Assessing Risk-Taking in a Driving Simulator Study: Modeling Longitudinal Semi-Continuous Driving Data Using a Two-Part Regression Model with Correlated Random Effects

Abstract

Signalized intersection management is a common measure of risky driving in simulator studies. In a recent randomized trial, investigators were interested in whether teenage males exposed to a risk-accepting passenger took more intersection risks in a driving simulator compared with those exposed to a risk-averse peer passenger. Analyses in this trial are complicated by the longitudinal or repeated measures that are semi-continuous with clumping at zero. Specifically, the dependent variable in a randomized trial looking at the effect of risk-accepting versus risk-averse peer passengers on teenage simulator driving is comprised of two components. The discrete component measures whether the teen driver stops for a yellow light, and the continuous component measures the time the teen driver, who does not stop, spends in the intersection during a red light. To convey both components of this measure, we apply a two-part regression with correlated random effects model (CREM), consisting of a logistic regression to model whether the driver stops for a yellow light and a linear regression to model the time spent in the intersection during a red light. These two components are related through the correlation of their random effects. Using this novel analysis, we found that those exposed to a risk-averse passenger have a higher proportion of stopping at yellow lights and a longer mean time in the intersection during a red light when they did not stop at the light compared to those exposed to a risk-accepting passenger, consistent with the study hypotheses and previous analyses. Examining the statistical properties of the CREM approach through simulations, we found that in most situations, the CREM achieves greater power than competing approaches. We also examined whether the treatment effect changes across the length of the drive and provided a sample size recommendation for detecting such phenomenon in subsequent trials. Our findings suggest that CREM provides an efficient method for analyzing the complex longitudinal data encountered in driving simulation studies.

1. Introduction

Driving simulations provide a safe and useful method for studying driving behavior that is highly associated with the on-road driving behavior (Fisher et al., 2007). Signalized intersection management is among the most complex and dangerous driving situations (Sifrit et al., 2010). A yellow light occurs as the vehicle approaches an intersection, requiring the driver to make an immediate decision to stop or continue on. Intersection management may be particularly difficult for novice drivers (Braitman et al., 2008), particularly in the presence of peer passengers. In a recent driving simulator study, interest focused on assessing the effects of peer passenger influence on teen driving behavior, where the outcomes were the number of stops for yellow lights and the time spent, by the drivers who did not stop, in the intersections when the light had turned red (Simons-Morton et al., 2014). These two measures describe different aspects of risky driving. A more cautious driver tends to stop at the yellow light; but if a driver decides to proceed through the light, the time spent in the intersection while the light is red is a direct measure of the risk of crashing, since cars from the other direction may have entered the intersection. Indeed, red light running is a major cause of side-impact crashes, which can cause serious injury and fatalities. Managing driving within the dilemma zone caused by the light turning yellow as the vehicle approaches the intersection is also a good measure of risk acceptance, which could be expected to vary according to driving conditions and driver characteristics. In this study we evaluated the effect of teenage passengers on male novice teenage drivers’ intersection management and the extent of risk they accepted as measured by time in the intersection during the red light.

This dual outcome is referred to as “semi-continuous”: it is right skewed, with a preponderance of zeroes indicating that many drivers stop when they approach a yellow light and greater than zero values for those who are in the intersection after the light turns red. There are two complexities of the analysis: first, the study used a longitudinal design, in which every driver is measured multiple times over the course of the simulated drive, so the outcomes measured on the same subject at different intersections are correlated. Second, the binary part and continuous part of the outcome may also be correlated, e.g. drivers who tend to stop also tend to spend less time in the intersections while the light is red when they do enter the intersection on yellow. To model the influence of experimental conditions on longitudinal, semi-continuous data, we may consider analyzing the outcome by modeling the discrete zero component separately from the nonzero continuous component. For example, a generalized linear mixed model (GLMM) can be used for the discrete outcome and a linear mixed model (LMM) for the continuous outcome. Such an approach ignores the potential dependency between the components, and hence can lead to biased effect estimates in the LMM (Albert and Shen, 2005; Su et al., 2009; Tom et al., 2013). In this case, it may be useful to jointly model these two outcomes for valid and efficient inference.

Different fields of research have developed methods to accommodate semi-continuous outcomes (Lachenbruch, 2002). Examples include health care demand in econometrics (Duan et al., 1983) and antibody assays (Moulton and Halsey, 1996) in cancer research. For longitudinal or repeated measures designs, Olsen and Shafer (2001) examined alcohol use, Albert and Shen (2005) studied emesis episodes from chemotherapy, and Tooze et al. (2002) analyzed medical expenditures. Although repeated semi-continuous outcomes have been addressed in other areas of research, this model has not been applied within driving simulator-based research. Our aim in this paper is to show how a two-part regression with correlated random effects can be used to make efficient and valid statistical inference in a driving simulator study with complex longitudinal semi-continuous outcomes. In addition, we perform numerical simulations to compare the performance of different methods in hypothesis testing problems, and make recommendations for sample size calculation in driving simulator studies.

In Section 2, we explain the design of the teen driving simulator study. Section 3 introduces the two-part regression with correlated random effects model, which we refer to as CREM, and discusses other analysis methods that ignore the correlation feature, including the GLMM, LMM and Wilcoxon rank sum test for estimating treatment effect. In Section 4, we apply CREM to the teen driving data and present the power and type I error numerical simulation study comparing CREM to other approaches. The software R (V 3.0.1), SAS (V 9.2), and SAS macro MIXCORR (Tooze et al., 2002) were used in the estimation and simulations. We summarize our findings and discuss implications of our work for future driving simulator studies in Section 5.

2. Teen Driving Simulator Study

The teen driving simulator study was a randomized control trial designed to study how peer passengers affect teen driving performance (Simons-Morton et al., 2014). The study investigated how the presence and the type of teen passenger, either risk-averse or risk-accepting, influenced risky-driving behavior. The participants were all male, aged 16 and 17 years old, who had previous driving experience and a Michigan driver license. A randomized two-by-two crossover design was used in which participants were randomly assigned to either a risk-averse or risk-accepting male confederate passenger. The confederate passenger interacted with the driver before the simulated drive according to a protocol designed to prime the driver with respect to the passenger’s risk preference. Then each study participant completed two drives, one alone and one with the assigned passenger, with the order of the two drives randomized and counterbalanced. The two study arms differed by passenger type and drives, one with and one without a passenger (solo and passenger drives, respectively). It should be noted that the predrive priming activity could affect behavior during the solo drive, as well as the passenger drive. Ultimately, it was expected that the study participants would have elevated risky behavior while driving with a peer passenger regardless of risk orientation relative to driving solo (Ouimet et al., 2013; Simons-Morton et al., 2014). The aim of this study was to determine if the effect of peer passenger was modified by the passenger type, which would be indicated by a significant interaction between passenger type and passenger presence. Throughout the paper, we refer to this interaction term as the “treatment effect.”

For the final analysis, there were a total of 58 participants with 31 assigned to a risk-averse passenger and 27 assigned to risk-accepting passenger. Participants were instructed to drive normally, follow the rules of the road, including driving speed, and speed limits were posted appropriately within the simulated drive. Each drive consisted of 42 intersections, 24 of which had traffic lights that turned yellow 2.6, 3.0, 3.4, or 6.0 seconds before the driver reached the mid-point of the intersections. All traffic lights remained yellow for 3.4 s, then turned red for 7.5 s before reverting to green. In the remaining intersections, the traffic lights stayed green. The intersections were spaced 200 meters apart and the order of the lights was chosen to minimize predictability. The 6.0 s intersections did not provide useful information because all drivers stopped before the traffic lights turned red. Therefore, we excluded all the 6.0 s intersections, resulting in 18 intersections for analysis per subject per drive.

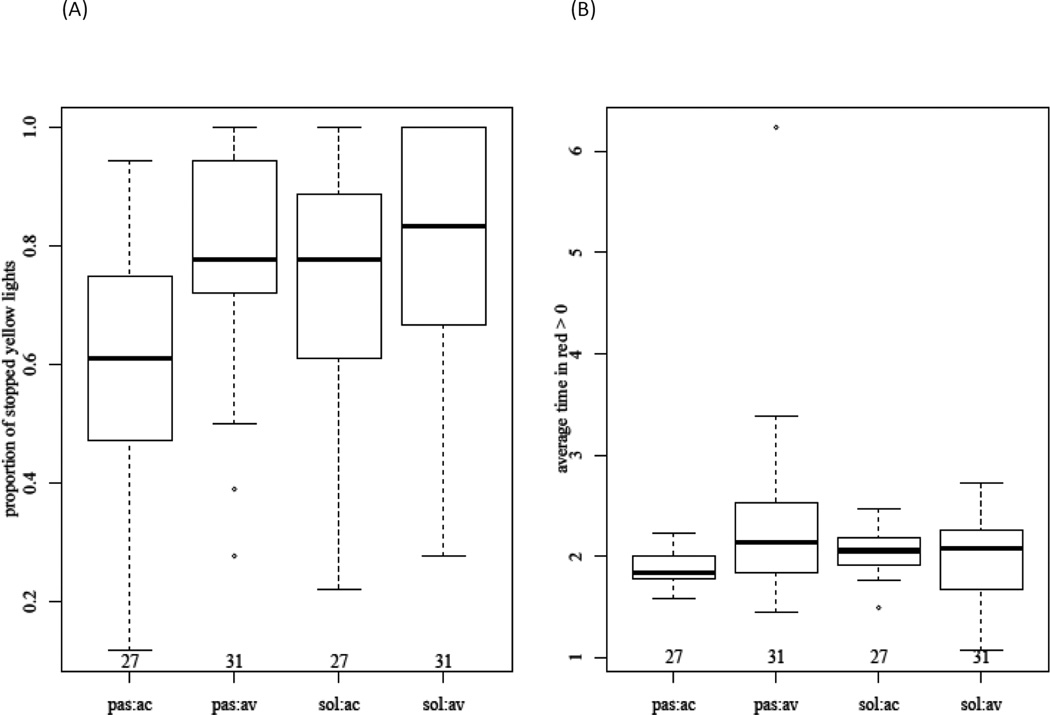
The primary outcome is risky-driving behavior measured by: (1) the frequency of stops for yellow traffic lights; and (2) the time spent in the intersections when the traffic lights were red. We refer to this outcome as time in red, where a time in red of zero indicates the driver stopped for a yellow light and time in red greater than zero is the time in the intersection while the light was red. A driver who stops more often and spends less time in the intersection while the light is red after entering the intersection on a yellow light would be considered less risky. The hypothesis of the experiment was that exposure to a risk-accepting peer passenger would cause the teen driver to engage in riskier driving behavior. A preliminary look at the data in Figure 1, panel (A) shows participants who were primed with a risk-averse passenger (sol:av) stopped more often at yellow lights when driving alone compared to other types of drives (solo risk-accepting (sol:ac), passenger risk-averse (pas:av) and passenger risk-accepting (pas:ac) drives). The participants accompanied by a risk-accepting passenger (pas:ac) stopped the least frequently. In panel (B), this same group had the lowest median time spent in an intersection when the light was red. Also, the drives including risk-averse passengers (pas:av and sol:av) had greater variability in their positive times in red.

Figure 1.

Boxplots for (A) proportion of stopped yellow lights by treatment group and (B) average positive time in red by treatment group. The four drives sol:av, sol:ac, pas:av, and pas:ac correspond to driving solo and primed with a risk-averse passenger, driving solo and primed with a risk-accepting passenger, driving with a risk-averse passenger, driving with a risk-accepting passenger. The number below each plot corresponds to the number of participants in that drive.

3. Material and Methods

3.1 The Correlated Random Effects Model (CREM)

Let Y_ij denote the response of the j^th(j = 1, …, n) observation in the i^th(i = 1, …, N) subject. Using similar language to Tooze et al. (2002), we refer to the zero/nonzero aspect of Y_ij as the occurrence variable S_ij defined as,

$$S_{ij}=\{\begin{array}{c}1,Y_{ij}=0\hfill \\ 0,Y_{ij}>0.\hfill \end{array}$$ (1)

The continuous part of Y_ij contributes to another piece of information that we call the intensity variable defined as R_ij ≡ [Y_ij | S_ij = 0]. It is natural to assume that Y_ij and S_ij are two correlated processes because they both intrinsically measure some aspects of the same individual characteristics. Tooze et al. (2002) and Su et al. (2009) proposed a two-part regression model with correlated random effects that makes use of both the occurrence and the intensity variables. The idea was to model the two longitudinal processes jointly with mixed effects models, while assuming the dependence was purely induced by the correlation of the random effects. Let p_ij be the probability of S_ij = 1 given the 1 × k vector of covariates X_ij. A generalized linear mixed model (GLMM) with a logit link function is used for p_ij and a linear mixed model (LMM) is used for R_ij:

$$\text{log}\left(\frac{p_{ij}}{1-p_{ij}}\right)={\mathbf{x}}_{\mathbf{i}\mathbf{j}}\mathbf{\alpha }+b_i,$$ (2)

$$R_{ij}={\mathbf{X}}_{\mathbf{i}\mathbf{j}}\mathbf{\beta }+c_i+{\mathrm{\epsilon }}_{\mathrm{i}\mathrm{j}},$$ (3)

where α and β are both a k × 1 coefficient vectors, the random error ε_ij is assumed i.i.d. $N(0,{\sigma }_{\epsilon }^2)$, and the subject level random intercepts b_i and c_i jointly follow a bivariate normal distribution:

$$[\begin{array}{c}\hfill b_i\hfill \\ \hfill c_i\hfill \end{array}]~N([\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}],[\begin{array}{cc}\hfill {\sigma }_b^2\hfill & \hfill \rho {\sigma }_b{\sigma }_c\hfill \\ \hfill \rho {\sigma }_c{\sigma }_b\hfill & \hfill {\sigma }_c^2\hfill \end{array}\left]\right).$$ (4)

By introducing a correlation structure between the random components, this model is able to convey the dependence between S_ij and R_ij, with ρ measuring the strength of the correlation. The two-part model can accommodate more random effects, but for simplicity we focused on the random intercepts. In addition, we show later that (4) characterizes the correlation structure in the driving data well. Henceforth we refer to this two-part correlated random effects model as CREM, the binary part (2) as CREM/GLMM and the continuous part (3) as CREM/LMM.

We denote the parameters of CREM as $\mathit{\theta }=(\mathit{\alpha },\mathit{\beta },\rho ,{\sigma }_b^2,{\sigma }_c^2)$, observation j = 1, …, n, and subject i = 1, …, N. Also, we denote the probability density function of the intensity variable as $f(R_{ij}|\mathit{\beta },{\sigma }_c^2)$, and the bivariate density of the random effects as $f(b_i,c_i|\rho ,{\sigma }_b^2,{\sigma }_c^2)$. Then the likelihood is

$$L(\mathit{\theta })=\prod _{i=1}^N\underset{{\mathit{b}}_i}{\int }\underset{{\mathit{c}}_i}{\int }\prod _{j=1}^n{(1-p_{ij})}^{1-s_{ij}}{p}_{ij}^{s_{ij}}f{(R_{ij}|\mathit{\beta },{\sigma }_c^2)}^{1-S_{ij}}f(b_i,c_i|\rho ,{\sigma }_b^2,{\sigma }_c^2)d{b}_{i}d{c}_i.$$ (5)

Due to the intractable integration, adaptive Gaussian quadrature can be used to approximate L(θ) and then θ is estimated by maximizing this approximation. Adaptive Gaussian quadrature is a numerical computational method that approximates integrals by a sum that contains terms evaluated at specified values on the integration domain. The procedure is adaptive in the sense that the domain where the integrand is not very close to zero is identified by centering the quadrature at the mode of the integrand. We use the SAS macro MIXCORR (Tooze et al., 2002), which employs the SAS PROC NLMIXED to implement the estimation procedure.

3.2 Other Traditional Methods

Alternative simpler approaches include fitting binary occurrence S_ij and continuous outcome R_ij separately as in models (2) and (3), respectively. In other words, the correlation between b_i and c_i is set to 0. These two approaches are referred to as GLMM and LMM. Both models can be fitted using SAS PROC NLMIXED or R function lmer of package lme4. A third alternative is to examine the entire outcome Y_ij in a nonparametric test like the Wilcoxon rank sum test (WRST) for a distributional difference between two treatment groups. In the case of a two by two crossover design, the observations over time are first averaged for each subject in each experimental period (in our example, solo drive and passenger drive). Denote the average for subject i in each drive by $Y_{i•}^{(0)}$ and $Y_{i•}^{(1)}$, respectively. Let Y_i• be the difference between $Y_{i•}^{(0)}$ and $Y_{i•}^{(1)}$. WRST uses the ranks of Y_i• from both experimental groups (in our example, risk-accepting and risk-averse passengers) to compute the test statistics, and examine whether the groups differ in treatment effect. For more than two treatment arms, the Kruskal-Wallis test can be used.

The main issue with modeling the outcome using S_ij or R_ij separately is the loss of information available in the other component. For example, in the teen driving simulator study, drivers with a risk-accepting passenger have lower proportions of stopping p_ij, and when they do not stop, they also have smaller positive times in red R_ij (See Figure 1) compared to drivers in other experimental conditions. The WRST uses both S_ij and R_ij, but collapses all the information into one variable per subject, which is often less powerful. In contrast, CREM makes full use of both outcomes in the longitudinal sequence, and models their dependence through the random effects. We would expect CREM to be the most accurate and powerful when the model assumptions are valid.

3.3 CREM: A Model for Teen Driving Simulator Study

The primary concern in the teen driving experiment was whether passenger type affected driving behavior. We were interested in a difference in the driving outcome between the randomly assigned risk-accepting and risk-averse passenger groups. In addition, we wanted to know whether the treatment effect was significant after adjusting for the intersection type (different time-to-intersection when the light turns yellow). With these questions in mind, CREM given by (2) and (3) were applied to the teen driving data to jointly model (a) the probability of a participant stopping at the intersection on a yellow light and (b) the time in red with a log transformation. The model included intersection type (2.6 s, 3.0 s, 3.4 s), passenger presence (solo or accompanied), passenger type (risk-averse or risk-accepting), and the interaction between passenger presence and passenger type. In this example, we assumed the covariate matrices were the same for models (2) and (3), but in other cases they could differ. The CREM/GLMM and CREM/LMM model components were assumed to have random intercepts only, which followed a bivariate normal distribution with a nonzero correlation. In other words, we expected some association between the number of times a subject entered the intersection on a yellow light and the time spent in the intersections when the light was red. The residuals in CREM/LMM were assumed normally distributed with constant variance. We refer to this as Model 1.

For a secondary analysis, we are interested in whether the driving behavior changed over time in each experimental group. For example, do the drivers in the risk-accepting group stop more often at the later intersections while driving solo? This could be due to either a learning effect (i.e., the driver gets more proficient with the simulator), or a washout of the confederate passenger’s influence over the course of the drive. Since the intersections were equally spaced 200 m apart, the intersection order was treated as a proxy for time. We used natural splines (Hastie and Tibshirani, 1990) to examine the time trend, with the spline basis generated using the ns function in R software. Model 1 was extended to include all two- and three-way interactions with the spline bases, passenger presence, and passenger type. We chose natural splines because this method results in better performance at the boundaries. The distributions of (b_i, c_i) and ε_ijk have the same form as those in Model 1. We refer to this as Model 2.

3.4 Power and Type I Error Analysis

To compare how the three traditional methods, GLMM, LMM and WRST, perform relative to CREM, we conducted a numerical simulation study to compute the power and type I error of each method when testing for treatment effect. In the context of the teen driving study, power is defined as the probability of concluding a treatment effect when the actual effect is not zero, and type I error is the probability of concluding a treatment effect when the actual effect is zero. Typically, .05 is set as the desired type I error, also referred to as the size of the test. Greater power and a type I error less than or equal to .05 are desired and indicative of a better test. The simulated data were generated from a simplified version of Model 1 that excluded the intersection type. Let α = (α₁, α₂, α₃)′ denote the coefficients of passenger presence, passenger type and their interactions in the CREM/GLMM parts of Model 1, respectively. Let β = (β₁, β₂, β₃)′denote the counterparts in the CREM/LMM portion of Model 1. Fixing (α₁, α₂) = (−.09, –.59) and (β₁, β₂) = (.08, –.01) to be close to the simplified model fit of the teen driving simulator study, we generated data sets for different parameters α₃, β₃ and ρ using R. For each data set, CREM was fitted to the data with Tooze’s SAS macro MIXCORR and the GLMM, LMM and WRST were fitted to the data using R. After we estimated the model parameters, a test for the treatment effect was conducted for all four methods. We used the Wald test for the interaction terms in GLMM, LMM, and CREM. The results of these simulations are presented in Section 4.2.

Another question of interest in the design of randomized driving simulation trials is how many participants are needed to detect a change in treatment effect over time. To address this question, we considered a simplified version of Model 2 by excluding the intersection type. Using simulation, we calculated the sample sizes needed to achieve different levels of power in detecting a treatment effect over time.

4. Results

4.1 Analyses of Teen Driving Data

The results of GLMM, LMM and CREM are shown in Table 1. Although the estimates from CREM do not differ much from the corresponding estimates in the logistic and linear regressions, the covariance ρσ_bσ_c between the random effects is marginally significant (Wald test p-value=.07). In our example, the inference of the treatment effect is similar whether CREM or the two uncorrelated models are used, as the correlation (ρ = .31) between the binary and continuous parts is relatively weak. However, as a general principle, we strongly recommend the CREM model over separate model fitting since we do know what the correlation will be until we fit the CREM model, and it is widely known that separate modeling can induce bias in this situation (Su et al., 2009).

Table 1.

Parameter estimates, standard errors and p-values for: (1) logistic regression and (2) linear regression, which are stacked in the first column, and (3) CREM in the second column.

	Uncorrelated		Correlated Random Effects
	Estimate(SE)	p >|t|	Estimate(SE)	p >|t|
Logistic regression (Binary)
Intercept	.76(.31)	.02	.75(.31)	.02
Intersection 3.0(s)	1.45(.14)	< .01	1.45(.14)	< .01
Intersection 3.4(s)	2.88(.18)	< .01	2.87(.18)	< .01
Passenger presence	−.08(.18)	.66	−.08(.18)	.65
Passenger type	−.72(.43)	.10	−.71(.44)	.10
Passenger presence*passenger type	−.81(.25)	< .01	−.80(.25)	< .01
${\sigma }_b^2$	2.17(.51)	< .01	2.17(.51)	< .01
Linear regression (Normal)
Intercept	.62(.04)	< .01	.64(.04)	< .01
Intersection 3.0(s)	.17(.01)	< .01	.17(.01)	< .01
Intersection 3.4(s)	.32(.02)	< .01	.33(.02)	< .01
Passenger presence	.07(.02)	< .01	.07(.02)	< .01
Passenger type	−.02(.05)	.67	−.04(.05)	.44
Passenger presence*passenger type	−.14(.03)	< .01	−.14(.03)	< .01
${\sigma }_c^2$	.02(.01)	< .01	.03(.01)	< .01
${\sigma }_e^2$	.02(.00)	< .01	.02(.00)	< .01
ρσbσc	-		.08(.04)	.07
−2×log likelihood	2064.08	-	2060.19	-

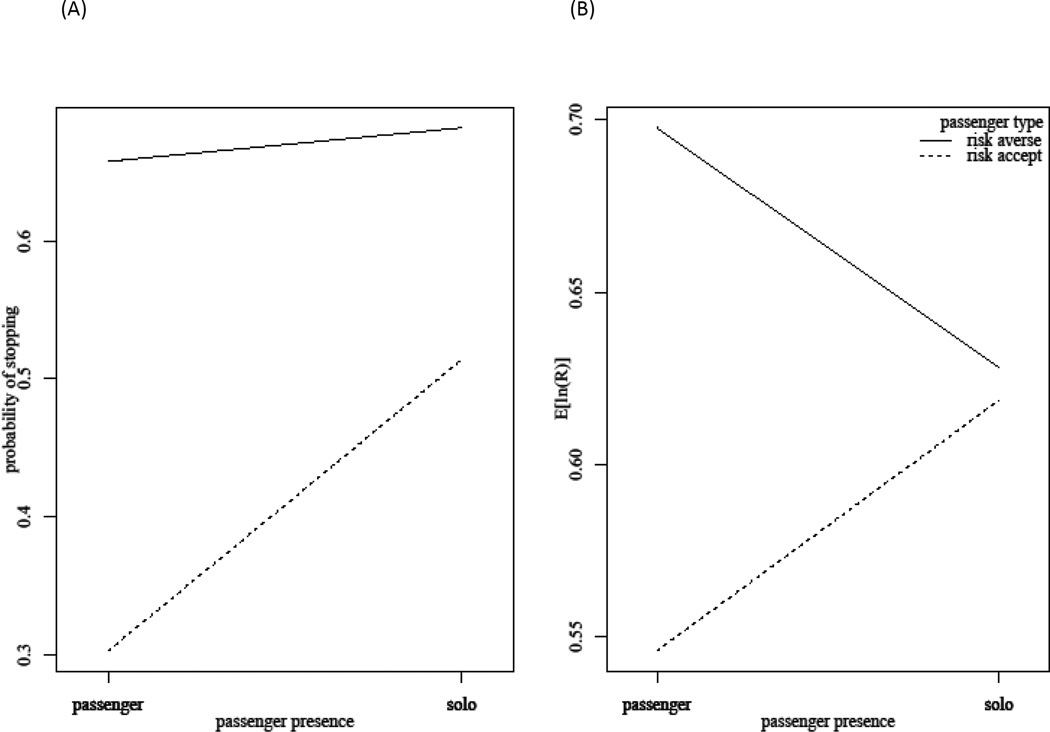
A visual description of the mean positive time in red and the probability of stopping at a yellow light for the two treatment conditions is presented in Figure 2. The two experimental groups were very different when they drove accompanied by a passenger. In panel (A), we observe that compared to the risk-accepting group, the risk-averse group was more likely to stop at the yellow lights. The risk-averse group on average stopped at 65%–70% of the 2.6 s intersections, regardless of the presence of the passenger. On the other hand, the risk-accepting group only stopped at 30% of the 2.6 s intersections while driving with the passenger; this probability increased to about 50% while driving alone, but it is still much lower than that of the risk-averse group. The group that drove with a risk-averse passenger spent greater positive time in red when they passed a yellow light compared to those with a risk-accepting passenger, particularly in the accompanied drive (panel (B)). Opposite directions of association between passenger presence and time in red are observed in the two passenger conditions. For the risk-averse group, more time in red was observed while driving with passenger compared to driving solo; it is the opposite for the risk-accepting group, who spent less time in red while driving with a passenger. The difference in the driving outcomes due to the experimental condition is significant, which is supported by the significant interaction (p-values < .01) between passenger presence and passenger type in both the logistic and linear regression components of CREM in Table 1. From these results, we observe a significant passenger effect on risky driving behavior, but the passenger effect is substantially modified by passenger type. As pointed out by Simons-Morton et al. (2014), because the interactions between the driver and confederate passenger were only done through predrive priming, and the passenger’s behavior in the car was the same for both treatment groups, the significant treatment effect on risky driving can be attributed to the driver’s perception of passenger norms.

Figure 2.

Using the estimates from the correlated random effects model of the teen driving data, the passenger type by passenger presence interaction is shown with (A) the probability of stopping and (B) the expected positive time in red at the 2.6 s intersections.

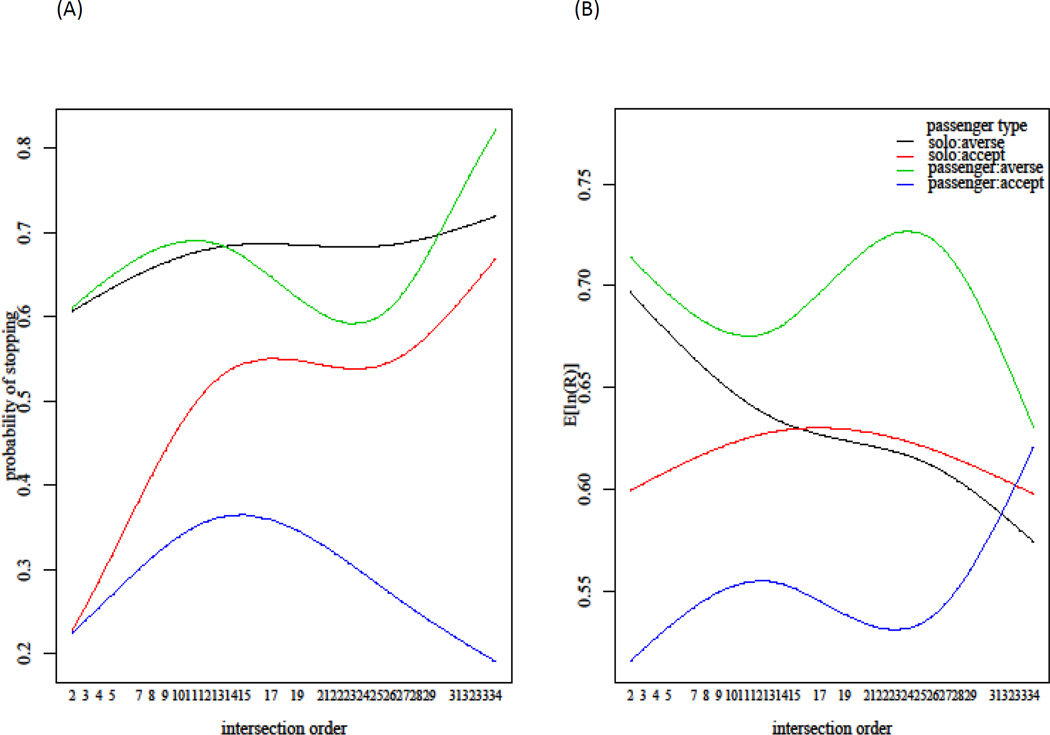
Given that the outcome was measured repeatedly over the course of a drive, we tested whether the treatment effect changed over time. We fit Model 2 incorporating the order of the intersection as the time variable and plotted the time trend of the four drives in Figure 3. The treatment effect was not found to vary significantly over the course of the drive, such that the difference in the response between the group assigned to a risk-averse passenger and the group assigned to a risk-accepting passenger was constant over the course of the drive. Nevertheless, there are interesting patterns, shown in Figure 3, that give additional insight into the study results. For example, the risk-averse group drove in a less risky manner in the solo condition over the course of the drive. A decreasing trend in time in red is obvious (black line in panel (B)), and the probability of stopping also slightly increases (black line in panel (A)) as the drive continues. For the same group, some fluctuations are seen in both time in red and stopping probability while driving with a passenger, but there was no obvious global trend (green lines). The solo drives in the risk-accepting group show behavioral change with respect to the probability of stopping (more stops made toward the end of the drive) but not the amount of time spent in red (red lines). Drives with passenger in the risk-accepting group, however, have an increasing trend with time in red, and demonstrated a surprising quadratic shape for making stops (blue lines). The risk-averse group drove more cautiously by making the most stops at yellow lights (black and green lines in panel (A)), but when they did not stop they spent more time in red compared to the risk-accepting group, particularly while driving with a passenger (green line in panel (B)). The risk-accepting group spent less time in red with a passenger, and made the fewest stops (blue lines). Given the relatively small sample size in this study, the difference in treatment effect over time is not statistically significant. It would be worthwhile to explore these patterns with a larger sample. We discuss the recommended sample size in the next section.

Figure 3.

Using the estimates of the correlated random effects model fit of the teen driving data, the treatment type by time interaction is shown with (A) the probability of stopping at 2.6-second intersections, and (B) the expected positive time in red spent in 2.6-second intersections.

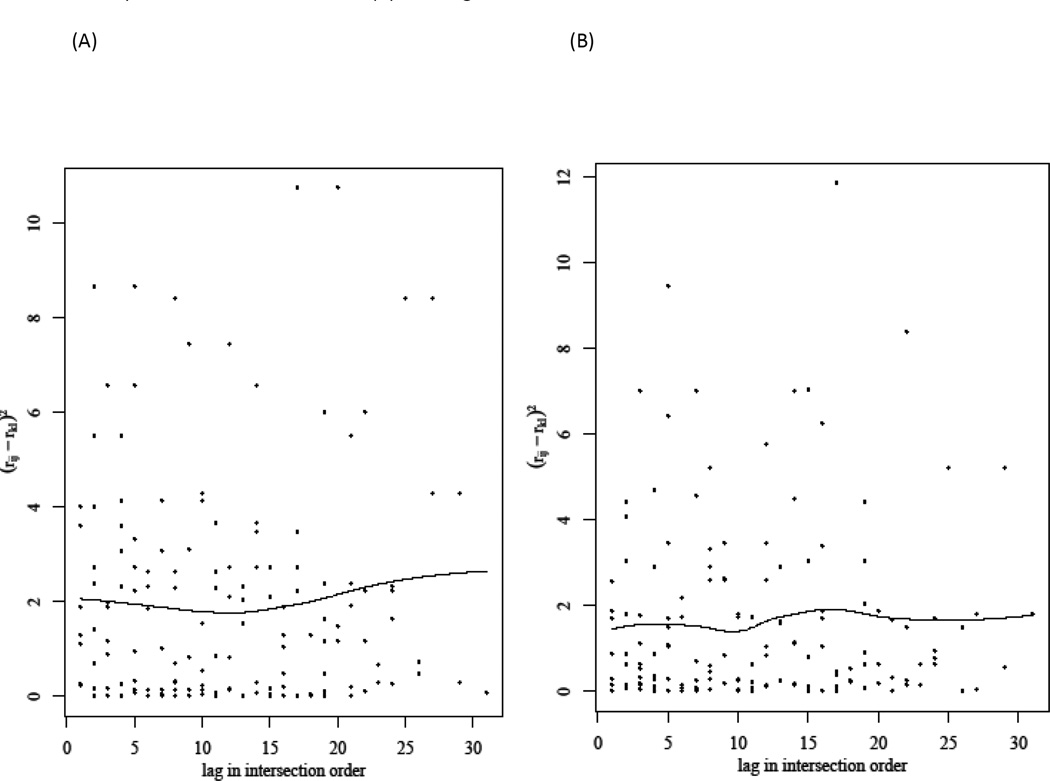
A check of the assumption of homoscedastic errors for the CREM/LMM component showed residuals that are distributed about zero with fairly constant variance (see Figure 4). A normal quantile plot of the residuals (not shown here) indicated no significant departures from normality. Finally, because the data are longitudinal, we checked for serial correlation in the residuals as seen in Figure 5. Not accounting for serial correlation in CREM can result in an inflated type I error (Albert and Shen, 2005). CREM residuals showed an approximately constant, non-increasing correlation regardless of the distance between any two intersections.

Figure 4.

(A) Linear regression residual plot where the residual for participant i, in drive j at intersection order k is the difference between the observed positive time in red and the estimated positive time in red.

Figure 5.

(A) A variogram for the first simulator drive, in which the residual r_ij for participant i at intersection order j is calculated as r_ij = Y_ij − Pr(S_ij = 0|b_i)E[ln(R_ij|c_i, ε_ij). Superimposed is a fitted polynomial curve to measure the trend in the squared residual differences. (B) A variogram for the second drive.

4.2 Power and Type I Error

We compared the performance of the test for treatment effect using CREM versus GLMM, LMM or WRST. The data were generated using Model 1, in which the treatment effects for the GLMM and LMM components (α₃ and β₃ respectively), and the random effects correlation ρ were varied. We used the likelihood ratio test for CREM, GLMM and LMM frameworks, and the measures of comparison were power and type I error. The higher the power of the test is, the more likely that the test concludes a treatment effect when the effect is non-zero. We fixed the size of all the tests at .05. The results in Table 2 show that the power under different models does not vary much with changing random effects correlation ρ. In the top panel of Table 2, where the treatment effect α₃ in the occurrence outcome remains constant while the treatment effect β₃ in the intensity outcome decreases in magnitude, power decreases for the test using LMM and CREM. Since GLMM does not estimate β₃, the power of its test remains fairly constant. The test associated with CREM has increased power compared to LMM, because CREM uses the additional information from the occurrence variable. Compared to GLMM and WRST, the test associated with CREM has greater power except for small values of β₃ such as .00 and .04. In these cases, the occurrence part of the outcome dominates the group means, and somewhat surprisingly, WRST attains better power than its parametric counterparts. In the middle panel of Table 2, where β₃ remains constant while α₃ decreases, the tests using LMM and CREM frameworks are not affected and achieve power very close to 1. The power of the test associated with GLMM decreases, as expected. Taken together, the top and middle panels indicate that the power of CREM is much more influenced by different parameter values of the treatment effect, β₃, in the intensity variable. In other words, compared to the occurrence variable, the intensity variable contributes more information in the detection of the treatment effect. The type I errors (bottom panel of Table 2) of the tests from CREM, LMM and WRST are close to .05. This result is in contrast with Su et al. (2009) who found that LMM could be biased with larger sample sizes. But in our simulation setting, all four methods of testing the interaction terms are consistent with the correct type I error. The sample size in the simulation is quite small to reflect the size of driving simulation studies in reality. When the sample size becomes larger, we would expect the LMM estimates to become biased. Despite the consistency of all candidate tests, CREM tends to have greater power in most cases, and hence is recommended for practical use.

Table 2.

Power and type I error from tests for treatment effects (interaction between Passenger Presence and Passenger Type) based on 500 data sets, each with a sample size of 60, under different models and different treatment effect α₃ in the occurrence outcome, treatment effect β₃ xin the intensity outcome, and random effects effect β₃ correlation ρ. The size for all the tests was set at .05. The rows represent the different parameterizations of α₃, β₃, and ρ. Columns 2 through 4 list the power corresponding to the different tests. Where effect α₃ = β₃ = 0, the values are type I errors.

Parameters (α3,β3,ρ)	Logistic Regression	Linear Regression	Correlated Random Effects Model	Wilcoxon Rank Sum Test
(−.62, −.14, .80)	.78	.98	1.00	.49
(−.62, −.14, .20)	.78	.98	1.00	.50
(−.62, −.14, .00)	.78	.99	1.00	.50
(−.62, −.14, – .20)	.77	.98	1.00	.49
(−.62, −.07, .80)	.78	.58	.90	.76
(−.62, −.07, .20)	.78	.60	.90	.72
(−.62, −.07, .00)	.78	.60	.90	.72
(−.62, −.07, – .20)	.77	.62	.88	.73
(−.62, −.04, .80)	.78	.22	.78	.83
(−.62, −.04, .20)	.78	.23	.77	.81
(−.62, −.04, .00)	.78	.23	.78	.82
(−.62, −.04, −.20)	.77	.23	.77	.80
(−.62, .00, .80)	.78	.05	.66	.92
(−.62, .00, .20)	.78	.04	.67	.89
(−.62, .00, .00)	.78	.05	.66	.89
(−.62, .00, −.20)	.77	.04	.67	.89
(−.30, −.14, .80)	.24	.99	.99	.08
(−.30, −.14, .20)	.26	.99	.99	.08
(−.30, −.14, .00)	.25	.99	.99	.07
(−.30, −.14, −.20)	.26	.99	.98	.08
(−.20, −.14, .80)	.13	.99	.98	.05
(−.20, −.14, .20)	.15	.98	.99	.06
(−.20, −.14, .00)	.14	.99	.98	.06
(−.20, −.14, −.20)	.14	.99	.98	.06
(.00, −.14, .80)	.06	.99	.98	.15
(.00, −.14, .20)	.07	.98	.98	.16
(.00, −.14, .00)	.07	.99	.98	.16
(.00, −.14, −.20)	.06	.99	.98	.14
(.00, .00, .80)	.06	.03	.06	.06
(.00, .00, .20)	.07	.05	.05	.06
(.00, .00, .00)	.07	.05	.06	.06
(.00, .00, −.20)	.06	.04	.06	.06
(.00, .00, −.80)	.05	.04	.05	.06

A common concern in the design of experiments is the sample size needed to detect a treatment effect difference over time. We extended the power analysis by simulating 200 data sets of sample size 60 using Model 2 and its estimates. The simulation was then repeated for a sample size of 120. The power associated with sample size 60 is .49. Doubling the sample size to 120 increases the power to .85. Applied to the driving data, these results show that if we are interested in uncovering the specified treatment difference over time, a greater sample size than the current 58 will be needed. These two sample sizes and their respective power can be used as a gauge in designing experiments that focus on a changing treatment effect over time.

5. Discussion

Signalized intersection management is a useful test of simulated driving skill and risk-taking. However, analyses of simulation data are complex, given the many variables involved, including potential learning effects, signal timing and spacing, and repeated measures that are semi-continuous with clumping at zero. In addition, given the relatively high expense involved, simulation studies generally involve relatively small samples. For these reasons, analyses must be carefully designed to capture actual/true effects. When the longitudinal or repeated outcome of a study is semi-continuous, as in our teen driving simulator study, we recommend using CREM as an efficient method for analysis. The discrete and continuous components of the outcome are modeled respectively by a logistic and a linear mixed effects regression. The dependence of the two components is captured in the covariance structure of the random effects from each regression model.

We applied CREM to the teenage driving data and found that the estimate of the correlation between the random effects is small and marginally significant. Our numerical simulation suggests that the power to detect a treatment effect can be greatly compromised if only one component of the outcome is analyzed. Both components should be modeled jointly for a valid and efficient inference. In our driving simulator example, we found that the analysis results were similar when we used the CREM as compared with separate modeling of the two components. This was in part due to the small to moderate correlation estimated between the two processes. That said, we believe that as a general rule, it is important to fit the CREM model since a priori it is impossible to know what the correlation is unless we fit the CREM model. Thus, at the very least, the CREM model provides a safe guard for avoiding bias in case of a large correlation.

Although we did not find power to vary with the random effects correlation there is no guarantee that this pattern holds under different circumstances, such as higher within subject variability in both the continuous and discrete components, higher proportions of subjects stopping for yellow lights in the control groups, or larger studies with more subjects having more repeated measurements. CREM should be used to minimize potential bias in parameter estimation (Su et al., 2009), which might otherwise result in spurious conclusions. If interest lies in studying the change in treatment effect over time, we would recommend a power simulation to estimate the sample size needed.

The findings provide evidence of an effect of male peer passengers, particularly the effect of risk-accepting passengers, on teenage simulated risky driving among novice teenage male drivers. The findings need to be confirmed in future experimental simulation studies, and possibly in naturalistic observational studies of on-road intersection management by drivers and passengers of varying age and sex. This research is important given the data from analyses of fatal crashes indicated that teenage passengers increase fatal crash risk among teenage drivers (Ouimet et al., 2013) and the growing emphasis in modern graduated driver licensing policies on limiting the number of teenage passengers among novice teenage drivers (IIHS, http://www.iihs.org/).

The current data available to us did not include vehicle speed. Including speed, in addition to time in red might make for an interesting extension of this methodology, i.e., two correlated semi-continuous outcomes, once this data is available in future driving simulator research. However, there are two primary and several secondary reasons why we do not formally consider speed in this particular data set. First, the simulated vehicle shared the roadway with several other vehicles, including vehicles traveling and/or passing in the inside lane (the left) going in the same direction as the simulated vehicle, and a lead vehicle. These set a pace for the drive and the lead vehicle, discouraged but did not absolutely prevent increased speed (the lead vehicle would increase speed if it was tailgated, but the participants were not informed of this). Knowing that a lead vehicle might influence intersection choices, or prohibit entering the intersection of it stopped at a yellow light, we programmed the simulator to coordinate the lead vehicle with the timing of the lights so that the lead vehicle would continue through the intersection. The simulated vehicle would then catch up with the lead vehicle after the light changed. Also, not only was the lead vehicle far enough ahead to not influence participants’ yellow light decisions, it was also far enough ahead so that the participant could increase their speed slightly when the light turned yellow so as to try to avoid being in the intersection when the light turned red, which is a common real-world tactic used by drivers. Second, in advance of driving the simulator, participants were instructed to follow the rules of the road, such as the speed limit, as they did in the real world. The speed limit of 35 mph was posted at multiple points along the drive. Observation of the participants by the experimenters confirmed that these strategies were effective in limiting speed, so we do not expect the driving speed to have varied much across subjects. Other reasons for not including speed in the analyses are that time in red is a more relevant measure of risk than the average speed. As mentioned previously, the longer the driver is exposed to the red light while in the intersection, the greater the risk of having a crash. Also, adjusting speed in the regression, which is a post-treatment variable, is problematic as it could bias the inference.

CREM with random intercepts is valid for describing the correlation structure between the discrete and continuous components of the driving outcome. A model with more random terms or from a non-normal distribution would require the development of new software. For example, Bhat and Eluru (2009) and Spissu et al. (2009) used a copula-based method to account for the correlation between a discrete and a continuous outcome variable. However, their approach was considered in the cross-sectional setting only, and the copula structure was imposed on the random errors. In order to make the extension to our longitudinal setting, we would need to assume the copula for the joint distribution of the random effects b_i and c_i, and then perform numerical integration. Wu and de Leon (2014) attempted to make such an extension assuming a Gaussian copula, but the computation is quite complicated and no software package is available yet. Furthermore, an analysis of model robustness to deviations from CREM assumptions such as non-normal random terms or errors is still needed.

Highlights.

• We examined the effect of peer passenger’s influence on teen simulated risky-driving behavior.

• We modeled the data with a two-part regression with a correlated random effects model (CREM).

• The correlation between the two components of the data was small to moderate in our example.

• The power to detect a treatment effect using CREM was usually higher than other approaches.

• Peer passenger presence, particularly risk-accepting passengers, increased risky driving.

Statement of Contribution/Potential Impact.

Signalized intersection management is complex and red light running is a common cause of crashes and a frequently used measure of risky driving in simulation research. We propose an innovative statistical methodology for analyzing complex longitudinal outcome data that is often encountered in driving simulator studies. Specifically, in our teen driving simulator study, we observe the length of time spent in an intersection when the traffic light is red following a dilemma scenario in which the traffic light was yellow as the driver approached the intersection. The resulting data have a repeated semi-continuous structure where many of the longitudinal outcomes are zero, reflecting a stop before entering the intersection. We introduce the use of a two-part correlated random-effects regression model, with one component measuring the probability of stopping before entering the intersection and the other measuring the mean duration spent in the intersection while the traffic light was red. The model is formulated to analyze data from a recent crossover trial examining the effect of a risk-accepting versus a risk-averse passenger on risky driving. We believe that this statistical methodology provides a useful technique for analyzing the complex data encountered in driving simulation studies.