Abstract
Computational knee models provide a powerful platform to investigate the effects of injury and surgery on functional knee behavior. The objective of this study was to use a multibody knee model to investigate the influence of ligament properties on tibiofemoral kinematics and cartilage contact pressures in the stance phase of walking. The knee model included 14 ligament bundles and articular cartilage contact acting across the tibiofemoral and patellofemoral joints. The knee was incorporated into a lower extremity musculoskeletal model and used to simulate knee mechanics during the stance phase of normal walking. A Monte Carlo approach was employed to assess the influence ligament stiffness and reference strains on knee mechanics. The ACL, MCL and posterior capsule properties exhibited significant influence on anterior tibial translation at heel strike, with the ACL acting as the primary restraint to anterior translation in mid-stance. The MCL and LCL exhibited the greatest influence on tibial rotation from heel strike through mid-stance. Simulated tibial plateau contact location was dependent on the ACL, MCL and LCL properties, while pressure magnitudes were most dependent on the ACL. A decrease in ACL stiffness or reference strain significantly increased average contact pressure in mid-stance, with the pressure migrating posteriorly on the medial tibial plateau. These ligament-dependent shifts in tibiofemoral cartilage contact during walking are potentially relevant to consider when investigating the causes of early onset osteoarthritis following knee ligament injury and surgical treatment.
Keywords: computational biomechanics, simulation, elastic foundation model, ACL, probabilistic analysis
Introduction
Computational knee models are useful for investigating joint mechanics in both injured and surgically repaired states. For example, prior studies have used knee models to study the influence of ACL tears, ligament reconstruction, and tendon transfers on knee kinematics and cartilage loading patterns [1, 2]. Accurate descriptions of soft tissue anatomy and mechanics are needed for these applications, which can make the models computationally demanding to solve [3, 4]. As a result, knee models often are only used to simulate simple loading scenarios, such as laxity tests and isolated quadriceps loading [5-7]. However, it is often important clinically to understand knee mechanics during functional multi-joint tasks such as walking.
Physics-based musculoskeletal modeling approaches have evolved with recent advancements in computational and medical imaging technologies and provide a consistent framework to simulate the muscular coordination of whole body movement. For example, simulations of subject-specific gait dynamics are now readily performed [8]. However, the musculoskeletal models used in most current gait simulations have simplified representations of the knee [9], which lack the anatomical detail needed to simulate soft tissue injuries or surgical procedures. To address this limitation, advanced multibody knee models have been introduced that include detailed representations of anatomical structures [10-13], but are less computationally demanding than finite element approaches [5, 14]. Multibody knee models are hence suitable for simulations of movement, and thus can be used to investigate the influence of soft tissue procedures on functional knee mechanics.
Subject-specific knee models can be created from high resolution MR images. A series of image slices is segmented to create 3D geometric representations of articular cartilage surfaces and ligament attachment sites, which are then used to characterize cartilage contact and ligamentous constraints acting about the tibiofemoral and patellofemoral joints [15]. In multibody knee models, the ligaments are typically represented as bundles of nonlinear springs acting between origin and insertion footprints [16]. Constitutive properties of the soft tissues are then needed to compute the internal tissue loads that arise with movement. However, these constitutive properties cannot currently be measured in vivo on a subject-specific basis. As a result, parametric uncertainty exists in the model which should be considered when simulating functional knee mechanics.
The objective of this study was to use a probabilistic approach to investigate the propagation of uncertain ligament constitutive properties onto knee mechanics in gait. Specifically, we assessed the effect of variations in ligament stiffness and reference strain on tibiofemoral kinematics and tibial contact when the quadriceps are loaded in the first half of stance. Additionally, we used a sensitivity analysis to determine the ligament constitutive properties that had significant effects on tibiofemoral kinematics and tibial contact.
Methods
To construct the knee model, we segmented the bone and cartilage surface geometries of the femur, tibia, and patella from MR images collected on a young adult female (age 23 yrs, height 1.65 m, mass 61 kg). Cartilage surfaces were represented by high resolution triangulated meshes and regions of contact between articulating cartilage surfaces were determined using ray-casting techniques together with hierarchical bounding boxes [17]. The combined thickness of the articulating cartilage was assumed to be 6 mm for both the tibiofemoral and patellofemoral joints. A nonlinear elastic foundation formulation [18] was used to compute pressure acting on each triangle face in contact based on the depth of penetration, the cartilage thickness, and assumed material properties (elastic modulus of 5 MPa, Poisson's ratio of 0.45 [19]) (Fig. 1). The tibiofemoral and patellofemoral joints were both modeled as 6 DOF.
Figure 1.
A multibody knee model was created that included six degree of freedom tibiofemoral and patellofemoral joints. Tibiofemoral and patellofemoral contact pressures were computed using an elastic foundation model, with local pressure calculated as a nonlinear function of the depth of penetration between articulating surfaces. To simulate walking, the knee was incorporated into a lower extremity musculoskeletal model with 44 muscles acting about the hip, knee and ankle.
The origins, insertions, and paths of the major knee ligaments were segmented from the MR images and included the: superficial and deep medial collateral ligament (sMCL, dMCL), lateral collateral ligament (LCL), anteriomedial and posteriolateral anterior cruciate ligament (aACL, pACL), anteriolateral and posteriomedial posterior cruciate ligament (aPCL, pPCL), patellar tendon (PT), medial and lateral patellofemoral ligaments (MPFL, LPFL), popliteofibular ligament (PFL), posteriomedial capsule (pmCAP), the posterior capsule (CAP), and the iliotibial band (ITB). Each ligament was represented by bundles of nonlinear springs spanning from origin to insertion. Ligament paths were reconstructed by using ellipsoidal and cylindrical wrap objects to model wrapping of the ligaments over bony geometries. The ligament force-strain relationship was assumed to be quadratic at low strains and linear at higher strains (Fig. 2) [20]. Linear stiffness was estimated from the ligament cross-sectional areas as measured from the MRI. Reference strains were adapted from the literature [21, 22].
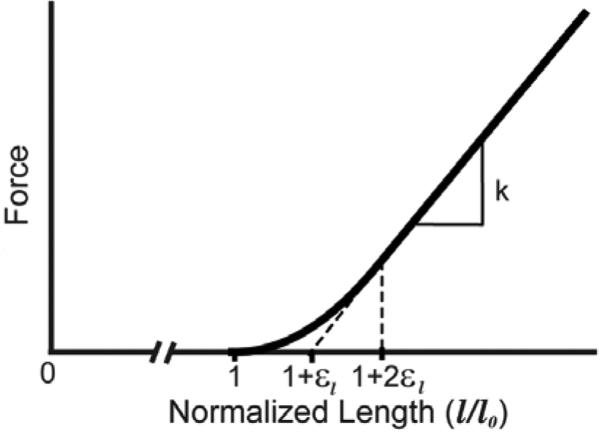
Figure 2.
The generic ligament force-strain curve was scaled by the ligament-specific stiffness (k) and slack length (l0). Slack length was computed from reference strain (εref) by scaling the ligament length in an extended knee reference configuration (lref) through the relationship l0 = lref/(1 + εref). The strain that defined the transition from nonlinear behavior to linear behavior was assumed to be εl=0.03.
The knee was integrated into an existing lower extremity musculoskeletal model [1], which included 44 muscles acting about the hip, knee, and ankle joints. The full model was implemented in SIMM [23] with the Dynamics Pipeline (Musculographics Inc., Santa Rosa, CA) and SD/Fast (Parametric Technology Corp., Needham, MA) used to generate code describing muscle-tendon dynamics and the multibody equations of motion. The predictive capacity of the model was previously validated by comparing simulated passive and active knee kinematics with subject-specific in vivo 3D knee kinematics measured with dynamic MRI [2].
Whole body kinematics and ground reactions were recorded while the subject walked overground in a motion analysis laboratory. The lower extremity model was scaled to the subject based on segment lengths determined in a standing upright posture. During walking, marker kinematics were collected at 100 Hz and then low-pass filtered at 12 Hz. Ground reaction forces were simultaneously collected at 2000 Hz (force plate model BP400600, AMTI, Watertown, MA) and then low-pass filtered at 50 Hz. A global optimization inverse kinematics routine determined pelvis translations, pelvis rotations, hip angles, knee flexion, and ankle dorsiflexion that best agreed with marker positions measured during gait [24]. At this stage, secondary tibiofemoral and all patellofemoral degrees of freedom (DOF) were assumed to be a constrained function of knee flexion, with these functions based on our simulated passive knee behavior [25].
At each frame of a gait cycle, an enhanced static optimization (ESO) routine was then used to calculate muscle forces, patellofemoral kinematics, and secondary tibiofemoral kinematics that minimized an objective function while satisfying overall dynamic constraints [26]. The objective function was a weighted sum of squared muscle activations, with a regularization term added to minimize frame-to-frame variations in secondary kinematics. The optimization constraints required that the muscle forces and internal knee loads (contact pressures, ligament forces) produced by the optimized knee kinematics generate the measured hip, knee (flexion), and ankle accelerations. The pelvis coordinates were prescribed to reproduce measured values, and measured ground reaction forces were applied directly to the feet. It should be explicitly noted that only knee flexion was prescribed in the gait simulation, with all other tibiofemoral and patellofemoral DOFs being allowed to evolve as a result of cartilage contact, ligament, and muscle forces. Each gait simulation provided a prediction of the tibiofemoral and patellofemoral kinematics and contact from heel strike through the mid-stance phase of walking (Fig. 3)
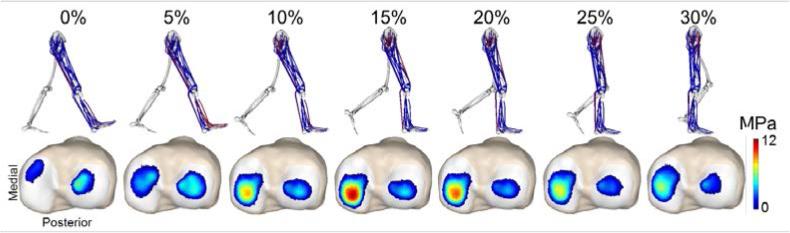
Figure 3.
Simulation of tibial plateau contact pressures from heel strike (0%) through mid-stance phase of gait. The first loading peak (~15%) preferentially loads the medial tibial plateau.
We used the Monte Carlo method to assess the propagation of uncertainties in ligament constitutive properties onto simulated tibiofemoral mechanics. The linear stiffness and reference strains of each of the ligament bundles was represented by independent Gaussian distributions centered at the nominal model values with standard deviations of 30% of the mean stiffness and 0.02 strain, respectively [5]. A total of 2000 simulations were performed on a high throughput computing grid using randomly selected values from the constitutive property distributions. The uncertainty in the predicted secondary tibiofemoral kinematics and tibial contact metrics (average pressure, contact area, center of pressure) was quantified by calculating the time varying means and standard deviations of all the simulations for each output (Fig. 4).
Figure 4.
The Monte Carlo analysis was performed by varying the linear stiffness and reference strain of the ligaments using independent Gaussian distributions, and repeating the gait simulations to determine the effect on tibiofemoral kinematics and tibial contact metrics. The output plots show the mean (solid line) ± 2 standard deviations (shaded region).
We performed a sensitivity analysis to determine the relative importance of the stiffness and reference strain of each ligament on simulated tibiofemoral kinematics and contact metrics. At heel strike and the first peak of tibiofemoral loading, we computed the Pearson's correlation coefficient (R) and corresponding p-value to quantify the correlation between the stiffness and reference strain of each ligament to both kinematics and contact metrics (Fig. 5). Correlations were considered statistically significant if p<0.05. The Pearson's correlation coefficients varied between −1 and 1, with values of 1 indicating a strong positive correlation, −1 indicating a strong negative correlation and 0 indicating no correlation. The absolute value of the Pearson's correlation coefficients was used to determine the relative influence of the stiffness and reference strain of each ligament on the output metrics.
Figure 5.
Sample scatter plots illustrating the sensitivity of tibiofemoral kinematics and tibial contact metrics to variations in ACL stiffness and reference strain. ACL properties exhibited significant influence on anterior tibial translation at heel strike. Medial tibial plateau contact pressures increased and migrated posteriorly in response to either a reduction in ACL stiffness or reference strain. ACL reference strain had a small, but significant, influence on tibial rotation at heel strike, with greater slack length (smaller reference strain) associated with internal tibial rotation.
Results
Variability in knee mechanics
Anterior tibial translation and internal tibial rotation exhibited marked variability when uncertainties in ligament parameters were considered. Tibial translation variability was posture dependent with a 95% confidence interval of ±1.5 mm at heel strike and ±3 mm at mid-stance (Fig. 4). The 95% confidence interval for tibial rotation was ±5 deg at heel strike and decreased slightly at mid-stance. The average tibial plateau contact pressure 95% confidence interval ranged from 5-6 MPa at the first peak of loading. The center of medial contact pressure exhibited a 95% confidence interval of ±2 mm in the anterior-posterior direction.
Kinematic Correlations (Fig. 6)
Figure 6.
Correlations between tibiofemoral kinematics and ligament stiffness (solid bars) and reference strains (open bars) at heel strike and first peak of tibiofemoral loading during stance. Notation: ACL – anterior cruciate ligament, PCL – anterolateral bundle of posterior cruciate ligament, MCL – medial collateral ligament, LCL – lateral collateral ligament, PT – patellar tendon, pCAP – posterior capsule. Significance denoted by * (p<0.05).
At heel strike, the ACL, MCL, and posterior capsule exhibited the greatest influence on anterior tibial translation. However by the time of first peak loading, anterior tibial translation was only significantly influenced by the ACL. Internal rotation at heel strike was primarily guided by the MCL and LCL, with the reference strains of these ligaments being more influential than the stiffness. ACL reference strains had secondary influence, being negatively correlated with internal rotation. At the time of first peak loading, tibial rotation remained significantly influenced by the MCL and LCL. The LCL, ACL and patellar tendon all exerted significant influence on lateral translation and adduction in midstance, with increased patellar tendon stiffness acting to adduct the knee. Both adduction and lateral tibial translation were most influenced by the LCL, with the ACL, PCL, MCL and PT also exhibiting significant influence.
Tibial Contact Correlations (Fig. 7)
Figure 7.
Correlations between tibial plateau contact metrics and ligament stiffness (solid bars) and reference strains (open bars) at first peak of tibiofemoral loading during stance. Abbreviations given in Fig. 6. Significance denoted by *p<0.05.
At mid-stance, an increase in ACL stiffness or reference strain was highly correlated with a decrease in contact pressure, with the effect being greater on the medial tibial plateau. Medial contact area was positively correlated with increased ACL, MCL, and LCL stiffness and reference strains. However, an increase in ACL stiffness or reference strain reduced contact area on the lateral side. The anterior-posterior location of center of pressure was highly correlated with ACL stiffness and reference strain on both the medial and lateral sides. MCL and LCL also exhibited influence on the anterior-posterior center of pressure location, with the reference strains again being more influential than the stiffness. The lateral center of pressure location was negatively correlated with ACL properties on the medial side, but positively correlated on the lateral side. The MCL reference strain also exerted a minor influence on medial-lateral center of pressure location.
Discussion
The objective of this study was to examine the sensitivity of tibiofemoral kinematics and contact metrics to variations in ligament constitutive properties. Previously, the influence of individual ligaments has been evaluated under isolated loading conditions using cadaveric experimentation [27-30] and computational models [6, 7, 31, 32]. We extended these prior studies by considering ligament influence during a functional task, walking, that involves time varying posture, muscle forces, and external loading. We found that ACL properties had the primary influence on average tibial cartilage contact pressure in mid-stance. The medial and lateral collateral ligament properties modulated tibial rotation at heel strike and exhibited secondary influence on cartilage contact location in mid-stance. Given the inherent uncertainty that exists in ligament properties, these sensitivities are important to consider when using computational models to investigate the surgical treatment of knee injuries and disease.
Anterior tibial translation and rotation were the most sensitive degrees of freedom to variations in ligament constitutive properties (Fig. 4). Cadaveric studies have previously demonstrated the importance of the ACL in restraining anterior translation [6, 7, 27]. Similarly, we found both the ACL stiffness and reference strain to have the greatest effect on anterior translation from heel strike through mid-stance. The influence of other ligaments on anterior translation were posture dependent, with the posterior capsule and MCL acting as secondary constraints to anterior translation at heel strike. Variations in MCL and LCL constitutive properties were more highly correlated with tibial rotation than the ACL. This finding is in agreement with experimental studies which have examined the combined effect of the ACL, MCL, and LCL [29-31]. For example, Markolf et al. found that while the ACL does provide rotational stability in an extended knee, its contribution was less than the MCL. Additionally, the contribution of the ACL decreased greatly in flexed postures [30], which is consistent with our sensitivity results suggesting the ACL influence on rotation diminishes as the knee is flexed in mid-stance.
Cartilage pressure, contact area, and contact location were most sensitive to the stiffness and reference strain of the ACL. An increase in ACL stiffness non-intuitively induced a reduction in cartilage contact pressure in mid-stance, particularly on the medial tibial plateau (Fig. 8). This result likely arises from the high degree of conformity between the curvatures of the medial femoral and tibial cartilage geometry, which makes contact pressure sensitive to small kinematic variations [33]. Specifically, a stiffer ACL provides a restraint to anterior tibial translation when the quadriceps are loaded in mid-stance, thereby maintaining contact in an area of high geometric conformity. In contrast, a compliant or longer ACL allows anterior tibial translation, such that contact pressure on the concave posterior aspect of the tibial plateau serves as a secondary restraint to anterior tibial translation. As a result, simulating gait with a reduced ACL stiffness or smaller reference strain induced an increase in contact pressure, particularly on the posterior aspect of the medial tibial plateau (Fig. 8).
Figure 8.
Illustration of the influence of ACL stiffness and reference strain on tibial plateau contact pressures at the first peak of tibiofemoral loading during stance. Tibial contact pressure patterns resulting from gait simulations with ±45% change in stiffness, or a ±0.03 shift in reference stiffness are shown. Note that a decrease in either ACL stiffness or reference strain results in both an increase in peak contact pressure and a posterior migration of the contact on the medial tibial plateau.
The sensitivity to ACL properties is of particular interest due to the prevalence of ACL injuries and associated long-term risk for osteoarthritis following ACL reconstruction [34, 35]. Surgical factors such as graft type, pretension, and fixation method can affect ligament stiffness and reference strains. Thus, a graft stiffness that is reduced compared to the native ACL could induce anterior tibial translation and elevated contact pressure during walking. It has been speculated that such altered cartilage loading mechanics could contribute to the initiation and progression of osteoarthritis [36].
A few limitations of the model and sensitivity analysis must be noted in order to properly interpret the results. The articular surface and ligament geometries were based on a single, healthy female subject. A more thorough exploration of multiple knee geometries is warranted to determine if the ligament sensitivities are geometry dependent. While we were not able to validate our simulations of knee mechanics in gait, we previously showed the nominal knee model predicted passive and active tibiofemoral and patellofemoral kinematics that were consistent with subject-specific dynamic MRI measures [12]. However, the nominal knee model relies on ligament properties derived from population based studies [37], which makes it critical to consider the propagation of this uncertainty when used in subject-specific models [38]. The sparsity and large range of experimental measures of ligament properties prevents a thorough analysis of their distribution within the population. An assumption of independent Gaussian distributions was therefore used, with previously assumed variances in ligament stiffness and reference strain [39]. Finally, our sensitivity metrics are first order correlation coefficients, which inherently do not account for nonlinearities or characterize interactions between ligaments. More advanced sensitivity analysis techniques exist [37], and will become more suitable for use as knee modeling and computational approaches needed to facilitate large scale explorations improve.
We conclude that probabilistic analysis of a multibody knee model is a powerful approach for exploring knee kinematic and cartilage contact sensitivities to knee ligament constitutive properties during functional movement. Our results highlight the strong influence that ligament stiffness and reference strain have on cartilage contact loading patterns during walking. As a result, the method and findings of this study are important to consider when using models to explore surgical treatments used to treat knee injury and disease.
References
- 1.Li G, Suggs J, Gill T. The effect of anterior cruciate ligament injury on knee joint function under a simulated muscle load: a three-dimensional computational simulation. Annals of biomedical engineering. 2002;30(5):713–20. doi: 10.1114/1.1484219. [DOI] [PubMed] [Google Scholar]
- 2.Barry MJ, Kwon TH, Dhaher YY. Probabilistic musculoskeletal modeling of the knee: A preliminary examination of an ACL-reconstruction.. Conference proceedings : ... Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference; 2010; pp. 5440–3. [DOI] [PubMed] [Google Scholar]
- 3.Gerus P, et al. Subject-specific knee joint geometry improves predictions of medial tibiofemoral contact forces. Journal of biomechanics. 2013;46(16):2778–2786. doi: 10.1016/j.jbiomech.2013.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Valente G, et al. Muscle discretization affects the loading transferred to bones in lower-limb musculoskeletal models. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 2011:0954411911425863. doi: 10.1177/0954411911425863. [DOI] [PubMed] [Google Scholar]
- 5.Dhaher YY, Kwon TH, Barry M. The effect of connective tissue material uncertainties on knee joint mechanics under isolated loading conditions. Journal of biomechanics. 2010;43(16):3118–25. doi: 10.1016/j.jbiomech.2010.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li G, Suggs J, Gill T. The effect of anterior cruciate ligament injury on knee joint function under a simulated muscle load: a three-dimensional computational simulation. Annals of Biomedical Engineering. 2002;30(5):713–720. doi: 10.1114/1.1484219. [DOI] [PubMed] [Google Scholar]
- 7.Suggs J, Wang C, Li G. The effect of graft stiffness on knee joint biomechanics after ACL reconstruction–a 3D computational simulation. Clinical biomechanics. 2003;18(1):35–43. doi: 10.1016/s0268-0033(02)00137-7. [DOI] [PubMed] [Google Scholar]
- 8.Delp SL, et al. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54(11):1940–50. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- 9.Arnold EM, et al. A model of the lower limb for analysis of human movement. Annals of biomedical engineering. 2010;38(2):269–79. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guess TM, et al. A multibody knee model with discrete cartilage prediction of tibio-femoral contact mechanics. Computer methods in biomechanics and biomedical engineering. 2013;16(3):256–70. doi: 10.1080/10255842.2011.617004. [DOI] [PubMed] [Google Scholar]
- 11.Lin YC, et al. Simultaneous prediction of muscle and contact forces in the knee during gait. Journal of biomechanics. 2010;43(5):945–52. doi: 10.1016/j.jbiomech.2009.10.048. [DOI] [PubMed] [Google Scholar]
- 12.Lenhart RL, et al. Prediction and validation of load-dependent behavior of the tibiofemoral and patellofemoral joints during movement. Annals of biomedical engineering. 2015 doi: 10.1007/s10439-015-1326-3. conditionally accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guess TM, et al. A subject specific multibody model of the knee with menisci. Medical engineering & physics. 2010;32(5):505–15. doi: 10.1016/j.medengphy.2010.02.020. [DOI] [PubMed] [Google Scholar]
- 14.Erdemir A. Open Knee: A Pathway to Community Driven Modeling and Simulation in Joint Biomechanics. Journal of medical devices. 2013;7(4):0409101–409101. doi: 10.1115/1.4025767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Weimer K, et al. Development and validation of a subject-specific computational human knee model in a dynamic knee simulator.. Summer Bioengineering Conference; Keystone, CO.. 2007. [Google Scholar]
- 16.Baldwin MA, et al. Efficient probabilistic representation of tibiofemoral soft tissue constraint. Computer methods in biomechanics and biomedical engineering. 2009;12(6):651–9. doi: 10.1080/10255840902822550. [DOI] [PubMed] [Google Scholar]
- 17.Thelen DG, Choi KW, Schmitz AM. Co-Simulation of Neuromuscular Dynamics and Knee Mechanics During Human Walking. Journal of biomechanical engineering. 2014;136(2):021033. doi: 10.1115/1.4026358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bei Y, Fregly BJ. Multibody dynamic simulation of knee contact mechanics. Medical engineering & physics. 2004;26(9):777–789. doi: 10.1016/j.medengphy.2004.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Askew M, Mow V. The biomechanical function of the collagen fibril ultrastructure of articular cartilage. Journal of biomechanical engineering. 1978;100(3):105–115. [Google Scholar]
- 20.Blankevoort L, et al. Articular contact in a three-dimensional model of the knee. Journal of Biomechanics. 1991;24(11):1019–1031. doi: 10.1016/0021-9290(91)90019-j. [DOI] [PubMed] [Google Scholar]
- 21.Shelburne KB, Torry MR, Pandy MG. Contributions of muscles, ligaments, and the ground-reaction force to tibiofemoral joint loading during normal gait. Journal of Orthopaedic Research. 2006;24(10):1983–1990. doi: 10.1002/jor.20255. [DOI] [PubMed] [Google Scholar]
- 22.Shin CS, Chaudhari AM, Andriacchi TP. The influence of deceleration forces on ACL strain during single-leg landing: a simulation study. Journal of Biomechanics. 2007;40(5):1145–1152. doi: 10.1016/j.jbiomech.2006.05.004. [DOI] [PubMed] [Google Scholar]
- 23.Delp SL, Loan JP. A computational framework for simulating and analyzing human and animal movement. Comput. Sci. Eng. 2000;2(5):46–55. [Google Scholar]
- 24.Lu TW, O’connor JJ. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J. Biomech. 1999;32(2):129–134. doi: 10.1016/s0021-9290(98)00158-4. [DOI] [PubMed] [Google Scholar]
- 25.Arnold EM, et al. A model of the lower limb for analysis of human movement. Ann. Biomed. Eng. 2010;38(2):269–279. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lenhart RL, et al. Influence of step rate and quadriceps load distribution on patellofemoral cartilage contact pressures during running. Journal of Biomechanics. 2015 doi: 10.1016/j.jbiomech.2015.04.036. in review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Melby A, et al. The effects of graft tensioning on the laxity and kinematics of the anterior cruciate ligament reconstructed knee. Arthroscopy: The Journal of Arthroscopic & Related Surgery. 1991;7(3):257–266. doi: 10.1016/0749-8063(91)90123-f. [DOI] [PubMed] [Google Scholar]
- 28.Fukubayashi T, et al. An in vitro biomechanical evaluation of anterior-posterior motion of the knee. Tibial displacement, rotation, and torque. The Journal of Bone & Joint Surgery. 1982;64(2):258–264. [PubMed] [Google Scholar]
- 29.Shoemaker SC, Markolf KL. Effects of joint load on the stiffness and laxity of ligament-deficient knees. An in vitro study of the anterior cruciate and medial collateral ligaments. The Journal of Bone & Joint Surgery. 1985;67(1):136–146. [PubMed] [Google Scholar]
- 30.Markolf KL, Mensch J, Amstutz H. Stiffness and laxity of the knee--the contributions of the supporting structures. A quantitative in vitro study. The Journal of Bone & Joint Surgery. 1976;58(5):583–594. [PubMed] [Google Scholar]
- 31.Li G, et al. A validated three-dimensional computational model of a human knee joint. Journal of biomechanical engineering. 1999;121(6):657–662. doi: 10.1115/1.2800871. [DOI] [PubMed] [Google Scholar]
- 32.Dhaher YY, Kwon T-H, Barry M. The effect of connective tissue material uncertainties on knee joint mechanics under isolated loading conditions. Journal of biomechanics. 2010;43(16):3118–3125. doi: 10.1016/j.jbiomech.2010.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Andriacchi TP, et al. Rotational changes at the knee after ACL injury cause cartilage thinning. Clinical orthopaedics and related research. 2006;442:39–44. doi: 10.1097/01.blo.0000197079.26600.09. [DOI] [PubMed] [Google Scholar]
- 34.Struewer J, et al. Knee function and prevalence of osteoarthritis after isolated anterior cruciate ligament reconstruction using bone-patellar tendon-bone graft: long-term follow-up. International orthopaedics. 2012;36(1):171–177. doi: 10.1007/s00264-011-1345-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Streich NA, et al. Long-term outcome of anterior cruciate ligament reconstruction with an autologous four-strand semitendinosus tendon autograft. International orthopaedics. 2013;37(2):279–284. doi: 10.1007/s00264-012-1757-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Andriacchi TP, et al. A framework for the in vivo pathomechanics of osteoarthritis at the knee. Ann Biomed Eng. 2004;32(3):447–57. doi: 10.1023/b:abme.0000017541.82498.37. [DOI] [PubMed] [Google Scholar]
- 37.Laz PJ, Browne M. A review of probabilistic analysis in orthopaedic biomechanics. Proceedings of the Institution of Mechanical Engineers. Part H. Journal of engineering in medicine. 2010;224(8):927–43. doi: 10.1243/09544119JEIM739. [DOI] [PubMed] [Google Scholar]
- 38.Anderson AE, Ellis BJ, Weiss JA. Verification, validation and sensitivity studies in computational biomechanics. Computer methods in biomechanics and biomedical engineering. 2007;10(3):171–84. doi: 10.1080/10255840601160484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Baldwin MA, et al. Efficient probabilistic representation of tibiofemoral soft tissue constraint. Computer methods in biomechanics and biomedical engineering. 2009;12(6):651–659. doi: 10.1080/10255840902822550. [DOI] [PubMed] [Google Scholar]