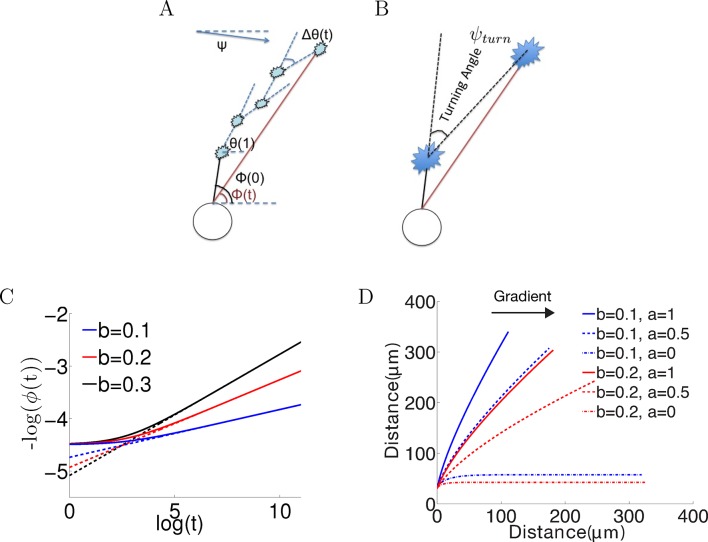
Figure 1. Model set-up and the noiseless case.

(A) The axon starts growing from the soma (black segment) at initiation angle ϕ(0). At each time point, the bearing is θ(t), and the bearing change between t and t + 1 is Δθ($t$). ϕ($t$) is the angle of the vector connecting the current position of the growth cone with the anchor point. Ψ is the fixed gradient direction. (B) The turning angle ψ_turn at time $t$ is the angle between the initial direction of growth, and the line joining the initial and current positions of the growth cone. (C) Simulation of the growth cone angle using Equation (1) in the noiseless case (ξ = 0) with the same $a$ = 1 and different values of b. The dashed line is the power law $\varphi \left(t\right)\propto t^{\frac{-b}{a+b}}$. In the long time limit, this law accurately describes the angle of the growth cone. (D) Simulations of the trajectories for different combinations of $a$ and $b$ in the absence of noise. Larger $b$ leads to stronger turning. When $a$ = 0, the growth cone very rapidly aligns with the gradient. The persistence term ($t$ > 0) leads to incomplete turning.

DOI: http://dx.doi.org/10.7554/eLife.12248.004