Radial Bias Is Not Necessary For Orientation Decoding

Abstract

Multivariate pattern analysis can be used to decode the orientation of a viewed grating from fMRI signals in early visual areas. Although some studies have reported identifying multiple sources of the orientation information that make decoding possible, a recent study argued that orientation decoding is only possible because of a single source: a coarse-scale retinotopically organized preference for radial orientations. Here we aim to resolve these discrepant findings. We show that there were subtle, but critical, experimental design choices that led to the erroneous conclusion that a radial bias is the only source of orientation information in fMRI signals. In particular, we show that the reliance on a fast temporal-encoding paradigm for spatial mapping can be problematic, as effects of space and time become conflated and lead to distorted estimates of a voxel’s orientation or retinotopic preference. When we implement minor changes to the temporal paradigm or to the visual stimulus itself, by slowing the periodic rotation of the stimulus or by smoothing its contrast-energy profile, we find significant evidence of orientation information that does not originate from radial bias. In an additional block-paradigm experiment where space and time were not conflated, we apply a formal model comparison approach and find that many voxels exhibit more complex tuning properties than predicted by radial bias alone or in combination with other known coarse-scale biases. Our findings support the conclusion that radial bias is not necessary for orientation decoding. In addition, our study highlights potential limitations of using temporal phase-encoded fMRI designs for characterizing voxel tuning properties.

Introduction

Orientation-selective neurons in the primary visual cortex (V1) are clustered at submillimeter scales to form cortical columns and pinwheel-like structures (Bartfeld and Grinvald, 1992; Blasdel, 1992; Ohki et al., 2006). Although orientation selectivity is predominantly organized at a fine spatial scale, Kamitani and Tong (2005) discovered that the orientation of a viewed grating can be accurately decoded from fMRI activity patterns in the human visual cortex. They hypothesized that orientation decoding was possible at standard fMRI resolutions due to local anisotropies in the distribution of orientation-selective columns, as this would lead to subtle imbalances in orientation preference at spatial scales exceeding the width of individual columns. Subsequent high-resolution fMRI studies have demonstrated the presence of orientation-selective signals in V1 at millimeter and submillimeter scales (Moon et al., 2007; Swisher et al., 2010; Yacoub et al., 2008). However, differential responses to orientation can also be found at much coarser spatial scales. For example, some studies have reported stronger overall V1 responses for cardinal than for oblique orientations (Furmanski and Engel, 2000), while others suggest that disproportionately more voxels prefer cardinal over oblique orientations (Sun et al., 2013). A retinotopically organized bias in favor of radial orientations (relative to the fovea) has also been found in human V1 (Sasaki et al., 2006). This radial bias appears quite prominent, and may originate from a bias evident in the elongated dendritic fields of retinal ganglion cells (Schall et al., 1986). Recent studies have revealed stronger responses for radial than tangential orientations in the human lateral geniculate nucleus (Ling et al., 2015), consistent with the possibility of a retinal contribution to the radial bias effects observed in V1.

In several recent studies, researchers have attempted to determine the extent to which fMRI decoding of stimulus orientation depends on fine-scale or coarse-scale biases (Alink et al., 2013; Kriegeskorte et al., 2010; Mannion et al., 2010; Op de Beeck, 2010; Swisher et al., 2010). This is an important question as it pertains not only to the functional organization of feature selectivity in the visual cortex, but also has direct relevance to understanding the types of information that can be detected in multivariate fMRI activity patterns (Swisher et al., 2010; Gardner, 2010; Shmuel et al., 2010; Tong and Pratte, 2012) and at the scale of individual voxels (Brouwer and Heeger, 2009; Kay et al., 2008; Kriegeskorte et al., 2010; Naselaris et al., 2011; Serences et al., 2009).

A recent study by Freeman et al. (2011) addressed this issue by using a temporal phase-encoding approach to measure V1 responses to periodic rotations of an oriented grating, and comparing these orientation preference maps with those evoked by a retinotopic radial-mapping stimulus (Fig. 1A, B). Orientation was accurately decoded from the original activity patterns obtained at standard fMRI resolutions, but after analytic removal of the radial bias component, orientation decoding fell to chance levels. From these results, Freeman et al. concluded that radial bias was the only source of orientation information in the fMRI signal, and thus necessary for orientation decoding. Curiously however, other fMRI studies have demonstrated the presence of other sources of orientation information in the visual cortex, distinct from radial bias (Alink et al., 2013; Freeman et al., 2013; Mannion et al., 2009; Swisher et al., 2010). Thus, conflicting results have emerged in the literature, and it has remained unclear as to why radial bias appears to be necessary for orientation decoding in some studies but not others.

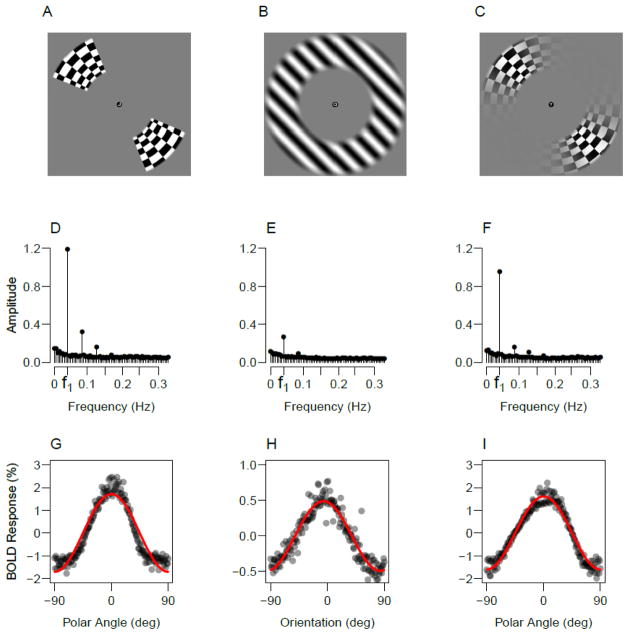
Figure 1.

Experimental stimuli and the resulting BOLD responses. Top row shows examples of the retinotopy wedge used in Experiments 1 and 3 (A), the oriented grating used in Experiments 1–3 (B) and the smoothed retinotopy wedge used in Experiment 2 (C). The middle row shows power spectrums of the BOLD signal in response to the wedge stimulus (D), oriented grating (E) and smoothed wedge (F), averaged over participants. The bottom row shows the corresponding BOLD signals from a representative participant to the wedge (G), grating (H) and smoothed wedge stimuli (I). The responses of individual voxels in V1 were phase locked to their retinotopic phase preference and averaged. The line shows the best-fitting cosine function to the data in each panel.

In the present study, our goal was to reconcile these disparate findings regarding whether radial bias might be necessary for orientation decoding. Our first step was to replicate the stimulus conditions, experimental parameters, and analytical procedure of Freeman et al. (2011), as their study was the first to report that orientation decoding depends entirely on radial bias. Across a series of experiments, we find that subtle but critical choices in experimental design led to erroneous conclusions in the Freeman et al. study. They relied on a temporal-encoding approach to characterize the orientation and polar-angle retinotopic preferences of individual voxels. Such an approach provides a fast, efficient method for spatial mapping (Engel, 2012), but has the potential to conflate effects of space and time. Moreover, different types of visual stimuli can evoke different spatiotemporal profiles of activity in the cortex, such that information about a stimulus may be conveyed not only at the fundamental frequency of the paradigm but also in the form of higher order temporal harmonics. Such considerations proved important when comparing the accuracy of decoding performance across orientation and polar-angle conditions.

In Experiment 1, we replicate the experimental results of Freeman et al., but show that the polar-angle retinotopy stimulus evokes higher-order harmonic responses, such that residual information persists about the retinotopy stimulus following removal of the fundamental component. In comparison, decoding of orientation is driven largely by the fundamental component. As a consequence, Freeman et al.’s approach of comparing decoding performance for orientation and polar angle, following the removal of the fundamental component, leads to an invalid procedure for estimating chance-level orientation decoding. In Experiments 2 and 3, we implemented minor changes to the spatiotemporal paradigm, by slowing the rotation of the stimulus or by smoothing the contrast-energy profile of the retinotopy stimulus to avoid evoking harmonic responses. These modest manipulations were sufficient to produce failures to replicate the original study, and suggest that orientation information persists following the removal of radial bias. In Experiment 4, orientations were presented using a blocked paradigm that avoided the possibility of conflating effects of space and time. Results from this experiment show that the orientation-tuning profiles for many individual voxels are more complex than would be predicted by radial bias alone. Based on these findings, we conclude that radial bias is not necessary for orientation decoding.

Materials and Methods

Participants

Eight healthy adult volunteers (aged 21–32, four females) with normal or corrected-to-normal vision participated in one or more of the experiments. These included four participants in Experiment 1, four in Experiment 2, three in Experiment 3, and four in Experiment 4. Three of the participants were authors. All participants gave written informed consent, and the study was approved by the Vanderbilt University Institutional Review Board.

MRI Acquisition

All MRI data were collected with a Philips 3T Intera Achieva scanner using an eight-channel head coil. Individual Experiments 1–4, and the retinotopic mapping of visual areas, were each performed in a separate MRI scanning session of 2.5 hrs in duration. Functional acquisitions were standard gradient-echo echoplanar T2*-weighted images, consisting of 22 slices aligned perpendicular to the calcarine sulcus (TR 1500 ms; TE 35 ms; flip angle 80°; FOV = 192 × 192 mm, slice thickness 3 mm with no gap; in-plane resolution 3 × 3 mm). This slice prescription covered the entire occipital lobe and parts of posterior parietal and temporal cortices with no SENSE acceleration. During a separate retinotopic mapping session, a high-resolution 3D anatomical T1-weighted image was acquired (FOV=256 × 256; resolution=1 × 1 × 1 mm) and this image was used to construct an inflated representation of the cortical surface. A custom bite-bar apparatus was used to minimize head motion.

MRI Preprocessing

Functional MRI data for each participant were simultaneously motion-corrected and aligned to the mean of one run using FSL’s MCFLIRT motion-correction algorithm (Jenkinson et al., 2002). The data were then high-pass filtered (cutoff, 90 s) in the temporal domain, and converted to percent signal change units by dividing the time series of each voxel by its mean intensity over each run.

Regions of Interest

In a session separate from the main experiment, standard retinotopic mapping procedures were used to delineate visual area V1 (DeYoe et al., 1996; Engel et al., 1997; Sereno et al., 1995) in the left and right hemispheres. These cortical visual areas were defined on the inflated surface, which was reconstructed using Freesurfer (Dale et al., 1999). The preprocessed experimental data were transformed to this surface using Freesurfer’s boundary-based registration (Greve and Fischl, 2009). Coherence values from the experimental polar-angle mapping runs were projected onto the flattened surface, and a region of interest was constructed by identifying voxels within V1 that responded to the experimental polar-wedge stimulus. The resulting ROI for each subject included between 224 and 335 voxels.

Task

During all runs in Experiments 1–3, participants performed an identification task on letters presented rapidly at fixation (5 letters/second, letter size 0.33° within a .5° fixation circle) by pressing a button to report whenever a ‘J’ or ‘K’ was presented. This task was used to encourage participants to maintain stable fixation and a steady level of alertness throughout the experiment. In Experiment 4, participants were required to maintain fixation while a randomly chosen stimulus orientation was presented on each 16-s block.

Polar-Angle Mapping

Each scanning session for Experiments 1–3 included 7–10 runs of polar-angle mapping. In Experiments 1 and 3, we used the same polar-angle mapping stimulus as Freeman et al. (Fig. 1A), which consisted of full-contrast counter-phase flickering (8 hz) checkerboard wedges that occupied 45° of polar angle and spanned an eccentricity from 4.5° to 9.5°. The inner and outer boundaries of the wedges included a 1° linear contrast ramp to mitigate aliasing artifacts at the edges. For Experiment 2, we applied a smooth contrast ramp to the checkerboard pattern along the polar-angle dimension (Fig. 1C), using a raised cosine function (5^th power).

In Experiments 1 and 2, the wedges rotated counterclockwise in 11.25° steps every 1.5 s, completing a cycle every 24 s. For both the double-wedge retinotopy stimulus and the orientation grating, 1 cycle of periodic stimulation refers to 180° of stimulus rotation. The wedge cycled through each of the 16 polar-angle positions 11 times in each run. In Experiment 3, the wedges rotated more slowly, completing a cycle in 72 s. To achieve this slower rotation, the wedges occupied each of the 16 positions for 4.5 seconds, completing 4.25 cycles per run.

To determine the polar-angle preference of each voxel, the data were averaged over the polar-angle mapping runs, and the Fourier transform was applied to the resulting mean time course for each voxel. The relative amplitude of the fundamental frequency indicates the strength of a given voxel’s response to periodic stimulation, and the temporal phase of that response provides an estimate of the polar-angle preference of that voxel.

Orientation Mapping

Each scanning session for Experiments 1–3 also included 14–15 runs of orientation mapping. For Experiments 1–3, we used the same visual stimulus for orientation mapping as Freeman et al. (Fig. 1B). A full-contrast sine-wave grating with a spatial frequency of 0.5 cpd was presented in an annular window that matched the eccentricity range of the polar-angle mapping stimulus. Stimulus eccentricity ranged from 4.5° to 9.5°, with a linear contrast ramp applied to the inner and outer 1° boundaries of the grating.

In each experiment, the grating rotated with the same temporal profile as the polar-angle wedges. In Experiments 1 and 2, the grating rotated by 11.25° every 1.5 s, so each cycle of stimulation required 24 s. In Experiment 3, the grating rotated at a slower rate of 11.25° every 4.5 s, so the period of stimulation was 72 s.

In Experiment 4, square-wave oriented gratings were presented in a blocked design. Each participant completed between 16 and 19 experimental runs, in addition to two localizer runs used to identify voxels in visual cortex with retinotopic preferences corresponding to the stimulus location. Each experimental run included 16 stimulus blocks with a duration 16s each. In each block, a grating was flashed on and off (250 ms on followed by 250 ms off) with a random spatial phase on each presentation. The orientation for each block was chosen pseudo-randomly, such that orientations within each run were sampled evenly from the orientation space. The stimulus consisted of a full-contrast square-wave grating that spanned from 1.5° to 10° in eccentricity, with a spatial frequency of 1.5 cpd, consistent with the stimulus parameters used by Kamitani & Tong (2005). No task was performed during this experiment; participants were instructed to maintain fixation on a central bull’s eye.

Decoding Orientation

The goal of the orientation decoding analyses in Experiments 1–3 was to measure the amount of orientation information present in a group of voxels, both prior to and following the analytic removal of radial bias. After fMRI preprocessing, we removed data corresponding to the first two rotations (Experiments 1 and 2) or the first quarter rotation (Exp. 3). This procedure removed transient responses resulting from the onset of the stimulus, and equated the number of functional acquisitions across the three experiments (144 functional volumes per run). Within each run, the data were then averaged over TRs corresponding to the same orientation, providing 16 responses for each voxel in each run corresponding to the 16 orientations for each voxel in the V1 ROI. To match the procedure of Freeman et al., we used a Naive Bayes classifier to identify which of the 16 orientations produced each activity pattern in a leave-one-run-out cross-validation scheme. The extent to which classification accuracy is above chance baseline (6.25% or 1/16) provides a measure of how much orientation information is present in a sample of voxels.

Removing Radial Bias From Orientation

The purpose of this analysis is to determine whether orientation decoding is driven entirely by the radial bias, or whether reliable orientation information remains available following the analytic removal of radial bias. Our first goal was to attempt to replicate Freeman et al.’s findings by adopting their procedures. We calculated the mean time series of every voxel across all polar-angle runs, and applied the Fourier transform to determine the preferred phase of each voxel (denoted ϕ_i for the ith voxel). Since the orientation mapping experiment followed the same temporal paradigm as the polar-angle mapping experiment, a voxel’s predicted radial bias in the orientation experiment should follow a cosine function with stimulus rotation frequency f cycles per run, and a preferred phase ϕ_i corresponding to that of the polar-angle mapping experiment. For every orientation-mapping run, we fitted the time series of each voxel using its predicted radial bias component by allowing the amplitude of the cosine function with phase ϕ_i to vary as a free parameter (β_i),

$$v_{ij}~{\beta }_{i}cos(f\ast {\theta }_j-{\varphi }_i)+{\epsilon }_{ij}.$$

The residuals of this regression analysis provide orientation-mapping data with the radial bias component removed. Orientation decoding was applied to this residual time series across all voxels in the ROI (i.e., fMRI activity patterns with radial bias removed), to assess whether any orientation information remained following this analytic procedure to remove radial bias.

Retinotopy Baseline

The critical question is whether V1 activity patterns with radial bias removed still contain reliable orientation information that can support decoding. If decoding of these residual activity patterns leads to chance-level performance (1/16 orientations, or 6.25% correct), then all orientation information in the original activity patterns must have arisen from radial bias. However, if decoding performance is greater than chance, this positive result could be due to either 1) the presence of orientation information that is truly distinct from radial bias, or 2) an inability to completely remove all of the radial bias information from the original orientation signal. Note that complete removal of radial bias is impossible unless one has knowledge of the true radial bias of every voxel in the ROI. Instead, estimates of a voxel’s true radial bias will be subject to some degree of estimation error, and the degree to which these estimates are imprecise will determine the amount of radial bias information that remains in the residual activity patterns.

To account for the possible presence of residual radial bias information, Freeman et al. devised a retinotopy baseline measure that specifies the level of decoding accuracy that would be expected if radial bias were the only source of orientation information in the orientation-mapping experiment, but the removal of the radial bias were imperfect. To construct this baseline, the level of decoding accuracy was first equated across polar-angle and orientation mapping experiments by adding independent Gaussian noise to every voxel for the polar-angle data. The level of noise was adjusted until performance levels were matched. Next, the polar-angle phase preference of each V1 voxel was used to regress out the radial bias component from the polar-angle fMRI data with noise added. Decoding of polar-angle retinotopic position from the residuals of this regression provides the retinotopy baseline – how much retinotopy information is left over after the analytical removal of retinotopy. This procedure of adding noise, regression and decoding was repeated 500 times for each participant, providing samples from the distribution that would arise under the hypothesis that no orientation information remains after removal of the radial bias.

The next step is to determine whether classification performance of orientation with radial bias removed is significantly higher than the retinotopy baseline. To do so, for each participant we simulated 500 accuracy scores from a binomial distribution with probability and size equal to the observed classification accuracy of the orientation-minus-radial-bias signal. A p-value is computed as the proportion of these simulations in which simulated orientation decoding was larger than the simulated retinotopy baseline. In addition to reporting these p-values for each subject, we combine them across subjects to compute a group-level p-value using Fisher’s method (Fisher, 1925).

Removing Harmonics

In Freeman et al.’s original analysis, the radial bias component was removed from the time series of every voxel by projecting out a cosine function with a phase corresponding to the polar-angle preference. However, as Fig. 3B of their paper indicates, voxel responses to the retinotopy wedge did not strictly follow a cosine function, as can be seen in the Fourier domain based on the elevated amplitudes observed in the second and third harmonics of the retinotopy signal. We replicate this finding in Experiment 1, and show that the presence of these harmonics poses a problem for calculating an appropriate retinotopy baseline, as these higher-order harmonics contain information to support decoding of polar-angle position even after the removal of the fundamental component. One way to address this problem is to construct the retinotopy baseline by removing these harmonic signals in addition to the fundamental cosine component. We used a multiple regression analysis to do so:

$$v_{ij}~{\beta }_{i1}cos(f\ast {\theta }_j-{\varphi }_i)+{\beta }_{i2}cos(2f\ast {\theta }_j-{\varphi }_{2i})+{\beta }_{i3}cos(3f\ast {\theta }_j-{\varphi }_{3i})+{\epsilon }_{ij}.$$

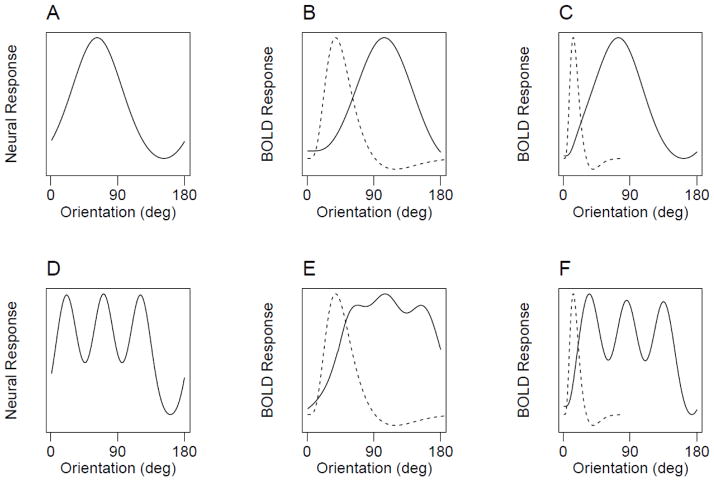
Figure 3.

Predicted effects of the hemodynamic response function on fMRI orientation signals. A) Hypothetical tuning curve that resembles a radial-bias like signal. B) The result of convolving the tuning curve in (A) with a hemodynamic response function (dashed curves), in which the oriented grating rotates through time over a 24 second period as in Freeman et al. and our Experiments 1 and 2. C) The result of convolving the hypothetical curve in (A) with the same HRF, but with a slower rotation period of 72 seconds. D) A hypothetical tuning curve that has a more complex signal, such as might reflect uneven sampling from the cortical columnar structure. E) In the 24-second design, convolution with the HRF filters out the complex aspects of the signal. F) Slowing the rotation period to 72 seconds greatly mitigates the filtering effect.

The first component represents the predicted signal at the fundamental frequency of the rotating stimulus (f) as in the original analysis. The additional components represent the second harmonic (2f) and the third harmonic (3f, with phases estimated from the retinotopy runs in the same manner as for the phase of the fundamental signal. The residuals from this regression serve as input for the harmonics-removed classification analysis of Experiment 1.

Tuning Curve Complexity

In Experiment 4, oriented gratings were presented in a blocked design, and our goal was to characterize how individual voxels responded to different orientations. If fMRI responses to orientation are solely determined by radial bias, then the orientation tuning curves for each voxel should reveal simple, unimodal response functions indicating a peak preference for a single orientation. Alternatively, more complex sources of orientation information, such as local anisotropies in the distribution of orientation columns or a combination of many disparate sources, should lead to the occurrence of more complex tuning curves. To characterize the complexity of voxel tuning curves, a series of models were fitted to each voxel, including an intercept model predicting no orientation tuning (M₀), a cosine function of orientation predicting a unimodal tuning curve (M₁), the sum of this cosine and a cosine with two cycles allowing for a bi-modal response function (M₂), and the sum of these and a cosine with three cycles allowing for a tri-modal response function (M₃). These cosine-based models were also compared with a von Mises tuning curve (VM). The von Mises allows for a unimodal response function, and has a free parameter that allows for tighter tuning bandwidths than the single cosine model.

Three approaches were used to determine which of these models provided the most accurate account of the orientation tuning curve data. First, a formal model-comparison approach was used to determine which model provided the best account of each voxel’s orientation tuning response profile. For each voxel, the merit of each model was characterized with the Akaike information criterion (AIC, Akaike, 1974). This statistic takes into account both how well each model fits the data and each model’s complexity, where overly flexible models are penalized for being able to capture any data pattern. By comparing the AIC values for each model within each voxel, we characterized how many voxels were best accounted for by each model for each participant.

Cross validation provides another common approach to determining how well a model fits data, while also ensuring that the model is not overly complex such that it is merely fitting noise. We adopted this approach by fitting each model to each voxel using data from all but one run, and then used the fitted model to predict the BOLD responses on the left-out run. This cross-validation procedure was performed in a leave-one-run-out approach, performed iteratively until every run was tested. The resulting variance accounted for by each model (as measured by R²) is taken as a measure of model accuracy. Whereas AIC aims to determine which model provides the best account of the data as defined by information theory, this cross-validation approach determines which model provides for the most powerful prediction performance. Although these approaches differ substantively in their goals, we find that the conclusions are largely in agreement across methods.

In addition to assessing how well each model could predict the responses of individual voxels, we constructed forward-encoding models to determine how well each model could be used to predict the viewed orientation from voxel response patterns (Brouwer and Heeger, 2009; Kay et al., 2008). Each model was fitted to each voxel’s response on all but one run, and the fitted models were used to predict the viewed orientations on the left-out run given the voxel activity patterns. The error in these predictions was measured as root mean squared error (RMSE) to quantify the accuracy of cross-validation performance. This is a multivariate approach as it pools information across voxels in order to produce predicted orientations, and as such is similar to orientation decoding (Kamitani and Tong, 2005). Because this approach relies on a cross-validation procedure, it will favor the simplest model that can accurately capture stable patterns in orientation responses.

Results

Experiment 1: Replication of Freeman et al. Study

In Experiment 1, we adopted the temporal phase-encoding approach used by Freeman et al. to characterize the retinotopic polar-angle preference and orientation preference of individual V1 voxels. Following their stimulus parameters and analytical procedures, we replicated the main patterns of results reported in their study.

Figure 2A shows classification performance from Experiment 1. The leftmost bar shows orientation classification from the original fMRI activity patterns. The middle bar shows orientation classification performance after analytic removal of radial bias, by regressing out the predicted cosine component. Removal of the radial bias component clearly lowers orientation classification performance, suggesting that at least some of the orientation information in these activity patterns can be attributed to radial bias. Residual decoding performance (mean accuracy, 26%) is significantly greater than chance-level performance (6.25%, indicated by the dashed line). However, as Freeman et al. noted, effective removal of radial bias depends on the accuracy with which one can estimate the true polar-angle preference of individual voxels. Thus, any noise or errors in these estimates would lead to incomplete removal of radial bias information, such that residual activity patterns could support above-chance decoding.

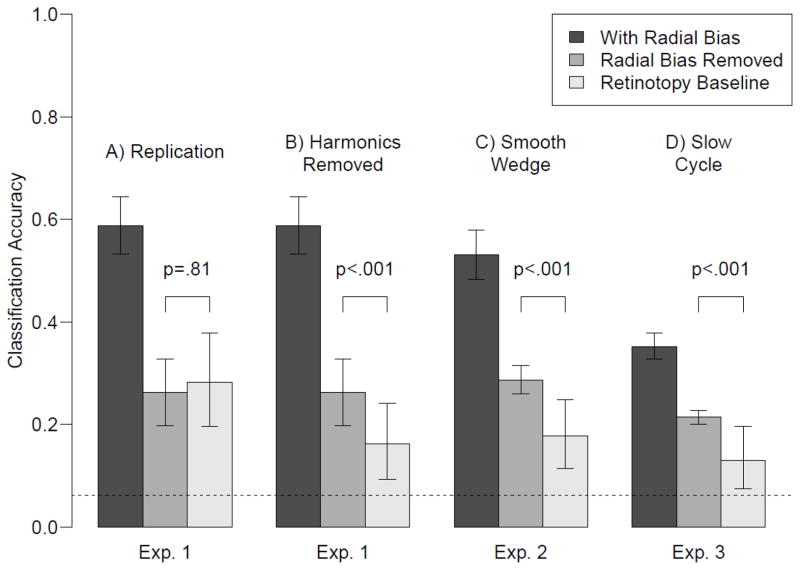
Figure 2.

Decoding results from Experiments 1–3. The leftmost bar in each panel shows decoding performance for the original orientation data. The middle bar shows decoding performance after removal of the radial bias. The third bar shows the retinotopy baseline, which represents the amount of residual retinotopy information left over after removal of the retinotopy signal. If orientation decoding after removing the radial bias is higher than this retinotopy baseline, then there must be orientation information in the signal that is not due to radial bias. Error bars denote standard errors for orientation decoding with and without radial bias. For the retinotopy baseline, the error bars denote the .025 and .975 percentiles of the simulated distribution, averaged across participants.

Freeman et al. devised a retinotopy baseline to specify how accurate orientation decoding should be if it were entirely due to radial bias, allowing for imperfect removal of radial bias via the regression procedure. Their baseline measure uses independent Gaussian noise to lower a participant’s retinotopy decoding performance to match orientation decoding performance, and then applies a bootstrapping procedure to determine the range of accuracies with which polar-angle can be decoded from the fMRI retinotopy experiment with radial biased removed. We computed this retinotopy baseline (third bar in Fig. 2A), and found that orientation classification performance was not significantly higher than the retinotopy baseline for any of the four subjects individually (p = .82, .73, .86 and .20), nor at the group level (p=.81). These data provide a compelling replication of the Freeman et al. result, which was interpreted to imply that removal of the radial bias effectively removes all orientation information from the fMRI activity patterns.

Experiment 1: Retinotopy information in harmonic components

A critical assumption underlying Freeman et al.’s analysis procedure is that all of the retinotopy information, and all of the radial bias orientation information conveyed by a voxel’s response, occur at the fundamental frequency of the stimulus paradigm. There are two ways in which this assumption might be violated. First, the retinotopy signal may exist only at the fundamental frequency, but the radial bias orientation signal contains information at other frequencies. If this were the case, then the regression procedure would fail to completely remove the radial bias signal from the orientation data, and orientation decoding would be above the retinotopy baseline even if the signal were driven by radial bias alone. However, this error did not occur because no difference was observed between orientation classification and the retinotopy baseline. The second possibility is that the radial bias orientation signal exists only at the fundamental frequency, but that the retinotopy signal contains information at other frequencies. Because the retinotopy baseline is a measure of residual retinotopy information after removing the fundamental component, the baseline in this case would include retinotopy information that is not present in the radial bias orientation signal. Consequently, the baseline would be too high, potentially resulting in no difference between orientation decoding and the retinotopy baseline, even if the orientation signal contained more than radial bias.

To investigate whether the retinotopy signal contains more information than the orientation signal at frequencies other than the fundamental, Figure 1 shows the power spectrums of the BOLD responses to the rotating wedge (Fig. 1D) and the rotating grating (Fig. 1E). In addition to power at the fundamental frequency of the rotating wedge (labeled f₁), there is also substantial power at frequencies corresponding to the 2^nd, 3^rd and 4^th harmonics of this signal.

To better understand the source of these harmonics, the bottom row of Figure 1 shows the corresponding BOLD responses, obtained by phase-locking each voxel to it’s retinotopic phase preference and averaging over voxels for a participant. Clearly, the response to the retinotopic wedge stimulus (Fig. 1G) does not follow a cosine function (shown as the line), but rather has a sharper tuning bandwidth (see also Dumoulin and Wandell, 2008). Alternatively, the BOLD response to the oriented grating (Fig. 2H) is described quite well by a cosine function.

Overall, the orientation signal nearly follows a cosine function, whereas the retinotopy signal does not. As a result, removing retinotopy by regressing out a cosine leaves more residual retinotopy information in the retinotopy time course than in the orientation time course. Consequently, the original retinotopy baseline is not a good benchmark for comparison with orientation decoding – Performance is too high due to residual information that is not present in the orientation signal. To better equate the signals we can simply regress out these harmonic components in addition to removing the fundamental (see Methods). Figure 2B shows the results (Harmonics Removed condition). As can be seen, removing these additional components from the retinotopy signal lowers the retinotopy baseline, demonstrating that these harmonics carry information in the retinotopy time course that can be removed via projection. Critically, a comparison of this harmonics-removed retinotopy baseline to classification performance for the orientation-minus-radial-bias activity pattern reveals significantly higher orientation decoding performance for three of the four individual subjects (all p<.001) and a marginally significant effect in the fourth subject (p=.10). Combining these results across subjects using Fisher’s method also indicates a significant difference across the two conditions at the group level (p<.001).

This significantly higher orientation decoding implies that there is orientation information that cannot be accounted for by radial bias when the proper baseline is used for comparison. Although we view this harmonics-removed baseline as more appropriate than removing only the fundamental component, our goal in Experiment 2 was to take an empirical approach, rather than an analytical approach, to construct a more appropriate baseline.

Experiment 2: Smooth Retinotopy Wedge

In Experiment 1, we showed that BOLD responses to the rotating retinotopy wedge carry harmonic information that is not present in the orientation signal. The stronger harmonic responses evoked by the retinotopy wedge stimulus (Fig. 1A) may be due to the hard leading and trailing edges of the stimulus along the polar-angle dimension, such that the contrast modulation of the stimulus display follows a square-wave pattern (i.e., at a given time a particular part of space is either background/zero-contrast or full-contrast stimulus). In comparison, the oriented sine-wave grating has no such edge (Fig. 1B), but rather, transitions smoothly through the orientation domain as the grating rotates. If the sharp contrast edge in the retinotopy stimulus is indeed responsible for the higher-order harmonics observed in the retinotopy signal, then we should be able to mitigate these harmonic responses by modifying the stimulus itself.

In Experiment 2, we attempted to better equate the temporal profile of BOLD responses evoked by the retinotopy and orientation stimuli. To do so, we employed a smoothed retinotopy wedge (Fig. 1C), which varied smoothly in stimulus contrast from 0% to 100% along the polar-angle dimension, following a raised cosine function. If the fMRI orientation signal arises entirely from radial bias as claimed by Freeman et al., then the decoding of orientation with radial bias removed should be no better than retinotopy baseline performance, and this should hold true even if one uses an appropriately modified retinotopy wedge that minimizes higher-order harmonic responses. Here, we evaluated this prediction.

Figure 2C shows the results of orientation decoding with radial bias included, orientation decoding with radial bias removed, and the retinotopy baseline decoding from Experiment 2. Note that the retinotopy baseline was constructed as in the original Freeman et al. analysis, removing only the fundamental frequency. Consequently, this experiment and analysis is identical to the original Freeman et al. study and our replication, with the exception of the smoothed contrast-ramp used for the retinotopy stimulus. This simple change in the retinotopy stimulus was sufficient to produce a failure to replicate Freeman et al.’s results: Orientation decoding after removing radial bias was significantly higher than the retinotopy baseline for each of the three participants (p = .03, .004 and .012) and at the group level (p < .001).

Figure 1F shows the power spectrum of the BOLD response to the smoothed wedge and Figure 1I shows the average phase-locked response for 1 cycle. As can be seen, smoothing the edges of the retinotopy stimulus leads to a reduction in power of the harmonic components relative to those of the hard-edged wedge. Moreover, qualitatively the average response looks more similar to the average response to the orientation stimulus. This analysis supports the supposition that the smoothed-wedge retinotopy stimulus provides for a more appropriate retinotopy baseline for comparison with orientation decoding. Taken together, the results of Experiments 1 and 2 suggest that there must be more orientation information in patterns of V1 BOLD responses than the radial bias.

Experiment 3: Stimulus Rotation Speed

A pure radial bias account makes a strong prediction about how a voxel should respond to various orientations – It should respond maximally to the orientation corresponding to it’s preferred radial axis, and its response should fall off as the orientation deviates from this radial preference. Figure 3A shows an example orientation-tuning curve for such a unimodal response function. Alternatively, other sources of voxel orientation information, such as from uneven sampling of orientation columns, would be expected to lead to more complex orientation tuning curves such as that shown in Figure 3D.

We considered how the hypothetical orientation tuning curves in the left panels of Figure 3 would respond in the phase-encoded design used by Freeman et al. In this design, the grating stimulus rotates through the orientation space in a 24-second period. To simulate how the true tuning curves in the left panels of Figure 3 would respond in this design, we convolved the tuning curves with a canonical hemodynamic response function (HRF, a double gamma function, shown as dashed lines) for a single 24-second rotation. Figure 3B shows the resulting hemodynamic time course for the radial-bias-like signal, and Figure 3E shows the time course for the more complex tuning curve. Whereas convolving the simple, unimodal curve with the HRF does little to change the shape of the function (other than a shift in time), its effect on the more complex tuning curve is to filter out the more complex information. This selective loss of complex information is a necessary consequence of the fact that this experimental design, like all phase-encoded designs, confounds orientation and time. Because the HRF acts as a low-pass filter in the time domain, removing higher-frequency information, this filtering effect will also occur in the orientation domain in the phase-encoded design. Consequently, this experimental design could disproportionately filter out orientation signals that deviate from simple, unimodal responses like the radial bias.

The potential loss of information due to temporal filtering can be lessened experimentally by simply slowing down the rotation speed of the grating. By doing so, each rotation through the 180° orientation domain becomes slower relative to the HRF, such that only very sharp or abrupt changes in the orientation tuning curve will be dampened by the HRF. For example, Figures 3C and 3F show the same hypothetical tuning curves convolved with the same HRF as before, but now with a 72-second rotation speed. Although the more complex response is still affected more than the unimodal response, much of the original information is preserved.

In Experiment 3 we replicated Freeman et al. in stimulus and analysis, but used a slower 72-second rotation period for both the oriented grating and the retinotopy wedge. The results are shown in Figure 2D. Orientation decoding performance is now significantly higher than the retinotopy baseline for three of the four participants (p = .014, .002, .008 and .30), and at the group level (p<.001). Note that this experiment utilized the original hard-edged retinotopy wedge, and the original retinotopy baseline. Consequently, this failure to replicate the original Freeman et al. result is due solely to the slower rotation speed, such that lowering this speed is sufficient to observe positive evidence for orientation information that is not driven by the radial bias. Slowing the rotation speed certainly had other effects, such as lowering overall decoding performance (likely because the signal of interest now lies more within the low-frequency fMRI noise). However, the design of the original paradigm renders such baseline effects immaterial, as they are effectively accounted for by the retinotopy baseline procedure.

Experiment 4: Estimating Orientation Tuning Curves

Whereas a pure radial bias account predicts a simple unimodal orientation-tuning curve for each voxel, evidence of more complex orientation tuning profiles would reject such an account. One approach to evaluate tuning complexity is to simply measure the tuning curves of individual voxels and to assess their complexity. The phase-encoding designs used in the previous experiments are ill suited for measuring how a voxel responds to different orientations, as the observed BOLD signal results from the convolution of the underlying orientation tuning curve and a hemodynamic response function. Without precise knowledge of this HRF for each voxel, however, the original response function remains elusive. Moreover, the use of a fast temporal-encoding paradigm could lead to a loss of information regarding the precise shape of the orientation-tuning profile across fine-scale variations in orientation space, even if the true HRF were known (cf. Fig. 3).

In Experiment 4, we avoid this problem by presenting oriented gratings in a blocked design. On each 16-second block a grating with random orientation was shown, and the average BOLD response of a voxel to each of these stimuli provides data for characterizing its orientation-tuning curve. Figure 4 shows examples of how individual voxels responded to the oriented gratings, with every data point indicating the response amplitude of that voxel to a single 16-s block of a particular orientation. The top row shows voxels that appear to have a simple, unimodal response profile. The next two rows, however, show voxels with preferences that appear to violate the simple unimodal response profile predicted by radial bias alone. The responses of individual voxels to single presentations of oriented gratings are noisy, but nonetheless appear to exhibit reliable tuning profiles that may be more complex than a simple unimodal curve.

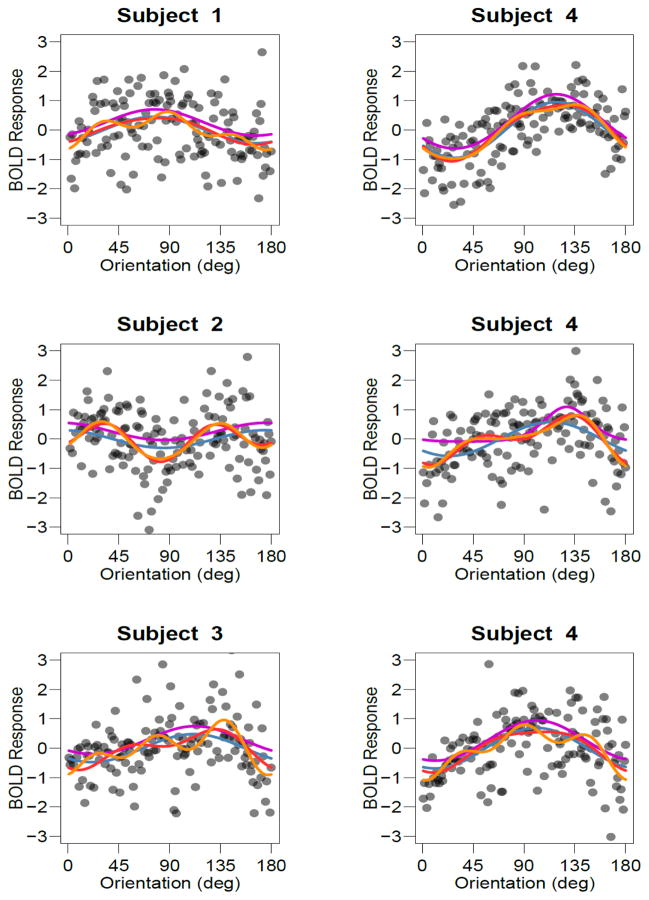
Figure 4.

Examples of tuning curves for individual voxels. Each point depicts the BOLD response of an individual voxel to an individual block in Experiment 4. Lines denote the best-fitting single-cosine (blue), two-cosine (red), three-cosine (orange) and von Mises (magenta) models overlaid as lines. The von Mises curves have been shifted up slightly so that they are not obscured by other curves. Top, middle and bottom rows depict voxels that were fit best by the single, double and triple-cosine complexity, respectively, where fit was assessed using AIC.

By fitting various models to the voxel responses and assessing how well each model accounts for the data, we can determine how to best characterize each voxel’s orientation tuning profile. In order to quantify the complexity of tuning for voxels in V1 for each participant, we fitted a series of models to each voxel’s response. These models varied in complexity from having no orientation tuning to models that allowed for fairly complex tuning profiles (see Methods). These models included no orientation tuning (M₀), tuning that followed a unimodal cosine function (M₁) or a unimodal Von Mises function (VM) allowing for variable tuning widths, and tuning that allowed for bi-modality (M₂) and for tri-modality (M₃). Whereas the simple cosine and von Mises tuning curves are concordant with the hypothesis that orientation information arises from a coarse-scale orientation signal such as radial bias, the more complex tuning curves cannot be readily explained by such an account.

To determine which model provides the best account of the orientation-tuning curves for a voxel’s responses to the gratings, it is necessary to consider both how well each model accounts for the data and how flexible each model is. Our goal was to provide a thorough comparison of the models, so we adopted three different approaches to assess model fit while taking model complexity into account (see Methods).

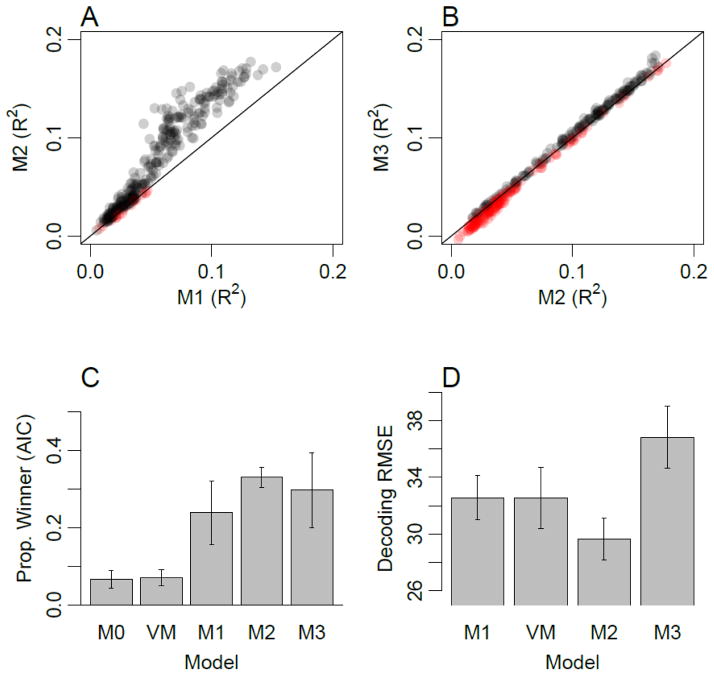
First, we used the AIC model comparison statistic to determine, for each voxel, which of these models provided the best account of the observed orientation responses. Figure 4 shows examples of voxels that were best characterized by M₁ (top), M₂ (middle) and M₃ (bottom). Figure 5C shows the proportion of voxels in V1 for which each model provided the best fit. The simple models that predicted unimodal response profiles (M₁ and VM) comprised about one third of the voxels in V1. With the exception of a small proportion of voxels that showed no orientation tuning (M₀), the remaining two thirds of voxels were best accounted for by a more complex model, such as the two-component and three-component cosine models shown in middle and bottom rows of Figure 4. These results imply that a majority of V1 voxels exhibit orientation tuning profiles that are more complex than simple unimodal functions.

Figure 5.

Experiment 4 modeling results. A) Cross-validation performance (R²) for model M₂ plotted as a function of performance for model M₁ for each V1 voxel. Colors indicate whether models M₁ (red) or M₂ (gray) exhibited higher cross-validation performance. Color intensity indicates density of overlapping points. B) Cross-validation performance for model M₃ plotted as a function of model M₂. Colors indicate whether models M₂ (red) or M₃ (gray) exhibited higher cross-validation performance. C) Proportion of voxels in V1 for which each of the models provided the best fit, as measured with AIC (error bars denote standard errors across participants). D) Leave-one-run-out decoding accuracy (RMSE), using each model as a forward-encoding model. Note that model M₀ cannot be used for decoding as it predicts no orientation tuning, and is therefore omitted.

In addition to conducting model comparison using AIC, we performed a straightforward cross-validation procedure to determine how well each model was able to capture the stable response patterns of individual voxels. Cross validation was performed by estimating the parameters of each model using all but one run, and measuring the goodness of fit (proportion variance explained, denoted by R²) between the model and the data for the left-out test run. With this cross-validation approach, overly complex models should lead to over-fitting of the data and lower R² values, on average, than simpler models with the appropriate number of parameters.

Figure 5A shows a scatterplot comparing goodness of fit values for the single-cosine model (abscissa) and the double-cosine model (ordinate). Data points indicate the cross-validated performance of every individual voxel; given that we were fitting the response amplitude of individual voxels to single-block presentations of orientation, relatively low R² values were to be expected. Nevertheless, highly consistent effects emerge from this analysis. First, all data points lie above zero for the single-cosine model, indicating that these voxels within the V1 ROI exhibit some orientation information. Second, the majority of data points (95%) lie above the line of unity, indicating that for these voxels the double-cosine model provides a better characterization of the orientation tuning functions than the single-cosine model. Our cross-validation procedure ensures that this advantage of the more complex double-cosine model is robust and captures replicable patterns in the data.

In Figure 5B, the scatterplot compares the performance of the two-cosine model (abscissa) and the three-cosine model (ordinate). The cross-validation results suggest that about half (51%) of the voxels in V1 are accounted for better with the three-component than with the two-component model. An interesting trend is prevalent for both the one vs. two and two vs. three component comparisons: voxels with lower overall cross-validation performance were better explained by the simpler model. In contrast, voxels with higher overall performance performed better in cross validation with the more complex model. These results imply that the ability to detect these more subtle components, or variations in orientation preference, depends upon the quality of fMRI data that one can obtain for responses to individual orientations.

Finally, we used each model in a forward-encoding approach (Brouwer and Heeger, 2009; Kay et al., 2008) to assess how well the models accounted for the multivariate response patterns in V1. For a given model (e.g., M₁), the model was fitted to each voxel on a subset of the data, and these fitted models were used to predict the viewed orientations given voxel activity patterns from the left-out data. Figure 5D shows average decoding errors for each model. Overall, the best-performing model is M₂, and the decoding error for M₂ is significantly lower than for the simpler unimodal models M₁ (t(3) = 3.56, p<.05) and VM (t(3) = 5.34, p<.05). This result is in line with the individual voxel analyses, suggesting that a simple unimodal model of voxel responses is not sufficiently complex to accurately capture all of the information in the data patterns. It should be noted that for this multivariate analysis, all voxels were forced to adopt the same model type. For this reason, the M₃ model may have performed more poorly as some proportion of voxels would been better described by a simpler model (M₁ or M₂), counteracting the potential benefits of applying the M₃ model to the subset of voxels with more complex tuning properties.

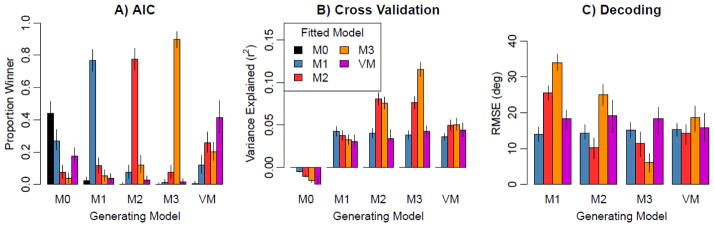
The above analyses take model complexity into account, which is important to ensure that the conclusions are not biased toward overly simple or overly complex tuning curves. In addition, we conducted simulations to ensure that this goal was met, by assessing how well each approach could identify the true model that was used to generate a simulated dataset. First, each model was used as a data-generating model: orientation responses were generated from these models with randomly chosen tuning parameters (e.g., randomized cosine phase preference), and a level of additive Gaussian noise (adjusted to match the fMRI data) was added to the simulated responses. For each simulated data set, each of the models was fitted and compared using the AIC approach (Fig. 6A), the individual voxel cross-validation procedure (Fig. 6B), and model comparison using the forward-encoding approach (Fig. 6C). Our simulations revealed that each of these approaches could successfully differentiate the data-generating model to some extent, but with varying degrees of success. As expected, AIC provided the most accurate approach. AIC is specifically designed to identify the correct model, whereas cross-validation approaches are more general tools that aim to identify the model that produces the best cross-validation performance. Nevertheless, each approach has merits, and all three approaches converge on a common set of results: A large proportion of voxels in V1 have more complex orientation tuning curves than can be explained by a unimodal preference for radial orientations.

Figure 6.

Results of simulation to evaluate the efficacy of identifying which model produced the simulated data, for model selection using AIC (A), cross-validation measuring proportion of variance explained (B), and cross-validated measures of orientation-decoding error (C).

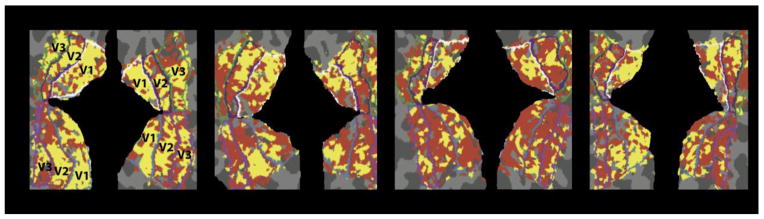
The analyses reported above focused on voxels in V1 that corresponded strongly to the retinotopic region of space occupied by the stimulus. As an addition to this ROI-based approach, Figure 7 shows the distribution of voxels throughout the early visual cortex that are best fit by simple and complex models, where the preferred model for each voxel was chosen using AIC. The models in this figure have been collapsed across voxels indicating a unimodal preference (M₁ or VM, red), and voxels with more complex tuning profiles (M₂ or M₃, yellow). Importantly, voxels with more complex tuning curves appear to be distributed throughout V1, and are also present in extrastriate visual areas V2 and V3.

Figure 7.

Winning model for each voxel as measured with AIC, projected onto the flattened surface representation of early visual cortex for each of the four participants. The models have been collapsed into groups that reflect a gross orientation preference like the radial bias (red; M₁ or VM) and those that have a more complex orientation-tuning curve (yellow; M₂ or M₃).

Discussion

Our goal was to elucidate why previous studies have led to conflicting reports regarding whether or not radial bias is necessary for orientation decoding. Across experiments, we successfully replicated the well documented finding that one source of orientation information in the fMRI signal arises from a radial bias (Ling et al., 2015; Mannion et al., 2010; Sasaki et al., 2006). We were also able to replicate the pattern of results initially reported by Freeman et al. (2011), finding that no orientation information appeared to remain in the residual fMRI signal after applying their analytic procedure to remove radial bias. However, we found that Freeman et al.’s procedure led to inflated estimates of chance-level performance in the retinotopic mapping experiment, because of residual information present in the higher-order harmonics of the fMRI time series. When this harmonic information was properly removed, either mathematically (Exp. 1) or experimentally by smoothing the contrast profile of the retinotopy wedge (Exp. 2), we found that significant orientation information remained present in V1 following the removal of radial bias. In addition, we demonstrated that the rapid nature of the temporal phase-encoding design used by Freeman et al. dampened the ability to detect orientation signals that are independent of coarse-scale radial bias. We mitigated these temporal filtering artifacts in Experiment 3 by slowing the rotation period of the mapping stimuli, which again led to a failure to replicate. Finally in Experiment 4, we used a standard block design that avoided these potential limitations, and found that many voxels exhibit orientation preferences that are too complex to be explained by a radial bias alone. Taken together, these results provide compelling evidence to refute the claim that radial bias is necessary for orientation decoding.

Our study demonstrates the persistence of orientation information in fMRI signals from V1, independent of radial bias. Such orientation information could arise from both local variability in orientation preference at a fine spatial scale (Alink et al., 2013; Kamitani and Tong, 2005; Swisher et al., 2010; Yacoub et al., 2008) and from other types of coarse-scale bias (Freeman et al., 2013; Furmanski and Engel, 2000; Sun et al., 2013). Regarding other potential sources of coarse-scale bias, a recent study reported a biased preference for vertical orientations prevalent near the foveal representation of V1 (Freeman et al., 2013). Although such a bias may have contributed to our decoding results to some extent, our results in Experiment 4 indicate that such coarse biases are not the only sources. We found that voxels with more than one peak orientation preference are distributed throughout the visual cortex (Fig. 7), ruling out explanations such as a combination of radial bias and vertical bias around the foveal representation. Another coarse-scale bias has recently been suggested to arise from artifacts at the borders of an oriented grating, based on an analysis of simulated V1 responses to orientation stimuli (Carlson, 2014). Although these simulation results suggest the possibility of such a bias contributing to orientation decoding, we find that significant orientation information is present throughout each visual area, rather than being isolated to either the foveal or the peripheral edges of the stimulus. Thus, these potential sources of coarse-scale bias do not provide an adequate account of the complexity of voxel orientation-tuning functions we observe throughout the visual cortex.

Since the initial finding that orientation signals can be decoded from the human visual cortex (Kamitani and Tong, 2005), there has been considerable interest in isolating the sources of this information. Recent proliferation of research in this area has uncovered the potential presence of multiple sources of information, though the extent to which each of these sources contributes to orientation decoding remains to be fully determined. The presence of orientation columns in non-human primates has been well-documented (Blasdel, 1992; Hubel and Wiesel, 1974; Hubel et al., 1978), and it has been show that high-resolution fMRI is capability of isolating these columns in animals and humans (Moon et al., 2007; Yacoub et al., 2008). Consequently, we expect that a portion of the orientation-selective fMRI signal should reflect the relationship between the physiological BOLD responses measured at coarse scales and the weighted sum of preferred orientations at finer columnar scales.

Phase-encoded designs are the standard paradigm for traditional retinotopic mapping, and they provide a powerful method for identifying the peak tuning preference of individual voxels (Engel, 2012). However, our results highlight important caveats to consider when using phase-encoded designs for the more ambitious goal of characterizing the tuning properties of voxels beyond their peak preferences. We show that by virtue of confounding the stimulus variable (e.g., orientation) with time, phase-encoded designs are sensitive to 1) Temporal artifacts that may arise from either the nature of the stimulus or the shape of the HRF, and 2) Filtering effects that result from the low-pass characteristics of the HRF. The latter problem is especially troublesome when the goal of a study is to characterize the complexity of a voxel’s response to different stimulus values, as the HRF will act to selectively remove the complex signals while retaining the simple ones. Here, for example, the effect of this filtering can be to smooth orientation-tuning curves, effectively removing signals such as might result from more fine-scale sources, such as orientation columns, while retaining gross information like the radial bias. The use of a slower temporal paradigm can help alleviate the effects of low-pass filtering, but with the associated cost of obtaining fewer cycles of data that is more contaminated by physiological noise.

Temporal-encoding paradigms have also grown in popularity in recent studies that use population receptive field (PRF) mapping to characterize the retinotopic preferences of individual voxels (e.g., Dumoulin and Wandell, 2008; Lee et al., 2013; Thirion et al., 2006; Zuiderbaan et al., 2012). Presumably, retinotopic receptive fields are simpler than orientation tuning curves at the voxel level. Nevertheless, it is possible that the use of rapid temporal-encoded designs could potentially mask or blur some fine-scale aspects of PRF model estimates. As the quantitative methods for mapping such receptive fields are developed to allow for more complexity in their shape (e.g., Greene et al., 2014; Lee et al., 2013), the way in which the experimental design acts to limit the data should also be considered.

In conclusion, our results suggest that there exist multiple sources of orientation information in the BOLD signal, even at standard fMRI resolutions. Characterizing these various sources of information is important, and may provide future insights into human orientation processing. In many fMRI studies, however, the goal is simply to measure and quantify the amount of orientation information present in the BOLD signal, regardless of its sources. Examples include studies of how attention modulates visual information processing (Jehee et al., 2011; Scolari et al., 2012), how perceptual learning affects stimulus representations (Jehee et al., 2012; Shibata et al., 2011), how working memory relies on early sensory systems (Ester et al., 2009; Harrison and Tong, 2009; Pratte and Tong, 2014; Serences et al., 2009), and those that examine the neural correlates of binocular rivalry and visual awareness (Haynes and Rees, 2005). In these and many other studies, multivariate pattern analysis techniques provide a powerful framework for quantifying the presence of information, by pooling all of the information available in the BOLD activity patterns across a broad range of spatial scales.

Highlights.

• Fast phase-encoding designs can distort fMRI measures of voxel tuning properties

• Such designs led to recent claims that fMRI orientation signals depend on radial bias

• With corrected designs, we find reliable orientation responses not due to radial bias