Abstract
Diffusion tensor imaging (DTI) is the most widely used method for characterizing non-invasively structural and architectural features of brain tissues. However, the assumption of a Gaussian spin displacement distribution intrinsic to DTI weakens its ability to describe intricate tissue microanatomy. Consequently, the biological interpretation of microstructural parameters, such as fractional anisotropy or mean diffusivity is often equivocal. We evaluate the clinical feasibility of assessing brain tissue microstructure with mean apparent propagator (MAP) MRI, a powerful analytical framework that efficiently measures the probability density function (PDF) of spin displacements and quantifies useful metrics of this PDF indicative of diffusion in complex microstructure (e.g., restrictions, multiple compartments). Rotation invariant and scalar parameters computed from the MAP show consistent variation across neuroanatomical brain regions and increased ability to differentiate tissues with distinct structural and architectural features compared with DTI-derived parameters. The return-to-origin probability (RTOP) appears to reflect cellularity and restrictions better than MD, while the Non-Gaussianity (NG) measures diffusion heterogeneity by comprehensively quantifying the deviation between the spin displacement PDF and its Gaussian approximation. Both RTOP and NG can be decomposed in the local anatomical frame for reference determined by the orientation of the diffusion tensor and reveal additional information complementary to DTI. The Propagator Anisotropy (PA) shows high tissue contrast even in deep brain nuclei and cortical gray matter and is more uniform in white matter than the FA, which drops significantly in regions containing crossing fibers. Orientational profiles of the propagator computed analytically from the MAP MRI series coefficients allow separation of different fiber populations in regions of crossing white matter pathways, which in turn improves our ability to perform whole brain fiber tractography. Reconstructions from subsampled data sets suggest that MAP MRI parameters can be computed from a relatively small number of DWIs acquired with high b-value and good signal-tonoise ratio in clinically achievable scan durations of less than 10 minutes. The neuroanatomical consistency across healthy subjects and reproducibility in test-retest experiments of MAP MRI microstructural parameters further substantiate the robustness and clinical feasibility of this technique. The MAP MRI metrics could potentially provide more sensitive clinical biomarkers with increased pathophysiological specificity compared to microstructural measures derived using conventional diffusion MRI techniques.
Keywords: Mean apparent propagator (MAP), diffusion propagator, tissue microstructure, non-Gaussianity, anisotropy, diffusion tensor imaging (DTI)
Graphical abstract
Introduction
Diffusion MRI is uniquely suited to characterize structural and architectural features of biological tissue in vivo due to its ability to quantify molecular displacements of water molecules noninvasively. Over the past decade diffusion tensor imaging (DTI) (Basser et al., 1994) has become the preferred method for analyzing diffusion weighted MR images (DWIs) in anisotropic tissues like white matter (WM). The scalar microstructural maps obtained from DTI, such as the mean diffusivity (MD) (Basser et al., 1994) and the fractional anisotropy (FA) (Basser and Pierpaoli, 1996) have become invaluable tools for studying normal brain (Pierpaoli et al., 1996), brain development and aging, and pathological conditions such as stroke, cancer, brain injury, and neurodegenerative diseases (Sundgren et al., 2004). However, the assumption of a Gaussian spin displacement distribution underlying DTI often renders the pathophysiological interpretation of changes in these parameters problematic. There is a growing clinical need for a comprehensive assessment of brain tissue changes using diffusion MRI based on intrinsic microanatomical parameters that have higher sensitivity and specificity than DTI-derived parameters.
A general description of water diffusion in complex neural structures is provided by the probability density function (PDF) of spin displacements, also known as the ensemble average propagator or the diffusion propagator, derived from the analysis of multiple DWIs. A reliable methodology for measuring the spin displacement PDF may better identify signatures of non-Gaussian, multi-compartmental, restricted and hindered diffusion in regions of complex WM, and potentially in gray matter (GM), potentially yielding novel and biologically more specific markers than FA and MD (Wu and Alexander, 2007, Liu et al., 2010, Wu and Cheung, 2010). Several techniques have been proposed to measure the PDF of spin displacements (Liu et al., 2003, Wedeen et al., 2005, Wu and Alexander, 2007, Assemlal et al., 2009, Descoteaux et al., 2011), some of which have been applied to in vivo brain imaging. However, most of these methods require long scan durations to accommodate the acquisition of numerous DWIs and, compared with DTI, often lack the necessary robustness and expediency for widespread clinical adoption. A general analysis framework that reliably extracts salient features of the spin displacement PDF as new microstructural biomarkers could improve the clinical potential of diffusion MRI.
Mean apparent propagator (MAP) MRI (Özarslan et al., 2013) was recently proposed as a quantitative physical and mathematical framework to measure the PDF of spin displacements in complex tissue microstructures. MAP MRI expands the diffusion MR signal analytically in the local DTI reference frame using a complete set of orthogonal basis functions closely related to the eigenfunctions of the Fourier transform. Because of the dual nature of these basis functions, both the measured signal in q-space (Callaghan, 1991) and the propagator in the reciprocal displacement r-space are represented with the same series coefficients resulting in increased robustness to noise and immunity from signal confounds. Moreover, relevant microstructural features can be reliably quantified with scalar descriptors of the propagator, e.g., zero-displacement probabilities, non-Gaussianity, and propagator anisotropy, which can be measured along the axes and planes of the anatomical reference frame defined by the orientation of the diffusion tensor. Finally, the MAP MRI framework conveniently allows direct comparisons between and among different propagators, potentially providing a unique opportunity for use in single subject, longitudinal, and multi-site -clinical investigations of microanatomical tissue changes.
In this study we quantify MAP microstructural parameters in brain tissues in vivo and evaluate their robustness, consistency, and reproducibility (test-retest variability) to establish MAP MRI as a clinically feasible and viable method for investigating brain structural anatomy.
Theory
MAP MRI represents both the measured diffusion MR signal attenuation E(q) in 3D q-space, q = (2π)−1γδG and its Fourier Transform, mean apparent propagator , in the local anatomical frame of reference defined by the diagonalized displacement covariance matrix (i.e., the diffusion tensor D).
| (1) |
where RT is a proper rotation matrix that diagonalizes the diffusion tensor, and ux, uy, uz are scaling parameters in the local frame of reference determined by the diffusion time td and the eigenvalues λk of: (Özarslan et al., 2013). Using a complete basis set of orthogonal Hermite-Gaussian functions separable in three spatial dimensions, the diffusion signal attenuation and the corresponding propagator can be expanded as:
| (2) |
where we are using compact column vector notations: a(A), Φ(A, q), and ψ (A, r) to represent the series coefficients an1n2n3, and corresponding 3D MAP MRI basis functions ϕn1 (ux, qx)ϕn2 (uy, qy)ϕn3 (uz, qz) in q-space and ψn1 (ux, x)ψn2 (uy, y)ψn3 (uz, z) in displacement r-space respectively, defined by indices n1, n2, n3 with n1 + n2 + n3 = N representing the total order in the expansion (truncated at Nmax),
| (3) |
and Hn (x) is the nth-order Hermite polynomial. The number of coefficients is (Nmax + 2)(Nmax + 4)(2Nmax + 3)/24 when the diffusion MR signal and propagator are assumed to be real and symmetric, assumptions generally applicable to clinical diffusion MRI experiments.
The analytical series expansions in q-space and r-space have the same coefficients an1n2n3, thereby providing robustness to the solution and a convenient way to enforce physical constraints, (e.g. symmetry, non-negativity and normalization of the propagator) when fitting the data (Özarslan et al., 2013). The expansion is dependent on the initial estimation of A, which is equivalent to estimating the diffusion tensor, but the infinite series expansion converges to the mean apparent propagator regardless of the choice of A. The first term in the expansion gives the Gaussian component of the propagator, while all higher-order terms successively approximate its non-Gaussian part using orthogonal basis functions. Once the matrix A is estimated, the coefficients a are obtained by solving the following quadratic minimization problem:
| (4) |
where y is a column vector containing the diffusion MR signals, S(q), while the rows of the encoding matrix, Q are the basis functions, ΦT(A, q) evaluated at the corresponding q-values, and the rows of the constraint matrix P are the basis functions ψT(A, r) evaluated, for example, on a uniform 35×35×17 Cartesian grid in the positive z half-space with .
The expansion in the MAP MRI functional basis enables the analytical computation of useful descriptors of the propagator which have been compiled in Table 1. For example, one type of zero-displacement probability (ZDP) called the return-to-origin probability (RTOP) has been suggested as an indicator for restricted diffusion (Assaf et al., 2000, Wu and Alexander, 2007, Özarslan et al., 2013) and can be easily computed from a weighted sum of the MAP MRI series coefficients. Similarly, the Non-Gaussianity (NG) index measures the deviation from Gaussian diffusion (i.e., the difference between the propagator P(r) and its Gaussian approximation PG(r)) as the relative power content of non-Gaussian terms in the MAP expansion.
Table 1.
MAP MRI parameters can be obtained directly from the MAP MRI series coefficients: RTOP – return-to-origin probability, RTAP – return-to-axis probability, RTPP – return-to-plane probability, NG – non-Gaussianity, NG⊥ – radial non-Gaussianity, NG‖ – axial non-Gaussianity, PA – propagator anisotropy, PADTI – anisotropy of the Gaussian propagator (DTI model), ΔθPO – difference between anisotropy measures of the full and Gaussian propagators.
| RTOP |
|
|
||
| RTAP |
|
|
||
| RTPP |
|
|
||
| NG |
|
|
||
| NG⊥ |
|
a⊥
= P⊥a |
||
| NG‖ |
|
a‖
= P‖a |
||
| PA | σ(sinθPA, 1.4) |
|
||
| PADTI | σ(sinθDTI, 0.4) |
|
||
| ΔθPO | θPA − θDTI |
Because the MAP basis functions are separable along three spatial dimensions, these propagator metrics can be decomposed along the axes and planes of the local anatomical reference frame A (Özarslan et al., 2013) using the formulas in Table 1. For example, the return-to-axis and return-to-plane probabilities (RTAP and RTPP, respectively) reflect the presence of restrictive barriers in the radial and axial orientation, while the parallel and perpendicular non-Gaussianity indices (NG⊥ and NG‖, respectively) are indicative of heterogeneous diffusion in the radial and axial direction. Similar to the radial and axial diffusivities derived from DTI, these scalar parameters encode directional information well-suited for characterizing complex diffusion in anisotropic tissues and could potentially provide discriminating WM biomarkers for axonal loss or demyelination.
With MAP MRI we can conveniently compare features of the propagators by disregarding their relative orientations (Özarslan et al., 2013). For two propagators P(r) and Q(r) described by coefficients a and b, and scaling matrices
| (5) |
respectively, we can define an angular measure of covariance, θPQ by analogy with the vector dot product
| (6) |
where the matrix Tζ is given in Appendix A. Using this angular measure of similarity we can extract useful microstructural features of the propagators, such as anisotropy. The propagator anisotropy (PA) is defined using the angular dissimilarity measure , where θPA quantifies the angular difference (Eq. 6) between the propagator and its isotropic counterpart represented using a set of isotropic basis function (Özarslan et al., 2009a) as described in detail in Appendix A. To allow comparison with DTI results, a similar angular measure θDTI (Özarslan et al., 2013) is defined for the Gaussian propagator (see Appendix A). Finally, the angular anisotropy metrics θPA and θDTI can be scaled to the dynamic range of the FA with a nonlinear function that emphasizes intensity variations in the desired range to obtain the propagator anisotropy measures PA and PADTI (Table 1).
To measure the orientational characteristics of the diffusion propagator we compute its radial moments analytically from the MAP MRI coefficients and visualize the resulting orientation distribution functions (ODF) using 3D glyphs (see Appendix B).
Methods
Four healthy volunteers were scanned on a conventional 3T scanner with a 32-channel radio frequency (RF) coil and a single-shot spin-echo diffusion-weighted EPI pulse sequence. All subjects participating in this study provided informed written consent in accordance with a clinical protocol approved by the Institutional Review Board within the National Institutes of Neurological Disorders and Stroke (NINDS). The volunteers were instructed to minimize head motion during the entire duration of the MRI exams. The imaging parameters were optimized to obtain, in a single average, in vivo DWIs with minimal image distortions and sufficient signal-to-noise ratio (SNR) at large diffusion weighting for accurate registration and post-processing. To this end, we acquired DWIs with 3mm isotropic resolution, field-of-view (FOV) 21×21 cm2, a 70×70 imaging matrix size, 42 slices for full-brain coverage, and parallel imaging acquisition (SENSE) with an acceleration factor of 2. The short echo spacing of 528 μs resulted in reduced image distortions due to magnetic field inhomogeneities, including gradient eddy currents, while the relatively low spatial resolution provided sufficient sensitivity for reliable distortion and motion correction with adequate tissue support even in DWIs with large diffusion weightings. Diffusion gradients with a maximum amplitude of 5 G/cm, a pulse width of δ = 34.5 ms and a separation of Δ = 40.5 ms were applied to acquire a large diffusion data set of 698 DWIs (including 14 non-diffusion weighted b = 0 s/mm2 baseline images) with maximum diffusion weighting bmax = 6,000 s/mm2 (qmax = 80 mm−1). The DWIs were sampled in 6 shells with b=1000, 2000, 3000, 4000, 5000 and 6000 s/mm2, along 23, 43, 83, 131, 148 and 256 directions respectively. In each shell the diffusion encoding directions were uniformly distributed on the unit sphere (Jones et al., 1999). Across shells, the directions were not collinear and were not optimized to be uniformly interleaved on the unit sphere. Images were obtained with full k-space coverage to prevent signal loss from subject motion and cardiac pulsation resulting in a minimum TE/TR = 94/5,800 ms. The non-diffusion weighted images were acquired throughout the scan to perform SNR computations and verify subject motion and measurement stability. The total scan time was 72 minutes. In addition, for each subject, we also acquired high resolution 1mm3 T2-weighted Fast-Spin-Echo and T1-weighted MP-RAGE scans to serve as anatomical templates for motion and distortion correction and tissue segmentation, respectively.
All DWIs (and the corresponding gradient orientations) were processed to correct for subject motion and EPI distortions due to magnetic field inhomogeneities (including gradient eddy currents), and registered to the high-resolution T2W anatomical scan using the Tortoise software package (Pierpaoli et al., 2010). After correction, the WM SNR was computed as the voxel-wise mean divided by the standard deviation of the signal in multiple non-diffusion weighted (baseline) images acquired during the experiments. This method was preferred over the standard region-of-interest (ROI) based SNR calculation because it quantifies contributions from multiple sources of error and artifacts that can accumulate during long in vivo experiments such as: subject motion, changes in tissue partial volume, physiological pulsations, hardware instabilities, etc. A diffusion tensor model was fit to the subset of 66 DWIs with b-values of up to 2,000 s/mm2, and maps of FA and MD were computed from the tensor components.
This initial DTI fit also represented the first step in the MAP MRI analysis determining, for each voxel, the scaling matrix A and the transformation (rotation R) from the laboratory to the anatomical reference frame (Eq. 1). On a voxel-by-voxel basis the scaling parameters (matrix A in Eq. 1) were then used to determine the MAP MRI coefficients in the anatomical DTI reference frame from the full DWI data set by solving the quadratic minimization problem in Eq. 4 with symmetry, normalization, and non-negativity constraints (enforced numerically using a grid 35×35×17 Cartesian grid in the positive z half-space with ) to ensure a physically plausible analytical solution of the propagator. To observe the convergence properties of the MAP series approximation and test its ability to resolve fine microstructural details, the calculation was repeated using different truncations for the MAP MRI series expansions Nmax = 4, 6, 8, and 10, yielding 22, 50, 95 and 161 unknown coefficients, respectively. Data were processed on the BIOWULF/HELIX computer cluster at the National Institutes of Health using in-house MATLAB (Mathworks Inc., Natick, MA, USA) and IDL (Exelis, Boulder, CO, USA) routines. Orientational profiles of the propagators were visualized with orientation distribution functions (ODF) computed analytically from MAP MRI series coefficients as the 2nd radial moment of the propagator. To illustrate the basic ability of using the MAP-derived ODFs to resolve crossing white matter fiber pathways we performed whole brain fiber tractography with DSI Studio and TrackVis (Wang et al., 2007).
From the MAP MRI series coefficients we computed scalar descriptors of the propagators (RTOP, NG and PA) and quantified them in anatomically defined regions-of-interest (ROIs). Zero-displacement probability and non-Gaussianity metrics were computed along and across the axes of the local reference frame determined by the diffusion tensor: RTAP, RTPP, axial (NG⊥) and planar (NG‖) non-Gaussianities, respectively. The high resolution T1W MP-RAGE data was processed with FreeSurfer’s automatic segmentation tool and used as a template to define anatomical ROIs in the cerebral GM, cerebral WM, corpus callosum (CC), basal ganglia (BG) and thalamus (TH). To minimize partial volume contamination in WM structures, the WM and CC ROIs were masked with an FA threshold of 0.3 and 0.7, respectively for each subject. ROI-averaged values of MAP MRI parameters were compared with corresponding values obtained from DTI-derived metrics such as FA and MD. All DTI and MAP MRI microstructural parameters were computed in the native subject coordinates and subsequently transformed to FreeSurfer coordinates for ROI analysis.
We evaluated the robustness of estimating MAP MRI parameters in the presence of different SNR using numerical Monte-Carlo experiments. MR diffusion weighted signals were generated for propagators defined by MAP MRI series expansions truncated at order Nmax = 10 (corresponding to 161 series coefficients) obtained from representative WM regions with diverse microstructure. These MAP MRI series coefficients describing a physical diffusion MAP function were used to numerically generate noiseless signals corresponding to the diffusion encoding scheme (i.e., diffusion gradient table) applied in this study. Rician noise of different amplitudes was added to the diffusion signals to simulate realistic experiments with different SNR levels. For each SNR level we generated 400 experimental instances, computed the MAP MRI series coefficients and microstructural parameters, and quantified the robustness of the measurement with relevant statistics (mean, standard deviation).
To investigate the clinical feasibility of the technique we subsampled the original diffusion MRI data set maintaining only 98 DWIs (including 3 baseline images) corresponding to clinical scan duration of less than 10 minutes. Specifically, the subsampled data sets contained diffusion measurements along 4, 7, 11, 17, 23, and 31 orientations in each shell with b=1000, 2000, 3000, 4000, 5000, and 6000 s/mm2, respectively. Within each shell, the subsampled set of diffusion measurements was selected so as to maximize the minimum angular difference between any two diffusion orientations, thereby maintaining a relatively uniform distribution on the unit sphere (Cheng et al., 2014). For each subject, the MAP MRI parameters and ODFs computed from the subsampled data sets using the same Nmax = 6 were compared to those obtained from the complete DWI data sets. Differences between MAP MRI scalar parameters were quantified using absolute error; while differences between the propagators were quantified more generally using the angular dissimilarity measure (Eq. 6). The consistency of MAP MRI metrics was determined by comparing ROI averaged MAP MRI parameter values across the four healthy volunteers, while reproducibility was evaluated with test-retest experiments in three healthy volunteers, each scanned in two separate exam sessions at least one week apart.
Results
No significant large subject motion was observed in any of the data sets over the course of the experiments. We carefully analyzed the image distortion due to gradient eddy currents in DWIs acquired with bmax = 6,000 s/mm2, and found no significant differences between DWIs acquired with the commonly used twice refocused spin echo (TRSE) and the conventional Stejskal-Tanner spin echo diffusion preparation employed in this study after motion and distortion correction were performed using Tortoise (Pierpaoli et al., 2010). The low spatial resolution allowed for the use of short echo spacing in the EPI readout, which along with parallel imaging, minimized distortions caused by magnetic field inhomogeneities, including gradient eddy currents. The conventional spin echo was also preferred over the TRSE sequence because of the shorter minimum echo time (TE) at large b-values TE = 94 ms, compared with TE = 111 ms for TRSE, resulting in improved tissue sensitivity.
The WM SNR was quantified as the mean over the standard deviation computed from several baseline images acquired throughout the experiment after post-processing and therefore included contributions from subject motion, physiological pulsations, image registration/post-processing, and scanner hardware instabilities. DWIs acquired at 3mm isotropic resolution had excellent baseline SNR even in white matter (above 80) and sufficient brain tissue signal in images with bmax = 6,000 s/mm2 to support reliable distortion correction and image registration. The corrected DWIs consistently showed good SNR and spatial accuracy when compared to the anatomical T2W images, suggesting that DWIs with sufficiently large diffusion weighting can be acquired for clinical MAP MRI. Regions of low SNR, such as the ventricles and tissue boundaries with significant partial volume contributions from cerebrospinal fluid (CSF) were excluded from the ROI analysis.
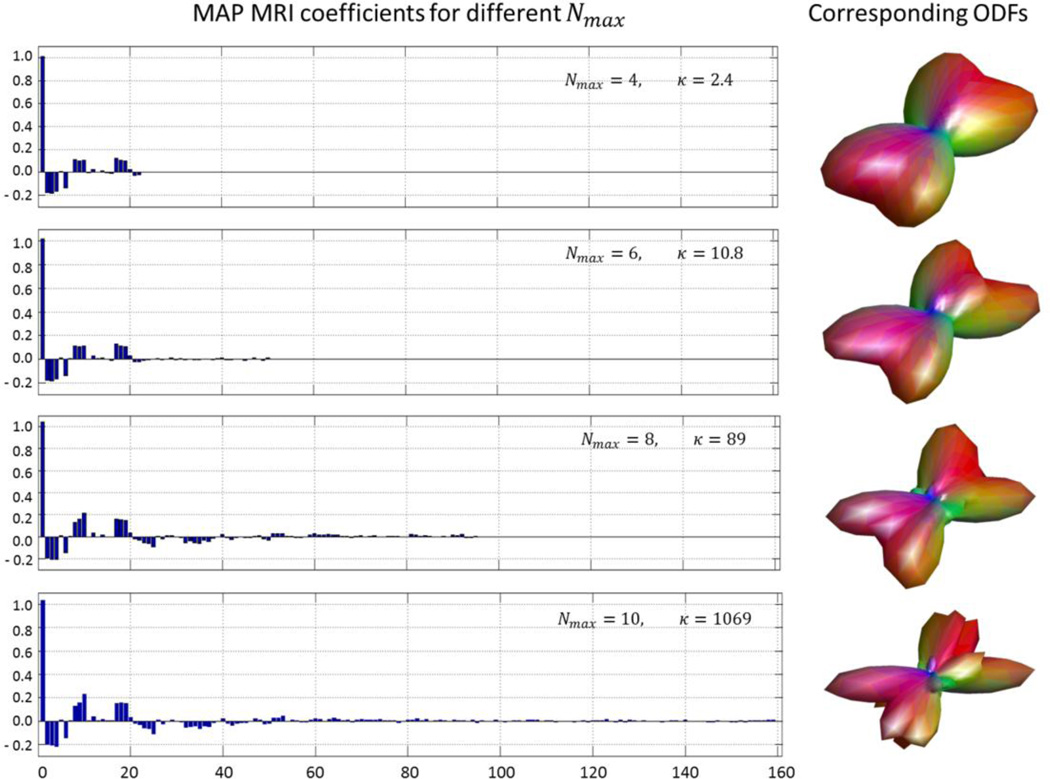
The in vivo DWIs were analyzed using different truncation orders (Nmax) of the MAP MRI series expansions. Regardless of Nmax, the first coefficient that represents the lowest-order (Gaussian) term, explains a large portion of the measured DWI signal even in WM regions containing crossing fibers. Figure 1 shows the calculated MAP MRI coefficients and corresponding ODFs for Nmax = 4, 6, 8, and 10 in a representative voxel from a region with complex neuronal microstructure. These results highlight the stability of the larger, lower order coefficients expected from the orthogonality of the MAP MRI basis functions (Özarslan et al., 2008, Özarslan et al., 2009a). As the number of estimated coefficients increases, the problem becomes more ill-posed, resulting in a larger condition number, κ (Fig. 1). While more coefficients provide a finer characterization of the propagator, the amount of additional detail in the reconstruction of the propagator does not increase significantly beyond a certain point. The trade-off between the level of detail in the propagator estimation and the amount of data acquired (and scan duration) is critical for clinical applications. Including terms up to order 6 was found to yield a sufficient level of detail in propagators from diverse brain regions, while allowing robust estimation of the MAP MRI coefficients even from subsampled data sets that simulate clinically feasible experiments. All further analysis of MAP MRI microstructural parameters described in this study uses Nmax = 6.
Figure 1.
MAP MRI reconstructions using different series truncation orders Nmax for a representative voxel containing complex WM microstructure. Left panel: Magnitude of MAP MRI coefficients computed with Nmax = 4, 6, 8, and 10 (corresponding to 22, 50, 95, and 161 coefficients, respectively). Right panel: corresponding diffusion orientation distribution functions (ODF). Due to the orthogonality of the MAP MRI basis functions, low-order coefficients do not change as the truncation order is successively increased, despite increasing condition number κ at larger.
The computation time for the reconstruction of MAP MRI parameters from whole-brain diffusion data sets with 3mm spatial resolution using Nmax = 6 was less than 3 hours on a single workstation with 32GB RAM and 8 cores × Intel i7-4770K at 3.5GHz. An acceleration of the MAP MRI analysis by a factor equal to the number of slices was achieved using the NIH BIOWULF computational cluster by simultaneously reconstructing all slices on multiple parallel nodes.
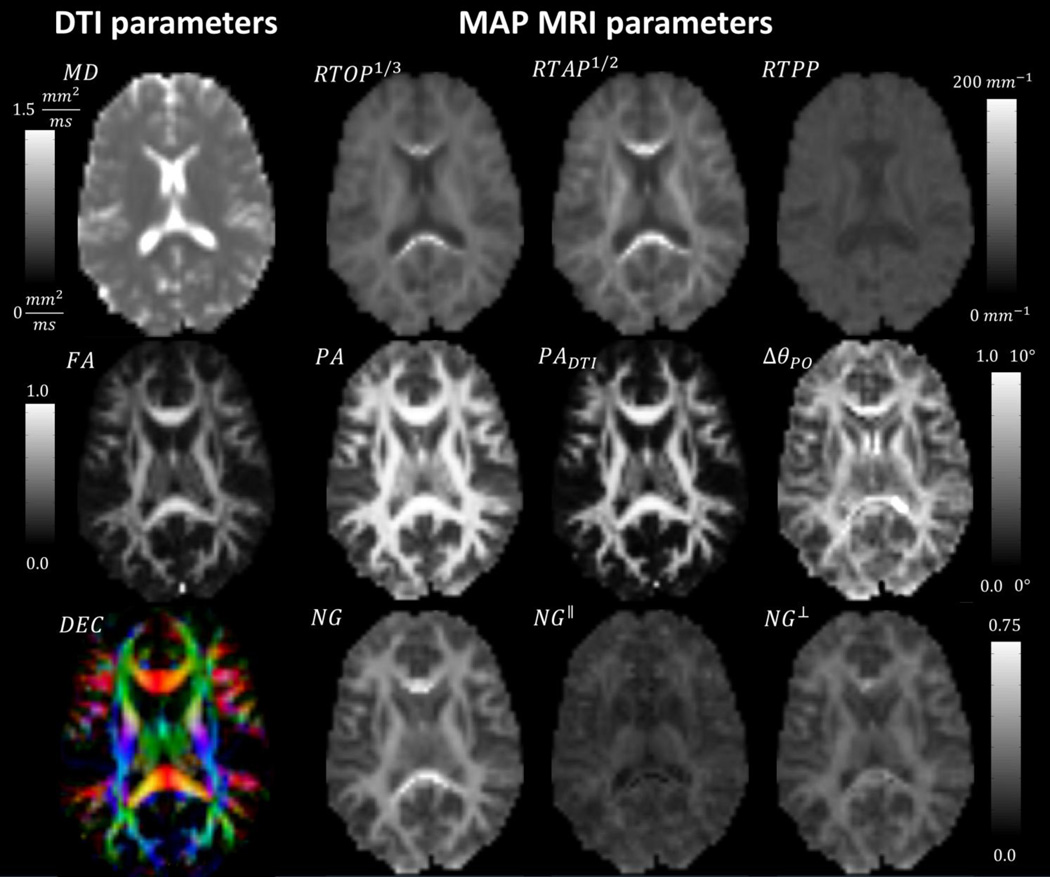
Across all healthy volunteers, the values of MAP-derived parameters were consistent in corresponding neuroanatomical regions with differing tissue features. In vivo RTOP images revealed larger values in WM (especially in the CC) than in GM, and very low values in regions with high partial volume of CSF. The RTOP tissue contrast may reflect overall restrictions and cellularity better than does the MD. RTAP was similar to RTOP in GM, but noticeably larger in regions of coherent tightly packed WM fibers such as the CC, where it is more sensitive to cylindrical restrictions potentially due to myelin. The RTPP was similar in GM and WM with slightly higher values in deep brain structures such as the thalamus. Overall deviations from Gaussianity (NG) were largest in WM fibers, potentially reflecting restriction perpendicular to the fiber orientation as indicated by large NG⊥, whereas diffusion along the axial direction was relatively Gaussian (low NG‖). PA and PADTI measure diffusion anisotropy based on the angular dissimilarity (θPA and θDTI) of the propagator relative to its isotropic counterpart for the general MAP MRI and Gaussian (DTI) approximations, respectively. The angular difference ΔθPO = θPA − θDTI directly quantifies the component of diffusion anisotropy that cannot be explained with the Gaussian model. As expected, the PADTI and FA correlated strongly, showing significantly lower values in WM regions of fiber crossings and in GM, where the Gaussian approximation determining these metrics cannot comprehensively quantify the complex orientational heterogeneity of the local microanatomy. The PA values on the other hand were uniformly high throughout WM, even in regions with large fiber orientation dispersions (i.e., crossing fibers) where the FA and PADTI dropped. Moreover, the PA as well as the angular difference measure ΔθPO revealed significant contrast in GM, suggesting that these metrics could potentially quantify morphological differences between distinct cortical regions. The quantitation of MAP MRI microstructural parameter in the WM and CC was not significantly affected by the choice of the FA threshold used to define these ROIs. Measured values for all microstructural parameters were in the expected ranges, in good agreement with previous studies with fixed brain specimen (Özarslan et al., 2013), supporting the clinical translatability of this technique. In regions containing high partial volume with CSF, such as the ventricles, the MAP MRI structural parameters are likely biased due to low signal intensity in DWIs even with low or moderate b-values. Accordingly, these regions were excluded from the subsequent ROI analysis.
ROI-averaged values of MAP MRI metrics (Fig. 3) were remarkably consistent across subjects and revealed significant contrast between cerebral GM and WM, coherent WM (CC), and deep brain gray matter nuclei such as the basal ganglia (BG) and the thalamus (TH). The relatively small standard deviations of these parameters across the group of all subjects in our preliminary results suggests little individual variability and good consistency of MAP MRI microstructural parameters in healthy individuals, supporting the possibility of clinical assessments. The RTOP was higher in WM than in GM and was mainly influenced by RTAP. The NG⊥ was high and uniform throughout the WM (including the CC) and showed intermediate values in subcortical regions. In the CC the mean PA was only slightly larger than in subcortical WM, whereas the mean FA and PADTI were significantly different between these two ROIs (Fig. 3), suggesting that the PA could be less sensitive to architectural features of WM (local orientational arrangement of fibers) than DTI-derived anisotropy measures and overall a more specific and robust measure for structural integrity. In the GM, BG, and TH, the PA was larger than the PADTI and showed larger dynamic range, potentially reflecting distinctions between cortical and/or subcortical regions (GM, BG, and TH). Compared with DTI-derived metrics such as FA and MD, MAP MRI parameters encode complementary information with different tissue contrast; the NG for instance, directly quantifies the difference between the MAP and DTI model approximations. While current results are consistent and reproducible, a separate study using a larger population must be conducted to establish normative values and construct anatomical atlases of MAP parameters in the brain tissue of healthy volunteers and patients.
Figure 3.
ROI analysis reveals the consistency of MAP MRI parameters across healthy volunteers (error bars indicate standard deviation across subjects) and good sensitivity to tissues with different structural and architectural features.
Fig. 4 illustrates a unique feature of MAP MRI – the computation of ZDP and non-Gaussianity indices from 2D and 1D projections of the propagator onto the planes and along the axes of the anatomical reference frame. These maps are analogous to the axial (parallel) and radial (perpendicular) diffusivities (eigenvalues) derived from DTI but reflect complex non-Gaussian diffusion processes and could provide integral clues for elucidating structural and architectural features in anisotropic tissues (restrictions, fiber dispersion, multiple compartments, etc.). For instance, in regions of fiber crossings, the RTPP measured along the orientation ê3 corresponding to the smallest DTI eigenvalue might be more indicative of radial restrictions (potentially due to myelin) compared with either RTAP or RTOP. In regions of coherent WM fibers RTPP or NG‖ measured along the orientation ê1of the largest DTI eigenvalue are likely modulated by the orientational dispersion of fibers. Future studies with higher spatial resolution will be able to investigate the microanatomical organization of different cortical regions and layers by quantifying the tangential and perpendicular components of propagator descriptors at the WM–GM interface (McNab et al., 2013).
Figure 4.
Decomposition of RTOP and NG measures along the axes of the local tissue frame of reference. In anisotropic tissues these parameters reveal directional information that complements the axial and radial diffusivities measured with DTI.
The ODFs revealed the characteristics of the local arrangement of microanatomical structures (Fig. 5A). Orientational profiles reflecting the complexity of arrangements of WM fibers were observed in regions with low FA along the superior fronto-occipital fasciculus, or in deep brain GM nuclei such as the putamen. Whole brain fiber tractography yielded satisfactory results but would benefit from improved spatial resolution. In general, increased spatial resolution and/or a large number of DWIs and MAP coefficients (Nmax) should be used for applications requiring high angular resolution of the ODFs, such as studies of whole brain structural connectivity. While Fig. 5B demonstrates the basic ability of MAP MRI to resolve crossing fibers (Fig. 5B, arrows), a rigorous evaluation of its potential for whole brain fiber tractography is beyond the scope of this manuscript and will be addressed in future studies. Although a truncation of order 6 provided sufficient detail in the ODFs for characterizing complex WM, regions of GM might benefit from reconstructions using more terms (larger Nmax). Due to likely partial volume contributions resulting from the relatively large voxel size, the orientational characteristics of the propagator in GM were not explored further in this study.
Figure 5.
Glyph representation of propagator ODFs reconstructed using MAP MRI in two regions of complex tissue microstructure (A). Whole brain tractography using ODFs derived from MAP MRI can be used to resolve crossing WM fiber pathways (B)
Numerical Monte-Carlo simulation experiments suggest that for small SNR values the MAP MRI parameters can be biased; generally, the ZDP and non-Gaussianity parameters are overestimated, whereas the anisotropy parameters are underestimated (Fig. 6). At higher SNR values these biases disappear and the variance of the estimated parameters is greatly reduced. These results confirm that metrics computed from projections of propagator on the axes (RTAP, axial NG) and planes (RTPP, planar NG) of the anatomical coordinate system are more susceptible to noise compared with the overall propagator measures (RTOP and NG), but also result in negligible biases at SNR levels above 75. Overall, the SNR dependence of MAP MRI metrics is comparable to that of DTI-derived parameters. Although Fig. 6 illustrates the simulation results for a representative propagator obtained in a region of complex WM, similar results were obtained for propagators in different brain tissues such as coherent WM, cortical GM, or deep brain nuclei. In voxels with significant CSF partial volume the signal noise floor is reach even for very low b-values significantly biasing the estimation of both DTI and MAP MRI parameters.
Figure 6.
Monte-Carlo simulation experiments reveal how at very low SNR the microstructural parameters measured with DTI (A) and MAP MRI (B) can be biased in a white matter region with complex microstructure (C). At higher SNR levels these parameters converge to unbiased values and exhibit reduced variances.
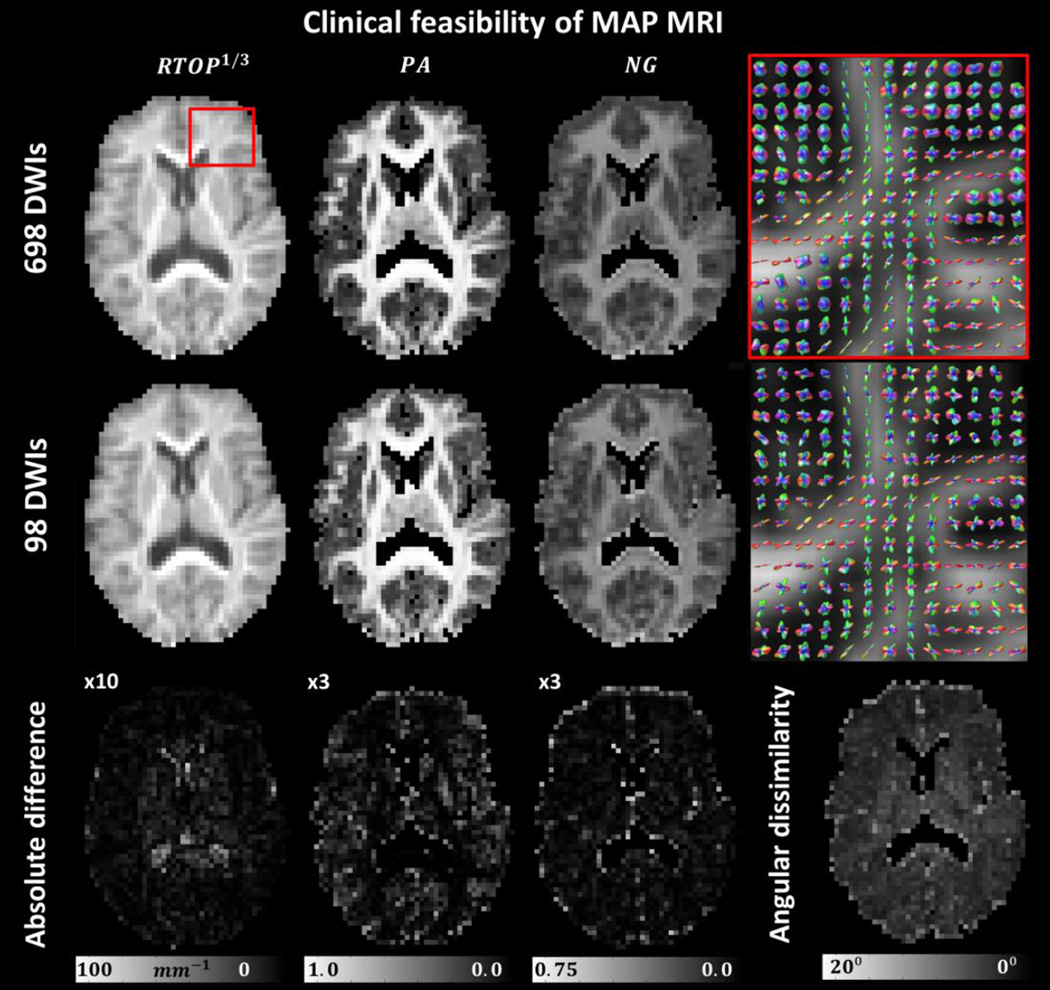
Drastically reducing the number of DWIs does not significantly affect the computation of MAP MRI microstructural parameters when images with bmax = 6,000 s/mm2 are included. The computations of integral and “integral-like” measures of the propagator such as the RTOP, NG, and PA, are remarkably stable and robust and can be obtained from as few as 98 DWIs (Fig. 7) suggesting that MAP MRI can be accelerated sufficiently for routine clinical applications and that relatively large b-values are beneficial. The largest discrepancies were found in regions close to the ventricles and at the cortical surface, where quantitation errors caused by motion/pulsation, gradient sampling scheme, and CSF partial volume contamination might lead to fitting errors. As expected, the orientational profiles of the propagator showed larger sensitivity to the number of DWIs and the gradient sampling schemes. Nevertheless, the small angular dissimilarity values measured between the propagators derived from the full and subsampled data sets underscore the robustness of the analytical MAP MRI framework and further corroborate its clinical feasibility (Fig. 7). The accuracy in measuring MAP MRI parameters from clinical data sets is expected to improve for future MAP MRI studies in which the diffusion sampling scheme (e.g. 95 direction protocol) is optimized from scratch by selecting diffusion encoding directions with uniform coverage both within and across shells with different b-values (Koay et al., 2012, Cheng et al., 2014), and confounds due to subject motion are greatly reduced due to shorter scan duration.
Figure 7.
Clinical feasibility of MAP MRI in a representative healthy volunteer. The MAP MRI metrics obtained from a highly subsampled data sets show very similar values to those obtained with the full data set. The largest differences occur in regions close to the ventricles and along sulci, where CSF partial volume contributions are more pronounced. PA and NG values in the ventricles were masked as these measurements are likely biased due to low SNR.
The test-retest experiments confirmed the reproducibility of MAP MRI experiments (Fig. 8). MAP MRI reconstructions of subsampled clinical (and full) data sets obtained in different scans yielded similar values for the propagator microstructural parameters and comparable orientation profiles. Fig. 8 summarizes the ROI-averaged DTI and clinical MAP MRI parameters in WM and GM obtained from the subsampled test-retest scans in each subject. Our results indicate that there is only a small variation of the measured MAP parameters in the same healthy volunteers across sessions (similar to that observed in DTI) that could be attributed to differences in subject head position and errors due to post-processing (e.g., image registration). The RTOP was the most robust parameter, while the NG and PA may be more sensitive to the estimation of the local reference frame (rotation matrix R), which can be affected by differences in subject head orientation and movement during the two sessions.
Figure 8.
Test-retest results for ROI-averaged clinical MAP MRI and DTI microstructural parameters in WM and GM derived from clinical data sets in three healthy volunteers. The test-retest reproducibility and consistency across subjects of MAP MRI metrics are similar to those of DTI-derived parameters. The values compare very well with those obtained from the ROI analysis of the full data sets (Fig. 3).
Discussion
This study accomplishes a critical step in the clinical translation of MAP MRI by demonstrating that it is possible to acquire MAP MRI data of sufficient quality to make a radiological assessment possible in a clinically feasible scanning period. To qualify the clinical potential of the microstructural parameters derived with MAP MRI several technical challenges and limitations deserve further consideration.
When clinical DWIs are acquired with large b-values, the range of in vivo water mobilities and tissue anisotropies can generate diffusion MR signals with a large dynamic range, potentially dropping below the noise floor in regions with significant CSF partial volume contributions. Evidently, such noisy signals bias the propagator estimation and should therefore be excluded from the MAP MRI analysis. Even in regions of highly coherent WM (e.g., CC), diffusion along the fiber orientation can sometimes lead to bias due to measurement noise. Therefore, increasing the spatial resolution to that of a typical clinical DTI scan (e.g., 2mm or 2.5mm isotropic) at the cost of lower SNR should be considered carefully (Fig. 6) and potentially used in conjunction with de-noising strategies (Koay et al., 2009) or regularization methods. Our current study aimed to provide an unbiased assessment of microstructural MAP MRI parameters in vivo. For that purpose, it was necessary to acquire large diffusion MRI data sets with a spatial resolution of 3mm isotropic that ensures sufficient sensitivity in brain tissues (Fig. 6). The commercialization of advanced gradient systems capable of achieving larger amplitudes and faster slew-rates will provide high SNR DWIs acquired with shorter TEs, likely enabling higher spatial resolutions (Setsompop et al., 2013) in clinical MAP MRI scans.
MAP MRI parameters provide a more comprehensive tissue characterization than DTI parameters reflecting physically meaningful microstructural features with greater neuroanatomical specificity. The family of zero displacement probability measures (e.g., RTOP, RTAP, RTPP) could become more specific biomarkers for cellularity, size of cell bodies and processes, or presence of restricting barriers (e.g., myelin) than the MD or the tensor eigenvalues derived with DTI (Gupta et al., 1999), while NG measures could more sensitively indicate additional sources of diffusional heterogeneity such as exchange, or multiple diffusing compartments. Metrics of ZDP and non-Gaussinaity computed from projections of the propagator in the anatomical reference frame could complement DTI measures of radial and axial diffusivities, which have been differentially associated with demyelination and axonal loss, respectively (Song et al., 2005). For instance, in brain regions with coherent WM such as the CC, most of the non-Gaussian diffusion behavior could be attributed to restriction orthogonal to the axons’ orientation as reflected by large values of NG⊥, a parameter that could prove to be a more powerful marker for demyelination than radial diffusivity. Compared to the FA, the PA provides a more proper assessment of anisotropy in regions with crossing WM fibers and has a larger dynamic range across different tissue types (including GM structures) possibly reflecting interesting cytoarchitectural and morphological features of potential clinical significance. The angular measure (Eq. 6) for quantifying differences between propagators in their individual reference frames could provide a unique clinical opportunity for longitudinally monitoring tissue microanatomical changes within individual subjects. Our preliminary results support the clinical potential of assessing brain microstructure using MAP MRI parameters and call for further studies on patient populations.
The decomposition of both RTOP and NG was performed in the frame of reference determined by the diffusion tensor (Eq. 1). RTAP, RTPP, NG‖ and NG⊥ were computed with respect to the direction with the largest diffusivity (i.e. the largest root-mean-squared spin displacement). In areas with multiple fiber orientations this direction is ill-defined, and, just like the DTI-derived axial and radial diffusivities, RTAP, RTPP, NG‖ and NG⊥ must be interpreted with caution (Avram et al., 2014). In those regions it is informative to also take into consideration the projections of RTOP and NG along and across the other eigenvectors of the diffusion tensor as shown in Fig. 4.
Viewing MAP MRI as a generalization of DTI allows one to directly appreciate the additional information it provides, as well as its limitations. For example, DTI-equivalent zero-displacement probabilities can be computed by truncating the series at Nmax = 0. The Gaussian RTOP is a function of the diffusion time and the geometric mean of the DTI eigenvalues and therefore correlates inversely with the MD. When the MAP RTOP is computed using a larger Nmax, a multiplicative “correction factor”, in the form of a weighted summation of the MAP coefficients, is added, sensitizing the measurement to complex diffusion processes (e.g. effects of restricting barriers). Compared with anisotropy measures derived from the DTI model such as the FA or the PADTI, the PA is generally sensitive to differences in orientational diffusion heterogeneity including angular variations in non-Gaussian diffusion. The additional anisotropy information added by MAP MRI compared to DTI is quantified directly by the angular difference measure ΔθPO = θPA − θDTI. The NG indices computed using Eq. 6 quantify “angular” deviations from the Gaussian propagators in a more general sense as compared with other similar techniques, such as the diffusion kurtosis (Jensen et al., 2005). Nevertheless, in MAP MRI too, the NG estimate can be influenced by the initial Gaussian approximation (i.e., scaling matrix A). While theoretically one could expand the propagator in an infinite MAP series using an arbitrary scaling matrix, the NG is only physically significant if the scaling parameters reflect the mean-squared displacements of tissue water spins undergoing Gaussian diffusion. For this reason in our study the scaling matrix was estimated by fitting a DTI model to a subset of the data comprising DWIs acquired with low b-values (Gaussian regime). If the scaling matrix is measured from large b-value DWIs the diffusivities no longer accurately quantify Gaussian diffusion and the measured NG does not represent a physically meaningful quantity. In this case one should transform the MAP coefficients to a different functional basis determined by appropriate scaling parameters that reflect Gaussian diffusion before computing the NG. In general, a MAP defined by scaling matrix A and coefficients a, can be represented in a new functional basis determined by scaling matrix B and coefficients b = Tζa, where the matrix Tζ is defined in Appendix A.
One exciting promise of MAP MRI is its ability to directly relate propagator descriptors such as the RTAP to physical features of the tissue microstructure if the geometry of the underlying microscopic restriction is well-characterized. For example, if we view myelinated axons in coherent WM as a collection of parallel impermeable cylinders and neglect extra-axonal signal contributions, we can infer the average axonal cross-sectional area, and implicitly the average axon diameter, directly from the RTAP (Özarslan et al., 2013). This physical interpretation of RTAP is predicated on two additional assumptions 1) a diffusion time that is sufficiently long to allow water molecules to completely sample microscopic compartments and 2) a diffusion gradient pulse duration δ that is sufficiently short to ensure the mean apparent propagator solution is a good approximation to the true mean propagator. The first condition is met for most in vivo experiments with human subjects, for which the inner diameters of myelinated axons are generally < 5µm, the tissue water diffusivity is on the order of 1.5 µm2/ms, and the duration of the diffusion preparation is generally longer than 50 ms. Due to gradient hardware limitations on whole-body MRI scanners the pulse width δ is relatively long (e.g., 32ms in our study) potentially leading to deviations from the short gradient pulse approximation underlying q-space analysis. This violation of the short pulse approximation represents a challenge that is inherent to the clinical translation of all diffusion MRI methods that acquire and analyze data in q-space (Liu et al., 2003, Wedeen et al., 2005, Wu and Alexander, 2007, Assemlal et al., 2009, Descoteaux et al., 2011), and results in measuring an approximation of the true mean propagator of the voxel microstructure. Nevertheless, for a well-characterized microstructure (e.g., parallel cylinders), the effect of finite δ can be overcome using numerical methods (Özarslan et al., 2009b, Avram et al., 2013). In WM tissue with more complex microstructure, the relation between RTAP and the average axon diameter can be affected by additional factors such as signal contributions from extra-axonal water, fiber orientation dispersion, membrane permeability, exchange between multiple compartments, and active cellular transport. Interestingly, these factors are expected to decrease the overall probability of spins to return to the axis parallel to the axon orientation (Pierpaoli and Basser, 1996) resulting in lower measurements of RTAP and implicitly an overestimation of the true average axon diameter. Consequently, in biological tissue, RTAP could provide an upper limit for the average axon diameter in the voxel (Avram and Basser, 2014). Reliable assessments of axon diameters at the whole-brain level using the RTAP measured with MAP MRI (Avram and Basser, 2014) might necessitate improved tissue specificity (Pasternak et al., 2009, Avram et al., 2010) and additional signal modeling (Jian et al., 2007, Zhang et al., 2012).
Parametric diffusion models such as NODDI (Zhang et al., 2012) or AxCaliber (Assaf et al., 2008) rely on a priori assumptions about the tissue microstructure and can therefore be very powerful tools for characterizing tissue regions where the microstructure is known and the parametric model is rich enough to embody it. In contrast, the non-parametric framework of MAP MRI aims to quantify diffusion in arbitrary tissue environments, and therefore may be more amenable to detecting and studying pathology or brain tissue changes during development or aging at the whole-brain level.
The analytical formulation of MAP MRI allows the reliable estimation of propagator metrics from diffusion MRI data sets that can be acquired within clinically achievable scan durations. The Hermite-Gaussian basis functions used in MAP MRI have desirable asymptotic behavior consistent with the physical requirements for the signal attenuation at small and large q-values, and are eigenfunctions of the Fourier Transform, thereby inherently describing the signal in both q-space and reciprocal (displacement) r-space (Özarslan et al., 2008). These properties make the complete set of orthogonal MAP MRI basis functions well-suited for characterizing complex (non-Gaussian) diffusion signals that occur in many in vivo situations. Propagator metrics obtained from drastically reduced data sets of DWIs show similar values as the corresponding metrics obtained from the complete data set, suggesting that MAP MRI can be sufficiently accelerated for clinical applications. Moreover, the MAP MRI parameters obtained from the subsampled data sets show a consistent neuroanatomical contrast in healthy volunteers, and can be reliably replicated in test-retest experiments. While these results suggest that the analytical MAP MRI framework is sufficiently powerful to measure propagator metrics from clinical data sets that can be acquired within 10 minutes, we expect that these parameters can be reliably estimated from even fewer DWIs by incorporating additional regularization constraints in the MAP reconstruction (L2 norm, low-rank matrix approximation, singular-value decomposition, compressed sensing reconstruction, L1 norm). Compared with other advanced diffusion MR techniques, MAP MRI framework also provides analytical metrics of various propagator features in the local reference frame of the tissue. Scalar propagator metrics of ZDP, non-Gaussianity, and anisotropy could potentially provide new insights into the microstructural organization of brain tissues during normal and abnormal development, aging, and disease.
Conclusions
Taken together, our results affirm in vivo MAP MRI as a feasible and viable technique for clinical applications and encourage future studies focusing on quantitative assessment, biophysical validation and clinical performance. MAP MRI subsumes DTI and provides a more comprehensive microstructural tissue characterization with complementary scalar indices that potentially could be more specifically related to features of tissue morphology (e.g., compartment size, cellularity, restriction). These novel MAP MRI parameters show consistent neuroanatomical contrast and are very reproducible in healthy volunteers, supporting the possibility of radiological assessments. Ultimately, they may provide biologically specific tissue markers in the early detection of demyelination pathologies (e.g., multiple sclerosis) or mild traumatic brain injury (mTBI), and improve our longitudinal characterization of structural brain tissue changes in neurological and psychiatric disorders, as well as during normal and abnormal brain development and aging.
Figure 2.
Neuroanatomical variation of MAP MRI and DTI microstructural parameters in a representative subject. DTI-derived parameters: MD, FA and Directionally-encoded color (DEC) map (Left). MAP MRI –derived zero-displacement probabilities, propagator anisotropy and non-Gaussianity indices (Right).
Highlights.
In vivo MAP metrics show consistent neuroanatomical contrast in healthy subjects
These microstructural scalar measures provide novel information compared with DTI
MAP parameters can be reconstructed from diffusion datasets acquired in 10 minutes
These metrics derived from clinical data sets show good test-retest repeatability
Acknowledgements
This work was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) and the National Institute of Neurological Disorders and Stroke (NINDS) at the National Institutes of Health (NIH), and the Department of Defense in the Center of Neuroscience and Regenerative Medicine (CNRM). EÖ was supported by TÜBİTAK-EU COFUND Project: 114C015, TÜBİTAK Project: 114E053, Boğaziçi University research funding BAP 8521, and NIH R01MH074794. We thank Dr. Jian Cheng for helpful discussions. In vivo MRI experiments were performed at the NIH MRI Research Facility (NMRF). This study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD. (http://biowulf.nih.gov).
Appendix A
Measures of Propagator Similarity and Anisotropy
The inner product between two propagator P(r) and Q(r) represented using Na and Nb coefficients in Cartesian functional bases defined by scaling matrices
| (A.1) |
, respectively, is defined as
| (A.2) |
Where and Tζ is a matrix with elements Tζ = Tm1n1(ζx)Tm2n2(ζy)Tm3n3(ζz) and
| (A.3) |
, with Km+n is 1 when m and n are even, and 0 otherwise. The similarity between the two propagators is measured as an angular measure of covariance in analogy with the vector dot product:
| (A.4) |
The isotropic part of the propagator Piso(r) can be represented using the isotropic simple harmonic oscillator reconstruction (iSHORE) basis functions in spherical coordinates with scaling parameter, which can be related to the expansion in the Cartesian anisotropic SHORE basis (Özarslan et al., 2013):
| (A.5) |
, where the κ(u0I), and ϒ(u0I, r) column vectors denote the iSHORE coefficients and
| (A.6) |
, respectively, while o(u0I), and Ψ (u0I, q) contain the equivalent anisotropic SHORE coefficients and basis functions in Cartesian coordinates, with . The PA is defined using a shape function to scale the angular θPO measure between P(r) and Piso(r) for adequate contrast:
| (A.7) |
To allow direct comparison with the FA, the PADTI is defined using Eqs. A.7 with the angular parameter θDTI quantifying the similarity between the anisotropic Gaussian propagator, with scaling parameters ux, uy, uz, and its isotropic counterpart, defined by the scaling parameter u0 that maximizes the similarity measure:
| (A.8) |
, where is the real positive root of the cubic polynomial in U
, and .
Appendix B
Orientation Distribution Functions
ODFs are computed analytically as radial moments of the propagators (Özarslan et al., 2013). For example, the 2nd radial moment is:
| (B.1) |
Where and C is a vector given by
| (B.2) |
| (B.3) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Assaf Y, Blumenfeld-Katzir T, Yovel Y, Basser PJ. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn Reson Med. 2008;59:1347–1354. doi: 10.1002/mrm.21577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf Y, Mayk A, Cohen Y. Displacement imaging of spinal cord using q-space diffusion-weighted MRI. Magn Reson Med. 2000;44:713–722. doi: 10.1002/1522-2594(200011)44:5<713::aid-mrm9>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Assemlal H-E, Tschumperlé D, Brun L. Efficient and robust computation of PDF features from diffusion MR signal. Medical Image Analysis. 2009;13:715–729. doi: 10.1016/j.media.2009.06.004. [DOI] [PubMed] [Google Scholar]
- Avram AV, Barnett A, Basser P. The Variation of MAP-MRI –derived Parameters Along White Matter Fiber Pathways in the Human Brain. Proc Intl Soc Magn Reson Med. 2014;23:2587. [Google Scholar]
- Avram AV, Basser P. Inferring Millisecond-Scale Functional Connectivity from Tissue Microstructure. Proc Intl Soc Magn Reson Med. 2014;23:3001. [Google Scholar]
- Avram AV, Guidon A, Song AW. Myelin water weighted diffusion tensor imaging. Neuroimage. 2010;53:132–138. doi: 10.1016/j.neuroimage.2010.06.019. [DOI] [PubMed] [Google Scholar]
- Avram AV, Ozarslan E, Sarlls JE, Basser PJ. In vivo detection of microscopic anisotropy using quadruple pulsed-field gradient (qPFG) diffusion MRI on a clinical scanner. Neuroimage. 2013;64:229–239. doi: 10.1016/j.neuroimage.2012.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Callaghan PT. Principles of Nuclear Magnetic Resonance Microscopy. Oxford: Clarendon Press; 1991. [Google Scholar]
- Cheng J, Shen D, Yap P-T. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2014. Springer; 2014. Designing single-and multiple-shell sampling schemes for diffusion MRI using spherical code; pp. 281–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Descoteaux M, Deriche R, Le Bihan D, Mangin J-F, Poupon C. Multiple q-shell diffusion propagator imaging. Medical Image Analysis. 2011;15:603–621. doi: 10.1016/j.media.2010.07.001. [DOI] [PubMed] [Google Scholar]
- Gupta RK, Sinha U, Cloughesy TF, Alger JR. Inverse correlation between choline magnetic resonance spectroscopy signal intensity and the apparent diffusion coefficient in human glioma. Magn Reson Med. 1999;41:2–7. doi: 10.1002/(sici)1522-2594(199901)41:1<2::aid-mrm2>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magnet Reson Med. 2005;53:1432–1440. doi: 10.1002/mrm.20508. [DOI] [PubMed] [Google Scholar]
- Jian B, Vemuri BC, Özarslan E, Carney PR, Mareci TH. A novel tensor distribution model for the diffusion-weighted MR signal. Neuroimage. 2007;37:164–176. doi: 10.1016/j.neuroimage.2007.03.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42:515–525. [PubMed] [Google Scholar]
- Koay CG, Ozarslan E, Johnson KM, Meyerand ME. Sparse and optimal acquisition design for diffusion MRI and beyond. Medical physics. 2012;39:2499–2511. doi: 10.1118/1.3700166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koay CG, Ozarslan E, Pierpaoli C. Probabilistic Identification and Estimation of Noise (PIESNO): a self-consistent approach and its applications in MRI. J Magn Reson. 2009;199:94–103. doi: 10.1016/j.jmr.2009.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Bammer R, Moseley ME. Generalized Diffusion Tensor Imaging (GDTI): A Method for Characterizing and Imaging Diffusion Anisotropy Caused by Non-Gaussian Diffusion. Israel Journal of Chemistry. 2003;43:145–154. [Google Scholar]
- Liu C, Mang SC, Moseley ME. In vivo generalized diffusion tensor imaging (GDTI) using higher-order tensors (HOT) Magn Reson Med. 2010;63:243–252. doi: 10.1002/mrm.22192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNab JA, Polimeni JR, Wang R, Augustinack JC, Fujimoto K, Stevens A, Janssens T, Farivar R, Folkerth RD, Vanduffel W, Wald LL. Surface based analysis of diffusion orientation for identifying architectonic domains in the in vivo human cortex. Neuroimage. 2013;69:87–100. doi: 10.1016/j.neuroimage.2012.11.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Özarslan E, Koay CG, Basser PJ. Simple harmonic oscillator based estimation and reconstruction for one-dimensional q-space MR. Proc Intl Soc Mag Reson Med. 2008;16:35. [Google Scholar]
- Özarslan E, Koay CG, Shepherd TM, Blackband SJ, Basser PJ. Simple harmonic oscillator based reconstruction and estimation for three-dimensional q-space MRI. Proc Intl Soc Mag Reson Med. 2009a;17:1369. [Google Scholar]
- Özarslan E, Koay CG, Shepherd TM, Komlosh ME, İrfanoğlu MO, Pierpaoli C, Basser PJ. Mean apparent propagator (MAP) MRI: A novel diffusion imaging method for mapping tissue microstructure. Neuroimage. 2013;78:16–32. doi: 10.1016/j.neuroimage.2013.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Özarslan E, Shemesh N, Basser PJ. A general framework to quantify the effect of restricted diffusion on the NMR signal with applications to double pulsed field gradient NMR experiments. J Chem Phys. 2009b;130:104702. doi: 10.1063/1.3082078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasternak O, Sochen N, Gur Y, Intrator N, Assaf Y. Free water elimination and mapping from diffusion MRI. Magn Reson Med. 2009;62:717–730. doi: 10.1002/mrm.22055. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Basser PJ. Toward a quantitative assessment of diffusion anisotropy. Magn Reson Med. 1996;36:893–906. doi: 10.1002/mrm.1910360612. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Walker L, Irfanoglu MO, Barnett A, Basser P, Chang L-C, Koay C, Pajevic S, Rohde G, Sarlls J, Wu M. ISMRM 18th Annual Meeting. Sweden: Stockholm; 2010. TORTOISE: an integrated software package for processing of diffusion MRI data; p. 1597. [Google Scholar]
- Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage. 2013;80:220–233. doi: 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S-K, Yoshino J, Le TQ, Lin S-J, Sun S-W, Cross AH, Armstrong RC. Demyelination increases radial diffusivity in corpus callosum of mouse brain. Neuroimage. 2005;26:132–140. doi: 10.1016/j.neuroimage.2005.01.028. [DOI] [PubMed] [Google Scholar]
- Sundgren PC, Dong Q, Gómez-Hassan D, Mukherji SK, Maly P, Welsh R. Diffusion tensor imaging of the brain: review of clinical applications. Neuroradiology. 2004;46:339–350. doi: 10.1007/s00234-003-1114-x. [DOI] [PubMed] [Google Scholar]
- Wang R, Bennen T, Sorensen AG, Wedeen VJ. Diffusion Toolkit: A Software Package for Diffusion Imaging Data Processing and Tractography. Proc Intl Soc Mag Reson. 2007 [Google Scholar]
- Wedeen VJ, Hagmann P, Tseng W-YI, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. 2005;54:1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- Wu EX, Cheung MM. MR diffusion kurtosis imaging for neural tissue characterization. NMR Biomed. 2010;23:836–848. doi: 10.1002/nbm.1506. [DOI] [PubMed] [Google Scholar]
- Wu Y-C, Alexander AL. Hybrid diffusion imaging. Neuroimage. 2007;36:617–629. doi: 10.1016/j.neuroimage.2007.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012;61:1000–1016. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]