Constitutive Modeling of Ascending Thoracic Aortic Aneurysms using Microstructural Parameters

Abstract

Ascending thoracic aortic aneurysm (ATAA) has been associated with diminished biomechanical strength and disruption in the collagen fiber microarchitecture. Additionally, the congenital bicuspid aortic valve (BAV) leads to a distinct extracellular matrix structure that may be related to ATAA development at an earlier age than degenerative aneurysms arising in patients with the morphological normal tricuspid aortic valve (TAV). The purpose of this study was to model the fiber-reinforced mechanical response of ATAA specimens from patients with either BAV or TAV. This was achieved by combining image-analysis derived parameters of collagen fiber dispersion and alignment with tensile testing data. Then, numerical simulations were performed to assess the role of anisotropic constitutive formulation on the wall stress distribution of aneurysmal aorta. Results indicate that both BAV ATAA and TAV ATAA have altered collagen fiber architecture in the medial plane of experimentally-dissected aortic tissues when compared to normal ascending aortic specimens. The study findings highlight that differences in the collagen fiber distribution mostly influences the resulting wall stress distribution rather than the peak stress. We conclude that fiber-reinforced constitutive modeling that takes into account the collagen fiber defect inherent to the aneurysmal ascending aorta is paramount for accurate finite element predictions and ultimately for biomechanical-based indicators to reliably distinguish the more from the less ‘malignant’ ATAAs.

Graphical Abstract

Introduction

Ascending thoracic aortic aneurysm (ATAA) is described at tissue level by medial degeneration and biomechanical weakening of the aneurysmal wall, ultimately leading to aortic dilatation and failure [1]. Elective surgery is indicated when the aortic diameter exceeds 5.5 cm since the yearly risk of dissection or rupture rises from 3% to 7% with aneurysms >6 cm [2]. Predisposing risk factors include poorly controlled hypertension, Marfan syndrome and importantly bicuspid aortic valve (BAV). Indeed, patients with BAV have a 9-fold increased risk of developing ATAA-related fatal complications compared with individuals with the tricuspid aortic valve (TAV) when matched for the degree of stenosis [3]. Although some authors suggest an intrinsic aortic wall disorder for BAV ATAAs [4], there is increasing evidence that hemodynamic flow abnormalities associated with BAV may also play a key role in the development of thoracic aortic aneurysms [5].

Our group recently reported altered biomechanical properties of ATAAs with either BAV or TAV [6, 7], and demonstrated that these differences are likely attributed to an altered collagen fiber microarchitecture that is distinct in ATAAs arising in the setting of BAV vs. TAV [8–10]. Moreover, numerical simulation showed high and locally varying wall shear stress for ATAAs, which may suggest a flow-induced vascular remodeling process as a basis for aneurysm formation [11, 12]. The present study was motivated by the need of accurate stress analysis incorporating the noted microstructural deficits in the aneurysmal aorta. Towards that end, we quantified the collagen fiber microarchitecture of the medial layer of experimentally-dissected aortic tissues obtained from ATAAs with either BAV or TAV. The fiber-reinforced constitutive framework proposed by Gasser et al. [13] was then employed to model the mechanical response of aneurysmal aorta by numerical simulations utilizing ATAA models composed by two aortic layers. The importance of a fiber-reinforced constitutive model versus a isotropic one and the influence of model parameters were quantified by error analysis.

Material and Methods

Aortic tissue specimen

All ascending aortic tissue specimens were gathered from our previous experimental study [6] according to guidelines of the University of Pittsburgh Institutional Review Board and the Center for Organ Recovery and Education. Segments of the non-aneurysmal (control) aorta were collected from organ donor/heart recipient subjects with TAV, whereas non-dissected ATAAs were obtained fresh from patients with either BAV or TAV undergoing elective repair of aneurysmal aorta at the University of Pittsburgh Medical Center. From the original study [6], we analyzed a subset of experimentally-dissected halves (ie, the one between the intimal surface and the dissected plane ([INT-DEL]) and the one between the adventitial surface and the dissected plane [ADV-DEL]), which were subjected to tensile testing of delaminated halves up to failure. Specifically, we included non-aneurysmal aorta (n.4), BAV ATAAs (n.8) and TAV ATAAs (n.6) with an age range of 42–72 years and aortic diameter range of 46–68 mm.

Tensile testing and multi-photon imaging

For the tensile tests, both ADV-DEL and INT-DEL dissected halves cut along either circumferential (CIRC) or longitudinal (LONG) orientation with respect to that of the aorta were tested on an Instron tensile system with a load cell of 25 N. Test specimens with rectangular shapes (approximately 30x6mm) were mounted in the tensile system and submerged in 0.9% physiologic saline solution at temperature of 37°C. The width, thickness and length of each specimen were measured at three different locations using a dial caliper and then averaged and recorded before testing. Surfalloy jaw faces with gritty, sandpaper-like surfaces were used to avoid slipping of the specimen in the pneumatic grips. Each specimen was preconditioned by loading to 7% strain and unloaded repeatedly for 10 cycles at a constant strain rate of 8.5% /min. Under displacement control, the specimen was stretched upon failure at constant crosshead speed of 1 mm/min. The Cauchy stress was calculated as the applied force normalized by the deformed cross-sectional area, and the stretch (λ) was calculated as the deformed length normalized by the original length of each specimen.

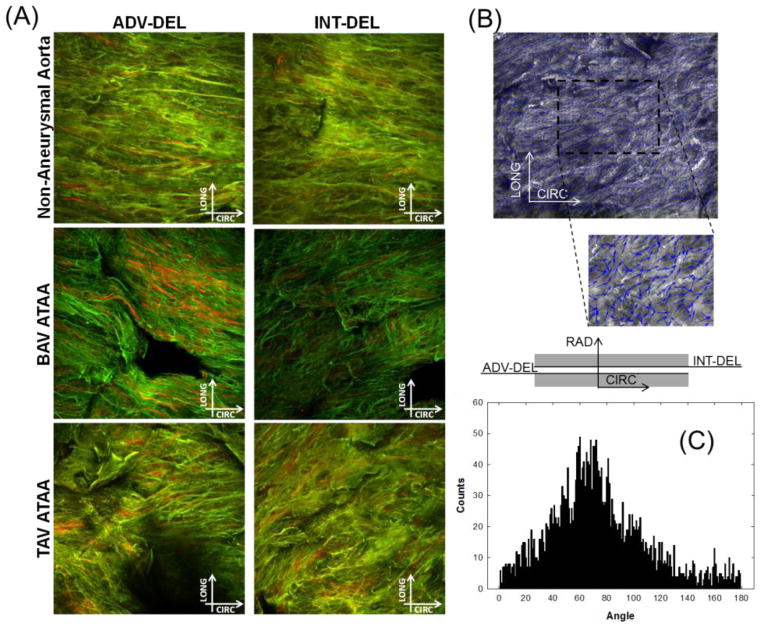
Tissue samples were fixed in 4% paraformaldehyde for 1.5 hour, approximately, and then stored in PBS solution at 4°C temperature prior imaging analysis. Fiber structural architecture of both ADV-DEL and INT-DEL halves in CIRC and LONG orientations were observed using an Olympus multi-photon microscope (Model FV10, ASW software). During imaging, the dissected planes of each tissue sample were faced to the microscope lens to allow for visualization of collagen and elastin fibers embedded in the medial plane. In this work, multi-photon imaging of tissue samples differs from that one reported previously by our group where we investigated the longitudinal and circumferential planes of the aneurysmal aorta [8]. Multi-photon stack images of dissected medial planes were taken on an area of 500μm x 500μm with a depth ranging 96–184 μm. Elastin (green) and collagen (red) fibers were automatically detected according to intrinsic fluorescence (channel RXD1, wavelength=525±25 nm) and second harmonic generation (channel RXD2, wavelength=400±50 nm), respectively.

Image-based fiber analysis

A custom automated image-based analysis tool developed in MATLAB (MathWorks, Inc., R2011a) by our group [14] was used to rigorously characterize the fiber microarchitecture from multi-photon images of aortic tissue samples. The algorithm detects objects of interest (collagen or elastin fibers) that are visualized by small arrows (blue) over object boundary. The zero degree corresponded to the circumferential direction of the ascending aorta. The fiber angle distribution (counts vs angle) was provided as a histogram with the peak showing the dominant fiber angle, which was then adopted for constitutive parameter estimation. Moreover, the fiber orientation index (OI) providing a measure of the fiber alignment was quantified [15]:

$$\text{OI}=\frac{1}{n}\sum {cos}^2({\theta }_i)$$ (1)

where θ_i is the angle of a fiber segment i = 1 … n with respect to the direction of supposed alignment. An OI=1 indicates a fiber set perfectly aligned towards a preferred angle direction or anisotropy, while OI=0.5 indicates random fiber alignment or isotropy. In order to include these structural parameters in the constitutive model, we averaged the values of both fiber angle and OI obtained separately in the CIRC and LONG directions as these values were determined from the same aortic tissue half.

Fiber-reinforced constitutive modeling

The stress–stretch response of aortic tissues in both CIRC and LONG orientations were fit by the fiber-reinforced structural model introduced by Gasser and collaborators [13] using the commercial software Hyperfit (Hyperfit v.1.16, Czech Science Foundation). The constitutive model adopted the strain energy function

$$\mathrm{W}=\frac{C}{2}(I_1-3)+\frac{k_1}{k_2}\left\{\mathit{exp}\left[k_2{({kI}_1+(1-3k)I_{4^i}-1)}^2\right]-1\right\}$$ (2)

where C, k₁ and k₂ were the material parameters, k and γ were the structural parameters, $I_1={\lambda }_{\mathit{CIRC}}^2+{\lambda }_{\mathit{LONG}}^2+{({\lambda }_{\mathit{CIRC}}{\lambda }_{\mathit{LONG}})}^{-2}$ was the first invariant of the right Cauchy-Green strain tensor, $I_{4^1}=I_{4^2}={\lambda }_{\mathit{CIRC}}^2{sin}^2\gamma +{\lambda }_{\mathit{LONG}}^2{cos}^2\gamma$ was a tensor invariant assuming that the two fiber families (i=1,2) were mechanically equivalent, symmetrically oriented with the same distribution parameter and embedded in the tangential dissected plane of the tissue (ie, no components in the radial direction). To account for OI in the constitutive model, a linear relationship was assumed between the multi-photon derived fiber parameter and the Gasser-Ogden-Holzapfel dispersion parameter. An OI=1 (ie, anisotropy) corresponded to a k=0 whereas an OI=0.5 (ie, isotropy) corresponded to a k=1/3.

Two regressions were performed: in the first one the material parameters were estimated with the structural parameters fixed at values determined by the imaged-based analysis and in the second one both material and structural parameters were estimated by the regression analysis (ie, mechanically-estimated structural parameters rather than histologically-derived). Each tissue half of both normal and aneurysmal aortic tissues were fit separately to model the aorta as an experimentally dissected bi-layered vessel. Regression adopted non-linear least squares method via the Levenberg–Marquardt algorithm to minimize the squared differences between the stress–stretch data and the theoretical strain energy function predictions. Optimization was performed in several steps starting from different constitutive parameter values, to guarantee that global rather than a local maximum was reached. The linear part of stress-stretch response was fitted first using the C parameter, and then the other parameters were derived with C kept in a certain range.

Finite element modeling

Numerical simulations were performed on two representative models of BAV ATAA and TAV ATAA, each with an aortic diameter of 54 mm. Electrocardiogram (ECG)-gated computed tomography angiography (CTA) scans were used to reconstruct ATAA geometries, according to our previously published finite element studies [11, 12]. Reconstructions included the aortic valve morphology modeled at fully opened shape. Then, ATAA geometries were imported in ABAQUS code (ABAQUS v6.12, SIMULIA Inc., Providence, RI) and meshed as shell by 4-node quadrilateral elements using a partitioning approach. Specifically, ~14,000 elements were adopted to mesh each model, and this can be considered a sufficient number according to convergence studies carried out by Nathan et al [16] to model the human thoracic aorta. The aortic wall was modeled as a bi-layered experimentally dissection (ie, both ADV-DEL and INT-DEL), hyperelastic material whose constitutive parameters were derived from regression analyses (see Table 1 and 2). Material parameters were calculated by two regression analyses: (I) based on structural parameters derived by imaged-based analysis, (II) based on both material and structural parameters estimated by mechanical response of aortic tissue specimens. Wall thicknesses were 1 mm and 0.7 mm for ADV-DEL and INT-DEL layers, respectively, as measured experimentally [6]. Tie contact conditions were used between the two aortic layers. Local material directions in each element were set using ABAQUS by means of multiple cylindrical coordinate systems with origins in the longitudinal axis of the ascending aorta. Large deformation was considered using Dynamic/Implicit formulation in ABAQUS software while the distal ends of supra-aortic vessels, the aortic valve and the descending aorta were fixed in all directions. ATAA models were loaded at mean aortic pressure of 80 mmHg. In order to assess the importance of accurate constitutive modeling, the mechanical properties derived by the fitting of the tensile testing data with the isotropic, strain energy function proposed by Raghavan and Vorp [17] were also used for comparison with fiber-reinforced constitutive model. The constitutive material parameters were set directly in ABAQUS using the implemented formulation of Gasser-Ogden-Holzapfel model while the isotropic material formulation was set using a user-defined UHYPER subroutine.

Table 1.

Material parameters of Gasser-Ogden-Holzapfel constitutive model and goodness of fit (ie, range of values) with the γ and k structural parameters obtained from multi-photon imaging analysis

	C (kPa)	k (kPa)	k	γ (deg)	k	OI	R	NRMSE
Non-Aneurysmal Aorta
ADV-DEL	5.5±4.8	417.32±175.7	16.8±17.2	11.0±4.8	0.23±0.02	0.66±0.03	0.98–0.89	0.21–0.45
INT-DEL	8.2±3.6	232.4±149.2	21.8±15.3	16.9±1.2	0.22±0.01	0.67±0.01	0.94–0.87	0.37–0.51
BAV ATAA
ADV-DEL	7.9±6.2	110.2±69.7	16.8±10.2	40.5±13.9	0.25±0.09	0.62±0.04	0.96–0.85	0.26–0.55
INT-DEL	6.6±8.2	138.3±88.4	17.6±12.2	29.5±14.3	0.26±0.09	0.63±0.03	0.99–0.87	0.16–0.53
TAV ATAA
ADV-DEL	4.0±3.0	113.8±51.5	14.6±5.2	34.1±10.1	0.27±0.02	0.60±0.04	0.98–0.92	0.21–0.41
INT-DEL	5.6±3.9	157.9±67.9	15.1±9.7	31.6±11.2	0.27±0.01	0.60±0.03	0.98–0.88	0.16–0.46

Table 2.

Material parameters of Gasser-Ogden-Holzapfel constitutive model and goodness of fit (ie, range of values) with the k and γ structural parameters derived from the macroscopic mechanical response of tensile testing rather than the multi-photon imaging analysis

	C (kPa)	k (kPa)	k	γ (deg)	k	R	NRMSE
Non-Aneurysmal Aorta
ADV-DEL	4.7±3.4	419.0±155.6	12.2±7.8	27.0±3.8	0.29±0.04	0.98–0.90	0.16–0.41
INT-DEL	6.3±2.3	413.7±120.1	3.1±2.1	29.4±11.2	0.30±0.02	0.99–0.91	0.10–0.39
BAV ATAA
ADV-DEL	5.4±4.2	132.9±98.1	7.4±8.2	42.9±13.5	0.17±0.14	0.98–0.91	0.15–0.41
INT-DEL	5.9±4.9	177.7±110.6	7.4±11.1	35.5±14.8	0.29±0.03	0.99–0.91	0.12–0.38
TAV ATAA
ADV-DEL	4.5±3.4	112.6±88.3	8.3±6.1	42.4±3.2	0.20±0.11	0.98–0.92	0.21–0.43
INT-DEL	5.4±4.2	168.9±73.5	8.5±5.9	58.3±17.8	0.27±0.05	0.99–0.92	0.15–0.40

Statistical analysis

One-way analysis of variance, followed by the Holm-Sidak post hoc test for all pair-wise comparisons, was performed to determine the significance among the image-based parameters as well as the constitutive parameters. A sensitivity analysis was performed to study the influence on the simulation response (ie, wall stress) of a change to one constitutive parameter. Specifically, one constitutive parameter was varied of ±10% with the others being fixed at constant values, and then the wall stress change was computed in the ATAA wall. Sensitivity to the selection of image-based microstructural parameters was also evaluated and compared to mechanically-derived microstructural parameters. Statistical analyses were performed using SPSS software (IBM SPSS Statistics, New York, NY) while data were presented as the mean±standard deviation. The correlation coefficient (R) and the normalized-root-mean-square-error (NRMSE) were used as a measure for the “goodness of fit”.

Results

Multi-photon imaging and analysis

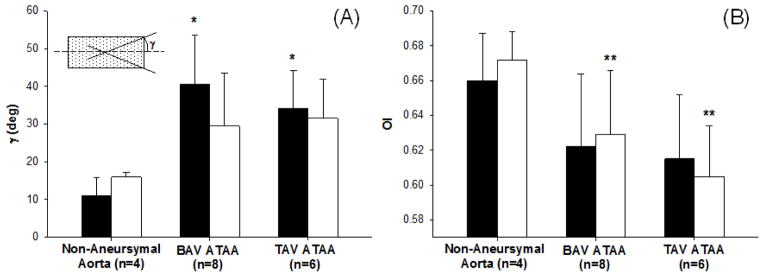
Digital image analysis of multi-photon images of the collagen and elastin fiber network of non-aneurysmal aorta and aneurysmal aorta with either BAV or TAV in the dissected medial plane of a specimen cut along CIRC direction revealed that both elastin and collagen fibers are oriented in parallel configurations (Fig. 1). A statistical significant change was noted for the average angle of collagen fiber orientation in ADV-DEL half of the non-aneurysmal aorta (γ_INT-DEL =11.0±4.8 deg, n=4) when compared with BAV ATAA (γ_INT-DEL =40.5±13.0 deg, n=8) and TAV ATAA (γ_INT-DEL =34.1±10.2 deg, n=6) (Fig. 2). For the INT-DEL half, the collagen fiber angle of non-aneurysmal aorta appeared to be smaller than both BAV ATAA and TAV ATAA. Overall, the OIs of non-aneurysmal experimentally-dissected half (OI_ADV-DEL=0.66±0.02 and OI_INT-DEL=0.67±0.01, n=4) were found significantly greater than that of both BAV ATAA (OI_ADV-DEL=0.62±0.04 and OI_INT-DEL=0.63±0.03, n=8) and TAV ATAA (OI_ADV-DEL=0.61±0.03 and OI_INT-DEL=0.60±0.03, n=6). These findings suggest that ATAAs have a less oriented collagen microstructure than non-aneurysmal aorta in experimentally-dissected specimens.

Fig 1.

(A) Example of multi-photon microscopy images (stack of 120 μm) of elastin (green) and collagen (red) fibers in the medial dissected plane of non-aneurysmal aorta, BAV ATAA and TAV ATAA in both ADV-DEL and INT-DEL layers; (B) processed image with small arrows in blue that follow the direction of collagen fibers and (C) histogram of fiber angle

Fig 2.

(A) Fiber angle for ADV-DEL (black squares) and INT-DEL (white squares) halves obtained by multi-photon imaging analysis, * significantly different from ADV-DEL non-aneurysmal aorta (P<.05); (B) orientation index for ADV-DEL (black squares) and INT-DEL (white squares) layers, ** significantly different from INT-DEL non-aneurysmal aorta (P<.05)

Tensile testing and constitutive parameters

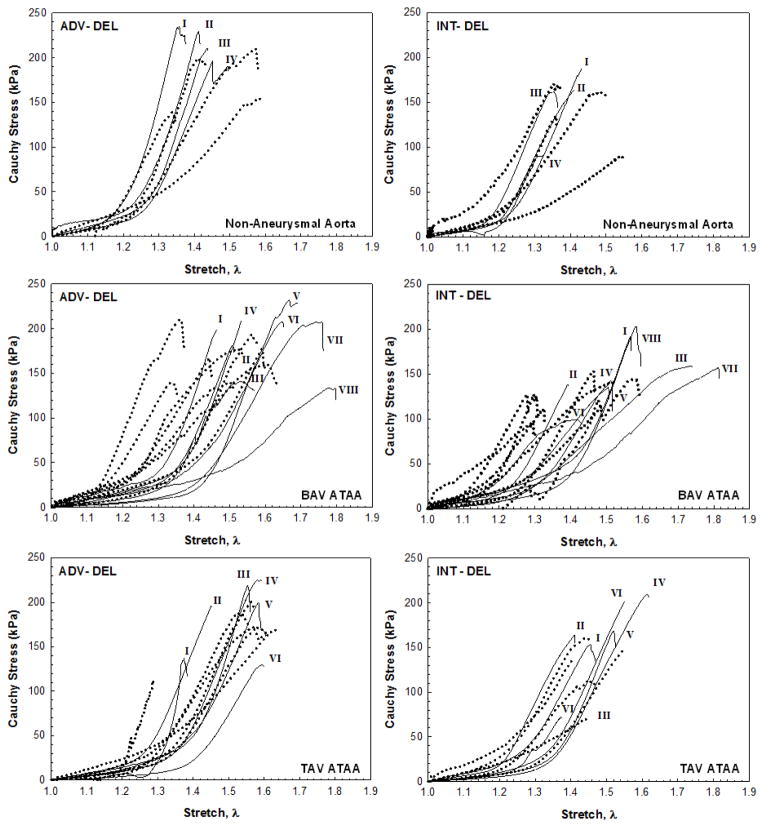
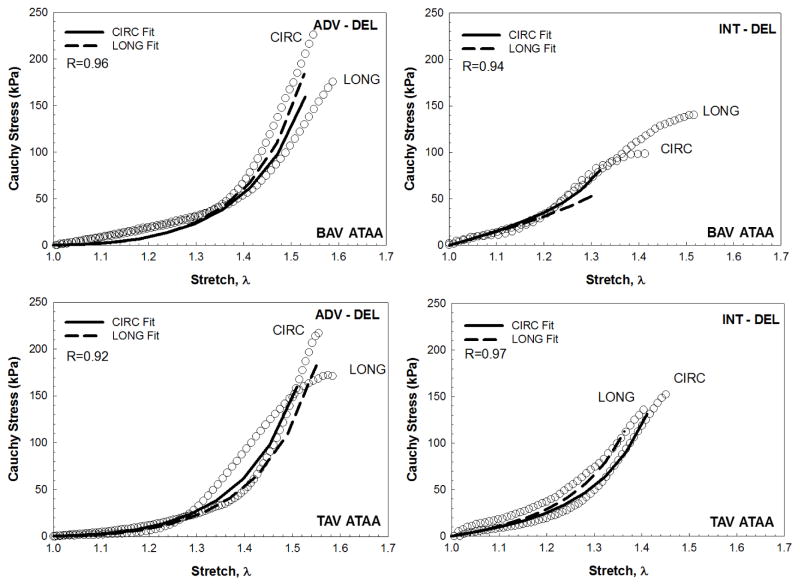
A highly non-linear mechanical response was exhibited by the experimentally-dissected tissue halves of the non-aneurysmal aorta and ATAAs with BAV and TAV (Fig. 3). The biomechanical behavior of ADV-DEL halves shows slightly higher strength than that exhibited by INT-DEL halves. The Cauchy stress–stretch curves were fit by the fiber-reinforced constitutive model with the structural parameters fixed at values quantified by multi-photon imaging analysis (Fig. 4 and Table 1). Material parameters were identified for the 1–1.4 stretch range or for lower values when specimens failed shortly. Fits provided values of R ranging between 0.98 and 0.85, and this span is likely caused by the constraining of both fiber angle and OI parameters. Such a result motivated a further fitting analysis with all five of Gasser-Ogden-Holzapfel parameters derived from the macroscopic mechanical response of both ADV-DEL and INT-DEL halves. Under this condition, the range of R was narrower than in the previous attempt while the NRMSE was low by suggesting a satisfactory fitting of tensile testing data (Table 2). The two sets of constitutive parameters differs mainly for both γ and k. Indeed, a significant difference was observed for the fiber angles of experimentally-dissected non-aneurysmal specimens predicted by the mechanical response (γ_ADV-DEL = 29.4±11.0 and γ_INT-DEL = 27.0±3.8) with those obtained from imaging analysis (γ_ADV-DEL = 11.0±4.8 and γ_INT-DEL =16.0±1.2, n=4, P<.05).

Fig 3.

Uniaxial stress-stretch responses for ADV-DEL and INT-DEL layers in CIRC (solid line) and LONG (dot line) orientations of non-aneurysmal aorta (top row), BAV ATAA (middle row) and TAV ATAA (bottom row); labels indicate specimens obtained from same tissue

Fig 4.

Representative fitting curve and corresponding stress-stretch data for ADV-DEL and INT-DEL layers of BAV ATAA (top row) and TAV ATAA (bottom row)

Finite element analysis and influence of constitutive parameters

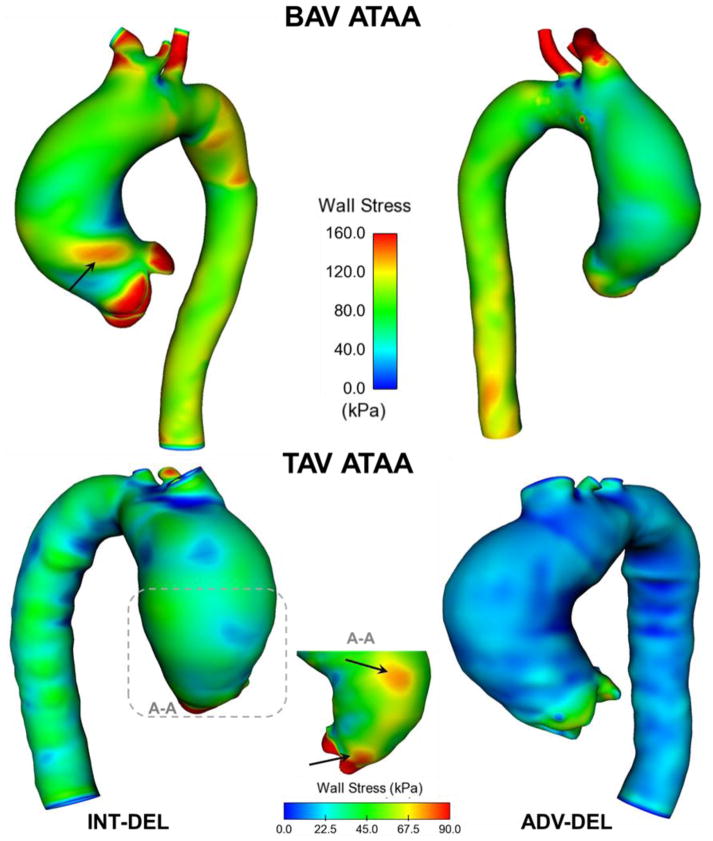
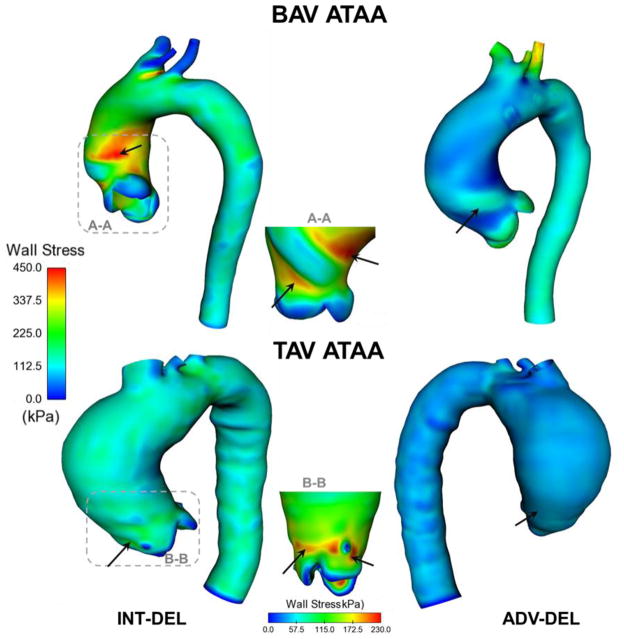
Local maxima of wall principal stress were found in the experimentally-dissected aneurysmal ascending aortic specimens (Fig. 5). Specifically, both the BAV ATAA and TAV ATAA exhibited peak of wall stress in regions corresponding to the sino-tubular junction, with BAV patients exhibiting a slightly higher stress magnitude than that of TAV ATAA. Although the INT-DEL half exhibited higher wall stress than ADV-DEL half, the stress distribution did not change appreciably between aortic layers of ATAA models. The isotropic strain energy function was found to alter the stress distribution of the aneurysmal wall when compared to that of the anisotropic formulation (Fig. 6). This difference was more remarkable for the isotropic modeling of the BAV ATAA, which displayed high wall stress even in the lesser curvature of the aneurysmal aorta. Most aortic dissections occur however with a transverse tear along the greater curvature of the aorta [18], and this may suggest the incapacity of the isotropic constitutive modeling to predict the location at greater risk to rupture or dissect.

Fig 5.

Comparison of maximum principal stress in both ADV-DEL (right models) and INT-DEL (left models) for both BAV ATAA and TAV ATAA simulations utilizing the anisotropic, fiber-reinforced structural model with structural parameters quantified by multi-photon imaging analysis; the black arrows indicate local maxima of wall stress

Fig 6.

Comparison of maximum principal stress in the ADV-DEL of both BAV ATAA and TAV ATAA simulations utilizing isotropic material properties (left models) and anisotropic material properties (right models); the black arrows indicate local maxima of wall stress

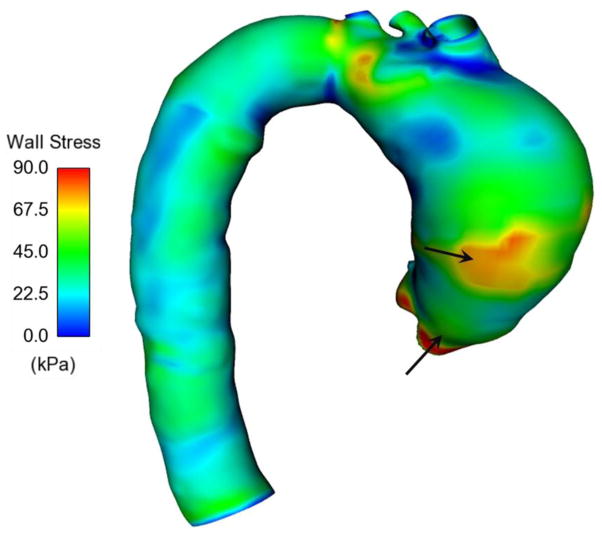
Sensitive analysis was performed using a subset of wall stress values determined in a stretch range between 1.06 and 1.35. This analysis allowed us to explore how the numerical model responded to the fitting errors that occur when the image-derived structural parameters were constrained during fitting analysis. We assumed the set of constitutive parameters derived from the mechanical response (see Table 2) as reference data since these parameters provided a low range of R values. Sensitive analysis revealed that the parameter set derived from both the mechanical response and multi-photon data affects the relative magnitudes of wall stress (NRMSE =0.383 for BAV ATAA and NRMSE =0.370 for TAV ATAA) as well as the stress distribution (Fig. 7). In a different way, the other sensitivity analysis to a change in one constitutive parameter demonstrated that the wall stress is relatively insensitive to errors related to ±10% change in the magnitude of constitutive parameters (Table 3).

Fig 7.

Distribution of maximum principal stress in TAV ATAA obtained with all five Gasser-Ogden-Holzapfel parameters derived from the macroscopic mechanical response of ADV-DEL halves; note that there is no appreciable difference in the wall stress distribution obtained with multi-photon derived parameters (see Fig 5).

Table 3.

NRMSE observed by a change of ±10% in the constitutive parameters; the wall stress in twenty nodes (corresponding to a stretch range of 1.06–1.35 close to maximum aortic diameter) was used for sensitivity analysis.

	C	k1	k2	γ	k
+10%	0.0267	0.0285	0.0026	0.0176	0.1091
−10%	0.0284	0.0288	0.0028	0.0180	0.1723

Discussion

In this study, the collagen fiber microarchitecture of the medial layer was quantified from multi-photon micrographs of experimentally-dissected human ascending aortic specimens obtained from ATAAs with different aortic valve morphology. Thus, the fiber-reinforced mechanical response of aneurysmal aorta was evaluated to assess the importance of accurate constitutive modeling using both error analysis and numerical simulations on a bi-layered ATAA model. The results support prior work that identified altered aortic medial microstructural properties for both BAV ATAA and TAV ATAA when compared with the normal ascending aorta [8, 9]. In this study, we utilized fiber distribution quantified from multi-photon microscopy to demonstrate an influence of vessel wall microstructural features on the resulting wall stress of patient-specific ATAA models.

In the aortic media, collagen fibers are generally organized in thick bundles in a parallel arrangement and thin fibers oriented perpendicularly to these bundles. However, a dramatic morphological change in collagen bundles may occur in presence of aneurysm or dissection, with fibers being more thin and scattered. Sariola et al [19] found that interlaminar collagen deposition in dissected specimens with cystic medial degeneration was more concentrated when compared with the non-aneurysmal aorta. Sokolis and collaborators [20] reported the presence of collagen fiber bundles even in the subintimal layers of the right-lateral region of TAV ATAA. Fiber microarchitecture was found to differ in the various tissue planes among ATAAs with different aortic valve phenotype [8]. Specifically, collagen fibers were found to be more oriented in the radial direction of the outer medial layers of BAV ATAA when compared with the non-aneurysmal aorta. Our findings are consistent with those documented by Phillippi et al. [9] who demonstrated that the collagen fibers of the intact aorta are more aligned in BAV ATAA specimens compared to TAV ATAA. Although collagen fibers distributions were not found statistically significant in this study, these differences in fibers orientation are expected to have a profound impact on the biaxial behavior and on the level of mechanical anisotropy. According to D’Amore et al. [21], numerical and experimental analyses provided evidence that a simple shift of 0.05 in fibers network OI might induce significant anisotropy. More specifically, while an isotropic polyurethane scaffold reported no difference in strain between the preferential and cross-preferential direction, an anisotropic polyurethane scaffold fabricated with the same material but characterized by a OI 0.05 higher than the previous one reported difference in strain between the preferential and cross-preferential of 20–30% (both scaffolds had a 7.5 MPa elastic modulus, strain were evaluated at 300 kPa equistress). Moreover, we observed that specimens from non-aneurysmal ascending aorta were found to exhibit a majority of fiber angles symmetrically oriented in the circumferential direction which was consistent with other reports [22, 23]. This supports the notion that ATAAs in patient with BAV implicate a matrix remodeling process distinct from that of TAV ATAAs [9].

Collectively, these data on the deranged collagen fiber architecture might explain the reduced biomechanical strength of the aneurysmal aorta compared to the normal ascending aorta found previously by our group [6]. Biaxial and uniaxial tensile tests have demonstrated a non-linear and stiffer behavior of ATAAs [24, 25] with BAV ATAA having greater failure strain and tensile strength than that of TAV ATAA [7], and with a decrease in dispensability varying with the patient age and aortic location [26–28]. In contrast, other studies documented comparable values of ultimate tensile stresses for the aneurysmal versus non-aneurysmal aorta [29, 30]. Haskett and collaborators [22] demonstrated that the increased stiffness of abdominal aorta is associated with decreased collagen fiber alignment in the circumferential direction, and this may predispose to aneurysm development. Such a result is consistent with the decreased circumferential fiber directionality and fiber alignment found in our study for the experimentally-dissected aneurysmal aorta compared to the non-aneurysmal aorta (see Figs 1 and 2). Additionally, the aorta is stiffer in the direction orthogonal to the preferred fiber orientation so that the decreased circumferential directionality may portend the tearing of aneurysmal aorta. However, most of these studies considered the aortic wall to be homogenous across aortic layers, an assumption that may lead to inaccurate predictions of wall stress distribution. Our results also revealed a weaker behavior of the inner, experimentally-dissected aortic layer when compared to that of the outer layer (Fig. 3). As it was shown by numerical simulations (Fig. 5), the fiber-reinforced and heterogeneous mechanical properties induces a dissimilar distribution of wall stress between aortic layers, and the stress discontinuity at interface layer can be considered a putative factor for tearing of the aneurysmal aorta. If the aorta is assumed to be homogenous and isotropic, disruption of layering and intermolecular or cellular forces cannot be considered. Heterogeneity of layer- and region-specific material properties of aneurysmal aorta have been documented by several groups [31–33]. The findings here suggest that isotropic modeling of ATAAs may also lead to an inability to accurately predict locations at the greatest risk of dissection or rupture (Fig. 6).

It is evident that accurate estimations of wall stress in ATAAs require not only the knowledge of the mechanical and structural properties in BAV versus TAV, but also the use of appropriate constitutive modeling. There is a growing interest in moving from basic phenomenological constitutive modeling to a microstructurally-based approach to provide constitutive parameters with a more natural and physical interpretation. Rodriguez et al. [34] compared the ability of an isotropic purely-phenomenological model and an anisotropic structurally motivated Gasser-type model to fit data for abdominal aortic aneurysms reported by Vande Geest et al [35]. The latter demonstrated that the Fung-type model was unable to fit the more isotropic behavior of young abdominal aortic tissues. Therefore, there is need for a new paradigm for stress analyses including microstructurally-based models since finite element stress estimation can provide better indicators of the likelihood for rupture or dissection than the clinically used maximum diameter criterion [36]. Towards this end, we emphasize the use of fiber-reinforced constitutive modeling to incorporate the microstructural defect of collagen fibers inherent to the aneurysmal ascending aorta.

Study limitations

Imaging of aortic media was performed after initial delamination testing [6], and this let presume fiber tissue damage that may have compromised our imaging findings. It should be noted that the highest Cauchy stress on the peel arms during delamination testing was 33 kPa for aneurysmal tissue specimens and 40 kPa for the non-aneurysmal aorta, according to our delamination testing on tissue samples collected from n.31 patients [6]. This suggests that the stress exerted on tissue specimens during delamination testing is quite low when compared to that occurring in the steep part of the stress-stretch curve in a tensile test. Therefore, it can be speculated that collagen fibers quantified by imaging analysis were not likely altered by the artificial delamination. Although delamination is destructive testing modality, the fiber bridging fracture mainly interests elastin rather than collagen [6]. Additionally, multi-photon images of intact aortic tissue samples collected by Phillippi et al. [9] showed a fiber distribution similar to that of experimentally-dissected tissue halves illustrated in this study. These facts support our hypothesis of minimal fiber damage after delamination testing. The standard protocol adopted in other studies [31, 37] consists to dissect the aortic tissue layers with a surgical scalpel or other medical instruments while pulling apart the dissected layer. Such procedure leads therefore to tissue damage as well and do not markedly differ from a delamination test using a controlled pulling force to dissect tissue layers. To our knowledge, this delamination testing represents the only available model of dissection.

Moreover, the limited number of aortic samples could have underscored potential differences in BAV ATAA versus TAV ATAA so that additional data are needed to strengthen the results of comparisons presented for different aortic valve morphology. The adopted fiber-reinforced constitutive model has not the flexibility to capture the full transversely isotropic material behavior induced by the transmural content and orientation of collagen fibers and may show low capability to characterize soft tissues with high fibers dispersion as found by our imaging analysis. Sensitivity analysis was performed at mean pressure of 80 mmHg when collagen fibers are not fully recruited so that error data can be affected by the adopted pressure boundary condition. The finite-element model partially considers the heterogeneity of layer-specific aortic mechanical properties and neglects the influence of residual stress and thickness changes.

Conclusions

Multi-photon imaging derived microstructural parameters of collagen fiber architecture were combined with uniaxial tensile testing on experimentally-dissected tissue halves to provide an anisotropic constitutive model of the aneurysmal aorta with either BAV or TAV. Numerical simulations on ATAA models with two aortic layers were performed to assess the role of both material and structural parameters on the wall stress distribution as well as the importance of anisotropic constitutive modeling. Our results support the hypothesis that an inherent defect in collagen fiber microarchitecture characterizes the aneurysmal aorta. This information is paramount for accurate finite element predictions of wall stress in ATAAs with either BAV or TAV. Future studies will be undertaken to incorporate more refined constitutive formulations including further descriptors of tissue microstructure [38] or based on multiscale homogenization approaches that couple microscale histological features with nanoscale biochemical properties [39]. Indeed, the use of more refined constitutive formulations can lead to better quantitative predictions of aortic wall stresses and thus to improved risk stratifications of ATAAs.