The Solution Structural Ensembles of RNA Kink-turn Motifs and Their Protein Complexes

Abstract

With the growing number of crystal structures of RNA and RNA/protein complexes, a critical next step is understanding the dynamic behavior of these entities in solution in terms of conformational ensembles and energy landscapes. To this end, we have used X-ray scattering interferometry (XSI) to probe the widespread RNA kink-turn motif and its complexes with the canonical kink-turn binding protein L7Ae. XSI revealed that the folded kink-turn is best described as a restricted conformational ensemble. The ions present in solution alter the nature of this ensemble, and protein binding can perturb the kink-turn ensemble without collapsing it to a unique state. This study demonstrates how XSI can reveal structural and ensemble properties of RNAs and RNA/protein complexes in solution and uncovers the behavior of an important RNA/protein motif. This type of information will be necessary to understand, predict, and engineer the behavior and function of RNAs and their protein complexes.

Introduction

The functional importance of RNA, beyond conveying genetic information, has become increasingly clear in the modern era of molecular biology. tRNAs play the central role in the so-called ‘second genetic code,’ structured RNAs act as enzymes, and abundant non-coding RNAs directly regulate gene expression^1–3. RNAs are essential to epigenetics, chromosome maintenance, alternative pre-mRNA splicing, protein synthesis, and protein export^3–9.

Over the past two decades, X-ray crystallography has increasingly provided invaluable atomic-level information about RNA and its complexes. These structures have enabled a new mechanistic understanding of RNA biology and driven the development of new, testable models. To raise our understanding of RNA and RNA-mediated processes to the next level, and to develop predictive quantitative models, the ensemble nature of RNA structure must be investigated. Folding, complex assembly, and function are determined by the probability of adopting particular structures on an energy landscape, but these landscapes and their resultant ensembles remain poorly understood for RNA and RNA/protein complexes. Crystal structures are points on these landscapes, and much of the extant structural data from solution-based approaches report on a most-populated state or an average structure^{10, 11}.

The need for solution structures and structural ensembles is particularly pressing for RNA, because RNA function typically requires a series of conformations and rearrangements between them. Moreover the structure of polyelectrolytes, like RNA, are expected to be highly sensitive to solution conditions^{12, 13}. NMR residual dipolar coupling (RDC) experiments in particular have underscored the importance of direct solution studies of RNA conformations¹⁴. They have revealed that simple helix-junction-helix (HJH) elements populate an ensemble of conformations dictated by the junction topology and populate a subspace of a larger sterically allowed space¹⁵. Understanding the structural range of these ensembles and their conformational entropy in unfolded, folded, and different functional states will be necessary for the development of a quantitative and predictive understanding of RNA behavior and function^{11, 16}.

While NMR RDC measurements have been invaluable in revealing the dynamic properties of simple isolated RNA junctions, it is difficult to apply RDCs to larger folded RNAs and to RNA/protein complexes, as will be needed to determine the properties of species that more closely resemble functional complexes. We therefore turned to an emerging structural method, X-ray scattering interferometry (XSI), which has previously been used to probe DNA conformational ensembles in solution and report on structure and structural plasticity^{10, 17, 18}. We utilized XSI to obtain information about a recurring RNA motif, the kink-turn, and its RNA/protein complexes.

The kink-turn is a common RNA motif typically consisting of a three-nucleotide bulge flanked by a GA/AG tandem base pair, which stabilizes a kink of more than 90 degrees and brings the two flanking helices together (Fig. 1a)^{19, 20}. Such sharp helix bends are necessary for RNAs to fold into compact three-dimensional structures. The kink-turn motif is extremely widespread in biology, and is found in almost all types of structured RNAs²⁰. Early studies showed that kink-turn RNAs can form a kinked structure independent of protein^{21, 22}, but naturally occurring kink-turns are often protein-associated. The most common kink-turn binding proteins are the L7Ae protein, studied herein, and its homologs. Complexes of kink-turn RNA and L7Ae-like proteins are widespread and conserved components of the ribosome, box C/D s(no) RNPs, RNase P and the spliceosome^{19, 23, 24}.

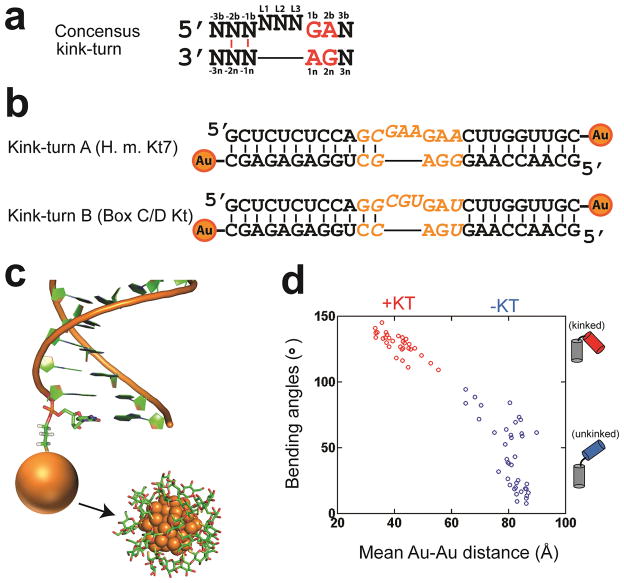
Figure 1. RNA kink-turns and Au-conjugated constructs.

(a) The consensus kink-turn sequence. The -1 and -2 positions are usually canonical base pairs (red lines)^{19, 23}. (b) Kink-turn sequences investigated in this study. Kink-turn A (KtA) and Kink-turn B (KtB) are also known as H.m. Kt7 and Box C/D kt, respectively. For simplicity, they are referred to as KtA and KtB herein. Au nanocrystals were attached to the 3′ ends of each strand. The varied kink-turn motif regions are shown in orange; the flanking sequences are the same for the two constructs. (c) Illustration of an RNA helix labeled with a Au nanocrystal (orange sphere) at its 3′ end through a three-carbon thiol linker (3′-thiol-modifer C3, Glen Research). A full representation of the nanocrystals (noted by arrow) is reproduced from Figure 2c of reference 18, including its thioglucose shell, and was generated based on a sub-structure of the nanocrystal reported in reference 48 and the experimental analysis of reference 49. (d) The distribution of inter-helical bending angles and the expected mean Au-Au distance for 70 crystal structures of 0–3 two-way junctions (i.e., 3 nt bulges) with (red) and without (blue) a kink-turn type 5′-flanking sequence: GA/AN (80% are GA/AG). See Online Methods for a detailed description of how these representative structures were selected and how the expected Au-Au distances were calculated.

There are abundant crystal structures of kink-turn RNAs, most of which are components of larger RNAs and RNA/protein (RNP) complexes.^{23, 25} Despite this wealth of information from crystal structures, we know little about the structures and structural ensembles of kink-turns and other folded RNAs in solution^{11, 16} and still less about the dynamic ensemble of RNAs within RNP complexes. For example, does a kink-turn motif, free or protein bound, adopt a single kinked conformation in solution, or populate a limited or diffusive ensemble of kinked conformations? Does the kink-turn structure change under different solution conditions and upon protein binding, and if so how? Do crystal structures match the true structures of kink-turns in solution? The answers to these questions are key to unraveling the fundamental molecular behavior of kink-turns and, in turn, to understanding their impact on the biological function of RNAs and RNA/protein complexes that contain kink turns.

To answer these questions, we determined the structural ensemble for two kink-turn motifs with and without the L7Ae protein across a range of solution conditions. We have shown that different counterion environments reshape the kink-turn structural ensemble, and that association with L7Ae protein steers the ensemble to a set of compact conformations.

RESULTS

Applying XSI to kink-turn RNA

We chose to study two well-studied kink-turn sequences, which we refer to as KtA and KtB for simplicity (Fig. 1b) ^{21, 26}. Study of these RNAs allow us to compare XSI data with prior data, to build on these prior studies, and to highlight the unique information that can be obtained by XSI. The KtA sequence (Kt7) occurs in ribosomes, and KtB (box-C/D kink-turn) is found in C/D box RNA and is a natural target of the L7Ae protein used in this study²⁷. We determined the effect of solution conditions and the L7Ae protein on the conformations of KtA and KtB.

We attached Au nanocrystrals to the ends of each kink-turn containing RNA duplex (Figs. 1b and 1c), following approaches used with DNA^{17, 18}. XSI works by isolating the scattering interference between these nanocrystals and then converting that interference pattern into a distance distribution by Fourier transformation^{10, 28}. XSI cannot, like X-ray crystallography, provide Ångstrøm-resolution information for all of the atoms in a structure, but it can provide Ångstrøm-level Au-Au distances in solution for specifically positioned Au nanocrystals. These distances can be determined across a range of solution conditions and for an ensemble of conformations^{10, 17}. For RNA, Au-Au positional information can be particularly revealing, because RNA helices are highly rigid and one is often interested in how junctions and/or bound proteins orient them; in turn, the positions of these helices and their attached tertiary motifs determine the overall architecture and conformational probabilities of an RNA^{12, 29, 30}.

As the RNA bends, the Au-Au distance is expected to decrease (Fig. 1d). The observed distance also depends, to a lesser extent, on the positions of the nanocrystal with respect to the helices to which they are attached, the geometry of the helices, and any dynamics associated with the helices and the attachments. These modest kink-turn independent effects have been measured, following approaches used for determining these parameters for DNA helices and their Au nanocrystal attachments,^{18, 31} and are modeled as described in Online Methods.

XSI reveals the solution distributions of kink-turn RNA

Our XSI data described below agree with the prior results suggesting that kink-turn RNA can exist as an equilibrium between kinked and unkinked RNA^{21, 32} and extend the previous results by revealing kink-turn structures and structural distributions in solution. These data provide strong evidence for complex, multi-state behavior within both the unkinked and kinked states–behavior that, in general, would be difficult to uncover with traditional approaches and to further parse into physical models.

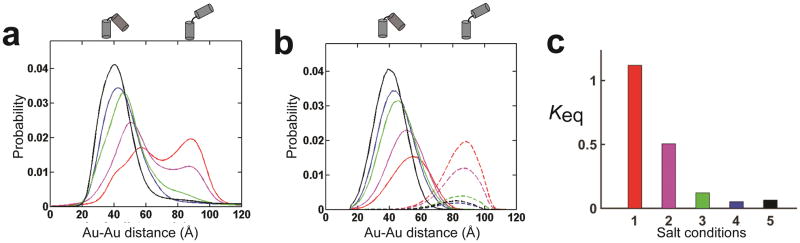
Figure 2a shows the Au-Au distances probability distribution for KtA (Fig. 1b) across a range of solution conditions (1–5 in Fig. 2, see legend of Fig. 2a for detail). The five solution conditions (legend of Fig. 2a) varied both salt type and concentration, from low to high monovalent cation concentrations (condition 1, 2 and 4), near physiological conditions (150 mM KCl and 1 mM MgCl₂;^{33, 34} condition 3), and high divalent cation concentration (condition 5). These salt conditions also allowed direct testing of whether a kink-turn responds specifically to Mg²⁺, as the only difference between conditions 2 and 5 is the presence or absence of 10 mM Mg²⁺. For convenience, we also ordered the salt conditions from 1 to 5 to give a monotonic effects on the kink-turn and helix conformational ensembles (Fig. 2 & Supplementary Results, Supplementary Table 1) and this provided a convenient way to depict the data. Also, given the monotonic conformational behavior of the helix and kink turns, this order likely reflects the relative degree of ionic screening of the salt solutions, including the far more efficient polyelectrolyte screening capability of Mg²⁺ and other divalent cations compared to monovalent ions for a given ionic strength ^{13, 35, 36} (Online Methods).

Figure 2. The salt dependence of the KtA (Kt7) kinking equilibrium.

(a) The measured Au-Au center-to-center distance distribution for KtA (Fig. 1b) under salt conditions 1–5 (see below) plotted in red (1), magenta (2), green (3), blue (4), and black (5). Salt conditions 1–5 are (1) 20 mM Na⁺ and 30 mM Tris·HCl, (2) 60 mM Na⁺ and 70 mM Tris·HCl, (3) 10 mM Na⁺, 1 mM Mg²⁺, 150 mM K⁺ and 70 mM Tris·HCl, (4) 510 mM Na⁺ and 70 mM Tris·HCl, and (5) 60 mM Na⁺, 10 mM Mg²⁺ and 70 mM Tris·HCl with the common conditions of pH 7.4 and 15 °C. Referred to as 1–5 in the text, salt conditions 1–5 have been ordered to simplify presentation of the results (Online Methods and Supplementary Table 1). (b) Ensemble models of KtA under salt conditions 1–5 for kinked (solid lines) and unkinked (dashed lines) states, with color coding as in a. Distributions were obtained using a basis set of X-ray crystallographic structures from the red and blue points, respectively, in Figure 1d (see Online Methods). Given the limited unkinked population under conditions other than salt condition 1, the compositions of the unkinked ensembles for salt condition 2 to 5 were modeled as the same as for condition 1. (c) The kinking equilibrium K_eq = [Unkinked]/[Kinked] for each salt condition calculated based on the analysis shown in b.

The kink turn RNA distribution is dependent on the ionic condition. Under conditions with weaker charge screening with only 20 or 60 mM Na⁺ (condition 1 and 2 in Fig. 2), we observed two peaks, one corresponding to distances expected for a standard junction (>60 Å, Fig. 1d and Fig. 2b) and one corresponding to a highly bent or ‘kinked’ state (<60 Å, Fig. 1d and Fig. 2b). The area of these two peaks were similar, with slightly less kinked state at 20 mM Na⁺ and slightly more at 60 mM Na⁺, similar to results from prior FRET data that gives a Na_1/2 of 72 mM for bending of this kink-turn sequence²¹. For solution conditions with stronger charge screening, with more Na⁺ (or K⁺) present and/or with Mg²⁺, the unkinked state nearly disappeared (Fig. 2a and 2c), also consistent with prior FRET and gel mobility data²¹.

Kinked KtA exhibits multiple and varying solution states

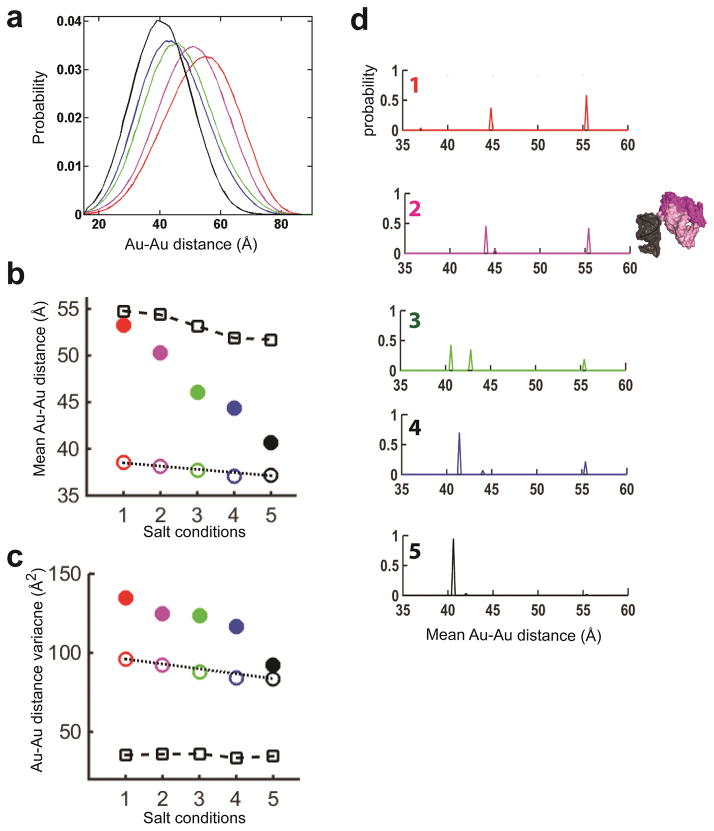
To assess the kinked state, we used a basis set of kinked and unkinked conformers like that in Figure 1c (see Online Methods for details) to deconvolute the distance distributions of Figure 2a into kinked and unkinked states (Fig. 2b). The kinked state distributions were re-plotted after normalization in Figure 3a. The change in the peak of the distance probability distribution for the kinked state as the salt conditions are changed (Fig. 3a) argues against any model that invokes only a single kinked conformation and instead supports a model in which there are multiple kinked conformations in solution.

Figure 3. The ensemble of the kinked state of KtA (Kt7) and its salt dependence.

(a) The kinked-state ensembles (solid lines in Fig. 2b) under salt conditions 1–5 (Fig. 2a legend) normalized to a total probability of 1. (The distributions appear broader than in Figure 2b (solid lines) because of a change in the x-axis scale.) (b, c) The mean (b) and variance (c) of the kinked-state distributions in a (closed circles; color-coding as in a). The standard error were 0.5 Å (b) and 10% of the total variance (c). Also plotted are the measured mean values (b) and variances (c) for a reference 12bp RNA duplex under salt conditions 1–5 (open squares; Online Methods) and the predicted mean values (b) and variances (c) for a single crystal structure of KtA (open circles, color-coded as in a; PDB 4BW0) to depict the small salt-dependent alterations in the Au-nanocrystal ensemble when only a single kink-turn conformation is present (Online Methods). (d) The kinked-state ensemble probability distribution under salt conditions 1–5 (top to bottom; color-coded as in a) determined from the fit to the basis set of Figure 1c. The mean Au-Au distances (binned in 1 Å increments) plotted in d use the expected Au-nanocrystal position for salt condition 5 to remove salt dependent variation in Au probe position, thereby allowing direct comparison of the kinked-state ensembles under different salt conditions. A three-dimensional representation of the two dominant conformers in the ensemble under salt condition 2 is included to the right of d2 to illustrate the range of helical orientations in the ensemble.

To analyze this shift more incisively, we plotted the salt dependent change in the mean Au-Au distance for the kinked population of KtA (Fig. 3b) and compared that to a hypothetical model in which the kinked KtA has a single kinked conformation (Fig. 3b) and this kinked form is salt independent such that the observed salt dependence of Au-Au distances would arise solely from the salt dependences of helix and Au nanocrystal. The helix and Au nanocrystal properties used in this comparison were determined using an RNA duplex control, as described in Online Methods. The mean distance changed from ~53 Å to ~41 Å for the kinked or ‘folded’ KtA (Fig. 3b), greatly exceeding the predicted change of ~2 Å for a kink with a fixed junction geometry (Fig. 3b) and the change of ~3 Å for a reference RNA helix (Fig. 3b). These data thereby provide strong evidence for the presence of multiple kink-turn conformers.

The shape of the conformational distributions at each condition provided additional structural information^{10, 17, 18}. Specifically, the larger variance of the kink-turn RNA, relative to the predicted variance for a single kink-turn conformer, provided evidence for the simultaneous occurrence of multiple kink-turn states at all but the highest salt condition where the observed variance and the predicted variance for a single kinked conformer were indistinguishable (Fig. 3c).

The above results indicate that the kinked kink-turn RNA cannot be accounted for by a single conformer and underscore the need to directly assess RNA conformations in solution. The XSI data for kinked population of KtA suggested that the average conformation becomes more kinked across the salt conditions studied (Fig. 3a, b, & d), consistent with increased electrostatic screening overcoming greater electrostatic repulsion in the more highly bent conformers^{10, 37}. Figure 3d shows that the conformations mainly fall in two regions of kink-turn Au-Au distances, one around 40–45 Å and the other around 55 Å. Varying occupancies of the conformers in these regions can account for the observed distributions across the salt conditions. Thus, the observed conformational ensembles could be reasonably described by a minimal model with two conformers. An ensemble with roughly evenly distributed conformers across a wide range of kink angles was ruled out. Although these XSI data cannot provide more detailed information about the distribution of states around 40–45 Å and 55 Å, pairwise distance distributions from additional Au nanocrystal pairs can help refine properties of conformational landscapes¹¹.

The ensemble nature of unkinked KtA and KtB

The results also provided evidence for an ensemble nature of the unkinked state of KtA from the data for the two lowest salt conditions where the unkinked state is sufficiently populated to obtain reliable ensemble information (Fig. 2b, Fig. 4a and Supplementary Fig. 1). To explore further the nature of the unkinked states and provide additional comparison of XSI data to more traditional approaches we investigated KtB (Fig. 1b), for which FRET studies indicated a failure to adopt the kinked state in the absence of bound protein³⁸.

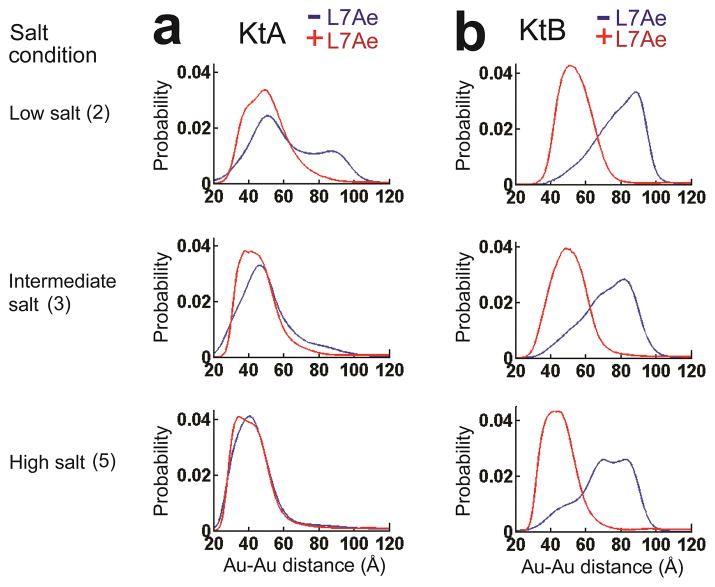
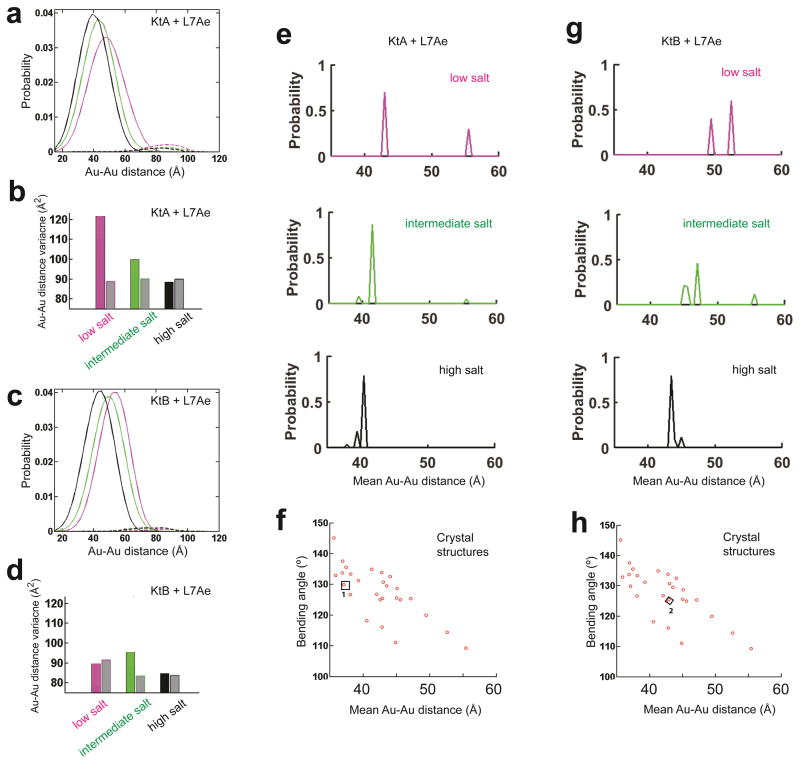
Figure 4. The KtA and KtB kink-turn conformational states without and with L7Ae.

The measured Au-Au center-to-center distance distribution for KtA (a) and KtB (b) without (blue) and with (red) bound L7Ae in 70 mM TrisHCl, pH 7.4, 10 mM sodium ascorbate and either 50 mM NaCl (low salt; Condition 2), 150 mM KCl and 1 mM MgCl₂ (intermediate salt; Condition 3), or 50 mM NaCl and 10 mM MgCl₂ (high salt; Condition 5). See the legend of Figure 2a and text for a description of the salt conditions, and see Online Methods for experimental details. The data for KtA without bound protein are reproduced from Figure 2a for comparison.

In agreement with analysis of folding by FRET²⁶, KtB remained predominantly in the unkinked rather than kinked state across the range of salt conditions studied (Fig. 4b). Nevertheless, a fraction of the molecules had an Au-Au distance of <60 Å, strongly suggesting the presence of a small amount of kinked RNA (cf. Fig. 4b and Fig. 1d), and this fraction increases as the electrostatic screening from the solution increases. The ability to detect a minor kinked population of KtB speaks to the power of XSI to provide distance information beyond an average value^{10, 28, 32}.

The peak Au-Au distance for unkinked KtB RNA changed with the solution condition, spanning a range of distances similar to that observed in crystallographic structures of non-kink RNA with three nucleotide bulges (Fig. 1d), and the Au-Au distances were much more broadly distributed than expected for a single conformation of the junction connecting the helices (Supplementary Fig. 1). The range of distances was similar to that for Tar RNA (Supplementary Fig. 1), which also has a three-nucleotide bulge and has been shown to be present in solution as a rather broad conformational ensemble³⁹. These results underscore the ability of XSI to deconvolute substates and to further reveal ensemble properties of those substates.

Kink-turn/L7Ae complexes retain a multiplicity of states

L7Ae is part of the box C/D sRNP, and its physiological target has the KtB sequence (Fig. 1b)²⁷. Biochemical studies have established that L7Ae binds its natural target KtB as well as KtA with nanomolar or stronger affinity^{21, 26}. Kink-turn RNA structures with bound protein exhibit a sharply kinked state, and solution studies have shown that kink-turn binding proteins can induce the kinked state^{26, 32}.

As expected, our XSI experiments showed that addition of L7Ae strongly promoted kinked states for both KtA and KtB (Fig. 4). Given their strong affinity and the general view of protein structure as selecting and restricting ligand conformations⁴⁰, one might have expected a common structure for each of the kink-turn RNA/L7Ae complexes across the range of salt conditions, although different conformations for the different RNAs complexed to L7Ae would have been reasonably expected given the range of conformations observed crystallographically for different complexes (Fig. 1d & ref 23).

We isolated the distance-probability distributions for the kinked state of the protein•RNA complexes, using basis sets of kinked and unkinked RNA structures as was done for the free kink-turn RNAs in Figure 2b above. These analyses, shown in Figures 5a–d, and the data of Figure 4 indicated that this simplest expectation was not met. I.e., the conformational states of the kink-turn RNAs within their complexes with the L7Ae protein changed across salt conditions (Figs. 4 & 5). The complexes of the two kink-turn RNAs also differed under matched solution conditions (Figs. 4 & 5). For KtA, which significantly populated the kinked state across all of the solution conditions, protein binding perturbed the kinked ensemble at the two lower salt conditions, further kinking it (Fig. 4a). Under these two conditions, low salt with no Mg²⁺ and a condition with Mg²⁺ that mimics the physiological condition, the distance variance for the KtA complexes was larger than predicted for a single kinked conformation (Fig. 5b). The variance decreased as ionic screening was further increased with the presence of 10 mM Mg²⁺ (high salt in Fig. 4a) consistent with multiple bound states that collapse to a single state or a set of similar states in the presence of high ion concentrations (Fig. 5b). The high salt state is consistent with the crystal structure of the isolated KtA•L7Ae complex (Fig. 5e, high salt & Fig. 5f)

Figure 5. The KtA•L7Ae and KtB•L7Ae ensemble and their salt dependence.

(a, c) The measured Au-Au center-to-center distance distribution for KtA•L7Ae and KtB•L7Ae (Fig. 1b) under low, intermediate, and high salt conditions (Condition 2, 3 and 5 in Fig. 2, colored in magenta, green, and black, respectively) decomposed into contributions from kinked (solid line in a and c) and unkinked (dashed line in a and c) conformations for KtA•L7Ae (a) and KtB•L7Ae (c). The very small amount of unkinked RNA (<6%; dashed lines) could represent damaged RNA or experimental noise. (b, d) The distance variance of the kinked ensemble for KtA•L7Ae (colored bar in b) and KtB•L7Ae (colored bar in d) compared with the predicted variance for a single kinked conformation (grey bars in b and d). (e, g) The probability distribution of the kinked ensemble for KtA•L7Ae (e) and KtB•L7Ae (g) at each solution condition, obtained by decomposing the kinked contributions (solid line in a and c) into contributions from basis set kinked conformations (f and h). The mean Au-Au distances of the conformers were binned with 0.5 Å intervals. (f, h) Basis set kinked conformations constructed using available crystal structures of kink-turns, including the isolated KtA·L7Ae (1 in f) and KtB·L7Ae (2 in h). f and h are aligned with e and g on their x-axes, respectively. The mean Au-Au distances plotted in e–h were obtained as described in Figure 3 in order to allow direct comparisons of the RNA structures without interference from salt-dependent Au-nanocrystal effects.

The complexes with KtA and KtB were different and behaved differently across the ionic conditions (Figs. 4 & 5, Supplementary Fig. 2). Unlike the progressive narrowing of KtA in its L7Ae complex with increasing ionic screening, KtB appeared to have distinct low and high salt distributions, each with narrow variance (Fig. 5d), and a broader distance distribution at intermediate ionic conditions. This behavior is consistent with a simple model, where KtB·L7Ae at the intermediate ionic condition, a mimic of the physiological condition, is a mixture of forms similar to the low and high salt forms, which are prevalent under conditions without and with 10 mM Mg²⁺, respectively (Fig. 5d & Fig. 5g). The KtB conformation when complexed with L7Ae in solution at high salt resembled the crystal structure of isolated KtB•L7Ae complex (Fig. 5g, high salt & Fig. 5h), as does that for KtA (see above).

The XSI data directly showed that differences between KtA and KtB in their crystal complexes with the L7Ae protein are also observed in solution, and that these conformations change across solution conditions. The results herein revealed a resemblance of the high salt KtA and KtB solution structures to their crystal structures, as might be expected for high salt crystallization conditions. Crystallization of RNA is often favored by high salt, likely in part due to the need to favor folded RNAs and RNA•protein complexes. In addition, a narrower conformational space of folded and complexed RNAs under high salt conditions in solution, such as the case with KtA, might facilitate crystallization and the formation of crystals that diffract well.

Kink-turn structures have been categorized as N1 or N3, representing the atomic positions on the adenine at position 2b (Fig. 1a) that alternatively accept a hydrogen bond from O2′ of the −1n nucleotide⁴¹. Structures within the N3 group span the entire range of bend angles observed herein, whereas N1 structures, at least those obtained crystallographically, correspond to only part of observed range (Fig. 6). The multiplicity of solution states observed for the kinked kink-turn and kink-turn/L7Ae complex could originate from different N3 or a mixture of N1 and N3 structures. These two models could be tested in the future with additional XSI experiments that are specifically designed to distinguish N1 and N3 structures.

Figure 6. The distribution of N1 and N3-type kink-turn conformations.

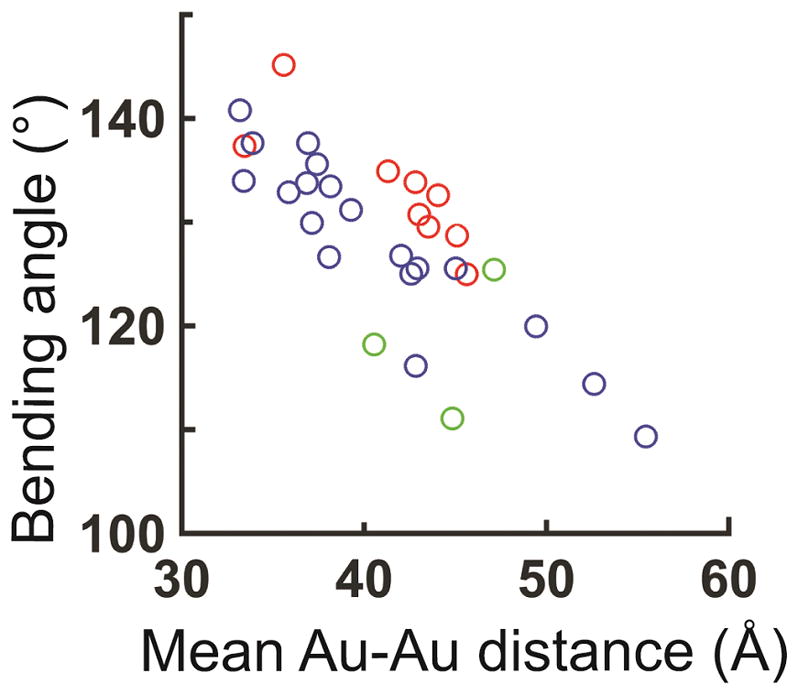
The distribution of inter-helical bending angles and the expected mean Au-Au distance for the crystal structures of N1 (red), N3 (blue), and kink-turn conformations that do not fall in either N1 or N3 class (green). Figure 6 is a replot of the red region in Figure 1d.

DISCUSSION

X-ray scattering interference (XSI) is an emerging and powerful technique that can be directly mapped –via a Fourier transform– into a distance distribution that in turn can be directly compared to predictions from models or computation^{10, 18, 28}. As a first application of XSI to RNA, the solution ensembles of two kink-turn RNA, KtA and KtB, were investigated. Our XSI results agree well with prior FRET studies, showing that KtA preferentially adopts the kinked conformation in the absence of bound protein whereas KtB does not, and that KtA and KtB are both preferentially kinked with bound L7Ae protein (Fig. 4)^{26, 38}. Further, XSI has allowed us to uncover conformational distributions for kink-turn RNAs in solution, both free and protein bound. The results underscore the ability of XSI to deconvolute substates and to reveal ensemble properties of those substates.

Although XSI lacks the all-atom structural precision attainable by X-ray crystallography and NMR, it can provide solution and ensemble information. As XSI provides distance distribution information about ensembles, it may complement NMR residual dipolar coupling (RDC) measurements that provide information on relative orientations but not distances^{11, 39}. XSI is also more readily scalable than NMR-RDC for the determination of ensembles for larger RNA and RNA•protein complexes. We anticipate that XSI may be particularly useful in the study RNA and RNA/protein systems because of the importance of knowing the relative positions and dynamic properties of RNA helices, information that is readily obtained as demonstrated in this study.

We observed that the unkinked state of KtA and KtB exhibit a range of bend angles across the range seen for non-structured RNAs of a similar junction topology, with the conformational preferences varying with solution conditions (Supplementary Fig. 1). We were able to detect a small amount of kinked KtB in solution in the absence of bound protein (Fig. 4). We showed that kink-turn RNA even in its folded state cannot be described as a single conformer (Fig. 3). The favored kinked conformation changed upon protein binding and across solution conditions (Figs. 3, 4 & 5). The folded kink turn, both free and protein-bound, was present as a mixture of states under most but not all conditions (Figs. 3 & 5). It will be of interest to determine if the narrowing to an apparent single conformation under high salt conditions for KtA reflects the site-specific binding of Mg²⁺ ion or other factors³⁸.

Ensemble descriptions can help in developing testable models for the underlying behavior of RNA/protein systems. The L7Ae protein binds both KtA and KtB with very high (sub-nanomolar to low nanomolar) affinity,^{26, 42} but it binds to KtA about 100-fold faster than it binds to KtB under low salt conditions^{42, 43}. Our results suggest that this difference in on-rate could arise from a conformational capture mechanism, where the slower association of KtB is due to the rarity of its kinked conformation compared to the large fraction of KtA that is kinked under similar conditions (Fig. 4). In addition, the L7Ae affinity for KtA increases ~2 fold from low to high salt, an effect similar to the increase in the fraction of kinked state in the free KtA ensemble and also consistent with a simple conformational capture mechanism⁴⁴. The slower dissociation of KtB than KtA from the L7Ae complex (7 x 10⁻⁴ s⁻¹ vs. 2 x 10⁻³ s⁻¹)^{42, 43} under low salt conditions may also be accounted for by our ensemble results. Stronger or additional RNA-protein interactions may be formed in the bound state with KtB, leading to the observed lower dynamics of the KtB/L7Ae complex than the KtA/L7Ae complex under similar low salt conditions (Figs. 5b and 5d). The models arising from this synergy of kinetic, thermodynamic and ensemble results provide an integrated framework that is testable and may be generally applicable to RNA/protein systems

Different kink-turn sequences are found across a considerable range of structural space (Fig. 6). Using the XSI data as a guide to identify appropriate solution conditions, NMR dynamic experiments can be designed to determine the nature and rate of the conformational change that allow kink-turn RNAs to explore their range of bend and kink angles (Fig. 6), both as free RNAs and in complexes with L7Ae and other proteins^{45, 46}.

The simplest rationale for the widespread occurrence of kink-turn sequences and structures in functional RNAs is their ability to allow RNAs to fold back upon themselves and promote the assembly of tertiary connections and globular-like, functional structures^{20, 47}. The dynamic nature of these structures may also be utilized in biological function. As RNA-mediated processes typically involve conformational transitions^{12, 47} and as the small local changes in kink-turns are amplified by the attached helices such that a large range of distances are possible, it will be fascinating to determine if RNA complexes utilize multiple kink-turn conformations within their functional cycles. XSI and other biophysical approaches will be key in developing hypotheses and tests to unravel the physical and energetic bases for complex biological processes carried out by RNA/protein complexes.

Online Methods

Materials

Au-labeled RNA oligonucleotides were prepared following previously described procedures^{17, 18}. Briefly, RNA oligonucleotides with 3′ thiol modifications (3′-Thiol-Modifier C3 S-S from Glen research) were synthesized by the PAN facility of Stanford University using ABI 394 DNA synthesizer and purified by Poly-Pak (Glen Research). RNA oligonucleotides were purified by anionic exchange HPLC, followed by DTT reduction. The thiolated RNA oligonucleotides were then coupled to thioglucose-bound Au nanocrystals for 2 h at pH 9.0, purified by anion exchange HPLC, and desalted by buffer exchange with water using centrifugal filters. The single-stranded RNA oligonucleotides were then annealed with their complementary strands at 40 °C for 30 minutes. The resulting RNA duplexes were then purified by anion exchange HPLC followed by centrifugal desalting.

A. fulgidus L7Ae protein was expressed and purified as previously described⁵⁰. Briefly, a modified pET-Duet1 plasmid (Novagen) containing gene sequence of a hexahistidine-L7Ae fusion protein was expressed in E. coli BL21-Gold (DE3) pLysS cells (Stratagene), induced with 0.2 mM IPTG at 20 °C for 12 h. Harvested cells were suspended in 20 mM Tris-HCl, (pH 8.0), 500 mM NaCl, 10 mM imidazole, 1 mM phenylmethylsulfonyl fluoride (PMSF) (buffer A) and lysed by sonication. The protein suspension was heated at 85 °C for 20 min in the presence of 10 mM MgCl₂ to denature endogenous protein, which was then removed by centrifugation at 18,000 rpm for 30 min at 4 °C. L7Ae was loaded onto a HisTrap column (GE Healthcare), washed with 25 mM imidazole in buffer A, and eluted with 500 mM imidazole in buffer A. The His₆ tag was cleaved from L7Ae by PreScission protease in 20 mM HEPES-Na (pH 7.6), 100 mM NaCl, 0.5 mM EDTA at 4–8 °C for 16 h. L7Ae was then applied to a heparin column (GE Healthcare) and eluted at 250 mM NaCl in a gradient from 50 to 2000 mM NaCl in 20 mM HEPES-Na (pH 7.6). The protein was further purified using a Superdex 200 gel filtration column (GE Healthcare), in a buffer containing 5 mM Tris-HCl (pH 8.0), 100 mM NaCl. The purified protein was buffer exchanged into XSI buffers before the SAXS measurements (see below).

SAXS measurements and data processing

Small-angle X-ray scattering data were acquired at the Stanford Synchrotron Radiation Lab (SSRL, Beamline 4–2) at 15 °C. A sample to detector distance of 1.1 meters was used for all measurement. The buffer conditions were 30 or 70 mM Tris-HCl, pH 7.4, 10 mM sodium ascorbate and 0–500 mM NaCl, 0–150 mM KCl and 0–10 mM MgCl₂. XSI measurements were carried out at an RNA concentration of 30 μM and a L7Ae concentration of 100 μM. With reported dissociation constants of low nanomolar or lower²⁶, L7Ae binding is expected to be saturating at 100 μM, as is consistent with the observed shifts in Au-Au distance distributions. Saturation was also confirmed experimentally by a titration of L7Ae to RNA, monitored by SAXS with unlabeled RNA (Supplementary Fig. 3). Representative scattering data were included in Supplementary Figures. 5 & 6. The scattering data were analyzed following procedures described previously to obtain Au-Au center-to-center distance distributions^{10, 28, 31}. Any contribution from protein scattering is expected to be very small compared to scattering from the gold nanocrystals and is nevertheless subtracted out in obtaining the XSI signal. The standard error of the mean and variance of the Au-Au center-to-center distance distributions (Figs. 3b, 3c, 5b and 5d) were 0.5 Å and 10% of the total variance, respectively. These errors represent the upper limits of the previously established normal range of errors associated from XSI measurements of multiple independently prepared samples^{17, 18}. This estimated level of uncertainty is consistent with results from two independent XSI measurements of KtA•L7Ae under salt condition 2 (Supplementary Fig. 7 and legend of Fig. 2a) and is larger than the uncertainty derived from technical replicates. In this work, X-ray scattering of each sample was measured 10 consecutive times to provide 10 technical replicates.

Determination of the conformation of a RNA kink-turn or bulge

The conformation of a RNA kink-turn or bulge was defined as the relative position of its 5′ and 3′ helical stems, which is uniquely described by a set of rotational (α, β, γ) and translational (x, y, z) degrees of freedoms. Of the three rotational parameters, β is the bending angle, γ indicates the bending direction and α + γ indicates the helical twist.¹⁰ The bending angle β can vary between 0 and 180° with a straight helix having β equal to 0°. For example, for a given crystal structure of a kink-turn, we determined its conformation by first aligning the 5′, C or bottom stem of the kink-turn structure at the −2b–2n base pair (Fig. 1a) to the bottom half of a canonical A-form helix in the reference coordinate, then the position of the 3′, NC or top stem of the kink-turn relative to the 5′, C or bottom stem of the kink-turn was defined as the movement, (α, β, γ, x, y, z), that aligns the top half of the canonical A-form helix to the 3′, NC or top stem of the kink-turn structure at the 3b3n base pair (Fig. 1a). The −2b–2n and 3b3n base pairs (Fig. 1a) define the boundary of the kink-turn motif.

Predicting the expected Au-Au distance distribution of a RNA conformation

The expected Au-Au distance distribution for a given kink-turn (or bulge) conformation in the context of the construct herein, a 25bp RNA with 3′ end-labeled Au nanocrystals (Fig. 1b), was predicted by statistical sampling of the Au nanocrystal linker conformation and structure ensemble of the RNA helices outside of the fixed kink-turn region, the region between the −2b–2n and the 3b3n base pair (Fig. 1a). Specifically, starting from a bottom and a top canonical A-form helix aligned with the kink-turn, we first generated two ensembles of 2000 conformations each for the bottom and the top RNA helices, respectively, with Au attached. The RNA helices were generated as previous described for DNA helices^{10, 18} using experimentally optimized RNA-specific parameters for the mean and variation in RNA base steps (Supplementary Table 2, X.S, P.B.H. and D.H., paper in preparation). To model the position of Au nanocrystals that are 3′-end attached, as is also needed, we first generated an initial Au coordinate cloud based on stochastic sampling of the linker conformation, removing conformations that would give steric clashes between the RNA, Au nanocrystals, and linker. The initial Au-coordinate cloud was then optimized against experimental data using four Au-nanocrystal variables, D, θ₀, axial₀, and ε_Au; D, θ₀, and axial₀ define the average position of the Au-nanocrystal cloud and ε_Au adjusts the overall size of this cloud, as described in (refs. 17, 18). To determine these four parameters and their salt dependence, we carried out XSI measurements on a series of RNA helix constructs containing 3′-end-labeled and internally labeled Au nanocrystals (Supplementary Fig. 8) under salt conditions 2 and 5 (Supplementary Table 1). Best-fit parameters for each salt condition were obtained by global optimization against the experimental data (Supplementary Table 2). For each of the 2000 helix conformations, the Au probe was added by randomly sampling the pre-built Au cloud. Thus, two sets of 2000 Au coordinates, one for the top helix and one for the bottom helix, were generated, and their pairwise distances were then pooled to generate the expected Au-Au center-to-center distance distribution. There is a small salt dependence of the RNA helix and Au linkers, which is described in detail in ‘Establishing a model for the salt dependence of RNA helix conformation and Au nanocrystal position’ immediately below.

Establishing a model for the salt dependence of RNA helix conformation and Au nanocrystal position

As only a weak salt dependence was observed for RNA helix and Au linkers (Supplementary Table 2), we used a simple salt-dependent model for helical and Au-nanocrystal position, based on linear extrapolation, to account for salt effects. We assumed that each of the nine parameters (Supplementary Table 2) defining the RNA/Au system is correlated with the relative salt screening strength of the solution (x) with the same linear correlation, as in Equation (1).

$${\mathit{Para}}_{i=1-9}(x)={\mathit{Para}}_i(x_{\mathit{low}})+(x-x_{\mathit{low}})\ast \frac{{\mathit{Para}}_i(x_{\mathit{high}})-{\mathit{Para}}_i(x_{\mathit{low}})}{(x_{\mathit{high}}-x_{\mathit{low}})}$$ (1)

In Equation (1), x is the relative salt strength of the solution; x_low and x_high are relative salt strength of the two salt conditions with experimentally determined parameter sets available. The subscripts, low and high, indicate that these two conditions are chosen at near the low and the high charging screening capability extrema of the range of salt conditions. For solutions containing only monovalent cations (e.g., Na⁺ and K⁺), the relative salt strength was assumed to be proportional to the total monovalent cation concentration. For solutions that also contain divalent cations (e.g., Mg²⁺), an equivalence factor N that equals the relative salt strength or electrostatic screening effects of 1 mM divalent cation relative to N mM of monovalent cation is needed to calculate the relative salt strength of the solution because the charge screening capability of divalent cations for nucleic acids is much stronger than monovalent cations of the same ionic strength^{13, 35, 36}. Thus, the relative salt strength of a solution was defined as x = [divalent]/[1 mM] + [monovalent]/[N mM] (Supplementary Table 1). The value of N was determined experimentally to be about 46 (Supplementary Figure 9), which is similar to the factor of ~40 previously determined from ion competition for occupancy of the ion atmosphere of a DNA duplex³⁵. The optimum equivalence factor value was obtained by a global fit of Equation (1) to the salt dependence in the mean Au-Au distances of a model 12bp RNA (Supplementary Figure 9). This equivalence factor was used, in turn, to calculate the relative salt strength x for each salt condition in Supplementary Table 1. These values of x along with the measured values of the nine parameters that describe the helix properties and Au nanocrystal position at low and high salt (Supplementary Table 2) were used in Equation (1) to obtain the helix geometry and Au position parameters for each experimental salt condition. We emphasize that the purpose of this model is to allow the small corrections for Au nanocrystal position and RNA helical parameters that occur with changing salt and not to render physical interpretations. Given that the salt effects on the Au nanocrystal and RNA helix to be corrected for are small relative to the changes observed by the kink turn RNAs, approximations in the model for correcting for the salt effects not arising from the kink-turn are not expected to affect the conclusions herein.

Comparison of the variance of the experimental Au-Au distance distribution with the expected Au-Au distance variance of a single RNA kink-turn conformation

The kink-turn conformer state from the X-ray crystallography structure pool (Fig. 1d) that best matches the mean Au-Au distance of the experimental Au-Au distance distribution was identified. The expected Au-Au distance distribution for this conformer was predicted following the procedure described above. The variance of the expected Au-Au distance distribution for this conformer was then used to represent the expected variance of a single kink-turn conformation (Fig. 5b and 5d).

Generation of an ensemble model of the kink-turn RNA

A basis set of bulge and kink-turn conformations was generated from a survey of RNA 0–3 two way junctions in the crystal structure database (see ‘Survey of kink-turn and other 0–3 two-way junctions in the crystal structure database’ and ‘Generation of a basis set of kink-turn and un-kinked 0–3 two-way junction structures’ below for detail) and their Au-Au distance distribution was predicted as described in “Predicting the expected Au-Au distance distribution of a RNA conformation” above. The ensemble conformational distribution of the kink-turn was generated by decomposing the experimental Au-Au distance distributions into a weighted sum of the basis set Au-Au distance distributions using MATLAB’s non-negative least-square fitting module.

Survey of kink-turn and other 0–3 two-way junctions in the crystal structure database

To survey the conformational distribution of 3nt bugles with and without the kink-turn sequence in the crystal structure database, all RNA-containing crystal structures with a resolution of ≤3.0 Å were downloaded from the Protein Data Bank²⁵. To identify two-way junctions, we first identified all helical 4mers in the downloaded pdb structures. A helical 4mer was defined as a stretch of RNA that is paired. We consider two bases to be paired if their C1′-C1′ distance was between 8 and 13 Å. We also required at least one of the three 2mers in the 4mer to be within 1.2 Å C1′ RMSD of a standard A-form 2mer. For comparison, helical 2mers of GC, AU or GU pairs in our 4mer database have C1′ RMSDs of 0.4 ± 0.2 Å. A total of about 103,000 helical 4mers were identified. With those helical 4mers, we were able to find two-way junctions in the database with identifiable helical stems.

We found 217 0–3 two-way junctions (i.e., 3nt bulges) with a consensus kink-turn sequence, which was defined as having a GA/AN stem immediately 3′ to the 3nt loop (Supplementary Fig. 10a). The N in GA/AN is most commonly a G (83%), and less commonly a U (16%) or a C (1%). All 0–3 two-way junctions with the kink-turn type 3′ stem sequence also have a well-formed helical 2mer immediately 5′ to the loop. These 5′ stem 2mers consist of canonical base pairs or GU wobble-pair and are all within 1.0 Å RMSD of a standard A-form 2mer. We also found 391 0–3 two-way junctions that do not have the consensus-kink-turn sequence but also have a 5′-helical 2mer that are canonical base pairs or one canonical base pair and one GU wobble pairs (Supplementary Fig. 10a). All 212 consensus GA/AN kink-turn sequences adopt a kink-turn like structure with a >100° bend (Supplementary Fig. 10b), and all 391 non-kink-turn two-way junction have a bending angle of <100° (Supplementary Fig. 10b) with the exception of one subclass of sequences that are kink-turn like. We referred to this sub-class as the A-cross (Supplementary Fig. 10a), as they have both consensus kink-turn A residues, but lacks G_1b of the GA/AN motif. The A-cross sub-class can be either kinked or non-kinked (Supplementary Fig. 10).

Generation of a basis set of kink-turn and un-kinked 0–3 two-way junction structures

For each of the kinked and un-kinked 0–3 two-way junctions, we calculated their inter-helical bending and twisting angles (see ‘Determination of the conformation of a RNA kink-turn or bulge’ above and Supplementary Fig. 10b) and predicted the corresponding mean Au-Au distances (see “Predicting the expected Au-Au distance distribution of a RNA conformation” above and Supplementary Fig. 10c). To generate a basis set of structures from the 217 and 391 structures with and without the kink-turn sequence, respectively, we removed over-represented structures. We first binned all structures based on the same RNA molecule (e.g., the same ribosome bound to different ligands). Within each bin, we clustered the structures based on their expected mean Au-Au distance into 1–3 clusters depending on how widely do these structures differ in their expected Au-Au distances. Only one representative structure from each cluster was kept. The final basis set included 31 and 39 structures with and without the kink-turn sequence. The 3 A-cross structures (Supplementary Fig. 10) were not used in the basis set.