Skip to main content
NCBI home page
Scientific Reports logoLink to Scientific Reports
. 2016 Feb 17;6:21461. doi: 10.1038/srep21461

One-way helical electromagnetic wave propagation supported by magnetized plasma

Biao Yang 1, Mark Lawrence 1, Wenlong Gao 1,2, Qinghua Guo 1,3, Shuang Zhang 1,a
PMCID: PMC4756303  PMID: 26883883

Abstract

In this paper we reveal the presence of photonic one-way helical surface states in a simple natural system- magnetized plasma. The application of an external magnetic field to a bulk plasma body not only breaks time-reversal-symmetry but also leads to separation of Equi-Frequency Contour surfaces (EFCs) to form topologically nontrivial gaps in k space. Interestingly, these EFCs support topologically protected surface states. We numerically investigate an interface between magnetized plasma, using a realistic model for parameter dispersion, and vacuum, to confirm the existence of one-way scatter-immune helical surface states. Unlike previous proposals for achieving photonic one-way propagation, our scheme does not require the use of artificial structures and should therefore be simple to implement experimentally.

The pursuit of one-way scatter-immune transportation of light has recently become a hot research topic not least because of the clear technological benefits of being able to manipulate electromagnetic waves while maintaining perfect transmission. Its apparent carrier is surface wave, by definition, is a wave bounded by the interface between two semi-infinite media. Traditional surface wave usually endures non-ignorable scattering loss when encountering any interfacial disorders, such as sharp bend. Recently, many kinds of photonic nontrivial surface wave, which show the robust property of one-way scatter-immune transportation, have been proposed by means of mimicking topological electronic system1,2. The defining feature of topological phases is bulk-edge correspondence. Bulk-edge correspondence, referring to the surprising dependence of boundary excitations on the characteristics of the bulk propagating modes rather than the local properties of the boundary, rebuilds our concepts on energy band theory. After Haldane proposed the photonic analogue of Quantum Hall Effect in 20083,4, several significant papers clarifying topological edge states both theoretically5,6,7,8,9 and experimentally10,11,12,13,14,15 have brought a whole new challenge to traditional optics. Simultaneously, magnetized near-zero-epsilon metamaterials16 was also proposed to prove one-way photonic states in 2-D plane. Obviously, a wholly new field-topological photonics17 has emerged. However, what cannot be neglected is that fabrication and assembly, especially 3D case for bulk photonic crystal or metamaterials, is still challenging and time consuming. Here, we propose a simple natural system-magnetized plasma to realize helical one-way surface propagation. More importantly, the topological transportation of electromagnetic surface waves can be reconfigurable by simply adjusting the external magnetic field or the plasma density.

Magnetized plasma has been recently investigated to show interesting electromagnetic properties such as sub-diffractional imaging18 and magnetic field induced transparency19. Under a strong magnetic field, the movement of the free electrons in the cold plasma is confined in the plane perpendicular to the applied magnetic field. On the other hand, the electrons can move freely along the direction of the magnetic field. It has been shown previously that with extremely strong magnetic field, the wave can propagate almost diffractionless along the direction of the magnetic field, in a similar way as wave propagate inside a hyperbolic metamaterials20,21, which currently is a very active research topic including subwavelength imaging22,23,24, negative refraction25, spontaneous emission enhancement with a large Purcell Factor26 and even topological ordered metamaterials9.

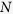For propagation of electromagnetic wave with angular frequency ω in the lossless plasma, the lossless plasma behaves as a free-electron model, whose electromagnetic response can be described by the Drude permittivity Inline graphic, where Inline graphic is the plasma frequency, Inline graphic being the electron concentration, e and m denote elementary electron charge and electron mass, respectively. As shown previously18, the applied external DC magnetic field leads the isotropic plasma to becoming extremely anisotropic medium because of electrons undergoing cyclotron orbits in the plane perpendicular to the field. If a magnetic field is aligned in the z direction, the electromagnetic response of the lossless magnetized plasma can be described by the following local, homogeneous permittivity tensor18,27,28,

graphic file with name srep21461-m4.jpg

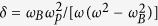where, Inline graphic, Inline graphic and Inline graphic. The cyclotron frequency Inline graphic is determined by the applied static magnetic field Inline graphic.

Considering a wave propagating along + z direction with circular polarizations as base states, this relative permittivity of the magnetized plasma can be reduced to a diagonal tensor Inline graphic, where Inline graphic, ‘Inline graphic’ correspond to right and left polarized states, respectively. To meet our hyperbolic demand in z direction which is parallel to the static magnetic field, the operating frequency must satisfy Inline graphic in the lossless condition. Whereas the applied magnetic field draws off-diagonal components into the relative permittivity, the magnetized plasma shows two bandgaps in k-space with condition of Inline graphic. So, the operating angle frequency has to be less than Inline graphic and satisfy Inline graphic. Based on these constraints, we can find Inline graphic, which means EFCs of vacuum is located in the EFCs’ bandgaps of the magnetized plasma, as shown in Fig. 1. In other words, these two materials have overlapped forbidden bands in k space, which is an essential condition to realize one-way scatter-immune transportation. Figure 1 shows corresponding hyperbolic properties and bandgaps of magnetized plasma, it can be seen as the result of a nontrivial transformation from normal hyperbolic metamaterials.

Figure 1. EFCs of magnetized plasma and vacuum.

Figure 1

Open in a new tab

The ordinary mode is wrapped by vacuum (indicated). There is a big gap between the extraordinary mode and vacuum. At the minimal point of upper pseudo hyperbolic branch, light propagates with strict left circular polarization states. However, for Inline graphic approaching infinity, polarization states become linear. The peak point of upper ordinary semi-sphere shows strict right circular polarization which is opposite to that of the minimal point, because these two states are lifted from a degeneracy point during nontrivial transformation from normal hyperbolic metamaterials. In the negative Inline graphic, polarization presents opposite properties. In the plane of Inline graphic, the z component of electric field is zero again, but its polarization is slightly elliptical compared with those pole locations. The permittivity is calculated with respect to Inline graphic. The wave vectors are in the unit of Inline graphic.

We now turn to studying how these topological features manifest themselves on the boundary of magnetized plasma. In what follows we investigate systems with continuous translational invariance in the z direction, thereby conserving Inline graphic. Here, by assuming the surface wave exponentially decays along either direction from y-z plane (i.e., the half space Inline graphic is occupied by isotropic media such as vacuum, whereas the magnetized plasma is located in Inline graphic), we use the method proposed by Dyakonov in 198829 to briefly calculate these surface wave. In the vacuum side, there are two orthogonal eigen modes which can be expressed as,

graphic file with name srep21461-m21.jpg

where Inline graphic is imaginary representing decay constant along positive x direction and q is the absolute value of in-plane propagation wave vector. Likewise, we can also write down the decay constant in magnetized plasma side Inline graphic as a function of vector Inline graphic. From two independent eigen modes of magnetized plasma it can be obtained through solving Maxwell’s Equations,

graphic file with name srep21461-m25.jpg

which both still are functions of Inline graphic. Until now, we have found four eigen modes that are localized on both sides of the surface. What combines them is the electromagnetic boundary condition. Postulating that the tangential components of these fields are continuous at the interface gives us the determinant problem of a Inline graphic constraint matrix,

graphic file with name srep21461-m28.jpg

After solving it, in Fig. 2a the results reveal that in the gap of EFCs any given surface can support just one propagating mode, which means that the spatial separation of left and right moving surface waves at certain Inline graphic prevents the occurrence of backscattering from any z-invariant disorder as shown in Fig. 2b. Topological order for magnetized plasma is attributed to the presence of a new type of plasmon Weyl points occurring at the plasma frequency of the system30.

Figure 2. Bulk states and surface states.

Figure 2

Open in a new tab

(a) Bulk states and surface states of this system. Top/Bottom refers to the configuration that vacuum is located on the top/bottom of magnetized plasma. (b) Schematic view of helical one-way back scattering-immune propagation in 3D. Chiral surface state propagating around the magnetized plasma with added cylindrical shape surrounded by vacuum, despite the existence of raised cylinder back-scattering is forbidden due to the absence of anticlockwise modes.

This immunity to backscattering has also been confirmed using full wave simulations shown in Fig. 3b in which a right moving surface wave propagates seamlessly around a sharp defect. The simulation is performed in the x-y plane for three different propagation constants Inline graphic in the shadow area as indicated by ‘A’, ‘B’ and ‘C’ in Fig. 3a. For point ‘A’ and ‘C’, since they are not located in the gap region, the electromagnetic wave can be scattered into the bulk states by z-invariant scatterers. On the other hand, at point ‘B’ where Inline graphic is in the middle of the gap, the surface wave is immune from scattering by the sharp edges, and therefore the numerical simulation confirms that it is a topologically nontrivial surface state. As expected, when the direction of the magnetic field is flipped, the propagation of the surface wave is also switched to the opposite direction. This may enable topological surface states with dynamically reconfigurable properties. Since the collision frequency is several orders of magnitude lower than the operating frequency, this realistic case can still be regard as lossless18.

Figure 3. Simulation of topologically protected surface states at the interface between a magnetic plasma and vacuum.

Figure 3

Open in a new tab

(a) Magnified shadow area of Fig. 2(a). (b) Field distribution simulated by commercial Comsol RF module. The parameter of the magnetized plasma are Inline graphic, Inline graphic and the operating frequency Inline graphic.

Interestingly, after zooming in the point ‘C’ shown in Fig. 3a where surface state is very close to the EFCs of vacuum, it is discovered that the surface state is not merging into the EFCs of vacuum, rather, it conformally bends around the EFCs of vacuum and goes parallel to the other branch of the EFCs of magnetized plasma. This indicates that even at 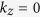Inline graphic Inline graphic, there exists a unidirectional surface state on each surface with dispersion relation expressed as16,

graphic file with name srep21461-m34.jpg

where Inline graphic and Inline graphic represents to top and bottom case, respectively. What’s important is that this surface mode can only be excited by magnetic current. After substituting the realistic parameters into Eq. 5, we get the mentioned subtle gap between surface state and vacuum bulk state at point ‘C’ is Inline graphic. However, since the surface states do not fall in the gap, they are not protected against z invariant defects.

For completeness, we show the polarization states of these nontrivial surface waves in Fig. 4. According to the boundary conditions, the tangential components of electric (E) and magnetic field (H) are continuous across the interface. However, the vertical components of the E and H fields are discontinuous. Specifically, they are related by Inline graphic. Therefore, the polarization states on the vacuum and the magnetized plasma sides are different. The polarization states on both side of the interface are generally elliptically polarized. Interestingly, the polarization ellipse lies in a plane that is perpendicular to the surface. Another interesting observation is that the polarization ellipse is generally not perpendicular to the Poynting vector. The angle formed between them varies monotonically from 0° for kz = 0 to 90° for k approaching infinity, as shown in Fig. 4b. Moreover, the plot of ellipticity shows that when k approaches infinity, the electric field in vacuum side becomes circularly polarized.

Figure 4. Electric field polarization of the surface states.

Figure 4

Open in a new tab

(a) The polarization states of the surface waves in vacuum and in the magnetized plasma. The polarization plane is perpendicular to the interface, therefore from top view, it is projected onto the interface as a linear vector. The insect shows that the polarization states are elliptical. (b) and (c) Direction of polarization plane and the ellipticities (Inline graphic) of the polarization states in vacuum and in the magnetized plasma. This figure corresponds to Fig. 3(a) for surface states at Inline graphic.

In conclusion, we have theoretically investigated the existence of one-way propagating surface wave between vacuum and magnetized plasma. The simulation confirms the presence of unidirectional backscattering-immune propagation of surface wave based on the simple natural system-magnetized plasma. Although the study has focused on free space magnetized plasma for manipulation of electromagnetic waves at microwave regime, it can be extended to terahertz regime by working with semiconductors with very small effect mass, such as InSb. Thus, this nontrivial edge states may also be observed in THz band by using magnetized semiconductors31.

Additional Information

How to cite this article: Yang, B. et al. One-way helical electromagnetic wave propagation supported by magnetized plasma. Sci. Rep. 6, 21461; doi: 10.1038/srep21461 (2016).

Acknowledgments

The work was supported by EPSRC (Grant No. EP/J018473/1), NSFC (Project 61328503), Leverhulme Trust (Grant No. RPG-2012-674), and China Scholarship Council (201306110041).

Footnotes

Author Contributions B.Y., M.L. and S.Z. conceived the original idea. B.Y., W.G. and Q.G. performed the surface states calculation and numerical simulation. All the authors analysed the data and wrote the manuscript.

References

  1. Hasan M. Z. & Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
  2. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  3. Haldane F. D. M. & Raghu S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys. Rev. Lett. 100, 013904 (2008). [DOI] [PubMed] [Google Scholar]
  4. Raghu S. & Haldane F. D. M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 78, 033834 (2008). [Google Scholar]
  5. Wang Z., Chong Y. D., Joannopoulos J. D. & Soljačić M. Reflection-Free One-Way Edge Modes in a Gyromagnetic Photonic Crystal. Phys. Rev. Lett. 100, 013905 (2008). [DOI] [PubMed] [Google Scholar]
  6. Hafezi M., Demler E. A., Lukin M. D. & Taylor J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011). [Google Scholar]
  7. Khanikaev A. B. et al. Photonic topological insulators. Nat. Mater. 12, 233–239 (2013). [DOI] [PubMed] [Google Scholar]
  8. Lu L., Fu L., Joannopoulos J. D. & Soljacic M. Weyl points and line nodes in gyroid photonic crystals. Nat. Photonics 7, 294–299 (2013). [Google Scholar]
  9. Gao W. et al. Topological Photonic Phase in Chiral Hyperbolic Metamaterials. Phys. Rev. Lett. 114, 037402 (2015). [DOI] [PubMed] [Google Scholar]
  10. Wang Z., Chong Y., Joannopoulos J. D. & Soljacic M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009). [DOI] [PubMed] [Google Scholar]
  11. Poo Y., Wu R.-x., Lin Z., Yang Y. & Chan C. T. Experimental Realization of Self-Guiding Unidirectional Electromagnetic Edge States. Phys. Rev. Lett. 106, 093903 (2011). [DOI] [PubMed] [Google Scholar]
  12. Rechtsman M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013). [DOI] [PubMed] [Google Scholar]
  13. Hafezi M., Mittal S., Fan J., Migdall A. & Taylor J. M. Imaging topological edge states in silicon photonics. Nat. Photonics 7, 1001–1005 (2013). [Google Scholar]
  14. Chen W.-J. et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 5, 10.1038/ncomms6782 (2014). [DOI] [PubMed] [Google Scholar]
  15. Lu L. et al. Experimental observation of Weyl points. Science 349, 622–624 (2015). [DOI] [PubMed] [Google Scholar]
  16. Davoyan A. R. & Engheta N. Theory of Wave Propagation in Magnetized Near-Zero-Epsilon Metamaterials: Evidence for One-Way Photonic States and Magnetically Switched Transparency and Opacity. Phys. Rev. Lett. 111, 257401 (2013). [DOI] [PubMed] [Google Scholar]
  17. Lu L., Joannopoulos J. D. & Soljacic M. Topological photonics. Nat. Photonics 8, 821–829 (2014). [Google Scholar]
  18. Zhang S., Xiong Y., Bartal G., Yin X. & Zhang X. Magnetized Plasma for Reconfigurable Subdiffraction Imaging. Phys. Rev. Lett. 106, 243901 (2011). [DOI] [PubMed] [Google Scholar]
  19. Gad R., Leopold J. G., Fisher A., Fredkin D. R. & Ron A. Observation of Magnetically Induced Transparency in a Classical Magnetized Plasma. Phys. Rev. Lett. 108, 155003 (2012). [DOI] [PubMed] [Google Scholar]
  20. Poddubny A., Iorsh I., Belov P. & Kivshar Y. Hyperbolic metamaterials. Nat. Photonics 7, 948–957, 10.1038/nphoton.2013.243 (2013). [DOI] [Google Scholar]
  21. Abelson Z., Gad R., Bar-Ad S. & Fisher A. Anomalous Diffraction in Cold Magnetized Plasma. Phys. Rev. Lett. 115, 143901 (2015). [DOI] [PubMed] [Google Scholar]
  22. Liu Z., Lee H., Xiong Y., Sun C. & Zhang X. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686 (2007). [DOI] [PubMed] [Google Scholar]
  23. Rho J. Spherical hyperlens for two-dimensional sub-diffractional imaging at visible frequencies. Nat. Commun. 1, 143 (2010). [DOI] [PubMed] [Google Scholar]
  24. Ishii S., Kildishev A. V., Narimanov E., Shalaev V. M. & Drachev V. P. Sub-wavelength interference pattern from volume plasmon polaritons in a hyperbolic medium. Las. Photon. Rev. 7, 265–271 (2013). [Google Scholar]
  25. Yao J. et al. Optical Negative Refraction in Bulk Metamaterials of Nanowires. Science 321, 930–930 (2008). [DOI] [PubMed] [Google Scholar]
  26. Jacob Z., Smolyaninov I. & Narimanov E. Broadband Purcell effect: radiative decay engineering with metamaterials. Appl. Phys. Lett. 100, 181105 (2012). [Google Scholar]
  27. Bellan P. M. Fundamentals of plasma physics. (Cambridge University Press, Cambridge, England, 2006). [Google Scholar]
  28. Bliokh Y. P., Felsteiner J. & Slutsker Y. Z. Total Absorption of an Electromagnetic Wave by an Overdense Plasma. Phys. Rev. Lett. 95, 165003 (2005). [DOI] [PubMed] [Google Scholar]
  29. Dyakonov M. I. New type of electromagnetic wave propagating at an interface. Soviet Physics JETP 67, 714–716 (1988). [Google Scholar]
  30. Gao W. et al. Plasmon Weyl Degeneracies in Magnetized Plasma. arXiv:1511.04875 [physics.optics] (2015).
  31. Han J. et al. The magneto-optical Kerr effect of InSb in Terahertz region. Phys. Lett. A 315, 395–398 (2003). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES