Methods for Dynamic Characterization of the Major Muscles Activating the Lower Limb Joints in Cycling Motion

Abstract

The functional activation, through electrical stimulation, of the lower limb consisting of several deficient muscles requires well-patterned and coordinated activation of these muscles. This study presents a method for characterizing the parameters of the major muscle groups controlling the ankle and knee joints in cycling motion, the latter having particular significance in the rehabilitation of locomotion. To lower mechanical indeterminacy in the joints the system is reduced by grouping the muscles acting in synergism. The joint torques were calculated by inverse dynamics methods from cycling motion data, including kinematics and foot/pedal reaction loads (forces, moments). The mechanical indeterminacy was resolved by applying optimization criteria and the individual muscle torques were parceled-out from the joint torques. System identification of the individual muscles, part of which being bi-articular, in this non-isometric condition was performed from the relationship between the evaluated force and the measured EMG of each the muscles, using both first and second order linear transfer functions. Feasibility of the presented method was demonstrated through the computation of the coefficients of the muscles involved and validating the results on the experimental data obtained from one subject.

Muscle characterization is an important factor in the quantitative modeling of motion. Of special interest is the case of muscle deficiency, in which the muscle may need to be activated by utilizing electrical stimulation (ES), either fully or partly for enhancement of the muscle force. The scope and limitations of ES to functionally activate paralyzed muscles have been extensively discussed in the literature.^1-4. However, ES can also be used to complement volitional activation in order to augment weakened muscle force such as in people with symptoms of impaired muscle capacity due to neuro-muscular disorders resulting from incomplete spinal cord injury, stroke, cerebral palsy, muscle atrophy and ageing.^5-12 In this mode, termed hybrid activation, the enhanced muscle force will generally result from the combined volitional and the ES-induced contributions. In either of these two modes of activation, i.e. the purely induced via ES alone, or the hybrid via combining induced and volitional activation, knowledge about the stimulation profiles (e.g. intensity, frequency, pulse duration, sequencing) is required to provide the activation torques for performing prescribed dynamic movements in non-isometric conditions, such as ambulating, cycling and the like. Thus, studying the characteristics of muscles during activity, through mathematical modeling seems essential in providing patterns of muscle activation for the generation of body movements.

The functional activation of the lower limb consists of several muscles, whose activations need to be patterned. Upon modeling the limb as a linkage with the muscles serving as actuators, biomechanical indeterminacy in the joints becomes apparent due to the fact that more than one muscle group is typically responsible for generating the joint torque. Thus, due to the lack of sufficient equations to describe the dynamics of the joint, the procedure of parceling out the individual contribution of each muscle group to the total joint torque is not straight forward. A common method to overcome this indeterminacy is to apply optimization principles,¹³ which can provide additional equations, enabling to resolve the muscle forces. The situation may become even more complex if the system properties of each of the participating muscles need to be identified and characterized, e.g. when muscle activation needs to be generated.

Cycling motion through pedaling is a common exercise in rehabilitation. Muscle characterization of the major muscle groups involved in cycling is thus essential if cycling motion is to be generated by stimulating these muscles either in pure FES-induced mode, such as maybe necessary in complete muscle denervation, or in hybrid mode, where weakened volitional activity is enhanced by induced activation of the muscles.

The general objective of this study is to present a method for characterizing the parameters of the major muscle groups controlling the ankle and knee joints in cycling motion, the latter having particular significance in the rehabilitation of locomotion. The specific objectives are: 1. System reduction, to reduce mechanical indeterminacy in the joints by grouping the muscles acting in synergism; 2. Calculation of the joint torques by inverse dynamics from cycling motion data, including kinematics and foot/pedal reaction loads (forces, moments); 3. Resolving the mechanical indeterminacy by applying optimization criteria to parcel-out the individual muscle torques from the joint torques; 4. System identification of the individual muscles, part of which being bi-articular, from the relationship between the evaluated force and the measured EMG of each the muscles; 5. Demonstration of feasibility of the presented method through the computation of the coefficients of the muscles involved and validating the results on the experimental data obtained from one subject.

In cycling motion, typically nine muscles in each leg take active part, including the gluteus maximus and adductor magnus (GMAX); medial hamstrings and biceps femoris long head (Hams); rectus femoris (RF); three-part vastus (VAS); biarticular gastrocnemius (GA); soleus and other plantarflexors (SOL); tibialis anterior (TA); biceps femoris short head (BFsh); iliacus and psoas (IL). Patterns of co-activation with synchronized ON/OFF switching times can be identified among these muscles. Thus, due to this synergistic activity, the nine muscles can be partitioned into four muscle groups for each leg.¹⁴

For instance, the knee extensors together with the rectus femoris are grouped as the quadriceps muscle (Quad), and the knee flexors together with the BFsh are grouped as the hamstrings (Hams). Thus, we have altogether four main muscle groups for actuating the ankle and knee, namely the TA, GA, Hams and Quad, of which the GA is bi-articular. The time sequence of the activity of these muscles, as revealed by their EMG tracings, indicates that at some phases of cycling more than one muscle group is involved in the actuation of each of the joints (see Figure 1).¹⁵ The muscles act in synchrony, but not simultaneously, to produce smooth function. Thus, despite the reduction in number of muscles the problem still remains indeterminate. Biomechanical modeling of bilateral pedaling is important for the design of protocols for the generation of cycling exercise, either with healthy muscles or in conjunction with ES. Information needed to understand the pedaling process includes identifying the leg muscles which participate, the pedal loads, and the kinematics of the leg segments.

Figure 1.

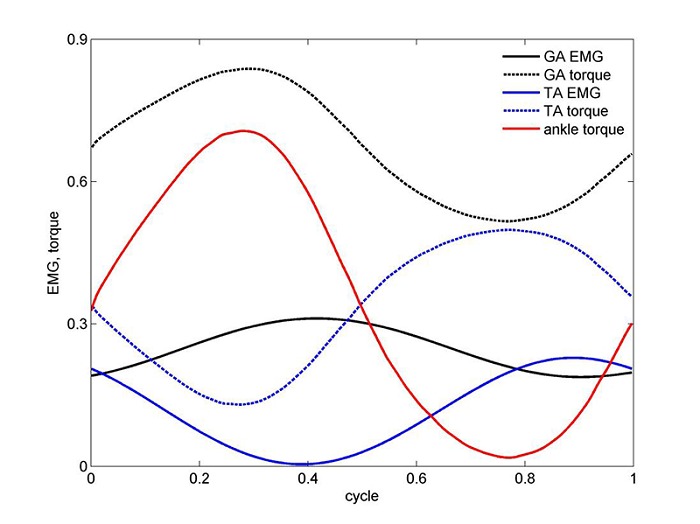
Net ankle torque as well as torque and EMG for each of the TA and GA muscles for one cycle, resulting from minimum stress optimization criterion (n = 3). Note that the EMG was normalized by dividing to the EMG at MVC and the torque was normalized by dividing by the maximal torque recorded in this experiment (cycling power was set here at 100 w).

Biomechanical models of cycling widely exist in the literature. A common model is the Two dimensional closed loop five-bar linkage mechanism for each of the legs, including thigh, shank, crank, seat support and pedal including the foot segment.^16-18 This is a two-degree-of-freedom model. It is assumed that the second leg moves synchronously, with a phase difference of 180°. The parameters measured in this model are the pedal load (force and moment), the angles of crank and pedal, each of the ankle, hip and knee joint angles and foot kinematics as collected by videography of markers attached to the shoe sole.

Materials and Methods

Ergometer equipped with optical encoder and force transducers

A friction-loaded cycle ergometer (Monark type 818E, Stockholm, Sweden) was equipped with an optical encoder module for crank angle measurement and cycling kinematics (US Digital type HEDS-9040-B00, WA, USA with separate disk assembly). The pedals were instrumented with multi-component strain gauge dynamometers,^12,19 for pedal load (force and moment) measurement. National Instrument’s SCC-SG24 Wheatstone Full bridge module on line collected the signals from pedals. Crank angle data were filtered (Butterworth third order zero lag filter with cutoff frequency of 15 Hz) allowing velocity to be calculated through differentiation.

Goniometers

Signals from goniometers placed on the subject’s ankle, knee and hip represent joint angle position were collected to determine the limb linkage kinematics. The goniometer data (Biometrics Ltd, Gwent, UK) were sampled at 1000 Hz via signal conditioning hardware to a PC.

Camera and image processing software.

Additional kinematic measurements (e.g. for pedal orientation) were made by using two spherical markers (2 cm dia), located on the shoe sole (one below the lateral malleolus and one opposite to the head of the fifth metatarsal). Video data are collected by a NM-M300EN Panasonic digital camera. Calibration was made using 4 control points by means of an Ariel Performance Analysis System (APAS) software. The optical axis of the camera was set centrally and perpendicular to the plane of motion.

Subject screen

The system was equipped with a subject screen for online bio-feedback during the cycling measurements.

EMG signals

EMG signals from the muscles were monitored and sampled at 1000 Hz for each of the 4 muscle groups during cycling motion using surface Ag-AgCl circular electrodes (1.5 cm diameter): two active electrodes for each muscle located on the muscle belly along its longitudinal axis, 2 cm apart, at mid-distance between the stimulation electrodes. One electrode is a ground electrode and placed on the bony medial epicondyle area of the knee femur. The skin surface is cleaned with alcohol, rubbed and gelled until the electrical impedance between each pair of electrodes is smaller than 5 kΩ.¹²

Results and Discussion

The model feasibility was demonstrated from measurements collected from an able-bodied subject, who was required to pedal at the steady speed of 60 rpm, with varying resistance powers of 50, 100, 150 and 200 w. Constancy of pedaling speed as secured by the subject screen providing speed feedback to the tested subject.

Inverse dynamics modeling

From the data collected in the above measurements on kinematics and pedal loads, the joint torques were calculated by applying inverse dynamics methods.^16-18,20 Next, the model combines implementation of a cost function with system identification in a two-step procedure, as follows.^14,21

Transformation of the joint torque to force within the individual muscles, using optimization criteria

System identification to characterize each of the four muscle groups studied, i.e. Gastrocnemius (GA), noting that this muscle is bi-articular, Tibialis Anterior (TA), Quadriceps (Quad) and Hamstrings (Hams), making use of the obtained muscle forces and their measured EMG’s.

Optimization

Different criteria were suggested for optimization.^22-27 In this study we applied the minimum stress criterion²⁵ as also suggested in cycling motion.^28,29 The muscle stress was evaluated from the muscle torque, the corresponding lever arm and the physiological cross sectional area (PCSA). This criterion thus reads:

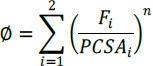(1)

Where Φ is to be minimized, i denotes the muscle index for each of the muscles of the joint involved (ankle, knee), F is the force within each of the muscles and the stress power n assumes the value 3.²⁵ The minimization procedure was performed using Matlab routine fmincon in the optimization toolbox, for each time point of an average cycle. Solutions including negative muscle forces were excluded, thus:

(2)

For the ankle joint with the TA and GA, the torque balance requires

(3)

Where d_GA and d_TA denote the lever arms for the GA and TA muscles, respectively. Note that the minus sign in the second term of the left hand side of the equation comes to account for the opposite torques applied by the TA and GA muscles.

In solving the above system of equations for the ankle joint, data about the moment arms for the TA and GA muscles were taken from Rugg et al.³⁰ and data for the cross sectional areas of these muscles were taken from Winter.³¹

It should be mentioned here that a somewhat different optimization criterion was applied by Raasch et al.¹⁴ for cycling motion at maximum speed pedaling. The cost function to be optimized was accordingly on muscle excitation, i.e. finding those muscle excitations that maximize the crank progress.

Figure 1 depicts sample results for the net ankle torque T_ank as well as torque and EMG for each of the TA and GA muscles in one typical cycle. EMG was normalized by dividing to the EMG value at MVC of each muscle. Torque was normalized by dividing by the maximal torque recorded in this experiment. It should be noted that the time delay observed in the traces of Figure 1 between torque and EMG may not reflect the expected neuro-mechanical delay in isolated muscle between mechanical contraction and neuro-excitation. Possible reasons for that include the following: (a) joint torque is being evaluated from the dynamic equations of the limb linkage, into which the measured kinematics is being fed and not of isolated muscle; (b) individual torque calculations go through an additional numerical calculation process, involving forces, lever arms and cross sectional areas, all potentially contributing to numerical errors; (c) unaccounted for factors, including activity of the contralateral leg, and inertial effects of the cycling device.

It should also be noted, though, that in the solution of the neuro-mechanical model system in the next section estimation of the physiological time delay values (with EMG preceding torque) will be accounted for.

From the optimization, an example for the maximal forces exerted in cycling motion in each of the joint muscles is shown in Figure 2, with the forces of the ankle muscles, TA and GA, in the upper panel. As noted from the figure, the maximal forces follow a linear increase with the cycling power.

Figure 2.

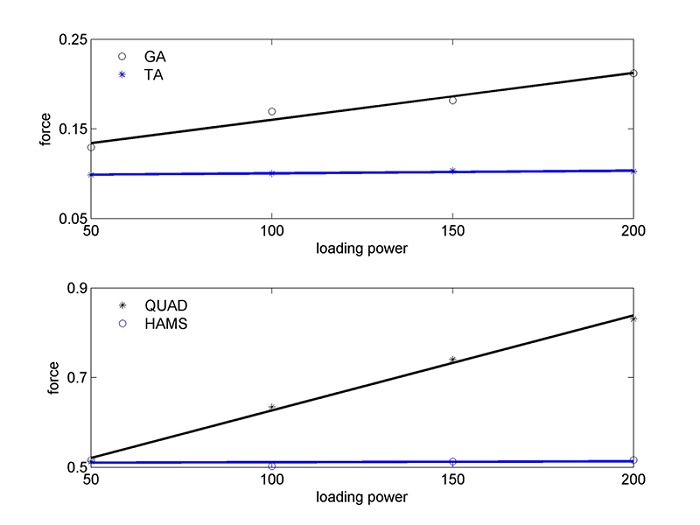
Maximal forces exerted in cycling motion for the TA and GA muscles (upper panel) and for the Quad and Hams muscles (lower panel), as a function of cycling power (w) (the force is expressed in 1/cm due to division of the dimensionless normalized torque by the moment arm, in cm).

Neuro-Mechanical System representation

In previous studies, neuro-mechanical muscle system representations relating EMG (input) to force or second order, with time delay^12,32-34 as follows, respectively

(4)

(5)

Where G(S) is the transfer function between output (torque/force) and input (EMG), d is the neuro-mechanical time delay and A, B, C are system coefficients for the characterized muscles, by means of the respective representations above. Note that the muscle torque here refers to the individual torque produced by each muscle, as obtained after optimization, as describe in equations (1 – 3).

Linear parameter estimation was performed after transforming each of the equations 4 and 5 into the time domain.³⁴ It consisted of an iteration process with assumed time delay between output and input, with target function to minimize the error between estimated and input EMG, by making use of the Matlab routine lsqlin (linear least squares with linear constraints) in the optimization toolbox. An alternative iteration approach is to minimize the error between estimated and output torque, after explicitly expressing the input EMG by means of an analytical function (e.g., fitting an n degree polynomial); this however would necessitate non-linear estimation procedures. Sample results for the linear estimations for the GA and TA muscle coefficients are summarized in Table 1. Validations of the muscle coefficients for each of the GA and TA muscles, through the reconstruction of their EMG signals and as linearly estimated for the second order transfer function, are presented in Figure 3 in the upper and lower panels, respectively.

Table 1.

Sample results for the linear estimations for the GA, TA, Quad and Hams muscle coefficients. Parameter A is expressed in sec for first order model and sec2 for second order model; B is dimensionless for first order and has sec units for second order model; C is dimensionless. Time delay d was nearly similar in both first and second order presentations; i.e. gave in both models the least SSE value.

muscle(load)	order	A	B	C	d	SSE
GA(100w)	1	5.55	0.37		0.83	0.009
	2	-184.14	5.70	0.37		0.008
TA(100w)	1	76.66	0.35		0.71	0.233
	2	695.03	76.08	0.35		0.219
QUAD(50w)	1	16.42	0.10		0.26	0.013
	2	-22.23	16.43	0.10		0.013
HAMS(150w)	1	8.75	0.12		0.20	0.083
	2	-4.34	8.76	0.12		0.083

Figure 3.

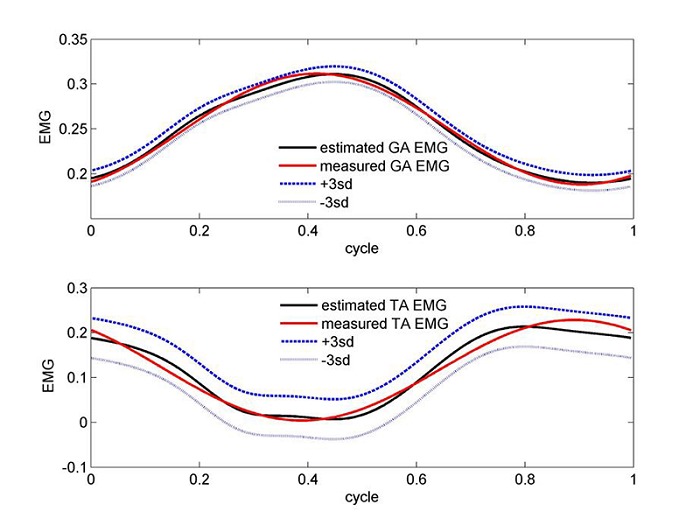
Validations of the muscle coefficients for the GA and TA muscles, through the reconstruction of their EMG signals and as linearly estimated for the second order transfer function in the upper and lower panels, respectively. The estimated curve is accompanied by an error strip of ± 3 sd (cycling power was 100 w).

Muscles of the knee joint and biarticular muscles

Different studies point to the significant role of biarticular muscles in power transfer from proximal to distal joints.³⁵ While the Hamstrings and quadriceps muscle groups are responsible for hip-to-knee transfer, the gastrocnemius is responsible to knee-to-ankle transfer.

It has been mentioned that the axial force within the biarticular muscle is maintained and may be considered constant across both joints. This, however, results in different torques in accordance with the respective different moment arms. Thus, the GA force estimated of at the ankle level is maintained at knee level, in which the quadriceps extends the knee joint and the hamstrings and gastrocnemius flex it. The knee torque resulting from the combined action of the quadriceps and hamstrings can be calculated as the difference between net total knee joint torque (as obtained from inverse dynamics) and gastrocnemius torque acting at knee joint.

To neutralize the contribution of the bi-articular GA in generating the knee joint torque, the GA force value obtained at the ankle level is multiplied by the moment arm as found in the literature.³⁶ Thus,

(6)

The net torque quad/hams is then parceled out using again the stress optimization criterion and taking data for the lever arms and cross sectional areas from Kellis, Baltzopoulos³⁷ and Ward et al.³⁸, respectively. The maximal forces exerted in cycling motion in each of the Quad and Hams muscles are shown in Figure 2, lower panel. The parameter estimation results of these two muscles are also presented in Table 1. Validations of the muscle coefficients for the Quad and Hams muscles, through the reconstruction of their EMG signals and as linearly estimated for the second order transfer function are presented in Figure 4 in the upper and lower panels, respectively.

Figure 4.

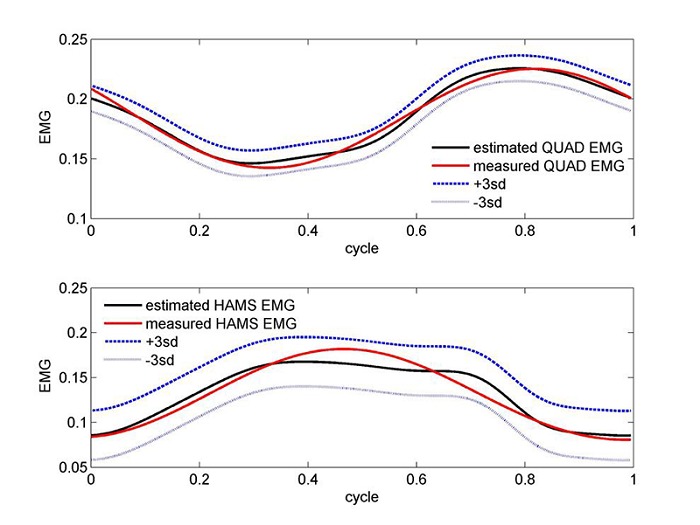
Validations of the muscle coefficients for the QUAD (upper panel) and HAMS (lower panel) muscles, through the reconstruction of their EMG signals and as linearly estimated for the second order transfer function in the upper and lower panels, respectively. The estimated curve is accompanied by an error strip of ± 3 sd (cycling power was 50 w for QUAD and 150 w for HAMS).

Muscle characterization is relevant if cycling motion is to be generated by electrically stimulated these muscles either in pure FES-induced mode, such as maybe required in complete muscle denervation, or in hybrid mode, where weakened volitional activity is enhanced by induced activation of the muscles. In this study we present a systematic method for characterizing the major muscle groups of the knee and ankle joints in cycling motion.

The mathematical simulation demonstrates how the developed models can be used to obtain the activation profiles that yield a required induced torque. Activation of the muscles, as expressed by their EMG’s (Figures 3 and 4), is generated from the muscle parameters obtained (e.g. Table 1), in accordance with the desired torques. This feature is important for flexibility of control, either in pure FES, or in hybrid activation when an enhancement torque is required. The model results suggested that the loading power affects the estimated muscle parameters. Future studies should focus on studying this effect more systematically.

The characterization of the muscle parameters was accomplished by a neuro-mechanical model for non-isometric activity of the lower limb in steady-state cycling motion. The linkage representing the lower limb included the ankle and knee joints, actuated by means of the TA, GA, Quad and Hams muscles, with the bi-articular GA being actuating both the ankle and knee joints. This typically indeterminate biomechanical problem was dealt with as follows: 1. Following the synergistic activity of the muscles involved in cycling motion, the system was reduced from nine to four muscles; 2. Solution of the GA bi-articular muscles was utilized when moving from the ankle to the knee joint; 3. Satisfaction of cost functions, as determined from optimization criteria, enabled us to overcome indeterminacy and determine the individual share of each muscle in the joint torques. For that, information about activation time of the muscles (Fig. 1) was useful.

The neuro-mechanical model makes use of the input (EMG, directly measurable) versus output (torque of muscle, estimated from experiment and optimization) to characterize the muscle dynamics in non-isometric activity, in a linear transfer function. Regarding the system order used, while experimenting with estimation of the muscle parameters in both first and second orders, the SSE errors turned smaller in the second order. It should, however, be kept in mind that a second order system includes an additional parameter, increasing the number of unknowns for the same input information.

The implementation of optimization criteria has been an ambiguous issue in the Biomechanics literature. To mention just a few, cost functions have included minimization of force (muscle, joint), stress, power, or a combination.^23,25 A somewhat different optimi-zation criterion was applied by Raasch et al.¹⁴ for cycling motion at maximum speed pedaling. The suggested cost function was on muscle excitation, i.e. find those muscle excitations that maximize the crank progress. In the present study we applied the minimum stress criterion, with power n = 3 (equation 1), after verifying that other criteria created inconsistencies of the forces obtained. It should be mentioned, though, that other values for the power n may provide better optimization results for different phases of the motion cycle, different muscles, different subjects, and the like. In fact, Collins²⁷ suggested that in level walking it would not be reasonable to assume that a unique optimization criterion dominates the entire course of movements and that it is more likely that there is a combination of several optimization criteria.

The procedure of parameter estimation could be performed with either the EMG or the torque as the target function. The presented estimated parameters shown in Table 1 were made while EMG served as the target function, as is also noted from the validation curves in Figures 3 and 4 in which the EMG is reconstructed. A selected delay time serves as the initial point of the linear iteration.³⁴ When following the second alternative, i.e. torque as the target function, the iteration becomes non-linear after expressing the input signal in function form and transforming to the time domain, making this approach less appealing compared to the selected one.

The presented model provides a systematic method to identify unambiguously muscle parameters in the non-isometric cycling activity. The identified parameters provides means of constructing activation patterns by means of activation profiles, as required in the complete activation of paralyzed muscles, or in the hybrid activation of partly deficient muscles.