BFLCRM: A BAYESIAN FUNCTIONAL LINEAR COX REGRESSION MODEL FOR PREDICTING TIME TO CONVERSION TO ALZHEIMER’S DISEASE

Abstract

The aim of this paper is to develop a Bayesian functional linear Cox regression model (BFLCRM) with both functional and scalar covariates. This new development is motivated by establishing the likelihood of conversion to Alzheimer’s disease (AD) in 346 patients with mild cognitive impairment (MCI) enrolled in the Alzheimer’s Disease Neuroimaging Initiative 1 (ADNI-1) and the early markers of conversion. These 346 MCI patients were followed over 48 months, with 161 MCI participants progressing to AD at 48 months. The functional linear Cox regression model was used to establish that functional covariates including hippocampus surface morphology and scalar covariates including brain MRI volumes, cognitive performance (ADAS-Cog), and APOE status can accurately predict time to onset of AD. Posterior computation proceeds via an efficient Markov chain Monte Carlo algorithm. A simulation study is performed to evaluate the finite sample performance of BFLCRM.

1. Introduction

Alzheimer’s Disease (AD) is a firmly incurable and progressive disease [14]. In the pathology of AD, mild cognitive impairment (MCI) is a clinical syndrome characterized by insidious onset and gradual progression, and commonly arising as a result of underlying neurodegenerative pathology [26]. Since MCI is considered as a risk state for AD, a major research focus in recent years has been to delineate a set of biomarkers that provide evidence of such a neurodegenerative pathology in living individuals, with the goal of specifying the likelihood that the pathophysiological process is due to Alzheimer’s disease (MCI due to AD; MCI-AD) and will lead to dementia within a few years [1]. Accordingly, increasing attention has been devoted to investigate the utility of various imaging, genetic, clinical, behavioral, and fluid data to predict the conversion from MCI to AD.

Several studies have utilized a small subset of biosignatures and then assessed the relative importance of different modalities in predicting the diagnostic change from MCI to AD [12, 21, 58, 61, 80]. For example, in [12], the authors simultaneously examined multiple features from different modalities, including structural magnetic resonance imaging (MRI) morphometry, cerebrospinal fluid biomarkers, and neuropsychological measures to assess an optimal set of predictors of conversion from MCI to AD. They observed that structural changes within the medial temporal lobe (MTL), particularly the hippocampus, as well as performance on cognitive tests that rely on MTL integrity (i.e., episodic memory), were good predictors of MCI to AD conversion.

Recently, most researchers have turned to the analysis of longitudinal data to assess the dynamic changes of various biomarkers associated with the MCI-to-AD transition across time. To begin, a prominent neural correlate of MCI-AD is volume loss within the MTL, especially within the hippocampus and entorhinal cortex [19], with increasing atrophy in these structures from normal aging to MCI to AD [54]. Longitudinal studies of individuals with MCI-AD have also highlighted the importance of assessing MTL changes in tracking the progression of MCI to AD. For example, several studies have documented diminished baseline hippocampal and entorhinal volumes that are associated with an increased likelihood of progressing to clinical dementia [29, 41]. Additionally, several modalities of disease indicators have been studied to assess progression to AD, including neuroimaging markers [61, 75, 79], biomedical markers [65], and neuropsychological assessments [55]. Finally, a number of structural MRI studies, covering region of interest (ROI), volume of interest, voxel-based morphometry, and shape analysis have reported that the degree of atrophy in several brain regions, such as the hippocampus and entorhinal cortex, is not only sensitive to disease progression, but also predicts MCI conversion [10, 16, 48].

Despite the importance of these investigations, a central question remains. Namely, how do we accurately predict the time to conversion in individuals who harbor AD pathology, as well as determine the optimal early markers of conversion? In [73], 148 MCI subjects were used to identify the most predictive neuropsychological measures. In [44], 139 MCI subjects in ADNI-1 were used to evaluate the predictive power of brain volume, ventricular volume, hippocampus volume, APOE status, cerebrospinal fluid (CSF) biomarkers, and behavioral scores. Their results show a moderately accurate prediction with the value of an area under the curve of 0.757 at 36 months, whereas they found that baseline volumetric MRI and behavioral scores were selectively predictive. Finally, in [13], 381 MCI subjects from ADNI 1 were examined to evaluate several biomarkers for predicting MCI to AD conversion including spatial patterns of brain atrophy, ADAS-Cog, APOE genotype, and cerebrospinal fluid (CSF) biomarkers. Their findings suggest that a combination of spatial patterns of brain atrophy and ADAS-Cog offers good predictive power of conversion from MCI to AD, whereas APOE genotype did not significantly improve prediction. To the best of our knowledge, no prior study has examined the role of functional covariates including hippocampus surface morphology in predicting time to conversion from MCI to AD with/without adjusting for low-dimensional behavioral and clinical measures.

To assess the predictability of hippocampus surface morphology in survival models, we develop a Bayesian functional linear Cox regression model (BFLCRM) with both functional and scalar covariates. The BFLCRM integrates a Cox proportional hazard regression and functional linear model into a single framework. First, BFLCRM can be an important extension of various statistical models including parametric, semiparametric and nonparametric models for handling survival response data and scalar covariates. See overviews of various survival models in [24, 33, 40] and the references therein. Recent advances in computation and prior elicitation have made Bayesian analyses of these survival models with scalar covariates feasible. For instance, nonparametric prior processes including the gamma process prior, the Beta process model, the correlated gamma process, and the Dirichlet process prior have been developed as the prior distribution of the baseline cumulative hazard function [33, 70]. Second, BFLCRM can be an important extension of various functional linear models for handling discrete or continuous response data and functional covariates. The existing literature focuses on the development of frequentist methods for functional linear models. Some examples include [23, 38, 59, 60, 78] and the references therein. Third, BFLCRM can be regarded as an important extension of high-dimensional survival models. However, most high-dimensional survival models focus on the identification of a small set of covariates and their overall effect on time-to-event outcomes [5, 39, 43]. These approaches can be sub-optimal for high-dimensional imaging data, since the effect of imaging data on clinical data and other imaging data is often non-sparse, which makes it notoriously difficult for many existing regularization methods [20, 74].

In Section 2, we will introduce BFLCRM and its associated Bayesian estimation procedure. In Section 3, we will introduce the NIH Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset and illustrate the use of BFLCRM in the prediction of time to conversion from MCI to AD by using both functional and scalar covariates. In Section 4, we conduct simulation studies to examine the finite sample performance of BFLCRM. In Section 5, we interpret the findings obtained from the analysis of ADNI dataset.

2. Bayesian Functional Linear Cox Regression Models

2.1. Setup.

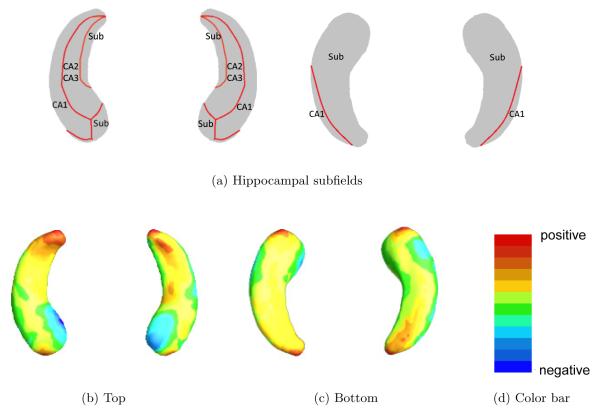
Consider imaging, genetic, and clinical data from n = 346 independent MCI patients in ADNI-1. For the i-th MCI patient, we observe a possibly right censored time to conversion to AD, denoted by y_i. Specifically, y_i = T_i∧C_i is the minimum of the censoring time C_i and the transition time T_i and ν_i = 1(y_i = T_i), where 1(·) is an indicator function. Moreover, we observe a p × 1 vector of scalar covariates, denoted by x_i = (x_i1, ··· , x_ip)^T, and a functional covariate, denoted by Z_i(·), on a compact set $\mathcal{S}$. In this paper, we focus on the noninformative censoring setting such that T_i and C_i are conditionally independent given all covariates of interest. The scalar covariates of interest include age at baseline, length of eduction, gender, handedness, marital status, retirement, and the well-known Apolipoprotein E (APOE) SNPs. The APOE has three major forms, ϵ2, ϵ3, and ϵ4, where ϵ3 is the most common form. The functional covariate of interest is the hippocampus surface morphology. Figure 1 shows the example hippocampus surface morphology data in ADNI-1 data.

Fig 1.

ADNI data: panel (a) is hippocampal subfields mapped onto a representative hippocampal surface [4], and panels (b) and (c), respectively, show the top and bottom views of the first subject’s hippocampal surface data color-coded by the colorbar in panel (d).

Our problems of interest are to establish the likelihood of conversion to Alzheimer’s disease (AD) in 346 MCI patients enrolled in the ADNI-1 and to select the optimal early markers of conversion from both the scalar covariates and the functional covariate. With the sole presence of x_i, it is common to consider Cox’s proportional hazards model [11], which assumes that the conditional hazard function of y_i given x_i is given by

$$h(y\mid {\mathbf{x}}_i)=h_0\left(y\right)\exp \left({\mathbf{x}}_i^T\beta \right)=h_0\left(y\right)\exp \left(\sum _{k=1}^p{x}_{\mathit{ik}}{\beta }_k\right),$$ (2.1)

where β = (β₁, ··· , β_p)^T is a p × 1 vector of regression coefficients and h₀(·) is an unknown baseline hazard function. However, the Cox proportional hazards model (2.1) does not incorporate the effect of the functional covariate Z_i(·) on the time to conversion.

2.2. Model Formulation

We propose a Bayesian functional linear Cox regression model with three main ingredients for handling both functional and scalar covariates as a natural extension of (2.1). Based on this formulation, we take a Bayesian approach to estimate the parameters of interest.

In the first component of BFLCRM, it is assumed that the hazard function of y_i given (x_i, Z_i(·)) is given by

$$h(y\mid {\mathbf{x}}_i,Z_i(\cdot \left)\right)=h_0\left(y\right)\exp \left(\sum _{k=1}^p{x}_{\mathit{ik}}{\beta }_k+{\int }_{\mathcal{S}}\gamma \left(s\right)\left(Z_i\right(s)-\mu (s\left)\right)\mathit{ds}\right),$$ (2.2)

where μ(s) is the mean function of Z_i(s) and γ(·) is an unknown coefficient function, a square integrable function on $\mathcal{S}$.

The second component of BFLCRM is the functional principal component analysis (fPCA) model of the Z_i(·)’s. It is assumed that the Z_i(s)’s are square integrable random functions and W_i(s) are measured at a set of grid points in $\mathcal{S}$ with measurement errors such that

$$W_i\left(s\right)=Z_i\left(s\right)+{ϵ}_i\left(s\right)=\mu \left(s\right)+{\stackrel{‒}{Z}}_i\left(s\right)+{ϵ}_i\left(s\right),$$ (2.3)

where ${\stackrel{‒}{Z}}_i\left(s\right)$ characterizes individual functional variations from μ(s). The ϵ_i(s)’s are measurement errors with mean zero and variance ${\sigma }_{ϵ}^2\left(s\right)$ at each s and independent of each other for s ≠ s′. Moreover, μ(s) can be consistently estimated by $\widehat{\mu }\left(s\right)={\sum }_{i=1}^n{W}_i\left(s\right)∕n$.

It is assumed that Z_i(s) and ϵ_i(s) are independent of each other and the covariance function of $\left\{{\stackrel{‒}{Z}}_i\right(s):s\in S\}$, denoted by $K(s,s^{\prime })=E\left\{\stackrel{‒}{Z}\right(s\left)\stackrel{‒}{Z}\right(s^{\prime }\left)\right\}$, is continuous on $\mathcal{S}\times \mathcal{S}$. According to Mercer’s theorem, K(s, s′) also admits a spectral decomposition $K(s,s^{\prime })={\sum }_{j=1}^{\infty }{\psi }_j{\varphi }_j\left(s\right){\varphi }_j\left(s^{\prime }\right)$, where (ψ_j, ϕ_j(s))’s are the eigenvalue-eigenfunction pairs of K(s, s′) such that {ψ_j : j ≥ 1} are the eigenvalues in decreasing order with ${\sum }_{j=1}^{\infty }{\psi }_j^2<\infty$. Thus, ${\stackrel{‒}{Z}}_i\left(s\right)$ admits the Karhunen-Loeve expansion as ${\stackrel{‒}{Z}}_i\left(s\right)={\sum }_{j=1}^{\infty }{\xi }_{\mathit{ij}}{\varphi }_j\left(s\right)$, where ξ_ij are referred to functional principal component (fPC) scores and ${\xi }_{\mathit{ij}}={\int }_{\mathcal{S}}{\stackrel{‒}{Z}}_i\left(s\right){\varphi }_j\left(s\right)\mathit{ds}$ are uncorrelated random variables with mean zero and variance ${\psi }_j=E\left({\xi }_{\mathit{ij}}^2\right)$. To estimate ξ_ij based on the observed covariate functions W_i(s), we first employ the cubic smoothing spline [30] to estimate the underlying signal Z_i(s). We then use the sample mean and covariance functions of the estimated Z_i(s) to estimate μ(s) and K(s, s′). Subsequently, we estimate ϕ_j(s) and ξ_ij for all i, j ≤ n.

The third component of the FLCRM is an approximation of ${\int }_{\mathcal{S}}\gamma \left(s\right)\stackrel{‒}{Z}\left(s\right)\mathit{ds}$. Since the eigenfunctions ψ_j(·) form a complete orthonormal system on the space of square-integrable functions on $\mathcal{S}$, the covariate function γ(s) can be expanded as

$$\gamma \left(s\right)=\sum _{j=1}^{\infty }{\varphi }_j\left(s\right){\gamma }_j\text{with}\sum _{j=1}^{\infty }{\gamma }_j^2<\infty .$$ (2.4)

Therefore, we have

$${\int }_{\mathcal{S}}{\stackrel{‒}{Z}}_i\left(s\right)\gamma \left(s\right)\mathit{ds}=\sum _{j=1}^{\infty }{\xi }_{\mathit{ij}}{\gamma }_j$$ (2.5)

and approximate h(y∣x_i, Z_i(·)) as

$$h_0\left(y\right)\exp \left(\sum _{k=1}^p{x}_{\mathit{ik}}{\beta }_k+\sum _{j=1}^{\infty }{\xi }_{\mathit{ij}}{\gamma }_j\right)\approx h_0\left(y\right)\exp \left(\sum _{k=1}^p{x}_{\mathit{ik}}{\beta }_k+\sum _{j=1}^{q_n}{\xi }_{\mathit{ij}}{\gamma }_j\right),$$ (2.6)

where q_n is a sufficiently large integer that may depend on n. As shown in the literature, such an approximation is accurate under some conditions on the decay rate of the γ_j’s. Practically, it is common to choose q_n such that the percentage of variance explained by the first q_n fPCA components is 70%, 85%, or 95%. Alternatively, we may formulate it as a model selection procedure and choose it by using some model selection criterion, such as the deviance information criterion (DIC) [34, 71].

2.3. Priors

To carry out a Bayesian analysis of model (2.6), we specify joint prior distributions for all unknown parameters (β, γ, h₀), where h₀(·) is the baseline hazard function. We first set p(β, γ, h₀) = p(β, γ)p(h₀) and assume (β, γ) ~ N(μ₀, Σ₀), where N(μ₀, Σ₀) is the multivariate Normal distribution with s (p + q_n) × 1 mean vector μ₀ and a (p + q_n) × (p + q_n) covariance matrix Σ₀.

We may specify different prior distributions for h₀(y). The most convenient and popular distribution for h₀(y) is the piecewise constant hazard model. Specifically, we first construct a finite partition of the time axis, 0 < s₁ < s₂ < ··· < s_J, with s_J > y_i for all i, which leads to J intervals (0, s₁], ···, (s_J−1, s_J]. In the j–th interval, we set h₀(y) = λ_j for y ∈ I_j = (s_j−1, s_j]. A common prior of the baseline hazard λ = (λ₁, ··· , λ_J)^T is the independent gamma prior ${\lambda }_j\sim \mathcal{G}({\alpha }_{0j},{\alpha }_{1j})$ for j = 1, ··· , J, where α_0j and α_1j are prior hyperparameters. Another approach is to build prior correlation among the λ_j’s using a prior ψ ~ N(ψ₀, Σ_J), where ψ_j = log(λ_j) for j = 1, ··· , J and ψ_j = (ψ₁, ··· , ψ_J). For notational simplicity, we focus on the piecewise constant hazard model with the independent gamma prior from here on.

We consider the strategy of choosing the hyperparameters Σ₀, α_0j and α_1j as follows. We can tune the eigenvalues of Σ₀ in order to control the prior information for the regression coefficients. If the smallest eigenvalue λ_min(Σ₀) converges to ∞, then N(μ₀, Σ₀) tends to be an improper prior. In contrast, if the largest eigenvalue λ_max(Σ₀) is very small, then N(μ₀, Σ₀) tends to be a strongly informative prior. In order to use a noninformative prior for the λ_j’s, the shape and scale parameters of the gamma distributions are set to be α_0j = 0.2 and α_1j = 0.4 for all j = 1, ··· , J [69]. Also setting either (α_0j, α_1j) = (0.5, 1) or (α_0j, α_1j) = (0.2, 1) would make the gamma distribution flat as well.

2.4. Posterior Computation

The log-posterior distribution of (β, γ, λ) (unnormalized) is given by

$$\sum _{i=1}^n\sum _{j=1}^J\left[u_{\mathit{ij}}{\nu }_i\right(\log {\lambda }_j+{\mathit{z}}_i^T\theta )-u_{\mathit{ij}}\{{\lambda }_j(y_i-s_{j-1})+\sum _{g=1}^{j-1}{\lambda }_g(s_g-s_{g-1})\left\}\exp \right({\mathit{z}}_i^T\theta \left)\right]-\{\log \mid {\Sigma }_0\mid +{(\theta -{\mu }_0)}^T{\Sigma }_0^{-1}(\theta -{\mu }_0\left)\right\}∕2+\sum _{j=1}^J\left\{\right({\alpha }_{0j}-1)\log {\lambda }_j-{\lambda }_j{\alpha }_{1j}+{\alpha }_{0j}\log ({\alpha }_{1j})-\log \Gamma ({\alpha }_{0j}\left)\right\},$$ (2.7)

where $\theta ={({\beta }^T,{\gamma }^T)}^T,{\mathit{z}}_i={({\mathit{x}}_i^T,{\xi }_{i1},\cdots ,{\xi }_{{\mathit{iq}}_n})}^T$, and s₀ = 0. Moreover, u_ij = 1 if the i–th subject is right censored in the j–th interval and 0 otherwise. We propose a Gibbs sampler for posterior computation after truncating the sum of the infinite series to have q_n < ∞ terms. The Gibbs sampler is computationally efficient and mixes rapidly. We first specify the hyperparameters μ₀, Σ₀, α_0j and α_1j for all j at appropriate values to represent prior opinion. Starting from the initiation step, the Gibbs sampler for model (2.6) with the truncated term q_n proceeds as follows:

1. Update (β, γ) according to their full conditional distribution in (2.7). Specifically, we employ the random walk Metropolis-Hastings (M-H) [31, 47] algorithm and choose a multivariate Normal proposal density yielding an average acceptance rate of 23.4% [27]. The mean of the proposal density is the posterior sample (β^t−1, γ^t−1) from the previous iteration. The covariance matrix is the inverse of the Fisher information matrix of the posterior distribution evaluated at (β^t−1, γ^t−1).

2. Update λ_j from its full conditional distribution

   $$p({\lambda }_j\mid {\lambda }_0^{(-j)},-)\sim \text{Gamma}({\alpha }_{0j}+\sum _{i=1}^n{u}_{\mathit{ij}}{\nu }_i,{\tilde{\alpha }}_{1j}),$$

   where ${\lambda }_0^{(-j)}$ is the vector λ₀ without the j-th element and ${\tilde{\alpha }}_{1j}$ is given by

   $${\tilde{\alpha }}_{1j}=\{\begin{array}{c}\hfill {\alpha }_{1j}+\sum _{i=1}^n\left\{u_{\mathit{ij}}\right(y_i-s_{j-1})+(s_j-s_{j-1}\left)\sum _{k=j+1}^J{u}_{\mathit{ik}}\right\}\exp \left({\mathit{z}}_i^T\theta \right),\hfill \\ \hfill \text{if}j\le J-1;\hfill \\ \hfill {\alpha }_{1J}+\sum _{i=1}^n\left\{u_{\mathit{iJ}}\right(y_i-s_{J-1}\left)\exp \right({\mathit{z}}_i^T\theta \left)\right\},\hfill \\ \hfill \text{if}j=J.\hfill \end{array}\phantom{\}}$$

3. Alzheimer’s Disease Neuroimaging Initiative Data Analysis

3.1. Alzheimer’s Disease Neuroimaging Initiative

The development of the BFLCRM is motivated by the analysis of imaging, genetic, and clinical data collected by ADNI. “Data used in the preparation of this article were obtained from the Alzheimers Disease Neuroimaging Initiative (ADNI) database (www.loni.usc.edu/ADNI). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (aMCI) and early Alzheimers disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, M.D., VA Medical Center and University of California - San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55 to 90, to participate in the research approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with aMCI to be followed for 3 years, and 200 people with early AD to be followed for 2 years. For up-to-date information see www.adni-info.org.”

3.2. Data Description

The aim of this ADNI data analysis is to examine the predictability of clinical, genetic, and imaging data for the time to conversion to AD in MCI patients. We focused on 346 MCI patients at baseline of the ADNI-1 database. Among the 346 MCI patients, 151 of them are converters and 195 are non-converters at 48 months.

For each MCI patient, we included his/her clinical, genetic, and imaging variables at baseline. The clinical characteristics include Gender (0=Male; 1=Female), Handedness (0=Right; 1=Left), Marital Status (1=Married; 2=Widowed; 3=Divorced; 4=Never married), Education length, Retirement (1=Yes; 0=No), Age, and Alzheimer’s Disease Assessment Scale-Cognition (ADAS-Cog) score. Marriage status is coded using 3 dummy variables: “Widowed”, “Divorced”, “Never married”. The ADAS-Cog test has been widely used to assess the severity of dysfunction in adults [62]. The genetic variables include the APOE genetic covariates, since it is well known that mutations in APOE raise the risk of progression from amnestic MCI to AD[56]. The Apolipoprotein E (APOE) SNPs, rs429358 and rs7412 were, separately, genotyped in ADNI-1. These two SNPs together define a 3 allele haplotype, namely the ϵ2, ϵ3, and ϵ4 variants and the presence of each of these variants was available in the ADNI database for all the individuals. Among these variants, APOE-ϵ3 is known to be most common allele, while APOE-ϵ4 has been turned out to be a risk factor for early onset of AD. [52]. In this model, we consider the presence of APOE-ϵ4 as a covariate to incorporate its effect on the time to conversion from MCI to AD. In addition, we selected 7 regions of interest (ROIs) which may significantly influence MCI progression among the 93 ROI volume data [6, 22, 37]. These 7 ROIs are bilateral hippocampal formation, bilateral amygdala, posterior limb of internal capsule, bilateral thalamus. In total, we have 17 scalar covariates. The imaging data include the hippocampal radial distances of 30,000 surface points on the left and right hippocampal surfaces. The hippocampal radial distance is a distance from its medial core to the hippocampal surface and measures hippocampal thickness.

In the demographic information, 220 participants are male, and 126 are female; 316 are right-handed, and 30 are left-handed. For Marital Status, 283 were married, 40 were widowed, 19 were divorced, and 4 were never married at baseline. Among these individuals, 276 were retired and 70 were not. On average, the subjects had 15.7 years of education with standard deviation 3.0 years, the minimum 6 years, and the maximum 20 years. The average age of subjects was 75.0 years with standard deviation of 7.3 years. The youngest person was 55 years old, while the oldest person was 90 years old. For the genetics information on the first allele of APOE, 25 subjects had genotype 2, 277 subjects had genotype 3, and 44 subjects had genotype 4. For the second allele, 156 subjects had genotype 3, while 190 subjects had genotype 4. The average ADAS-cog score was 11.5, with standard deviation of 4.4. The lowest score was 2 and the highest score was 27.67.

3.3. Hippocampus Image Preprocessing

We used a hippocampal image analysis package to calculate hippocampal surface data as follows [8, 46, 50,66, 67, 68, 77]. Given the 3D MRI scans, we used FIRST [53] to segment hippocampal substructures and then applied the marching cube method [45] to automatically reconstructing hippocampal surfaces. Then, an automatic algorithm, called topology optimization, was used to introduce two cuts on a hippocampal surface in order to convert it into a genus zero surface with two open boundaries. The two cuts, whose locations were at the front and back of the hippocampal surface, represent its anterior junction with the amygdala and its posterior limit as it turns into the white matter of the fornix. We then computed holomorphic 1-form basis functions [76]. It allows us to induce conformal grids of the hippocampal surfaces which were consistent across subjects. The conformal representation of the surface was computed with this conformal grid [66]. We also computed the “feature image” of a surface by combining the conformal factor and mean curvature and linearly scaling the dynamic range into [0, 255]. Finally, the feature image of each surface in the dataset was registered to a common template by using an inverse consistent fluid registration algorithm [68]. It establishes high-order correspondences between 3D surfaces. Finally, we computed various surface statistics based on the registered surface, such as multivariate tensor-based morphometry (mTBM) statistics [76].

3.4. Data Analysis

We focused on 346 MCI patients in the ADNI-1 data in order to examine the predictability of clinical, genetic, and imaging covariates for the time to conversion to AD from MCI. The patients consist of 151 converters and 195 non-converters. We fit BFLCRM with time to conversion to AD as the response y_i, the clinical, genetic, and ROI volume data as scalar covariates in x_i, and the hippocampus surface data based on radial distance as functional covariates in Z_i(·) for the i-th subject. In all posterior computations, we centered the scalar covariates x_i using their mean. We chose the first 14 eigenfunctions of hippocampal surface data, which explain about 73.48% of the variance in the hippocampus surface data. The first 14 largest eigenfunctions projected on the hippocampal surfaces were presented in Figure 3 in the supplementary document. For the piecewise constant hazards model of h₀(·), we chose J = 70 intervals so that each interval contains at least one failure or censored observation. The full BFLCRM model (2.6) contains 19 scalar covariates and the first 14 fPC scores.

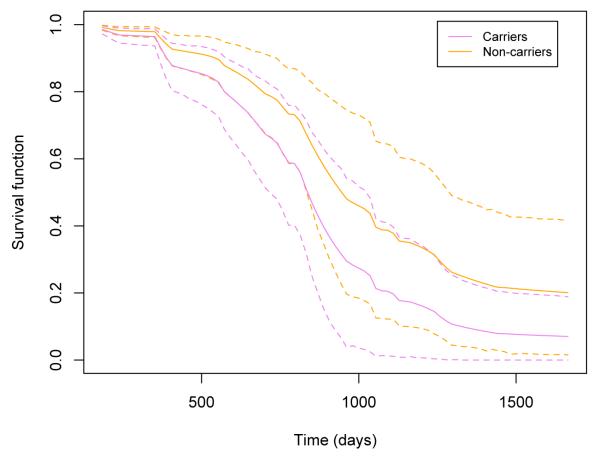
Fig 3.

ADNI data analysis results: the estimated survival curves of APOE-ϵ4 carriers and non-carriers under the full BFLCRM model. Other continuous or categorical covariates are fixed at the mean values or reference levels. The dotted lines show the 95% HPD intervals of the estimated survival functions.

Due to the lack of prior information, all hyperparameters were chosen to reflect nearly noninformative priors. For regression coefficients, the hyperparameters of the multivariate Normal priors were set as μ₀ = (0, ··· , 0) and Σ₀ = diag(5, ··· , 5). For the γ_j’s, the shape and scale parameters of the Gamma priors were set to be α_0j = 0.2 and α_1j = 0.4 for j = 1, ··· , 70 [69]. We ran the Gibbs sampler for 25,000 iterations after 5,000 burn-in iterations. Based on the 20,000 MCMC samples, we calculated various posterior quantities of (β, γ, λ). For the full BFLCRM model, we also conducted sensitivity analyses in order to investigate the influence of different choices of hyperparameters in the prior distributions. From the results shown in Tables 1 and 2 in the supplementary document, we found that the proposed priors were robust to various choices of the hyperparameters in the prior distributions. The computational time (in C/C++ using an 8-cores 2.80 GHz Intel processors) was 350 seconds for running the Gibbs sampler for the full BFLCRM model with 25,000 iterations.

Table 1.

ADNI data analysis results for the full BFLCRM model : the posterior quantities of 19 regression coefficients β_ks, that correspond to x_i =(Gender, Handedness, Widowed, Divorced, Never married, Length of Education, Retirement, Age, APOE-ϵ4 carrier, ADAS-cog Score, posterior limb of internal capsule, Right hippocampal formation, Left hippocampal formation, Left thalamus, Left amygdala, Right amygdala, and Right thalamus). Mean denotes ‘posterior mean’, SD denotes ‘posterior standard deviation’, and lower and upper, respectively, represent the ‘lower and upper limits’ of a 95% highest posterior density interval.

	β 1	β 2	β 3	β 4	β 5	β 6	β 7	β 8
Mean	0.4344	0.2255	0.3119	0.2729	0.7203	−0.0874	0.3455	−0.0519
SD	0.2513	0.3647	0.3827	0.4663	0.7867	0.0367	0.2482	0.0178
lower	−0.0495	−0.5248	−0.4632	−0.6789	−0.9383	−0.1691	−0.0919	−0.0873
upper	0.9478	0.8628	1.0138	1.1195	2.2009	−0.0244	0.8608	−0.0188

	β 9	β 10	β 11	β 12	β 13	β 14	β 15	β 16	β 17
Mean	0.5550	0.1568	0.0008	0.0006	−0.0011	−0.0004	0.0018	−0.0012	0.0003
SD	0.2341	0.0265	0.0005	0.0004	0.0004	0.0004	0.0009	0.0005	0.0004
lower	0.1258	0.1030	−0.0002	−0.0002	−0.0019	−0.0012	0.0000	−0.0023	−0.0004
upper	1.0258	0.2075	0.0019	0.0014	−0.0004	0.0003	0.0036	−0.0002	0.0010

Table 2.

ADNI data analysis results under the four models: Deviance Information Criterion (DIC) and the empirical means of iAUC values and their corresponding standard errors in the parenthesis calculated from the Monte Carlo cross-validation (MCCV).

	the full BFLCRM model	Model 1	Model 2	Model 3
DIC	427.19	413.08	417.04	438.22
iAUC	0.840 (0.003)	0.836 (0.003)	0.809 (0.003)	0.751 (0.004)

Table 1 shows the posterior means of the regression coefficients β and their standard deviations, as well as the lower and upper limits of the 95% highest posterior density (HPD) intervals based on the full BFLCRM model. Six scalar covariates including “Length of Education”, “Age”, “APOE-ϵ4 carrirer”, “ADAS-cog score”, “Left Hippocampal formation”, and “Right amygdala” have 95% HPD intervals that do not contain 0. This implies that we can expect a worse prognosis of AD for MCI patients with lower ROI volume in the left hippocampal formation and the right amygdala. This finding supports the finding that atrophy of the hippocampal formation is a significant diagnostic marker [35, 42]. It also confirms the previous finding that the amygdala volume tends to be reduced in the early stage of AD[49,57]. Moreover, the 95% HPD intervals of the 1st, 7th, and 14th fPCs do not contain 0. This may indicate that the hippocampal radial distance is an important functional covariate for predicting the time to conversion to AD in MCI subjects.

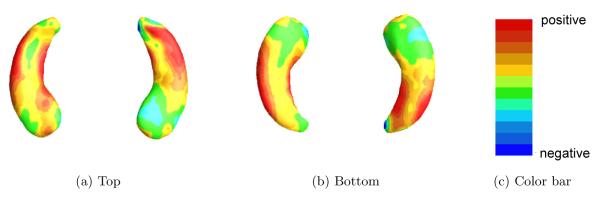
We estimated the coefficient function γ(·) by using $\widehat{\gamma }\left(s\right)={\sum }_{j=1}^{14}{\widehat{\varphi }}_j\left(s\right){\widehat{\gamma }}_j$, where ${\widehat{\gamma }}_j$ is the posterior mean of γ_j for each j. Figure 4 shows the estimated coefficient function $\widehat{\gamma }(\cdot )$ associated with the hippocampal surface data. When hippocampal atrophy in a red region is greater, a risk of progressing from MCI to AD is expected to be increased. A blue region suggests that the thicker the area is on the hippocampus, the shorter the time to conversion to AD is. Inspecting Figure 4 reveals that the subfields of CA1 and subiculum on the hippocampi have positive effects on the hazard function, indicating that the thinner these areas on the hippocampus are, the shorter the time is to conversion to AD.

Fig 4.

ADNI data analysis results for the full BFLCRM model: panels (a) and (b), respectively, show the top and bottom views of the estimated coefficient function associated with the hippocampal surface data color-coded by the colorbar in panel (c).

Figure 3 shows the estimated survival functions of the APOE-ϵ4 carriers and non-carriers, when the values of the continuous covariates are set at their mean values and the categorical variables are set at their reference levels. The dotted lines show the 95% HPD intervals of survival functions. The APOE-ϵ4 carriers are expected to convert from MCI to AD faster than non-carriers. These results are consistent with several prior studies suggesting that the presence of the APOE-ϵ4 allele increases the risk of developing AD [9, 63, 72].

We compared the full BFLCRM model with three reduced models in terms of their predictive performance. For Model 1, we excluded the ROI volume covariates from the full BFLCRM model. For Model 2, we only included all the scalar covariates. For Model 3, we only included the clinical covariates, APOE-ϵ4 status, and the ADAS-cog score. For all three reduced models, we set J = 70 intervals so that each interval contains at least one failure or censored observation. For the regression coefficients, the hyperparameters of the multivariate Normal priors were set as μ₀ = (0, ··· , 0) and Σ₀ = diag(5, ··· , 5). We set α_0j = 0.2 and α_1j = 0.4 for j = 1, ··· , 70. We ran the Gibbs sampler for 25,000 iterations after 5,000 burn-in iterations. We also calculated the Deviance Information Criterion (DIC) and integrated AUC (iAUC) for all four models, where AUC denotes the area under the Receiver Operating Characteristic (ROC) curve. The DIC can be estimated within the MCMC iterations. More details can be found in [34, 71].

Table 2 shows the values of DIC and iAUC for the four models. The full BFLCRM model yields the DIC value of 427.19, which is smaller than those of Models 3, but larger than those of Model 1 and 2. The Model 1 had the smallest DIC value as 413.08. For Model 1, as shown in Table 3, “Age”, “APOE-ϵ4 carrier”, and “ADAS-cog score” have their 95% HPD intervals that do not contain 0. See additional estimation results associated with Models 1-3 in Tables 3-4 and Figures 1 and 2 of the supplementary document. Based on the iAUC values, however, the full BFLCRM model achieves the best predictive performance. Moreover, the full model and Model 1, that include the hippocampal surface data as functional covariates, provide better predictive performance than Models 2 and 3. This may indicate that the hippocampal surface data contributes significantly to the time of conversion from MCI to AD. We estimated the iAUC by using a Monte Carlo cross-validation (MCCV) method [32]. Specifically, the full data set was randomly split into a training set with 200 subjects and a test set with 146 subjects. For each such split, we fitted each model to the training set and then calculated iAUC based on the test set. This random split was repeated 100 times yielding the estimated iAUC values for all models.

Table 3.

ADNI data analysis results for Model 1: the posterior quantities of 12 regression coefficients β_ks, that correspond to x_i =(Gender, Handedness, Widowed, Divorced, Never married, Length of Education, Retirement, Age, APOE-ϵ4 carrier, and ADAS-cog Score). Mean denotes ‘posterior mean’, SD denotes ‘posterior standard deviation’, and lower and upper, respectively, represent the ‘lower and upper limits’ of a 95% highest posterior density interval.

	β 1	β 2	β 3	β 4	β 5	β 6	β 7	β 8	β 9	β 10
Mean	0.3943	0.2826	0.2422	0.1409	0.5174	−0.0577	0.4045	−0.0406	0.5143	0.1572
SD	0.2016	0.3317	0.3121	0.4377	0.7682	0.0341	0.2442	0.0156	0.2190	0.0239
lower	−0.0157	−0.3488	−0.4151	−0.7356	−0.9930	−0.1260	−0.0610	−0.0699	0.1069	0.1104
upper	0.7842	0.9094	0.8308	0.9196	1.9468	0.0045	0.8900	−0.0089	0.9634	0.2030

Table 4.

Simulation results corresponding to h₀₁(·) under different censoring rates and sample sizes: the deviance information criterion (DIC), the mean squared errors (MSE) of $\widehat{\beta }$ and $\widehat{\gamma }$ and the estimated integrated area under the curve (iAUCs) and their standard errors in parentheses calculated from the 100 simulated data sets. The Gibbs sampler was run for 20,000 iterations with 5,000 burn-in iterations for each simulated data set.

sample size	censoring rate		${\mathrm{MSE}}_{\widehat{\beta }}$	${\mathrm{MSE}}_{\widehat{\gamma }}$	iAUC	DIC
200	0.3	FPCA	0.109 (0.009)	0.614 (0.016)	0.935 (0.001)	42.99 (3.46)
		PCA	0.113 (0.010)	0.847 (0.020)	0.934 (0.001)	44.66 (3.58)
	0.5	FPCA	0.181 (0.014)	0.696 (0.021)	0.933 (0.002)	−93.80 (3.44)
		PCA	0.186 (0.014)	0.913 (0.025)	0.932 (0.002)	−92.21 (3.46)
500	0.3	FPCA	0.045 (0.003)	0.445 (0.012)	0.932 (0.001)	83.52 (4.52)
		PCA	0.047 (0.003)	0.581 (0.015)	0.930 (0.001)	85.50 (4.57)
	0.5	FPCA	0.052 (0.004)	0.454 (0.013)	0.928 (0.001)	−260.93 (4.58)
		PCA	0.052 (0.004)	0.600 (0.015)	0.927 (0.001)	−259.37 (4.63)

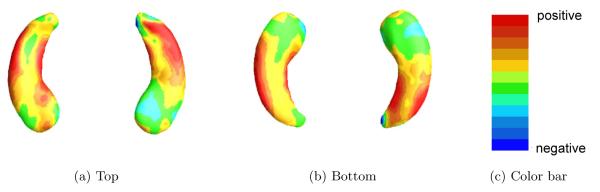
Fig 2.

ADNI data analysis results for the full BFLCRM model: panels (a) and (b), respectively, show the top and bottom views of the estimated coefficient function associated with the hippocampal surface data color-coded by the colorbar in panel (c).

4. Simulation Studies

We conduct Monte Carlo simulations to evaluate the proposed BFLCRM across different censoring rates and sample sizes. Moreover, we will evaluate the predictability of our BFLCRM compared to proportional hazards models without the use of functional covariates.

4.1. Setup

We generated all simulated data sets according to model (2.1). The x_i is a 4 × 1 vector and its corresponding elements were independently generated from N(0, 0.5). We set the true value of β to be (0.7, 0.2, −0.5, −1)^T. The functional covariate Z_i(s) was generated from model (2.3), where its underlying function follows the standard Gaussian process with the covariance function K(s, t) = exp(−3(s − t)²). The observed functional covariate data W_i(s) consists of noisy observations evaluated at 100 equally spaced grids in the interval [−4,4] with some measurement errors. Specifically, the measurement errors ϵ_i(s) were independently generated from a N(0, 0.5) across s. The functional coefficient γ(s) was generated from the standard Gaussian process with covariance function K_γ(s, t) = exp(−2(s − t)²). To generate the survival time, we considered two different baseline hazard functions h₀₁(·) and h₀₂(·) as follows.

$$h_{01}\left(t\right)=1\text{if}t>0,$$ (4.1)

$$h_{02}\left(t\right)=\{\begin{array}{cc}\kappa \omega \hfill & \text{if}0<t\le 2;\hfill \\ \kappa \omega {(t-1)}^{\omega -1}\hfill & \text{if}2<t\le 3;\hfill \\ \kappa \omega 2^{\omega -1}\hfill & \text{if}t>3.\hfill \end{array}\phantom{\}}$$ (4.2)

The first baseline hazard function h₀₁(·) assumes that it is constant over time. As a more general form of hazard function, we consider a mixed form of baseline hazard functions for the exponenetial and Weibull distributions. The hazard function h₀₂(·) depends on κ and ω. In this simulation study, we set κ = 1/3 and ω = 2. Finally, the censoring times were independently generated from a uniform distribution with parameter chosen to achieve a desired censoring rate of 30% or 50%. We considered sample sizes of n = 200 and n = 500 for each censoring rate and simulated 100 data sets for each case.

4.2. Simulation Results

We used the piecewise constant hazard model for h₀(s), in which we set J = 5 and subintervals (s_j−1, s_j] to be of equal length. We set (α_0j, α_1j) = (0.2, 0.4) for all j, Σ₀ = diag(5, ··· , 5), and μ₀ = diag(0, ··· , 0)^T. We calculated the first 12 fPC scores explaining 95% of the variation of the functional covariates, and then compared the estimation results using the first 12 PC scores in order to investigate the efficacy of using fPCA. For each simulated data set, we ran the Gibbs sampler for 20,000 iterations with 5,000 burn-in iterations.

To examine the estimation and prediction performance of BFLCRM, we calculated mean squared errors (MSEs) and time-dependent integrated area under the curve (iAUC)[32] based on 100 simulated data sets for each scenario. The computational time (in C/C++ using an 8-cores 2.80 GHz Intel processor) was 50.3 seconds for BFLCRM with sample size 200 for one repetition. We let $\widehat{\beta }$ denote the posterior mean of β. The MSE of $\widehat{\beta }$ is defined by ${\mathrm{MSE}}_{\widehat{\beta }}={\sum }_{j=1}^p{({\widehat{\beta }}_j-\beta )}^2$, whereas the MSE for γ(·) is defined by ${\mathrm{MSE}}_{\widehat{\gamma }}={\int }_{-4}^4{\left\{\widehat{\gamma }\right(s)-\gamma (s\left)\right\}}^2\mathit{ds}$, where $\widehat{\gamma }\left(s\right)$ denotes the posterior mean of γ at time s. A smaller MSE implies better estimation accuracy, and a large value of iAUC implies a better predictive model. To evaluate the predictive value of the functional covariate to the hazard function, we calculated iAUC for two nested models including a reduced BFLCRM model with solely scalar covariates in x_i and a full BFLCRM model with both W_i(·) and x_i.

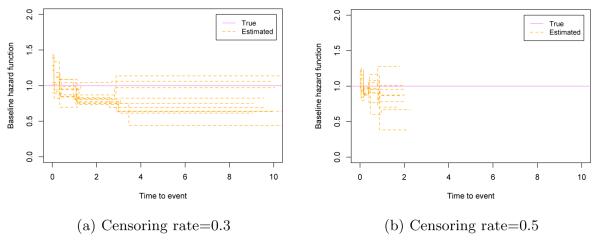
Table 4 presents the estimation results with h₀₁(·) in (4.1) based on 100 simulated data sets for each scenario. The MSE values of both $\widehat{\beta }$ and $\widehat{\gamma }(\cdot )$ are fairly small in all the cases. The values of iAUC indicate reasonable predictive performance of our BFLCRM. The MSE value decreases as either the sample size gets larger or the censoring rate gets smaller. Also, estimation results of fPCA are better than those of PCA in both MSE and iAUC. When the functional covariate has moderate measurement noise, fPCA will lead better estimation and prediction results since the use of smoothing step in fPCA can dramatically reduce measurement errors. Table 5 presents the means and standard errors of iAUC for the reduced and full BFLCRM models under each scenario. The iAUC value of the full BFLCRM model is generally larger than that of the reduced model in all scenarios. This may indicate that the use of functional covariates can improve predictability of the hazard function. Figure 5 shows the baseline hazard functions estimated by the full BFLCRM from the first 10 data sets in the sample size 500 cases. The dotted lines show the estimated baseline hazard functions, and the true baseline hazard function h₀₁(·) is plotted as a solid line on each plot. When the true baseline hazard function is constant, our model estimates the true function well in low to moderate censoring cases.

Table 5.

Simulation results corresponding to h₀₁(·): the mean iAUC and the corresponding standard error in the parenthesis calculated from the 100 simulated data sets for each scenario. The Gibbs sampler was run for 20,000 iterations with 5,000 burn-in iterations for each simulated data set.

n Censoring rate	200		500
	0.3	0.5	0.3	0.5
reduced	0.675 (0.004)	0.612 (0.006)	0.668 (0.002)	0.666 (0.002)
full	0.935 (0.001)	0.933 (0.002)	0.932 (0.001)	0.928 (0.001)

Fig 5.

Simulation results corresponding to h₀₁(·): panels (a) and (b) respectively show the first 10 estimated baseline hazard functions with 0.3 and 0.5 censoring rates based on the size 500 samples. The solid line is the true baseline hazard function, h₀₁(·).

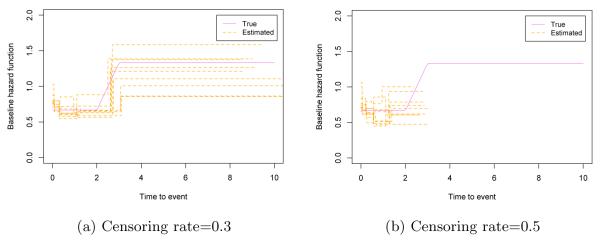
Table 6 presents the estimation results with h₀₂(·) in (4.1) based on 100 simulated data sets for each scenario. Table 7 shows iAUC values for the two nested models. These results in Tables 6 and 7 are consistent with those based on h₀₁(·). The estimated baseline hazard functions are presented in Figure 6 for the sample size 500 cases. We plot the estimated baseline hazard functions of the first 10 data sets using the full BFLCRM model. The solid line shows the true baseline hazard function h₀₂(·) on each plot. When the true baseline hazard function is not piecewise constant, it is well approximated by the estimated baseline hazard function in the low censoring case. In the moderate censoring case, our model captures the general pattern of the true baseline hazard function. It may indicate that our BFLCRM approximates the general form of the baseline hazard function fairly well and therefore it is applicable for most of the practical settings.

Table 6.

Simulation results corresponding to h₀₂(·) under different censoring rates and sample sizes: the deviance information criterion (DIC), the mean squared errors (MSE) of $\widehat{\beta }$ and $\widehat{\gamma }$ and the estimated integrated area under the curve (iAUC), and their standard errors in parentheses calculated from the 100 simulated data sets. The Gibbs sampler was run for 20,000 iterations with 5,000 burn-in iterations for each simulated data set.

sample size	censoring rate		${\mathrm{MSE}}_{\widehat{\beta }}$	${\mathrm{MSE}}_{\widehat{\gamma }}$	iAUC	DIC
200	0.3	FPCA	0.112 (0.009)	0.618 (0.018)	0.934 (0.001)	128.21 (3.57)
		PCA	0.112 (0.010)	0.854 (0.021)	0.933 (0.001)	129.02 (3.66)
	0.5	FPCA	0.183 (0.017)	0.698 (0.023)	0.933 (0.002)	−15.26 (3.37)
		PCA	0.189 (0.018)	0.913 (0.023)	0.932 (0.002)	−13.70 (3.38)
500	0.3	FPCA	0.048 (0.003)	0.453 (0.012)	0.931 (0.001)	306.94 (4.46)
		PCA	0.049 (0.005)	0.586 (0.015)	0.930 (0.001)	308.62 (4.49)
	0.5	FPCA	0.054 (0.004)	0.457 (0.013)	0.927 (0.001)	−69.55 (4.50)
		PCA	0.054 (0.004)	0.611 (0.016)	0.926 (0.001)	−68.00 (4.54)

Table 7.

Simulation results corresponding to h₀₂(·): the mean iAUC and the corresponding standard error in the parenthesis calculated from the 100 simulated data sets for each scenario. The Gibbs sampler was run for 20,000 iterations with 5,000 burn-in iterations for each simulated data set.

n Censoring rate	200		500
	0.3	0.5	0.3	0.5
reduced	0.673 (0.004)	0.612 (0.006)	0.668 (0.002)	0.665 (0.002)
full	0.934 (0.001)	0.933 (0.002)	0.931 (0.001)	0.927 (0.001)

Fig 6.

Simulation results corresponding to h₀₂(·): panels (a) and (b) respectively show the first 10 estimated baseline hazard functions with 0.3 and 0.5 censoring rates based on the size 500 samples. The solid line is the true baseline hazard function, h₀₂(·).

5. Discussion

The BFLCRM was developed to predict the time of conversion from MCI to AD, as well as to determine the optimal set of predictors at baseline that effect the time of conversion. We obtained estimation and prediction results for functional and scalar predictors. This study has examined a very large set of predictors for predicting the time of conversion from MCI to AD. We observed several important predictors including (i) gender, (ii) handedness, (iii) APOE status, and (iv) surface morphology changes with the right and left hippocampi. These findings highlight the importance of including not only demographic and clinical information, but also high-dimensional imaging data, in statistical analyses of MCI-AD conversion. These results are also consistent with newly published clinical research criteria which incorporate the use of an array of biomarkers in research settings and clinical trials [1].

Several prior studies have highlighted the importance of hippocampal changes in the context of AD-related neurodegeneration and prediction of MCI-AD conversion [18]. These studies, however, commonly assess changes to hippocampal volume rather than surface morphology. The current analysis includes both measures of volume and surface area, with the changes in surface morphology adding additional predictive value.

As shown in Figure 4, the changes in surface area occur more prominently on the anterior portion of the long axis of the hippocampus. Functional MRI studies in healthy adults suggest that anterior portions of the hippocampus are critical for the mnemonic binding processes that are engaged in tasks of episodic (day-to-day) memory. Since episodic memory tasks, particularly those that require binding operations, are some of the earliest cognitive impairments observed in MCI-AD [2], the anterior surface changes identified in the current analysis may underlie these early memory changes and serve as an important predictor of time of conversion.

From Figure 4, we observed that when hippocampal atrophy was greater in the CA1 subfield and subiculum of the hippocampi, it took shorter to progress to AD. Similar to our finding, it was reported that greater atrophy of CA1 and subicular subfields in hippoocampi was related to increased risk for conversion from MCI to AD [3]. The subregional atrophy rate in the CA1 and subicular subfields was also turned out to be the best predictor to explain the progression to AD from MCI [25]. Also, it was revealed that left hippocampal body volume was associated with delayed verbal memory [7], where the delayed verbal memory was one of important predictor for determining whether a subject was a MCI converter or not [28]. Thus, our finding in Figure 4 supports these research results.

Beyond the important effects on hippocampal surface morphology, we observed important volumetric changes in the left hippocampal formation and the right amygdala. There has been extensive research to diagnose Alzheimer’s disease by using atrophy of various brain regions [15, 17, 36,64]. In particular, it was reported that the volume hippocampal formation showed significant reduction in patients with clinically diagnosed Alzheimer’s disease [35, 42]. It was also found that the amygdala volume was reduced in very early AD, which suggested that MRI-based amygdaloid volumetric measurement was a relevant biomarker [49]. Also, as shown in [57], the level of amygdala atrophy is related to global illness severity in the early stage of AD. Our ADNI-1 data analysis results agree with these findings in that volumetric changes in the hippocampal formation is an important variable to predict the time to conversion from MCI to AD.

The analysis also shows that APOE status exerts important effects on the time of conversion. Our results also agree with several prior studies that have documented that the presence of the APOE ϵ4 allele increases the risk of developing Alzheimer’s disease. Particularly, if a subject has APOE ϵ4, then MCI progression more likely occurs.

We have demonstrated the utility of BFLCRM as a valuable method for identifying optimal early markers of conversion to AD in patients with MCI. The early markers identified from our analysis could be used in case selection for various clinical trials for evaluating drug/therapeutic efficiency in slowing or modifying AD-related pathophysiology, when such drugs and therapeutic treatments are available.

There are some limitations to our analysis. Our findings survived internal cross validation, but they need replication in an independent community-based sample. We did not include measures of pathology (e.g. beta-amyloid) in our models since CSF and amyloid-PET were available only in a small subset of individuals in ADNI-1. However, a study of ADNI-2 subjects has shown a robust correlation between the APOE e4 allele and cortical amyloid burden [51], suggesting that APOE e4 may have served as a surrogate for cortical amyloid plaque load in our analysis.

We have developed BFLCRM for the use of functional and scalar covariates to predict time-to-event outcomes. Several important methodological issues need to be addressed in future research. First, it would be interesting to investigate the theoretical properties of our Bayesian procedure, including the support of the prior and truncation approximation bounds q_n. Second, it is interesting to develop a new Bayesian method to automatically determine the distribution of q_n. Third, it is interesting to incorporate high-dimensional scalar covariates (e.g., genetic markers in the whole genome) in FLCRM and develop its associated estimation and testing procedures. Developing such statistical methods poses many new challenges both computationally and theoretically.