FACS-style detection for real-time cell viscoelastic cytometry

Abstract

Cell mechanical properties have been established as a label-free biophysical marker of cell viability and health; however, real-time methods with significant throughput for accurately and non-destructively measuring these properties remain widely unavailable. Without appropriate labels for use with fluorescence activated cell sorters (FACS), easily implemented real-time technology for tracking cell-level mechanical properties remains a current need. Employing modulated optical forces and enabled by a low-dimensional FACS-style detection method introduced here, we present a viscoelasticity cytometer (VC) capable of real-time and continuous measurements. We demonstrate the utility of this approach by tracking the high-frequency cell physical properties of populations of chemically-modified cells at rates of ~ 1 s⁻¹ and explain observations within the context of a simple theoretical model.

Introduction

Because physiological changes are known to affect their mechanical properties^1,2, cell deformability has emerged as a label-free biomarker for cell health and disease^3–5. Traditional bulk testing techniques such as ektacytometry^6,7 provide macro-scale mechanical properties which combine culture-medium cell interactions, cell-cell interactions and individual cell properties. However, it is now known that individual cell properties when measured separately can provide markers for diseases including cancer and malaria⁸. To measure mechanical properties at the individual cell level, a number of techniques have been developed including micromanipulation⁹, microchannel filters^10,11, electric fields¹², inertial forces^5,13, cell collisions⁷, and attached beads¹⁴. With these approaches, cell systems including leukocytes¹⁵, fibroblasts¹⁶, and cancer cells^17,18have shown clear distributions of individual cell mechanical properties that evolve with both disease progression or treatment. When fluorescent biomarker labels are available, expression heterogeneity in such cell samples can be readily evaluated with flow cytometers or fluorescent activated cell sorters (FACS) capable of measuring and sorting populations one cell at a time with throughputs > 10,000 cells/s. Complementing these techniques are flow cytometers with 2-D imaging capability which, and though they have lower throughputs, can be used to identify morphology and characterize intracellular structure directly where other methods cannot. Efforts to obtain comparable throughputs with mechanical property testing have combined hydrodynamic shear forces with fast 2-D image-processing^5,19to achieve rates ranging from 10² – 10⁵ cells/s. These methods rely on measuring cell physical response to applied hydrodynamic stresses with high-speed cameras and computationally-intensive image analysis in either real-time or post-processing modalities. While the infrastructure associated with this can be substantial, cameras and computational tools continue to become faster and less expensive making the approach promising for broader implementation. However, because these methods are 2D characterization-based, they will appropriately integrate with imaging and not traditional flow cytometers or FACS when correlation with complementary fluorescent or scattering signals is desired. To develop mechanical property testing tools that can be most broadly used therefore, FACS-compatible detection schemes must be employed and, because of the speed with which these cytometers function, new and rapid mechanical property markers will be required. For cell systems such as malaria-infected red blood cells (RBCs), we have shown that cell viscoelasticity is a more appropriate biomarker than its purely elastic response (used in most high-throughput techniques) at shorter timescales (< 100 ms for RBCs) that are required as one pushes to higher throughputs⁴. Building on other work where we have shown that linear stretchers can be used to stretch and measure low frequency relaxation in both red and much stiffer white blood cells^20–25, the dynamic viscoelasticity can be measured using modulated optical forces to probe the high-frequency mechanical response of individual cells⁴. This work demonstrated that, to extract frequency-dependent cell viscoelasticity at reasonable accuracy, multiple measurements per cell are required (~ 40/cell)⁴, throttling maximum throughput, and creating a significant hurdle for data and computationally intensive camera-based 2-D image detection schemes. Here and enabled by a simple detection approach designed around the linear optical trap, we demonstrate a real-time implementation of this viscoelasticity biomarker with a simple FACS-style photodetection scheme to measure individual cell viscoelastic properties at throughputs of up to 1 cell/s. While not comparable to simple deformability based markers, rates are sufficient to screen statistically significant populations and track 10% changes. By drastically reducing the detection footprint and data processing times we provide a route for integration of mechanical/viscoelastic property detection with traditional flow cytometers.

To demonstrate our approach, we study RBCs both as a well-established model with known mechanical properties and as a target of pharmacological research^2,26, blood-borne disease diagnosis including malaria and sickle cell^10,27, and for the day-to-day monitoring of donated and stored blood. RBCs have three primary structural components: a lipid bilayer, a membrane cytoskeleton, and an internal cytoplasm^28,29 and decoupling the individual contributions of these components to overall cell mechanical properties may confirm proposed physiological mechanisms and lead to potential markers for disease or cell health. We use diamide and glutaraldehyde to selectively stiffen cell mechanical components and measure the resulting changes in dynamic viscoelasticity while employing a Kelvin-Voigt model, though not required for qualitative comparisons, to aid data interpretation.

Materials and methods

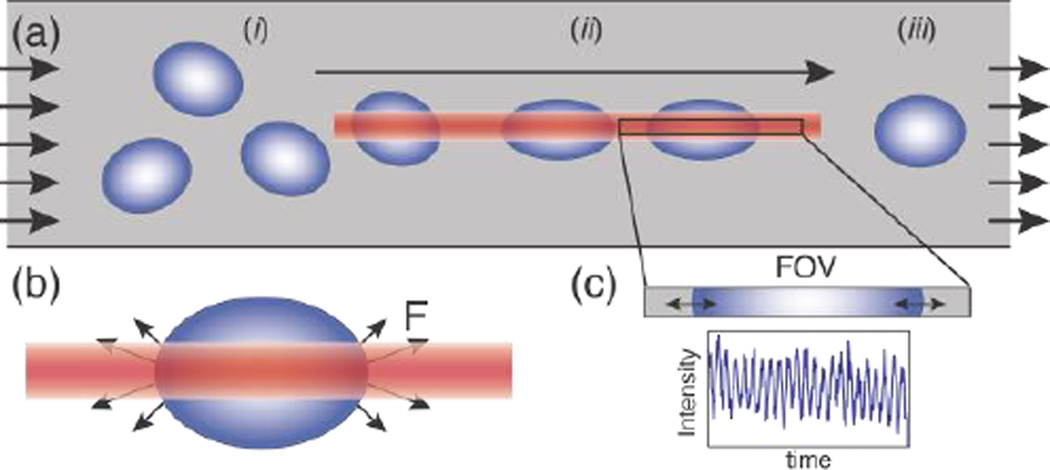
In our cytometer, RBC suspensions are flowed through a simple microfluidic channel where a linear optical trap applies aligning and deforming forces on cells while facilitating a novel and lightweight detection scheme for tracking cell mechanical response. Figure 1a demonstrates the approach where the optical trap aligns cells and applies sinusoidal stress as they flow down the trap length.

Figure 1.

a) Schematic of the microfluidic device demonstrating cell alignment and RBC stretching, the direction of flow, and the fixed field-of-view (FOV) of the detector. Cells flowing at random orientation (i) are trapped, aligned via torque experienced in the optical trap and stretched (ii) by the optical trap (OT) until they pass through the trap and relax back to their original shape (iii). b) Antipodal stretching optical forces (F) generated on the two edges of the cell that are in the laser focus on an RBC in the OT²³. c) The FOV with the light intensity measured by the photodetector directly proportional to the oscillating size of the cell blocking the light (Supplementary Video 1).

Optical trap for cell stretching

We employ a linear diode-bar based optical stretcher to generate the asymmetric intensity profile necessary to apply antipodal deformation forces (Figure 1b) required to stretch cells in flow and generate small non-destructive perturbations (~ 1%) in their size (Figure 1c)^4,23. Figure 1 illustrates the direction of forces on a cell, where cells are pulled into the linear optical trap and exposed to oscillating stress generated by the modulated optical intensity as they translate down the trap length. We generate the optical trap using a linear diode bar laser (2495-Y-5.0 W, 810 nm, JDSU, Milpitas, CA) with an emitter of size 1 µm×100 µm. The laser light is collimated using a 20× objective (Aplan 20×/0.45, Zeiss, Jena, Germany) and focused within the sample plane using a 40×/.85 Olympus UplanApo objective. A frequency generator (DS 360 Stanford Research Systems) is used to modulate the laser intensity and generate sinusoidal stretching forces of ~20 pN⁴.

Time-dependent cell strain measurement and analysis

RBCs appear as dark objects when slightly out of focus, increasing contrast, with an effective shadow that can be used to track relative cell size change (Supplementary Video 1). Here, the phase of the cell oscillation is a robust signal as it does not depend on the absolute signal amplitude and is independent of moderate changes in refractive index or z-focus. Further, the measured intensity is a sine function at the applied frequency allowing for noise filtering and oversampling by averaging multiple cycles to increase signal to noise. In using tight error limits on the sine fit, we also filter out any signal from cells still reorienting when they arrive at the detection zone, an artefact which would appear as a low/zero frequency shift of the baseline in the 20 Hz signal. These factors allow for an effective resolution of 1–3% stretch⁴.

In our setup, as cells flow down the microfluidic channel, trapped and anisotropic cells align preferentially along the length of the linear optical trap to minimize optical torque. In this, cells may translate and flow freely along the trap long axis as fluid drag precisely directs them through a fixed field of view (Figure 1a). This design allows for the tracking of the time-dependent cell strain oscillation by simply measuring the percentage of the FOV blocked by the cell (Figure 1c) using a single photodetector measuring total light intensity in the FOV. To emulate such a large rectangular detector, we sum the measured intensities of 150 pixels of a high-speed CMOS camera along the FOV (Silicon Video high-speed SV643M camera, EPIX, Buffalo Grove, IL coupled to a 40× objective capable of 1000 frames/s (fps) paired to a custom-made data acquisition program, Supplementary material 1). This approach mimics the zero-dimensional detection scheme of a FACS instrument by relying on a single pixel photodetector (rectangular pixel ~100×1 aspect ratio matched to the linear diode bar). In this simplified approach, the sum of pixel intensities along the chosen line length is representative of the cell size. When an individual cell is detected in the field of view, the pixel sum over 250 frames at 20 Hz modulation frequency and 1000 fps for 5 cycles along with the modulation signal from the frequency generator are fit to sine functions to extract the phase lag and amplitude of cell size oscillation. This approach of extracting cell response from a simple photodetector mimic, instead of 2-D image processing and detection normally used to track and measure cell size^4,5, reduces signal-processing times to ~10 ms/cell. Also, and without the need for storage of large videos, the maximum number of cells measured is unconstrained and currently determined only by the time a microfluidic experiment can be sustained.

Theoretical model

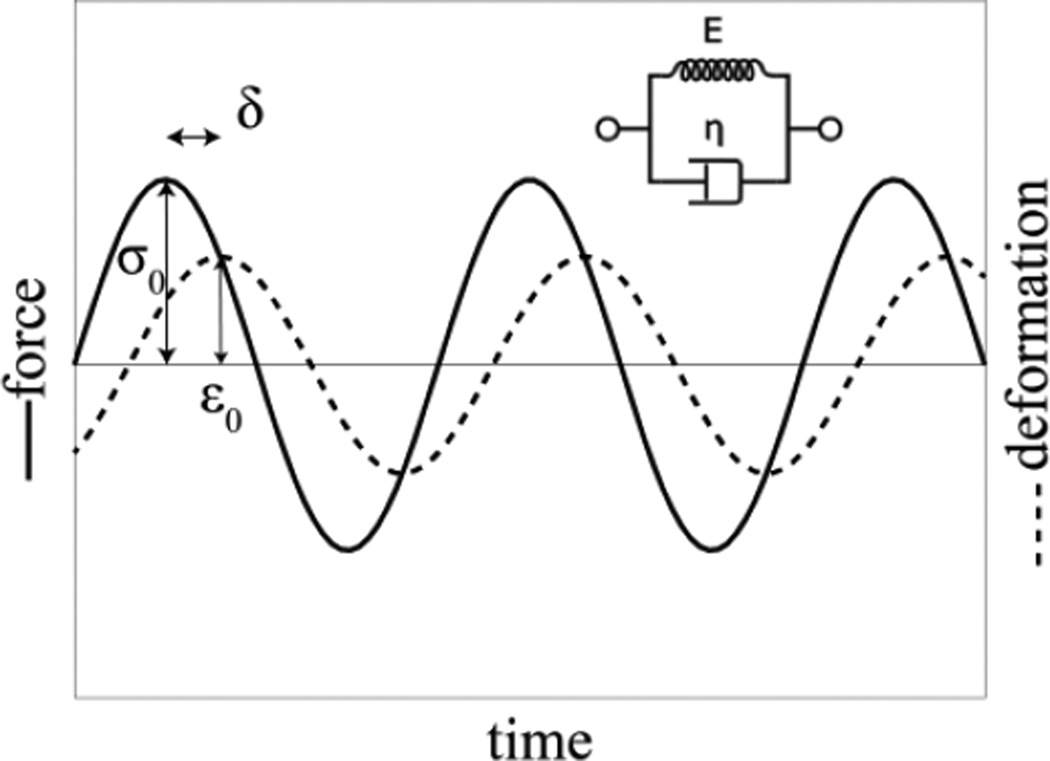
To interpret the measured viscoelastic behavior of unmodified and chemically-modified RBCs, we define a simplified Kelvin-Voigt (KV) model where the dominant contributions to cell mechanical behavior are from the cytoskeleton, dominating the elastic behavior and modeled as a spring, and the membrane viscosity which dictates the overall cell viscous behavior³⁰modeled as a dashpot (Figure 2).

Figure 2.

Schematic of the KV model and its response to harmonic stress.

In this, the cell response to a harmonic stress σ₀ cos (ωt) is a harmonic strain ε₀ cos (ωt − δ) which trails the applied stress by a characteristic phase lag δ at a strain amplitude ε₀. Both of these depend on the dynamic viscosity of the dashpot η, the elastic modulus of the spring E, and the oscillation frequency ω as³¹:

$$\delta ={\text{tan}}^{-1}\frac{G\prime \prime }{G\prime }={\text{tan}}^{-1}\frac{\omega \eta }{E}$$ Equation 1

$${\epsilon }_0\propto \frac{1}{\sqrt{E^2+{\omega }^2{\eta }^2}}$$ Equation 2

where tan δ is the loss tangent, G′′ and G′ are the loss and storage moduli³¹ and τ = η/E is the time constant of the system measured to be ~ 0.1 s for unmodified RBCs²⁸. These dependencies of the measured variables δ and ε₀ on the viscosity and elastic modulus can be employed to predict changes in measured values when cell physical properties change.

Materials

Experiments were performed in microfluidic channels (2 cm × 1000 µm × 10 µm) fabricated in polydimethylsiloxane (PDMS) (Sylgard 184, Dow Corning) on glass slides using standard soft- lithography techniques³². In this, chrome-plated glass masks were printed and used to selectively polymerize KMPR 1010 and 1050 photoresist (Kayaku Microchem) via UV exposure in a mask aligner (Karl Suss MJB3) on a silicon wafer to form the masters. These templates were then used to mold PDMS that was subsequently irreversibly bonded to glass slides using oxygen plasma. Channels were soaked with buffer solution for 3 hr before experiments. For experiments on RBCs, 7.5 µl blood was diluted in 500 µl of 300 mOsm phosphate buffered saline with 1.5% sodium citrate to prevent coagulation and 0.2% w/v bovine serum albumin to prevent sticking. Because the time with which chemical modification is applied can influence cell properties, consistent conditions were employed. For our studies, cells were fixed with increasing concentrations (0.001 – 0.0035% v/v) of glutaraldehyde, soaked for 30 min, and washed twice in 300 mOsm buffer. For experiments with diamide-treated cells, unmodified RBCs were soaked in 3.8 mM diamide in 300 mOsm buffer solution for 20 min and washed twice before injection into the microfluidic device for measurement. For any experiments requiring longer than 2 hrs, samples were replenished with identical preparations from the same donor to avoid any artifacts due to cell properties changing with time as activated cells were observed after 2 hr.

Results and discussion

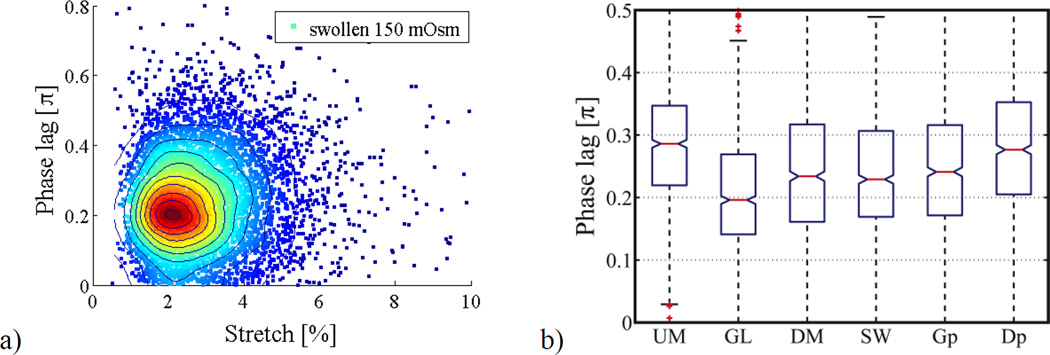
We have shown that by detecting only a simple signal we can probe mechanical properties including phase lag and strain amplitude of individual cells real-time. To test accuracy and resolution of these measurements and to estimate potential throughput, we measured δ and ε₀ of RBCs with known phase lag and strain amplitude. Figure 3a shows the observed distribution of 6500 swollen RBCs probed real-time during a single experiment in 3 hr at 20 Hz, exposed to laser powers of < 20 mW for 0.1 s/cell to measure 2 cycles/cell. The results show that phase lag and deformation are in expected ranges for swollen RBCs⁴ at the applied frequency and laser powers with a mean phase lag of 0.24 π ± 0.13 π and mean strain amplitude of 2.9% ± 1.4% for 150 mOsm swollen RBCs.

Figure 3.

(a) FACS-style scatter plot of swollen RBCs in hypotonic 150 mOsm buffer (n = 6500 cells, cells were replaced after 2 hr with fresh samples from the same donor to prevent drift due to effects of storage at room temperature on cell mechanical properties). (b) Population data (n = 1000) for unmodified (UM), 0.0025 % v/v glutaraldehyde fixed (GL), 3.8 mM diamide fixed (DM), 150 mOsm swollen (SW), mixed population glutaraldehyde:unmodified 70:30 (Gp), mixed population diamide:unmodified 70:30 (Dp) RBCs respectively. All populations tested the null hypothesis in a two-sample t-test vs unmodified RBCs (UM) at 5 % significance level, where samples GL, DM, SW and Gp had p < 0.001 while Dp had a p value of 0.08. Standard box plots show the middle 50 percentile of each population, the red line is the median and notches mark the 5% significance level around the median. Non-overlapping notches signify statistically different populations at 5% significance level.

We also employ the rapid nature of the detection scheme to probe statistically significant cell numbers and track the effect of selective chemical stiffening on overall dynamic behavior of RBCs to identify the contribution of various components of cell structure to overall viscoelastic behavior. We summarize observed trends averaged over 1000 measured RBCs subjected to three different chemical modifications: glutaraldehyde to alter overall viscosity and elasticity of the cell, diamide which fixes only cytoskeleton proteins modifying the viscosity and elastic modulus of the cytoskeleton alone, and swelling in hypotonic buffer which alters the cytoplasmic viscosity to generate pretension in the cell membrane. The results of these experiments are provided in Figure 3b and summarized in Table 1. Using theoretical predictions of the measured dynamic properties of the KV model we identify relative contributions of internal mechanical components to overall properties.

Table 1.

Summary of measured deviations of mean phase lag and strain amplitude of fixed cells and property changes (ω = 20 Hz).

Chemical modification	δ	ε0	E	η
	Measured variable		Property changes due to fixation
Unmodified	0.284 ± 0.097 π	2.80 % ± 1.09 %	-	-
Glutaraldehyde (0.0025% v/v)	0.208 ± 0.096 π	2.24 % ± 0.90 %	Increase	Increase
Diamide (3.8mM)	0.241 ± 0.113 π	3.08 % ± 1.25 %	Increase	Constant
Swelling (150 mOsm)	0.239 ± 0.097 π	2.47 % ± 1.00 %	Increase	Constant

Statistical analysis and limits of detection

In dynamic mechanical analysis as implemented here, phase lag depends on the relative strength of the elastic (E) and viscous (η) material components. A purely viscous material’s response has a phase lag of 0.5 π while a purely elastic material’s response has zero phase lag relative to the applied oscillating stress. For viscoelastic biological cells one expects a frequency-dependent phase lag 0 < δ < 0.5 π. The lower bound is reached at frequencies far below the time constant of the system or in systems of very high elasticity including stiff or fixed cells. The higher bound is reached at large frequencies where the viscous component dominates however, based on the inverse tangent dependence suggested by the KV model, we expect these frequencies to be large where the strain amplitude will be too small to measure. Most mammalian and microbial cells with a nucleus and internal organelles are generally much stiffer than RBCs and we therefore expect smaller phase lags. With this understanding and using our measured results for δ and ε₀, we quantify changes in η and E and compare results with reported literature. For unmodified RBCs, our measured mean phase lag of 0.28 ± 0.10 π at 20 Hz modulation frequency, corresponds to a relaxation time of τ = 0.06 ± 0.03 s (Equation 2), a value that compares well to reported values of 0.1 s in literature²⁸.

Despite the known broad distribution (± 45%) of mechanical properties within the same cell sample due to inherent differences in cells such as age and the difference between samples from different donors (±18%)³³, we identified statistically significant changes in measured properties of chemically-modified RBCs relative to unmodifed RBCs. We also recognise that real-time sinusoidal function fit-error due to averaging over only 2 cycles/cell contributes to the scatter in Figure 3a. To reduce this noise and improve sensitivity to smaller changes in mechanical properties at the cost of reduced throughput (only 1000/hr vs. 3000/hr), we have collected 5 cycles/cell, 0.25 s/cell @ 20 Hz vs. 0.1 s/cell @ 20 Hz, for all measurements reported in Figure 3b and Table 1. This reduced the noise in a test case of swollen cells from 0.24 ± 0.13 π (±54%) at 2 cycles/cell to 0.24 ± 0.10 π (±42%) at 5 cycles/cell. The cost of averaging over higher number of cycles to reduce sampling noise (for the same cell, standard deviation of averaged cycles σ_avg = σ / √cycles)⁴ is the increase of probing time per cell, which leads to reduced throughput. With this limitation, to achieve throughputs > 1000/hr, one could move to higher modulation frequencies with the help of more sensitive photodetectors for reliable measurement of smaller strain amplitudes⁴. We use basic statistical principles to estimate the sample size required to track expected mechanical property changes. Minimum sample size required to estimate the mean of a population with standard deviation σ within ± δ from the actual value with 95% confidence is N > [(1.96 * σ)/δ]^2. To estimate the mean within ±5% error for our measurements with ~50% standard deviation, the minimum sample size required is ~ 400 or 1600 cells for ±2.5% error. With this expected minimum measurement resolution of 10% based on at least 400 cells, we investigated the sensitivity of VC by using it to quantify different types/magnitudes of changes in mechanical properties of cells generated using known RBC chemical modifications. We employ paired two-sample student’s t-test at 5% significance level to validate differences between populations and report corresponding p values. The run-to-run variation is within the 95% confidence interval around overall the population mean (k sample means Tukey-Kramer test at α = 0.05 significance showed no statistical difference between multiple runs).

Sensitivity to alteration of membrane and cytoskeleton mechanical properties by glutaraldehyde

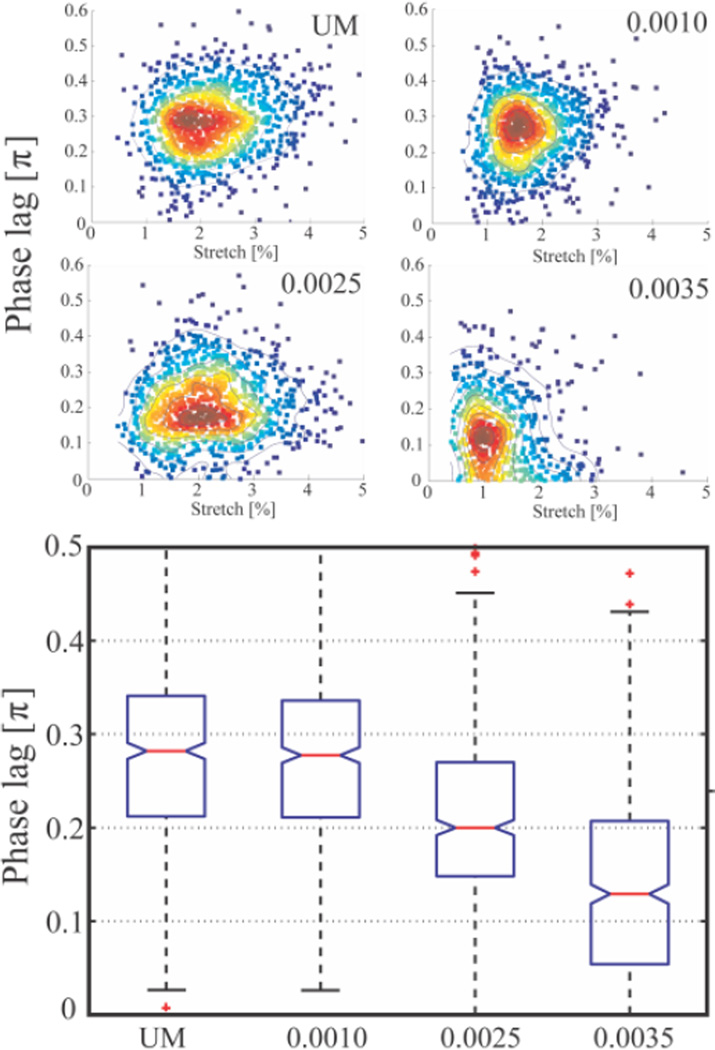
In measurements of glutaraldehyde fixed cells, we observed 26% reduction in δ in comparison to unmodifed cells (p < 0.0001). Because glutaraldehyde is a non-specific fixative that crosslinks membrane skeletal proteins, phospholipids, and the cytoplasm, it is expected to increase the cytoskeletal elasticity E and decrease membrane viscosity η²⁹. However, the contribution of the 20% change in cytoplasmic viscosity caused by the glutaraldehyde fixation³⁴ to the overall viscosity is expected to be negligible^28,29. A 26% reduction in measured mean phase lag relative to unmodifed cells corresponds to 35% reduction in τ. With this and using static elastic modulus measurements, one can quantify changes in membrane viscosity. We have also used VC to distinguish RBCs modified with a range of concentrations of glutaraldehyde (Figure 4) to further demonstrate sensitivity to small changes in mechanical properties. Additionally, we observed that a mixed population of 70% fixed (0.0025% v/v) and 30% unmodified cells is statistically different from both the pure unmodified (p<0.0001) and pure fixed samples (p <0.0001), further demonstrating the sensitivity of the approach.

Figure 4.

Population data (n = 550) box plots (5% significance notch) for unmodified (UM), 0.001% v/v glutaraldehyde fixed (0.0010), 0.0025% v/v glutaraldehyde fixed (0.0025), 0.0035% v/v glutaraldehyde fixed (0.0035) respectively.

Sensitivity to alteration of cytoskeleton mechanical properties using diamide

In previous mostly-static studies on diamide, with different range/direction of forces applied at different rates, vastly different measured values of membrane shear modulus (8× increase) and bending modulus (2 or 3×) have been reported³³. Despite this, the general consensus is that cross- linking of cytoskeletal spectrin leads to an increase of cell elasticity E with cell viscosity η remaining essentially constant. Dynamic measurements have demonstrated the ability to differentiate diamide-fixed cells using arbitrary parameters but have not been able to quantify its influence on specific mechanical structures²⁹. These properties are often not accessible from deformability studies in pressure driven flows because they only measure the effective cellular viscosity while this approach can selectively probe the elastic modulus and the viscosity of the membrane²⁹. With VC we observe a 15% reduction in mean phase lag compared to unmodified cells (p < 0.0001) corresponding to a 15% reduction in τ which, at constant η, implies an increase in cytoskeletal elasticity E by ~17%. While this is not consistent with reported magnitudes in the literature, these results demonstrate that the effects of diamide fixation may not be limited to cytoskeletal elasticity. Additionally, we also observe that a mixed population of 70% fixed and 30% unmodified cells is statistically different from both the pure unmodified (p<0.08) and pure fixed samples (p <0.0001).

Sensitivity to alteration of cell properties due to pre-tension induced by swelling

RBC swelling is well known to have a significant influence on mechanical properties; in our studies, we observed 16% reduction in δ in comparison to unmodifed cells (p < 0.0001). Swelling reduces cytoplasmic viscosity, ignored in this KV model, while causing pre-tension in the membrane/cytoskeleton that may increase elastic modulus E but should not influence membrane viscosity η. A 16% reduction in mean phase lag measured at 20 Hz corresponds to a 14% reduction in relaxation time τ which compares well with reported values³³ and, with no expected change in η, implies that swelling increases cytoskeletal elasticity by ~16%, consistent with the literature³³.

For the sake of completeness we also identified and addressed potential additional sources of noise in the data including changes in focal plane of cells and differences in cell refractive index. While cells that enter the trap at the upstream end are pulled into and held within focus by the optical trap before they arrive within the detection zone, cells that are pulled into the trap closer to the detection zone could still be reorienting or out of focus during detection and are filtered out by the sine function fit. Differences in cell index could lead to different forces and stretch amplitudes; however, as we have shown in previous work, cells of different stiffness (equivalent to applying different optical forces due to differences in refractive index) do not have a significantly different amplitude at stretch frequencies > 5 Hz⁴.

Currently, our resolution is limited by the detector dynamic range and resolution. Despite this, our studies demonstrate the sensitivity of VC in tracking changes in mechanical properties in cells and its utility for large population screening. While we observe similar trends in mechanical property changes with chemical fixation as reported in the literature, differences in actual magnitudes of mechanical properties are expected. This is due both to the wide variety of predominantly static techniques employed to probe RBC mechanical properties that report vastly different magnitudes^29,35 and because VC is based on measuring small deformations and corresponding weak cell perturbations. Also, in our technique and unlike imaging methods, cell viscoelastic properties are available within 10 ms of the cell passing the optical trap. At a sample flow rate of 1000 µm/s, a cell could be selected for real-time sorting 10 µm downstream of the detection area using techniques such as those previously developed in our group. These include microfluidic-sorting systems based on “traditional” optical traps³⁶, DVD player optics³⁷ and using linear diode bars such as those employed here^38,39 potentially with the same diode bar used for stretching. Currently throughput is limited to a few thousand cells/hr largely due to the microfluidics and the inconsistent arrival of perfectly spaced cells to the optical trap. While this technique could never match the 10,000 cells/s rates that can be achieved by some FACS machines, it could be deployed with reasonable throughput (up to 10,000 cells/sample) for applications where available combinations of fluorescent markers are not adequate. The simplicity in both the mechanisms used for applying forces and tracking cell response makes this system appropriate for significant parallelization with multiple optical trap/detector combinations coupled to a single microfluidic channel by adapting multi-trap systems already demonstrated in the literature⁴⁰ and available commercially (E3500 Optical Tweezers System Elliot systems, TWEEZ 200si by ARESIS). When these approaches are coupled with available higher modulation frequencies (20 Hz to 200 Hz⁴), an increase in a few orders of magnitude throughput is feasible. Also, by reducing the hardware to a single photodetector/laser diode bar combination, we demonstrate a path towards eventual integration into existing flow cytometer instrumentation.

Conclusions

We demonstrate real-time dynamic mechanical property measurement of single cell viscoelastic properties of statistically significant populations of RBCs at throughputs of ~1000 cells/hr. The simplified FACS-style zero-dimensional measured signal provides a direct route to high frequency (>1000 Hz) studies by rapidly increasing sampling rate at low cost and computing requirements with potential for integration into existing cytometers. We explore the scope, detection sensitivity, and maximum throughput of the VC, in the context of population level screening for cytometry, by investigating and identifying the mechanisms of diamide and glutaraldehyde fixation of RBCs.