Characterizing RNA Excited States using NMR Relaxation Dispersion

Abstract

Changes in RNA secondary structure play fundamental roles in the cellular functions of a growing number of non-coding RNAs. This chapter describes NMR-based approaches for characterizing microsecond-to-millisecond changes in RNA secondary structure that are directed toward short-lived and low-populated species often referred to as “excited states”. Compared to larger-scale changes in RNA secondary structure, transitions towards excited states do not require assistance from chaperones, are often orders of magnitude faster, and are localized to a small number of nearby base pairs in and around non-canonical motifs. Here we describe a procedure for characterizing RNA excited states using off-resonance R_1ρ NMR relaxation dispersion utilizing low-to-high spin-lock fields (25–3000 Hz). R_1ρ NMR relaxation dispersion experiments are used to measure carbon and nitrogen chemical shifts in base and sugar moieties of the excited state. The chemical shift data is then interpreted with the aid of secondary structure prediction to infer potential excited states that feature alternative secondary structures. Candidate structures are then tested by using mutations, single-atom substitutions, or by changing physiochemical conditions, such as pH and temperature, to either stabilize or destabilize the candidate excited state. The resulting chemical shifts of the mutants or under different physiochemical conditions are then compared to those of the ground and excited state. Application is illustrated with a focus on the transactivation response element (TAR) from the human immune deficiency virus type 1 (HIV-1), which exists in dynamic equilibrium with at least two distinct excited states.

1. Introduction

Many regulatory RNAs (Storz, 2002; Serganov et al., 2007; Cech et al., 2014) undergo conformational changes that play essential roles in their biological functions (Mandal et al., 2004; Tucker et al., 2005; Schwalbe et al., 2007; Cruz et al., 2009; Rinnenthal et al., 2011; Dethoff, Chugh, et al., 2012). Among many functionally important motional modes, changes in RNA secondary structure can expose or sequester key regulatory elements, and thereby provide the basis for molecular switches that regulate and control a wide range of biochemical processes (Serganov & Patel, 2007; Breaker, 2011; Dethoff, Chugh, et al., 2012).

For example, riboswitches (Grundy et al., 2002; Winkler et al., 2002) are RNA-based genetic elements typically embedded in the 5′ untranslated region (5′ UTR) of bacterial genes that employ changes in secondary structure in order to regulate expression of metabolic genes in response to changes in cellular metabolite concentration (Schwalbe et al., 2007; Serganov & Patel, 2007). In a prototypical metabolite riboswitch (Tucker & Breaker, 2005), a ligand metabolite, such as adenine, binds the aptamer domain and induces a conformational change, which typically sequesters an RNA element into a helix (Fig 1A). The unavailability of this element in turn changes the folding pathway of a downstream decision-making expression platform, directing it towards structures that turn off (and in some cases, on) gene expression, either by forming a transcription terminating helix or by sequestering the Shine-Dalgarno sequence where the ribosome binds, thereby inhibiting translation (Fig 1A) (Haller et al., 2011). Changes in RNA secondary structure can also affect access to RNA sites and thereby allow regulation of post-transcriptional processing, including splicing (Fig 1B) (Cheah et al., 2007), gene silencing by microRNA (miRNA) (Kedde et al., 2010), and RNA editing (Polson et al., 1996). RNA secondary structural switches are also widely used by the RNA genomes of retroviruses to transition between different roles required by various steps of the viral lifecycle (Huthoff et al., 2001; D’Souza et al., 2004). For example, a pH dependent secondary structural RNA equilibrium was recently shown to regulate translational recoding in the murine leukemia virus (Fig 1C) (Houck-Loomis et al., 2011).

Figure 1.

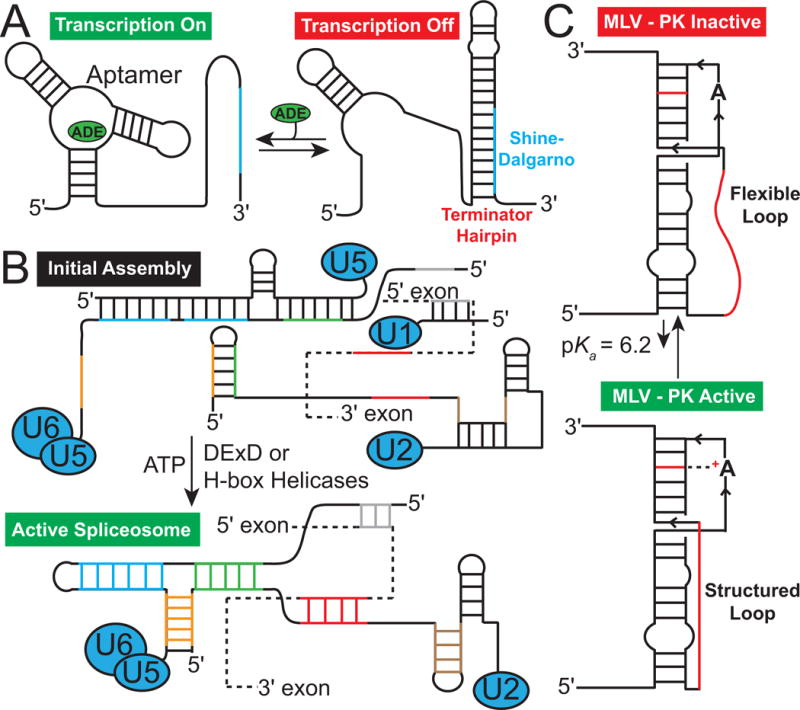
Secondary structural changes in RNA (A) Adenine riboswitch secondary structure with and without the adenine metabolite, which binds to the aptamer domain stabilizing a specific secondary structure turning on transcription. In the absence of metabolite the Shine-Dalgarno sequence (blue) is sequestered turning off transcription (Reining, A. et al., 2013). (B) Secondary structural transitions of mRNA (dashed line) and a spliceosome catalyzed by chaperones (DExD or H-box helicases) that are key for splicing. (C) pH dependent secondary structural equilibrium in the murine leukaemia virus pseudoknot (MLV-PK) mRNA that regulates translational miscoding.

Most RNA secondary structural switches require the melting of several base pairs and result in the creation and disruption of entire helices and hairpins. They can therefore be energetically costly and often require assistance from protein chaperones (Herschlag, 1995; Rajkowitsch et al., 2007) or otherwise must take place during co-transcriptional folding (Garst et al., 2009; Lai et al., 2013). Recently, a new mode of RNA secondary structural transitions has been uncovered through application of solution state NMR spectroscopy (Hoogstraten et al., 2000; Venditti et al., 2009; Dethoff, Petzold, et al., 2012; Lee et al., 2014). These transitions are directed toward low populated (typically <5%) and short-lived (lifetime typically <2 ms) alternative secondary structures that feature local reshuffling of base pairs (bps) in and around non-canonical motifs (Fig 2) (Dethoff, Petzold, et al., 2012; Lee et al., 2014). These transient species are often referred to as “excited states” (ES) (Sekhar et al., 2013) because they represent a higher free energy state (typically destabilized by 1–3 kcal/mol) as compared to the energetically more favorable ground state (GS).

Figure 2.

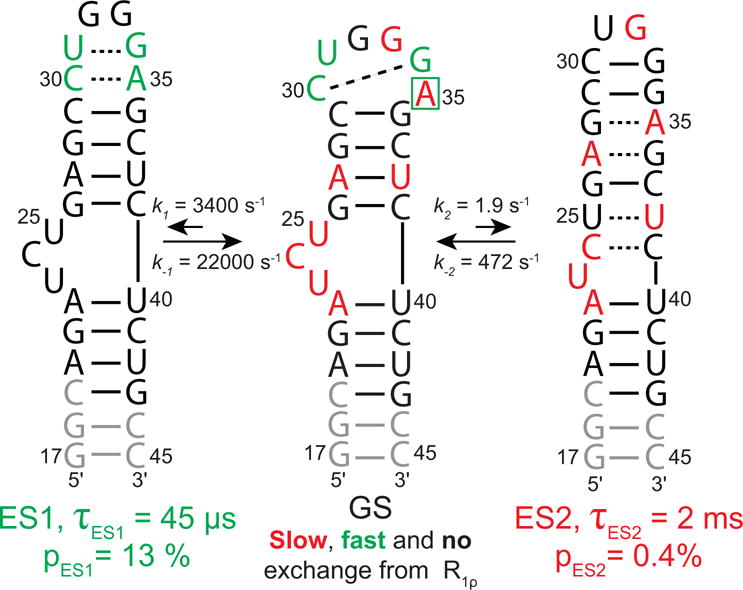
HIV-1 TAR exists in dynamic equilibrium with two excited states (ES1 and ES2). Shown are the ES secondary structure, population (p_ES), lifetime (τ), as well as the forward (k₁/k₂) and reverse (k₋₁/k₋₂) rate constants. The GS is labeled to show sites with slow (red), fast (green) and no chemical change (black) measured by R_1ρ relaxation dispersion. Note that A35 shows a combination of fast (C1′) and slow (C8) exchange. Sites in grey were not measured due to spectral overlap.

An example of such RNA transitions is shown in Figure 2 for the transactivation response element (TAR) RNA from the human immune deficiency virus type 1 (HIV-1) (Weeks et al., 1990; Puglisi et al., 1992; Aboul-ela et al., 1996). TAR has been shown to exist in dynamic equilibrium with two distinct excited states (ES1 and ES2) (Dethoff, Petzold, et al., 2012; Lee et al., 2014). ES1 is 13% populated, has a short lifetime of ~45 μs and features localized changes in base pairing within an apical loop (Fig 2). ES1 sequesters apical loop residues by base pairing interactions that would otherwise be available to interact with proteins (Fig 2) (Dethoff, Petzold, et al., 2012). ES2 is only ~0.4% populated, but has a longer lifetime of ~2 ms (Fig 2) (Lee et al., 2014). It features longer-range reshuffling of base pairs that span the bulge and apical loop that are separated by a four bp helix, remodeling all non-canonical features of the TAR structure (Fig 2) (Lee et al., 2014).

Recent studies suggest that transitions toward ESs are common in many regulatory RNAs (Hoogstraten et al., 2000; Venditti et al., 2009; Zhang et al., 2011; Dethoff, Petzold, et al., 2012; Lee et al., 2014; Tian et al., 2014; Zhao et al., 2014). Compared to conventional secondary structural rearrangements, transitions towards RNA ESs are orders of magnitude faster, occur without assistance from external co-factors, and result in smaller, yet significant, changes in RNA secondary structure, which can include changes in base protonation state (Lee et al., 2014). They can therefore meet unique demands for RNA biological functions (Lee et al., 2014). In addition to playing new roles in RNA-based regulation, the unique features of RNA ESs make them potentially attractive targets for the development of RNA-targeting therapeutics (Lee et al., 2014). Here, we review NMR methods that can be used to characterize structural and energetic properties (population and lifetime) of RNA ESs.

2. NMR Relaxation Dispersion

2.1 Chemical Exchange

NMR relaxation dispersion (RD) experiments, which probe line-broadening contributions to NMR resonances arising from chemical exchange, can be used to characterize ESs of biomolecules. Several excellent reviews (Palmer et al., 2001; Palmer et al., 2006; Korzhnev et al., 2008; Bothe, Nikolova, et al., 2011; Sekhar & Kay, 2013; Palmer, 2014) describe the theoretical underpinnings of RD NMR techniques. They are briefly reviewed here to make the basic concepts accessible to the general reader. Readers are referred to the above reviews for a more rigorous treatment of these experiments.

The key NMR interaction underlying the RD experiments is the chemical shift. Nuclei behave as tiny magnets and due to quantization of the nuclear spin angular momentum, they align parallel (α state) or anti-parallel (β state) relative to the static NMR magnetic field (B₀). Since the parallel alignment is more energetically favorable (for nuclei with a positive gyromagnetic ratio), a net bulk magnetization over an ensemble of spins build up parallel to the magnetic field. In a basic 1D NMR experiment, radiofrequency (RF) pulses are used to realign this bulk magnetization along a direction perpendicular to the B₀ field. The bulk magnetization then precesses about the B₀ field at a characteristic resonance Larmor frequency and gives rise to a detectable oscillating magnetic field. This time-domain signal is then Fourier transformed to yield the standard frequency-domain NMR spectrum, in which unique signals at characteristic frequencies are observed for various spins for a given nuclei. These frequencies are referenced against a standard frequency (e.g. tetramethylsilane for ¹H) at that given B₀ field and this field-independent parameter is called the “chemical shift”.

The chemical shift is directly proportional to the energy gap between the a and b states, which in turn is proportional to the magnetic field strength experienced by the nucleus. Because electronic clouds surrounding nuclei “shield” or “deshield” the nucleus from the external magnetic field by variable amounts that are highly dependent on the specific electronic environment, a wide range of chemical shifts are typically observed for different sites in a molecule. This makes the NMR chemical shifts exquisitely sensitive to structure (e.g. torsion angles, sugar pucker, etc.), protonation state, and interactions (hydrogen bonding, electrostatic interactions, etc.). For nucleic acid applications, one is typically interested in the NMR active nuclei ¹H, ¹³C, ¹⁵N, ²H, and ³¹P, with ¹³C, ¹⁵N, and ²H introduced during synthesis, typically by using labeled nucleotide triphosphates (NTPs) in in vitro transcription reactions.

To understand how exchange between a GS and ES gives rise to line-broadening of the NMR resonance, consider an RNA molecule exchanging between two states; a major GS, in which a base is flipped in, and a minor ES, in which the base is flipped out (Fig 3A). Nuclei belonging to this base (along with its immediate neighbors) will experience different electronic environments before and after the flip, therefore will be associated with distinct NMR chemical shifts, ω_GS and ω_ES (Fig 3B). In the absence of exchange between the GS and ES, two NMR peaks are observed centered around ω_GS and ω_ES with integrated volumes reflecting the relative populations of the GS and ES (Fig 3B). However, when the GS and ES exchange at rates (k_ex = k₁ + k₋₁) comparable to their NMR frequency difference (Δω = ω_GS−ω_ES), the chemical shift of a given nucleus fluctuates back and forth between ω_GS and ω_ES. Because the fluctuation is stochastic, nuclei in different molecules spend varying amounts of time in the GS and ES, and therefore spend differential amounts of times with ω_GS and ω_ES frequencies. This results in the broadening of the NMR signal, reflecting a wide range of apparent frequencies due to variable admixing of ω_GS and ω_ES (Fig 3B). Because of its lower starting population and signal intensity, this broadening often puts the minor ES outside NMR detection limits (Fig 3B).

Figure 3.

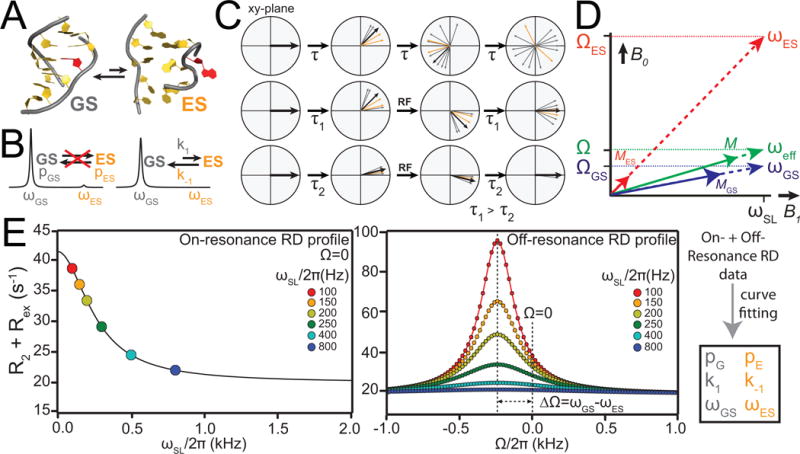
Characterizing chemical exchange using NMR relaxation dispersion. (A) Example of an equilibrium between a GS and ES. (B) Chemical exchange between GS and ES leads to broadening of resonances and disappearance of minor ES signal. (C) Bulk magnetization aligned along the Y-axis of the lab frame, followed by magnetization dephasing due to transverse relaxation. The middle and lower panel show the dephasing of bulk magnetization due to chemical exchange suppressed by application of RF fields for long (τ₁) and short (τ₂) delays in the CPMG experiment. (D) Resonance offset (Ω), effective field (ω) and magnetization (M) vectors for the GS and ES in R_1ρ experiment (denoted by the subscripts GS and ES, respectively). ω_eff, Ω and M represent the effective field, average offset and magnetization, (M), respectively. (E) Simulated examples of on-resonance (left) and off-resonance (right) RD profiles showing the dependence R_1ρ on spin-lock power ω_SL and offset Ω.

It is instructive to conceptualize chemical exchange in terms of magnetization precession (Fig 3C). Here, nuclei in the sample are associated with a bulk “magnetization” vector that is initially aligned along an axis in the laboratory frame by a “preparation” pulse. The individual magnetization vectors from nuclei in different molecules are initially co-aligned along the Y- (or X-) axis via phase coherence of the nuclear spins. The magnetization vector then precesses about the B₀ field (Z-axis) with the frequency ω (Fig 3C). In the absence of chemical exchange, two species precess at their respective chemical shift frequencies, ω_GS and ω_ES. However, in the presence of exchange, the precessing frequency of a given magnetization vector varies stochastically between ω_GS and ω_ES. Since nuclei from different molecules spend varying amounts of time precessing with frequencies ω_GS and ω_ES, they no longer precess in synchrony. Rather, they “fan out” and cause phase decoherence or “dephasing” (Fig 3C). This dephasing leads to an additional exchange contribution referred to as R_ex to the observed transverse relaxation rate R_2,obs = R₂+R_ex describing the rate at which the Y (or X) component of the magnetization vector decays over time. The NMR line width is directly proportional to R₂+R_ex, and exchange manifests as a line-broadening contribution.

2.2 Relaxation Dispersion Experiments

RD NMR experiments can be used to characterize properties of the often invisible ES by measuring the exchange broadening contribution to the visible GS resonance (reviewed in (Palmer et al., 2001; Palmer & Massi, 2006; Korzhnev & Kay, 2008; Bothe, Nikolova, et al., 2011; Palmer, 2014)). In particular, experiments are used to measure the chemical exchange contribution to line-broadening (R_ex) during a relaxation period (T_relax) during which the sample is subjected to radiofrequency frequency (RF) irradiation. Various types of RD experiments differ in the initial state of the magnetization and the type of RF irradiation that is used.

In the Carr-Purcell-Meiboom-Gill (CPMG) experiment (Carr et al., 1954; Meiboom et al., 1958; Loria et al., 1999a; F. A. Mulder et al., 2001), the initial state generally consists of transverse magnetization (e.g. aligned along the Y-axis) and the RF irradiation consists of a series of equally spaced high-power 180° refocusing pulses. In the case of the spin relaxation in the rotating frame experiment, or R_1ρ (Deverell et al., 1970; Akke et al., 1996; F. A. A. Mulder et al., 1998; Korzhnev et al., 2002), the initial magnetization is typically aligned along an effective field direction (which is defined by both the RF irradiation power and offset) and the irradiation consists of a weaker, but continuous RF with a specified power level (ω_SL) and frequency or offset (Ω) (Fig 3D).

The RF field employed in this case is called a “spin-lock” (SL), as it locks the magnetization along its effective field. In both the CPMG and R_1ρ experiments, the RF irradiation perturbs the precession of magnetization so as to diminish the efficiency with which chemical exchange results in dephasing of the magnetization, and therefore exchange broadening. For example, in the CPMG experiment, the series of 180° pulses effectively “invert” the precession of magnetization at a constant time interval (τ_CPMG); in this manner, some of the dephasing occurring prior to the 180° pulse is refocused in the period following the pulse, with the degree of refocusing increasing with shorter τ_CPMG delays (Fig 3C). In the case of the R_1ρ experiment, the two effective field directions associated with the GS and ES are brought into closer alignment by application of a continuous RF field (Fig 3D), thereby decreasing the extent of dephasing arising due to precession around the GS and ES effective fields. The dependence of the exchange broadening contribution (R_ex) on τ_CPMG in the case of CPMG and ω_SL, as well as Ω in the case of R_1ρ (Fig 3E), can be used to extract exchange parameters of interest. For slow (k_ex << |Δω| to intermediate (k_ex~|Δω|) exchange, these experiments can be used to determine the population (p_ES), lifetime (τ_ES = 1/[(1−p_ES)k_ex]), and chemical shift of the ES (ω_ES). For fast exchange (k_ex>>|Δω|), it becomes more difficult to reliably determine exchange parameters though one can typically accurately measure the factor Φ = p_GSp_ESΔω² where additional experiments are needed to resolve the ES chemical shift and population (Bothe et al., 2014). It is important to note the chemical shift of the ES carries the desired structural information.

CPMG relaxation dispersion experiments can be used to characterize processes with exchange rates (k_ex = k₁+k₋₁) in the range of ~10 s⁻¹ < k_ex < ~6000 s⁻¹ (Palmer et al., 2001; Korzhnev & Kay, 2008). CPMG data is typically measured at multiple magnetic field strengths and combined with additional experiments (e.g. HSQC/HMQC) in order to determine the sign of the excited state chemical shift (Skrynnikov et al., 2002). Although widely used in studies of proteins, the CPMG experiment proves difficult to apply to nucleic acids. This is due to a paucity of ideal imino nitrogens, and because ¹³C experiments are complicated by extensive C–C interactions that are difficult to suppress due to challenges in achieving selective carbon excitation with hard pulses (Yamazaki et al., 1994; Johnson et al., 2008). The exchange timescale accessible to R_1ρ is broader than CPMG (~60 s⁻¹ < k_ex < ~100,000 s⁻¹) (Palmer & Massi, 2006) and for slow-intermediate exchange, the sign of excited state chemical shift sign can deduced at a single magnetic field strength (Trott et al., 2002). For processes occurring at even slower timescales (~20 s⁻¹ < k_ex < ~300 s⁻¹) chemical-exchange saturation transfer (CEST) experiments employing weak RF spin-lock fields have recently been shown to be a robust approach to characterize lowly populated conformational states in both proteins and nucleic acids (Fawzi et al., 2011; Vallurupalli et al., 2012; Long et al., 2014; Zhao et al., 2014).

2.3 R_1ρ with Low-to-High Spin-Lock Fields

The application of low ω_SL is required in order to characterize ESs with exchange rates slower than k_ex < ~2,000 s⁻¹. However use of lower ω_SL (<1000 Hz) in the conventional 2D R_1ρ experiment is complicated due to the fact that one has many spins with a broad range of chemical shift frequencies, each with a distinct effective field (Fig 3D) that have to be aligned along their individual effective fields during the preparation phase of the experiment. For relatively high ω_SL (>1000 Hz), there is a limited range of effective field orientations for the various spins, and it is possible to align the magnetization efficiently using adiabatic ramps, which are generally 3–4 ms long (Zinn-Justin et al., 1997; F. A. A. Mulder et al., 1998; Kim et al., 2004; Massi et al., 2004; Igumenova et al., 2006; Hansen et al., 2007). However, for low spin-lock fields (<1000 Hz), one has a broader range of orientations, and proper alignment of the magnetization requires longer delays of the adiabatic ramps, resulting in severe sensitivity loss due to relaxation (Kim & Baum, 2004; Massi et al., 2004; Palmer & Massi, 2006). For a spin-lock field of 275 Hz, the alignment of initial magnetization is efficient only for offset values >325 Hz (Kim & Baum, 2004).

Recent advances in the ¹⁵N R_1ρ experiment introduced by the groups of Palmer and Kay address these limitations and allow use of much lower spin-lock fields (Massi et al., 2004; Korzhnev et al., 2005), on the order of 25–150 Hz, thus extending sensitivity to exchange timescales on the order of tens of milliseconds comparable to those accessible by CPMG. These advances have been integrated into an NMR experiment for measuring ¹³C (Hansen et al., 2009) and ¹⁵N (Nikolova et al., 2012) R_1ρ in nucleic acids (Fig 4). These experiments have so far been applied in the characterization of systems in fast to intermediate exchange in both proteins and nucleic acids (k_ex ~ 300 – 30000Hz, Δω ~ 20 – 800Hz), and will be discussed in this chapter in the context of characterizing RNA ESs.

Figure 4.

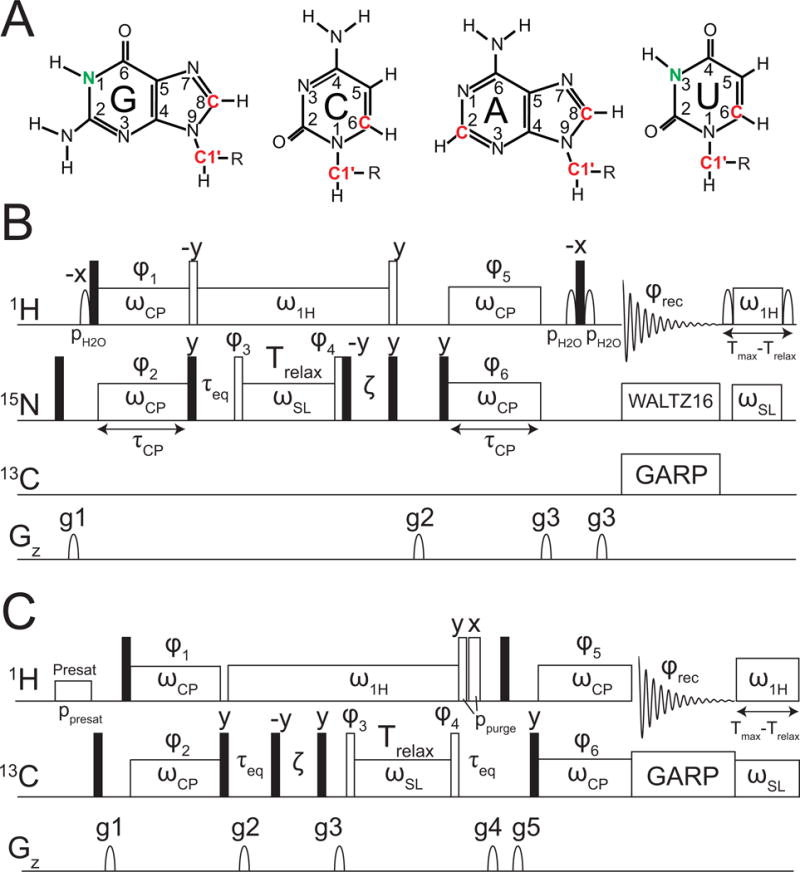
Pulse sequences for the measurement of ¹⁵N and ¹³C R_1ρ in uniformly ¹³C/¹⁵N labeled nucleic acids (A) The carbon and nitrogen nuclei that are targeted in RNA for R_1ρ measurements are highlighted. Pulse sequences for 1D (B) ¹⁵N (Nikolova, E. N., et al., 2012) and (C) ¹³C (Hansen, A. L., et al., 2009) R_1ρ experiments are as shown.

The basic experiment uses selective Hartmann-Hahn polarization transfers developed by Bodenhausen (Pelupessy et al., 1999; Ferrage et al., 2004) to excite specific spins of interest and collect data in a 1D manner. Both the GS and ES magnetization is aligned along the average effective field (ω_eff, Fig 3D) through application of a hard 90° pulse (Fig 4B,C) (Bothe et al., 2014). Upon application of the spin-lock, magnetization in states GS and ES will evolve about their respective effective fields ω_GS and ω_ES (Fig 3D). In cases of highly asymmetric exchange (p_GS >> p_ES) the effective fields of the GS and ω_eff are essentially the same and it has been shown that the effective field can be considered to be on the GS (Korzhnev et al., 2005; Bothe et al., 2014).

Because only one spin is aligned along its effective field, it is possible to use significantly weaker RF fields, for a full range of 25–3500 Hz (Massi et al., 2004; Korzhnev et al., 2005; Hansen et al., 2009). The lowest spin-lock power attainable is predominately limited by ~3-times the largest homonuclear scalar coupling (J_CC/J_NN) (Zhao et al., 2014): G-N1 and U-N3 ~50 Hz, A/G-C8 ~45 Hz, C1′ ~150 Hz, and A-C2 ~40 Hz. By using a continuous low spin-lock RF field rather than hard 180° pulses, it is also possible to suppress or eliminate unwanted C-C and N-C interactions in uniformly ¹³C/¹⁵N labeled samples (Hansen et al., 2009). The C-H (or N-H) scalar coupling evolution and cross-correlated relaxation between C-H (or N-H) dipole-dipole and carbon chemical shift anisotropy (CSA) are efficiently suppressed by using a strong ¹H continuous-wave field applied on the resonance of interest (Fig 4B,C). Consistent heating throughout a given experiment is maintained by a heat-compensation element (Korzhnev et al., 2005; Hansen et al., 2009) that applies far off-resonance ¹H and ¹³C/¹⁵N spin-locks for a given amount of time (T_max−T_relax), where T_max is the longest time delay and T_relax is the time delay in a given scan. Water is efficiently suppressed using either low power presaturation during inter-scan delay or with a WATERGATE element (Piotto et al., 1992) before acquisition. The same ¹⁵N R_1ρ experiment introduced by Kay and co-workers (Korzhnev et al., 2005) can be used to measure RD in imino nitrogens in DNA (Nikolova et al., 2012) and RNA (Lee et al., 2014). Unlike the ¹³C resonances, it is generally possible to assign the imino N1/3 resonances in much larger RNA systems. This, combined with the fact that the ¹⁵N chemical shift is extremely sensitive to RNA secondary structure makes imino ¹⁵N R_1ρ an ideal approach for characterizing the secondary structure of RNA excited states. These experiments have so far been applied to measure R_1ρ data for base (N1, N3, C2, C6, and C8) and sugar (C1′) nuclei in RNA and DNA (see Fig 4A).

3. General Protocol for Characterizing RNA ESs using Low-to-High Spin-Lock Field ¹³C and ¹⁵N Off-resonance NMR R_1ρ and Uniformly Labeled Nucleic Acid Samples

3.1 Construct Design

It is common practice for transcription reactions using T7 RNA polymerase (T7 RNAP) to add two G residues at the 5′ end of the RNA in order to maximize transcription yields. RNA secondary structure prediction is used to make sure that such sequence modifications do not interfere with the RNA GS or ES.

3.2 Sample Preparation and Purification

Because the R_1ρ experiment is sensitivity demanding, we typically require NMR samples with ≥1 mM concentration of ¹³C/¹⁵N uniformly labeled RNA. This typically yields spectra with ≥40 signal-to-noise ratios (S/N) at 16 scans (the minimum phase-cycling steps involved in the experiment) and with an inter-scan delay (d1) of ~1.4–2.0 sec, allowing acquisition of ~140 R_1ρ data points at various ω_SL and within ~12 hrs. This requirement for high sensitivity can also make it challenging to record R_1ρ data on slowly tumbling systems such as large RNAs (>70 nt) or RNA-protein complexes. TROSY-based R_1ρ experiments can be used to improve sensitivity in such large systems (Loria et al., 1999b; Igumenova & Palmer, 2006). Samples can be prepared by in vitro transcription employing commercially available ¹³C/¹⁵N labeled nucleotide triphosphates (NTPs), followed by polyacrylamide gel electrophoresis (PAGE) purification or other purification methods. It is important to ensure that all running buffers, reagents, glassware, and equipment used are RNAse-free. Protocols for preparation of uniformly ¹³C/¹⁵N labeled RNA samples are described elsewhere (Easton et al., 2010; Petrov et al., 2013; Alvarado et al., 2014).

3.3 Protocol for Measuring R_1ρ RD in Uniformly Labeled Nucleic Acids

The RNA nuclei that are typically targeted for R_1ρ measurements by the methods described here are depicted in Figure 4A. Well established NMR approaches (reviewed in (Furtig et al., 2003)) are initially used to assign resonances in the RNA.

3.3.1 Calibrating Spin-Lock Power

When setting up the R_1ρ experiment on a new spectrometer or newly installed probe/console, it is critical to calibrate ¹³C and ¹⁵N spin-lock powers (Palmer et al., 2001). In general, spin-lock power calibration is not necessary when switching samples or changing temperature.

Prepare a modified version of R_1ρ pulse sequence by removing the pulses with phase φ₃ and φ₄ flanking the spin-lock element (Fig 4B,C). This can be done by setting their duration to zero or by omitting the pulses from the pulse program. The following protocol can then be used to calibrate ¹⁵N or ¹³C spin-lock powers.

1. Select a sharp and well-resolved resonance to perform calibration. This resonance should exhibit minimal to no chemical exchange to avoid complication from exchange processes.

2. Compile a table containing spin-lock powers ω_SL (in Hz) to be calibrated and associated power levels P (in dB). The power levels can be estimated based on the calibrated ¹⁵N or ¹³C rectangular 90° pulse values.

3. Record 1D experiments for an array of spin-lock durations, T_relax (Fig 4B,C). Typically 33 durations are used in increments of 1/(4ω_SL) from 0 to 8/ω_SL (Hansen et al., 2009). For example, a 100 Hz spin-lock power would be incremented 33 times from 0–80 ms in increments of 2.5 ms.

4. Measure the resultant peak intensity. It should be modulated by exp(iω_SL,realT_realx) where ω_SL,real is the real ω_SL.

5. Calculate the real ω_SL by fitting the intensities to the equation I (τ) = I₀ exp(−R·T_relax) cos(ω_SL,realT_realx + φ), where T_realx is the duration of spin-lock, is the relaxation rate, and I is the peak intensity.

6. Repeat Step 4–5 for all ω_SL in the table, and obtain ω_SL,real for all preset P values.

7. Fit P and ω_SL,real to a logarithmic equation P = a log₁₀(ω_SL,real) + b. Ideal curve would give an R² > 0.99. If the data points deviate from linear curve, a polynomial fitting can be adopted instead. An example is shown in Figure 5.

8. Use the calibration equation given by the fit in 7 to back-calculate P for a desired spin-lock power within the range of powers tested.

Figure 5.

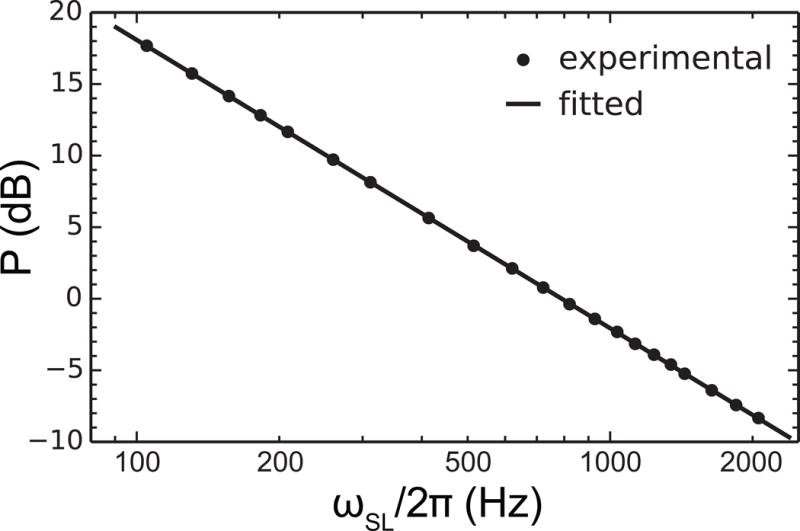
Example of spin-lock power calibration curve. Calibration shown was carried out for ¹⁵N on Bruker 600 MHz, fitted with to show a linear regression.

3.3.2 Measurement of ¹⁵N R_1ρ Data

Figure 4B shows the pulse sequence employed to measure RD for imino ¹⁵N nuclei. The RF pulses along with their characteristic power and duration are defined as they appear in the pulse sequence. The key parameters to be optimized are listed below.

• p_H2O: Sinc shaped pulse for manipulation of water magnetization (for flip-back and WATERGATE). p_H2O should be optimized to achieve optimal peak intensity and efficient water suppression. It can be initially set to a value calculated from ¹H 90° pulse, and then optimized by arraying 5~7 values of the pulse power centered around the initial guess.

• ω_CP: strength of ¹H/¹⁵N RF field for selective Hartman-Hahn polarization transfer pulses. Optimal transfer is achieved when ω_CP ≈ 90 Hz for both ¹H and ¹⁵N pulses. Estimate the power levels for ¹H and ¹⁵N ω_CP pulses corresponding to 90 Hz from the spin-lock power calibration curve of ¹⁵N (Fig 5) and from ¹H 90° pulse. Fine tune the power levels for both the ¹H and ¹⁵N pulses around that value to maximize the intensity of the desired peak with T_relax set to 0 ms. Efficient heteronuclear cross polarization can be achieved when ω_CP (in Hz) is set to values larger than $\left|{ }^1{J}_{\mathrm{NH}}\right|\sqrt{3}/4$. (Korzhnev et al., 2005).

• τ_CP: duration of polarization transfer delay is set to ~ 1/|¹J_NH| and further optimized to obtain the maximum peak intensity of the desired resonance.

• ω_1H: ¹H spin-lock field used to suppress scalar coupling (¹J_HN), and N-H/N DD/CSA cross-correlated relaxation during the ¹⁵N spin-lock period (T_relax). It is set to ~5000 Hz for ¹⁵N R_1ρ experiment. ω_1H should also be chosen to be larger than the effective spin-lock field to avoid polarization transfer during the spin-lock period (Korzhnev et al., 2005). In practice, when setting up ¹⁵N R_1ρ experiment for the first time, several different ω_1H values are tested until dispersion data with minimum artifacts are obtained.

• ζ delay (optional calibration): Nearby ¹⁵N resonances that have overlapping ¹H chemical shifts can be suppressed by using the ζ delay (Fig 4B,C), wherein ζ=π/(2δ) and δ/(2π) is the ¹⁵N offset (Hz) of the resonance to be suppressed (Korzhnev et al., 2005; Hansen et al., 2009).

• τ_eq: time delay for equilibration of GS and ES and is set to ~3/k_ex.

• T_max: the maximum duration of the relaxation time used to measure the R_1ρ monoexponential decay. It varies from resonance to resonance, and is typically set to a value that results in decay in the peak intensity to ~30–40% of the intensity measured at T_min = 0 ms. Care must be taken to ensure the combination of ω_SL and T_relax does not exceed the tolerance of the probe.

The following protocol is employed to collect ¹⁵N R_1ρ

1. Optimize pulse sequence parameters as described above.

2. Record on-resonance data by setting Ω = 0 Hz and measure R_1ρ decay curves at ~20 powers ranging from 50–2000 Hz. To do this, measure R_1ρ monoexponential decay curves at individual power levels and zero offset by acquiring the peak intensity as a function of ~8–10 spin-lock durations (T_relax). Preform duplicate measurements at T_min and T_max to help estimate R_1ρ uncertainty. Note that the absence of relaxation dispersion – or a dependence for R_ex on spin-lock power in the on-resonance profile does not imply absence of chemical exchange. It is possible that the exchange involves a very large Δω such that the carrier offset is not optimally positioned near ω_ES where the R_ex contribution is maximum (Trott & Palmer, 2002). Off-resonance data (see Fig 6 below) must be collected to verify absence of chemical exchange at a given site.

3. Measure off-resonance R_1ρ data by varying both ω_SL (typically 3 or more values spanning the limits described above) and Ω (≥20 values per ω_SL probed). The maximum value for Ω (hereinafter referred as Ω_max) is generally ~3–4 times the ω_SL. Beyond this offset range, R_1ρ will be dominated by R₁ relaxation contributions, resulting in significant uncertainty when extracting R_ex. In general, ≥20 values of Ω are chosen with equal spacing to span ± Ω_max symmetrically about the zero offset.

4. It may be important to calibrate sample temperature (see note in 3.4.7) when carrying out the R_1ρ measurements since small differences (~5 °C) can have significant effect on the observed RD profiles.

Figure 6.

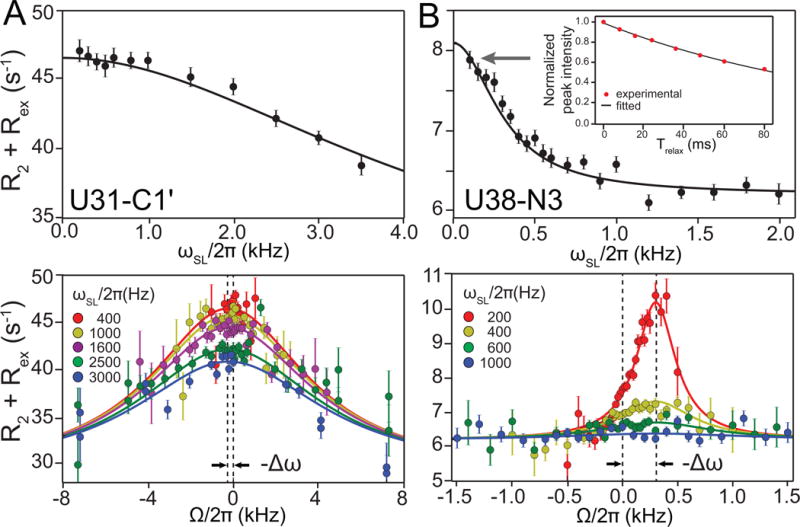
Representative on- (top) and off-resonance (bottom) 1D R_1ρ RD profiles for uridine residues from HIV-1 TAR. (A) U31-C1′ exhibiting fast exchange between GS and ES1 measured using 1D ¹³C R_1ρ experiment. (B) U38-N3 exhibiting slow exchange between GS and ES2 measured using 1D ¹⁵N R_1ρ experiment. The RD data are fitted to Laguerre equation. The inset shows the magnetization decay, as a function of relaxation delay (T_relax), of the first point in the on-resonance profiles, which is fit to a monoexponential to obtain the R_1ρ value.

3.3.3 Measurement of ¹³C R_1ρ data

The ¹³C R_1ρ pulse sequence (Fig 4C) can be set up in a similar manner as described for ¹⁵N R_1ρ (3.3.2) to target the carbon nuclei shown in Figure 4A. A presaturation approach (PRESAT) can be used for water suppression of these non-exchangeable resonances (Hansen et al., 2009). ¹³C nuclei typically require much shorter relaxation delays (T_relax <50 ms), and a broader range of ω_SL can be used (typically 150 – 3500 Hz). Care has to be taken to limit Hartmann-Hahn matching condition with other neighboring carbons that have sizable scalar couplings. See Hansen et al. for an involved discussion (Hansen et al., 2009). Below, we describe the basic elements that differ from those of the ¹⁵N R_1ρ experiment (3.3.2).

• p_presat: presaturation power level. Optimize power level to achieve good water suppression in combination with p_purge (see below). Typically lower power (~100–150 Hz) is used to achieve selective suppression. It is critical to avoid using high power levels for probe safety.

• ω_CP: strength of ¹H/¹³C RF field of polarization transfer. It is set to ~100 Hz in ¹³C R_1ρ experiment. See 3.3.2.

• τ_CP: duration of polarization transfer. The optimal value is ~ 1/|¹J_CH|. See 3.3.2.

• ω_1H: ¹H spin-lock field. See 3.3.2. For ¹³C, ~8–10 kHz ω_1H is typically needed to completely suppress unwanted ¹J_CH and DD/CSA effects (Hansen et al., 2009).

• ζ delay (optional calibration): See 3.3.2. It is noted that the effectiveness of the ζ delay is significantly compromised for resonances with strong homonuclear scalar couplings (primarily applicable for ¹³C resonances such as C6) (Hansen et al., 2009).

• p_purge: Water purge element. p_purge need to be optimized by varying their power and duration for every experiment to maximize water suppression.

The protocol for ¹³C R_1ρ measurements is the same as the case of ¹⁵N, except for the following points.

1. On-resonance data are collected at ω_SL ranging from 45–3500 Hz or 150–3500 Hz for C2/C8 spins and C1′/C6 spins, respectively.

2. C-C Hartmann-Hahn transfers need to be computed as described previously (Hansen et al., 2009) in order to avoid spin-lock powers and offset combinations that can result in transfers to neighboring or distant C resonances with significant J_CC couplings. For example, lower ω_SL are not feasible for C1′ because of sizeable ¹J_C1′C1′ and need to avoid Hartmann-Hahn transfers (Hansen et al., 2009).

3.3.4 Trouble Shooting R_1ρ

• Expected peak is absent. Either the Hartmann-Hahn polarization transfer failed or resulted in negligible signal. Make sure ¹H and ¹³C/¹⁵N carrier positions have been set properly, and that a well estimated τ_CP has been given based on ¹J_CH or ¹J_NH. Try increasing the number of scans and array both ω_CP pulses around power levels estimated for a 90–100 Hz transfer.

• Oscillations are seen in the monoexponential decay of peak intensity. Check that the lowest ¹³C/¹⁵N spin-lock power used is at least 3 times the largest J_CC/J_NN. For slow exchanging systems with large ES populations (k_ex <250 s⁻¹, and p_ES >10%), oscillations can arise due to precession of the ES magnetization. It may be possible to suppress such oscillations by reducing the length of the τ_eq (see Fig 4) to ~5 ms (Qi Zhang, University of North Carolina, personal communication).

3.4 Data Analysis

3.4.1 Fitting Monoexponentials to Obtain R_1ρ Values

The R_1ρ data is collected as a series of 1D spectra for each combination of ω_SL and Ω. The procedure below is used to extract the R_1ρ data from each set of 1D spectra recorded using different spin-lock durations, T_relax.

1. Spectra are processed by nmrPipe (Delaglio et al., 1995) and then are assembled into a single pseudo-2D spectrum using an nmrPipe script.

2. The pseudo-2D spectrum is fitted to Gaussian or Lorentzian line-shape using nmrPipe autoFit script. This fitting scheme assumes that all 1D peaks share the same line-width and resonance frequency. We find that this global approach to curve fitting improves accuracy and robustness.

3. Peak intensities are extracted from the Step 2, and are subsequently fitted against T_relax according to equation I = I₀ exp(−R_1ρ·T_relax) using a non-linear fitting algorithm. The nonlinear fitting could be sensitive to the initial values of I₀ and R_1ρ, especially when the signal-to-noise is poor. To address this potential problem, carry out Steps 4 and 5.

4. Normalize the peak intensities in the 1D arrays by scaling down these intensities so that the intensity at the shortest delay (T_min) equal to 1.0. The initial estimate for I₀ is thus set to 1.0.

5. The initial estimation for R_1ρ is obtained by linearly fitting these intensities to the equation ln I = ln I₀ − R_1ρT_relax. The non-linear fitting is then performed under these initial guess, and R_1ρ is extracted. An example of a fit is shown in Figure 6B (inset).

6. Monte-Carlo method or Jackknife algorithms can be used to estimate the uncertainty of the fitted R_1ρ value. These errors will be used in the fitting of R_1ρ data described value. in 3.4.2 and 3.4.3.

3.4.2 Fitting Off-Resonance R_1ρ Data using Algebraic Equations

Several algebraic expressions, derived using various approximations, can be used to fit the dependence of R_1ρ on ω_SL and Ω to extract the desired exchange parameters (reviewed in (Palmer & Massi, 2006)). These equations can be used to extract exchange parameters from the R_1ρ data, and also, can provide a powerful tool for exploring the experiment. The most versatile expression uses the Laguerre approximation developed by Palmer and co-workers (Miloushev et al., 2005):

$$R_{1\rho }=R_1{\cos }^2\theta +R_2{\sin }^2\theta +\frac{{\sin }^2\theta p_{\mathrm{GS}}{p}_{\mathrm{ES}}\mathrm{\Delta }{\omega }_{\mathrm{ES}}^2{k}_{\mathrm{ex}}}{\left\{\frac{{\omega }_{\mathrm{GS}}^2{\omega }_{\mathrm{ES}}^2}{{\omega }_{\text{eff}}^2}+k_{\mathrm{ex}}^2-{\sin }^2\theta p_{\mathrm{GS}}{p}_{\mathrm{ES}}\mathrm{\Delta }{\omega }_{\mathrm{ES}}^2\left(1+\frac{2k_{\mathrm{ex}}^2\left(p_{\mathrm{GS}}{\omega }_{\mathrm{GS}}^2+p_{\mathrm{ES}}{\omega }_{\mathrm{ES}}^2\right)}{{\omega }_{\mathrm{GS}}^2{\omega }_{\mathrm{ES}}^2+{\omega }_{\text{eff}}^2{k}_{\mathrm{ex}}^2}\right)\right\}}$$ (1)

where ${\omega }_{\text{eff}}^2=\mathrm{\Delta }{\mathrm{\Omega }}^2+{\omega }_{\mathrm{SL}}^2$, ${\omega }_{\mathrm{GS}}^2={\left({\mathrm{\Omega }}_{\mathrm{GS}}-{\omega }_{\mathrm{rf}}\right)}^2+{\omega }_{\mathrm{SL}}^2$, ${\omega }_{\mathrm{ES}}^2={\left({\mathrm{\Omega }}_{\mathrm{ES}}-{\omega }_{\mathrm{rf}}\right)}^2+{\omega }_{\mathrm{SL}}^2$, $\mathrm{\Delta }{\omega }_{\mathrm{ES}}={\mathrm{\Omega }}_{\mathrm{ES}}-{\mathrm{\Omega }}_{\mathrm{GS}}$, $\theta ={\tan }^{-1}\left({\omega }_{\mathrm{SL}}/\mathrm{\Delta }\mathrm{\Omega }\right)$, $\mathrm{\Delta }\mathrm{\Omega }=\overline{\mathrm{\Omega }}-{\omega }_{\mathrm{rf}}$, where R₁ and R₂ are the longitudinal and transverse relaxation rates, respectively, Ω_GS and Ω_ES are the resonance offsets from the spin-lock carrier for the respective states, ω_rf and ω_SL are reference frequency and the strength of the spin-lock carrier, $\overline{\mathrm{\Omega }}=p_{\mathrm{GS}}{\mathrm{\Omega }}_{\mathrm{GS}}+p_{\mathrm{ES}}{\mathrm{\Omega }}_{\mathrm{ES}}$ k_ex is the exchange rate, all in units of s⁻¹. The Laguerre equation is valid under conditions of fast exchange, and deviations can arise in slow to intermediate exchange with a large excited state population (p_ES >10%). These deviations generally increase with slower exchange rates and increasing populations, particularly for low spin-lock fields (ω_SL ≤400 Hz) (Miloushev & Palmer, 2005).

For >2-state exchange, there can be a range of exchange topologies (Palmer & Massi, 2006). Typically, the R_1ρ data is analyzed assuming ES1⇌GS⇌ES2 with or without minor exchange between ES1 and ES2. It should be noted that under certain exchange regimes, the R_1ρ data will be sensitive to the presence of minor exchange between ES1 and ES2, and therefore, under favorable exchange conditions can in principle be used to define the topology of the exchange process (Palmer & Massi, 2006). For 3-state without minor exchange, one can use the following equation (Palmer & Massi, 2006):

$$R_{1\rho }=R_1{\cos }^2\theta +R_2{\sin }^2\theta +{\sin }^2\theta \left(\frac{k_1\mathrm{\Delta }{\omega }_{\mathrm{ES}1}^2}{{\mathrm{\Omega }}_{\mathrm{ES}1}^2+{\mathrm{\Omega }}_{\mathrm{SL}}^2+k_{-1}^2}+\frac{k_2\mathrm{\Delta }{\omega }_{\mathrm{ES}2}^2}{{\mathrm{\Omega }}_{\mathrm{ES}2}^2+{\mathrm{\Omega }}_{\mathrm{SL}}^2+k_{-2}^2}\right)$$ (2)

where Δω_ES1 = ΔΩ_ES1−Ω_GS, Δω_ES2 = ΔΩ_ES2−Ω_GS, k₁ and k₋₁ are the GS-ES1 forward and reverse rate constants, respectively, and k₂ and k₋₂ are the GS-ES2 forward and reverse rate constants, respectively.

A Laguerre approximation has also been used to analyze 3-state exchange (Dethoff, Chugh, et al., 2012), and has shown excellent agreement with numerical solutions, though its range of validity has not been fully examined:

$$\begin{array}{l}{R}_{1\rho }=R_1{\cos }^2\theta +R_2{\sin }^2\theta +\\ {\sin }^2\theta \left(\frac{p_{\mathrm{GS}}{p}_{\mathrm{ES}1}\mathrm{\Delta }{\omega }_{\mathrm{ES}1}^2{k}_{\mathrm{ex}1}}{\left\{{\omega }_{\mathrm{GS}}^2{\omega }_{\mathrm{ES}1}^2/{\omega }_{\text{eff}}^2+k_{\text{ex}1}^2-{\sin }^2\theta p_{\mathrm{GS}}{p}_{\mathrm{ES}1}\mathrm{\Delta }{\omega }_{\mathrm{ES}1}^2\left(1+\frac{2k_{\text{ex}1}^2\left(p_{\mathrm{GS}}{\omega }_{\mathrm{GS}}^2+p_{\mathrm{ES}1}{\omega }_{\mathrm{ES}1}^2\right)}{{\omega }_{\mathrm{GS}}^2{\omega }_{\mathrm{ES}1}^2+{\omega }_{\text{eff}}^2{k}_{\text{ex}1}^2}\right)\right\}}+\frac{p_{\mathrm{GS}}{p}_{\mathrm{ES}2}\mathrm{\Delta }{\omega }_{\mathrm{ES}2}^2{k}_{\mathrm{ex}2}}{\left\{{\omega }_{\mathrm{GS}}^2{\omega }_{\mathrm{ES}2}^2/{\omega }_{\text{eff}}^2+k_{\text{ex}2}^2-{\sin }^2\theta p_{\mathrm{GS}}{p}_{\mathrm{ES}2}\mathrm{\Delta }{\omega }_{\mathrm{ES}2}^2\left(1+\frac{2k_{\text{ex}2}^2\left(p_{\mathrm{GS}}{\omega }_{\mathrm{GS}}^2+p_{\mathrm{ES}2}{\omega }_{\mathrm{ES}2}^2\right)}{{\omega }_{\mathrm{GS}}^2{\omega }_{\mathrm{ES}2}^2+{\omega }_{\text{eff}}^2{k}_{\text{ex}2}^2}\right)\right\}}\right)\end{array}$$ (3)

Other expressions for 3-state exchange with minor exchange have been reported (Trott et al., 2004).

When carrying out a fit to the R_1ρ data, one starts out with broad estimates of initial exchange parameters and performs a fit using the equations described above. However, starting estimates combined with conventional local-minimum optimization methods (such as the Levenberg-Marquadt algorithm) can lead to fits being trapped in local minima. In such cases, use of simulated annealing and basin-hopping (Wales et al., 1997) schemes can prove very beneficial for finding global minima.

The quality of the fit is assessed using a χ² analysis, for which reasonable fits typically yield values below 1.5, though care should be taken if a fit gives a χ² of <1 as this may indicate over-fitting. A poor fit may suggest deviations from a two-state model or from the range of validity of the Laguerre equation or >2-state exchange. Statistical tests (e.g. F-Test and Akaike information criterion) (Akaike, 1974) can provide insights in to the likelihood of one model over the other.

3.4.3 Fitting Off-Resonance R_1ρ Data using Bloch McConnell Equations

Alternatively, one can fit the R_1ρ data directly by numerical integration of the Bloch-McConnell (B-M) equations (McConnell, 1958). The B-M equation does not rely on any algebraic approximations and makes it possible to compute R_1ρ data for arbitrarily complex exchange models consisting of many ESs with distinct exchange topologies. The disadvantage of this method is the high computational cost. Typically, we find that using parameters from the Laguerre fit simplifies the search for the global minimum. More typically, we use the B-M equations to establish the validity of the Laguerre approximation through comparison of computed R_1ρ given a set of ω_SL and Ω around a given set of speculated exchange parameters (for example see (Bothe, Lowenhaupt, et al., 2011)). B-M simulations can also be used to examine effects arising from >2-state exchange.

3.4.4 Determining the chemical shifts of the ES

Fitting of the R_1ρ data yields Δω and p_ES. This together with the observed chemical shift, $\overline{\mathrm{\Omega }}$, can be used to determine the ES chemical shift, Ω_ES:

$${\mathrm{\Omega }}_{\mathrm{ES}}=\overline{\mathrm{\Omega }}+(1-p_{\mathrm{ES}})\mathrm{\Delta }\omega$$ (3)

It worth noting that the same unit should be used for Ω_ES, $\overline{\mathrm{\Omega }}$ and Δω either in Hz or in ppm. To convert Δω from Hz to ppm, one can use equation Δω (ppm) = Δω(Hz)×10⁶/ω_Lamor where ω_Lamor (in Hz) is Larmor frequency of the spin of interest. For example, if Larmor frequency of a ¹⁵N spin is 60.772 MHz, then a Δω=−257 Hz will be translated to −4.23 ppm. The GS chemical shift can be calculated by ${\mathrm{\Omega }}_{\mathrm{GS}}=\overline{\mathrm{\Omega }}-p_{\mathrm{ES}}\mathrm{\Delta }\omega$.

3.4.5 Plotting RD profiles

When displaying RD profiles, we plot R₂ + R_ex versus spin-lock offset frequency (Ω) for various (typically color coded) spin-lock powers. This omits the R₁ contribution to R_1ρ, which does not provide any information regarding exchange parameters. Note that Ω is the ¹³C or ¹⁵N resonance offset frequency from the carrier position, and ΔΩ = −Δω. An example plot is shown in Figure 6 for fast (ES1, Fig 6A) and slow (ES2, Fig 6B) exchange processes in HIV-1 TAR. Note that in general, the maximum R_ex occurs when the carrier is on resonance with the ES chemical shift, thus simple inspection of the profile can be used to estimate the chemical shift of the ES. For fast exchange, one generally sees a broader line and it becomes more difficult to pinpoint the position of peak maximum and therefore the chemical shift of the ES (Bothe et al., 2014).

3.4.6 Estimating Uncertainties in Exchange Parameters

Bootstrap and Monte Carlo based approaches can be used to estimate uncertainties in the measured exchange parameters (Bothe, et al., 2014). A parent data set of R_1ρ data points (Ω, ω_SL, R_1ρ, R_1ρ error) is used for both methods.

In the Bootstrap approach:

1. 1000 child data sets of the same size as the parent data set are generated by randomly choosing data points from the parent data set. Here, each data point can be either excluded or chosen multiple times.

2. Each child data set and the parent data set are fit to the Laguerre equation to obtain the five exchange parameters: R₁, R₂ p_ES, k_ex and Δω

3. The uncertainty in the exchange parameters is then determined by calculating the standard deviation of the individual parameters of the child data sets relative to parameters of the parent data set.

In the Monte Carlo approach:

1. The parent data set is fit to the Laguerre equation to obtain the five exchange parameters.

2. 1000 child data sets are generated using the exchange parameters, the Laguerre equation, and the Ω and ω_SL values of the parent data set.

3. Each child data set is noise corrupted according to the R_1ρ error from the parent data set.

4. The child data sets are fit to the Laguerre equation.

5. The uncertainty in the exchange parameters is then determined by calculating the standard deviation of the individual parameters of the child data sets relative to parameters of the parent data set.

3.4.7 Kinetic-Thermodynamic Analysis

Valuable kinetic-thermodynamic information can be obtained from the exchange parameters (Korzhnev et al., 2007; Nikolova et al., 2011). This can also provide important insights into the nature of the ES and transition state (TS). For a 2-state system, the free energy difference between the GS and ES at a given temperature can readily be obtained using the following equation:

$$\mathrm{\Delta }{G}_{\mathrm{ES}}(T)=-k_{B}T\ln \left(\frac{p_{\mathrm{ES}}}{p_{\mathrm{GS}}}\right)$$ (4)

where ΔG_ES is the relative free energy difference between the GS (arbitrarily referenced to 0) and the ES, T is the experimental temperature (in Kelvin), and k_B is Boltzmann’s constant.

The free energy difference relative to the transition state can be obtained by:

$$\ln \left(\frac{k_i(T)}{T}\right)=\ln \left(\frac{k_{\mathrm{B}}\kappa }{h}\right)-\frac{\mathrm{\Delta }{G}_i^T(T)}{RT}$$ (5)

where (i = 1 or −1) are the forward and reverse rate constants, respectively. T is the experimental temperature (in Kelvin), k_B is Boltzmann’s constant, κ is the transmission coefficient (assumed to be 1), h is Planck’s constant, ΔG^T is the forward or reverse activation barrier, and R is the gas constant.

The enthalpies and entropies can also be obtained through temperature dependent R_1ρ measurements.

$$\ln \left(\frac{k_i(T)}{T}\right)=\ln \left(\frac{k_{\mathrm{B}}\kappa }{h}\right)-\frac{\mathrm{\Delta }{G}_i^T(T_{\mathrm{hm}})}{R{T}_{\mathrm{hm}}}-\frac{\mathrm{\Delta }{H}_i^T}{R}\left(\frac{1}{T}-\frac{1}{T_{\mathrm{hm}}}\right)$$ (6)

Where k_i (i = 1 or −1) are the forward and reverse rate constants, respectively. T is the experimental temperature (in Kelvin), k_B is Boltzmann’s constant, κ is the transmission coefficient (assumed to be 1), h is Planck’s constant, R is the gas constant, ΔG^T is the forward or reverse activation barrier, ΔH^T is the forward or reverse enthalpy of activation, and T_hm is the harmonic mean of the experimental temperatures measured:

$$T_{\mathrm{hm}}=n{\left({\displaystyle \sum _{i=1}^n\left(\frac{1}{T_i}\right)}\right)}^{-1}$$ (7)

Finally, $T\mathrm{\Delta }{S}_i^T=\mathrm{\Delta }{H}_i^T-\mathrm{\Delta }{G}_i^T(T_{\mathrm{hm}})$ Where ΔS^T is the forward or reverse entropy of activation.

Note: Here it is critical to ensure the spectrometer temperature is calibrated to match the sample temperature. This can be achieved by recording spectra of 99.8% methanol-d₄ (Cambridge Isotope Laboratories, Inc.) at varying spectrometer temperatures. Here, the actual sample temperature is given by T = −16.7467Δδ² – 52.5130Δδ+ 419.1381, where Δδ is the difference in chemical shift (ppm) between the hydroxyl and methyl proton (Findeisen et al., 2007).

3.5. Inferring Structures of RNA Excited States using NMR Chemical Shifts and Secondary Structure Prediction

3.5.1 ¹³C and ¹⁵N Chemical Shift-Structure Relationships in RNA

The ¹³C and ¹⁵N chemical shifts of the ES carry rich structural information. Base carbon chemical shifts (C2/C6/C8) are sensitive to changes in the glycosidic angle χ (anti versus syn) as well as stacking (Dejaegere et al., 1998; Xu et al., 2000; Ebrahimi et al., 2001; Fares et al., 2007; Ohlenschlager et al., 2008). The adenine C2 is sensitive to protonation of N1. Sugar C1′ chemical shifts are sensitive to both sugar pucker and the glycosidic bond angle (Dejaegere & Case, 1998; Xu & Au-Yeung, 2000; Ebrahimi et al., 2001; Fares et al., 2007; Ohlenschlager et al., 2008). The ¹⁵N chemical shifts are sensitive to the properties of H-bonding (see below) (Goswami et al., 1993) and also directly report on changes in ¹⁵N protonation states (Büchner et al., 1978).

In Figure 7, we show 2D HSQC-style representation that capture key ¹³C (Fig 7A) and ¹⁵N (Fig 7B) chemical-shift-structure relationships in RNA (McBrairty et al., 2015). As can be seen, resonances belonging to Watson-Crick (WC) bps that are surrounded by other WC bps (A-form residues) fall within a narrow region of ¹³C chemical shifts for both base (C2, C6, C8) and sugar (C1′) resonances (Dejaegere & Case, 1998; Xu & Au-Yeung, 2000; Ebrahimi et al., 2001; Fares et al., 2007; Ohlenschlager et al., 2008). Non-canonical residues have ¹³C and ¹⁵N chemical shifts that deviate from the narrow range defined by the WC A-form conformation. For example, residues in bulges and apical loops have C6/C8 resonances that are downfield shifted in both carbon and proton dimensions. The C1′ chemical shifts in non-A-form regions are also upfield shifted, consistent with changes in sugar pucker from C3′-endo toward C2′-endo. In general, non-canonical bps that resemble the A-form helix geometry will show carbon chemical shifts that fall within the A-form helical distributions, whereas more flexible base-pairing and differences in backbone conformation can lead to differences in both C6/C8 (downfield) and C1′ (upfield) chemical shifts.

Figure 7.

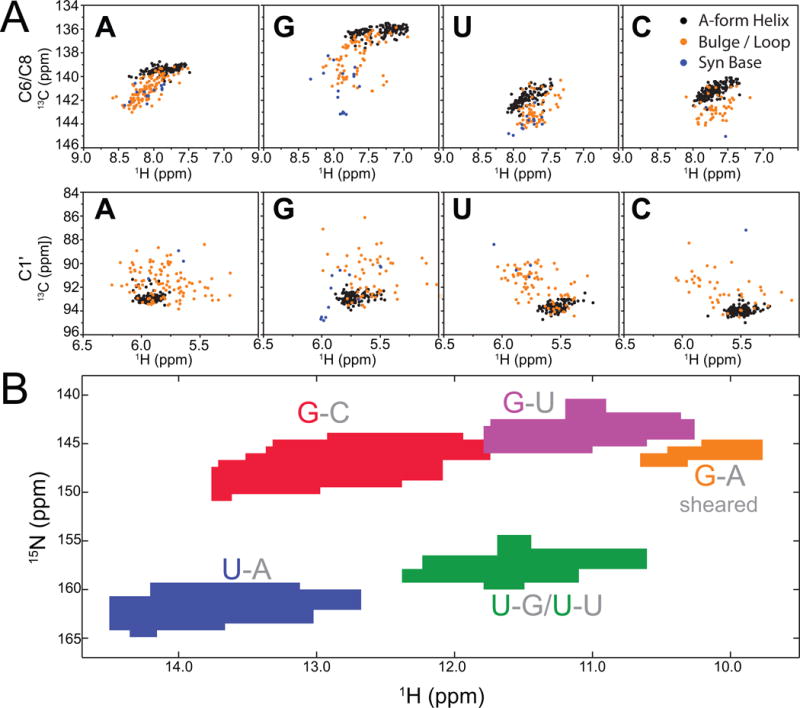
Chemical shift-structure relationships in RNA (A) Distribution of C-H chemical shifts derived from BMRB database (McBrairty, 2015) for different regions of RNAs: A-form helical Watson-Crick base pairs (black); bulge, internal loop or apical loop (gold); residues with a syn base conformation (blue). (B) Distribution of N-H chemical shifts of RNA imino groups for guanine and uracil nucleotides in different base pair contexts: G-C Watson-Crick base pairs (red), G-U wobbles (purple), sheared G-A pairs (gold), U-A Watson-Crick base pairs (blue), and U-G wobbles or U-U mispairs (green).

In addition, the imino (G-N1/U-N3) and amino (A-N6/C-N4/G-N2) ¹⁵N chemical shifts are sensitive to changes in base-pairing, including changes in hydrogen bonding partner, as well as the hydrogen bonding distance, which give rise to predictable changes in chemical shift from the standard WC bps to other types of base-pairing (Fig 7B). Guanine N1 in G-C bps resonates in a region downfield (Δω_N1 ~2–5 ppm) from the chemical shifts of the same spin in G-U wobble mispairs. Likewise, uracil N3 chemical shifts of A-U pairs resonate downfield (Δω_N3 ~2–5 ppm) from that of U-N3 in G-U mispairs. In general, G-N1 and U-N3 display upfield shift from the canonical G-C/A-U region upon partial or complete loss of stable nitrogen H-bonding. Therefore, if a base pair involving G/U changes from canonical pair to non-canonical pair or an unpaired base, or vice versa, it is likely to produce a detectable RD profile, providing a clue about the change of base-pairing in the excited state.

It is also possible to capture motif-specific chemical shift signatures. For example, the UUCG apical loop features a syn G that has an unusual C8 resonance that is ~7 ppm downfield shifted from the reference A-form helical chemical shifts (Dethoff, Petzold, et al., 2012). Other common motifs such as GNRA tetraloops can also be readily identified through a combination of the C8, C2, C1′ chemical shifts that remain consistent throughout these motifs.

3.5.2 Secondary Structure Prediction

The information regarding which residues undergo an exchange process and direction and magnitude of the ES change in chemical shift form a “chemical shift fingerprint”, which can be used to infer potential models for the ES structure. The chemical shift fingerprints can be used to infer which residues become more/less helical upon formation of the ES. For example, in the HIV-1 TAR ES1, the G-C8 shows clear signs of a syn G analogous to that seen in the UUCG apical loop, while A35 and many other apical loop residues show signs of moving away from non-helical sugar pucker in the GS (i.e. C2′-endo) toward more helical C3′-endo sugar pucker in ES1. In HIV-1 TAR ES2, the U28-N3 shows clear signs of a weakened hydrogen bond, as the A27-U38 moves towards a non-canonical U25-U38 bp.

RNA ESs often arise due to localized changes in secondary structure (Fig 2). For this reason, it is instructive to test the possibility that the ES represents an alternative secondary structure. A powerful approach for obtaining a list of candidate ES structures is to use commonly available secondary structure prediction programs such as Mfold (Zuker, 2003) or MC-Fold (Parisien et al., 2008) to examine higher energy secondary structures that can be adopted by an RNA (Fig 8A). These alternative secondary structures are examined to see if they can qualitatively explain the observed ES chemical shift fingerprints. For example, in the case of HIV-1 TAR, one finds that the second energetically most favorable structure features a more compact loop that can explain the chemical shift fingerprints measured for ES1 (Fig 8A) (Dethoff, Petzold, et al., 2012). A higher energy secondary structure that features remodeling of bulge, upper helix, and apical loop is also observed that can explain the more broad distribution exchange observed for ES2, and the unique chemical shift fingerprints (Lee et al., 2014). In general, a given secondary structure is interrogated to examine whether it addresses the following questions:

1. Does the alternative secondary structure result in changes in the environment of all residues showing signs of exchange broadening?

2. Does the alternative secondary structure preserve the environment of all residues showing no signs of exchange broadening?

3. Do the specific changes in structure and, specifically, transitions from helical to non-helical residues or inter-conversion of G-C to G-U bps agree with the specific ES chemical shifts?

Figure 8.

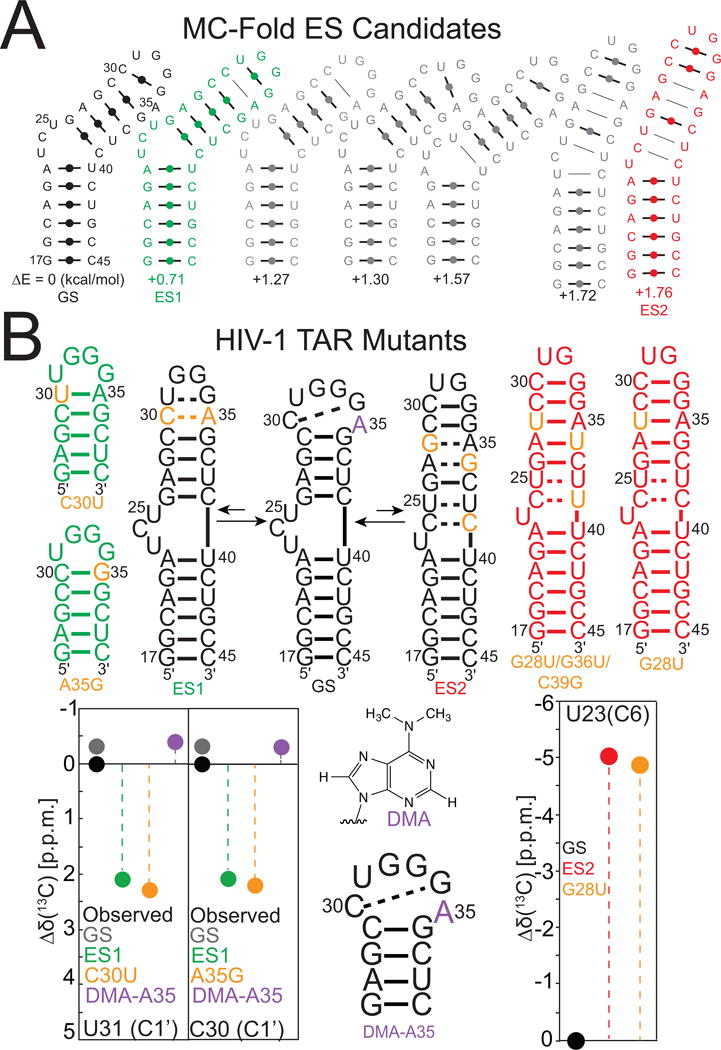
(A) Using secondary structure prediction to generate a list of candidate excited states. Shown are the seven lowest energy secondary structures with estimated energies referenced to the GS of HIV-1 TAR predicted from MC-Fold (Parisien & Major, 2008). The second and the seventh predicted secondary structures are ES1 (green) and ES2 (red), respectively as determined by R_1ρ and chemical shift finger prinitng. (B) Mutate and chemical shift fingerprinting analysis of RNA ESs. Shown are TAR mutants designed to stabilize ES1 (green), ES2 (red) or the GS (black) with residue color indicating substitution (orange), chemically modified substitution (purple). Chemical shift fingerprinting is shown as a comparison of chemical shifts determined by HSQC spectra of TAR mutants and R_1ρ relative to the chemical shift of HIV-1 TAR.

In this manner, a candidate ES model is generated and tested as described below.

3.6 Testing Model RNA ESs

3.6.1 Stabilizing GS and ES Using Mutations

A candidate ES model with alternative secondary structure is tested using mutations and single atom substitutions that are designed to stabilize the ES and in some cases the GS. Generally, it is possible to design substitution mutations that, for example, convert a non-canonical bp in the ES, such as an A-C bp, into a more stable canonical bp, such as G-C or A-U. This is shown in Figure 8B, where the HIV-1 TAR ES1 is stabilized using two mutations that convert A-C into WC bps. Likewise, mutating the A-G mismatch to a WC A-U can stabilize the TAR ES2. ESs with low energetic stability that have very low populations (<1%) can require more severe mutations in order to completely stabilize the ES. Indeed, complete stabilization of the low populated TAR ES2 (~ 0.4%) required a triple mutant (Fig 8B) (Lee, J., et al., 2014). An ES or GS can also be stabilized through deletion of a residue. For example, in HIV-1 TAR deletion of the three-nucleotide bulge stabilizes the GS of HIV-1 TAR so there is no exchange with ES2, but still allows exchange with ES1. Replacement of the apical loop to a stable UUCG loop stabilizes the GS completely so there is no exchange between either ES1 or ES2 (Fig 8B). All designed mutants are subjected to secondary structure prediction. Ideally, two or more ES-stabilizing mutations should be used independently, each targeting a different region of the RNA (see below). Each mutant is prepared and analyzed by NMR as described below. Because only 2D HSQC spectra are needed for chemical shift fingerprinting, unlabeled RNA samples can be used and obtained by in vitro transcription or by solid-phase chemical synthesis. 2D HSQC NMR measurements at natural abundance can be performed with optimal sensitivity using SOFAST-HMQC (Farjon et al., 2009; Sathyamoorthy et al., 2014) and BEST-TROSY (Ying et al., 2011) that yield higher sensitivity per unit time.

All mutants are subjected to the following analysis:

1. The secondary structure is determined using 2D NOESY NMR experiments. The goal is to determine whether the mutation stabilizes the proposed ES secondary structure. If the secondary structure does not match that predicted for the ES model, the mutant is not studied further, and the ES model is refined or a new mutant is selected to stabilize it.

2. The ¹³C and ¹⁵N chemical shifts are assigned and compared (see below for factors that influence this agreement) to the chemical shifts measured for the ES (or GS) in the wild-type construct. Examples of such chemical shift fingerprint comparisons are shown in Figure 8B.

3. For a concerted exchange directed to a single ES, any ES-stabilizing mutation should affect all of the resonances experiencing exchange, including those that may be distant from the site of mutation (Fig 8B). Moreover, these perturbations should be specifically directed toward the ES chemical shifts fingerprints determined by R_1ρ (Fig 8B).

4. All resonances showing no signs of chemical exchange should experience little chemical shift perturbation upon mutation (typically <1 ppm). At this point, it is possible to examine if a given resonance does not sense a given ES because of too small Δω. For example, the HIV-1 TAR ES2 stabilizing mutant (G28U) shows small Δω values for a number of resonances (U42-N3 and A22-C8) explaining why these residues show little to no sign of chemical exchange in the R_1ρ measurements (Lee et al., 2014).

ES-stabilized mutants are not expected to have chemical shifts that perfectly match those of the ES, since the mutation itself is expected to cause changes on the order of 1 ppm (Dethoff, Petzold, et al., 2012; Lee et al., 2014). The ES-stabilized mutant could also be in fast exchange with other higher energy conformations, and this could also impact the observed chemical shifts relative to the ES.

3.6.2 Stabilizing GS and ES Using Single-Atom Substitutions

The GS or ES can be stabilized by chemical modifications, including those that occur naturally. Many chemically modified RNA samples can be obtained commercially (e.g. ChemGenes, Glen Research, Berry and Associates). Typically the sample is lyophilized, to get rid of impurities, and buffer exchanged. Chemical modifications can be used to disrupt base pairing and favor “bulged out” or “flipped out” conformations. For example, N6-N6-dimethyl substituted adenine (DMA) was used to disrupt A-C type H-bonding in the TAR ES1 and to favor the GS in which the adenine is bulged out (Fig 8B) (Dethoff, Chugh, et al., 2012). Indeed, the modification leads to perturbations in the chemical shifts directed toward the GS (Fig 8B). In studies of DNA, ES that feature Hoogsteen (HG) base pairs have been stabilized in G-C and A-T base pairs through methylation of guanine and adenine N1 (Nikolova et al., 2011). Conversely, the single atom substitution converting purine N7 to a carbon (deaza-purine) was used to destabilize the HG bps and trap the WC GS (Nikolova et al., 2012).

3.6.3 Stabilizing GS and ES by Changing pH

In some cases, an ES may be associated with a protonation event. For example, many non-canonical A-C bps are protonated, and therefore their formation can be favored by lowering pH. The HIV-1 TAR ES1 features formation of an A⁺-C bp, which is absent in the GS, where it is possible lowering the pH will favor the ES over the GS. Indeed, one finds decreasing the pH results in chemical shift perturbations directed toward the ES1, while increase the pH results in perturbations directed toward the GS. In addition, decreasing/increasing the pH results in an increase/decrease in the HIV-1 TAR ES1 population. In general, changing the pH is a powerful approach to obtain insights into any ES that may involve protonation or deprotonation.