Structure of Particle Networks in Capillary Suspensions with Wetting and Nonwetting Fluids

Abstract

The mechanical properties of a suspension can be dramatically altered by adding a small amount of a secondary fluid that is immiscible with the bulk phase. The substantial changes in the strength of these capillary suspensions arise due to the capillary force inducing a percolating particle network. Spatial information on the structure of the particle networks is obtained using confocal microscopy. It is possible, for the first time, to visualize the different types of percolating structures of capillary suspensions in situ. These capillary networks are unique from other types of particulate networks due to the nature of the capillary attraction. We investigate the influence of the three-phase contact angle on the structure of an oil-based capillary suspension with silica microspheres. Contact angles smaller than 90° lead to pendular networks of particles connected with single capillary bridges or clusters comparable to the funicular state in wet granular matter, whereas a different clustered structure, the capillary state, forms for angles larger than 90°. Particle pair distribution functions are obtained by image analysis, which demonstrate differences in the network microstructures. When porous particles are used, the pendular conformation also appears for apparent contact angles larger than 90°. The complex shear modulus can be correlated to these microstructural changes. When the percolating structure is formed, the complex shear modulus increases by nearly three decades. Pendular bridges lead to stronger networks than the capillary state network conformations, but the capillary state clusters are nevertheless much stronger than pure suspensions without the added liquid.

1. Introduction

Capillary suspensions are particle suspensions with a small amount of added secondary fluid that is immiscible with the bulk phase.¹ The added fluid can cause the creation of a sample-spanning particle network, leading to dramatic alterations of the suspension rheology and stability.¹⁻⁸ This effect can be used as a simple option for tuning the flow behavior of suspensions, which would otherwise require the addition of binding agents, surfactants, or other additives.⁹ Capillary suspensions can be used for various applications, such as the preparation of novel food products with reduced fat content and improved temperature stability,⁶ precursors for ceramic or glass filters with high porosity and simultaneously small pore size,¹⁰⁻¹² improved polymer blends,^5,13,14 and slurries for printable electronics with accurately molded edge shape and good charge-transfer properties.¹⁵ The modified rheological properties also can be detrimental, for example, when capillary suspensions appear as hydrate slurries formed from water in mineral oil emulsions during oil recovery.^16,17

Capillary suspensions can be formed either with the secondary phase wetting better than the bulk phase, which is referred to as the pendular state, or wetting less well in the capillary state. In both cases, a percolating particle network arises, leading to a transition in rheological properties due to network gelation.¹ In the pendular state, two neighboring particles are connected by a concave bridge, which induces a capillary force.⁴ In the capillary state, no binary bridges between two particles are formed. Instead, for energy reasons, small secondary phase droplets serve as a center for tetrahedral or octahedral particle clusters with small particle numbers, as was calculated numerically.¹⁸ The binary bridged particles of the pendular state or the small clusters of the capillary state serve as generic building blocks for the formation of sample-spanning networks. Network percolation with increasing amounts of secondary phase content in the capillary state was calculated numerically by Fortini.¹⁹ Experimental proof and visualization of this calculated structure had not yet been achieved prior to the present study.

Capillary suspensions are to some extent similar to well-studied wet granular matter.²⁰ However, there are some major differences between wet granular matter and capillary suspensions.^2,8,20 In capillary suspensions, the particles are typically much smaller than in granular matter and the density difference between the surrounding bulk phase and solid particles is reduced. These two factors can be readily seen in the difference in the Eötvös number (Eo, also called the Bond number) between the two systems, which relates the system’s surface tension forces to body forces. Wet granular matter typically has an Eötvös number smaller than unity (Eo ≈ 0.01 to 0.1) but much larger than for capillary suspensions (Eo ≈ 10^–5 to 10^–6) using typical values for each system. This means that capillary wetting is of more relative importance in capillary suspensions. These differences in the Eötvös numbers are readily apparent in the differences in the solid volume fraction, which is typically much lower for capillary suspensions (as low as 10%) and adjustable over a wide range.^1,9 Additionally, wet granular media is usually studied in air rather than in liquid. Thus, viscous forces transmitted via the bulk fluid can lead to differences during mixing and in the rheological response of capillary suspensions, while these forces are absent when air is the bulk phase. However, for very high solid volume fractions approaching close packing, capillary suspensions also show granular-like behavior due to a restriction of relative particle motion.^2,8

When preparing capillary suspensions, proper mixing to achieve good droplet breakup of the second fluid is important,⁵ as is the deliberate choice of volume ratios of the solid and liquid phases. In particular, the secondary liquid volume has to be small compared to the bulk liquid volume and droplet sizes must be comparable to the particle size.^2,13 Apart from mixing conditions and dispersed phase and secondary fluid volume fractions, the structure of capillary suspensions and their strength depend on the particle radius R, the interfacial tension Γ between the fluids, and the wetting properties of both liquids.⁹ These wetting properties result in the three-phase contact angle θ that the liquid–liquid interface forms with respect to the solid surface, as described by the Young equation.²¹ The capillary force F_c in a concave bridge of volume V between two equally sized spherical particles with separation h can be computed either by solving the Young–Laplace equation or by assuming a certain bridge shape. Typically, the capillary force is orders of magnitude higher than the van der Waals force² as well as gravity.²⁰ This leads to increased cohesion between particles in capillary suspensions compared to suspensions without added secondary fluid, resulting in the observed marked changes in flow behavior and prevented particle sedimentation.⁶ For a toroidal bridge shape and a small bridge volume, the force in good approximation is given by

1

with f (V, h) = 1 for spheres in contact.^22,23 The toroidal approximation leads to errors smaller than 10% for concave bridges.²⁴ The equations for the force may, with slight modification, also be applied for spheres of different sizes using a Derjaguin approximation.²² Furthermore, different particle shapes or surface roughness values can be introduced into the calculations.^25,26 The capillary force of single bridges can be related to the macroscopic stress of a percolated capillary suspension network. For equally sized particles in direct contact and using eq 1 for the capillary force calculation, the relationship between capillary force and yield stress σ_y is given by

2

with f (ϕ) being a function of the particle volume fraction.^2,27 This function contains information about the network structure such as the coordination number, i.e., the number of bridges per particle, which strongly influences the network strength.^23,27

When the secondary fluid wets better than the bulk fluid, the three-phase contact angle θ is smaller than 90°. For small bridge volumes, this leads to a concave bridge shape and therefore to the pendular state. For contact angles larger than 90°, the bridge shape would geometrically have to be convex, leading to a positive Laplace pressure and particle repulsion, especially at short particle distances.²⁸ Therefore, the transition between the pendular and capillary states is expected at approximately 90°. For larger bridge volumes, it should take place at smaller contact angles due to the curvature of the particle surface.²⁹ While eq 2 predicts the strength of capillary suspensions in the pendular state to scale with cos θ, the contact angle dependence in the capillary state is uncertain. Simulations in this case indeed give some hints as to the dependence,¹⁸ but these are experimentally unproven. As the percolated network is not directly based on capillary forces between binary sphere contacts but on interconnected energetically favored clusters of several particles, eqs 1 and 2 cannot be used to predict the strength of such capillary state suspensions correctly, particularly since cos θ is negative for θ > 90°. Additionally, eq 1 was validated only up to 40° in the original publication.²² Thus, for pendular state suspensions with contact angles larger than 40°, the use of this equation is not thoroughly warranted.

In recent work, the strength of capillary suspensions has been characterized by rheological measurements.^1−7,9,10 These papers show the impact of the secondary fluid on the flow behavior. A marked increase in the yield stress occurs when the particle network is formed. The low-frequency complex shear modulus |G*| shows the same increasing trend due to the addition of the secondary fluid.¹ Direct observation of the samples is necessary to elucidate the underlying structure and fully understand the rheological findings. In the present work, this task is accomplished using confocal microscopy, which is a powerful method for the visualization of three-dimensional sample structures in situ.³⁰ If the refractive index of the sample is matched, then spatial imaging deep within the sample is possible. By using a Crocker–Grier algorithm³¹ which had been further improved by Weeks,³² it is possible to determine the positions of all of the particles which can be used to determine the fractal dimension D_f of particulate gels by direct evaluation of the particle pair distribution function.³³

Recently, several confocal studies on different ternary solid–liquid–liquid systems have been performed. Gögelein et al. imaged the buildup of capillary bridges in wet granular media.³⁴ Lee et al. clarified the structure of colloidal gels that arise due to the bridging of Pickering emulsion droplets and compared this gelled structure to van der Waals colloidal gels.³⁵ Leunissen et al. examined Pickering emulsions by means of dyeing the particles and the droplet phase with two fluorescent dyes with different emission wavelengths while leaving the bulk phase undyed.³⁶ Also using two different dyes for particles and droplets, Wenzl studied the influence of shear and compression forces on particle clusters held together by a secondary fluid immersed in another bulk fluid.³⁷

In the present study, we examine how the three-phase contact angle affects the structure of capillary suspensions in both the pendular and capillary states. An index-matched model system of fluorescently dyed silica microspheres in oil is used, to which small amounts of aqueous glycerol are added that contain another fluorescent dye. For contact angle variations, the silica surface has been chemically modified while leaving the liquids unchanged. The modification and dyeing of particles are detailed in the Materials and Methods section of this paper, as are the methods used for sample preparation and measurement data acquisition. Three-dimensional confocal images of the resulting capillary suspensions are recorded, and particle pair correlation functions of the percolating networks are calculated (section 3.1). This allows, for the first time, the pendular and capillary states to be imaged directly inside the sample. The influence of particle porosity on the structure has also been investigated by different particle treatments (section 3.2). The observed structure is compared to rheological measurements, which provide insight into the network strength (section 3.3).

2. Materials and Methods

2.1. Materials

The index-matched capillary suspensions were prepared using silica microspheres in an oil mixture with added aqueous glycerol. As the solid phase, we used monomodal silica spheres (Kromasil 10-7-SIL, batch no. 9043, Akzo Nobel, Bohus, Sweden; purchased from MZ-Analysentechnik GmbH, Mainz, Germany) with a mean particle size of d_50,3 = 6.40 ± 0.02 μm and a polydispersity of (d_90,3 – d_10,3)/d_50,3 = 0.697 ± 0.005. The nanoporous particles were fluorescently dyed with rhodamine B isothyocyanate (Sigma-Aldrich, Steinheim, Germany) and chemically modified before sample preparation as outlined in section 2.2. The refractive index of the particles after the reaction was 1.455 ± 0.006. The procedure used to determine this refractive index is described in section 1.4 of the Supporting Information.

The ratio of the components of the oil as well as the water phase was chosen to fit the refractive index of the chemically modified silica particles. Index matching is necessary to obtain high-quality confocal images. A mixture of 1,2-cyclohexane dicarboxylic acid diisononyl ester (refractive index n = 1.463, Hexamoll DINCH, BASF, Ludwigshafen, Germany) and n-dodecane (n = 1.421, Alfa Aesar, Karlsruhe, Germany) was used as the oil phase. The proper Hexamoll to dodecane volume ratio for index matching (n = 1.455) was found to be 83.8/16.2. Both oil phase components are fully miscible, as was confirmed by detecting no emulsion drops when the mixture is observed with bright-field light microscopy. Additionally, no phase separation of the oil mixture is noted after 6 months in a closed vessel. The aqueous phase consisted of a mixture of glycerol (n = 1.474, purity >99.5%, Carl Roth, Karlsruhe, Germany) and ultrapure water (n = 1.333) with a glycerol/water weight ratio of 86.4/13.6. PromoFluor-488 premium carboxylic acid (PromoKine, Heidelberg, Germany) was added as a fluorescent dye to the aqueous phase. This dye is insoluble in the oil phase and does not adsorb to the particle surface. Hexamoll is immiscible with the aqueos glycerol but tends to adsorb to the interface with the aqueous phase as it is a slightly polar ester. A characterization of the interfacial adsorption is given in section 2 of the Supporting Information. All chemicals were used as delivered from the suppliers.

2.2. Chemical Modification of Silica Particles

The silica spheres are highly porous as delivered, with a pore volume of 0.9 mL/g, consisting of greater than 97% open pores and a mean pore size of 11 nm. This porosity was utilized for fluorescently dyeing not just the surface but also the interior of the particles. A modified Stöber synthesis was used to covalently bind the dye to the particles.³⁸⁻⁴⁰ A detailed description of the synthesis is given in the Supporting Information, section 1.1. Wenzl et al. recently used a very similar procedure to prepare the same Kromasil silica microspheres for their confocal study.⁴¹ The modified Stöber synthesis did not lead to a change in particle shape, as all of the particles are still perfectly spherical, as shown in Supporting Information Figure S1.a. The dyeing process does not lead to a significant change in particle size, with the mean particle diameter being d_50,3 = 6.43 ± 0.03 μm after treatment (Supporting Information Figure S2). BET (Brunauer–Emmett–Teller adsorption method) surface measurements show a reduction from 295 to 249 m²/g. Therefore, although the porosity of the dyed particles has decreased, it remains very high.

Additional reaction steps were completed using the dyed porous silica particles to further modify the particle surface. An overview of the prepared particle types used in this study is shown in the Supporting Information in Table S1, including both porous and nonporous particles. To produce nonporous particles, the modified Stöber reaction was repeated using small numbers of dyed particles, with some differences in the reaction scheme: no more coupled dye was added, and higher concentrations of tetraethyl orthosilicate (TEOS) were used (3 mL TEOS per gram of dyed silica spheres). The measured particle density remained nearly unchanged during all of the reactions at 2.04 ± 0.07 g/mL. Particle densities have been measured at 20 °C using helium gas pycnometry (MultiVolume Pycnometer 1305, Micromeritics Instrument Corporation, Norcross, GA, USA), and the results were cross-checked by liquid pycnometry in water.

To change the contact angle, the silica surface of either porous or nonporous particles was treated with trimethyl chlorosilane (TMCS, Alfa Aesar, Karlsruhe, Germany). When exposed to TMCS, the −OH groups on the silica surface are replaced by trimethylsilyl groups (−Si–(CH₃)₃), making the particle surface more hydrophobic.⁴² A detailed description of the completed method is given in section 1.3 of the Supporting Information.

2.3. Sample Preparation

In this study, the oil phase (mixture of Hexamoll DINCH and n-dodecane) was used as a bulk fluid, and the fluorescently dyed aqueous glycerol as a secondary fluid. The particle dispersed phase volume fraction ϕ_solid = V_solid/V_total is defined as the particle volume divided by the total sample volume. The secondary phase volume fraction ϕ_sec = V_secondary/V_total is analogously defined as the volume of the secondary phase divided by the total sample volume. Therefore, the bulk phase volume fraction ϕ_b is given by ϕ_b = 1 – (ϕ_solid + ϕ_sec). The volume ratios were kept constant for all of the prepared capillary suspension samples at a secondary fluid volume of ϕ_sec = 0.0225 and a particle dispersed phase volume of ϕ_solid = 0.25. Additionally, some pure suspensions without secondary fluid were prepared, i.e., ϕ_sec = 0. One should be aware that the particle volume V_solid is defined as the actual rather than the effective solid volume V_eff using the particle density, where the density had been measured to be 2.04 g/mL. This value has been used here for the porous as well as the nonporous particles. Only the solid silica parts of the particles are treated as being part of V_solid as only these have a density of 2.04 g/mL. The volume of the internal pores V_pore inside the particles is not part of the solid particle volume. The rheology of the samples is governed by the apparent particle volume V_eff = V_solid + V_pore. While the effective solid volume fraction ϕ_solid,eff = V_eff/V_total for nonporous particles with V_pore = 0 equals ϕ_{solid,eff,nonporous} = ϕ_solid = 0.25, it is significantly higher than 0.25 for the porous particles with V_pore > 0 and was measured by imaging to be close to ϕ_{solid,eff,porous} = 0.55 as discussed later in section 3.2.

For sample preparation, an ultrasound sonifier (Digital Sonifier model 250, Branson Ultrasonics Corporation, Danbury, CT, USA) with an ultrasonic horn of 12.5 mm diameter and a maximum available output power of 200 W was used. The bulk and secondary phases were placed together into a small vessel (18 mm inner diameter), and the fluids were emulsified at an amplitude of 35% for 30 s. For the pure suspension preparation, the same energy input was also applied to the bulk phase to ensure that any temperature changes were equivalent in each preparation. After this first step, silica particles were stirred into the fluid with a spatula, and another ultrasonic mixing step was applied to the sample using an amplitude of 10% for another 30 s. The measured overall sample temperature after the second sonication was approximately 40 to 50 °C; however, the local temperature near the ultrasonic horn was probably much higher. A small total sample volume of 0.75 mL was used for all preparations to ensure homogeneity as ultrasonic emulsification and mixing decrease sharply away from the tip of the horn.⁴³

2.4. Confocal Microscopy and Image Analysis

The confocal images were taken with a Leica TCS SP8 inverted confocal laser scanning microscope (Leica Microsystems, Mannheim, Germany). The microscope is equipped with two lasers with wavelengths of 488 and 552 nm. The PromoFluor-488 premium carboxylic dye in the capillary suspension secondary phase is excited by the 488 nm laser, and the rhodamine B isothiocyanate in the particles is excited by the 552 nm laser. The microscope is equipped with a spectral detector allowing the detected wavelength range to be adjusted in order to minimize crosstalk between the emission signals of the dyes in the two different detection channels. The secondary phase dye emission was detected in a wavelength range of 495–520 nm, and the particles at 650–700 nm. A glycerol immersion objective with a correction collar with a numerical aperture of 1.3 and 63× magnification (HC PL APO 63×/1.30 GLYC CORR CS2, Leica Microsystems, Mannheim, Germany) was used, as this matches the sample refractive index of 1.455 best and therefore should lead to negligibly small optical distortions.⁴⁴ Additionally, the discrepancy between the covered distance of the vertically moving objective and the focal point was negligible (lower than 0.5%), which would have been much higher and would have needed later correction in the image data if the immersion medium would not have been sufficiently index matched to the sample.⁴⁵ The sample was deposited onto a coverslip (170 μm thickness), which was then placed on the inverted confocal microscope for 3D image acquisition.

Image analysis was completed using MATLAB. Particle localization was based on a modification of the 2D particle tracking algorithm of Crocker and Grier,³¹ which had been further developed for 3D detection by Weeks.^32,46 As the particles in this study have a broad size distribution and some confocal images were too noisy (taking the much larger pixel number per particle into account, compared to that in the original Crocker and Grier study), some more elaborate processing steps were necessary. A detailed description of these steps for particle localization and the determination of particle pair distribution functions is given in section 3.1 of the Supporting Information.

2.5. Contact Angle Determination

The dependence of the three-phase contact angle on the surface coverage of hydrophobic groups and therefore on the TMCS concentration during particle hydrophobization is highly nonlinear.⁴² This fact together with the variable reaction kinetics makes contact angle measurements of each surface-treated particle type necessary. A very small quantity (≲0.5 mg) of dyed particles was distributed in both 10 μL of the oil phase as well as in 10 μL of the aqueous glycerol phase. These sparse dispersions were brought into contact in a custom-built microchannel on top of a microscope coverslip and were allowed to rest for at least 10 min to reach an equilibrium state. Many particles migrated to the fluid interface during this period. The coverslip with the sample was placed on top of the confocal microscope, and 3D confocal pictures of individual particles sitting in the interface were taken. The 3D images were adjusted to show a 2D projection directly perpendicular to the interface (example image in Figure 1). Three-phase contact angle θ was calculated directly via the geometry of a circular segment due to the spherical particle shape. The contact angle is always defined as the angle that the secondary phase makes with respect to the solid surface. For every particle type, the contact angle data is based on at least three observed particles at different positions on the interface. The values determined are listed in Supporting Information Table S1.

Figure 1.

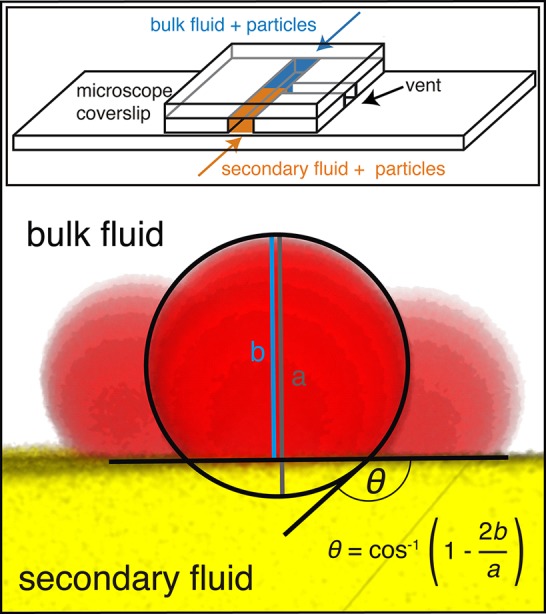
Determination of contact angle θ. The main figure shows an example 2D projection of a confocal 3D image of single particles (red) in the interface between the bulk (uncolored) and secondary (yellow) fluid. The circle and lines are added for better visualization of the geometry. The inset shows a schematic drawing of the custom-built microchannel on the microscope coverslip.

2.6. Rheological Measurements

The rheological measurements were carried out with a stress-controlled rheometer (Physica MCR 501, Anton Paar GmbH, Filderstadt, Germany) using a plate–plate geometry with 8 mm plate diameter and a gap width of 0.5 mm. As the plates employed were smooth, only oscillatory measurements were conducted to minimize the influence of wall slip, which should certainly be expected in highly filled suspension systems with oil as the bulk phase.⁴⁷ Oscillatory strain-sweep measurements were completed at a constant angular frequency of 10 rad·s^–1. Frequency-sweep measurements were made in a frequency range of 100–0.1 rad·s^–1 at a strain amplitude of 0.01%, which was within the linear viscoelastic domain for all samples. All measurements were conducted at 20 °C.

3. Results and Discussion

3.1. Structure of Systems with Nonporous Particles

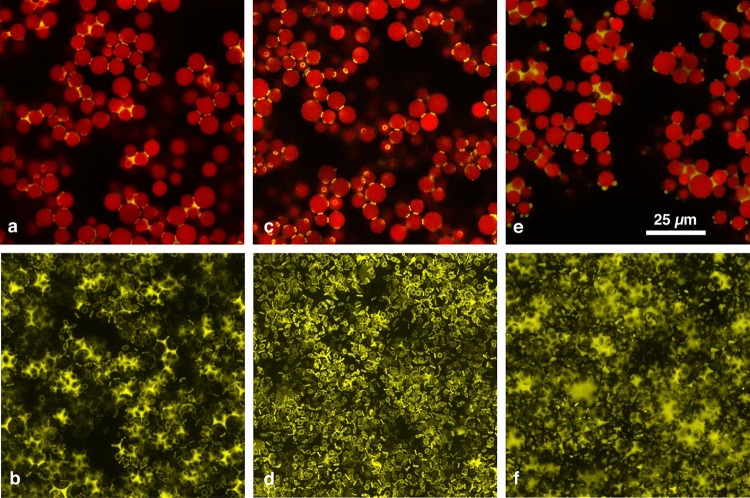
In the present study, three different treatments of nonporous silica particles have been used to produce capillary suspensions. These particles have three-phase contact angles of 40°, 61°, and 94°. Confocal images of capillary suspensions prepared with these three particle types are shown in Figure 2. In the top row (Figure 2a,c,e) a single x–y slice of the three-dimensional image is shown. Both detection channels of the confocal microscope have been overlaid so that the positions of the dyed particles (shown in red) and the dyed secondary fluid (shown in yellow) can be seen simultaneously. In the bottom row (Figure 2b,d,f), only the detected secondary phase is depicted to further clarify the sample structure. These images of the secondary fluid are projections of the 3D image along the vertical z image axis, containing all of the secondary fluid detected in the corresponding part of the 3D image, which allows the distribution and shape of the separate secondary phase droplets to be visualized. Three-dimensional images of both detection channels overlaid, reconstructed with ImageJ, are shown in Supporting Information Figure S4. Additionally, videos that further clarify the 3D structure are provided in the Supporting Information.

Figure 2.

Confocal images of capillary suspensions with nonporous particles and contact angles of 40° (a, b), 61° (c, d), and 94° (e, f). The scale bar shown in (e) is valid for all six images. The top row shows example 2D slices with a size of 102 × 102 μm². The particles are shown in red and the second fluid is shown in yellow, and black regions belong to the undyed bulk fluid. The bottom-row images show projections of the detected second fluid from 3D image stacks, which have a depth of 100 μm perpendicular to the image plane.

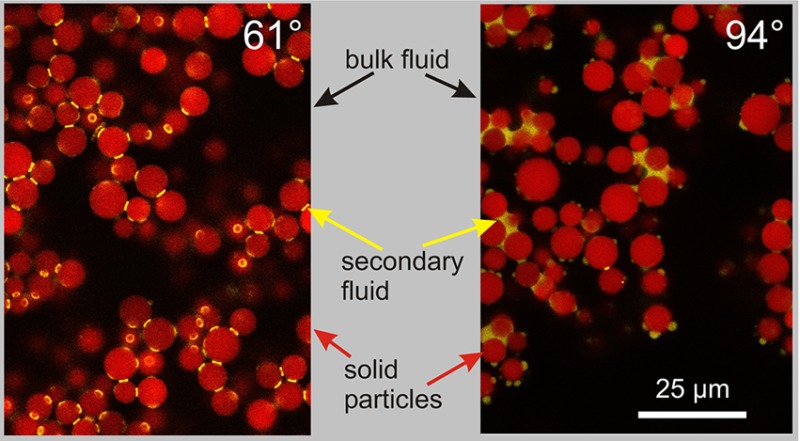
For the sample with a contact angle of 61°, a network structure induced by single pendular bridges between the spherical silica particles is evident. There are neither any particle clusters visible nor large secondary phase droplets. The 2D projection of the spatially distributed secondary phase (Figure 2d) shows that the structure indeed arises from binary bridges with a toroidal shape, which also gives a clear hint that the bridged particles have zero or close to zero separation. This further indicates that this structure is induced by strong attractive capillary forces. Network percolation can be seen in the 3D reconstructed image (Figure S4b). This confocal image set is the first direct three-dimensional visualization of the pendular state in capillary suspensions. Previous images of capillary suspensions either illustrated some individual bridges between very few particles in diluted samples¹ or could show only capillary suspension sample surfaces by scanning electron microscopy after immobilizing the sample system, achieved by solidification of the secondary phase^5,7 or sintering of the particles,^11,12 both of which can lead to structural changes in the sample. These studies were sufficient to deduce and verify the existence of the pendular state in capillary suspensions for contact angles smaller than 90°, but none of the studies could provide information on the network in the wet sample.

There are many toroidal bridges visible in the 40° contact angle sample (Figure 2a,b), which is expected for such a low contact angle. However, there are also numerous clustered structures where one larger secondary phase droplet binds three or more particles. This clustered structure is comparable to the funicular state described in wet granular matter.^13,23,48,49 The funicular state, in general, is very similar to the pendular state as both appear for low contact angles and their main difference lies in the secondary phase volume. Funicular state clusters appear when the volume of neighboring pendular bridges becomes too large to prevent aggregation.⁴⁸ Adjacent bridges coalesce upon contact, leading first to particle trimers and later to larger agglomerated structures when the secondary phase volume is further increased.

The transition from the pendular to the funicular state normally occurs when the secondary phase volume fraction ϕ_sec is increased,^8,13,48 but as the 40° and 61° samples both had ϕ_sec = 0.0225, there has to be another reason for this transition. The contact angle influences the bridge shape and can, even for a constant volume, geometrically facilitate bridge coalescence. Heidlebaugh et al. proposed that the transition occurs when a third particle contacts an existing binary bridge.¹³ A different criterion for the pendular–funicular transition was suggested by Flemmer,⁴⁸ who stated that coalescence between two adjacent bridges leads to the funicular conformation. The critical volume V_sec,crit of a secondary fluid bridge in this case is reached when the three-phase contact lines of two bridges touch. The increased volume of the droplets connecting multiple particles suggests that the Flemmer criterion is more appropriate. In a triangular particle configuration, the particle contact points have an angular distance of 60° leading to the pendular–funicular transition with the Flemmer criterion as soon as the half-filling angle of adjacent bridges reaches 30°;⁴⁹ see section 4 of the Supporting Information for details. Using a toroidal approximation to calculate the contact-angle-dependent bridge volume V_sec,crit of a bridge with a 30° half-filling angle²⁹ and the volume V_sphere of one particle, we computed a volume ratio of V_sec,crit/V_sphere = 0.021 ± 0.001 for a contact angle of 40° in the sample system used here whereas it is V_sec,crit/V_sphere = 0.025 ± 0.001 in the 61° system. Thus, in the 40° system about 15% less secondary fluid volume is necessary for the pendular–funicular transition than in the 61° system, assuming the coordination number is the same in both cases. The actual secondary phase volume used in this study is larger than the necessary critical transition volume for the 40° sample, but less than this critical volume for the 61° sample. As the transition is dependent on the coordination number, this value should also be subsequently explored.

The network structure of the 94° sample (Figure 2e,f) clearly differs from that of the 61° sample. The secondary fluid is mainly located between clusters consisting of three or more particles. Presumably, the secondary fluid induces small particle number clusters around these secondary phase droplets. The confocal image proves the existence of the capillary state for this sample. Its existence in real sample systems before was inferred only from simulations and rheological measurements.^1,18,19 There are still some binary bridges visible, which are in principle not expected for θ > 90°, but as the mean contact angle of 94° is not too far above the expected transition value of 90° from the pendular to the capillary state, this could be caused by inhomogeneous particle surface reactions during particle modification, with some less hydrophobic particles still exhibiting contact angles smaller than 90°. Recently, a possible standard deviation of 19.3° in the three-phase contact angle distribution of interfacially adsorbed chemically homogeneous spherical particles was experimentally found by Snoeyink et al., which strongly supports this hypothesis.⁵⁰

Figure 3 shows some magnified details of the reconstructed 3D images (Supporting Information Figure S3). In the capillary state sample (Figure 3c), there are many separate droplets of secondary fluid that interact with only single particles, with some particles even showing several such droplets. These singly connected droplets may be caused by the rupture of clusters during the vigorous mixing required to form the capillary suspension. They do not contribute to the sample-spanning network and therefore have no influence on the material strength. In the pendular state samples (Figure 3a,b), no such singly connected droplets are visible, and the entire secondary fluid volume contributes to the particle network structure.

Figure 3.

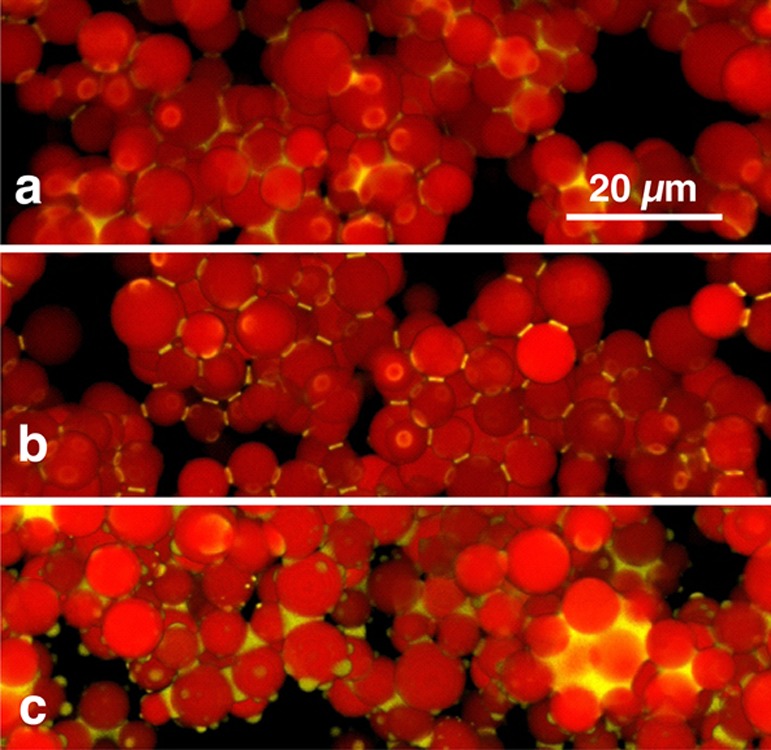
Detailed view showing parts of the reconstructed 3D network structure of capillary suspensions with nonporous particles with contact angles of 40° (a), 61° (b), and 94° (c). The scale bar is valid for all three images.

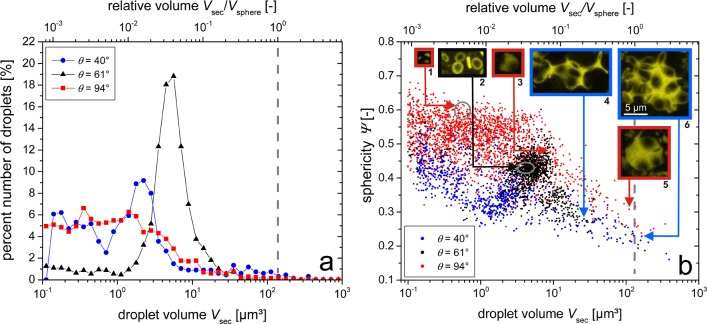
The qualitative differences among the three samples which can be seen in the confocal images of Figures 2 and 3 can also be quantified. The volume and surface of each of the secondary fluid droplets detected by the 495–520 nm channel of the confocal microscope have been determined using ImageJ.^51,52 The confocal images of the second fluid were made binary with missing voxels inside the droplets filled prior to calculations of the surface area and volume. The threshold used for binarization has some influence on the results. If the threshold is chosen to be too low, then noise in the images is incorrectly detected as small droplets and some separated adjacent droplets can be mistakenly detected as forming a single large connected droplet. Noise near single droplets can also result in the volume and surface area of these droplets being overestimated. If the threshold chosen is too high, then the droplet volumes are underestimated and the surface area is overestimated. Single droplets can also be computationally split into several separated small droplets (e.g., a dimer split into two pendular bridges or a single pendular bridge split into several parts). None of these effects can be completely avoided by choosing any single threshold value, but the effects can be minimized. The same intermediate threshold value of 30 related to an intensity value range of 0 to 255 has been used for all samples to ensure the comparability of results. The detection of larger droplets seems to be quite accurate for the chosen threshold value: errors in droplet connectedness were minimized and the droplet smoothness was maximized (minimizing the surface area). Nevertheless, there remain small droplets visible in the data. While a portion of these droplets may be linked to the wetting of asperities, especially for smaller contact angles, many more, especially the smallest of these droplets, should be attributed to misdetections mainly caused by the partitioning of larger bridges. Therefore, we chose to eliminate any droplets smaller than 0.1 μm³ (close to the smallest resolution of the microscope which is ∼0.02 μm³) and do not rely on these small droplets when comparing the samples. The number of detected droplets was greater than 600 for all of the samples. A histogram of the droplet numbers, evaluated from the determined droplet volume data, is shown in Figure 4a. The Wadell sphericity Ψ, which is defined as

3

with V_sec and A_sec representing the volume and surface area of the droplet, respectively, was calculated for each droplet. A perfectly spherical droplet has a sphericity of Ψ = 1, while nonspherical droplets have values of less than unity. The calculated sphericity, as a function of droplet volume, for each secondary fluid droplet in all three samples is shown in Figure 4b.

Figure 4.

Droplet number percent distribution (a) and Wadell sphericity Ψ (b) of the individual second fluid droplets with 40° (blue), 61° (black), and 94° (red). Both parameters are shown as a function of the droplet volume (bottom axis of abscissae) and as a function of the droplet to particle volume ratio V_sec/V_sphere (upper axis of abscissae). The dashed gray lines denote the mean volume of a single solid particle. The insets (1–6) in (b) show projections of example droplets from the 3D confocal images with volumes and sphericities as marked. Gray circles denote the regions containing all of the separate droplets of insets 1 and 2. The scale bar in inset 6 is valid for all of the droplet images.

The data in Figure 4b reveal three distinct populations among the pendular (61°), funicular (40°), and capillary state (94°) samples. The pendular state sample shows a narrow range of drop volumes between 2 and 10 μm³ with sphericities in the range of 0.35–0.50. This narrow distribution in volume is seen even better in the volume histogram (Figure 4a) with a very pronounced peak with few larger or smaller droplets. A total of 77% of the total number of drops, representing 64% of the total secondary fluid volume, falls within this range of 2–10 μm³. When compared to the mean volume V_sphere of the solid silica particles, most of the second fluid droplet volumes in the pendular state are around 2–5% of the particle volume. This is in good agreement with the maximum size ratio for binary bridge coalescence. In Figure 4b, inset 2 shows some of these binary bridges that fall into this volume and sphericity peak.

For both the funicular and capillary state samples, the volume distributions are much wider. The capillary state sample (94°) shows the most spherical droplets over the entire volume range. The large number of smaller droplets with V_sec < 2 μm³ (V_sec/V_sphere < 0.015) and sphericities of approximately 0.5–0.6 can be identified as singly connected droplets. In this sample, about 25 ± 10% of the droplets in the volume range below approximately 0.5 μm³, however, have to be considered to be misdetections from binarization, as determined by comparing 300 of these detections to the original 3D confocal image. Three correctly detected droplets are shown in inset 1 of Figure 4b. While these singly connected droplets account for 70% of the total number and 12% of the total second fluid volume, they cannot contribute to the network strength. The 94° capillary state sample also exhibits a population of larger bridging droplets, two examples of which are given in insets 3 and 5. The sphericity strongly decreases with increasing droplet size due to the increase in droplet surface area as the droplets fill the narrow voids between particles as particle clusters are built.

The funicular state sample (40°) also shows such large droplets, but their sphericity is even lower than in the capillary state sample, as such large droplets (inset images 4 and 6) are even less compact than their capillary state counterparts (inset image 5). Even though particle clusters are visible in both the capillary and funicular samples, the difference in the sphericity is most likely due to the different clustering mechanisms. Large particle clusters with single large droplets in the capillary state are energetically favorable but less so than for multiple, noninterconnected droplets, and such large droplets would not form close-packed particle clusters.¹⁸ Large funicular state clusters are expected to consist of one interconnected droplet with a compact particle configuration due to the attractive capillary force from the negative Laplace pressure.⁵³ Further proof of the capillary-force-induced interaction for the 40° sample can be found in Figure 4b in the clear peak at 2 μm³, implying that a large number of binary bridges also exist in this sample. Their slightly smaller volume compared to that of the pendular state bridges of the 61° sample can be explained by the pendular–funicular transition at lower volumes for this lower contact angle. A closer look at 230 droplets below 0.5 μm³ revealed that in this volume range only 35 ± 10% were correct detections, mostly denoting small wetted regions of particle surface asperities. The other 65 ± 10% are mostly, apart from a small amount of noise, incorrectly detected pendular bridges that have been separated into two or more smaller volumes due to the image binarization. In this funicular sample, the correctly detected binary bridges account for 42% of the total number of droplets but only 15% of the total second liquid volume. Larger clusters with a size greater than 10 μm³ (V_sec/V_sphere > 0.07) account for 83% of the liquid volume in the funicular sample.

The funicular sample with a 40° contact angle seemingly resembles the 94° capillary state sample, but this is misleading. Clustering through bridge coalescence in the 40° sample leads to a droplet whose interface toward the bulk fluid still has a concave curvature. The Laplace pressure inside such a droplet is negative, so these droplets still exhibit attractive capillary forces between the adjacent particles. This is not the case for the droplets in the capillary state seen at 94° due to their convex interface toward the bulk phase, leading to positive Laplace pressures. This leads to a loss of symmetry for small clusters, as shown in inset 3 in Figure 4b, or to a less compact particle arrangement around larger droplets (inset 5 in Figure 4b). Both of these effects lead to higher droplet sphericities compared to those for the funicular state and hint at key physical differences between these two states. In reality, the 40° funicular sample more closely resembles the 61° pendular state sample. Scheel et al.⁴⁹ showed for low contact angles that the interacting attractive forces among three particles are nearly equivalent, regardless of if there are three separate bridges or if there is only a central single concave droplet binding the three particles together. This finding also is valid for larger funicular clusters. That is, the force on each particle of the cluster is independent of the number of particles in the cluster.^23,49 This implies that a plateau in strength is reached as soon as the binary bridge pendular state transitions to the funicular state, a conclusion also supported by previous experiments that investigated the tensile strength of wet granular matter⁵⁴ and the yield stress of capillary suspensions.^7,11

Figure 5 shows the results of the computational image analysis of the spatial arrangement of solid particles in the three different network structures. Radial particle pair distribution functions g(r/R) are shown up to a distance of r/R = 7, where radial coordinate r is normalized by a single particle radius R.³³ The mean particle size R = d_50,3/2 = 3.21 μm has been used for calculation, thus neglecting the effects of the particle size distribution. Nevertheless, all three samples show typically shaped pair distribution functions with a large first peak at direct particle contact (r/R = 2) and a smaller peak slightly lower than r/R = 4 and approaching g(r/R) = 1 for large distances. As detailed at the end of this section, there remain open challenges in the determination of the radial pair distribution function. Thus, the data in Figure 5 should be treated as preliminary results, particularly for large r/R. However, this data suggests the usefulness of such computational analyses for further structural research on capillary suspensions. Keeping the limitations in mind, we hypothesize that structural differences between the samples can be deduced from pair correlation functions. Individual peak positions r/R and peak heights g(r/R) were determined from the discrete data points of the calculated pair distribution function, which had the highest g(r/R) values near the analyzed peak position. While the actual pair correlation function is not a discrete function, the data points can give a fair estimate of the peak positions and heights. Peak widths were not quantified but were examined qualitatively in comparison to the three different samples.

Figure 5.

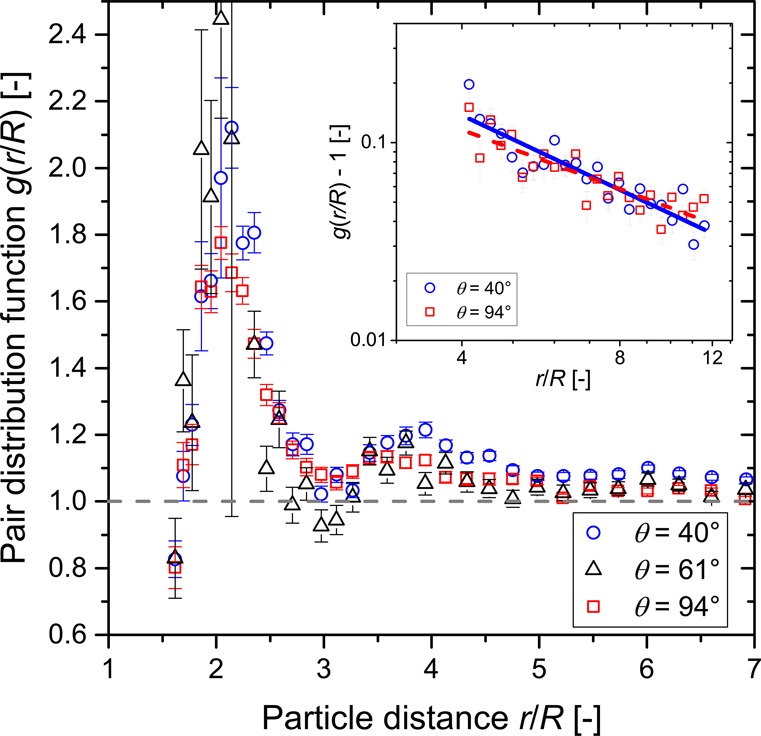
Pair distribution function g(r/R) of capillary suspensions with three-phase contact angle θ of 40° (blue circles), 61° (black triangles), and 94° (red rectangles) for small particle distances r/R < 7, where the radial coordinate r is normalized by the particle radius R. The dashed gray line denotes the asymptote g(r/R) = 1. The inset shows a double-logarithmic plot of the same data set (asymptote is subtracted) for 40° and 94° in an intermediate distance range between 4R and 12R. The solid blue line and the dashed red line are power law fits to the 40° and 94° data points, respectively.

For the 94° capillary state sample, both peaks in Figure 5 are more shallow and widened. The widening of the second peak with a maximum at ∼3.6R likely implies a landscape with larger and more varied clusters as had been shown by calculations of particle distances in different close-packed clusters;⁵⁵ see section 3.3 in the Supporting Information for more details. The 40° funicular-like sample also shows a widening with a significant shoulder at higher separations but with the peak maximum being around a separation of 4R. This implies that while a clustered structure still exists, these clusters are less compact than for the capillary state. The smaller peak width also implies that the clusters consist of fewer particles and have fewer conformations than in the capillary state sample, a conclusion which is substantiated by the direct images of the bridges shown in Figure 2b. The binary-bridged pendular 61° sample has a peak at ∼3.75R. While this may imply some clustering, which is unlikely given the trough around 3R, it more likely shows that the binary connections are quite flexible and the network is tortuous. At intermediate distances between 4R and 12R, shown as a double-logarithmic plot in the inset of Figure 5, the pair distribution function convergence toward g(r/R) = 1 can be described by power law behavior with exponents of −1.2 ± 0.1 for the 40° sample and −1.0 ± 0.1 for the 94° sample. Using the approach from Dinsmore et al.,³³ one is tempted to deduce fractal dimensions D_f of 1.8 ± 0.1 for the 40° sample and 2.0 ± 0.1 for the 94° sample, which then is another indication of the more compact clustering of the capillary state in comparison to the funicular-like cluster structure. However, due to the large standard errors one should be quite careful with this data. The covered distance range here is too short to pose thorough statements about sample fractality. Also, the total number of considered particles per sample (∼3100 for the 40° and 94° samples and ∼750 for the 61° sample) appears to be insufficient. The lower particle number considered in the 61° sample also manifests itself in the larger error bars and stronger scattering of data points of this sample. We cross checked pair distribution functions determined from images with both lower (∼750) and higher (∼3100) particle numbers for the 40 and 94° samples. The images resulted in very consistent shapes of the pair correlation function independent of the particle number at low r/R but much larger scattering and error bars for the images with lower particle numbers. Thus, the particle number (i.e., the size of the evaluated confocal images) should be further increased in subsequent studies to minimize the pronounced scattering and errors in the data. This should also reduce errors in the exponents shown in the inset diagram of Figure 5, leading to smoother shapes of the pair distribution functions and enabling a fit to larger distances >12R. Determinations of the dimensionality, however, may be further complicated by a transition in the growth of the capillary state clusters, as was shown by Fortini where small clusters were characterized by D_f = 1.8 and continuing growth, by D_f = 2.6.¹⁹ The impact of the particle size distribution also has to be taken into account.^41,56 While these points are beyond the scope of this study and should be investigated in future research, these first results show the general applicability and usefulness of such computational image analysis methods in gaining valuable insight into capillary suspension sample microstructures and in evaluating structural differences.

3.2. Structure of Systems with Porous Particles

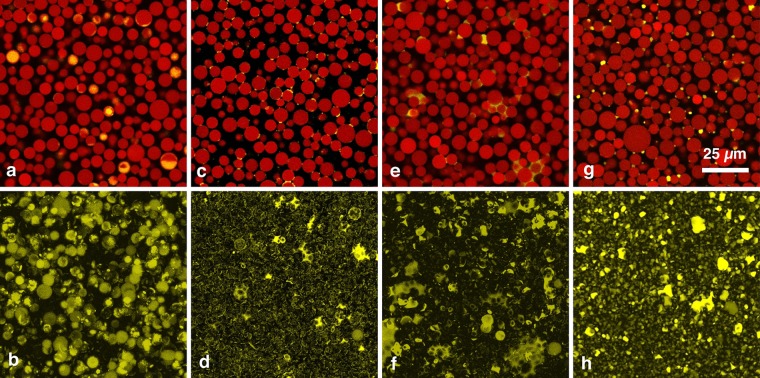
The use of porous particles can lead to pronounced changes in the observed behavior of capillary suspensions. Figure 6 shows confocal images of samples prepared with porous particles having four different apparent contact angles of 72°, 115°, 133°, and 147°. For particles with 72°, no sample spanning network is obtained. The added secondary phase is completely absorbed into the particle pores, as can be deduced from the overlay image (Figure 6a). The corresponding projection of the secondary phase (Figure 6b) further confirms these findings. The imbibition of the secondary fluid into the pores is determined by different parameters, the main one being the Laplace pressure which depends on the pore size and the contact angle of the wetting fluid with respect to the pore walls. Lower contact angles lead to faster absorption.⁵⁷ Therefore, the secondary phase will preferentially intrude into the pores as long as it is better wetting than the bulk phase. For apparent three-phase contact angles higher than 90°, the bulk phase imbibition is favored while the secondary phase stays at the particle surface. Accordingly, a pendular state particle network is achieved for an apparent contact angle of 115° (Figure 6c,d). The toroidal bridges are clearly visible and resemble the 61° nonporous sample described in the previous section. Most bridges are binary, thus the added secondary fluid volume at that contact angle is below the value that would cause the pendular–funicular transition. At 147° (Figure 6g,h), the capillary state is obtained. The droplets, which serve as the cluster center, appear more convex than those reported for the 94° nonporous sample. The transition from pendular to the capillary state using porous particles seems to occur at a value of around 133° (Figure 6e,f), which is surprising since it is expected to occur at 90° or slightly below in both systems. The particle porosity obviously has a strong influence on the contact angle dependence of capillary suspension structure formation, shifting the transition between the pendular and capillary configuration to apparently higher values.

Figure 6.

Confocal images of capillary suspensions with porous particles and contact angles of 72° (a, b), 115° (c, d), 133° (e, f), and 147° (g, h). The scale bar shown in (g) is valid for all eight images. The top row shows example 2D slices with a size of 102 × 102 μm². The particles are shown in red, the second fluid is shown in yellow, and black regions belong to the undyed bulk fluid. The bottom-row images show projections of the detected second fluid from 3D image stacks, which have a depth of 100 μm perpendicular to the image plane.

At contact angles of less than 90°, the secondary fluid is absorbed into the particle pores where it should no longer be available for interparticulate bridging. This would suggest a transition from nonbridged particles at θ < 90° to a capillary state system for θ > 90°. Therefore, the pendular state should not be accessible for a porous particle system without saturating the pores. This is clearly not the case, as the 115° samples clearly show a pendular state structure with concave binary bridges. For a sample system with different fluids but using the same silica particles with a slightly different treatment, Wenzl observed a similar behavior in wet granular media.³⁷ Wenzl reported that the three-phase contact angle measured for particles sitting on the surface of a large emulsion droplet of the secondary phase had a value of ∼130°, whereas the exact same sample system showed a three-phase contact angle of only ∼90° when the secondary phase droplet volume was much smaller than the particle volume and each droplet bridged only two particles.³⁷ This discrepancy of 40° in the contact angle likely occurred due to particle surface roughness. This roughness can lead to pronounced contact angle hysteresis,^21,58,59 particularly in combination with three-phase contact line pinning.⁶⁰ As we determined the contact angle values at flat interfaces, the real contact angle in the pendular bridged conformation visible in Figure 6c,d can be expected to actually have a much lower value than the measured 115°. The actual contact angle for each bridge cannot be measured accurately due to the inadequate resolution of the images. Nevertheless, the bridge shape looks concave rather than convex, implying that it actually is less than 90°. If, as in Wenzl’s work, a discrepancy of 40° exists here, then the real contact angle would be around 75° and the pendular state would indeed be expected. If the observed value marking the transition between the pendular and capillary states (θ = 133°) is also reduced by 40°, then a much more reasonable value close to 90° (θ = 93°) is calculated. While this contact angle discrepancy clearly depends on the use of porous particles, the exact cause nevertheless remains unclear. It also remains unclear as to whether the measured contact angles in the actual study are equilibrium contact angles or systematically higher angles measured inside the possible value range given by the hysteresis.

The differences in surface roughness are not the only factor that can influence the contact angle hysteresis. Chemical surface heterogeneities are also likely due to the variations in reaction kinetics during particle preparation. Some particles might be more hydrophobic than others, leading to an overall contact angle distribution in the sample, or there also could be chemical inhomogeneity on each particle surface. In the latter case, the heterogeneous surface wetting is described by the Cassie–Baxter model, which predicts an intermediate contact angle with hysteresis.^61,62 In the porous sample system, the surface heterogeneity is further intensified if the oil phase fills the pores at θ > 90°. The secondary phase must then form a partial interface with the oil phase at the pore apertures, leading to even more heterogeneous wetting. If these pores are partially filled with a single phase and the porous particle then migrates to the interface between both fluids, as in the contact angle measurement, then this might lead to a different contact angle if rewetting inside the pores is hindered compared to that in pores that are wet by both fluid phases simultaneously, as is the case when these experimental samples are prepared.

Because of the high particle porosity, the effective dispersed phase volume fraction ϕ_solid,eff, which determines the capillary suspension’s flow properties in the porous particle system, is much higher than the real solid volume of ϕ_solid = 0.25 used for sample preparation. By calculating the ratio of voxels containing an emitted rhodamine B signal to the total number of voxels of the image, we determined the effective dispersed volume ϕ_solid,eff for all of the porous systems to be between 0.53 and 0.57. As the particles as delivered by the supplier have a porosity of around 65% and the BET surface only decreased from 295 to 249 m²/g during dyeing, it is reasonable to assume a porosity greater than 50% for the dyed porous particles. The determined volume ϕ_solid,eff = 0.55 ± 0.02 indicates an average particle porosity of 55 ± 2% for the treated particles, which is in good agreement with the BET surface reduction.

3.3. Coupling Structure and Rheology

To couple the observed structural changes seen in the confocal images to the samples’ flow behavior, we made rheological measurements using the porous particle system. Figure 7 shows strain-sweep as well as frequency-sweep experimental data for two systems with ϕ_sec = 0.0225 and particles with contact angles of 38° and 117°. In both systems, G′ is nearly frequency-independent and much greater than G″, which is typical for a strongly gelled sample. In total, 10 samples with porous particles having different contact angles were examined. The two samples shown in Figure 7 had the maximum and minimum |G*| values of these samples, with all of the other intermediate samples also having a frequency-independent complex shear modulus. If we are to assume a power law dependence of the shear modulus on the frequency, |G*| ∝ ωⁿ, then exponent n is smaller than 0.08 in all cases. Therefore, the magnitude of the complex shear modulus 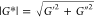in the linear viscoelastic regime, which here is approximately equal to G′, can be considered to be a single value, and the magnitude of the complex shear modulus at 10 rad·s^–1 and a strain amplitude of 0.01% is considered to be a function of only the contact angle in the following experiments.

Figure 7.

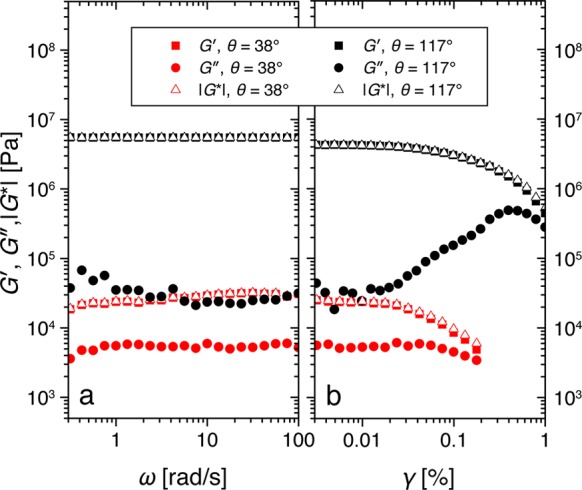
Storage modulus G′, loss modulus G″, and magnitude of the shear modulus |G*| as a function of (a) the oscillation angular frequency ω and (b) the strain amplitude γ for two capillary suspension samples using porous particles with contact angles of 38 (red symbols) and 117° (black symbols). The effective solid dispersed phase content was ϕ_solid,eff = 0.55 ± 0.02, and the second fluid content was ϕ_sec = 0.0225 for both samples.

The magnitude of the shear moduli for different capillary suspensions with ϕ_sec = 0.0225 and different contact angles is shown in Figure 8 with corresponding values for some of the samples without added secondary fluid. The samples with an added secondary phase show a very slight increase in |G*| between 38° and 72° from 1.9 × 10⁴ to 2.7 × 10⁴ Pa. Above 90°, the complex shear modulus increases by more than two decades to 4.6 × 10⁶ Pa, where it remains nearly constant for contact angles between 109° and 133°. At contact angles above 133°, |G*| decreases again, dropping by one decade to 5.4 × 10⁵ Pa at 147°. It is obvious that this strong nonmonotonic dependence of the modulus on the contact angle, and especially the large increase at 90°, for these capillary suspension samples (red circles) arises from the addition of small amounts of secondary fluid when compared to the pure suspension values (blue rectangles). The secondary fluid clearly leads to an increased network stability even though the samples already form gels without the added second fluid.

Figure 8.

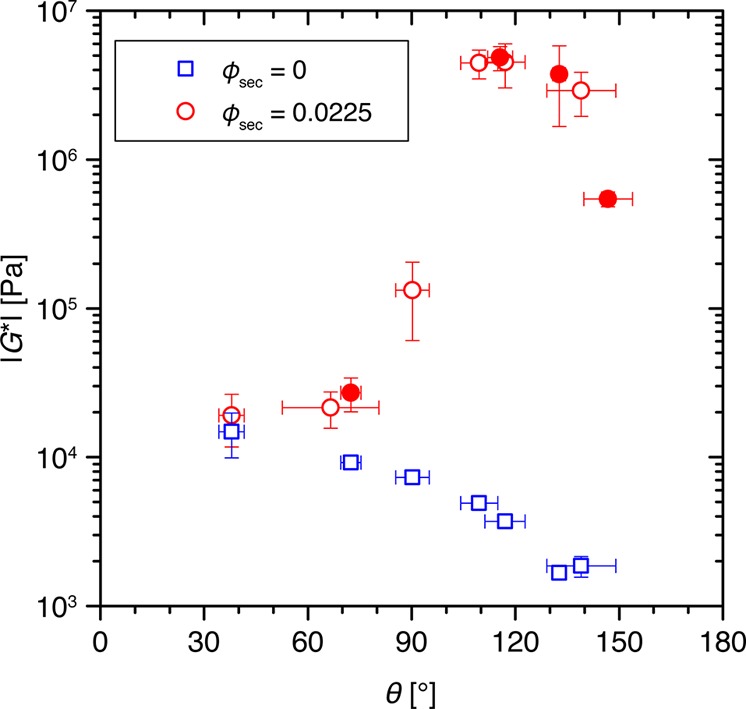
Dependence of the complex shear modulus magnitude |G*| (at 10 rad·s^–1 and 0.01% strain amplitude) on the three-phase contact angle θ for capillary suspensions using porous particles at ϕ_sec = 0.0225 (red circles) and 0 (blue rectangles). Data points with corresponding confocal images shown in Figure 6 are denoted using filled symbols. The effective solid dispersed phase content was ϕ_solid,eff = 0.55 ± 0.02 for all of the samples. Pure suspension data points (ϕ_sec = 0) are shown as a function of the three-phase contact angle corresponding to the same surface treatment.

For the suspensions without secondary fluid prepared from particles with surface treatments identical to those of their corresponding capillary suspensions, the complex shear modulus decreases monotonically with increasing contact angle. The complex shear modulus decreases by nearly one decade from 1.5 × 10⁴ Pa for the hydrophilic particles (38° contact angle) to 1.9 × 10³ Pa for the sample with a contact angle of 139°. This reduction occurs as a result of weakening particle interactions. Similar behavior has been demonstrated previously for other systems.^63,64 It is worth noting that, when compared to the capillary suspension samples, the shear moduli in the pure suspensions (ϕ_sec = 0) have a stronger frequency dependence with exponent n between 0.16 and 0.27. This is nevertheless quite weak such that only a single |G*| value obtained at 10 rad·s^–1 and 0.01% is shown.

The dependence of the shear modulus on contact angle in the capillary suspensions can be explained by comparing the rheological data to the confocal images as discussed in the previous section. The four samples imaged in Figure 6 are highlighted using filled circles in Figure 8. For the 72° sample, the complex shear modulus is only slightly higher than the corresponding value for the sample without the secondary fluid. In the images, all of the fluid visible is inside the particle pores where it cannot form capillary bridges and therefore does not lead to a significant increase in network strength. As there is some increase in |G*| compared to the pure suspension as the contact angle approaches 90°, it is likely that the secondary fluid is not entirely located inside the pores. Very small microdroplets of fluid could be adhering to small asperities on the particle surfaces where they form very small bridges upon contact with a second particle.²⁵ These bridges are able to transmit capillary forces, which are stronger than van der Waals interactions. However, the magnitude of the transmitted force is low compared to full particle bridging.²⁵ The microdroplets and microbridges cannot be seen in these confocal images because of their small number, a small size that exceeds the resolution limit of the microscope, and the very low dye content in each droplet. Section 3.4 in the Supporting Information shows an example where the visualization of such small droplets was achieved by increasing the laser intensity and detector gain of the microscope. The absorption of the secondary phase into the particle pores decreases and slows as the contact angle increases, which leads to more fluid available on the particle surface to form bridges corresponding to the drastic increase in |G*| near 90°. While it is possible that additional changes in the van der Waals or electrostatic interaction contribute to the increase in |G*|, there is no increase in the corresponding samples without secondary fluid, implying that these possible contributions are very minor. Above 90°, the secondary phase is no longer preferentially wetting and absorption of this fluid into the pores ceases. All of the secondary phase is outside of the particle pores for the 115° sample where it bridges the particles. The corresponding |G*| value at this angle is maximal and has a value that is about three decades higher than the suspension without added secondary fluid. This is very clear proof of the strong adhesion force induced by capillary bridges in the pendular state. The reduction in |G*| at very high contact angles can be attributed to the weakening of the bridges and the transition from the pendular to the capillary state. The sample with a contact angle of 147° shows particle agglomeration by capillary state clusters, and the corresponding rheological data also shows a decrease from the maximum value. The capillary state admixture is weaker on an absolute scale than the pendular state but is nevertheless much stronger than the suspensions without any secondary fluid.

There remains some ambiguity as to the extent of the reduction in strength for the capillary suspension (ϕ_sec = 0.0225) between 133° and 147° when the decrease in the pure suspensions’ complex shear modulus is taken into account. It is possible that this trend arises in part from the same changes occurring in the pure suspension, but this is unlikely to be the case. First, the dominant attractive interaction mechanism is different between these two systems as evidenced by the change from concave bridges to convex clusters. Second, the drop in strength for the capillary suspensions between 133° and 147° of nearly one decade is more pronounced than for the pure suspension. In fact, since the van der Waals force is much smaller than the capillary force, changes to the van der Waals force can account for a drop in the magnitude of the shear modulus by only a few percent. Therefore, the cause of this downturn must be due to a change in the capillary force that we hypothesize is due to the transition from the pendular to capillary state as is observed in the confocal images. To elucidate this decrease in the strength between the pendular and capillary states more clearly, force measurements of pendular bridged particles as well as clustered particles in the capillary state should be completed using this system in some future study. The capillary state sample, nevertheless, has a much higher complex shear modulus than the pure suspension without added fluid. Although the droplets in the capillary state have a convex shape and positive Laplace pressure, the strong attractive interaction can be assigned to the presence of the droplets clustering the particles and forming a percolating particle network.

4. Conclusions

Model capillary suspension systems covering a wide range of three-phase contact angles between 38° and 147° were examined by confocal microscopy and rheology in the present work. The confocal measurements made it possible, for the first time, to image entire unmodified sample volumes of capillary systems and gain insight into the 3D network structure. Using this method, structural differences that occur with the variation in the contact angle were elucidated. For nonporous particles, the confocal images prove the existence of the capillary state for three-phase contact angles slightly higher than 90°. Clusters with small numbers of particles, held together by the secondary phase, are visible. Images of such structures clearly show the existence of a sample-spanning clustered network as had been proposed previously using simulations.¹⁹ The pendular state was imaged for samples with contact angles lower than 90°. These images demonstrate the transition between systems consisting only of binary bridges to systems with bridges binding more than two particles, a state that is analogous to the funicular state in wet granular media. The transition from a binary bridge pendular state to a funicular-like pendular state occurs for geometrical reasons when the contact angle is decreased rather than from an increase in the secondary fluid volume. Computational image analysis provides pair distribution functions that give further insight into the structural differences, where the clustered structures lead to a broadening of the characteristic second peak. The funicular-like clustering seems to be less compact than the capillary state clustering, as the peak for the funicular-like sample is shifted to a higher particle distance. This finding is further corroborated by a lower apparent fractal dimension in the funicular-like sample compared to that in the capillary state sample. For highly porous particles, the transition from the pendular to the capillary state changes from 90° to a much higher apparent contact angle near 130°. The reason for this shift is not yet known but is likely due to a change in wetting behavior caused by surface roughness and chemical inhomogeneity, including the existence of contact angle hysteresis. Further research on these bridges and their shape is of considerable interest. For samples with porous particles and contact angles below 90°, a strong network caused by the capillary force is not formed as the added secondary fluid is absorbed into the particle pores. There is a slight increase in the shear modulus at angles of less than 90° due to small microdroplets that remain on the surface in the asperities, but this increase is dwarfed by the change at θ > 90°. The sample images show numerous pendular bridges at apparent contact angles above 90°, and the modulus dramatically increases by three decades compared to the suspension without secondary fluid, reaching a maximum at θ = 115°. Samples that are identified as being in the capillary state by the confocal measurements also showed an increase in shear modulus when compared to the pure suspensions but have a modulus one decade below that of the maximal pendular state samples.

Droplets that are connected to only a single particle are observed in the nonporous capillary state system (Figure 3c). The loss in secondary phase volume that contributes to network stability due to the singly connected droplets leads to a reduction in the binding force and corresponding macroscopic rheological parameters, but these droplets could also play an important role in the aging processes of capillary state systems. If these droplets can migrate to other positions and gradually bind more and more particles, then an increase in the network strength with time should be observed. Such an increase in the shear modulus over hours and even days was documented in a previous study using a capillary state system containing calcium carbonate particles.⁶⁵ The confocal observation of such samples over a long time period could help to elucidate the underlying processes and confirm the role of these droplets in this aging.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.5b04246.

• Preparation and properties of silica particles. Interfacial properties of the liquid phases. Imaging of capillary suspensions. Contact-angle-dependent coalescence criterion for the pendular–funicular transition. (PDF)

• Movie for better visualization of the three-dimensional network structure in the funicular state (40°). (AVI)

• Movie for better visualization of the three-dimensional network structure in the pendular state (61°). (AVI)

• Movie for better visualization of the three-dimensional network structure in the capillary state (94°). (AVI)

The authors declare no competing financial interest.