Abstract
By investigating a square-shaped metamaterial structure we discover that wave diffraction at diagonal corners of such a structure excites transverse magnetic harmonics of 210 mode (TM210 harmonics). Multi-layer overlapping and deliberately regulating period length between adjacent unit cells can significantly enhance TM210 harmonics, leading to a strong absorption waveband. On such a basis, a design strategy is proposed to achieve broadband, thin-thickness multi-layered metamaterial absorbers (MMAs). In this strategy big pyramidal arrays placed in the “white blanks” of a chessboard exhibit two isolated absorption bands due to their fundamental and TM210 harmonics, which are further connected by another absorption band from small pyramidal arrays in the “black blanks” of the chessboard. The as-designed MMA at a total thickness (h) of 4.36 mm shows an absorption of above 0.9 in the whole frequency range of 7–18 GHz, which is 38% broader with respect to previous design methods at the same h. This strategy provides an effective route to extend the absorption bandwidth of MMAs without increasing h.
Metamaterials possess exotic electromagnetic properties, and have important applications in diverse areas, such as sensors1,2,3, invisibility cloaks4,5,6, camouflage7,8 and energy harvesting9,10,11. Among them, metamaterial absorbers (MMAs) have attracted considerable attention from radio to optical frequency by virtue of the perfect absorption, thin thickness and flexible design ability of the metamaterials9,10,11,12,13,14. However, most of the microwave MMAs developed so far show a narrow absorption bandwidth, though many efforts including by optimizing artificial structure design15,16,17,18,19,20,21,22,23 have been made on the broadening of the absorption bandwidth of MMAs. In fact, the design of a broadband MMA is intractable due to the complicated interaction among different metamaterial resonant units, the limited room to place various metamaterial resonant units, as well as the intrinsic contradiction between the bandwidth and absorption strength by using too many kinds of metamaterial resonant units24. Thus, our research group has recently proposed a novel concept to skillfully integrate non-planar metamaterials with traditional magnetic absorbing materials and effectively manufactured absorbers with a significantly broadened absorption bandwidth in GHz frequencies. However, the dependency on the intrinsic dispersion and magnetic properties of the traditional magnetic absorber (TMA)25,26 restricts extension of the so-defined composite MMAs to other frequency ranges.
On the other hand, vertically assembling multiple layer metamaterials can merge their resonance absorption peaks from every layer of metamaterial structures, and consequently extend the absorption bandwidth of metamaterials without decreasing absorption strength27,28,29,30,31,32,33. But it generally has an disadvantage of a large thickness since the availability of a broad absorption bandwidth requires a number of layers. A multi-unit pattern method was used on the design of a pyramidal multi-layered MMA, reducing the MMA thickness by half in condition of the same absorption bandwidth34. Nevertheless, in all of these vertically assembling multiple layer metamaterials, every layer only contributes one narrow resonance peak to the absorption bandwidth34,35. Metal-dielectric-metal cavity structures can theoretically excite resonant absorption of multiple orders36,37,38,39,40, exhibiting multi-peak or multi-band absorption41,42,43. For example, a two different-sized hyperbolic metamaterial waveguide array has demonstrated a strong absorption in most of the frequency range between 2.3–40 GHz when the thickness is 11.52 mm44. However, the absorption band above 0.9 is separated and relative narrow. This is because the employed harmonic frequency adjacent to the fundamental harmonic one is twice larger than the latter, suggesting few possibility for these two kinds of resonance peaks to form a continuous high absorption band in limited thickness.
In this work, it is discovered that square-shaped metal-dielectric-metal cavities are able to excite weak TM210 harmonics, which are between the fundamental and third order harmonics. These weak harmonics can be remarkably enhanced by multi-layer overlapping into pyramidal arrays and deliberate regulation of period length between adjacent unit cells. The as-enhanced TM210 harmonic absorption can easily be connected with the fundamental harmonic absorption to form a singificantly broadened continuous strong absorption waveband by alternately inserting another pyramidal arrays of small sizes. The as-proposed multi-layered pyramidal MMAs have taken full use of both the fundamental and TM210 harmonics, and thus have a bandwidth of twice wider than those of the original simple counterparts. They have significant advantages of a highly absorption efficiency or a broad strong absorption bandwidth, even compared with the multi-unit MMAs reported previously34,35,44.
Results and Discussion
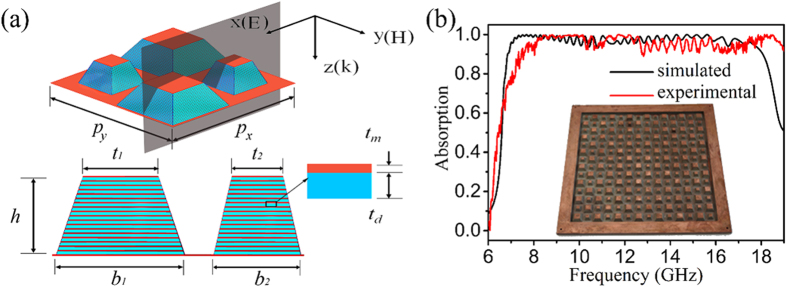
We achieve broadband, thin-thickness metamaterial absorbers (MMAs) by fully taking advantages of both the fundamental and TM210 harmonics. This is quite different from the recently reported two different-sized hyperbolic metamaterial waveguide array44, despite the apparently similar structure between them. In the latter hyperbolic metamaterial waveguide array structure, no high order harmonic is empolyed between the third order and fundamental harmonics, only resulting in a few of separated strong absorption bands in a wide frequency range. To illustrate the effectiveness of our designing strategy, we take a broadband multi-layered MMA in the range of 6–19 GHz for an example. Figure 1 depicts the structure and absorption spectra of the MMA. It consists of two different-sized pyramids, which are arranged in a chessboard manner. Each pyramid is composed of 20 layers of metal-dielectric-metal resonance cavities with their sizes tapered linearly from top to the bottom. Each thin layer of metal-dielectric- metal resonance cavity is made of a lossy dielectric material epoxy-based FR4 sandwiched between two copper foils. The copper foils have an electric conductivity of 5 × 107 S/m while the FR4 has a relative permittivity of 4.3(1-0.025i). Figure 1(a) shows the schematics of the three-dimensional structure and a typical cross-section parallel to x-z plane for a unit cell of the MMA. In the simulations, periodic boundary conditions are used in the x and y directions, and a plane wave is incident downward on the MMA with the electric field polarized along the x-direction (TE wave, transverse electric) as indicated in Fig. 1(a). The designed dimensions of a unit cell shown in Fig. 1(a) are px = 24 mm, py = 24 mm, t1 = 6.3 mm, t2 = 3.6 mm, b1 = 11 mm, b2 = 6.6 mm, tm = 0.018 mm, td = 0.2 mm, and h = 4.36 mm. As the MMA is backed with a copper foil, no transmission could be made and the absorption can be calculated by A = 1 − R. Figure 1(b) shows the simulated and measured absorption spectra of the as-designed MMA under normal incidence in frequencies (f) of 6–19 GHz. The MMA shows a strong simulated and measured absorption of above 0.9 in a wide frequency range of more than 11 GHz. The good agreement between the experimental and simulated results indicate that our design method is viable. The calculated absorption bandwidth (7–18 GHz) has a small shift to a low frequency with respect to the measured one (8–19 GHz). This could be reasonably explained by the unavoidable but acceptable fabrication errors. The fluctuation in the simulated curve indicates that the broadband absorption spectrum resulted from the combination of many neighbour absorption peaks together, consistent with the previous finding for the metamaterials made of truncated pyramids10,27.
Figure 1.
(a) 3-dimensional structure diagram (top) as well as a typical cross-section along x-z shadow plane (bottom) for the repeating unit of the as-designed metamaterial absorber (MMA) labelled with sizes. The red brown represents metal copper foils and the light blue represents dielectric FR-4. px = 24 mm, py = 24 mm, t1 = 6.3 mm, t2 = 3.6 mm, b1 = 11 mm, b2 = 6.6 mm, tm = 0.018 mm, td = 0.2 mm, and h = 4.36 mm. (b) The simulated and experimental absorption spectra of the as-designed MMA. The inset shows a photograph of the fabricated MMA.
For our designing MMA, the relative absorption bandwidth (WRAB = 2(fU − fL) ⁄ (fU + fL), where fU and fL are the upper and lower frequency bounds of a continuous band with absorption above 0.9) is calculated to be as large as 88%, surpass the planar microwave MMAs reported so far27,28,41,44. However, WRAB cannot fully evaluate the absorption efficiency of MMAs as it does not take into account the MMA thickness. Here a ratio of operational bandwidth to thickness Wob/t = (λU − λL)/t is proposed, where λU and λL are the upper and lower wavelength bounds of a continuous band with absorption above 0.9, t is the thickness of the MMA. Wob/t involves wavelength and the thickness of MMAs, and is a dimensionless value. Thus, it is more reasonable to use Wob/t rather than WRAB to assess the absorption efficiency of MMAs even in different frequency ranges. In our example, the MMA exhibits a Wob/t as big as 6.01, as listed in Table 1. This value is the biggest one among all the reported MMAs including the multi-sized pyramidal MMA28,33, suggesting that the MMA proposed here is more effective in broadening the strong absorption bandwidth. This originates from our unique size regulation of the chessboard-arranged pyramids. Specifically, these regulations include three points. First, the period length (p) between the pyramidal units is carefully optimized to significantly enhance TM210 harmonics. Second, b1 is set to make a fundamental resonance corresponding to the lower frequency bound of the target absorption band (fL) and t1 to (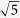 +1)fL/2. In this way, the frequency band between fL and
+1)fL/2. In this way, the frequency band between fL and 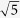 fL is divided into 2 frequency bands and thus the fundamental and TM210 harmonics form two isolated strong absorption wavebands, respectively. Third, by alternately inserting small pyramidal arrays on the chessboard with b2 almost equal to t1 and t2 a little smaller than b1/
fL is divided into 2 frequency bands and thus the fundamental and TM210 harmonics form two isolated strong absorption wavebands, respectively. Third, by alternately inserting small pyramidal arrays on the chessboard with b2 almost equal to t1 and t2 a little smaller than b1/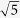 , the two isolated strong absorption bands are connected to obtain a broadened continuous absorption band in a greatest efficiency. In contrast, for the previously designed pyramidal MMAs, either b2
, the two isolated strong absorption bands are connected to obtain a broadened continuous absorption band in a greatest efficiency. In contrast, for the previously designed pyramidal MMAs, either b2
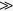 t133 or t2 ≥ b1/
t133 or t2 ≥ b1/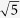 34. Moreover, p is seldom optimized for the deliberate enhancement of TM210 harmonics. Consequently, several absorption units and resonance modes contribute to only one frequency, leading to inferior absorption efficiencies. To confirm the above statements, we will demonstrate the physical implication and originality of this design strategy in the following.
34. Moreover, p is seldom optimized for the deliberate enhancement of TM210 harmonics. Consequently, several absorption units and resonance modes contribute to only one frequency, leading to inferior absorption efficiencies. To confirm the above statements, we will demonstrate the physical implication and originality of this design strategy in the following.
Table 1. Comparison of absorption properties of the planar MMAs reported in literatures and this work proposed here.
| Feature of MMAs | Absorption waveband | Thickness | Wob/t | Reference |
|---|---|---|---|---|
| Truncated pyramidal | 7.8–14.7 GHz | 5 mm | 3.61 | 27 |
| Double-corrugated structure | 7.8–16 GHz | 5 mm | 3.94 | 28 |
| 1-layer donut-shape | 5.03–5.13 GHz | 0.8 mm | 1.45 | 41 |
| 3-layer crosses structure | 4.45–4.95 THz | 3.8 μm | 1.79 | 17 |
| Double-layered grating | 0.25–2.5 THz | 620 μm | 1.74 | 45 |
| Saw-toothed multi-layer slab | 0.3–4.7 μm | 1 μm | 4.40 | 10 |
| Multiple-layer pyramidal | 1–14 μm | 3 μm | 4.33 | 30 |
| Hyperbolic waveguide taper array | 2.9–5 μm | 40 μm | 5.00 | 33 |
| Multi-sized sow-wave hyperbolic | 0.5–2.5 μm | 56 μm | 3.75 | 34 |
| Truncated pyramidal | 0.2–5.8 μm | 56 μm | 1.00 | 35 |
| 1-layer mixed-size square hole | 583–613 nm | 15 μm | 0.20 | 14 |
| Multi-sized Pyramidal using TM210 | 7–18 GHz | 4.36 mm | 6.01 | This work |
For vertically stacked multiple-layered metamaterials, the continuous broadband absorption waveband comes from the simply merged absorption peaks of the unit cells in each layer27,44. As every layer in the stack has a similar structure but different sizes, they absorb microwaves in an alike mechanism. Therefore, without loss of generality, we have selected a middle layer of the MMA with side length (L) of 9.825 mm to analyse the resonance behaviour for understanding the broadband absorption mechanism of the proposed MMA. Figure 2(a) indicates that there exist two absorption peaks: a strong one located at f1 = 7.4 GHz and a relatively weak one at f2 = 17.0 GHz.
Figure 2.
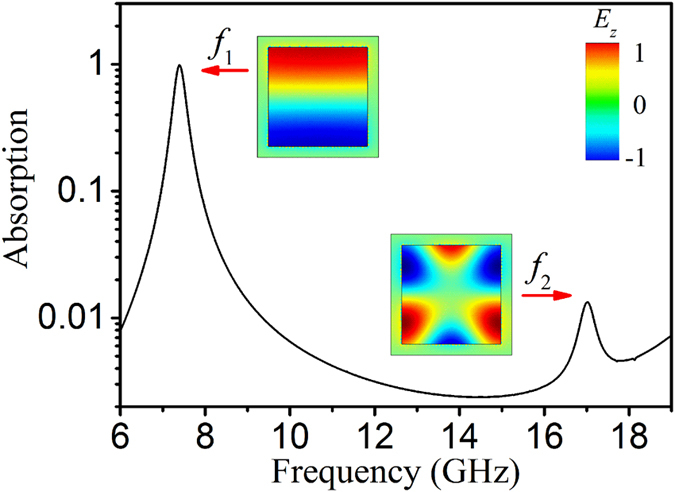
Simulated absorption spectrum of a metal-dielectric-metal resonator unit cell with L = 9.825 mm, which indicates that there are two resonances at frequency (f) at 7.4 and 17.0 GHz. The insets show the corresponding electric field distribution patterns in the unit cell at the resonance frequencies of f1 = 7.4 GHz and f2 = 17.0 GHz, respectively.
When the incident waves diffract from opposite edges into a dielectric slit sandwiched by two parallel conducting metal patches, they will propagate oppositely and may excite standing waves. The resonance frequency of the standing wave can be described with equation (1)39.
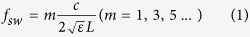 |
where c, ε, L and m are the speed of light in vacuum, the permittivity and length of the dielectric slit, and mode number of the harmonic, respectively. Note that only odd mode harmonics exist in this model. After substituting the parameters in the above equation with the specific dimensions of the metamaterial layer, the fundamental harmonic frequency can be calculated to be 7.36 GHz, which agrees well with f1. This indicates that the strong absorption peak results from the first order standing wave harmonic. The inset pointing to f1 reveals that the electric field distribution at f1 shows the typical characteristic of fundamental standing wave harmonics, further approving that the strong absorption peak originates from the fundamental resonance of the standing waves.
However, the absorption peak located at f2 does not fit any resonance modes predicted by Eq. (1), implying that there is a new absorption mechanism besides the fundamental harmonic resonance for the metal-dielectric-metal cavity. The E distribution pattern at f2 is alike a TM210 mode of a rectangular waveguide cavity resonator45,46. For rectangular waveguide cavity resonators, the resonance frequencies (fmnl) can be calculated by
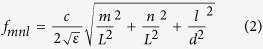 |
where the indices m, n, l represent the variation number in the standing wave patterns along the x, y, z directions, respectively; L and d are the resonator sizes. Equation (2) implies all the possible resonant modes along three directions. For the middle layer of the MMA with L = 9.825 mm, f1 corresponds to the fundamental harmonic f010 while f2 (=17.0 GHz) almost equals to 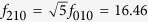 GHz (the deviation is 3.2%), suggesting that the metamaterial unit cells behave similar to rectangular waveguide cavity resonators.
GHz (the deviation is 3.2%), suggesting that the metamaterial unit cells behave similar to rectangular waveguide cavity resonators.
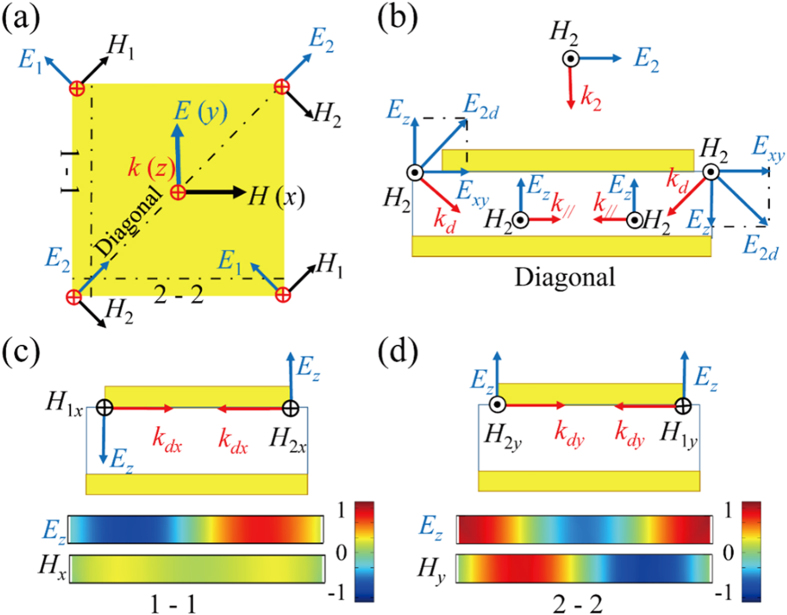
To excite TM210 mode, it is necessary for waves to diffract from both x and y directions. Furthermore, the diffracted waves should have an electric field (E) along z direction. Therefore, the excitation of TM210 resonance mode can only originate from the diffraction at the corners of the metal patches. Figure 3(a) shows the scheme of the diffractions at corners. It illustrates that the incident waves are decomposed into two component waves 1 and 2. Component 1 will diffract at the top-left and bottom-right corners, while component 2 will diffract at the top-right and bottom-left corners. As shown in Fig. 3(b), the waves diffracted from diagonal corners superpose to form standing waves, resulting in TM210 resonance mode. To clearly show the resonance, we decompose the diffracted waves into two components along x and y directions, and the decomposition of the wave vectors are certified by the electric field and magnetic field distribution, which clearly display the phase of the vectors. As shown in Fig. 3(c), the components along +y and −y directions are out of phase, which only enables odd mode harmonics. But the components along +x and −x directions are in phase according to the decomposition indicated in Fig. 3(d). As a result, standing waves of even harmonics are able to form. This clearly manifests that it is possible to generate TMmn0 modes, where m and n are even and odd numbers, respectively. Furthermore, it also explains well why only TM210 but not TM200 or TM020 exists in our design. It is the first time to discover that resonant mode TM210 exists in the metal-dielectric-metal unit cells. This is instructive and beneficial to extend the absorption bandwidth of their-based MMAs, though such a single unit cell only exhibits a weak intensity of the TM210 harmonic, as indicated by Fig. 2.
Figure 3.
(a) A schematic shows the incident EM wave (EHk) is decomposed into two components, which diffract at four corners of the rectangular waveguide cavity resonator: for component 1 at left-top and right-bottom corners, for component 2 at right-top and left-bottom corners. (b) Diffracted waves from diagonal cross section. Decomposition of the diffracted wave vectors and normalized E field and H field distribution at resonance frequency of TM210 along (c) x direction at 1 - 1 cross section (d) along y direction at 2 - 2 cross section.
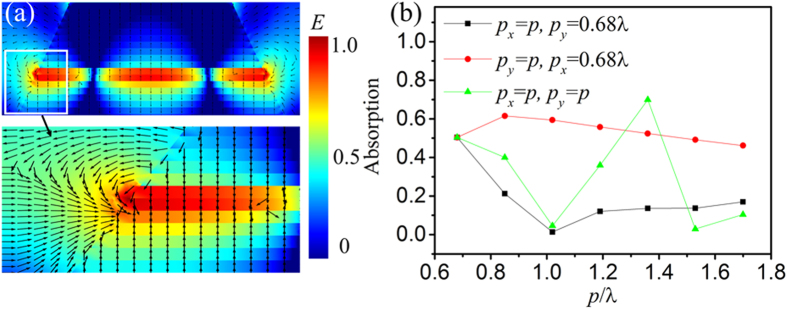
The absorption of TM210 harmonics in a metal-dielectric-metal unit cell can be significantly enhanced by vertically stacking multiple layers of unit cells. Figure 4(a) represents that for a vertically stacked multiple-layered metamaterials consisting of the big pyramids shown in Fig. 1 with px = py = 12 mm, the incident waves at the edges of metal patches are diffracted in various directions and some of the diffraction waves of neighbouring layers could access the resonance layer. Thus, the electric field intensities in the layer with TM210 harmonics are substantially enhanced by the diffracted electromagnetic waves of the vicinal layers. Consequently, the absorption of the MMA at 17 GHz could reach about 0.5 due to the TM210 harmonics (corresponding to the first left date point in Fig. 4(b)). This value is one to two orders of magnitude larger than that of the metal-dielectric-metal single layered metamaterials shown in Fig. 2.
Figure 4.
(a) Normalized electric field distribution with diffracted electric field vectors of the 20-layer MMA at 17 GHz along yz plane. (b) Influence of the periodic length of the MMA on the simulated absorption at 17 GHz (λ = 17.65 mm).
The periodic length (p) between the pyramidal units has also strong influences on the electromagnetic wave diffraction property of the MMA unit cells and thus on the TM210 harmonic absorption. For the electromagnetic waves with f = 17 GHz (corresponding to λ = 17.65 mm), Fig. 4(b) indicates that when p along x direction (px, E//x) increases from 0.68 to 1.7λ, the harmonic absorption at 17 GHz exhibits a minimum value of 0.01 at px = λ. As illustrated in Fig. 4(a), the absorption at 17 GHz took place in the 6th layer of the pyramid with L = 9.825 mm, and the 1st to 8th layers also contribute to it. In this case, the above 12 layers work as a grating. When px = λ, the grating will reflect nearly all the incident waves according to the diffraction theory47, leading to a weakest absorption (see Supplementary Fig. S1 online). When p along y direction (py, E⊥y) increases from 0.68 to 1.7λ, the absorption shows a maximum value of 0.62. This is because when E is parallel to the slit, wider slit allows more waves to permeate, enhancing TM210 harmonics. On the other hand, increasing p decreases the occupation ratio of the pyramid and thus the absorption. If the effect of the occupation ratio are excluded, increasing px and py will both increase the absorption except at px = λ (see Supplementary Fig. S2 online). There occurs a maximum absorption of 0.7 when px = py = 1.36λ. This suggests that the TM210 harmonic absorption could also be enhanced by the optimization of p.
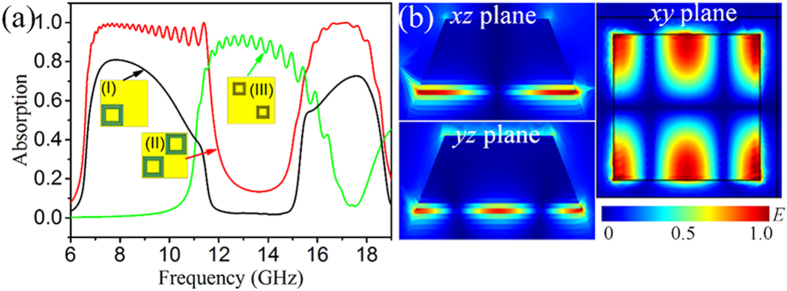
Curve I in Fig. 5(a) shows the simulated absorption spectrum of the MMA based on the big pyramids shown in Fig. 1 with p optimized to be 24 mm. Obviously, it exhibits two absorption wavebands with the absorption within 0.4–0.8 at 7–11 GHz and 15–19 GHz. In this case, the pyramids only occupy half of the space in the “white blanks” of the chessboard and about 3/4 space in the structure is vacant. Thus, we could double the big pyramids to increase the occupancy ratio in condition that the gap between the adjacent units remains unchanged, as described by inset II of Fig. 5(a). Curve II in Fig. 5(a) indicates that when all the “white blanks” of the chessboard are filled with the big pyramids, the as-designed MMA exhibits two separated strong absorption wavebands at 7–11 GHz and 15–19 GHz due to the fundamental and TM210 harmonics. All the absorptions in these two wavebands are almost above 0.9.
Figure 5.
(a) Simulated absorption spectra of the MMAs consisting of pyramids with p = 1.36λ: big pyramid arrays half (I) and full filling (II) “white blanks” of a chessboard, small pyramid arrays full filling “black blanks” of a chessboard (III). (b) Normalized electric field distribution of structure II at 17 GHz: (left up) cross section along xz plane, (left down) cross section along yz plane and (right) central cross section of the 6th layer.
While it is well-accepted that the strong absorption waveband at 7–11 GHz comes from the merging of the fundamental harmonics of various metal-dielectric-metal unit cells, we here pay attention to the rigorous evidence that the strong absorption waveband at 15–19 GHz is mainly attributed to the TM210 harmonics. According to Eq. (2), the absorption at 17 GHz may come from TM210 harmonic of the metal-dielectric-metal resonator with L = 9.825 mm, which is just the 6th layer of the big pyramids (Layer 6). As shown in Fig. 5(b), the electric field (E) at f = 17 GHz is mainly located at Layer 6 as well as its adjacent layers, and it manifests a typical field distribution of TM210 harmonics. Similar E distributions are also observed at f = 15, 16 and 18 GHz for the layers with L corresponding to the frequency of TM210 harmonics. No other resonance modes are found except for a weak TM030 harmonic at 19 GHz, where the absorption is only 0.2 (see Supplementary Fig. S3 online). This fully confirms that it is the TM210 harmonics that dominate the absorption in 15–19 GHz. Since the MMA has a size comparable with the working wavelength, some of the incident waves may possibly scatter in various directions rather than be absorbed. To exclude this, we have calculated the absorption of the chessboard arranged the big pyramids by two different ways of calculating the volume integration of the energy loss density within the MMA and the (1 – S112) of the MMA (see Supplementary Fig. S4 online). The two values almost equal with each other, implying that the scattering hardly occurs.
To further obtain a continuous strong absorption waveband, there is only a bandwidth of 4 GHz to compensate the absorption between them. This can be easily completed by filling the “black blanks” of the chessboard with small pyramidal arrays33. As a matter of fact, when the small pyramidal arrays with L of around 6.6 to 3.6 mm from the bottom to top are occupied in the “black blanks” of the chessboard, they exhibit a strong absorption in 11–15 GHz as indicated by curve III in Fig. 5(a). Therefore, after simultaneously arranging the two kind of pyramidal unit cells in the “white blanks” and “black blanks” of the chessboard, the fulfilled metamaterial can display a strong absorption of above 0.9 in the whole frequency range of 7–18 GHz. This is verified both in simulation and experiment as shown in Fig. 1(b).
Above all, the broad absorption bandwidth comes from three sources: the fundamental harmonics of the big and small pyramids, as well as the TM210 harmonics of the big pyramids. The as-designed broadband pyramidal MMAs should make full use of TM210 harmonics of the big pyramids at the high frequency absorption by regulating p to ensure the excellent absorption efficiency. In addition, the sizes of the big and small pyramids should approximately obey the following equations: 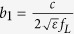 to follow Eq. (1);
to follow Eq. (1); 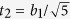 to ensure the connection of the absorption bands provided by the fundamental harmonics of the small pyramids and the TM210 harmonics of the big pyramids;
to ensure the connection of the absorption bands provided by the fundamental harmonics of the small pyramids and the TM210 harmonics of the big pyramids; 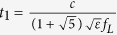 to make the big and small pyramids contribute to half of the frequency band from
to make the big and small pyramids contribute to half of the frequency band from 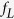 to
to 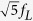 , respectively;
, respectively; 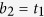 to ensure the connection of the absorption bands provided by fundamental harmonics of the big and small pyramids. Under the above conditions, the size parameters should be made some further optimization to achieve a continuous strong absorption waveband. In our example, we obtain a strong absorption bandwidth of 11 GHz from 7 to 18 GHz. In contrast, if ignoring the contribution from TM210 harmonics, the absorption waveband only covers the frequency range of 7–15 GHz, which is around 8 GHz in width. This means that the bandwidth is increased by 38% due to TM210 harmonics of the big pyramids. Compared with the traditional simple design which uses only the fundamental harmonic absorption in 7–11 GHz and 11–15 GHz from the big and small pyramids respectively, our MMA designed here has a tripled bandwidth. According to Eq. (2), there are higher order harmonics at higher frequencies for the metal-dielectric-metal resonance cavity unit cells. Therefore, some isolated strong absorption wavebands are expected at frequencies exceeding 19 GHz44, where we do not have a focus here.
to ensure the connection of the absorption bands provided by fundamental harmonics of the big and small pyramids. Under the above conditions, the size parameters should be made some further optimization to achieve a continuous strong absorption waveband. In our example, we obtain a strong absorption bandwidth of 11 GHz from 7 to 18 GHz. In contrast, if ignoring the contribution from TM210 harmonics, the absorption waveband only covers the frequency range of 7–15 GHz, which is around 8 GHz in width. This means that the bandwidth is increased by 38% due to TM210 harmonics of the big pyramids. Compared with the traditional simple design which uses only the fundamental harmonic absorption in 7–11 GHz and 11–15 GHz from the big and small pyramids respectively, our MMA designed here has a tripled bandwidth. According to Eq. (2), there are higher order harmonics at higher frequencies for the metal-dielectric-metal resonance cavity unit cells. Therefore, some isolated strong absorption wavebands are expected at frequencies exceeding 19 GHz44, where we do not have a focus here.
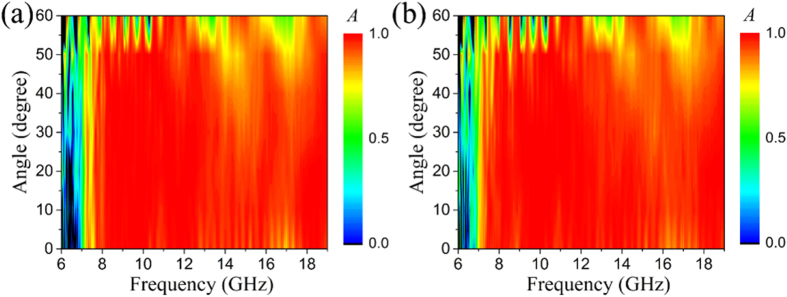
The measured absorption contour map for TE and TM polarization with incident angle versus frequency is plotted in Fig. 6. When the incident angle is smaller than 50°, the MMA maintains its absorption of above 0.9 in the frequency range of 8–19 GHz, manifesting the excellent angular independence of absorption. Comparison of Fig. 6(a) with (b) indicates that the MMA presents polarization insensitivity even at an incident angle of 60 °. The angular and polarization insensitivity of the MMA are beneficial for many applications such as stealth, electromagnetic compatibility and solar energy collection1,8,19. The as-proposed design method is expected to be flexible as it can be extended to other frequency ranges due to the form-invariance of Maxwell equations.
Figure 6.
Measured absorption of the proposed MMA under illumination of (a) TE and (b) TM waves with incident angles from 0 ° to 60 ° in the frequency range of 6–19 GHz.
Conclusion
In conclusion, commonly used metamaterial unit cells of square-shaped metal-dielectric-metal cavities behave like rectangular waveguide cavity resonators. By the wave diffraction at diagonal corners they may excite TM210 harmonics, which can be further enhanced by multi-layer overlapping and regulation of period length between adjacent unit cells. On such a basis, a design method to achieve broadband metamaterial absorbers is proposed by employing both fundamental and TM210 harmonics from the unit cells of metal-dielectric-metal cavities. A broadband metamaterial absorber (MMA) is accordingly designed and experimentally verified to show an absorption of above 0.9 in the frequency range of 7–18 GHz, whose bandwidth is tripled with respect to the original simple configuration which only uses fundamental harmonics. The as-proposed design strategy provides a general route to greatly extend the absorption bandwidth of MMAs without increasing the total thickness.
Methods
The absorptions and field distributions of the MMAs are numerically simulated and calculated using a Finite-Element-Method based software package Comsol Multiphysics. The MMA is fabricated by a computer assisted mechanical engraving machine. First, 20 layers of 200 × 200 mm printed circuit boards (PCBs), each of which consists of a copper film with a thickness of 0.018 mm covered on a 0.15-mm-thick FR4 board, are bounded together to form a stack using an adhesive with a thickness of 0.05 mm and almost the same dielectric constant as FR4. A copper film is added to the bottom of the stack to suppress the transmission. Afterwards, the above PCB stack is subjected to mechanical engraving, a 200 × 200 mm sample containing 49 units is obtained as shown in Fig. 1(a). The reflection (R) of the MMA is measured in a microwave anechoic chamber using an Agilent Network Analyzer N5230A.
Additional Information
How to cite this article: Long, C. et al. Broadening the absorption bandwidth of metamaterial absorbers by transverse magnetic harmonics of 210 mode. Sci. Rep. 6, 21431; doi: 10.1038/srep21431 (2016).
Supplementary Material
Acknowledgments
This work is supported by the National Natural Science Foundation of China (No. 11204225, 51577138 and 51521001), the Top Talents Lead Cultivation Project and the Innovative Group Project of Hubei Province (2015CFA003), the Yellow Crane talent plan of Wuhan municipal government, Equipment Development Pre-research Shared Technology Fund Project (9140A10031212QT69120).
Footnotes
Author Contributions C.L., W.W. and W.L. performed the theoretical analysis and simulation; S.Y. and J.Z. performed the fabrication and characterization of the samples; C.L., W.L. and J.G. wrote the manuscript; J.G. initiated and supervised the project; All authors discussed the results and reviewed the manuscript.
References
- Liu N., Mesch M., Weiss T., Hentschel M. & Giessen H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 10, 2342–2348 (2010). [DOI] [PubMed] [Google Scholar]
- Yang J. J., Huang M., Tang H., Zeng J. & Dong L. Metamaterial Sensors. Int. J. Antenn. Propag 2013, 1–16 (2013). [Google Scholar]
- Zhou G. Y., Lee A. W., Chang J. Y., Huang C. H. & Chen J. K. Fabrication of metamaterial absorber using polymer brush - gold nanoassemblies for visualizing the reversible pH-responsiveness. J. Mater. Chem. C 2, 8226–8234 (2014). [Google Scholar]
- Pendry J. B., Schurig D. & Smith D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006). [DOI] [PubMed] [Google Scholar]
- Schurig D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006). [DOI] [PubMed] [Google Scholar]
- Li W., Guan J., Sun Z., Wang W. & Zhang Q. A near-perfect invisibility cloak constructed with homogeneous materials. Opt. Express 17, 23410–23416 (2009). [DOI] [PubMed] [Google Scholar]
- Guan J., Li W., Wang W. & Fu Z. General boundary mapping method and its application in designing an arbitrarily shaped perfect electric conductor reshaper. Opt. Express 19, 19740–19751 (2011). [DOI] [PubMed] [Google Scholar]
- Li W., Guan J. & Wang W. Homogeneous-materials-constructed electromagnetic field concentrators with adjustable concentrating ratio. J. Phys. D: Appl. Phys. 44, 125401 (2011). [Google Scholar]
- Hedayati M. K. et al. Design of a Perfect Black Absorber at Visible Frequencies Using Plasmonic Metamaterials. Adv. Mater. 23, 5410–5414 (2011). [DOI] [PubMed] [Google Scholar]
- Cui Y. et al. Ultrabroadband Light Absorption by a Sawtooth Anisotropic Metamaterial Slab. Nano Lett. 12, 1443–1447 (2012). [DOI] [PubMed] [Google Scholar]
- Li W. et al. Refractory Plasmonics with Titanium Nitride: Broadband Metamaterial Absorber. Adv. Mater. 26, 7959–7965 (2014). [DOI] [PubMed] [Google Scholar]
- Tao H. et al. A metamaterial absorber for the terahertz regime: Design, fabrication and characterization. Opt. Express 16, 7181–7188 (2008). [DOI] [PubMed] [Google Scholar]
- Avitzour Y., Urzhumov Y. A. & Shvets G. Wide-angle infrared absorber based on a negative-index plasmonic metamaterial. Phys. Rev. B 79, 045131 (2009). [Google Scholar]
- Hu C., Liu L., Zhao Z., Chen X. n. & Luo X. Mixed plasmons coupling for expanding the bandwidth of near-perfect absorption at visible frequencies. Opt. Express 17, 16745–16749 (2009). [DOI] [PubMed] [Google Scholar]
- Rhee J., Yoo Y., Kim K., Kim Y. & Lee Y. Metamaterial-based perfect absorbers. J. Electromagnet. Wave 28, 1541–1580 (2014). [Google Scholar]
- Wen Q. Y., Zhang H. W., Xie Y. S., Yang Q. H. & Liu Y. L. Dual band terahertz metamaterial absorber: Design, fabrication, and characterization. Appl. Phys. Lett. 95, 241111 (2009). [Google Scholar]
- Ye Y. Q., Jin Y. & He S. Omnidirectional, polarization-insensitive and broadband thin absorber in the terahertz regime. J. Opt. Soc. Am. B 27, 498–504 (2010). [Google Scholar]
- Li H. et al. Ultrathin multiband gigahertz metamaterial absorbers. J. Appl. Phys. 110, 014909 (2011). [Google Scholar]
- Zhu L. et al. Broadband absorption and efficiency enhancement of an ultra-thin silicon solar cell with a plasmonic fractal. Opt. Express 21, A313–A323 (2013). [DOI] [PubMed] [Google Scholar]
- Zhu J. et al. Ultra-broadband terahertz metamaterial absorber. Appl. Phys. Lett. 105, 021102 (2014). [Google Scholar]
- Li M., Yang H.-L., Hou X.-W., Tian Y. & Hou D.-Y. Perfect metamaterial absorber with dual bands. Prog. Electromagn. Res. 108, 37–49 (2010). [Google Scholar]
- Huang L. & Chen H. Multi-band and polarization insensitive metamaterial absorber. Prog. Electromagn. Res. 113, 103–110 (2011). [Google Scholar]
- Guo Y., Yan L., Pan W., Luo B. & Luo X. Ultra-Broadband Terahertz Absorbers Based on 4× 4 Cascaded Metal-Dielectric Pairs. Plasmonics 9, 951–957 (2014). [Google Scholar]
- Wen D. E. et al. Broadband metamaterial absorber based on a multi-layer structure. Phys. Scr. 88, 15402–15408 (2013). [Google Scholar]
- Li W., Wu T., Wang W., Guan J. & Zhai P. Integrating non-planar metamaterials with magnetic absorbing materials to yield ultra-broadband microwave hybrid absorbers. Appl. Phys. Lett. 104, 022903 (2014). [Google Scholar]
- Li W., Wu T., Wang W., Zhai P. & Guan J. Broadband patterned magnetic microwave absorber. J. Appl. Phys. 116, 044110 (2014). [Google Scholar]
- Ding F., Cui Y., Ge X., Jin Y. & He S. Ultra-broadband microwave metamaterial absorber. Appl. Phys. Lett. 100, 103506 (2012). [Google Scholar]
- Pang Y., Cheng H., Zhou Y. & Wang J. Double-corrugated metamaterial surfaces for broadband microwave absorption. J. Appl. Phys. 113, 084907 (2013). [Google Scholar]
- Meng L., Zhao D., Li Q. & Qiu M. Polarization-sensitive perfect absorbers at near-infrared wavelengths. Opt. Express 21, A111–A122 (2013). [DOI] [PubMed] [Google Scholar]
- Liang Q. et al. Metamaterial-Based Two Dimensional Plasmonic Subwavelength Structures Offer the Broadest Waveband Light Harvesting. Adv. Opt. Mater 1, 43–49 (2013). [Google Scholar]
- Ma W., Wen Y. & Yu X. Broadband metamaterial absorber at mid-infrared using multiplexed cross resonators. Opt. Express 21, 30724–30730 (2013). [DOI] [PubMed] [Google Scholar]
- Bouchon P., Koechlin C., Pardo F., Haïdar R. & Pelouard J.-L. Wideband omnidirectional infrared absorber with a patchwork of plasmonic nanoantennas. Opt. Lett. 37, 1038–1040 (2012). [DOI] [PubMed] [Google Scholar]
- He S., Ding F., Mo L. & Bao F. Light Absorber with an Ultra-Broad Flat Band Based on Multi-Sized Slow-Wave Hyperbolic Metamaterial Thin-Films. Prog. Electromagn. Res. 147, 69–79 (2014). [Google Scholar]
- Ji D. X. et al. Broadband absorption engineering of hyperbolic metafilm patterns. Sci. Rep. 4, 7 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lobet M., Lard M., Sarrazin M., Deparis O. & Henrard L. Plasmon hybridization in pyramidal metamaterials: a route towards ultra-broadband absorption. Opt. Express 22, 12678–12690 (2014). [DOI] [PubMed] [Google Scholar]
- Sellier A., Teperik T. V. & de Lustrac A. Resonant circuit model for efficient metamaterial absorber. Opt. Express 21, A997–A1006 (2013). [DOI] [PubMed] [Google Scholar]
- Moreau A. et al. Controlled-reflectance surfaces with film-coupled colloidal nanoantennas. Nature 492, 86–89 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu C., Li X., Feng Q., Chen X. N. & Luo X. Investigation on the role of the dielectric loss in metamaterial absorber. Opt. Express 18, 6598–6603 (2010). [DOI] [PubMed] [Google Scholar]
- Peng X. Y., Wang B., Lai S., Zhang D. H. & Teng J. H. Ultrathin multi-band planar metamaterial absorber based on standing wave resonances. Opt. Express 20, 27756–27765 (2012). [DOI] [PubMed] [Google Scholar]
- Lockyear M. J., Hibbins A. P., Sambles J. R., Hobson P. A. & Lawrence C. R. Thin resonant structures for angle and polarization independent microwave absorption. Appl. Phys. Lett. 94, 041913 (2009). [Google Scholar]
- Yoo Y. J. et al. Polarization-independent dual-band perfect absorber utilizing multiple magnetic resonances. Opt. Express 21, 32484 (2013). [DOI] [PubMed] [Google Scholar]
- Yoo Y. J. et al. Triple-band perfect metamaterial absorption, based on single cut-wire bar. Appl. Phys. Lett. 106, 071105 (2015). [Google Scholar]
- Kim Y. J. et al. Dual broadband metamaterial absorber. Opt. Express 23, 3861 (2015). [DOI] [PubMed] [Google Scholar]
- Yin X., Long C., Chen L., Guan J. G. & Li X. Ultra-wideband microwave absorber by connecting multiple absorption bands of two different-sized hyperbolic metamaterial waveguide arrays. Sci. Rep. 5, 15367 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y. et al. Ultra-broadband terahertz perfect absorber by exciting multi-order diffractions in a double-layered grating structure. Opt. Express 23, 2032–2039 (2015). [DOI] [PubMed] [Google Scholar]
- Pozar D. M. Microwave engineering. (John Wiley & Sons, 2009). [Google Scholar]
- Born M. & Wolf E. Principles of Optics. The Mathematical Gazette, 986 (1999). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.