Abstract
Objective.
The primary objective was to determine whether age deficits in implicit sequence learning occur not only for second-order probabilistic regularities (event n − 2 predicts n), as reported earlier, but also for first-order regularities (event n − 1 predicts event n). A secondary goal was to determine whether age differences in learning vary with level of structure.
Method.
Younger and older adults completed a nonmotor sequence learning task containing either a first- or second-order structure. Learning scores were calculated for each subject and compared to address our research objectives.
Results.
Age deficits in implicit learning emerged not only for second-order probabilistic structure, but also for simple, first-order structure. In addition, age differences did not vary significantly with structure; both first and second order yielded similar age deficits.
Discussion.
These findings are consistent with the view that there is an associative binding deficit in aging and that this deficit occurs for implicit as well as explicit learning and across simple and more complex sequence structures.
Key Words: Aging, Implicit learning, Sequence learning, Structure.
Implicit learning refers to the ability to acquire environmental regularities without conscious effort or awareness of what has been learned (Reber, 1989). Implicit probabilistic sequence learning is a specific type of implicit learning in which people acquire regularities among events that occur sequentially, thus requiring associations over time. Such learning is essential because it underlies abilities such as learning language and adapting to new routines and environments, functions that hinge upon our ability to detect and make use of reoccurring patterns in environmental input (Newport & Aslin, 2004; Norman & Price, 2012).
Environmental regularities are frequently probabilistic (as opposed to deterministic), meaning that events often, but not always, predict later ones. In addition, regularities vary in complexity; events that tend to co-occur can be temporally adjacent, or they can be separated by one or more random, intervening events. Despite the traditional view that all implicit types of learning are spared in aging, more recent studies have found age differences in implicit probabilistic sequence learning, particularly when the regularities are probabilistic and/or more complex (Bennett, Howard, & Howard, 2007; Howard et al., 2004; Howard Jr. & Howard, 1997; Howard Jr. & Howard, 2013; Janacsek, Fiser, & Nemeth, 2012; Seaman, Howard, & Howard Jr., 2014). However, whether age deficits also exist for learning simple probabilistic regularities remains unclear. In this study, we compare younger and older adults’ learning of simple (first order) and more complex (second order) probabilistic regularities.
Implicit probabilistic sequence learning can be measured in the laboratory using tasks in which participants respond via corresponding button press to stimuli that appear sequentially in one of multiple spatial locations on a computer screen. Unbeknownst to participants, certain sequences occur with high probability (HP) and others with low probability (LP). Implicit learning is demonstrated by faster reaction times to the HP when compared with LP sequences, without evidence of explicit knowledge about the regularity. As in the real world, these regularities can be made to vary in terms of the temporal and/or spatial distance between related events, a characteristic referred to as their “structure” (Remillard and Clark, 2001). In regularities with a first-order structure, an event predicts the occurrence of another event that immediately follows (event n − 1 predicts event n), such that the to-be-associated items are temporally adjacent. In higher order regularities, such as those with second-order structure where an event predicts another that occurs two items later (event n − 2 predicts n), an association must be made over one (or more) random, intervening events.
Structure may affect implicit sequence learning because processing and memory demands increase with the separation between the to-be-associated items. Moreover, structure may affect learning more in older adults who are experiencing cognitive deficits associated with normal aging than in younger adults. Indeed, there is evidence to support these ideas; age deficits in learning are larger for third when compared with second-order probabilistic structures (Bennett et al., 2007; Howard et al., 2004), and older adults sometimes fail to learn third-order structure at all (Howard et al., 2004). These findings suggest that there may be an upper limit to the level of structure that older adults can acquire. Might there also be a lower limit at which age deficits in implicit probabilistic sequence learning are reduced or disappear entirely? This remains an open question because most studies comparing younger and older adults have used second-order structures.
Studies assessing the effects of aging on learning second-order probabilistic structures find that both young and older adults learn the regularities, but older adults learn less about the regularity than younger adults, particularly when training is extended. Specifically, learning of the sequence is often comparable early in training, but in late training older adults’ sequence learning appears to asymptote, whereas younger adults continue to learn. This suggests that the overall capacity to learn probabilistic regularities (and not just rate of learning per se) is reduced in old age. Because age differences typically emerge in late training when the age-vulnerable striatal system is thought to dominate performance, they are hypothesized to reflect deterioration/dysfunction of the striatal learning system responsible for forming probabilistic associations (Bennett, Madden, Vaidya, Howard, & Howard, 2011; Janacsek et al., 2012; Simon, Vaidya, Howard Jr., & Howard, 2012). If age differences in learning are due to older adults’ impaired ability to form associations, then a deficit should also be observed even when the to-be-associated items are temporally adjacent.
To date, no studies have directly compared younger and older adults’ learning of first- and second-order probabilistic structures within the same study when all other study factors are held constant. Without such a comparison it is possible, for example, that age deficits in learning second and higher order structures actually reflect more general cognitive impairments, such as age differences in working memory capacity, or general slowing (Salthouse, 1996). Thus, examining whether there are also age deficits in learning first-order probabilistic regularities will determine if there is a fundamental deficit in learning of probabilistic sequential regularities—even among adjacent events—or whether declines in other cognitive processes may disrupt an otherwise intact learning system.
One earlier study has reported age deficits in probabilistic sequence learning for first-order structure (Howard Jr., Howard, Dennis, & Kelly, 2008; Experiment 2), but there were also age differences in overall task accuracy, making it impossible to distinguish between age deficits in learning and the willingness to make errors (e.g., speed/accuracy tradeoffs). Howard Jr. and coworkers (2008) also examined learning of second-order structure in a different experiment (Experiment 1), but a number of other factors, including the probability of HP versus LP triplets, differed between the experiments making it impossible to isolate the effects of structure.
This study tested younger and older adults on either a first- or second-order version of the Triplets Learning Task (TLT), a probabilistic sequence learning task explained in detail in the Method section (Howard Jr. et al., 2008). Importantly, all other study factors were held constant across structural conditions. Our primary goal was to examine whether age deficits in implicit sequence learning are exclusive to higher order regularities (i.e., second order), or whether they are also found for simpler regularities (i.e., first order). A secondary goal was to determine if age deficits in learning vary with structure; that is, whether age deficits are larger for one level of structure when compared with the other.
Method
Participants
Twenty-six college-aged adults (M = 19.5 years; SD = 1.1) and 28 older adults (M = 70.9 years; SD = 5.5) participated. They were recruited through the Georgetown Psychology Department participant pool or from the community by advertisement in the Washington Post. Their demographics and neuropsychological performance are in Table 1. Older adults were highly educated and differed from the younger adults only in processing speed, as assessed by the Digit Symbol Substitution Test (DSST; Wechsler, 1997). Young adults were compensated with course credit or $25 and older adults with $25. Participants were tested individually in sessions lasting 90min.
Table 1.
Mean (SD) Demographic and Neuropsychological Characteristics of Participants Separated by Age Group
| Older adults | Younger adults | |||
|---|---|---|---|---|
| First order | Second order | First order | Second order | |
| Age* | 70.2 (4.9) | 71.6 (6.1) | 19.0 (1.0)* | 20.0 (.90) |
| Education | 16.7 (2.3) | 16.9 (2.2) | 13.4 (1.2) | 14.1 (1.1) |
| BDS | 7.2 (1.9) | 7.5 (2.9) | 7.7 (2.6) | 8.4 (2.6) |
| DSST* | 59.9 (14.7) | 68.3 (17.6) | 96.6 (21.1) | 89.4 (7.7) |
| NAARTa | 14.4 (7.4) | 12.8 (6.3) | 15.6 (8.0) | 14.3 (6.8) |
| MMSE | 28.2 (1.7) | 28.4 (1.3) | — | — |
Notes. BDS = Backwards Digit Span; DSST = Digit Symbol Substitution Test; MMSE = Mini Mental State Examination. Means that are statistically different between age groups are denoted with an asterisk. Means that are statistically different between structural conditions within an age group are denoted by an asterisk in the first-order column.
aThe North American Adult Reading Test (NAART) is scored such that higher scores reflect poorer performance. For all other neuropsychological tests, higher scores indicate better performance.
The TLT
Participants completed 1,500 trials of the TLT (Howard Jr. et al., 2008). A schematic of the TLT is shown in Figure 1. Participants view a horizontal row of four open circles centered on a computer screen. On each trial, a three-event sequence of the circles (a “triplet”) fills in sequentially red, red, and green. Participants are instructed to observe the first two red “cues” and to indicate the location of the green “target” by pressing a spatially corresponding button. Importantly, they are not informed of the presence of any regularities and are only told to respond as quickly as possible. Cues are displayed for 120ms each (150ms ISI) followed by the target, which remains in view until a correct response. The next trial begins 650ms after the response.
Figure 1.
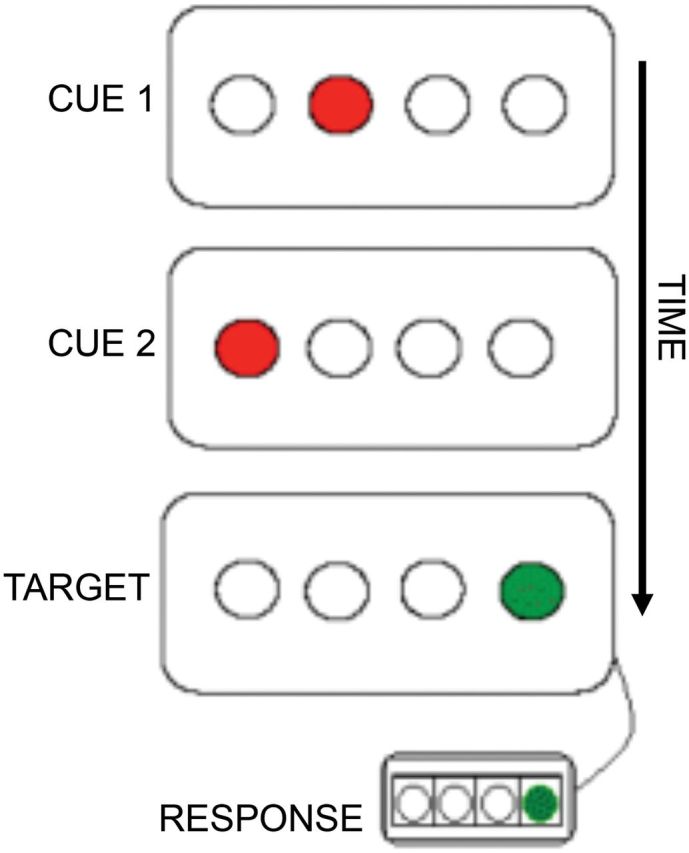
Schematic of the Triplets Learning Task. Each trial, or “triplet,” consists of the sequential presentation of two red cues and a green target. Subjects are instructed to view the first two red cues of each triplet and to respond only to the location of the green target using a corresponding response button.
This task is particularly well suited for comparing age groups with different motor capabilities. In contrast to more traditional sequence learning tasks, participants do not respond to every event; so, the motor demands of the task and the possibility for motor sequencing are minimized. In addition, the time between events within a triplet is controlled, because event timing is not determined by the participant’s response time.
Unbeknownst to participants, the location of one of the red cues probabilistically predicts the target’s location, whereas the location of the other red cue is random. For first-order regularities, the second red cue (i.e., the one immediately preceding the target) is predictive, whereas the first red cue is predictive for second order. Specifically, for a given cue on 80% of the trials, the target appeared in the HP location and on the other 20% of trials it occurred in one of the three LP locations. This resulted in 16 triplets occurring with HP (80% frequency) and 48 triplets occurring with LP (20% frequency) for both the first- and second-order conditions.
The HP triplets were not determined randomly, but rather followed one of six possible patterns (i.e., 1–2–3–4; 2–3–4–1; 3–4–1–2, etc., where numbers correspond to spatial position). For example, a participant in the second-order condition receiving the regularity 1–2–3–4 would see 1r 2 and 4r 1 (where r indicates the position of the second, nonpredictive red cue) with HP, and 2r 1 and 1r 4 with LP. In contrast, a participant in the first-order condition with 1–2–3–4 would see r 12 and r 41 with HP and r 21 and r 14 with LP. This ensured that the cue–target relationships were counterbalanced across participants and that all of the possible target locations occurred equally often (Howard Jr. et al., 2008). Thus, the only factor that differed between the first and second-order conditions was which of the two red cues preceding the target was predictive; all other factors were held constant.
Each session contained 10 blocks of 50 trials each (500 trials per session) and lasted approximately 20min. Participants therefore completed three sessions of the TLT for a total of 1,500 trials. At the end of each block, participants’ average response time was displayed, along with instructions to either “focus more on speed” or “focus more on accuracy.” This was done to drive both younger and older adults to 92% accuracy, with the instruction they received determined by overall accuracy on that block (e.g., Howard Jr. et al., 2008; Simon, Howard Jr., & Howard, 2011).
Procedure
The experiment employed a mixed design with age (young, old) and level of structure (first order, second order) as between subject factors. Session (1–3) and triplet probability (HP, LP) were within subject factors. After obtaining consent, 14 of the 26 younger adults were assigned to the first-order condition and 12 to the second-order condition. The 28 older adults were evenly divided into the first- and second-order conditions.
After they heard and indicated that they understood the task instructions, participants completed three sessions of the TLT. To minimize fatigue, brief breaks occurred at the end of each block and longer breaks between sessions. After the third session, participants completed neuropsychological tests measuring working memory (Backwards Digit Span—BDS; Wechsler, 1997), verbal intelligence (North American Adult Reading Test–NAART; Blair & Spreen, 1989), and processing speed (Digit Symbol Substitution Test--DSST; Salthouse, 1996). Older adults also completed the Mini Mental State Examination (Stern, Sano, Paulson, & Mayeux, 1987) to screen for signs of cognitive impairment. The study was approved by the Georgetown University Institutional Review Board.
Quantifying Implicit Sequence Learning
As in earlier studies using the TLT, we used Implicit Associative Learning IAL) scores, which measure learning unbiased by individual or group differences in overall RT (Howard Jr. et al., 2008). Prior to calculating these scores, and consistent with previous studies, we eliminated certain types of trials from all analyses, including “repetitions” from both first- and second-order conditions (e.g., 111, 333), “trills” from the second-order condition (e.g., 121, 343) and “doubles” from the first-order condition (e.g., 122, 311). We eliminated these because people have pre-existing response tendencies to these triplets (Boyer, Destrebecqz, & Cleeremans, 2005; Cleeremans & McClelland, 1991; Howard Jr. et al., 2008). In addition, due to the nature of the regularity, these triplet types cannot be counterbalanced across subjects. Therefore, unlike the other triplet types, they occur with LP for all participants, so the effects of learning cannot be separated from pre-existing response tendencies for these triplet types. We also eliminated errors before calculating IAL scores.
To determine individual IAL scores we calculated the median RT for all correct responses for each of the remaining 48 triplets and then correlated this with the observed triplet frequency for each individual. People with higher negative correlations between RT and triplet frequency reveal greater sequence-specific learning, in that they are responding faster to the more frequent triplets and, thus, more predictable targets. For ease of interpretation, the correlations were multiplied by –1 so that higher IAL scores reflect greater learning. IAL scores were calculated for each participant on each of the three task sessions.
Results
Overall, mean accuracy was high (M ± SD = 0.94±0.05) and did not differ across age groups or structure (all Fs < 2.3, ps > .14), thus, we eliminated few trials due to errors, and results were calculated using a similar number of trials for each group. The absence of an age effect on overall task accuracy is important because any age differences in learning we observe in the response time data cannot be attributed to age differences in the willingness to make errors. Overall, young adults responded faster (M ± SD = 337.7±51.1ms) than older adults (M ± SD = 554.3±141.5ms; F(1, 50) = 72.8, = 0.59, p < .0001). There was also a main effect of session, such that response speed improved over sessions of the task; F(2, 100) = 81.4, = 0.62, p <.0001. However, mean response times did not differ by structure (F(1, 50) = 1.12, = 0.02, p = .31),suggesting that overall task speed was not influenced by structure. No interactions were reliable.
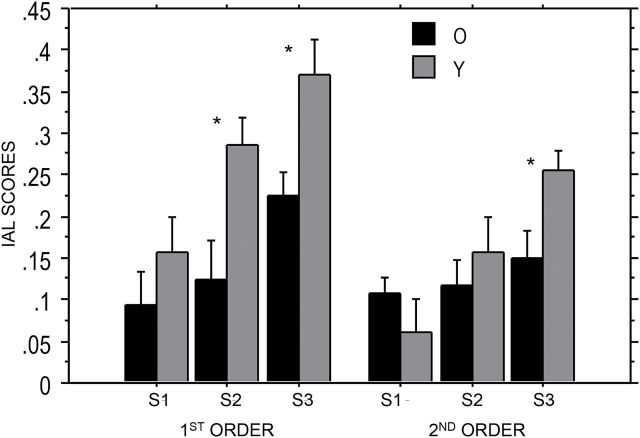
To examine sequence learning, we submitted IAL scores, which are shown in Figure 2, to a mixed design 2×2 × 3 ANOVA with Age and Structure varying between subjects and Session varying within subjects. There was a main effect of Session (F(2, 100) = 26.74; = 0.35; p < .0001); mean IAL scores increased across sessions, suggesting that learning increased over training (Session 1: M ± SD = 0.11±0.13, Session 2: M ± SD = 0.17±0.15, Session 3: M ± SD = 0.25±0.14). All pairwise comparisons between the sessions were reliable (ts > 3.00, ps < .004). There was a main effect of Age (F(1, 50) = 7.96; = 0.12; p = .007), such that younger adults had higher IAL scores on average (M ± SD = 0.22±0.17) compared with older adults (M ± SD = 0.14±0.13). Finally, there was also a main effect of Structure (F(1, 50) = 6.16; = 0.11; p = .017); participants in the first-order condition had higher scores on average (M ± SD = 0.21±0.17) than those in the second-order condition (M ± SD = 0.14±0.13).
Figure 2.
Mean Implicit Associative Learning scores for young and older adults separated by structure and session. Means that are significantly different (p < .05) are denoted with an *.
There was also an Age × Session interaction, which indicated that IAL scores increased more across sessions for the younger than the older adults (F(2, 100) = 4.83; = 0.09; p = .01). However, neither the Age × Structure (F(1, 50) = 2.67; = 0.05; p = .10) nor the Age × Structure × Session interaction (F(2, 100) = 0.626; = 0.03; p = .54) was significant, suggesting that the age-related deficit in sequence learning did not vary with the level of structure.
Even though the omnibus ANOVA revealed no interactions involving Age and Structure, we also conducted separate Age × Sessions ANOVAs on each level of structure. This was particularly important for the first-order structure; our primary research question concerns whether there are age differences in this level of structure, and so we wanted to confirm that there are significant age differences even when first-order structure is examined alone. The ANOVA on first-order structure revealed a main effect of Session (F(1, 52) = 7.75; = 0.42; p = .010) with scores increasing over sessions. Most important, there was a main effect of Age (F(1, 26) = 7.75; = 0.23; p = .001); with younger adults revealing higher IAL scores (M ± SD = 0.27±0.17) than older adults (M ± SD = 0.15±0.15). The lack of a Session × Age interaction (F(2, 52) = 1.8; = 0.07; p = .17),suggests that the effect of age did not differ across sessions. For this first-order structure, significant age deficits were detected in both the second (t(26) = 2.82, p = .009) and third (t(28) = 2.92, p = .007) sessions. Thus, it is clear that there are age deficits in learning first-order regularities.
The separate ANOVA on the second-order groups was also important to determine whether we replicated the pattern of age difference in second-order learning we have found in earlier research. This ANOVA yielded a main effect of Session (F(1, 48) = 8.78; = .27; p = .0006), with IAL scores increasing as training progressed. There was no main effect of Age (F(1, 24) = 1.05; = .04; p = .32), but there was a Session × Age interaction (F(1, 48) = 3.59; = .13; p = .035); age deficits in learning were not detected in the first two sessions (ts < 1.07, ps > .29), but emerged in the last session of training (t(24) = 2.44, p = .023; Figure 2). This late-emerging age deficit in learning replicates our earlier studies comparing learning of second-order TLT regularities in young versus older adults after similar amounts of training (Howard Jr. et al., 2008; Simon et al., 2011, 2012).
Discussion
In this study, older and younger adults completed either a first- or second-order version of the TLT, a probabilistic sequence learning task. This is the first study to compare the effects of age on learning of first- and second-order structures directly while holding all other study factors constant. In the following, we discuss our findings in terms of our primary and secondary research objectives.
Do Age Deficits Occur for First-Order Probabilistic Structures?
The findings from this study provide a clear answer to our main research question; there were age differences in learning first-order structure. This finding is consistent with Howard Jr. and coworkers (2008), but, unlike the earlier study, in this study the age groups had equal overall accuracy, and the ratio of HP:LP triplets was the same across the two structural conditions.
Crucially, we not only detected age deficits for learning first-order structure, but also observed the expected pattern of age deficits for second-order structure. Age differences in learning second-order structure were late-emerging (detected in Session 3 only), replicating the results of earlier studies using the TLT (Simon et al., 2011, 2012), as well as those using more motor-based sequence learning tasks (Howard et al., 2004). Thus, the age differences we detected in the first-order condition were likely not due to special characteristics of our sample.
Not only are there age deficits in learning first-order structure, but also these deficits are at least as large as those in learning second-order structure; significant age deficits first appeared in the second session for first order, but not until the third session for second order.
Do Age Deficits Vary With Level of Structure?
The lack of any significant interactions involving Age × Structure in the omnibus ANOVA suggests that the magnitude of the age deficits in learning did not depend on the level of structure—that is, similar age differences emerged for learning both second-order and first-order structures. As discussed in the following, however, whether there are age differences in the effects of structure is still an open question. This is because there is evidence suggesting that the effect of structure on learning may be influenced by multiple factors.
The fact that the omnibus Age × Structure and Age × Structure × Session interactions were not significant was at first surprising because motor-based sequence learning tasks have found that learning is better for second when compared with third-order structure, and that older adults learn very little from third-order structure, suggesting that age deficits might be exacerbated by higher order regularities (Howard et al., 2004).
In addition, the lack of an Age × Structure interaction is seemingly at odds with findings from an earlier report using the TLT (Howard Jr. et al., 2008). Through a cross-experiment (first vs. second order) comparison, Howard Jr. and coworkers (2008) had proposed that there might be smaller age deficits for first- than second-order regularities; the IAL scores reported in that comparison suggested that younger adults learned similar amounts from both first- and second-order versions of the task, whereas the older adults learned more from first-order relationships. However, a number of factors differed across the 2008 experiments in addition to structure, confounding the comparison. First, the ratio of HP to LP triplets varied across the 2008 experiments; it was 80:20 in the second-order experiment and 90:10 in the first-order experiment. Second, the age groups were not matched for overall task accuracy (unlike the present study). Finally, and perhaps most important, because the Howard Jr. and coworkers (2008) study was the first to use the TLT, participants were given very extended training—6,000 trials, instead of the 1,500 trials given in the present study— and the IAL scores reported were from the last 3,000 of those trials. A retrospective reanalysis of the IAL scores for the 2008 studies using the first 1,500 trials yielded results very similar to those reported here; there were similar main effects of age (favoring young), session, and structure (favoring first order, though this effect was only marginal in the 2008 data). In addition, the interactions involving age × structure were not significant for the 2008 data, consistent with the present findings. In fact, age differences were in the direction of being larger in the first-order condition, just as in this study.
The fact that the conclusions drawn from the 2008 experiments are different depending on the stage of learning considered suggests that length of training may be one factor influencing how age differences in learning are affected by structure. However, as will be discussed more later, length of training is not likely to be the only important factor. Thus, it seems that the question of how structure influences age differences in learning is a complex issue, likely requiring additional studies to address.
Do Other Cognitive Factors Affect Age Deficits in Learning First- and Second-Order Structure?
The finding of age differences in learning for both first- and second-order structures supports the notion that there is a fundamental age deficit in the system underlying the formation of associations and that this associative deficit occurs for implicit as well as explicit domains of learning (Kilb & Naveh-Benjamin, 2007; Naveh-Benjamin, Brav, & Levy, 2007; Naveh-Benjamin et al., 2009). Several studies showing age differences in the implicit learning of second-order probabilistic structures have proposed this explanation (for review, see Howard Jr. & Howard, 2013). However, without also showing age deficits for first-order structures, these studies are unable to rule out the possible contribution of age differences in working memory capacity. If age-related working memory deficits were causing the age deficits in learning, then in this study age differences would be expected to be larger for the second- than first-order structure as there are more intervening events, but they were not. Moreover, we found no age differences in working memory as assessed by BDS across groups and/or conditions in our sample, and BDS scores were neither correlated with the learning scores within any group, nor when all the groups were combined. Thus, age-related declines in working memory cannot account for the age differences in learning we report. This finding is also consistent with earlier research that has shown working memory to be more important for explicit rather than implicit sequence learning, as well as for skill learning than sequence-specific learning (for review see Janacsek & Nemeth, 2013). However, future work could include multiple/more sensitive working memory tasks to examine whether specific components of working memory (e.g., attentional refreshing) relate to age differences in sequence learning (Loaiza, Rhodes, & Anglin, 2013; Sylvain-Roy, Lungu, & Belleville, 2014).
Although they did not differ in working memory, younger and older adults in our sample did differ in processing speed, as assessed through the DSST. Although this study was not designed to investigate this, processing speed was associated with individual differences in learning but only in the first-order groups: There were significant correlations across all individuals in the first-order condition between DSST scores and Sessions 2 (r(26) = .47, p = .01) and 3 (r(26) = .46, p = .01) IAL scores, such that those with better DSST performance (faster processing speed) had higher IAL scores in the TLT. These correlations were not significant in the second-order condition (all ps > .33). It is possible that slower speed might make learning first-order probabilistic associations especially challenging for older adults because they must associate immediately adjacent events (i.e., the second cue and the target) that occur rapidly. Although performance on the DSST relates to motor speed, it is also thought to index general information processing capacity, which has been shown to influence cognitive abilities above and beyond motor speed (Bryan & Luszcz, 1996; Joy, Kaplan, & Fein, 2004). The fact that DSST scores were associated with IAL scores from the TLT—a task in which motor demands are minimized—supports this idea.
We next examined how processing speed may have contributed to the age deficits in learning we observed. We performed a mediation analysis to test whether participants’ scores on the DSST mediated the relationship between Age (the predictor) and IAL scores (the outcome). We tested several mediation models, using IAL scores from Sessions 1–3, respectively, as the outcome variables. The first three models collapsed across structure in consideration of power. However, we also tested three models for each level of structure separately given the correlations between DSST and first–but not second order—scores reported earlier. We found no evidence that processing speed mediated the relationship between age and sequence learning in any model; the indirect effect of Age on IAL scores (i.e., through DSST scores) was not significant. Therefore, there is no evidence that DSST scores mediate the age differences in sequence learning we report, even though DSST did correlate with first-order learning. It is possible that this failure to find mediation reflects low power as this study was not specifically designed to investigate this issue. Future work could examine this possibility further by including larger sample sizes, as well as more sensitive tests of processing speed and additional cognitive measures.
Limitations
Our finding that processing speed correlates with learning of first-order, but not second-order, structure suggests that event timing could affect age differences in learning, but this study used only one presentation rate. It will be useful to vary timing in future studies to assess the generalizability of the present findings across various stimulus presentation rates. For example, one potential way in which learning might be maximized for older adults would be to increase the amount of time that they have to process stimuli. However, numerous studies using more motor-based sequence learning tasks have demonstrated that increasing the time between stimuli actually makes learning the regularities more difficult for young adults (Frensch, Buchner, & Lin, 1994; Frensch & Miner, 1994; Howard Jr., Howard, Dennis, & Yankovich, 2007; Stadler, 1995), and this might also turn out to be the case for the TLT. Nonetheless, future work could explore the possible tradeoffs between timing of the to-be-associated events and learning outcomes, and whether timing might have different effects for younger versus older adults.
Another limitation of this study is that our findings concerning the effects of structure may hold for only relatively short training—it is not clear how the results would change if the groups were given a longer period of training, such as the extensive, 3-day training used in Howard Jr. and coworkers (2008). The fact that the published pattern of results from the 2008 data that were based on much longer training was different than that observed in our reanalysis of the data (i.e., using comparable length of training to that given here) highlights this point.
Finally, we did not collect a recognition measure from our participants. Thus, we do not have direct evidence that the learning was implicit, in the sense that people have no explicit knowledge of the regularities they learned. We did not collect such a recognition measure, because all participants also took part in a second day of testing on implicit learning tasks. Thus, we did not want them to be alerted to the fact that regularities were present in the tasks they were encountering. We judged it reasonable to prioritize this goal (i.e., goal of the larger protocol) over administering an explicit recognition test immediately following the TLT because evidence from several published studies with the task indicates that virtually no one becomes aware of the probabilistic regularity in the TLT, even when several sensitive measures are used. For example, neither young nor older adults have been able to distinguish between high and low frequency triplets in a recognition task given at the end of training (Howard Jr. et al., 2008; Simon et al., 2011; 2012).
Conclusions
This study is the first to compare the effects of age on implicit learning of first- and second-order probabilistic regularities when all other task factors are held constant. Age deficits in implicit learning emerged not only for second-order probabilistic regularities, but also for simple, first-order regularities, suggesting that there is a fundamental deficit in the older group’s ability to form probabilistic sequential associations. These results are consistent with the view that there is an associative binding deficit in aging and that this deficit occurs not only for explicit learning and memory (Naveh-Benjamin, 2000; Naveh-Benjamin et al., 2007, 2009), but also for implicit learning. These findings suggest that the aging of implicit learning might compromise essential everyday functions (e.g., habit formation, decision making) that are subserved by the ability to implicitly learn probabilistic regularities occurring sequentially in the environment, and they also highlight the need for research on how to preserve and/or promote implicit forms of learning.
Funding
This work was supported by National Institutes of Health/National Institute on Aging grants R01AG036863 to D. V. Howard and J. H. Howard Jr. and F31AG047037 to C. M. Stillman.
Acknowledgments
The authors would like to thank Lauren Westbay and Halley Feldman for assistance with data collection.
References
- Bennett I. J., Howard J. H., Jr., Howard D. V. (2007). Age-related differences in implicit learning of subtle third-order sequential structure. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences, 62, 98–103. 10.1093/geronb/62.2.P98 [DOI] [PubMed] [Google Scholar]
- Bennett I. J., Madden D. J., Vaidya C. J., Howard J. H., Jr., Howard D. V. (2011). White matter integrity correlates of implicit sequence learning in healthy aging. Neurobiology of Aging, 32, 2317.e1–2317.e12. 10.1016/j.neurobiolaging.2010.03.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair J. R., Spreen O. (1989). Predicting premorbid IQ: A revision of the National Adult Reading Test. The Clinical Neuropsychologist, 3, 129–136. 10.1080/13854048908403285 [Google Scholar]
- Boyer M., Destrebecqz A., Cleeremans A. (2005). Processing abstract sequence structure: Learning without knowing, or knowing without learning? Psychological Research, 69, 383–398. 10.1007/s00426-004-0207-4 [DOI] [PubMed] [Google Scholar]
- Bryan J., Luszcz M. A. (1996). Speed of information processing as a mediator between age and free-recall performance. Psychology and Aging, 11, 3–9. 10.1037/0882-7974.11.1.3 [DOI] [PubMed] [Google Scholar]
- Cleeremans A., McClelland J. L. (1991). Learning the structure of event sequences. Journal of Experimental Psychology: General, 120, 235–253. 10.1037/0096-3445.120.3.235 [DOI] [PubMed] [Google Scholar]
- Frensch P. A., Buchner A., Lin J. (1994). Implicit learning of unique and ambiguous serial transitions in the presence and absence of a distractor task. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 567–584. 10.1037/0278-7393.20.3.567 [Google Scholar]
- Frensch P. A., Miner C. S. (1994). Effects of presentation rate and individual differences in short-term memory capacity on an indirect measure of serial learning. Memory & Cognition, 22, 95–110. 10.3758/BF03202765 [DOI] [PubMed] [Google Scholar]
- Howard J. H., Jr., Howard D. V. (1997). Age differences in implicit learning of higher order dependencies in serial patterns. Psychology and Aging, 12, 634–656. 10.1037/0882-7974.12.4.634 [DOI] [PubMed] [Google Scholar]
- Howard J. H., Jr., Howard D. V. (2013). Aging mind and brain: Is implicit learning spared in healthy aging? Frontiers in Psychology, 4, 817. 10.3389/fpsyg.2013.00817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. H., Howard D. V., Dennis N. A., Kelly A. J. (2008). Implicit learning of predictive relationships in three-element visual sequences by young and old adults. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 1139–1157. 10.1037/a0012797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. H., Jr., Howard D. V., Dennis N. A., Yankovich H. (2007). Event Timing and age deficits in higher-order sequence learning. Neuropsychology, Development, and Cognition, Section B: Aging, Neuropsychology and Cognition, 14, 647–668. 10.1080/13825580601186635 [DOI] [PubMed] [Google Scholar]
- Howard D. V., Howard J. H., Jr., Japikse K., DiYanni C., Thompson A., Somberg R. (2004). Implicit sequence learning: Effects of level of structure, adult age, and extended practice. Psychology and Aging, 19, 79–92. 10.1037/0882-7974.19.1.79 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janacsek K., Fiser J., Nemeth D. (2012). The best time to acquire new skills: Age-related differences in implicit sequence learning across the human lifespan. Developmental Science, 15, 496–505. 10.1111/j.1467-7687.2012.01150.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janacsek K., Nemeth D. (2013). Implicit sequence learning and working memory: Correlated or complicated? Cortex, 49, 2001–2006. 10.1016/j.cortex.2013.02.012 [DOI] [PubMed] [Google Scholar]
- Joy S., Kaplan E., Fein D. (2004). Speed and memory in the WAIS-III Digit Symbol–Coding subtest across the adult lifespan. Archives of Clinical Neuropsychology, 19, 759–767. 10.1016/j.acn.2003.09.009 [DOI] [PubMed] [Google Scholar]
- Kilb A., Naveh-Benjamin M. (2007). Paying attention to binding: Further studies assessing the role of reduced attentional resources in the associative deficit of older adults. Memory & Cognition, 35, 1162–1174. 10.3758/BF03193486 [DOI] [PubMed] [Google Scholar]
- Loaiza V. M., Rhodes M. G., Anglin J. (2013). The influence of age-related differences in prior knowledge and attentional refreshing opportunities on episodic memory. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences. Advance online publication. 10.1093/geronb/gbt119 [DOI] [PubMed] [Google Scholar]
- Naveh-Benjamin M. (2000). Adult age differences in memory performance: Tests of an associative deficit hypothesis. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26, 1170–1187. 10.1037/0278-7393.26.5.1170 [DOI] [PubMed] [Google Scholar]
- Naveh-Benjamin M., Brav T. K., Levy O. (2007). The associative memory deficit of older adults: The role of strategy utilization. Psychology and Aging, 22, 202–208. 10.1037/0882-7974.22.1.202 [DOI] [PubMed] [Google Scholar]
- Naveh-Benjamin M., Shing Y. L., Kilb A., Werkle-Bergner M., Lindenberger U., Li S. C. (2009). Adult age differences in memory for name-face associations: The effects of intentional and incidental learning. Memory (Hove, England), 17, 220–232. 10.1080/09658210802222183 [DOI] [PubMed] [Google Scholar]
- Newport E. L., Aslin R. N. (2004). Learning at a distance I. Statistical learning of non-adjacent dependencies. Cognitive Psychology, 48, 127–162. 10.1016/S0010-0285(03)00128-2 [DOI] [PubMed] [Google Scholar]
- Norman E., Price M. C. (2012). Social intuition as a form of implicit learning: Sequences of body movements are learned less explicitly than letter sequences. Advances in Cognitive Psychology, 8, 121–131. 10.2478/v10053-008-0109-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reber A. S. (1989). Implicit learning and tacit knowledge. Journal of Experimental Psychology: General, 118, 219–235. 10.1037/0096-3445.118.3.219 [Google Scholar]
- Remillard G., Clark J. M. (2001). Implicit learning of first-, second-, and third-order transition probabilities. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27, 483–498. 10.1037//0278-7393.27.2.483 [DOI] [PubMed] [Google Scholar]
- Salthouse T. A. (1996). The processing-speed theory of adult age differences in cognition. Psychological Review, 103, 403–428. 10.1037/0033-295X.103.3 [DOI] [PubMed] [Google Scholar]
- Seaman K. L., Howard D. V., Howard J. H., Jr. (2014). Adult age differences in learning on a sequentially cued prediction task. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences, 69, 686–694. 10.1093/geronb/gbt057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon J. R., Howard J. H., Jr., Howard D. V. (2011). Age differences in implicit learning of probabilistic unstructured sequences. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences, 66, 32–38. 10.1093/geronb/gbq066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon J. R., Vaidya C. J., Howard J. H., Howard D. V. (2012). The effects of aging on the neural basis of implicit associative learning in a probabilistic triplets learning task. Journal of Cognitive Neuroscience, 24, 451–463. 10.1162/jocn_a_00116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler M. A. (1995). Role of attention in implicit learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 21, 674–685. 10.1037/0278-7393.21.3.674 [Google Scholar]
- Stern Y., Sano M., Paulson J., Mayeux R. (1987). Modified mini-mental state examination: Validity and reliability. Neurology, 3, 179. [Google Scholar]
- Sylvain-Roy S., Lungu O., Belleville S. (2014). Normal aging of the attentional control functions that underlie working memory. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences. Advance online publication. 10.1093/geronb/gbt166 [DOI] [PubMed] [Google Scholar]
- Wechsler D. (1997). Wechsler Adult Intelligence Scale (3rd ed.). San Antonio, TX: Harcourt Assessment. [Google Scholar]