Designing alternative splicing RNA-seq studies. Beyond generic guidelines

Abstract

Motivation: Designing an RNA-seq study depends critically on its specific goals, technology and underlying biology, which renders general guidelines inadequate. We propose a Bayesian framework to customize experiments so that goals can be attained and resources are not wasted, with a focus on alternative splicing.

Results: We studied how read length, sequencing depth, library preparation and the number of replicates affects cost-effectiveness of single-sample and group comparison studies. Optimal settings varied strongly according to the target organism or tissue (potential 50–500% cost cuts) and, interestingly, short reads outperformed long reads for standard analyses. Our framework learns key characteristics for study design from the data, and predicts if and how to continue experimentation. These predictions matched several follow-up experimental datasets that were used for validation. We provide default pipelines, but the framework can be combined with other data analysis methods and can help assess their relative merits.

Availability and implementation: casper package at www.bioconductor.org/packages/release/bioc/html/casper.html, Supplementary Manual by typing casperDesign() at the R prompt.

Contact: rosselldavid@gmail.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

The design of an RNA-seq experiment is crucial for its validity and an adequate use of resources but is typically not assessed in detail. General guidelines ignore critical aspects such as the specific research goals or the nature of the studied phenomenon, e.g. ENCODE guidelines recommend 30 million (m) paired-end reads of >30 base pairs (bp) for expression estimation and 200 m read pairs of >76 bp for novel transcript discovery [ENCODE Project Consortium, 2012 (encodeproject.org/ENCODE/protocols/dataStandards/ENCODE\_RNAseq\_Standards\_V1.0.pdf)]. As we show below the adequacy of such guidelines can change significantly between studies. Several experimental design strategies were recently proposed. Grant et al. (2011) and Li and Dewey (2011) developed an RNA-seq simulator for single sample studies, considering mapping issues and situations where a reference transcriptome is unavailable, respectively. Given a series of experimental protocols, the simulation pipeline of Griebel et al. (2012) can explore the potential effects of various biases and settings. Busby et al. (2013) and Rossell and Müller (2013) proposed sample size calculations to compare overall gene expression across two groups, where interestingly these can be based on pilot or public data and hence incorporate some of the characteristics of this study. These strategies focus mostly on specific settings such as one sample studies, a given data analysis or technology (e.g. short reads). Here we propose a general framework for either single- or multi-sample studies targeting gene or isoform expression that is flexible to accommodate any goal, technology (including long reads) and data analysis. The approach is guided by Bayesian decision theory, where key characteristics of the phenomenon under study or the technology are learnt as data become available and, importantly, the uncertainty associated to these unknown characteristics is formally taken into account in a mathematically coherent manner. The goal is to provide recommendations tailored to each study, such as sequencing settings, the potential benefits of conducting further experimentation or the relative merits of different data analysis strategies. Additionally, the framework can also pinpoint general principles such as the balance between increasing sample size versus sequencing depth or assess the cost-effectiveness of short reads versus long reads from the latest sequencing technologies.

2 Approach

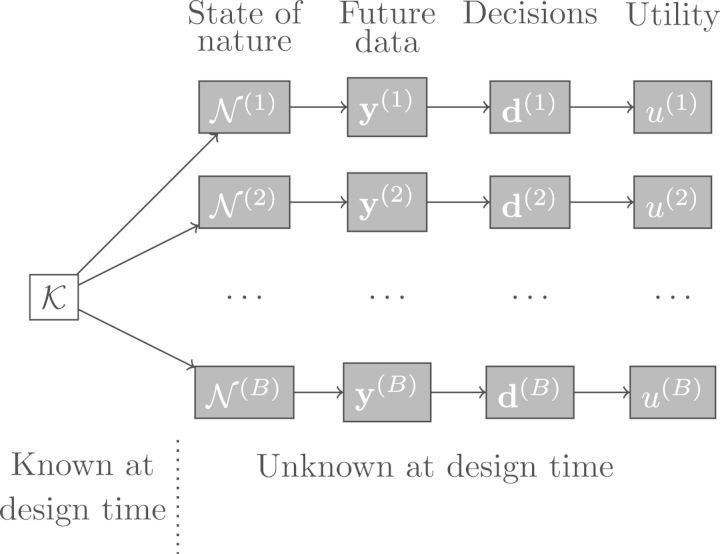
A main difficulty to design RNA-seq or similar high-throughput studies is the substantial uncertainty regarding its biological background (e.g. variability, actual expression levels, extent of differences between groups) and the sequencing process itself (e.g. distribution of reads or insert sizes, mappability). We refer to the collection of these unknown characteristics as the state of nature $\mathcal{N}$. Bayesian predictive simulation reflects this uncertainty by generating various possible values of $\mathcal{N}$ according to their probability given current knowledge $\mathcal{K}$, and subsequently generating future experimental data $y$ that could be obtained under a given experimental design $e$ and associated analysis results $d$. Figure 1 gives a schematic representation. Ideally $\mathcal{K}$ contains pilot data from the same or a similar study, but we provide default human and mice samples and a strategy for other tissues and species (Supplementary Section 6). The simulation results can guide the design of a single-stage study where all samples are collected simultaneously or a two- or multi-stage study that collects data batches in a sequential fashion. We emphasize that each of such batches should contain samples from all the groups under comparison, else artifacts such as batch effects can render the data useless. Given that deciding the sequencing settings and number of replicates upfront can be challenging, $\mathcal{K}$ can be a first data batch that is used to guide the simulation and assess the benefits of collecting further data. Upon obtaining any further additional data one may add it to $\mathcal{K}$ and repeat the simulation using the updated knowledge. For simplicity in our examples we consider one- or two-stage designs.

Fig. 1.

Representing uncertainty via simulation. States of nature ${\mathcal{N}}^{(1)},\dots ,{\mathcal{N}}^{(B)}$ are probabilistically generated given current knowledge $\mathcal{K}$. ${\mathcal{N}}^{(b)}$ includes isoform expression, insert sizes, read distribution along transcripts and mappability. Given ${\mathcal{N}}^{(b)}$ and an experiment design, future data $y^{(b)}$ are generated and data analysis decisions $d^{(b)}$ are made. The utility $u^{(b)}$ measures how good decisions were and any incurred costs. The expected utility is estimated with $\widehat{U}=B^{-1}{\displaystyle {\sum }_{b=1}^B{u}^{(b)}}$

Formally, simulations are based on a probability model for $(\mathcal{N},y)$ given $\mathcal{K}$ (Section 3) and, after they are obtained, they can be analysed with any user-specified strategy to make decisions $d$ (e.g. expression estimates, differential expression calls). Simulations for individual samples are based on casper (Rossell et al., 2014), which extends a standard RNA-seq probabilistic representation (Salzman et al., 2011), and multiple samples are linked via the LogNormal-Normal with Modified Variance (LNNMV) model (Yuan and Kendziorski, 2006), or alternatively the GaGa model (Rossell, 2009). Briefly, casper records the full exon path visited by each read to avoid the loss of information from counting single exons or exon pairs (in particular rendering it applicable to short and long reads alike) and does not impose parametric assumptions on read and insert size distributions (e.g. uniform reads, Normal or Poisson inserts). Further, being a count-based model renders it computationally efficient, which is critical to simulate many datasets under potentially numerous experimental settings. Regarding LNNMV and GaGa, they appealingly do not impose any relationship between mean and variance and, while strictly models for continuous data, as discussed below after an adequate transformation (essentially, log-fragments per kilobase per million [FPKM]) we found that they can provide a better fit to experimental data than count-based distributions (e.g. Poisson or Negative Binomial). See Section 3.5 for a discussion of preprocessing and goodness-of-fit.

Once simulations have been obtained one can report any sensible criteria related to the study goals such as the error in estimating isoform expression, false discoveries or statistical power, and the experimenter can informally decide which design offers a better trade-off between accuracy and the cost of the experiment. Alternatively, one may formally define a utility function u that combines these competing goals (accuracy versus cost) into a single summary and adopt Bayesian decision theory to optimize the expected value of u (Berger, 1985). The approach is flexible in that the utility can incorporate any criteria reflecting the experimenter’s preferences, and is straightforward to implement using our posterior simulation approach. To facilitate the use of our framework we provide two default utilities. For single-sample studies, the utility considers the mean absolute error (MAE) in estimating isoform (or gene) expression and a cost term that depends on the chosen sequencing depth. MAE is a measure of overall estimation precision that is robust to outliers, e.g. preventing a few isoforms from having an unduly large effect on the final design, but naturally other choices are possible. We also illustrate an alternative based on the proportion of correctly identified dominant isoforms (with highest relative expression within a gene). For multi-sample studies, the utility considers the statistical power to find isoforms that are differentially expressed (DE) by a user-defined relevant margin (e.g. 2-fold), false discoveries and a cost that depends on the sample size and sequencing depth. In principle these utilities require setting certain parameters, but these have a simple interpretation and inverse decision theory (Swartz et al., 2006) bypasses the need to specify a single parameter value (Section 3.2, Supplementary Section 3). So far we kept technical discussion to a minimum, Section 3 outlines the methods, data preprocessing and model goodness-of-fit (see also Supplementary Sections 1–4). The Supplementary Material contains a summary of our mathematical notation.

3 Methods

3.1 Probability model

The basis for individual samples is casper. Let G be the number of genes of interest and ${\tilde{n}}_{gj}$ be the read count for gene $g=1,\dots ,G$ in sample j, then ${\tilde{n}}_j=({\tilde{n}}_{1j},\dots ,{\tilde{n}}_{\text{Gj}})\sim \text{Multinomial}({\tilde{N}}_j,{\mathit{\theta }}_j)$, where ${{\displaystyle \mathit{\theta }}}_j=({\theta }_{1j},\dots ,{\theta }_{Gj})$ are the true proportions of molecules from each gene and ${\tilde{N}}_j$ the total aligned reads. ${\tilde{N}}_j$ is the number of reads in single-end experiments and read pairs in paired-end experiments. We assume that gene g has I_g isoforms (from genome annotations or de novo predictions) and that reads come from each isoform with probabilities ${\mathit{\pi }}_{gj}=({\mathit{\pi }}_{g1j},\dots ,{\pi }_{g{I}_{g}j})$. That is, ${\mathit{\pi }}_{gj}$ are relative expressions of all known or predicted isoforms of gene g for sample j. The distribution of reads along a transcript is estimated non-parametrically from the data, and likewise for the distribution of insert sizes (length of RNA molecules after fragmentation). We set default symmetric Dirichlet priors ${\mathit{\theta }}_j\sim \text{Dir}(2),\hspace{0.17em}{\mathit{\pi }}_{\text{gj}}\sim \text{Dir}(2)$ which, while being non-informative, induce a mild form of shrinkage to improve parameter estimates (Rossell et al., 2014). The extension to multiple samples uses LNNMV model. Let ${\widehat{\eta }}_{\text{gij}}$ be any expression estimate of interest for isoform i in sample j, e.g. log-FPKM ${\widehat{\eta }}_{\text{gij}}=\text{log}({10}^9{\pi }_{\text{gij}}{\theta }_{\text{gj}}/w_{\text{gi}})$ where w_gi is the isoform length (bp). Then ${\widehat{\eta }}_{gij}\sim N({\mu }_{gik},{\varphi }_{gi})$ with group mean ${\mu }_{\text{gik}}\sim N({\mu }_0,{\tau }_0^2)$ and ${\varphi }_{\text{gi}}^{-1}\sim \text{Gamma}({\nu }_0/2,{\sigma }_0^2/2)$, where $({\mu }_0,{\tau }_0^2,{\nu }_0,{\sigma }_0^2)$ are estimated via empirical Bayes (Yuan and Kendziorski, 2006). We note that ${\varphi }_{\text{gi}}$ models flexibly isoform-specific variance, as it does not impose any relationship with the mean μ_gik, and that $\text{Var}({\widehat{\eta }}_{\text{gij}})$ includes the true variability in expression η_gij across samples and that due to estimation error of ${\widehat{\eta }}_{\text{gij}}$ given η_gij. Alternatively, GaGa assumes ${\widehat{\eta }}_{\text{gij}}\sim \text{Gamma}({\alpha }_{\text{gi}},{\alpha }_{\text{gi}}/{\mu }_{\text{gik}})$ with hierarchical Gamma distributions on α_gi and μ_gik (Supplementary Section 1.2). Both casper, LNNMV and GaGa lead to computationally tractable model fitting and posterior simulation, rendering the approach practical.

3.2 Default utilities

We consider utility functions $u=u(e,\mathit{\gamma },\widehat{\mathit{\gamma }})$ that measure usefulness of a design $e$ based on its cost, a (unknown) characteristic $\mathit{\gamma }$ of interest related to gene/isoform expression and its estimate $\widehat{\mathit{\gamma }}$ based on data eventually produced by $e$. We use the generic notation $\mathit{\gamma }$ to emphasize that this can be any quantity deemed relevant by the researcher, but as shown below $\mathit{\gamma }$ will often be a simple function of $\mathit{\pi }$ or $\mathit{\theta }$ (e.g. relative expression, differences across groups). We propose default $u(e,\mathit{\gamma },\widehat{\mathit{\gamma }})$ but the user can easily incorporate alternatives. In studies with a single sample j we let $\mathit{\gamma }={\mathit{\pi }}_j$ be the vector with genome-wide relative expressions for that sample. Denote the read length by r and the desired number of reads by N (i.e. as indicated to the sequencing facility), which is different from the eventually mapped reads ${\tilde{N}}_j$, then our default utility is $u(e,\widehat{\mathit{\gamma }},\mathit{\gamma })=-c_0-c_{1}2Nr-\text{MAE}$ for paired-end experiments (for single-ends replace 2 N by N), where the fixed cost c₀ does not depend on the design and can be ignored, c₁ is a cost per base sequenced to be defined and

$$\text{MAE}=\frac{1}{G}{\displaystyle {\sum }_{g=1}^G\frac{1}{I_{\text{g}}}}{\displaystyle {\sum }_{i=1}^{I_{\text{g}}}|{\widehat{\pi }}_{\text{gij}}}-{\pi }_{\text{gij}}|$$

is the MAE in estimating ${\mathit{\pi }}_{\text{j}}$. To help the experimenter set c₁ we note that it has a simple interpretation. Setting $c_1=0.01/(2r{\Delta }_N)$ means that the experimenter is willing to pay for Δ_N extra reads to reduce MAE by $\ge$0.01. The quotes given by sequencing facilities usually depend on the number of reads N, hence c₁ can be easily translated to money. As an alternative we consider studies that aim to identify the dominant isoform ${\gamma }_{\text{gj}}={\text{argmax}}_{\text{i}}{\pi }_{\text{gij}}$ across $i=1,\dots ,I_{\text{g}}$, in which case we set $u(e,\widehat{\mathit{\gamma }},\mathit{\gamma })=-c_0-c_{1}2rN+D$, where $D=G^{-1}{\sum }_{g=1}^G\mathcal{I}\left({\widehat{\gamma }}_{\text{gj}}={\gamma }_{\text{gj}}\right)$ is the proportion of genes for which we correctly identified the dominant isoform, $\mathcal{I}(·)$ is the indicator function and $c_1=0.01/(2r{\Delta }_N)$ means that the experimenter will pay for Δ_N extra reads to increase D by $\ge 0.01$.

In multi-sample studies we let ${\gamma }_{\text{gi}}=1$ if isoform i is truly DE across K groups by a user-defined margin (else ${\gamma }_{\text{gi}}=0$) and ${\widehat{\gamma }}_{\text{gi}}$ are DE calls obtained from any desired data analysis method. For instance, for K = 2 groups we may set ${\gamma }_{\text{gi}}=\mathcal{I}(|{\mu }_{\text{gi}1}-{\mu }_{\text{gi}2}|>\text{log}(t))$ where t is the minimal fold change (FC) between groups that the experimenter deems to be relevant. We introduce t rather than testing strict equality across groups (${\mu }_{\text{gi1}}={\mu }_{\text{gi}2}$) to reflect the custom in the field of not reporting FCs below a certain threshold t. In our examples we use t = 2 and t = 3 and set DE calls ${\widehat{\gamma }}_{\text{gi}}=1$ when LNNMV posterior probabilities (PP) of ${\gamma }_{\text{gi}}=1$ were $>1-\alpha$ or alternatively when TREAT Benjamini-Hochberg (BH) adjusted P-values (McCarthy and Smyth, 2009; Benjamini and Hochberg, 1995) were $\le \alpha$, where α is the desired false discovery proportion (FDP). Both LNNMV-PP and TREAT-BH test the equivalence null hypothesis $|{\mu }_{\text{gi}1}-{\mu }_{\text{gi}2}|\le \text{log}(t)$ versus the alternative $|{\mu }_{\text{gi1}}-{\mu }_{\text{gi}2}|>\text{log}(t)$. The cutoff PP$>1-\alpha$ ensures that the posterior expected FDP$\le \alpha$, whereas TREAT-BH targets the usual frequentist FDR control. As a technical comment, according to decision theory one should set ${\widehat{\gamma }}_{\text{gi}}$ to maximize posterior expected utility, but instead we adopt a pragmatic standpoint and acknowledge that the data analyst may have other preferred data analysis strategies. See Supplementary Section 2 for further discussion. Let S_k be the sample size (number of replicates) in group $k=1,\dots ,K$ and $S={\sum }_{k=1}^K{S}_{\text{k}}$ the total sample size. The default utility for multi-sample studies is $u(e,\widehat{\mathit{\gamma }},\mathit{\gamma })=-(c_0+c_{1}2rN)S+{\sum }_{g,i}{\widehat{\gamma }}_{\text{gi}}$, which rewards having a larger number of DE calls ${\sum }_{g,i}{\widehat{\gamma }}_{\text{gi}}$. This utility does not explicitly include a penalty for false positives but recall that ${\widehat{\gamma }}_{gi}$ are set to control the FDP$\le \alpha$, and incorporates a sampling cost $(c_0+c_{1}2rN)S$. Setting $c_0+c_{1}2rN={\Delta }_{\text{DE}}/{\Delta }_S$ means the experimenter would pay for Δ_S more samples if she were to obtain $\ge {\Delta }_{\text{DE}}$ new DE calls (Supplementary Table S4 has an example). As shown in our examples, often we do not need to set c₀, c₁ as it is clear from the context whether the increase in DE calls offsets the cost of additional samples.

3.3 Simulation

The utility $u(e,\mathit{\gamma },\widehat{\mathit{\gamma }})$ obtained from conducting a study with design $e$ is a random variable that depends on the unknown state of nature $\mathit{\gamma }$ and decisions $\widehat{\mathit{\gamma }}$ based on the eventual data (also unknown at the time of study design). Following certain axioms, Bayesian decision theory dictates that one should choose the design $e$ maximizing $U(e)=E(u(e,\mathit{\gamma },\widehat{\mathit{\gamma }})|\mathcal{K})$, the expected utility with respect to $(\mathit{\gamma },\widehat{\mathit{\gamma }})$ given current knowledge $\mathcal{K}$ Algorithms 1 and 2 below simulate B realizations of $(\mathit{\gamma },\widehat{\mathit{\gamma }})$ and thus of $u(e,\mathit{\gamma },\widehat{\mathit{\gamma }})$ from their distribution given $\mathcal{K}$ for single- and multi-sample studies, respectively. In Algorithm 1 the user specifies a read length r, target number of reads N, mean insert size f (bp) and, optionally, pilot data consisting of a vector with exon path counts $y_0$ and total reads ${\tilde{n}}_0$ for each gene. Long single-end reads (e.g. $r=$1500 bp) are simulated as two paired-ends of length $r/2$ with insert size f = r, which gives rise to the same exon path that would be observed with a single read of length r. Although we recommend using pilot data whenever possible, and in the absence of related RNA-seq data it could come from microarrays or some other technology (see the Supplementary Manual for an example), if no pilot data are available one may conduct prior predictive simulation in Step 1 of Algorithm 1 (i.e. set $\tilde{n}=(0,\dots ,0)$, draw ${\mathit{\pi }}_j^{(b)}\sim \text{Dir}(2)$). We now outline the algorithms and give them in full detail in Supplementary Section 3.

Algorithm 1. Simulation of one RNA-seq sample j. For $b=1,\dots ,B$

1. Simulate gene expressions ${\mathit{\theta }}_j^{(b)}\sim \text{Dir}(2+{\tilde{n}}_0)$ and relative isoform expressions ${\mathit{\pi }}_j^{(b)}$ given $({\tilde{n}}_0,y_0)$ via Metropolis-Hastings (Rossell et al., 2014). Find ${\mathit{\gamma }}_j^{(b)}$ associated to $({\mathit{\theta }}_j^{(b)},{\mathit{\pi }}_j^{(b)})$.

2. Simulate ${\tilde{N}}_j^{(b)}=N{p}_{r}my$ reads, where p_r is a known proportion of uniquely mappable r-long reads (Li et al., 2014), $m\sim \text{Unif}(0.6,0.9)$ that of actually aligned reads and $y\sim \text{Unif}(0.8,1.2)$ a ±20% random read yield. See Supplementary Section 1.4 for details.

3. Simulate future data $(y_j^{(b)},{\tilde{n}}_j^{(b)})$ given ${\mathit{\pi }}_j^{(b)},{\mathit{\theta }}_j^{(b)}$, i.e. ${\tilde{n}}_j^{(b)}\sim \text{Multinomial}({\tilde{N}}_j,{\mathit{\theta }}_j^{(b)})$, reads per isoform $\sim \text{Multinomial}({\tilde{n}}_j^{(b)},{\mathit{\pi }}_j^{(b)})$. Get expression estimates ${\widehat{\mathit{\gamma }}}_j^{(b)}$ (by default using casper, but BAM files Li et al. (2009) can be generated for combination with other software).

4. Record $u^{(b)}=u(e,{\mathit{\gamma }}_j^{(b)},{\widehat{\mathit{\gamma }}}_j^{(b)})$.

Algorithm 1 can be used either in single-stage studies where we consider a single sequencing experiment and in multi-stage studies where we consider sequencing a sample of interest multiple times to increase precision. In single-stage studies ${\widehat{\mathit{\gamma }}}_j^{(b)}$ in Step 3 is based only on the new data $(y_j^{(b)},{\tilde{\mathit{n}}}_j^{(b)})$, whereas as in multi-stage studies ${\widehat{\mathit{\gamma }}}_j^{(b)}$ also uses the pilot data $(y_0,{\tilde{\mathit{n}}}_0)$ as these came from the sample of interest.

Algorithm 2 below requires setting (r, N, f) and the number of replicates S_k in each group $k=1,\dots ,K$, where K is the number of groups that one wishes to compare expression across. To estimate statistical power accurately we recommend that Algorithm 2 uses pilot data from the groups of interest, given that power depends critically on the size of the differences between groups relative to the within-groups variance (pooled variance when variability is different in each group). Although using pilot data from a different study is also possible, this may lead to under-estimating the number of DE calls (i.e. sequence too many samples) or over-estimating them (i.e. sequence too few samples). Hence we envision a use of Algorithm 2 in two- or multi-stage studies, where batches are collected sequentially and become the pilot data to decide if further replicates are needed.

Algorithm 2. Simulation of multiple samples. For $b=1,\dots ,B$

1. Draw ${\mu }_{\text{gik}}^{(b)}\sim N(m_{\text{gik}},v_{\text{gik}})$, $1/{\varphi }_{\text{gi}}^{(b)}\sim \text{Gamma}(a_{\text{gi}},b_{\text{gi}})$ for all g, i, k, where $(m_{\text{gik}},v_{\text{gik}},a_{\text{gi}},b_{\text{gi}})$ depend on the pilot data and are given in Supplementary Section 1.2. Compute ${\mathit{\gamma }}^{(b)}$.

2. Draw ${\eta }_{\text{gij}}^{(b)}\sim N({\mu }_{\text{gik}}^{(b)},{\varphi }_{\text{gi}}^{(b)})$ for all g, i, k, $j=1,\dots ,S_{\text{k}}$. Find corresponding ${\mathit{\pi }}_j^{(b)},{\mathit{\theta }}_j^{(b)}$ (Supplementary Section 1.2).

3. Use Steps 2 and 3 in Algorithm 1 to obtain ${\widehat{\eta }}_{\text{gij}}^{(b)}$ for all g, i, j.

4. Obtain DE calls ${\widehat{\mathit{\gamma }}}^{(b)}$, record $u^{(b)}=u(e,{\widehat{\mathit{\gamma }}}^{(b)},{\mathit{\gamma }}^{(b)})$

From Algorithms 1-2 we obtain the Monte Carlo estimate $\widehat{U}(e)={\sum }_{b=1}^B{u}^{(b)}/B$ for any given design $e$. To choose amongst several possible designs $e$ one can apply Algorithms 1 and 2 for each of them and choose that maximizing $\widehat{U}(e)$. An advantage of these simulation-based algorithms is that one may easily evaluate $\widehat{U}(e)$ for all values of the utility coefficients (c₀, c₁). That is, one may report the optimal $e$ for each (c₀, c₁) to find the best design for the range of (c₀, c₁) values deemed reasonable, which avoids the need to set a single (c₀, c₁) (Swartz et al., 2006). Another advantage is that one may examine the distribution of the individual components in $u(e,\mathit{\gamma },\widehat{\mathit{\gamma }})$ for various $e$, e.g. the MAE in single-sample studies or DE calls and FDP in multi-sample studies, as illustrated in our examples. Algorithm 1 is implemented in the casper function simMAE and Algorithm 2 in simMultSamples (Supplementary Manual).

3.4 Data

The FASTQ files for the K549 cell line and mouse bladder tissue used as pilot data in Section 4 were obtained from the ENCODE Project Consortium (2012), samples wgEncodeEH002625 and wgEncodeEM003062, respectively. The human lymphoblastoids sample was from the 1000 genomes project (Lappalainen et al., 2013), sample ERS185276. For the multi-sample example we obtained GSE37704 SRA files from ncbi.nlm.nih.gov/sra?term=SRP012607, converted them to FASTQ format with SRA toolkit 2.2.2 (eutils.ncbi.nih.gov/Traces/sra) command fastq-dump –split-3 filename.sra, and aligned to the human genome hg19 with Tophat2 version 2.0.2 (Trapnell et al., 2012) (default parameters and -a 5). GSE49712 SRA files (ncbi.nlm.nih.gov/sra?term=SRP028705) were aligned to hg19 with STAR 2.3.0 (Dobin et al., 2013) (default parameters). We imporated the GENCODE v18 (Engström et al., 2013) isoforms.gtf file into Bioconductor and used casper function wrapKnown to import the data and obtain isoform expression estimates (Supplementary Manual).

3.5 Preprocessing and goodness-of-fit

Our multi-sample model assumes that data are preprocessed to remove systematic differences between samples and potential biases due to batches or other covariates. We used quantile normalization, which Bullard et al. (2010) found useful for RNA-seq data, followed by the linear model adjustment ${\widehat{\eta }}_{\text{gij}}={\tilde{\eta }}_{\text{gij}}-x_{\text{j}}{\widehat{\mathit{\beta }}}_{\text{gi}}$, where ${\tilde{\eta }}_{\text{gij}}$ are raw expression estimates, $x_j$ a covariate vector (e.g. batches) and ${\widehat{\mathit{\beta }}}_{\text{gi}}$ the least-squares estimate from regressing ${\tilde{\eta }}_{\text{gij}}$ on $x_j$ and the group indicator. ${\widehat{\eta }}_{\text{gij}}$ are the adjusted expression estimates fed into LNNMV or GaGa (for the latter we add an offset to guarantee ${\widehat{\eta }}_{\text{gij}}>0$). We used casper function mergeExp to quantile-normalize and mergeBatches for batch effect adjustment. We emphasize the importance of an adequate normalization, e.g. if it cannot be safely assumed that differences between samples are solely due to artifacts one may consider alternatives such as quantro (Hicks and Irizarry, 2015).

Another important point is to assess that the assumptions posed by our model are reasonable, as these drive the simulation. For the multi-sample LNNMV/GaGa models we implemented genome-wide residual quantile–quantile plots and asymmetry checks for ${\widehat{\eta }}_{\text{gij}}$, i.e. the first hierarchical level of the model. The LNNMV assumptions for log-FPKM held fairly well in datasets GSE37704 and GSE49712, whereas GaGa had a slightly worse fit and Poisson or Negative binomial qq-plots revealed a substantially poorer fit to the aligned read counts (Supplementary Sections 4.2 and 4.3). These checks include the hierarchical level that isoform means μ_gik arise from a common Normal (LNNMV) or inverse Gamma (GaGa) distribution. Usually the fit was satisfactory for genes with aligned read count above a certain minimum (roughly  > 10). For our single-sample model we compared the number of mapped reads $\tilde{n}$ with posterior predictive simulations, again finding a good fit (Supplementary Section 4.1). As further validation, the examples in Section 4.2 compare observed DE calls with out-of-sample predictions in GSE37704 and GSE49712, finding a reasonably good agreement. For further details see Supplementary Sections 4–5. We note that while the main role of LNNMV/GaGa for us is as a simulation engine, an interesting side implication is that data analysis strategies devised for continuous data often remain reasonable for RNA-seq. See also Law et al. (2014) for the more advanced voom strategy based on incorporating weights to consider that measurement precision increases with read count.

4 Results

4.1 Single-sample studies

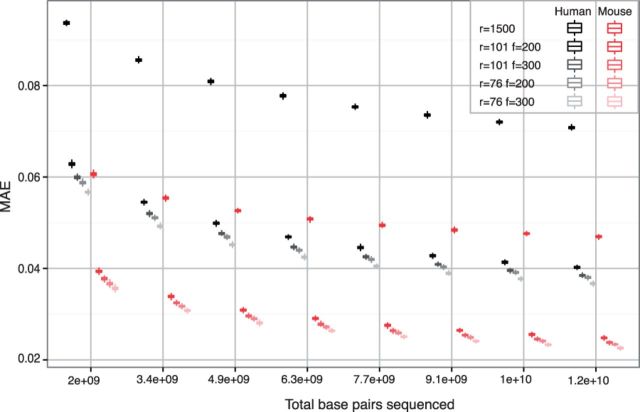
As a first example we consider single sample-studies that aim to estimate relative isoform expression and measure the MAE in (1). The characteristics of the design to be decided are the number of reads N, read length r and average insert size f (bp). N and r depend on the sequencing settings and f on the fragmentation protocol used to preprocess the sample. We consider r = 76, 101 short reads with either f = 200 or 300, and also r = 1500 long reads (e.g. as arising from modern sequencing technologies). For each of these settings we consider a total of 2–12 sequenced gigabases (Gb) and compare several organisms and cell types. We used pilot data from the ENCODE Project Consortium (2012) to design studies for UCSC hg19 isoform expression in the human K549 cell line and mouse mm10 isoforms in bladder tissue. Figure 2 summarizes the results. Both for human (black) and mouse (red), for any fixed total sequenced Gb the lowest MAE is given by r = 76, f = 300 and the largest by r = 1500. A potential reason is that the proportion of non-mappable paired-end reads changes little for r > 76, e.g. from 2.1% for r = 76 to 2.4% for r = 101 according to the piecewise-linear power law of Li et al. (2014) (Supplementary Section 1.4), hence for fixed fragment length and total sequenced Gb shorter reads may imply sampling more molecules and estimating low expression isoforms better. Indeed, we observed largest differences between experimental settings for low-FPKM isoforms (Supplementary Figs S16b and S18b). Note that non-mappability can be substantially higher with shorter or single-end reads, e.g. 12.8% for single-end 36 bp reads. Although this is taken into account by parameter p_r in Algorithm 1, one may also consider more advanced strategies to reflect mappability (e.g. gene-specific). We view our global mappability parameter p_r as a reasonable computationally tractable compromise.

Fig. 2.

Evaluating single-sample designs. Relative isoform expression MAE versus total sequenced bp for r = 76, 101 short reads with insert sizes f = 200, 300 and r = 1, 500 long reads. Grey: human K549 cell line (hg19). Red: mouse bladder tissue (mm10)

Regarding r = 1500 long reads, if one also considers that they currently have a higher cost per sequenced bp than short reads (Quail et al., 2012), these results strongly suggest that the latter are more efficient in terms of genome-wide estimation of isoform abundance. However, we also found that long reads can be beneficial for complex genes such as those with overlapping transcripts in opposite strands (Supplementary Fig. S18), and may also be the more natural choice for other analysis goals (e.g. validation of de novo isoform discovery). Because of its lower transcriptome complexity mouse isoform estimates were substantially more precise than for human, e.g. a MAE = 0.05 (±5% error in relative expression) required 3.24 Gb for human but only 0.67 Gb for mouse, which can allow to cut costs by $\approx$500%. Although it may not be surprising that different organisms require distinct sequencing depths, the observation also applies to different tissues from the same organism. For instance, in human lymphoblastoids MAE = 0.05 requires 1.8 Gb, which is only 55.6% of the 3.24 Gb for K549. This can be explained by K549 isoform expression being more asymmetric than in lymphoblastoids (Supplementary Fig. S15, bottom), which causes a higher representation of certain molecules in the RNA library and makes it harder to sample lowly-expressed isoforms. Even within K549, $r=76,f=300$ achieves MAE = 0.058 with $2\times {10}^9$ total sequenced bp whereas $r=101,f=200$ requires $>3\times {10}^9$, a > 50% increase in cost. As another example, consider that the goal is to determine the dominant isoform of each gene in K549. The proportion of correctly identified major isoforms increases with number of sequenced bp (Supplementary Fig. S19). As before, sequencing shorter reads and longer fragment sizes gives better results and interestingly even with low coverage we expect to achieve  > 90% correct detections.

These examples show the importance of considering individual characteristics of each study such as the target transcriptome, distribution of expression levels and sample preparation, which can all have a non-negligible effect on expression estimates.

4.2 Multi-sample studies

We now consider differential expression studies. Akin to sequential clinical trials, rather than spending all resources upfront we consider starting with a pilot study and collecting data incrementally. Additionally to (r, f, N) here we need to set the number of samples S_k per group. We consider the pilot MiSeq study in GSE37704 (Trapnell et al., 2013), which has 3 HOXA1 knock-down and 3 scramble samples (roughly 2.5 m aligned reads per sample). As a preliminary exploration, we used the LNNMV-PP  > 0.95 rule (Section 3.2) to find hg19 isoforms that were DE by  > 3-folds, obtaining 640 significant calls (Fig. 3, top). These findings suggest that even based on relatively low-yield MiSeq data there are noticeable differences in isoform expression between the two groups, which is further confirmed by a Principal Components plot (Supplementary Fig. 3). Next we used Algorithm 2 to design a follow-up study with either 3 or 6 more samples per group for a total of S_k = 6 or S_k = 9, respectively. We considered a HiSeq experiment with either N = 16 or 32 m short reads (r = 101), and also long reads (r = 1, 500) with the equivalent number of total sequenced bp (N = 2.1 m). The combinations of $(S_{\text{k}},N,r)$ gave eight possible experimental designs. Figure 3 (top) shows the predicted number of DE calls (gray) under six of those designs and Supplementary Table S2 gives DE calls, average FDP and power for all eight designs. For instance, we predicted that S_k = 6 with r = 101 and N = 16 m (9.7–18.2 m actual alignments) would increase DE calls from 640 to 884.5 (970 for S_k = 9). As a validation, GSE37704 has three HiSeq samples with r = 101 and 10.9–16.4 m aligned reads each. These gave 870 DE calls (Fig. 3, top), in close agreement with the predicted 884.5. The results also suggest that doubling the number of new replicates (S_k = 6–9) improves statistical power to a much larger extent than doubling sequencing depth (N = 16–32 m), consistently with previous findings [e.g. Rapaport et al. (2013); Busby et al. (2013)]. We note that the LNNMV-PP rule adequately controlled the average FDP below the target 0.05. Interestingly, we also found that long r = 1, 500 bp reads offer a very limited increase in the ability to find DE isoforms, again likely due to the fact that for a fixed total sequenced bp longer reads sample much fewer molecules and hence cannot estimate expression so accurately. In practice long reads are more costly than short reads [e.g. per bp cost with Pacbio RS is > 4 than for MiSeq/HiSeq (Quail et al., 2012)], so a more realistic cost-equivalent of N = 16 m, r = 101 bp short reads is $N=2.1/4=0.52$ m long reads, which gives even lower power (Supplementary Tables S2 and S3). To assess robustness we repeated the simulations under the GaGa model, obtaining very similar results (Supplementary Figs S21 and S22, Supplementary Table S5).

Fig. 3.

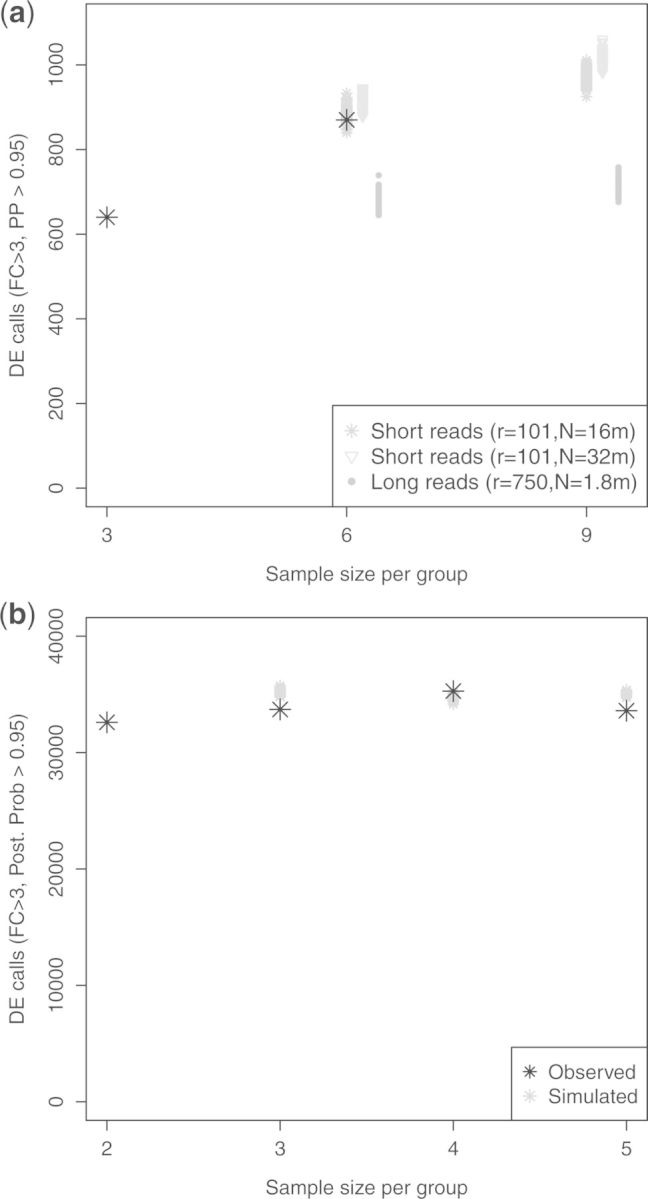
Evaluating multi-sample studies. (a) Number of hg19 isoform DE calls ($|\text{FC}|>3$) with S_k = 3 MiSeq samples per group, 3 MiSeq + 3 HiSeq from GSE37704 (black) and simulations for $S_{\text{k}}=6,9$ based on S_k = 3 (grey). (b) DE calls for GENCODE v18 transcripts with $S_{\text{k}}=2,3,4,5$ per group from GSE47912 (black) and simulations based on S_k = 2 (grey)

Given the simulation output it is straightforward to evaluate other FC cutoffs and analyses, which can be useful to further assess robustness and also to compare the performance of several analysis methods. We considered lowering the FC threshold to  > 2 and also using TREAT-BH (Section 3.2) instead of LNNMV-PP to make DE calls. LNNMV-PP with the  > 2 cutoff gave a higher number of DE calls than for the more stringent  > 3, but results were analogous in terms of the optimal design (Supplementary Table S2). Regarding TREAT-BH for  > 3 and  > 2 cutoffs we again found that adding independent replicates was preferable to increasing sequencing depth and that long reads were not cost-effective (Supplementary Fig. S20, Supplementary Tables S2 and S3). The predicted number of DE calls in the simulations matched those in the validation HiSeq data also for TREAT-BH. The FDP was adequately controlled but relative to LNNMV-PP there was a sharp decrease in DE calls. This is not surprising given that equivalence testing P-values control false positives under the worst possible case that the FC lies at the boundary $|{\mu }_{\text{gi}1}-{\mu }_{\text{gi}2}|=\text{log}(t)$ for all genes g, which results in a conservative behavior when many FCs truly are of a smaller magnitude. So far our discussion was informal, but these results are easily integrated with decision theory (Supplementary Section 5). For instance, S_k = 9 would only be preferable to S_k = 6 if the experimenter believed that as few as 14 new DE calls already make it worth sequencing one extra sample. That is, for most experimenters the decision S_k = 6 has higher expected utility than S_k = 9.

The previous example illustrates a situation where continuation beyond the pilot ($S_{\text{k}}>3$) clearly improves statistical power, and that this can be detected even when using MiSeq pilot data to assess a HiSeq follow-up. It is equally important to detect situations where little benefits are expected beyond the pilot, as then one can stop experimentation. To illustrate this we selected 2 of the 5 universal human and 5 brain reference samples from GSE49712 (Rapaport et al., 2013) as pilot data and used Algorithm 2 to predict the number of DE calls when increasing the sample size to S_k = 3,4,5. GSE49712 is a distinct example from GSE37704 due to having higher read yield (roughly 61 m aligned reads per sample) and that here we considered 194 820 isoforms from GENCODE v18 (Engström et al., 2013) rather than the 40 892 UCSC hg19 isoforms studied in GSE37704. Further, the Principal Components plot reveals the existence of stronger differences between groups (Supplementary Fig. S11). In fact, 32 596 DE calls were found by LNNMV-PP with a fold-change > 3 based only on the S_k = 2 pilot samples per group. Figure 3 (bottom), Supplementary Table S6 and Supplementary Figure S23 show that little benefits were predicted for increasing S_k further. For instance the 32 596 LNNMV-PP calls were predicted to only increase to 35 037 for S_k = 5, a prediction that was confirmed when analysing the five available experimental samples per group, where in fact even slightly fewer DE calls were made (33 595). Analogous results were found for a  > 2 cutoff and when making DE calls with TREAT-BH. Interestingly, for a  > 3 cutoff LNNMV-PP offered better statistical power than TREAT-BH at a low FDP but for a  > 2 cutoff LNNMV-PP was overly liberal with an FDP around 0.12–0.13, whereas TREAT-BH showed an FDP = 0.05–0.06 much closer to the target 0.05. This example shows that, beyond choosing an experimental design, the simulations can help assess which amongst various analysis strategies may be more appropriate for the problem at hand.

5 Discussion

In an era when high-throughput technologies and Big Data are having a profound impact on biomedical research, experimental design continues to be critical for the validity of science. Unfortunately design considerations are often overlooked, perhaps encouraged partly by a naive feeling that with good enough technology design considerations are less important and partly by practical difficulties such as the lack of available tools. To address these challenges, we proposed a general framework for RNA-seq experiments firmly grounded in Bayesian decision theory and statistical design of experiments. We focused on RNA-seq, but the framework can serve as a basis to design other experiments, e.g. proteomics, genome-wide association studies etc. The key components for such extensions are a model that offers a good probabilistic representation of the data-generating process, a utility function or multiple criteria that assess cost-effectiveness taking into account the characteristics of the problem at hand and a computational strategy that produces answers within a practical time frame. Although there are other possible routes to specify these components, Bayesian models equipped with posterior and posterior predictive sampling algorithms become a convenient choice that allow implementing our framework in a straightforward manner.

Our results indicate that it is important to go beyond default guidelines to consider each individual study, i.e. to customize the design. By taking into account the target organism or likely expression levels for the tissue of interest one may cut sequencing costs by a factor of 2–5 and still estimate expression at a good precision. Similarly for multi-sample studies, where the ability to find differential expression depends critically on between-groups differences relative to within-groups variability and other characteristics. For instance, the contrast between GSE37704 and GSE49712 resembles differences between studies encountered in practice in the underlying biology, technology used or even the target transcriptome that one wishes to make inference for. By adapting to such context-specific characteristics, customized designs are a promising and currently under-explored framework to help researchers decide if and how to conduct high-throughput studies in a statistically principled manner. The associated savings in time and experimentation are not only ethical, but also help focus research efforts where they are more likely to yield useful results.

Funding

D.R. was partially funded by National Institutes of Health (R01 CA158113-01>) and Ministerio de Economía y Competitividad of Spain (MTM2012-383337>). C.S-O. was partially supported by AGAUR Beatriu de Pinós fellowship BP-B 00068>.

Conflict of Interest: none declared.