An experimentalist's guide to computational modelling of the Min system

Summary

Spatio-temporal oscillations of the Min proteins are essential for selecting the cell division site in Escherichia coli. These oscillations are a key example of a biological phenomenon that can only be understood on a systems level rather than on the level of its individual components. Here, we review the key concepts that mathematical modelling has added to our understanding of the Min system. While several different mechanisms have been proposed, in all cases the oscillations emerge from a dynamic instability of a uniform protein distribution. To generate this instability, however, the various mechanisms rely on different features of Min protein interactions and transport. We critically evaluate these mechanisms in light of recent experimental evidence. We also review the effects of fluctuations caused by low cellular concentration of Min proteins, and describe how stochastic effects may potentially influence Min protein dynamics.

In recent years, the remarkable oscillatory dynamics of the Min proteins MinC, MinD and MinE in Escherichia coli have emerged as a key example of self-organization inside bacterial cells (Howard and Kruse, 2005). As a result of their periodic migration from one cell pole to the other (Fig. 1A), the assembly of the Z ring, which ultimately drives cytokinesis, is suppressed near the cell poles by the division inhibitor MinC and instead is accurately directed to midcell (Lutkenhaus, 2002; Errington, 2003; Rothfield et al., 2006). This precise positioning of the Z ring may also be aided by nucleoid occlusion, which inhibits division in regions close to the nucleoids (Margolin, 2005). Much is now known about the interactions and cellular localization of the Min proteins. However, prior to the introduction of mathematical modelling, an understanding of the fundamental origins of the Min oscillations remained elusive. Through recent theoretical work, it has become clear that just a few key properties of the Min proteins are sufficient for self-organization and to generate oscillations (Howard and Kruse, 2005).

Fig. 1. Min oscillations in E. coli.

A. Time-lapse fluorescence micrographs of an E. coli cell synthesizing a green fluorescent protein fusion to MinD, along with extra MinE, showing one full oscillation cycle.

B. Distribution of membrane-bound MinD (blue dots) and MinE (red) obtained from a stochastic simulation. Dots represent individual molecules.

C. Concentration of MinD (blue, lower half) and MinE (red, upper half) obtained from a deterministic analysis. The concentration is colour-coded, with darker colours signifying larger concentrations. B and C were modified from Fange and Elf (2006).

We emphasize that understanding this organization requires a mathematical analysis on a systems level, as the observed dynamics rely on the interaction of many protein molecules that individually are incapable of oscillating. In this respect, simple ‘cartoon’ like pictures or qualitative models are inadequate to analyse the complex dynamics of the Min proteins, making a computational analysis indispensable. An already large and still growing number of models have been proposed (Howard et al., 2001; Meinhardt and de Boer, 2001; Kruse, 2002; Howard and Rutenberg, 2003; Huang et al., 2003; Huang and Wingreen, 2004; Drew et al., 2005; Meacci and Kruse, 2005; Fange and Elf, 2006; Kerr et al., 2006; Pavin et al., 2006; Tostevin and Howard, 2006). Conceptually, most models incorporate the idea that a dynamic instability leads to self-organized patterning (Howard and Kruse, 2005). In other words, a homogenous distribution of Min proteins in the cytoplasm and on the membrane is unstable. In such a situation, a small perturbation of the uniform distribution will not decay away but instead grows and leads in this case to an oscillatory pattern. Such a pattern is truly self-organized, because the patterning is determined by the intrinsic properties of the proteins and their interactions rather than being imposed from above. However, there are important mechanistic differences among the various models. For example, the treatment of protein binding kinetics differs fundamentally between the models. Moreover, the transport of membrane-bound molecules is essential in some models, whereas for others it is not. For biologists not trained in computational analysis, it is often hard to identify the essential differences between the various models as compared with mere technical differences. Therefore, the impact of the theoretical analysis on experiments, which can only be fully developed by comparing the different models, has been somewhat limited. In this review, we will provide a guide to the ensemble of models and highlight the important similarities and differences among the various models.

One fundamental property of a model is whether it is stochastic or deterministic. In a stochastic model, the state of the system is usually specified by the positions of the individual molecules. This is illustrated in Fig. 1B, with the positions of the molecules on the membrane marked by coloured dots. Consequently, the dynamics are also described on a molecular level: at each point in time, the particles probabilistically undergo one of several possible transitions, for example, moving to a neighbouring location or binding to the membrane. This allows for a straightforward implementation of details of the molecular scale dynamics, where the inherent randomness of biochemical processes can be properly incorporated.

In contrast, in a deterministic model, the state of the system is given by the local concentrations of molecules and their changes over time from averaged rates. Figure 1C shows the local concentration of membrane-bound Min proteins by colour coding. A detailed specification of the underlying elementary events is often not necessary in this case, and the study of one deterministic model captures the behaviour of a whole class of detailed molecular models. Therefore, in spite of its technical nature, the difference between a stochastic and a deterministic analysis can have important consequences for our understanding of Min protein dynamics. A thorough understanding of model similarities and differences on these various levels is important when designing new experiments. Ideally, these experiments should provide new insights into Min dynamics, which can in turn be fed back into improved models in a cycle beneficial for both theory and experiments.

Attempts to explain the spatio-temporal oscillations of the Min proteins are based on the exchange of MinD and MinE between the cytoplasm and the membrane. The dynamics of MinC are known to closely follow that of MinD, and are therefore normally not modelled separately. When bound to ATP, MinD attaches to the membrane and subsequently recruits MinE. MinE in turn catalyses ATP hydrolysis, such that MinD (and MinE) are released back into the cytoplasm, where both MinD and MinE diffuse. The ATP hydrolysis involved in the exchange of MinD and MinE between the cytoplasm and the membrane provides the energy driving the oscillations. The first important result of mathematical analysis was that these processes alone are not sufficient to explain the observed oscillatory pattern of the Min proteins (Howard et al., 2001; Meinhardt and de Boer, 2001; Kruse, 2002).

Other ingredients leading to a dynamic instability have been proposed. Roughly, they fall into two classes: either attachment of MinD to the membrane is cooperative, or there are attractive interactions between MinD molecules bound to the membrane. Accordingly, we will divide the existing models into either cooperative attachment (CA) or aggregation current (AC) models. Interestingly, the models of both classes suggest that neither the observed MinE ring nor the helical arrangement of membrane-bound MinD is essential for the generation of the oscillations. Nevertheless, these structures do provide important hints about molecular mechanisms.

To discuss the proposed mechanisms in more detail, we start with deterministic models that rely on only a few basic assumptions about the molecular interactions. We consider first the class of CA models. In these models the instability follows from cooperativity in the binding/unbinding kinetics of MinD and MinE to the membrane, in addition to MinD-induced binding of MinE and MinE-induced release of MinD (Fig. 2A). The model proposed in Howard et al. (2001) assumes that the unbinding of MinD depends on the concentration of MinE bound to the membrane. Furthermore, binding and unbinding of MinE depends on the concentration of cytosolic MinD. So far, there is no direct experimental evidence for such dependence. The mechanism underlying the oscillations is roughly the following: after expulsion of MinD from the membrane at one end of the cell by MinE, MinD diffuses rapidly in the cytoplasm and rebinds where the MinE concentration is lowest. In sufficiently short cells, this is at the far end of the cell. After some time, the MinE removes most of the MinD from one cell end and subsequently dissociates from the membrane. As MinE requires MinD for membrane binding, MinE is then forced to relocate to the MinD patch at the other end. Importantly this model is conservative, i.e. it assumes a constant overall number of MinD and MinE proteins. Experiments strongly suggest that protein synthesis and degradation is indeed irrelevant for the oscillation mechanism (Raskin and de Boer, 1999).

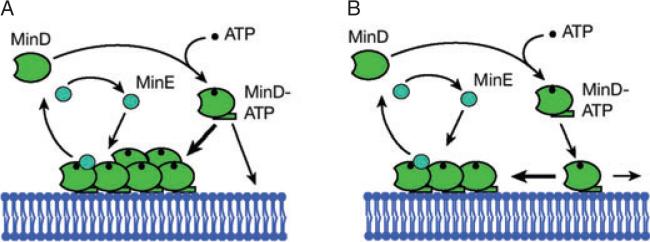
Fig. 2. Schematic representation of the Min dynamics in CA and AC models.

A. Reaction diffusion with CA. Cytoplasmic MinD (green) binds to ATP (black) and a subsequent conformational change increases its affinity for binding to the membrane. Attachment to the membrane occurs preferentially in regions already covered by MinD (thick arrow). MinE (blue) binds to membrane-bound MinD. It induces ATP hydrolysis, which eventually leads to detachment of the MinDE complex from the membrane.

B. Aggregation current. In its ATP-bound form, MinD attaches anywhere to the membrane. Attractive interactions between membrane-bound MinD moving on the membrane lead to the formation of MinD aggregates (thick arrow). MinE binds to membrane-bound MinD and releases it from the membrane as in CA models. Note that the preferential movement of membrane MinD towards MinD aggregates is the principal difference between the CA and AC models: in CA models, membrane movement either is absent or occurs purely by diffusion.

In the simulations of Huang et al. (2003) and Meinhardt and de Boer (2001), the presence of membrane-bound MinD increases the rate of further MinD binding. Experiments in vitro have shown that the amount of bound MinD does not increase linearly with the concentration of MinD in the system (Lackner et al., 2003; Mileykovskaya et al., 2003), suggesting cooperativity during MinD binding. However, the first of these models (Meinhardt and de Boer, 2001) crucially depends on protein synthesis and degradation, while the model of Huang et al. (2003) and all other CA models of Min protein dynamics similar to Howard et al. (2001) assume a constant number of MinD and MinE molecules. In the model of Huang et al. (2003), MinD proteins are directed to the opposite cell half, because in the presence of membrane-bound MinE, MinD is quickly released back into the cytoplasm, while in the absence of membrane-bound MinE, MinD binds to the membrane. This mechanism is again similar to Howard et al. (2001) and leads to an accumulation of MinD at the new pole. Finally, the model makes a crucial prediction: in numerical simulations it has been found that the charac teristic striped pattern in filamentous cells is stable only if the exchange of ATP for ADP bound to cytosolic MinD is not too fast. The reason for this behaviour remains to be explored.

In contrast to CA models, AC models postulate that the dynamic instability is a consequence of attractive interactions between membrane-bound MinD molecules (Fig. 2B). This attraction causes membrane-bound MinD to preferentially move towards regions of high MinD concentration, leading to the formation of MinD aggregates (Kruse, 2002; Meacci and Kruse, 2005). Such directed movement does not occur in CA models, in which membrane-bound MinD either is immobile or moves purely by diffusion, and excess mobility of these proteins can abolish the oscillations. There is indeed some evidence for the formation of MinD aggregates on the membrane. Unilamellar vesicles form tubes encircled by attached MinD which assemble into a tightly wound helix (Hu et al., 2002). Helices, although with a much larger pitch, have also been observed in E. coli (Shih et al., 2003). Experiments using the non-hydrolysable ATP analogue ATPgS suggest a two-step process for the formation of MinD aggregates (Hu et al., 2002). It involves first binding of MinD to the phospholipid membrane, and a subsequent conformational change of the molecule that allows for the formation of MinD filaments. Recent yeast two-hybrid studies provide strong evidence for an enhanced interaction between pairs of MinD molecules after membrane binding of both partners (Taghbalout et al., 2006). The binding of one partner does not seem to be sufficient for this effect, an observation that is clearly compatible with an AC mechanism. Note that in all AC models the number of MinD and MinE molecules is conserved.

How is MinD then targeted towards the opposite pole in the AC models proposed in Kruse (2002) and Meacci and Kruse (2005)? In these models it is assumed that the number of binding sites for MinD on the membrane is limited. Therefore, MinD released from the membrane in the cell half with the higher MinD concentration preferentially binds close to the opposite cell pole because of more available binding sites in this area. The AC models predict that if the levels of MinD or MinE are sufficiently high, oscillations should cease. This prediction is similar to those from CA models; however, in AC models an inhomogenous stationary distribution results (Kruse, 2002; Meacci and Kruse, 2005), as opposed to the homogeneous stationary distribution found in many CA models. Furthermore, in contrast to CA models, oscillations persist in AC models for homogenous distributions of cytoplasmic MinD and MinE. Clearly, in order to determine if either CA or AC mechanisms dominate in vivo, experimental testing of these types of predictions would be very useful.

All the models presented above consider general properties of Min protein dynamics, but are independent of many of the detailed molecular interactions. More recently, models have attempted to account for these details more accurately (Drew et al., 2005; Fange and Elf, 2006; Kerr et al., 2006; Pavin et al., 2006; Tostevin and Howard, 2006). However, they have not introduced fundamentally new mechanisms. Rather, they can be seen as variants of the model suggested in Huang et al. (2003) in so far as they modify the dependency of the MinD binding rate on membrane-bound MinD. As these models consider molecular details, most of them are stochastic descriptions. Inclusion of stochastic effects is potentially relevant, as the Min proteins are present at relatively low concentrations of a few mM in E. coli (Shih et al., 2002). However, for these protein concentrations, the stochastic versions broadly confirm the analysis of the deterministic models, although several interesting new features have arisen. Howard and Rutenberg (2003) considered a stochastic version of the model introduced in Howard et al. (2001). These authors found that the accuracy of cell division positioning is compromised if the number of molecules is too low, even if the oscillations continue. They also found that oscillations could sometimes be detected at low protein concentrations, even though no oscillations are generated in the deterministic model for the same parameter values. This phenomenon is termed a fluctuation-induced instability. In a stochastic analysis of the model introduced in Huang et al. (2003), the opposite effect was found: fluctuations destroy the oscillations found in the deterministic model (Kerr et al., 2006). For the AC model introduced in Meacci and Kruse (2005), fluctuations can have both effects (Meacci, 2006).

As the stochastic computations essentially confirm the results of the deterministic analysis, one might wonder why a biologist should be interested in them. The reason is that the stochastic analysis can predict quantities that can be obtained experimentally, but which are impossible to obtain in a deterministic analysis. Examples are variations in the positional accuracy of the Z ring (Howard and Rutenberg, 2003; Kerr et al., 2006), in the oscillation period (Fange and Elf, 2006; Kerr et al., 2006), or in the number of particles partitioned into the daughter cells (Tostevin and Howard, 2006). For example, Tostevin and Howard (2006) found large variations in the number of protein molecules partitioned into daughter cells after a simulated cell division event. Comparison of these results with experimental data will likely provide valuable insights into the oscillation mechanism. Recent modelling paper has already shed light on the origin of some unusual oscillation behaviours. For example, during oscillations of the Min proteins in spherical mutants of E. coli, the oscillation axis often drifts (Corbin et al., 2002). Stochastic analysis has shown that this effect can be entirely attributed to fluctuations (Fange and Elf, 2006). These authors also showed that the dynamic MinD spots observed in a mutant lacking phosphatidylethanolamine (Mileykovskaya et al., 2003) could be readily explained with a stochastic analysis.

As more experimental details are revealed, stochastic models should provide a more realistic description of the Min dynamics in E. coli. In particular, there have been attempts to understand the formation of helical MinD structures on the cytoplasmic membrane (Pavin et al., 2006; Tostevin and Howard, 2006). The formation of helices is, however, not essential for the oscillations, as earlier models without membrane filaments were able to generate oscillatory dynamics. Nevertheless, the helices are such a prominent feature that they should ideally be incorporated into the modelling. Models with MinD filament formation generally assume that membrane MinD binding is favoured at the ends of MinD filaments. With this assumption, it was found that the Min oscillations were still generated. Furthermore, filamentous MinD aggregates were formed, but a three-dimensional analysis did not reveal any spirals (Pavin et al., 2006). Clearly, more work will be required to generate realistic helical membrane filaments. Attempts have also been made to model filaments using a deterministic model (Drew et al., 2005); however, this model incorporated additional assumptions not confirmed by experiments, such as the existence of special nucleation sites.

We next consider the question of dimensionality: namely, whether a full three-dimensional analysis is required or whether a simpler one-dimensional approach suffices. If we assume that the distribution of Min proteins is homogenous around the circumference of the bacterium, then an essentially one-dimensional analysis is appropriate. In this case, the membrane and the cytosol are described as a line. This has been the first step in all analyses. In contrast to the other models, reduction of the cytosol to a line destroys the striped pattern observed in filamentous cells in the CA model of Huang et al. (2003). This finding indicates that for this model, inhomogeneities of the cytosolic MinD-ATP and MinD-ADP distribution along the radial co-ordinate are essential. However, in other models that permit inhomogeneities in this radial direction, no deviations from a homogenous distribution have been reported so far (Meinhardt and de Boer, 2001; Fange and Elf, 2006; Kerr et al., 2006; Pavin et al., 2006).

In wild-type cells, the MinE ring is one of the most prominent features of the Min oscillations. However, as stated above, according to theoretical analysis, this structure is not essential for generating oscillations (Huang et al., 2003). This finding agrees with experiments with MinE mutants, which exhibit MinD oscillations even in the absence of a MinE ring (Shih et al., 2002). Nevertheless, when MinE rings are present, two mechanisms for their formation are suggested by the models. In the CA models (Howard et al., 2001; Huang et al., 2003; Fange and Elf, 2006; Kerr et al., 2006; Tostevin and Howard, 2006), MinE that is diffusing after being released at one pole will attach to the membrane as soon as the membrane concentration of MinD is sufficiently high. This leads to an accumulation of MinE at the end of a MinD polar zone. In the models presented in Kruse (2002) and Meinhardt and de Boer (2001), a particularly high affinity for binding of MinE to a certain range of MinD concentrations has to be assumed. This is supposed to mimic preferential binding of MinE to ends of MinD filaments.

In conclusion, mathematical modelling has provided us with testable models that explain the Min oscillations as emerging from collective interactions of the Min proteins. The models predict that the oscillations arise from simple principles and should therefore be reconstructable in vitro. The models have also made predictions about the partitioning of the Min proteins at cell division, and also predict that the accuracy of division is compromised as the Min protein concentration levels are reduced, even if the oscillations persist (see above). These predictions would be very interesting to investigate experimentally and would form a stringent test of the modelling approach. In order to put the models to a real test, however, it is essential to obtain experimental values for the parameters that enter the models. In turn, they will provide information about the molecular mechanism (AC versus CA) generating the oscillations. A first step has been taken in this direction by measuring the diffusion constants of cytoplasmic and membrane-bound MinD and MinE, as well as their residence times in the cytoplasm (Meacci et al., 2006).

The theoretical analysis of Min dynamics also has important consequences for other systems, most of all the observation that only a few key properties of the proteins are needed to generate complex dynamic patterns in living bacteria. As these properties are not particularly sophisticated, one might expect that patterns similar to the Min oscillations might be involved in many other processes in bacteria, such as the Spo0J/Soj-system in Bacillus subtilis (Doubrovinski and Howard, 2005). Progress on the Min system has also shown that an understanding of complex dynamic patterns in bacteria will likely require mathematical analysis. Such analyses are rapidly becoming a genuine and powerful tool of modern microbiology.