Unsupervised lineage‐based characterization of primate precursors reveals high proliferative and morphological diversity in the OSVZ

ABSTRACT

Generation of the primate cortex is characterized by the diversity of cortical precursors and the complexity of their lineage relationships. Recent studies have reported miscellaneous precursor types based on observer classification of cell biology features including morphology, stemness, and proliferative behavior. Here we use an unsupervised machine learning method for Hidden Markov Trees (HMTs), which can be applied to large datasets to classify precursors on the basis of morphology, cell‐cycle length, and behavior during mitosis. The unbiased lineage analysis automatically identifies cell types by applying a lineage‐based clustering and model‐learning algorithm to a macaque corticogenesis dataset. The algorithmic results validate previously reported observer classification of precursor types and show numerous advantages: It predicts a higher diversity of progenitors and numerous potential transitions between precursor types. The HMT model can be initialized to learn a user‐defined number of distinct classes of precursors. This makes it possible to 1) reveal as yet undetected precursor types in view of exploring the significant features of precursors with respect to specific cellular processes; and 2) explore specific lineage features. For example, most precursors in the experimental dataset exhibit bidirectional transitions. Constraining the directionality in the HMT model leads to a reduction in precursor diversity following multiple divisions, thereby suggesting that one impact of bidirectionality in corticogenesis is to maintain precursor diversity. In this way we show that unsupervised lineage analysis provides a valuable methodology for investigating fundamental features of corticogenesis. J. Comp. Neurol. 524:535–563, 2016. © 2015 The Authors The Journal of Comparative Neurology Published by Wiley Periodicals, Inc.

During evolution the cerebral cortex has undergone tangential expansion accompanied by an increase in the number of cortical areas. In addition, in both human and nonhuman primate cortex there has been a selective enlargement of the supragranular layer compartment (Marín‐Padilla, 1992), which has an important role in the computational processes of the brain (reviewed in Douglas and Martin, 2004; Kennedy et al., 2007). The enlarged supragranular layers of the primates arise from a specialized precursor pool, the outer subventricular zone (OSVZ) (Smart et al., 2002; Lukaszewicz et al., 2005). The OSVZ is the major germinal zone of the developing primate cerebral cortex and harbors the bulk of cortical progenitors from midcorticogenesis onward (Smart et al., 2002; Lukaszewicz et al., 2005; Fietz et al., 2010; Hansen et al., 2010; Fietz and Huttner, 2011; Lui et al., 2011; Reillo and Borrell, 2012; Betizeau et al., 2013). Although significant progress has been made in identifying the OSVZ precursor types in human (Hansen et al., 2010; Fietz and Huttner, 2011) and non‐human (Betizeau et al., 2013) primates, understanding the cellular and molecular properties of OSVZ precursors that drive its expansion in the primate lineage remains a major challenge (Lui et al., 2011; Dehay et al., 2015).

Lipophilic dye deposit on the basal membrane and adenoviral infection in human tissue shows that the primate OSVZ includes a large fraction of basal radial glia cells (bRGs) that greatly outnumber intermediate progenitors (IPs) (Fietz et al., 2010; Hansen et al., 2010). bRGs were described as monopolar precursors with a basal process contacting the basal lamina, but lacking an apical process contacting the ventricle (Fietz et al., 2010; Hansen et al., 2010; Fietz and Huttner, 2011; Reillo and Borrell, 2012). A recent study in embryonic macaque, combining real‐time imaging of retrovirally infected green fluorescent protein (GFP)‐expressing progenitors from long‐term organotypic slice cultures with immunohistochemistry, showed that the bRG population is more diverse than previously reported in human studies (Betizeau et al., 2013). This study showed that, in addition to the previously described basal process bearing bRG precursor (the bRG‐basal‐P precursor), three additional categories of bRGs can be observed: 1) bipolar bRG precursors exhibiting an apically directed process in addition to the basal process (bRG–both‐P precursors); 2) monopolar bRG precursors lacking a basal process and exhibiting an apically directed process (bRG–apical‐P precursors); and 3) transient bRGs (tbRG precursors) where either a well‐developed apical or basal process (or both) retract or are formed during the lifetime of the precursor (Betizeau et al., 2013). Note that in macaque, bRG apically directed processes do not reach the ventricular border and therefore contain only basolateral plasma membrane (reviewed in Florio and Huttner, 2014). By contrast, bRG basal processes can either extend all the way to the basal lamina or just be basally directed.

This work reveals complex lineages of the primate OSVZ precursor subtypes involving many successive rounds of proliferative divisions. Importantly, statistical analysis showed that each bRG subtype has a distinct proliferative behavior and neurogenic capacity. This unanticipated diversity in the OSVZ progenitor pool has prompted a revised view of prevailing models of primate corticogenesis (Florio and Huttner, 2014).

To explore the diversity of OSVZ precursors and the robustness of the morphology‐based classification, we have implemented an unsupervised probabilistic clustering approach based on Hidden Markov Trees (HMTs) (Crouse et al., 1998; Durand et al., 2004). Compared with conventional parametric or hierarchical clustering models (Polo et al., 2010), the HMT approach takes the tree‐based nature of the data into account when identifying clusters, revealing the order relationships in lineages. These order relationships are then used to better define progeny. HMTs are thus well suited for modeling data with natural growth and branching processes, and have been used for diverse applications such as analyzing branching patterns during tree growth (Durand et al., 2005) and reconstruction of pluripotent stem cell lineage trees from incomplete gene expression measurements (Olariu et al., 2009). The method is widely used in technical applications such as wavelet‐based signal processing for acoustic and visual denoising and reconstruction (Crouse et al., 1998; Choi et al., 2000; Willsky, 2002; Duarte et al., 2008), image modeling (Romberg et al., 2001), or pattern recognition (He et al., 2008). Here we present the first application of HMT models to the analysis of cortical precursor types. HMTs encode in their structure the underlying assumption that there exist discrete types of precursors that can be characterized both by their observable characteristic morphology and by the fate of their progeny. In this way the unsupervised machine learning algorithms for HMTs are able to identify unobservable precursor types when lineage‐based clustering is applied to a large database of monkey cortical precursors, collected for Betizeau et al. (2013). One can speculate that molecular markers would identify these unobserved precursor types. In the Betizeau et al. (2013) database each cell is characterized by its observed features as well as its position in the lineage trees. Despite the simplicity of the HMT model, the learned probabilistic model accurately identifies and explains the roles of diverse morphological precursor types and their lineage relations in monkey cortex, reproducing the diversity revealed by empirical (manual) observation (Betizeau et al., 2013). In addition, HMT predicts the type of cells that previously could not be characterized because of their unknown fate.

A novelty of the HMT prediction is that the automated method simultaneously takes into account morphological and lineage information including progeny, thereby suggesting slight deviations from a purely morphology‐based characterization. The HMT model also predicts the possibility of a higher diversity than so far observed in the database. This larger diversity, largely resulting from subdividing existing categories, could correspond to precursors with as yet to be determined specialized developmental roles. In accordance with the previously reported nature of precursor type transitions (Betizeau et al., 2013), the HMT shows that each precursor type generates characteristic frequencies of daughter types. Importantly, the HMT transition diagrams confirm the presence of loops connecting members at different lineage depths, thereby speaking against a strict direction of transitions from less toward more fate‐constrained precursors. By using the HMT, we have been able to show that these loops serve to ensure the high precursor diversity observed in the data. As larger datasets of progenitor and stem cells for different species with a diversity of morphological and genetic measurements become available (Costa et al., 2011; Betizeau et al., 2013), automated methods such as HMT models will be able to provide an invaluable generic tool for identifying hidden patterns of proliferation.

Glossary of terms and synonyms

Root: the first node of the lineage tree, i.e., the first observed precursor.

Lineage depth, rank of division: number of divisions between the root and the cell.

Normalized depth: depth divided by the length of the longest branch of the tree, so that the root has normalized depth 0, and the maximum normalized depth is 1.

Observer classification, manual classification: classification of precursors into discrete categories by a human expert, according to manually defined criteria, such as morphology. Also refers to the classification in Betizeau et al. (2013).

Type, category, cluster: synonyms for discrete categories of real objects or abstract data. We use the term “type” to denote a category of real cells, and “cluster” when talking about groups of data points that share statistical similarities in the abstract feature representation space.

Transition diagram: graph showing proportions of cell types and the frequencies of transitions between types. Arrows in the transition diagram show for each precursor type the proportion of daughter cell types after divisions. The precursor types in a transition diagram are vertically arranged according to their normalized depth.

MATERIALS AND METHODS

Animals

Fetuses from timed‐pregnant cynomolgus monkeys (Macaca fascicularis, gestation period 165 days) were delivered by caesarian section as described elsewhere (Lukaszewicz et al., 2005). All experiments are in compliance with national and European regulations as well as with institutional guidelines concerning animal experimentation. Surgical procedures are in accordance with European requirements 2010/63/UE. The experimental protocol C2EA42‐12‐11‐0402‐003 was reviewed and approved by the Animal Care and Use Committee CELYNE (C2EA #42).

Organotypic slice culture, adenoviral, and retroviral infection

Occipital poles of embryonic hemispheres were isolated and embedded in 3% low melting agarose (Sigma, Saint‐Quentin‐Fallavier, France) in supplemented Hanks balanced salt solution (HBSS) at 37°C. Then 300‐μm‐thick parasagittal slices were cut in 4°C supplemented HBSS using a vibrating blade microtome (Leica VT1000 S). Slices were incubated in Glasgow minimum essential medium (GMEM) containing porcine cytomegalovirus–enhanced GFP (pCMV–EGFP) retrovirus (1–5.10⁵ pi/ml) (Betizeau et al., 2013) or Ad‐CMV‐GFP (1 × 10¹⁰ PFU; Vector, Nanterre, France), for 2–3 hours at 37°C. Slices were then mounted on laminin/poly‐lysine–coated 0.4‐μm Millicell culture inserts (Millipore, Molsheim, France) in a drop of type I collagen (BD Biosciences, Allschwil, Switzerland) and cultured at 37°C, 7.5% CO₂, in 6‐well plates in GMEM supplemented with 1% sodium pyruvate, 7.2 μM beta‐mercaptoethanol, 1% nonessential amino acids, 2 mM glutamine, 1% penicillin/streptomycin, and 10% fetal calf serum (FCS; GE Healthcare, Vélizy‐Villacoublay, France).

Following 1–4 days of in vitro culture, slices were fixed for 1 hour in phosphate‐buffered (0.1 M) paraformaldehyde solution (PFA 2%) and cryoprotected with 10% and then 20% sucrose in phosphate buffer (PB). Sections were cut at 20 μm on a cryostat (Microm HM550) after embedding in O.C.T. compound (Tissue‐Tek, Sakura Finetek, Alphen aan Den Rijn, The Netherlands).

Antibodies

The primary antibody used in these studies is listed and described in Table 1. Fluorophore‐conjugated secondary antibodies, goat anti‐chicken/Alexa 488 (1:1,000), goat anti‐mouse/Alexa 555 (1:800), and goat anti‐rabbit/Alexa 647 (1:400) were obtained from Molecular Probes (Lyon, France).

Table 1.

Primary Antibody Used in This Study

Antibody	Immunogen	Manufacturer, cat.#, host species, mono‐ vs. polyclonal, RRID	Dilution
Green fluorescent protein (GFP)	GFP isolated directly from the jellyfish Aequorea victoria	Molecular Probes, #A10262, chicken, RRID AB11180610	1:800

Antibody characterization: GFP

This antibody is the purified IgY fraction from chicken serum raised against GFP directly from the jellyfish Aequorea victoria (RRID:AB_11180610). GFP antibodies are suitable for the detection of native GFP, GFP variants, and most GFP fusion proteins. This antibody allows the highlighting of cells positive for GFP‐adenovirus or GFP‐retrovirus (Hansen et al., 2010; Betizeau et al., 2013).

Immunohistochemistry

Cryosections were air‐dried for 30 minutes and hydrated in Tris‐buffered saline (TBS; pH 7.6) for 30 minutes. Slices were treated with Antigen Retrieval (Dako, Les Ulis, France) for 15 minutes at 95–96°C and then cooled to room temperature during 20 minutes. Nonspecific binding was blocked by incubation in TBS + bovine serum albumin (BSA) 1% + normal goat serum (10%, Gibco/Life Technologies, Grand Island, NY) for 30 minutes. The primary antibody was incubated overnight in TBS + 1% BSA at 4°C for 12 hours. After washing in TBS, fluorophore‐conjugated secondary antibodies were coincubated in Dako Diluent (Dako) for 1 hour at room temperature. After washing in TBS, sections were stained with 4′,6 diamidino‐2‐phenylindole (DAPI; Molecular Probes, Eugene, OR; 1:4,000 in TBS) for 10 minutes at room temperature. Sections were mounted in Fluoromount G (SouthernBiotech, Birmingham, AL).

Image acquisition

Images were collected by confocal microscopy using a Leica DM 6000 CS SP5. Acquisitions were performed using a Leica HCX PL AP immersion oil 40×/1.25 0.75 with a digital zoom of 2. Tiled scans were automatically acquired using the LAS AF software (Leica). For cryosections, stacks of five optical sections spaced 2 μm apart were taken. For the morphology analysis on 80‐μm‐thick sections, stacks throughout the entire section thickness were acquired spaced 1 μm apart. All image analyses were performed in ImageJ software (Schneider et al., 2012).

Collection of the dataset

The dataset comprising positively identified precursors via immune staining and video recording was collected for Betizeau et al. (2013), and is described in detail there. The dataset is the result of approximately 7,000 hours of video recordings of organotypic slice cultures from developing macaque cortex. Images were taken every 1–1.5 hours for up to 15 days. We analyzed cells from embryonic (E) day 65 (i.e., 65 days post conception) and E78 derived from four hemispheres at each time point (34 lineages, 216 cells at E65, 57 lineages, 479 cells at E78 for a total of 91 lineages, 695 cells). Table 2 lists the features measured for each cell and their possible discrete values.

Table 2.

Description of measured morphological and proliferative features per cell

Feature	Description	Possible values
Morphology at birth	Presence/absence of apical/basal processes at birth	• No processes • Apical process only • Basal process only • Apical and basal process
Morphology at mitosis	Presence/absence of apical/basal processes prior to mitosis	• No processes • Apical process only • Basal process only • Apical and basal process
Cell type	Cycling/postmitotic	• Unknown • Cycling • Postmitotic • Dead cell
Process stability	Process stability between birth and mitosis	• No process • Minimum one transient process • Permanent (at least one process during at least 85% of the cell's lifetime)
Process retraction	Retraction of processes during mitosis	• No mitosis • No retraction • Minimum one process retracts
Cell‐cycle length	Cell‐cycle length in hours	• No mitosis • Time bins for 20–40, 40–60, 60–80, 80–100 h
Mitotic plane angle	Orientation of mitotic plane	• No mitosis • 0–30, 30–60, 60–90 deg
Translocation	Translocation movement prior to mitosis	• No mitosis • Downward translocation • No translocation • Upward translocation
Zone	Zone where cell is located at onset	• Apical VZ (ventricular zone) • ISVZ (inner subventricular zone) • IFL (inner fiber layer) • OSVZ (outer subventriculsar zone) • OFL (outer fiber layer) • SP (subplate)
Mitosis location	Cell following mitosis	• Lower daughter cell • Upper daughter cell
Division type	Proliferative or differentiative division: the values indicate the daughter cell types (proliferative, postmitotic, unknown type)	• Absence of mitosis • 2 postmitotic • 1 postmitotic, 1 unknown • 1 postmitotic, 1 proliferative • 1 proliferative, 1 unknown • 2 proliferative • unknown

Data preprocessing and annotation

Continuous features of the dataset were rounded and converted into discrete values. Bins of 20 hours for the cell‐cycle length were used, with a maximum of 100 hours. For the mitotic plane, bins of 30° between 0° and 90° were used. The presence of a process was evaluated at each time point. A process was noted present if detected on the image. A process was considered stable if at least one process was present in at least 85% of the precursor's lifetime, transient if it was present between 15 and 85% of the lifetime, and absent if not detected for more than 15% of the lifetime. Because of the focus of the present study on the precursor types of the OSVZ and inner (I)SVZ, lineage trees originating in the apical VZ (22.3% of all recorded lineage trees) were removed.

Hidden Markov Trees

A Hidden Markov Tree (Crouse et al., 1998) is a graphical model, closely related to the Hidden Markov Model (HMM). It models the probabilistic relationship between observable variables and a hidden state variable, as well as the probabilistic dependencies between hidden states of different observations. Whereas in an HMM every hidden state has exactly one successor, an HMT models the relationship between different observations with a tree structure. For simplicity, only binary trees, i.e., trees in which every non‐leaf node has exactly two successors, are considered here. In the context of cell lineage analysis, the measured features of a single cell are considered as so many observations, and allow a discrete hidden state to be attributed to each cell. The vector of features of each cell constitutes the observable variables, which are dependent uniquely on the hidden state. The lineage is directly translated into the HMT structure, and the hidden state of each cell is modeled to depend stochastically uniquely on the hidden state of the mother cell (Fig. 1). The hidden state of each cell is an abstraction of internal and external signaling that the cell experiences. This state, which is not directly observed, expresses itself through observable features such as the morphology, behavior of cells before mitosis, and observed daughter cell types.

Figure 1.

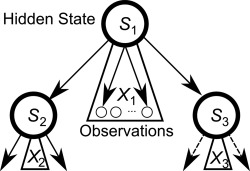
Graphical model structure of a Hidden Markov Tree (HMT) model, with hidden states S_u and observation vectors X_u. The representation shows statistical dependencies assumed by the model: the hidden states of the two daughter cells (S₂ and S₃) are conditionally independent given the hidden state of the mother cell (S₁), and the distribution of observation variables depends only on the hidden state of the cell.

Hidden Markov Tree notation

The data for a single lineage are given by observations X, and the lineage tree structure. Following the notation of Durand et al. (2004), we denote by $\overline{{\mathbf{X}}_1}=(X_1,\dots , X_n)$ a single tree rooted in $X_1$. In addition, we define the tree of hidden states (with the same structure as $\overline{{\mathbf{X}}_1}$) by $\overline{{\mathbf{S}}_1}=(S_1, \dots , S_n)$, where each $S_i$ can take on discrete values from 1 to K, corresponding to the number of hidden states (Fig. 1). For each node u we denote the set of children as c(u), the parent of u as ρ(u), and the sub‐trees rooted at u as $\overline{{\mathbf{X}}_u}$ and $\overline{{\mathbf{S}}_u}$. An HMT is defined through two properties: 1) for each observation in a node $X_u$ the observation probability is given as a mixture model dependent on the hidden states via

$$P\left(X_u=x\right)= {\displaystyle \sum }_{j=1}^{K}P(S_u=j)\cdot P(X_u=x|S_u=j)$$

and 2) for given observations $\overline{{\mathbf{X}}_1}$ and hidden states $\overline{{\mathbf{S}}_1}$ of the whole tree, the likelihood factorizes according to the Markov property for a tree structure

$$\begin{array}{l}P\left(\overline{{\mathbf{X}}_1}=\overline{x_1},\overline{{\mathbf{S}}_1}=\overline{s_1}\right)\\ =P\left(S_1=s_1\right)\cdot \left({\displaystyle \prod }_{u\ne 1}P\left(S_u=s_u|S_{\rho \left(u\right)}=s_{\rho \left(u\right)}\right)\right)\cdot {\displaystyle \prod }_{u}P\left(X_u=x_u|S_u=s_u\right)\end{array}$$

The task required here is to infer automatically an HMT model that explains the morphological subtypes observed, as well as stochastic lineage relationships between the discrete types. This requires defining in advance the parameter K that determines the number of possible hidden states for each cell. The HMT algorithm then infers three sets of parameters:

1. A multinomial prior distribution π = (π ₁, …, π _K), so that π _j is the probability that the hidden state of the root node in a lineage is j, i.e., ${\pi }_i=P(S_1=j)$.

2. A transition matrix A = (a _ij), where a _ij describes the probability that the hidden state of a daughter cell is type j, under the condition that the mother cell's hidden state is of type i, i.e., $a_{ij}=P(S_{u+1}=j|S_u=i)$, where u+1 is a child of u.

3. An observation model θ = (θ₁, …, θ_K), in which each θ_j describes a multivariate discrete probability distribution for the observed variables x under the condition that the hidden state is type j, i.e., ${\theta }_j\left(x_u\right)=P(X_u=x_u|S_u=j)$. For simplicity, a discrete mixture‐of‐multinomials model is assumed. All observed variables are conditionally independent given the hidden state (this is equivalent to the Naïve Bayes model commonly used in machine learning). In this case, the likelihood model factorizes over all observed attributes, i.e., for $x_u=(x_u^1, \dots , x_u^p)$ one can calculate ${\theta }_j\left(x_u\right)=\prod _{i=1}^{p}P(X_u^i=x_u^i|S_u=j)$. In principle, other models, e.g., Gaussians for continuous variables, or modeled dependencies, could be equally used (Bishop, 2006).

The likelihood for given parameters can thus be factorized as

$$P\left(\overline{{\mathbf{X}}_1}=\overline{x_1},\overline{{\mathbf{S}}_1}=\overline{s_1}\right)=\pi (s_1)\cdot {\displaystyle \prod }_{u\ne 1}A(s_u,s_{\rho \left(u\right)})\cdot {\displaystyle \prod }_u{\theta }_{s\left(u\right)}(x_u).$$

Given an HMT model, a variant of the well‐known Viterbi algorithm adapted to the tree structure is used to infer the most likely hidden state assignment for each cell from known observations and the lineage relationship (Durand et al., 2004). For our application it is necessary to learn the most likely model (π, A, θ) that explains all the measured data, given by multiple lineage trees and the morphological measurements. For this, a variant of the unsupervised expectation–maximization (EM) algorithm called the upward–downward algorithm is used (described below) (Crouse et al., 1998; Durand et al., 2004). The algorithm iterates multiple times through the whole dataset, consisting of multiple lineages, and adapts the three sets of parameters to maximize the likelihood of the observations. Our analysis was performed with Matlab (Mathworks, Natick, MA).

The algorithm is initialized with a predefined number of cell types between 2 and 20. The algorithm proceeds to perform 50 iterations of the upward–downward algorithm to learn (π, A, θ), after which convergence is reached in all cases. As for every EM‐type algorithm, the parameters to be learned need to be initialized randomly. This leads to different but qualitatively similar results following multiple iterations. Twenty repetitions on each dataset are performed, and the most representative result is selected for further analysis.

To choose the most representative result of the 20 repetitions for a fixed number of clusters K, the distances between the θ vectors are computed for all clusters of one clustering to all θ vectors of the other 19 clusterings. For each cluster the most similar cluster in every other experiment is determined. Distances between clusterings are defined as the sum of minimum distances between clusters. The clustering with the minimum median distance to all other clusterings is selected as the representative clustering for the fixed number of clusters K.

Model constraints

The HMT algorithm can easily be modified to impose specific constraints on the lineage relationships, such as a directionality of precursor type transitions. Typically A is initialized as a random matrix with entries between 0 and 1 that are normalized to represent proper probabilities. If, however, an entry in A is set to 0, it will remain 0 throughout model learning, making certain transitions between states impossible. If A is thus initialized as a (random) triangular matrix, where a _ij = 0 for i > j, the resulting model will impose a directionality in the possible hidden state transitions, whereby precursors in state i cannot generate daughter cells with a state j < i. This implies that larger state indices correspond to more differentiated cells, whereas precursors of states with low indices can still differentiate into many different cell types. Unlike stem cells, precursors have a limited potential to self‐renew prior to differentiating into distinct cell types (Hirabayashi and Gotoh, 2010). Cortical progenitors also exhibit bidirectional state transitions that are not compatible with a directional model (Betizeau et al., 2013). Therefore in our analysis we tested both models and found similar precursor types but in significantly different proportions.

Upward–downward algorithm

The upward–downward algorithm is a variant of the unsupervised EM algorithm that learns the optimal parameters (π, A, θ) for an HMT model of a given dataset. The main difficulty is estimating the distribution of the hidden states of each node, from which the updated parameters of the HMT model can be relatively easily estimated. The smoothed‐probability variant (Durand et al., 2004) was used to obtain the distribution of hidden states. This method avoids the numerical problems arising from multiplication of small probabilities along the tree paths. It computes the auxiliary smoothed probabilities, where 1\u denotes the whole tree without the subtree rooted at node u:

$${\beta }_u\left(j\right)=P\left(S_u=j|\overline{{\mathbf{X}}_u}=x_u\right)$$

$${\beta }_{\rho \left(u\right),u}\left(j\right)=\frac{P(\overline{{\mathbf{X}}_u}=\overline{x_u}|S_{p\left(u\right)}=j)}{P(\overline{{\mathbf{X}}_u}=\overline{x_u})}$$

$${\alpha }_u\left(j\right)=\frac{P(\overline{{\mathbf{X}}_{1\backslash u}}=\overline{x_{1\backslash u}}|S_u=j)}{P(\overline{{\mathbf{X}}_{1\backslash u}}=\overline{x_{1\backslash u}}|\overline{{\mathbf{X}}_u}=\overline{x_u})} .$$

As the name of the algorithm implies, these quantities can be computed in two passes through the tree, one in the upward and the other in the downward direction. In addition, the marginal distribution $P(S_u=j)$ is required. This is computed by starting with $P\left(S_1=j\right)={\pi }_j$ at the root, and then using the recursion $P\left(S_u=j\right)=\sum _{i}P(S_u=j|S_{\rho \left(u\right)}=i)\cdot P(S_{\rho \left(u\right)}=i)$.

In the upward recursion, the leaf nodes are initialized to ${\beta }_u\left(j\right)=\frac{{\theta }_j(x_u)\cdot P(S_u=j)}{N_u}$, where $N_u=\sum _j{\theta }_j\left(x_u\right)\cdot P(S_u=j)$ is a normalizing factor. For the internal nodes one computes ${\beta }_u\left(j\right)=\frac{{\theta }_j(u)\cdot P(S_u=j)\cdot {\prod }_{v\in c(u)}{\beta }_{u,v}(j)}{N_u}$, where the normalizing factor $N_u=\sum _j{\theta }_j(x_u)\cdot P(S_u=j)\cdot \prod _{v\in c(u)}{\beta }_{u,v}(j)$. The ${\beta }_{u,v}$ are calculated recursively as ${\beta }_{\rho \left(u\right),u}\left(j\right)=\sum _k\frac{{\beta }_u(k)\cdot P(S_u=k|S_{p\left(u\right)}=j)}{P(S_u=k)}$.

In the downward recursion, the quantities ${\alpha }_u\left(j\right)$ are computed, starting with the initialization ${\alpha }_1\left(j\right)=1$ for the root node. Subsequently, ${\alpha }_u\left(j\right)$ is computed as ${\alpha }_u\left(j\right)=\frac{1}{P(S_u=j)}\cdot \sum _i\frac{{\alpha }_{\mathrm{\rho }\left(u\right)}\left(i\right)\cdot {\beta }_{\rho \left(u\right)}(i)\cdot P(S_u=j|S_{\rho (u)}=i)}{{\beta }_{\rho \left(u\right),u}(i)}$.

Once ${\alpha }_u(j)$ and ${\beta }_u(j)$ are known for every node in a single tree, the probabilities for the hidden states are obtained as $P(S_u=j|\overline{{\mathbf{X}}_1}=\overline{x_1})={\alpha }_u\left(j\right)\cdot {\beta }_u(j)$. By doing this for all lineage trees, the parameters of the HMT model can be updated in the M‐step of the EM algorithm with rather straightforward calculations of weighted sums and subsequent normalization, given that the parameters describe probability distributions that sum to 1 (Crouse et al., 1998; Durand et al., 2004).

Viterbi algorithm

The purpose of the Viterbi algorithm is to assign for a given HMT model the most likely tree of hidden states $\overline{{\mathbf{S}}_1}$ to a lineage tree with observations $\overline{{\mathbf{X}}_1}$. We give a brief summary of the implementation suggested by others (Durand et al., 2004). The algorithm calculates the assignment $\overline{s_1}=\text{arg}\underset{\overline{\mathrm{s}}}{\text{max}}P(\overline{{\mathbf{S}}_1}=\overline{s},\overline{{\mathbf{X}}_1}=\overline{x_1})$ that maximizes the likelihood given $\overline{x_1}$. For this, auxiliary variables ${\delta }_u\left(j\right)=\underset{\overline{s_{c\left(u\right)}}}{\text{max}} P(\overline{{\mathbf{X}}_{\mathbf{u}}}=\overline{{\mathrm{x}}_{\mathrm{u}}}, \overline{{\mathbf{S}}_{\mathbf{c}\left(\mathbf{u}\right)}}=\overline{{\mathrm{s}}_{\mathrm{c}\left(\mathrm{u}\right)}}|S_u=j)$ and ${\delta }_{\rho \left(u\right),u}\left(j\right)=\underset{\overline{s_{c\left(u\right)}}}{\text{max}} P(\overline{{\mathbf{X}}_{\mathbf{u}}}=\overline{{\mathrm{x}}_{\mathrm{u}}}, \overline{{\mathbf{S}}_{\mathbf{c}\left(\mathbf{u}\right)}}=\overline{{\mathrm{s}}_{\mathrm{c}\left(\mathrm{u}\right)}}|S_{\rho (u)}=j)$ are computed for every node u, respectively each parent–child node pair, starting at the leaf nodes where ${\delta }_u\left(j\right)={\theta }_j(x_u)$. For the internal nodes, the values are computed in an upward recursion as

$${\delta }_u\left(j\right)={\theta }_j\left(x_u\right)\cdot {\displaystyle \prod }_{v\in c\left(u\right)}{\delta }_{u,v}\left(j\right)$$

$${\delta }_{\rho \left(u\right),u}\left(j\right)=\underset{k}{\text{max}}{\delta }_u\left(k\right)\cdot P(S_u=k|S_{\rho \left(u\right)}=j).$$

In a subsequent downward pass, the optimal hidden state sequence is retrieved by first maximizing ${\pi }_j\cdot {\delta }_1\left(j\right)$ to find the optimal state S ₁ for the root node, and then assigning the states that maximized ${\delta }_{\rho \left(u\right),u}\left(j\right)$ for the given state of the parent node, until the leaf nodes are reached.

Cluster initialization

The unsupervised HMT learning algorithm is initialized by setting the parameters A and θ to random values between 0 and 1, followed by normalization to obtain proper probability distributions. For A, different types of constraints are defined (see above). The prior distribution π is initialized to a uniform distribution. Identified postmitotic cells are initially assigned to a single cluster, and remain there throughout the clustering. Without this initialization, multiple clusters of postmitotic cells are identified for larger numbers of clusters, but this effect does not qualitatively change the types of identified precursors, which are the focus of the present study. Different sets of features are used for the data matrix, but features that had no effect on the clustering (such as the germinal zone or the cortical area) are removed.

Evaluation of cluster analysis

Silhouette values (Rousseeuw, 1987) were computed as indicators of clustering quality. The silhouette value s(x _i) for a single data point x _i is computed as $s\left(x_i\right)=\frac{b\left(x_i\right)-a(x_i)}{\text{max}(a\left(x_i\right),b\left(x_i\right))}$, where a(x _i) is the average distance of x _i to all points in the same cluster, and b(x _i) is the minimum average distance of x _i to all other clusters in which x _i is not a member. Hence low values of a(x _i) indicate that x _i is representative of the cluster, whereas high values of b(x _i) indicate that x _i is very different from the other clusters. s(x _i) is restricted to lie between −1 and +1, and high values indicate good clustering quality, whereas negative values indicate that the data point should rather belong to a different cluster. By computing $S_k=\frac{1}{n_k}\sum _{x_i\in C_k}s(x_i)$ as the average of s(x _i) over all n _k points in cluster C _k, one obtains an indicator of how well separated the cluster is from all others. An indicator for the complete clustering is obtained by averaging S _k over all K clusters. These values are used to compare clustering results with different numbers of clusters, becausee increasing K reduces both a(x _i) and b(x _i) simultaneously, and thus a larger number of clusters does not necessarily improve the silhouette score. This property makes the silhouette a better indicator for cluster quality than, for example, the log‐likelihood of the data, because the latter merely increase with larger K.

RESULTS

Unbiased sampling of OSVZ cortical precursors

Empirically capturing the full repertoire of OSVZ progenitors requires an unbiased sampling method. Previous reports on human fetal cortex reported that the OSVZ was populated by two precursors types: bRG‐basal‐P and nonpolar IPs (Fietz et al., 2010; Hansen et al., 2010; Reillo et al., 2011; LaMonica et al., 2013; Ostrem et al., 2014). Using 1,1′‐dioctadecyl‐3,3,3′,3 (Dil) deposits on the pia, these researchers detected back‐labeled cell bodies in the OSVZ, leading them to describe only those OSVZ precursors as bRGs that possess a basal process attached to the basal membrane (Fietz et al., 2010; Hansen et al., 2010). In addition, the Kriegstein group used adenoviral labeling (Hansen et al., 2010; LaMonica et al., 2013; Ostrem et al., 2014) to label OSVZ precursors. Adenoviruses infect noncycling and cycling cells but are preferentially internalized in precursors bearing integrins (Wickham et al., 1993). Integrins are concentrated at the distal tip of the basal process of the bRG that extends a process up to the basal membrane (Fietz et al., 2010). Hence, the bias in the adenovirus method results from a procedure that only labels a specific subset of the OSVZ precursors. By contrast, retroviral vectors allow labeling of all cycling cells—and no postmitotic cells—in a truly unbiased fashion. The comparison of the diversity of precursors encountered 24 hours after infection of an organotypic slice by retrovirus or adenovirus (Fig. 2G) clearly demonstrates the bias of the adenovirus infection technique due to labeling uniquely bRG‐basal‐P precursors. The progeny of the adenoviral infected precursors 4 days after infection (i.e., after one to two cell cycles) include the range of morphotypes that are observed following retroviral infection (Fig. 2H) (Betizeau et al., 2013). Of note, bRGs bearing an apical process have been observed in human live‐imaging data in the rare instances in which the slice survival has been sufficiently long to allow division of the infected precursor (LaMonica et al., 2013). The focus of human studies on bRG precursors bearing a basal process led the authors of these studies to overlook apically directed mitotic somal translocation (MST) (Ostrem et al., 2014), although careful examination of their data reveals apical MST, as shown, for instance, in Movie S6 in LaMonica et al. (2013). However, bRGs with a basal process correspond to 16% of the OSVZ bRG population, and MST directionality is uniquely determined by the presence of an apical or a basal process, with apical MST being as frequent as basal MST (Betizeau et al., 2013).

Figure 2.

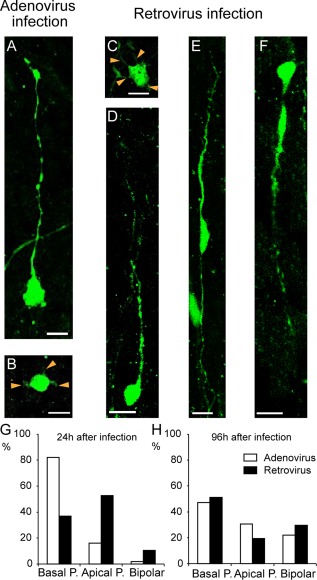
Examples of the different morphotypes of OSVZ EGFP+ precursors on organotypic slices immunostained for EGFP after 1 day in vitro following EGFP adenoviral infection (A,B) or EGFP retroviral infection (C–F) at E76. Following adenoviral infection, two main types of precursors were observed: (A) bRG with only a basal process, referred to as bRG‐basal‐P and (B) multipolar cell with thin processes (orange arrowheads). Following retroviral infection, four different precursor types were observed: (C) multipolar cell with processes (orange arrowheads), (D) bRG‐basal‐P, (E) bRG bearing both an apical and a basal process referred to as bRG‐both‐P (note that the two processes have different thickness and they extend through the OSVZ depth, and (F) bRG cells bearing a well‐developed apical process referred to as bRG‐apical‐P. G: Proportions of morphologies observed 24 hours following infection. Adenoviral infection results in GFP being selectively expressed in bRG‐basal‐P (>80%) (n = 132). By contrast, GFP is expressed in all three stable morphotypes after retroviral infection. H: 96 hours after adenoviral or retroviral infection, similar frequencies of bRG‐basal‐P, bRG‐apical‐P, and bRG‐both‐P are observed (n = 96). Scale bar = 10 μm in A–F.

Analysis of the dataset

The global statistics of the dataset obtained from unbiased sampling (see Materials and Methods) were initially analyzed. As we are primarily interested in OSVZ and ISVZ precursors, all lineage trees that had their root (first) precursor in the apical VZ (22%) were removed. Cells that derive from precursors in the VZ can migrate into higher regions, but this is very rare (0.7%), the vast majority originating in the ISVZ. Hence 90% of all cells descending from the root precursor remain in the same zone as the root while migrating cells invariably terminate in more basally located zones.

The global statistics of the dataset are shown in Fig. 3. The dataset combines measurements from two developmental stages (E65 and E78), with the majority of cells coming from E78 (69%). The observed lineages include between two and seven generations of divisions. (Lineages in which the first observed cell does not divide are excluded.) E78 lineages are longer (average depth 3.5) compared with E65 lineages (average depth 3.2). Among the observed cells, 43% are cycling cells and 12% are postmitotic. There are significantly more postmitotic cells in the E65 (20%) dataset than at E78 (8%). Seven percent of cells died and therefore could not be classified as cycling or postmitotic. At both time points the cells came mostly from the OSVZ (71%) and ISVZ (20%), with small contributions from the apical VZ, inner fiber layer (IFL), outer fiber layer (OFL), and subplate. bRG precursor morphology was annotated with respect to apical and basal processes, and distinguishing the morphology prior to and following mitosis. Prior to mitosis, cells typically have more processes than at birth, and at E65 there are altogether fewer cells without processes. At mitosis 28% of the precursors are nonpolar (IP), 17% are bipolar (bRG‐both‐P), and similar percentages of precursors have apical (bRG‐apical‐P) (47%) or basal processes (bRG‐basal‐P) (42%). The proportion of IP precursors is higher at E78 than at E65 (33% vs. 18%), whereas at E65 slightly more bipolar precursors are observed (19% vs. 16%). Only a few bipolar precursors are observed at birth (4%), the majority being nonpolar precursors (36%). Of the precursors, 56% had at least one observed process during at least 85% of the observation period (denoted as “permanent processes”), and 24% were identified as having transient processes; the rest did not have processes. Soma translocation prior to mitosis (MST) occurred in 25% of all cells, with slightly more moving down (15%) (apical MST) than up (10%) (basal MST). Nineteen percent of precursors retracted at least one process prior to mitosis; the rest either did not retract or failed to develop processes.

Figure 3.

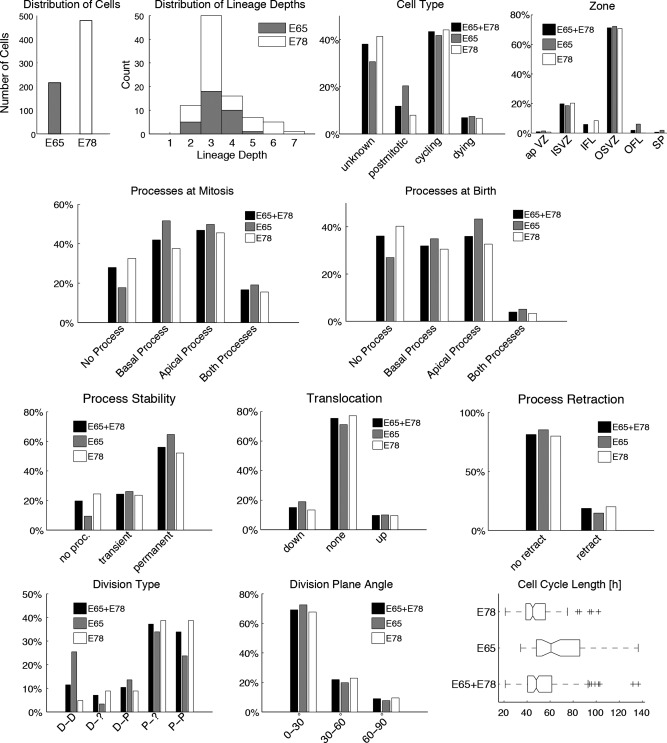
Analysis of the global statistics of the dataset at E65 (31% of all cells, gray bars) and E78 (69%, white bars), as well as for the combined dataset (E65+E78, black bars). The first two diagrams show for both developmental stages the counts of cells and the distribution of lineage depths, respectively. The following histograms show for each developmental stage and the combined dataset the distribution of the discrete parameter values for each feature, as described in Table 2. For cell cycle lengths the boxplots indicate the continuous feature distribution at each stage.

For cycling cells in which the fate of the daughter cell was known, 29% were found to perform differentiative divisions. Included in these precursors are 12% in which both daughters are postmitotic (25% at E65), 7% in which the fate of one cell is unknown, and 10% that have one postmitotic and one proliferative successor. Thirty‐four percent of precursors perform purely proliferative divisions, and 37% have one proliferative daughter and one daughter of unknown fate. The mitotic plane angle was horizontal (between 0 and 30°) in 69% of all dividing precursors. Comparison of cell‐cycle times reveals substantially longer durations at E65 (67 hours on average) than at E78 (48 hours).

Unsupervised characterization of cell types

The HMT algorithm was applied to the pooled E65 and E78 datasets (Fig. 3), using the features listed in Table 2 and the lineage relationship of cells as input. Individual clustering for both sets led to qualitatively similar results. To be compatible with the nomenclature in Betizeau et al. (2013), in which five types of progenitors and one type of postmitotic cells were identified, the algorithm was first initialized to use K = 6 clusters, and no constraint on precursor transitions was imposed. This procedure permits stochastic, bidirectional transitions between precursor types to be learnt, on condition that they best explain the observed dataset. In Fig. 4 we present detailed characterizations of each cell type using the statistics of the measured morphological and proliferative features. In particular, the first part of each panel presents the percentages of precursors of each type that possess apical or basal morphology, or are bipolar (indicated by lighter colors). From these visualizations it is apparent that the five precursor clusters identified by the HMT are in good agreement with previously described manual categorizations of progenitor types. In particular, one cluster contained mostly postmitotic cells (labeled “Neurons”). This is shown in the “Cell Type” histogram. Four of the six precursor types are defined to a large extent by their morphology, corresponding to the bRG‐apical‐P, bRG‐basal‐P, bRG‐both‐P, and IP precursor types previously described in Betizeau et al. (2013). The final precursor type is characterized by the transient character of its processes (see “Process” statistics), and was previously identified as the tbRG type (Betizeau et al., 2013). These findings confirm that the automatic extraction of cell types by the HMT algorithm leads to similar results as the manual categorization by human experts. Fig. 4 provides the statistics of the other features, described in Table 2, as a further resource for revealing characteristics of different progenitor types. The results of this analysis are summarized below:

Figure 4.

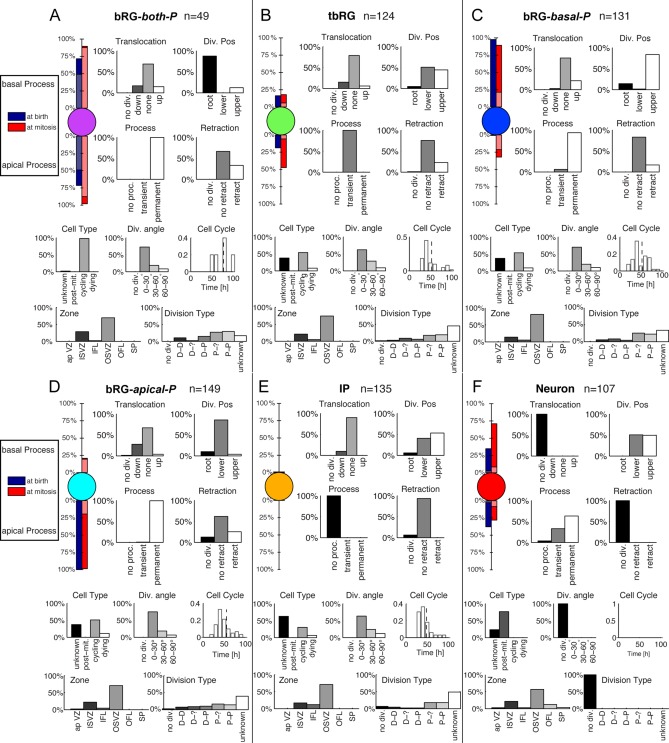
A–F: Automatically extracted cell types for the combined E65 and E78 dataset, using K= 6 different types and allowing all state transitions. The visualizations of morphology show the percentage of cells that have apical and basal processes at birth (blue) and prior to mitosis (red). Light blue and red bars indicate the percentage of bipolar cells. Histograms of morphological and proliferative features of the cells in each cluster further specify the different cell types (see Table 2 for interpretation of features). The features drawn on the bottom (Zone and Division Type) were not used for clustering. The automatic clustering result validates previously described precursor types (Betizeau et al., 2013). Lineage properties of the precursor types are analyzed in Fig. 5.

bRG‐both‐P (Fig. 4A) comprise 7% (49/695) of the observed cells and are bipolar precursors both at birth and prior to mitosis. The percentage of bipolar precursors increases between first observation and mitosis (from 49% to 88%). Precursors of this type have longer cell cycles than all other types (77.6 hours on average). They are often found at the root of the observed lineage trees (normalized depth 0.05; Fig. 5B), and are highly proliferative, creating on average almost twice as many progenies as the other precursor types (4.8 cells on average; Fig. 5C). A third of the precursors of this type retract at least one process prior to mitosis, and translocations in both directions are possible (17% down, 15% up).

Figure 5.

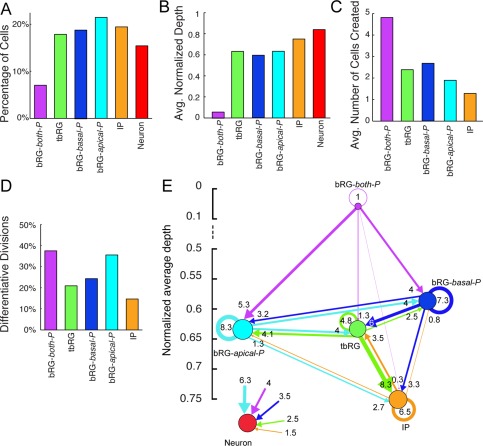
Analysis of the lineage properties of automatically extracted precursor types, obtained by the HMT algorithm using K = 6 types and allowing all state transitions. Types and colors correspond to Fig. 4. A: Distribution of cell types. B: Average normalized depth of cells of each type. C: Average number of cells in the progeny. D: Percentage of differentiative divisions per precursor type. E: Transition diagram between the precursor types. Node size indicates proportions of cells of that type. Edge thickness is proportional to the frequency of the transition in the dataset. The y‐axis represents the average normalized lineage depth where the precursor type is found. The neuron type is placed in insert for clarity. The transition diagram shows that almost all transitions are possible, except for transitions into bRG‐both‐P, which has a unique function at the roots of lineages, creating the largest progeny, and frequently differentiating. Bidirectional transitions are possible in most cases, and self‐renewal is frequent for all precursor types with the exception of bRG‐both‐P. All precursor types can produce neurons, but the three bRG types have the strongest contribution.

tbRG (Fig. 4B) constitute 18% (124/695) of all observed cells, characterized by at least one transient process. At birth, only 16–19% of these precursors have apical or basal processes (never both). The percentage of these precursors with basal processes is stable, but 47% will have apical processes prior to mitosis. tbRG precursors are almost equally likely to be either the upper or lower precursor at birth. When mitosis was observed, 21% of these precursors undergo translocations in either direction, and about 23% retract a process. bRG‐basal‐P (Fig. 4C) constitute 19% (131/695) of all observed cells. At birth it is typically the upper precursor that inherits the basal process, which is stable throughout its lifetime. Although these precursors do not inherit the apical process, 32% of them proceed to develop an apical process, and prior to mitosis 21% will have a bipolar morphology. Twenty‐one percent undergo upward translocations, and 17% perform process retractions prior to mitosis. bRG‐apical‐P (Fig. 4D) constitute the largest cluster at 21% (149/695) of all observed cells. They invariably inherit an apical but never a basal process, and are typically the lower daughter (86%). The apical process is stable in 99% of the precursors of this type, and 21% grow a basal process (in addition to the apical process) prior to mitosis. 28% of all dividing precursors of this type perform downwards translocations, and 25% retract processes.

IP (Fig. 4E) constitute 19% (135/695) of the observed cells and these precursors are characterized by being nonpolar both at birth and prior to mitosis. They are found as both lower and upper precursors after division, and are found toward the ends of the lineage trees (normalized depth 0.75). Because of their position in the lineage, they produce fewer cells than all other types (1.3 observed cells on average in the progeny).

Neurons (Fig. 4F) constitute 15% (107/695) of the observed cells and by definition do not include cycling cells. They are not clearly defined by their morphology, although 71% have basal processes at the final observation, and only 8% are bipolar. They include cells with both transient (33%) and permanent (63%) processes. They are equally likely to be upper or lower cells following mitosis.

The proportions of cell types defined by the HMT are summarized in Fig. 5A, which shows that four of the five precursor types occur in almost equal numbers, although bRG‐both‐P are notably less frequent. The normalized depth in Fig. 5B indicates where cell types occur in the lineage tree (with 0 being the root, and 1 being the deepest leaf of the tree). As expected, bRG‐both‐P precursors are predominantly near the root, and neurons are at the leaves of the trees. Because of occasional early asymmetric divisions, where one daughter is a neuron, and the other is a precursor that divides multiple times, neurons do not always have normalized depth 1, so that some lineage trees include precursors that have larger depth than the neurons, which explains the small difference in depth between IPs and neurons, given that IP precursors are closer to the end of the tree than are the other bRG and tbRG precursors. The number of cells in the progeny (Fig. 5C) is highest for bRG‐both‐P, and lowest for IP precursors, despite the high rate of differentiative divisions for bRG‐both‐P precursors, and the lowest rate of differentiative divisions for IP precursors (Fig. 5D).

The lineage relationships between the different precursor types are best and most compactly described by a state transition diagram as displayed in Fig. 5E. Transition diagrams are graphs showing the proportions of all cell types by the size of the respective node, and the frequency of transitions between types. Arrows indicate that precursors of a particular type can create daughter cells of the target type, and the thickness of the arrow, as well as numbers near arrows showing the percentage of all divisions that are of this type, indicate how frequently such transitions occur. Self‐renewing transitions are displayed by a loop, and the percentage of divisions that create neurons is presented in a separate inset. The vertical order of the cell types corresponds to their average normalized depth (Fig. 5B).

Most of the possible transitions (26/30) are observed. Bidirectional transitions are detected between all precursor types except for the bRG‐both‐P, which receives no contribution from any other precursor type, and is usually located at the root of the lineages. In the transition diagrams the normalized depth shows that the bRG‐both‐P has a high stemness. As expected, bRG‐both‐P frequently split up into an upper bRG‐basal‐P and a lower bRG‐apical‐P precursor, but rarely generate IP or tbRG precursors directly, nor do they self‐renew. bRG‐basal‐P often self‐renew, and commonly generate tbRG precursors. tbRG most commonly generate IP daughters. IP precursors often self‐renew, and differentiate less frequently than all other types. bRG‐apical‐P precursors also frequently self‐renew, and are the largest source of differentiated cells. tbRG and bRG‐apical‐P constitute hubs participating in the highest number of transitions. All categories of precursors are competent to generate neurons albeit with very different frequencies. Interestingly, IP precursors exhibit the lowest frequency of neuron generation and bRG‐apical‐P the highest (insert, Fig. 5E).

Both the definition of precursor types and their proliferative behavior resemble the earlier manual classification of precursors based purely on their morphology (Betizeau et al., 2013). A notable difference is the bRG‐both‐P type, which is characterized slightly differently by the HMT algorithm. Even though it is still predominantly bipolar, it is less frequent, occurs almost exclusively at the root of lineages, and does not exhibit bidirectional transitions. In the Discussion section we analyze in depth the reasons and significance of this result.

Identifying new precursor types

Our results show that when the HMT algorithm is initialized with K = 6 clusters (Fig. 4) it returns, on average, the same cell clusters obtained by manual classification (Betizeau et al., 2013). If K is set to larger values, new precursor types emerge. Under these conditions it is not guaranteed that all previously found precursor types are exactly reproduced, as they could be split up into more refined clusters. However, overall we do find that the most characteristic features are retained. Fig. 6 shows the results for K = 8 clusters of cells. The retained precursor types are: bRG‐basal‐P, bRG‐apical‐P, IP, bRG‐both‐P. Three new precursor types emerge as subclusters from previously found types for K = 6. The tbRG type of precursors with transient processes is now split into two subtypes. A new type (9% of cells), referred to as “tbRG+” (Fig. 6C), exhibits transient features and is mostly found in the OSVZ (86%). tbRG+ is born with nonpolar characteristics, prior to developing apical (73%) or basal processes (38%), and in 11% of cases both processes. Forty‐one percent of the processes retract prior to mitosis. The other new transient precursor type (6% of cells) is referred to as “tbRG−” (Fig. 6D), and is the inverse of tbRG+: it is born with apical (38%) or basal (48%) processes, but never both. tbRG− mostly lose processes prior to mitosis; 7% maintain an apical process. These precursors do not translocate or retract.

Figure 6.

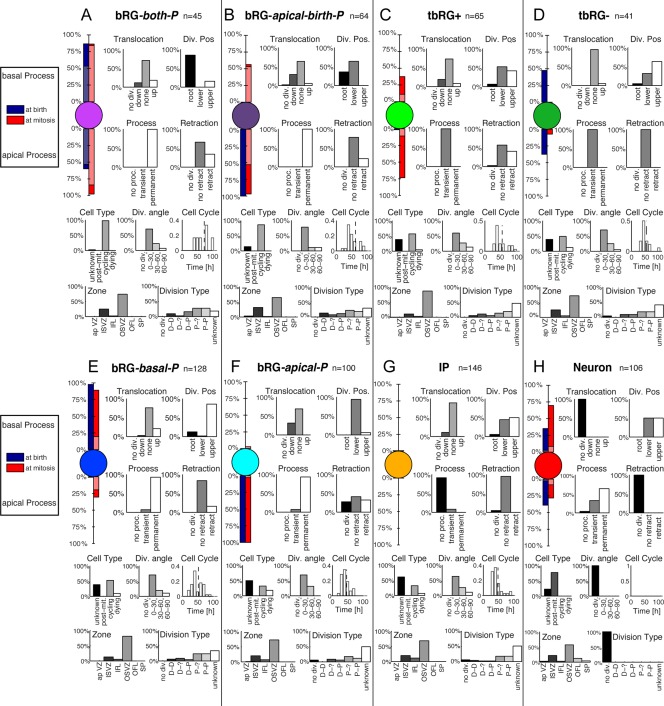
A–H: Automatically extracted cell types, using K = 8 different types and allowing all transitions. See Fig. 4 for an interpretation of the visualization. Compared with the K = 6 case, most precursor types remain (bRG‐basal‐P, bRG‐apical‐P, IP, bRG‐both‐P, Neurons), but with K = 8 clusters new precursor types (bRG‐apical‐birth‐P, tbRG+, tbRG‐) are identified. Lineage properties of the precursor types are analyzed in Fig. 7.

The remaining new precursor type (9% of cells) is referred to as “bRG‐apical‐birth‐P” (Fig. 6B), and combines features of bRG‐apical‐P and bRG‐both‐P types. At K = 6, 87% of bRG‐apical‐birth‐P precursors were categorized as bRG‐apical‐P and the rest as bRG‐both‐P. They are born uniquely with an apical process, and they are invariably the lower cell following mitosis. In these precursors, the cell‐cycle is 63 ± 26 hours, which is longer than that of bRG‐apical‐P (47 ± 13 hours), but shorter than that of those seven bRG‐both‐P type for which the cell cycle duration (73 ± 22 hours) could be reliably measured, because they were not the first cells in lineages. This difference is consistent with bRG‐apical‐P's increased number of proliferative divisions and shorter cell‐cycle lengths (Pilaz et al., 2009). Prior to mitosis, 53% of the bRG‐apical‐birth‐P precursors develop bipolar morphology. Figure 7B shows that bRG‐apical‐birth‐P precursors (normalized depth 0.35) occur at deeper levels of lineage trees than bRG‐both‐P precursors (normalized depth 0.07), which occur almost exclusively at the root of lineage trees, but significantly higher than bRG‐apical‐P precursors, which are now found toward the ends of lineage trees (normalized depth 0.77). Furthermore, the number of progeny of new bRG‐apical‐birth‐P precursors (3.5; Fig. 7C) is the second highest, lower only than for bRG‐both‐P precursors (5.1), but higher than for bRG‐apical‐P precursors (1.2). This implies that there are two types of precursors born with uniquely apical processes: those bearing an apical process at mitosis and that can regrow a basal process (bRG‐apical‐birth‐P), and those developing an apical process soon after mitosis (bRG‐apical‐P). Interestingly, bRG‐apical‐birth‐P precursors also perform substantially more differentiative divisions (Fig. 7D), and are the largest source of neurons, whereas the remaining bRG‐apical‐P have only a small contribution to this pool, showing only a minimally higher rate of differentiation than IPs.

Figure 7.

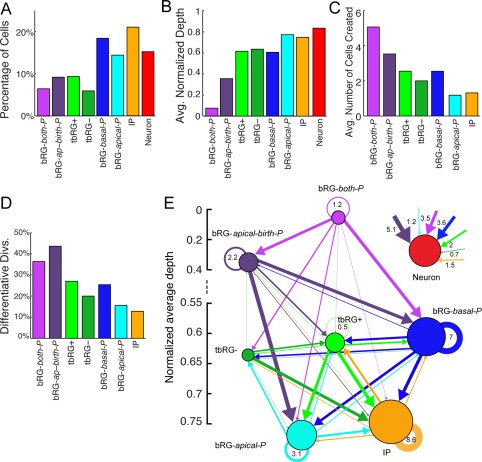
Analysis of the lineage properties of automatically extracted precursor types, obtained by the HMT algorithm using K = 8 types without constraints on transitions. A: Distribution of cell types, showing how precursor types from the K = 6 case are split up. B: Average normalized depth of cells of each type. C: Average number of cells in the progeny. D: Percentage of differentiative divisions per precursor type. E: Transition diagram between the precursor types. Most transitions are possible, with the exception of transitions into bRG‐both‐P and bRG‐apical‐birth‐P. The strongest contribution to the neuron pool comes from bRG‐apical‐birth‐P precursors, followed by bRG‐basal‐P and bRG‐both‐P. The lineage properties reproduce the key properties of the K = 6 case, and make common division patterns more visible by introducing precursor subtypes.

The transition diagram (Fig. 7E) for K = 8 shows a similar picture to K = 6 and in both cases the bRG‐both‐P precursors do not receive contributions from any other precursor type. A notable feature of the K = 8 case is the strong transition from bRG‐both‐P to bRG‐apical‐birth‐P: the latter now capture those precursors that regrow their basal process and maintain their inherited apical process. bRG‐apical‐birth‐P precursors are either at the root of a lineage or daughters of bRG‐both‐P, but are rarely daughters of other types. In the K = 8 analysis, there are fewer transitions from bRG‐both‐P into bRG‐apical‐P precursors, and almost none to IP and tbRG+ precursors. bRG‐apical‐birth‐P is a source of bRG‐apical‐P, and also of bRG‐basal‐P and neurons, but never tbRG− and rarely IP precursors. bRG‐basal‐P precursors constitute a hub as for K = 6, receiving contributions from all clusters, and generating all types except bRG‐both‐P precursors, but having more transitions into bRG‐apical‐P than into bRG‐apical‐birth‐P precursors. bRG‐apical‐P precursors have their main source in the bRG‐apical‐birth‐P and tbRG+ precursor, often self‐renew and generate IP or tbRG− precursors, but rarely differentiate. Both tbRG types rarely self‐renew, but frequently generate IP precursors. There is a stronger transition from tbRG− to tbRG+ than vice versa, and tbRG− differentiate less frequently than do tbRG+ precursors. As in the K = 6, in K = 8 IP precursors show the highest levels of self‐renewal, and once again rarely differentiate.

Imposed directionality of cell type transitions

The HMT algorithm makes it possible to impose constraints on the directionality of precursor transitions (see Materials and Methods). By initializing the transition matrix A to a triangular structure, precursors of type i can only produce daughters of type j with j ≥ i, but not types of lower order. This restriction corresponds to enforcing increased levels of differentiation with every division, and a natural ordering of precursor types according to their proliferative potential. Enforcing this constraint leads to a reduction of the numbers of parameters to be learnt by the HMT algorithm, which facilitates statistical model learning. Comparing the results of a constrained and unconstrained model to fit the biological observations can thus provide insights into the validity of the assumption of unidirectional progressive differentiation. When the restriction mechanism is added to the HMT algorithm for K = 6 clusters, there is little change in precursor types identified, but there are important changes in the lineage structure and proportions of cells (compare Fig. 5 and 9). By definition of the constraints, the precursor types are ordered by the position in the lineages (Fig. 9B), whereas in the unconstrained case of Fig. 5 and Fig. 7 the order is arbitrary (but was matched manually for easier comparison).

Figure 9.

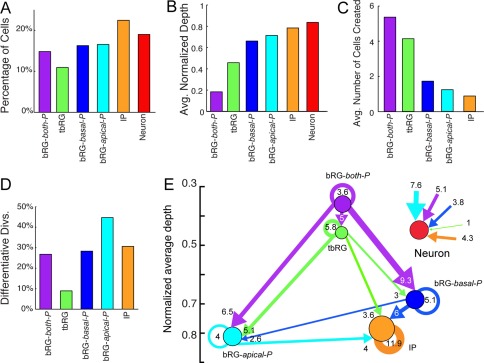
Analysis of the lineage properties of automatically extracted precursor types, obtained by the HMT algorithm using K = 6 types and imposed directionality of possible transitions. A: Distribution of cell types: imposing directionality leads to a shift of cell type proportions. B: Average normalized depth of cells of each type. C: Average number of cells in the progeny. D: Percentage of differentiative divisions per cell type. E: Transition diagram between precursor types. All allowed transitions except for direct bRG‐both‐P to IP transitions are observed, but proportions are very different from previous results in Fig. 5 and Fig. 7, as well as for manual classification (Betizeau et al., 2013). The constrained transition diagram cannot capture the observed bidirectionality of transitions.

Imposed directionality leads to occasional changes in the statistics of clusters. For example, the bRG‐both‐P cluster is more than twice as large (Fig. 9A), but is less homogeneous than the bRG‐both‐P cluster in Fig. 4. Only 64% of all precursors of this type are bipolar, compared with 88% without directionality constraints. This is an effect of precursors in this cluster being forced to be at the beginning of lineages, which leads to non‐bipolar precursors at the roots of lineage trees being categorized into this cluster. In particular, 63% of the precursors from the bRG‐apical‐birth‐P type (identified for K = 8 in Fig. 7) are now categorized as bRG‐both‐P precursors, compared with only 13% in the unconstrained case. Similarly, precursors with transient morphology at later stages of lineages can switch from the tbRG to the IP type, because this might better explain their lineage position. Therefore the tbRG cluster shrinks and becomes the least frequent type, whereas IP grows. Also the normalized depth of tbRG is reduced (Fig. 9B), and because tbRG have to occur prior to all other types except bRG‐both‐P, their progeny is larger than in the unconstrained classification, whereas the progeny of bRG‐apical‐P and bRG‐basal‐P shrinks. Comparing this characterization with the results for K = 8 (Fig. 7) shows that 60% of the tbRG+ precursors, but only 32% of the tbRG− precursors fall in the new tbRG cluster (the rest are classified as IP or neuron cells). Also the proportion of neurons is increased, possibly due to the capture of the small number of uncertain cells at the ends of lineages. The percentage of differentiative divisions (Fig. 9D) shrinks for tbRG types, because of their early position in lineages, and increases for bRG‐apical‐P and IP precursors.

Blurring the distinction between types can be avoided by increasing the number of clusters, because the HMT algorithm can uncover types that have similar morphological distributions, but different positions in the lineage as different cell types, or find non‐overlapping paths, where cells of one type can never occur as progeny of a particular mother cell type. An increase to K = 10, for example, finds two types of bRG‐basal‐P, bRG‐apical‐P, and IP, which occur at different depths within the lineage. This also separates basal‐only precursors at the roots of lineage trees from bRG‐both‐P precursors, thereby leading to more homogeneous clusters. In conclusion, the assumption of a strict, unidirectional progressive differentiation of precursors does not appear to match the biological reality, unless a significantly higher diversity of precursor types is accepted, and more data will be necessary to clearly describe such types. A reasonable model with K = 6 types can be identified, which resembles the unconstrained model, as well as manual classification based on morphology. However there is a less clear distinction between types, and a failure to capture bidirectional transitions, which occur at least for unipolar bRG and tbRG types in all other models, including the manual classification (Betizeau et al., 2013).

Detection of new hidden cell types

As we have shown above, the number of clusters with which the HMT algorithm is initialized determines the subsequent types of cells identified. In particular, smaller clusters of cell types are only found if they are either sufficiently different from all other cells with respect to their features or proliferative behavior, or if the number of clusters of cell types is sufficiently large. If these conditions are not fulfilled, then smaller clusters of cell types are merged with the larger clusters, as this maximizes the likelihood of the data under the learned model. A stepwise increase in the number of clusters leads to an increase in the cell types, according to their prominence in the dataset. Figure 10 shows how increasing the number of cell types from 2 to 10 impacts on the proportions of clusters (indicated by the corresponding node size) and the relationships between cell types found for different parameters (indicated by lines connecting two cell types); an illustration of the morphology of each cell type at mitosis is shown at the bottom). No constraints on transitions are imposed, the color codes are matched with the conventions used in Fig. 5 and Fig. 7, and precursor types with a transient morphology are marked with a dashed circle. Fig. 10 shows that at K = 2, only cycling and postmitotic cells are distinguished. At K = 3 a new cluster for nonpolar IP‐like precursors is obtained, which is also observed at higher K values. At K = 4, the polar cycling precursors are subdivided into a group with predominantly apical and another with predominantly basal processes. At K = 5, tbRG precursors with transient (growing) processes emerge as a separate progenitor type. At K = 6 the bipolar progenitor type emerges as a separate small cluster (for color code, see Fig. 5), and the tbRG type now includes precursors that both grow and retract processes. At K = 7 two types of progenitors with transient processes appear. At K = 8, the bRG‐apical‐birth‐P type (Fig. 6) is found as a new cluster with permanent apical processes from birth to mitosis, of which 53% develop a bipolar morphology. Furthermore, the two types of transient process–bearing precursors are discriminated into two categories, one that grows (tbRG+) and one that retracts processes (tbRG−). At K = 9, IP‐like precursors are split into a cluster that self‐renews, and another predominantly neurogenic cluster. At K = 10, a new neurogenic type appears, which is born with only a basal permanent process, but around 50% of all precursors grow an additional apical process, and most precursors perform upward translocations prior to mitosis. Even though HMT can in principle be run for arbitrary values of K, a more finely grained analysis that could reveal more meaningful cell types would require larger datasets.

Figure 10.

Increasing the number of potential clusters for the HMT algorithm reveals new precursor types. For different numbers of types (from K = 2 [left]) to K = 10 [right]), the node size indicates proportion of cells falling into each cluster, and dashed circles indicate types with transient morphology. Lines indicate the proportion of cells of a previous cluster (at lower K) that fall into the new cluster (for larger K). For simplicity, only transitions that account for at least 10% of cells in each cluster are indicated. As the number of clusters increases, previous precursor types split up to form better discriminated clusters, whereas other types remain mostly unchanged. Bottom: cartoon of average morphology at mitosis for each type (red bars are proportional to the percentage of cells with apical or basal processes; colors of cell bodies for K = 6 also correspond to cell types in Fig. 4; for K = 8 to Fig. 6).

Objective evaluation of clustering quality

The different cell types identified by the HMT algorithm correspond to well‐separated clusters in the data space. Fig. 10 shows that the cell types identified by the HMT algorithm crucially depend on the number of clusters to be learned, but are in good agreement with previously described characterizations of progenitor types. The choice of the appropriate number of clusters for HMT and other free parameters can be based on a variety of objective criteria for evaluating clustering quality. Unlike the evaluation of supervised machine learning techniques, in which classification error on a test set is a universal criterion for performance comparison, there is no such unique criterion for unsupervised clustering methods. The choice of the “best” clustering method depends on the desired application, in our case exploratory data analysis. Although quantitative criteria can strongly support this choice, it is important to evaluate several objective criteria that should be met by a successful model, and to accompany them by an expert interpretation of the learnt model (von Luxburg et al., 2012). Different methods are likely to capture different aspects of the dataset, and the results may depend on the size of the dataset, as well as the noise level of the data (Buhmann, 2010). Furthermore, hyperparameters such as the overall number of clusters are not known a priori and need to be chosen according to heuristics.

In machine learning, several heuristics for evaluation metrics have been developed, which largely focus on two clustering criteria: 1) data points within the same cluster should be as similar as possible; and 2) data points in different clusters should be as dissimilar as possible, i.e., clusters should be well separated. An often used criterion that takes both aspects into account is the silhouette score described in Materials and Methods (Rousseeuw, 1987). The silhouette score intuitively compares the similarity of points within each cluster (which should be high in a good clustering) with the similarity between different clusters (which should be low). The silhouette score turns this into a score between −1 (bad clustering quality) and +1 (best quality). Higher silhouette values indicate that each datapoint in a cluster is closer to other datapoints within that cluster, and farther away from datapoints in other clusters. Values close to zero indicate that data points are close to the borders of clusters, and negative values indicate that datapoints are closer to datapoints in other clusters than to their own, thereby indicating a clustering defect. In Figure 11A the silhouette values for different numbers of clusters are compared for HMT models without constraints (HMT undirected) or with imposed directionality (HMT directed). For all values of K, the unconstrained model performs better, and a peak between K = 4 and K = 6 is found, which is also the parameter range in which the identified cell types correspond to previously identified types (compare Fig. 10). For smaller K values, the clusters overlap, and for larger K values the clusters become similar, which leads to lower silhouette scores. This was compared with a completely random assignment of cells to clusters with uniform probabilities, and a shuffling of labels that preserves the proportions of clusters. The HMT algorithm leads to significantly better clustering. For large numbers of clusters K the silhouette values approach zero, meaning that in such fine‐grained clusterings many data points can be switched between clusters without much effect. This also indicates that more data would be needed to reliably detect more clusters, by measuring either more cells, or more features per cell, which could facilitate the distinction between otherwise similar types. However, even with larger numbers of clusters, the HMT results are significantly above chance. Figure 11B shows an analysis of the silhouette values for individual cell types in the HMT result for K = 6 cell types, presented in Fig. 4. IP and postmitotic clusters are best separated from the rest, whereas the tbRG precursors have the smallest silhouette value due to the variable morphology of these precursors. The silhouette score is one objective criterion to evaluate the clustering quality of the learnt model, and is helpful for choosing an appropriate range for the number of types, but should not be the only criterion, because it does not take lineage relationships into account.

Figure 11.

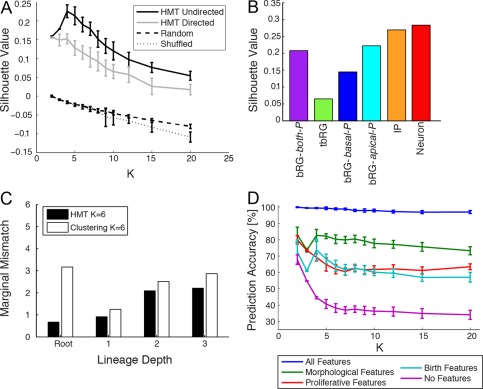
Quantitative evaluation of clustering quality provides a guideline for selecting model parameters. A: Evaluation of clustering results with different K by their silhouette values (shown are means and standard errors for 20 repetitions). HMT models without constraints (HMT undirected) perform better at discrimination than models with imposed directionality (HMT directed). For comparison, results of random and shuffled assignments of cells to clusters are shown, verifying that the clustering is significantly better than chance, even for large K. B: Silhouette values per cell type for the K = 6 clusters from Fig. 4, learned without constraints. C: Mismatch between predicted and actual statistics of all features at different depths of lineage trees (comparing marginal distributions, i.e., statistics irrespective of cell type). For every lineage depth, the HMT model with an equal number of clusters predicts the distribution of features in the original dataset better than a clustering model without lineage structure. D: Accuracy of cell type prediction for different numbers of clusters K, given the mother precursor type and different sets of features (all features = full dataset; morphological features = use only features about apical and basal processes at birth and at mitosis; birth features = use only features available at birth of the cell (processes at birth, division position); no features = use only mother precursor type).

Comparison of HMT and feature‐based clustering

HTM models fit the tree‐like nature of the dataset well, but cell types could also be inferred based on clustering of the attributes alone. Although this is successful for capturing the overall distribution of attributes in the dataset, HMT models in addition capture lineage relationships and can thus better predict the distribution of features at different depths of lineage trees. Pure clustering models instead have no notion of transitions or lineage depths, and would predict the same distribution at all levels. Because Fig. 5B, 7B, and 9B show that different cell types occur preferably at specific lineage depths, this is obviously not the case. The mismatch can be quantified through the marginal distribution of features at different depths, which predicts the distribution of each feature in Table 2 using a weighted average across cell types. The weight corresponds to the likelihood of finding cells of each type at every lineage depth; thus the distribution at the root is dominated by bRG‐both‐P, and near the leaves by IPs and neurons. Figure 11C shows the mismatch of the marginal distributions between the actual distribution of features in the dataset at each depth, the marginal distribution predicted by the HMT, and a clustering model, learned with standard EM (Bishop, 2006), which ignores lineage information. The mismatch is computed as the sum of the absolute differences in predicted probability tables for the discrete attributes. (Other measures lead to similar results.) HMT performs better in matching the marginal distributions at all lineage depths when compared with a cluster model. The difference is particularly striking for root nodes, which account for only 13% of all cells, but have a very distinct morphology, in particular a much higher fraction of bipolar precursors (42%) than in the overall dataset (17%). This difference is only captured by the HMT model, but not by clustering alone. We can therefore conclude that tree‐structured models like HMT capture important lineage‐related properties of the dataset better than purely feature‐based clustering.

Prediction of daughter cell types

The silhouette analysis focuses only on the homogeneity of clusters according to the measured features, but does not take into account the lineage information that is simultaneously learned by the HMT algorithm. Apart from the marginal analysis (Fig. 11C), which compares the overall statistics at different depths, a successful model of cell differentiation should also be able to predict daughter cell types from both feature and lineage information. We therefore introduce an alternative criterion for the evaluation of tree‐based clustering quality, namely, the prediction accuracy of the daughter cell type, based on the type of the mother cell, and different subsets of features. Due to the randomness involved in mitosis, perfect prediction cannot be expected, but in a meaningful model it must be possible to predict the daughter cell types significantly above the chance level of 1/K, e.g., due to the likelihood of certain cell type transitions, described by the transition matrix A in the HMT algorithm. Table 3 shows the prediction accuracy for K = 6 types, measured as the percentage of correctly predicted daughter cell types, given the mother cell type and different features. Table 3 shows the prediction accuracy if only a single feature, or if all other features (“Without Feature”) are used. One can see that morphological features prior to mitosis and at birth are highly predictive, but every feature contributes to a prediction well above chance level. The accuracy is also shown for different groups of features: “Features at Birth” uses only features that the cell inherits when it is born (morphology at birth and position after division). These indicators are not significantly better predictors than the morphology alone. If the morphological features (at birth and at mitosis) are combined, a prediction accuracy of 80% is achieved, which indicates that morphology is indeed a strong indicator of cell type. In comparison, predictions using only proliferative features (length of the cell cycle, cell type [postmitotic or cycling], mitosis location, and mitotic plane angle) show lower accuracy (62%). Finally, using all features, cells can be correctly categorized almost perfectly with 98.9% accuracy. If no features are used, i.e., if prediction is only based on the cell type of the mother cell and the probability of state transitions in A, one can still predict the daughter cell type with an accuracy of 38.2%, which is well above the chance level of 16.6%.

Table 3.

Influence of features on the prediction of daughter cell type (%)^a

	Morphology at mitosis	Morphology at birth	Cell type	Process stability	Process retraction	Cell cycle	Mitotic plane angle	Trans‐location	Mitosis location
Only feature	62	63.9	49.7	60.3	51.4	50	49.5	51.2	48.3
Without feature	91.4	92.8	98.4	93.5	96.8	98.2	98.6	98.7	97.2

	Features at birth	Morphological features	Proliferative features	All/no features
Only feature	64	80.3	62	98.9
Without feature	86.2	86.7	93.7	38.2

^aFor the nine features used for clustering, the percentage of correct predictions is shown, using mother cell type and a single feature resp. all features except one. For comparison we display the prediction accuracy if only features known at birth (processes and division position), morphological features (processes at birth and at mitosis), proliferative features (cell‐cycle length, mitosis location, mitotic plane angle, cell type), or all or no features are used for prediction. Bold numbers indicate the best, italic numbers the lowest prediction result. Results are for the combined E65 and E78 dataset, using K = 6 clusters of cell types without constraints, averaged over 20 trials with random cluster initializations. All features have similar influence on the prediction accuracy, with values around or over 50%. Morphological features are the best predictors, yielding accuracies over 62%. The combination of features allows for prediction of the daughter cell type with more than 90% accuracy (98.9% if all features are used).

The prediction accuracy is also dependent on the number of cell types. Whereas with fewer clusters the chance of randomly predicting the correct cluster is higher, more types allow for more specialization, which could limit the number of choices for the type of the daughter cell, given the type of the mother cell. In the extreme case of deterministic transitions between cell types and many types of cells, an almost perfect prediction should thus be achieved based solely on the mother cell type, but this was not found to be the case. Fig. 11D shows the prediction accuracy for different numbers of clusters, and using different sets of features. One can see that using all features, almost perfect predictions (above 96.9%) of the daughter cell type are achieved even for 20 different types, which indicates that even in this case clusters do exhibit too great an overlap. For all other groups of features the prediction accuracy decays as the number of clusters K approaches 20. Very good performance of over 70% is reached when morphological features alone are used. If no features are used, i.e., predictions are only based on the mother's type, the performance monotonically decreases with increasing K, but is still well above the chance level of 1/K.

DISCUSSION

The present study shows that an HMT lineage‐based clustering method provides an objective and quantitative characterization of different discrete precursor types in the developing primate cortex. This has been made possible by the exploitation of an extensive dataset of morphological, proliferative features, and lineage relationships of precursors in the fetal macaque cortex using an unbiased sampling method. Our results validate the previously reported diversity of primate cortical precursors using manual classification, and show that nondeterministic transitions, defined via transition probabilities between many different cell types, are the rule, rather than the exception. The HMT model allows the testing of hypotheses concerning the number of distinct progenitor types, hinting at a greater diversity than previously reported, as well as exploring the significance of non‐unidirectional progressive differentiation.

Validation of manual characterization of precursors

Our present understanding of corticogenesis is largely the result of experimental reports of distinct classes of precursors based mostly on morphology (Fietz et al., 2010; Hansen et al., 2010, 2013; Betizeau et al., 2013; Florio and Huttner, 2014). Our quantitative analysis validates this approach, as the cell types obtained from HMT‐based clustering largely correspond to manually defined categories, with precursors divided into five bRG types corresponding to permanent, transient, and nonpolar morphologies (Betizeau et al., 2013). HMT analysis has the advantage in that it can push characterization further than the manual classification: the HMT model not only clusters cells according to their observable morphological features, but also takes into account the possibility that each cell type has internal predispositions for the types of daughter cells it can generate.

There is good agreement between the manual and HMT classifications, and upward of 85% of cells are put into the same categories when HMT is run without constraints and with the same number of precursor types as were previously identified manually (Betizeau et al., 2013). However, there are also potentially important differences between the two sets of results, which are explored in Fig. 12. Figure 12A shows the HMT model as developed here, which contrasts with Figure 12C, which is the manual classification (Betizeau et al., 2013). Comparison of the two models shows important differences. One reason for this disagreement is that in Betizeau's study, labels were only assigned to clearly identified cycling and postmitotic cells, whereas the HMT can compute a prediction for all cells in the lineage trees, including those cells at the end of the observation of the lineage, where the fate of the cell is unknown. This prediction can be based on the available measurements of morphology and other features, as well as the categorization of the mother cell. This completion of partially observed and labeled lineages is an important advantage of the HMT method.

Figure 12.

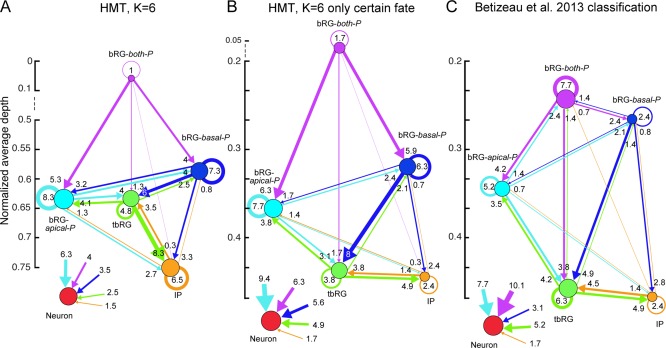
Comparison of transition diagrams for HMT‐based and manual classification into K = 6 types, for the combined datasets from E65 and E78. A: Transition diagram for the HMT results with K=6 types and no constraints, equivalent to Fig. 5E, shown for comparison. B: Same as A, but only showing transitions for precursors with certain fate, i.e., when either mitosis could be observed or cells could be defined as neurons. Changes in the average normalized depth are due to the exclusion of leaf nodes of lineage trees, which leads to the change of vertical layout. C: Transition diagram for precursors with certain fate (same cells as in B), using the manual classification from (Betizeau et al., 2013). Comparison of B and C shows that many characteristics, such as bidirectionality of transitions, are shared, but also reveals differences in the proportions of precursor types and the possibility of transitions into bRG‐both‐P.

A major difference between the manual and HMT analysis concerning the proportions of cell types lies mainly in the bRG‐both‐P and IP precursor types. Whereas in the manual classification based uniquely on morphology, bRG‐both‐P precursors account for 26% of the total, this figure drops to 7% for the HMT analysis (Fig. 5A, 12A). Do the differences between the manual and HMT models stem uniquely from the HMT predicting the cells that were not fully characterized in the manual classification? Fig. 12B shows the transition diagrams for the HMT without predicted leaf nodes. Here the proportions of cell types become closer to those reported in the manual classification, in particular for bRG‐both‐P (increased to 12%) and IP (decreased to 18%). Therefore this analysis shows that the inference of the uncharacterized cells by the HMT method is not the only source of difference in the results of the two methods.

A potential important reason for differences in the two methods is the consideration of lineage position by the HMT algorithm. This defines the bRG‐both‐P type as appearing only at or at least very near the beginning of observed lineages (Fig. 5B), suggesting that this precursor category shows a strong stemness. In the transition diagram for the HMT with K = 6 (Fig. 12A,B), this has the effect that the bRG‐both‐P type has uniquely outgoing transitions, i.e., a bRG‐both‐P precursor can only occur as the daughter of a precursor of the same type, but not of any other type. This is different from the manual classification (Fig. 12C), in which the bRG‐both‐P cluster receives contributions from other bRG types, thus forming bidirectional connections. When we analyzed how often transitions over two levels occur, we found that there are no transitions in which a grandmother precursor becomes a bRG‐both‐P precursor after two divisions, unless the first daughter is bRG‐both‐P. This implies that once a bRG‐both‐P precursor has differentiated into a different type, the ability to become bRG‐both‐P is definitively lost. This holds for both HMT and manual classification. Although such dependencies across two or multiple generations are not directly modeled by the HMT, they are nevertheless captured for our dataset. Below we will discuss possible extensions to the HMT that could explicitly capture higher order dependencies.

An important conceptual difference between the two categorizations shown in Fig. 12 is that the HMT model has probabilistic assignments to types, which means that the types do not have to be completely homogeneous. In the HMT's bRG‐both‐P type, only 88% are bipolar, not 100% as in the morphology‐based assignment, so that we occasionally find bipolar precursors being assigned to the bRG‐apical‐P and bRG‐basal‐P types. The reason why HMT assigns such a cell to a specific cluster also depends on whether the behavior of the cell in terms of the fate of its progeny is closer to that of other cells in that cluster, or is due to the similarity in terms of other measured features. There are two sorts of reasons for a cell to behave differently than its morphology suggests. It could result from an annotation error. For example, a cell's processes could have been incorrectly experimentally evaluated because of partial or complete occlusion by other cells. It could, however, reflect a more profound cause, whereby morphology and fate of progeny are viewed as two stochastic expressions of an internal genetic program (Kennedy and Dehay, 2012). According to this view, a cell type would then merely correspond to a discrete representation of this expression pattern, and could be seen as the default or most likely expression pattern of the state. This would still allow occasional random deviations, and thus give rise to a continuum of morphological and lineage patterns. The HMT model, because of the probabilistic nature of observation and transition models, is ideally suited to capture such variability in the features and proliferation patterns of cells belonging to the same type (see below for interpretation of this developmental flexibility).

Diversity of precursor types

An important conclusion of the HMT analysis for K greater than 6 (Fig. 7, 10) is the evidence for a potentially larger diversity of precursor types with different roles during development. For K = 8 we identify three new types: the tbRG precursors with transient morphology are subdivided into tbRG+ and tbRG−, which exhibit differences in their progeny and their ability to differentiate into neurons. Furthermore, we identify the novel bRG‐apical‐birth‐P type, which is, like bRG‐apical‐P, uniquely born with an apical process, but in 50% of cases acquires a bipolar morphology prior to mitosis. Unlike bRG‐apical‐P, bRG‐apical‐birth‐P precursors occur much earlier in lineages, and have greater neurogenic potential than the remaining precursors with apical processes. This raises the question of how many types of precursors one should expect. The HMT algorithm provides an easy to use tool for such explorations, but due to the finite size of the dataset, the number of clusters cannot be set arbitrarily large. The qualitative analysis of Fig. 10 shows that reasonable types are identified for K lower than 10, and the quantitative criteria in Fig. 11 show that satisfactory performance for cluster separation and prediction of cell types is maintained at these K values. Nevertheless, the automatically extracted types will necessarily become more similar, which is shown in the silhouette plot of Fig. 11C, and they may eventually degenerate into clusters with very few cells. In this case, a combination of objective and qualitative analysis using expert knowledge combined with larger datasets is required for reliable fine discrimination between larger numbers of cell types.

The ability of the unsupervised method to identify previously unreported precursor types as new categories as in Fig. 6 depends crucially on the size of the available dataset. The dataset of progenitors in the developing monkey cortex is the largest of its kind to date, containing 91 lineages with 695 cells and measurements of their morphology and proliferative behavior (Betizeau et al., 2013). Applying the HMT algorithm with more clusters will require even larger datasets so as to avoid overfitting, by which tiny clusters consisting of very few cells would be formed. A further complication for large K values is that, due to the random initialization of clusters, results may vary significantly from trial to trial. Alternatively, clusters obtained for large K may be merged a posteriori according to their similarity, which leads to results similar to those shown in Fig. 10.

Impact of directionality

A useful feature of HMTs and other Bayesian graphical models is their ability to include prior knowledge as well as constraints in a principled fashion. For this study we tested the impact of constraining the directionality of differentiation, so that precursors after each division become progressively more fate constrained. Although this is a common hypothesis concerning the nature of corticogenesis (Qian et al., 1998; Noctor et al., 2004; Tyler and Haydar, 2013), we found that an explicit inclusion of this assumption leads to a model (Fig. 9) that does not match the biological reality as well as fully unconstrained models, suggesting that bidirectional transitions between most (but not all) of the precursor types would be a fundamental property that a model of primate corticogenesis should capture. The HMT model, as well as morphology‐based manual classification, finds that monopolar bRGs and tbRGs exhibit bidirectional transitions. The exception is the bRG‐both‐P precursor, which indeed seems to differentiate unidirectionally under all HMT conditions.

One can use an adaptation of the HMT model to explore the consequences of directionality. The effect of imposing directionality is a blurring of precursor types (Fig. 8), which occurs because precursors that should differentiate into a precursor type that is upstream in the directed HMT model get merged with other cells. As a consequence, several other properties, such as the proportions of the cell types, or the percentages of differentiative divisions, differ from all other assignments. A clear indication of the differences between the directed and undirected case is illustrated in Fig. 13, which shows the distribution of cell types in the progeny of specific precursors, i.e., all cells resulting directly or indirectly from a division of each precursor. In the unconstrained case (Fig. 13A, following the transition diagram of Fig. 12), a large diversity of types can be observed for all types of precursors, which is also the case following manual classification. This is clearly different for the constrained HMT model (Fig. 13B, following the transition diagram of Fig. 9), in which more committed types such as IP are restricted to a small subset of types in their progeny. In both cases bRG‐both‐P can only be generated through self‐renewal. The progeny of the more committed precursors is much less diverse than for early precursors. This can be easily seen in Fig. 13B by noticing the predominance of the warm colors when comparing the rows for bRG‐both‐P and IP precursors.

Figure 8.

A–F: Automatically identified cell types, using K = 6 different types, but with imposed directionality of possible transitions. See Fig. 4 for an interpretation of the visualization. Compared with the unconstrained case, the cell types are similar, but slightly less homogeneous (see, e.g., bRG‐both‐P). This is an effect of the imposed directionality of transitions. Lineage properties of the precursor types are analyzed in Fig. 9.

Figure 13.

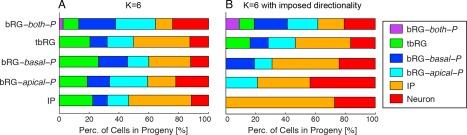
Distribution of cell types in the progeny of precursor cells for unconstrained and constrained HMT models. A: Nature of the progeny of the different precursor types identified in the clustering for K = 6 without constraints on transitions (Figs. 4, 5). B: Same as A, but with imposed directionality (Figs. 8, 9). The progeny in B is far less diverse than in the results of other HMT or manual classification.

There is a subtle relationship between directionality and the number of distinct precursor types. In the case of K = 8 types (Fig. 7), the results show that the occurrence of the new precursor types such as bRG‐apical‐birth‐P, tbRG+, and tbRG−, leads to a sparser transition diagram. For example, there are only weak transitions from other types back into bRG‐apical‐birth‐P, but strong forward connections into other bRG types, and a strong contribution coming from bRG‐both‐P. This could hint at a progressive differentiation pathway from bRG‐both‐P via bRG‐apical‐birth‐P to bRG‐apical‐P, in which the strongly neurogenic bRG‐apical‐birth‐P type could be responsible for asymmetric divisions.

Until the recent study of Betizeau et al. (2013) describing bidirectional transitions in primate cortical precursors, the prevailing view was that the early stages of cortical development unfold according to hierarchical principles. The dominant theory of a hierarchical development from stem cell toward differentiated cell types perceives lineage progression as a progressive restriction in stemness and cell potential caused by a series of (irreversible fate) decisions. However, this restrictive view of unidirectional lineage progression has been challenged by a number of experimental and conceptual studies (Rolink et al., 1999; Sato et al., 1999; Heyworth et al., 2002). It has been argued that a mechanism of lineage progression, which includes the potential for reversibility, is much more flexible in response to different environmental signals (Huang et al., 2005; Zipori, 2005). The frequent occurrence of bidirectional transitions between cortical precursor types during corticogenesis introduces stochasticity, and might therefore be indicative of a certain degree of flexibility. We do not know whether the observed reversibility entails going backward in developmental potential. However, imposing directionality constraints reduces the diversity of precursor types (Fig. 13). The observed reversibility might be made possible by the unique stem cell properties such as high self‐renewal ability and proliferative potential of primate precursors (Betizeau et al., 2013). Instances of reversibility are described in case of both transdifferentiation and dedifferentiation, in which the cell behavior appears to oppose the major developmental pathway. Contrary to strict hierarchical lineages, in which once a decision is made a cell is committed to a particular differentiation stage, primate cortical precursors have the ability to reverse. However, due to the lack of molecular analysis at the single cell level, we do not know to which extent the bidirectional transitions occur between more primitive cell stages and more committed progeny.

The present results favor a concept of stem cell organization based on flexible and self‐organizing cellular units, which are not restricted to a unidirectional flow through a sequence of compartments. Such an adaptive system could allow for self‐organization and thereby provide the plasticity and robustness needed to generate the complexity of the adult cortex (Chang et al., 2008; Huang, 2009; Kennedy and Dehay, 2012; Zubler et al., 2013).

Potential and limitations of the HMT for corticogenesis

Although tested here on morphological features and lineage relationships for primate precursors, our method could be applied more generally to datasets of different species, including datasets with different types of recordings, such as genetic expression markers (Olariu et al., 2009; Costa et al., 2011). In our dataset, measurements of every cell are available. However, other studies (Olariu et al., 2009) have shown that it is possible to infer the characteristics of intermediate precursors, even when there is only information about cells at the end of lineages.

Given the complexities of real cell lineages and the observed diversity of precursor types, the HMT model clearly is a simplification. As we have shown in Fig. 10, the number of clusters to be formed (the parameter K) can play a crucial role in determining which precursor types are identified by the unsupervised method. The number of precursor types is linked to how one conceptualizes corticogenesis. Because it is unknown exactly how many discrete types of precursors one should expect to find in the developing cortex, there is no clear a priori choice for K. One possibility is to base the choice of free parameters on model comparison methods like the silhouette value for clusters, which evaluates the cluster separation and within‐cluster similarity, and the ability of the model to predict the type of daughter cells (Fig. 11). We also based our choice of K on exploratory analysis and the observation that the results for K = 6 correspond qualitatively to previously reported precursor types with different proliferative roles (Hansen et al., 2010; Betizeau et al., 2013). Alternatively, one could explore the additional categories of precursors obtained with k = 8 for explaining certain aspects of corticogenesis. Other studies using HMTs have used alternative criteria for model selection; such as the Bayesian information criterion or integrated completed likelihood (Biernacki et al., 2000; Durand et al., 2005), or selected K according to known properties of the data (Olariu et al., 2009).

Limitations of the probabilistic model

Although the HMT model captures lineage dependencies better than pure clustering models (Fig. 11C), it has limitations. The HMT model makes the simplifying assumption that the types of each of the two daughter cells are conditionally independent, given the type of the mother cell. This means that the HMT in its standard form is not able to capture the preference for certain patterns of division, such as the frequently observed division into one upper bRG‐basal‐P and one lower bRG‐apical‐P daughter cell. Although such common patterns have high likelihood in the HMT, other relatively infrequent patterns such as the generation of two daughters with only basal processes are given too high a likelihood. Apparently, this problem does not affect the capability of HMTs to extract meaningful cell types, but it would affect its suitability as a generative model to predict new lineages through random sampling, and could improve the accuracy of predicted cell types (Table 3). One potential solution would be to modify the model and introduce a probabilistic dependency between the two daughter cell types. In this case the transition matrix A would predict not only the cell types of the two daughters independently, but also provide a joint probability distribution for pairs of daughter cell types, conditioned on the type of the mother, as proposed, for example, by Durand et al. (2005). Similarly, dependencies of daughter types across multiple generations could be modeled by a higher order Markov process, in which the daughter types are conditioned on the types of mother, grandmother, or earlier precursors in the lineage, thus increasing the number of parameters in A. As the discussion of the deviation of the HMT model from morphology‐based manual classification has shown, there are indeed some seemingly important second‐order or higher order relationships, such as the inability of precursors to become bRG‐both‐P precursors after differentiation into another type. A second‐order Markov model could allow this aspect to be captured explicitly.

Another shortcoming of the HMT model is that it does not permit modeling dependencies of daughter cell types on features of the mother cell, such as, for example, the cell‐cycle length or the angle of the mitotic plane. Introducing such dependencies would further complicate the probabilistic model, because the assumption of a hidden Markov state would be violated. Given enough data, it could be best avoided by increasing the number of available precursor types K, such that mother cells with similar morphologies but different proliferative features could end up in different clusters, and thus have different transition probabilities for daughters. An example is the occurrence of the bRG‐apical‐birth‐P type for K = 8 and its difference in progeny compared with the bRG‐both‐P and bRG‐apical‐P types (Fig. 6, 7).

Another simplifying assumption of the HMT is that the observed features are conditionally independent, given the type of the cell. Clearly there are correlations between the morphologies prior to and after mitosis, or between the inherited processes and the location of mitosis. Such dependencies are still captured in our results, because features are quite homogeneous within clusters and can thus be analyzed after assigning types to all cells with the Viterbi algorithm (Durand et al., 2005). However, dependencies could in principle be modeled also by a more complex observation model that replaces the Naïve Bayes assumption for θ with additional dependencies between attributes.

Related work

The HTM method used for the present study relies on the algorithms derived by Crouse et al. (1998) and refined by Durand et al. (2004). HMT models for biological growth processes were first proposed by Durand et al. (2005) as a statistical model for plant architectures. HMTs have been used by Olariu et al. (2009) to reconstruct cell lineage trees for human pluripotent stem cells. In their study, phenotypes of cells were only known for cells at the root and at the end of lineages, and measured by the expression of a cell surface antigen. The HMT was used to predict survival of a cell and two levels of the unobservable antigen expression level at intermediate precursors; and also to infer division patterns that lead to the observed expressions at the leaves. That approach differs from the present study, in which the set of observations for each cell is much richer, and thus the HMT model provides a prediction not only for lineages, but also for morphologically different categories of cells.

CONCLUSIONS

Analysis of large cellular developmental databases is a challenge to experimental and theoretical biologists. In this context, the development of a powerful automated analysis pipeline such as the one presented here illuminates our understanding of corticogenesis. The HMT model presented here confirms that primate corticogenesis is characterized by diverse precursor morphologies and complex lineages. In contrast, rodent corticogenesis is thought to exhibit few precursor types and linear lineages (Tyler and Haydar, 2013). In this context it would be interesting to apply the HMT model to a large rodent database, which should be able to inform us whether the observed primate rodent differences are qualitative or merely quantitative.

Finally, exploring a large database that has fine‐grain genetic profiling would better inform us about the flexibility of the lineages and give further insights into mechanisms of self‐organization predicted to be linked to cortical complexity (Chang et al., 2008; Huang, 2009; Kennedy and Dehay, 2012; Dehay et al., 2015).

CONFLICT OF INTEREST STATEMENT

The authors declare they have no competing financial interests.

ROLE OF AUTHORS

All authors had full access to all the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis. Study concept and design: MP, MB, SP, HK, RJD, CD. Analysis and interpretation of data: MP, SP, MB, JW, CD. Drafting of the manuscript: MP, MB, SP, HK, RJD, CD. Statistical analysis: MP, MB, SP. Obtained funding: RJD, HK, CD. Study supervision: CD, RJD, HK.