Abstract
Spatially continuous predictions of seabed hardness are important baseline environmental information for sustainable management of Australia’s marine jurisdiction. Seabed hardness is often inferred from multibeam backscatter data with unknown accuracy and can be inferred from underwater video footage at limited locations. In this study, we classified the seabed into four classes based on two new seabed hardness classification schemes (i.e., hard90 and hard70). We developed optimal predictive models to predict seabed hardness using random forest (RF) based on the point data of hardness classes and spatially continuous multibeam data. Five feature selection (FS) methods that are variable importance (VI), averaged variable importance (AVI), knowledge informed AVI (KIAVI), Boruta and regularized RF (RRF) were tested based on predictive accuracy. Effects of highly correlated, important and unimportant predictors on the accuracy of RF predictive models were examined. Finally, spatial predictions generated using the most accurate models were visually examined and analysed. This study confirmed that: 1) hard90 and hard70 are effective seabed hardness classification schemes; 2) seabed hardness of four classes can be predicted with a high degree of accuracy; 3) the typical approach used to pre-select predictive variables by excluding highly correlated variables needs to be re-examined; 4) the identification of the important and unimportant predictors provides useful guidelines for further improving predictive models; 5) FS methods select the most accurate predictive model(s) instead of the most parsimonious ones, and AVI and Boruta are recommended for future studies; and 6) RF is an effective modelling method with high predictive accuracy for multi-level categorical data and can be applied to ‘small p and large n’ problems in environmental sciences. Additionally, automated computational programs for AVI need to be developed to increase its computational efficiency and caution should be taken when applying filter FS methods in selecting predictive models.
Introduction
Seabed substrate data is important baseline environmental information for supporting the sustainable management of Australia’s marine jurisdiction. Seabed substrate is an important factor controlling the spatial distribution of benthic marine communities as it influences the colonisation and formation of ecological communities and the abundance of benthic organisms [1–6]. Seabed hardness is an important character of seabed substrate as it may influence the nature of attachment of an organism to the seabed [6]. Hard substrates provide environments that generally support sessile suspension feeders, while soft (unconsolidated) substrates generally support discrete motile invertebrates [5]. Hence, a spatially continuous measurement of seabed hardness would be a significant aid in predicting the spatial distribution of benthic marine communities and thus to marine ecosystem management. Moreover, it can also be used for the sustainable exploitation of marine resources and planning infrastructure (e.g. selection of pipeline routes).
Despite its importance, seabed hardness data is often difficult to acquire [7]. It can be directly measured at (often widely-dispersed) discrete locations, inferred from underwater video footage at discrete locations over small areas [8], or inferred from multibeam backscatter data [9–11]. However, there are disadvantages associated with these methods. For example, the direct measurements are only available at point locations, and the inferred data are either only available at discrete locations over small areas or their accuracy is unknown and may be affected by many factors [7, 12]. Therefore, predictive modelling provides an alternative approach to generate spatially continuous data of seabed hardness [7], where seabed hardness was classified into two classes (i.e. hard/soft binary data) according to the approach by Stein et al. [8] that is however difficult to use for certain substratum compositions. Moreover, all mixed classes were classified into hard class [7], so the relevant information of the mixed classes is missing for the management of associated habitats. However, no study has been conducted on predicting seabed hardness based on four classes data yet.
Predictive variables are essential to making predictions of seabed hardness. Physical properties derived from multibeam backscatter and bathymetry have proven to be useful predictors for predicting seabed hardness [7, 12]. Multibeam data collection can result in hardness and roughness maps which differentiate between different substrate types of the seabed [13]. At regional and continental scales, seabed sediments are often strongly correlated to bathymetry [14, 15]. At these scales, bathymetry and its derived properties are informative predictors of seabed substrate types. Moreover, recent technological advancements in sonar equipment have significantly increased the amount of biophysical data for making spatially continuous predictions of seabed hardness.
To predict seabed hardness, one of the most important decisions to make is to identify the best modelling technique that can generate a surface to truthfully represent seabed hardness. Random forest (RF) developed by Ho [16, 17] and Breiman [18, 19] has proven to have high predictive accuracy (PA) in data mining and many other disciplines [20–24]. It outperformed a number of statistical modelling techniques for spatial prediction using continuous data in the marine environmental sciences [14, 25, 26]. Hence, it was applied to predicting the spatial distribution of seabed hardness based on two classes and again achieved high PA [7]. In a recent study, seabed substrate types were predicted based on four textural classes derived from relative proportions of sediment grain size and their ratio [27]; and RF was again found to be one of the most accurate methods. However, its predictions were for grain size ranging from mud to gravel, which falls into the soft class according to Li et al. [7]. In addition, a Self-Organising Map and a hierarchical clustering method were jointly applied to angular backscatter response curves and produced seabed hardness classification with multiple classes, but its accuracy was less than RF and the results were not spatially continuous [12].
Model selection is essential for identifying an optimal predictive model and various methods have been developed [28–30]. However, it is often argued that model selection is less important for RF, because: 1) RF is insensitive to un-important variables, as it selects the most important variable at each node split [23]; 2) it is of high predictive performance even when most predictive variables are noisy [21]; and 3) its PA depends only on the number of strong features and not on the number of noisy variables if sample sizes are large (500 to 1000) [31]. It was found that excluding the correlated variables may improve the PA [25, 32, 33]. In contrast, it was observed that including some correlated variables could improve the PA [7, 15, 34, 35], suggesting that correlated variables may be able to compensate for the small number of predictors generally found in the environmental sciences. These contradictory findings demonstrate that model selection is necessary for identifying an optimal predictive model for RF.
A model selection procedure for RF was developed previously by Li et al. [7] and it selects the predictors based on the variable importance produced from RF [36]. This is a stepwise procedure using both forward and backward selection to add or eliminate predictors, which is similar to what has been proposed in recent studies [37, 38], but uses PA to determine the selection of each predictive variable. In the environmental sciences, predictive variables are often correlated, which may affect the observed variable importance for the predictors when using RF. To deal with this, an R package ‘extendedForest’ [39] was developed to compensate for the shortcomings in the existing RF package by Liaw and Wiener [36]. Furthermore, two R functions, Boruta [40] and RRF (i.e. regularized RF) [41], were developed to automatically search for the important predictors for RF. All these studies provide fundamental tools for selecting the important predictors in this study.
In this study, we aim to select the most accurate model to predict the spatial distribution of seabed hardness based on four classes of seabed hardness. To achieve this, we: 1) introduced two new classification schemes for seabed video classification; 2) tested the effects of various predictor sets on the accuracy of RF predictive models based on video classifications and seabed biophysical variables; and 3) examined the influence of five feature selection (FS) methods on the most accurate predictive model identified. Finally, the most accurate models were used to predict the spatial distribution of seabed hardness and the predictions were visually examined and compared with the predictions of hardness in two classes [7].
Methods
Study region
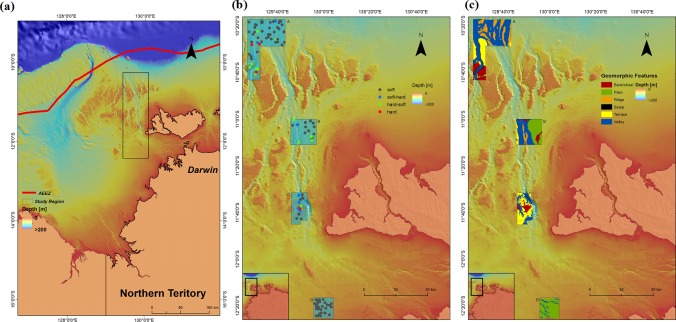
The study region is located in the eastern Joseph Bonaparte Gulf, northern Australian marine margin (Fig 1A). Four areas (A—D) in the region were used in this study (Fig 1B), which were surveyed in 2009 [42] and 2010 [43] under the permissions of Geoscience Australia and Department of the Environment, Water Heritage and the Arts. In these surveys, high-resolution multibeam bathymetry and backscatter data and co-located underwater video transects were acquired across the four areas (Fig 1B). The areas comprise a spatially complex suite of geomorphic features including shallow flat-topped banks, terraces, ridges, deep valleys and plains (Fig 1C).
Fig 1.
a) Location of the study region in the eastern Joseph Bonaparte Gulf, northern Australian marine margin overlaid with bathymetry; b) location of the four study areas (A, B, C, and D) in the study region and seabed hardness types (hard, hard-soft, soft-hard and soft) based on hard90 overlaid with bathymetry at video transect; and c) the geomorphic features of the four study areas.
Schemes for deriving seabed hardness from underwater video observations
Estimation of substratum composition
The seabed and associated epibenthos (Fig 1B) were recorded along underwater video transects using a forward-facing towed-video system. The video footage was analysed based on a 15-second window for each transect to classify substratum composition [44]. The substratum composition was visually estimated to 5% precision [45] in terms of seven size-class categories of rock, boulders, cobble, rubble, gravel, sand and mud as defined by [46]. While this method is subjective and may not be as precise as the regularly used point-count method, previous studies have proven it to be highly comparable and less time-consuming [45]. The definitions and representative images of these categories are provided in S1 File.
We grouped substratum composition into two categories: soft and hard materials. Anything larger than gravel (i.e. rubble, cobbles, boulders and bedrock) was classified as ‘hard’ material, while mud, sand and gravel were classified as ‘soft’ material according to Stein et al. [8]. For a given location, the sum of total hard and total soft cover (i.e. the percentage of ‘hard’ and ‘soft’ materials) was always 100%. Additionally, the presence of epibenthic communities provides additional information to correctly classify substratum. For instance, biota/benthic organisms (i.e. sessile organisms like sponges, hard corals and octocorals) that require hard substratum for growth [1, 3, 4, 47, 48] were found in amongst soft substratum according to the video data alone.
Seabed hardness classification
Seabed substratum is usually classified based on the video footage according to the approach by Stein et al. [8]. However for certain substratum compositions, it is difficult to apply. For example, for a substratum composition with 40% sand, 45% pebble and 15% gravel, it is impossible to apply this approach. Therefore, to overcome such issues we developed two new systems by modifying Stein et al.’s approach as below.
On the basis of Stein et al. [8], we developed a new system to classify the seabed substrate into four categories: hard, hard-soft, soft-hard and soft. If a substratum consisted of >70% hard material, it was classed as ‘hard’. If it consisted of ≤70% and >50% hard material, it was classed as ‘hard-soft’. If it consisted of <50% and ≥30% hard material, it was classed as ‘soft-hard’. And if it consisted of <30% hard material, it was classed as ‘soft’. This classification system is hereinafter referred to as ‘hard70’ in this study. This system would produce similar results as Stein et al. [8], but could avoid some issues associated with the concepts of primary and secondary substrate in Stein et al. [8] as discussed above.
Our initial assessment showed that our samples were mostly classified as ‘soft’, while a small number of samples were ‘hard’, leaving a limited number of samples for the mixed classes when hard70 was employed. Hence, another new classification system is proposed in this study. If a substratum consisted of ≥90% hard material, it was classed as ‘hard’. If it consisted of <90% and >50% hard material, it was classed as ‘hard-soft’. If it consisted of <50% and >10% hard material, it was classed as ‘soft-hard’. And if it consisted of ≤ 10% hard material, it was classed as ‘soft’. This system is hereinafter referred to as ‘hard90’.
In these two classification systems, a substrate consisting of 50% ‘hard’ and 50% ‘soft’ materials was assumed to be non-existent. If it indeed exists in reality, we would need to re-examine the video images and decide which one has greater cover or assign a fifth class to the system(s). However, this is not the case in this study. In total, 140 samples of seabed hardness were considered in this study. Of the 140 samples, 9 and 6 samples were recorded as hard, 11 and 14 hard-soft, 6 and 9 soft-hard and 114 and 111 soft based on hard70 and hard90 systems respectively. The resultant datasets were used to predict seabed hardness, with hardness classes based on hard90 presented in Fig 1B.
Predictive variables
Following a preliminary analysis based on data availability and the relationships with seabed hardness as discussed above and in previous studies [7, 9–12], 41 predictive variables (i.e. features) were initially selected for this study. They are:
-
1
Easting,
-
2
Northing,
-
3
Bathymetry (bathy): a measure of depth of bodies of water,
-
4
Local Moran I of bathymetry(bathy.moran): a measure of local spatial autocorrelation in bathymetry,
-
5
Planar curvature (planar.curv): a curvature of the surface perpendicular to the slope direction (second derivative of bathymetry),
-
6
Profile curvature (profile.curv): a curvature of the surface in the direction of slope (second derivative of bathymetry),
-
7
Topographic relief (relief): a measure of difference between the highest and the lowest points (variance) in the surrounding cells,
-
8
Seabed slope (slope): slope gradient (first derivative of bathymetry),
-
9
Surface area (surface): the ratio of the “true” surface area and its “planar” surface area,
-
10
Topographic position index (tpi): a measure of difference between a cell elevation and the average of the elevation values in the surrounding cells,
-
11–37
Backscatter (bs10 to bs36): a diffused reflection of acoustic energy due to scattering process back to the direction from which it's been generated, measured as the ratio of the acoustic energy sent to a seabed to that returned from the seabed, normalised to incidence angles between 10° and 36°,
-
38
Homogeneity of backscatter (homogeneity): a measure of closeness of the distribution of elements in the Gray-Level Co-occurrence Matrix (GLCM) to the GLCM diagonal,
-
39
Variance of backscatter (variance): a measure of the dispersion of the values around the mean within the GLCM,
-
40
Local Moran I of backscatter (bs.moran): a measure of local spatial autocorrelation in backscatter, and
-
41
Prock: the probability of hard substrate.
The first two variables are the coordinates of sample locations. The next eight variables are bathymetry and its derived variables. The remaining 31 variables are backscatter and its derived variables. Acquisition and processing of multibeam bathymetry, backscatter and their derived variables, and prock have been detailed in previous studies [12] and in relevant online metadata [49–61]. All these variables were available at each grid cell to a 10 m resolution in the four study areas for generating the spatial predictions of seabed hardness and are freely available [49–61]. These 41 variables were also available at 140 sample locations for developing models to predict seabed hardness. The dataset for developing predictive models in this paper is provided as S2 File, where the study areas and hardness are factors and all the variables are numerical.
Selecting predictors based on correlation analysis
There were strong correlations among some predictive variables based on Spearman’s rank correlation that was used due to non-linear relationships between some variables. We removed 21 backscatter (bs) variables that were perfectly correlated with other variables or with a ρ = 0.99, which is usually called a correlation-based filter FS method [28, 62]. The selection was also according to their relation with the total hard (i.e., whether they displayed a better relationship with total hard) and their correlation coefficients with other bs variables. The bs25 should have been removed according to the above selection criteria, but was retained because it was used in a previous study [7]. The Pearson’s correlation (r) was also derived for the remaining bs variables. The correlations of the remaining 20 variables (Table 1) and seabed hardness (i.e., hard total, the percentage cover of hard materials) were presented in Table 2.
Table 1. Predictive variables and their corresponding number.
| No. | Predictive variable | No. | Predictive variable |
|---|---|---|---|
| 1 | easting | 11 | tpi |
| 2 | northing | 12 | bs13 |
| 3 | prock | 13 | bs21 |
| 4 | bathy | 14 | bs25 |
| 5 | bathy.moran | 15 | bs27 |
| 6 | planar.curv | 16 | bs32 |
| 7 | profile.curv | 17 | bs35 |
| 8 | relief | 18 | homogeneity |
| 9 | slope | 19 | variance |
| 10 | surface | 20 | bs.moran |
Table 2. Spearman correlation coefficients (ρ) among 20 predictive variables and seabed hardness (i.e. hard total) (n = 140).
| easting | northing | prock | bathy | bathy.moran | planar.curv | profile.curv | relief | slope | surface | tpi | bs13 | bs21 | bs25 | bs27 | bs32 | bs35 | homogeneity | variance | bs.moran | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hard.total | -0.28 | 0.05 | 0.46 | -0.37 | 0.34 | -0.07 | -0.14 | 0.23 | 0.16 | 0.28 | -0.21 | 0.45 | 0.43 | 0.45 | 0.47 | 0.49 | 0.48 | 0.23 | -0.13 | 0.34 |
| easting | 1 | -0.85 | 0.36 | -0.53 | 0.08 | -0.01 | 0.01 | -0.3 | -0.25 | -0.29 | 0.07 | 0.4 | 0.43 | 0.4 | 0.38 | 0.36 | 0.4 | 0.31 | -0.27 | 0.04 |
| northing | -0.85 | 1 | -0.52 | 0.71 | -0.23 | 0.01 | -0.01 | 0.17 | 0.2 | 0.15 | -0.04 | -0.6 | -0.62 | -0.61 | -0.6 | -0.6 | -0.63 | -0.43 | 0.35 | -0.16 |
| prock | 0.36 | -0.52 | 1 | -0.81 | 0.48 | 0.06 | 0.03 | -0.13 | -0.17 | -0.08 | 0.03 | 0.78 | 0.79 | 0.78 | 0.77 | 0.74 | 0.78 | 0.41 | -0.3 | 0.45 |
| bathy | -0.53 | 0.71 | -0.81 | 1 | -0.26 | -0.05 | 0.03 | 0.18 | 0.22 | 0.14 | 0.02 | -0.88 | -0.89 | -0.88 | -0.88 | -0.83 | -0.87 | -0.53 | 0.42 | -0.31 |
| bathy.moran | 0.08 | -0.23 | 0.48 | -0.26 | 1 | -0.11 | 0.1 | 0.24 | 0.17 | 0.25 | 0.14 | 0.35 | 0.28 | 0.31 | 0.32 | 0.36 | 0.33 | 0.02 | 0.04 | 0.56 |
| planar.curv | -0.01 | 0.01 | 0.06 | -0.05 | -0.11 | 1 | -0.18 | -0.13 | -0.13 | -0.09 | -0.45 | 0.05 | 0.06 | 0.05 | 0.04 | 0.01 | 0.04 | 0.07 | -0.04 | -0.09 |
| profile.curv | 0.01 | -0.01 | 0.03 | 0.03 | 0.1 | -0.18 | 1 | 0.03 | -0.08 | -0.01 | 0.65 | 0 | -0.03 | -0.03 | -0.04 | -0.01 | -0.05 | -0.13 | 0.13 | 0.08 |
| relief | -0.3 | 0.17 | -0.13 | 0.18 | 0.24 | -0.13 | 0.03 | 1 | 0.88 | 0.92 | -0.06 | -0.04 | -0.06 | -0.02 | -0.01 | 0 | -0.04 | -0.33 | 0.44 | 0.19 |
| slope | -0.25 | 0.2 | -0.17 | 0.22 | 0.17 | -0.13 | -0.08 | 0.88 | 1 | 0.83 | -0.07 | -0.07 | -0.09 | -0.05 | -0.04 | -0.03 | -0.07 | -0.27 | 0.37 | 0.09 |
| surface | -0.29 | 0.15 | -0.08 | 0.14 | 0.25 | -0.09 | -0.01 | 0.92 | 0.83 | 1 | -0.08 | 0.02 | -0.02 | 0.03 | 0.05 | 0.07 | 0.02 | -0.29 | 0.43 | 0.15 |
| tpi | 0.07 | -0.04 | 0.03 | 0.02 | 0.14 | -0.45 | 0.65 | -0.06 | -0.07 | -0.08 | 1 | 0 | -0.03 | -0.03 | -0.03 | -0.01 | -0.05 | -0.13 | 0.08 | 0.16 |
| bs13 | 0.4 | -0.6 | 0.78 | -0.88 | 0.35 | 0.05 | 0 | -0.04 | -0.07 | 0.02 | 0 | 1 | 0.98 | 0.98 | 0.98 | 0.94 | 0.97 | 0.51 | -0.43 | 0.21 |
| bs21 | 0.43 | -0.62 | 0.79 | -0.89 | 0.28 | 0.06 | -0.03 | -0.06 | -0.09 | -0.02 | -0.03 | 0.98 | 1 | 0.99 | 0.98 | 0.92 | 0.96 | 0.52 | -0.44 | 0.19 |
| bs25 | 0.4 | -0.61 | 0.78 | -0.88 | 0.31 | 0.05 | -0.03 | -0.02 | -0.05 | 0.03 | -0.03 | 0.98 | 0.99 | 1 | 0.99 | 0.95 | 0.97 | 0.51 | -0.42 | 0.21 |
| bs27 | 0.38 | -0.6 | 0.77 | -0.88 | 0.32 | 0.04 | -0.04 | -0.01 | -0.04 | 0.05 | -0.03 | 0.98 | 0.98 | 0.99 | 1 | 0.96 | 0.98 | 0.51 | -0.42 | 0.22 |
| bs32 | 0.36 | -0.6 | 0.74 | -0.83 | 0.36 | 0.01 | -0.01 | 0 | -0.03 | 0.07 | -0.01 | 0.94 | 0.92 | 0.95 | 0.96 | 1 | 0.96 | 0.5 | -0.4 | 0.25 |
| bs35 | 0.4 | -0.63 | 0.78 | -0.87 | 0.33 | 0.04 | -0.05 | -0.04 | -0.07 | 0.02 | -0.05 | 0.97 | 0.96 | 0.97 | 0.98 | 0.96 | 1 | 0.54 | -0.44 | 0.22 |
| homogeneity | 0.31 | -0.43 | 0.41 | -0.53 | 0.02 | 0.07 | -0.13 | -0.33 | -0.27 | -0.29 | -0.13 | 0.51 | 0.52 | 0.51 | 0.51 | 0.5 | 0.54 | 1 | -0.85 | -0.06 |
| variance | -0.27 | 0.35 | -0.3 | 0.42 | 0.04 | -0.04 | 0.13 | 0.44 | 0.37 | 0.43 | 0.08 | -0.43 | -0.44 | -0.42 | -0.42 | -0.4 | -0.44 | -0.85 | 1 | 0.15 |
| bs.moran | 0.04 | -0.16 | 0.45 | -0.31 | 0.56 | -0.09 | 0.08 | 0.19 | 0.09 | 0.15 | 0.16 | 0.21 | 0.19 | 0.21 | 0.22 | 0.25 | 0.22 | -0.06 | 0.15 | 1 |
Seabed hardness (total hard) was strongly correlated with prock, bathy, and bs and its derived variables; while it was weakly correlated with northing, planar.curv, profile.curv, slope and variance (Table 2). The relationships among the 20 variables were further illustrated in S1 Fig. High prock values were typically associated with “hard” substrate (S1 Fig). In contrast, low prock values were associated with “soft” substrate. While a similar pattern was observed for backscatter, bathymetry showed an opposite pattern with a negative correlation (Table 2). These relationships were typically non-linear. These variables could potentially be good predictors of seabed hardness.
Application of RF
Random forest, as briefly described in [7], is an ensemble machine learning method that combines many individual regression or classification trees in the following way: from the original sample, many bootstrap samples and portions of predictive variables are drawn, and an unpruned regression or classification tree is fit to each bootstrap sample using the sampled variables. From the complete forest, the status of the response variable is usually predicted either as an average of the predictions of all trees for regression or as the class with the majority vote for classification [18, 63].
The R function, randomForest by Liaw and Wiener [36], was employed to develop a model to predict the spatial distribution of seabed hardness. The default values of mtry, ntree and nodesize are often good options [21, 36] that were also observed in marine environmental sciences [7, 15], so the default values were used for these parameters.
Feature selection
The model selection was based on a procedure developed for RF in previous studies [7, 34, 64], which involved two steps. One step was to select predictors to form a model that is often termed as feature selection, and the other was to estimate the predictive accuracy of the model formed that is addressed in the next section. To select predictive variables, we adopted the same principle used in rfcv, a cross-validation function in the randomForest package [36], that is, identifying and removing the least important variables based on the importance of predictive variables.
Five FS methods were used to select predictors in this study based on all 140 samples. These methods are: 1) the variable importance (VI), 2) averaged variable importance (AVI), 3) knowledge informed AVI (KIAVI), 4) Boruta and 5) RRF. The first method (i.e., VI) was based on the procedure in a previous study [7] as detailed below and was applied to hard90 data with 20 variables. For this FS method, we initially used all 20 variables to establish the full model. We then reduced the full model by gradually removing the least important variable(s) from the previous model based on the variable importance measure by RF (see Fig A in S3 File), which resulted in 22 models (see Table 3). Two exceptions to this are that: 1) for model 18 and 19, since bs25 and bs27 are equally important, we excluded them from model 17 respectively; and 2) for model 22, we included it because prock was the most important predictor in a previous study [7]. After reaching the model with minimum number of predictors (i.e. only one predictor remained), we then identified the important predictor(s) based on the PA of the models developed. The important predictor(s) were defined as follows: if their exclusion reduced the PA of the subsequent model, they were determined to be important (i.e. variance, surface and relief). We also identified the unimportant predictor(s) (i.e. bs27) that increased the PA when they were excluded. We then repeated above procedure by adding these important predictors and removing the unimportant predictor to the most accurate model so far (i.e., model14) to develop predictive models until no further improvement in the PA could be achieved.
Table 3. A brief summary of RF modelling process for hard90 data using various FS methods and predictive variables.
1) models 1–25 based on the VI using 20 variables; 2) models 26–29 based on the AVI using 20 variables; 3) models 30–31 based on KIAVI using 20 variables; 4) models 32–43 based on the AVI using 41 variables; and 5) models 44–45 based on the Boruta and model 46 based on the RRF using 41 variables. Model.fit is the predictive accuracy (ccr) of training samples by each RF model developed. The corresponding predictor for each number is listed in Table 1.
| Model | Modelling.process | Predictors | No.predictors | Model.fit |
|---|---|---|---|---|
| 1 | All 20 predictive variables | All 20 variables | 20 | 100 |
| 2 | model 1:—planar.curv | 1–5,7–20 | 19 | 100 |
| 3 | model 2:—surface | 1–5, 7–9, 11–20 | 18 | 100 |
| 4 | model 3:—slope | 1–5, 7–8, 11–20 | 17 | 100 |
| 5 | model 4:—relief | 1–5, 7, 11–20 | 16 | 100 |
| 6 | model 5:—bathy.moran | 1–4, 7, 11–20 | 15 | 100 |
| 7 | model 6:—profile.curv | 1–4, 11–20 | 14 | 100 |
| 8 | model 7:—bs.moran | 1–4, 11–19 | 13 | 100 |
| 9 | model 8:—bathy | 1–3, 11–19 | 12 | 100 |
| 10 | model 9:—homogeneity | 1–3, 11–17, 19 | 11 | 100 |
| 11 | model 10:—variance | 1–3, 11–17 | 10 | 100 |
| 12 | model 11:—northing | 1, 3, 11–17 | 9 | 100 |
| 13 | model 12:—tpi | 1, 3, 12–17 | 8 | 100 |
| 14 | model 13:—bs13 | 1, 3, 13–17 | 7 | 100 |
| 15 | model 14:—bs21 | 1, 3, 14–17 | 6 | 100 |
| 16 | model 15:—easting | 3, 14–17 | 5 | 100 |
| 17 | model 16:—bs32 | 3, 14–15, 17 | 4 | 100 |
| 18 | model 17:—bs27 | 3, 14, 17 | 3 | 96.43 |
| 19 | model 17:—bs25 | 3, 15, 17 | 3 | 96.43 |
| 20 | model 18:—bs25 | 3, 17 | 2 | 96.43 |
| 21 | model 20:—prock | 17 | 1 | 100 |
| 22 | model 20:—bs35 | 3 | 1 | 91.43 |
| 23 | model 14: + variance | 1, 3, 13–17, 19 | 8 | 100 |
| 24 | model 23: + surface | 1, 3, 10, 13–17, 19 | 9 | 100 |
| 25 | model 24: + relief | 1, 3, 8, 10, 13–17, 19 | 10 | 100 |
| 26 | Six most important predictors | 1, 10, 16–19 | 6 | 100 |
| 27 | model 26: + prock and bs27 | 1, 3, 10, 15–19 | 8 | 100 |
| 28 | model 27: + planar.curv | 1, 3, 6, 10, 15–19 | 9 | 100 |
| 29 | model 27:—prock | 1, 10, 15–19 | 7 | 100 |
| 30 | Combine model 24 and 27 | 1, 3, 10, 13–19 | 10 | 100 |
| 31 | model 30:—bs21 | 1, 3, 10, 14–19 | 9 | 100 |
| 32 | The 13 predictors most important | 1, 10, 18, 19, bs28-bs36 | 13 | 100 |
| 33 | model 32: + bs10 | 1, 10, 18, 19, bs10, bs28-bs36 | 14 | 100 |
| 34 | model 33: + planar.curv | 1, 6, 10, 18, 19, bs10, bs28-bs36 | 15 | 100 |
| 35 | model 34: + northing | 1, 2, 6, 10, 18, 19, bs10, bs28-bs36 | 16 | 100 |
| 36 | model 35: + prock, bs.moran, bs27 | 1–3, 6, 10, 18–20, bs10, 15, bs28-bs36 | 19 | 100 |
| 37 | model 36:—bs27 | 1–3, 6, 10, 18–20, bs10, bs28-bs36 | 18 | 100 |
| 38 | model 37:—bs.moran | 1–3, 6, 10, 18, 19, bs10, bs28-bs36 | 17 | 100 |
| 39 | model 37:—prock | 1, 2, 6, 10, 19–20, bs10, bs28-bs36 | 17 | 100 |
| 40 | model 35:—planar.curv | 1, 2, 10, 18, 19, bs10, bs28-bs36 | 15 | 100 |
| 41 | model 40:—northing | 1, 10, 18–19, bs10, bs28-bs36 | 14 | 100 |
| 42 | model 41:—bs34 | 1, 2, 10, 17–19, bs10, bs28-bs33, bs36 | 14 | 100 |
| 43 | All 41 predictors | All 41 predictors | 41 | 100 |
| 44 | 30 predictors | 1–3, 7, 11, 20, bs12, bs14:bs36 | 30 | 100 |
| 45 | model 44: +bs13 | 1–3, 7, 11, 20, bs12:bs36 | 31 | 100 |
| 46 | 31 predictors | 1–3, 5, 7–11, 18–20, bs15, bs17-bs18, bs20-bs25, bs27-bs36 | 31 | 100 |
We then applied the second model selection method (i.e., AVI). Due to the randomness associated with the importance of predictive variables generated by RF algorithm, the least important variable(s) may change with individual iterations; meanwhile, correlated variables may also affect the order of the least important variable(s); so an R package ‘extendedForest’ [39] was used and repeated 100 times to generate the average values of variable importance (Fig B in S3 File) that were used to select the predictors. This approach was applied to hard90 using 20 variables, which led to four models (i.e. models 26 to 29; see Table 3). We initially selected the most importance predictors when the level was 4 or 6 according to Fig B in S3 File, then added the next important predictor(s) until no further improvement in PA was gained. We then removed the least important predictor from the most accurate model to determine if further improvement was possible.
We also used KIAVI (i.e. applied AVI to a combined model that was based on two most accurate models identified via VI and AVI using 20 predictive variables) to see if we could further improve the accuracy. Since AVI can deal with correlated variables, we also applied this approach to the whole dataset (i.e. using 41 variables) (Fig C in S3 File) by adopting the rationale for adding and removing predictor(s) as stated above.
We also applied AVI to hard70 data using 20 and 41 variables. We also applied AVI to a combined model based on the most accurate model identified for hard90 and the most accurate model based on AVI approach using 20 variables for hard70 to see if we could further improve the PA, which is also a kind of KIAVI and hereinafter referred to as the ‘KIAVI’.
We then used Boruta [40] to search for the important predictors for hard90 and hard70 data using all 41 variables because it is an all-relevant FS algorithm. For hard90 data, the default value (i.e., 100) was used for the maximal number of importance source runs in the final round. To resolve predictive variables left as ‘Tentative’, we increased the number of importance source runs to 2000 and 5000 respectively, but they selected the same variables. For hard70 data, we used the default value as well as the values of 2000 and 5000 for the maximal number of importance source runs. The selected variables were then used in the randomForest function.
Lastly, we used RRF [41] to search the important predictors for hard90 and hard70 data using 41 variables because it is also an all-relevant FS algorithm. This is hereinafter referred to as RRF approach in this study. The selected variables were then used in the randomForest function.
Model validation
To identify the most accurate predictive model, we need to know the PA of each model formed from the above FS methods. To achieve this, we used rf.cv that validates one model with fixed predictive variables for all iterations for a given number of predictive variables [7]. This function allows variations in datasets generated by cross-validation and ensures the model select relevant predictors from a list of the fixed predictive variables. Given that the response variable is categorical, the correct classification rate (ccr) [65] and kappa [66] were used to measure the accuracy of the predictive model and were calculated using the built-in functions in rf.cv.
To assess the predictive ability of each model, we used 10-fold cross-validation [67]. To deal with the random error associated with each 10-fold cross validation [7, 34, 64], the cross validation procedure was repeated 100 times. The choice of this iteration number was based on findings in previous studies [7, 34] and that the dynamics of the predictive accuracies with iterations of relevant models in this study suggested that averaged accuracies stabilised after 20–80 iterations. The final results were based on the average of 100 iterations of the cross validation.
Model comparison and spatial predictions
Since the data of ccr and kappa were not normally distributed based on the Shapiro-Wilk normality test, with heterogeneous variance based on Fligner-Killeen test of homogeneity of variances, or both, Mann-Whitney tests were used to compare the PA in terms of ccr and kappa between the most accurate models for both hard90 and hard70 data.
Finally, the most accurate predictive models for hard90 and hard70 data were used to predict seabed hardness at each 10m grid cell in the study areas. A portion of area A (A1) that comprises a variety of seabed geomorphic features was selected to illustrate and compare the predictions.
All relevant computing work was implemented in R 2.15.2 [68]. Relevant maps were then produced using ArcGIS (ESRI ® ArcMap TM 10.0) [69].
Results
Predictive model for hard90 data
Model selection using VI for 20 predictive variables (VI & filter)
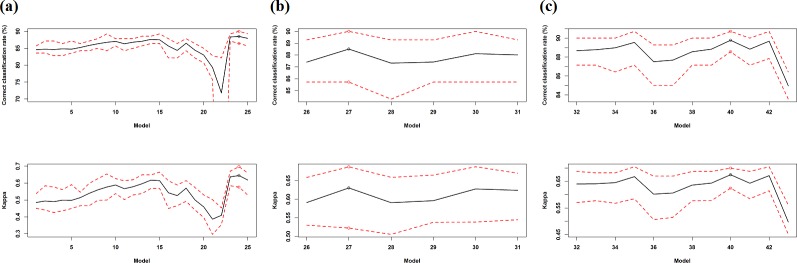
In total, 25 models were developed based on the model selection approach using variable importance of 20 variables (models 1–25 in Table 3, Fig 2A). Correct classification rates gradually increased from model 1 and reached a maximum mean (i.e. 87.64%) for model 14, except that the PA of models 3, 5 and 11 slightly decreased after the removal of surface, relief and variance respectively. It then began to decrease from model 15 onwards with an abrupt increase for model 18 due to the exclusion of bs27, and reached the lowest value for model 22 that contained only one predictor. After adding variance and surface to model 14, the PA was further improved and reached the highest mean value of 88.53% for model 24 (Fig 2A, Table 3). Kappa displayed a similar pattern as ccr and reached the highest mean value of 0.6449 for model 24, with the exception of that the lowest value was attained for model 21 that again contained only one predictor. It showed that bs35 was the most important predictor based on ccr while prock was the most important predictor based on kappa. Overall, model 24 was more accurate than other models in terms of both of ccr and kappa. This model contained nine predictors (Fig 2A, Table 3). In addition, most models perfectly predicted the training samples. Removing bs27 from model 24 did not improve the accuracy, so it was not presented in the results.
Fig 2. Correct classification rate (%) and kappa (mean: black line; minimum and maximum: dash red lines) of 43 RF models with different predictor sets based on the averages over 100 iterations of 10-fold cross validation for seabed hardness based on hard90 data; and the model with the maximum mean ccr and mean kappa (circle).
a) models 1–25 based on the VI using 20 predictive variables; b) models 26–29 based on the AVI and models 30–31 based on KIAVI using 20 variables; c) models 32–43 based on the AVI using 41 variables.
Model selection using AVI and KIAVI for 20 predictive variables (AVI & filter and KIAVI & filter)
On the basis of the AVI using 20 variables, further four models were developed (models 26–29 in Table 3, Fig 2B). Correct classification rates reached the highest mean value of 88.51% for model 27 after the inclusion of bs27 and prock. It then started to decrease after adding planar.curv (i.e. model 28) and excluding prock (i.e. model 29). It showed that adding or excluding a further variable reduced the PA of model 27. Kappa displayed an identical pattern to ccr and reached the highest mean value of 0.6304 for model 27. Combing the two best performing models identified so far (i.e. models 24 and 27) resulted in two further models (models 30 and 31 in Table 3) that did not improve the PA in comparison with model 27. Overall, model 27, containing eight predictors, was more accurate than other models in terms both of ccr and kappa (Fig 2B, Table 3).
Model selection using AVI for 41 predictive variables
On the basis of the AVI using 41 variables, a further 12 model were developed (models 32–43 in Table 3, Fig 2C). The PA increased after adding bs10, planar.curv and northing, which resulted in a highly accurate model (i.e. model 35). After adding the next three most important predictors, the PA decreased. Further tuning to model 36 by removing the next less important predictor(s) resulted in models 37 to 39. The PA of all these models was less than that of model 35. Further tuning to model 35 by removing the least important predictor (i.e. planar curv) resulted in the most accurate model 40 (with a mane ccr of 89.78%). Model 43, which used all 41 variables, was much less accurate than all other models (Fig 2C). Kappa displayed an identical pattern as ccr and reached the highest mean value of 0.6753 for model 40. Overall, model 40 was relatively more accurate than other models in terms both of ccr and kappa and contained 15 predictors (Table 3). In addition, model 40 could not be further improved by removing either the next less important predictor (model 41) or the highly correlated predictor (model 42).
Model selection using Boruta for 41 predictive variables
On the basis of the Boruta approach, two models were developed (models 44–45 in Table 3). Model 44 contained 30 predictors with a mean ccr of 85.79% (ranging from 85% to 86.43%) and a mean kappa of 0.5279 (ranging from 0.4897 to 0.5616). Model 45 contained 31 predictors with a mean ccr of 85.83% (ranging from 85% to 87.14%) and a mean kappa of 0.5301 (ranging from 0.4986 to 0.5845), which was slightly more accurate than model 44.
Model selection using RRF for 41 predictive variables
On the basis of the RRF approach, a further model was developed (model 46 in Table 3). Model 46 contained 31 predictors with a mean ccr of 85.27% (ranging from 83.57% to 87.14%) and a mean kappa of 0.5078 (ranging from 0.4511 to 0.5853).
In summary, 46 models were developed for hard90 data. Model 24 was the most accurate model based on the VI and model 27 was the most accurate model based on the AVI using 20 variables; and model 40 was the most accurate model based on the AVI and model 45 was the most accurate model based on the Boruta using 41 variables. Overall, model 40 was the most accurate model.
Agreement of the observed and predicted values of the most accurate model
The predicted values based on the most accurate model (i.e., model 40) and the observed values matched well for most classes in terms of both user’s accuracy and producer’s accuracy, although producer’s accuracy was poor for the hard-soft class (Table 4). When the hard-soft and soft-hard classes were merged into the hard class, the accuracies were improved, especially for the user’s accuracy for the hard class (Table 5). The user’s accuracy was higher than the producer’s accuracy for non-soft classes (Tables 4 and 5). Non-soft classes, particularly hard-soft, were under-predicted while the soft class was over-predicted.
Table 4. Confusion matrix between the observed and predicted values of four hardness classes based on the average of 100 times of 10-fold cross validation using the most accurate predictive model (i.e., model 40) for hard90.
| Observed | |||||||
|---|---|---|---|---|---|---|---|
| Hard | Hardsoft | Softhard | Soft | Total | User's accuracy | ||
| Predicted | Hard | 4 | 1 | 0.42 | 0 | 5.42 | 73.80 |
| Hardsoft | 0 | 6.84 | 0.86 | 1.89 | 9.59 | 71.32 | |
| Softhard | 0 | 0 | 5.87 | 0.13 | 6 | 97.83 | |
| Soft | 2 | 6.16 | 1.85 | 108.98 | 118.99 | 91.59 | |
| Total | 6 | 14 | 9 | 111 | 140 | ||
| Producer's Accuracy | 66.67 | 48.86 | 65.22 | 98.18 | 89.78 | ||
Table 5. Confusion matrix between the observed and predicted values of two hardness classes based on the average of 100 times of 10-fold cross validation using the most accurate predictive model (i.e., model 40) for hard90.
| Observed | |||||
|---|---|---|---|---|---|
| Hard | Soft | Total | User's accuracy | ||
| Predicted | Hard | 18.99 | 2.02 | 21.01 | 90.39 |
| Soft | 10.01 | 108.98 | 118.99 | 91.59 | |
| Total | 29 | 111 | 140 | ||
| Producer's Accuracy | 65.48 | 98.18 | 91.41 | ||
Predictive model for hard70 data
Model selection using AVI for 20 predictive variables (AVI & filter)
Twenty five models were developed based on the AVI for 20 variables (models 1–25 in Table 6, Fig 3A). The first twenty models were developed by removing the least important variable based on AVI. Correct classification rates reached a local maximum for model 11. Two predictors (i.e. bs21 and bathy.moran) were identified as important variables and a few predictors were identified as unimportant variables (e.g. profile.curv, bs.moran, variance).
Table 6. A brief summary of RF modelling process for hard70 data using various FS methods and predictive variables.
1) models 1–25 based on the AVI using 20 variables; 2) models 26–38 based on the AVI using 41 variables; 3) models 39–49 based on KIAVI using 41 variables; and 4) models 50–52 based on the Boruta with the maximal number of importance source runs of 2000, 100 and 5000, and model 53 based on the RRF using 41 variables. The model fit is the predictive accuracy (ccr) of training samples by each RF model developed. The corresponding predictor for each number is listed in Table 1.
| Model | Modelling.process | Predictors | No.predictors | Model.fit |
|---|---|---|---|---|
| 1 | All 20 predictive variables | All 20 variables | 20 | 100 |
| 2 | model 1: -relief | 1–7, 9–20 | 19 | 100 |
| 3 | model 2: -northing | 1, 3–7, 9–20 | 18 | 100 |
| 4 | model 3: -bs13 | 1, 3–7, 9–11, 13–20 | 17 | 100 |
| 5 | model 4: -bs27 | 1, 3–7, 9–11, 13–14, 16–20 | 16 | 100 |
| 6 | model 5: -slope | 1, 3, 4–7, 10–11, 13–14, 16–20 | 15 | 100 |
| 7 | model 6: -bs25 | 1, 3–7, 10–11, 13, 16–20 | 14 | 100 |
| 8 | model 7: -bs21 | 1, 3–7, 10–11, 16–20 | 13 | 100 |
| 9 | model 8: -bathy.moran | 1, 3–4, 6–7, 10–11, 16–20 | 12 | 100 |
| 10 | model 9: -surface | 1, 3–4, 6–7, 11, 16–20 | 11 | 100 |
| 11 | model 10: -bathy | 1, 3, 6–7, 11, 16–20 | 10 | 100 |
| 12 | model 11: -tpi | 1, 3, 6–7, 16–20 | 9 | 100 |
| 13 | model 12: -bs35 | 1, 3, 6–7, 16, 18–20 | 8 | 100 |
| 14 | model 13: -variance | 1, 3, 6–7, 16, 18, 20 | 7 | 100 |
| 15 | model 14: -bs.moran | 1, 3, 6–7, 16, 18 | 6 | 100 |
| 16 | model 15: -bs32 | 1, 3, 6–7, 18 | 5 | 100 |
| 17 | model 16: -easting | 3, 6–7, 18 | 4 | 100 |
| 18 | model 17: -profile.curv | 3, 6, 18 | 3 | 96.43 |
| 19 | model 18: -homogeneity | 3, 6 | 2 | 95 |
| 20 | model 19: -planar.curv | 3 | 1 | 91.43 |
| 21 | model 11: +bs21 | 1, 3, 6–7, 11, 13, 16–20 | 11 | 100 |
| 22 | model 21: +bathy.moran | 1, 3, 5–7, 11, 13, 16–20 | 12 | 100 |
| 23 | model 21: -profile.curv | 1, 3, 6, 11, 13, 16–20 | 10 | 100 |
| 24 | model 21: -bs.moran | 1, 3, 6–7, 11, 13, 16–19 | 10 | 100 |
| 25 | model 24: -variance | 1, 3, 6, 7, 11, 18, 13, 16, 17 | 9 | 100 |
| 26 | All 41 predictors | 1–11, 18–20, bs10-bs36 | 41 | 100 |
| 27 | model 26:—bs25, bs10:bs14 | 1–11, 18–20, bs15-bs36 | 35 | 100 |
| 28 | model 27:—bathy, relief, bs24,bs26, bs27 | 1–3, 5–7, 9–11, 18–20, bs15-bs23, bs28-bs36 | 30 | 100 |
| 29 | model 28:—bs20, bs29, bs30, bs36 | 1–3, 5–7, 9–11, 18–20, bs15-bs19, bs21-bs23, bs28, bs31-bs35 | 26 | 100 |
| 30 | model 29:—nothing and bs28 | 1, 3, 5–7, 9–11, 18–20, bs15-bs19, bs21-bs23, bs31-bs35 | 24 | 100 |
| 31 | model 30:—slope and bs34 | 1, 3, 5–7, 10, 11, 18–20, bs15 to bs19, bs21-bs23, bs31-bs33, 17 | 22 | 100 |
| 32 | model 31-—bs15, bs16, bs19, bs21, bs32, bs33 and bs 35 | 1, 3, 5–7, 10, 11, 18–20, bs17, bs18, bs22, bs23, bs31 | 15 | 100 |
| 33 | model 32-—bathy.moran, surface, bs17 and bs22 | 1, 3, 6–7, 11, 18–20, bs18, bs23, bs31 | 11 | 100 |
| 34 | model 33-—homogeneity | 1, 3, 6–7, 11, 19–20, bs18, bs23, bs31 | 10 | 100 |
| 35 | model 34-—tpi | 1, 3, 6–7, 19–20, bs18, bs23, bs31 | 9 | 100 |
| 36 | model 35-—bs23 | 1, 3, 6–7, 19–20, bs18, bs31 | 8 | 100 |
| 37 | model 36-—bs18 | 1, 3, 6–7, 19–20, bs31 | 7 | 100 |
| 38 | model 37-—bs.moran | 1, 3, 6–7, 19, bs31 | 6 | 100 |
| 39 | Variables for model 24, 33, and model 40 for hard90 | 1–3, 6–7, 10–11, 13, 18–20, bs10, bs18, bs23, bs28-bs36 | 23 | 100 |
| 40 | model 39-—bs10 | 1–3, 6–7, 10–11, 13, 18–20,bs18, bs23, bs28-bs36 | 22 | 100 |
| 41 | model 40-—bs28, bs30 abd bs36 | 1–3, 6–7, 10–11, 13, 18–20, bs18, bs23, bs29, bs31-17 | 19 | 100 |
| 42 | model 41-—northing | 1, 3, 6–7, 10–11, 13, 18–20, bs18, bs23, bs29, bs31-17 | 18 | 100 |
| 43 | model 42-—bs35 | 1, 3, 6–7, 10–11, 13, 18–20, bs18, bs23, bs29, bs31-bs34 | 17 | 100 |
| 44 | model 43-—bs29 and bs34 | 1, 3, 6–7, 10–11, 13, 18–20,bs18, bs23, bs31-bs33 | 15 | 100 |
| 45 | model 44-—bs21 | 1, 3, 6–7, 10–11, 18–20,bs18, bs23, bs31-bs33 | 14 | 100 |
| 46 | model 45-—bs33 | 1, 3, 6–7, 10–11, 16, 18–20,bs18, bs23, bs31 | 13 | 100 |
| 47 | model 46-—surface | 1, 3, 6–7, 11, 16, 18–20,bs18, bs23, bs31 | 12 | 100 |
| 48 | model 47-—tpi | 1, 3, 6–7, 16, 18–20,bs18, bs23, bs31 | 11 | 100 |
| 49 | model 47-—tpi and bs31 | 1, 3, 6–7, 16, 18–20, bs18, bs23 | 10 | 100 |
| 50 | 27 predictors | 1, 3, 7, 11, bs12, bs13, bs16-bs36 | 27 | 100 |
| 51 | model 50-—easting, bs12 | 2–3, 7, 11, 20, bs13, bs16-bs36 | 25 | 100 |
| 52 | model 50- +bs10, bs14 | 1, 3, 7, 11, bs10, bs12-bs14, bs16-bs36 | 29 | 100 |
| 53 | 31 predictors | 1–3, 5, 7–11, 18–20, bs15, bs17-bs18, bs20-bs25, bs27-bs36 | 31 | 100 |
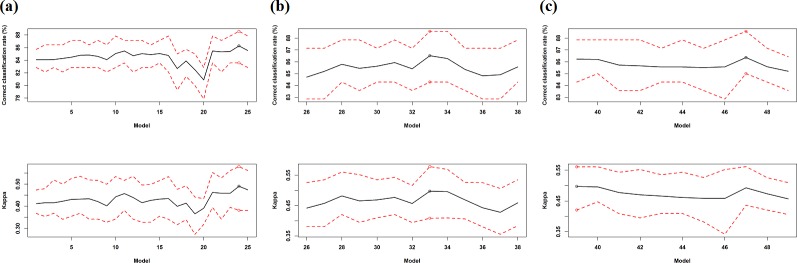
Fig 3. Correct classification rate (%) and kappa (mean: black line; minimum and maximum: dash red lines) of 49 RF models with different predictor sets based on the averages over 100 iterations of 10-fold cross validation for seabed hardness based on hard70 data; and the model with the maximum mean ccr and mean kappa (circle).
a) models 1–25 based on the AVI using 20 predictive variables; b) models 26–38 based on the AVI using 41 variables; c) models 39–49 based on KIAVI using 41 variables.
After further adding the important variables to model 11 and removing the unimportant predictors from subsequent models, ccr increased and reached the highest mean value of 86.27% for model 24. Kappa displayed a similar pattern as ccr and reached the highest mean value of 0.4905 for model 24. Overall, model 24 with 10 predictors was more accurate than other models. In addition, most models perfectly predicted the training samples.
Model selection using AVI and KIAVI for 41 predictive variables
On the basis of the AVI for 41 variables, a further 13 models were developed (models 26–38 in Table 6, Fig 3B). The AVI of model 38 for hard70 data using 41 variables showed that easting should be excluded, while on the basis of model 24 for hard70 data it should be included. Hence no further model development was conducted for hard70 data using 41 variables. The most accurate model was model 33 with a mean ccr of 86.52%. Kappa displayed an identical pattern as ccr and reached the highest mean value (i.e. 0.4976) for model 33. This model contained 11 predictors.
On the basis of model 24 for hard70 and also model 40 for hard90 (i.e. the most accurate model), we further tuned model 33 by including additional predictors that were used in these two models. This resulted in a further 11 models (models 39–49 in Table 6). Model 39 was the most accurate model in terms of kappa (i.e. 0.4973) while model 47 is the most accurate model in terms of ccr (i.e. 86.36) (Table 6 and Fig 3C). Overall, model 33 was relatively more accurate than other models.
Model selection using Boruta for 41 predictive variables
On the basis of the Boruta approach, three models were developed (models 50–52 Table 6). Model 50 contained 25 predictors with a mean ccr of 87.04% (ranging from 85.71% to 87.86%) and a mean kappa of 0.5328 (ranging from 0.4836 to 0.5609). Model 51 contained 27 predictors with a mean ccr of 86.85% (ranging from 84.29% to 87.86%) and a mean kappa of 0.5318 (ranging from 0.4538 to 0.5692). Model 52 contained 29 predictors with a mean ccr of 86.99% (ranging from 84.29% to 87.86%) and a mean kappa of 0.5309 (ranging from 0.4434 to 0.5609). Model 50 was slightly more accurate than model 51 and model 52.
Model selection using RRF for 41 predictive variables
On the basis of the RRF, one model was developed (model 53 in Table 6). Model 53 contained 31 predictors with a mean ccr of 85.14% (ranging from 82.86% to 87.14%) and a mean kappa of 0.4533 (ranging from 0.3949 to 0.5351).
In summary, 53 models were developed for hard70 data. Model 24 was the most accurate model based on AVI using 20 variables, and model 33 was the most accurate model based on AVI and model 50 was the most accurate model based on Boruta using 41 variables. Of these 53 models, model 50 was the most accurate model.
Agreement of the observed and predicted values of the most accurate model
The predicted values based on the most accurate model (i.e., model 50) and the observed values matched very well for the soft class in terms of both user’s accuracy and producer’s accuracy; and producer’s accuracy was poor for non-soft classes, especially for the hard-soft class (Table 7). When the hard-soft and soft-hard classes were merged into the hard class, the accuracies were improved, especially the user’s accuracy for the hard class (Table 8). The user’s accuracy was higher than the producer’s accuracy for non-soft classes (Tables 7 and 8). All non-soft classes were under-predicted while the soft class was over-predicted.
Table 7. Confusion matrix between the observed and predicted values of four hardness classes based on the average of 100 times of 10-fold cross validation using the most accurate predictive model (i.e., model 50) for hard70.
| Observed | |||||||
|---|---|---|---|---|---|---|---|
| Hard | Hardsoft | Softhard | Soft | Total | User's accuracy | ||
| Predicted | Hard | 4 | 1.22 | 0.01 | 2.08 | 7.31 | 54.72 |
| Hardsoft | 1.02 | 4.22 | 0 | 1.24 | 6.48 | 65.12 | |
| Softhard | 0 | 0.3 | 3 | 0.04 | 3.34 | 89.82 | |
| Soft | 3.98 | 5.26 | 2.99 | 110.64 | 122.87 | 90.05 | |
| Total | 9 | 11 | 6 | 114 | 140 | ||
| Producer's Accuracy | 44.44 | 38.36 | 50.00 | 97.05 | 87.04 | ||
Table 8. Confusion matrix between the observed and predicted values of two hardness classes based on the average of 100 times of 10-fold cross validation using the most accurate predictive model (i.e., model 50) for hard70.
| Observed | |||||
|---|---|---|---|---|---|
| Hard | Soft | Total | User's accuracy | ||
| Predicted | Hard | 13.77 | 3.36 | 17.13 | 80.39 |
| Soft | 12.23 | 110.64 | 122.87 | 90.05 | |
| Total | 26 | 114 | 140 | ||
| Producer's Accuracy | 52.96 | 97.05 | 88.86 | ||
Comparison of FS methods based on the most accurate predictive models identified for hard90 and hard70 data
The accuracy of full models (i.e. model 43 for hard90, and model 26 for hard70) and the most accurate models identified based on various FS methods have been summarised in Table 9 and Fig 4. The models developed from 41 variables were more accurate than the models from the pre-selected 20 variables for both hard90 and hard70 (Table 9). The most accurate models based on various FS techniques were significantly more accurate than the models using either all 41 variables or the pre-selected 20 variables in terms of both ccr and kappa for both hard90 and hard70 (Table 9).
Table 9. Comparison of the accuracy of full models (i.e. model 43 for hard90, and models 26 for hard70) with the most accurate models based various FS methods.
The differences between these comparisons based on the Mann-Whitney tests (n = 100 for each model).
| Data | Model | FS method | ccr | kappa | ||||
|---|---|---|---|---|---|---|---|---|
| ccr | models | p-value | kappa | models | p-value | |||
| Hard90 | 43 | 41 variables | 84.97 | 0.4973 | ||||
| 1 | Filter (20 variables) | 84.62 | 1 vs. 43 | 0.0000 | 0.4852 | 1 vs. 43 | 0.0000 | |
| 24 | VI & filter | 88.53 | 24 vs. 1 | 0.0000 | 0.6449 | 24 vs. 1 | 0.0000 | |
| 27 | AVI & filter | 88.51 | 27 vs. 1 | 0.0000 | 0.6305 | 27 vs. 1 | 0.0000 | |
| 30 | KIAVI | 88.11 | 30 vs. 1 | 0.0000 | 0.6278 | 30 vs. 1 | 0.0000 | |
| 40 | AVI | 89.78 | 40 vs. 43 | 0.0000 | 0.6753 | 40 vs. 43 | 0.0000 | |
| 45 | Boruta | 85.83 | 44 vs. 43 | 0.0000 | 0.5301 | 44 vs. 43 | 0.0000 | |
| 46 | GRF | 85.28 | 46 vs. 43 | 0.0010 | 0.5078 | 46 vs. 43 | 0.0013 | |
| Hard70 | 26 | 41 variables | 84.71 | 0.4421 | ||||
| 1 | Filter | 84.09 | 1 vs. 26 | 0.0000 | 0.4116 | 1 vs. 26 | 0.0000 | |
| 24 | AVI & Filter | 86.27 | 24 vs. 1 | 0.0000 | 0.4905 | 24 vs. 1 | 0.0000 | |
| 33 | AVI | 86.52 | 33 vs. 26 | 0.0000 | 0.4976 | 33 vs. 26 | 0.0000 | |
| 47 | KIAVI | 86.36 | 47 vs. 26 | 0.0000 | 0.4927 | 47 vs. 26 | 0.0000 | |
| 50 | Boruta | 87.04 | 50 vs. 26 | 0.0000 | 0.5328 | 50 vs. 26 | 0.0000 | |
| 53 | GRF | 85.14 | 53 vs. 26 | 0.0002 | 0.4533 | 53 vs. 26 | 0.0028 | |
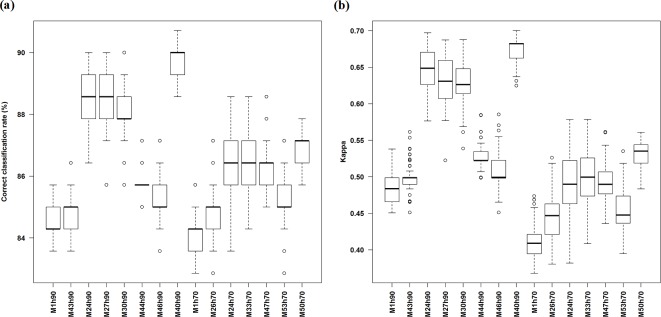
Fig 4.
Correct classification rate (%) (a) and kappa (b) of the most accurate models based on the averages over 100 iterations of 10-fold cross validation for hard90 and hard70 data.
The most accurate models based on the FS methods were compared in Table 10 and Fig 4. For hard90, models 24 and 27 were not significantly different in terms of ccr and models 27 and 30 were not significantly different in terms of kappa. For hard70, models 24, 33 and 47 were not significantly different. All other models were significantly different in terms of PA. Their accuracy changed with FS methods in the following order: for hard90, AVI > VI & filter > AVI & filter > KIAVI & filter > Boruta > RRF; and for hard70, Boruta > AVI, AVI & filter, KIAVI > RRF.
Table 10. Comparison of the accuracy of the most accurate models (i.e. model 40 for hard90 and model 50 for hard70) with the most accurate models based various FS techniques, and also model 40 with model 50.
The differences between these comparisons based on the Mann-Whitney tests (n = 100 for each model).
| FS method Hard90 | Models | p-value for ccr | p-value for kappa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Developed | Model | 24 | 27 | 30 | 45 | 46 | 24 | 27 | 30 | 45 | 46 | |
| VI & filter | 25 | 24 | ||||||||||
| AVI & filter | 4 | 27 | 0.8881 | 0.0010 | ||||||||
| KIAVI | 2+25+4 | 30 | 0.0003 | 0.0006 | 0.0000 | 0.4450 | ||||||
| Boruta | 2 | 45 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||||
| GRF | 1 | 46 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||
| AVI | 11 | 40 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Hard70 | Model | 24 | 33 | 47 | 53 | 24 | 33 | 47 | 53 | |||
| AVI & filter | 25 | 24 | ||||||||||
| AVI | 13 | 33 | 0.1079 | 0.3001 | ||||||||
| KIAVI | 11+25+13 | 47 | 0.6253 | 0.1820 | 0.9357 | 0.2328 | ||||||
| GRF | 1 | 53 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||||
| Boruta | 3 | 50 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||
| Hard90/Hard70 | Model | 40 | 40 | |||||||||
| 50 | 0.0000 | 0.0000 | ||||||||||
The ccr and kappa of the most accurate model (i.e. model 40) for hard90 were significantly higher than the rest five models (i.e. models 24, 27, 30, 44 and 46) based on the Mann-Whitney tests (with p values < 0.0001). The ccr and kappa of the most accurate model (i.e. model 50) for hard70 were significantly higher than those of the remaining four models (i.e. models 24, 33, 47 and 53) based on the Mann-Whitney tests (with p values < 0.0001). In addition, the most accurate model for hard90 was significantly more accurate than the most accurate model for hard70 based on the Mann-Whitney test (with a p value < 0.0001).
In terms of computing efficiency as measured by the number of models developed for identifying the most accurate model for each FS method, RRF and Boruta were much higher than AVI, VI and KIAVI.
Comparison of spatial predictions of seabed hardness based on hard90 and hard70 data
The spatial predictions of the most accurate models for hard90 and hard70 were similar, with a match rate between corresponding hardness classes as high as 92.31% (i.e. with a corresponding mismatch rate of 7.69%, Table 11). Hard and soft were predicted less often, while hard-soft and soft-hard were predicted in greater number based on hard90 data than hard70. Of the mismatched predictions, about 1.3% of hard predictions for hard70 were predicted as hard-soft and soft-hard for hard90, while about 5.18% of soft predictions for hard70 were predicted as hard-soft and soft-hard for hard90, leading low match rates for certain classes between hard90 and hard70.
Table 11. Confusion matrix between predictions for individual classes based on hard90 and hard70 data for all study areas and for a portion of area A (A1).
| All four areas- Hard70 (17,418,262 grid cells) | Correctly matched by hard70 (%) | ||||||
| Hard | Hard-soft | Soft-hard | Soft | Total | |||
| Hard90 | Hard | 0.85 | 0.23 | 0.00 | 0.09 | 1.17 | 72.60 |
| Hard-soft | 1.26 | 3.68 | 0.10 | 2.06 | 7.12 | 51.77 | |
| Soft-hard | 0.04 | 0.13 | 2.65 | 3.12 | 5.95 | 44.60 | |
| Soft | 0.41 | 0.06 | 0.17 | 85.12 | 85.77 | 99.25 | |
| Total | 2.57 | 4.10 | 2.93 | 90.41 | 100.00 | ||
| Correctly matched by hard90 (%) | 33.15 | 89.91 | 90.56 | 94.16 | 92.31 | ||
| Area A1- Hard70 (3,083,153 grid cells) | Correctly matched by hard70 (%) | ||||||
| Hard | Hard-soft | Soft-hard | Soft | Total | |||
| Hard90 | Hard | 2.01 | 0.12 | 0 | 0.46 | 2.59 | 77.78 |
| Hard-soft | 5.24 | 14.82 | 0.29 | 6.66 | 27.01 | 54.85 | |
| Soft-hard | 0 | 0.14 | 2.45 | 7.17 | 9.76 | 25.09 | |
| Soft | 1.62 | 0.01 | 0.21 | 58.8 | 60.64 | 96.96 | |
| Total | 8.87 | 15.09 | 2.95 | 73.09 | 100 | ||
| Correctly matched by hard90 (%) | 22.66 | 98.22 | 82.90 | 80.45 | 78.07 | ||
The predictions of the most accurate models for hard90 and hard70 were illustrated in Fig 5 using a portion of study area (A1) to visually compare the predictions of the RF predictive models. This area was chosen as an example as it contains highly contrasting geomorphic features. For this particular portion, the match rate is 78.07% (i.e. with a corresponding mismatch rate of 21.93%, Table 11). Of the mismatched predictions, about 5.24% of hard predictions for hard70 were predicted as hard-soft for hard90, while about 13.83% of soft predictions for hard70 were predicted as hard-soft and soft-hard for hard90, resulting in low match rates for some classes between hard90 and hard70. Their predictions captured similar major patterns, while the some hard predictions for hard70 in the high banks were predicted as hard-soft or soft-hard for hard90 in the southern portion, and some soft predictions for hard70 on the terrace in the northeast corner were predicted as soft-hard and hard-soft for hard90. The hard substrates were found mostly on banks that were associated with the highest backscatter values (Fig 5D). The hard-soft and soft-hard substrates were also mostly found on banks as well as on portions of terraces. In comparison, soft substrates were mostly found on valleys that were often associated with the lowest backscatter values; and portions of terraces were also predicted as soft.
Fig 5.
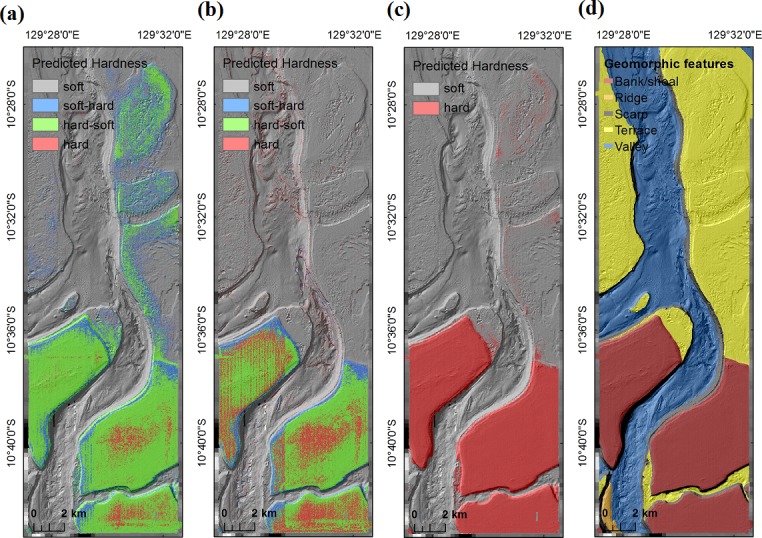
Spatial predictions of seabed hardness for a section of area A (A1): a) hard90, b) hard70, c) hardness with two classes, and d) geomorphic features.
Comparison of spatial predictions: four classes vs. two classes
The spatial predictions for hard90 and hard70 were similar with the predictions based on two hardness classes [7, 70]. The match rates were 92.06% and 93.18% respectively when the predictions of hard, hard-soft and soft-hard were pooled into one category (i.e. hard) for hard90 and hard70.
The spatial predictions for hard90 and hard70 in area A1 were similar with the predictions based on two hardness classes [7] (Fig 5), with the match rates of 81.53% and 89.42% respectively when the predictions of hard, hard-soft and soft-hard were combined into a single category (i.e. hard) for hard90 and hard70.
Discussion and Conclusions
Predictive accuracy of seabed hardness
All the models developed produced a good to perfect fit to the data (Tables 3 and 6); and their PA is also high (Figs 2 and 3). There is no definite relationship between the models’ fit and their PA, which is consistent with the findings in our previous study [7]. The PA of the most accurate models based on various FS techniques varies from 0.4852 to 0.6753 for hard90 and from 0.4116 to 0.5328 for hard70 in terms of kappa (Tables 9 and 10). According to Fielding & Bell [65], the agreement between the predicted and the tested values is good if kappa is between 0.4 and 0.75. This demonstrates that the PA of the models developed for predicting the seabed hardness is high. The PA of the most accurate models is even more notable in terms of ccr; and it varies from 84.62% to 89.78% for hard90 and from 84.09% to 87.04% for hard70. The high PA implies that: 1) seabed substrate was properly classified based on underwater video footage, and the data produced for the response variable is of high quality; 2) the hardness classification schemes developed (i.e. hard90 and hard70) are robust; and 3) the predictors used were informative. Furthermore, the PA for each model is stable and reliable because it is an averaged PA based on 100 repetitions of 10-fold cross-validation. Hence we can confirm that:
sample size used in this study was adequate for modelling the seabed hardness;
RF is an effective modelling method with high PA not only for presence/absence data but also for multi-level categorical data;
robust predictive models were developed;
seabed hardness of four classes can be predicted with a high accuracy; and
RF can be applied to ‘small p and large n’ problems in environmental sciences, with the number of predictive variables as low as only one.
This study further affirms the superior performance of RF in marine environmental sciences [14, 15, 25, 26, 32]. The excellent performance of RF has been attributed to a number of features associated with RF including the ability to model non-linear relationships commonly found in the environmental sciences as discussed in previous studies [25, 26, 32].
It is apparent that non-soft classes were under-predicted while the soft class was over-predicted for both hard90 and hard70 data, which could be attributed to the unbalanced sample size of the hardness classes. The hard-soft class was under-predicted and approximately 50% of observed hard-soft samples were predicted as the soft class for both datasets, which was unexpected as it is anticipated to be more similar to hard or soft-hard classes than to the soft class. Although the limitations discussed in [7] could be potential factors resulting in such phenomenon, further studies are recommended to investigate this phenomenon. Approximately 50% of the non-soft classes were predicted as the soft class for hard70 data, which could be also attributed to the limitations discussed in [7]. This finding highlights the difference between hard90 and hard70, suggesting that hard90 data may have more accurately classified the seabed substrate and should be adopted in the future studies.
When the hard-soft and soft-hard classes were merged into the hard class, the user’s and producer’s accuracy between the observed and the predicted values was improved but still slightly lower than the previously published findings, particularly for hard70 data [7, 12]. This reduction in the accuracy could be attributed to that bathymetry was an important predictor in the previous studies [7, 12], but it is no longer an important predictor in this study. This change is because banks and terraces are mostly located in shallow water and are most often associated with hard substrates. However, the hard class in the previous study was split into three classes in the current study, which are located at similar water depths, thus bathymetry can no longer differentiate these classes and was not found to be an important predictor in this study.
Predictive accuracy and correlated predictive variables
The PA changes with highly correlated predictors for models developed for hard90 and hard70 data. Their influence on the PA changes with individual predictors. The phenomenon that the inclusion of highly correlated predictors (i.e. ρ≥0.99 and r≥0.95) could improve the PA was observed for many models in this study (e.g. model 1 vs. model 43 and model 17 vs. model 19 for hard90, model 1 vs. model 26 for hard70, and those models compared in Table 10). This could be explained by the fact that these correlated predictors are informative as they have high variable importance (S3 File) and their inclusion can increase the number of informative predictors selected for each individual tree in RF, thus improving the PA. It was observed that including some correlated variables improved the PA in previous studies [7, 15, 34], suggesting that correlated variables may be able to compensate for the small number of predictors in environmental sciences, and more often than not we only have correlated proxy predictive variables in environmental sciences instead of causal predictors as seen in simulation studies [31].
In contrast, the exclusion of some highly correlated predictors may improve the PA in some other cases. It was observed for hard70 where bs27 and bs25 were highly correlated (ρ = 0.99, r = 1.00), but the exclusion of bs27 from model 4 led to a slight increase in PA for the subsequent model (i.e. model 5) containing bs25. The exclusion of bs25 from model 6 for hard70 also resulted in slight improvement in PA for model 7 that contains bs21. This phenomenon was further evidenced in Fig 2C after removing bs27 that was highly correlated with bs28 and bs33 (with ρ≥0.99 and r = 0.98). Similar findings were observed in previous studies [25, 32, 33, 35].
Contradictory findings were observed in previous studies in the marine environmental sciences as well as in this study regarding correlated predictors for RF. These opposite effects imply that not all highly correlated predictors should be used even if there are of high VI or excluded, and that there are no short-cuts in identifying the optimal predictive model. The extendedForest [39] package can efficiently deal with the correlated variables in terms of the variable importance, but selecting predictors that can improve PA from correlated predictive variables is a challenging task. No free lunch theorems [71] still apply even if the predictors are highly correlated. This finding also suggests that the typical approach used in pre-selecting predictors by excluding correlated variables (i.e. r≥0.95 or the inflation factor ≥20) needs to be re-examined for identifying predictive models using machine learning methods, at least for the application of random forest in marine environmental sciences. These applications further demonstrate that feature selection is essential for identifying an optimal predictive model for RF in marine environmental sciences [15, 25].
Predictive accuracy and important and unimportant predictors
Some important and unimportant predictors were identified based on the VI for hard90 and the AVI for hard70. They were excluded during the initial FS process, which may obviously lead to the exclusion of some important predictors and thus result in less accurate predictive models which has also been observed in previous studies [7, 64]. Adding the important predictors and removing the unimportant ones could partially solve this problem. However, the accuracy of predictive models in this study showed inconsistent response patterns to the inclusion or removal of the important or unimportant predictors. Of the three important predictors identified for hard90, two of them (i.e. variance and surface) further improved the PA after adding them back while the inclusion of the remaining one (i.e. relief) reduced the PA (Table 3 and Fig 2A). Of the two identified important variables for hard70, the inclusion of bs21 further improved the PA while the inclusion of bathy.moran reduced the PA; and of the three unimportant variables, removing profile.curv and bs.moran further improved the PA, whereas removing variance reduced the PA (Table 6 and Fig 3A). It is apparent that their influence on PA changes with individual predictors. It was also observed that reliance upon variable importance only can lead to suboptimal predictive model and the most accurate predictive model may be overlooked in previous studies [7, 64]. These findings suggest that the predictor(s) with the least variable importance should not be excluded without further testing. The detection of the important and unimportant predictors provides signals of potential candidates or establishes prior information for further improvement of the PA. However efforts are required to select relevant predictors from them to further improve the PA.
Feature selection methods
Five FS methods, VI, AVI, KIAVI, Boruta and RRF, were tested in terms of PA in this study. They are essentially all VI-based wrapper methods according to Janecek et al. and Saeys et al.[28, 62]. These methods were applied to the full dataset and a pre-selected sub-dataset. Since the VI was obtained from RF, these methods are also embedded techniques [28]. To develop the final predictive models based on VI and AVI, the contribution to the PA of relevant predictors was used to determine their inclusion or elimination in the backward or forward stepwise selection. Hence, these applications cover three different FS techniques: filter, wrapper and embedded. In this study, filter and/or wrapper FS techniques were used in combination with embedded FS techniques within RF.
It is apparent that all FS techniques used in this study improved the PA except that the filter FS method significantly reduced the PA with respect to the full models. The effects of these techniques are however different for hard90 and hard70. For hard90, the model developed by applying AVI to 41 variables is significantly more accurate than other FS techniques. For hard70, the model developed by applying Boruta to 41 variables is significantly more accurate than other FS techniques. These findings highlight that: 1) these FS techniques are data sensitive and data-specific, and 2) to obtain an optimal predictive model for a given dataset, relevant FS techniques should be tested to select the most appropriate FS technique, otherwise sub-optimal models may be produced. All the most accurate models identified in Tables 9 and 10 are believed to be the local optimum, which were identified under the FS methods with the limited resources used. In fact, all optimal models identified based on FS methods are believed to be local optimal. A complete search for the global optimal model(s) is time consuming and at times, impossible, especially when there are a large number of predictive variables. This is because the computational requirements have a factorial increase with the number of variables, highlighting the importance of FS methods. Although the application of KIAVI did not further improved the PA, it was found that informing knowledge to VI can further improve the PA [7, 64]. Again no free lunch theorems [71] are still effective when using FS methods. In general, AVI and Boruta show their effectiveness in searching for the most accurate predictive models and are recommended for future studies. It may be worth testing whether applying the AVI to the variables selected by Boruta could further improve the PA in future studies. However, caution should be taken when applying the filter FS method because: 1) the number of predictive variables is usually small in environmental sciences; and 2) inclusion of highly correlated predictors (with r ≥ 0.99) could improve the PA as discussed above.
Computational demand is critical in choosing a FS method. Among the five methods, the computational time decreases from VI, AVI, KIAVI, Boruta to RRF in terms of the number of models tested to find the final model. Three advantages of VI were discussed previously [34]. KIAVI and AVI share these advantages and AVI led to the most accurate model for hard90 in this study, but apparently their computational demand is high and automated programs need to be developed to increase their computational efficiency in the future. Moreover, these FS methods are applicable to datasets with small number of features such as those tested in this study. For datasets with large number of features (e.g. from thousands to millions), dimension reduction methods may be required to reduce the computing demand. However, caution needs to be taken when non-linear correlations exist [72].
As discussed in the previous study [7], the PA is the ultimate measure for selecting the predictive model. Model selection via these FS methods is based on the PA. These FS methods will produce models that are the most accurate or optimal instead of the most parsimonious as discussed above and previously [7]. The traditional model selection methods such as AIC and BIC for regression models (e.g. linear model, generalised linear model) attempt to select the most parsimonious models that are not necessarily the most accurate models, especially when proxy variables are used as predictors instead of causal variables. Since the ultimate goal of predictive modelling is to identify the most accurate model(s), these FS methods are more appropriate than AIC and BIC methods in selecting predictive model(s). The principles underpinning these FS methods can be easily applied to other machine learning methods as well as regression models. Therefore, they are recommended for selecting predictive model(s) for RF and other modelling techniques in future studies.
Hardness classification methods and prediction maps of seabed hardness
Hard90 vs hard70
Two seabed hardness classification schemes, hard90 and hard70, were proposed in this study. In comparison with hard70, the advantages of Hard90 were presumed to be that: 1) the probabilities of ‘hard’ and ‘soft’ are increased accordingly by using a threshold of 90% or 10%, which ensured the ‘hard’ or ‘soft’ substratum classification to be composed mostly of the representative substratum (i.e. ‘hard’ or ‘soft’); and 2) number of samples for the mixed classes of hardness are increased and samples are more evenly distributed among four classes. Thus the PA was expected to be higher for models based on hard90 than on hard70, which were confirmed by the findings in this study (Tables 9 and 10).
Less hard and soft and more mixed classes were also anticipated to be predicted for hard90 than for hard70, which are confirmed by the findings in Table 11. Hard predictions for hard70 predicted as the hard-soft class for hard90 was less than soft predictions for hard70 predicted as the soft-hard class for hard90 (1.26% vs. 3.12%); even a portion of soft predictions for hard70 (2.06%) was predicted as hard-soft for hard90. However, the majority of the predictions are similar for hard90 and hard70, with a match rate as high as 92.31% between these two schemes (Table 11). By comparing the distribution of the hardness classes in the hard70 and hard90, there were three samples that shifted from hard to hard-soft, and from soft to soft-hard respectively, but the resultant changes in predictions are not as even as the samples.
Four classes vs. two classes
The PA for four hardness classes in this study seems less than that for two classes in the previous study [7]. A few factors were expected to affect the PA either positively or negatively:
The hard class in the previous study was further divided into three classes in this study, so the PA was expected to be reduced.
Since the locations of the video tracks are again different to their true locations (thus to the locations of backscatter data), we should not expect to reduce the predictive error much by using the predictive variables at video locations directly.
The predictive variables derived in this study are expected to be more reliable than those in previous studies [7, 12], because in previous studies the variables were derived for the sample locations that are usually a few meters to a few kilometres away from the video track, while in this study all variables were generated for the location of the video locations to remove the possible effects of the inaccuracy in the variables caused by the distance. Hence an accuracy improved model is expected.
Bathymetry was an important predictor for hard and soft in the previous study [7] but not in the current study as discussed above in 4.1. This may further explain why the PA was slightly reduced in this study.
The spatial predictions for hard90 and hard70 were similar with the predictions based on two hardness classes [7], with match rates as high 92.06% and 93.18% respectively. They are also as high as 81.53% and 89.42% respectively for A1. These findings show that major patterns were captured in their predictions, although predictions based on hard70 as expected are more similar to the predictions based on two classes than the predictions based on hard90. This is because both the two hardness class system in the previous study [7] and hard70 scheme in this study used the same 70% and 30% thresholds to classify hard and soft classes.
Geomorphic features
The predicted maps reflect the influence of various geomorphic features such as banks, terraces, and valleys (Figs 1C and 5). The associations of the predicted hardness with geomorphic features are generally similar to those discussed in previous studies [7, 12]. These associations were supported by ecological studies because certain organisms expected to be found on hard [43, 73] or soft substrates [43, 73] were observed in the corresponding substrates in this study.
The predictions that were illustrated using a portion of study area (A1) (Fig 5) highlight the difference in predictions among all geomorphic features for hard90 and hard70, with a lower match rate than that for all areas (78.07% vs 92.31%) and with more mixed classes predicted for hard90 (Table 11). Such differences were mainly observed on banks and terraces (Figs 1C and 5).
Limitations and other issues
The nature of the seabed is a fundamental factor in controlling the acoustic returns (i.e. backscatter). Soft seabed substrates generally produce lower backscatter intensity; in contrast, hard seabed substrates generally produce higher backscatter intensity [74–77]. However, the strength of the acoustic returns can be significantly attenuated or even lost because of scattering from surface topography and the sessile benthic organisms, causing an apparent reduction in the backscatter intensity. Likewise, very strong seabed reflections can be observed due to well-sorted unconsolidated sediments in the absence of any surface topography or the presence of hard surface underneath a veneer of soft materials. The existence of these factors can affect the reliability of acoustic data and classification of video images [12], thus affecting the PA.
In addition, the limitations discussed in relation to using video footage to validate substrate grounds and to the nature of backscatter intensity in Li et al. [7] are also applicable to this study.
Conclusions
Two seabed hardness classification schemes proposed in this study, hard90 and hard70, are effective and they all led to high PA for seabed hardness predictions. Seabed hardness is predictable and can be predicted into a spatially continuous layer with a high accuracy, especially to large areas where multibeam acoustic data exist and predictions of seabed classes are needed for marine planning and management.
Not all highly correlated predictive variables should be used or excluded. The usual approach used in pre-selecting variables by excluding correlated ones should be re-examined for identifying predictive models using machine learning methods, at least for the application of RF in the environmental sciences.
The identification of the important and unimportant predictors provides guideline for further improving the predictive models, although additional effort is required to select relevant predictors from the important and unimportant predictors.
FS is essential for identifying an optimal predictive model for RF in environmental sciences but is a challenging task as a complete search for the global optimal model(s) is time consuming and sometimes impossible. AVI and Boruta show their effectiveness in searching for the most accurate predictive models and are recommended for future studies. Automated computational programs for AVI are recommended to be developed to improve its computational efficiency in the future. However, caution should be taken when applying filter FS method in selecting optimal predictive models.
This study further affirms the superior performance of RF in marine environmental sciences. RF is an effective modelling method with high PA not only for presence/absence data and but also for multi-level categorical data. RF can be applied to ‘small p and large n’ problems in environmental sciences. It is recommended for generating spatially continuous predictions of categorical variables like seabed hardness when the information of relevant predictive variables is available.
Supporting Information
(DOCX)
(DOCX)
(CSV)
Fig A: measured by RF using randomForest package for 20 predictive variables [1]; Fig B: averaged VI from 100 iterations of RF using extendedForest package for 20 variables [2]; and Fig C: averaged VI from 100 iterations of RF using extendedForest package for 41 variables [2].
(DOCX)
Acknowledgments
We would like to thank Dale Roberts and Peter Tan for their valuable comments and suggestions. This study was undertaken as an activity of the Seabed Mapping and Coastal Information Section, National Earth and Marine Observations Group, Environmental Geoscience Division, Geoscience Australia (GA). We thank the Master and crew of the RV Solander and scientific staff at the Australian Institute of Marine Science (AIMS) for their support in conducting the survey, Marcus Stowar (AIMS) for towed-video and still photography acquisition, and the Field and Engineering Support staff at GA. This study is published with the permission of the Chief Executive Officer, Geoscience Australia.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This study was internally funded by Geoscience Australia.
References
- 1.Post AL, Wassenberg TJ, Passlow V. Physical surrogates for macrofaunal distribution and abundance in a tropical gulf. Marine and Freshwater Research. 2006;57:469–83. [Google Scholar]
- 2.Mortensen PB, Dolan M, Buhl-Mortensen L. Prediction of benthic biotopes an a Norwegian offshore bank using a combination of multivariate analysis and GIS classification. ICES Journal of Marine Science. 2009;66:2026–32. [Google Scholar]
- 3.Newell RC, Seiderer LJ, Robinson JE. Animal/sediment relationships in coastal deposits of the eastern English Channel. Journal of the Marine Biological Association of the United Kingdom. 2001;81:1–9. [Google Scholar]
- 4.Warwick RM, Davies JR. The distribution of sublitoral macrofauna communities in the Bristol Channel in relation to the substrate. Estuarine, Coastal and Shelf Science. 1977;5:267–88. [Google Scholar]
- 5.McArthur MA, Brooke BP, Przeslawski R, Ryan DA, Lucieer VL, Nichol S, et al. On the use of abiotic surrogates to describe marine benthic biodiversity. Estuarine, Coastal and Shelf Science. 2010;88:21–32. [Google Scholar]
- 6.Williams IM, Leach JHJ. The relationship between depth, substrate and ecology: a drop video study from the southeastern Australian coast. Oceanologica Acta. 1999;22:651–62. [Google Scholar]
- 7.Li J, Siwabessy J, Tran M, Huang Z, Heap A . Predicting Seabed Hardness Using Random Forest in R In: Zhao Y, Cen Y, editors. Data Mining Applications with R: Elsevier; 2013. p. 299–329. [Google Scholar]
- 8.Stein DL, Tissot BN, Hixon MA, Barss WH. Fish–habitat associations on a deep reef at the edge of the Oregon continental shelf. Fisheries Bulletin. 1992;90:540–51. [Google Scholar]
- 9.Anderson JT, Van Holliday D, Kloser R, Reid DG, Simard Y. Acoustic seabed classification: current practice and future directions. ICES Journal of Marine Science. 2008;65:1004–11. [Google Scholar]
- 10.Kloser RJ, Penrose JD, Butler AJ. Multi-beam backscatter measurements used to infer seabed habitats. Continental Shelf Research. 2010;30:1772–82. [Google Scholar]
- 11.Basu A, Saxena NK . A review of shallow-water mapping systems. Marine Geodesy. 1999;22:249–57. [Google Scholar]
- 12.Siwabessy PJW, Daniell J, Li J, Huang Z, Heap AD, Nichol S, et al. Methodologies for seabed substrate characterisation using multibeam bathymetry, backscatter and video data: A case study from the carbonate banks of the Timor Sea, Northern Australia. Geoscience Australia, Record 2013/11, 82pp: 2013.
- 13.Gray JS, Elliot M. Ecology of Marine Sediments: From Science to Management New York: Oxford University Press; 2009. [Google Scholar]
- 14.Li J, Potter A, Huang Z, Daniell JJ, Heap A. Predicting Seabed Mud Content across the Australian Margin: Comparison of Statistical and Mathematical Techniques Using a Simulation Experiment. Record. Geoscience Australia, 2010/11, 146pp, 2010.
- 15.Li J, Potter A, Huang Z, Heap A. Predicting Seabed Sand Content across the Australian Margin Using Machine Learning and Geostatistical Methods. Geoscience Australia, Record 2012/48, 115pp, 2012 Contract No.: Geoscience Australia, Record 2012/48, 115pp.
- 16.Ho TK. The random subspace method for constructing decision forests IEEE Trans on Pattern Analysis and Machine Intelligence. 1998;20(8):832–44. [Google Scholar]
- 17.Ho TK, editor Random decision forests. Proceedings of the Third International Conference on Document Analysis and Recognition; 1995 14–16 Aug 1995; Montreal, Que., Canada.
- 18.Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- 19.Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and regression trees. Belmont: Wadsworth; 1984. [Google Scholar]
- 20.Cutler DR, Edwards TCJ, Beard KH, Cutler A, Hess KT, Gibson J, et al. Random forests for classification in ecology. Ecography. 2007;88(11):2783–92. [DOI] [PubMed] [Google Scholar]
- 21.Diaz-Uriarte R, de Andres SA. Gene selection and classification of microarray data using random forest. BMC Bioinformatics. 2006;7(3):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marmion M, Luoto M, Heikkinen RK, Thuiller W. The performance of state-of-the-art modelling techniques depends on geographical distribution of species. Ecological Modelling. 2009;220(24):3512–20. [Google Scholar]
- 23.Okun O, Priisalu H, editors. Random forest for gene expression based cancer classification: overlooked issues. Pattern Recognition and Image Analysis: Third Iberian Conference, IbPRIA 2007 2007 June 6–8, 2007; Girona, Spain: Lecture Notes in Computer Science 4478, Springer-Verlag, Berlin.
- 24.Prasad AM, Iverson LR, Liaw A. Newer classification and regression tree techniques: bagging and random forests for ecological prediction. Ecosystems. 2006;9:181–99. [Google Scholar]
- 25.Li J, Heap AD, Potter A, Daniell J. Application of machine learning methods to spatial interpolation of environmental variables. Environmental Modelling & Software. 2011;26:1647–59. [Google Scholar]
- 26.Li J, Heap AD, Potter A, Huang Z, Daniell J. Can we improve the spatial predictions of seabed sediments? A case study of spatial interpolation of mud content across the southwest Australian margin. Continental Shelf Research. 2011;31:1365–76. 10.1016/j.csr.2011.05.015 [DOI] [Google Scholar]
- 27.Stephens D, Diesing M. A Comparison of Supervised Classification Methods for the Prediction of Substrate Type Using Multibeam Acoustic and Legacy Grain-Size Data. PLOS ONE. 2014;9(4):e93950:14. 10.1371/journal.pone.0093950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Saeys Y, Inza I, Larrañaga P. A review of feature selection techniques in bioinformatics. Bioinformatics. 2007;23(19):2507–17. [DOI] [PubMed] [Google Scholar]
- 29.Dougherty E, Hua J, Sima C. Performance of feature selection methods. Current Genomics. 2009;10:365–74. 10.2174/138920209789177629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Guyon I, Lemaire V, Boullé M, Dror G, Vogel D, editors. Analysis of the KDD Cup 2009: Fast scoring on a large Orange customer database. JMLR: Workshop and Conference Proceedings; 2009.
- 31.Biau G. Analysis of a random forest method. Journal of Machine Learning Research. 2012;13:1063–95. [Google Scholar]
- 32.Li J, Heap A, Potter A, Daniell JJ. Predicting Seabed Mud Content across the Australian Margin II: Performance of Machine Learning Methods and Their Combination with Ordinary Kriging and Inverse Distance Squared. Geoscience Australia, Record 2011/07, 69pp, 2011 Contract No.: Geoscience Australia, Record 2011/07, 69pp.
- 33.Li J, Sanabria LA. Advances in spatial statistical modelling with applications to terrestrial and marine environments in Australia Canberra: Geoscience Australia Wednesday Seminar; 2013. p. 47. [Google Scholar]
- 34.Li J. Predictive Modelling Using Random Forest and Its Hybrid Methods with Geostatistical Techniques in Marine Environmental Geosciences. In: Christen P, Kennedy P, Liu L, Ong K-L, Stranieri A, Zhao Y, editors. The proceedings of the Eleventh Australasian Data Mining Conference (AusDM 2013), Canberra, Australia, 13–15 November 2013; 13–15 November 2013: Conferences in Research and Practice in Information Technology, Vol. 146; 2013.
- 35.Li J, Potter A, Heap A. Irrelevant Inputs and Parameter Choices: Do They Matter to Random Forest for Predicting Marine Environmental Variables? Australian Statistical Conference 2012; 9–12 July 2012; Adelaide2012.
- 36.Liaw A, Wiener M. Classification and regression by randomForest. R News. 2002;2(3):18–22. [Google Scholar]
- 37.Hapfelmeier A, Ulm K. A new variable selection approach using random forests. Computational Statistics & Data Analysis. 2013;60:50–69. [Google Scholar]
- 38.Genuer R, Poggi JM, Tuleau-Malot C. Variable selection using random forest. Pattern Recognition Letters. 2010;31:2225–36. [Google Scholar]
- 39.Smith SJ, Ellis N, Pitcher CR. Conditional variable importance in R package extendedForest. R vignette <http://gradientforestr-forger-projectorg/Conditional-importancepdf>. 2011.
- 40.Kursa MB, Rudnicki WR. Feature Selection with the Boruta Package. Journal of Statistical Software. 2010;36(11):1–13. [Google Scholar]
- 41.Deng H. Guided random forest in the RRF package. arXiv:13060237. 2013.
- 42.Heap AD, Przeslawski R, Radke L, Trafford J, Battershill C, Party S. Seabed Environments of the Eastern Joseph Bonaparte Gulf, Northern Australia. Sol4934—Post-survey Report. Geoscience Australia, Record 2010/09, 78pp, 2010.
- 43.Anderson TJ, Nichol S, Radke L, Heap AD, Battershill C, Hughes M, et al. Seabed Environments of the Eastern Joseph Bonaparte Gulf, Northern Australia: GA0325/Sol5117—Post-Survey Report. Geoscience Australia, Record 2011/08, 59pp, 2011.
- 44.Anderson TJ, Cochrane GR, Roberts DA, Chezar H, Hatcher G. A rapid method to characterize seabed habitats and associated macro-organisms. In: Todd BJ, Greene HG, editors. Mapping the Seafloor for Habitat Characterization. Special Paper 47: Geological Association of Canada; 2008. p. 71–9.
- 45.Mortensen P, Buhl-Mortensen L. Distribution of deep-water gorgonian corals in relation to benthic habitat features in the Northeast Channel (Atlantic Canada). Marine Biology. 2004;144(6):1223–38. 10.1007/s00227-003-1280-8 [DOI] [Google Scholar]
- 46.Wentworth CK. A scale of grade and class terms for clastic sediments. Journal of Geology. 1922;30:377–92. [Google Scholar]
- 47.Buhl-Mortensen L, Buhl-Mortensen P, Dolan MFJ, Danmheim J, Bellec V, Holte B. Habitat complexity and bottom fauna composition at different scales on the continental shelf and slope of northern Norway. Hydrobiologia. 2012;685:191–219. [Google Scholar]
- 48.Thrush SF, Hewitt JE, Funnell GA, Cummings VJ, Ellis J, Schultz D, et al. Fishing disturbance and marine biodiversity: role of habitat structure in simple soft-sediment systems. Marine Ecology Progress Series. 2001;221:255–64. [Google Scholar]
- 49.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Backscatter Local Moran I Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76727); 2013. [Google Scholar]
- 50.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Bathymetry Local Moran I Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76727); 2013. [Google Scholar]
- 51.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Backscatter Variance Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76726); 2013. [Google Scholar]
- 52.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Backscatter Homogeneity Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76725); 2013. [Google Scholar]
- 53.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Profile Curvature Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76722); 2013. [Google Scholar]
- 54.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Planar Curvature Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76721); 2013. [Google Scholar]
- 55.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Topographic Position Index Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76717); 2013. [Google Scholar]
- 56.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Surface Area Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76716); 2013. [Google Scholar]
- 57.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Relief Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76715)2013. [Google Scholar]
- 58.Siwabessy J, Huang Z. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Slope Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76714); 2013. [Google Scholar]
- 59.Siwabessy J. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Backscatter Grids Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76340); 2013. [Google Scholar]
- 60.Siwabessy J. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Bathymetry Grids Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76400); 2013. [Google Scholar]
- 61.Siwabessy J. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Probability of Seabed Hardness Grids Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76347); 2013. [Google Scholar]
- 62.Janecek AG, Gansterer WN, Demel MA, Ecker GF, editors. On the relationship between feature selection and classification accuracy. JMLR: Workshop and Conference Proceedings; 2008.
- 63.Strobl C, Boulesteix A, Zeileis A, Hothorn T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinformatics. 2007;8(25):25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Li J. Predicting the spatial distribution of seabed gravel content using random forest, spatial interpolation methods and their hybrid methods. The International Congress on Modelling and Simulation (MODSIM) 2013; 1–6 December 2013; Adelaide2013. p. 394–400.
- 65.Fielding AH, Bell JF. A review of methods for the assessment of prediction errors in conservation presence/absence models. Environmental Conservation. 1997;24(1):38–49. . [Google Scholar]
- 66.Cohen J. A coefficient of agreement for nominal scales. Educational and Psychological Measurement. 1960;20:37–46. [Google Scholar]
- 67.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction 2nd ed. New York: Springer; 2009. 763 p. [Google Scholar]
- 68.R Development Core Team (2012) R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing; 2012.
- 69.ESRI Inc (2002) ArcGIS 10.0. ESRI Inc., Redlands, CA.
- 70.Li J, Siwabessy J. Methodologies for multibeam seabed hardness mapping in the Timor Sea—Hardness Prediction Grids Canberra: Geoscience Australia; (http://www.ga.gov.au/metadata-gateway/metadata/record/gcat_76401); 2013. [Google Scholar]
- 71.Wolpert D, Macready W. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation. 1997;1:67–82. [Google Scholar]
- 72.Austin MP, Belbin L, Meyers JA, Doherty MD, Luoto M. Evaluation of statistical models used for predicting plant species distributions: Role of artificial data and theory. Ecological Modelling. 2006;199:197–216. [Google Scholar]
- 73.Przeslawski R, Daniell J, Anderson T, Vaughn Barrie J, Heap A, Hughes M, et al. Seabed Habitats and Hazards of the Joseph Bonaparte Gulf and Timor Sea, Northern Australia. Geoscience Australia, Record 2008/23, 69pp, 2011 Contract No.: Geoscience Australia, Record 2008/23, 69pp.
- 74.Hamilton LJ, Parnum I. Acoustic seabed segmentation from direct statistical clustering of entire multibeam sonar backscatter curves. Continental Shelf Research. 2011;31:138–48. [Google Scholar]
- 75.Goff JA, Olson HC, Duncan CS. Correlation of side-scan backscatter intensity with grain-size distribution of shelf sediments, New Jersey margin. Geo-Marine Letters. 2000;20:43–9. [Google Scholar]
- 76.De Falco D, Tonielli R, Di Martino G, Innangi S, Simeone S, Parnum IM. Relationships between multibeam backscatter, sediment grain size and Posidonia oceanica seagrass distribution. Continental Shelf Research. 2010;30:1941–50. [Google Scholar]
- 77.Ferrini VL, Flood RD. The effects of fine-scale surface roughness and grain size on 300 kHz multibeam backscatter intensity in sandy marine sedimentary environments. Marine Geology. 2006;228:153–72. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
(CSV)
Fig A: measured by RF using randomForest package for 20 predictive variables [1]; Fig B: averaged VI from 100 iterations of RF using extendedForest package for 20 variables [2]; and Fig C: averaged VI from 100 iterations of RF using extendedForest package for 41 variables [2].
(DOCX)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.