A new phase diagram of water under negative pressure: The rise of the lowest-density clathrate s-III

Researchers predict a new ice clathrate structure as the most stable ice polymorph with the lowest density in a negative-pressure region.

Abstract

Ice and ice clathrate are not only omnipresent across polar regions of Earth or under terrestrial oceans but also ubiquitous in the solar system such as on comets, asteroids, or icy moons of the giant planets. Depending on the surrounding environment (temperature and pressure), ice alone exhibits an exceptionally rich and complicated phase diagram with 17 known crystalline polymorphs. Water molecules also form clathrate compounds with inclusion of guest molecules, such as cubic structure I (s-I), cubic structure II (s-II), hexagonal structure H (s-H), tetragonal structure T (s-T), and tetragonal structure K (s-K). Recently, guest-free clathrate structure II (s-II), also known as ice XVI located in the negative-pressure region of the phase diagram of water, is synthesized in the laboratory and motivates scientists to reexamine other ice clathrates with low density. Using extensive Monte Carlo packing algorithm and dispersion-corrected density functional theory optimization, we predict a crystalline clathrate of cubic structure III (s-III) composed of two large icosihexahedral cavities (8⁶6⁸4¹²) and six small decahedral cavities (8²4⁸) per unit cell, which is dynamically stable by itself and can be fully stabilized by encapsulating an appropriate guest molecule in the large cavity. A new phase diagram of water ice with TIP4P/2005 (four-point transferable intermolecular potential/2005) model potential is constructed by considering a variety of candidate phases. The guest-free s-III clathrate with ultralow density overtakes s-II and s-H phases and emerges as the most stable ice polymorph in the pressure region below −5834 bar at 0 K and below −3411 bar at 300 K.

INTRODUCTION

Water molecules are the third most abundant molecular species in the universe (1). Ice, the form of water in condensed state, is the most common molecular solid on Earth and can be also detected in the giant planetary interior. The existence of water and ice has implication to the diversity of nature and possible presence of life. Because of the flexible hydrogen bonds, water ice exhibits an exceptionally rich and complicated phase diagram (2–10). Under different conditions of pressure (P) and temperature (T), there are 17 experimentally established crystalline phases of ice so far (2, 3, 11). Among them, ice XI has the lowest mass density of 0.930 g/cm³ and forms a proton-ordered phase at zero temperature and ambient pressure (12). At elevated temperature (72 K), ice XI transforms into a proton-disordered phase, that is, the well-known ice Ih (12). In addition, many hypothetical ice phases are also predicted and wait experimental confirmation, for example, virtual ices i and i′ with low density (13), ice 0 as a precursor to ice nucleation (5), silica-like ice polymorphs (14), and partially ionic phase of water ice under extremely high pressure (5 to 50 Mbar) (6–10).

Apart from pure water ices, water and various gas molecules (such as Ne, Ar, H₂, CO₂, CH₄, C₂H₆, adamantane, and methylcyclohexane) can form a class of nonstoichiometric inclusion compounds, namely, the gas hydrate or ice clathrate (15–18). In the ice clathrates, water molecules form loosely hydrogen-bonded framework connected by interlinked cages whose inner cavities are either completely or partially occupied by guest molecules. So far, at least five types of ice clathrate structures have been experimentally identified (11, 15, 19) or theoretically proposed (20), namely, cubic structure I (s-I) with 2 5¹² cages and 6 5¹²6² cages per unit cell; cubic structure II (s-II) with 16 5¹² cages and 8 5¹²6⁴ cages; hexagonal structure H (s-H) with 3 5¹² cages, 2 4³5⁶6³ cages, and 1 5¹²6⁸ cage; tetragonal structure T (s-T) with 2 4²5⁸6⁴ cages; and tetragonal structure K (s-K) with 6 5¹² cages, 4 5¹²6³ cages, and 4 5¹²6² cages per unit cell, respectively. Usually, the clathrate hydrates are considered as hypothetical phases of water (21, 22) and have to be stabilized by favorable van der Waals (vdW) interactions between guest molecules and host water cages (16–18, 23). However, Falenty and co-workers (11) recently synthesized guest-free s-II clathrate (also named ice XVI) by leaching Ne atoms from the s-II Ne clathrate. The guest-free s-II clathrate is mechanically stable at atmospheric pressure up to a temperature of 145 K and exhibits negative thermal expansion with good mechanical stability and larger lattice constants than the filled clathrate. The experimental realization of empty s-II lattice not only confirms that water molecules themselves can form loose crystalline phase with density lower than ice XI but also motivates us to further explore other possible low-density polymorphs of water ice that are stable at low temperatures and negative pressures.

In contrast to the comprehensive knowledge of phase diagram of water under positive pressures, the negative-pressure region of the diagram is much less explored (21, 22, 24, 25). Some efforts have been devoted to determining the limiting mechanical tension that the stretched liquid water can sustain before the event of nucleation occurs, namely, the cavitation pressure (24–28). Classical nucleation theory predicted a cavitation pressure of about −1900 bar for water at room temperature (25, 26). A large negative pressure of about −1400 bar in the microscopic aqueous inclusions inside a quartz matrix was reported (27). A negative pressure of −1600 bar in water capillary bridges was also measured with an atomic force microscope (28).

Besides the stretched liquid water, guest-free clathrates can be regarded as low-density phases of water ice that exist in the negative-pressure region of the phase diagram (21, 22, 29, 30) and have been investigated by classical molecular dynamics (MD) simulations. Jacobson et al. (29) established a P-T phase diagram with inclusion of liquid water, ice Ih, and s-I and s-II clathrates and concluded that guest-free s-II clathrate is the stable phase of water at P ≤ −1320 bar and T ≤ 275 K. Using TIP4P/2005 (four-point transferable intermolecular potential/2005) model (31), Conde et al. (21) found that the sequence of stable phases of water at negative pressure is ice XI, s-II, and s-H clathrates. At 0 K, the critical pressures for transitions from ice XI to s-II and from s-II to s-H were −3639 and −7775 bar, respectively. Bai et al. (30) reported evidence of spontaneous formation of monolayer guest-free clathrate within a hydrophobic nanoslit at low temperatures.

So far, only three known phases of empty ice clathrates (s-I, s-II, and s-H) have been considered in the negative-pressure phase diagram of water. Here, we report a guest-free clathrate with cubic structure, named structure III (s-III), which is dynamically stable and can be fully stabilized by encapsulating suitably sized guest molecules. A new phase diagram of water under negative pressure is constructed, where s-III clathrate replaces the previously believed s-H phase and dominates the region of deeper negative pressures. The discovery of this ice clathrate not only reestablishes the phase diagram of water but also motivates experimentalists to explore possibly new ice clathrate phases with low density.

RESULTS AND DISCUSSION

Full density functional theory (DFT) optimization with vdW-DF2 functional yielded an equilibrium lattice parameter of 13.431 Å for the guest-free s-III unit cell. The fractional coordinates of the s-III clathrate are given in table S1. Real-space force constants of the guest-free s-III clathrate were calculated by using the density functional perturbation theory as implemented in Vienna Ab initio Simulation Package (VASP). The phonon dispersion was then computed from the real-space force constants using the Phonopy package (32) (see fig. S1). No imaginary frequency is found within the entire Brillouin zone, confirming its dynamic stability.

To investigate the competition of different low-density ice polymorphs, here we took ice XI (12) as reference and considered a number of guest-free ice clathrates, that is, s-I, s-II, s-H (19), s-K (20), SGT (sigma-2) as a silica analog (33), s-T (15), and s-III, as well as virtual ice i (13) for comparison, which are displayed in fig. S2. Their equilibrium volume of unit cell, average O-O distance, mass density, and lattice cohesive energy from DFT calculations are summarized in Table 1 and compared with available experiments. For ice XI, the calculated mass density (0.9 g/cm³) is slightly lower than the experimental data (0.93 g/cm³) (12), and the theoretical O-O distance (2.765 Å) between neighboring water molecules is slightly longer than the experimental one (2.735 Å). Moreover, the theoretical lattice cohesive energy (E_latt) of ice XI deviates from the measured value (34) by only 3.98 kJ/mol. For the empty lattice of s-II clathrate, the mass density of 0.804 g/cm³ and average O-O distance of 2.765 Å from our DFT calculations are also rather close to the experimental values of 0.81 g/cm³ and 2.751 Å (11), respectively. Overall, the vdW-DF2 functional is reasonable to describe the intermolecular hydrogen bonding interactions of water ices.

Table 1. Number of water molecules per unit cell (Z_cell), equilibrium volume of unit cell (V_cell), average distance between oxygen atoms in adjacent water molecules (d_O-O), mass density (ρ), and lattice cohesive energy per water molecule (E_latt) for various ice and guest-free clathrate phases.

The values in parentheses are experimental data.

Phase	Zcell	Vcell (Å3)	dO-O (Å)	ρ (g/cm3)	Elatt (kJ/mol)
Ice XI	8	266 (257*)	2.785 (2.735*)	0.900 (0.930*)	62.84 (58.86†)
Ice i	8	280	2.785	0.855	61.31
s-I	46	1692	2.765	0.813	61.38
s-K	80	2962	2.765	0.808	60.76
s-II	136	5059 (5022‡)	2.765 (2.751‡)	0.804 (0.81‡)	61.37
s-T	12	453	2.795	0.792	60.23
s-H	34	1325	2.785	0.768	60.79
SGT	64	2650	2.765	0.722	59.27
s-III	48	2423	2.765	0.593	55.77

*Results of the study by Leadbetter et al. (12) obtained from neutron diffraction at 5 K.

†Results of the study by Whalley (34) with zero-point energy contributions removed.

‡Results of the study by Falenty et al. (11) obtained from neutron diffraction at 5 K.

On the whole, the lattice cohesive energy of these nine ice polymorphs is nearly proportional to the mass density (see Table 1); that is, the denser phase of water ice has larger cohesive energy. Among all crystalline phases of water considered here, the E_latt of ice XI phase (62.84 kJ/mol) with the highest mass density (0.9 g/cm³) is the largest, whereas the E_latt of s-III (55.77 kJ/mol) with the lowest density (0.593 g/cm³) is the smallest (only three-fourths of s-II). The average O-O distance is 2.765 Å for s-III clathrate and is nearly identical to those of the known clathrate phases of s-I (2.765 Å), s-II (2.765 Å), s-K (2.765 Å), s-H (2.785 Å), s-T (2.795 Å), and SGT (2.765 Å). In addition, the average lengths of O–H covalent bonds (d_O–H) and hydrogen bonds (d_O…H) in the s-III clathrate and in the other ice phases are about the same (see table S2). Therefore, the ultralow density of s-III ice clathrate is mainly originated from the unique icosihexahedral water cage rather than the longer distance between adjacent water molecules.

The lattice cohesive energies as a function of volume per water molecule (E_latt-V) for ice XI, ice i, and clathrates of s-K, SGT, s-T, s-I, s-II, s-H, and s-III are given in fig. S3. One can see that the E_latt-V curve for each phase exhibits quadratic behavior at its equilibrium volume. Figure 1 further depicts the relative enthalpy as a function of negative pressure for various candidate phases by taking ice XI as a reference. The cross point between the H-P curves of two phases defines their transition pressures at 0 K. In the negative-pressure range from zero to −4009 bar, ice XI is the most stable crystalline phase of water with the lowest enthalpy. Then, s-II clathrate becomes more favorable at more negative pressure. This transition pressure coincides well with −3639 bar previously obtained by Conde et al. using a TIP4P/2005 model (21). At deeper pressures beyond −5500 bar, s-III clathrate eventually prevails over s-II. From the H-P diagram, one can also see that s-H clathrate becomes more stable than s-II clathrate at −7614 bar, as previously predicted by Conde et al. at −7775 bar (21), whereas SGT clathrate surpasses s-H at deeper pressure over −8804 bar. However, s-II, s-H, and SGT clathrates are always less stable than s-III clathrate if P ≤ −5500 bar. In brief, our DFT calculations at zero temperature demonstrate that the newly disclosed s-III clathrate (instead of s-H and SGT) is the most favorable low-density phase of water ice under deeply negative pressures.

Fig. 1. Relative enthalpy per water molecule (DFT computation) versus negative pressure for clathrate phases of s-I, s-II, s-H, s-III, SGT, s-K, s-T, and ice i, with ice XI as a reference.

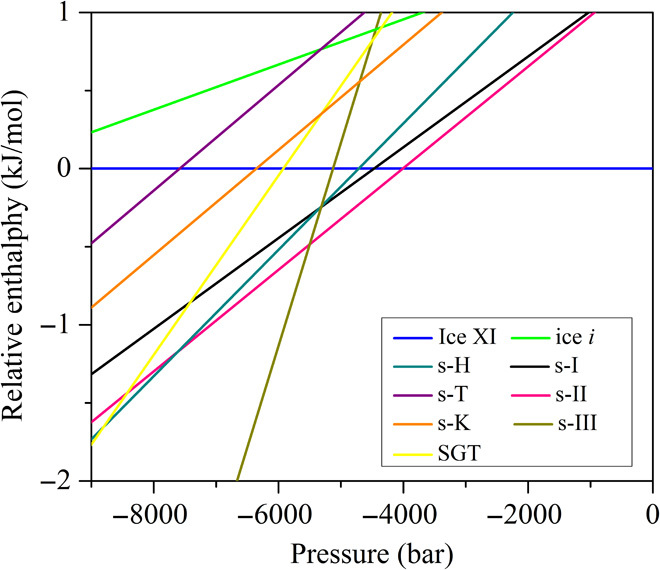
The crossover pressures between ice XI and s-II, s-II and s-III, s-II and s-H, and s-H and SGT are −4009, −5500, −7614, and −8804 bar, respectively.

Monte Carlo/MD simulations of P-T phase diagram

The above P-H curves only provide information at zero temperature. To obtain a complete P-T diagram, here we perform free energy calculations and Gibbs-Duhem integration by using a TIP4P/2005 water model (31). As given in table S3, the lattice cohesive energies and mass densities of various ice/clathrate phases (including ices XI and i, s-I, s-II, s-H, s-IIII, s-T, SGT, and s-K clathrates) from DFT calculations are well consistent with the calculated results using TIP4P/2005 potential at zero temperature and zero pressure, with average deviations of 1.28% in lattice cohesive energy. Therefore, it is reasonable to further explore the P-T phase diagram of water using comprehensive MD simulations with the TIP4P/2005 potential, which has been demonstrated to describe the relative energy, critical temperature, and surface tension of liquid water and ice phases well (35).

The P-T phase diagram of water ice polymorphs (including ice XI, ice Ih, ice i, s-I, s-II, s-H, s-III, s-T, SGT, and s-K clathrates) was constructed on the basis of the Einstein molecule method with the TIP4P/2005 potential. First, to obtain reliable configurations of the ice polymorphs, isothermal-isobaric Monte Carlo simulations at temperatures from 1 to 200 K (with 5-K increment) and pressures from −6000 to 2000 bar (with 1000-bar increment) were performed using a homemade code. For each candidate structural phase, the configurations from Monte Carlo (MC) simulations were used to calculate free energy on the basis of the Einstein molecule approach with the GROMACS (GROningen MAchine for Chemical Simulations) program (36). At each P-T condition, the Ewald sum method with a real-space cutoff of 8.5 Å was adopted to treat the electrostatic interactions, and the pair potential was truncated at 8.5 Å (see fig. S4). For the ice Ih and clathrate phases of s-I, s-II, s-H, s-III, s-T, s-K, and SGT, we considered the effect of proton disorder (11, 37) in the free energies. Once the free energy at a reference point was determined, thermodynamic integration method could be used to explore the free energy under other thermodynamic conditions. Specifically, an initial coexistent point was located by equating the chemical potentials between two phases at a certain temperature and pressure (38). Then, the Gibbs-Duhem integration based on the trapezoid predictor-corrector formulas (39) was performed to compute the phase boundaries.

The water phase diagram by TIP4P/2005 potential is plotted in Fig. 2. Four ice polymorphs, namely, ice XI, ice Ih (which is the proton-disordered phase of ice XI), s-II, and s-III clathrates, arise under negative pressures, in agreement with the DFT results above. Other candidate phases, including ice i and clathrates of s-I, s-K, SGT, s-T, and s-H, no longer show up in the phase diagram of water ice because of their higher free energies. At different temperatures (0 to 300 K), s-II clathrate emerges as the most stable phase below ice XI, ice Ih, and liquid water, in agreement with previous observations (21, 22, 29). By extrapolation to 0 K, ice XI transforms into s-II clathrate at a pressure of −3357 bar, close to the critical pressure of −3639 bar obtained by Conde et al. (21). At more negative pressures, s-II phase further transforms into s-III at −5834 bar (T = 0 K) or −3411 bar (T = 300 K), and the phase boundary between s-II and s-III clathrates rises with increasing temperature. Below the s-II/s-III boundary line, the new s-III clathrate, instead of the previously believed s-H phase (21), dominates the deeper region of the diagram. Also note that the zero-temperature transition pressures for ice XI/s-II and s-II/s-III transformations from the P-H curves in Fig. 1 (DFT calculations) are −4009 and −5500 bar, respectively, which are close to the results based on the TIP4P/2005 potential, that is, −3357 and −5834 bar, respectively. In short, both empirical MD simulations at finite temperature and DFT calculations at 0 K validate the existence of s-III ice clathrate in the phase diagram of water at deeply negative pressures.

Fig. 2. P-T phase diagram of TIP4P/2005 water model in the region of negative pressures.

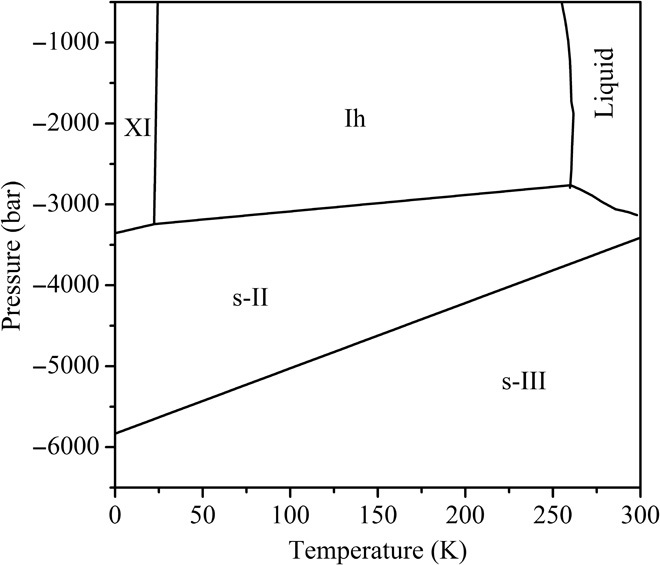
The phase boundaries between liquid water and Ih or s-II ice phases are taken from the study of Conde et al. (21) using the same TIP4P/2005 potential.

Stabilization of s-III clathrate by guest molecules

In the laboratory, applying and maintaining very large tension or negative pressure up to −6000 bar would be very difficult. Similar to the clathrate hydrates (16), s-III clathrate can be fully stabilized by encapsulating suitable guest molecules that fit the size of a larger 8⁶6⁸4¹² cavity. For example, as shown in Fig. 3, by inserting a dodecahedrane molecule (C₂₀H₂₀) (40) into the interior of each 8⁶6⁸4¹² cage, the guest-host (attractive) interaction energy in (C₂₀H₂₀)₂@(H₂O)₄₈ clathrate is −131.7 kJ/mol per C₂₀H₂₀ molecule by vdW-DF2 calculation, which is favorable to maintain the s-III clathrate lattice. The equilibrium lattice constant (13.262 Å) of (C₂₀H₂₀)₂@(H₂O)₄₈ clathrate slightly shrinks from the empty clathrate (13.431 Å), similar to a recent experimental observation of the s-II clathrate hydrate of neon (11). Note also that C₂₀H₂₀ molecule is one possible guest molecule that can fit the size of the 8⁶6⁸4¹² cavity. Encapsulation of other molecules with comparable sizes, for example, fullerenes with 40 to 60 carbon atoms (41), coronene (C₂₄H₁₂), corannulene (C₂₀H₁₀), and 4,4-dipropylheptane (C₁₃H₂₈), might serve well for the stabilization purpose. In other words, the predicted s-III clathrate can form an inclusion compound phase of water with appropriately sized guest molecules and may be synthesized in the laboratory under accessible conditions.

Fig. 3. Configuration of filled s-III clathrate.

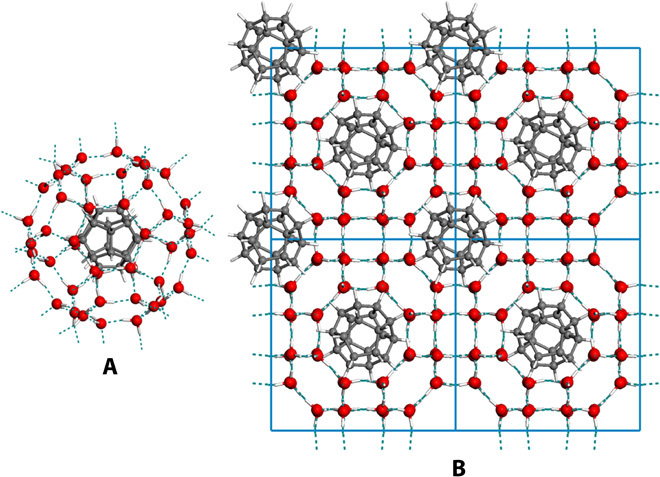
(A) Structure of an individual 8⁶6⁸4¹² water cage with a C₂₀H₂₀ molecule encapsulated. (B) Structure of the s-III clathrate with one C₂₀H₂₀ molecule encapsulated in each large cavity (2 × 2 unit cell is shown for a clearer view).

CONCLUSION

To summarize, using extensive DFT calculations as well as MC and MD simulations, we predict the thermodynamic stability of s-III ice clathrate, which is composed of unprecedented large icosihexahedral cavities and small decahedral cavities. The guest-free s-III clathrate is also proven to be dynamically stable on the basis of phonon-spectrum computation. We show that the guest-free s-III clathrate phase dominates the deeply negative-pressure region in the P-T phase diagram (below −5834 bar at 0 K and below −3411 bar at 300 K). This new ultralow-density phase of clathrate can be fully stabilized and possibly synthesized by incorporating appropriately sized molecules in the icosihexahedral cavities. If the guest-free clathrate s-III could be achieved in experiments, as done recently to achieve guest-free clathrate s-II (11), the guest-free s-III could be a potential candidate as ice XVII. In closing, the finding of the s-III ice clathrate not only brings in new insights into the less-explored negative-pressure regime of the phase diagram of water but also can stimulate future experiments to synthesize new clathrate hydrates with ultralow density and to explore applications such as gas storage or CO₂ sequestration.

MATERIALS AND METHODS

MC search of new clathrate phases

To search for possible crystalline phases of water under negative pressure, we used the MC packing algorithm and simulated annealing procedure (42) combined with the consistent valence force field. To achieve low-density structures with loose frameworks, we adopted (CH₄)(H₂O)_x (x = 2, 3, 4) stoichiometries with higher methane content than the conventional clathrates, for example, (CH₄)(H₂O)_5.75 for s-I (19). The methane molecules were finally removed from the obtained lattice structures to create the guest-free polymorphs of ice frameworks. For each stoichiometry, all 230 space groups were explored. However, most searches ended up with either dense-packed structures similar to the previously reported filled ice (43) or clathrate structures with density comparable to the known clathrate phases but less favorable energy.

Among all candidate structures from MC searches, only a cubic structure, named s-III clathrate, stands out for its ultralow density and unique geometry. As displayed in Fig. 4, s-III clathrate with P$\overline{4}$3n space group has 48 water molecules per unit cell, which is composed of two kinds of cages, that is, two large icosihexahedral 8⁶6⁸4¹² cages (6 octagonal faces, 8 hexagonal faces, and 12 quadrangular faces) and six small decahedral 8²4⁸ cages (2 octagonal faces and 8 quadrangular faces). The quadrangle face links adjacent 8²4⁸ cages, the hexagon face connects the neighboring cavities of 8⁶6⁸4¹², and the quadrangle or octagon face combines the smaller 8²4⁸ cage and the larger 8⁶6⁸4¹² cage. Topologically, s-III phase can be related to the silica analog of zeolite RHO, whereas s-I, s-II, and s-H clathrates correspond to the zeolite frameworks of MEP (melanoplilogite), MTN (dodecasil-3C), and DOH (dodecasil-1H), respectively (14). Compared with the other types of clathrate (including s-I, s-II, s-H, s-T, and s-K), the 48-member icosihexahedral cage as the major building unit of s-III clathrate is the largest, resulting in the lowest density, as summarized in Table 1.

Fig. 4. Structure of s-III ice clathrate.

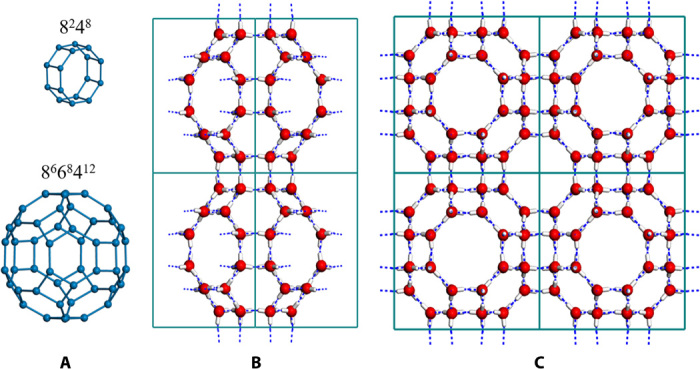
(A) Two types of building water cages (bottom: 8⁶6⁸4¹², 48-molecule with O symmetry; top: 8²4⁸, 16-molecule with D₂ symmetry; only oxygen frameworks are shown). (B and C) Repeated unit cells (1 × 2) (B) and 2 × 2 unit cells (C) (the hydrogen bond network is shown with blue dash line, red for oxygen, and white for hydrogen).

DFT calculations of the energies and stabilities

The energies and stabilities of guest-free clathrates and selected ice phases were investigated by DFT calculations with the VASP 5.3 software package (44). The electron-ion interactions were described by the projector augmented wave (PAW) potential (45). To account for the intermolecular dispersion interactions, the exchange-correlation interaction was described by the vdW-DF2 functional (46), with inclusion of a long-range term of the correlation energy. The electron wave function was expanded by plane-wave basis up to 700 eV, and the Brillouin zones were sampled by k point grids with a uniform spacing of 2π × 0.04 Å⁻¹.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/2/e1501010/DC1

Table S1. Fractional coordinates of the structure III (s-III) clathrate with cubic lattice (space group: P$\overline{4}$3n, lattice constant: 13.431 Å) from vdW-DF2 DFT calculation.

Table S2. Average lengths of O–H covalent bond (d_O–H) and hydrogen bond (d_O…H) for different phases (ice XI, ice i, s-I, s-II, s-H, SGT, s-K, s-T, and s-III clathrates) based on vdW-DF2 DFT computation.

Table S3. Mass density (ρ) and lattice cohesive energy per water molecule (E_latt) for different phases (ice XI, ice i, s-I, s-II, s-H, SGT, s-K, s-T, and s-III clathrates) based on vdW-DF2 (DFT) optimization, and another independent optimization using the TIP4P/2005 water model (at zero temperature and zero pressure).

Fig. S1. Phonon dispersion for guest-free s-III ice clathrate based on vdW-DF2 DFT computation.

Fig. S2. Crystal structures (2 × 2 unit cells) of ice i, ice XI, and clathrates of s-T, s-I, s-II, s-K, SGT, and s-H phases (blue dash lines for hydrogen bonds, red for oxygen, and white for hydrogen).

Fig. S3. Lattice cohesive energies (E_latt) for structures ice XI, ice i, s-K, s-I, s-II, s-H, s-III, SGT, and s-T clathrates as a function of volume per water molecule.

Fig. S4. Computed Helmholtz energy (A_sol) of the s-III clathrate based on the TIP4P/2005 potential, using the Einstein method, as a function of real-space cutoff distance r_cutoff.