Skip to main content
PMC home page
Functional Neurology logoLink to Functional Neurology
. 2016 Jan 3;30(4):245–256. doi: 10.11138/FNeur/2015.30.4.245

Multi-channel registration of fractional anisotropy and T1-weighted images in the presence of atrophy: application to multiple sclerosis

Eloy Roura a,✉, Torben Schneider b, Marc Modat c, Pankaj Daga c, Nils Muhlert b, Declan Chard b,d, Sebastien Ourselin c, Xavier Lladó a, Claudia Gandini Wheeler-Kingshott b,e
PMCID: PMC4758777  PMID: 26727703

Summary

Co-registration of structural T1-weighted (T1w) scans and diffusion tensor imaging (DTI)-derived fractional anisotropy (FA) maps to a common space is of particular interest in neuroimaging, as T1w scans can be used for brain segmentation while DTI can provide microstructural tissue information. While the effect of lesions on registration has been tackled and solutions are available, the issue of atrophy is still open to discussion. Multi-channel (MC) registration algorithms have the advantage of maintaining anatomical correspondence between different contrast images after registration to any target space. In this work, we test the performance of an MC registration approach applied to T1w and FA data using simulated brain atrophy images. Experimental results are compared with a standard single-channel registration approach. Both qualitative and quantitative evaluations are presented, showing that the MC approach provides better alignment with the target while maintaining better T1w and FA co-alignment.

Keywords: neuroimaging, registration, multiple sclerosis, atrophy

Introduction

Nowadays, research studies in multiple sclerosis (MS) (Ashtari et al., 2014) involve the use of both conventional magnetic resonance imaging (MRI) (Goruku et al., 2011) and quantitative MRI methods such as diffusion-weighted (DW) imaging (DWI); these new MRI techniques are also used in other diseases affecting the brain (Baglieri et al., 2013). A key challenge in quantitative MRI analysis is the registration of scans to structural images that can be used to segment gray matter (GM), white matter (WM) and lesions. However, both lesions and tissue atrophy can adversely affect registration. While in this study we focus on MS, this can also be seen in other neurological conditions, particularly in older cohorts where age-related or vascular lesions are seen in combination with disease-related tissue atrophy, for example in subjects with Alzheimer’s disease. The effects of lesions on registration and tissue segmentation have already been assessed on T1-weighted (T1w) volumetric scans, and techniques for minimizing them developed (Sdika et al. 2009; Chard et al., 2010; Battaglini et al., 2012; Ceccarelli et al., 2012). However, MS-associated atrophy (as shown in Fig. 1) is also a substantial issue, making registration inaccurate. This is particularly apparent when the target is a template based on healthy control data and the source scan is from a person with progressive MS, where ventricular enlargement may be prominent (as shown in Fig. 2) (Derakhshan et al., 2010). In such a situation very large deformations are required to bring the ventricles into alignment, and methods developed to work with healthy controls may fail.

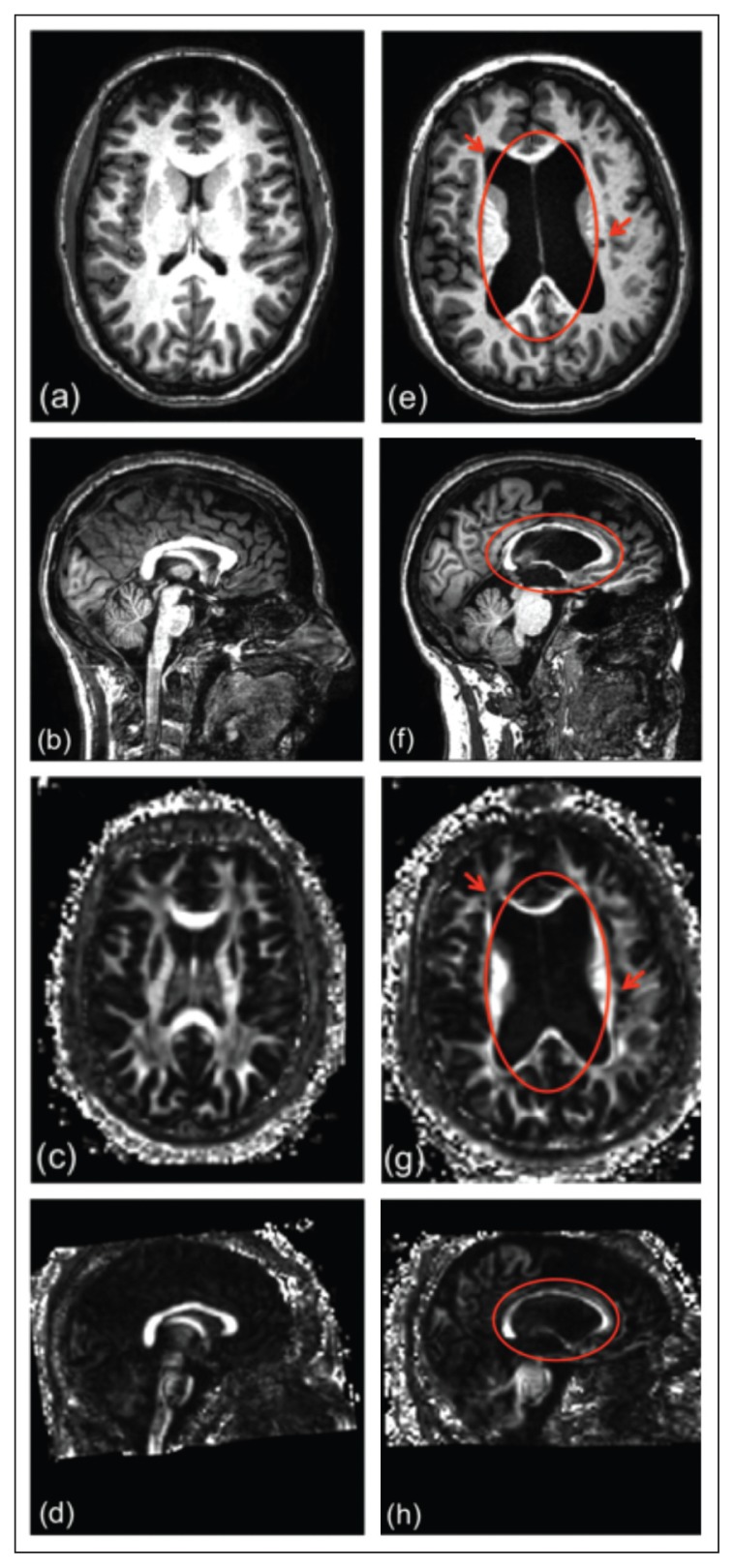
Figure 1.

Figure 1

Open in a new tab

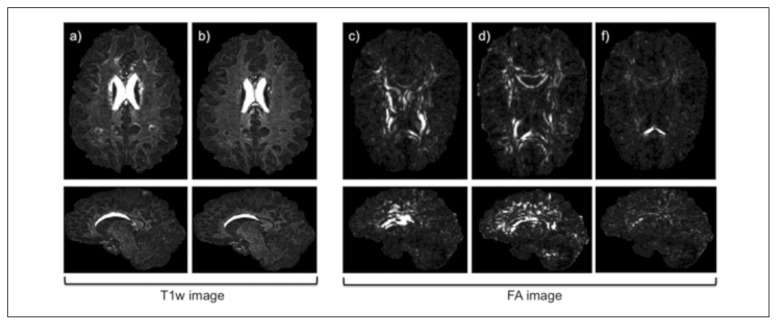
Images in a healthy subject (on the left) and in an MS patient with ventricular enlargement and lesions (on the right).

a,e) T1w axial images; b,f) T1w sagittal images; c,g) FA axial images; d,h) FA sagittal images. The lesions are circled in red.

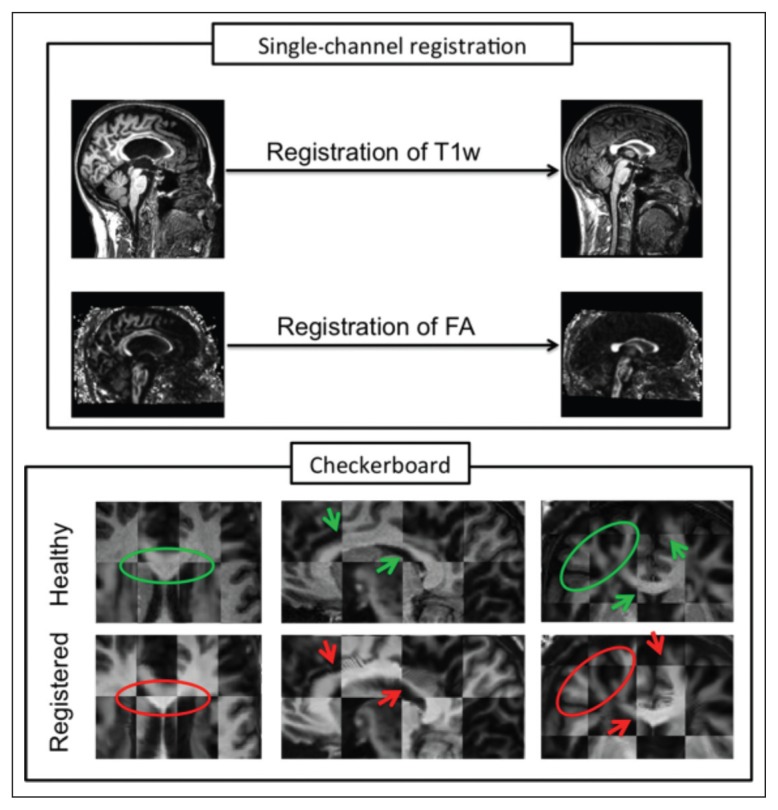
Figure 2.

Figure 2

Open in a new tab

Misalignment between T1w and FA brain images of an MS patient after registration to a healthy subject.

The box at the top shows the input images (original MS patient on the left and target healthy subject on the right). The box at the bottom shows: the checkerboard between T1w and FA of the original healthy subject (top row) and the checkerboard between the two output images of the single-channel registration (bottom row).

In the case of multi-contrast regional studies a registration step is often also required to align several subjects to a template space while maintaining intra-subject alignment of images with different contrasts such as T1w scans and diffusion MRI-derived indices. Registration of multi-spectral MRI data is usually undertaken either independently for each modality or using transformations determined by registering T1w structural scans. However, diffusion MRI metrics, such as fractional anisotropy (FA), also contain structural information complementary to that of T1w scans, and so using both simultaneously to guide image registration may improve alignment in multi-modal analysis (Park et al., 2003; Geng et al., 2012). Several registration strategies have been proposed over the last few years:

  1. Single-channel (SC), where individual different contrast datasets are deformed independently. In situations where source and target images belong to different modalities, e.g., T1w, T2-weighted (T2w), DW, diffusion tensor (DT), the registration is considered multi-modal (Wells et al., 1996; Ourselin et al., 2000; Guimond et al., 2001; Archip et al., 2007; Studholme, 2008; Klein et al., 2010; Walimuni et al., 2011), while if source and target images correspond to the same image modality the registration is mono-modal (Thirion, 1996, 1998; Rueckert et al., 1999, 2003; Studholme et al., 2004; Vercauteren et al., 2007, 2008; Modat et al., 2010a). In this work, a multi-modal strategy is used when intra-subject registration is performed, and a mono-modal one when we perform SC inter-subject registrations.

  2. Single modality-based approaches, where only one dataset is used to estimate the deformations and the other datasets are deformed according to the first. In this work, we based the deformations on the T1w sequence (T1w-based).

  3. Multi-channel (MC) registration processes where each space contains more than one modality to compute the deformation. A previous co-alignment between the images in each space (source and target) is needed. The MC approach performs a simultaneous registration of two different modalities to a specific target (Park et al., 2003; Miller et al., 1993; Guimond et al., 2002; Avants et al., 2007), exploiting the complementary information in images of different modalities. This solution was previously developed by Studholme (2008), who combined structural and full DT information into the same registration process. More recently, Daga et al. (2011) proposed a normalised mutual information (NMI) expression able to perform this MC registration in a more computationally efficient manner, although only using the FA information rather than the full tensor. The latter approach (Daga et al., 2011) is the one used in this work.

Registration of MRI images affected by lesions and atrophy to a healthy target space is challenging, but can be improved by taking care of some of the problems. There exist freely available algorithms that include lesion filling, e.g. at the websites of FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/lesion_filling), SPM-LST (http://www.applied-statistics.de/lst.html), and SPM-SLF (http://eia.udg.edu/salem/slfToolbox/software.html), which allow lesion inpainting of T1w images in order to minimize biases in image intensity distributions. However, such algorithms have not yet been developed for other modalities, in particular for DT imaging (DTI)-derived indices. Fewer studies have proposed solutions to the issue of registering multiple images of different contrast also affected by severe atrophy to a common space. In this study we tackle the specific issue of improving alignment between T1w and FA data for a single subject after registration to a common space. This is a particular concern when dealing with MS subjects because of the differences in the extent of atrophy across subjects, who sometimes also show large ventricular enlargement (Fig. 2). In such cases, the substantial anatomical structural difference between the source and target images requires very large deformations. Furthermore, in MS, both MS lesions and atrophy affect the different MRI processing tasks. However, as shown elsewhere (Battaglini et al., 2012; Roura et al., 2012), the presence of lesions does not significantly affect the quality of the registration process, while atrophy may introduce large segmentations and registration errors. Hence, in this work we will focus on the effects of atrophy on registration and propose techniques to limit this.

Multi-channel approaches may help by maintaining anatomical correspondence between T1w and FA images of each subject, after registration to any target space (e.g. to a healthy subject from the same study or to a common standard space). This is true even when large-scale deformations are necessary to match patient data to healthy targets. However, the specific registration of T1w and FA maps within the subject’s space is not a simple task since the tissue contrast of these images is very different. In addition, these two modalities are often affected by different levels of partial volume effects due to differences in voxel sizes, as well as by sequence-specific image distortions.

The aim of our study is two-fold: first to demonstrate the validity of the MC registration approach for the registration of T1w and FA images to a target space, and second, to test whether the results obtained from the MC approach outperform those obtained with mono-modal SC registration or with the T1w-based approach. We therefore developed a new pipeline that includes a co-registration step between T1w and FA images followed by MC registration to a standard space. In order to achieve a good co-registration of T1w and FA images in the subject’s space, T2w and non-DW (b0) images are also used.

In line with the work of Modat et al. (2010b), we propose to generate simulated brain atrophy images by using healthy control scans deformed to match scans from MS patients. This approach enables us to evaluate different registration approaches by registering these simulated images back to the unaltered healthy control scans. Previous studies have outlined a number of different algorithms that can be used to simulate atrophy for different specific applications (Camara et al., 2006; Karaçali and Davatzikos, 2006). However, there is no established method for simulating MS lesions on both T1w and FA images. In this study, therefore, we propose a simple method in which MS brains are simulated using Demons registration (DReg) of healthy subjects to MS subjects (Thirion, 1998; Vercauteren et al., 2008), whose images contain both MS lesions and atrophy, and an independent method is then used to test the registration of each atrophied dataset back to its original healthy subject. To evaluate the registration pipeline we performed both qualitative and quantitative analysis of the registration results, comparing the MC approach with standard SC registrations back to the original healthy subject images. In our study, 10 healthy subjects and 10 MS patients were used to generate 100 brain atrophy simulations. A qualitative evaluation using checkerboards and difference images as well as a quantitative analysis using the mean intensity difference are included in this work. Furthermore, in order to evaluate the impact of the lesions in the MS subjects, we also analyzed registration results when the MS lesions on T1w had been filled prior to the atrophy simulation.

Methods

MRI data

Subjects

Ten healthy subjects (mean age: 41.8 years, 4 males and 6 females) and 10 patients with MS (6 relapsing-remitting, 3 secondary progressive, 1 primary progressive, mean age: 41.6 years, 3 males and 7 females, mean disease duration: 13.2 years, median Expanded Disability Status Scale score = 2.5) were scanned on a 3T Philips Achieva scanner (Philips, Best, The Netherlands), with a 32-channel head coil.

MRI protocol

i) Dual echo proton density T2w scan: voxel size = 1 × 1 × 3 mm, TR = 3500 ms, TE = 19/85 ms; ii) three-dimensional (3D) fast-field echo T1w structural scan: voxel size = 1 × 1 × 1 mm, TR = 6.9 ms, TE = 3.1 ms, inversion time TI = 824 ms, field of view 256 × 256 × 180 sagittal slices; iii) DTI acquisition: cardiac-gated SE-EPI, TR ≊ 24 s (depending on the subject’s heart rate), TE = 68 ms, number of DW directions = 61 (b = 1200 s/mm2), number of non-DW (b0) scans = 7, voxel size = 2 × 2 × 2 mm, SENSE acceleration factor = 3.1.

Atrophy simulations

From the 10 healthy subjects we generated a total of 100 simulations of atrophied brains. This was done by deforming the 10 healthy subjects into the native space of each of the 10 patients in order to introduce different rates of MS atrophy; for this purpose we used DReg. To generate the data for the testing purposes, T1w, FA, T2w and b0 images were used, although here we evaluate only the performance of the registrations done using the T1w and FA images. Furthermore, another set of 100 simulations was generated after first filling the MS lesions (Chard et al., 2010) on the T1w images, prior to performing the atrophy simulation.

Image processing

The image processing strategy presented in this work consists of three parts: i) pre-processing steps; ii) registration of T1w and FA images to a target space; and iii) evaluation of different registration pipelines (SC, MC and T1w-based).

Pre-processing

Pre-processing involves calculation of the DT maps, including FA maps, from the DW images (DTI processing), and the creation of MC datasets for each subject (intra-subject registration) to be used in the creation of the simulated atrophy data (simulated atrophy data).

DTI processing

The DTI dataset was first corrected for eddy current distortions using the eddy_correct command from the FMRIB Software Library (http://www.fmrib.ox.ac.uk/fsl), assuming a linear co-registration between all the 3D volumes, with the first b0 image being taken as the reference image. The free open-source toolkit Camino (http://www.camino.org.uk) was then used to fit the DT and compute the FA in each voxel in the space of the first b0 image. For anatomical reference and registration purposes, we also computed the average b0 image, after the co-registration step, from seven non-DW b0 images acquired as part of the DTI dataset.

Intra-subject registration

To perform the registration of T1w and FA images to a common space, it is essential to first align these images in the subject’s native space. We registered the FA images to the T1w data in native space in order to retain the information from the higher resolution of these scans.

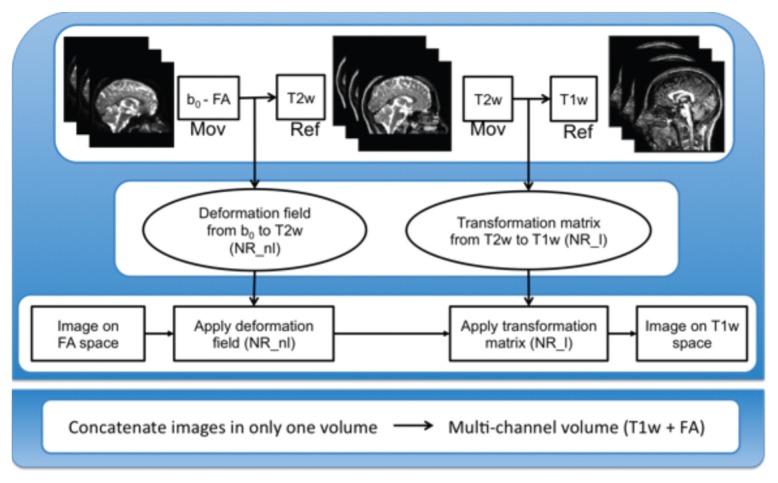
Figure 3 shows the overall scheme for co-registering T1w and FA images. For each of the 10 healthy subjects and 10 MS patients’ datasets we performed the following steps:

Figure 3.

Figure 3

Open in a new tab

Pipeline for the generation of the multi-channel data (T1w + FA).

Ref = reference image; Mov = moving image; NR_l = NiftyReg linear; NR_nl = NiftyReg non-linear.

  1. The average b0 volume was aligned to the corresponding anatomical T2w using a non-rigid registration method from NiftyReg (http://cmic.cs.ucl.ac.uk/home/software) (Modat et al., 2010a) to correct for EPI-induced distortions in the DW data (Muhlert et al., 2013).

  2. The T2w images were then aligned with the T1w images via affine registration with NiftyReg (Ourselin et al., 2000, 2001, 2002).

  3. The composition of the deformation field (b0 to T2w, computed at step 1) and the transformation matrix (T2w to T1w, computed at step 2) allows us to transform images from the DTI space to the T1w space (and vice versa). This transformation was then applied to FA maps to obtain FA co-registered to T1w data in native space. The co-registered images (FA and T1w) obtained in this step were used as target images in the SC and T1w-based registration strategies of the simulated atrophy datasets, and concatenated to generate the MC data of T1w and DW images in native space, needed as the input for the MC registration.

Once the MC data had been created, we had all the data needed to test the registration of T1w and FA images to a target space using either an MC or an SC registration method. We always combined subsequent transformations in order to apply a single interpolation to the data and avoid interpolation-related biases and errors.

Simulated atrophy data

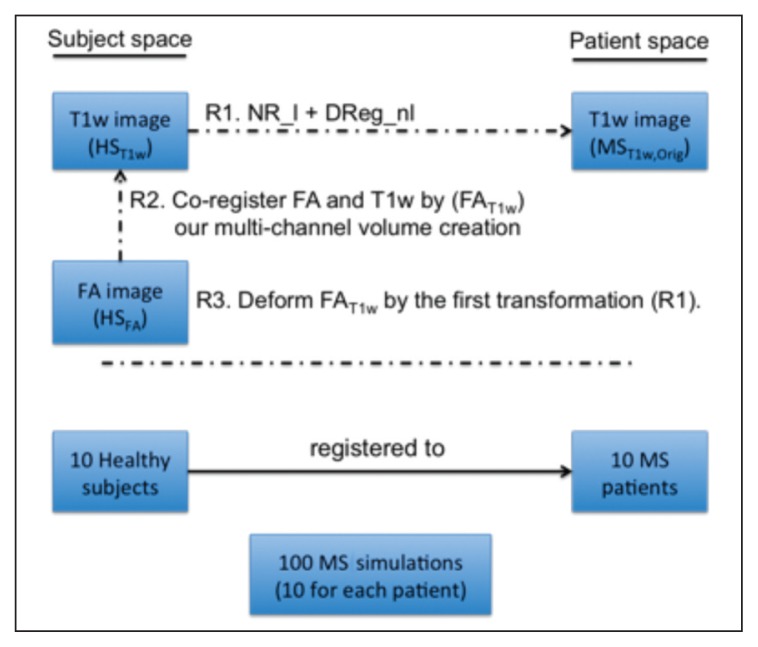
The strategy used to generate these simulations consists of three steps (Fig. 4):

Figure 4.

Figure 4

Open in a new tab

Pipeline used to simulate atrophy in healthy subjects.

NR_l = NiftyReg linear registration (rigid+affine); DReg = Demons registration. R1, R2, and R3 refer to the three registration steps performed in this pipeline.

  1. Deformation of each T1w image from a healthy subject space to each MS patient space. This registration uses the NiftyReg software (Ourselin et al., 2000, 2001, 2002; Modat et al., 2010a) for rigid and affine registration and DReg (Vercauteren et al., 2008) for the deformation process.

  2. Transportation of each healthy subject’s FA map into the same subject’s T1w space using the intra-subject registration pipeline as detailed above (Fig. 3).

  3. Application of atrophy deformation, obtained in step 1 using the T1w image, to the aligned FA map resulting from step 2.

These three steps were performed for each of the 10 healthy subjects to match them to each of the 10 MS patients (Fig. 4) in such a way that we obtained 100 simulated atrophy datasets, derived from original MS subjects and also containing MS lesions. This set of data was used for evaluating the registration performance. Henceforth we will refer to the 10 healthy subjects’ dataset as HST1w, HSFA and HSMC. The original 10 MS subjects’ datasets will be referred to as MST1w,Orig, MSFA,Orig (an MC dataset from the original MS patients was not created as they were used only as the targets to simulate atrophy). The 100 datasets deformed to simulate MS will be the input of the registrations and will be referred to as MST1w,Sim, MSFA,Sim and MSMC,Sim. Note that first subindex refers to the image modality and the second to the specific subset.

It is important to note that DReg is a symmetric log-domain diffeomorphic registration algorithm that deforms the input source image (Isource(x,y,z)) into the target image (Itarget(x,y,z)) returning both the deformation field T and the inverse deformation field T−1 (both consisting of a vector field where each vector is applied to each voxel). Those two deformations allow transformation of either the input Isource(x,y,z) into the resultant image (RD(x,y,z)) by T, or the inverse by T−1. The inverse transformation of the atrophy generation provides us with the ground truth that is needed to evaluate how well our registration approach can recover the simulated atrophy.

To summarize, DReg receives Isource(x,y,z) and Itarget(x,y,z) and outputs:

DReg(Isource(x,y,z),Itarget(x,y,z))→[RD(x,y,z),TD,TD-1]; [1]

where RD(x,y,z), TD and TD−1 are the output image and the transformations T mentioned earlier. Here Isource, Itarget and RD are HST1w, MST1w,Orig and MST1w,Sim, respectively.

The non-linear registration method used in this step of atrophy generation was performed using the Symmetric Log-Domain Diffeomorphic Demons Algorithm (Vercauteren et al., 2008), which has the advantage over previous Demons algorithms of providing the inverse of the spatial transformation. Demons is an iterative optimization procedure, which tries to minimize the cost function based on the sum of squared differences of the two images (Isource and Itarget) plus the regularization of a Gaussian kernel by a second order optimization method.

Using this atrophy simulation procedure we also created another set of 100 simulations in which, in accordance with the approach of Chard et al. (2010), the lesions on MST1w,Regj (with j = SC, T1w-based and MC) images were filled before performing the registration of the HST1w to each MS patient space (step 1).

Registration

In this section we focus on the main purpose of this work, which is to use an MC approach based on the work of Daga et al. (2011), which, in turn, is based on the Free Form Deformation (FFD) algorithm of Rueckert et al. (1999), and to compare it with classical SC approaches. The three different strategies evaluated in this study and explained here below all start from the co-registered MST1w,Sim and MSFA,Sim images, and the MSMC,Sim obtained from the data preparation in the pre-processing step, as well as the HST1w, the HSFA and the HSMC. Note that Demons is based on a non-parametric approach that includes a Gaussian smoothing kernel, while FFD is a parametric model that uses B-Splines. Therefore, the two transformation models are independent, and recovering simulated deformation created with the Demons using FFD is appropriate and unbiased.

The FFD algorithm consists of the same main registration steps, i.e. the optimization of a cost function, transformation of the moving image and interpolation function. The similarity measure used by Modat et al. (2010b) is based on the NMI. This measure is regularized by adding a penalty term (bending energy) computed at the control point positions in order to smooth the transformation. This cost function is optimized by the conjugate gradient ascent. The transformation model locally deforms the moving image using cubic B-Splines. Moreover, as stated by Daga et al. (2011), when the MC approach is used a reformulation of the NMI is needed.

Therefore, after deforming the original healthy subject images (Isource(x,y,z)) into simulated atrophy images (RD(x,y,z)) by registering them to the MS patients (Itarget(x,y,z)) we recovered the simulated atrophy with the NiftyReg software, NReg, by registering the RD(x,y,z) images back to the original subject data (Isource(x,y,z)). NReg receives RD(x,y,z) and Isource(x,y,z) and outputs:

NReg(RD(x,y,z),Isource(x,y,z))→[RN(x,y,z),TN]; [2]

The result of this registration, where RN(x,y,z) is the warped image and TN is the deformation field, is compared with the original image, Isource, where an ideal registration should give:

TN(RD(x,y,z))=TD-1(RD(x,y,z)); [3]

where RD = MSi,Sim, Isource = HSi and RN = MSi,Regj, with i = T1w, FA, MC and j = SC, T1w-based, MC respectively. The process explained above is used to compare the performance of the three different registration strategies, when registering the 100 simulations to the original healthy subjects:

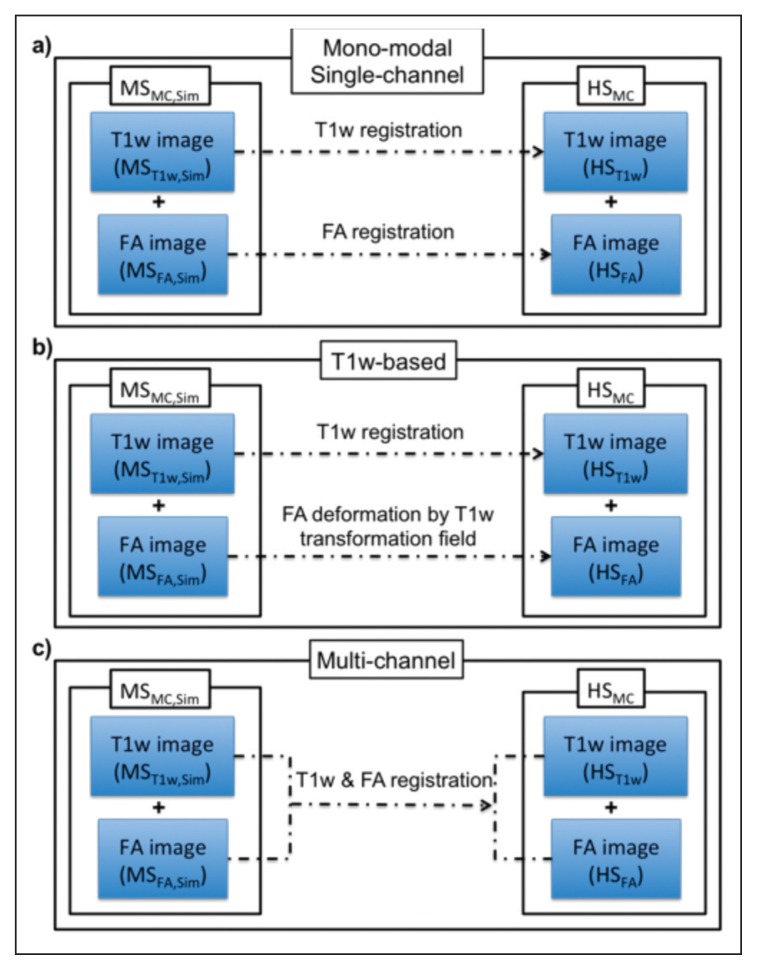
  1. Mono-modal single-channel registration. Each specific modality, MST1w,Sim and MSFA,Sim, is registered to its corresponding target modality, HST1w and HSFA respectively, as schematically shown in figure 5a. We use the registration of Modat et al. (2010a). The output of these registrations are noted as MST1w,RegSC and MSFA,RegSC respectively.

  2. T1w-based registration. In this registration approach the deformation of one modality is used as a transformation model for all the source images. We refer to this strategy as a one modality-based SC approach, which in our experiments applies the transformations from MST1w,Sim to HST1w also to transform MSFA,Sim into the target space, HSFA. This strategy is schematically represented in figure 5b. The output of this registration will be MST1w,RegT1w-based and MSFA,RegT1w-based.

  3. Multi-channel registration. Conversely to the SC approaches 1) and 2), here the different modalities are merged into one MC dataset for both source, MSMC,Sim, and target, HSMC, images. This approach is based on the work presented by Daga et al. (2011) where the NMI similarity measure from Modat et al. (2010a) was re-edited to share the information of different modalities during registration. Figure 5c illustrates the MC approach, where the images are simultaneously registered to the target. The output of this registration will be MST1w,RegMC and MSFA,RegMC.

Figure 5.

Figure 5

Open in a new tab

Three different registration strategies compared in the analysis of the experimental results.

Evaluation

We evaluate the performance of the registration in two ways using simulated atrophy and its recovery: i) using a qualitative analysis based on a checkerboard image (visual agreement); ii) calculating the mean intensity of the absolute value of the difference images.

Checkerboard image

The checkerboard between the registered T1w and FA images allows visual inspection of alignment accuracy based on the continuity of structural features and it shows: i) how well the registration process works in terms of matching the source image to the target image; ii) how well different source image modalities, e.g. T1w and FA, are aligned to each other in the target space.

Difference image

Here the registration performance is assessed within each modality using a global rather than a local index. A difference image D(x,y,z) is calculated using the target (Itarget(x,y,z)) and the registered image (RN(x,y,z)) of the same modality (e.g. HSFA and MSFA,Regj respectively, or HST1w and MST1w,Regj with j = SC, T1w-based, MC), and it is assumed that better registration corresponds to a lower overall mean value.

These difference images have been used in previous applications, i.e. to help localize MS lesion changes in longitudinal studies (Lladó et al., 2012) or to detect anatomical structures in medical images (Díez et al., 2011). For each registration method (Fig. 5) we computed D(x,y,z), performing a voxel-wise subtraction between the original subject (target in each registration) and the registration result. To compute D(x,y,z), the results of each registration method were normalized due to the vastly different intensities that may appear in the T1w images. We chose to normalize to the CSF, because WM and GM may differ in T1w images from healthy and from MS subjects. Therefore, we considered the ratio: intensity voxel divided by mean of the CSF. Furthermore, we quantified the mean of D(x,y,z), MeanD, which provides a quantitative measure of the goodness of the registration methods, where the smaller MeanD is, the more accurate the registration. Note that to compute the difference we always used the absolute values.

In order to assess the registration performance at tissue-class level, MeanD was computed for the whole brain as well as for WM and GM masks. The whole brain mask was obtained using the Brain Extraction Tool (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/BET) (Smith, 2002) while the tissue class segmentation was performed using the SPM8 toolbox (http://www.fil.ion.ucl.ac.uk/spm) (Ashburner and Friston, 2005). However, as the result of the segmentation is a probability map per tissue type, we performed a maximum likelihood operation to identify voxels belonging to masks of GM and WM, which were computed by assigning each voxel the class of maximum likelihood (probability threshold 0.5).

To assess whether MeanD values were significantly different when calculated for each registration method, the Bonferroni correction test (Holm, 1979) was performed to counteract multiple comparisons. To analyze the statistical significance of these comparisons, we carried out a one-way ANOVA to compare the performance of the different methods, considering as a null hypothesis (H0) that the means are equal with a 5% confidence level (α = 0.05).

Results

Data processed in the pre-processing section were then used for all the registration experiments, with original healthy subjects (10 cases) as target and simulated MS subjects (100 cases) as source. We repeated these experiments with the MS subjects in which lesions had first been filled, before simulation. Figure 6 shows an example of the images through the various steps for SC registration (original, simulated and registered).

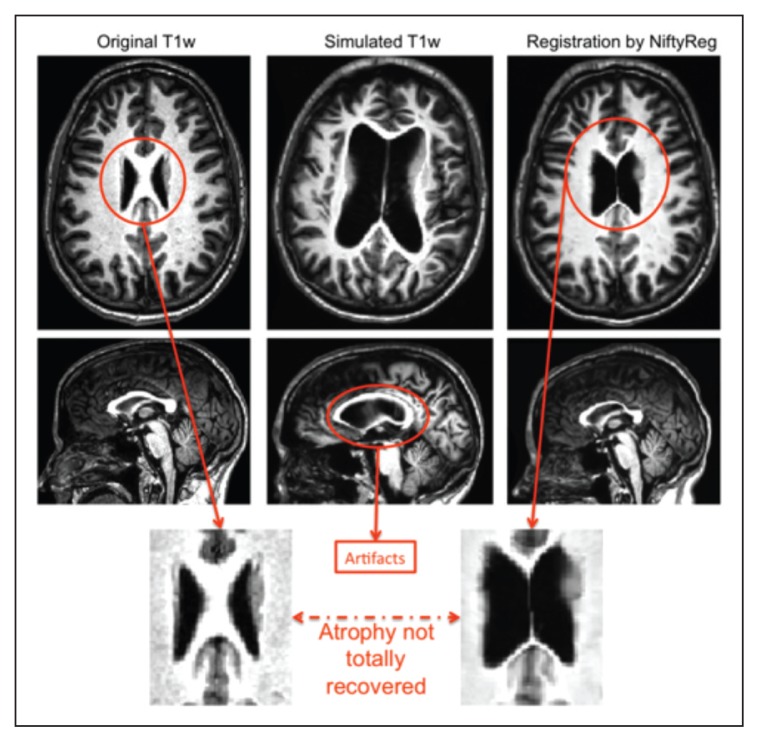
Figure 6.

Figure 6

Open in a new tab

Original atrophied and registered T1w images.

The bottom row illustrates the problem of the registration back to the original healthy subject, using a single-channel registration pipeline, where the software is not able to recover the ventricles.

Checkerboard evaluation

The first assessment was based on qualitative analyses using the checkerboard images to compare how the structures were aligned with each other for each combination of images: i) T1w result vs T1w target; ii) FA result vs FA target; and iii) T1w result vs FA result. This was performed for SC, MC and T1w-based registrations (as summarized in figure 4). In this stage, as well as comparing against the target, we checked whether the registration process kept the original alignment between T1w and FA for each registration approach.

In particular, we carefully inspected the alignment of the corpus callosum, which is very close to the ventricles, and can therefore be affected by their large enlargement, and can undergo thinning as a result of pathology but also of large image processing deformations, especially when registered to a healthy brain. Also, we assessed the cortical regions because their low FA values make them challenging to register properly with T1w. Figure 7 provides an illustration of the combined results for each registration strategy and each modality for one of the simulated MS datasets, with large deformations due to severe simulated atrophy.

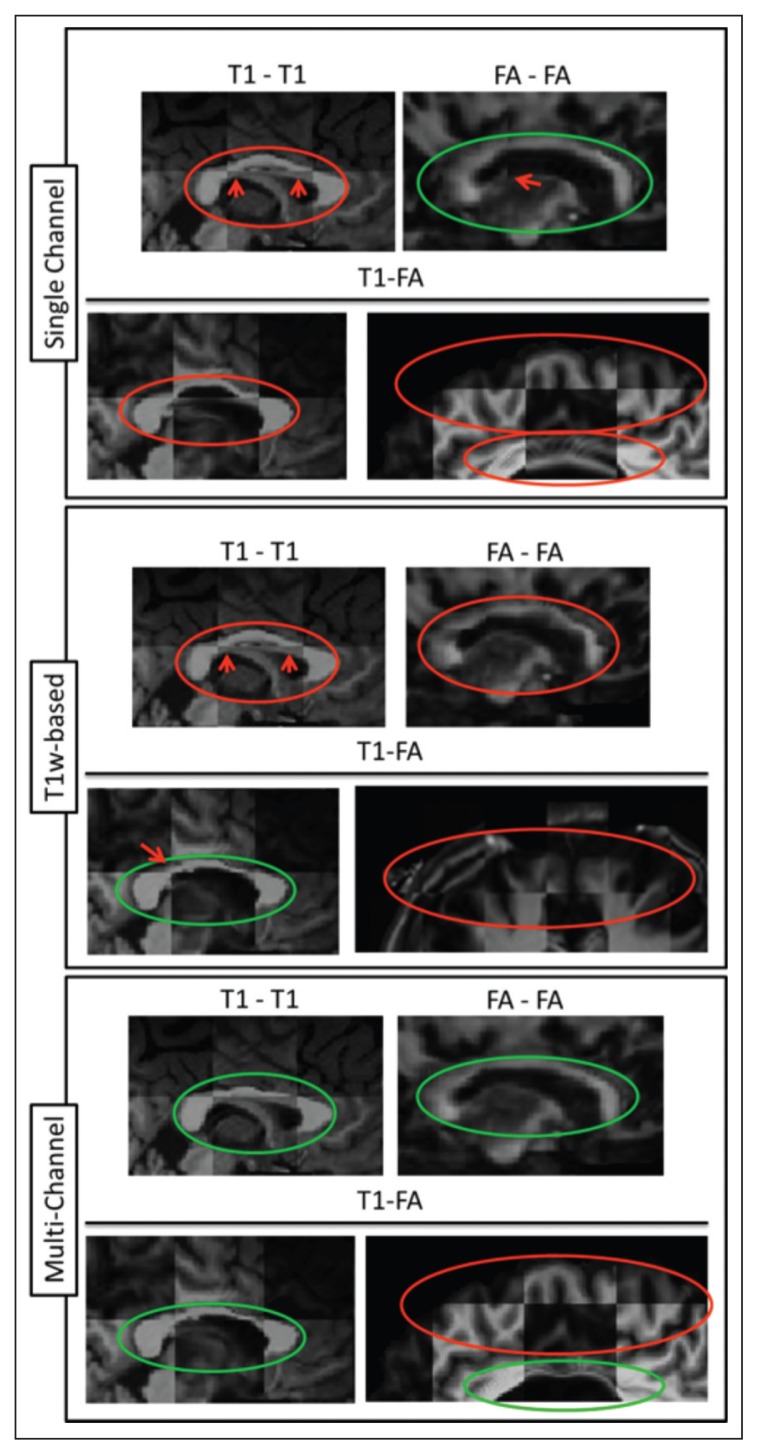
Figure 7.

Figure 7

Open in a new tab

Checkerboard images of all the combinations for the three strategies (SC, T1w-based and MC).

The top row of each strategy corresponds to T1w-T1w and FA-FA comparisons separately while the second row corresponds to comparison of T1w-FA results. Orange circles show regions of poor registration, whereas green circles show regions of accurate registration.

On visual inspection we observed that:

  1. When employing the SC approach in the presence of a high level of atrophy the registration cannot recover structures like the corpus callosum and therefore the alignment with the target image is not accurate. Moreover, poor structure alignment is also observed when comparing the co-alignment of MST1w,RegSC and MSFA,RegSC in the target space, e.g. the FA WM structures do not match the WM structures on the T1w image.

  2. When employing the T1w-based registration approach, similar results are noticeable when comparing the results of the registration between the same modality source and target images, e.g. MSFA,RegT1w-based and HSFA or MST1w,RegT1w-based. As expected, though, the co-alignment of T1w and FA images in the target space, e.g. of MSFA,RegT1w-based with MST1w,RegT1w-based, is better due to their initial co-registration.

  3. Finally, when employing the MC approach the corpus callosum of the registered images, MSFA,RegMC and MST1w,RegMC, is better aligned with the corresponding target images, HSFA and HST1w, compared to what is observed with the SC method, for both T1w and FA data. Due to the inherent co-registration of MSFA,RegMC and MST1w,RegMC, structures are well matched even across modalities.

Difference image evaluation

The difference image between MST1w,Regj and HST1w was computed for all simulated data and for j = SC, MC (Fig. 8), while the difference image for FA was computed for j = SC, T1w-based, MC (Fig. 8).

Figure 8.

Figure 8

Open in a new tab

Difference image of T1w and FA from SC, MC and T1w-based approach.

Difference of T1w images from a) SC and b) MC results. Difference between FA images for c) SC registration, d) T1w-based approach, and e) MC registration. The brighter the voxels the greater the differences. All the images are from the same subject at the same location where first row are axial and second row are sagittal image orientations. The range of intensities has been optimized for better visualization of the differences (voxel values range in all the images from 0 to 1).

On visual inspection, SC registration was associated with higher intensity differences between registered and target T1w images in the corpus callosum and periventricular areas. T1w-based registration was associated with higher intensity differences for FA images. The MC approach provided the lowest intensity differences for both T1w and FA images. This was confirmed in all the simulated data and registration tests.

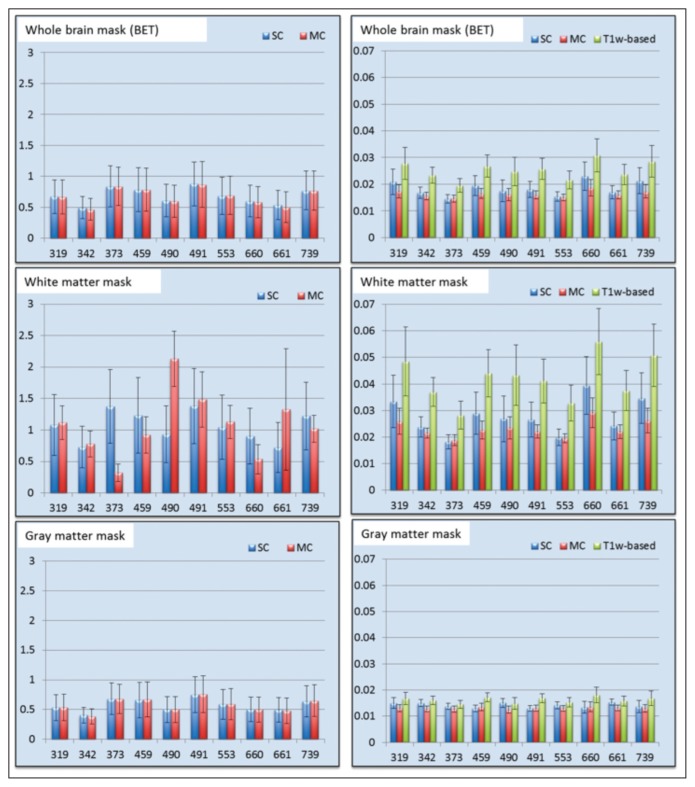
To corroborate the visual results, we compared the MeanD image between the different registration methodsas shown in figure 9. SC and MC registrations produced similar results on T1w over the whole brain or the GM mask. No consistent pattern was observed on the T1w registrations of the WM mask. For registration of FA images, the MC approach presented lower mean difference values for all cases (whole brain, WM mask and GM mask; Fig. 9).

Figure 9.

Figure 9

Open in a new tab

Bar plot of the mean intensity of the difference image for the T1w images on the left and FA images on the right.

Values for each patient (319, 342, ... 739) are the mean of the 10 MS simulations; the error bar illustrates the standard deviation.

Last, we assessed whether the MeanD scores differed between the SC and MC registrations. Analyzing the Bonferroni test, we observed that for T1w images, SC and MC approaches showed no significant differences. Instead, for FA images, the MC approach led to significantly lower MeanD for whole brain, GM and WM masks (p<<0.01). This can be explained by the fact that the T1w image provides information for example in GM regions where FA presents very low contrast. We conclude that MC registration provides better alignment to a target as well as better T1w and FA co-alignment in target space.

Simulated images with lesions filled

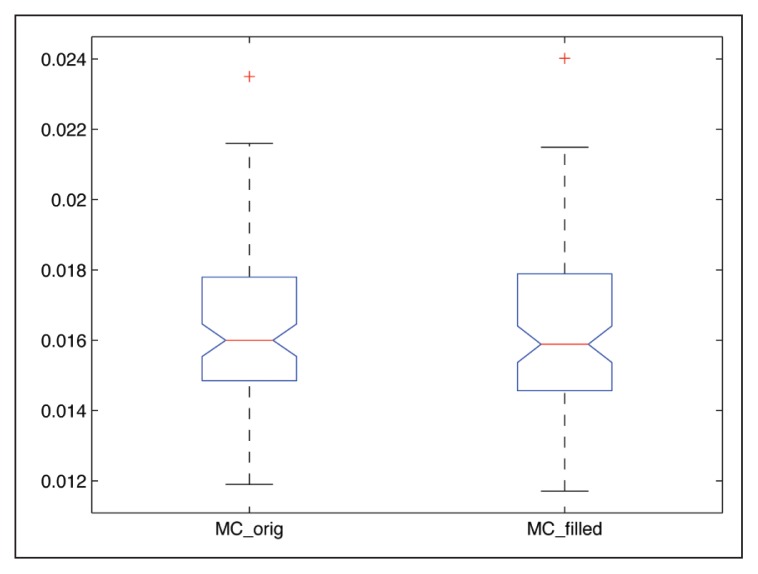
Similarly to the results presented before, the registration strategies for both T1w and FA images followed a similar trend when registering the simulated images with the MS lesions-filled T1w dataset, obtaining better FA and T1w image alignment with MC. We performed statistical analysis using the Bonferroni test obtaining significant differences between strategies (p<<0.01). On the other hand, we also performed a balanced one-way ANOVA analysis individually for each registration strategy (SC, T1w-based and MC) between simulated images with lesions and simulated images with lesions filled. The p-values obtained in all cases did not suggest to reject the null hypothesis (p>>0.05), confirming that the effect of the MS lesions was not significant in the proposed atrophy simulation. Figure 10 illustrates the results obtained for the MSFA,RegMC when using both the original and lesion-filled simulations.

Figure 10.

Figure 10

Open in a new tab

Boxplot of the MC registration results when using the original and lesion-filled simulations.

Differences are computed between the MSFA, RegMC result image and the original HSFA.

Discussion

Registration of the individual T1w images to the target space showed similar performances between the mono-modal SC, T1w-based and MC approaches. This may relate to the well-defined tissue contrast between GM and WM on these images, but could also be due to preserved signal in GM, allowing the SC approach to perform well. On the FA maps, however, both qualitative and quantitative evaluations demonstrated significantly better registration when the MC approach was used. This was apparent on whole brain, GM and WM alignment. It was also reflected in the alignment of FA with T1w data after registration, which provided substantially greater accuracy when using the MC strategy. We also demonstrated that MC, compared to SC and T1w-based, offers improved results of T1w and FA co-registration in common space; even though both MC and T1w-based strategies rely on initial co-registration of FA and T1w in native space, the final direct alignment, i.e. T1w and FA alignment, in common space was significantly better for MC techniques.

An important point to consider in this experimental analysis is that the SC approach provided good co-registration between the input image and the target space. This may not be the case in real patient data, where it is well known that WM and GM contain lesions, causing localized and sometimes diffuse intensity changes across the whole brain. In our simulations we evaluated the effect of atrophy, but not focal intensity changes, such as the WM lesions that are characteristic of MS. The rationale for our choice to concentrate on atrophy was highlighted in the introduction and rested on the fact that the influence of WM lesions on registration outcomes is limited when it comes to the whole brain (Roura et al., 2012). This was also shown when repeating the experiments using simulations created using previously lesion-filled T1w images from MS subjects. Moreover, strategies to cope with lesions, such as inpainting, have been proposed and validated only for the T1w modality (Sdika and Pelletier, 2009; Chard et al., 2010; Battaglini et al., 2012), while they still need to be developed for DTI-derived indices such as FA where local properties of signal intensities are far from uniform even within a specific tissue type. Furthermore, it is important to consider standard target spaces such as the MNI atlas or a group-specific atlas built with MS patient data, which could simplify registration of patient scans.

Despite the clear improvements presented in this work, there are some limitations that should be addressed in future studies. For instance, we generated simulated atrophy by registering T1w images of healthy controls to T1w images of MS patients and then we applied the same transformation to FA images of the same subjects. This procedure ensured that the FA and T1w images were deformed equally, but it did not accurately reproduce the presence of MS lesions. Previous evaluations, though, confirmed that lesions have minimal effect on MC (T1w and FA) registration to a common space (Battaglini et al., 2012; Roura et al., 2012), therefore justifying the use of the proposed strategy as a simple means of atrophy generation without having to explicitly consider MS lesions. Following previous work presented by Daga et al. (2011), we focused on the evaluation of an MC pipeline applied to T1w and FA images. However, it is well known that other indices from the DTI matrix or even other imaging modalities could provide complementary information and could also be used for the MC registration pipeline.

In conclusion, this paper has presented an MC registration approach for moving T1w and FA images to a healthy control target space. The registration pipeline was tested in people with MS with atrophy and marked ventricular enlargement. For the experimental evaluation, we proposed our own atrophy generation framework based on deforming healthy subjects by registering them to real MS patients with MS lesions and atrophy. We created 100 simulated atrophy images from original healthy subjects who were registered to the patients. A comparison between SC and MC registration with qualitative and quantitative analysis has been presented. We have shown that for FA, more than for T1w images, MC registration offers significant improvements in alignment accuracy over SC or T1w approaches. Studies registering FA maps to common space should consider using MC registrations in preference to SC or T1w-based pipelines.

Acknowledgments

E. Roura holds a UdG BR-GR13 grant. The International Federation of MS (Du Pré Grant 2012) granted E. Roura for a research stay in IoN/UCL. Declan Chard has received research support from the MS Society of Great Britain and Northern Ireland, and the UCLH/UCL NIHR Biomedical Research Centre. This work has also been partially supported by “La Fundació la Marató de TV3” and by Retos de Investigación TIN2014-55710-R.

References

  1. Archip N, Clatz O, Whalen S, et al. Non-rigid alignment of pre-operative MRI, fMRI, and DT-MRI with intra-operative MRI for enhanced visualization and navigation in image-guided neurosurgery. Neuroimage. 2007;35:609–624. doi: 10.1016/j.neuroimage.2006.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ashburner j, Friston Kj. Unified segmentation. Neuroimage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
  3. Ashtari F, Bahreini SA, Zahendnasab H. Co-occurrence of multiple sclerosis and Thomsen’s myotonia: a report of two cases. Funct Neurol. 2014;29:269–271. [PMC free article] [PubMed] [Google Scholar]
  4. Avants BB, Duda jT, Zhang H, et al. Multivariate normalization with symmetric diffeomorphisms for multivariate studies. Med Image Comput Comput Assist Interv. 2007;10:359–366. doi: 10.1007/978-3-540-75757-3_44. [DOI] [PubMed] [Google Scholar]
  5. Baglieri A, Marino MA, Morabito R, et al. Differences between conventional and non-conventional MRI techniques in Parkinson’s disease. Funct Neurol. 2013;28:73–82. doi: 10.11138/FNeur/2013.28.2.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Battaglini M, jenkinson M, De Stefano N. Evaluating and reducing the impact of white matter lesions on brain volume measurements. Hum Brain Mapp. 2012;33:2062–2071. doi: 10.1002/hbm.21344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Camara O, Schweiger M, Scahill RI, et al. Phenomenological model of diffuse global and regional atrophy using finite-element methods. IEEE Trans Med Imaging. 2006;25:1417–1430. doi: 10.1109/TMI.2006.880588. [DOI] [PubMed] [Google Scholar]
  8. Ceccarelli A, jackson jS, Tauhid S, et al. The impact of lesion in-painting and registration methods on voxel-based morphometry in detecting regional cerebral gray matter atrophy in multiple sclerosis. AjNR Am j Neuroradiol. 2012;33:1579–1585. doi: 10.3174/ajnr.A3083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chard DT, jackson jS, Miller DH, et al. Reducing the impact of white matter lesions on automated measures of brain gray and white matter volumes. j Magn Reson Imaging. 2010;32:223–228. doi: 10.1002/jmri.22214. [DOI] [PubMed] [Google Scholar]
  10. Daga P, Winston G, Modat M, et al. Integrating structural and diffusion MR information for optic radiation localisation in focal epilepsy patients. Proc IEEE Int Symp Biomed Imaging. 20112011:353–356. [Google Scholar]
  11. Derakhshan M, Caramanos Z, Giacomini PS, et al. Evaluation of automated techniques for the quantification of grey matter atrophy in patients with multiple sclerosis. Neuroimage. 2010;52:1261–1267. doi: 10.1016/j.neuroimage.2010.05.029. [DOI] [PubMed] [Google Scholar]
  12. Díez y, Oliver A, Lladó X, et al. Revisiting intensity-based image registration applied to mammography. IEEE Trans Inf Technol Biomed. 2011;15:716–725. doi: 10.1109/TITB.2011.2151199. [DOI] [PubMed] [Google Scholar]
  13. Geng X, Styner M, Gupta A, et al. Multi-contrast diffusion tensor image registration with structural MRI. Proc IEEE Int Symp Biomed Imaging. 20122012:684–687. [Google Scholar]
  14. Goruku y, Albayram S, Balci B, et al. Cerebrospinal fluid flow dynamics in patients with multiple sclerosis: a phase contrast magnetic resonance study. Funct Neurol. 2011;26:215–222. [PMC free article] [PubMed] [Google Scholar]
  15. Guimond A, Guttmann CRG, Warfield SK, et al. Deformable registration of DT-MRI data based on transformation invariant tensor characteristics. Proc IEEE Int Symp Biomed Imaging. 20022002:1–4. [Google Scholar]
  16. Guimond A, Roche A, Ayache N, et al. Three-dimensional multimodal brain warping using the demons algorithm and adaptive intensity corrections. IEEE Trans Med Imaging. 2001;20:58–69. doi: 10.1109/42.906425. [DOI] [PubMed] [Google Scholar]
  17. Holm S. A Simple Sequentially Rejective Multiple Test Procedure. Scand Stat Theory Appl. 1979;6:65–70. [Google Scholar]
  18. Karaçali B, Davatzikos C. Simulation of tissue atrophy using a topology preserving transformation model. IEEE Trans Med Imaging. 2006;25:649–652. doi: 10.1109/TMI.2006.873221. [DOI] [PubMed] [Google Scholar]
  19. Klein S, Staring M, Murphy K, et al. Elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imaging. 2010;29:196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
  20. Lladó X, Ganiler O, Oliver A, et al. Automated detection of multiple sclerosis lesions in serial brain MRI. Neuroradiology. 2012;54:787–807. doi: 10.1007/s00234-011-0992-6. [DOI] [PubMed] [Google Scholar]
  21. Miller MI, Christensen GE, Amit y, et al. A mathematical textbook of deformable neuroanatomies. Proc Natl Acad Sci USA. 1993;90:11944–11948. doi: 10.1073/pnas.90.24.11944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Modat M, Ridgway G, Hawkes D, et al. Nonrigid registration with differential bias correction using normalised mutual information. Proc IEEE Int Symp Biomed Imaging. 2010a2010:356–359. [Google Scholar]
  23. Modat M, Ridgway GR, Taylor ZA, et al. Fast free-form deformation using graphics processing units. Computer Methods Programs Biomed. 2010b;98:278–284. doi: 10.1016/j.cmpb.2009.09.002. [DOI] [PubMed] [Google Scholar]
  24. Muhlert N, Sethi V, Schneider T, et al. Diffusion MRI-based cortical complexity alterations associated with executive function in multiple sclerosis. j Magn Reson Imaging. 2013;38:54–63. doi: 10.1002/jmri.23970. [DOI] [PubMed] [Google Scholar]
  25. Ourselin S, Stefanescu R, Pennec X. Robust registration of multi-modal images: towards real-time clinical applications. In: Dohi T, Kikinis R, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2002. Berlin Heidelberg: Springer; 2002. pp. 140–147. [Google Scholar]
  26. Ourselin S, Roche A, Subsol G, et al. Reconstructing a 3D structure from serial histological sections. Image and Vision Computing. 2001;19:25–31. [Google Scholar]
  27. Ourselin S, Roche A, Prima S, et al. Block matching: a general framework to improve robustness of rigid registration of medical images. In: Delp SL, DiGioia AM, jaramaz B, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2000. Berlin Heidelberg: Springer; 2000. pp. 557–566. [Google Scholar]
  28. Park Hj, Kubicki M, Shenton ME, et al. Spatial normalization of diffusion tensor MRI using multiple channels. Neuroimage. 2003;20:1995–2009. doi: 10.1016/j.neuroimage.2003.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Roura E, Schneider T, Daga P, et al. Multi-channel registration of FA and T1-weighted images to standard space: patients with multiple sclerosis. ISMRM (abstract 2525) 2012. ( http://discovery.ucl.ac.uk/1410585)
  30. Rueckert D, Frangi AF, Schnabel jA. Automatic construction of 3-D statistical deformation models using non-rigid registration. IEEE Trans Med Imaging. 2003;22:1014–1025. doi: 10.1109/TMI.2003.815865. [DOI] [PubMed] [Google Scholar]
  31. Rueckert D, Sonoda LI, Hayes C, et al. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans Med Imaging. 1999;18:712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
  32. Sdika M, Pelletier D. Nonrigid registration of multiple sclerosis brain images using lesion inpainting for morphometry or lesion mapping. Hum Brain Mapp. 2009;30:1060–1067. doi: 10.1002/hbm.20566. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Studholme C. Dense feature deformation morphometry: incorporating DTI data into conventional MRI morphometry. Med Image Anal. 2008;12:742–751. doi: 10.1016/j.media.2008.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Studholme C, Cardenas V, Song E, et al. Accurate tem-plate-based correction of brain mri intensity distortion with application to dementia and aging. IEEE Trans Med Imaging. 2004;23:99–110. doi: 10.1109/TMI.2003.820029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Thirion jP. Image matching as a diffusion process: an analogy with Maxwell’s demons. Med Image Anal. 1998;2:243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
  37. Thirion jP. Non-rigid matching using demons. Proceedings of the 1996 Conference on Computer Vision and Pattern Recognition. 1996:245–251. doi: 10.1109/CVPR.1996.517081. [DOI] [Google Scholar]
  38. Vercauteren T, Pennec X, Perchant A, et al. Symmetric log-domain diffeomorphic Registration: a demons-based approach. Med Image Comput Comput Assist Interv. 2008;11:754–761. doi: 10.1007/978-3-540-85988-8_90. [DOI] [PubMed] [Google Scholar]
  39. Vercauteren T, Pennec X, Perchant A, et al. Non-parametric diffeomorphic image registration with the demons algorithm. Med Image Comput Comput Assist Interv. 2007;10:319–326. doi: 10.1007/978-3-540-75759-7_39. [DOI] [PubMed] [Google Scholar]
  40. Walimuni IS, Abid H, Hasan KM. A computational framework to quantify tissue microstructural integrity using conventional MRI macrostructural volumetry. Comput Biol Med. 2011;41:1073–1081. doi: 10.1016/j.compbiomed.2010.10.009. [DOI] [PubMed] [Google Scholar]
  41. Wells WM, Viola P, Atsumi H, et al. Multi-modal volume registration by maximization of mutual information. Med Image Anal. 1996;1:35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]

Articles from Functional Neurology are provided here courtesy of CIC Edizioni Internazionali

RESOURCES