Quantitative evaluation of positive ϕ angle propensity in flexible regions of proteins from three-bond J couplings

Abstract

³J_HNHα and ³J_C′C′ couplings can be readily measured in isotopically enriched proteins and were shown to contain precise information on the backbone torsion angles, ϕ, sampled in disordered regions of proteins. However, quantitative interpretation of these couplings required the population of conformers with positive ϕ angles to be very small. Here, we demonstrate that this restriction can be removed by measurement of ³J_C′Hα values. Even though the functional forms of the ³J_C′Hα and ³J_HNHα Karplus equations are the same, large differences in their coefficients enable accurate determination of the fraction of time that positive ϕ angles are sampled. A four-dimensional triple resonance HACANH[C′] E.COSY experiment is introduced to simultaneously measure ³J_C′Hα and ³J_HNC′ in the typically very congested spectra of disordered proteins. High resolution in these spectra is obtained by non-uniform sampling (in the 0.1-0.5% range). Application to the intrinsically disordered protein α-synuclein shows that while most residues have close-to-zero positive ϕ angle populations, up to 16% positive ϕ population is observed for Asn residues. Positive ϕ angle populations determined with the new approach agree closely with consensus values from protein coil libraries and prior analysis of a large set of other NMR parameters. The combination of ³J_HNC′ and ³J_C′C′ provides information about the amplitude of ϕ angle dynamics.

1 Introduction

A survey of experimentally determined protein structures contained in the protein structure databank (PDB) shows that, with the exception of Gly, the vast majority of residues adopt negative values for the backbone torsion angle, ϕ. Well-ordered residues with positive ϕ angles are mostly restricted to type I′, type II, and type II′ tight β-turns and helix-terminating C-cap motifs. Transient occupation of conformations where one or more residues adopt positive ϕ angles may be of high functional relevance, and has been implicated in substrate recognition.^1,2,3 Moreover, molecular dynamics simulations on folded proteins indicate that peptide plane flips associated with a change in the sign of ϕ are energetically feasible,^4,5 suggesting that transient formation of conformations with a positive ϕ backbone torsion angle could be more common than implied by the analysis of static PDB X-ray structures. Adoption of positive ϕ values has been proposed to be particularly relevant in intrinsically disordered proteins (IDPs) and intrinsically disordered regions (IDRs) of amyloidogenic proteins, where they may impact the kinetics of fibril formation.^6,7

Analysis of chemical shifts and other NMR parameters of IDPs and IDRs suggests low but non-vanishing populations of positive ϕ angle conformers,^8,9,10,11,12 mostly following what is seen in statistical coil libraries extracted from the PDB.^13,14 Traditionally, the primary markers for positive ϕ conformations are ¹J_CαHα, which is at a minimum in the α_L region of Ramachandran space,¹⁵ and strong intraresidue H^N-H^α NOEs.¹⁶ However, neither of these parameters provides reliable fractional populations of the positive ϕ conformations as the variations in their values associated with negative ϕ angles usually are large and not very well defined. The Karplus equation relating ³J_C′Hα to ϕ indicates that positive ϕ angles, associated with a trans C′-N-C^α-H^α arrangement, have much larger ³J_C′Hα values than those observed for negative ϕ angles.¹⁷ Here, we demonstrate that ³J_C′Hα, in particular when used in conjunction with ³J_HNHα and ³J_C′C′, provides a precise quantitative measure for the fractional positive ϕ population of any given residue. We demonstrate that, even for the typically very poorly resolved spectral regions of disordered proteins, nearly complete sets of ³J_C′Hα values can be obtained by recording the HACANH[C′] E.COSY spectrum in a four-dimensional (4D) fashion. This experiment then also yields ³J_HNC′, providing yet another parameter to define the ϕ angle distribution. Relatively recently introduced non-uniform sampling (NUS) strategies permit the recording of 4D spectra at very high resolution and in relatively limited amounts of measurement time.^18,19,20 This approach is used in our study, and the accuracy at which J couplings can be extracted from such NUS-reconstructed spectra is shown to scale approximately inversely with the square root of the sparsity of the acquired data. Thus, the accuracy depends inversely on the square root of measurement time, following the same rules as in fully sampled NMR spectra.

2 Experimental Section

2.1 NMR sample preparation

Uniformly ¹³C/¹⁵N-enriched, N-terminally acetylated²¹ wild-type α-synuclein (aS) protein was expressed and purified as described previously.²² The NMR sample contained 0.6 mM aS in 20 mM sodium phosphate, pH 6.0, 50 mM NaCl, and 5% D₂O. The NMR sample of the third IgG-binding domain of protein G (GB3, 1.2 mM, uniformly ¹³C/¹⁵N-enriched) was prepared in 50 mM sodium phosphate, pH 6.5, 50 mM NaCl, and 5% D₂O. The NMR sample of uniformly ¹³C/¹⁵N-enriched ubiquitin (2.8 mM) was prepared in 20 mM imidazole buffer, pH 6.0, containing 7% D₂O.

2.2 NMR measurements

The 4D HACANH[C′] E.COSY spectrum of α-synuclein was recorded using the pulse sequence of Fig. 1, using a Bruker Avance III 600-MHz spectrometer equipped with a TCI cryogenic probe and a z-axis gradient coil. Non-uniform sampling with a sparsity of 0.55% was employed in order to achieve high resolution and thereby the most reliable peak positions and J coupling measurements, while keeping the total measuring time restricted to about three days. The time domain matrix consisted of 80* × 62* × 250* × 1024* complex data points, or acquisition times of 112 ms (t₁, ¹H^α), 28 ms (t₂, ¹³C^α), 179 ms (t₃, ¹⁵N), and 102 ms (t₄, ¹H^N). The ¹H^α, ¹³C^α and ¹⁵N carrier frequencies were set at 4.2, 56, and 118 ppm, respectively and 4 scans per FID were recorded. Additionally, 3D HA(CA)NH[C′] E.COSY spectra were recorded for ubiquitin and GB3, again using the pulse scheme of Fig. 1, but keeping the ¹³C^α evolution time t₂ = 0. The 3D HN(COCO)NH pulse sequence²³ was used at 900 MHz using a 2.5% NUS scheme, in order to obtain additional ³J_C′C′ coupling values for α-synuclein residues that were previously inaccessible due to resonance overlap. The new 3D HN(COCO)NH spectrum was recorded with 200 ms acquisition times in both the t₁ (¹⁵N) and t₂ (¹⁵N) dimensions.

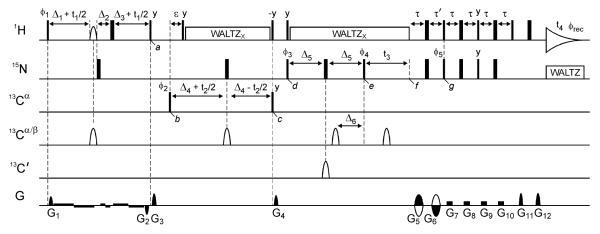
Fig. 1.

Pulse scheme of the HACANH[C′] E.COSY experiment. Narrow and wide lines indicate non-selective 90° and 180° pulses, respectively, except for the 90° pulses on ¹³C^α that have their duration adjusted to have no excitation of ¹³C'. ¹H decoupling (γ_HB₁ = 3.1 kHz; phase x) is applied using the WALTZ16 scheme.³⁸ The carrier frequencies for ¹H, ¹⁵N, ¹³C^α, ¹³C^α/β and ¹³C' are 4.7, 119, 56, 46 and 176 ppm, respectively. The ¹H^α shaped pulse is of the ReBURP-type and has a duration of 3.5ms. The ¹³C' shaped pulse is of the hyperbolic-secant type and has a duration of 2 ms. The ¹³C^α/β shaped pulses are G3-shaped⁵³ with a duration of 350μs, except for the pulse during ¹³C^α evolution (t₂) which is of the ReBURP-type⁵⁴ and has a duration of 420 μs. Note that the durations of all shaped pulses presented here are for measurements at 600 MHz ¹H frequency; these values scale inversely with field strength and should be adjusted accordingly when experiments are recorded at a field strength that differs from 14.1 T. Delays: ε = 2.5 ms, τ = 2.6 ms, τ' = τ + t₃(0), Δ₁ = 1.7 ms - 0.92 × P_rb/2 where P_rb is the duration of the ¹H^α ReBURP pulse and the scaling factor of 0.92 for ¹J_CαHα dephasing was measured experimentally for a pair of centered ¹H ReBURP and ¹³C G3 shaped pulses with a duration ratio of 10:1, Δ₂ = Δ₁+Δ₃, Δ₃ = 0.17 ms, Δ₄ = 14 ms, Δ₅ = 15 ms and Δ₆ = 14 ms. All pulse phases are x, unless specified. Phase cycling: ϕ₁ = x; ϕ₂ = x,-x; ϕ₃ = x,x,-x,-x; ϕ₄ = y,-y; ϕ₅ = x; and ϕ_rec = x,-x,-x,x. The gradient pulses G₁-G₁₂ (z axis) have strengths of 7, −7, 30.1, 28.7, 25.9, 25.9, 3.5, 3.5, 4.9, 4.9, 25.9 and 25.9 G/cm, with durations of 0.05, 0.05, 2, 1.3, 1, 2, 2.4, 2.4, 2.4, 2.4, 0.2 and 0.503 ms, respectively. Weak gradients (0.35 G/cm) with a polarity indicated in the figure were applied during ¹H^α evolution (t₁) to minimize radiation damping of the solvent signal. Quadrature detection in the t₁ and t₂ dimensions was achieved by increasing ϕ₁ and ϕ₂, respectively, in the regular States-TPPI manner. Quadrature detection in the t₃ dimension is obtained by the Rance-Kay method,³⁷ inverting G₅, G₆ and ϕ₅.

For NUS processing of the HACANH[C′] E.COSY and HN(COCO)NH spectra, we used the in-house written SMILE routine (Ying et al., unpublished), incorporated in the data processing software package NMRPipe.²⁴ The digital resolution of the final 4D spectra was 1.4 Hz (¹H^α, F₁), 8.7 Hz (¹³C^α, F₂), 1.4 Hz (¹⁵N, F₃) and 2.4 Hz (¹H^N, F₄) for aS, and 1.0 (¹⁵N, F₁), 1.0 (¹⁵N, F₂) and 2.4 Hz (¹H^N, F₃) for the α-synuclein HN(COCO)NH spectrum. Peak picking and spectrum analysis was carried out with the programs NMRPipe and SPARKY.²⁵

2.3 Coil Database

For all comparisons with backbone torsion angle distributions expected in disordered regions of proteins we used the recently introduced coil library of Mantsyzov et al. which consists of all longer (> 3 residue) segments that lack intramolecular H-bonding in the PDB.¹⁴ This library differs from the widely used Fitzkee coil library¹³ mostly by the absence of tight β-turns and was developed as a reference for the MERA program,¹⁴ which aims to provide a residue-specific ϕ/ψ distribution of IDPs and IDRs.

3 Measurement of ³J_C'Hα from HACANH[C′] E.COSY

The exclusive-COSY (E.COSY) principle provides a convenient and accurate method for measurement of unresolved scalar coupling, J_AB, between a pair of nuclear spins A and B. E.COSY experiments require the presence of a third nuclear spin, C, that has a large, resolvable coupling to spin A and whose chemical shift can be correlated in a multi-dimensional NMR experiment with spin B.^26,27 Numerous E.COSY experiments have been introduced over the past few decades that permit the measurement of virtually every possible type of three-bond ¹H-¹H and heteronuclear J coupling in isotopically enriched proteins.^{17,28,29,30,31,32} A condition for accurate measurement of the J_AB coupling from a B-C cross peak is that the spin-state of the passive spin, A, remains unperturbed. A reduction in the apparent coupling will result if the longitudinal relaxation time of spin A is insufficiently long relative to the delay durations used in the pulse scheme.^33,17 So, on the one hand it is important to select from the two spins, A and B, the spin with the longest T₁ relaxation time to function as the passive, unperturbed spin. On the other hand, as the J_AB displacement is read out from the relative displacement in resonance frequency of spin B when monitoring the components of the B-C cross peak, it is important that the line width of spin B is narrow. For measurement of ³J_C′Hα by an E.COSY experiment, the choice is whether the ¹³C′ or the ¹H^α should act as the passive spin. The ¹³C′ T₁ relaxation times for IDPs at 600 MHz ¹H frequency and above are typically longer than 1 s, which is considerably longer than those of ¹H^α in ¹³C-enriched proteins, thus favoring ¹³C′ to be the passive spin. On the other hand, the transverse relaxation time of ¹³C′ is longer than for ¹H^α, favoring it to be the actively detected spin because it potentially offers higher frequency resolution. In our experiments, we have selected ¹³C′ to be the passive spin, but enhance the spectral resolution of the ¹H^α spin by homonuclear decoupling it from ¹H^N and ¹H^β in a band-selective manner.^34,35

3.1 Description of the pulse scheme

We here used the HACANH[C′] E.COSY pulse scheme (Fig. 1) for measurement of the ³J_C′Hα and ³J_HNC′ couplings. This triple resonance pulse scheme transfers magnetization in a unidirectional fashion from ¹H^α via ¹³C^α and ¹⁵N to ¹H^N and is similar in design to the early H(CA)NNH experiment,³⁶ but it lacks ¹³C′ decoupling and it uses gradient-enhanced transfer from ¹⁵N to ¹H for sensitivity enhancement and improved solvent signal suppression.³⁷ Other small but important differences will be discussed below. To minimize resonance overlap in crowded IDP spectra, we carry out the experiments in a 4D fashion, with evolution of ¹H^α, ¹³C^α and ¹⁵N chemical shifts in the indirect dimensions, and direct detection of ¹H^N. The ¹³C^α evolution period can be omitted if the measurement is carried out as a 3D experiment, potentially useful for small proteins such as ubiquitin and GB3, where resonance overlap is less of a concern. However, this will remove the possibility to also measure ³J_HNC′ from such a spectrum.

During the (t₁, ¹H^α) evolution period, a ¹H^α band-selective pulse is paired with a non-selective ¹H 180° pulse (separated by the short Δ₂ delay, Fig. 1) to effectively invert all ¹H spins other than ¹H^α, thereby removing ¹H-¹H J-dephasing during t₁ evolution and enhancing the attainable ¹H^α spectral resolution. Note that ¹H^α-¹H^β J-dephasing for Ser and Thr residues is not refocused during t₁ because their ¹H^β resonate within the bandwidth that is inverted by the ¹H^α band-selective pulse. Similarly, the geminal ¹H^α-¹H^α dephasing remains active for Gly residues. Evolution of ¹J_CαHα coupling during t₁ is adjusted to be active for ~3.4 ms, with most of the ¹J_CαHα dephasing actually taking place during the pair of simultaneously applied band-selective ¹H^α and ¹³C^α pulses. As indicated in Figure 1, very weak, antiphase gradients are also applied during the t₁ evolution period to prevent radiation damping of the ¹H₂O magnetization, which otherwise would rotate ¹H^α spins that resonate under the water resonance back to the z axis, making them effectively disappear from the spectrum. The antiphase G₁/G₂ gradient pulse pair serves to remove the effect of imperfections in the band-selective and non-selective 180° ¹H pulses, applied during t₁, while also eliminating any transverse ¹³C magnetization. At time point a, the relevant, selected magnetization then is described by 2C_z^α(i)H_z^α(i) cos(δ_Hαt₁) (π²J_HαC′t₁) cos(π³J_HαC′t₁), where δ_Hα is the ¹H^α chemical shift frequency, and ²J_HαC′ and ³J_HαC′ are the two- and three-bond J couplings from ¹H^α to the intraresidue and preceding ¹³C′, respectively.

During the subsequent (t₂, ¹³C^α) constant-time evolution period between time points b and c, ¹J_CαN and ²J_CαN are active for the full constant-time duration 2Δ₄, and ¹J_CαHα rephasing is active for the duration ε, which is set to a compromise value (2.5 ms) that enables magnetization transfer to occur for both ¹³C^α methine and methylene (Gly) groups. The constant-time duration is set to 2Δ₄ ≈ 1/¹J_CαCβ ≈ 28 ms such that the net effect of ¹J_CαCβ dephasing is eliminated. Broad-band ¹H-decoupling with the WALTZ16 modulation scheme³⁸ is used while care is taken that the water magnetization remains in a well-defined state, parallel to the decoupling radiofrequency field, thereby facilitating suppression of the intense water signal during the detection period. At time point c, following the ¹³C^α evolution period, the 2C_z^α(i)H_z^α(i) terms from time point a are converted to 2C_z^α(i)N_z(i) sin(2π ¹J_CαNΔ₄) cos(2π ²J_CαNΔ₄) + 2C_z^α(i)N_z(i+1) sin(2π ²J_CαNΔ₄) cos(2π ¹J_CαNΔ₄). Undesired transverse magnetization terms are eliminated at this point by pulsed field gradient G₄. Between time points d and e, prior to (t₃, ¹⁵N) evolution, a ¹²C' filter is applied to ensure removal of any signals from isotopomers where ¹⁵N is bonded to a ¹²C' isotope (due to incomplete isotope labeling). In the absence of such a filter, we found that in the ¹⁵N dimension of the final spectrum, the ¹⁵N-{¹²C′} signal approximately overlaps with the downfield component of the ¹⁵N-{¹³C′} doublet,³⁹ causing an artificial reduction in the apparent ³J_C′Hα E.COSY splitting. A hyperbolic-secant-shaped ¹³C′ pulse is used during this ¹²C′ filter, such that complete ¹³C′ inversion is not adversely impacted by RF inhomogeneity.⁴⁰ During the ¹²C′ filter, a ¹³C^α pulse is applied which rephases a significant fraction of the 2C_z^α(i)N_y(i) + 2C_z^α(i)N_y(i+1) terms present at time point d to yield 2C_z'(i-1)N_y(i) and 2C_z'(i)N_y(i+1) at point e. Therefore, at time point e, (t₃, ¹⁵N) evolution starts from antiphase ¹⁵N-{¹³C′} magnetization, which is in-phase with respect to ¹H^N. Following t₃ evolution (time point f) ¹⁵N magnetization is converted to the requisite antiphase 2N_yH_z terms during the duration τ + τ′, which also serves as the gradient-encoding delay (by oppositely signed gradient pulses G₅ and G₆), followed by standard gradient-enhanced transfer to ¹H^N,³⁷ which is detected during the time t₄. Note that ¹³C' decoupling is absent during all chemical shift evolution periods, leading to the desired E.COSY effect. However, since both ¹³C′(i) and ¹³C′(i-1) play a role in the evolution of the various terms, discussed above, the 4D E.COSY multiplet pattern is somewhat more complex than in typical E.COSY applications. Below, we will therefore briefly discuss the fine structure observed in these 4D multiplets.

3.2 J couplings contained in the HACANH[C′] E.COSY spectrum

The 4D HACANH[C′] E.COSY spectrum contains a rich array of J coupling information involving the backbone carbonyl nuclei. Next to the “active” ¹J_NC′ coupling, which yields the requisite well-resolved antiphase E.COSY splitting in the ¹⁵N dimension and which contains potentially useful information on H-bonding,⁴¹ the spectrum yields ¹J_C′Cα, ²J_C′N, ³J_HNC′, ²J_C′Hα, and the main purpose of our study: ³J_C′Hα. The values of ¹J_C′Cα, ²J_C′N, and ²J_C′Hα show relatively little variation with structure, and so far have not yet found much use in terms of protein structure analysis.^42-44 Both ³J_HNC′ and ³J_C′Hα correlate with ϕ via well-defined Karplus equations and are of most immediate structural value. Below, we therefore briefly illustrate how these couplings are manifested in the 4D spectrum.

3.3 Measurement of ³J_C′Hα and ²J_C′Hα

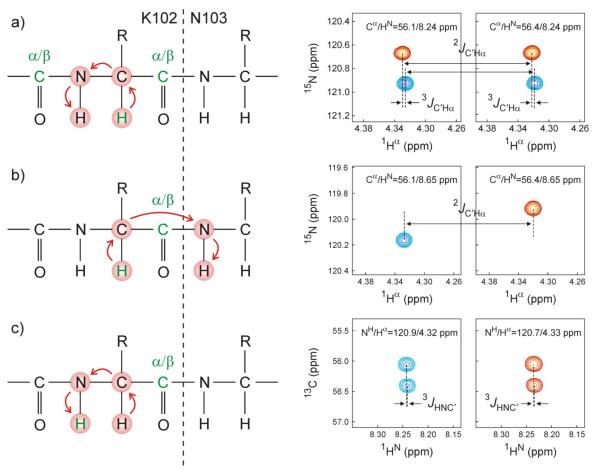
As discussed above, two types of magnetization transfer take place from ¹³C^α to ¹⁵N: intraresidue, mediated by ¹J_CαN and sequential, to ¹⁵N of residue i+1, mediated by ²J_CαN. Figure 2a concerns the intraresidue correlation observed for K102, and illustrates the relevant magnetization transfer pathway. Note that in the ¹⁵N dimension, the cross peak is split by the presence of ¹J_C′N to the ¹³C′(i-1) of the preceding residue. The splitting is antiphase due to the presence of the ¹²C′ filter (between time points d and e in Fig. 1), and the displacement in the ¹H^α dimension corresponds to the desired ³J_C′Hα coupling. The spin state of the ¹³C′ is inverted between ¹H^α and ¹⁵N evolution, giving rise to the negative slope of the doublets in Fig. 2a. However, after accounting for this sign inversion, and knowing that the sign of ¹J_C′N is negative (due to the negative magnetogyric ratio of ¹⁵N), this slope corresponds to a positive value for the ³J_C′Hα(i-1,i) coupling. The H^α(i)➔H^N(i) cross peak appears twice, as it is split in the ¹³C^α dimension by ¹³C′(i), therefore providing duplicate measurements for each 3J_C′Hα coupling (Fig. 2a). Comparison of such pairs of measured 3J_C′Hα couplings provides a measure for their reproducibility, and averaging their values is used to reduce their random uncertainty by √2.

Fig. 2.

Analysis of the 4D HACANH[C′] E.COSY spectrum, shown for couplings involving residue K102 in aS. The left hand side of each panel denotes the magnetization transfer pathway, with active and passive nuclei whose pairwise J coupling is measured shown in green. The right hand side of each panel shows small cross sectional regions through the 4D NMR spectrum, illustrating the measurement of various J couplings. (a) Measurement of ³J_C'Hα and ²J_C'Hα from ¹⁵N-¹H^α cross sections. Two independent measurements are shown, separated in the orthogonal ¹³C^α dimension by 1J_CαC'. Relative ¹H^α displacement within each panel corresponds to ³J_C'Hα; relative ¹H^α displacement between the two panels corresponds to ²J_C'Hα. (b) Alternative measurement of ²J_C'Hα from the sequential ¹³C^α-¹H^α (K102) to ¹⁵N-¹H^N (N103) cross peak. Relative displacement in the ¹H^α dimension corresponds to ²J_C'Hα. ¹⁵N displacement corresponds to ¹J_NC′, and ¹³C^α displacement to ¹J_CαC'. (c) Measurement of ³J_HNC' from a ¹³C^α-¹H^N cross section. Relative ¹H^N displacement within each panel equals ³J_HNC' and relative ¹³C^α displacement equals ¹J_CαC'. ¹⁵N displacement between the two panels equals ¹J_NC′; relative ¹H^N displacement between the two panels equals ²J_HNC′.

Analogous to the ¹J_CαN transfer pathway discussed above, transfer via ²J_CαN yields a H^α(i)➔H^N(i+1) cross peak (Fig. 2b). Here, the ¹⁵N(i+1) and ¹³C^α(i) frequencies of the cross peak depend on the spin state of ¹³C′(i) only, yielding a single measurement of ²J_C′Hα when extracting this value from the difference in ¹H^α frequency of the two multiplet components. An upfield ¹H^α displacement together with a downfield ¹³C^α displacement for the red versus the blue multiplet component in Fig. 2b points to opposite signs for ¹J_CαC′ and ²J_C′Hα. Note that ²J_C′Hα can also be obtained from Fig. 2a, from the relative ¹H^α displacement of the duplicate doublets shown in its two panels.

3.4 Measurement of ³J_HNC′

As mentioned above, the intraresidue H^α(i)➔H^N(i) cross peak is split in the ¹³C^α dimension by ¹J_CαC′, with the upfield and downfield components corresponding to ¹³C′ in the ∣α> and ∣β> spin states, respectively. Therefore, when viewing ¹³C^α-¹H^N cross-sections of the 4D spectrum taken through the cross peak of Fig. 2a, an E.COSY tilt reflecting the intraresidue ³J_HNC′ is seen, with the ¹J_CαC′ splitting in the ¹³C^α dimension, and ³J_HNC′ in the ¹H^N dimension (Fig. 2c). Again this coupling is obtained in duplicate by viewing the two cross-sections obtained at δ_N±¹J_NC′/2 (Fig. 2c).

As with most 4D NMR experiments, the HACANH[C′] E.COSY spectrum can also be recorded in fewer dimensions, and here this can be done most conveniently by not incrementing the duration the ¹³C^α evolution period (i.e., keeping t₂=0). However, in practice we find that overlap between the sequential and intraresidue H^α➔H^N cross peaks is rather common, in particular in disordered proteins. In folded proteins, the 3D version of the experiment is a viable option, although reducing the dimensionality of the experiment in this manner removes the ability to measure ³J_HNC′ from the spectrum.

3.5 Reproducibility of the measured ³J_C′Hα and ³J_HNC′ values

The random measurement uncertainty, σ, of a peak position in a frequency domain spectrum is directly proportional to the resonance line width, LW, and inversely related to the signal-to-noise ratio, SNR. To a fair approximation, it is given by:⁴⁵

$$\sigma =\mathrm{LW}∕\left(\text{2SNR}\right)$$ (1)

The uncertainty in the J splitting requires propagation of the uncertainty in both of its components and is therefore √2 larger. For time domain signals that have not fully decayed, as typically applies in the indirect dimensions of multi-dimensional NMR experiments, the attainable line width is approximately given by 1/AT, where AT is the length of the acquisition time in the dimension considered. This consideration indicates that it is important to sample the signals in the dimension where the coupling is measured for as long as practically feasible (up to ca 2×T₂, where T₂ is the decay constant of the signal), and that it is desirable to minimize the apparent decay rate through the removal of ¹H-¹H J splittings, as is done in the scheme of Fig.1 by band-selective homonuclear decoupling in the ¹H^α dimension. Band-selective homonuclear decoupling in the detected ¹H^N dimension of the spectrum would be advantageous for enhancing ¹H^N resolution and thereby the accuracy of ³J_HNC′. However, this mode of decoupling in the directly detected dimension is technically more challenging in terms of water signal suppression on cryogenic probes, which typically have only a single-axis pulsed field gradient accessory, and therefore was not used in our experiments. Note also that ¹H^N is only split by ¹H^α, making homonuclear decoupling less advantageous than it is for ¹H^α, where the couplings to both ¹H^N and ¹H^β are removed. Overall, the line width in the ¹H^N dimension remains somewhat larger than in the homonuclear decoupled ¹H^α dimension, and with the applicable SNR (cf eq 1) being the same for defining the peak position precision, the random error in the ³J_HNC′ will be correspondingly larger than for ³J_C′Hα.

Each intraresidue H^α➔H^N cross peak consists of four multiplet components, corresponding to the splitting by ¹³C′(i) and ¹³C′(i-1) (Fig. 2a,c) whereas each sequential H^α(i)➔H^N(i+1) cross peak is split into doublets by ¹³C′(i) (Fig. 2b). Therefore, the number of resonances in the 4D spectrum approximately equals 6N, where N is the number of residues in the protein. This number typically is small relative to the total number of time domain data points sampled in the indirect frequency dimensions, meaning that the HACANH[C′] E.COSY spectrum is relatively sparse and well suited for the use of non-uniform sampling (NUS) techniques^{18,19,20,46,47,48}. Here, spectral reconstruction was carried out by the in-house written SMILE routine of the NMRPipe program²⁴ which integrates accurate spectral reconstruction with spectral resolution enhancement by using a method that effectively mimics multi-dimensional linear prediction.⁴⁹

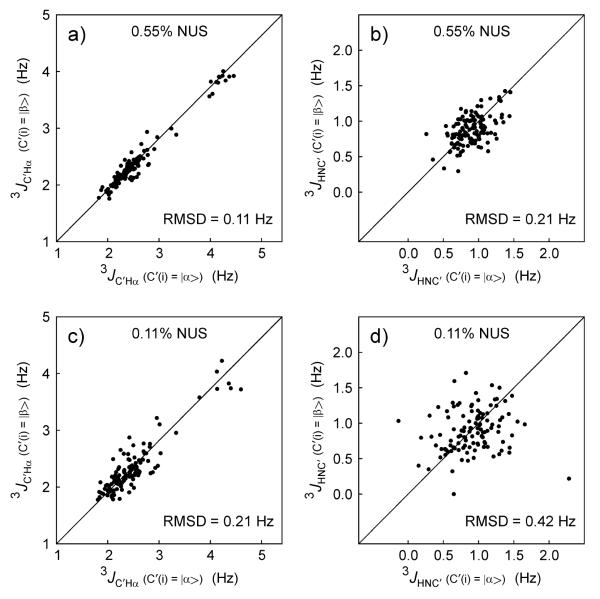
The availability of duplicate measurements for ³J_HNC′ and ³J_C′Hα makes evaluation of their random uncertainty straightforward, and permits evaluation of how closely this random error approaches the theoretical limit set by eq 1. As can be seen in Figure 3a, the pairwise root-mean-square deviation (RMSD) between the two sets of ³J_C′Hα is 0.11 Hz, and averaging the two sets of values therefore reduces the random uncertainty to 0.06 Hz.

Fig. 3.

Reproducibility of the duplicate measurements of ³J couplings from the 4D NUS HACANH[C′] E.COSY spectrum of α-synuclein. Comparisons of the duplicate ³J_C'Hα measurements (see right panels of Fig. 2a) obtained when (a) using 0.55% NUS sampling and (c) 0.11% NUS sampling. Analogous comparisons of the two ³J_HNC' measurements (see right two panels of Fig. 2c) obtained when using (b) 0.55% and (d) 0.11% NUS sampling.

The average signal-to-noise ratio for intra-residue cross peaks is ca 120:1, and line widths are approximately 10 Hz (¹H^α of non-T/S/G), ca 15-20 Hz for T/S/G; 25 Hz (¹³C^α), 5 Hz (¹⁵N) and 15-20 Hz (¹H^N). Eq 1 can then be used to predict precisions of ca 0.1 and 0.06 Hz for ³J_HNC′ and ³J_C′Hα, respectively. As can be seen from the pairwise RMSD values observed for the duplicate sets of ³J_HαC′ and ³J_HNC′ (Fig. 3), these predicted precisions fall close to their theoretical limit, indicating that the NUS reconstruction process used in our analysis faithfully reproduces peak positions.

The processed NMR spectrum containing the ³J_HαC′ and ³J_HNC′ splittings were generated from a 4D NUS time domain matrix that included measured data for only 0.55% of its elements, i.e., with 99.45% of them initially set to zero and subsequently adjusted during the iterative NUS processing procedure to values that approach those that would have been sampled if measurements for these time points had been made. As mentioned above, with only ca 800 resonances in the HACANH[C′] E.COSY spectrum of aS, the total number of time domain data points sampled in the indirect dimensions is far larger than this number of 800 resonances, making the NUS reconstruction feasible. It is therefore interesting to test whether a similar quality spectrum can be reconstructed from even fewer sampled data. For this purpose, we also reconstructed a 0.11% sampled data set, representing 20% of the same data used above for spectral reconstruction, and consequently yielding √5 lower SNR. As can be seen in Fig. 3c,d, the reproducibility of the measured J couplings then also decreases by a factor of ca √5, indicating that no additional uncertainty in extracted peak position is added by the NUS processing over what is expected on the basis of simple signal-to-noise considerations, even for a sparsity as low as 0.11%.

4 Karplus equation for ³J_C′Hα

An empirically parameterized ³J_C′Hα Karplus equations was introduced on the basis of values measured for ubiquitin using a 3D E.COSY method conceptually analogous to the 4D experiment of Fig. 1.³² Comparison of the previously measured and new ubiquitin data shows pairwise RMSD values of 0.29 Hz relative to the earlier measurements. Considering that this RMSD is more than √2 higher than the estimated uncertainty in the newly acquired data, we conclude that the newer data is of higher accuracy than the earlier data, and we will only use the new data for any fitting and analysis.

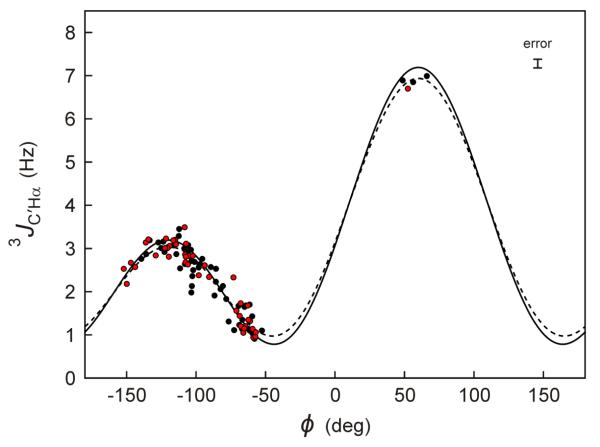
Best fits of the Karplus equation to the experimental ³J_C′Hα values and the coordinates of the NMR-determined structure of ubiquitin (PDB entry 2MJB)⁵⁰ and the RDC-refined structure of GB3 (PDB entry 2OED)²³ are shown in Figure 4 (dashed lines). The RMSD between observed and Karplus-predicted ³J_C′Hα values (dashed lines) equals 0.25 Hz, respectively. As expected on the basis of the higher measurement precision reached in the current study, this value is somewhat lower than obtained previously.¹⁷ However, it remains considerably higher than the random uncertainties in the measurement. This latter observation indicates that, similar to what was previously noted for the ³J_C′C′ coupling,²³ parameters other than ϕ can also influence these couplings. These other factors, which may include valence angle distortion of, for example, the τ angle (N-C^α-C′) and/or H-bonding of amide and carbonyl groups, are difficult to account for in experimental structures, and therefore limit the extent to which agreement between experimental ³J_C′Hα and predicted values can be enforced during the calculation of structures of folded proteins. In IDPs and IDRs, the effects of factors other than ϕ on the ³J couplings are expected to average to roughly zero, and should permit interpretation of these couplings in a more quantitative fashion, which then can approach the experimental uncertainty in the measurement of these ³J couplings.¹⁴

Fig. 4.

Plot of experimental ³J_C'Hα coupling values against the backbone torsion angle ϕ, for ubiquitin (black symbols) and GB3 (red). The backbone ϕ values are derived from RDC-refined structures of GB3 (PDB entry 2OED) and ubiquitin (PDB entry 2MJB), both obtained without ³J_C'Hα data. The superimposed best-fit Karplus equation, shown as a dashed curve, is given by ³J_C'Hα = 3.76 × cos²(ϕ−60°) + 1.95 × cos(ϕ−60°) + 1.23. After factoring out the effect of Gaussian ϕ angle fluctuations (σ = 0.226),^52,51 the rigid limit Karplus equations (solid line) is given by: ³J_C'Hα = 4.17 × cos²(ϕ−60°) + 2.00 × cos(ϕ−60°) + 1.02. Residues with elevated backbone dynamics (L12, D40, and G41 for GB3; T9-K11, D32-G35, G47, D52, and R72-G76 for ubiquitin) are excluded from the plot and the fitting process. The error bar (top right) corresponds to the random error (±1 standard deviation) based on the reproducibility of the ³J_C'Hα measurements. The considerably larger RMSD of 0.25 Hz relative to the best-fitted Karplus curve (dashed line) reflects the impact of factors other than ϕ on the ³J_C'Hα value.

The best-fit Karplus curve, described above, was derived using a single, static representation of the protein structure. However, it is well recognized that proteins are subject to modest amplitude ϕ-angle fluctuations, previously estimated to have an RMS amplitude of ca 13° in regions of well-ordered structure.⁵¹ When factoring out the effect of these backbone fluctuations,⁵² slightly different, “rigid-limit” Karplus parameters are obtained that should be applicable when refining a structure in terms of an ensemble of perfectly static conformers (solid lines in Fig. 4), and these latter curves are therefore used when describing an IDP or IDR in terms of an ensemble representation.¹⁴

Tables containing the experimental ³J_C'Hα and ²J_C'Hα values for α-synuclein, ubiquitin, and GB3, together with the α-synuclein ³J_HNC′ values are included as Electronic Supplementary Information (ESI).

5 Fractional population of positive ϕ angles from ³J couplings

Under the assumption that all ϕ angles are negative, we previously were able to extract two parameters, the average <ϕ⁻> and its standard deviation σ, from two experimental observables: ³J_HNHα and ³J_C'C'.⁵¹ Although a small population, P⁺, of conformers with positive ϕ values in IDPs was shown to have minimal impact on the extracted <ϕ⁻> and σ values, the actual value of P⁺ could not be determined from that data. As we will show below, the large difference between ³J_C'Hα coupling values for negative and positive values of ϕ now allows determination of P⁺. To this extent, we name the ³J_C'Hα values that would correspond to the fractions of conformers with only negative and only positive ϕ angles ³J_C'Hα(−) and ³J_C'Hα(+), respectively. Considering that the positive ϕ angles sampled in the PDB, and in particular in the coil library,^13,14 cluster relatively tightly around <ϕ⁺> values, this permits us to make an amino-acid-type-specific estimate for the average, <³J_C'Hα(+)>, by using the positive-ϕ conformers of the coil library in concert with the rigid-limit Karplus equation. Note that the effect of dynamic averaging is included when calculating <³J_C'Hα(+)> over the coil library distribution of positive ϕ conformers, and that it therefore is the rigid-limit parameterization of the Karplus curve that needs to be used for predicting <³J_C'Hα(+)>.

5.1 Iterative procedure for determination of P⁺

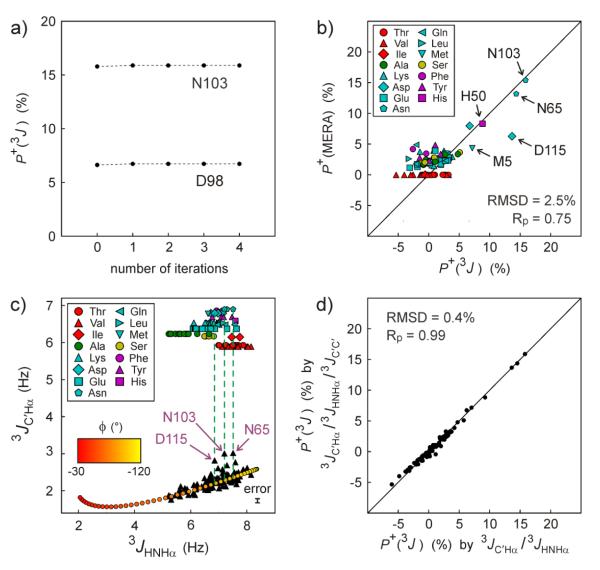
Since ³J_HNHα and ³J_C'C' coupling values for averaged negative ϕ angles in coil regions (<ϕ⁻>, typically between −80 and −100°) are similar to the coupling values averaged for positive ϕ angles, experimental ³J_HNHα and ³J_C'C' couplings are not much impacted by a small fraction of conformers with positive ϕ values. Therefore, to a first approximation, they may be ignored when calculating residue-specific <ϕ⁻> and σ values.⁵¹ These <ϕ⁻> and σ values then can be used to calculate ³J_C'Hα(−) from the dynamics-corrected⁵² form of the ³J_C'Hα Karplus equation (see also Section 6, eqn (4)). Next, P⁺ for each residue can be derived from

$${}^{3}J_{{\mathrm{C}}^{\text{'}}\mathrm{H}\alpha }=P^{+}<{}^{3}J_{{\mathrm{C}}^{\text{'}}\mathrm{H}\alpha }(+)>+(1-P^{+}){}^{3}J_{{\mathrm{C}}^{\text{'}}\mathrm{H}\alpha }(-),$$ (2)

where ³J_C'Hα is the experimentally observed value. In a subsequent iteration, this P⁺ value can be used to recalculate the ³J_HNHα(−) and ³J_C'C'(−) values, yielding an improved estimate for <ϕ⁻> and σ, and an improved ³J_C'Hα(−) value. This then allows a better estimate of P⁺ in this second iteration. More iterations could be carried out, but in practice the procedure converges rapidly (Fig. 5a) and a single iteration suffices. With an RMSD of only 2.5%, excellent agreement is seen (Fig. 5b) between the P⁺ values derived in this manner and those previously obtained by MERA analysis¹⁴ of a large set of NMR input parameters (incl. ¹³C and ¹⁵N chemical shifts, ¹H-¹H NOEs, and five different types of ¹J, ²J and ³J couplings).

Fig. 5.

Deriving the fractional population of positive ϕ angles, P⁺, in IDPs and IDRs. (a) P⁺ for α-synuclein residues N103 and D98 during successive iterations of ³J_HNHα, ³J_C'C', and ³J_C'Hα analysis (see main text). (b) Comparison of the P⁺ derived from iterative ³J analysis (³J_C'Hα, ³J_HNHα, and ³J_C'C') with P⁺ obtained with the MERA webserver¹⁴ without using ³J_C'Hα as input parameter. Different residue types are presented by the symbols shown in the inset. Full results are listed in ESI Table S5. (c) Extracting P⁺ from only ³J_C'Hα and ³J_HNHα by interpolation. Red-to-yellow color shaded points correspond to the calculated correlation between ³J_C'Hα and ³J_HNHα dynamic Karplus equations (eqn 4), assuming σ = 29.5° (average IDP σ value previously derived for α-synuclein⁵¹). Shaped symbols mark the residue-type specific <³J_C'Hα> values calculated from the Mantsyzov coil library for residues with ϕ >0.¹⁴ Pairs of ³J_HNHα and ³J_C'Hα values are shown as black filled triangles, all in the ³J_C'Hα = 2-3 Hz range. Residues with ³J_C'Hα that are significantly higher than expected from ³J_HNHα when assuming P⁺ = 0 are marked by arrows and residue number. The error bar (bottom right) corresponds to the random error (±1 standard deviation) in the ³J_C'Hα measurements. The random error in ³J_HNHα (±0.05 Hz) is too small for display purposes. (d) Comparison of P⁺ calculated by iterative analysis of ³J_C'Hα, ³J_HNHα and ³J_C'C' with those of simplified analysis (panel c method) of ³J_C'Hα and ³J_HNHα.

5.2 Direct determination of P⁺ from ³J_HNHα and ³J_C'Hα

As an alternative to the above iterative method, a good approximation for P⁺ can be obtained directly from the experimental ³J_HNHα and ³J_C'Hα values without requiring knowledge of ³J_C'C': The fact that to a good approximation ³J_HNHα and ³J_C'Hα are linearly correlated over the range from −60° < ϕ < −120° (Fig. 5c) permits a direct prediction of ³J_C'Hα (³J_C'Hα^pred,neg) under the assumption that only this range of ϕ is populated. In practice, higher values may be observed, and P⁺ can be calculated from

$$P^{+}=({}^{3}J_{{\mathrm{C}}^{\text{'}}\mathrm{H}\alpha }{}^{\text{obs}}-{}^{3}J_{{\mathrm{C}}^{\text{'}}\mathrm{H}\alpha }{}^{\text{pred},\text{neg}})∕({}^{3}J_{{\mathrm{C}}^{\text{'}}\mathrm{H}\alpha }{}^{\text{pred},\text{pos}}-{}^{3}J_{{\mathrm{C}}^{\text{'}}\mathrm{H}\alpha }{}^{\text{pred},\text{neg}})$$ (3)

where ³J_C'Hα^pred,pos is the residue-type-specific predicted value for positive coil angles, spanning a narrow range from 6 to 7 Hz for the different residue types (Fig. 5c; ESI Table S4). In practice, the iterative analysis of ³J_C'Hα ³J_C'C' and ³J_HNHα and the simple interpolation method of Fig. 5c yield very similar P⁺ values (Fig. 5d).

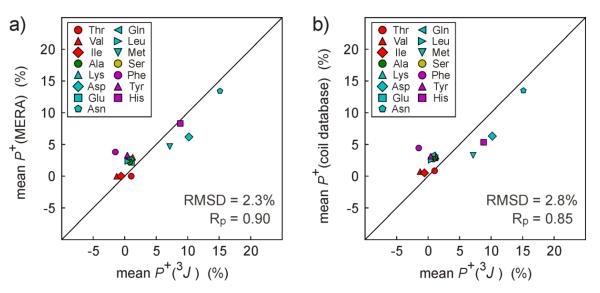
The newly acquired ³J_C'Hα data allows us to revisit the propensities to adopt positive ϕ angles for different residue types in the IDP α-synuclein. We find that P⁺ values, averaged by residue type, agree very closely with those obtained from MERA analysis (Fig. 6a), which did not use ³J_C'Hα as an input parameter. The only slight outlier in the correlation concerns Phe residues, which show a weak propensity (~4%) for positive ϕ angles, both in the MERA results and in the coil database (Fig. 6b), whereas ³J_C'Hα points to a vanishingly low population. However, with ³J_C'Hα data available for only two Phe residues in α-synuclein, the statistical uncertainty in the Phe <P⁺> values obtained for α-synuclein is rather large.

Fig. 6.

Positive ϕ angle propensity in α-synuclein for different residue types. (a) Comparison of P⁺ obtained from MERA analysis (lacking ³J_C'Hα as input) with results of iterative analysis of ³J_C'Hα, ³J_HNHα and ³J_C'C'. (b) Comparison of P⁺ obtained from iterative analysis of ³J_C'Hα, ³J_HNHα and ³J_C'C' with residue-type averaged P⁺ values of the Mantsyzov coil library.¹⁴

6 Amplitudes of ϕ angle fluctuations from ³J couplings

Assuming that ³J_HNHα and ³J_C'C' couplings only depend on the intervening backbone torsion angle, ϕ, the amplitude of ϕ angle fluctuations (assumed to follow a Gaussian distribution) can be extracted from such a pair of measurements.⁵¹ This approach relies on the motion-corrected Karplus equation,⁵²

$${}^{3}J=A^{\prime }{\cos }^2\theta +B^{\prime }\cos \theta +C^{\prime }$$ (4)

where A'=A exp(−2σ²), B' =B exp(−σ²/2), and C'=C+A[1-exp(−2σ²)]/2 , with A, B, and C being the rigid limit Karplus coefficients, θ is the averaged intervening dihedral angle, and σ is its standard deviation.

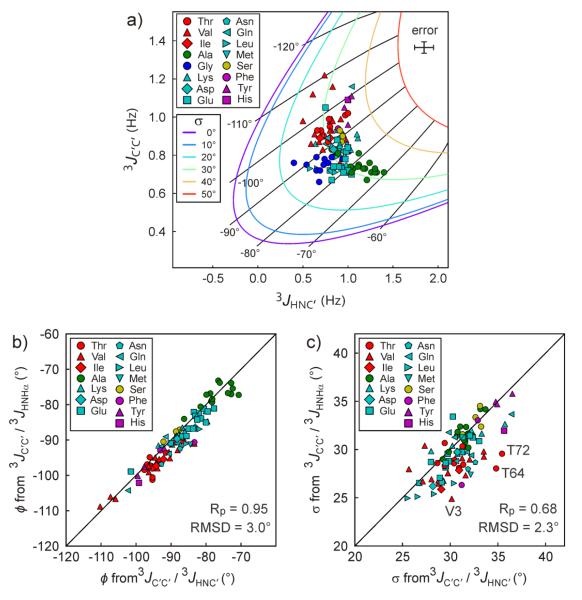
Our current study measures ³J_C′Hα and ³J_HNC′ and this pair of couplings, or any other pairwise combination of the four sets of ³J_C′Hα, ³J_HNC′, ³J_C'C', or ³J_HNHα can be used for analysis of the amplitude of σ, provided that their respective Karplus equations are not linearly related. Previously, we used the combination of ³J_HNHα and ³J_C'C' to extract residue-specific σ values for α-synuclein.⁵¹ Here, we demonstrate that σ values can be extracted from pairs of ³J_C′C′ and ³J_HNC′ values (Fig. 7). Colored lines in Figure 7a correlate the ³J_HNHα and ³J_C'C values predicted by their respective Karplus equations for different values of <ϕ> (marked by black, radial spokes), with different colors corresponding to different amplitudes of σ. As can be seen from the figure, the plot of ³J_HNC′ versus ³J_C′C′ values for α-synuclein places the σ values of all residues in the 25-35° range. With an RMSD of only 3°, the residue-specific <ϕ> values extracted from this figure agree closely with the corresponding <ϕ> values previously obtained from ³J_HNHα and ³J_C′C′ analysis (Fig. 7b), and similarly, with an RMSD of only 2.3°, the σ values also agree very well with our prior study (Fig. 7c).⁵¹

Fig. 7.

Extracting the amplitude of ϕ angle fluctuations from ³J_C′C′ and ³J_HNC'. (a) Plot of ³J_C′C′ versus ³J_HNC′ for α-synuclein. The rigid limit (after factoring out σ=13° motions) ³J_HNC′ Karplus parameterization¹⁷ was used: ³J_HNC′ = 4.78 × cos²(ϕ) + 0.86 × cos(ϕ) − 0.23 Hz. Solid lines show correlations between ³J_C′C′ and ³J_HNC′ predicted by the dynamics-corrected Karplus equations for ϕ angles (ϕ values marked by black “radial spokes”), with the different colors representing the amplitude of σ. The error bars (top right) corresponds to the random error (±1 standard deviation) of the ³J_C'Hα and ³J_{C' C'} measurements. (b) ϕ and (c) σ values that are extracted from the ³J_C′C′ and ³J_HNC' analysis are compared to those from ³J_C′C′ and ³J_HNHα analysis, reported previously.⁵¹

7 Concluding Remarks

We have shown that ³J_C'Hα and ³J_HNC' can be measured simultaneously and at high precision by using a 4D NMR pulse sequence. Only when such experiments are carried out in conjunction with very sparse non-uniform sampling does it become experimentally feasible to use long acquisition times in all four dimensions. These long acquisition times are required for obtaining the very high spectral resolution that is needed for precise measurement of very small J couplings. Although many of the widely used spectral analysis software packages are not yet fully optimized for convenient analysis of the extremely large 4D matrices, there is no conceptual or technical problem in obtaining resonance positions at the same accuracy as in spectra of lower dimensionality. Our analysis shows that the uncertainty in the extracted 4D peak positions is primarily determined by the intrinsic signal to noise ratio in the acquired time domain data. Indeed, the uncertainty in peak positions when using only a fraction of this data for NUS reconstruction is found to scale approximately with the inverse square root of the size of this fraction.

The large difference in ³J_C'Hα values for residues with negative and positive ϕ angles makes this coupling particularly useful for identifying fractional populations of positive ϕ angles in disordered regions of a protein. In particular, when used in conjunction with ³J_HNHα, the uncertainty in populations of positive ϕ conformers can be detected with uncertainties of only a few percent. Positive ϕ populations determined in this manner for α-synuclein agree well with those from the recent MERA analysis¹⁴ which used far more experimental data, but not ³J_C'Hα. Results obtained for α-synuclein are also in very close agreement with positive ϕ propensities seen in a recently introduced large coil library, extracted from non-H-bonded residues in the PDB, suggesting that the new method is not only precise but also accurate.

As previously shown for the combination of ³J_HNHα and ³J_C'C', the newly measured ³J_C'Hα and ³J_HNC' values can be combined with either ³J_HNHα or ³J_C'C' to extract the average of the negative ϕangles sampled by a given IDP or IDR residue, and the standard deviation relative to this average value. Comparison of <ϕ⁻> and σ values derived from ³J_C'C' and ³J_HNC' agree very well with the earlier analysis and confirm that such an analysis is quite robust.

It has been hypothesized, mostly based on molecular dynamics simulations, that formation of α-pleated sheet structures may be a common conformational transition intermediate on the pathway to amyloid formation.⁶ The requisite Ramachandran map flips from α_Rα_L to ββ for pairs of adjacent residues is commonly observed when comparing X-ray crystal structures of closely related proteins,⁷ providing some experimental support that such transitions are energetically feasible. α-Synuclein clearly falls in the category of amyloidogenic proteins, but its intrinsic disorder previously made it difficult to assess the presence of elevated transient population of α-pleated sheet backbone conformations. Analysis of our ³J_C'Hα data finds no evidence for elevated population of the positive ϕ angles associated with α-pleated sheet, and propensities of its residues to adopt positive ϕ angles closely correlate with the residue-type specific propensities seen in the coil library. We note, however, that this observation does not preclude the formation of α-pleated sheet structures as an intermediate, but simply that if present the population of such structures must be very low.

For folded proteins, factors other than the intervening torsion angle ϕ are found to have a non-negligible impact on ³J_C'Hα. Although this limits the accuracy at which ϕ angles can be extracted from ³J_C'Hα, it also offers new opportunities to gain access to these additional factors, which include deviations from idealized geometry, H-bonding, and χ₁ angles. We are currently exploring the feasibility of developing quantitative relations that extend the Karplus equations to take these additional factors into account.