Abstract
Purpose
To propose and evaluate a model for the blood water T1 that takes into account the effects of hematocrit fraction, oxygenation fraction, erythrocyte hemoglobin concentration, methemoglobin fraction and plasma albumin concentration.
Methods
Whole blood and lysed blood T1 data were acquired at magnetic fields of 3T, 7T, 9.4T and 11.7T using inversion-recovery measurements and a home-built blood circulation system for maintaining physiological conditions. A quantitative model was derived based on multi-variable fitting of this data.
Results
Fitting of the model to the data allowed determination of the different parameters describing the blood water T1 such as those for the diamagnetic and paramagnetic effects of albumin and hemoglobin, and the contribution of methemoglobin. The model correctly predicts blood T1 at multiple fields, as verified by comparison with existing literature.
Conclusion
The model provides physical and physiological parameters describing the effects of hematocrit fraction, oxygenation, hemoglobin concentration, methemoglobin fraction and albumin concentration on blood water T1. It can be used to predict blood T1 at multiple fields.
Keywords: longitudinal relaxation, in vitro blood, hematocrit, oxygenation, hemoglobin concentration, methemoglobin, albumin, relaxivity, T1 model
Introduction
The longitudinal relaxation rate (R1 = 1/T1) of water proton in blood plays an important role in various quantitative MRI applications, such as measuring cerebral blood flow using arterial spin labeling (1) as well as determining the appropriate nulling point for black blood imaging (2) and vascular space occupancy (VASO) MRI, a cerebral blood volume weighted functional MRI approach (3). It is also a valuable diagnostic parameter for staging hematoma (4,5).
Under physiological conditions, blood is composed mainly of plasma and erythrocytes with the erythrocyte volume fraction referred as hematocrit fraction (Hct). The intracellular volume of erythrocyte consists mainly of a high concentration (~5mM tetramer) hemoglobin solution. Regular hemoglobin with Fe2+ in the heme is a diamagnetic protein when binding O2 (HbO2), but paramagnetic when not coordinated to O2 (deoxyHb). Methemoglobin (MetHb) with Fe3+ in the heme, which is a trace amount in physiological blood but has high concentration in methemoglobinemia (6,7) and aged blood such as hematoma (4), is also paramagnetic with high relaxivity. In terms of water 1H magnetic properties at a certain magnetic field, blood can be considered as consisting of two water compartments separated by the erythrocyte membrane: (i) the plasma, characterized by a constant water T1 depending on the albumin concentration, and (ii) the erythrocyte cytoplasm characterized by a water T1 depending on the hemoglobin concentration in the erythrocyte (mean corpuscular hemoglobin concentration, MCHC), methemoglobin fraction (fMetHb) and oxygenation fraction (Y). The hemoglobin concentration in the erythrocyte and the albumin concentration in the plasma determine the water fractions in these two compartments.
To date, the longitudinal relaxation rate of water in blood has been measured in vivo and in vitro at multiple magnetic fields, showing a linear dependence of longitudinal relaxation rate R1 = 1/T1 on Hct, and Y (8–29). Several calibration equations (14,17,19,20,23,26–29) have been derived as a function of hematocrit fraction (Hct) and oxygenation fraction (Y). In addition to these two parameters, R1 depends on the hemoglobin concentration in erythrocytes (MCHC), which is generally constant under physiological conditions (30), but may vary under pathological situations. The methemoglobin fraction (fMetHb) may also greatly affect R1, but this effect was previously measured only at magnetic fields below 3T (13,31–37). Therefore, we measured a series of lysed and whole blood water T1 data and derived and evaluated a general theory that describes the effects of Hct, Y, MCHC and fMetHb on blood water R1 at higher magnetic fields (≥3T).
METHODS
Sample Preparation
Bovine blood, an analogue of human blood with similar hemoglobin structure (38), erythrocyte permeability (39), MCHC (40) and viscosity (40), was obtained from a local slaughterhouse. Fresh blood (3.5L) was mixed with 300mL 83mM sodium citrate solution to prevent coagulation. The samples were stored at 4°C, and used within 8 days. Samples with different hematocrit fractions were prepared by centrifuging blood samples and separating them into erythrocytes and plasma at 10,000G for 15min at 4°C, and recombining them in appropriate volume ratios. The lysed blood samples with different hemoglobin concentrations were prepared through lysing the whole blood with target hemoglobin concentration by sonication (Branson Ultrasonics, Danbury, CT) on ice for 6min with 45% amplitude and 10s “on”, 5s “off” working cycles. The cell lysate after centrifugation (10,000G, 15min at 4°C) was immediately used for T1 measurements. For the experiments to determine methemoglobin’s relaxivity, concentrated sodium nitrite solution (23mM) was added into fully oxygenated lysed blood and equilibrated at room temperature for 2 hours to prepare samples with different methemoglobin concentrations (1 mole sodium nitrite can roughly transfer 1 mole hemoglobin to methemoglobin). The phosphate buffered saline (PBS) solution was prepared by diluting 10 times in PBS liquid (Fisher) with deionizing water.
A home-built blood circulation system (14,17,41) was used to prevent sedimentation of erythrocytes, and to control temperature and oxygenation fraction. Temperature was maintained at 37+/−0.3°C for all experiments. Oxygenation was controlled by blowing N2/O2 mixture into the mixing chamber in the blood circulation system and measured in the flow system using a fiber-optic pO2 sensor (Oxford Optronix) placed outside the coil. Whole or lysed blood samples were circulated with a flowing speed of ~30 mL/min (~0.5 cm/s). During experiments, we used a flow-stop-flow pattern, i.e. a flowing blood sample for the first 5–10 seconds, after which the flow was stopped 5–10 seconds before MR signal acquisition and resumed after acquisition. This strategy prevented erythrocyte precipitation and “washout” effects during T1 measurement. A cylinder sample tube (inner diameter 11 mm) was connected with the circulation system at both ends, and positioned vertically inside the RF coil. Experiments for determination of methemoglobin’s relaxivity and water T1 in saline solution were performed in a tube not connected to the perfusion system. Samples were equilibrated in the 37. 5°C water bath for 20min, and then quickly put into the magnet for T1 experiments (5–10min). Sample temperatures after experiments were measured as 36.5–37.0°C.
During the experiment, the O2 needs to be carefully controlled because the free O2 dissolved in the blood can decrease T1 as reported before (14,28,42). In venous blood samples, the pO2 is tightly related to Y following the oxygen-hemoglobin dissociation curve, but for arterial blood more free O2 will be present at higher pO2, leading to a reduction in T1. This extra relaxation enhancement by free O2 has been studied in arterial blood, plasma and CSF (14,28,42) and found to depend linearly on R1 as described by: R1=0.00027xpO2 (mmHg) + 0.2263 in CSF at 1.5T (42), R1 = 0.00041xpO2 (mmHg) + 0.56 in arterial blood at 3T (28) and R1 = 0.00020xpO2 (mmHg) + 0.31 in plasma at 7T (14).. The slopes of these equations represent the pO2 dependence of R1. Therefore, a variation of arterial blood pO2 over the typical physiological range of 95+/−13 mmHg (43) can induce R1 differences of 0.002–0.004 s−1, which are within the experimental error range. Most of our whole blood data were in this range, but some of the fully oxygenized lysed blood data used for calculating r1dia,Hb over this range were not. To correct for the pO2 effect, the R1 of these lysed blood data with pO2 outside the mentioned range were calibrated to the condition of pO2=95 mmHg using the equation R1,cal = R1,exp – 0.00020 (pO2 – 95). The pO2 of the fully lysed blood samples for calculating r1para,MetHb were not measured, because the samples with different MetHb concentrations for the same magnetic field were prepared by pouring 50mL lysed blood from the same batch and ~1mL sodium nitrite into 50mL tubes and tightly sealed. The experiments at the same magnetic field were finished at nearly the same time, so pO2 across different samples were nearly the same. Fortunately, the lack of this value will not affect the calculation of r1para,MetHb, which is the slope of R1 change with the concentration of MetHb.
A blood analyzer (Radiometer, ABL700) was used to monitor hematocrit fraction (Hct), oxygen partial pressure (pO2), oxygenation saturation (sO2), total hemoglobin concentration (ctHb) and methemoglobin fraction (fMetHb) immediately before and after every experiment. Note that Hct value reported by the blood analyzer is calculated based on total hemoglobin concentration in the blood (ctHb) according to an empirical relationship Hct = 0.00301 × ctHb (g/L) (reference manual of the ABL700 blood analyzer). This corresponds to a hemoglobin concentration in erythrocyte (mean corpuscular hemoglobin concentration, MCHC) of 332 g/L (44). The oxygen saturation (sO2) is the ratio between oxygenated hemoglobin concentration and total hemoglobin concentration (the sum of oxygenated and deoxygenated hemoglobin concentration). The oxygenation fraction (Y) is defined as sO2/100%.
MR Methods
The MR experiments were conducted on 3T and 7T whole body scanners (Philips Medical Systems, Best, The Netherlands) as well as on 9.4T, 11.7T spectrometers (Bruker Biospin, Billerica, USA). A conventional inversion recovery sequence was used to measure T1, with recovery time of 15s after each acquisition to relax the system back to equilibrium and have a consistent initial magnetization. The total TR thus increases with the inversion time (TI), but the initial magnetization is always the same. TI-values used were 0.1s, 0.4s, 0.7s, 1s, 1.4s, 1.9s, 2.5s, 4s, 6s, 9s for 3T and 7T scanners, and 0.1s, 0.2s, 0.4s, 0.8s, 1s, 1.2s, 1.5s, 1.8s, 2.2s, 2.5s, 3s, 4s, 5s, 8s, 12s, 15s, 20s for 9.4T and 11.7T spectrometers. The experiments performed at 3T used a quadrature head coil and the following imaging parameters: FOV=32×32mm2, matrix=32×32, single-short EPI, 10ms no-slice-selection hyperbolic secant inversion pulse. A single slice (10mm thick) in the center region of the tube was imaged. A small dephasing gradient (0.6 mT/m) was applied continuously during the inversion delay time to minimize possible radiation damping effects (17,45,46). A similar protocol was applied on the 7T human scanner, as detailed in a previous paper (14). The experiments performed on spectrometers used quadrature volume coils with a 60μs 180° inversion pulse and a small dephasing gradient (0.10 G/cm) during the inversion delay time.
Blood T1 Model
Here we build up the theory from basic principles to combine the individual components that are needed to describe the contributions of water in the erythrocyte (affected by the diamagnetic and paramagnetic relaxation of hemoglobin and the paramagnetic relaxation of methemoglobin) and water in plasma (affected by albumin and free O2). The hemoglobin relaxation is affected by the oxygenation fraction Y and the iron oxidative state (Fe2+ versus Fe3+), while the relative contribution of the two compartments depends on the water fraction (fwater) in each compartment, often approximated using the Hct but more accurately calculated from the hemoglobin and albumin concentrations for erythrocytes and plasma, respectively. The addition of the components depends on the exchange regime for the MRI measurement. A two-compartment “fast exchange” model (47) has been applied to describe blood T1 measured by inversion recovery experiments because the water exchange rate between plasma and cytoplasm is much faster than difference between the longitudinal relaxation rates between these two compartments (14,48). The baseline equation for the resulting single-compartment rate then is:
| [1] |
with fery,water the water fraction in the erythrocyte, which can be derived to be (14,49,50)
| [2] |
based on the fact that hemoglobin occupies about 30% of the volume (51) in the erythrocyte and water volume fraction in the plasma is about 95% (49,50) mainly due to the high concentration of albumin. R1,plasma is the longitudinal relaxation rate of water in plasma, and R1,ery is the water longitudinal relaxation rate of water in the erythrocyte.
Diamagnetic relaxation enhancement
In a protein solution like plasma (albumin solution) and cytoplasm in the erythrocyte (hemoglobin solution), the large protein will slow down the water tumbling and increase the water longitudinal relaxation rate. This diamagnetic effect is a short range effect limited to a thin “hydration shell” (52), where water tumbling is slow and the cross relaxation between water and protein is strong (53–55). Due to the fast exchange between water in this hydration shell and bulk water, the diamagnetic relaxation enhancement (relative to plasma) ΔR1,dia can be expressed as
| [3] |
ΔR1dia,shell is the relaxation enhancement (relative to saline solution) of water in the hydration shell. Vshell and Vbulk are the water volumes in the hydration shell and in protein solution. Because the hydration shell is thin and its volume proportional to the protein volume, ΔR1,dia can be rewritten as
| [4] |
where a is the volume ratio between the hydration shell and protein molecule, and mprotein, Vprotein, ρprotein, nprotein, Mprotein are the mass, volume, density, number of moles and molecular weight of the protein, mwater is the water mass in the protein solution. Therefore, the diamagnetic relaxation enhancement of protein can be expressed as
| [5] |
where and bprotein = nprotein/m protein are the diamagnetic relaxivity and molality of the protein, respectively. The molality can be related to the mass concentration of protein (cprotein g/L) via:
| [6] |
with the solution volume V, the solution mass m and the solution density ρ. The protein in plasma is mainly albumin (56), therefore the longitudinal relaxation of water in plasma can be written as
| [7] |
in which R1saline is the water longitudinal relaxation rate in saline solution and r1dia,Alb is the diamagnetic relaxivity of water due to albumin. According to Eq. [6], the molality concentration of albumin bAlb can be calculated via:
| [8] |
The coefficient of 0.501 in the plasma density ρplasma was obtained from linear extrapolation between the density with the protein (1025g/L) (57) and the water density (i.e. zero protein concentration). This can be done because the protein solution density has a linear dependence on the protein concentration (58) and the albumin concentration is known: cAlb=0.75mM×66.5kg/mol=49.9g/L (14).
The diamagnetic relaxation enhancement (relative to saline water) in the erythrocyte is mainly attributed to the hemoglobin, and can be expressed as
| [9] |
r1dia,Hb is the diamagnetic relaxivity of hemoglobin. The molality bHb can be related to the concentration of hemoglobin (cHb) via
| [10] |
The factor 0.377 in the cytoplasm density ρcytoplasm was determined from linear extrapolation between solution and pure water, similar to albumin above but now using the erythrocyte cytoplasm density of 1125g/L (44,59) and the erythrocyte hemoglobin concentration of 332g/L. Notice that the overall structures of oxyhemoglobin, deoxyhemoglobin and methemoglobin are comparable under the same physiological conditions (temperature, pH, etc), causing these three types of hemoglobin to share the same diamagnetic relaxivity r1dia,Hb.
Paramagnetic relaxation enhancement
Similar to the diamagnetic effect, the paramagnetic relaxation enhancements of methemoglobin and deoxyhemoglobin, which also depend linearly on their concentration, can be expressed as
| [11a] |
| [11b] |
where r1para,MetHb and r1para,deoxyHb are the paramagnetic relaxivities of methemoglobin and deoxyhemoglobin respectively. bMetHb and bdeoxyHb are the molalities of methemoglobin and deoxyhemoglobin in the erythrocyte, that can be related to the total molality of hemoglobin bHb through
| [12a] |
| [12b] |
Under physiological conditions, the hemoglobin protein is a tetramer (60). While multiple possible tetramers can exist (e.g. binding one, two, three or four O2), it can be calculated from the binding constants that hemoglobin exists predominantly as a mixture of the fully oxygenated state (all four O2 binding sites occupied) and the fully deoxygenated state in the normal oxygenation range (61–64). Thus, thanks to this well-known cooperative binding process, one relaxivity parameter (r1para,deoxyHb) is sufficient to approximate the paramagnetic effect of deoxy-hemoglobin. Therefore the water R1 in erythrocyte can be expressed as
| [13] |
and the blood water R1 can be written as
| [14] |
Data Fitting
Averages of the magnitude intensities at the center of the slice profiles (scanners) and the integrals of the water peaks (spectrometers) were fitted as a function of inversion time (TI) using the following model valid under conditions of TR > 5T1:
| [15] |
The equilibrium signal S0, the inversion efficiency C and blood 1H2O R1 (1/T1) were fitted using a nonlinear-least squares algorithm. The errors of fitted R1 were calculated as 95% confidence interval in the fitting.
In whole blood, multiple T1 data at 3T, 7T, 9.4T, 11.7T, at various Y (0.48 – 1.00), Hct (0.31 – 0.75) and fMetHb (0.016–0.028) were fitted using Eq. [14]. The blood sample Hct, Y and fMetHb were read directly from the blood analyzer. Albumin’s concentration was set as 0.75 mM (14) or 0.77 mmol/kg (Eq. [6]). The hemoglobin molalities bHb were calculated to be 6.49 mmol/kg (Eq. [10]) assuming that the hemoglobin concentration (cHb) in erythrocytes was the normal MCHC of 332 g/L (34,35). The water fractions in erythrocyte fery,water were calculated from Hct according to Eq. [2]. The r1dia,Alb, r1dia,Hb and r1para,MetHb obtained from the linear fits of plasma and lysed blood samples were directly used in the fitting. A Matlab (Mathworks, Natick, MA) function fmincon was used to minimize the relative error |R1,exp – R1,fitted|/R1,exp.
Results
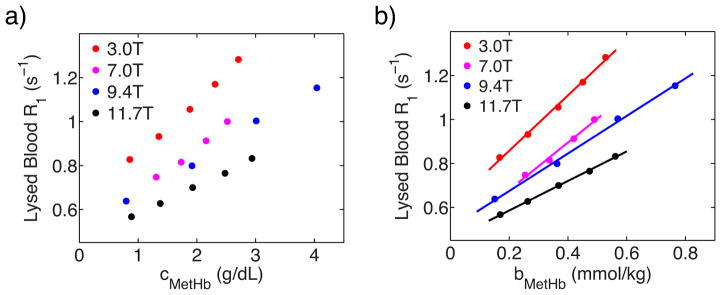
The paramagnetic effect of methemoglobin was studied by measuring R1 of fully oxygenated lysed blood samples with different methemoglobin fractions and the same total hemoglobin concentration (Figure 1). Because the diamagnetic effects from normal hemoglobin and methemoglobin are the same, r1para,MetHb could be directly derived from the slope as listed in Table 1.
Figure 1.
a) The dependence of lysed blood R1 values on the methemoglobin’s concentration. b) Linear fitting of lysed blood R1 values as a function of methemoglobin’s concentration under fully oxygenated conditions.
Table 1.
Fitted paramagnetic relaxivities of methemoglobin and deoxyhemoglobin, diamagnetic relaxivities of albumin and hemoglobin, and relaxation rate of saline, with error indicating 95% confidence interval of fitting.
| B0 (T) | 3.0 | 7.0 | 9.4 | 11.7 |
|---|---|---|---|---|
| r1para,MetHb/103 (mol/kg×s) −1 | 1.26+/−0.13 | 1.08+/−0.30 | 0.854+/−0.13 | 0.672+/−0.040 |
| r1dia,Alb (mol/kg×s) −1 | 172+/−9 | 114+/−13 | 114+/−8 | 96.2+/−5.2 |
| r1dia,Hb (mol/kg×s) −1 | 62.9+/−2.4 | 45.1+/−9.1 | 47.2+/−5.4 | 43.3+/−9.9 |
| r1para,deoxyHb (mol/kg×s) −1 | 65.6+/−8.8 | 56.2+/−8.1 | 64.9+/−8.9 | 58.2+/−5.0 |
| R1,saline (s−1) | 0.287+/−0.009 | 0.263+/−0.007 | 0.232+/−0.007 | 0.235+/−0.004 |
Combining water R1 data in plasma and saline solution at 37 °C (Table 2), the diamagnetic relaxivity of albumin at cAlb = 0.75 mM (14) was calculated as
Table 2.
Measured longitudinal relaxation rates of plasma and saline solution at 37°C with error indicating 95% confidence interval in the fitting of inversion-recovery curves.
| B0 (T) | 3.0 | 7.0 | 9.4 | 11.7 |
|---|---|---|---|---|
| R1plasma (s−1) | 0.383+/−0.003 | 0.328+/−0.005 | 0.318+/−0.003 | 0.296+/−0.003 |
| R1saline (s−1) | 0.251+/−0.004 | 0.240+/−0.005 | 0.229+/−0.003 | 0.222+/−0.001 |
| [16] |
and listed in Table 1.
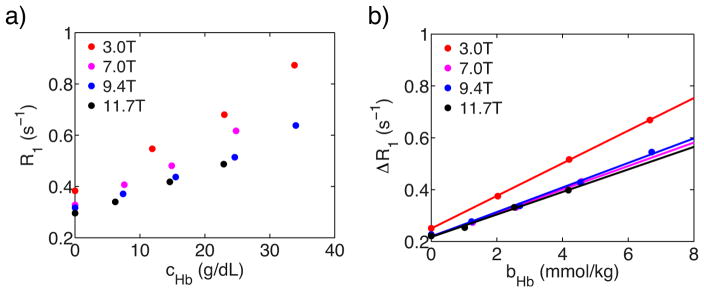
The diamagnetic effect of hemoglobin r1dia,Hb was studied by measuring R1 of fully oxygenated lysed blood samples with different hemoglobin concentrations (Figure 2). Because the lysed blood samples with targeted hemoglobin concentrations were prepared by mixing plasma, albumin concentrations in different samples were different. Moreover, the methemoglobin concentrations in different samples were different. Therefore, the measured R1 should be corrected by removing contributions of albumin’s diamagnetic relaxation and methemoglobin’s paramagnetic relaxation following Eq. [17].
Figure 2.
a) The dependence of lysed blood R1 values on the hemoglobin’s concentration. b) Linear fitting of the corrected lysed blood relaxation rate ΔR1 as a function of hemoglobin’s molality concentration at fully oxygenated conditions.
| [17] |
Fig. 2b shows the linear fitting of this corrected lysed blood ΔR1 (Table 3) as a function of hemoglobin concentration. The r1dia,Hb was derived from the slope (Table 4).
Table 3.
Measured (R1) and corrected (ΔR1) lysed blood relaxation rates at fully oxygenated conditions.
| B0 (T) | bHb (mM/kg) | fMetHb | pO2(mmHg) | bAlb (mM/kg) | R1 (s−1) | ΔR1 (s−1) |
|---|---|---|---|---|---|---|
| 3.0 | 6.66 | 0.024 | 111 | 0.00 | 0.873 | 0.672 |
| 4.20 | 0.022 | 97 | 0.27 | 0.680 | 0.517 | |
| 2.03 | 0.028 | 144 | 0.53 | 0.547 | 0.385 | |
| 0.00 | 0 | 95 | 0.77 | 0.383 | 0.251 | |
| 6.44 | 0.026 | 0.01 | 0.827 | |||
| 6.44 | 0.041 | 0.01 | 0.932 | |||
| 6.44 | 0.057 | 0.01 | 1.056 | |||
| 6.44 | 0.070 | 0.01 | 1.170 | |||
| 6.44 | 0.082 | 0.01 | 1.282 | |||
|
| ||||||
| 7.0 | 4.58 | 0.022 | 350 | 0.23 | 0.617 | 0.482 |
| 2.59 | 0.021 | 288 | 0.46 | 0.481 | 0.369 | |
| 1.26 | 0.021 | 268 | 0.62 | 0.407 | 0.307 | |
| 0.00 | 0 | 167 | 0.77 | 0.328 | 0.240 | |
| 6.36 | 0.040 | 0.01 | 0.747 | |||
| 6.36 | 0.053 | 0.01 | 0.815 | |||
| 6.36 | 0.066 | 0.01 | 0.912 | |||
| 6.36 | 0.077 | 0.01 | 1.000 | |||
|
| ||||||
| 9.4 | 6.72 | 0.016 | 102 | 0.00 | 0.638 | 0.546 |
| 4.54 | 0.015 | 105 | 0.23 | 0.514 | 0.429 | |
| 2.70 | 0.020 | 104 | 0.45 | 0.437 | 0.339 | |
| 1.23 | 0.020 | 103 | 0.62 | 0.371 | 0.279 | |
| 0.00 | 0 | 106 | 0.77 | 0.317 | 0.229 | |
| 5.58 | 0.027 | 0.10 | 0.638 | |||
| 5.58 | 0.065 | 0.10 | 0.799 | |||
| 5.58 | 0.102 | 0.10 | 1.003 | |||
| 5.58 | 0.137 | 0.10 | 1.153 | |||
|
| ||||||
| 11.7 | 4.18 | 0.021 | 113 | 0.27 | 0.487 | 0.402 |
| 2.53 | 0.022 | 114 | 0.47 | 0.418 | 0.335 | |
| 1.02 | 0.022 | 139 | 0.65 | 0.340 | 0.263 | |
| 0.00 | 0 | 98 | 0.77 | 0.296 | 0.222 | |
| 5.84 | 0.029 | 0.07 | 0.567 | |||
| 5.84 | 0.045 | 0.07 | 0.627 | |||
| 5.84 | 0.063 | 0.07 | 0.700 | |||
| 5.84 | 0.081 | 0.07 | 0.765 | |||
| 5.84 | 0.096 | 0.07 | 0.832 | |||
Table 4.
Measured relaxation rates of blood water at different fields, Hct, oxygenation fraction, metHb fraction and pO2
| 3T | 7T | 9.4T | 11.7T | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||||||||
| Hct | Y | fMetHb | pO2 | R1(s) | Hct | Y | fMetHb | pO2 | R1(s) | Hct | Y | fMetHb | pO2 | R1(s) | Hct | Y | fMetHb | pO2 | R1(s) |
| 0.32 | 0.80 | 0.015 | 47 | 0.525 | 0.31 | 0.88 | 0.019 | 58 | 0.429 | 0.30 | 0.98 | 0.017 | 85 | 0.400 | 0.31 | 1.00 | 0.018 | 108 | 0.385 |
| 0.68 | 0.015 | 44 | 0.531 | 0.74 | 0.019 | 42 | 0.436 | 0.89 | 0.017 | 57 | 0.408 | 0.88 | 0.017 | 50 | 0.393 | ||||
| 0.59 | 0.013 | 37 | 0.550 | 0.62 | 0.014 | 31 | 0.447 | 0.77 | 0.016 | 40 | 0.411 | 0.88 | 0.017 | 50 | 0.391 | ||||
| 0.59 | 0.013 | 40 | 0.549 | 0.51 | 0.015 | 29 | 0.458 | 0.61 | 0.016 | 35 | 0.423 | 0.75 | 0.019 | 88 | 0.408 | ||||
| 0.45 | 0.98 | 0.019 | 109 | 0.589 | 0.45 | 0.79 | 0.017 | 45 | 0.487 | 0.53 | 0.016 | 31 | 0.440 | 0.59 | 0.018 | 34 | 0.434 | ||
| 0.96 | 0.018 | 86 | 0.590 | 0.75 | 0.018 | 45 | 0.501 | 0.39 | 0.99 | 0.019 | 90 | 0.426 | 0.38 | 1.00 | 0.018 | 99 | 0.395 | ||
| 0.81 | 0.017 | 74 | 0.615 | 0.61 | 0.014 | 31 | 0.509 | 0.80 | 0.016 | 43 | 0.440 | 0.83 | 0.016 | 48 | 0.405 | ||||
| 0.77 | 0.016 | 48 | 0.618 | 0.50 | 0.013 | 29 | 0.515 | 0.75 | 0.015 | 40 | 0.444 | 0.72 | 0.014 | 40 | 0.420 | ||||
| 0.72 | 0.014 | 45 | 0.615 | 0.56 | 0.80 | 0.017 | 47 | 0.545 | 0.66 | 0.014 | 34 | 0.453 | 0.39 | 1.00 | 0.018 | 106 | 0.403 | ||
| 0.72 | 0.014 | 42 | 0.617 | 0.68 | 0.015 | 35 | 0.561 | 0.57 | 0.013 | 31 | 0.461 | 0.99 | 0.018 | 80 | 0.399 | ||||
| 0.63 | 0.014 | 42 | 0.639 | 0.58 | 0.014 | 30 | 0.577 | 0.44 | 0.99 | 0.017 | 88 | 0.443 | 0.90 | 0.017 | 53 | 0.409 | |||
| 0.52 | 0.012 | 38 | 0.648 | 0.45 | 0.013 | 23 | 0.597 | 0.84 | 0.017 | 49 | 0.454 | 0.82 | 0.013 | 44 | 0.415 | ||||
| 0.56 | 0.98 | 0.019 | 34 | 0.627 | 0.63 | 0.87 | 0.018 | 51 | 0.569 | 0.82 | 0.017 | 50 | 0.455 | 0.72 | 0.015 | 40 | 0.438 | ||
| 0.81 | 0.018 | 93 | 0.661 | 0.76 | 0.017 | 38 | 0.579 | 0.75 | 0.016 | 41 | 0.470 | 0.61 | 0.014 | 36 | 0.451 | ||||
| 0.8 | 0.017 | 52 | 0.668 | 0.63 | 0.016 | 31 | 0.599 | 0.65 | 0.015 | 39 | 0.489 | 0.50 | 0.013 | 33 | 0.461 | ||||
| 0.71 | 0.016 | 49 | 0.679 | 0.50 | 0.015 | 28 | 0.607 | 0.55 | 0.013 | 32 | 0.504 | 0.51 | 0.013 | 32 | 0.452 | ||||
| 0.62 | 0.014 | 43 | 0.685 | 0.75 | 0.86 | 0.019 | 55 | 0.618 | 0.53 | 0.98 | 0.018 | 83 | 0.469 | 0.44 | 0.99 | 0.017 | 98 | 0.414 | |
| 0.54 | 0.013 | 38 | 0.693 | 0.71 | 0.017 | 37 | 0.651 | 0.93 | 0.018 | 63 | 0.476 | 0.98 | 0.017 | 94 | 0.416 | ||||
| 0.67 | 0.97 | 0.019 | 33 | 0.685 | 0.63 | 0.016 | 31 | 0.673 | 0.80 | 0.016 | 44 | 0.497 | 0.95 | 0.017 | 91 | 0.421 | |||
| 0.9 | 0.019 | 84 | 0.699 | 0.50 | 0.014 | 27 | 0.694 | 0.70 | 0.014 | 39 | 0.505 | 0.86 | 0.016 | 57 | 0.424 | ||||
| 0.76 | 0.016 | 68 | 0.700 | 0.63 | 0.014 | 38 | 0.517 | 0.74 | 0.015 | 50 | 0.440 | ||||||||
| 0.71 | 0.016 | 52 | 0.737 | 0.56 | 0.013 | 35 | 0.530 | 0.69 | 0.014 | 47 | 0.450 | ||||||||
| 0.62 | 0.014 | 49 | 0.740 | 0.64 | 0.98 | 0.017 | 81 | 0.518 | 0.64 | 0.014 | 44 | 0.456 | |||||||
| 0.53 | 0.014 | 41 | 0.784 | 0.97 | 0.016 | 74 | 0.519 | 0.55 | 0.013 | 38 | 0.464 | ||||||||
| 0.49 | 0.013 | 39 | 0.763 | 0.82 | 0.016 | 49 | 0.554 | 0.54 | 0.013 | 38 | 0.455 | ||||||||
| 0.71 | 0.014 | 41 | 0.574 | 0.53 | 1.00 | 0.018 | 94 | 0.433 | |||||||||||
| 0.63 | 0.014 | 38 | 0.602 | 0.98 | 0.018 | 93 | 0.436 | ||||||||||||
| 0.51 | 0.012 | 34 | 0.639 | 0.86 | 0.016 | 56 | 0.454 | ||||||||||||
| 0.75 | 0.98 | 0.017 | 87 | 0.54 | 0.81 | 0.015 | 44 | 0.466 | |||||||||||
| 0.98 | 0.017 | 87 | 0.541 | 0.69 | 0.014 | 38 | 0.487 | ||||||||||||
| 0.79 | 0.016 | 52 | 0.598 | 0.67 | 0.013 | 36 | 0.505 | ||||||||||||
| 0.74 | 0.016 | 50 | 0.609 | 0.60 | 0.014 | 36 | 0.499 | ||||||||||||
| 0.65 | 0.015 | 41 | 0.628 | 0.53 | 0.012 | 32 | 0.506 | ||||||||||||
| 0.51 | 0.012 | 31 | 0.511 | ||||||||||||||||
| 0.64 | 0.99 | 0.017 | 89 | 0.468 | |||||||||||||||
| 0.79 | 0.016 | 43 | 0.506 | ||||||||||||||||
| 0.69 | 0.013 | 36 | 0.531 | ||||||||||||||||
| 0.53 | 0.012 | 29 | 0.538 | ||||||||||||||||
| 0.71 | 0.98 | 0.017 | 78 | 0.483 | |||||||||||||||
| 0.85 | 0.016 | 50 | 0.513 | ||||||||||||||||
| 0.78 | 0.017 | 46 | 0.532 | ||||||||||||||||
| 0.67 | 0.015 | 39 | 0.563 | ||||||||||||||||
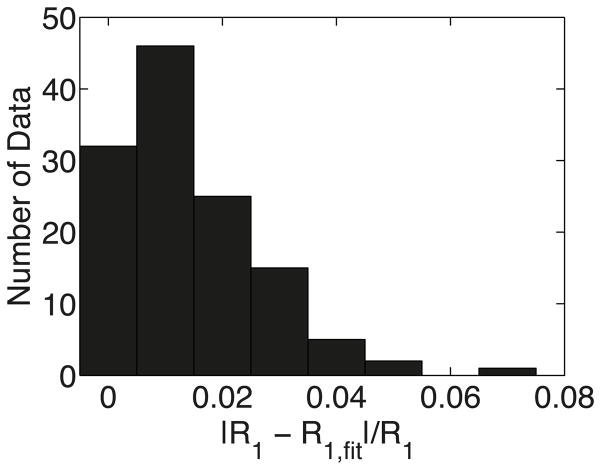
To verify our model for whole blood, multiple whole blood R1 data (Table 4) at 3T, 7T, 9.4T, 11.7T, at various Y (0.48 – 1.00), Hct (0.31 – 0.75) and fMetHb (0.016–0.028) were fitted using Eq. [14]. Figure 3 shows a summary of the fitting accuracy, indicating that our model fitted the experimental data well, with average relative error (R1-R1,fit)/R1 of 1.4%. The fitted parameters r1para,deoxyHb and R1saline are listed in Table 1, and the fitted R1saline agreed with the R1saline measured separately in experiments (Table 2).
Figure 3.
Histogram summarizing the relative errors between the experimental whole blood R1 and fitted R1.
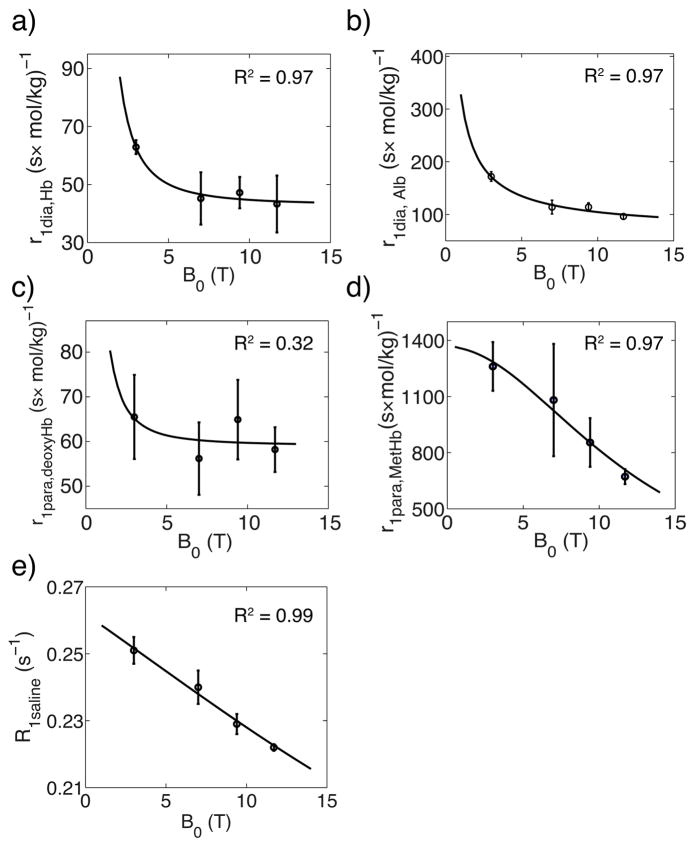
Fig. 4 shows the magnetic field dependence of the diamagnetic relaxivity of hemoglobin (Fig. 4a), diamagnetic relaxivity of albumin (Fig. 4b), paramagnetic relaxivity of deoxyhemoglobin (Fig. 4c) and paramagnetic relaxivity of methemoglobin (Fig. 4d), and the water R1 of saline solution (Fig. 4e). The diamagnetic relaxivities of albumin and hemoglobin were fitted (Figs 4a,b) using the following empirical equation proposed by Lindstrom and Koenig (16).
Figure 4.
The magnetic field dependence of r1dia,Hb (a), r1dia,Alb (b), r1para,deoxyHb (c) r1para,MetHb (d) and R1saline (e), and numerical fitting using Freed’s equation (65,66) (paramagnetic relaxivity, solid line) and Lindstrom and Koenig’s Equation (16) (diamagnetic relaxivity and R1saline, solid line)
| [18] |
with the 1H gyromagnetic ratio γH and empirical constants P1 = 9.45×109 s−2×kg/mol, P2 = 2.88×10−4 s, P3 = 0.822 and P4 = 64.9 (s×mol/kg) −1 for r1dia,Alb and P1 = 4.22×1015 (s−2×kg/mol), P2 = 4.55×10−4 s, P3 = 1.97 and P4 = 42.9 (s×mol/kg) −1 for r1dia,Hb. The water T1 in saline solution R1saline also can be predicted using Eq. [18] with P1 = 3.88×109 s−2, P2 = 6.68×10−11 s, P3 = 1.11 and P4 = 2.41×10−3 s−1. The paramagnetic relaxivities of deoxyhemoglobin and methemoglobin were fitted (Figs 4c,d) using the outer sphere model of Freed (65,66) which described the water molecules diffusing around the paramagnetic complex:
| [19] |
with the proton and electron Larmor frequencies ωH and ωS, and empirical constants P1 = 6.40×106 (s×mol/kg) −1, τ = 9.72×10−6 s, τS = 3.07×10−10 s for r1para,MetHb, and P1 = 8.55×103 (s×mol/kg) −1, τ = 8.68×10−9 s, τS = 8.97×10−12 s for r1para,deoxyHb.
Discussion
Lysed and whole blood experimental R1 data were used to validate a simple longitudinal relaxation model for blood water and to evaluate the paramagnetic and diamagnetic effects of albumin, hemoglobin and methemoglobin at multiple fields. For the diamagnetic relaxivities of hemoglobin, previous studies (8,10,14,17,20,21,23,26–28) have quantitatively described the diamagnetic relaxation enhancement of hemoglobin as Hct dependence using the empirical equation R1=A×Hct+B. In our model, this Hct dependent coefficient A can be approximated by the product of the diamagnetic relaxivity r1dia,Hb and the hemoglobin concentration in the erythrocyte (bHb = 6.49mmol/kg), which is 0.41 s−1 at 3T and 0.29 s−1 at 7T. This is comparable to the reported A value as ~0.5 s−1 at 3T (17,20) and 0.34 s−1 at 7T (19) in the previous human or bovine blood studies. As shown in Fig 4, the diamagnetic longitudinal relaxivities of albumin and hemoglobin decrease as magnetic field increases, which follows the trend observed by Lindstrom and Koenig (16) in the CO bound hemoglobin solution. Therefore, the equation from Lindstrom and Koenig (16) (Eq. [18]) was used to fit r1dia,Alb and r1dia,Hb in the Fig 4. Note that we have only limited number of field data for this multiple parameter fit, but can be used to numerically extrapolate and estimate diamagnetic relaxivity values at unknown magnetic fields around our measured magnetic field range.
Our paramagnetic relaxivities of deoxyhemoglobin r1para,deoxyHb (per hemoglobin complex) at 3T (65.6 (mol/kg×s) −1) and 7T (56.2 (mol/kg×s) −1) agree reasonably with r1para,deoxyHb reported by Blockley et al. (10) as 14.6×4 (mol/L×s) −1 per hemoglobin at 3T and 10.6×4 (mol/L×s) −1 per hemoglobin at 7T. Our paramagnetic relaxivities of methemoglobin r1para,MetHb (per hemoglobin complex) are also comparable to the r1para,MetHb of 175×4 (M×s) −1 per hemoglobin measured at 220MHz (67). At the same time, the paramagnetic relaxivity of methemoglobin r1para,MetHb decreases with increasing magnetic field following the NMR relaxation dispersion curve measured by Koenig et al. (68), while the paramagnetic relaxivities of deoxyhemoglobin r1para,deoxyHb have weak magnetic field dependence which was also observed by Blockley et al. (10). Although initial studies about the paramagnetic relaxation in methemoglobin attributed the relaxation enhancement to the “inner sphere” (67,69) mechanism, i.e. only water ligated with heme relaxes fast, and then exchange with bulk water. However, an extensive investigation of proton relaxation dependence on temperature (70) had shown that the exchange rate between ligated water and bulk water was not fast enough to induce the fast relaxation, and Koenig et al. (36) measured the relaxation dispersion curve at multiple magnetic fields and proved the “outer sphere” mechanism, i.e. the fluctuation of the dipolar coupling between water and paramagnetic protein due to water diffusion, dominated the paramagnetic relaxation. Therefore, Freed’s diffusion model (65,66) which described water molecules diffusing around the paramagnetic complex was used to fit the field dependence of the paramagnetic relaxivities of methemoglobin and deoxyhemoglobin in Fig 4. Similar to the fitting of diamagnetic relaxivity dependence on the magnetic field, the fit of Eq. [19] should be considered as a numerical extrapolation due to the limited number of experimental data.
The good fitting of our model in terms of the difference between the experimental and predicted T1 values over a large number of blood data (Fig. 3) supports our model and thus should allow the fitted relaxivities at multiple fields (3.0 T, 7.0 T, 9.4 T and 11.7 T) to be used to calculate the blood T1 for quantitative MRI experiments. Table 5 compares the blood T1 calculated from our model and the human blood T1 measured by other groups. They agree well except for a venous blood T1 measured at 7T by Rooney et al. (29). Therefore, the blood T1 calculated from our model (Table 6) can be a reference for studies on 9.4T and 11.7T animal scanners as well as on ultra high human field scanners that are now becoming available. In addition to adult blood, the results in Table 5 show that our model is also able to predict blood T1 in neonates. In neonate blood, the fetal erythrocyte’s cell volume (MCV) is 20% larger than adult erythrocyte (71), and the most of hemoglobin is hemoglobin F, which replaces two beta subunits with two gamma subunits, but has similar overall structure as the adult hemoglobin. This shows the versatility of our model to predict abnormal blood T1.
Table 5.
Comparison between human blood T1 measured in vivo and blood T1 calculated by our model.
| B0 | Hct | Exp. T1 (ms) | Cal. T1 (ms) | ||
|---|---|---|---|---|---|
| Adult (20) | Arterial | 1.5T | 0.47+/−0.03 | 1499+/−74 | 1439 |
| Adult Male(25) | Venous | 1.5T | 1429+/−21 | 1229–1387 | |
| Adult Female(25) | Venous | 1.5T | 1531+/−29 | 1317–1462 | |
| Adult (20) | Arterial | 3T | 0.47+/−0.03 | 1779+/−80 | 1849 |
| Adult (20) | Venous | 3T | 0.47+/−0.03 | 1694+/−77 | 1668 |
| Adult Male (24) | Venous | 3T | 1677+/−120 | 1597–1743 | |
| Adult Female (24) | Venous | 3T | 1769+/−100 | 1680–1809 | |
| Adult Male (25) | Venous | 3T | 1618+/−30 | 1597–1743 | |
| Adult Female (25) | Venous | 3T | 1681+/−87 | 1680–1809 | |
| Adult (18) | Venous | 3T | 1825+/−104 | 1597–1809 | |
| Neonate (22) | Venous | 3T | 0.423 | 1757 | 1726 |
| Sickle Cell Patient | Venous | 3T | 0.233+/−0.039 | 1910+/−89 | 1990 |
| Female (18) | |||||
| Sickle Cell Patient | Venous | 3T | 0.235+/−0.029 | 1938+/−82 | 1987 |
| Male (18) | |||||
| Adult Male (25) | Venous | 7T | 2012+/−119 | 1945–2116 | |
| Adult Female (25) | Venous | 7T | 2163+/−94 | 2043–2193 | |
| Adult (29) | Venous | 7T | 2587+−283 | 1945–2193 |
In the calculation, all relaxivities and R1saline were obtained from Table 1. fMetHb was set as the average value 0.004 (73) in normal adult blood. The oxygenation fraction Y was 1.0 for arterial blood and 0.65 for venous blood, based on published range of 0.55 – 0.75 (74,75). If Hct is not specified, T1 range was calculated according to the physiological range of 0.41 – 0.53 for male and 0.36 – 0.46 for female (71).
Table 6.
The predicted arterial and venous blood T1 in the physiological range of health human. The calculation parameters are the same as the calculation in Table 5.
| Hct | Y | T1 (ms)
|
||||
|---|---|---|---|---|---|---|
| 3.0 T | 7.0 T | 9.4 T | 11.7 T | |||
| Male | 0.41–0.53 | 1.00 | 1789–1910 | 2191–2329 | 2472–2691 | 2585–2810 |
| Female | 0.36–0.46 | 1.00 | 1859–1963 | 2271–2388 | 2597–2789 | 2714–2910 |
| Male | 0.41–0.53 | 0.65 | 1597–1743 | 1945–2116 | 2122–2373 | 2239–2497 |
| Female | 0.36–0.46 | 0.65 | 1680–1809 | 2043–2193 | 2264–2490 | 2385–2616 |
| Male | 0.47 | 0.55–0.75 | 1623–1716 | 1971–2090 | 2163–2330 | 2283–2449 |
| Female | 0.41 | 0.55–0.75 | 1700–1788 | 2063–2173 | 2296–2456 | 2420–2579 |
Besides predicting blood T1 values at 3T, 7T, 9.4T, 11.7T, the blood T1 at other fields can also be predicted from the curves in Fig 4. For example, using Eq. [18], Eq. [19] and our fitted parameters, we can extrapolate the relaxivities at 4.7T as r1dia,Hb of 51.1 (mol/kg×s) −1, r1dia,Alb of 138 (mol/kg×s) −1, r1para,deoxyHb of 61.7 (mol/kg×s) −1, r1para,MetHb of 1.19×103 (mol/kg×s) −1 and R1saline of 0.246 s−1. Meyer et al. (27) measured at 4.7T the oxygenation dependence of bovine blood (Hct=0.4) as R1 = A × (1-Y) + B, where A=0.12+/−0.03 s−1 was defined as the paramagnetic coefficient of deoxyhemoglobin. According to Eq. [14], this paramagnetic coefficient A can be expressed as fery,water×bHb×r1para,deoxyHb, which can be calculated as 0.13 s−1 based on our fitted parameters r1para,deoxyHb (61.7 (mol/kg×s) −1) and agrees well with the result from Meyer et al. (27). At the same time, Dobre et al. (11) measured bovine blood T1 as 1833+/−49 ms at Hct=0.43+/−0.03 and Y=0.81+/−0.13. Assuming a fMetHb=2% for the regular bovine blood, we calculated blood T1 as 2004 ms under the same conditions based on our fitted relaxivities, which is similar to the result from Dobre et al. (11). Extrapolating to relaxation times at 1.5T is less accurate due to the nonlinear steeper field dependence of the diamagnetic albumin and diamagnetic and paramagnetic hemoglobin relaxivities (Figs. 4a-c). When extrapolating relaxivities at 1.5 T, we found r1dia,Hb = 121 (mol/kg×s) −1, r1dia,Alb = 253 (mol/kg×s) −1, r1para,,deoxyHb = 80.3 (mol/kg×s) −1, r1para,MetHb = 1.34×103 (mol/kg×s) −1 and R1saline = 0.257 s−1. Using these numbers to estimate the arterial blood T1 at Hct = 0.36–0.53 at 1.5 T, we found it to be 1367–1585 ms for a methemoglobin fraction of 0.004. This is comparable with a previous in vivo human study (1499+/−74ms, (20)), in vitro human blood study (1435 ms (9), measured at 23°C) and in vitro bovine blood study (1400 ms, (72)). The venous blood T1 measured in sagittal sinus (25) is also comparable to our prediction (Table 2).
The blood T1 predicted from our model can also be used to evaluate the MRI experiments related to blood T1 such as the VASO experiment to determine the relative cerebral blood volume (CBV) change during activation (3) and the ASL experiment to measure cerebral blood flow (CBF) (77). The quantification in both experiments depends on the accuracy of the blood T1 value used because the VASO experiment uses blood T1 to calculate an inversion time (TI) to null the blood signal while blood T1 is an important parameter in ASL experiment to calculate the label decay. When performing these experiments, the blood T1 is generally considered to be a constant at certain magnetic field, but as we discussed, even in a healthy human, the blood T1 could vary in a range due to different Hct, Y (venous blood) and fMetHb. For example, in healthy people, Hct has a ~10% variation (71), fMetHb has a ~1% variation (73) while Y in venous blood has a range of 0.55–0.75 (74,75). The blood T1 could change 100–150ms at 3T for these blood parameters’ variation. Using the typical experiment conditions (76,77), the CBV change during the activation could have a 1%–2% difference based on the equations in (76) while the CBF could have ~20% difference for PCASL and ~10% difference for QUIPSS II PASL based on the simple model in ASL “white paper” (77).
There are several assumptions in our model. The key assumption is that a single R1 dominates the inversion-recovery process of the blood despite the erythrocyte and plasma compartments having different R1 and that this single blood R1 can be simply expressed as the weighted sum of R1 in plasma and erythrocyte (Eq. 1). According to chemical exchange theory (48), this assumption is valid when
| [20] |
in which kexch is the water exchange rate between plasma and erythrocyte. Using a lifetime of about 8 ms for water inside the erythrocyte (78), the exchange life time (1/τexch= 1/τery + 1/τplasma) for this system would be 6.8 ms for hematocrit fraction (Hct) = 0.3 and 2.5 ms for Hct = 0.75, corresponding to kexch (= 1/τexch) values of 147 and 400 Hz, respectively. This exchange rate is much faster than the R1 difference in erythrocyte and in plasma as measured in this study and many other studies. Note that this fast-exchange condition for R1 is different from the exchange-narrowing condition for R2 which requires water exchange rate between plasma and erythrocyte to be much faster than the water chemical shift difference in plasma and in erythrocyte. Even if the peaks for water in plasma and in erythrocyte are separated, they still share the same averaged longitudinal relaxation time as shown in Eq. 1. (48).
Another assumption in our model is that all hemoglobins are homogenous. This assumption is valid for the normal adult blood. But for sickle cell disease, the hemoglobin is mutated as HbS and forms fibers in its deoxy-state (79,80). This different hemoglobin, especially the fibers formed by polymerization could change the water-protein interaction and thus the blood T1. According to a previous in vivo study, the blood T1 of patients with sickle cell disease is comparable to normal volunteers and thus the values found with our model (Table 5), but caution needs to be taken when using our model for sickle cell disease until more measurements of blood R1 under this condition confirm the above result.
Conclusion
We derived a comprehensive model for the effects of hemoglobin concentration, hematocrit fraction, oxygenation fraction, methemoglobin fraction and albumin concentration on the water 1H T1 in blood, and confirmed the equations experimentally in whole blood samples at 3T, 7T, 9.4T and 11.7T. The fitted parameters presented here provide a good calibration for calculating human blood T1, as demonstrated by excellent agreement with human blood T1 values measured in vivo by other groups. Our model should be useful to predict blood T1 for arbitrary hemoglobin concentration, hematocrit fraction, oxygenation, methemoglobin fraction and albumin concentration at multiple fields.
Acknowledgments
Grant support: NIH: P41 EB015909, NIH: K25 HL121192
We are grateful to Drs. James Pekar and Paul Bottomley for helpful discussions. Grant support was provided by the National Institute of Health (NIH) (P41EB015909 and K25 HL121192).
References
- 1.Detre Ja, Leigh JS, Williams DS, Koretsky AP. Perfusion imaging. Magn Reson Med. 1992;23:37–45. doi: 10.1002/mrm.1910230106. [DOI] [PubMed] [Google Scholar]
- 2.Edelman RR, Chien D, Kim D. Fast selective black blood MR imaging. Radiology. 1991;181:655–660. doi: 10.1148/radiology.181.3.1947077. [DOI] [PubMed] [Google Scholar]
- 3.Lu H, Golay X, Pekar JJ, Van Zijl PCM. Functional magnetic resonance imaging based on changes in vascular space occupancy. Magn Reson Med. 2003;50:263–274. doi: 10.1002/mrm.10519. [DOI] [PubMed] [Google Scholar]
- 4.Bradley WG. MR appearance of hemorrhage in the brain. Radiology. 1993;189:15–26. doi: 10.1148/radiology.189.1.8372185. [DOI] [PubMed] [Google Scholar]
- 5.Cohen M, McGuire W, Cory D, Smith J. MR appearance of blood and blood products - an in vitro study. Am J Roentgenol. 1986;146:1293–1297. doi: 10.2214/ajr.146.6.1293. [DOI] [PubMed] [Google Scholar]
- 6.Bodansky O. Methemoglobinemia and methemoglobin-producing compounds. Pharmacol Rev. 1951;3:144–196. [PubMed] [Google Scholar]
- 7.Prchal JT, Gregg XT. Red cell enzymes. Hematology Am Soc Hematol Educ Program. 2005:19–23. doi: 10.1182/asheducation-2005.1.19. [DOI] [PubMed] [Google Scholar]
- 8.Atalay MK, Reeder SB, Zerhouni EA, Forder JR. Blood oxygenation dependence of T1 and T2 in the isolated, perfused rabbit heart at 4.7T. Magn Reson Med. 1995;34:623–627. doi: 10.1002/mrm.1910340420. [DOI] [PubMed] [Google Scholar]
- 9.Barth M, Moser E. Proton NMR relaxation times of human blood samples at 1.5 T and implications for functional MRI. Cell Mol Biol. 1997;43:783–791. [PubMed] [Google Scholar]
- 10.Blockley NP, Jiang L, Gardener AG, Ludman CN, Francis ST, Gowland PA. Field strength dependence of R1 and R2* relaxivities of human whole blood to ProHance, Vasovist, and deoxyhemoglobin. Magn Reson Med. 2008;60:1313–1320. doi: 10.1002/mrm.21792. [DOI] [PubMed] [Google Scholar]
- 11.Dobre MC, Ugurbil K, Marjanska M. Determination of blood longitudinal relaxation time (T1) at high magnetic field strengths. Magn Reson Imaging. 2007;25:733–735. doi: 10.1016/j.mri.2006.10.020. [DOI] [PubMed] [Google Scholar]
- 12.Bryant RG, Marill K, Blackmore C, Francis C. Magnetic relaxation in blood and blood clots. Magn Reson Med. 1990;13:133–144. doi: 10.1002/mrm.1910130112. [DOI] [PubMed] [Google Scholar]
- 13.Gomori J, Grossman R, Yuip C, Asakura T. NMR relaxation times of blood: dependence on field strength, oxidation state, and cell integrity. J Comput Assist Tomogr. 1987;11:684–690. [PubMed] [Google Scholar]
- 14.Grgac K, van Zijl PCM, Qin Q. Hematocrit and oxygenation dependence of blood (1)H2O T1 at 7 tesla. Magn Reson Med. 2013;70:1153–1159. doi: 10.1002/mrm.24547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lin AL, Qin Q, Zhao X, Duong TQ. Blood longitudinal (T1) and transverse (T2) relaxation time constants at 11.7 Tesla. Magn Reson Mater Phys Biol Med. 2012;25:245–249. doi: 10.1007/s10334-011-0287-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lindstrom TR, Koenig SH. Magnetic-field-dependent water proton spin-lattice relaxation rates of hemoglobin solutions and whole blood. J Magn Reson. 1974;15:344–353. [Google Scholar]
- 17.Lu H, Clingman C, Golay X, van Zijl PCM. Determining the longitudinal relaxation time (T1) of blood at 3.0 Tesla. Magn Reson Med. 2004;52:679–82. doi: 10.1002/mrm.20178. [DOI] [PubMed] [Google Scholar]
- 18.Qin Q, Strouse JJ, van Zijl PCM. Fast measurement of blood T1 in the human jugular vein at 3 Tesla. Magn Reson Med. 2011;65:1297–304. doi: 10.1002/mrm.22723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rane SD, Gore JC. Measurement of T1 of human arterial and venous blood at 7T. Magn Reson Imaging. 2013;31:477–9. doi: 10.1016/j.mri.2012.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shimada K, Nagasaka T, Shidahara M, Machida Y, Tamura H. In vivo measurement of longitudinal relaxation time of human blood by inversion-recovery fast gradient-echo MR imaging at 3T. Magn Reson Med Sci. 2012;11:265–71. doi: 10.2463/mrms.11.265. [DOI] [PubMed] [Google Scholar]
- 21.Thulborn KR, Waterton JC, Matthews PM, Radda GK. Oxygenation Dependence of the Transverse Relaxation Time of Water Protons in Whole Blood at High Field. Biochim Biophys Acta. 1982;714:265–270. doi: 10.1016/0304-4165(82)90333-6. [DOI] [PubMed] [Google Scholar]
- 22.Varela M, Hajnal JV, Petersen ET, Golay X, Merchant N, Larkman DJ. A method for rapid in vivo measurement of blood T1. NMR Biomed. 2011;24:80–8. doi: 10.1002/nbm.1559. [DOI] [PubMed] [Google Scholar]
- 23.De Vis JB, Hendrikse J, Groenendaal F, de Vries LS, Kersbergen KJ, Benders MJNL, Petersen ET. Impact of neonate haematocrit variability on the longitudinal relaxation time of blood: Implications for arterial spin labelling MRI. NeuroImage Clin. 2014;4:517–525. doi: 10.1016/j.nicl.2014.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wu WC, Jain V, Li C, Giannetta M, Hurt H, Wehrli FW, Wang DJJ. In vivo venous blood T1 measurement using inversion recovery true-FISP in children and adults. Magn Reson Med. 2010;64:1140–7. doi: 10.1002/mrm.22484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang X, Petersen ET, Ghariq E, De Vis JB, Webb aG, Teeuwisse WM, Hendrikse J, van Osch MJP. In vivo blood T1 measurements at 1.5 T, 3 T, and 7 T. Magn Reson Med. 2012;70:1082–1086. doi: 10.1002/mrm.24550. [DOI] [PubMed] [Google Scholar]
- 26.Janick P, Hackney D, Grossman R, Asakura T. MR Imaging Various Oxidation States of Intracellular and Extracellular Hemoglobin. Am J Neuroradiol. 1991;12:891–897. [PMC free article] [PubMed] [Google Scholar]
- 27.Meyer M-E, Yu O, Eclancher B, Grucker D, Chambron J. NMR relaxation rates and blood oxygenation level. Magn Reson Med. 1995;34:234–241. doi: 10.1002/mrm.1910340215. [DOI] [PubMed] [Google Scholar]
- 28.Silvennoinen MJ, Kettunen MI, Kauppinen RA. Effects of hematocrit and oxygen saturation level on blood spin-lattice relaxation. Magn Reson Med. 2003;49:568–71. doi: 10.1002/mrm.10370. [DOI] [PubMed] [Google Scholar]
- 29.Rooney WD, Johnson G, Li X, Cohen ER, Kim S-G, Ugurbil K, Springer CS. Magnetic field and tissue dependencies of human brain longitudinal 1H2O relaxation in vivo. Magn Reson Med. 2007;57:308–18. doi: 10.1002/mrm.21122. [DOI] [PubMed] [Google Scholar]
- 30.Uthman E. Understanding anemia (understanding health and sickness series) University Press of Mississippi; 1998. [Google Scholar]
- 31.Hayman LA, Taber KH, Ford JJ, Bryan RN. Mechanisms of MR signal alteration by acute intracerebral blood: old concepts and new theories. AJNR Am J Neuroradiol. 12:899–907. [PMC free article] [PubMed] [Google Scholar]
- 32.Aime S, Fasano M, Paoletti S, Arnelli A, Ascenzi P. NMR relaxometric investigation on human methemoglobin and fluoromethemoglobin. An improved quantitative in vitro assay of human methemoglobin. Magn Reson Med. 1995;33:827–31. doi: 10.1002/mrm.1910330613. [DOI] [PubMed] [Google Scholar]
- 33.Eisenstadt M. NMR relaxation of protein and water protons in methemoglobin solutions. Biophys J. 1981;33:469–74. doi: 10.1016/S0006-3495(81)84907-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bradley WG, Schmidt PG. Effect of methemoglobin formation on the MR appearance of subarachnoid hemorrhage. Radiology. 1985;156:99–103. doi: 10.1148/radiology.156.1.4001427. [DOI] [PubMed] [Google Scholar]
- 35.Day RW, White KS, Hedlund GL. Nitric oxide increases the signal intensity of the T1-weighted magnetic resonance image of blood. J Cardiovasc Magn Reson. 2005;7:667–669. [PubMed] [Google Scholar]
- 36.Koenig S, Brown R, Lindstrom T. Interactions of solvent with the heme region of methemoglobin and fluoro-methemoglobin. Biophys J. 1981;34:397–408. doi: 10.1016/S0006-3495(81)84858-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nummi P, Alanen A, Näntö V, Kormano M. Effect of hemolysis and clotting on proton relaxation times of blood. Acta Radiol Diagn (Stockh) 27:225–30. doi: 10.1177/028418518602700217. [DOI] [PubMed] [Google Scholar]
- 38.Safo MK, Abraham DJ. The X-ray structure determination of bovine carbonmonoxy hemoglobin at 2.1 A resoultion and its relationship to the quaternary structures of other hemoglobin crystal froms. Protein Sci. 2001;10:1091–9. doi: 10.1110/ps.48301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Benga G, Borza T. Diffusional water permeability of mammalian red blood cells. Comp Biochem Physiol B Biochem Mol Biol. 1995;112:653–9. doi: 10.1016/0305-0491(95)00116-6. [DOI] [PubMed] [Google Scholar]
- 40.Jikuya T, Tsutsui T, Shigeta O, Sankai Y, Mitsui T. Species differences in erythrocyte mechanical fragility: Comparison of human, bovine, and ovine cells. ASAIO J. 1998;44:452. [PubMed] [Google Scholar]
- 41.Zhao JM, Clingman CS, Närväinen MJ, Kauppinen Ra, van Zijl PCM. Oxygenation and hematocrit dependence of transverse relaxation rates of blood at 3T. Magn Reson Med. 2007;58:592–7. doi: 10.1002/mrm.21342. [DOI] [PubMed] [Google Scholar]
- 42.Zaharchuk G, Martin AJ, Rosenthal G, Manley GT, Dillon WP. Measurement of cerebrospinal fluid oxygen partial pressure in humans using MRI. Magn Reson Med. 2005;54:113–21. doi: 10.1002/mrm.20546. [DOI] [PubMed] [Google Scholar]
- 43.Medical R. The blood gas handbook. Denmark: Radiometer Medical; 2011. [Google Scholar]
- 44.Kokholm G. Simultaneous measurements of blood pH, pCO2, pO2 and concentrations of hemoglobin and its derivates-a multicenter study. Scand J Clin Lab Invest Suppl. 1990;203:75–86. doi: 10.3109/00365519009087494. [DOI] [PubMed] [Google Scholar]
- 45.Zhou J, Mori S, van Zijl PCM. FAIR excluding radiation damping (FAIRER) Magn Reson Med. 1998;40:712–719. doi: 10.1002/mrm.1910400511. [DOI] [PubMed] [Google Scholar]
- 46.Bloembergen N, Pound R. Radiation damping in magnetic resonance experiments. Phys Rev. 1954;95:8–12. [Google Scholar]
- 47.Zimmerman JR, Brittin WE. Nuclear magnetic resonance studies in multiple phase systems: lifetime of a water molecule in an adsorbing phase on silica gel. J Phys Chem. 1967;61:1328–1333. [Google Scholar]
- 48.McLaughlin A, Leigh J. Relaxation times in systems with chemical exchange: Approximate solutions for the nondilute case. J Magn Reson. 1973;9:296–304. [Google Scholar]
- 49.Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJH. Water Proton MR Properties of Human Blood at 1.5 Tesla_: Magnetic Susceptibility, T1, T2, T*2, and Non-Lorentzian Signal Behavior. Magn Reson Med. 2001;45:533–542. doi: 10.1002/mrm.1072. [DOI] [PubMed] [Google Scholar]
- 50.Silvennoinen MJ, Clingman CS, Golay X, Kauppinen RA, van Zijl PCM. Comparison of the dependence of blood R2 and R2* on oxygen saturation at 1.5 and 4.7 Tesla. Magn Reson Med. 2003;49:47–60. doi: 10.1002/mrm.10355. [DOI] [PubMed] [Google Scholar]
- 51.Kageyama K, Onoyama Y, Kogawa H, Goto E, Tanabe K. The maximum and minimum water content and cell volume of human erythrocytes in vitro. Biophys Chem. 1989;34:79–82. doi: 10.1016/0301-4622(89)80044-4. [DOI] [PubMed] [Google Scholar]
- 52.Klotz IM. Protein hydration and behavior: many aspects of protein behavior can be interpreted in terms of frozen water of hydration. Science. 1958;128:815–822. doi: 10.1126/science.128.3328.815. [DOI] [PubMed] [Google Scholar]
- 53.Koenig SH, Schillinger WE. Nuclear magnetic relaxation dispersion in protein solutions. I. Apotransferrin. J Biol Chem. 1969;244:3283–9. [PubMed] [Google Scholar]
- 54.Nandi N, Bagchi B. Dielectric Relaxation of Biological Water. J Phys Chem B. 1997;101:10954–10961. [Google Scholar]
- 55.Otting G, Liepinsh E. Protein hydration viewed by high-resolution NMR spectroscopy: implications for magnetic resonance image contrast. Acc Chem Res. 1995;28:171–177. [Google Scholar]
- 56.Chanarin I, Brozovic M, Tidmarsh E, Waters D. Blood and its disease. New York: Churchill Livingstone; 1984. [Google Scholar]
- 57.Rhoades RA, Bell DR. Medical phisiology: principles for clinical medicine. 4. Wolters Kluwer; 2008. [Google Scholar]
- 58.Adair GS, Adair ME. The density increments of proteins. Proc R Soc Lond A Math Phys Sci. 1947;190:341–56. doi: 10.1098/rspa.1947.0080. [DOI] [PubMed] [Google Scholar]
- 59.Lentner Co; Ciba-Geigy, editor. Geigy Scientific Tables, Vol 3: Physical Chemistry Composition of Blood, Hematology Somatometric Data. 1985. [Google Scholar]
- 60.Fanelli A, Antonini E, Caputo A. Hemoglobin and myoglobin. Adv Protein Chem. 1964;19:73–222. doi: 10.1016/s0065-3233(08)60189-8. [DOI] [PubMed] [Google Scholar]
- 61.Eaton WA, Henry ER, Hofrichter J, Mozzarelli A. Is cooperative oxygen binding by hemoglobin really understood. Nat Struct Mol Biol. 1999;6:351–358. doi: 10.1038/7586. [DOI] [PubMed] [Google Scholar]
- 62.Imai K. Adair fitting to oxygen equilibrium curves of hemoglobin. Methods Enzymol. 1994;232:559–576. doi: 10.1016/0076-6879(94)32064-0. [DOI] [PubMed] [Google Scholar]
- 63.Johnson CR, Ownby DW, Gill SJ, Peters KS. Oxygen binding constants and stepwise enthalpies for human and bovine hemoglobin at pH 7.6. Biochemistry. 1992;31:10074–10082. doi: 10.1021/bi00156a030. [DOI] [PubMed] [Google Scholar]
- 64.Klotz IM. Hemoglobin-oxygen equilibria: retrospective and phenomenological perspective. Biophys Chem. 2003;100:123–9. doi: 10.1016/s0301-4622(02)00273-9. [DOI] [PubMed] [Google Scholar]
- 65.Freed JH. Dynamic effects of pair correlation functions on spin relaxation by translational diffusion in liquids. II. Finite jumps and independent T1 processes. J Chem Phys. 1978;68:4034–4037. [Google Scholar]
- 66.Bennett HF, Brown RD, Koenig SH, Swartz HM. Effects of nitroxides on the magnetic field and temperature dependence of 1/T1 of solvent water protons. Magn Reson Med. 1987;4:93. doi: 10.1002/mrm.1910040202. [DOI] [PubMed] [Google Scholar]
- 67.Gupta RK, Mildvan AS. Nuclear relaxation studies on human methemoglobin. Observation of cooperativity and alkaline Bohr effect with inositol hexaphosphate. J Biol Chem. 1975;260:240. [PubMed] [Google Scholar]
- 68.Koenig SH, Brown D, Brown RD. Relaxation of solvent protons by paramagnetic ions and its dependence on magnetic field and chemical environment: implications for NMR imaging. Magn Reson Med. 1984;1:478–95. doi: 10.1002/mrm.1910010407. [DOI] [PubMed] [Google Scholar]
- 69.Davidson N, Gold R. The nuclear magnetic relaxation time of water protons in ferrihemoglobin solutions. Biochim Biophys Acta. 1957;26:370–3. doi: 10.1016/0006-3002(57)90018-5. [DOI] [PubMed] [Google Scholar]
- 70.Pifat G, Marici S, Grandja S. A proton magnetic relaxation study of human ferrihaemoglobin in aqueous salt solutions. Biopolymers. 1973;12:905–20. doi: 10.1002/bip.1973.360120418. [DOI] [PubMed] [Google Scholar]
- 71.Hoffman R, Furie B, McGlave P, Silberstein, Leslie E, Shattil SJ, Benz EJJ, Heslop H. Normal blood values: selected reference values for neonatal, pediatric, and adult populations. Hematology: Basic Principles and Practice. 2008 [Google Scholar]
- 72.Lu H, Golay X, van Zijl PCM. Intervoxel heterogeneity of event-related functional magnetic resonance imaging responses as a function of T(1) weighting. Neuroimage. 2002;17:943–55. [PubMed] [Google Scholar]
- 73.Van Slyke DD, Hiller A, Weisiger J, Cruz W. Determination of carbon monoxide in blood and of total and active hemoglobin by carbon monoxide capacity; inactive hemoglobin and methemoglobin contents of normal human blood. J Biol Chem. 1946;166:121–48. [PubMed] [Google Scholar]
- 74.Gibbs E, Lennox W, Nims L, Gibbs F. Arterial and cerebral venous blood: arterial-venous differences in man. J Biol Chem. 1942;144:325–332. [Google Scholar]
- 75.Jain V, Langham MC, Wehrli FW. MRI estimation of global brain oxygen consumption rate. J Cereb Blood Flow Metab. 2010;30:1598–607. doi: 10.1038/jcbfm.2010.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Lu H, Hua J, van Zijl PCM. Noninvasive functional imaging of cerebral blood volume with vascular-space-occupancy (VASO) MRI. NMR Biomed. 2013;26:932–48. doi: 10.1002/nbm.2905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Alsop DC, Detre JA, Golay X, et al. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn Reson Med. 2015;73:102–116. doi: 10.1002/mrm.25197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Herbst MD, Goldstein JH. A review of water diffusion measurement by NMR in human red blood cells. Am J Physiol. 1989;256:1097–1104. doi: 10.1152/ajpcell.1989.256.5.C1097. [DOI] [PubMed] [Google Scholar]
- 79.Stetson CA. The state of hemoglobin in sickled erythrocytes. J Exp Med. 1966;123:341–6. doi: 10.1084/jem.123.2.341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Finch JT, Perutz MF, Bertles JF, Döbler J. Structure of sickled erythrocytes and of sickle-cell hemoglobin fibers. Proc Natl Acad Sci U S A. 1973;70:718–22. doi: 10.1073/pnas.70.3.718. [DOI] [PMC free article] [PubMed] [Google Scholar]