Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Feb 19;6:21302. doi: 10.1038/srep21302

Structural and electronic features of binary Li2S-P2S5 glasses

Koji Ohara 1,a, Akio Mitsui 1,2, Masahiro Mori 1, Yohei Onodera 3, Shinya Shiotani 1, Yukinori Koyama 1, Yuki Orikasa 4, Miwa Murakami 1, Keiji Shimoda 1, Kazuhiro Mori 3, Toshiharu Fukunaga 3, Hajime Arai 1, Yoshiharu Uchimoto 4, Zempachi Ogumi 1
PMCID: PMC4759574  PMID: 26892385

Abstract

The atomic and electronic structures of binary Li2S-P2S5 glasses used as solid electrolytes are modeled by a combination of density functional theory (DFT) and reverse Monte Carlo (RMC) simulation using synchrotron X-ray diffraction, neutron diffraction, and Raman spectroscopy data. The ratio of PSx polyhedral anions based on the Raman spectroscopic results is reflected in the glassy structures of the 67Li2S-33P2S5, 70Li2S-30P2S5, and 75Li2S-25P2S5 glasses, and the plausible structures represent the lithium ion distributions around them. It is found that the edge sharing between PSx and LiSy polyhedra increases at a high Li2S content, and the free volume around PSx polyhedra decreases. It is conjectured that Li+ ions around the face of PSx polyhedra are clearly affected by the polarization of anions. The electronic structure of the DFT/RMC model suggests that the electron transfer between the P ion and the bridging sulfur (BS) ion weakens the positive charge of the P ion in the P2S7 anions. The P2S7 anions of the weak electrostatic repulsion would causes it to more strongly attract Li+ ions than the PS4 and P2S6 anions, and suppress the lithium ionic conduction. Thus, the control of the edge sharing between PSx and LiSy polyhedra without the electron transfer between the P ion and the BS ion is expected to facilitate lithium ionic conduction in the above solid electrolytes.

Lithium ion batteries (LIBs) have been widely used in many applications such as mobile phones, electric vehicles (EVs), and plug-in hybrid electric vehicles (PHVs). To improve their performance in such applications, solid electrolytes have attracted attentions1,2,3, because the realization of an all solid-state battery will enable the miniaturization of battery packages and increase the safety of battery components, compared with that of LIBs with an organic electrolyte. Binary Li2S-P2S5 glasses, which consist of PSx polyhedral anions, are well-known superionic conductors, and are also candidates for such solid electrolytes owing to their high ionic conductivity at room temperature4,5. Recently, novel solid lithium electrolytes such as 70Li2S-29P2S5-1P2S36, 75Li2S-25P2S5-50Li2S-25GeS2 (Li10GeP2S12)7,8, and 75Li2S-25P2S5-200Li2S-100SiS2 (Li11Si2PS12)9 have been reported, which feature liquidlike Li+ ion conduction. All these materials are derived from Li2S-P2S5 glasses. Therefore, the nature of Li2S-P2S5 glasses must be classified in detail to continue the development of advanced Li ionic conductors targeted at the realization of all-solid-state batteries. To clarify the origin of the ionic conduction, the structures of Li2S-P2S5 glasses have been thoroughly explored10,11,12 by reverse Monte Carlo (RMC) simulation13,14. A structural analysis of 70Li2S-30P2S5 glass by RMC simulation based on X-ray and neutron diffraction suggests that a large number of vacancies, which are recognized as fully acceptable units of a Li+ ion, are found around the PS4 tetrahedral anion10 and this structural feature is associated with high Li ionic conductivity15,16. Furthermore, the conduction pathways of the Li+ ions for 50Li2S-50P2S5, 60Li2S-40P2S5, and 70Li2S-30P2S5 glasses were also determined using a combination of RMC simulation and the bond valence sum method11, which suggests that the activation energy of Li+ ion conduction depends on the conduction pathway. However, structural models based on RMC simulation usually do not take the electronic structure into account, which could lead to incorrect electronically conductive structures for solid electrolyte materials that should be insulators.

In this paper, we present a comparative fundamental study of the structures of the 67Li2S-33P2S5 (67Li2S), 70Li2S-30P2S5 (70Li2S), and 75Li2S-25P2S5 (75Li2S) glasses. The lithium ionic conductivities of 67Li2S, 70Li2S, and 75Li2S were 5.6 × 10−5 S/cm, 1.4 × 10−4 S/cm, and 3.0 × 10−4 S/cm, respectively. We also analyze the environment of the Li+ ions on the basis of structural analyses combining X-ray and neutron diffraction with the aid of density functional theory (DFT)/RMC simulation and Raman spectroscopy to reveal the relationship between structural properties and Li ionic conduction.

Results and Discussion

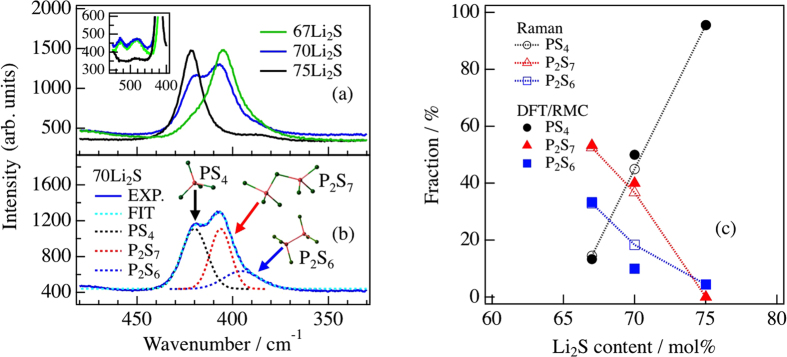
To quantitatively evaluate the fraction of PSx polyhedral anions, the Raman spectra of the 67Li2S, 70Li2S, and 75Li2S glasses were obtained, as shown in Fig. 1a. It is known that bands in the frequency range of 330–480 cm−1 are sensitive to the S-P-S bond angle. On the basis of previous studies4,17, we assigned the three bands at approximately 425 cm−1, 410 cm−1, and 390 cm−1 to the stretching vibration of the P-S bonds in the 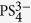Inline graphic (ortho-thiophosphate) ion, 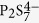Inline graphic (pyro-thiophosphate) ion, and 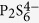Inline graphic (an ethanelike structure with a P-P bond) ion, respectively. 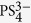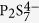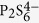Since the scattering coefficient of the Raman spectroscopy is affected by each PSx polyhedral anion18,19, the ratios of the Inline graphic, Inline graphic, and Inline graphic ions were estimated by a Lorentzian function, shown as dotted lines in Fig. 1b, and are summarized as open circles, open triangles, and open squares in Fig. 1c, respectively. 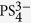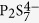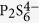It is clear that the ratio of Inline graphic ions increases with the Li2S content, while the ratios of Inline graphic and Inline graphic ions decrease. This tendency is in good agreement with that observed in previous studies4,20. Furthermore, the band corresponding to the stretching vibration of the P-P bond also disappears at approximately 530 cm−1 in the 75Li2S glass, as shown in the inset of Fig. 1a. Since the band at 547 cm−1 for polycrystalline Li4P2S6 is characterized by the stretching vibration of the P-P bonds21, the bands observed at 530 cm−1 in the glasses are related to the P-P stretching vibration. The disappearance of this band is consistent with the decrease in the ratio of 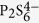Inline graphic ions. Intriguingly, it was found that 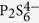Inline graphic ions exist in these glasses with ratios of approximately 33.0%, 18.3% and 4.4% in 67Li2S, 70Li2S, and 75Li2S, respectively, whereas they should not be contained in the stoichiometric compositions (0PS4:100P2S7 in 67Li2S, 50PS4:50P2S7 in 70Li2S, and 100PS4:0P2S7 in 75Li2S). This means that there is a sulfur deficiency in these glasses. The sulfur deficiency was confirmed by an Inductively Coupled Plasma (ICP) analysis, as shown in Fig. S1. Hayashi et al. found by NMR measurement22 that a small number of 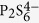Inline graphic ions are formed in the glass ceramic 70Li2S-28P2S5-2P2S3, and the degradation of conductivity is expected to be caused by the formation of 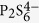Inline graphic ions.

Figure 1.

Figure 1

Open in a new tab

(a) Raman spectra in the range of 330–480 cm−1 for Li2S-P2S5 glasses. Black, blue, and green lines represent 75Li2S, 70Li2S, and 67Li2S glasses, respectively. The spectra in the range of 400–560 cm−1 are enlarged in the inset for clarity. (b) Spectral decomposition of Raman spectrum for 70Li2S glass. Blue line, experimental data; dotted lines, the fitting result for all PS polyhedra (right-blue), PS4 (black), P2S7 (red), and P2S6 (blue) anions. (c) PSx polyhedral fractions for Li2S-P2S5 glasses derived from Raman spectra (open marks) and DFT/RMC model (filled marks).

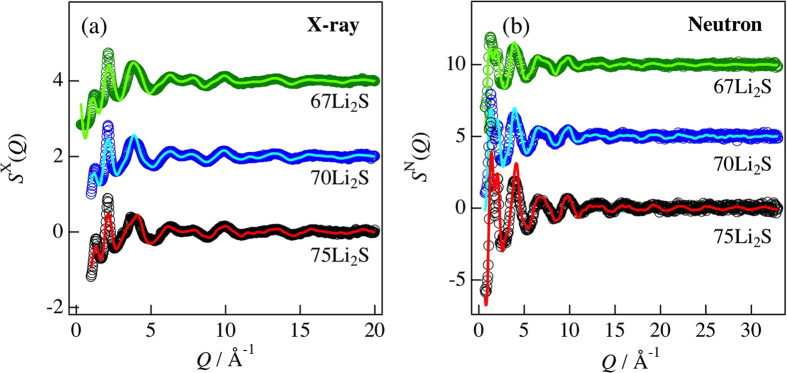
Figure 2a,b show experimental X-ray and neutron total structure factors, SX(Q) and SN(Q), respectively, for the 67Li2S, 70Li2S, and 75Li2S glasses. Oscillations in both SX(Q) and SN(Q) remain up to the high Q region, which is evidence for well-defined short-range order in the formation of P-S bonds. The difference between the three compositions is not significant in both sets of diffraction data, but the contrast between the diffraction data for SX(Q) and SN(Q) is apparent in the low-Q region. To extract quantitative information from the diffraction regarding the atomic arrangements in the glassy materials, the total pair distribution functions, T(r), were calculated for each glass by Fourier transformation of the total structure factor, SX,N(Q). Figure S2 shows T(r) for 75Li2S glass. From the negative coherent scattering length of neutrons for 7Li (hereafter the superscript is omitted), it is possible to identify the P-S and Li-S correlation lengths. The first peak at approximately 2.0 Å in both sets of diffraction data is related to the P-S correlation associated with the PS4 tetrahedral anions, while the second negative peak at approximately 2.5 Å is related to the Li-S correlation length. Both of these lengths are similar for all compositions and hence do not provide any specific information to help identify the structural features.

Figure 2.

Figure 2

Open in a new tab

Total structure factors S(Q) at room temperature for Li2S-P2S5 glasses derived from (a) X-ray and (b) neutron diffraction. Circles, experimental data; lines, DFT/RMC model. The circle and line colors correspond to those in Fig. 1.

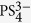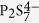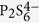To uncover the relationship between the glassy structure and the high ionic conductivity for these glasses4,7,9,23, we modeled the atomic structure of the Li2S-P2S5 glasses by DFT/RMC simulation using X-ray and neutron diffraction data, fixing the ratios of the Inline graphic, Inline graphic, and Inline graphic ions on the basis of Raman spectroscopy measurements to reproduce the plausible glassy structures. The total structure factors SX,N(Q) of the Li2S-P2S5 glasses derived from the DFT/RMC model are shown in Fig. 2 as lines. The DFT/RMC model is consistent with the experimental data. The peak observed at approximately Q = 1.2–1.3 Å−1 is usually called the first sharp diffraction peak (FSDP) and is thought to be a signature of the network structure formed in glassy materials. In phosphate glasses the FSDP is principally found approximately Q = 1.3 Å−1 24, suggesting an intermediate range order of ~4.8 Å. This scale is larger than length between the centers of bonded PO4 tetrahedral anions (P-P correlation length, ~2.9 Å). This is related to the formation of a strong network mainly comprising corner-shared interconnections of regular PO4 tetrahedral anions (sp3 bonding)25. The GeS2-P2S5 glasses also have an FSDP at approximately Q = 1.1–1.2 Å−1, suggesting intermediate range order between GeS4 or PS4 tetrahedral anions26. On the other hand, the FSDP in the Li2S-P2S5 glasses was observed at approximately Q = 1.2 Å−1, corresponding to an intermediate range order of ~5.0 Å. However, note that the corner-shared interconnections of the regular PS4 tetrahedral anions are not related to the FSDP in this system. Because we fixed the ratios of the PxSy tetrahedral anions and the interconnections of the regular PS4 tetrahedral anions in the DFT/RMC simulations. To understand the origin of the FSDP, the partial structure factors for the 70Li2S glass were calculated from the DFT/RMC model as shown in Fig. S3. As can be seen in this figure, SP−P(Q) has an FSDP at approximately Q = 1.2 Å−1, indicating that the P-P correlation contributes to the formation of the FSDP. According to a previous study10, the X-ray weighting factor for the P-P Faber-Ziman partial structure factor is 0.0346 (as evaluated from the form factor values at Q = 0), whereas the corresponding neutron weighting factor is 0.2438 for the 70Li2S glass. Actually, the heights of the FSDP in SN(Q) are greater than those in SX(Q). Not only glasses, but also the molecular liquids CCl4, SiCl4, GeCl4, and SnCl4 with the regular XCl4 tetrahedral anion (X = C, Si, Ge, and Sn) have a similar FSDP at approximately Q = 1.2 Å−1, despite these liquids not having the interconnections of regular XCl4 tetrahedral anions27. Although the relationship between the FSDP and the topology of the network is still not well understood, it is suggested that a pseudo network of P-P correlations contributes to the stabilization of the glassy structure.

To obtain information on the partial correlation in real space, the partial pair distribution functions (PDFs), gij(r), for the Li2S-P2S5 glasses were calculated from the DFT/RMC model as shown in Fig. S4. gij(r) for P-S correlation, gP−S(r), has a peak at approximately r = 2.0 Å and a shoulder on the high-r side. This bond length is consistent with that of a bridging sulfur (BS) in a P-S-P bond. gLi−S(r) also has a peak at approximately r = 2.5 Å, which is consistent with the experimental results for the PDF. Furthermore, gP−P(r) has two peaks at r = 2.2 Å and r = 3.5 Å, corresponding to the bond length of the 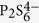Inline graphic ion and the correlation length of the 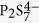Inline graphic ion, respectively. All the gij(r) peaks except for Li-Li correlation are well defined and sharp because the combination of X-ray diffraction, neutron diffraction, and DFT calculation provides us with a sufficient number of factors for each correlation. Note that the difference between the three glasses is very small, suggesting that their atomic correlations are very similar. This behavior is consistent with the structure factors, SX,N(Q), obtained from the DFT/RMC simulations, where the data are similar for the three glasses.

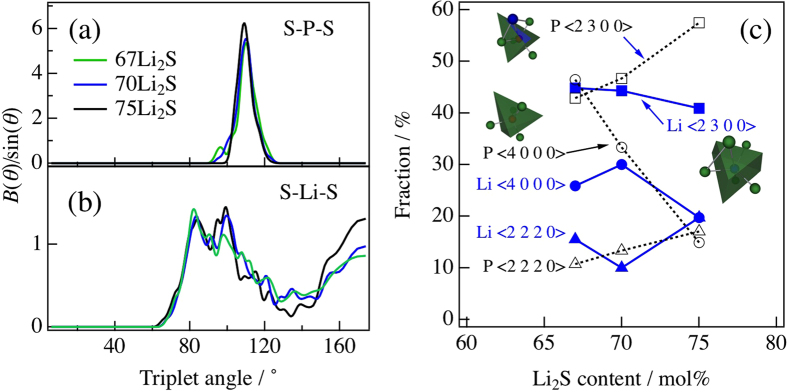
To understand the short-range correlation in detail, the coordination numbers in the Li2S-P2S5 glasses calculated up to 3.2 Å are summarized in Table 1. The coordination number of S around P, NP−S, increases with increasing Li2S content owing to the disappearance of the 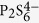Inline graphic ions. NP−Li also increases, while NLi−P and NLi−S remains almost constant in the three compositions. Furthermore, as the simplest analysis beyond two-body correlations, the bond angle distributions of the S-P-S and S-Li-S triplets for the 67Li2S, 70Li2S and 75Li2S glasses were calculated from the DFT/RMC model as shown in Fig. 3a,b, respectively. The S-P-S has a peak at 109° for all compositions owing to the formation of the regular PS4 tetrahedral anion with sp3 bonding. It also has a peak at approximately 95° except for the 75Li2S glass, which is related to the existence of BS ions. The S-Li-S bond angle distribution also shows a similar trend for all compositions regardless the BS ions of the existence, but the magnitude of the peak at approximately 100° significantly increases at a higher Li2S content. This increase is closely related to the change in the coordination environment of the Li+ ions.

Table 1. Average coordination numbers in Li2S-P2S5 glasses up to r = 3.2 Å derived from the DFT/RMC model.

Samples 67Li2S glass 70Li2S glass 75Li2S glass
NP−Li 2.04 2.20 3.23
NP−P 0.36 0.13 0.09
NP−S 3.64 3.87 3.92
NLi−Li 0.55 0.66 0.79
NLi−P 0.98 0.94 1.11
NLi−S 4.74 4.57 4.58
NS−Li 2.93 2.96 3.41
NS−P 1.09 1.07 1.00
NS−S 0.40 0.28 0.21
Open in a new tab

Ni−j: partial coordination number of j atoms around i atoms.

Figure 3.

Figure 3

Open in a new tab

Bond angle distributions for (a) S-P-S and (b) S-Li-S derived from DFT/RMC model. Line colors correspond to those in Fig. 1. (c) Comparison between the P-centered (open marks with dotted line) and Li-centered Voronoi polyhedra (filled marks with solid line) for Li2S-P2S5 glasses derived from DFT/RMC model.

To obtain the coordination environment of the Li+ ions in detail, Voronoi polyhedron statistics were calculated by Voronoi tessellation analysis28,29, in which it is assigned by a Voronoi index 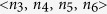Inline graphic, where 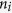Inline graphic denotes the number of i-edged faces and 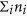Inline graphic is the total coordination number. The results for Li-centered Voronoi polyhedra calculated up to 3.2 Å are shown in Fig. 3c, together with results for P-centered polyhedra. This calculation length corresponds to the first coordination length of the Li-S correlation determined by the DFT/RMC model. Therefore, the calculation of P-centered Voronoi polyhedra includes information about the coordination environment beyond the first coordination of P-S correlation. The P-centered Voronoi polyhedra up to the first coordination environment have no composition dependence as shown in Fig. S5. It is clear that the fractions of <2 3 0 0> and <2 2 2 0> P-centered Voronoi polyhedra beyond the first coordination environment increase relative to that of <4 0 0 0> Voronoi polyhedra in the Li2S-P2S5 glasses, as shown by black dotted lines in Fig. 3c, which is consistent with the coordination number for P-Li correlation, NP−Li. This increase in the fraction of higher-index Voronoi polyhedra occurs with increasing Li2S content, which indicates that the number of Li+ ions increases at around the PSx polyhedral anion. On the other hand, the Li-centered Voronoi polyhedra are shown in Fig. 3c as blue solid lines and have no dependence on the Li2S content, which is also consistent with the coordination number for Li-P correlation, NLi−P. Although the distribution of Li+ ions has not been characterized, it has been found that the simple Voronoi polyhedra for Li-centered polyhedra are dominant in the DFT/RMC model owing to the consideration of the electron state for Li+ ions in the DFT calculation. It is suggested that the free volume around PSx polyhedral anions allows the distribution of Li+ ions at a higher Li2S content.

The extent of polyhedral connection between PSx and LiSy polyhedra in the Li2S-P2S5 glasses through corner, edge, and face sharing is calculated as shown in Fig. 4a. The results were classified on the basis of PSx polyhedral anions. The filled and hatched bars indicate corner and edge sharing, respectively. The fraction of edge sharing increases relative to that of corner sharing with increasing Li2S content, which is related to the bond angle distribution of the S-Li-S triplet. This means that an increase of the Li2S content does not affect the local coordination environment of Li+ ions, and free volume around the PSx polyhedral anion decreases. On the other hand, each fraction of the PSx polyhedral anions in the 67Li2S and 70Li2S glasses is almost the same, although we expected a distinct difference between the compositions. This result shows the distribution of Li+ ions in each PSx polyhedral anion. Strangely, the ratio (the number of Li ions sharing S with P2S7 anions/the number of Li ions sharing S with PS4 anions) in 70Li2S was found to be about 1.28, which is larger than the value of 1.11 for 67Li2S. The ratios of the molecular anions (P2S7/PS4) are 0.82 and 3.62 for 70Li2S and 67Li2S, respectively. This suggests that the P2S7 anion attracts the Li+ ions more than the PS4 and P2S6 anions. To evaluate the free volume, we calculated the bond length to the coordination number of the S around Li, NLi−S, and Li around S, NS−Li, as shown in Fig. 4b,c. The maximum bond length of 5.7 Å was determined from the Li-S-P bond length (3.2 Å + 2.5 Å), corresponding to the calculation length of polyhedral connection statistics. As can be seen in Fig. 4b, the NLi−S in this system has no composition dependence, which is consistent with the Li-centered Voronoi polyhedra. On the other hand, the NS−Li in 75Li2S is found to be larger than that of others as shown in Fig. 4c, which suggests that the free volume around S ions decreases in 75Li2S. Intriguingly, the NS−Li increase in 70Li2S compared to that in 67 Li2S at 3.8 Å and over. Thus, as the Li2S content increases in this system, the free volume around Li ion has no composition dependence, while that around S decreases. The DFT/RMC structure is consistent with both the diffraction data and the Raman data (Fig. 5a), and we compared the electronic structure in terms of each PSx polyhedral anion for the 70Li2S glass. Figure 5b,c show the partial density of states (p-DOS) of the 70Li2S glass for the S 3p-orbital and P 3p-orbital, respectively. It is apparent that the orbitals form a hybrid orbital between the phosphorus and sulfur; the highest occupied molecular orbital (HOMO) is located at −4.0–−0.5 eV and the lowest unoccupied molecular orbital (LUMO) is located at 1.5–5.0 eV. The positive charge of the P ion is large owing to the hybrid orbital. However, the p-DOS plots of P ion reveal that the P2S7 anion only differs from the PS4 and P2S6 anions (Fig. 5c). A shallow level appears near the bottom of the LUMO at approximately 2.0 eV in the P2S7 anion, which relates to a covalent bond between the P ion and the BS ion in the P2S7 anion. This electron transfer is expected to weaken the positive charge of the P ions, which attract Li+ ions to the P2S7 anions more strongly than the other PSx polyhedral anions. Furthermore, the attracted Li+ ions are easy to stay around the P2S7 anions, which may suppress the lithium ionic conduction in solid electrolytes. On the other hand, the P2S6 anion is almost the same to the PS4 anion in terms of the electronic structure and does not suppress the Li ion conduction compared to the P2S7 anion, although we expected a strong suppression to Li ion as shown Hayashi et al.22. It is well known that the diffusion of cations is accelerated by the polarization of anions30,31,32. Also, the Li+ ion distribution is clearly affected by the polarization of anions33, which means that the edge sharing between PSx and LiSy polyhdera is related to the lithium ionic conduction. Actually, the lithium ionic conductivity of 75Li2S without P2S7 anions is higher than that of the other glasses. Furthermore, Li2S-SiS2 glasses with added LiI with exhibiting large polarization have a high ionic conductivity34. Thus, the control of the edge sharing between PSx and LiSy polyhdera without the electron transfer between the P ion and the BS ion is expected to facilitate the lithium ionic conduction in a solid electrolyte, which should contribute to the development of all-solid batteries.

Figure 4.

Figure 4

Open in a new tab

(a) Polyhedral connection statistics for Li2S-P2S5 glasses calculated using DFT/RMC model. All connections are between PSx and LiSy polyhedra. Red, green, and blue represent 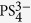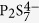Inline graphic, Inline graphic, and Inline graphic ions, respectively. Filled and hatched bars represent corner and edge sharing. Relationship between the bond length and the coordination number for the Li-S (b) and S-Li (c) correlations derived using the DFT/RMC model.

Figure 5.

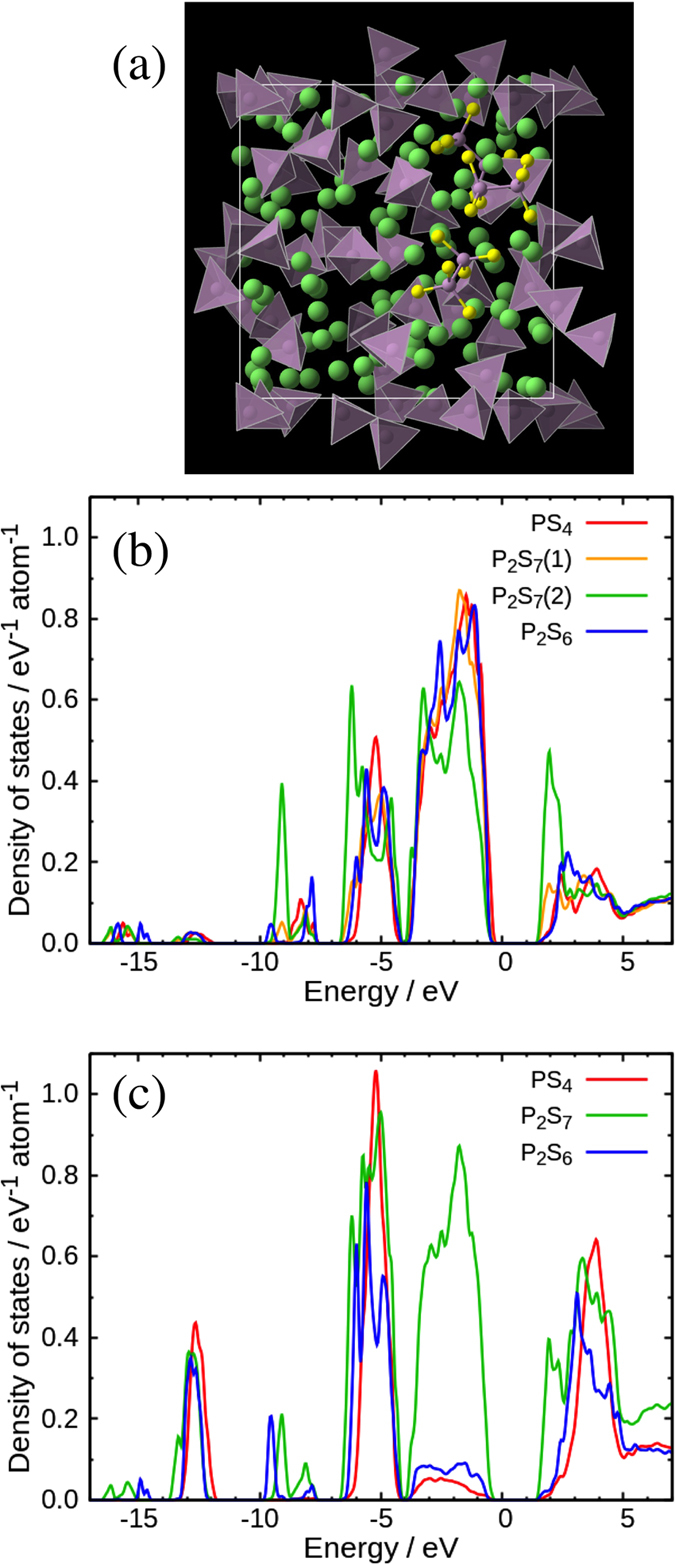
Figure 5

Open in a new tab

(a) DFT/RMC model of 70Li2S glass. Green, Li; Purple, P and PS polyhedral anions; Yellow, S. Polyhedral partial DOS for (b) S p-orbital and (c) P p-orbital of 70Li2S glass.

Conclusion

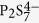In this study, we found that Inline graphic ions as well as Inline graphic and Inline graphic ions are present in 67Li2S-33P2S5 (67Li2S), 70Li2S-30P2S5 (70Li2S), and 75Li2S-25P2S5 (75Li2S) glasses on the basis of Raman spectroscopy measurement. 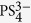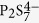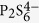Density functional theory and reverse Monte Carlo simulations (DFT/RMC) quantitatively reproduced the results of high-energy X-ray diffraction, neutron diffraction, and Raman spectroscopy, fixing the ratios of Inline graphic, Inline graphic, and Inline graphic ions. The DFT/RMC model indicates that the P-P correlation contributes to the formation of the first sharp diffraction peak, suggesting that the structure can be stabilized by this correlation in the three glasses. The distinct peak at approximately 100° for the S-Li-S bond angle distribution at a high Li2S content is consistent with the increase in the edge sharing polyhedral connection between PSx and LiSy, which means that the free volume around the PSx polyhedral anion allows the distribution of Li+ ions. It is conjectured that Li+ ions around the face of the PSx polyhedra are affected by the polarization of anions. The electronic structure of the DFT/RMC model suggests that the existence of the P2S7 anion may suppress lithium ionic conduction. Thus, it has been demonstrated that the observation of the local structure is important for understanding the origin of high lithium ionic conduction. We suggest that the high ionic conduction in solid electrolytes can be controlled by the edge sharing between PSx and LiSy polyhedra without the electron transfer between the P ion and the BS ion. This finding is a crucial key concept for designing new solid electrolytes.

Methods

Sample preparation

The Li2S-P2S5 glasses were prepared by the mechanical milling method. 7Li2S (Kojundo Chemical lab., Ltd., 99.8%) and P2S5 (Aldrich, 99%) crystalline powders were used as the starting materials. A mixture of these materials was mechanically milled at room temperature by a planetary ball mill using a zirconia pot (45 ml) with 10 zirconia balls (diameter: 10 mm). The rotation speed was 370 rpm and the milling time was about 80 h. All the processes were performed in a dry Ar atmosphere. Ionic conductivity was measured by the AC impedance method in an Ar atmosphere at room temperature with an applied frequency range of 100 Hz to 1 MHz using a Solartron 1260 frequency response analyzer. Carbon-coated blocking the electrode was painted on both sides of the sample. The observed ionic conductivities of 67Li2S, 70Li2S, and 75Li2S were 5.6 × 10−5 S/cm, 1.4 × 10−4 S/cm, and 3.0 × 10−4 S/cm, respectively. Densities of Li2S-P2S5 glasses were measured using a gas pycnometer (Accupyc 1330, Micromeritics) under a high purity He atmosphere at room temperature.

Raman spectroscopic measurement

Raman spectra for the Li2S-P2S5 glasses were acquired at room temperature on a LabRAM HR-800 (Horiba-Jobin Yvon) spectrometer equipped with a 100× lens (NA = 0.90, Olympus), a 1800 grooves/mm grating, and an excitation wavelength of 632.8 nm (He-Ne laser). The laser power was reduced to less than 1 mW to avoid laser-induced degradation on the focused particles (laser spot size; 4 μm in diameter). The exposure time was 30 s × 10 times for several particles.

High-energy X-ray diffraction measurement

The high-energy X-ray diffraction experiments for the Li2S-P2S5 glasses were carried out at room temperature at the SPring-8 high-energy XRD beamline BL04B2 using a two-axis diffractometer35. The incident X-ray energy obtained from a Si 220 crystal monochromator was 61.4 keV. The diffraction patterns of the samples and an empty tube were measured in the transmission geometry with an angle from 0.3 to 40°, corresponding to a Q-range from 0.2 to 20 Å−1. The intensity of the incident X-ray was monitored in an ionization chamber filled with Ar gas and the scattered X-rays were detected by a Ge detector. A vacuum electric chamber was used to suppress air scattering around the sample. The collected datasets were corrected for the absorption, background, and polarization effects. Details of the data correction and normalization procedures are given in ref. 35.

Time-of-flight neutron diffraction measurement

The time-of-flight neutron diffraction experiments for the Li2S-P2S5 glasses were carried out at room temperature using the General Materials Diffractometer (GEM) at ISIS, Rutherford Appleton Laboratory, UK36,37. The data were reduced and corrected for attenuation and multiple scattering using the Gudrun program38.

Density functional theory and Reverse Monte Carlo simulations

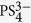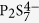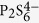To obtain a plausible structural model, we evaluated the densities of the glasses (Fig. S6). DFT/RMC simulations of the Li2S-P2S5 glasses were carried out from an initial atomic configuration prepared by an Amorphous Cell code (BIOVIA) in a cubic box with the corresponding densities listed in Table 2. The ratios of the Inline graphic, Inline graphic, and Inline graphic ions in the Li2S-P2S5 model structures were fixed on the basis of the Raman spectroscopic results. The numbers of Li+ ion was fixed to satisfy the stoichiometry of the PSx polyhedral anions. DFT and RMC calculations were performed iteratively until the difference in the atomic coordination between DFT and RMC became less than 0.2 Å. DFT calculations were performed using the projector augmented wave (PAW) method39 implemented in VASP40,41. The generalized gradient approximation (GGA) functional of Perdew, Burke, and Ernzerhof (PBE)42 was used for the exchange correlation term. A plane-wave cutoff energy of 260 eV was used. Internal atomic positions were optimized until the residual forces became less than 5 × 10−2 eV/Å. The experimental S(Q) obtained from the high-energy X-ray and neutron diffraction measurements were fitted simultaneously by employing the RMC++ code43. The cut off radius, i.e., the minimum allowed distance between atom pairs, was estimated from the experimental pair distribution function. The simulations were performed for different initial configurations for each composition, and their validity was verified.

Table 2. Details of Li2S-P2S5 glasses; compositions, densities, atomic number densities, particle numbers, and box lengths used in DFT/RMC simulation.

Samples 67Li2S glass 70Li2S glass 75Li2S glass
Composition (Li2S)67(P2S5)33 (Li2S)70(P2S5)30 (Li2S)75(P2S5)25
Density (g/cm3) 1.950 1.938 1.935
Atomic number density (Å−1) 0.0487 0.0496 0.0518
Particle number 180 208 368
Box length (Å) 15.39 16.11 18.35
Open in a new tab

Additional Information

How to cite this article: Ohara, K. et al. Structural and electronic features of binary Li2S-P2S5 glasses. Sci. Rep. 6, 21302; doi: 10.1038/srep21302 (2016).

Supplementary Material

Supplementary Information
srep21302-s1.pdf (2.1MB, pdf)

Acknowledgments

This work was supported by the Research and Development Initiative for Scientific Innovation of New Generation Batteries (RISING) project of the New Energy and Industrial Technology Development Organization (NEDO) of Japan. The synchrotron radiation experiments were approved by the Japan Synchrotron Radiation Research Institute (proposal Nos 2011B1457, 2012B1540, 2013B1010, 2013B7600, 2014A7600). The neutron diffraction measurements were approved by the Rutherford Appleton Laboratory, UK (proposal No. RB1255026). This work was partially supported by JSPS Grand-in-Aid for Research Activity Start-up (No. 15H06919). We thank Alex Hannon for assistance in the measurement and Shinji Kohara, Eugene Bychkov, Iwao Watanabe, and Yoshio Ukyo for helpful discussions.

Footnotes

Author Contributions The manuscript was written through contributions of all authors; K.O., A.M., T.F., Y.U. and Z.O. conceived this research; A.M. and S.S. prepared samples; K.O. and A.M. performed high-energy X-ray measurements; K.O., A.M. and Y.O. performed neutron diffraction measurements; A.M., S.S. and K.S. performed Raman spectroscopic measurements; K.O. and M.M. carried out DFT/RMC simulations; K.O., A.M., M.M., Y.O., Y.K., Y.O. and K.S. analyzed the results; K.O., A.M., M.M., Y.O., S.S., Y.K., Y.O., M.M., K.S., K.M., T.F. and H.A. contributed to discussions of the results; K.O., M.M., Y.O., Y.O., K.S. and H.A. wrote the paper with help from all authors. All authors reviewed the manuscript.

References

  1. Tarascon J. M. & Armand M. Issues and challenges facing rechargeable lithium batteries. Nature 414, 359–367 (2001). [DOI] [PubMed] [Google Scholar]
  2. Masquelier C. Solid electrolytes: Lithium ions on the fast track. Nat. Mater. 10, 649–650 (2011). [DOI] [PubMed] [Google Scholar]
  3. Han F., Gao T., Zhu Y., Gaskell K. J. & Wang C. A Battery Made from a Single Material. Adv. Mater. 27, 3473–3483 (2015). [DOI] [PubMed] [Google Scholar]
  4. Mizuno F., Hayashi A., Tadanaga K. & Tatsumisago M. New, Highly Ion-Conductive Crystals Precipitated from Li2S-P2S5 Glasses. Adv. Mater. 17, 918–921 (2005). [Google Scholar]
  5. Hayashi A., Hama S., Morimoto H., Tatsumisago M. & Minami T. Preparation of Li2S-P2S5 amorphous solid electrolytes by Mechanical Milling. J. Am. Ceram. Soc. 84, 477–479 (2001). [Google Scholar]
  6. Minami K., Hayashi A., Ujiie S. & Tatsumisago M. Structure and properties of Li2S-P2S5-P2S3 glass and glass-ceramic electrolytes. J. Power Sources 189, 651–654 (2009). [Google Scholar]
  7. Kamaya N. et al. A lithium superionic conductor. Nat. Mater. 10, 682–686 (2011). [DOI] [PubMed] [Google Scholar]
  8. Mo Y., Ong S. P. & Ceder G. First Principles Study of the Li10GeP2S12 Lithium Super Ionic Conductor Material. Chem. Mater. 24, 15–17 (2012). [Google Scholar]
  9. Kuhn A. et al. A new ultrafast superionic Li-conductor: ion dynamics in Li11Si2PS12 and comparison with other tetragonal LGPS-type electrolytes. Phys. Chem. Chem. Phys. 16, 14669–14674 (2014). [DOI] [PubMed] [Google Scholar]
  10. Onodera Y., Mori K., Otomo T., Sugiyama M. & Fukunaka T. Structural Evidence for High Ionic Conductivity of Li7P3S11 Metastable Crystal. J. Phys. Soc. Jpn. 81, 044802 (2012). [Google Scholar]
  11. Mori K. et al. Visualization of conduction pathways in lithium superionic conductors: Li2S-P2S5 glasses and Li7P3S11 glass-ceramic. Chem. Phys. Lett. 584, 113–118 (2013). [Google Scholar]
  12. Onodera Y. et al. Structural origin of ionic conductivity for Li7P3S11 metastable crystal by neutron and X-ray diffraction. J. Phys. Conf. Ser. 502, 012021 (2014). [Google Scholar]
  13. McGreevy R. L. & Pusztai L. Reverse Monte Carlo Simulation: A new technique for the determination of disordered structures. Mol. Simul. 1, 359–367 (1988). [Google Scholar]
  14. Keen D. A. & McGreevy R. L. Structural modelling of glasses using reverse Monte Carlo simulation. Nature 344, 423–425 (1990). [Google Scholar]
  15. Swenson J. & Börjesson L. Correlation between Free Volume and Ionic Conductivity in Fast Ion Conducting Glasses. Phys. Rev. Lett. 77, 3569–3572 (1996). [DOI] [PubMed] [Google Scholar]
  16. Dzugutov M. A universal scaling law for atomic diffusion in condensed matter. Nature 381, 137–139 (1996). [Google Scholar]
  17. Tachez M., Malugani J.-P., Mercier R. & Robert G. Ionic Conductivity of and Phase Transition in Lithium Thiophosphate Li3PS4. Solid State Ionics 14, 181–185 (1984). [Google Scholar]
  18. Umesaki N., Takahashi M., Tatsumisago M. & Minami T. Structure of rapidly quenched glasses in the system Li2O-SiO2. J. Mat. Sci. 28, 3473–3481 (1993). [Google Scholar]
  19. Iwamoto N., Umesaki N., Takahashi M., Tatsumisago M. & Minami T. Molecular dynamics simulation of Li4SiO4 melt and glass. J. Non-Cryst. Solids 95–96, 233–240 (1987). [Google Scholar]
  20. Hayashi A., Minami K. & Tatsumisago M. Development of sulfide glass-ceramic electrolytes for all-solid-state lithium rechargeable batteries. J. Solid State Electrochem. 14, 1761–1767 (2010). [Google Scholar]
  21. Mercier R., Malugani J. P., Fahys B., Douglande J. & Robert G. Synthese, structure cristalline et analyse vibrationnelle de l’hexathiohypodiphosphate de lithium Li4P2S6. J. Solid State Chem. 43, 151–162 (1982). [Google Scholar]
  22. Hayashi A., Minami K., Ujiie S. & Tatsumisago M. Preparation and ionic conductivity of Li7P3S11−z glass-ceramic electrolytes. J. Non-Cryst. Solids 356, 2670–2673 (2010). [Google Scholar]
  23. Sakuda A., Hayashi A. & Tatsumisago M. Sulfide Solid Electrolyte with Favorable Mechanical Property for All-Solid-State Lithium Battery. Sci. Rep. 2261, 1–5 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Suzuya K., Price D. L., Loong C.-K. & Martin S. W. Structure of vitreous P2O5 and alkali phosphate glasses. J. Non-Cryst. Solids 232–234, 650–657 (1998). [Google Scholar]
  25. Hoppe U. et al. Combined neutron and X-ray scattering study of phosphate glasses. J. Non-Cryst. Solids 293–295, 158–168 (2001). [Google Scholar]
  26. Cherry B., Zwanziger J. W. & Aitken B. G. The structure of GeS2-P2S5 glasses. J. Phys. Chem. B 106, 11093–11101 (2002). [Google Scholar]
  27. Pothoczki S., Temleitner L., Jóvári P., Kohara S. & Pusztai L. Nanometer range correlations between molecular orientations in liquids of molecules with perfect tetrahedral shape: CCl4, SiCl4, GeCl4, and SnCl4. J. Chem. Phys. 130, 064503 (2009). [DOI] [PubMed] [Google Scholar]
  28. Finney J. L. Random packings and the structure of simple liquids. I. the geometry of random close packing. Proc. R. Soc. London, Ser. A 319, 479–493 (1970). [Google Scholar]
  29. Borodin V. A. Local atomic arrangements in polytetrahedral materials. Philos. Mag. A 79, 1887–1907 (1999). [Google Scholar]
  30. Wilson M. & Madden P. A. Polarization effects in ionic systems from first principles. J. Phys. Condens. Matter 5, 2687–2706 (1993). [Google Scholar]
  31. Trullàs J., Alcaraz O., González L. E. & Silbert M. Structure and dynamics of molten agcl. the inclusion of induced polarization. J. Phys. Chem. B 107, 282–290 (2003). [Google Scholar]
  32. Alcaraz O., Bitrián V. & Trullàs J. Molecular dynamics study of polarizable point dipole models for molten sodium iodide. J. Chem. Phys. 127, 154508 (2007). [DOI] [PubMed] [Google Scholar]
  33. Tahara S. et al. Intermediate-range chemical ordering of cations in molten RbCl-AgCl. J. Chem. Phys. 143, 044509 (2015). [DOI] [PubMed] [Google Scholar]
  34. Kennedy J. H. & Yang Y. A Highly Conductive Li+ -Glass System: (1-x)(0.4SiS2 -0.6Li2S) -xLiI. J. Electrochem. Soc. 133, 2437–2438 (1986). [Google Scholar]
  35. Kohara S. et al. Structural studies of disordered materials using high-energy x-ray diffraction from ambient to extreme conditions. J. Phys. Condens. Matter 19, 506101 (2007). [Google Scholar]
  36. Williams W. G., Ibberson R. M., Day P. & Enderby J. E. GEM - General materials diffractometer at ISIS. Physica B: Condensed Matter 241–243, 234–236 (1998). [Google Scholar]
  37. Hannon A. C. Results on disordered materials from the GEneral Materials diffractometer, GEM, at ISIS. Nucl. instrum. methods phys. res., A Accel. spectrom. detect. assoc. equip 551, 88–107 (2005). [Google Scholar]
  38. GUDRUN. doi: http://www.isis.stfc.ac.uk/instruments/gem/software/software.html.
  39. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
  40. Kresse G. & Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
  41. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  42. Perdew J. P., Burke K. & Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  43. Gereben O., Jóvári P., Temleitner L. & Pusztai L. A new version of the RMC++ Reverse Monte Carlo programme, aimed at investigating the structure of covalent glasses. J. Optelect. Adv. Mater. 9, 3021–3027 (2007). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep21302-s1.pdf (2.1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES