Abstract
Many MRI techniques require prior knowledge of the T1-relaxation time of blood (T1bl). An assumed/fixed value is often used; however, T1bl is sensitive to magnetic field (B0), haematocrit (Hct), and oxygen saturation (Y). We aimed to combine data from previous in vitro measurements into a mathematical model, to estimate T1bl as a function of B0, Hct, and Y. The model was shown to predict T1bl from in vivo studies with a good accuracy (±87 ms). This model allows for improved estimation of T1bl between 1.5–7.0 T while accounting for variations in Hct and Y, leading to improved accuracy of MRI-derived perfusion measurements.
Keywords: ASL, cerebral blood flow measurement, MRI, perfusion weighted MRI, mathematical modelling
Introduction
The spin-lattice relaxation time of blood (T1bl) plays a critical role in a range of MRI applications. In particular, the accuracy of blood flow measurements made using arterial spin labelling (ASL)1 depends directly on accurate knowledge of T1bl in a given subject. Black blood angiography, vascular space occupancy imaging, dynamic contrast-enhanced magnetic resonance imaging, cardiac MRI applications, and MR-based temperature monitoring also rely on accurate estimation of this parameter.
A number of factors influence spin-lattice relaxation time (T1). T1 increases with Larmor frequency, and therefore magnetic field strength (B0), which in single phase homogeneous substances can be described using the Bloembergen-Purcell-Pound theory.2 In human tissues and blood, the relationship is more complex, as macromolecules such as proteins provide relaxation pathways which speed up T1 relaxation. One such protein is haemoglobin, which is an oxygen transport protein that resides in erythrocytes (red blood cells), and hence haematocrit (Hct), which describes the volume fraction of erythrocytes in whole blood, will influence T1bl. Proteins residing in blood plasma, such as albumin and globulin, will similarly effect T1bl. In addition, paramagnetic materials provide a further T1 relaxation pathway, and, as deoxyhaemoglobin is weakly paramagnetic, the oxygen saturation fraction of blood (Y) will also influence T1 relaxation. Lastly, the T1 relaxation time is temperature-dependent, with longer relaxation times found at higher temperatures.
In general, an assumed value of T1bl will be used in the MRI techniques described above, particularly in the clinic, where technical and scan time constraints prevent measurement of T1bl on a patient-by-patient basis. Although many previous studies have determined values of T1bl empirically (see Table 1), these have generally been performed under differing physiological/experimental conditions (magnetic field strength, blood oxygenation, haematocrit, etc.), often without direct measurement of all the influencing factors. The aim of this study was to bring together the results of previous studies into a general mathematical model for predicting T1bl, as a function of B0, Hct, and Y. This will provide estimates of T1bl values in arterial and venous blood, over the range of magnetic field strengths used in clinical practice (1.5–7.0 T). This should lead to subsequent improvements in the accuracy of ASL-derived blood flow measurements, particularly in pathologies where the constitution of the blood is known to be outside the normal range.
Table 1.
Sources of literature values of R1bl.
| Ref. | B0 (T) | No. data points | Blood source | Age range (years) | Gender | Hct | Y |
|---|---|---|---|---|---|---|---|
| Stefanovic and Pike6 | 1.5 | 8 | Human (22℃) | – | – | Measured (0.51 ± 0.004) | Measured (0.42–0.93) |
| Lu et al.5 | 3.0 | 9 | Bovine (37℃) | – | – | Measured (0.38–0.46) | Measured (0.69–0.99) |
| Rane and Gore7 | 7.0 | 10 | Human (37℃) | – | – | Measured (0–1) | Measured (0.66–0.97) |
| Grgac et al.3 | 7.0 | 13 | Bovine (37℃) | – | – | Measured (0–1) | Measured (0.4–1.0) |
| Dobre et al.8 | 4.7,7.0 | 2 | Bovine (37℃) | – | – | Measured (0.43) | Measured (0.79–0.81) |
| Zhang et al.4 | 1.5, 3.0, 7.0 | 18 | Human in vivo | 24–38 | M, F | Estimated | Estimated (venous) |
| Wu et al.9 | 3.0 | 8 | Human in vivo | 7–39 | M, F | Estimated | Estimated (venous) |
| Varela et al.10 | 3.0 | 19 | Human in vivo | 0.4–37 | M, F | Measured | Estimated (venous) |
| De Vis et al.11 | 3.0 | 3 | Human in vivo | 0.05–0.24 | M,F | Measured | Estimated (venous) |
Note: The range of Hct and Y are shown if these parameters were measured, if not estimated values were used, adjusted for the age and gender of the subject (for Hct), and whether the blood was arterial or venous (for Y).
Materials and methods
Theory
A two-compartment blood model, consisting of erythrocytes and plasma in fast exchange, was previously described in Grgac et al.3 In this model, the longitudinal relaxation rate of whole blood (R1bl, equivalent to T1bl−1) is given by
| (1) |
where Hct is the haematocrit (0–1), Y is the oxygen saturation fraction (0–1), fe is the fraction of water in whole blood that resides in erythrocytes (0–1), R1e is the longitudinal relaxation rate of erythrocytes (s−1), and R1p is the longitudinal relaxation rate of plasma (s−1). Under normal physiological conditions, water volume fraction in erythrocytes is approximately 70%, and water volume fraction in plasma is 94–95%,3 which allows fe to be expressed as a function of Hct as follows3
| (2) |
In addition, because deoxyhaemoglobin acts as a weak paramagnetic contrast agent, we can express R1e as a function of Y
| (3) |
where R1eox is the longitudinal relaxation rate of erythrocytes when Y = 1 (100% oxygen saturation), [Hb] is the mean corpuscular haemoglobin concentration (5.15 mmol Hb tetramer/L plasma3), and r1deoxyHb is the molar relaxivity of deoxyhaemoglobin (s−1 L plasma in erythrocyte/mmol Hb tetramer).
When analysing data collected over a range of magnetic field strengths, the possible dependence of R1eox, R1p and r1deoxyHb on B0 must also be accounted for. The relationship between whole blood R1 and B0 between 1.5 and 7.0 T has been shown to be linear,4 and as such linear regression terms for the above parameters were substituted into equations (1) and (3) as follows (β0 represents the ‘intercept’ term, β1 represents the ‘gradient’ with respect to B0)
| (4) |
| (5) |
| (6) |
By combining equations (1)–(6), a general model was constructed, with R1bl as the dependent variable, B0, Hct and Y as independent variables, and the following as fitted parameters: β0,R1eox, β1,R1eox, β0,r1deoxyHb, β1,r1deoxyHb, β0,R1p, β1,R1p.
Data analysis
All data analysis was performed using Matlab R2014a (MathWorks Inc., Natick, MA, USA), and Matlab’s fminsearch algorithm was used for model fitting. Forty-two literature values of T1bl,3,5–8 acquired in vitro between 1.5 and 7.0 T in conjunction with empirically controlled variations in Hct and Y (see Table 1), were fit simultaneously to the model. The T1bl values in Stefanovic and Pike6 were increased by 12% to account for the shift in T1bl between 22℃ and 37℃.5,6 Following initial model fitting, a Monte Carlo simulation was performed to determine the uncertainty on the fitted parameters. Here, the pool of N = 42 raw data points were randomly sampled N times (with replacement), and the model was fit to this synthetic raw data set. This process was iterated 1000 times, and the median and 95% confidence interval (CI) of the distribution of fitted values for each parameter were used as the final parameter estimate and its uncertainty, respectively. Parameters for which the 95% CI crossed zero were classified as non-significant, and the process was repeated with these terms set to zero.
Following this, the fitted parameter values were substituted into equations (1) to (6), and the ability of the model to predict values of T1bl taken from further literature sources4,9–11 (Table 1), in which measurements were made in vivo, was tested. These comprised 48 values of T1bl, taken from human studies performed between 1.5 and 7.0 T. In these studies, measurements were made in blood in the sagittal sinus, so normal values of Y = 0.68 (for venous blood) were assumed,12 and, where not measured, a value of Hct, corrected for age and gender, was estimated based on literature values.13,14
Results
The Monte Carlo simulation showed that the 95% CI around the fitted value of β1,r1deoxyHb crossed zero, and as such this parameter was non-significant (i.e. there was no evidence to suggest r1deoxyHb changes with B0). With this term set to zero, the following values were obtained for the remaining fitted parameters (95% lower and upper CIs shown in brackets):
β0,R1eox: 1.10 (0.97, 1.28) s−1, β1,R1eox: −0.058 (−0.085, −0.038) s−1T−1, β0,r1deoxyHb: 0.033 (1.8 × 10−9, 0.056) s−1 L plasma in erythrocyte/mmol Hb tetramer, and β0,R1p: 0.49 (0.40, 0.57) s−1, β1,R1p: −0.023 (−0.035, −0.0079) s−1 T−1.
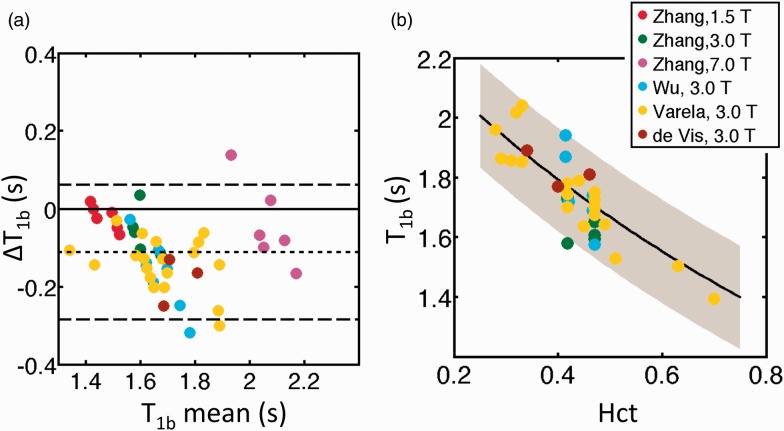
With the above values substituted into equations (1) to (6), the difference between predicted and measured T1bl values (ΔT1bl), taken from the in vivo literature sources,4,9,10 is illustrated in Figure 1(a). Predicted T1bl values were slightly underestimated compared to in vivo literature values, with a mean ΔT1bl of −108 ms (predicted minus literature values, mean 6% under-estimation), and a standard deviation in ΔT1bl of 89 ms. As such, an offset of +108 ms should be added to the model when predicting in vivo T1b values (see Discussion). The final model, valid between 1.5 and 7.0 T, is therefore
where
| (7) |
and
| (8) |
where ΔT1bl = 0 and 108 ms for in vitro and in vivo studies respectively. Note that if a full blood analysis has been performed, a measured value for [Hb] (mean corpuscular haemoglobin concentration) can be used in equation (7), rather than the assumed value of 5.15 mmol Hb tetramer/L plasma.
Figure 1.
(a) Bland-Altman plot illustrating the difference between modelled and measured values of T1bl (ΔT1bl), between 1.5 and 7.0 T. The horizontal dashed lines show the mean value of ΔT1bl (short dashes) and the limits of agreement (long dashes, mean(ΔT1bl) ± (1.96xSD(ΔT1bl)). (b) Variation in modelled values of T1bl (black line, with grey shading indicating limits of agreement), with literature values overlaid (legend indicates literature source in (a) and (b)). All data in (b) represent in vivo T1bl values, and as such the ΔT1bl = 180 ms offset has been added to the modelled values (equation (8)).
Figure 1(b) illustrates the change in both modelled and measured in vivo T1bl values as a function of Hct, shown here at 3.0 T.
Discussion
After correcting for the ΔT1bl offset, our model was able to predict literature measurements of in vivo T1bl with a good degree of accuracy (root mean square error = 87 ms). For example, in Zhang et al.,4 the measured T1bl values in venous blood in the sagittal sinus of healthy subjects (mean age 31 years) at 1.5 T, 3.0 T, and 7.0 T were 1480 ms, 1650 ms and 2088 ms, respectively (males and females combined). The equivalent values predicted using our model were 1565 ms, 1688 ms, and 2147 ms, respectively (data in Zhang et al.4 were not used to ‘train’ the model). Our model fitting indicated that both the T1 of plasma and fully oxygenated erythrocytes increase with B0, and our results agree with previous findings that T1bl is highly sensitive to haematocrit, but only weakly dependent on oxygenation.15 Also, our fitted value for r1deoxyHb of 0.033 s−1 L plasma in erythrocyte/mmol Hb tetramer lies between the mean fitted values of 0.052 in Grgac et al.3 and 0.012 in Blockley et al.15 (s−1 L plasma in erythrocyte/mmol Hb tetramer).
The offset between predicted and literature T1bl values arose from the fact that our model was ‘trained’ using data from in vitro studies (necessary to control the Hct and Y levels in the blood), then used to predict values from in vivo studies. Trisodium citrate was added to the blood in the in vitro studies to prevent coagulation, and higher osmolarity sodium concentrations will draw water out of erythrocytes via osmosis, shortening T13. In Grgac et al.,3 the addition of anti-coagulant was estimated to reduce T1bl by 7%, which agrees very well with the average underestimation of 6% when our model was used to predict literature values acquired in vivo.
Implications for arterial spin labelling
When processing ASL data, an assumed value of T1bl is used in the conversion of raw signal into cerebral blood flow (CBF) values (see Alsop et al.16 for details). Certain pathologies may result in a patient having a haematocrit outside the normal range expected for their age/gender, and assuming a normal Hct value in these patients will result in an incorrect estimation of T1bl, which in turn will lead to an incorrect calculation of CBF. For instance, sickle cell anaemia is a genetic condition in which patients have atypical haemoglobin molecules, resulting in a low number of red blood cells (anaemia). In a severely anaemic patient (say Hct = 0.20), the calculated value of T1bl in arterial blood (Y = 0.97) using our model would be 2.09 s at 3.0 T. If we assumed a normal Hct value in this subject (say Hct = 0.47 for a 30 year old male), the calculated value of T1bl drops to 1.70 s. This 18% underestimation of T1bl, resulting from an assumed normal value for T1bl rather than a Hct-corrected value, would lead to an overestimation in the calculated CBF of approximately 30%, based on a typical pseudo-continuous ASL acquisition (see equation 1 in Alsop et al.16).
Conclusions
MRI applications such as ASL are dependent on accurate knowledge of T1bl, which is rarely measured on a patient-by-patient basis. We have presented a mathematical model which brings together previous empirical measurements of T1bl, and provides a general tool for estimation of this parameter in individual subjects, adjusted for magnetic field strength, haematocrit and oxygenation of the blood. In healthy subjects, this model can be used with assumed normal values of Hct (corrected for age/gender) and Y, whereas in patients measured Hct and Y values may be required, which will require blood sampling and non-trivial steps for accurate assessment. Following this, the model presented here will account for the influence of a patient’s atypical Hct and Y values on the estimated value of T1bl. This in turn will have a significant influence on the quantification of CBF using ASL, and considerable errors in CBF quantification will occur if normal values of T1bl are assumed.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was funded by Great Ormond Street Hospital Children’s Charity.
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Authors’ contributions
PWH designed the research, analysed data and wrote the manuscript; CAC, FJK edited the manuscript and provided clinical input. All authors approved the final manuscript.
References
- 1.Williams DS, Detre JA, Leigh JS, et al. Magnetic resonance imaging of perfusion using spin inversion of arterial water. Proc Natl Acad Sci 1992; 89: 212–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bloembergen N, Purcell E, Pound R. Relaxation effects in nuclear magnetic resonance absorption. Phys Rev 1948; 73: 679–712. [Google Scholar]
- 3.Grgac K, van Zijl PCM, Qin Q. Hematocrit and oxygenation dependence of blood 1H2O T1 at 7 tesla. Magn Reson Med 2013; 70: 1153–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang X, Petersen ET, Ghariq E, et al. In vivo blood T(1) measurements at 1.5 T, 3 T, and 7 T. Magn Reson Med 2013; 70: 1082–1086. [DOI] [PubMed] [Google Scholar]
- 5.Lu H, Clingman C, Golay X, et al. Determining the longitudinal relaxation time (T1) of blood at 3.0 Tesla. Magn Reson Med 2004; 52: 679–682. [DOI] [PubMed] [Google Scholar]
- 6.Stefanovic B, Pike GB. Human whole-blood relaxometry at 1.5T: Assessment of diffusion and exchange models. Magn Reson Med 2004; 52: 716–723. [DOI] [PubMed] [Google Scholar]
- 7.Rane S, Gore JC. Measurement of T1 of human arterial and venous blood at 7T. Magn Reson Imaging 2013; 31: 477–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dobre MC, Uğurbil K, Marjanska M. Determination of blood longitudinal relaxation time (T1) at high magnetic field strengths. Magn Reson Imaging 2007; 25: 733–735. [DOI] [PubMed] [Google Scholar]
- 9.Wu W-C, Jain V, Li C, et al. In vivo venous blood T1 measurement using inversion recovery true-FISP in children and adults. Magn Reson Med 2010; 64: 1140–1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Varela M, Hajnal JV, Petersen ET, et al. A method for rapid in vivo measurement of blood T1. NMR Biomed 2011; 24: 80–88. [DOI] [PubMed] [Google Scholar]
- 11.De Vis JB, Hendrikse J, Groenendaal F, et al. Impact of neonate haematocrit variability on the longitudinal relaxation time of blood: Implications for arterial spin labelling MRI. NeuroImage Clin 2014; 4: 517–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Keys A. The oxygen saturation of the venous blood in normal human subjects. Am J Physiol Leg Content 1938; 124: 13–21. [Google Scholar]
- 13.Lubin BH. Reference values in infancy and childhood. In: Nathan DG, Oski FA (Eds). Hematology of Infancy and Childhood. 2nd edition. Philadelphia, PA, USA: WB Saunders; 1981, pp.1552–1574.
- 14.Devine B. Mean blood hematocit of adults: United States 1960–1962. Natl Cent Health Stat Ser Public Health Serv Publ 1967; 1000: 1–36. [Google Scholar]
- 15.Blockley NP, Jiang L, Gardener AG, et al. Field strength dependence of R1 and R 2* relaxivities of human whole blood to prohance, vasovist, and deoxyhemoglobin. Magn Reson Med 2008; 60: 1313–1320. [DOI] [PubMed] [Google Scholar]
- 16.Alsop DC, Detre JA, Golay X, et al. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn Reson Med 2014; 73: 102–116. [DOI] [PMC free article] [PubMed] [Google Scholar]