Abstract
With heart and cardiovascular diseases continually challenging healthcare systems worldwide, translating basic research on cardiac (patho)physiology into clinical care is essential. Exacerbating this already extensive challenge is the complexity of the heart, relying on its hierarchical structure and function to maintain cardiovascular flow. Computational modelling has been proposed and actively pursued as a tool for accelerating research and translation. Allowing exploration of the relationships between physics, multiscale mechanisms and function, computational modelling provides a platform for improving our understanding of the heart. Further integration of experimental and clinical data through data assimilation and parameter estimation techniques is bringing computational models closer to use in routine clinical practice. This article reviews developments in computational cardiac modelling and how their integration with medical imaging data is providing new pathways for translational cardiac modelling.
Keywords: cardiac mechanics, data–model fusion, heart mechanics, patient-specific modelling, translational cardiac modelling
1. Introduction
Heart function is the orchestration of multiple physical processes occurring across spatial scales that must act in concert to carry out its principal role: the transport of blood through the cardiovascular system. Interest in cardiac physiology stretches beyond scientific curiosity to genuine need, with diseases of the heart posing significant challenges to the vitality of societies, healthcare systems and economies worldwide. Discord in cardiac function leading to pathology can occur at every spatial scale (figure 1). Changes in protein isoforms in the contractile unit of the heart (sarcomere), in gene expression and organization of proteins, in the constitution of the extracellular tissue scaffold, in the flow of blood through the muscle, in the excitation of the muscle or in the anatomy of the organ highlight a few of many examples. The cumulative effect of pathology in heart disease—often an ensemble of multiple modifications—ultimately re-tunes cardiac function, leading to a progressive deterioration in performance as the heart struggles to maintain output. Cardiology has advanced significantly, improving care and outcomes in patients. However, our ability to diagnose specific mechanisms, plan or adapt therapy, and/or predict treatment outcomes in patients continues to present challenges, reflecting a need to improve how we use knowledge of cardiology to analyse—or model—the heart.
Figure 1.
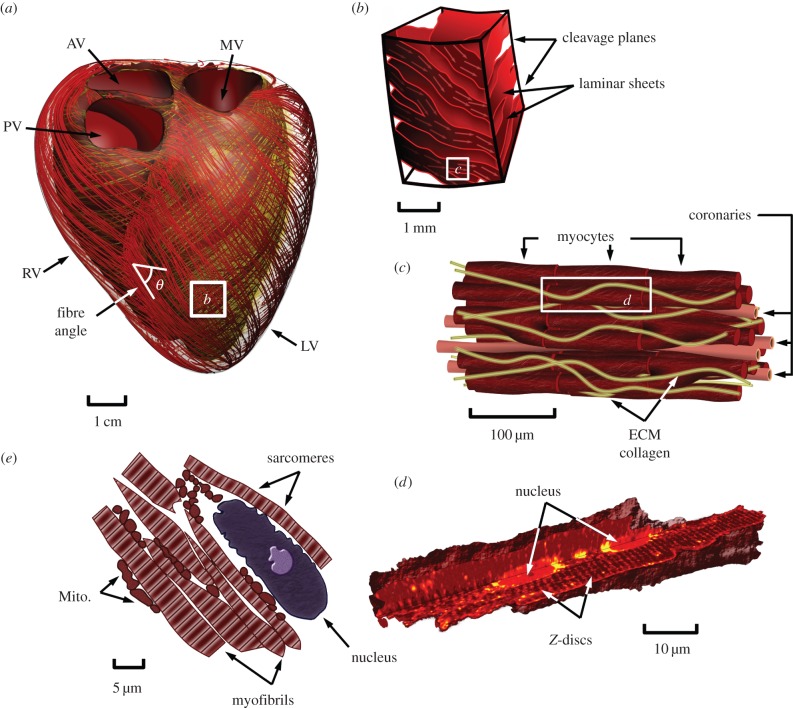
Illustrative representation of multiscale cardiac anatomy. (a) Geometric representation of the biventricular anatomy of the heart with streamlines illustrating its fibre architecture, (b) tissue block illustrating the laminar structure of the heart comprising fibre bundles arranged into sheets separated by cleavage planes, (c) local structural arrangement of myocytes and coronary capillaries, (d) 3D view of the cardiomyocyte cut to view internal structures (data courtesy of Dr Rajagopal and Dr Soeller [1,2]), (e) anatomy of the cell illustrating nucleus, myofibres (comprising crossbridges) and mitochondria. RV, right ventricle; LV, left ventricle; PV, pulmonary valve; AV, aortic valve; MV, mitral valve; ECM, extracellular matrix; Mito., mitochondria.
The use of modelling for understanding cardiac physiology and mechanics has a long history, with work stretching back to Woods [3], who estimated the stress in the heart wall by approximating the ventricle as a thin-walled spherical shell (known as the Law of Laplace). Modelling has since progressed to better approximate the underlying anatomical and physiological complexities. Geometric models of the heart evolved from thin-walled spheres to ellipsoids [4], axisymmetric idealized ventricles [5] and eventually to three-dimensional (3D) anatomically accurate geometries [6,7]. Studies illustrated the importance of accounting for nonlinearity in tissue mechanical properties [8–10] and structure [10,11] to understand the motion and load response of the heart. With experimental data on myocardial load response [12,13] and structure [14], more detailed structure-based models were introduced [15–17]. Experimental studies illustrating length [18], velocity [19] and frequency-dependent [20] modulation of muscle force were also integrated into models [21], broadening the scope of these models to simulate the mechanical function of the heart.
The biomechanical aspects of cardiac function cannot be fully isolated, instead they are interlinked with numerous physiological processes. At its core, the heart is a multiphysics organ [22] with electrical activation stimulating muscle contraction [23,24], muscle contraction interacting with intraventricular blood to promote outflow [25,26] and coronary perfusion [27], transporting metabolites and clearing waste products. These physical phenomena—involving reaction–diffusion, nonlinear mechanics, hemodynamics and biotransport—are tightly integrated, influencing the mechanical action of the heart. Heart function is dynamically regulated and modulated through interactions with the circulatory system, nervous system and endocrine system to change cardiac output [28–30]. Like other muscles, the heart's functional capacity and structure is also dynamic, responding to chronic changes in loading conditions and metabolic demand by altering cell structures, structural content, size, shape and vascular transport, among others. These physical and regulatory processes (which have been modelled to varying degrees) operate collectively to effectively deliver blood over decades and under extreme changes in functional demand. Understanding the influence of these factors on the biomechanics of the heart is important for deciphering the heterogeneous pathologies of the heart.
As the computational modelling community has explored various aspects of cardiac function at a fundamental level, parallel advancements in medical imaging and other diagnostic tools have enabled acquisition of an impressive range of datasets. Modern imaging is capable of recording the anatomy and motion of the heart, its tissue architecture, blood flow and perfusion, metabolism as well as numerous other pictures potentially useful in characterizing the state of a patient's heart [31]. With such a wealth of data, however, the challenge becomes integration and contextualization. Addressing this challenge is the primary aim of data assimilation, fusing cardiac models with these disparate data sources. While the complexity of a model is, in many ways, no simpler than the data it is founded upon, the advantage is its ability to link observed behaviour to the underlying physiology, providing potential mechanistic explanations of patient pathology. After the challenges of data–model fusion are met and model analysis provides novel insight, the difficulty then turns to translating these findings into clinically useable decision-making tools that can be robustly tested through clinical trials, proving their efficacy and superiority compared to existing techniques. This effort is the principle aim of translational cardiac modelling (TCM), bringing cardiac modelling and model-based outcomes into the clinical routine. TCM, however, remains in its infancy, grappling with the challenges of using real data and striking the balance between necessary and known complexity to deliver tools that address clinical needs. While the road to translation is challenging, the potential for significant impact has fuelled scientific progress forward towards this aim.
In this review, we consider the recent advances in ventricular cardiac mechanics modelling and translation to clinical applications. Section 2 provides an overview of the current state-of-the-art in biomechanical heart modelling, addressing the various aspects of multiphysics physiology explored in the literature. Emerging work in the areas of multiscale modelling as well as growth and remodelling applied to cardiac mechanics are also reviewed. Section 3 continues by reviewing available clinical data, the challenges in model parametrization as well as data–model fusion techniques commonly used in TCM. Finally, current translational efforts appearing in the literature are reviewed (§4) and future directions for TCM are discussed (§5). Exhaustive, in-depth review of each of these subjects could be an article in and of itself. Instead, this article gives an overview of the road to translation in cardiac mechanics, touching on the important aspects which span research disciplines and examining those future directions required to realize the potential impact of modelling. While this article focuses on translation of ventricular mechanics models in the heart, this discussion reviews tools and advancements that may facilitate other translational modelling efforts.
2. Modelling paradigms in the heart
The multiscale anatomy and physiology of the heart play an integral role to cardiac function [28] (figure 1). The cardiac muscle (or myocardium) is a highly structured collection of cells known as cardiomyocytes. Within these cells, the fundamental contractile unit is the sarcomere, consisting of inter-digitating lattices of thick and thin filaments. The cyclic interaction between the thick and thin filaments, triggered and regulated by intracellular calcium, determines the amount of force generated during active muscle contraction. Electrical excitation of the myocytes cyclically modulates intracellular calcium concentration, releasing calcium from internal stores that are subsequently replenished.
Myocytes are arranged axially through the extracellular matrix, providing the heart's necessary elastic structure. These fibres run in parallel and are separated by cleavage planes [14,32], interconnecting to form a 3D network allowing the heart to undergo complex motions during each cardiac cycle. The tissue organization enables fast propagation of electrical waves in the direction of fibres through gap junctions that interlink cells. The integrated electromechanical action of the heart is essential for the efficient transfer of blood through the cardiac chambers, coronary arteries and the entire circulatory system. The introduction of disease can occur through a variety of mechanisms, often leading to remodelling of the shape, structure and function of the heart as it aims to preserve output. However, long-term remodelling is often debilitative, leading to the progressive deterioration of cardiac performance and the development of heart disease. In this section, we review modelling efforts presented in the literature aimed at addressing the varying physiological aspects of the heart.
2.1. Modelling cardiac anatomy and structure
Personalized ventricular mechanics analyses rely on anatomically realistic geometric models. Since the early 1970s, sophisticated imaging techniques, such as cine-angiography and echocardiography (ECHO), have been used to provide detailed descriptions of the ventricular anatomy. Concurrently, experimental methods were designed that were capable of obtaining detailed 3D measurements of ex vivo cardiac geometry as well as myocardial microstructural information. This approach enabled the creation of high fidelity 3D anatomical models of dog [14,15], pig [33] and rabbit [34] hearts with embedded descriptions of the myocardial tissue architecture.
With the development of non-invasive 3D cardiac imaging techniques, the construction of subject-specific 3D anatomical models of the heart is now widespread. The availability of in vivo imaging has not only ensured that computational models can accurately represent the shape of intact hearts, but has also enabled in vivo mechanics analyses to be performed on a wide range of species (e.g. dog [35], sheep [36] and human [37–40]). Methods for constructing 3D anatomical models can be broadly categorized into three main approaches: (1) iterative nonlinear least-squares fitting [15,33,40–42], combining medical image registration with free-form deformation techniques to customize a generic mesh [43]; (2) volume mesh generation from binary masks or surface meshes of the myocardium performed by software packages such as Tarantula (http://www.meshing.at/), GHS3D (http://www-rocq.inria.fr/gamma/ghs3d/ghs.html), CGAL (http://www.cgal.org/) and Simpleware (http://www.simpleware.com/); and (3) cardiac atlases used for the construction of 3D models of the heart from non-invasive medical images [44,45]. While each approach has proved effective, limitations remain. Fitting techniques working from template meshes can struggle to preserve mesh quality and perform poorly when dissimilarity between the template and target geometry exists. In contrast, volume mesh generation from masks or surface segmentations usually have good mesh quality but are more sensitive to potential segmentation errors.
In addition to constructing anatomy, models must also incorporate myocardial tissue structure. Our basic understanding of 3D myocardial architecture has been built up from detailed histological studies [14,15,46]. These data are still widely used as the basis for rule-based algorithms to represent myocardial fibre orientation [47,48]. High spatial resolution data have been made available by scanning electron microscopy and confocal microscopy [14,32,41,42], and this has enabled quantitative characterization of myocardial laminae, which have been shown to play a significant role in cardiac mechanics [49,50]. Diffusion tensor imaging techniques have been developed to estimate myocyte orientations [51]. Recently, high spatial resolution images of ex vivo hearts have provided another means to study myofibre structure [52] and to examine the organization of laminae throughout the whole heart volume [53]. While progress towards more comprehensive methods for characterizing cardiac microstructure (particularly in vivo) are in development, lack of tissue structure information remains an important gap in computational models and a likely confounding factor influencing model results.
2.2. Passive myocardial constitutive equations
It is generally accepted that the mechanical response of ventricular myocardium can be described by anisotropic, hyperelastic (or viscoelastic) constitutive equations [12,54] (table 1). Transversely isotropic constitutive equations have been proposed by Humphrey & Yin [54] and Guccione et al. [60]—which has become one of the most cited and used cardiac constitutive models. The existence of myocardial sheetlets motivated the development of an orthotropic Fung-type exponential strain energy density function [74]. The model aimed to account for the relative shear (sliding) between adjacent sheetlets that have been shown to contribute to the total LV wall thickening during systole. Dokos et al. [66] confirmed that myocardium exhibits orthotropic mechanical response using carefully designed shear experiments on myocardial tissue blocks excised from the mid-ventricular wall. Similar material response was observed in shear testing experiment of human myocardium [75,76]. However, the level of statistical significance suggesting an orthotropic response was not as strong as that reported by Dokos et al. [66], with the mechanical response appearing transversely isotropic under large strain loads. Extending the approach pioneered for characterization of arteries [77,78], Holzapfel & Ogden [67] proposed a constitutive modelling framework, based on the underlying morphology of the heart tissue, to model the orthotropic passive mechanical response. Many constitutive equations in table 1 employ exponential forms, which generally suffer from a strong correlation between constitutive parameters. Criscione et al. [62] addressed these issues, in part, by using mutually independent strain invariants to define a transversely isotropic constitutive equation, minimizing the covariance between each of the response terms. However, this technique is yet to be used by the cardiac mechanics research community for predictive mechanics simulations.
Table 1.
Table of sample of cardiac constitutive equations published and used in the literature. HE, hyperelastic; VE, viscoelastic; 1D, one-dimensional; ISO, isotropic; TISO, transversely isotropic; ORTH, orthotropic; UA, uni-axial; BA, bi-axial; MA, multi-axial; SH, shear; PV, pressure–volume; ES, epicardial strains; LitVals, various literature values.
| model | type | structure | par no. | data | references | year |
|---|---|---|---|---|---|---|
| Humphrey & Yin | HE | TISO | 4 | BA [13] | [55] | 1987 |
| Horowitz | HE | TISO | 8 | BA [13] | [56] | 1988 |
| Humphrey | HE | TISO | 5 | BA [57] | [58] | 1990 |
| Guccione | HE | TISO | 5 | ES [59] | [60] | 1991 |
| Lin & Yin | HE | TISO | 4 | MA | [61] | 1998 |
| Criscione | HE | TISO | — | — | [62] | 2001 |
| Costa | HE | ORTH | 7 | — | [49] | 2001 |
| Pole-zero | HE | ORTH | 18 | LitVals, BA [63] | [17] | 2001 |
| Kerckhoffsa | HE | TISO | 4 | BA [57], PV [64] | [65] | 2003 |
| Holzapfel & Ogden | HE | ORTH | 8 | SH [66], BA [13] | [67] | 2009 |
| Loeffler | VE | 1D | 5 | UA | [68] | 1975 |
| Yang | VE | ISO | 5 | UA | [69] | 1991 |
| Huyghe | VE | TISO | 11 | UA [70], BA [12] | [71] | 1991 |
| Holzapfel | VE | ORTH | 4 | LitVals | [72] | 1991 |
| Cansiz | VE | ORTH | 17 | SH [66] | [73] | 2015 |
aLaw also contains additional parameters for modelling tissue compressibility not included in the table.
Cardiac tissue comprises cells (principally myocytes and fibroblasts) surrounded by extracellular fluid and held together structurally through extracellular matrix proteins [79]. The tissue–fluid interaction gives rise to viscous effects, which have been experimentally demonstrated by the appearance of hysteresis in stress–strain [12] and force–displacement [66] curves during cyclic loading. Modelling the complex viscous effect poses challenges since the mechanical behaviour is time-dependent and the constituents of the computational models need to take into account a mixture of solids and fluids. Several methods have been proposed to represent viscoelastic function in passive constitutive models (table 1) ranging from relatively simple arrangements using Maxwell's constitutive equation [68] to more complex variants incorporating known orthotropic hyperelastic models [73]. Current viscoelastic models tend to provide capacity to appropriately model cyclic loading conditions. However, validation of these types of models demands further experiments specifically targeted for hysteresis and creep phenomena. These experiments can be challenging, particularly ex vivo where tissue viability and changes to the extracellular fluid environment can confound the recordings.
2.3. Active contraction constitutive equations
Sliding filament theory by Huxley [80] has formed the foundation of many modern myocyte contraction models. Some of the first models that used this theory were proposed by Wong [81]. Subsequent models have concentrated on relating the active fibre tension to muscle length, time following stimulus, the interaction between Ca2+ and troponin C [82], and the effects of sarcomere length on Ca2+ binding and tension [83]. Guccione & McCulloch [84] estimated the active fibre stress using a deactivation contraction model, which placed specific emphasis on the deactivating effect of shortening velocity, as well as the dependence on shortening history. This model formed the basis of a time-varying elastance model [16] that was dependent on sarcomere length and length-dependent calcium concentration.
Hunter et al. [21] proposed an empirical cellular mechanics model (the HMT model), which considered the passive mechanical properties of the tissue, the rapid binding of Ca2+ to troponin C and its tension-dependent release (which occur at a slower rate), the length-dependent tropomyosin movement, the availability of Ca2+ binding sites and the crossbridge tension development. This model was shown to reproduce the response to isotonic loading and dynamic sinusoidal loading experiments. Based on the HMT model, Niederer et al. [85] proposed a more detailed time-dependent model with descriptions of contractile stress by taking the dynamics of calcium binding into account. Both models used a fading memory model to compute the active tension resulting from crossbridge kinetics. The Rice contraction model [86] instead used phenomenological representations to approximate the spatial arrangement of crossbridges, creating a compact ordinary differential equation model capable of replicating a wide range of experiments. The Bestel–Clement–Sorine (BCS) contraction model (proposed in [87] and further developed in [88]) considered myosin molecular motors, was chemically controlled and consistent with the sliding filament theory. The passive component was designed to be transversely isotropic by combining an elastic model of the Z-discs with a viscohyperelastic component model representing the extracellular matrix. The active contractile component was also coupled with a viscous element. Transverse active stresses (orthogonal to the myocyte axis) have also been predicted by the arrangement of the myosin crossbridge [89] and applied in contraction models to achieve better matching of measured systolic strains [90].
In comparison to the active stress framework whereby passive and contractile stresses are summed, an active strain framework has also been proposed. Using concepts from the growth and remodelling literature, this approach defines the deformation gradient tensor as the product of a passive elastic component and an active component [91]. This approach aims to preserve convexity in the material strain energy by avoiding the stress superposition found in more traditional active contraction mechanics models. However, these theoretical results rely on the complete decoupling between active components and length-/velocity-dependent mechanisms, which may present challenges for the model's consistency when comparing to physiological experiments.
2.4. Incompressible versus nearly incompressible formulations
Myocardial models introduced in the literature vary in their treatment of myocardial mass and its conservation. Physiologically, this debate stems from the fact that experimental studies have shown intravascular blood flow may account for changes of 5–10% in ventricular wall volume during each cycle [92]. A common approach used in a number of models [17,49,93] is to approximate the tissue as incompressible using the so-called mixed u–p formulation [94], which neglects these minor variations in mass content. An equally common alternative considers the myocardium as compressible (or nearly incompressible), whereby myocardial volume is lost or gained as a function of the effective hydrostatic pressure based on a pressure–volume constitutive equation. This approach is commonly applied using a displacement only formulation with additional parameter(s) (i.e. bulk modulus and, potentially, others) which scale terms that penalize changes in volume [65,90,95]. An alternative employed in some cardiac mechanics studies is the perturbed Lagrangian approach, whereby pressure and displacement are solved with the pressure–volume constitutive relation given as the required constraint [73,96,97]. Numerical considerations for these models, in the context of cardiac mechanics, were discussed in [98]. Use of different models seems often motivated by numerical considerations, leaving an open question of which strategy is most applicable when modelling cardiac tissue.
2.5. Electromechanics
Contraction of the heart is induced by electrical activation initiating in the sinoatrial node and propagated through the myocardium by an electrophysiological depolarization wave. Coupling electrophysiology and mechanics allows models to account for known length-dependent alterations in wave propagation and resultant contraction. Electromechanical models (figure 2a) enable investigations of the role of abnormal electrical activity on mechanical performance of the heart as well as mechanical factors that contribute to arrhythmogenesis [24]. There are a wide variety of mathematical models of cardiac cell electrophysiology ranging from: low-order phenomenological models such as the FitzHugh–Nagumo (FHN) type models [103,104]; multivariate representations such as the Beeler–Reuter model [105] and biophysical ionic current models governed by ordinary differential equations [106], such as Hodgkin–Huxley type models [107] and human ventricular cell models [108]. The modified FHN model proposed in [104] has been widely adopted in electromechanics modelling studies [109–113], and species-specific models have been applied to study electromechanics during myocardial infarction [114] and dyssynchronous heart failure [115]. Mechano-electrical feedback plays an important role in the heart [116]. In particular, the state of deformation of the heart muscle is known to modulate the electrical properties of myocytes via the stretch-activated channels [113,117] and has the potential to modulate arrhythmogenesis. Although the electrical and mechanical function of the heart operate at significantly different timescales, coupled electromechanical simulations have been made possible via two numerical strategies. A common approach considers numerical partitioning of the electromechanical system, decoupling the electrical and mechanical problems using implicit–explicit methods [109,111,113,115,118,119]. Alternatively, a monolithic approach based on finite-element methods (FEMs) has been proposed [112], enabling stable integration of length-dependent effects of motion on electrical wave propagation. While quantitative comparisons between partitioned and monolithic approaches suggest the two forms tend to yield compatible results, these comparisons are likely to depend strongly on the selected model problem, with some responding more strongly to electromechanical coupling effects.
Figure 2.
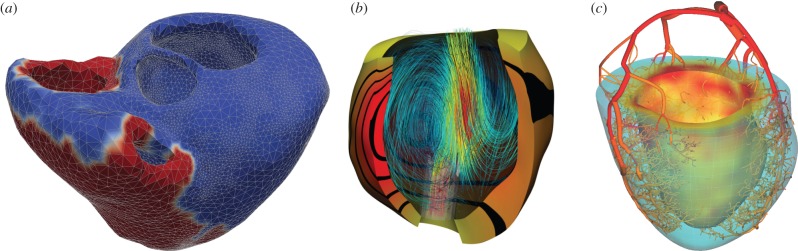
Samples of multiphysics modelling in the heart. (a) Biventricular electromechanical model of the heart illustrating the propagation of electrical potential over the heart [99]. (b) Fluid–solid mechanical model of the assisted LV. Fluid flow streamlines (coloured blue-red indicating increasing velocity magnitude) and myocardial displacements (yellow-red with equally spaced bands illustrating displacement magnitude) are illustrated [100,101]. (c) Coupled 1D flow-poroelastic perfusion model shown at early systole. Flow velocities are shown in the vessel segment. The pore pressure in the myocardium shows increased systolic compressive forces preferentially towards the subendocardium [102].
2.6. Fluid–structure interaction in the ventricles
Intraventricular blood flow and its influence on heart function has been the focus of numerous studies in the literature (see reviews by Khalafvand et al. [120] and Chan et al. [121]). Georgiadis et al. [122] did some of the first flow-specific work, considering the left ventricle as an axisymmetric ellipsoid. Similar models were later presented by Baccani et al. [123], Domenichini et al. [124] and Pedrizzetti & Domenichini [125], who suggested a possible link between ventricular vortical dynamics and disease. Saber et al. [126] and Merrifield et al. [127] presented some of the first patient-specific flow models of the LV using arbitrary Lagrangian–Eulerian (ALE) finite volume methods that integrated motion derived from images. Doenst et al. [128] and Oertel & Krittian [129] presented patient-specific flow models, incorporating left ventricle and atria, along with aortic structures for simulating left ventricular flow dynamics. Blood flow simulations have also been used to study diseases, such as myocardial infarction [130], congenital heart disease [131] and hypertrophic cardiomyopathy [132].
Some of the first models considering flow and tissue motion in the heart were done by Peskin [133], who focused on the interaction of flow with valves. This initial work spawned numerous subsequent studies examining the mechanical heart valves [134,135], mitral valves [136], both mitral and aortic valves [137] as well as recent work studying trileaflet biomechanical tissue valves [138,139]. Extension of fluid–structure interaction (FSI) techniques to study the interaction between blood flow and the ventricles was achieved by McQueen & Peskin [140,141], which was subsequently used for later studies of the heart [142–144]. These models, representing the myocardium as a collection of 1D fibres, were used to study coupling between flow and tissue along with the interaction between chambers of the heart [25,145–147]. One of the first attempts at modelling ventricular fluid–solid coupling using the FEM was presented by Chahboune & Crolet [148], where a two-dimensional (2D) model incorporating an anatomically based cross—section of the heart was used to analyse the effects of coupled flow and hemodynamics. Other 2D axisymmetric models were later used to study FSI effects under assist device support [149], in patients with DCM [150] and to examine the sensitivity of myocardial stiffness on clinical parameters [151].
Watanabe et al. [152,153] presented a 3D FEM model of an idealized left ventricle, incorporating myocardial biomechanics based on the work of Lin & Yin [61], representing the first work to incorporate state-of-the-art biomechanical models. This work used conforming low-order finite-elements to approximate the FSI problem, simplifying the intraventricular flow dynamics compared to comparable hemodynamics models. Cheng et al. [154] presented a partitioned passive filling model which coupled refined finite volume blood flow with a thin-walled isotropic hyperelastic wall model. Biventricular models were later developed which treated the heart as a passive Mooney–Rivlin material with an isotropic exponential term [155,156], driving systole and diastole through inflow/outflow boundary conditions. This model was later extended to incorporate an anisotropic term and emulate contraction by scaling passive material stiffness parameters with time [157]. A non-conforming monolithic FSI method and model [26,158] were used to simulate passive/active cardiac mechanics on patient-specific geometries using the Costa constitutive equation [49]. This model was later applied to study congenital heart diseases [159,160] and assisted left ventricles [100,101,161] (figure 2b). Krittian et al. [162] presented some of the first validation work, developing an experimental heart setup and modelled using both FSI and boundary-driven flow modelling, illustrating good qualitative agreement between data and model particularly for the boundary-driven flow model. Gao et al. [163] recently merged FEM models of the ventricle with the immersed boundary techniques of Peskin to enable use of current constitutive models within this framework.
While FSI models enable simulation of a multiphysics phenomenon at the core of cardiac function, such simulations often require substantial computational resources. Moreover, due to the low viscosity of blood and dominance of pressure, approximations of ventricular mechanics that ignore hemodynamics (considering the ventricle as a pressure-filled chamber) have proved effective in many modelling scenarios. While it is established that intraventricular pressure gradients are present in the ventricle, the spatial variation in pressure is often small relative to the absolute pressure scale. On the other hand, FSI models become increasingly important when studying specific pathologies, such as valve stenosis or hypoplastic left heart syndrome where significant increases in shear stress or decreases in ventricular filling pressures are observed, respectively.
2.7. Poromechanical modelling
The coupling of myocardial deformation and coronary blood flow (perfusion) has long been an area of interest motivated, in large part, by the significant influence of the crosstalk on their respective function (for review, see [164]). Coronary perfusion, essential for delivering metabolites to the myocardium, is functionally altered by muscle contraction with changes in muscle stiffness and deformation influencing the vascular resistance and compliance. From a mechanical modelling standpoint, one may conceptualize this multiphysics coupling within a classical FSI framework, explicitly resolving each vessel in the tissue [165]. However, this approach presents challenges given the anatomical complexity of the coronary vasculature [102] and significant variation in scale—from epicardial arteries (on the scale of millimetre) to coronary capillaries (on the scale of micrometre). An alternative is to consider flow below some spatial scale as a continuum, no longer resolved on the basis of individual vessels but as a continuous phenomenon present over the myocardial volume [166,167]. Two main families of this multiscale approach are classically used: homogenization and mixture theory.
Homogenization refers to a family of mathematical methods in which the contribution of smaller scale flows is simplified by seeking an asymptotic limit for the problem solution assuming a scale separation between microscopic and macroscopic domains. A typical underlying assumption is the presence of periodicity in the geometry and material properties of the microstructure, which can be described by the spatial repetition of a basic unit cell (often referred to as a representative volume element in mechanical literature). Various asymptotic methods can then be used to mathematically characterize the limit solution. The limit formulation generally takes the form of a coupled problem between variables at both macroscopic and microscopic scales. In certain restrictive situations, i.e. cases involving linear microscale problems with constant coefficients, the microscopic problem can be solved independently of the macroscopic one. More generally, the formulation requires an iterative solution process, whereby variables in the unit cell are calculated assuming a given macroscopic solution and resultant quantities are passed to the macroscopic problem. This increases the computational demand for practical problems significantly; however, this approach has been successfully explored for perfusion modelling [168,169].
In contrast, mixture theory is directly formulated at the macroscopic level assuming that a given number of distinct solid and fluid phases coexist and interact at each point in the continuum. This approach differs from the previous approach by directly embedding the functional effect of the unit cell into the governing poromechanical system through the use of constitutive equations governing the kinematic–kinetic interaction within (and between) phases. This approach originated in the pioneering work of Biot [170] and has been further enhanced and refined over the decades, using general descriptions of continuum mechanics to express the fundamental principles of conservation laws and thermodynamics [171–173]. More recently, the particular challenges present in the heart (e.g. large strains and rapid fluid flows) have been specifically addressed [174]. This leads to a coupled formulation that resembles ALE FSI [175], except that here the fluid and solid domains are the same and a volume-distributed coupling term is present [176].
When considering the application of these poromechanical approaches to the heart, experimental observations reveal a number of important additional features. Regarding the passive behaviour, cardiac tissue displays strongly anisotropic swelling and stiffening effects under perfusion pressure [177], similar to that of skeletal muscle [178]. The active behaviour of the heart is also seen to exhibit notable coupling effects—such as the well-known flow impediment phenomenon occurring during cardiac systole [179]—that modelling must incorporate. Perfusion is also highly compartmentalized, with flow in a region of tissue fed by a specific set of larger arteries [180]. To address this, the explicit solution of the flow in larger arteries has been coupled to a distal poromechanical tissue model yielding a multiscale representation that accounts for the distribution of inflow sites [102] (figure 2c). Additionally, different scales of the vasculature—exhibiting largely different flow characteristics—often inhabit the same volume, pointing to the need for so-called multi-compartment formulations [169,181] that allow for generations of vessels to be treated independently. The relationship between the explicit vascular structure and permeability and porosity must also be either quantified from high-resolution microvascular imaging [182,183] or from perfusion imaging [184].
2.8. Multiscale modelling strategies for contraction
The ejection of blood occurring with each beat of the heart depends on a cascade of functions spanning multiple scales. The power stroke of each myosin head (motion on the nanometre scale) aggregates through the hierarchical structure of the organ to produce each heart beat (motion at the centimetre scale). As a result, understanding the biochemistry of the heart and its influence on mechanical function requires use of multiscale, or micro-macro, approaches. Many multiscale modelling approaches, particularly in electrophysiology [185–187], have been introduced to enable the integration of biophysical models through the hierarchy illustrated in figure 1. Here, we focus our discussion particularly on multiscale modelling for contraction.
2.8.1. Subcellular contraction modelling
A crossbridge in itself can be seen as a special chemical entity having internal mechanical variables (or degrees of freedom) pertaining to the actual geometric configuration. In this context, whether a crossbridge is in an attached or detached state implies a conformational change of these internal variables and a change in the inherent free energy [188], providing a thermodynamically consistent basis for modelling the complex interplay of chemical and mechanical phenomena at the sarcomere level. This framework is appropriate for analysing the Huxley models of muscle contraction, based on the so-called sliding filament theory. In [80], the crossbridge is seen as a system with one mechanical degree of freedom associated with a linear spring that is under tension as soon as the myosin head attaches to the actin filament, which collectively induces muscle contraction. This model was later refined in [189], including additional chemical states in the attached configuration that accounted for the so-called power-stroke phenomenon, a key concept in the attachment–detachment cycle described in [190] (see also [191]). An alternative approach was recently proposed in [192], where a purely mechanical model was substituted for the chemical states of the attached crossbridge, with 2 degrees of freedom corresponding to one bi-stable element in series with a linear spring.
2.8.2. Multiscale/micro-macro approaches for contraction
Once the crossbridge behaviour has been modelled, the major challenge is to aggregate the behaviour of a single crossbridge over myofibrils, myocytes, myofibres to motion at the tissue and whole-organ scales (figure 1). Given the large number of crossbridges at the sarcomere level and above, it is quite natural to adopt a statistical description, as proposed in [80], by which the total active force/stress is given by the mean of the individual crossbridge forces with an appropriate scaling factor. This approach naturally leads to considering dynamical equations representing the evolution of the underlying probability density functions (PDFs). In order to mitigate the resulting computational costs in the simulation process, some approximations can be made by representing the PDF by a limited number of so-called moments [193]. In fact, under certain modelling assumptions, the moments equations are exact, and directly provide the active stresses themselves as solutions of a dynamical equation [88,194]. In any case, active stresses need to be eventually considered in conjunction with passive behaviour ingredients, resulting from various constituents other than sarcomeres at the cell level and outside of cells. Use of homogenization could be envisioned for this purpose, albeit it is more standard in mechanics to resort to rheological modelling, by which various components can be combined in an energy-consistent formalism, e.g. in the three-element muscle model proposed by Hill [195] and used in [88] to formulate a complete macroscopic cardiac tissue model.
An important consideration is the adequacy of such multiscale modelling approaches and whether they appropriately link cardiac function across scales. It has been demonstrated in [80] that a 1 degree of freedom muscle contraction model is adequate for representing important features of muscle physiology, such as the Hill force–velocity dependence. Furthermore, the extension of this model proposed in [88] was shown to correctly reproduce length-dependence effects namely, the so-called Frank–Starling mechanism and the scaled elastance properties evidenced by Suga et al. [196] and observed in experimental measurements [197]. Nevertheless, an important motivation for a more refined microscopic model resides in the shorter time scale effects observed in fast transients, such as under force or length clamp [189,198]. In addition, transient deactivation may be a critical determinant of mechanical heterogeneity in asynchronous activation [199].
2.9. Growth and remodelling
The form and function of the heart changes continuously–during development and aging or in response to training, disease and clinical intervention [200]. These phenomena are collectively referred to as growth and remodelling [201]. Specifically, the notion of growth is commonly related to changes in cardiac dimensions, whereas the notion of remodelling refers to changes in cardiac structure, composition or muscle fibre orientation [202]. Modelling the long-term, chronic response of the heart through growth and remodelling is challenging, and far from being completely understood.
Proposed more than two decades ago [203], the first mathematical model for growth within the framework of nonlinear continuum mechanics is now well established and widely used for various biological structures [204]. These models are based on the conceptual idea to decompose the deformation gradient into a reversible elastic and an irreversible growth part. Only the elastic part (a product of the deformation gradient and the inverse growth tensor) is used in the constitutive equations, which then enters the equilibrium formulation in the standard way [201]. The growth part, a second-order tensor, can be prescribed using constitutive equations relating the growth kinematics and growth kinetics, two equations that characterize how and why the system grows [205]. As an alternative to model growth at the continuum level, is the constrained mixture approach [206], based on the original mixture theory of Truesdell & Noll [207], where each of the continuum's constituents possesses its own reference configuration, physical properties and rate of turnover, but deforms as a whole with the continuum.
Cardiac growth is associated with a wide variety of pathologies, which can conceptually be classified into two categories [208]: concentric and eccentric hypertrophy. Concentric hypertrophy is associated with thickening of the ventricular walls, impaired filling and diastolic heart failure. Eccentric hypertrophy is associated with a dilation of the ventricles, reduced pump function and systolic heart failure [209]. While the causes for cardiac growth are generally multifactorial, concentric hypertrophy is commonly believed to be a consequence of pressure overload, while eccentric hypertrophy is thought to be related to volume overload [210]. Both conditions can affect the left and/or right side of the heart [211]. Left-sided overload triggers growth and remodelling of the left ventricle and may cause the symptoms of left heart failure (pulmonary oedema, reduced ejection fraction or cardiogenic shock). Right-sided overload triggers right ventricular growth and remodelling and may cause symptoms of right heart failure (compromised pulmonary flow, stagnation venous blood flow and poor LV preload). These different manifestations of cardiac growth and remodelling are chronic and can progressively worsen over time, ultimately proving fatal.
A variety of different models for cardiac growth have been proposed throughout the past decade [212]. Some simply prescribe a growth constitutive equation and study its impact on cardiac function [213] without feedback mechanisms based on the physiological status of the heart. Others allow growth to evolve naturally in response to pressure overload or volume overload [210]. While initial conceptual models used idealized ellipsoidal single ventricles [213] or bi-ventricular geometries [205], more recent approaches use personalized human heart geometries with all four chambers [209]. Using whole heart models allows us to explore clinically relevant secondary effects of growth and remodelling including papillary muscle dislocation, dilation of valve annuli with subsequent regurgitant flow and outflow obstruction [209]. Growth models may also explain residual stress which is known to be present in the myocardium [214,215].
Multiscale modelling holds the potential to link the clinical manifestation of cardiac growth to molecular and cellular level events and integrate data from different sources and scales. Studies of explanted failing human hearts revealed that the type of cardiac growth is directly linked to changes in cellular ultrastructure [216]: in concentric hypertrophy, individual cardiomyocytes thicken through the parallel addition of myofibrils; in eccentric hypertrophy, cardiomyocytes lengthen through the serial addition of sarcomeres [217]. Eventually, integrating these chronic alterations of cardiomyocyte structure and morphology into multiscale models of cardiac growth could help elucidate how heart failure progresses across the scales. It would also allow us to fuse data from various sources—clinical, histological, biochemical and genetic—to gain a comprehensive, holistic understanding of the mechanisms that drive disease progression.
3. Towards translation: data–model fusion
Models adapted to a patient's cardiac anatomy and function are being proposed for use in diagnostic medicine—providing new or improved biomarkers for indicating or stratifying disease—as well as predictive medicine—allowing for virtual testing of treatment both acutely and longitudinally. Underpinning this translational approach are the significant advancements made in medical imaging which are now capable of providing a wealth of information about the anatomy, structure and kinematics of the heart. While the concept of leveraging this information to define patient-specific models is straightforward, the execution of fusing images and models remains a key challenge in many TCM projects. This process depends critically on the type of data used, image processing of data into quantifiable terms and assimilation of this data within a model.
3.1. Clinical data and acquisition
Since the first X-ray image acquired in 1895, medical imaging data have grown to play a key role in patient diagnosis, treatment planning and follow-up in the clinic. This is thanks, in large part, to the advent of new modalities, reduced cost of imaging, prevalence of systems in clinics worldwide and substantial body of evidence from clinical trials highlighting the improvement in patient outcomes for specific treatments using image-derived quantities. The main non-invasive imaging techniques used in cardiology and applied in cardiac modelling are ECHO, computed tomography (CT) and magnetic resonance imaging (MRI) [31].
Out of these three modalities, ECHO is by far the most accessible in clinics. It combines safety, low price and versatility for a wide range of cardiovascular disorders (assessment of anatomy and function of heart and valves, anatomy of large vessels, measurement of flow using Doppler effect and others). The excellent temporal resolution is compromised by a lower signal-to-noise ratio and contrast-to-noise ratio (figure 3a) and limitations in the reproducibility of exams, which are often operator-dependent. Although there are no real contraindications for the ECHO exam, the hearts of larger patients can be difficult to image. Regardless, the prevalence of ECHO in clinics worldwide and current use in assessment of heart conditions suggests that models capable of successfully exploiting this data source have a large potential for translational impact.
Figure 3.
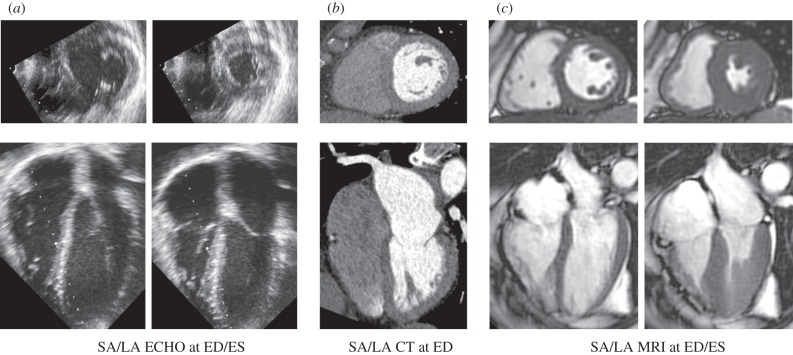
Example of typical medical images of short-axis and long-axis views of the heart. (a) ECHO images at two points in the cardiac cycle. (b) CT images at end diastole (single time point usually acquired due to radiation dose) with contrast bolus illuminating the LV blood pool. (c) CINE MRI at two points in the cardiac cycle. SA, short-axis; LA, long axis; ED, end diastole; ES, end systole.
Current cardiac CT imaging (multi-slice and multi-source systems) has the advantage of fast acquisition, excellent spatial resolution and reproducibility (figure 3b). These factors enable morphological and functional assessment of the heart (including valves) even for larger patients. The superior spatial resolution of CT and fast acquisition times make it the modality of choice for the non-invasive assessment of detailed anatomy, such as stenosis in arteries or valves. CT can also provide dynamic information throughout the cardiac cycle, though this is usually avoided in patients due to the significant radiation dose. Indeed, the main drawbacks of CT are the patient exposure to ionizing radiation and application of iodine contrast agents. These drawbacks are, in particular cases, outweighed by the potential benefit of CT; for example, coronary angiography and other vascular stenoses as well as valve disorders.
MRI provides similar functional and morphological information as CT without the use of ionizing radiation (figure 3c). A higher temporal resolution (in comparison to CT) contributes to accurate functional imaging of heart [218,219]. In addition, MRI is capable of imaging tissue characteristics such as presence of infarction scar [220], fat infiltration or inflammation [221], fibrosis [222,223], iron-loading [224], 3D myocardial strains [225,226] and potentially vascular tree structure [227]. MRI is limited in the speed of acquisition, relying on cardiac gating, respiratory navigation or breath-holds to acquire images of the heart. As a result, typical MRI images are averages over multiple heartbeats. Speed of acquisition and signal-to-noise remain key factors that limit the spatio-temporal resolution of MRI. Advances in MRI acceleration techniques and improved motion correction, however, have led to substantial progress in imaging of fine anatomical structures (e.g. coronaries [228]). The main drawbacks of MRI are in contraindication for some patients (e.g. MRI incompatible pacemakers), longer acquisition times and the cost of exams.
While the spatio-temporal resolution of these modalities is often adapted for a given patient (e.g. breath-hold duration in MRI or X-ray dose in CT), table 2 provides some typical values. The details of image acquisition often play a significant role in later processing and present practical considerations important for translation. The lack of reproducibility in repetitive breath holding in MRI as well as differences in breath-hold and free breathing scans often lead to images that are not easily co-registered into the same orientation and space. Even in common short-axis cine MRI stacks, differences in a patient's breath-hold position can yield significant misalignment between 2D slices, an issue that is not problematic for clinical processing, but challenging for TCM. As a result, it is important to carefully adapt imaging protocols to optimize them when used in modelling.
Table 2.
Sources of image data used in TCM. Resp.comp., respiratory compensation; RT, real time; PI(n), parallel imaging (acceleration factor); BH, breath-hold; FB, free breathing; NAV, breathing navigator; excl.NAVeff., excluding navigator efficiency (total scanning time needs to be multiplied 2–3×), kt, kt-blast/kt-sense/kt-PCA; NSA, number of signal averages; HB, heartbeat; PC MRI, phase contrast MRI. Note that the X-ray dose of non-dynamic CT is approximately 10-folds lower than in dynamic CT.
| modality (MRI sequence) | acceleration (MRI) | resp. comp. | duration | resolution (mm) × (ms) |
|---|---|---|---|---|
| BH Cine MRI (bSSFP) | PI(2) | BH | 5–8 s/slice | (2 × 2 × 8) × (20) |
| FB Cine MRI | PI(2) | FB(NSA) | 60 s/slice | (2 × 2 × 8) × (20) |
| RT Cine MRI | PI(3–4) | FB | RT | (3.5 × 3.5 × 10) × (70) |
| 3D morphology (bSSFP) [228,229] | PI(3) | FB, NAV | 4 min excl.NAVeff | 1.5 × 1.5 × 1.5 |
| 2D tagged [230] | PI(2) | BH | 15 s/slice | (2 × 2 × 8) × (30) |
| 3D tagged [225] | PI(2) | BH | 15 s/volume × 3 | (3 × 3 × 7) × (20) |
| T1-mapping (MOLLI) | — | BH | 20 s/slice | 2 × 2 × 8 |
| MR perfusion (2D) [231] | kt(5) | BH/FB | 3 slices/HB | (2.5 × 2.5 × 10) × (1000) |
| MR Perfusion (3D) [232] | kt(7) | BH/FB | volume/HB | (2.5 × 2.5 × 5) × (1000) |
| 2D echo (RT) | — | FB | RT | (below 0.5 mm) × (20) |
| 3D echo | — | BH | 10 s | (below 1 mm) × (60) |
| CT (single time image) | — | BH | 15 s | below 1 mm |
| CT (dynamic) | — | BH | 15 s | (below 1 mm) × (70) |
| 2D MRI flow | PI(2) | BH/FB(NSA) | 15 s (in BH) | (2 × 2 × 8) × (20) |
| 4D MRI flow [233] | kt(8) | FB | 7 min excl.NAVeff | (2.3 × 2.3 × 2.3) × (30) |
| echo Doppler | — | FB | RT | (10 × 10 × 10) |
| in vivo DTI [234] | — | BH/FB | 60 min/5 slices | (2.7 × 2.7 × 6) |
Other advanced imaging methods in development could further enhance the data available for modelling. Dual positron emission tomography (PET) MRI or PET-CT are enabling the imaging of functions (such as metabolism and perfusion) in the heart along with co-registration to anatomical information. Elastography techniques using ECHO or MRI [235–237] introduce the potential of directly measuring apparent tissue stiffness at multiple points in the cardiac cycle [235]. Advancement of diffusion tensor imaging into the heart in vivo [234,238] provides the possibility to measure specific structural characteristics of the heart. While not yet used in the clinic, these modalities may play a role in future model-based parameter estimation.
Beyond imaging, a range of alternative data sources have proved useful in TCM. Pressure in the heart cavities (important for instance to obtain quantitative values of tissue stresses) can be measured by invasive catheterization. The non-invasive blood pressure measurement in periphery by using a transfer function [239] can provide the proximal aortic pressure over the cardiac cycle. Electrophysiology models can be constrained by invasively measured intracavity extracellular potentials, non-invasive body surface mapping procedures, as well as electrocardiogram recordings. The former was applied in CRT modelling [39,99] and the latter is a current challenge for a number of research groups.
3.2. Image processing
The use of acquired image data in developing patient-specific cardiac models is preceded by image processing. Often image processing is necessary for the personalization of model anatomy and the extraction of information from the data (e.g. motion pattern) that can be used in the personalization of the model (e.g. data assimilation).
As the information used in modelling is often combined using several types of data, spatial and temporal registration of the acquired images is necessary. Given the fast dynamics of a heart beat and the relatively small displacements involved, achieving a robust and accurate multi-modal registration of all the available data is core to the accuracy and robustness of model outputs. While within a single modality, the techniques of spatial registration are quite robust [240], the registration in between modalities often requires manual input/corrections.
An important step of image processing is image segmentation used to extract relevant anatomical details and extracting motion information, for instance displacement of points (out of 3D tagged MRI), motion of endo- and epicardial surfaces (cine MRI, 3D ECHO) or tag-plane motion (2D tagged MRI [241]). There are a number of existing segmentation and motion-tracking methods relying on manual, semi-automated or fully automated procedures. A move towards full automation is essential for wider use of personalized modelling techniques [242,243]. The uncertainty of image processing impacts the accuracy of the personalized model. Recent projects combining synthetic images and biophysical models proposed a way to estimate the accuracy of motion tracking in medical images [244].
Table 3 summarizes selected studies in which modelling was successfully combined with real or synthetic datasets. Typical image data modalities applied in these studies were cine or tagged MRI and myocardial passive and active properties were estimated. In some of the studies, parameters of an electrophysiological model (typically regional tissue conductivities) were estimated. Both ex vivo [255,256] and in vivo diffusion tensor imaging [238,257] data have been processed to estimate myocardial fibre orientations and used for simulations. Certain difficulties of using ex vivo images (including inter-subject registration, and the differences in tissue properties between excised and living organs) may be circumvented in vivo with the development of imaging [258] and reconstruction [48,238] techniques.
Table 3.
Examples of works presented in the literature targeted at TCM and data–model fusion. CE, constitutive equation; est. meth., estimation methods; SA, sensitivity analysis; NH, neo-Hookean; GL, Guccione constitutive equation (law); NF, neo-Fibre; HO, Holzapfel–Ogden; V, variational; PS, parameter sweep; RO-UKF, reduced-order unscented Kalman filter; ML, manifold learning; DFO, derivative-free optimization; P, passive; A, active; BCS, Bestel–Clement–Sorine.
| data | subject | CE | est. meth. | phase | SA | references |
|---|---|---|---|---|---|---|
| 2D tagged | phantom | NH | V | P | — | [245] |
| 2D tagged | phantom | GL | V | P | — | [245] |
| 2D tagged | human | GL | V | P | — | [246] |
| 3D tagged and cine MRI | human | GL | RO-UKF | P | — | [247] |
| cine MRI and pressure | human | A | — | [248] | ||
| 2D tagged | in silico | — | [241] | |||
| cine MRI | pig | BCS | RO-UKF | P, A | X | [249] |
| cine MRI | human | BCS | UKF | P, A | X | [250] |
| cine MRI | human | BCS | ML | P, A | — | [251] |
| 3D tagged and cine MRI | in silico and human | NH, NF, GL, HO | PS | P | X | [244,252] |
| cine MRI | human | BCS | DFO | A | X | [253] |
| cine MRI (low res.) | human | BCS | RO-UKF | A | — | [254] |
3.3. Model parametrization
Model parametrization is typically achieved by optimization, attempting to match some target data with model result(s) using the goodness of fit gauged by an objective function. What is deemed a successful parametrization depends on the purpose. For some applications, the goal is simply to find a set of parameters that yield an acceptably low objective function, providing a model which appropriately matches data. However, when the parameters themselves are the target of an analysis, then the process of model parametrization should also consider the uniqueness and identifiability of parameters.
Model parameter uniqueness and identifiability depend on the model, the data and the objective function [244]. Important for parameter uniqueness is that a model be structurally and practically identifiable. Structural identifiability ensures that given endless, error-free data, one could determine model parameters uniquely. In contrast, practical identifiability ensures that parameters can be determined uniquely based on the type of data available in experiments. Demonstrating practical identifiability is often straightforward for simple models, but becomes increasingly challenging as models become more complex. Even if a model demonstrates practical identifiability, experimental or clinical data can introduce problems. Noise and bias artefacts in data can reduce parameter identifiability and make model predictions unreliable. Adding to the challenge is model fidelity, or whether the model is sufficiently rich to represent that data. Model simplicity can lead to a poor match between the simulation and data and potential non-uniqueness in parameters. In contrast, complex models may rectify issues with model fidelity but at the expense of parameter identifiability. The objective function also plays an important role, acting as the yardstick indicating whether model and data agree. If this objective is too relaxed, it may be possible for multiple parameter sets to be valid minima despite parameters being, theoretically, uniquely identifiable. Considering these factors is critical for studies wishing to use model parameters themselves.
Parameter identification using in vivo imaging data of the beating heart has challenged many researchers, especially when using the exponential-type strain energy density functions to model the passive mechanical behaviour of myocardium. The lack of 3D kinematic measurements, or of certain modes of deformation during normal in vivo motion, may result in poor practical identifiability. For example, during diastolic filling, the motion information captured during in vivo imaging may not adequately span into the nonlinear range of the stress–strain (or pressure–volume) curve to enable the underlying material parameters to be fully characterized [245]. Schmid et al. [259] conducted simulation studies to examine the suitability of five strain-based constitutive models and determined the orthotropic exponential constitutive model developed by Costa et al. [49] to best represent different shear deformations [260]. However, several studies have reported strong correlations between the material constants [244,246,247].
3.4. Data assimilation
The previous sections illustrated the wealth of models and data available for simulating the heart. These models can be calibrated (parametrized) based on patient data to produce patient-specific simulations. In mathematical terms, the process becomes an inverse problem, whereby data that is generally a potential output of the model system is used to help retrieve specific model inputs (e.g. unknown initial conditions, physical parameters, etc). Cardiac models, by their nature, are dynamical systems of partial differential equations (PDEs) and their integration with data to solve inverse problems falls into the general class of methods referred to as data assimilation techniques. Historically, data assimilation arose in geophysics in the 1970s [261], but nowadays has reached new fields of science [262]. From its inception, data assimilation relates to numerous theoretical fields: statistical estimation, optimization, control and observation theory, modelling and numerical analysis, as well as data processing. In cases where the complete solution, for example the entire motion of the heart, is known, some have suggested direct use of the data to determine unknown parameters by the direct use of these quantities within the governing PDE [263]. More often, however, data assimilation aims to reconstruct the trajectory of an observed PDE system from a time sequence of heterogeneous measurements. In data assimilation, there are two classes of methods: variational and sequential [262].
Variational methods seek to minimize a least-squares criterion combining a comparison term between the actual data and the simulation, with additional regularization terms accounting for the confidence in the model. The comparison-term or data-fitting-term is usually called similarity/discrepancy measure, whereas the model confidence terms are called a priori. This is known as the variational approach as reflected in the popular 4D-Var method [264]. The most effective minimization strategies compute the criterion gradient through an adjoint model integration corresponding to the dynamical model constraint under which the criterion is minimized. Then, the minimization problem is classically solved by a gradient descent algorithm, involving numerous iterations of the combination of the model and adjoint dynamics. Gradient-free approaches can also be used, simplifying the use of variational methods in complex codes, but involving still more evaluations of the functional [253,265].
Sequential methods can be inspired from the point of view of feedback control theory. The key concept is to define an observer (also referred to as estimator in the stochastic context) that uses the data as a control to track the actual trajectory, and concurrently retrieve the unknown parameters. This so-called sequential approach gives a coupled model–data system solved similarly to a usual PDE-based model, with a comparable computational cost. Indeed, this approach can provide significantly improved efficiency assuming the feedback is designed specifically for the system at hand. Two main classes of feedback have been developed: (1) reduced-order Kalman-based feedbacks (or filters) which cumulate the advantage of their genericity with a reduced computation cost for PDE-based models [266,267]; (2) Luenberger feedbacks where the filter is specifically tuned by analysing the dissipative properties of the physical system described by the models [268,269]. Note that these two classes can be used concurrently to define, for instance, joint state and parameters estimators [266] where the Luenberger filter is devoted to the stabilization of the state errors (initial conditions, modelling errors) and the reduced-order Kalman-like feedback handles the parameter identification. We can also combine these two feedbacks for coupled physical systems, for instance in cardiac electromechanics where a Luenberger feedback is used in the mechanics and a reduced-order feedback is employed on the electrophysiology [270]. Use of established data assimilation techniques for cardiac mechanics requires some special considerations. The most fundamental one is to establish the observability of the system, namely the amount of information that can be retrieved from the data at hand. This question is vast and must be addressed using sensitivity analysis and uncertainty quantification.
3.4.1. Methodological issues in cardiac data assimilation
Use of established data assimilation techniques for cardiac mechanics requires some special considerations. Heart models present a major difficulty in that they are strongly nonlinear, with phase changes throughout the cardiac cycle. These changes in the physical nature of the heart can introduce challenges in the use and convergence of data assimilation methods [250]. In this respect, the (sequential) methods that rely on particles for the model sensitivity computations have proved to improve robustness [247,249,250]. Other constraints on the system (e.g. tissue incompressibility discussed in §2.4) or the parameters that often lack direct observations must also be handled appropriately. Moreover, it is often beneficial to add physical constraints (such as positivity for material stiffness constants) by adjusting the physical system or through a change of variables [249,250].
Another difficulty arises due to the data at hand. In cardiac mechanics, the first source of data is image sequences providing motion through the cardiac cycle. The information contained in images is very different from the classical model outputs, which makes the definition of similarity measures challenging. In essence, the model computes displacements with respect to a reference configuration. In contrast, the images show the deformed domain over time. With some imaging modalities, such as tagged MRI or 3D ECHO, image processing techniques allow one to reconstruct a measured 3D displacement sequence more directly comparable to the model displacements [244,246]. However, for standard MRI or CT sequences, we must define a discrepancy measure between the deformed model domain and the observed shape. In this respect, the data assimilation community may benefit from the data fitting definitions already well developed in the image processing and registration community [271].
4. Bringing translational cardiac modelling to the clinic
The advancements made in modelling, imaging, image processing and data assimilation provide an impressively diverse range of tools and data. Extending these developments beyond academic and research realms and into the hospital requires careful consideration of specific clinical questions and the requirements of the end-user. The specific clinical application and desired outcome, in turn, guide the selection of required models and data, influencing the necessary processing and assimilation tools, theoretical considerations, etc. (figure 4). The pathways for TCM to make an impact clinically are numerous. In this section, we highlight some of these active TCM efforts.
Figure 4.
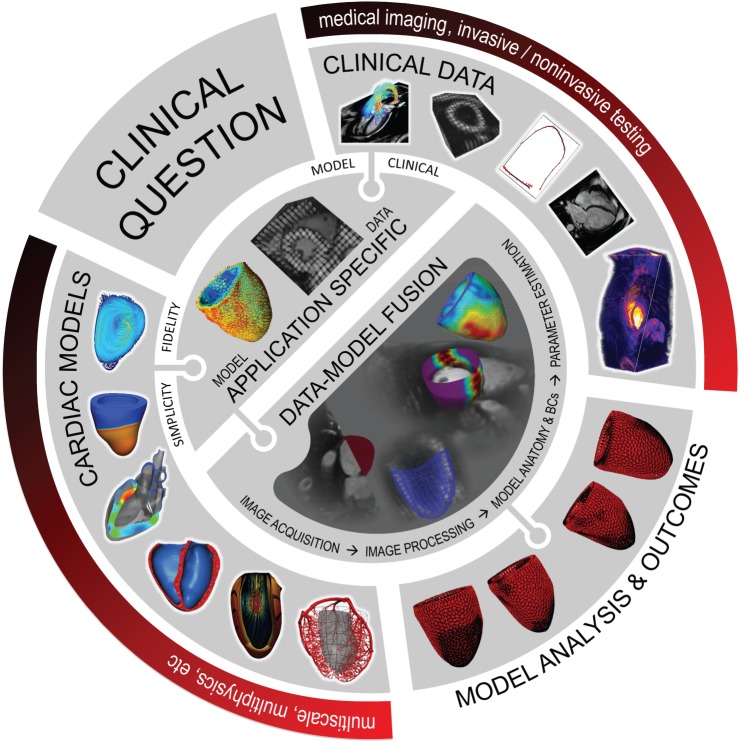
TCM pathway, illustrating the formative steps of model-based analysis. The driver for TCM efforts starts with the clinical question, informing the selection of an application-specific model that brings together the appropriate data and model components. Data–model fusion is then required, personalizing the model with sufficient data (either patient-specific or population average data) to address the clinical need. Once formulated, modelling can be executed and used to generate specific clinically relevant outcomes, informing diagnosis, treatment optimization or treatment planning.
4.1. Device assessment
Device-based treatment and therapy are playing an increasingly important role in the clinic [272]. Considering the significant time and investment required to bring medical devices to market, thorough vetting of a device's design is critical before it enters into clinical trial. Modelling, with encouragement from regulatory agencies [273], has played a significant role in device evaluation, particularly in the testing of mechanical- and tissue-based heart valves [134] which were simulated in idealized geometries to examine performance, damage and fatigue.
Increasingly, modelling is being used to consider how a device interacts with the mechanics of the heart itself. Figure 5a illustrates the use of an electromechanical model used to access the efficacy of a mitral valve annuloplasty device that aims to reduce mitral regurgitation. FSI models have been applied to assess left ventricular assist devices [100,101,161], examining how alterations in device settings influence myocardial unloading as well as the potential for LV thrombus formation. Electromechanical modelling has been used to assess the AdjuCor (http://www.adjucor.com/home.html) extravascular ventricular assist device, whereby pneumatic cushions are used to improve ventricular stroke volume while unloading the heart [275]. Biomechanical modelling has also been used for trans-catheter aortic valve replacement, using an anatomically accurate aortic model to simulate valve deployment [276].
Figure 5.
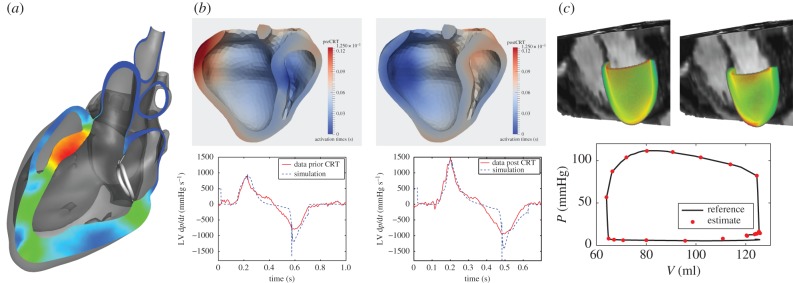
Example applications bringing TCM to the clinic. (a) Evaluation of mitral annuloplasty device using a four chamber electromechanical heart model, assessing the degree to which the device improves mitral valve regurgitation [274]. (b) Examination of biventricular CRT, using an electromechanical model tuned to baseline data to predict therapy response of left ventricular dp/dt [99]. (c) Left ventricular mechanics model parametrization using CINE, 3D tagged and 4D PC MRI providing estimates of tissue properties through the cardiac cycle [244,252].
These examples illustrate the potential of TCM to provide a platform for the rapid evaluation of medical devices. Further advancement of computational techniques [277–279] enhances the ability of models to resolve fine details influential in the operation of devices. In this context, models rely on anatomically accurate (as opposed to patient-specific) geometries and literature-based values to effectively represent the heart. Here, the purpose is a model with representative patient physiology, providing a means for evaluating efficacy and suggesting design modifications. This shift in focus dramatically simplifies data–model fusion and provides a more straightforward platform for exploiting complex cardiac models.
4.2. Therapy planning
Another avenue for TCM is through therapy planning, where models are used to predict the outcomes of different therapies. A prime example is Cardiac Resynchronization Therapy (CRT), where the placement of leads to excite the heart are currently evaluated during device implantation to maximize the rate of left ventricular pressure at early systole [280]. The peak left ventricle pressure time derivative (max LV dp/dt) is a standard clinical measure of a short-term effect of CRT. Electromechanical models tuned to pre-therapy imaging data were shown to accurately predict the effect of biventricular pacing (figure 5b) [99]. Modelling results also provided insight into therapy, suggesting that length-dependence (Frank–Starling mechanism) might be a key factor in treatment efficacy [39]. Both the studies used non-invasive MRI data as well as invasive electrophysiological data. Use of these tools to optimize treatment prior to surgery requires reducing the dependence on invasive data, a direction currently being explored.
Modelling is also being pursued as a way to evaluate pharmacological interventions, particularly when multiple drugs may be combined to deliver an optimal therapy. The syndrome of heart failure would once more be a typical example [281]. Significant efforts are also spent on electrophysiological side, searching for potential cellular proteins that could be targeted for drug development [282–284]. Inherently, this effort requires multiscale models to effectively examine the cascade of a drug operating on a subcellular target to a functional at the organ level. Extending these models beyond the development stage towards patient-specific planning introduces challenges and will likely require significant investment into the identification of key alterations required for personalization.
While many therapy models focus on the acute response, consideration of growth and remodelling effects is extremely attractive in predicting the long-term viability of therapy. These models are increasingly important as many therapies, such as CRT, are known to result in reverse remodelling and thus fundamentally change the responsiveness of the heart to treatment over time. Growth and remodelling could also play a role in therapy planning, where often the decision of whether or not to treat a patient is made based on the likely deterioration in a patient's condition [285]. Using these modelling approaches could provide much more reliable predictors of disease progression, enabling appropriate staging of therapy. Key to this development is the appropriate identification of remodelling mechanisms through either animal experiments or clinical studies where invasive tissue samples can be collected.
4.3. Biomarkers and diagnosis
Beyond addressing specific therapies, TCM has been proposed as a novel path for patient assessment and potential diagnosis through the use of model-based biomarkers. Advances in cardiac imaging and catheterization techniques have resulted in a wealth of clinical data contributing to the design of numerous biomarkers for cardiac dysfunction. Leveraging these data using patient-specific cardiac models provides a useful tool to better understand cardiac dysfunction on an individualized basis [99,244,246]. While estimation of quantities, such as stress and work, from direct measurements is not currently feasible, these quantities can be directly estimated using personalized models, providing a wealth of information that could be exploited to stratify patients.
Further, the data assimilation and model personalization processes require the tuning of model parameters. Often these parameters are quantities of interest, such as myocardial tissue stiffness or contractility [249,252,254] (figure 5c). Unlike other clinical indices that only reflect global chamber performance, myocardial mechanical properties provide tissue-specific biomarkers elucidating potential muscle tissue fibrosis, scar, reduced contractility and/or delayed relaxation. In vivo measurement of tissue mechanical properties is not readily available; therefore, estimates derived from model-based analysis integrating available personalized clinical data can offer more insight into the mechanisms and potential stage of disease. Recently, quantifying myocardial tissue properties has become the focus of much research to better understand the causes of ventricular dysfunction in several cardiac diseases such as myocardial infarction, heart failure [255], heart failure with preserved/reduced ejection fraction and hypertensive heart disease. In vivo estimates of tissue mechanical properties combined with other subject-specific measurements of cardiac function may assist with more effective stratification of different types of heart failure. Moreover, use of model-based biomarkers that can be rigorously tested against current clinical standards [286] would enable the design of mechanism-specific treatment strategies.
5. Realizing translational potential
5.1. The clinical question and data/model selection
With the wealth of available models and data, it becomes evermore critical that TCM is guided by the requisite outcome required to address a clinical question (figure 4). Identification of the problem and the intended outcome enables the appropriate identification of a model and set of data that ensures accuracy and robustness. This interplay introduces a delicate balance between the clinical question, available data, model fidelity and the final outcome desired from the model. A model must be rich enough in function to address the question of interest. It may be richer than necessary so long as the additional complexity does not yield uncertainty (or non-uniqueness) in the outcome. In contrast, simplicity often yields robustness but this can come at the expense of accuracy. As a consequence, realizing the potential of TCM requires careful consideration of the key factors important for addressing the clinical question at hand.
The examples of models applied into clinical problems from §4 fall into two general groups: direct translation to clinics and an indirect TCM employing the models in the development of new techniques (e.g. devices or drugs). Both application types require a very tight collaboration between the modelling team and end-customer, whether it be clinicians or commercial partners. Building bridges between these historically disjunct cultures is beginning at centres around the globe, as clinicians, industrial partners and modellers work more closely together to address relevant problems. Such a tight collaboration is necessary to ensure TCM addresses core needs and end-customers know what can be reliably derived from model-based outcomes. A successful example of translational modelling is HeartFlow (https://www.heartflow.com), illustrates the need for inter-disciplinary teamwork well, being co-founded by both a cardiovascular surgeon and engineer.
Clinical data, in particular medical image-based data, remain a necessary component to the progression of TCM. Improving imaging and image processing techniques will have a significant influence on the accuracy and robustness of model-based outcomes. This integration must begin at a much more fundamental level, making image acquisition and processing account for modelling needs and adapting models to robustly use these outputs. Imaging modalities (such as elastography [235–237] and in vivo diffusion tensor imaging [234,238]) present new opportunities to further engage modelling and imaging towards clinical outcomes, providing more direct measures of tissue properties and structure. However, the combination of imaging and modelling must also remain cognizant of clinical constraints, balancing outcomes with the complexity of patient assessment, cost and timescales. Nowadays, TCM often relies on the most advanced data available, which are often far from those acquired through standard care. In a research context, efforts to exploit the wealth of available data are essential to explore the potential for TCM outcomes. However, for clinical practice to shift towards such complex exams, the value of a model must be demonstrably better than the current standard of care. Using routine clinical data may limit the information for TCM, but would significantly improve uptake by facilitating the organization of multi-centre clinical studies. In this context, information-rich databases of standard data (e.g. UK Biobank; http://www.ukbiobank.ac.uk) will likely prove invaluable for guiding TCM efforts.
The selection of a cardiac model needs to balance the clinical question and available data. Importantly, the model-based outcome must address the question, capitalize on the available data, be robust and minimize uncertainties. Even the most efficient data assimilation methods become significantly more challenging and computationally intensive as the number of personalized parameters grows or the computational problem itself increases in demand. As a consequence, simplified models are often being used to parametrize components of more complex models; as was the case in [100] where a solid mechanics–Windkessel model was used to tune model parameters prior to simulating the full FSI-Windkessel model. Moreover, very complex models encompassing the widest range of physiological knowledge through integration many smaller models are not necessarily more predictive or reliable. The trade-off between model fidelity and simplicity remains application-specific. A simplistic (or complex) model may provide valuable outcomes in one application but be completely flawed in another.
While multiphysics models are necessary for addressing some phenomena in the heart, such integrated models often come with a greater demand for personalization and increased computational complexity. Examining the added value of such a model becomes increasingly important in TCM, where clinical timescales are short and computational resources in the majority of clinical centres are limited. While computational techniques and hardware continue to improve at rapid pace, it is likely that the most significant impact for multiphysics models will occur in the assessment of devices. By using population average models, the need for personalization would be eliminated, while still providing a valuable in silico environment for testing.
Despite broad support for multiscale modelling and simulations of cardiac growth and remodelling, the difficulty of model validation, mainly caused by the lack of appropriate experimental and clinical data, remains a point of concern [287]. Determining the genesis of physiological changes due to drug-based interventions and validating currently proposed hypotheses on governing principles is critical to the long-term use of modelling for guiding therapy. One important step is to extract the important cardiac modifications due to remodelling in order to guide modelling. Recent developments in statistical shape models for longitudinal analysis can help extracting this information [285,288]. However, exploiting the full potential of these techniques will require longitudinal animal experiments, collecting imaging and biopsy data to quantify alterations across scales.
5.2. Application-specific models and data–model fusion
Once an application-specific model and suitable type of data are selected, data collection and data–model fusion present a number of practical challenges that must be addressed to maximize translational potential. Imaging protocols, though typically standardized, are often adjusted to the patient's status and may be negatively influenced by the compliance of the patient or skill of the operator. These factors can significantly degrade image quality or precision, reducing the efficacy of TCM. Mitigating these factors through more straightforward imaging protocols, better identification of image quality measures, or using data redundancy to identify the confidence in image-derived quantities would greatly improve reliability of imaging data. Another core challenge is the streamlining and automation of image processing and data assimilation pipelines. While many tools exist in the research environment, few can be robustly applied by clinicians across many datasets. Moreover, manual intervention is often necessary, introducing uncertainty which must be quantified to practically ensure the quality of results.
As model-based tools continue to advance, efforts have been initiated to cross validate and benchmark methods. In the domain of image processing, algorithms to track motion from tagged MRI were systematically evaluated and compared with manually segmented results [289], showing comparable accuracy among the methods tested. Comparison of different cardiac mechanical models was recently conducted on the same extensive pre-clinical dataset (STACOM 2014 challenge; http://stacom.cardiacatlas.org) to evaluate predictive capacity and compare model produced outcomes [290]. While quantities such as displacements were well-predicted, strong variations were observed in myocardial stress predictions across models. Recent work in FSI benchmarking has also been organized, using 3D printing and measured materials to test the predictive accuracy of these methods (http://cheart.co.uk/other-projects/fsi-benchmark/). Benchmarking and validation will be increasingly necessary for TCM to convince the clinical community and the regulatory agencies of the validity and robustness of application-specific models.
5.3. Model analysis and outcomes
For TCM to realize its potential, it is crucial that simulation results are mapped into appropriate quantities that can guide clinical decision-making. Many of the modelling results target standard clinical metrics (e.g. FFR, max dp/dt), enabling a more straightforward pathway for TCM to make a clinical impact. Novel biomarkers will likely arise from TCM (e.g. myocardial stiffness or contractility); however, beyond being robust and reliable, these quantities must be demonstrated to provide diagnostic or prognostic value beyond the current clinical norm. Identification of these potential targets requires strong collaboration between clinicians and modellers, mixing practical hypotheses with deliverable model metrics to assess a patient's state or therapy plan.
While uptake of TCM into clinical care would take significant time and resource, the advent of large databases storing longitudinal data on patient treatment and outcomes provides a pathway to significantly accelerate translation of model-based outcomes. An alternative pathway for identifying TCM targets is through large-scale statistical methods. In this context, model-based outcomes could be used along with other measures typically embedded in Big Data approaches, examining potential correlations between derived model-based outcomes and specific clinical conditions or responses to therapy. As model-based outcomes integrate data and physical principles, these could provide essential metrics that are non-trivially related to typical clinical measures. Replicating these measures using statistical methods alone would likely require significantly larger amounts of data and increasingly complex, nonlinear regression techniques.
5.4. Uncertainty quantification
Model-based approaches need to provide a measure of confidence in their predictions. As measurement on living tissue is, by nature, sparse and noisy, there is a strong need to integrate all the sources of error in the process and quantify their impact on model outcomes. This requires an important shift from the current deterministic approaches to more probabilistic strategies, where uncertainties in input data are modelled to understand their impact on outcomes. The challenge of determining the impact of uncertainty permeates through the entire translational modelling pathway (figure 4). Uncertainty in model boundary conditions and anatomical construction stemming from data requires careful consideration of likely errors inherent in the data and processing pipeline. Similarly, examination of data assimilation techniques and the variation of model parameters to uncertainty in data must also be considered. This can create challenges both methodologically, as deriving stochastic models of such complex phenomena is non-trivial, and computationally, as such approaches are much more demanding. While comprehensive assessment of all uncertainties presents significant challenges, better clarification of model outcomes is mandatory to hone the focus of these efforts. Verification that all model parameters and quantities maintain a certain accuracy is an ideal, but far away goal. However, more immediate confidence may be obtained through demonstration that targeted outcomes are robust and reliable. Uncertainty quantification methods have started to be applied in the cardiac community [187,249,291–293] and these techniques will play an increasingly important role in TCM.
6. Conclusion
Addressing current clinical limitations in diagnosis, prognosis, treatment and therapy planning in heart and cardiovascular disease remains a significant translational goal driving cardiac research. In this paper, we reviewed modelling efforts aimed at addressing various physiological mechanisms influential for cardiac mechanics—spanning spatial scales and physical principles. The substantial growth in medical imaging and the techniques for leveraging this data for modelling were also reviewed. These parallel developments have opened a broad range of possibilities for bringing TCM into the clinic.
Acknowledgements
D.N. thanks Dr Ashley Nordsletten for assistance in revision, Dr Vijayaraghavan Rajagopal and Dr Christian Soeller for cellular imaging data, and Dr Eric Kerfoot for assistance with data visualization. R.C. and D.N. would like to thank Dr Eva Sammut for assistance in revision.
Authors' contributions
This article was organized by D.N. All authors participated in the writing and editing of the manuscript.
Competing interests
We have no competing interests.
Funding
D.N., L.A. and M.H. acknowledge funding from the BHF New Horizons programme (NH/11/5/29058) and EPSRC Research grant (EP/N011554/1). D.C., J.L., P.M. and R.C. acknowledge funding from the European Union's Seventh Framework Program for research, technological development and demonstration, under grant agreement no. 611823 (VP2HF Project). M.N., A.Y. and V.W. acknowledge New Zealand Government funding from the Health Research Council of New Zealand, and the Marsden Fund administered by the Royal Society of New Zealand. D.N., J.L., L.A., M.H. and R.C. acknowledge support from the National Institute for Health Research (NIHR) Biomedical Research Centre at Guy's and St Thomas' NHS Foundation Trust in partnership with King's College London, and by the NIHR Healthcare Technology Co-operative for Cardiovascular Disease at Guy's and St Thomas' NHS Foundation Trust.
Disclaimer
The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.
References
- 1.Hou Y, Crossman DJ, Rajagopal V, Baddeley D, Jayasinghe I, Soeller C. 2014. Super-resolution fluorescence imaging to study cardiac biophysics: α-actinin distribution and z-disk topologies in optically thick cardiac tissue slices. Prog. Biophys. Mol. Biol. 115, 328–339. ( 10.1016/j.pbiomolbio.2014.07.003) [DOI] [PubMed] [Google Scholar]
- 2.Rajagopal V, et al. 2015. Examination of the effects of heterogeneous organization of RyR clusters, myofibrils and mitochondria on Ca2+ release patterns in cardiomyocytes. PLOS Comput. Biol. 11, e1004417 ( 10.1371/journal.pcbi.1004417) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Woods RH. 1892. A few applications of a physical theorem to membranes in the human body in a state of tension. Trans. R. Acad. Med. Ireland 10, 417–427. ( 10.1007/BF03171228) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mirsky I. 1969. Left ventricular stresses in the intact human heart. Biophys. J. 9, 189–208. ( 10.1016/S0006-3495(69)86379-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ghista DN, Patil KM, Gould P, Woo K. 1973. Computerized left ventricular mechanics and control system analyses models relevant for cardiac diagnosis. Comput. Biol. Med. 3, 27–46. ( 10.1016/0010-4825(73)90017-6) [DOI] [PubMed] [Google Scholar]
- 6.McCulloch A, Smaill B, Hunter P. 1987. Left ventricular epicardial deformation in the isolated arrested dog heart. Am. J. Physiol. 252, 233–241. [DOI] [PubMed] [Google Scholar]
- 7.Hunter P, Smaill B. 1988. The analysis of cardiac function: a continuum approach. Prog. Biophys. Mol. Biol. 52, 101–164. ( 10.1016/0079-6107(88)90004-1) [DOI] [PubMed] [Google Scholar]
- 8.Mirsky I. 1973. Ventricular and arterial wall stresses based on large deformations analyses. Biophys. J. 13, 1141–1159. ( 10.1016/S0006-3495(73)86051-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Janz R, Kubert B, Moriarty T, Grimm A. 1974. Deformation of the diastolic left ventricle. II. Nonlinear geometric effects. J. Biomech. 7, 509–516. ( 10.1016/0021-9290(74)90085-2) [DOI] [PubMed] [Google Scholar]
- 10.Hunter P. 1975. Finite element analysis of cardiac muscle mechanics. Oxford, UK: University of Oxford. [Google Scholar]
- 11.Panda S, Natarajan R. 1977. Finite-element method of stress analysis in the human left ventricular layered wall structure. Med. Biol. Eng. Comput. 15, 67–71. ( 10.1007/BF02441577) [DOI] [PubMed] [Google Scholar]
- 12.Demer LL, Yin F. 1983. Passive biaxial mechanical properties of isolated canine myocardium. J. Physiol. 339, 615–630. ( 10.1113/jphysiol.1983.sp014738) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yin FC, Strumpf RK, Chew PH, Zeger SL. 1987. Quantification of the mechanical properties of noncontracting canine myocardium under simultaneous biaxial loading. J. Biomech. 20, 577–589. ( 10.1016/0021-9290(87)90279-X) [DOI] [PubMed] [Google Scholar]
- 14.LeGrice IJ, Smaill B, Chai L, Edgar S, Gavin J, Hunter PJ. 1995. Laminar structure of the heart: ventricular myocyte arrangement and connective tissue architecture in the dog. Am. J. Physiol. Heart. Circ. Physiol. 269, H571–H582. [DOI] [PubMed] [Google Scholar]
- 15.Nielsen P, Le Grice I, Smaill B, Hunter P. 1991. Mathematical model of geometry and fibrous structure of the heart. Am. J. Physiol. Heart. Circ. Physiol. 260, H1365–H1378. [DOI] [PubMed] [Google Scholar]
- 16.Guccione JM, Costa KD, McCulloch AD. 1995. Finite element stress analysis of left ventricular mechanics in the beating dog heart. J. Biomech. 28, 1167–1177. ( 10.1016/0021-9290(94)00174-3) [DOI] [PubMed] [Google Scholar]
- 17.Nash M, Hunter P. 2000. Computational mechanics of the heart. J. Elast. 61, 113–141. ( 10.1023/A:1011084330767) [DOI] [Google Scholar]
- 18.Vahl C, Timek T, Bonz A, Fuchs H, Dillman R, Hagl S. 1998. Length dependence of calcium- and force-transients in normal and failing human myocardium. J. Mol. Cell. Cardiol. 30, 957–966. ( 10.1006/jmcc.1998.0670) [DOI] [PubMed] [Google Scholar]
- 19.de Tombe PP, Ter Keurs H. 1990. Force and velocity of sarcomere shortening in trabeculae from rat heart. Effects of temperature. Circul. Res. 66, 1239–1254. ( 10.1161/01.RES.66.5.1239) [DOI] [PubMed] [Google Scholar]
- 20.Lewartowski B, Pytkowski B. 1987. Cellular mechanism of the relationship between myocardial force and frequency of contractions. Prog. Biophys. Mol. Biol. 50, 97–120. ( 10.1016/0079-6107(87)90005-8) [DOI] [PubMed] [Google Scholar]
- 21.Hunter P, McCulloch A, Ter Keurs H. 1998. Modelling the mechanical properties of cardiac muscle. Prog. Biophys. Mol. Biol. 69, 289–331. ( 10.1016/S0079-6107(98)00013-3) [DOI] [PubMed] [Google Scholar]
- 22.Nordsletten D, Niederer S, Nash M, Hunter P, Smith N. 2011. Coupling multi-physics models to cardiac mechanics. Prog. Biophys. Mol. Biol. 104, 77–88. ( 10.1016/j.pbiomolbio.2009.11.001) [DOI] [PubMed] [Google Scholar]
- 23.Panfilov AV, Holden AV. 1997. Computational biology of the heart. New York, NY: Wiley. [Google Scholar]
- 24.Trayanova NA. 2011. Whole-heart modeling applications to cardiac electrophysiology and electromechanics. Circul. Res. 108, 113–128. ( 10.1161/CIRCRESAHA.110.223610) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.McQueen DM, Peskin CS. 2000. A three-dimensional computer model of the human heart for studying cardiac fluid dynamics. ACM SIGGRAPH Comput. Graph. 34, 56–60. ( 10.1145/563788.604453) [DOI] [Google Scholar]
- 26.Nordsletten D, McCormick M, Kilner P, Hunter P, Kay D, Smith N. 2011. Fluid–solid coupling for the investigation of diastolic and systolic human left ventricular function. Int. J. Numer. Methods Biomed. Eng. 27, 1017–1039. ( 10.1002/cnm.1405) [DOI] [Google Scholar]
- 27.Lee J, Smith NP. 2012. The multi-scale modelling of coronary blood flow. Ann. Thorac. Surg. Biomed. Eng. 40, 2399–2413. ( 10.1007/s10439-012-0583-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Opie LH. 2004. Heart physiology: from cell to circulation. Philadelphia, PA: Lippincott Williams and Wilkins. [Google Scholar]
- 29.Suga H. 1990. Ventricular energetics. Physiol. Rev. 70, 247–277. [DOI] [PubMed] [Google Scholar]
- 30.Clerico A, Recchia FA, Passino C, Emdin M. 2006. Cardiac endocrine function is an essential component of the homeostatic regulation network: physiological and clinical implications. Am. J. Physiol. Heart. Circ. Physiol. 290, H17–H29. ( 10.1152/ajpheart.00684.2005) [DOI] [PubMed] [Google Scholar]
- 31.Lamata P, Casero R, Carapella V, Niederer SA, Bishop MJ, Schneider JE, Kohl P, Grau V. 2014. Images as drivers of progress in cardiac computational modelling. Prog. Biophys. Mol. Biol. 115, 198–212. ( 10.1016/j.pbiomolbio.2014.08.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Young A, Legrice I, Young M, Smaill B. 1998. Extended confocal microscopy of myocardial laminae and collagen network. J. Microsc. 192, 139–150. ( 10.1046/j.1365-2818.1998.00414.x) [DOI] [PubMed] [Google Scholar]
- 33.Stevens C, Remme E, LeGrice I, Hunter P. 2003. Ventricular mechanics in diastole: material parameter sensitivity. J. Biomech. 36, 737–748. ( 10.1016/S0021-9290(02)00452-9) [DOI] [PubMed] [Google Scholar]
- 34.Vetter FJ, McCulloch AD. 1998. Three-dimensional analysis of regional cardiac function: a model of rabbit ventricular anatomy. Prog. Biophys. Mol. Biol. 69, 157–183. ( 10.1016/S0079-6107(98)00006-6) [DOI] [PubMed] [Google Scholar]
- 35.Wang V, Lam H, Ennis D, Young A, Nash M. 2008. Passive ventricular mechanics modelling using MRI of structure and function. In Medical image computing and computer-assisted intervention–MICCAI 2008 (eds D Metaxas, L Axel, G Fichtinger, G Székely), pp. 814–821. Berlin, Germany: Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Walker JC, Ratcliffe MB, Zhang P, Wallace AW, Hsu EW, Saloner DA, Guccione JM. 2008. Magnetic resonance imaging-based finite element stress analysis after linear repair of left ventricular aneurysm. J. Thorac. Cardiovasc. Surg. 135, 1094–1102. ( 10.1016/j.jtcvs.2007.11.038) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sermesant M, Forest C, Pennec X, Delingette H, Ayache N. 2003. Deformable biomechanical models: application to 4D cardiac image analysis. Med. Image Anal. 7, 475–488. ( 10.1016/S1361-8415(03)00068-9) [DOI] [PubMed] [Google Scholar]
- 38.Hoogendoorn C, Sukno FM, Ordás S, Frangi AF. 2009. Bilinear models for spatio-temporal point distribution analysis. Int. J. Comput. Vis. 85, 237–252. ( 10.1007/s11263-009-0212-6) [DOI] [Google Scholar]
- 39.Niederer SA, Plank G, Chinchapatnam P, Ginks M, Lamata P, Rhode KS, Rinaldi CA, Razavi R, Smith NP. 2011. Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovasc. Res. 89, 336–343. ( 10.1093/cvr/cvq318) [DOI] [PubMed] [Google Scholar]
- 40.Wenk JF, et al. 2010. First finite element model of the left ventricle with mitral valve: insights into ischemic mitral regurgitation. Ann. Thorac. Surg. 89, 1546–1553. ( 10.1016/j.athoracsur.2010.02.036) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Helm P, Beg MF, Miller MI, Winslow RL. 2005. Measuring and mapping cardiac fiber and laminar architecture using diffusion tensor MR imaging. Ann. Thorac. Surg. NY Acad. Sci. 1047, 296–307. ( 10.1196/annals.1341.026) [DOI] [PubMed] [Google Scholar]
- 42.Gurev V, Lee T, Constantino J, Arevalo H, Trayanova NA. 2011. Models of cardiac electromechanics based on individual hearts imaging data. Biomech. Model. Mechanobiol. 10, 295–306. ( 10.1007/s10237-010-0235-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lamata P, Niederer S, Barber D, Norsletten D, Lee J, Hose R, Smith N. 2010. Personalization of cubic hermite meshes for efficient biomechanical simulations. In Medical image computing and computer-assisted intervention–MICCAI 2010 (eds T Jiang, N Navab, JPW Pluim, MA Viergever), pp. 380–387. Berlin, Germany: Springer. [DOI] [PubMed] [Google Scholar]
- 44.Fonseca CG, et al. 2011. The Cardiac Atlas Project—an imaging database for computational modeling and statistical atlases of the heart. Bioinformatics 27, 2288–2295. ( 10.1093/bioinformatics/btr360) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang Y, et al. 2012. An atlas-based geometry pipeline for cardiac hermite model construction and diffusion tensor reorientation. Med. Image Anal. 16, 1130–1141. ( 10.1016/j.media.2012.06.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Streeter DD, Spotnitz HM, Patel DP, Ross J, Sonnenblick EH. 1969. Fiber orientation in the canine left ventricle during diastole and systole. Circul. Res. 24, 339–347. ( 10.1161/01.RES.24.3.339) [DOI] [PubMed] [Google Scholar]
- 47.Bayer J, Blake R, Plank G, Trayanova N. 2012. A novel rule-based algorithm for assigning myocardial fiber orientation to computational heart models. Ann. Biomed. Eng. 40, 2243–2254. ( 10.1007/s10439-012-0593-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nagler A, Bertoglio C, Gee M, Wall W. 2013. Personalization of cardiac fiber orientations from image data using the unscented Kalman filter. In Functional imaging and modeling of the heart (eds S Ourselin, D Rueckert, N Smith), pp. 132–140. Berlin, Germany: Springer. [Google Scholar]
- 49.Costa KD, Holmes JW, McCulloch AD. 2001. Modelling cardiac mechanical properties in three dimensions. Phil. Trans. R. Soc. Lond. A 359, 1233–1250. ( 10.1098/rsta.2001.0828) [DOI] [Google Scholar]
- 50.LeGrice I, Takayama Y, Covell J. 1995. Transverse shear along myocardial cleavage planes provides a mechanism for normal systolic wall thickening. Circul. Res. 77, 182–193. ( 10.1161/01.RES.77.1.182) [DOI] [PubMed] [Google Scholar]
- 51.Basser PJ, Mattiello J, LeBihan D. 1994. MR diffusion tensor spectroscopy and imaging. Biophys. J. 66, 259 ( 10.1016/S0006-3495(94)80775-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Plank G, et al. 2009. Generation of histo-anatomically representative models of the individual heart: tools and application. Phil. Trans. R. Soc. A 367, 2257–2292. ( 10.1098/rsta.2009.0056) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gilbert SH, Benoist D, Benson AP, White E, Tanner SF, Holden AV, Dobrzynski H, Bernus O, Radjenovic A. 2012. Visualization and quantification of whole rat heart laminar structure using high-spatial resolution contrast-enhanced MRI. Am. J. Physiol. Heart. Circ. Physiol. 302, H287–H298. ( 10.1152/ajpheart.00824.2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Humphrey J, Yin F. 1989. Biomechanical experiments on excised myocardium: theoretical considerations. J. Biomech. 22, 377–383. ( 10.1016/0021-9290(89)90052-3) [DOI] [PubMed] [Google Scholar]
- 55.Humphrey J, Yin F. 1987. A new constitutive formulation for characterizing the mechanical behavior of soft tissues. Biophys. J. 52, 563–570. ( 10.1016/S0006-3495(87)83245-9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Horowitz A, Lanir Y, Yin FC, Perl M, Sheinman I, Strumpf RK. 1988. Structural three-dimensional constitutive law for the passive myocardium. J. Biomech. Eng. 110, 200–207. ( 10.1115/1.3108431) [DOI] [PubMed] [Google Scholar]
- 57.Novak VP, Yin FCP, Humphrey JD. 1994. Regional mechanical properties of passive myocardium. J. Biomech. 27, 403–412. ( 10.1016/0021-9290(94)90016-7) [DOI] [PubMed] [Google Scholar]
- 58.Humphrey J, Strumpf R, Yin F. 1990. Determination of a constitutive relation for passive myocardium. II. Parameter estimation. J. Biomech. Eng. 112, 340–346. ( 10.1115/1.2891194) [DOI] [PubMed] [Google Scholar]
- 59.McCulloch AD, Smaill BH, Hunter PJ. 1989. Regional left ventricular epicardial deformation in the passive dog heart. Circul. Res. 64, 721–733. ( 10.1161/01.RES.64.4.721) [DOI] [PubMed] [Google Scholar]
- 60.Guccione JM, McCulloch AD, Waldman L. 1991. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J. Biomech. Eng. 113, 42–55. ( 10.1115/1.2894084) [DOI] [PubMed] [Google Scholar]
- 61.Lin D, Yin F. 1998. A multiaxial constitutive law for mammalian left ventricular myocardium in steady-state barium contracture or tetanus. J. Biomech. Eng. 120, 504–517. ( 10.1115/1.2798021) [DOI] [PubMed] [Google Scholar]
- 62.Criscione JC, Douglas AS, Hunter WC. 2001. Physically based strain invariant set for materials exhibiting transversely isotropic behavior. J. Mech. Phys. Solids 49, 871–897. ( 10.1016/S0022-5096(00)00047-8) [DOI] [Google Scholar]
- 63.Smaill B, Hunter P. 1991. Structure and function of the diastolic heart: material properties of passive myocardium. In Theory of heart (eds L Glass, P Hunter, A McCulloch), pp. 1–29. New York, NY: Springer. [Google Scholar]
- 64.Nikolić S, Yellin EL, Tamura K, Vetter H, Tamura T, Meisner JS, Frater RW. 1988. Passive properties of canine left ventricle: diastolic stiffness and restoring forces. Circul. Res. 62, 1210–1222. ( 10.1161/01.RES.62.6.1210) [DOI] [PubMed] [Google Scholar]
- 65.Kerckhoffs R, Bovendeerd P, Kotte J, Prinzen F, Smits K, Arts T. 2003. Homogeneity of cardiac contraction despite physiological asynchrony of depolarization: a model study. Ann. Biomed. Eng. 31, 536–547. ( 10.1114/1.1566447) [DOI] [PubMed] [Google Scholar]
- 66.Dokos S, Smaill BH, Young AA, LeGrice IJ. 2002. Shear properties of passive ventricular myocardium. Am. J. Physiol. Heart. Circ. Physiol. 283, H2650–H2659. ( 10.1152/ajpheart.00111.2002) [DOI] [PubMed] [Google Scholar]
- 67.Holzapfel GA, Ogden RW. 2009. Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Phil. Trans. R. Soc. A 367, 3445–3475. ( 10.1098/rsta.2009.0091) [DOI] [PubMed] [Google Scholar]
- 68.Loeffler L, Sagawa K. 1975. A one-dimensional viscoelastic model of cat heart muscle studied by small length perturbations during isometric contraction. Circul. Res. 36, 498–512. ( 10.1161/01.RES.36.4.498) [DOI] [PubMed] [Google Scholar]
- 69.Yang M, Taber LA. 1991. The possible role of poroelasticity in the apparent viscoelastic behavior of passive cardiac muscle. J. Biomech. 24, 587–597. ( 10.1016/0021-9290(91)90291-T) [DOI] [PubMed] [Google Scholar]
- 70.van Heuningen R, Rijnsburger WH, ter Keurs HE. 1982. Sarcomere length control in striated muscle. Am. J. Physiol. Heart. Circ. Physiol. 242, H411–H420. [DOI] [PubMed] [Google Scholar]
- 71.Huyghe JM, van Campen DH, Arts T, Heethaar RM. 1991. The constitutive behaviour of passive heart muscle tissue: a quasi-linear viscoelastic formulation. J. Biomech. 24, 841–849. ( 10.1016/0021-9290(91)90309-B) [DOI] [PubMed] [Google Scholar]
- 72.Holzapfel GA, Gasser TC. 2001. A viscoelastic model for fiber-reinforced composites at finite strains: Continuum basis, computational aspects and applications. Comput. Methods Appl. Mech. Eng. 190, 4379–4403. ( 10.1016/S0045-7825(00)00323-6) [DOI] [Google Scholar]
- 73.Cansz FBC, Dal H, Kaliske M. 2015. An orthotropic viscoelastic material model for passive myocardium: theory and algorithmic treatment. Comput. Methods Biomech. Biomed. Eng. 18, 1160–1172. ( 10.1080/10255842.2014.881475) [DOI] [PubMed] [Google Scholar]
- 74.Costa KD, Takayama Y, McCulloch AD, Covell JW. 1999. Laminar fiber architecture and three-dimensional systolic mechanics in canine ventricular myocardium. Am. J. Physiol. Heart. Circ. Physiol. 276, H595–H607. [DOI] [PubMed] [Google Scholar]
- 75.Sommer G, Haspinger DCh, Andrä M, Sacherer M, Viertler C, Regitnig P, Holzapfel GA. 2015. Quantification of shear deformations and corresponding stresses in the biaxially tested human myocardium. Ann. Thoroc. Surg. Biomed. Eng. 43, 2334–2348. ( 10.1007/s10439-015-1281-z) [DOI] [PubMed] [Google Scholar]
- 76.Sommer G, Schriefl AJ, Andrä M, Sacherer M, Viertler C, Wolinski H, Holzapfel GA. 2015. Biomechanical properties and microstructure of human ventricular myocardium. Acta biomaterialia 24, 172–192. ( 10.1016/j.actbio.2015.06.031) [DOI] [PubMed] [Google Scholar]
- 77.Holzapfel GA, Gasser TC, Ogden RW. 2000. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids 61, 1–48. ( 10.1023/A:1010835316564) [DOI] [Google Scholar]
- 78.Gasser TC, Ogden RW, Holzapfel GA. 2006. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 3, 15–35. ( 10.1098/rsif.2005.0073) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Mescher AL. 2010. Junqueira‘s basic histology: text and atlas, vol. 12 New York, NY: McGraw-Hill Medical. [Google Scholar]
- 80.Huxley A. 1957. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 7, 255–318. [PubMed] [Google Scholar]
- 81.Wong AY. 1971. Mechanics of cardiac muscle, based on Huxley's model: mathematical simulation of isometric contraction. J. Biomech. 4, 529–540. ( 10.1016/0021-9290(71)90042-X) [DOI] [PubMed] [Google Scholar]
- 82.Tözeren A. 1985. Continuum rheology of muscle contraction and its application to cardiac contractility. Biophys. J. 47, 303–309. ( 10.1016/S0006-3495(85)83920-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Ter Keurs HE, Rijnsburger WH, Van Heuningen R, Nagelsmit MJ. 1980. Tension development and sarcomere length in rat cardiac trabeculae: evidence of length-dependent activation. In Cardiac dynamics (eds J Baan, AC Arntzenius), pp. 25–36. The Hague, The Netherlands: Martinus Nijhoff Publishers. [DOI] [PubMed] [Google Scholar]
- 84.Guccione J, McCulloch A. 1993. Mechanics of active contraction in cardiac muscle: part I—constitutive relations for fiber stress that describe deactivation. J. Biomech. Eng. 115, 72–81. ( 10.1115/1.2895474) [DOI] [PubMed] [Google Scholar]
- 85.Niederer S, Hunter P, Smith N. 2006. A quantitative analysis of cardiac myocyte relaxation: a simulation study. Biophys. J. 90, 1697–1722. ( 10.1529/biophysj.105.069534) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Rice JJ, Wang F, Bers DM, De Tombe PP. 2008. Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys. J. 95, 2368–2390. ( 10.1529/biophysj.107.119487) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Bestel J, Clément F, Sorine M. 2001. A biomechanical model of muscle contraction. In Medical image computing and computer-assisted intervention–MICCAI 2001 (eds WJ Niessen, MA Viergever), pp. 1159–1161. Berlin, Germany: Springer. [Google Scholar]
- 88.Chapelle D, Le Tallec P, Moireau P, Sorine M. 2012. Energy-preserving muscle tissue model: formulation and compatible discretizations. Int. J. Multiscale Comput. Eng. 10, 189–211. ( 10.1615/IntJMultCompEng.2011002360) [DOI] [Google Scholar]
- 89.Tangney JR, et al. 2013. Novel role for vinculin in ventricular myocyte mechanics and dysfunction. Biophys. J. 104, 1623–1633. ( 10.1016/j.bpj.2013.02.021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Usyk T, Mazhari R, McCulloch A. 2000. Effect of laminar orthotropic myofiber architecture on regional stress and strain in the canine left ventricle. J. Elast. Phys. Sci. Solids 61, 143–164. ( 10.1023/A:1010883920374) [DOI] [Google Scholar]
- 91.Rossi S, Ruiz-Baier R, Pavarino LF, Quarteroni A. 2012. Orthotropic active strain models for the numerical simulation of cardiac biomechanics. Int. J. Numer. Methods Biomed. Eng. 28, 761–788. ( 10.1002/cnm.2473) [DOI] [PubMed] [Google Scholar]
- 92.Yin F, Chan C, Judd RM. 1996. Compressibility of perfused passive myocardium. Am. J. Physiol. Heart. Circ. Physiol. 271, H1864–H1870. [DOI] [PubMed] [Google Scholar]
- 93.Omens JH, MacKenna DA, McCulloch AD. 1993. Measurement of strain and analysis of stress in resting rat left ventricular myocardium. J. Biomech. 26, 665–676. ( 10.1016/0021-9290(93)90030-I) [DOI] [PubMed] [Google Scholar]
- 94.Bathe K-J. 2006. Finite element procedures. Englewood Cliffs, NJ: Klaus-Jurgen Bathe. [Google Scholar]
- 95.Vetter FJ, McCulloch AD. 2000. Three-dimensional stress and strain in passive rabbit left ventricle: a model study. Ann. Thor. Surg. Biomed. Eng. 28, 781–792. ( 10.1114/1.1289469) [DOI] [PubMed] [Google Scholar]
- 96.Thorvaldsen T, Osnes H, Sundnes J. 2005. A mixed finite element formulation for a non-linear, transversely isotropic material model for the cardiac tissue. Comput. Methods Biomech. Biomed. Eng. 8, 369–379. ( 10.1080/10255840500448097) [DOI] [PubMed] [Google Scholar]
- 97.Asner L, Hadjicharalambous M, Lee J, Nordsletten D. 2015. Stacom challenge: simulating left ventricular mechanics in the canine heart. In Statistical atlases and computational models of the heart-imaging and modelling challenges (eds O Camara, T Mansi, M Pop, K Rhode, M Sermesant, A Young), pp. 123–134. Basel, Switzerland: Springer. [Google Scholar]
- 98.Hadjicharalambous M, Lee J, Smith NP, Nordsletten DA. 2014. A displacement-based finite element formulation for incompressible and nearly-incompressible cardiac mechanics. Comput. Methods Appl. Mech. Eng. 274, 213–236. ( 10.1016/j.cma.2014.02.009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Sermesant M, et al. 2012. Patient-specific electromechanical models of the heart for the prediction of pacing acute effects in CRT: a preliminary clinical validation. Med. Image Anal. 16, 201–215. ( 10.1016/j.media.2011.07.003) [DOI] [PubMed] [Google Scholar]
- 100.McCormick M, Nordsletten D, Kay D, Smith N. 2013. Simulating left ventricular fluid–solid mechanics through the cardiac cycle under LVAD support. J. Comput. Phys. 244, 80–96. ( 10.1016/j.jcp.2012.08.008) [DOI] [Google Scholar]
- 101.McCormick M, Nordsletten D, Lamata P, Smith NP. 2014. Computational analysis of the importance of flow synchrony for cardiac ventricular assist devices. Comput. Biol. Med. 49, 83–94. ( 10.1016/j.compbiomed.2014.03.013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Lee J, Cookson A, Chabiniok R, Rivolo S, Hyde E, Sinclair M, Michler C, Sochi T, Smith N. 2015. Multiscale modelling of cardiac perfusion. In Modeling the heart and the circulatory system (ed. A Quarteroni), pp. 51–96. Basel, Switzerland: Springer. [Google Scholar]
- 103.FitzHugh R. 1961. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1, 445 ( 10.1016/S0006-3495(61)86902-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Aliev RR, Panfilov AV. 1996. A simple two-variable model of cardiac excitation. Chaos Solitons Fractals 7, 293–301. ( 10.1016/0960-0779(95)00089-5) [DOI] [Google Scholar]
- 105.Beeler GW, Reuter H. 1977. Reconstruction of the action potential of ventricular myocardial fibres. J. Physiol. 268, 177–210. ( 10.1113/jphysiol.1977.sp011853) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Winslow RL, Rice J, Jafri S, Marban E, O'Rourke B. 1999. Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, II model studies. Circul. Res. 84, 571–586. ( 10.1161/01.RES.84.5.571) [DOI] [PubMed] [Google Scholar]
- 107.Hodgkin AL, Huxley AF. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. ( 10.1113/jphysiol.1952.sp004764) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Ten Tusscher K, Noble D, Noble P, Panfilov A. 2004. A model for human ventricular tissue. Am. J. Physiol. Heart. Circ. Physiol. 286, H1573–H1589. ( 10.1152/ajpheart.00794.2003) [DOI] [PubMed] [Google Scholar]
- 109.Sermesant M, Delingette H, Ayache N. 2006. An electromechanical model of the heart for image analysis and simulation. IEEE Trans. Med. Imag. 25, 612–625. ( 10.1109/TMI.2006.872746) [DOI] [PubMed] [Google Scholar]
- 110.Rogers JM, McCulloch AD. 1994. Nonuniform muscle fiber orientation causes spiral wave drift in a finite element model of cardiac action potential propagation. J. Cardiovasc. Electrophysiol. 5, 496–509. ( 10.1111/j.1540-8167.1994.tb01290.x) [DOI] [PubMed] [Google Scholar]
- 111.Nash MP, Panfilov AV. 2004. Electromechanical model of excitable tissue to study reentrant cardiac arrhythmias. Prog. Biophys. Mol. Biol. 85, 501–522. ( 10.1016/j.pbiomolbio.2004.01.016) [DOI] [PubMed] [Google Scholar]
- 112.Göktepe S, Kuhl E. 2010. Electromechanics of the heart: a unified approach to the strongly coupled excitation–contraction problem. Comput. Mech. 45, 227–243. ( 10.1007/s00466-009-0434-z) [DOI] [Google Scholar]
- 113.Keldermann RH, Nash MP, Gelderblom H, Wang VY, Panfilov AV. 2010. Electromechanical wavebreak in a model of the human left ventricle. Am. J. Physiol. Heart. Circ. Physiol. 299, H134–H143. ( 10.1152/ajpheart.00862.2009) [DOI] [PubMed] [Google Scholar]
- 114.Wall ST, Guccione JM, Ratcliffe MB, Sundnes JS. 2012. Electromechanical feedback with reduced cellular connectivity alters electrical activity in an infarct injured left ventricle: a finite element model study. Am. J. Physiol. Heart. Circ. Physiol. 302, H206–H214. ( 10.1152/ajpheart.00272.2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Aguado-Sierra J. 2011. Patient-specific modeling of dyssynchronous heart failure: a case study. Prog. Biophys. Mol. Biol. 107, 147–155. ( 10.1016/j.pbiomolbio.2011.06.014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Kohl P, Sachs F. 2001. Mechanoelectric feedback in cardiac cells. Phil. Trans. R. Soc. A 359, 1173–1185. ( 10.1098/rsta.2001.0824) [DOI] [Google Scholar]
- 117.Kuijpers NH, ten Eikelder HM, Bovendeerd PH, Verheule S, Arts T, Hilbers PA. 2007. Mechanoelectric feedback leads to conduction slowing and block in acutely dilated atria: a modeling study of cardiac electromechanics. Am. J. Physiol. Heart. Circ. Physiol. 292, H2832–H2853. ( 10.1152/ajpheart.00923.2006) [DOI] [PubMed] [Google Scholar]
- 118.Xia H, Wong K, Zhao X. 2012. A fully coupled model for electromechanics of the heart. Comput. Math. Methods Med. 2012, 927279–1172. ( 10.1155/2012/927279) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Vigueras G, Roy I, Cookson A, Lee J, Smith N, Nordsletten D. 2014. Toward GPGPU accelerated human electromechanical cardiac simulations. Int. J. Numer. Methods Biomed. Eng. 30, 117–134. ( 10.1002/cnm.2593) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Khalafvand S, Ng E, Zhong L. 2011. CFD simulation of flow through heart: a perspective review. Comput. Methods Biomech. Biomed. Eng. 14, 113–132. ( 10.1080/10255842.2010.493515) [DOI] [PubMed] [Google Scholar]
- 121.Chan BT, Lim E, Chee KH, Osman NAA. 2013. Review on CFD simulation in heart with dilated cardiomyopathy and myocardial infarction. Comput. Biol. Med. 43, 377–385. ( 10.1016/j.compbiomed.2013.01.013) [DOI] [PubMed] [Google Scholar]
- 122.Georgiadis J, Wang G, Pasipoularides A. 1992. Computational fluid dynamics of left ventricular ejection. Ann. Biomed. Eng. 20, 81–97. ( 10.1007/BF02368507) [DOI] [PubMed] [Google Scholar]
- 123.Baccani B, Domenichini F, Pedrizzetti G, Tonti G. 2002. Fluid dynamics of the left ventricular filling in dilated cardiomyopathy. J. Biomech. 35, 665–671. ( 10.1016/S0021-9290(02)00005-2) [DOI] [PubMed] [Google Scholar]
- 124.Domenichini F, Pedrizzetti G, Baccani B. 2005. Three-dimensional filling flow into a model left ventricle. J. Fluid Mech. 539, 179–198. ( 10.1017/S0022112005005550) [DOI] [Google Scholar]
- 125.Pedrizzetti G, Domenichini F. 2005. Nature optimizes the swirling flow in the human left ventricle. Phys. Rev. 95, 1–4. ( 10.1103/physrevlett.95.108101) [DOI] [PubMed] [Google Scholar]
- 126.Saber NR, Wood NB, Gosman A, Merrifield RD, Yang G-Z, Charrier CL, Gatehouse PD, Firmin DN. 2003. Progress towards patient-specific computational flow modeling of the left heart via combination of magnetic resonance imaging with computational fluid dynamics. Ann. Biomed. Eng. 31, 42–52. ( 10.1114/1.1533073) [DOI] [PubMed] [Google Scholar]
- 127.Merrifield R, Long Q, Xu X, Kilner PJ, Firmin DN, Yang G-Z. 2004. Combined CFD/MRI analysis of left ventricular flow. In Medical imaging and augmented reality (eds G-Z Yang, T Jiang), pp. 229–236. Berlin, Germany: Springer. [Google Scholar]
- 128.Doenst T, Spiegel K, Reik M, Markl M, Hennig J, Nitzsche S, Beyersdorf F, Oertel H. 2009. Fluid-dynamic modelling of the human left ventricle: methodology and application to surgical ventricular reconstruction. Ann. Thorac. Surg. 87, 1187–1197. ( 10.1016/j.athoracsur.2009.01.036) [DOI] [PubMed] [Google Scholar]
- 129.Oertel H, Krittian S. 2011. Modelling the human cardiac fluid mechanics. Karlsruhe, Germany: KIT Scientific Publishing. [Google Scholar]
- 130.Khalafvand SS, Ng EY-K, Zhong L, Hung T. 2012. Fluid-dynamics modelling of the human left ventricle with dynamic mesh for normal and myocardial infarction: preliminary study. Comput. Biol. Med. 42, 863–870. ( 10.1016/j.compbiomed.2012.06.010) [DOI] [PubMed] [Google Scholar]
- 131.de Vecchi A, Gomez A, Pushparajah K, Schaeffter T, Nordsletten D, Simpson J, Penney G, Smith N. 2014. Towards a fast and efficient approach for modelling the patient-specific ventricular haemodynamics. Prog. Biophys. Mol. Biol. 116, 3–10. ( 10.1016/j.pbiomolbio.2014.08.010) [DOI] [PubMed] [Google Scholar]
- 132.Su B, Zhang J-M, Tang HC, Wan M, Lim CCW, Su Y, Zhao X, San Tan R, Zhong L. 2014. Patient-specific blood flows and vortex formations in patients with hypertrophic cardiomyopathy using computational fluid dynamics. In Biomedical Engineering and Sciences (IECBES), 2014 IEEE Conf., Kuala Lumpur, Malaysia, 8–10 December, pp. 276–280. New York, NY: IEEE.
- 133.Peskin C. 1972. Flow patterns around heart valves: a numerical method. J. Comput. Phys. 10, 252–271. ( 10.1016/0021-9991(72)90065-4) [DOI] [Google Scholar]
- 134.Yoganathan A, He Z, Jones S. 2004. Fluid mechanics of heart valves. Annu. Rev. Biomed. Eng. 6, 331–362. ( 10.1146/annurev.bioeng.6.040803.140111) [DOI] [PubMed] [Google Scholar]
- 135.Le TB, Sotiropoulos F. 2013. Fluid–structure interaction of an aortic heart valve prosthesis driven by an animated anatomic left ventricle. J. Comput. Phys. 244, 41–62. ( 10.1016/j.jcp.2012.08.036) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Cheng Y, Zhang H. 2010. Immersed boundary method and lattice Boltzmann method coupled FSI simulation of mitral leaflet flow. Comput. Fluids 39, 871–881. ( 10.1016/j.compfluid.2010.01.003) [DOI] [Google Scholar]
- 137.Su B, Zhong L, Wang X-K, Zhang J-M, San Tan R, Allen JC, Tan SK, Kim S, Leo HL. 2014. Numerical simulation of patient-specific left ventricular model with both mitral and aortic valves by FSI approach. Comput. Methods Prog. Biomed. 113, 474–482. ( 10.1016/j.cmpb.2013.11.009) [DOI] [PubMed] [Google Scholar]
- 138.Hsu M-C, Kamensky D, Bazilevs Y, Sacks MS, Hughes TJ. 2014. Fluid–structure interaction analysis of bioprosthetic heart valves: significance of arterial wall deformation. Comput. Mech. 54, 1055–1071. ( 10.1007/s00466-014-1059-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Kamensky D, Hsu M-C, Schillinger D, Evans JA, Aggarwal A, Bazilevs Y, Sacks MS, Hughes TJ. 2015. An immersogeometric variational framework for fluid–structure interaction: application to bioprosthetic heart valves. Comput. Methods Appl. Mech. Eng. 284, 1005–1053. ( 10.1016/j.cma.2014.10.040) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.McQueen D, Peskin C. 1989. A 3D computational method for blood flow in the heart. I. Immersed elastic fibers in a viscous incompressible fluid. J. Comput. Phys. 81, 372–405. ( 10.1016/0021-9991(89)90213-1) [DOI] [Google Scholar]
- 141.McQueen D, Peskin C. 1989. A 3D computational method for blood flow in the heart. II. Contractile fibers. J. Comput. Phys. 82, 289–297. ( 10.1016/0021-9991(89)90050-8) [DOI] [Google Scholar]
- 142.Yoganathan A, Lemmon J, Kim Y, Walker P, Levine R, Vesier C. 1994. A computational study of a thin-walled three-dimensional left ventricle during early systole. J. Biomech. Eng. 116, 307–314. ( 10.1115/1.2895735) [DOI] [PubMed] [Google Scholar]
- 143.Taylor T, Suga H, Goto Y, Okino H, Yamaguchi T. 1996. The effects of cardiac infarction on realistic three-dimensional left ventricular blood ejection. J. Biomech. Eng. 118, 106–110. ( 10.1115/1.2795934) [DOI] [PubMed] [Google Scholar]
- 144.Jones T, Metaxas D. 1998. Patient-specific analysis of left ventricular blood flow. Lect. Notes Comput. Sci. 1496, 156–166. ( 10.1007/BFb0056198) [DOI] [Google Scholar]
- 145.Lemmon J, Yoganathan A. 2000. Computational modeling of left heart diastolic function: examination of ventricular dysfunction. J. Elast. 122, 297–303. ( 10.1115/1.1286559) [DOI] [PubMed] [Google Scholar]
- 146.Kovacs SJ, McQueen DM, Peskin CS. 2001. Modelling cardiac fluid dynamics and diastolic function. Phil. Trans. R. Soc. Lond. A 359, 1299–1314. ( 10.1098/rsta.2001.0832) [DOI] [Google Scholar]
- 147.Vigmod E, Clements C, McQueen D, Peskin C. 2008. Effect of bundle branch block on cardiac output: a whole heart simulation study. Prog. Biophys. Mol. Biol. 97, 520–542. ( 10.1016/j.pbiomolbio.2008.02.022) [DOI] [PubMed] [Google Scholar]
- 148.Chahboune B, Crolet J. 1998. Numerical simulation of the blood-wall interaction in the human left ventricle. Eur. Phys. J. Appl. Phys. 2, 291–297. ( 10.1051/epjap:1998195) [DOI] [Google Scholar]
- 149.Ong C, Chan B, Lim E-G, Abu Osman N, Abed A, Dokos S, Lovell NH. 2012. Fluid structure interaction simulation of left ventricular flow dynamics under left ventricular assist device support. In Engineering in Medicine and Biology Society (EMBC), 2012 Annual Int. Conf. of the IEEE, San Diego, CA, 28 August–1 September, pp. 6293–6296. New York, NY: IEEE. [DOI] [PubMed]
- 150.Chan B, Ong C, Lim E-G, Abu Osman N, Al Abed A, Lovell NH, Dokos S. 2012. Simulation of left ventricle flow dynamics with dilated cardiomyopathy during the filling phase. In Engineering in Medicine and Biology Society (EMBC), 2012 Annual Int. Conf. of the IEEE, San Diego, CA, 28 August–1 September, pp. 6289–6292. New York, NY: IEEE. [DOI] [PubMed]
- 151.Chan BT, Abu NA, Lim E, Chee KH, Abdul YF, Abed AA, Lovell NH, Dokos S. 2013. Sensitivity analysis of left ventricle with dilated cardiomyopathy in fluid structure simulation. PLoS ONE 8, e67097 ( 10.1371/journal.pone.0067097) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Watanabe H, Sugiura S, Kafuku H, Hisada T. 2004. Multiphysics simulation of left ventricular filling dynamics using fluid–structure interaction finite element method. Biophys. J. 87, 2074–2085. ( 10.1529/biophysj.103.035840) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Watanabe H, Sugiura S, Hisada T. 2008. The looped heart does not save energy by maintaining the momentum of blood flowing in the ventricle. Am. J. Physiol. 294, 2191–2196. ( 10.1152/ajpheart.00041.2008) [DOI] [PubMed] [Google Scholar]
- 154.Cheng Y, Oertel H, Schenkel T. 2005. Fluid-structure coupled CFD simulation of the left ventricular flow during filling phase. Ann. Biomed. Eng. 8, 567–576. ( 10.1007/s10439-005-4388-9) [DOI] [PubMed] [Google Scholar]
- 155.Yang C, Tang D, Haber I, Geva T, Pedro J. 2007. In vivo MRI-based 3D FSI RV/LV models for human right ventricle and patch design for potential computer-aided surgery optimization. Comput. Struct. 85, 988–997. ( 10.1016/j.compstruc.2006.11.008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Tang D, Yang C, Geva T, Pedro J. 2010. Image-based patient-specific ventricle models with fluid–structure interaction for cardiac function assessment and surgical design optimization. Prog. Pediatr. Cardiol. 30, 51–62. ( 10.1016/j.ppedcard.2010.09.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Tang D, Yang C, Geva T, Gaudette G, Pedro J. 2011. Multi-physics MRI-based two-layer fluid–structure interaction anisotropic models of human right and left ventricles with different patch materials: cardiac function assessment and mechanical stress analysis. Comput. Struct. 89, 1059–1068. ( 10.1016/j.compstruc.2010.12.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Nordsletten D, Kay D, Smith N. 2010. A non-conforming monolithic finite element method for problems of coupled mechanics. J. Comput. Phys. 229, 7571–7593. ( 10.1016/j.jcp.2010.05.043) [DOI] [Google Scholar]
- 159.De Vecchi A, Nordsletten D, Razavi R, Greil G, Smith N. 2013. Patient specific fluid–structure ventricular modelling for integrated cardiac care. Med. Biol. Eng. Comput. 51, 1261–1270. ( 10.1007/s11517-012-1030-5) [DOI] [PubMed] [Google Scholar]
- 160.de Vecchi A, Nordsletten DA, Remme EW, Bellsham-Revell H, Greil G, Simpson JM, Razavi R, Smith NP. 2012. Inflow typology and ventricular geometry determine efficiency of filling in the hypoplastic left heart. Ann. Thorac. Surg. 94, 1562–1569. ( 10.1016/j.athoracsur.2012.05.122) [DOI] [PubMed] [Google Scholar]
- 161.McCormick M, Nordsletten D, Kay D, Smith N. 2011. Modelling left ventricular function under assist device support. Int. J. Numer. Methods Biomed. Eng. 27, 1073–1095. ( 10.1002/cnm.1428) [DOI] [Google Scholar]
- 162.Krittian S, Schenkel T, Janoske U, Oertel H. 2010. Partitioned fluid–solid coupling for cardiovascular blood flow: validation study of pressure-driven fluid-domain deformation. Ann. Thor. Surg. Biomed. Eng. 38, 2676–2689. ( 10.1007/s10439-010-0024-4) [DOI] [PubMed] [Google Scholar]
- 163.Gao H, Carrick D, Berry C, Griffith BE, Luo X. 2014. Dynamic finite-strain modelling of the human left ventricle in health and disease using an immersed boundary-finite element method. IMA J. Appl. Math. 79, 978–1010. ( 10.1093/imamat/hxu029) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Westerhof N, Boer C, Lamberts RR, Sipkema P. 2006. Cross-talk between cardiac muscle and coronary vasculature. Physiol. Rev. 86, 1263–1308. ( 10.1152/physrev.00029.2005) [DOI] [PubMed] [Google Scholar]
- 165.Quarteroni A, Formaggia L. 2004. Mathematical modelling and numerical simulation of the cardiovascular system. In Computational models for the human body, volume 12 of handbook of numerical analysis (eds PG Ciarlet, N Ayache), pp. 3–127. Amsterdam, The Netherlands: Elsevier. [Google Scholar]
- 166.Huyghe JM, van Campen DH, Arts T, Heethaar RM. 1991. A two-phase finite element model of the diastolic left ventricle. J. Biomech. 24, 527–538. ( 10.1016/0021-9290(91)90286-V) [DOI] [PubMed] [Google Scholar]
- 167.Vankan W, Huyghe J, Janssen J, Huson A. 1996. Poroelasticity of saturated solids with an application to blood perfusion. Int. J. Eng. Sci. 34, 1019–1031. ( 10.1016/0020-7225(96)00009-2) [DOI] [Google Scholar]
- 168.Hornung U. 2012. Homogenization and porous media, vol. 6 Munich, Germany: Springer Science & Business Media. [Google Scholar]
- 169.Rohan E, Cimrman R. 2010. Two-scale modeling of tissue perfusion problem using homogenization of dual porous media. Int. J. Multiscale Comput. Eng. 8, 81–102. ( 10.1615/IntJMultCompEng.v8.i1.70) [DOI] [Google Scholar]
- 170.Biot MA. 1941. General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164. ( 10.1063/1.1712886) [DOI] [Google Scholar]
- 171.Bowen RM. 1980. Incompressible porous media models by use of the theory of mixtures. Int. J. Eng. Sci. 18, 1129–1148. ( 10.1016/0020-7225(80)90114-7) [DOI] [Google Scholar]
- 172.Coussy O. 2004. Poromechanics. Chichester, UK: John Wiley and Sons. [Google Scholar]
- 173.Loret B, Simões FM. 2005. A framework for deformation, generalized diffusion, mass transfer and growth in multi-species multi-phase biological tissues. Eur. J. Mech. A Solids 24, 757–781. ( 10.1016/j.euromechsol.2005.05.005) [DOI] [Google Scholar]
- 174.Chapelle D, Moireau P. 2014. General coupling of porous flows and hyperelastic formulations: From thermodynamics principles to energy balance and compatible time schemes. Eur. J. Mech. B Fluids 46, 82–96. ( 10.1016/j.euromechflu.2014.02.009) [DOI] [Google Scholar]
- 175.Hughes T, Liu W, Zimmermann T. 1981. Lagrangian–Eulerian finite element formulation for incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 29, 329–349. ( 10.1016/0045-7825(81)90049-9) [DOI] [Google Scholar]
- 176.Vuong A-T, Yoshihara L, Wall W. 2015. A general approach for modeling interacting flow through porous media under finite deformations. Comput. Methods Appl. Mech. Eng. 283, 1240–1259. ( 10.1016/j.cma.2014.08.018) [DOI] [Google Scholar]
- 177.May-Newman K, Omens JH, Pavelec RS, McCulloch AD. 1994. Three-dimensional transmural mechanical interaction between the coronary vasculature and passive myocardium in the dog. Circul. Res. 74, 1166–1178. ( 10.1161/01.RES.74.6.1166) [DOI] [PubMed] [Google Scholar]
- 178.Reeve AM, Nash MP, Taberner AJ, Nielsen PM. 2014. Constitutive relations for pressure-driven stiffening in poroelastic tissues. J. Biomech. Eng. 136, 081011 ( 10.1115/1.4027666) [DOI] [PubMed] [Google Scholar]
- 179.Chapelle D, Gerbeau J-F, Sainte-Marie J, Vignon-Clementel I. 2010. A poroelastic model valid in large strains with applications to perfusion in cardiac modeling. Comput. Mech. 46, 91–101. ( 10.1007/s00466-009-0452-x) [DOI] [Google Scholar]
- 180.Spaan JA, et al. 2005. Visualisation of intramural coronary vasculature by an imaging cryomicrotome suggests compartmentalisation of myocardial perfusion areas. Med. Biol. Eng. Comput. 43, 431–435. ( 10.1007/BF02344722) [DOI] [PubMed] [Google Scholar]
- 181.Michler C, et al. 2013. A computationally efficient framework for the simulation of cardiac perfusion using a multi-compartment Darcy porous-media flow model. Int. J. Numer. Methods Biomed. Eng. 29, 217–232. ( 10.1002/cnm.2520) [DOI] [PubMed] [Google Scholar]
- 182.Smith AF, Shipley RJ, Lee J, Sands GB, LeGrice IJ, Smith NP. 2014. Transmural variation and anisotropy of microvascular flow conductivity in the rat myocardium. Ann. Biomed. Eng. 42, 1966–1977. ( 10.1007/s10439-014-1028-2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Hyde ER, et al. 2014. Multi-scale parameterisation of a myocardial perfusion model using whole-organ arterial networks. Ann. Biomed. Eng. 42, 797–811. ( 10.1007/s10439-013-0951-y) [DOI] [PubMed] [Google Scholar]
- 184.Cookson A, Lee J, Michler C, Chabiniok R, Hyde E, Nordsletten D, Smith N. 2014. A spatially-distributed computational model to quantify behaviour of contrast agents in MR perfusion imaging. Med. Image Anal. 18, 1200–1216. ( 10.1016/j.media.2014.07.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Carusi A, Burrage K, Rodriguez B. 2012. Bridging experiments, models and simulations: an integrative approach to validation in computational cardiac electrophysiology. Am. J. Physiol. Heart. Circ. Physiol. 303, H144–H155. ( 10.1152/ajpheart.01151.2011) [DOI] [PubMed] [Google Scholar]
- 186.Sadrieh A, et al. 2014. Multiscale cardiac modelling reveals the origins of notched T waves in long QT syndrome type 2. Nat. Commun. 5, 5069 ( 10.1038/ncomms6069) [DOI] [PubMed] [Google Scholar]
- 187.Pathmanathan P, Shotwell MS, Gavaghan DJ, Cordeiro JM, Gray RA. 2015. Uncertainty quantification of fast sodium current steady-state inactivation for multi-scale models of cardiac electrophysiology. Prog. Biophys. Mol. Biol. 117, 4–18. ( 10.1016/j.pbiomolbio.2015.01.008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Hill TL. 2012. Free energy transduction and biochemical cycle kinetics. New York, NY: Springer Science and Business Media. [Google Scholar]
- 189.Huxley AF, Simmons RM. 1971. Proposed mechanism of force generation in striated muscle. Nature 233, 533–538. ( 10.1038/233533a0) [DOI] [PubMed] [Google Scholar]
- 190.Lymn R, Taylor EW. 1971. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry 10, 4617–4624. ( 10.1021/bi00801a004) [DOI] [PubMed] [Google Scholar]
- 191.Eisenberg E, Hill TL. 1979. A cross-bridge model of muscle contraction. Prog. Biophys. Mol. Biol. 33, 55–82. ( 10.1016/0079-6107(79)90025-7) [DOI] [PubMed] [Google Scholar]
- 192.Marcucci L, Truskinovsky L. 2010. Mechanics of the power stroke in myosin II. Phys. Rev. E 81, 051915 ( 10.1103/PhysRevE.81.051915) [DOI] [PubMed] [Google Scholar]
- 193.Zahalak GI. 1981. A distribution-moment approximation for kinetic theories of muscular contraction. Math. Biosci. 55, 89–114. ( 10.1016/0025-5564(81)90014-6) [DOI] [PubMed] [Google Scholar]
- 194.Guerin T, Prost J, Joanny J-F. 2011. Dynamical behavior of molecular motor assemblies in the rigid and crossbridge models. Eur. Phys. J. E 34, 1–21. ( 10.1140/epje/i2011-11060-5) [DOI] [PubMed] [Google Scholar]
- 195.Hill A. 1938. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B 126, 136–195. ( 10.1098/rspb.1938.0050) [DOI] [Google Scholar]
- 196.Suga H, Sagawa K, Shoukas AA. 1973. Load independence of the instantaneous pressure-volume ratio of the canine left ventricle and effects of epinephrine and heart rate on the ratio. Circul. Res. 32, 314–322. ( 10.1161/01.RES.32.3.314) [DOI] [PubMed] [Google Scholar]
- 197.Caruel M, Chabiniok R, Moireau P, Lecarpentier Y, Chapelle D. 2014. Dimensional reductions of a cardiac model for effective validation and calibration. Biomech. Model. Mechanobiol. 13, 897–914. ( 10.1007/s10237-013-0544-6) [DOI] [PubMed] [Google Scholar]
- 198.Piazzesi G, Lombardi V. 1995. A cross-bridge model that is able to explain mechanical and energetic properties of shortening muscle. Biophys. J. 68, 1966 ( 10.1016/S0006-3495(95)80374-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Tangney JR, Campbell SG, McCulloch AD, Omens JH. 2014. Timing and magnitude of systolic stretch affect myofilament activation and mechanical work. Am. J. Physiol. Heart. Circ. Physiol. 307, H353–H360. ( 10.1152/ajpheart.00233.2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Mann DL, Zipes DP, Libby P, Bonow RO, Braunwald E. 2015. Braunwald's heart disease. Philadelphia, PA: Sauders, Elsevier. [Google Scholar]
- 201.Ambrosi D, et al. 2011. Perspectives on biological growth and remodeling. J. Mech. Phys. Solids 59, 863–883. ( 10.1016/j.jmps.2010.12.011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Taber LA. 1995. Biomechanics of growth, remodeling, and morphogenesis. Appl. Mech. Rev. 48, 487–545. ( 10.1115/1.3005109) [DOI] [Google Scholar]
- 203.Rodriguez EK, Hoger A, McCulloch AD. 1994. Stress–dependent finite growth in soft elastic tissues. J. Biomech. 27, 455–467. ( 10.1016/0021-9290(94)90021-3) [DOI] [PubMed] [Google Scholar]
- 204.Menzel A, Kuhl E. 2012. Frontiers in growth and remodeling. Mech. Res. Commun. 42, 1–14. ( 10.1016/j.mechrescom.2012.02.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Göktepe S, Abilez OJ, Kuhl E. 2010. A generic approach towards finite growth with examples of athlete's heart, cardiac dilation, and cardiac wall thickening. J. Mech. Phys. Solids 58, 1661–1680. ( 10.1016/j.jmps.2010.07.003) [DOI] [Google Scholar]
- 206.Humphrey JD, Rajagopal KR. 2002. A constrained mixture model for growth and remodeling of soft tissues. Math. Models Methods Appl. Sci. 12, 407–430. ( 10.1142/S0218202502001714) [DOI] [Google Scholar]
- 207.Truesdell C, Noll W. 2004. The non-linear field theories of mechanics. Berlin, Germany: Springer. [Google Scholar]
- 208.Göktepe S, Abilez OJ, Parker KK, Kuhl E. 2012. A multiscale model for eccentric and concentric cardiac growth through sarcomerogenesis. J. Theor. Biol. 265, 433–442. ( 10.1016/j.jtbi.2010.04.023) [DOI] [PubMed] [Google Scholar]
- 209.Genet M, Lee LC, Baillargeon B, Guccione JM, Kuhl E. 2015. Modeling pathologies of systolic and diastolic heart failure. Ann. Biomed. Eng. 44, 112–127. ( 10.1007/s10439-015-1351-2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 210.Kerckhoffs RCP, Omens JH, McCulloch AD. 2012. A single strain-based growth law predicts concentric and eccentric cardiac growth during pressure and volume overload. Mech. Res. Commun. 42, 40–50. ( 10.1016/j.mechrescom.2011.11.004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Rausch MK, Dam A, Göktepe S, Abilez OJ, Kuhl E. 2011. Computational modeling of growth: systemic and pulmonary hypertension in the heart. Biomech. Model. Mechanobiol. 10, 799–811. ( 10.1007/s10237-010-0275-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212.Boovendeerd PHM. 2012. Modeling of cardiac growth and remodeling of myofiber orientation. J. Biomech. 45, 872–882. ( 10.1016/j.jbiomech.2011.11.029) [DOI] [PubMed] [Google Scholar]
- 213.Kroon W, Delhaas T, Arts T, Bovendeerd PHM. 2009. Computational modeling of volumetric soft tissue growth: application to the cardiac left ventricle. Biomech. Model. Mechanobiol. 8, 301–309. ( 10.1007/s10237-008-0136-z) [DOI] [PubMed] [Google Scholar]
- 214.Omens JH, McCulloch AD, Criscione JC. 2003. Complex distributions of residual stress and strain in the mouse left ventricle: experimental and theoretical models. Biomech. Model. Mechanobiol. 1, 267–277. ( 10.1007/s10237-002-0021-0) [DOI] [PubMed] [Google Scholar]
- 215.Genet M, Rausch M, Lee L, Choy S, Zhao X, Kassab G, Kozerke S, Guccione J, Kuhl E. 2015. Heterogeneous growth-induced prestrain in the heart. J. Biomech. 48, 2080–2089. ( 10.1016/j.jbiomech.2015.03.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216.Gerdes AM, Kellerman SE, Moore JA, Muffly KE, Clark LC, Reaves PY, Malec K, McKeown PP, Schocken DD. 1992. Structural remodeling of cardiac myocytes in patients with ischemic cardiomyopathy. Circulation 86, 426–430. ( 10.1161/01.CIR.86.2.426) [DOI] [PubMed] [Google Scholar]
- 217.Savinova OV, Gerdes AM. 2012. Myocyte changes in heart failure. Heart Fail. Clin. 8, 1–6. ( 10.1016/j.hfc.2011.08.004) [DOI] [PubMed] [Google Scholar]
- 218.Atkinson DJ, Edelman R. 1991. Cineangiography of the heart in a single breath hold with a segmented turboflash sequence. Radiology 178, 357–360. ( 10.1148/radiology.178.2.1987592) [DOI] [PubMed] [Google Scholar]
- 219.Usman M, Atkinson D, Heathfield E, Greil G, Schaeffter T, Prieto C. 2015. Whole left ventricular functional assessment from two minutes free breathing multi-slice cine acquisition. Phys. Med. Biol. 60, N93 ( 10.1088/0031-9155/60/7/N93) [DOI] [PubMed] [Google Scholar]
- 220.Wesbey G, Higgins C, McNamara M, Engelstad B, Lipton M, Sievers R, Ehman R, Lovin J, Brasch R. 1984. Effect of gadolinium-DTPA on the magnetic relaxation times of normal and infarcted myocardium. Radiology 153, 165–169. ( 10.1148/radiology.153.1.6473778) [DOI] [PubMed] [Google Scholar]
- 221.Delfaut EM, Beltran J, Johnson G, Rousseau J, Marchandise X, Cotten A. 1999. Fat suppression in MR imaging: techniques and pitfalls. Radiographics 19, 373–382. ( 10.1148/radiographics.19.2.g99mr03373) [DOI] [PubMed] [Google Scholar]
- 222.Mewton N, Liu CY, Croisille P, Bluemke D, Lima JA. 2011. Assessment of myocardial fibrosis with cardiovascular magnetic resonance. J. Am. Coll. Cardiol. 57, 891–903. ( 10.1016/j.jacc.2010.11.013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223.Ugander M et al. 2012. Extracellular volume imaging by magnetic resonance imaging provides insights into overt and sub-clinical myocardial pathology. Eur. Heart J. 33, 1268–1278. ( 10.1093/eurheartj/ehr481) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 224.Carpenter J-P, et al. 2014. On T2* magnetic resonance and cardiac iron. Circulation 123, 1519–1528. ( 10.1161/CIRCULATIONAHA.110.007641) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 225.Rutz AK, Ryf S, Plein S, Boesiger P, Kozerke S. 2008. Accelerated whole-heart 3D CSPAMM for myocardial motion quantification. Magn. Reson. Med. 59, 755–763. ( 10.1002/mrm.21363) [DOI] [PubMed] [Google Scholar]
- 226.Young AA. 1999. Model tags: direct three-dimensional tracking of heart wall motion from tagged magnetic resonance images. Med. Image Anal. 3, 361–372. ( 10.1016/S1361-8415(99)80029-2) [DOI] [PubMed] [Google Scholar]
- 227.Lambert SA et al. 2015. Bridging three orders of magnitude: multiple scattered waves sense fractal microscopic structures via dispersion. Phys. Rev. Lett. 115, 094301 ( 10.1103/PhysRevLett.115.094301) [DOI] [PubMed] [Google Scholar]
- 228.Henningsson M, Koken P, Stehning C, Razavi R, Prieto C, Botnar RM. 2012. Whole-heart coronary MR angiography with 2D self-navigated image reconstruction. Magn. Reson. Med. 67, 437–445. ( 10.1002/mrm.23027) [DOI] [PubMed] [Google Scholar]
- 229.Giorgi B, Dymarkowski S, Maes F, Kouwenhoven M. 2002. Improved visualization of coronary arteries using a new three-dimensional submillimeter MR coronary angiography sequence with balanced gradients. Am. J. Roentgenol. 179, 901–910. ( 10.2214/ajr.179.4.1790901) [DOI] [PubMed] [Google Scholar]
- 230.Axel L, Dougherty L. 1989. Improved method of spatial modulation of magnetization (SPAMM) for MRI of heart wall motion. Radiology 172, 349–350. ( 10.1148/radiology.172.2.2748813) [DOI] [PubMed] [Google Scholar]
- 231.Plein S, Ryf S, Schwitter J, Radjenovic A, Boesiger P, Kozerke S. 2007. Dynamic contrast-enhanced myocardial perfusion MRI accelerated with k-t SENSE. Magn. Reson. Med. 58, 777–785. ( 10.1002/mrm.21381) [DOI] [PubMed] [Google Scholar]
- 232.Jogiya R, Kozerke S, Morton G, De Silva K, Redwood S, Perera D, Nagel E, Plein S. 2012. Validation of dynamic 3-Dimensional whole heart magnetic resonance myocardial perfusion imaging against fractional flow reserve for the detection of significant coronary artery disease. J. Am. Coll. Cardiol. 60, 756–765. ( 10.1016/j.jacc.2012.02.075) [DOI] [PubMed] [Google Scholar]
- 233.Pedersen H, Kozerke S, Ringgaard S, Nehrke K, Kim W. 2009. k-t PCA: Temporally constrained k-t BLAST reconstruction using principal component analysis. Magn. Reson. Med. 62, 706–716. ( 10.1002/mrm.22052) [DOI] [PubMed] [Google Scholar]
- 234.Stoeck CT, von Deuster C, Genet M, Atkinson D, Kozerke S. 2015. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart. Magn. Reson. Med. 17(Suppl. 1), P81 ( 10.1186/1532-429X-17-S1-P81) [DOI] [PubMed] [Google Scholar]
- 235.Robert B, Sinkus R, Gennisson J-L, Fink M. 2009. Application of DENSE-MR-elastography to the human heart. Magn. Reson. Med. 62, 1155–1163. ( 10.1002/mrm.22124) [DOI] [PubMed] [Google Scholar]
- 236.Mariappan YK, Glaser KJ, Ehman RL. 2010. Magnetic resonance elastography: a review. Clin. Anat. 23, 497–511. ( 10.1002/ca.21006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 237.Pernot M, Couade M, Mateo P, Crozatier B, Fischmeister R, Tanter M. 2011. Real-time assessment of myocardial contractility using shear wave imaging. J. Am. Coll. Cardiol. 58, 65–72. ( 10.1016/j.jacc.2011.02.042) [DOI] [PubMed] [Google Scholar]
- 238.Toussaint N, Stoeck CT, Schaeffter T, Kozerke S, Sermesant M, Batchelor PG. 2013. In vivo human cardiac fibre architecture estimation using shape-based diffusion tensor processing. Med. Image Anal. 17, 1243–1255. ( 10.1016/j.media.2013.02.008) [DOI] [PubMed] [Google Scholar]
- 239.Brett SE, Guilcher A, Clapp B, Chowienczyk P. 2012. Estimating central systolic blood pressure during oscillometric determination of blood pressure: proof of concept and validation by comparison with intra-aortic pressure recording and arterial tonometry. Blood Press. Monit. 17, 132–136. ( 10.1097/MBP.0b013e328352ae5b) [DOI] [PubMed] [Google Scholar]
- 240.Shi W, et al. 2012. A comprehensive cardiac motion estimation framework using both untagged and 3D tagged MR images based on non-rigid registration. IEEE Trans. Med. Imag. 31, 1263–1275. ( 10.1109/TMI.2012.2188104) [DOI] [PubMed] [Google Scholar]
- 241.Imperiale A, Chabiniok R, Moireau P, Chapelle D. 2011. Constitutive parameter estimation methodology using tagged-MRI data. In Functional imaging and modeling of the heart (eds D Metaxas, L Axel), pp. 409–417. Berlin, Germany: Springer. [Google Scholar]
- 242.Ecabert O, Peters J, Walker M, Ivan T, Lorenz C, von Berg J, Lessick J, Vembar M. 2011. Assessment of myocardial fibrosis with cardiovascular magnetic resonance. Med. Image Anal. 15, 863–876. ( 10.1016/j.media.2011.06.004) [DOI] [PubMed] [Google Scholar]
- 243.Shi W, Jantsch M, Aljabar P, Pizarro L, Bai W, Wang H, O'Regan D, Zhuang X, Rueckert D. 2013. Temporal sparse free-form deformations. Med. Image Anal. 17, 779–789. ( 10.1016/j.media.2013.04.010) [DOI] [PubMed] [Google Scholar]
- 244.Hadjicharalambous M, et al. 2015. Analysis of passive cardiac constitutive laws for parameter estimation using 3D tagged MRI. Biomech. Model. Mechanobiol. 14, 807–828. ( 10.1007/s10237-014-0638-9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 245.Augenstein KF, Cowan BR, LeGrice IJ, Nielsen PM, Young AA. 2005. Method and apparatus for soft tissue material parameter estimation using tissue tagged magnetic resonance imaging. J. Biomech. Eng. 127, 148–157. ( 10.1115/1.1835360) [DOI] [PubMed] [Google Scholar]
- 246.Wang VY, Lam H, Ennis DB, Cowan BR, Young AA, Nash MP. 2009. Modelling passive diastolic mechanics with quantitative MRI of cardiac structure and function. Med. Image Anal. 13, 773–784. ( 10.1016/j.media.2009.07.006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 247.Xi J, Lamata P, Lee J, Moireau P, Chapelle D, Smith N. 2011. Myocardial transversely isotropic material parameter estimation from in-silico measurements based on a reduced-order unscented Kalman filter. J. Mech. Behav. Biomed. Mater. 4, 1090–1102. ( 10.1016/j.jmbbm.2011.03.018) [DOI] [PubMed] [Google Scholar]
- 248.Wang L, Dawoud F, Wong KC, Zhang H, Liu H, Lardo AC, Shi P. 2011. Transmural electrophysiologic and scar imaging on porcine heart with chronic infarction. In STACOM (eds O Camara, E Konukoglu, M Pop, K Rhode, M Sermesant, A Young), pp. 23–32. Berlin, Germany: Springer. [Google Scholar]
- 249.Chabiniok R, Moireau P, Lesault P-F, Rahmouni A, Deux J-F, Chapelle D. 2012. Estimation of tissue contractility from cardiac cine-MRI using a biomechanical heart model. Biomech. Model. Mechanobiol. 11, 609–630. ( 10.1007/s10237-011-0337-8) [DOI] [PubMed] [Google Scholar]
- 250.Marchesseau S, et al. 2013. Personalization of a cardiac electromechanical model using reduced order unscented Kalman filtering from regional volumes. Med. Image Anal. 17, 816–829. ( 10.1016/j.media.2013.04.012) [DOI] [PubMed] [Google Scholar]
- 251.Chabiniok R, Bhatia KK, King AP, Rueckert D, Smith N. 2015. Manifold learning for cardiac modeling and estimation framework. In statistical atlases and computational models of the heart-imaging and modelling challenges (eds O Camara, T Mansi, M Pop, K Rhode, M Sermesant, A Young), pp. 284–294. Basel, Switzerland: Springer. [Google Scholar]
- 252.Asner L, et al. In press. Estimation of passive and active properties in the human heart using 3D tagged MRI. Biomech. Model. Mechanobiol. ( 10.1007/s10237-015-0748-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 253.Wong KC, Sermesant M, Rhode K, Ginks M, Rinaldi CA, Razavi R, Delingette H, Ayache N. 2014. Velocity-based cardiac contractility personalization from images using derivative-free optimization. J. Mech. Behav. Biomed. Mater. 43, 35–52. ( 10.1016/j.jmbbm.2014.12.002) [DOI] [PubMed] [Google Scholar]
- 254.Chabiniok R, Sammut E, Hadjicharalambous M, Asner L, Nordsletten D, Razavi R, Smith N. 2015. Steps towards quantification of the cardiological stress exam. In Functional imaging and modeling of the heart (eds H van Assen, P Bovendeerd, T Delhaas), pp. 12–20. Basel, Switzerland: Springer. [Google Scholar]
- 255.Krishnamurthy A, et al. 2013. Patient-specific models of cardiac biomechanics. J. Comput. Phys. 244, 4–21. ( 10.1016/j.jcp.2012.09.015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 256.Rohmer D, Sitek A, Gullberg GT. 2007. Reconstruction and visualization of fiber and laminar structure in the normal human heart from ex vivo. Invest. Radiol. 42, 777–789. ( 10.1097/RLI.0b013e3181238330) [DOI] [PubMed] [Google Scholar]
- 257.Eggen MD, Swingen CM, Iaizzo PA. 2009. Analysis of fiber orientation in normal and failing human hearts using diffusion tensor MRI. In IEEE Int. Symp. on Biomedical Imaging: From Nano to Macro, Boston, MA, 28 June–1 July, pp. 642–645. New York, NY: IEEE.
- 258.Gamper U, Boesiger P, Kozerke S. 2007. Diffusion imaging of the in vivo heart using spin echoes–considerations on bulk motion sensitivity. Magn. Reson. Med. 57, 331–337. ( 10.1002/mrm.21127) [DOI] [PubMed] [Google Scholar]
- 259.Schmid H, Nash M, Young A, Hunter P. 2006. Myocardial material parameter estimation—a comparative study for simple shear. J. Biomech. Eng. 128, 742–750. ( 10.1115/1.2244576) [DOI] [PubMed] [Google Scholar]
- 260.Schmid H, O'Callaghan P, Nash M, Lin W, LeGrice I, Smaill B, Young A, Hunter P. 2008. Myocardial material parameter estimation. Biomech. Model. Mechanobiol. 7, 161–173. ( 10.1007/s10237-007-0083-0) [DOI] [PubMed] [Google Scholar]
- 261.Blum J, Le Dimet F-X, Navon IM. 2009. Data assimilation for geophysical fluids. Handb. Numer. Anal. 14, 385–441. ( 10.1016/S1570-8659(08)00209-3) [DOI] [Google Scholar]
- 262.Chapelle D, Fragu M, Mallet V, Moireau P. 2013. Fundamental principles of data assimilation underlying the Verdandi library: applications to biophysical model personalization within euheart. Med. Biol. Eng. Comput. 51, 1221–1233. ( 10.1007/s11517-012-0969-6) [DOI] [PubMed] [Google Scholar]
- 263.Perotti LE, Ponnaluri AV, Krishnamoorthi S, Balzani D, Klug WS, Ennis DB. 2015. Identification of unique material properties for passive myocardium. Auckland, New Zealand: Cardiac Physiome Workshop. [Google Scholar]
- 264.Le Dimet F-X, Talagrand O. 1986. Variational algorithms for analysis and assimilation of meteorological observations: theoretical aspects. Tellus A 38, 97–110. ( 10.1111/j.1600-0870.1986.tb00459.x) [DOI] [Google Scholar]
- 265.Delingette H, Billet F, Wong KC, Sermesant M, Rhode K, Ginks M, Rinaldi CA, Razavi R, Ayache N. 2012. Personalization of cardiac motion and contractility from images using variational data assimilation. IEEE Trans. Biomed. Eng. 59, 20–24. ( 10.1109/TBME.2011.2160347) [DOI] [PubMed] [Google Scholar]
- 266.Moireau P, Chapelle D, Le Tallec P. 2008. Joint state and parameter estimation for distributed mechanical systems. Comput. Methods Appl. Mech. Eng. 197, 659–677. ( 10.1016/j.cma.2007.08.021) [DOI] [Google Scholar]
- 267.Moireau P, Chapelle D. 2011. Reduced-order unscented Kalman filtering with application to parameter identification in large-dimensional systems. ESAIM Control Optimisation Calc. Var. 17, 380–405. ( 10.1051/cocv/2010006) [DOI] [Google Scholar]
- 268.Lakshmivarahan S, Lewis JM. 2013. Nudging methods: a critical overview. In Data assimilation for atmospheric, oceanic and hydrologic applications, vol. II (eds S Ki Park, L Xu), pp. 27–57. Berlin, Germany: Springer. [Google Scholar]
- 269.Moireau P, Chapelle D, Le Tallec P. 2009. Filtering for distributed mechanical systems using position measurements: perspectives in medical imaging. Inverse Probl. 25, 035010 ( 10.1088/0266-5611/25/3/035010) [DOI] [Google Scholar]
- 270.Corrado C, Gerbeau J-F, Moireau P. 2015. Identification of weakly coupled multiphysics problems. Application to the inverse problem of electrocardiography. J. Comput. Phys. 283, 271–298. ( 10.1016/j.jcp.2014.11.041) [DOI] [Google Scholar]
- 271.Imperiale A, Routier A, Durrleman S, Moireau P. 2013. Improving efficiency of data assimilation procedure for a biomechanical heart model by representing surfaces as currents. In Functional imaging and modeling of the heart (eds S Ourselin, D Rueckert, N Smith), pp. 342–351. Berlin, Germany: Springer. [Google Scholar]
- 272.Mancini D, Burkhoff D. 2005. Mechanical device–based methods of managing and treating heart failure. Circulation 112, 438–448. ( 10.1161/CIRCULATIONAHA.104.481259) [DOI] [PubMed] [Google Scholar]
- 273.Food and D. Administration. 2014. Reporting of computational modeling studies in medical device submissions. In Draft guidance for industry and food and drug administration staff. See http://www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/GuidanceDocuments/ucm371016.htm. [Google Scholar]
- 274.Rausch M, Bothe W, Kvitting J-P, Swanson J, Miller D, Kuhl E. 2012. Mitral valve annuloplasty. Ann. Biomed. Eng. 40, 750–761. ( 10.1007/s10439-011-0442-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 275.Gee MW, Hirschvogel M, Basilious M, Wildhirt S. 2015. A closed loop 0D-3D model of patient specific cardiac mechanics for cardiac assist device engineering. In 4th Int. Conf. on Computational and Mathematical Biomedical Engineering, Paris, France, 9 June–1 July. Swansea, UK: CMBE Zeta Computational Resources Ltd.
- 276.Wang Q, Sirois E, Sun W. 2012. Patient-specific modeling of biomechanical interaction in transcatheter aortic valve deployment. J. Biomech. 45, 1965–1971. ( 10.1016/j.jbiomech.2012.05.008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 277.Lafortune P, Ars R, Vázquez M, Houzeaux G. 2012. Coupled electromechanical model of the heart: parallel finite element formulation. Int. J. Numer. Methods Biomed. Eng. 28, 72–86. ( 10.1002/cnm.1494) [DOI] [PubMed] [Google Scholar]
- 278.Gurev V, Pathmanathan P, Fattebert J-L, Wen H-F, Magerlein J, Gray RA, Richards DF, Rice JJ. 2015. A high-resolution computational model of the deforming human heart. Biomech. Model. Mechanobiol. 14, 829–849. ( 10.1007/s10237-014-0639-8) [DOI] [PubMed] [Google Scholar]
- 279.Augustin CM, Neic A, Liebmann M, Prassl AJ, Niederer SA, Haase G, Plank G. 2016. Anatomically accurate high resolution modeling of human whole heart electromechanics: a strongly scalable algebraic multigrid solver method for nonlinear deformation. J. Comput. Phys. 305, 622–646. ( 10.1016/j.jcp.2015.10.045) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 280.Kayvanpour E, et al. 2015. Towards personalized cardiology: multi-scale modeling of the failing heart. PLoS ONE 10, e0134869 ( 10.1371/journal.pone.0134869) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 281.Chapelle D, Felder A, Chabiniok R, Guellich A, Deux J-F, Damy T. 2015. Patient-specific biomechanical modeling of cardiac amyloidosis–a case study. In Functional imaging and modeling of the heart (eds H van Assen, P Bovendeerd, T Delhaas), pp. 295–303. Basel, Switzerland: Springer. [Google Scholar]
- 282.Qu Z, Garfinkel A, Chen P-S, Weiss JN. 2000. Mechanisms of discordant alternans and induction of reentry in simulated cardiac tissue. Circulation 102, 1664–1670. ( 10.1161/01.CIR.102.14.1664) [DOI] [PubMed] [Google Scholar]
- 283.Sato D et al. 2009. Synchronization of chaotic early afterdepolarizations in the genesis of cardiac arrhythmias. Proc. Natl Acad. Sci. USA 106, 2983–2988. ( 10.1073/pnas.0809148106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 284.Moreno JD, et al. 2011. A computational model to predict the effects of class I anti-arrhythmic drugs on ventricular rhythms. Sci. Transl. Med. 3, 98ra83. ( 10.1126/scitranslmed.3002588) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 285.Mansi T, et al. 2011. A statistical model for quantification and prediction of cardiac remodelling: application to tetralogy of Fallot. IEEE Trans. Med. Imag. 30, 1605–1616. ( 10.1109/TMI.2011.2135375) [DOI] [PubMed] [Google Scholar]
- 286.Hlatky MA, et al. 2009. Criteria for evaluation of novel markers of cardiovascular risk a scientific statement from the American heart association. Circulation 119, 2408–2416. ( 10.1161/CIRCULATIONAHA.109.192278) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 287.Tsamis A, Cheng A, Nguyen TC, Langer F, Miller D, Kuhl E. 2012. Kinematics of cardiac growth: In vivo characterization of growth tensors and strains. J. Mech. Behav. Biomed. Mater. 8, 165–177. ( 10.1016/j.jmbbm.2011.12.006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 288.Zhang X, et al. 2014. Atlas-based quantification of cardiac remodeling due to myocardial infarction. PLoS ONE 9, e110243 ( 10.1371/journal.pone.0110243) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 289.Tobon-Gomez C, et al. 2013. Benchmarking framework for myocardial tracking and deformation algorithms: an open access database. Med. Image Anal. 17, 632–648. ( 10.1016/j.media.2013.03.008) [DOI] [PubMed] [Google Scholar]
- 290.Camara O, Mansi T, Pop M, Rhode K, Sermesant M, Young A. 2015. Statistical atlases and computational models of the heart-imaging and modelling challenges: 5th International Workshop, STACOM 2014. In Held in Conjunction with MICCAI 2014,Boston, MA, USA,18 September 2014, revised Selected Papers, vol. 8896. Cham, Switzerland: Springer.
- 291.Konukoglu E, et al. 2011. Efficient probabilistic model personalization integrating uncertainty on data and parameters: application to eikonal-diffusion models in cardiac electrophysiology. Prog. Biophys. Mol. Biol. 107, 134–146. ( 10.1016/j.pbiomolbio.2011.07.002) [DOI] [PubMed] [Google Scholar]
- 292.Zettinig O, et al. 2014. Data-driven estimation of cardiac electrical diffusivity from 12-lead ECG signals. Med. Image Anal. 18, 1361–1376. ( 10.1016/j.media.2014.04.011) [DOI] [PubMed] [Google Scholar]
- 293.Neumann D, et al. 2014. Robust image-based estimation of cardiac tissue parameters and their uncertainty from noisy data. In Medical image computing and computer-assisted intervention–MICCAI 2014 (eds P Golland, N Hata, C Barillot, J Hornegger, R Howe), pp. 9–16. Basel, Switzerland: Springer. [DOI] [PubMed] [Google Scholar]