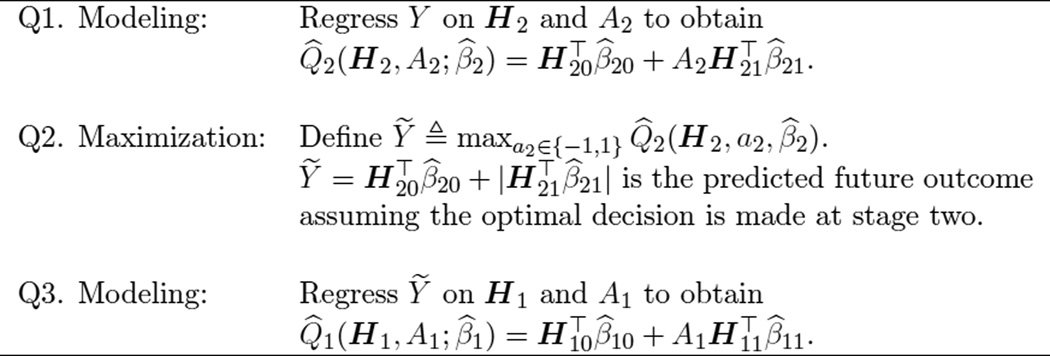iqLearn: Interactive Q-Learning in R

Abstract

Chronic illness treatment strategies must adapt to the evolving health status of the patient receiving treatment. Data-driven dynamic treatment regimes can offer guidance for clinicians and intervention scientists on how to treat patients over time in order to bring about the most favorable clinical outcome on average. Methods for estimating optimal dynamic treatment regimes, such as Q-learning, typically require modeling nonsmooth, nonmonotone transformations of data. Thus, building well-fitting models can be challenging and in some cases may result in a poor estimate of the optimal treatment regime. Interactive Q-learning (IQ-learning) is an alternative to Q-learning that only requires modeling smooth, monotone transformations of the data. The R package iqLearn provides functions for implementing both the IQ-learning and Q-learning algorithms. We demonstrate how to estimate a two-stage optimal treatment policy with iqLearn using a generated data set bmiData which mimics a two-stage randomized body mass index reduction trial with binary treatments at each stage.

1. Introduction

In practice, clinicians and intervention scientists must adapt treatment recommendations in response to the uniquely evolving health status of each patient. Dynamic treatment regimes (DTRs) formalize this treatment process as a sequence of decision rules, one for each treatment decision, which map current and past patient information to a recommended treatment. A DTR is said to be optimal for a prespecified desirable outcome if, when applied to assign treatment to a population of interest, it yields the maximal expected outcome.

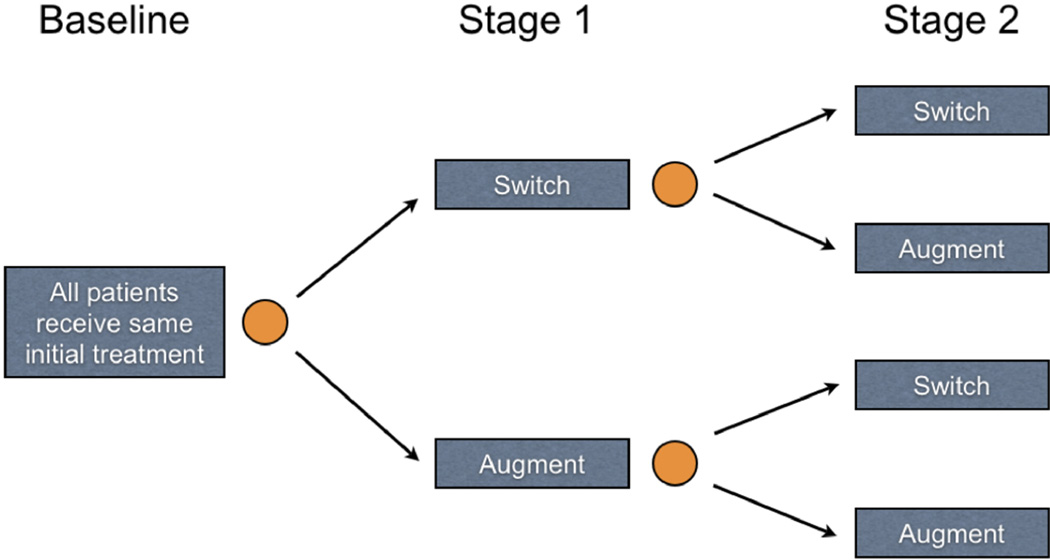
With the potential for better patient outcomes, reduced treatment burden, and lower cost, there is growing interest in personalized treatment strategies (Hamburg and Collins 2010; Abrahams 2010). Sequential multiple assignment randomized trials (SMARTs; Lavori and Dawson 2004; Murphy 2005a) are designed for the estimation of optimal DTRs. In a SMART, subjects are randomized to treatment at each decision point or stage of the trial. Figure 1 contains a visual representation of a SMART design toy example where all subjects receive the same treatment at baseline (e.g., possibly a standard of care). After some period of time in the baseline stage, patients are then randomized (represented by gold circles) at the start of the first stage to one of two treatment categories: “switch” or “augment” current treatment. After some period of time in the first stage, subjects are again randomized to either switch or augment their current treatment(s) in the second stage. There are many variations of this design; for example, more than two treatments can be offered at each stage, and for ethical reasons it is common to include an option for baseline or first-stage responders to continue their currently successful treatment. Although it is possible to design a trial with additional stages, two stage SMARTs are common, as evidenced by many recently completed and ongoing SMARTs. For a list of SMARTs that have finished or are in the field, see The Methodology Center at Pennsylvania State University (2012) and Eric Laber’s current list (Laber 2013). With additional randomizations beyond one or two stages, the number of patients assigned to each sequence of treatments decreases, along with the power to estimate optimal decisions in the later stages. In principle, the sequential randomization scheme in SMARTs guarantees that there are no confounders that influence which types of subjects follow each of the possible treatment sequences. To keep our discussion focused, we will work under the assumption of a two-stage SMART with randomized binary treatments at each stage. However, all the methods discussed here apply to observational data when additional assumptions are made on the treatment assignment mechanism (see, for example, Murphy 2003; Moodie, Chakraborty, and Kramer 2012).

Figure 1.

SMART design toy example with two randomized stages and two treatment options at each stage. Patients progress from left to right and are randomized to one of two treatment options just prior to Stages 1 and 2. Randomizations are represented by gold circles; treatments are displayed in blue boxes.

We introduce the R (R Core Team 2014) package iqLearn (Linn, Laber, and Stefanski 2015) for estimating optimal DTRs from data obtained from a two stage trial with two treatments at each stage using interactive Q-learning (IQ-learning; Laber, Linn, and Stefanski 2014). The package is available from the Comprehensive R Archive Network (CRAN) at http://CRAN.R-project.org/package=iqLearn. Although we recommend using IQ-learning instead of Q-learning in most practical settings based on developments in Section 2 and Laber et al. (2014), a comparison of the regimes estimated by the two methods may be of interest to some data analysts. Thus, functions for estimating a regime using the Q-learning algorithm are also included in iqLearn for completeness. Introductions to both Q- and IQ-learning are provided in Section 2. Section 3 provides a case-study illustrating the iqLearn package. A brief discussion of future work concludes the paper in Section 4.

2. Q-learning and interactive Q-learning

We assume data are collected from a two-stage randomized trial with binary treatments at each stage, resulting in n i.i.d. patient trajectories of the form (X₁, A₁, X₂, A₂, Y), where X₁ and X₂ are vectors of dimension p₁ and p₂, respectively. The variables in the trajectory are: baseline covariates, X₁ ∈ ℝ^p₁ ; first-stage randomized treatment, A₁ ∈ {−1, 1}; covariates collected during the first-stage but prior to second-stage treatment assignment, X₂ ∈ ℝ^p₂ ; second-stage randomized treatment, A₂ ∈ {−1, 1}; and the response, Y ∈ ℝ, collected at the conclusion of the trial. We assume Y has been coded so that higher values indicate more positive clinical outcomes. To simplify notation, we group variables collected prior to each treatment randomization into a history vector H_t, t = 1, 2. That is, H₁ = X₁ and ${\mathit{H}}_2={({\mathit{X}}_1^{\top },A_1,{\mathit{X}}_2^{\top })}^{\top }$.

A DTR is a pair of functions π = (π₁, π₂) where π_t maps the domain of H_t into the space of available treatments {−1, 1}. Under π a patient presenting at time t with history H_t = h_t is assigned treatment π_t (h_t). The goal is to estimate a DTR that when applied in a population of patients of interest, the expected outcome is maximized. Define the value of a fixed regime π as V^π ≜ 𝔼^π(Y), where 𝔼^π denotes the expectation when treatment is assigned according to the policy π. The optimal treatment regime, π^opt, maximizes the value function:

$${𝔼}^{{\mathit{\pi }}^{\text{opt}}}(Y)=\underset{\mathit{\pi }}{\text{sup}}{𝔼}^{\mathit{\pi }}(Y).$$

In Sections 2.1 and 2.2, we explain how an optimal regime can be estimated from data using Q-learning and IQ-learning. The IQ-learning estimated optimal decision rules will be denoted by ${\pi }_t^{\mathrm{I}\mathrm{Q}-\text{opt}}$ and the Q-learning analogs by ${\pi }_t^{\mathrm{Q}-\text{opt}}$. Both methods are implemented in the iqLearn package.

2.1. Q-learning

Q-learning (Watkins 1989; Watkins and Dayan 1992; Murphy 2005b) is an approximate dynamic programming algorithm that can be used to estimate an optimal DTR from observational or randomized study data. Define the Q-functions:

$$Q_2({\mathit{h}}_2,a_2)\triangleq 𝔼(Y|{\mathit{H}}_2={\mathit{h}}_2,A_2=a_2),$$

$$Q_1({\mathit{h}}_1,a_1)\triangleq 𝔼(\underset{a_2\in \{-1,1\}}{\text{max}}{Q}_2({\mathit{H}}_2,a_2)|{\mathit{H}}_1={\mathit{h}}_1,A_1=a_1).$$

The Q-function at stage two measures the Quality of assigning a₂ to a patient presenting with history h₂. Similarly, Q₁ measures the quality of assigning a₁ to a patient with h₁, assuming an optimal decision rule will be followed at stage two. Were the Q-functions known, dynamic programming (Bellman 1957) gives the optimal solution, π_t^opt (h_t) = arg max_{at∈{−1,1}} Q_t (h₁, a_t). Since the underlying distribution of the patient histories is not known, the conditional expectations that define the Q-functions are unknown and must be approximated. Q-learning approximates the Q-functions with regression models; commonly linear models are chosen in practice because they yield simple, interpretable models. We will consider linear models of the form: $Q_t({\mathit{h}}_t,a_t;{\beta }_t)={\mathit{h}}_{t0}^{\top }{\beta }_{t0}+a_t{\mathit{h}}_{t1}^{\top }{\beta }_{t1}$, t = 1, 2, where h_t0 and h_t1 each include an intercept and a subset of variables collected in h_t. Define ${\beta }_t\triangleq {({\beta }_{t0}^{\top },{\beta }_{t1}^{\top })}^{\top }$. The Q-learning algorithm is given in Figure 2.

Figure 2.

Q-learning algorithm.

The tth-stage optimal decision rule then assigns the treatment a_t that maximizes the estimated Q_t-function,

$${\hat{\pi }}_t^{\mathrm{Q}-\text{opt}}({\mathit{h}}_t)=\text{arg}\underset{a_t}{\text{ max }}{\hat{Q}}_t({\mathit{h}}_t,a_t;{\hat{\beta }}_t).$$

In Q-learning with linear models, this can be written as

$${\hat{\pi }}_t^{\mathrm{Q}-\text{opt}}({\mathit{h}}_t)=\text{sign}({\mathit{h}}_{t1}^{\top }{\hat{\beta }}_{t1}).$$

The first modeling step in the Q-learning algorithm is a standard multiple regression problem to which common model building and model checking techniques can be applied to find a parsimonious, well-fitting model. The absolute value in the definition of Ỹ arises when A₂ is coded as {−1, 1}, since arg max_a2 ${\hat{Q}}_2({\mathit{H}}_2,a_2;{\hat{\beta }}_2)=\text{sign}({\mathit{H}}_{21}^{\top }{\hat{\beta }}_{21})$. The second modeling step (Q3) requires modeling the conditional expectation of Ỹ. This can be written as

$$Q_1({\mathit{H}}_1,A_1)=𝔼(\tilde{Y}|{\mathit{H}}_1,A_1)=𝔼({\mathit{H}}_{20}^{\top }{\beta }_{20}+|{\mathit{H}}_{21}^{\top }{\beta }_{21}||{\mathit{H}}_1,A_1).$$ (1)

Due to the absolute value function, Ỹ is a nonsmooth, nonmonotone transformation of H₂. Thus, the linear model in step Q3 is generally misspecified. In addition, the nonsmooth, nonmonotone max operator in step Q2 leads to difficult nonregular inference for the parameters that index the first stage Q-function (Robins 2004; Chakraborty, Murphy, and Strecher 2010; Laber, Lizotte, Qian, Pelham, and Murphy 2010; Song, Wang, Zeng, and Kosorok 2015; Chakraborty, Laber, and Zhao 2013). In the next section, we develop an alternative to Q-learning, which we call IQ-learning, that addresses the applied problem of building good models for the first-stage Q-function and avoids model misspecification for a large class of generative models.

2.2. Interactive Q-learning (IQ-learning)

IQ-learning differs from Q-learning in the order in which the maximization step (Q2 in the Q-learning algorithm) is performed. We demonstrate how the maximization step can be delayed, enabling all modeling to be performed before this nonsmooth, nonmonotone transformation. This reordering of modeling and maximization steps facilitates the use of standard, interactive model building techniques because all terms to be modeled are linear, and hence smooth and monotone, transformations of the data. For a large class of generative models, IQ-learning more accurately estimates the first-stage Q-function, resulting in a higher-quality estimated decision rule (Laber et al. 2014). Another advantage of IQ-learning is that in many cases, conditional mean and variance modeling techniques (Carroll and Ruppert 1988) offer a nice framework for the necessary modeling steps. These mean and variance models are interpretable, and the coefficients indexing them enjoy normal limit theory. Thus, they are better suited to inform clinical practice than the misspecified first-stage model in Q-learning whose indexing parameters are nonregular. However, the mean-variance modeling approach we advocate here is not necessary and other modeling techniques may be applied as needed. Indeed, a major advantage and motivation for IQ-learning is the ability for the seasoned applied statistician to build high-quality models using standard interactive techniques for model diagnosis and validation.

IQ- and Q-learning do not differ at step one (Q1), which we refer to as the second-stage regression. Define $m({\mathit{H}}_2;{\beta }_2)\triangleq {\mathit{H}}_{20}^{\top }{\beta }_{20}$, and $\mathrm{\Delta }({\mathit{H}}_2;{\beta }_2)\triangleq {\mathit{H}}_{21}^{\top }{\beta }_{21}$. We call the first term the main effect function and the second the contrast function. Δ(H₂; β₂) “contrasts” the quality of the second-stage treatments: $\mathrm{\Delta }({\mathit{H}}_2;{\beta }_2)=\frac{1}{2}\{Q_2({\mathit{H}}_2,A_2=1)-Q_2({\mathit{H}}_2,A_2=-1)\}$. In the IQ-learning framework, the first-stage Q-function is defined as

$$Q_1({\mathit{h}}_1,a_1)\triangleq 𝔼(m({\mathit{H}}_2;{\beta }_2)|{\mathit{H}}_1={\mathit{h}}_1,A_1=a_1)+\int |z|g(z|{\mathit{h}}_1,a_1)dz,$$ (2)

where g(· | h₁, a₁) is the conditional distribution of the contrast function Δ(H₂; β₂) given H₁ = h₁ and A₁ = a₁. In fact, Equation 2 is equivalent to the representation of Q₁ in Equation 1; the conditional expectation has been split into two separate expectations and the second has been written in integral form. Instead of modeling the conditional expectation in Equation 1 directly, IQ-learning separately models 𝔼(m(H₂; β₂) | H₁ = h₁, A₁ = a₁) and g(· | h₁, a₁). Although IQ-learning trades one modeling step (Q3) for two, splitting up the conditional expectation in Equation 1 is advantageous because the terms that require modeling are now smooth, monotone functionals of the data. The maximization occurs when the integral in Equation 2 is computed, which occurs after the conditional density g(· | h₁, a₁) has been estimated. The IQ-learning algorithm is described in Figure 3.

Figure 3.

IQ-learning algorithm.

The IQ-learning estimated optimal DTR assigns the treatment at stage t as the maximizer of the estimated stage-t Q-function ${\hat{\pi }}_t^{\mathrm{I}\mathrm{Q}-\text{opt}}({\mathit{h}}_t)=\text{arg}{\text{ max}}_{a_t}{\hat{Q}}_t^{IQ}({\mathit{h}}_t,a_t;{\hat{\beta }}_t)$.

We note that it is possible to obtain ${\hat{Q}}_1^{IQ}$ in IQ4 by modeling the bivariate conditional distribution of m(H₂; β₂) and Δ(H₂; β₂) given H₁ and A₁ instead of separate modeling steps IQ2 and IQ3. However, it is often easier to assess model fits using standard residual diagnostics and other well-established model checking tools when $𝔼({\mathit{H}}_{20}^{\top }{\beta }_{20}|{\mathit{H}}_1,A_1)$ and g(· | H₁, A₁) are modeled separately.

2.3. Remark about density estimation in IQ3

Step IQ3 in the IQ-learning algorithm requires estimating a one-dimensional conditional density. In Laber et al. (2014) we accomplish this using mean-variance, location-scale estimators of g(· | h₁, a₁) of the form

$$ĝ(z|{\mathit{h}}_1,a_1)=\frac{1}{\hat{\sigma }({\mathit{h}}_1,a_1)}\hat{\varphi }(\frac{z-\hat{\mu }({\mathit{h}}_1,a_1)}{\hat{\sigma }({\mathit{h}}_1,a_1)}),$$

where μ̂(h₁, a₁) is an estimator of μ(h₁, a₁) ≜ 𝔼{Δ(H₂; β₂) | H₁ = h₁, A₁ = a₁}, σ̂²(h₁, a₁) is an estimator of σ²(h₁, a₁) ≜ 𝔼 {(Δ(H₂; β₂) − μ(h₁, a₁))² | H₁ = h₁, A₁ = a₁}, and ϕ̂ is an estimator of the density of the standardized residuals {Δ(H₂; β₂) − μ(h₁, a₁)} /σ(h₁, a₁), say ϕ_h1,a1, which we assume does not depend on the history h₁ or the treatment a₁. Mean-variance function modeling tools are well-studied and applicable in many settings (Carroll and Ruppert 1988). Currently, iqLearn implements mean-variance modeling steps to estimate g(· | h₁, a₁) with the option of using a standard normal density or empirical distribution estimator for ϕ̂.

3. Using the iqLearn package

3.1. Preparing dataset bmiData

The examples in this section will be illustrated using a simulated dataset called bmiData which is included in the iqLearn package. The data are generated to mimic a two-stage SMART of body mass index (BMI) reduction with two treatments at each stage. The patient characteristics, treatments, and outcomes in bmiData are based on a small subset of patient covariates collected in a clinical trial studying the effect of meal replacements (MRs) on weight loss and BMI reduction in obese adolescents; see Berkowitz et al. (2010) for a complete description of the original randomized trial. Descriptions of the generated variables in bmiData are given in Table 1. Baseline covariates include gender, race, parent_BMI, and baseline_BMI. Four- and twelve-month patient BMI measurements were also included to reflect the original trial design. In the generated data, treatment was randomized to meal replacement (MR) or conventional diet (CD) at both stages, each with probability 0.5. In the original study, patients randomized to CD in stage one remained on CD with probability one in stage two. Thus, our generated data arises from a slightly different design than that of the original trial. In addition, some patients in the original data set were missing the final twelve-month response as well as various first- and second-stage covariates. Our generated data is complete, and the illustration of IQ- and Q-learning with iqLearn that follows is presented under the assumption that missing data have been addressed prior to using these methods (for example, using an appropriate imputation strategy).

Table 1.

Description of variables in bmiData.

Variable	Support	Description
gender	{0, 1}	Patient gender, coded female (0) and male (1).
race	{0, 1}	Patient race, coded African American (0) or other (1).
parent_BMI	ℝ	Parent BMI measured at baseline.
baseline_BMI	ℝ	Patient BMI measured at baseline.
A1	{−1, 1}	First-stage randomized treatment, coded so that A1 = 1 corresponds to meal replacement (MR) and A1 = −1 corresponds to conventional diet (CD).
month4_BMI	ℝ	Patient BMI measured at month 4.
A2	{−1, 1}	Second-stage randomized treatment, coded so that A2 = 1 corresponds to meal replacement (MR) and A2 = −1 corresponds to conventional diet (CD).
month12_BMI	ℝ	Patient BMI measured at month 12.

After installing iqLearn, load the package:

R> library("iqLearn")

Next, load bmiData into the workspace with

R> data("bmiData", package = "iqLearn")

For reproducibility, set the seed of the random number generator:

R> set.seed(1)

The generated dataset bmiData is a data frame with 210 rows corresponding to patients and 8 columns corresponding to covariates, BMI measurements, and assigned treatments.

R> dim(bmiData)

[1] 210   8

R> head(bmiData)

  gender race parent_BMI baseline_BMI month4_BMI month12_BMI A1 A2
1      0    1   31.59683     35.84005   34.22717    34.27263 CD MR
2      1    0   30.17564     37.30396   36.38014    36.38401 CD MR
3      1    0   30.27918     36.83889   34.42168    34.41447 MR CD
4      1    0   27.49256     36.70679   32.52011    32.52397 CD CD
5      1    1   26.42350     34.84207   33.72922    33.73546 CD CD
6      0    0   29.30970     36.68640   32.06622    32.15977 MR MR

Recode treatments meal replacement (MR) and conventional diet (CD) as 1 and −1, respectively.

R> bmiData$A1 <- ifelse(bmiData$A1 == "MR", 1, −1)
R> bmiData$A2 <- ifelse(bmiData$A2 == "MR", 1, −1)

We use the negative percent change in BMI at month 12 from baseline as our final outcome:

R> y <- −100 * (bmiData$month12_BMI -
+    bmiData$baseline_BMI) / bmiData$baseline_BMI

Thus, higher values indicate greater BMI loss, a desirable clinical outcome. We will next show how to implement IQ-learning with the iqLearn package to obtain an estimate of the optimal DTR, ${\hat{\mathit{\pi }}}^{\mathrm{I}\mathrm{Q}-\text{opt}}=({\hat{\pi }}_1^{\mathrm{I}\mathrm{Q}-\text{opt}},{\hat{\pi }}_2^{\mathrm{I}\mathrm{Q}-\text{opt}})$, that maximizes the expected BMI reduction.

3.2. IQ-learning functions

The current version of the iqLearn package only allows specification of linear models at all modeling steps. An advantage of IQ-learning over Q-learning is that for a large class of generative models, linear models are correctly specified at each modeling step (Laber et al. 2014). In general, this is not true for Q-learning at the first-stage. In our illustrations, we skip some of the typical exploratory techniques that a careful analyst would employ to find the best-fitting models. These steps would not be meaningful with the bmiData dataset since it was simulated with linear working models and would only detract from our main focus which is to present the steps of the IQ-learning algorithm using the functions in iqLearn. Analysts who use IQ-learning should employ standard data exploration techniques between each modeling step. Another consequence of using generated data is that we will not interpret any coefficients or comment on model fit. In fact, most of the R² statistics are nearly 1 and many terms appear highly significant, reflecting the fact that the data are not real. All models and decision rules estimated in this section are strictly illustrative. In addition, the results in this section are not representative of the results of the original meal replacement study.

Step IQ1: Second-stage regression

The first step in the IQ-learning algorithm is to model the response as a function of second-stage history variables and treatment. We model the second-stage Q-function as a linear function of gender, parent_BMI, month4_BMI, and A2, fitting the model using least squares.

R> fitIQ2 <- learnIQ2(y ˜ gender + parent_BMI + month4_BMI +
+    A2 * (parent_BMI + month4_BMI), data = bmiData, treatName = "A2",
+    intNames = c("parent_BMI", "month4_BMI"))

The function learnIQ2() creates an object of type ‘learnIQ2’ that contains a ‘lm’ object of the linear regression in addition to several other components. We have implemented the formula specification above. The user can specify any formula admissible to lm(), but it must include the main effect of treatment A2 and at least one treatment interaction term. The second and third arguments specify which variable codes the second-stage treatment and covariates interacting with treatment, respectively. If exploratory work suggests there are no treatment-by-covariate interactions at the second stage, IQ-learning has no advantage over Q-learning, and it would be appropriate to model the conditional expectation of Ỹ directly at the first stage. The default method for learnIQ2() requires a matrix or data frame of variables to use as main effects in the linear model. Below, we create this data frame.

R> s2vars <- bmiData[, c(1, 3, 5)]
R> head(s2vars)

  gender parent_BMI month4_BMI
1      0   31.59683   34.22717
2      1   30.17564   36.38014
3      1   30.27918   34.42168
4      1   27.49256   32.52011
5      1   26.42350   33.72922
6      0   29.30970   32.06622

The default method also requires a vector of indices that point to the columns of s2vars that should be included as treatment interactions in the model.

R> s2ints <- c(2, 3)

The default method for learnIQ2() is

R> fitIQ2 <- learnIQ2(H2 = s2vars, Y = y, A2 = bmiData$A2, s2ints = s2ints)

To print the regression output we can call summary() on the ‘learnIQ2’ object.

R> summary(fitIQ2)

Stage 2 Regression:

Call:
lm(formula = Y ˜ s2. - 1)

Residuals:
     Min       1Q   Median       3Q      Max
−20.5929  −3.7614  −0.1526   4.4436  17.4479

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)
s2.intercept     41.28845    3.98789  10.353  < 2e-16 ***
s2.gender        −0.64891    0.89924  −0.722   0.4714
s2.parent_BMI    −0.15509    0.10236  −1.515   0.1313
s2.month4_BMI    −0.82067    0.13992  −5.865  1.8e-08 ***
s2.A2            −7.38709    3.97545  −1.858   0.0646 .
s2.parent_BMI:A2  0.20223    0.10201   1.983   0.0488 *
s2.month4_BMI:A2  0.02816    0.13982   0.201   0.8406
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.437 on 203 degrees of freedom
Multiple R-squared:  0.605,        Adjusted R-squared:  0.5914
F-statistic: 44.42 on 7 and 203 DF,  p-value: < 2.2e-16

The plot() function can be used to obtain residual diagnostic plots from the linear regression, shown in Figure 4. These plots can be used to check the usual normality and constant variance assumptions. The ‘learnIQ2’ object is a list that contains the estimated main effect coefficients,

R> fitIQ2$betaHat20

 s2.intercept     s2.gender s2.parent_BMI s2.month4_BMI
   41.2884512    −0.6489144    −0.1550899    −0.8206701

and interaction coefficients,

R> fitIQ2$betaHat21

           s2.A2 s2.parent_BMI:A2 s2.month4_BMI:A2
     −7.38708909       0.20223376       0.02815973

Figure 4.

Residual diagnostic plots from the second-stage regression in IQ-learning.

The first term of $betaHat20 is the intercept and the first term of $betaHat21 is the main effect of treatment A2. Other useful elements in the list include the vector of estimated optimal second-stage treatments for each patient in the dataset ($optA2), the ‘lm’ object ($s2Fit), the vector of estimated main effect terms ($main), and the vector of estimated contrast function terms ($contrast).

Step IQ2: Main effect function regression

The next step in the IQ-learning algorithm is to model the conditional expectation of the main effect term given first-stage history variables and treatment. We accomplish this by regressing ${\{{\mathit{H}}_{20,i}^{\top }{\hat{\beta }}_{20}\}}_{i=1}^n$ on a linear function of ${\{{\mathit{H}}_{1,i},A_{1,i}\}}_{i=1}^n$ using the function learnIQ1main() which creates an object of type ‘learnIQ1main’. The learnIQ1main() function extracts the estimated vector of main effect terms from the ‘learnIQ2’ object to use as the response variable in the regression.

R> fitIQ1main <- learnIQ1main (˜ gender + race + parent_BMI + baseline_BMI +
+    A1 * (gender + parent_BMI), data = bmiData, treatName = "A1",
+    intNames = c("gender", "parent_BMI"), s2object = fitIQ2)
R> summary(fitIQ1main)

Main Effect Term Regression:

Call:
lm(formula = mainResp ˜ s1m. - 1)

Residuals:
    Min      1Q  Median      3Q     Max
−4.0200 −1.2126  0.1407  1.1547  5.2493

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)
s1m.intercept     40.29745    1.25558  32.095  < 2e-16 ***
s1m.gender        −0.62882    0.24014  −2.619   0.0095 **
s1m.race          −0.14183    0.24233  −0.585   0.5590
s1m.parent_BMI    −0.37081    0.02276 −16.292  < 2e-16 ***
s1m.baseline_BMI  −0.54769    0.03475 −15.761  < 2e-16 ***
s1m.A1             5.05355    0.72522   6.968 4.44e-11 ***
s1m.gender:A1      0.18455    0.24083   0.766   0.4444
s1m.parent_BMI:A1 −0.16380    0.02115  −7.746 4.51e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.725 on 202 degrees of freedom
Multiple R-squared:  0.9519,        Adjusted R-squared:   0.95
F-statistic: 499.6 on 8 and 202 DF,  p-value: < 2.2e-16

The user can specify any right-hand sided formula admissible by lm(), but it must include the main effect of treatment A1. If no treatment interactions are desired, intNames can be omitted or specified as NULL (the default). The default method for learnIQ1main() requires a matrix or data frame of variables to use as main effects in the linear model. Below, we create this data frame.

R> s1vars <- bmiData[, 1:4]
R> head(s1vars)

  gender race parent_BMI baseline_BMI
1      0    1   31.59683     35.84005
2      1    0   30.17564     37.30396
3      1    0   30.27918     36.83889
4      1    0   27.49256     36.70679
5      1    1   26.42350     34.84207
6      0    0   29.30970     36.68640

The default method also requires a vector of indices that point to the columns of s1vars that should be included as treatment interactions in the model. If no interactions are desired, s1mainInts can be omitted, as the default is NULL.

R> s1mainInts <- c(1, 3)

The default method for learnIQ1main() is

R> fitIQ1main <- learnIQ1main(object = fitIQ2, H1Main = s1vars,
+    A1 = bmiData$A1, s1mainInts = s1mainInts)

where the first argument is the ‘learnIQ2’ object. Again, plot() gives residual diagnostic plots from the fitted regression model, shown in Figure 5. Elements of the list returned by learnIQ1main() include the estimated main effect coefficients,

R> fitIQ1main$alphaHat0

   s1m.intercept       s1m.gender       s1m.race   s1m.parent_BMI
      40.2974492       −0.6288155     −0.1418311       −0.3708085
s1m.baseline_BMI
      −0.5476887

and estimated interaction coefficients,

R> fitIQ1main$alphaHat1

           s1m.A1     s1m.gender:A1 s1m.parent_BMI:A1
        5.0535529         0.1845549        −0.1637973

Other elements are used in future steps of the algorithm.

Figure 5.

Residual diagnostic plots from the regression model for the main effect term.

Step IQ3: Contrast function density modeling

The final modeling step in IQ-learning is to model the conditional density of the contrast function given first-stage history variables and treatment. We will accomplish this by considering the class of location-scale density models and employing standard conditional mean and variance modeling techniques. Thus, we begin by modeling the conditional mean of the contrast function using learnIQ1cm().

R> fitIQ1cm <- learnIQ1cm(˜ gender + race + parent_BMI + baseline_BMI +
+    A1 * (gender + parent_BMI + baseline_BMI), data = bmiData,
+    treatName = "A1", intNames = c("gender", "parent_BMI", "baseline_BMI"),
+    s2object = fitIQ2)
R> summary(fitIQ1cm)

Contrast Mean Regression:

Call:
lm(formula = cmResp ˜ s1cm. - 1)

Residuals:
      Min        1Q    Median        3Q       Max
−0.140304 −0.040954 −0.002024  0.038278  0.140948

Coefficients:
                       Estimate Std. Error  t value Pr(>|t|)
s1cm.intercept       −7.3287896  0.0425272 −172.332  < 2e-16 ***
s1cm.gender          −0.0044590  0.0080960   −0.551 0.582407
s1cm.race             0.0072002  0.0081239    0.886 0.376517
s1cm.parent_BMI       0.2094135  0.0007631  274.428  < 2e-16 ***
s1cm.baseline_BMI     0.0183059  0.0011694   15.654  < 2e-16 ***
s1cm.A1              −0.0520737  0.0425007   −1.225 0.221918
s1cm.gender:A1       −0.0090028  0.0080828   −1.114 0.266683
s1cm.parent_BMI:A1    0.0066622  0.0007675    8.681 1.35e-15 ***
s1cm.baseline_BMI:A1 −0.0040765  0.0011732   −3.475 0.000626 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.05765 on 201 degrees of freedom
Multiple R-squared:  0.9981,        Adjusted R-squared:  0.998
F-statistic: 1.183e+04 on 9 and 201 DF,  p-value: < 2.2e-16

The user can specify any right-hand sided formula admissible by lm(), but it must include the main effect of treatment A1. The default method for learnIQ1cm() requires a matrix or data frame of variables to use as main effects in the linear model and indices indicating the treatment interaction effects. intNames can be omitted or specified as NULL if no interactions are desired. We will use s1vars and specify the interactions with a vector for s1cmInts below.

R> s1cmInts <- c(1, 3, 4)

The default method is

R> fitIQ1cm <- learnIQ1cm(object = fitIQ2, H1CMean = s1vars,
+    A1 = bmiData$A1, s1cmInts = s1cmInts)

Figure 6 displays the residual diagnostics produced by plot(). The learnIQ1cm() function returns a list with several elements. The residuals from the contrast mean fit are stored in $cmeanResids. Estimated main effect coefficients can be accessed,

R> fitIQ1cm$betaHat10

   s1cm.intercept       s1cm.gender        s1cm.race
     −7.328789639      −0.004459014      0.007200203
  s1cm.parent_BMI s1cm.baseline_BMI
      0.209413508       0.018305862

as well as the interaction coefficients,

R> fitIQ1cm$betaHat11

             s1cm.A1       s1cm.gender:A1  s1cm.parent_BMI:A1
        −0.052073685         −0.009002806         0.006662162
s1cm.baseline_BMI:A1
        −0.004076464

Figure 6.

Residual diagnostic plots from the linear regression model for the contrast function mean.

Other items in the list are used in upcoming steps of the algorithm.

After fitting the model for the conditional mean of the contrast function, we must specify a model for the variance of the residuals. Standard approaches can be used to determine if a constant variance fit is suficient. If so,

R> fitIQ1var <- learnIQ1var(fitIQ1cm)

is the default for estimating the common standard deviation. Equivalently, the homo method can be specified to indicate homoskedastic variance,

R> fitIQ1var <- learnIQ1var(object = fitIQ1cm, method = "homo")

but this additional statement is unnecessary since it is the default. A list is returned with the estimated common standard deviation of the contrast mean fit residuals ($stdDev), the vector of standardized residuals for each patient in the dataset ($stdResids), and several other elements, some of which are NULL when the homoskedastic variance method is specified.

If the variance is thought to be non-constant across histories and/or treatment, the "hetero" method allows specification of a log-linear model for the squared residuals. As before, the formula should be only right-hand sided and must include the main effect of treatment A1. The default for s1varInts is NULL, which should be used if no interactions are desired in the model. The formula and default specifications are displayed below.

R> fitIQ1var <- learnIQ1var(˜ gender + race + parent_BMI +
+    baseline_BMI + A1 * (parent_BMI), data = bmiData, treatName = "A1",
+    intNames = "parent_BMI", method = "hetero", cmObject = fitIQ1cm)
R> s1varInts <- c(3, 4)
R> fitIQ1var <- learnIQ1var(object = fitIQ1cm, H1CVar = s1vars,
+    s1sInts = s1varInts, method = "hetero")
R> summary (fitIQ1var)

Variance Model:

Call:
lm(formula = lRes2 ˜ s1v. - 1)

Residuals:
    Min      1Q  Median      3Q     Max
−8.5694 −0.8962  0.4247  1.4247  2.9195

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)
s1v.intercept       −8.241606   1.484122  −5.553 8.77e-08 ***
s1v.gender           0.077415   0.285104   0.272   0.7863
s1v.race             0.075925   0.286549   0.265   0.7913
s1v.parent_BMI      −0.002661   0.026917  −0.099   0.9213
s1v.baseline_BMI     0.036738   0.040900   0.898   0.3701
s1v.A1               1.921779   1.478243   1.300   0.1951
s1v.parent_BMI:A1   −0.053469   0.027035  −1.978   0.0493 *
s1v.baseline_BMI:A1 −0.002528   0.041195  −0.061   0.9511
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.033 on 202 degrees of freedom
Multiple R-squared:  0.9222,        Adjusted R-squared:  0.9191
F-statistic: 299.4 on 8 and 202 DF,  p-value: < 2.2e-16

Figure 7 displays the residual diagnostics produced by plot(). The ‘learnIQ1var’ object is a list that includes the estimated main effect coefficients,

R> fitIQ1var$gammaHat0

   s1v.intercept       s1v.gender         s1v.race   s1v.parent_BMI
    −7.138610546      0.077414538      0.075925188     −0.002661492
s1v.baseline_BMI
     0.036738083

and interaction coefficients,

R> fitIQ1var$gammaHat1

             s1v.A1   s1v.parent_BMI:A1 s1v.baseline_BMI:A1
        1.921779012        −0.053468524        −0.002528188

when the "hetero" option is specified. The vector of standardized residuals can be found in $stdResids. Other elements in the list are used in the next IQ-learning step.

Figure 7.

Residual diagnostic plots from the log-linear variance model.

The final step in the conditional density modeling process is to choose between the normal and empirical density estimators. Based on empirical experiments (see Laber et al. 2014), we recommend choosing the empirical estimator by default, as not much is lost when the true density is normal. However, iqResids() can be used to inform the choice of density estimator. The object of type ‘iqResids’ can be plotted to obtain a normal QQ-plot of the standardized residuals, displayed in Figure 8.

R> fitResids <- iqResids(fitIQ1var)

Figure 8.

Normal QQ-plot of the standardized residuals obtained from the contrast mean and variance modeling steps.

Step IQ4: Combine first-stage estimators

The function learnIQ1() has four inputs: the previous three first-stage objects and the method to use for the density estimator, either "norm" or "nonpar", which may be chosen based on the normal QQ-plot of the standardized residuals described previously. learnIQ1() combines all the first-stage modeling steps to estimate the first-stage optimal decision rule.

R> fitIQ1 <- learnIQ1(mainObj = fitIQ1main, cmObj = fitIQ1cm,
+    sigObj = fitIQ1var, dens = "nonpar")

A vector of estimated optimal first-stage treatments for patients in the study is returned ($optA1).

Recommend treatment with IQ1() and IQ2()

After estimating the optimal regime using the IQ-learning algorithm, the functions IQ1() and IQ2() can be used to recommend treatment for future patients. To determine the recommended first-stage treatment for a patient with observed history h₁, we must form vectors h1main, h1cm, and h1var that match the order of main effects in each of the corresponding first-stage modeling steps. We suggest checking summary() for each of the first-stage modeling objects to ensure the new patient’s history vectors have the correct variable ordering. If the "homo" method was used to fit a constant variance, h1var can be left unspecified or set to NULL. In our examples, the main effects used in each of the three first-stage modeling steps all happened to be the same variables in the same order. Thus, in this example h1main, h1cm, and h1var are equivalent.

R> h1 <- c(1, 1, 30, 35)
R> h1main <- h1
R> h1cm <- h1
R> h1var <- h1
R> optIQ1 <- IQ1(mainObj = fitIQ1main, cmObj = fitIQ1cm, sigObj = fitIQ1var,
+    dens = "nonpar", h1main = h1main, h1cm = h1cm, h1sig = h1var)
R> optIQ1

$q1Pos
[1] 9.964656

$q1Neg
[1] 9.308351

$q1opt
[1] 1

As displayed above, a list is returned by IQ1() that includes the value of the first-stage Q-function when A₁ = 1 ($q1Pos) and A₁ = −1 ($q1Neg) as well as the recommended first-stage treatment for that patient, $q1opt.

For a patient with second-stage history h₂, we only need to check the order of the main effects in the second-stage regression and form a corresponding vector based on the new patient’s observed history.

R> h2 <- c(1, 30, 45)
R> optIQ2 <- IQ2(fitIQ2, h2)
R> optIQ2

$q2Pos
[1] −0.9962029

$q2Neg
[1] −0.8904261

$q2opt
[1] −1

Similar to IQ1, a list is returned that contains the value of the second-stage Q-function when A₂ = 1 ($q2Pos) and A₂ = −1 ($q2Neg) as well as the recommended second-stage treatment, $q2opt.

3.3. Q-learning functions

For convenience, when a comparison of IQ- and Q-learning is desired, functions are available in iqLearn to estimate and recommend optimal treatment strategies using Q-learning. Function qLearnS2() implements the second-stage regression in the same manner as learnIQ2(), with the minor exception that a treatment-by-covariate interaction is not required but rather only the main effect of treatment A2. Examples of the default and formula implementations are given below.

R> fitQ2 <- qLearnS2(H2 = s2vars, Y = y, A2 = bmiData$A2, s2ints = s2ints)
R> fitQ2 <- qLearnS2(y ˜ gender + parent_BMI + month4_BMI +
+    A2 * (parent_BMI + month4_BMI), data = bmiData, treatName = "A2",
+    intNames = c("parent_BMI", "month4_BMI"))

Methods summary() and plot() can be used in the same way as demonstrated with the IQ-learning functions; see the discussion of learnIQ2() in Section 3.2 for more details and examples.

The function that estimates the first-stage Q-function is qLearnS1(). It can be implemented with either a right-hand sided formula specification or the default method. Both options are demonstrated below.

R> fitQ1 <- qLearnS1(object = fitQ2, H1q = s1vars, A1 = bmiData$A1,
+    s1ints = c(3, 4))
R> fitQ1 <- qLearnS1(˜ gender + race + parent_BMI + baseline_BMI +
+    A1 * (gender + parent_BMI), data = bmiData, treatName = "A1",
+    intNames = c("gender", "parent_BMI"), qS2object = fitQ2)

It is necessary to include the main effect of treatment A1, but s1ints (intNames in the formula version) can be omitted or specified as NULL if no interactions are desired in the model. Both ‘qLearnS2’ and ‘qLearnS1’ objects are lists that include the estimated parameter vectors for the main effects and treatment interactions.

R> fitQ2$betaHat20

 s2.intercept     s2.gender s2.parent_BMI s2.month4_BMI
   41.2884512    −0.6489144    −0.1550899    −0.8206701

R> fitQ2$betaHat21

           s2.A2 s2.parent_BMI:A2 s2.month4_BMI:A2
     −7.38708909       0.20223376       0.02815973

R> fitQ1$betaHat10

   s1.intercept       s1.gender         s1.race   s1.parent_BMI
    38.83160227     −0.70842181      0.01415719     −0.26714110
s1.baseline_BMI
    −0.57425620

R> fitQ1$betaHat11

           s1.A1     s1.gender:A1 s1.parent_BMI:A1
       4.5484118        0.3189128       −0.1501112

In addition, Ỹ can be accessed from ‘qLearnS2’ with $Ytilde, and the ‘lm’ objects at each stage are also included ($s2Fit and $s1Fit). Finally, the ‘qLearnS1’ object contains a vector of estimated optimal first-stage treatments for patients in the dataset ($optA1), and the ‘qLearnS2’ object contains the corresponding second-stage vector ($optA2).

To recommend the Q-learning estimated optimal treatments for a new patient based on observed histories, functions qLearnQ1() and qLearnQ2() are available and are similar to IQ1() and IQ2(). They require the observed history vectors for the new patient to have the same variables in the same order as the main effects in the regressions used to build the Q-learning regime. Checking the summary() of the Q-learning objects is recommended to ensure the histories are set up properly. Examples are given below.

R> summary(fitQ1)

Stage 1 Regression:

Call:
lm(formula = Ytilde ˜ s1. - 1)

Residuals:
    Min      1Q  Median      3Q     Max
−4.3604 −1.3291  0.0098  1.3419  4.8536

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)
s1.intercept     38.83160    1.34129  28.951  < 2e-16 ***
s1.gender        −0.70842    0.25653  −2.762  0.00628 **
s1.race           0.01416    0.25887   0.055  0.95644
s1.parent_BMI    −0.26714    0.02431 −10.987  < 2e-16 ***
s1.baseline_BMI  −0.57426    0.03712 −15.470  < 2e-16 ***
s1.A1             4.54841    0.77473   5.871 1.76e-08 ***
s1.gender:A1      0.31891    0.25727   1.240  0.21657
s1.parent_BMI:A1 −0.15011    0.02259  −6.645 2.76e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.843 on 202 degrees of freedom
Multiple R-squared:  0.9547,        Adjusted R-squared:  0.9529
F-statistic:   532 on 8 and 202 DF,  p-value: < 2.2e-16

R> h1q <- c(1, 1, 30, 35)
R> optQ1 <- qLearnQ1(fitQ1, h1q)
R> optQ1

$q1Pos
[1] 10.38813

$q1Neg
[1] 9.660148

$q1opt
[1] 1

R> summary (fitQ2)

Stage 2 Regression:

Call:
lm(formula = Y ˜ s2. - 1)

Residuals:
     Min       1Q   Median       3Q      Max
−20.5929  −3.7614  −0.1526   4.4436  17.4479

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)
s2.intercept     41.28845    3.98789  10.353  < 2e-16 ***
s2.gender        −0.64891    0.89924  −0.722   0.4714
s2.parent_BMI    −0.15509    0.10236  −1.515   0.1313
s2.month4_BMI    −0.82067    0.13992  −5.865  1.8e-08 ***
s2.A2            −7.38709    3.97545  −1.858   0.0646 .
s2.parent_BMI:A2  0.20223    0.10201   1.983   0.0488 *
s2.month4_BMI:A2  0.02816    0.13982   0.201   0.8406
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.437 on 203 degrees of freedom
Multiple R-squared:  0.605,        Adjusted R-squared:  0.5914
F-statistic: 44.42 on 7 and 203 DF,  p-value: < 2.2e-16

R> h2q <- c(1, 30, 45)
R> optQ2 <- qLearnQ2 (fitQ2, h2q)
R> optQ2

$q2Pos
[1] −0.9962029

$q2Neg
[1] −0.8904261

$q2opt
[1] −1

Elements in the returned lists are the same as those returned by IQ1() and IQ2().

3.4. Estimating regime value

We may wish to compare our estimated optimal regime to a standard of care or constant regime that recommends one treatment for all patients. One way to compare regimes is to estimate the value function. A plug-in estimator for V^π in the randomized treatment setting is

$${\hat{V}}^{\mathit{\pi }}\triangleq \frac{{\sum }_{i=1}^n{Y}_i𝟙\{A_{1,i}={\pi }_1({\mathit{h}}_{1,i})\}𝟙\{A_{2,i}={\pi }_2({\mathit{h}}_{2,i})\}}{{\sum }_{i=1}^n𝟙\{A_{1,i}={\pi }_1({\mathit{h}}_{1,i})\}𝟙\{A_{2,i}={\pi }_2({\mathit{h}}_{2,i})\}},$$

where Y_i is the ith patient’s response, (A_1i, A_2i) the randomized treatments and (h_1i, h_2i) the observed histories. This estimator is a weighted average of the outcomes observed from patients in the trial who received treatment in accordance with the regime π. It is more commonly known as the Horvitz-Thompson estimator (Horvitz and Thompson 1952). The function value() estimates the value of a regime using this plug-in estimator and also returns value estimates corresponding to four non-dynamic regimes under randomization: $valPosPos (π₁ = 1, π₂ = 1); $valPosNeg (π₁ = 1, π₂ = −1); $valNegPos (π₁ = −1, π₂ = 1); and $valNegNeg (π₁ = −1, π₂ = −1). The function value() takes as input d1, a vector of first-stage treatments assigned by the regime of interest; d2, a vector of second-stage treatments assigned by the regime of interest; Y, the response vector; A1, the vector of first-stage randomized treatments received by patients in the trial; and A2, the vector of second-stage randomized treatments.

R> estVal <- value(d1 = fitIQ1$optA1, d2 = fitIQ2$optA2, Y = y,
+    A1 = bmiData$A1, A2 = bmiData$A2)
R> estVal

$value
[1] 6.650607

$valPosPos
[1] 6.201568

$valPosNeg
[1] 3.523643

$valNegPos
[1] 8.063114

$valNegNeg
[1] 7.917462

attr(,"class")
[1] "value"

4. Conclusion

We have demonstrated how to estimate an optimal two-stage DTR using the IQ-learning or Q-learning functions and tools in the R package iqLearn. As indicated by its name, interactive Q-learning allows the analyst to interact with the data at each step of the IQ-learning process to build models that fit the data well and are interpretable. At each model building step, the IQ-learning functions in iqLearn encourage the use of standard statistical methods for exploratory analysis, model selection, and model diagnostics.

Future versions of iqLearn will implement more general model options; in particular, the functions will be generalized to handle data with more than two treatments at each stage.