Bacterial predator–prey dynamics in microscale patchy landscapes

Abstract

Soil is a microenvironment with a fragmented (patchy) spatial structure in which many bacterial species interact. Here, we explore the interaction between the predatory bacterium Bdellovibrio bacteriovorus and its prey Escherichia coli in microfabricated landscapes. We ask how fragmentation influences the prey dynamics at the microscale and compare two landscape geometries: a patchy landscape and a continuous landscape. By following the dynamics of prey populations with high spatial and temporal resolution for many generations, we found that the variation in predation rates was twice as large in the patchy landscape and the dynamics was correlated over shorter length scales. We also found that while the prey population in the continuous landscape was almost entirely driven to extinction, a significant part of the prey population in the fragmented landscape persisted over time. We observed significant surface-associated growth, especially in the fragmented landscape and we surmise that this sub-population is more resistant to predation. Our results thus show that microscale fragmentation can significantly influence bacterial interactions.

1. Introduction

Bacterial habitats, such as soil, our gastrointestinal tract, and even the ocean are spatially structured at the microscale [1,2]. Soil typically contains particles with sizes that vary between 2 µm or less for clay and 1 mm for sand [3,4] (figure 1a). It is within the confines of the interconnected cavities in between soil particles that microorganisms, such as bacteria, interact. Most of our knowledge of population dynamics in such highly structured landscapes comes from a large body of theoretical [5–7] and experimental studies [8–11] concerning macroscopic organisms in macroscopic landscapes. Due to technical challenges, however, experimental study and even a clear theoretical framework of the population dynamics of microorganisms in spatially structured microhabitats such as soil is lacking, especially for interacting bacterial populations such as predator–prey communities.

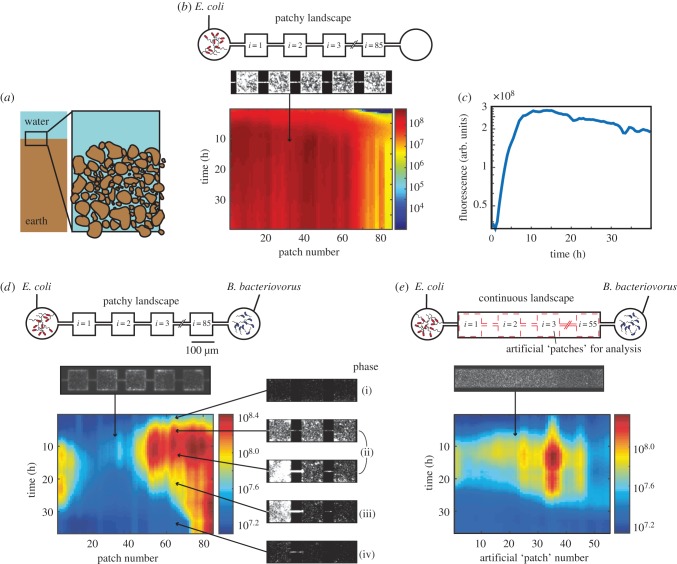
Figure 1.

On-chip predator–prey system. (a) Soil consists of a three-dimensional network of micrometre-sized patches. (b) A control experiment, in which only prey is introduced to a patchy landscape, consisting of coupled patches (top). A heatmap of a kymograph (depicting space horizontally and time vertically, the colour bar indicates logarithmically scaled fluorescent intensity in arbitrary units) showing the population dynamics of fluorescently labelled E. coli. (c) The mean prey growth dynamics over all patches shows the familiar phases of bacterial growth: exponential phase and entry into stationary phase (at t = 10 h). (d,e) Predator–prey dynamics in the presence of predator in a patchy landscape (d) and a ‘continuous’ landscape (e). Software-generated ‘virtual’ patches that are used in data analysis of the continuous habitat are indicated by red dashed lines. In both habitats there initially is a steep rise in fluorescence which corresponds to the growth of E. coli, followed by a death phase in which E. coli lyse after predation. Each pixel represents a single habitat patch. Microscopy images show representative snapshots of the population dynamics in phases (i)–(iv), arrows indicate the approximate space and time of image acquisition.

One may hypothesize that for bacteria, a landscape with constrictions with a size of only a few micrometres can be considered fragmented. This hypothesis predicts that the population dynamics differ significantly between individual patches and that the dynamics of interacting bacteria at the local (patch) level become decorrelated quickly with increasing distance [12]. Habitat fragmentation may also influence the lifetime of the population as a whole [5,8,12,13]. However, bacteria differ in important ways from ‘large’ animals: bacteria grow to higher densities, possibly reducing stochastic fluctuations that may lead to local extinction. Bacteria are also highly mobile, in terms of their swimming speed [14] as well as in terms of their ability to pass through small constrictions [15]. Furthermore, while diffusion of signalling molecules, food, and waste is very efficient at microscopic scales, diffusion at larger scales is negligible. Finally, bacteria can adopt very different lifestyles, living clustered together in biofilms with greatly reduced mobility, or as motile planktonic individuals [16]. For these reasons, it is unclear whether bacterial habitats that are spatially structured at the microscale can be considered ‘fragmented’ or not. Because macroscopic fragmentation has been shown to affect key parameters such as the global lifetime of a population [8–11], we believe there is reason to assume that microscopic fragmentation could be of importance for understanding bacterial life in natural structured habitats such as soil. However, the question of how fragmentation affects predator–prey dynamics at the microscale has remained unanswered.

Over the past few years, microfabrication techniques have allowed for the creation of microscale synthetic ecosystems that are structured at the spatial scales relevant to bacterial populations [17–21]. It thus has become technically feasible to quantify bacterial predator–prey interactions in each of the individual micrometre-scale patches of a landscape under controlled conditions over many generations. Taking advantage of these recent advances, we fabricated a microscale fragmented habitat and a non-fragmented habitat and contrasted bacterial predator–prey dynamics in these two habitat types. We studied the bacterial predator Bdellovibrio bacteriovorus preying upon Escherichia coli. Bdellovibrio bacteriovorus is a small (0.4 × 1 µm) and highly motile (it can swim over 160 µm s⁻¹, or 160 body lengths per second [22]) predator of Gram-negative bacteria, that occurs, for example, in soil, in the human gut and in water [23]. To complete its life cycle, B. bacteriovorus inserts itself into the periplasmic space of its prey and converts it into a round-shaped ‘bdelloplast’ [24]. Bdellovibrio bacteriovorus subsequently extracts and ingests solutes from its prey and increases in length, after which it divides and four to six progeny are produced per E. coli prey. Approximately 3–4 h after invasion, B. bacteriovorus lyses its host and swims away to hunt for the next prey [23]. While B. bacteriovorus are ferocious predators, a small fraction of prey may survive predation due to plastic phenotypic resistance, preventing the total eradication of the prey population [25].

Studying the B. bacteriovorus–E. coli interaction in both fragmented and continuous landscapes allows us to test the hypothesis that a bacterial habitat featuring microscale constrictions is fragmented and as such influences the predator–prey interaction. Specifically, we address the question to what extent a spatially structured microhabitat gives rise to variations in predation rates, and at what scale predator–prey dynamics are spatially correlated in a microstructured landscape such as soil. Can B. bacteriovorus predate effectively in spatially structured landscapes? Does fragmentation increase the persistence of the prey population? Furthermore, given that B. bacteriovorus has shown potential to protect crops and reduce biofouling [26–29], it would be useful to know how its effectiveness in structured habitats relates to its effectiveness as measured in well-mixed (unstructured) culture flasks [30–32]. In this regard, B. bacteriovorus has also attracted significant interest because of its potential to eradicate bacterial biofilms which are spatially structured at the microscale [33,34].

2. Material and methods

(a). Strains and growth conditions

(i). Growth of Escherichia coli

We used strain JEK 1036 previously described in [18], which is wild-type E. coli W3110 labelled with a green fluorescent protein (lacZY::GFPmut2). JEK 1036 was grown overnight (O/N) from glycerol in Luria-Bertani (LB) broth at 30°C whilst shaken at 200 r.p.m., diluted 1 000-fold the next morning in Diluted Nutrient Broth (DNB, 0.8 g l⁻¹ NB, 2 mM CaCl₂ · 2H₂O, 3 mM MgCl₆ · 2H₂O, pH 7.6) and grown to OD₆₀₀ ∼ 1. Fluorescence expression was induced by adding 100 µM of isopropyl β-d-1-thiogalactopyranoside (IPTG, Promega) to the medium.

(ii). Growth of Bdellovibrio bacteriovorus and microhabitat inoculation

Escherichia coli JEK 1036 [18] was cultivated to maximum turbidity (OD₆₀₀ ∼ 4) in LB broth, then concentrated to OD₆₀₀ = 10 by centrifugation and subsequently resuspended in HEPES buffer (25 mM HEPES, 2 mM CaCl₂ · 2H₂O, 3 mM MgCl₆ · 2H₂O, pH 7.8). Bdellovibrio bacteriovorus HD100, with a chromosomal fusion of the HuaA histone-like protein gene [24] to monomeric Teal protein (mTeal), was added to this medium from glycerol stock and was incubated O/N in a volume of 2 ml while shaking at 280 r.p.m. at 28°C, until a transparent liquid was obtained. The culture's transparency indicates that all E. coli, except for a fraction that is phenotypically resistant, have been lysed. The culture was then spun down at 3 000 r.p.m. for 10 min and resuspended in 2 ml fresh DNB, at 28°C. The microhabitat was simultaneously inoculated with approximately 3 µl of resuspended B. bacteriovorus culture and approximately 3 µl of pure E. coli culture in DNB medium in a 1 : 1 ratio (measured by optical density) from opposite sides.

(b). Experimental set-up

(i). Microfabrication of microhabitats

To emulate the patchy geometry of natural bacterial habitats with relevant spatial dimensions (figure 1a), and to allow for the quantitative study of predator–prey interactions as a function of space and time, we created a well-defined linear array of habitat patches on a silicon chip, that are connected to each other by narrow corridors (figure 1b,d, top) [18,35]. As a control for the patchiness of the patchy geometry, we also designed a continuous landscape of identical volume that consisted of one large habitat without internal constrictions (figure 1e). Microhabitats were fabricated in silicon using a two-step procedure of photolithography and reactive ion etching following a previously published protocol [18,35]. The patchy microhabitats consisted of 85 patches (each 100 µm in length, 100 µm in width, and 15 µm in depth) connected by corridors (50 × 5 × 15 µm), the continuous microhabitats consisted of a single patch (8 500 × 100 × 15 µm) with a total volume identical to the volume of the patchy habitat. The 180 nm deep slits are too shallow for the passage of bacteria and thus preclude them from leaving the microhabitats and entering the reservoirs. On the other hand, the slits do allow for the diffusion of, for example, nutrients and waste [18,35]. At the start of an experiment, the reservoirs (having a volume approx. 15 times the habitat) were filled with fresh DNB medium (supplemented with 100 µM IPTG) to ensure that plenty of nutrients were available to the E. coli for the entire duration of the experiment. Two ports to inoculate bacteria were drilled through the silicon, one at each end of the habitat, furthermore, ports were drilled to allow for the filling of the reservoirs. After short exposure to O₂-plasma to facilitate proper bonding, a silicon microhabitat was bonded to a polydimethylsiloxane (PDMS) coated coverslip. The microhabitats and reservoirs were then filled with fresh DNB medium (supplemented with 100 µM IPTG). Subsequently, cultures of B. bacteriovorus and E. coli were inoculated from opposite ends as described above. The medium in the device was not replenished during the experiment. After the habitat and reservoirs had been filled and the habitat had been inoculated with bacteria, the inlet holes were sealed with quick-drying PDMS. Data were acquired for periods up to 3 days, the exact duration of each experiment is shown on the time axis of the relevant figures. All experiments were performed in triplicate.

(ii). Microhabitat imaging

To capture the dynamics of the prey population in the presence (and absence) of the predator, microhabitats were imaged every 20 min using an Olympus IX81 inverted microscope controlled with MicroManager v. 1.4.14 software [36], equipped with a 20× 0.75 numerical aperture (NA) objective, an Andor Neo sCMOS camera and a motorized stage (Marzhauser). The sample was illuminated using an X-cite 120 Q (Lumen dynamics) light source. We used the total fluorescence intensity in the GFP channel as a proxy for prey density which was previously shown to be a valid approach [35,37]. Due to the limited brightness of B. bacteriovorus, predator cells were not continuously monitored. The fluorescent mTeal fusion, however, allowed us to periodically verify the presence of B. bacteriovorus using a 100× objective. The set-up was enclosed in an incubator set to 28°C.

(iii). Image processing and data analysis

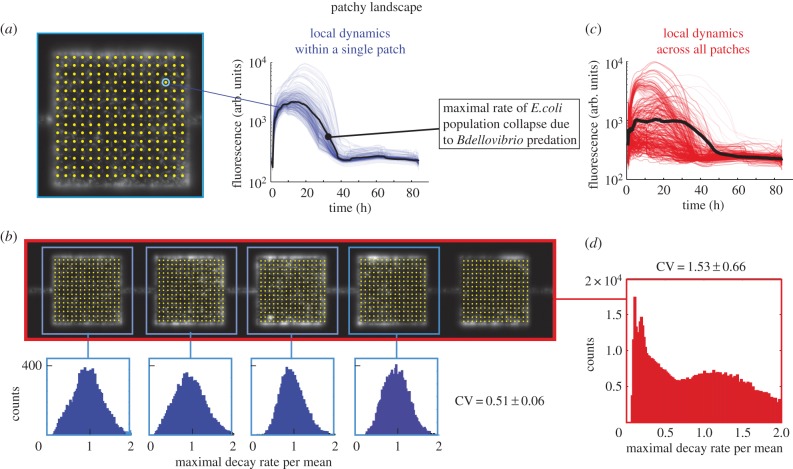
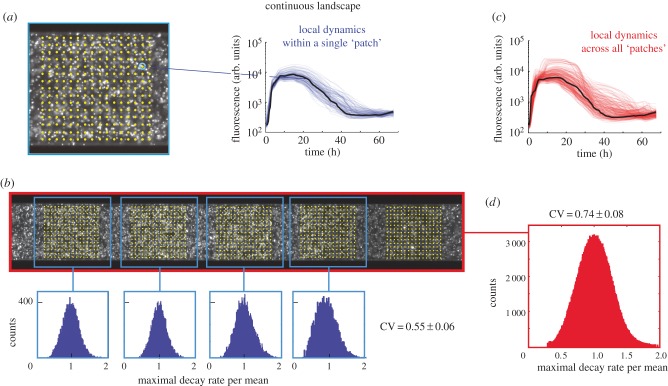
Images were processed in Matlab using a custom script. Briefly, each patch was subdivided in 98 × 98 regions (we left out a margin from the edges of the patches to remain unbiased by the limited precision of the microscope stage movement) from which fluorescence time traces were obtained by binning into bins of 3 × 3 pixels. By dividing the patches into subregions, we are able to quantify the variation of predation rates within individual patches (see Results), while the binning reduces noise in the fluorescence signal. To render the analysis of the continuous landscape as comparable as possible to the patchy landscape, artificial ‘virtual patches’ of identical size and inter-patch spacing were computationally generated in the continuous landscape during analysis (figure 1b). In designing the habitat geometries, we chose to keep the total habitat volume of the patchy and continuous landscapes identical, and therefore, given the different geometries of the two landscapes, the continuous landscape consisted of 55 ‘virtual patches’ versus 85 patches for the patchy landscape. Next, we performed a background correction for each time trace and smoothed the time traces using a five-point window. Subsequently, the maximal predation rates were calculated for each time trace by calculating the maximal negative slope (maximal predation rate) beyond the maximum value of a time trace (figures 2a and 3a). Using this algorithm, each of the patches yields 10⁴ values for the maximal predation rates. We exclude time traces originating from empty regions within the patch (typically a few per cent of the traces, defined by a maximum that is 10% or less than the most frequent maximal value of all time traces in the patch). The values for the maximal predation rates were then plotted in histograms such as the blue histograms in figures 2b and 3b. To usefully compare the variance of this distribution between patches, also in cases where the mean values differ, we divided the maximal predation rate by its mean. We thus describe the variation as the coefficient of variation (CV), defined as the standard deviation of the distribution divided by the mean of the distribution. The within-patch CV thus obtained for each patch was averaged over all patches yielding two values: one for all of the patches in the patchy geometry (CV_l,p), and one for all of the ‘virtual patches’ in the continuous geometry (CV_l,c). To compare the local CV of the patches with the CV of the landscape as a whole, we generated two more numbers: one that described the global CV for the entire landscape for a patchy geometry (CV_g,p) and one that described the global CV of the entire landscape for the continuous geometry (CV_g,c). The degree to which the global CV for the entire landscape and that of the individual patches (local CV) differ is expressed in terms of their ratio R according to R = Global CV/Local CV for each repeat experiment where a ratio equal to one means that the variation at the local scale is equal to the variation at the global scale. This analysis yielded six ratios: three repeat measurements for the patchy landscape R_p and three repeat measurements for the continuous landscape R_c. To test whether R_p and R_c differed significantly, we used a Wilcoxon rank-sum test.

Figure 2.

Predation rates in a patchy landscape. (a) Yellow dots indicate 98×98 points (for clarity, only 16×16 are shown) that were used to generate time traces (thin blue lines show single time traces for one patch, the fat black line represents the mean) from patches of the fragmented landscape. The maximum predation rate is extracted from individual traces. (b) Distribution of the maximal rate of decay of four patches. (c) All time traces of all patches within a patchy habitat (thin red lines show single time traces for one patch, the fat black line represents the mean). (d) The distributions of the maximum decay rates calculated for all points in all patches within the patchy landscape.

Figure 3.

Predation rates in the continuous landscape. (a) Yellow dots indicate 98 × 98 points (for clarity, only 16 × 16 are shown) that were used to generate time traces (thin blue lines show single time traces for one virtual patch, the fat black line represents the mean) from patches of the continuous landscape. The maximum predation rate is extracted from individual traces. (b) Distribution of the maximal rate of decay of four virtual patches. (c) All time traces of all virtual patches within a continuous habitat (thin red lines show single time traces for one patch, the fat black line represents the mean). (d) The distributions of the maximum decay rates calculated for all points in all virtual ‘patches’ within the continuous landscape.

(iv). Spatial correlation

To calculate the spatial correlation between patches, time traces were used as shown in figure 1, where a single fluorescence time trace represents the dynamics in a single patch. Spatial correlations were calculated as a function of increasing inter-patch distance using the corrcoef function in Matlab.

(v). Survival analysis

For the survival analysis, we used the fluorescence signal originating from all 98 × 98 subregions in the patches. As is described in the ‘Results’ section, the typical fluorescence signal rises first (due to bacterial growth) and subsequently reaches a maximum, after which it declines (due to predation). First, the time-point associated with the maximum value in the fluorescence is determined. Second, the time-point at which the fluorescence crosses the cut-off fluorescence value associated with a region that does not contain any bacteria is determined. This time-point is recorded and designated as the ‘time-of-death’ for that particular region in space. This procedure is repeated for all time traces, and Kaplan–Meier survival curves are generated using the log-rank function of Matlab. As the patchy- and continuous-habitat experiments were performed in triplicate, we obtained three sets of survival curves (electronic supplementary material, figure), each quantifying the surviving population fractions in the patchy and continuous landscapes over time. The log-rank algorithm determines this fraction, as well as whether the two survival curves for the patchy and continuous landscapes are statistically different, including the associated p-value. Additionally, the algorithm determines the residual values, i.e. the population fraction that persists.

The survival analysis as described above was also performed separately for the periphery (the outer rim of the habitat patch, measuring 15 µm or less to the closest sidewall) and centre (the remaining 70 × 70 × 10 µm³ central volume element) of the habitat patches. The centre of the habitat patches has a low surface to volume ratio (0.20 µm⁻¹) as only a top and bottom surface are present, whereas the periphery is enclosed by the sidewalls increasing the surface to volume ratio (0.28 µm⁻¹ and 0.27 µm⁻¹ for the patchy and continuous habitats, respectively).

(vi). Real-time movies

Real-time and time-lapse movies provide additional insights beyond those extracted from total fluorescence intensity time traces. For example, movies help to identify different modes of prey growth such as surface-associated growth, which manifests itself as an increase in fluorescence at the edges of an observed microcolony in combination with limited (or even the absence of) motility. Furthermore, the process and timing of predation can be followed. While we are unable to observe the exact time of entry of the predator, we clearly observed the formation of bdelloplasts when rod-shaped prey were converted into round-shaped bdelloplasts, followed by their sudden disappearance due to lysis (electronic supplementary material, movies S1, S4, and S5).

3. Results

Prior to studying the dynamics between predator and prey, we performed a control experiment in which the landscape was only inoculated with prey (figure 1b,c). This experiment shows that E. coli quickly populates the entire landscape, though some spatial variation is present (figure 1b). The mean fluorescence intensity of all patches over time (figure 1c) shows that the prey initially grows exponentially, until it reaches stationary phase approximately 10 h after inoculation. In the following 30 h, the population did not collapse, as evidenced by an approximately constant mean fluorescent intensity. We conclude that in the absence of predator, and in good agreement with previous studies of E. coli in microfabricated landscapes [18,38], the bacterial prey population inoculated in the microfabricated landscape exhibited all the familiar phases of growth and did not show population collapse even after 2 days.

A different picture emerges when predator and prey are both inoculated from opposite sides. Figure 1 shows prey dynamics as a function of space and time in the presence of the predator, for the patchy landscape (figure 1d) and for the continuous landscape (figure 1e). An experiment is typically characterized by four phases in the predator–prey dynamics (labelled (i) through (iv) in figure 1d). Initially, (phase (i)), growth of the prey population is dominant over predation and consequently the population density increases. During phase (i), the majority of E. coli bacteria are planktonic, motile, and migrate between patches rapidly, whereas in phase (ii), the majority of E. coli become sessile and show an increase in surface-associated growth [16]. Without predator (figure 1b,c), one observes phases (i) and (ii) only (see [38] for a detailed analysis of the colonization process). When prey and predator are both (simultaneously) inoculated, predation starts to dominate in phases (ii) and (iii) and the population density of E. coli starts to decline approximately 10–20 h after inoculation. In the final phase (iv), the prey density reaches a steady-state, where most of the prey population is eradicated, except for a small number of prey that is presumably characterized by plastic phenotypic resistance to predation [25]. We note that while the specific spatial pattern, e.g. the presence of two separated predation foci in the patchy landscape in figure 1d, varies from experiment to experiment (see electronic supplementary material, figure), all six independent experiments showed the four phases described above. Electronic supplemental material, movie S1, shows the predation process in more detail, including the formation of round bdelloplasts and their sudden disappearance as they get lysed by B. bacteriovorus. We conclude that B. bacteriovorus do indeed predate E. coli populations in the structured landscapes and that the prey population is decimated.

We then asked how habitat topology influences the variation of prey dynamics at local versus global spatial scales. To address this, we first quantified how much the maximal predation rate of the prey population varied within patches in the patchy landscape (local scale), where the conditions are presumably uniform, and compared this quantity to the spread of the maximal decay rate across patches (global scale). To compare spreads with slightly different means, we used the CV as a measure of the spread (see the ‘Image processing and data analysis’ section for details). We calculated four values of the CV: (1) CV_l,p (local, patchy; variation within patches in the patchy landscape), (2) CV_g,p (global, patchy; variation in the entire patchy landscape), (3) CV_l,c (local, continuous; variation within the virtual ‘patches’ in the continuous landscape), and (4) CV_g,c (global, continuous; variation in the entire continuous landscape). The values obtained, as well as a schematic of the regions for which the CVs were calculated, are summarized in table 1.

Table 1.

Local and global coefficients of variation in the patchy and continuous landscape. Values are the mean±standard error of the mean (s.e.m.) of three independent experiments.

First, we observed that in the patchy landscape the variation within a patch (local scale) was smaller than the variation between patches (CV_l,p < CV_g,p). A statistical comparison of CV_l,p and CV_g,p is provided below. This observation is consistent with the notion that conditions that affect predator–prey dynamics, for example fluctuations in predator and prey densities, vary across patches in a patchy landscape. The source of the increased variation across the landscape is not obvious as both the limited migration due to the patchiness of the landscape and the increasing physical distance between ever more distant regions could contribute to this result. To uncouple the influences of the patchy structure and physical distance, we compared the patchy landscape to the continuous landscape that does not contain structural patchiness. We found that the local CV of the decay rates within the ‘virtual patches’ in the continuous landscape, CV_l,c, is 0.55 ± 0.06, were very similar to the local CV in the patchy landscape (CV_l,p ≈ CV_l,c). This similarity is expected since both distributions represent local dynamics within an identical area (and volume) in the landscapes. The maximal decay rates of all time traces across the entire continuous landscape (red traces in figure 3c) have a relatively narrow distribution (figure 3d) and has a global CV_g,c of 0.74 ± 0.08. This number is larger than the average local CV_l,c of the ‘virtual patches’ in the continuous landscape, indicating that conditions in the entire continuous landscape are somewhat more diverse than in a small fraction of the entire landscape. However, it is important to note that the global CV_g,c of the continuous landscape is considerably smaller than the global CV_g,p of the patchy landscape (CV_g,p = 1.53 ± 0.66).

To properly address the question whether the patchiness of the patchy landscape increases variation, we calculated the ratios R_p = CV_g,p/CV_l,p for the patchy landscape and R_c = CV_g,c/CV_l,c for the continuous landscape. This assessment shows that R_p is indeed larger than R_c (R_p = 2.8 ± 0.9, R_c = 1.3 ± 0.02 mean ± s.e.m. of n = 3 experiments, R_p > R_c p = 0.05, using a single-sided Wilcoxon rank-sum test). We may thus conclude that our findings support the hypothesis that patchiness increases the variation in population decay rates of the prey by approximately a factor of two.

While the measurements described above show that patchiness influences the predator–prey interaction at the global level, these measurements do not provide insight into the extent to which the prey dynamics is correlated in space. Spatial correlation gives insights into the connectivity between patches and the ease with which bacteria can move between patches. To quantify this, we analysed the correlation between the time traces of patches as a function of patch distance. Figure 4a shows the dependence on distance of the Pearson's correlation coefficient, for the patchy (red) and continuous (black) landscapes (see the ‘Spatial Correlation’ section). As expected, both landscapes show a decrease in correlation with increasing distance. However, while the two landscapes lose correlation similarly for distances up to approximately 15 patches, this analysis also shows that the patchy landscape loses correlation faster than the continuous landscape beyond 15 patches. Spatial dynamics in the patchy landscape thus extend beyond a single patch, yet are correlated over shorter distances than in the continuous landscape, a high migration rate of bacteria between adjacent patches in the initial phases of the experiment may explain correlations beyond the patch size. A high migration rate between patches would be expected to contribute to a high coupling between patches and synchronization in the dynamics between patches. Indeed, real-time movies of the initial phases of the experiment (electronic supplementary material, movies S2 and S3) show that up to hundreds of bacteria can migrate between patches per minute, depending on bacterial density. This finding suggests that the migration rate in the patchy landscape is apparently sufficiently high to generate correlation in the dynamics between a few adjacent patches, but over long (more than 15 patches) distances, the effects of the patchy landscape on the dynamics become apparent. As such, the present spatial configuration represents an unexplored intermediate regime between a coherent well-mixed state and an entirely fragmented state [12].

Figure 4.

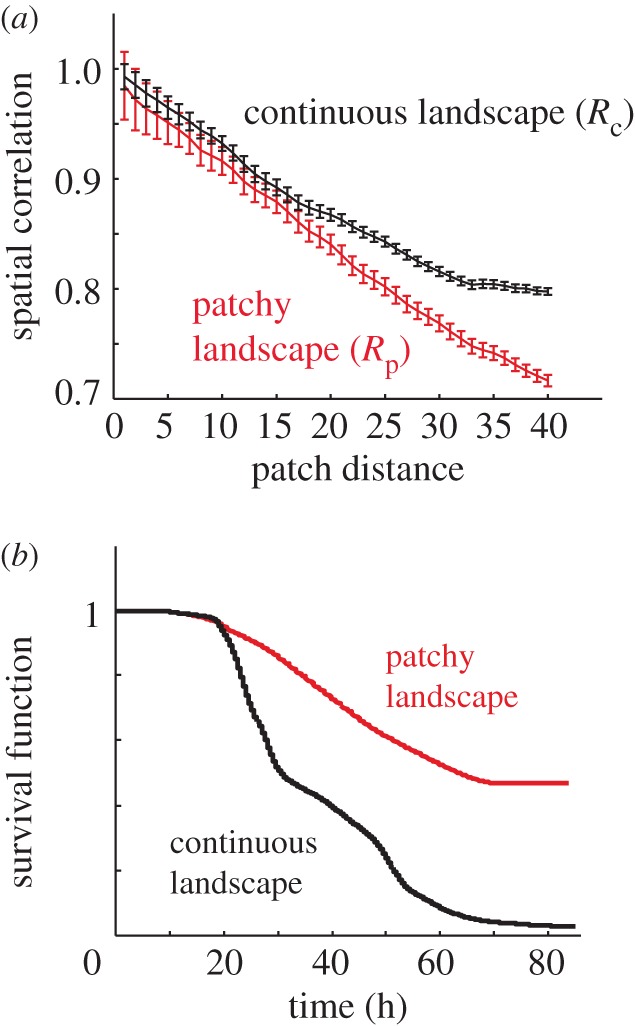
Correlation in patchy and continuous habitats. (a) The temporal correlation of the population dynamics decreases with increasing patch distance. Beyond approximately 15 patches, correlation in the patchy landscape (red) is lost more rapidly than in the continuous landscape (black). (b) Kaplan–Meier survival functions for a patchy landscape (red) and a continuous landscape (black). The two functions differ (p < 0.00001) and the fraction of prey population that remains in the patchy landscape is higher than in the continuous landscape (p = 0.05), see Results.

Given our finding that patchiness affects variation and spatial correlation of the prey dynamics, we then asked what the ramifications of these findings were for the survival of prey. Does patchiness, like in various macroscopic systems [5,8,12,13] give rise to an increased persistence of the prey population, or do specific bacterial properties (such as high mobility, high density, and surface growth) render the analogy to macroscopic organisms invalid? To answer this question, we performed a survival analysis for prey in both the patchy and continuous landscapes. Using fluorescence as a proxy for prey persistence, we generated survival curves representing the spatial fraction of the prey population that survives (see figure 4b and the ‘Survival Analysis’ section for details). After the onset of predation (in this experiment approx. after 10 h), survival curves in both the patchy and continuous landscape start to decline. Interestingly, the survival functions of the patchy and continuous populations are not equal, (p < 0.00001 using a log-rank test). Survival curves for all the experiments are displayed in electronic supplementary material, figures g–i. These results show that while almost the entire population dies in the continuous landscape (residual value = 0.04 ± 0.04, n = 3), a significant fraction of the population in the patchy landscape survives (0.36 ± 0.10, n = 3) demonstrating that prey survival in the patchy landscape is increased compared with the continuous landscape (p = 0.05, using a single-sided Wilcoxon rank-sum test). The increased survival in the patchy landscape is not caused by a lower per capita predation rate as the absolute values for the per capita predation rates are 0.06 ± 0.01 and 0.05 ± 0.01 per hour for the patchy geometry and continuous landscapes, respectively, in good agreement with previously measured batch values [30–32]. This control shows that (i) the geometry of the landscape does not influence the kinetics of the predator–prey interaction and that (ii) the rates measured in the microchip are comparable to those previously measured.

4. Discussion

This work was inspired by studies on macro-scale patchy landscapes showing that patchiness can greatly impact the spatio-temporal dynamics of predator–prey systems, such as an extended lifetime of a macroscopic population [8–11]. We investigated to what extent bacterial predator–prey systems in microfragmented landscapes exhibit similar behaviours. The present patchy landscape can be considered ‘mildly’ fragmented as on the one hand fragmentation increases the variation in predation rates, but on the other hand spatial correlations extend over multiple patches. The presence of this intermediate regime should perhaps be considered in the context of the fundamental differences between macroscopic animals inhabiting macroscopic landscapes and microscopic organisms inhabiting microscopic landscapes. First, compared to macroscopic animals, bacteria (and especially B. bacteriovorus) move through space fast and grow to high densities. If one were to simply scale up the microfragmented landscape and its microbial inhabitants to macroscopic proportions, one would obtain the following (rather absurd) large-scale animal equivalent: hundreds of cheetahs racing at approximately 500 km h⁻¹ in random directions while hunting a few hundred antelopes that run around at 100 km h⁻¹ in a square field of only 100 × 100 m. Such exceedingly high density and mobility would likely give rise to relatively homogeneous spatial dynamics within the field and result in spatial correlations that extend beyond it. Moreover, bacteria can adopt distinct lifestyles, existing as individual planktonic cells that swim freely, or growing as multi-cellular surface-associated colonies. Bacteria exhibiting one of these two lifestyles differ in a myriad of ways including cellular mobility, capacity to forage, resistance to environmental insults, and physiology. By impacting core processes like colonization, survival, and extinction, lifestyle switching plays a central role in bacterial ecology. Another distinction between the microscopic and macroscopic worlds is that signalling molecules, nutrients, and waste diffuse across space highly efficiently. For example, a small molecule such as glucose traverses the length of a patch (100 µm) in approximately 10 s and a distance of 15 patches in approximately an hour (which is in the order of one bacterial division time). Such environmental homogenization may be less apparent for macroscopic animals. A future theory of microbial ecology that draws from macroscopic theory would have to take into account these fundamental differences.

Perhaps the most salient effect described in this manuscript is the observation that a significant fraction of prey in the fragmented landscape persists, in contrast to the prey population in the continuous landscape that is nearly eradicated (surviving prey population fraction of 0.04 ± 0.04 n = 3). As this effect cannot be attributed to a difference in predation rates (the maximal predation rates in the two landscapes are equal), the increased persistence may be attributed to the geometry of the patchy landscape. Classical metapopulation dynamics, in which a given patch becomes extinct after which it is ‘rescued’ by migration of prey from an adjacent patch, could be responsible for the increased survival in the patchy landscape. However, while this scenario cannot be ruled out completely, the limited extent to which lateral movement (migration) is visible in the kymographs leads us to favour a different explanation.

Previous work has shown that while B. bacteriovorus can predate an E. coli biofilm, a significant fraction of the biofilm often remains [39], in contrast to predation on planktonic E. coli cultures where only a minute fraction of the population survives due to phenotypic resistance. In the microhabitats under investigation here, part of the prey population grows as a surface-associated biofilm (see electronic supplementary material, movies S1, S4, and S5). Surface-associated growth concentrates in the periphery of habitat patches where, due to the presence of sidewalls, the surface to volume ratio is higher when compared with the centre of habitat patches. An increase in the population fraction adopting a surface-associated lifestyle may render it more resistant to predation and could result in an increased survival in the periphery of patches. To test this hypothesis, we performed a survival analysis for the periphery and centre of habitat patches separately. This analysis revealed that prey persistence in the patchy habitat is indeed significantly higher in the periphery compared with the centre of patches (peripheral residual fraction of 0.49 ± 0.14, versus 0.30 ± 0.10, p < 0.02 using a one-tailed paired t-test). In contrast, we did not observe a significant difference when comparing survival in the periphery and centre of (virtual) patches in the continuous habitat (0.05 ± 0.05 and 0.04 ± 0.05, respectively). Two effects may explain the difference observed between the patchy and continuous habitats: (i) patches in a patchy habitat have four sidewalls, whereas (virtual) patches in the continuous habitat only have two, lowering the surface to volume ratio and (ii) patches in a patchy habitat have corners facilitating bacterial adhesion [40], while corners are absent in the continuous habitat. Both the increase in surface to volume ratio and the presence of corners facilitate surface-associated growth. As a result, geometry-induced enhancement of surface-associated growth may be responsible for the increased persistence of prey we observe in the patchy habitat. While in our experiments the persisting bacteria did not divide, the exact physiological state of these remaining bacteria remains unknown. Assessing the capacity of these persisting prey to grow and divide will be of importance when using B. bacteriovorus for water cleaning, crop protection, and as an additional means to fight bacterial infections.

Authors' contributions

F.J.H.H., E.J., C.D., and D.A.K. conceived and designed the experiments. F.J.H.H. and D.A.K. performed experiments and analysed the data. O.R. designed and contributed protocols. F.J.H.H. and D.A.K. wrote the manuscript. All authors read and approved the final manuscript.

Competing interests

We have no competing interests.

Funding

Supported by grants from the Minerva Foundation for Movement Ecology and the Dean of the faculty of Science of the Hebrew University to D.A.K. European Research Council grant NanoforBio No. 247072 and the Netherlands Organisation for Scientific Research (NWO/OCW) as part of the Frontiers of Nanoscience programme to C.D.