There is no fitness but fitness, and the lineage is its bearer

Abstract

Inclusive fitness has been the cornerstone of social evolution theory for more than a half-century and has matured as a mathematical theory in the past 20 years. Yet surprisingly for a theory so central to an entire field, some of its connections to evolutionary theory more broadly remain contentious or underappreciated. In this paper, we aim to emphasize the connection between inclusive fitness and modern evolutionary theory through the following fact: inclusive fitness is simply classical Darwinian fitness, averaged over social, environmental and demographic states that members of a gene lineage experience. Therefore, inclusive fitness is neither a generalization of classical fitness, nor does it belong exclusively to the individual. Rather, the lineage perspective emphasizes that evolutionary success is determined by the effect of selection on all biological and environmental contexts that a lineage may experience. We argue that this understanding of inclusive fitness based on gene lineages provides the most illuminating and accurate picture and avoids pitfalls in interpretation and empirical applications of inclusive fitness theory.

1. Introduction

In the half-century since its initial development [1], inclusive fitness theory has played a central role in behavioural and evolutionary ecology and now forms the core of the interdisciplinary field of social evolution. Yet, this period also saw repeated controversies over the theory's status and interpretation. Much of the early criticism came from theoretical population genetics (e.g. [2,3]), which helped identify the limitations of the initial models of inclusive fitness theory and led to generalizations (e.g. [4]) and integration with population genetics and evolutionary game theory (e.g. [3,5,6]). As a result, modern inclusive fitness theory is a well-integrated and central component of broader evolutionary theory and population genetics (see [7–9], for reviews).

Curiously, the theoretical developments in inclusive fitness theory and its integration with evolutionary theory over the past half-century seem to have had limited impact on how the theory is understood and used, particularly by empirical researchers. This is likely in part because much of the mathematical theory remains inaccessible to many empirical researchers and sometimes appears disconnected from empirical issues. In this article, we wish to highlight an important theme in the modern theory of inclusive fitness that we believe is underappreciated: rather than a generalization of Darwinian fitness, inclusive fitness is a tool for measuring Darwinian fitness in a social context. We argue that this notion of inclusive fitness has important consequences for its biological interpretation and tests of Hamilton's rule. We propose that using a ‘lineage's eye view’ of inclusive fitness may help to avoid some of these pitfalls of interpretation and may help highlight important biological considerations when measuring inclusive fitness.

We begin by discussing different concepts of fitness and arguing against the commonly held view that inclusive fitness is a generalization or extension of classical Darwinian fitness. Instead, the modern theory of inclusive fitness shows that it is precisely classical Darwinian fitness averaged across the social environments and demographic states in which members of a lineage may find themselves. Both direct effects on the fitness of focal individual due its own behaviour and any indirect fitness effects due the behaviour of other individuals are accounted for in this averaging process. A few corollaries of this view of inclusive fitness immediately follow. First, inclusive fitness cannot be construed as an individual-level quantity; rather, it belongs to the gene lineage. This view is close to the ‘gene's eye view’ of selection [10,11]; we discuss parallels between the ‘lineage’ view and the gene's eye view in §6a. Second, Hamilton's rule (in its general form), by measuring whether or not a mutant lineage has a higher expected fitness than an alternative allele, is simply an expression of whether an allele is adaptive or not.

Finally, measuring Hamilton's rule is as complex as measuring fitness and requires properly averaging over relevant social environments and demographic states. Thus, there is no single Hamilton's rule that is suitable for all empirical systems. While this is well-known theoretically, there has been a tendency in the empirical literature to use the ‘canonical Hamilton's rule’, which is based on additive costs and benefits and lacks demographic structure, and therefore applies only for a very specific scenario. To quantify Hamilton's rule or inclusive fitness using field or experimental data, one needs to carefully specify the structure of the social interaction, which will determine the relevant condition to be met for the trait in question to be adaptive. We illustrate these complexities using the example of cooperative courtship in wild turkeys [12].

2. Fitness

Many different definitions of fitness exist, designed for different aspects of evolutionary analyses and used in different conceptual frameworks (e.g. [11, ch. 10]). In this section, we review several standard notions of fitness and clarify how they are connected by considering how each concept emerges from theoretical evolutionary analyses. Although the various points we make in this section hold more generally, we focus for simplicity of presentation on haploid populations and on the condition for increase of a rare mutant allele. This basic scenario is commonly used to characterize evolutionarily stable states, which can be viewed as adaptations [13].

(a). Invasion fitness: the growth rate of a mutant lineage

One of the standard problems in evolutionary theory is to predict the fate of a mutant allele or trait in a population composed of some resident allele or trait. If a resident trait resists invasion by any alternative mutant trait, then this trait characterizes an evolutionarily stable state. Such states are likely to be observed in a population over the long term. This type of long-term analysis underlies most social evolution theory, e.g. models of the evolution of sex ratio [14], dispersal [15], interspecific mutualism [16], to name just a few.

‘Fitness’ in this context is the measure that determines the invasion of a mutant trait and is therefore called invasion fitness. Because evolution is a dynamical (and stochastic) process, the characterization of evolutionary stability and the computation of invasion fitness is usually carried out using methods from dynamical systems and stochastic processes [7,17,18]. In this framework, the proper measure of invasion fitness (assuming the population is censused at discrete intervals) is the expected geometric growth rate of a rate mutant trait in the population, which we denote by ρ. When the geometric growth rate of a lineage is greater than one, ρ > 1, a rare mutant will increase in frequency and invade.

The invasion fitness ρ takes into account all relevant biotic and abiotic factors that may affect the growth rate of a mutant when rare in a population. Insofar as fitness should be a single number allowing one to predict the fate of a mutant, ρ is the most comprehensive measure of fitness, and it is the relevant quantity for predicting the long-term outcome of evolution. However, being a mathematical object that describes the outcome of a complex dynamical system, it is frequently hard to interpret in biological terms. Therefore, it needs to be unpacked and related to what we can measure and observe more easily, which is the reproductive success of individuals.

(b). Individual fitness

Behavioural and evolutionary ecology often defines fitness as the number of offspring of an individual that survive to reproductive age and uses this definition as a measure of how individual behaviours and other traits are adapted to the environment. This is the classical Darwinian notion of fitness. The fitness of any given individual depends on all relevant biotic and abiotic factors that affect the survival and reproduction of that individual. In general, these factors are stochastic, so evolutionary theorists almost always work with expected (or averaged) individual fitness, which we denote by w, and drop the word ‘expected’ from the phrase hereafter. Since we are usually interested in how the genetic composition of the population affects individual fitness, the expectation is taken over all other biological and environmental factors affecting fitness and is conditioned on the genetic composition of the population at the beginning of the life cycle (i.e. genotypes may vary among individuals in the population but individual genotypes are assumed to take fixed or ‘realized’ values). It is also important to emphasize that w is the number of surviving offspring after a complete life cycle, not just offspring produced by an individual (although the latter is usually what is practically measured in the field). In other words, we assume that offspring are counted after processes such as competition for limited local resources [19] have affected the recruitment of juveniles to the adult stage.

(c). Inclusive fitness

Given a focal individual's genotype, the only remaining source of variation in individual fitness w comes from the genotypes of an individual's social partners. These social partners form the ‘social environment’ of the focal individual. Suppose that we write the fitness of a mutant individual as a linear function of the frequency of the mutant allele among the social partners of that mutant individual, p_n:

2.1

where c is the direct fitness effect of the mutant's own genotype on its own fitness, b is the effect of others' genotypes on the mutant individual's fitness, i.e. the indirect fitness effect, and e is an error term. The first term, ‘1’, reflects the baseline fitness of the resident genotype. We can always write down such an expression by defining c and b as average effects (i.e. partial regression coefficients; [4,20–22]), with the error terms absorbing any deviations from linearity such that (which is given by the method of least squares).

The quantity on the right-hand side of equation (2.1) is still a random variable because the frequency of the mutant allele among the social partners of any specific mutant individual will vary stochastically as those social partners are typically randomly sampled from the individuals that might interact with the mutant. To predict the expected fate of a mutant's lineage, we need to take an expectation of the mutant fitness in equation (2.1) over all possible values of the frequency of the mutant allele among social partners, p_n, where the likelihood of a particular value of p_n is determined by the population structure and demography.¹ Effectively, this expectation can be calculated by averaging replicates of the evolutionary process, just as one sets up replicate lines in microbial evolution experiments (see figure 1 for more detail). Taking this expectation of w_m, we obtain the inclusive fitness w_IF:

2.2

where

2.3

is the probability that the randomly drawn neighbour of a local gene lineage (mutant or resident) will be of the same lineage; that is, the probability that the lineages are identical by descent. We put the subscript m on the expectation operator to emphasize that the expectation is over replicate mutant lineages.

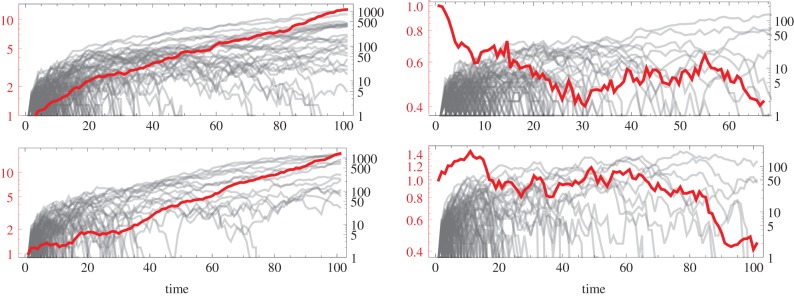
Figure 1.

Simulations of the fates of lineages founded by a single mutant in an additive social dilemma (i.e. when b = b and c = c from equation (2.2) with b and c constant). In each of the panels, the grey lines represent one instance of the invasion process, whereas the thicker red line is the average of 500 simulations. When a grey line disappears below vertically, the mutant lineage has gone extinct. In all panels, r = 0.2. In the top row, there is no class structure and c = 0.2. The top left has b = 1.1 and top right b = 0.9. The two benefit values straddle the threshold for the invasion fitness ρ to be greater than one (i.e. satisfying Hamilton's rule, or equivalently, the mutant trait being adaptive). These figures demonstrate that while plenty of lineages either increase or go extinct in each case, Hamilton's rule predicts the average behaviour of many such invasions, hence the expected outcome of the evolutionary process. In the bottom row, we simulate a case with two classes of individuals, subordinates and dominants (as described in §3) with where subordinates forgo almost all reproduction (s = 0.01) to help the dominants and pay a cost , while dominants do not help subordinates, 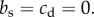In the bottom left panel, the benefit to the dominant is 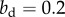and in the bottom right, it is 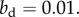As in the non-class-structured case, individual lineages might increase or go extinct, and the class-structured version of Hamilton's rule (equation (3.1)) predicts the expected success of the lineage in the bottom left and extinction in the bottom right. (Online version in colour.)

Equation (2.2) is a general measure of inclusive fitness conditional on the current frequency of the mutant allele since the partial regression coefficients b and c capture average fitness effects [8,25,26]. When fitness effects are additive or the mutant is rare in the population, the benefit b and cost c are constants independent of mutant allele frequency, and equation (2.2) boils down to inclusive fitness as originally defined by Hamilton [1]. When fitness effects are non-additive and the mutant is not vanishingly rare, the benefit and cost coefficients are frequency dependent, which can lead to additional complexity in analysing the dynamics of selection on behaviour [9,27]. We provide an example of this in §5c.

We can now connect inclusive fitness with invasion fitness. During the initial stage of the invasion, the mutant remains rare and mutant fitness will be linear in mutant allele frequency. This means that 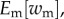which is averaged over replicates of the evolutionary process, is the mean expected number of offspring of the invading mutant lineage and therefore corresponds² to the expected invasion fitness ρ (figure 1) [23]:

2.4

Thus, the growth rate of the mutant is the inclusive fitness of a mutant lineage member. Since a mutant is favoured by selection when ρ > 1, we have that the mutant spreads in the population if 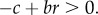Equation (2.4) also connects ρ as the comprehensive measure of invasion success and the behavioural ecology notion of individual fitness w. As our derivation above makes clear, the growth rate ρ, or equivalently the inclusive fitness w_IF, is simply the expectation of individual fitness, taken over both any biological and environmental factors that affect fitness and over replicates of evolutionary process.

We note that the derivation above, although perhaps presented slightly differently than is usual, does not contain a novel extension or generalization of inclusive fitness. Instead, we present it to emphasize two general points about the nature of inclusive fitness and how to measure it. The first point is that inclusive fitness is not an extension of classical Darwinian fitness in the sense that the former does not add or subtract anything from the latter. Rather, inclusive fitness is simply the expected individual fitness of individuals belonging to a gene lineage. Regardless of social interactions or population structure, the relevant quantity for an allele to increase is the invasion fitness ρ, which is the expectation given in equation (2.2). Second, although expressed in terms of individual fitness, inclusive fitness is not an ‘individual-level’ property. The key to this point is in the phrase ‘expectation taken over replicates of the evolutionary process’. This means that we need to consider all potential situations in which a member of a mutant lineage might find itself (e.g. different genetic backgrounds for the focal individual, groups of different sizes with different genotype compositions and different classes of individual, etc.), calculate the expected probabilities of each such situation and compute the average individual fitness weighted by these probabilities. Inclusive fitness as the quantity resulting from this exercise therefore cannot be ascribed to any single individual, or even to a given class of individuals, except as an approximation or average. Inclusive fitness is thus inherently tied to the dynamics of a lineage and how its members transition from one social and demographic situation to another. It is worth noting that Hamilton was aware of the nature of inclusive fitness as an average from the start [1, p. 8], even though he proposed the individual-based view as a heuristic (see Discussion for more on this issue).

3. Fitness in heterogenous populations: the importance of reproductive value

In the simple derivation of invasion and inclusive fitness above, we assumed that the only thing distinguishing individuals was their own genotype and that of their interaction partners. In other words, we assumed that demographic factors such as age and life stage do not affect survival or fertility. This assumption also precludes the existence of different reproductive classes or castes such as workers and queens in eusocial insects since such classes have systematic differences in survival and/or fertility as a result of different developmental trajectories. The simple framework above might apply for the evolution of some phenotypes in some species, such as adult phenotypes in semelparous plants and animals. However, many of the most interesting social phenotypes, such as eusociality and cooperative breeding, have evolved in species with age, stage or class structure. These sources of biological variation create variation in the individual fitness of each stage or class, and this variation must be properly averaged using reproductive value in order to produce the invasion fitness of a given allele [23,28–30]. This is because invasion fitness looks at what happens to the lineage over many generations as the mutant either invades the population or goes extinct. Therefore, different demographic classes need to be weighted by their relative contributions to the lineage far in the future, which is their reproductive value. Invasion fitness using reproductive value to account for class structure then leads to a general version of Hamilton's rule that predicts the direction of selection on the underlying gene. Importantly, this class-structured view of fitness and Hamilton's rule resolves some persistent conceptual confusions regarding inclusive fitness and the evolution of helping by subordinates in cooperatively breeding species or altruistic helping by sterile workers in eusocial species.

Rather than presenting invasion fitness and Hamilton's rule for the most general case of class-structure, we will illustrate how these two expressions differ from the symmetric case in a simple scenario where there is one class of individuals (dominants) that consistently reproduces more than another class (subordinates). Dominants could be cooperatively breeding vertebrates (e.g. [31,32]) who produce more offspring than subordinates. For every surviving offspring of the dominant, assume that the subordinate gets only s offspring, where s < 1; further assume that the chance of becoming a subordinate individual is σ and is independent of whether the parent was a dominant or subordinate. Given this class structure, we can determine when an allele that results in an increase in cooperation by the subordinate or the dominant will invade the population. Suppose that the dominant gets an indirect fitness benefit b_d from the change in behaviour by mutant subordinates and the subordinate gets b_s for the change in behaviour by mutant dominants. The change in behaviour by the mutant also incurs a direct fitness cost of c_d for the dominant and c_s for the subordinate. Theory for evolution in class-structured populations [6,29] shows that the allele for this change in cooperation between dominants and subordinates will increase in frequency when

3.1

where r is the genetic relatedness between a dominant and subordinate individual (this result can be derived using the methods of Taylor & Frank [6]). The brackets in equation (3.1) are the inclusive fitness effects for the subordinates and dominants. Each inclusive fitness effect is then multiplied by the proportion of individuals of each class, 1 − σ and σ for the dominant and subordinate, respectively. The inclusive fitness effect of the subordinate is further multiplied by its reproductive value relative to the dominant s. This reveals immediately the crucial role of reproductive value. As s decreases, the subordinate systematically contributes fewer offspring to the population and its fitness costs and benefits contribute less to invasion fitness. In the case of sterile subordinates (analogous to sterile female workers in eusocial insects), s = 0 and these individuals can contribute to any fitness benefit b_d received by the dominant at any direct cost c_s to themselves. This is analogous to the case of somatic cells in a multicellular organism that contribute no ‘offspring’ and may benefit the germ cells at any cost to themselves.

The essential role of reproductive value in averaging inclusive fitness effects across different classes of individuals, such as subordinates and dominants, in equation (3.1) highlights the fact that invasion fitness cannot ‘belong’ to any one individual since individuals belong to only one class at a time. Rather, fitness can only be measured at the gene lineage level where gene lineages pass through each class over time as they are transmitted repeatedly from parents to offspring. Thus, statements regarding the inclusive fitness of any single class of individual, such as a worker or queen, are necessarily incomplete as they cannot determine whether a gene is under positive selection resulting in the corresponding trait becoming better adapted. This suggests that arguments that the ‘individual organism is the privileged unit of adaptation’ (e.g. [33,34]) are problematic since one cannot, for example, view solely the queen or the worker in an insect colony as adapting to their environment. Instead, one must view the expression of a gene lineage expressed in both queens and workers as adapting to its environment. Such a view could correspond to a ‘gene's eye view’ [10,11] if invasion fitness is used to measure evolutionary success (for more on this connection, see §6a).

4. Inclusive fitness and adaptedness

Our definition of fitness in §2 based on gene lineages gives us a very general ruler with which we can measure the adaptedness of a phenotype or trait produced by a given gene. Mutant alleles with higher fitness than residents (when in competition with residents) will invade the population and increase in frequency. In the long run, those alleles whose fitnesses are high enough so that no mutants can invade are evolutionarily stable and produce phenotypes that are ‘adaptations' ([13]; see [35] for alternative notions of adaptation). Thus, measuring fitness is really a way of measuring a gene's adaptedness for a given distribution of abiotic, biotic and social environments. Genes that are adaptive will tend to increase in frequency when rare due to positive selection, whereas maladaptive genes will tend to go extinct due to negative selection. Since, as we emphasize above, inclusive fitness is simply a way of writing down fitness where ‘direct’ effects are separated from ‘indirect’ effects and genetic relatedness, measuring inclusive fitness is also just a way of measuring the adaptedness of a gene. Thus, in principle, all that is required for measuring inclusive fitness is an accurate measurement of individual fitness (as defined in §2c) that averages across all potential abiotic and biotic (individual and social) environments. Such a measurement may not require the delicate accounting necessary for measuring separately direct and indirect fitness effects. This relationship between adaptedness and inclusive fitness is obscured when inclusive fitness is described as an ‘extension of the concept of Darwinian fitness’ [36, p. 192] or a ‘generalization of Darwinian fitness’ [37, p. 417]³ or when the direct fitness component alone is referred to as ‘classical Darwinian/Fisherian’ fitness [38, p. 13]. Obscuring this direct relationship between adaptedness and inclusive fitness could be the source of some of the confusion about how inclusive fitness relates to natural selection [25,39].

5. Identifying the correct condition for adaptiveness: a case study

As we argue in §4, quantifying adaptedness of a behaviour does not necessarily need quantifying direct and indirect fitness effects, provided that one averages classical fitness appropriately. Nonetheless, in many cases quantifying the direct and indirect fitness effects and putting them together into some version of Hamilton's rule may be easier or conceptually more illuminating than alternative methods [40,41]. The problem then is that how one empirically measures the direct and indirect effects depends on assumptions about the structure of the social interaction, where different assumptions can give dramatically different answers as to the adaptiveness of a trait or behaviour.

To be more specific, despite many elaborations on the original Hamilton's rule (e.g. [42]), the overall tendency in the field is to use the ‘canonical’ Hamilton's rule, the inequality 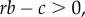with b and c defined as additive fitness effects and r the pairwise relatedness. Most debate over empirical quantification of Hamilton's rule is about how to measure r, b and c properly [43]. We argue that a more fundamental problem is the assumption that the canonical Hamilton's rule applies without considering whether its assumptions apply. The canonical Hamilton's rule applies when the social interaction is symmetric, fitness effects of the behaviour are additive, and there is no class structure. These assumptions are unlikely to apply to many interactions in nature for which the canonical Hamilton's rule is used. While some authors (e.g. [43]) do explicitly recognize the specific assumptions behind the canonical Hamilton's rule, they also assert that this form of Hamilton's rule nonetheless represents a good approximation to many interactions in nature. This assertion, to our knowledge, remains untested empirically. Worryingly, the conclusions from the same data can be very different depending on whether or not these assumptions hold, even if the costs, benefits and relatedness are quantified properly. We illustrate our point by considering a seemingly straightforward case, that of cooperative courtship of wild turkeys [12].

(a). Cooperative male courtship in wild turkeys

Wild turkeys have a lek-like mating system where males defend small territories close to one another and females visit these territories to mate with males. Many of these males display to females by themselves, but some form pairs (or rarely, bigger groups) that jointly display and defend females from other males. One of the males in these pairs (the dominant) gets many or all of the matings and offspring, whereas the subordinate often gets few or none. This kind of cooperative courtship system has been documented in several bird species in addition to wild turkeys including manakins [44,45], ruffs [46] and Tasmanian native hens [47,48].

An early account of cooperative courtship in wild turkeys by Watts & Stokes [49] documented that males in pairs tend to be brothers, which suggests that indirect benefits might help to explain why subordinates forgo their own reproduction in helping dominants. This idea was not tested quantitatively until Krakauer [12] measured the reproductive success of males in singletons and pairs along with the relatedness of males within a pair. In particular, he measured the average siring success of singleton males and the dominant male in pairs. He assumed that the siring success of singletons represents the opportunity cost of being a subordinate, corresponding to c in Hamilton's rule, while the difference between the success of dominants and singletons is the benefit provided by the subordinate to the dominant, i.e. b. He used mean relatedness in pairs, r, to calculate the canonical version of Hamilton's rule, obtained 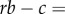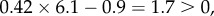and concluded that kin selection does indeed explain the evolution of cooperative courtship in wild turkeys.

We wish to use this case to highlight the fact that the ‘correct’ condition to check for adaptedness, and therefore the conclusions from empirical data, depends non-trivially on assumptions about how the social interaction works. We focus on two issues: accounting for class structure and reproductive value and the potential for non-additive pay-offs. We leave aside other important issues, such as local competition between kin that might negate some or all of the inclusive fitness effects, since that issue has been already discussed in the literature at some length [19,50,51].

Consider the well-known model that underlies canonical Hamilton's rule: two individuals have the option of providing a fertility benefit 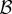to each other while forsaking some personal fertility 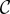as the cost of helping. 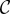in this matrix is the additional fertility a player can get if it defects (relative to when it cooperates), in other words, the opportunity cost of cooperation. In wild turkeys, helping would correspond to joining a courting pair (hence giving up reproducing singly) and acting cooperatively towards females, abstaining from within-pair conflict, etc. We can summarize this game using the pay-off matrix given in (5.1), where C denotes the cooperator strategy, D the non-cooperator (defector) and the entries are the fertility pay-offs to a player whose strategy is given by the row when the partner's strategy is given by the column.

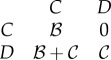5.1

(b). Reproductive value

The problem with the model given (5.1) is that it is prima facie inconsistent with what we know about wild turkeys: each individual in a cooperative pair gets fertility pay-off 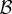; in other words, there is no skew within cooperative pairs. One way to make the model compatible with the observation of complete skew within groups is to assume the game is played between two individuals from different classes. Watts & Stokes [49] observed in the Rio Grande population that dominance hierarchies within and among male courtship groups (i.e. pairs, triplets or quartuplets) are established early in life and remain unchanged until death. They report rigid adherence to both within- and between-group hierarchies for displaying and mating (although in other populations, perhaps due to environmental stress, social roles might be reversed; A. Krakauer 2015, personal communication). Thus, it seems probable that dominant and subordinate members of a pair belong to different social classes with different expected matings and reproduction. Therefore, we need to use a class-structured model such as the one given in equation (3.1). Consider a simple model where all individuals are in pairs and each pair has one dominant and one subordinate male so that the proportion of subordinates in the population is 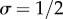. We further assume, to be consistent with the observed pattern in wild turkeys, that dominants only receive help and do not help the subordinates: 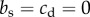. From equation (3.1), the increase condition for cooperation becomes

5.2

where for ease of presentation, we equate the fertility benefit 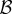and cost 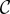in the pay-off matrix to the fitness benefit 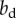and cost c_s, respectively, by ignoring local competition between kin.

Equation (5.2) is different from the canonical Hamilton's rule in that the cost term is weighted by s, the relative reproductive value of the subordinates, which is also how many offspring each subordinate produces relative to a dominant. If s were close to one, the computations in Krakauer would apply. For wild turkeys, however, we can expect that s is much less than one, and may even be close to zero. If, as described by Watts & Stokes [49], turkeys live in a rigid hierarchy set early in life, then subordinate males are likely to be kept to low reproduction by social factors outside their control. Furthermore, Krakauer reports that the distribution of reproduction for singleton males is bimodal, with most males (70%; 10 out of 14) not reproducing. If these non-reproducing males are those who would otherwise be subordinates in pairs, then very few offspring would be produced per capita by subordinates relative to the dominants, i.e. s would be much less than one. Consequently, viewed from the lineage's perspective, any costs incurred by the subordinates are likely to be of little consequence for the maintenance of cooperation once a strict hierarchy and reproductive skew are established and the relevant condition for adaptedness of helping is much relaxed relative to the canonical Hamilton's rule. One can argue that this simply makes the original analysis conservative, which is true if we are interested in whether the behaviour is adaptive or not, but not true if we are interested in whether high relatedness is essential for cooperative courtship being adaptive. This is a biologically relevant point: the class-structured model predicts that in species with similar breeding systems, we should not see relatedness being the crucial factor explaining the presence or absence of cooperative courtship; rather it should be the social system that constrains the outside options (and therefore the reproductive value) of subordinates that should be operative. An example of this might be found in occelated wrasses (Symphodus ocellatus), where satellite males help territorial males in courtship and territory defence [52], despite having only a small share of paternity and not being related to the territorial males (M. Taborsky 2015, personal communication). This is likely due to the fact that in a size-structured population, satellite males (who are smaller than territorial males) have little chance of defending a territory themselves, which reduces both their opportunity cost of helping and reproductive value, though the latter may not be zero, since satellite males can grow to be territorial in the next season [53].

(c). Non-additive pay-offs

As argued above, it is likely that class structure plays an important role in wild turkeys. However, at least theoretically, one could observe different breeding success among individuals in a cooperating pair even if the population lacked class structure and the social interaction were initially symmetric. Nevertheless, the correct condition for adaptedness will not in general be the canonical Hamilton's rule. To illustrate this point, suppose that when two cooperators pair up, one is selected at random to be the helper (or the subordinate), the other the receiver (or the dominant). When a cooperator pairs with a non-cooperator, the non-cooperator gets all the pay-off. This could be, for example, because non-cooperators fight to monopolize copulations while cooperators avoid such competitive behaviours. The expected pay-offs from different pairings are now:

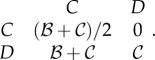5.3

The upper left entry reflects that an individual in a cooperative pair obtains zero or 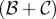with equal probability. This pay-off matrix represents a non-additive game: i.e. a game where the benefit a cooperator gives to its partner depends on the partner's type. The condition for cooperation to increase is given by [42,54,55]:

5.4

where the last term is not found in the canonical Hamilton's rule and is a result of cooperators receiving less benefit from pairing with a cooperator than defectors receive from pairing with a cooperator. This non-additive term depends on p, the frequency of cooperators in the population. Importantly, the definition (and measurement) of and 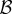in this model is precisely the same as in the canonical model (and [12]). When cooperation is rare (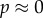), the condition for increase becomes 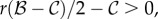and when it is common (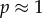), 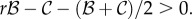Both conditions are harder to satisfy than 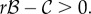Using Krakauer's estimates (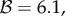 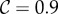and r = 0.42), the conditions for low and high cooperator conditions evaluate to 0.192 and −1.838, respectively, indicating that cooperative courtship would get selected for at low frequency, but against at high frequency. Thus, cooperation in this case would not be unconditionally selected, and we would expect a stable polymorphism of cooperators under this model (the stable equilibrium frequency of cooperation can be calculated to be ).

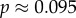Overall, depending on how one assumes cooperation plays out in the social setting, one can arrive at significantly different conclusions as to whether and when cooperation is adaptive using the same data. This is problematic, since the canonical version of Hamilton's rule is usually applied without checking whether its assumptions hold in the system. In many cases (like wild turkeys), the assumption underlying the canonical Hamilton's rule almost certainly does not hold, and a different condition for adaptedness is required. We emphasize that highlighting this issue in no way detracts from the novelty or significance of Krakauer's study [12] in particular, which is a good example of the painstaking work required to quantify the fitness consequences of social behaviour in the wild. More generally, this issue is not a reason to stop quantifying inclusive fitness or Hamilton's rule. Rather, the mismatch between real social interactions and overly simple versions of Hamilton's rule emphasizes that the careful and painstaking empirical work that measures fitness effects of a behaviour needs to be coupled with some elementary modelling of the empirical features of the social interaction in order to more accurately construct a condition for the adaptedness of the behaviour.

6. Discussion

Although inclusive fitness is sometimes described as an ‘extension of Darwinian fitness’, we use a ‘lineage view’ to show that inclusive fitness is in fact best understood as Darwinian fitness averaged over the distribution of different social and environmental states in which members of a lineage find themselves. When there are different demographic classes, the expectation also needs to be weighted by the relative contribution of each class to the long-term persistence of the lineage (i.e. reproductive value). While these are well-known points in theory, their ramifications for interpretation and empirical measurement of inclusive fitness remain obscure in the field more generally. For example, it is common to claim (and teach) that inclusive fitness is an individual-level quantity, which is strictly speaking false, as inclusive fitness is an expectation over lineage-level properties. Hamilton himself pointed this out multiple times [1,56]; however, he also consistently favoured a perspective that imagines individuals maximizing their inclusive fitness as a useful heuristic. This heuristic has indeed been important in the development of the field as it provided an important and easily accessible insight to the action of selection in complex interactions. Yet over time, the heuristic seems to have taken on the status of the theory itself, being the only exposure to inclusive fitness that most people have. This is problematic, since the individual-level heuristic can fail to account for the inherent complexity of evolution in populations with age and class structure where the fitness consequences of a social behaviour may depend non-additively on the phenotypes of individuals in the social interaction.

(a). Lineage's eye or gene's eye?

The lineage view of fitness given by the equation for invasion fitness (2.4) is very close to the popular concept of the ‘gene's eye view’ of evolution [10,11]. In fact, we believe that the gene's eye view, properly understood, is coincident with the lineage view, where the gene is the marker of a lineage. For example, Dawkins [11, ch. 10] discusses five different notions of fitness. Our expected individual fitness from §2b corresponds to Dawkins’ ‘fitness[2]’ concept that measures the fitness of genotypes.⁴ However, Dawkins does not explicitly discuss an averaging process akin to the one leading to our equation (2.4). The closest Dawkins comes to this is when he considers his ‘fitness[3]’, by which he means the fitness of an organism (as opposed to a genotype), and points out that the best fitness measure is the number of descendants far into the future. Although Dawkins applies this long-term measure to organisms, this is the same perspective used in lineage fitness, which is the expected long-term success of a lineage. The lineage view combines the ‘gene's eye view’ focus on the effect of selection on a single gene with a long-term perspective that measures the success of that gene across all possible future social and environmental states that the gene may experience. Both the lineage and gene view emphasize that fitness (or inclusive fitness) is best viewed as a property of the gene lineage rather than the individual organism [11,57].

(b). Conflicts of interests in the lineage view

It is common in evolutionary biology and behavioural ecology to talk about the conflicts between the fitness interests of different classes of individuals (e.g. parents and offspring). At face value, a lineage view of fitness could be seen to imply that conflicts of interest between individuals are epiphenomenal or even non-existent. The lineage view does not negate the potential utility of analysing conflicts of interest at the individual level; however, it does say that, properly understood, conflicts of interests are not between individuals, but between roles in an interaction where different genes may come to be expressed in different roles. A role is a particular social or demographic context that can be occupied by an individual in an interaction (e.g. parent versus offspring or dominant versus subordinate). A conflict of interest (in the ‘battle-ground’ sense) between roles exists when (a gene in) an individual in one role can obtain a higher fitness only by lowering the fitness of (a gene in) an individual in another role. For instance, in parental care, one can speak of a conflict of interest between the role of the parent and that of the offspring.⁵ The conflicts of interests between roles will certainly play a role in determining the evolutionary outcome, and thinking about them can yield important insights, as was the case for research in parent–offspring conflict, which helps making sense of phenomena such as costly begging or genomic imprinting.

At the same time, thinking purely at the level of individual conflicts of interests can lead to inaccuracies. Considering again parent–offspring conflict, few studies account for the passing of lineages both through parents and offspring [58,59], which has led to an overestimation of the level of conflict [59]. This example reinforces our view that individual-level heuristics (including those based on conflict or alignment of interests) are useful but ultimately need to be backed up with a full analysis of the evolutionary process, for which the appropriate criterion is the lineage fitness.

(c). Quantitative genetics, regression and Hamilton's rule

Although Hamilton's rule provides an intuitive partition of the effect of selection on social traits, its original derivation by Hamilton [1] was and remains relatively inaccessible. Hamilton simplified his derivation considerably in 1970 [60] by using the Price equation [61], which is a general approach for calculating mean trait change in a population and was derived independently in the context of quantitative genetics by Robertson [62]. Essentially, the Price equation expresses the effect of natural selection as a covariance between fitness and the trait of interest. Transforming this covariance into Hamilton's rule can easily be done using quantitative genetic methods where fitness and traits can be expressed as linear regressions on an underlying heritable genetic component [4,20–22] in a manner similar to equation (2.1). Combining these regressions with the Price equation yields a general Hamilton's rule where the fitness costs and benefits are partial regression coefficients of fitness on focal and social partner genotypes, respectively, and relatedness (in simple cases) is a regression of social partner genotypes on the focal genotype. This derivation of Hamilton's rule emphasizes that the important quantities in Hamilton's rule can be viewed as regression coefficients, which can be estimated via the well-developed statistical tools of quantitative genetics [63].

In addition to its accessibility, this derivation also shows that Hamilton's rule can be interpreted as a quite general condition in that it can summarize the potentially complex genetic and social interactions in a population via their average additive effects. A recent controversy around Hamilton's rule and inclusive fitness centres around this generality and questions whether Hamilton's rule is a general tool for understanding natural selection or whether it is restricted and only applies under some circumstances [25,39,64]. However, this is not the first time divergent views have been expressed about whether a rule of the 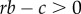structure is generally valid. When Queller [42] extended Hamilton's rule to account explicitly for non-additive interactions, Grafen [65] responded by pointing out the additive version still holds defining the costs and benefits as average additive effects and implicitly invoked the regression approach described above. More recently, Gardner et al. [25] explicitly invoked the regression approach to argue that Hamilton's rule is as general as ‘the theory of natural selection itself’. In contrast, Allen et al. [66] regard the regression formulation much less valuable and argue that it conflates correlation with causality.

We do not take a strong position on the generality of Hamilton's rule, which to us seems mostly a matter of semantics. We do find it non-trivial that, regardless of the processes affecting fitness, one can decompose the response to selection using linear regression coefficients on self and partner genotypes. At the same time, we wonder if the debate regarding the generality of Hamilton's rule has had unintended consequences where repeated affirmations of the possibility of writing some rule of the form 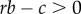led to a sort of complacency among researchers that kept using the simple, canonical version without considering whether its assumptions hold. As we have discussed, the canonical Hamilton's rule is insufficient in the presence of class structure and cannot reflect non-additive pay-offs in a simple way without subsuming them into average additive effects that are frequency dependent. These are well-known facts in the theoretical literature, but we find that empirical research has rarely used these elaborations on the canonical Hamilton's rule (with few exceptions, e.g. [67]).

Whatever the cause, this disconnect between theoretical results and their application in empirical research hinders progress in the study of social behaviour. We believe that the lineage view of invasion fitness that we espouse here provides a useful and accurate biological interpretation of the mathematical theory of inclusive fitness that will begin to bridge this disconnect and stimulate progress in the field.

Competing interests

We declare we have no competing interests.

Funding

This work was supported in part by an National Academies Keck Futures Initiatives grant no. CB13 to J.V.C., E.A. and Timothy Linksvayer. E.A. is supported by the University of Pennsylvania and by NSF grant no. EF-1137894.