Individual variation behind the evolution of cooperation

Abstract

Life on Earth has two remarkable properties. The first is variation: even apart from the vast number of extant species, there are considerable differences between individuals within a single species. The second property is cooperation. It is surprising that until recently the interactions between these two properties have rarely been addressed from an evolutionary point of view. Here, I concentrate on how inter-individual differences influence the evolution of cooperation. First, I deal with cases where individuality is maintained by random processes like mutation or phenotypic noise. Second, I examine when differences in state cause differences in behaviour. Finally, I investigate the effects of individual role specialization. Variation can be important in several ways. Increased random variation can change the expectation about cooperativeness of future partners, altering behaviour in a current relationship. Differences in state may serve as a book-keeping mechanism that is necessary for the evolution of reciprocity. If the cost of cooperation can depend on state then strategic regulation of state makes it possible to coerce partners to cooperate. If conditions force individuals to specialize, cooperation becomes more valuable. My review of theoretical models suggests that variation plays an important role in the evolution of cooperation.

1. Cooperation and the importance of assortment

Since Darwin's seminal work [1], natural selection has been widely accepted as a principal evolutionary force shaping the living world. Natural selection, however, is based on competition; therefore, it poses a problem for evolutionary biology to explain the emergence of cooperation, i.e. when an individual helps their potential competitors at a cost to itself [2]. Decades of research have shown that a crucial aspect of the evolution of cooperation is how strong the assortment between cooperators is; in other words, how probable it is that cooperators interact exclusively with cooperators and defectors only with defectors [3–5]. If the cost-to-benefit ratio (c/b) of cooperation is smaller than the degree of assortment (A),

4.5

then cooperation can evolve [3,4]. Of course, this condition is based on overly simplified assumptions but still provides useful insights into the evolution of cooperation. The left-hand side of the above condition emphasizes the role of ecology and life history in the evolution of cooperation, as the magnitudes of the cost and benefit of cooperation largely depend on ecological circumstances and life-history characteristics of the individuals [6]. The right-hand side of the condition stresses the importance of assortment. Several mechanisms can facilitate a high level of assortment [3,4]. Examples include kin discrimination, limited dispersal, social network structure, partner choice, competitive altruism and generalized, direct and indirect reciprocity [7]. From these, an important observation can be made: most if not all of these mechanisms can also be under selection. This raises two crucial questions. First, which mechanism of assortment is expected to evolve under what circumstances [5,8]? Second, how does the evolution of cooperation influence the evolution of assortment: is there any coevolution between the two traits [9,10]?

Assortment assumes inter-individual variation, at least in cooperativeness itself [11]. But variation in many other traits may also influence assortment and hence the emergence of cooperation. This is the focus of this paper. This is not meant to be a comprehensive review, and there are many more studies in this wide topic that could have been cited.

2. Variation

The magnitude of life's immense variability is well illustrated by the fact that taxonomists sort living creatures into millions of species mainly on the basis of their morphology alone [12]. Variation, however, is not restricted to morphology. Species are characterized by a multitude of life histories, physiological processes and behaviours. Variation also goes beyond the level of species: individuals of the same species, even if they are of the same sex, age and size, can be different [13]. Morphological polymorphisms within species, such as wing dimorphism and weaponry variability in insects, or plumage polymorphisms in birds such as the ruff (Philomachus pugnax), have been recognized for a long time [14–16]. Recent studies have also found consistent behavioural differences between individuals of the same species, sex, age and size, a phenomenon that is similar to human personality [17–19]. The individuals' internal state, such as energy reserves, hormone levels or mental mood, may serve as a basis for many of these inter-individual differences [20–22].

Individual differences are especially important in a social context. The existence of variation in the social environment opens up new behavioural options for individuals which in turn may result in new selective forces [21]. For instance, in a uniform population it is not worth choosing between possible partners because they are all the same. On the other hand, it may pay off to be choosy in a variable population because, for instance, it can be worth leaving a below-average partner as there is a good chance of finding a better one [21]. Individual differences may also facilitate task specialization.

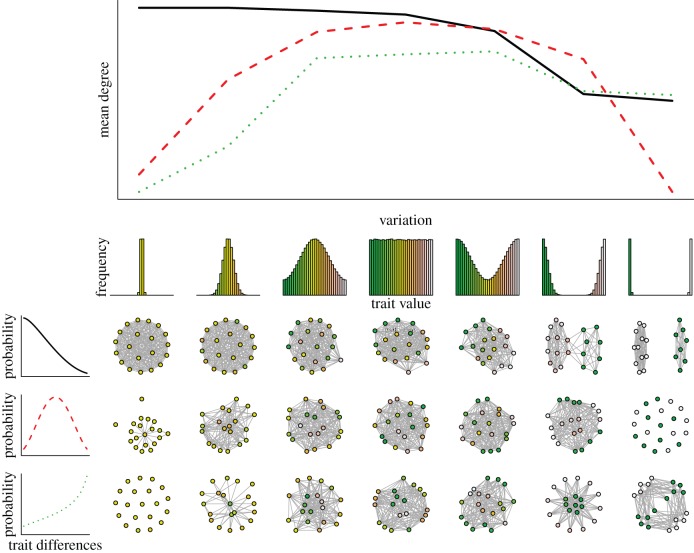
Partner choice and inter-individual variation can determine an individual's social environment. To illustrate this possibility, I develop a toy example of network formation (figure 1). I assume that individuals differ in a quantitative trait but they follow the same rule to choose interaction partners. The rule gives the probability of interaction between two individuals as the function of the difference between their trait values. Based on these assumptions, an adjacency matrix can be constructed for a given rule and a given distribution of the trait in the population. This then allows me to plot the interaction network between individuals. Computations show that changing the variance of the trait in the population can dramatically alter the structure of the interaction network (figure 1). These results are important because they illustrate that variation, through its effects on social structure, can influence the evolution of social behaviours in general, and cooperation in particular [7].

Figure 1.

The relationship between within-population variation and social networks generated by different inter-individual preference curves. The upper panel shows how the mean degree (i.e. mean number of neighbours) of individuals changes as a function of the population variation illustrated by the histograms under the x-axis for different preference curves, given by panels on the left. A preference curve gives the probability of interaction between a pair of individuals as a function of their difference. Network plots are representative examples of a group drawn randomly from the population with the given variation above the plot and the preference rule given left to the plot. (Online version in colour.)

Inter-individual variation can arise in different ways. The most important ones are (i) random processes like mutations or phenotypic noise, (ii) variation caused by differences in an individual's state, and (iii) task specialization. In what follows I review selected models of cooperation centred around these sources of variation.

3. Random variation and partner choice

Partner choice is an important mechanism behind assortment, not only in the context of cooperation but also for mate choice and sexual selection [23]. In a cooperative context, the simplest form of partner choice is the so-called exit strategy. An individual following an exit strategy finishes an interaction as soon as its partner defects, i.e. stops to help [24]. Several studies suggested that exit strategies do surprisingly well in terms of facilitating cooperation under a range of conditions [24,25].

McNamara et al. [26] showed that within-population variation is especially important for the success of exit strategies. They modelled an infinite population where variation in individuals' cooperativeness was maintained by extrinsic factors like mutation and phenotypic noise. Individuals paired up at random and played a maximum of N rounds of the Prisoner's Dilemma. If any member of the pair defected at any round then the pair split up. The computations showed that a population of defectors evolved if within-population variation was low. In this case, because every individual plays the same strategy, an individual can be certain that their partner will defect at the population mean of cooperativeness. In such a situation, it is best to pre-empt the partner's defection and to defect one round ahead. This quickly led to a population where everybody was a defector. The situation dramatically changed if the level of variation was high. In this case, there is a good chance that an individual will meet a partner who is much more cooperative than the population average. Interacting with such a partner means a long period of cooperative interactions leading to high benefits. These benefits offset the costs caused by interacting with a partner who is less cooperative than the population average. Consequently, under high variation the best response of an individual became to be more cooperative than the average level of cooperativeness in the population. Therefore, a population of cooperators evolved.

The above model illustrates that partner choice can facilitate the evolution of cooperation in variable populations. This model was, however, based on the assumption that individuals who have been cheated opt out from the interaction. But how realistic is this assumption? It is reasonable to assume that cooperation emerges from the ancestral strategy of no cooperation. In such a uniform population, however, an exit strategy has no selective advantage (see above) so it is unlikely that exiting is part of an individual's behavioural repertoire at this stage. This means that the emergence of cooperation would require the evolution of ‘two complementary functions' [27]: cooperation and exiting. The problem is that, in terms of selective advantage, neither of them makes sense without the other, an ‘evolutionary problem of bootstrapping’ [27]. McNamara et al. [28] show that a gradual coevolution between cooperation and choosiness can be a solution to this bootstrapping problem.

In their model, McNamara et al. [28] considered an infinite population. Individuals were characterized by two genetically determined traits, cooperativeness and choosiness. Cooperativeness defined the effort an individual invested in a pairwise game. An individual's gain from the dilemma depended on (at least partly) the effort of their partner, while its cost was determined by their own effort alone. As a consequence, there was a conflict of interest, i.e. each partner preferred the other to invest more. After playing the game, both members reproduced proportionally to their payoffs. The offspring entered the pool of single individuals. After each round of investment, paired individuals decided whether to continue with the current partner or not. This decision was governed by the individual's other trait, choosiness which defined the minimum acceptable effort of the partner. If the partner provided less effort than this threshold, then the individual discontinued the interaction and both members became single. Zero choosiness means that an individual is non-discriminatory: it accepts anyone as a partner. Single individuals paid a search cost to establish a new interaction with a randomly chosen new partner. It can be shown that the non-cooperative, non-discriminatory state is evolutionarily stable in this model if the level of variation is small [28]. On the other hand, when there is considerable individual variation in both cooperativeness and choosiness, a cooperative and choosy population evolved. In this case, a positive correlation between cooperation and choosiness emerged because individuals having opposing traits obtained particularly low payoffs. Those who were more cooperative but less choosy were easily exploited. On the other hand, choosy and non-cooperative individuals spent most of their time searching for cooperative individuals who then likely rejected them. From those individuals who had similar traits, the ones who were cooperative and choosy had a higher payoff than those who were non-cooperative and non-discriminatory, because the former ones could take part in long periods of cooperation while the latter could not exploit them. This resulted in a cooperative and choosy population.

This model nicely illustrates how coevolution between assortment (choosiness) and helping leads to the emergence of stable cooperation. Here, evolution could overcome the problem of bootstrapping because the two traits gradually changed and high within-population variation made possible a well-defined positive correlation between them.

To conclude this section, we should note that cooperative traits seem to be variable in many populations [11] and, at least in humans, individuals frequently break off links to defectors [29].

4. State differences

An individual can be characterized by many attributes, such as colour, size or age. Out of this myriad of attributes we label as state variables those that can heavily influence the costs and benefits of an individual's behaviour [30]. As a consequence, an organism's fitness maximizing behaviour should depend on the state variables [30]. These variables may include characteristics of the individual itself such as its morphology, levels of hormones or parasite load. Attributes of the individual's environment, such as spatial position or territory quality, can also contribute to its state. Furthermore, state can include aspects of the social environment such as aggressiveness of group mates, number of social ties or quality of mate [30].

State can influence behaviour: for instance, feather quality may alter flight efficiency and hence foraging behaviour. Behaviour can also affect state: for instance, a bird can improve the quality of its feathers by moulting [30]. State may also change as a consequence of environmental effects like UV radiation that continuously degrades feather quality. Owing to the inherent stochasticity in behaviour and the environment, individuals are usually not in identical states. In §§4(a–c), I investigate how these state differences influence cooperative behaviour.

(a). Food sharing

Sharing food is a common behaviour in humans, such as at feasts at gatherings of relatives or friends. It is likely that this is not just a modern behaviour. Studies in hunter–gatherers suggest that food sharing may have been common in the past. For instance, successful Hadza hunters regularly share meat with others, often non-relatives [31]. The two best documented examples in animals are those of blood sharing in vampire bats [32] and meat sharing in chimpanzees [33]. In both cases, the owners of food actively offer a meal to others. If we define food sharing in a broader sense, without the requirement for active offering [34], many other common behaviours can qualify as food sharing. A prominent example can be the extensively studied behaviour of scrounging (see below) [35].

Even early models emphasize the role of inter-individual variation in the evolution of food sharing. For instance, Blurton Jones [36] argued that additional food items are worth less and less for the discoverer of a food patch as it becomes satiated. As a consequence, it tolerates theft by a hungry latecomer. Winterhalder [37] showed that food sharing can reduce the risk of starvation in strongly stochastic environments, where each individual's foraging success varies erratically and independently of others. These early analyses were, however, not based on a game theoretical argument [34]. In Winterhalder's model, for instance, all individuals searched for food and shared it with all other individuals in the group, meaning that a sharer could be sure that its help would be returned.

Whitlock et al. [38] provided a game theoretical treatment of food sharing based on explicit individual differences in resources. They assumed that the value of additional resources diminishes with increasing resources. As a consequence, the cost of sharing is small for an individual with a high level of resources while the benefit of receiving food is large for an individual with low resources. By investigating pairs of individuals interacting, Whitlock et al. [38] found that reciprocal food sharing can be evolutionarily stable if an individual's level of resources changes frequently and unpredictably. Their model, however, does not contain enough ecological details to reveal under what environmental circumstances these results are plausible.

The producer–scrounger paradigm can provide a way to model food sharing in a more detailed ecological setting [35]. In these models, individuals can choose one of the two foraging tactics, producer and scrounger. Producers actively search for food, consume part of each patch they find and share the remainder with scroungers. Scroungers, on the other hand, search for individuals who have just found food, then rush in and take their share. A producer can only feed from patches it found itself, while scroungers are assumed to feed only from patches found by producers. Hence, producers can be considered as cooperators producing public goods (food patches), while scroungers are free-riders. By explicitly modelling the foraging process in a stochastic environment, Caraco & Giraldeau [39] were able to calculate the probability of survival for both producers and scroungers. Over most of the parameter space, they found that producers and scroungers could coexist as in an evolutionarily stable strategy, although the probability of survival was lower in the mixed groups (where food is shared) than in the unstable pure producer groups (where food is not shared). Because of this, producer–scrounger games are usually considered as games of exploitation [35]. This argument suggests that food sharing, at least under the producer–scrounger scenario, is far from being a cooperative act that increases the individual's payoffs. This should not always have to be so, however.

In a state-dependent dynamic game model of producing and scrounging, Barta & Giraldeau [40] found that food sharing could increase an individual's payoffs at evolutionary stability. In the model, individuals based their strategy on their energy reserves. In the evolutionarily stable strategy, individuals with low reserves played scrounger while individuals with high reserves played producer. This differential use of tactics is rooted in the risk-sensitive properties of the foraging process. Using the scrounger tactic provides a relatively small but reliable amount of food, because scroungers could feed from many patches discovered by several producers, but they also had to share the food with other scroungers and the producer who originally found the patch. On the other hand, producers obtained more food from a patch than scroungers because they could consume part of the patch alone before the arrival of scroungers. Nevertheless, they found patches at a low rate because they could only rely on their own search effort. Consequently, an individual with low reserves should play scrounger because the small but reliable amount of food obtained can prevent starvation. Although a producer gains more food from a patch than a scrounger, the high variance in its patch-finding success results in a high probability of starvation when reserves are low. Therefore, individuals play scrounger if reserves are low. When many in the group use the scrounger tactic then it pays off to play producer. This can be safely done if reserves are high.

By explicitly modelling the environment, the authors found that this reserve-dependent food sharing strategy yielded higher daily survival than if all food obtained from a patch was retained by its producer when the distribution of food was highly aggregated or patches contained many food items. Under these circumstances, the cost of sharing is small if the sharer has high reserves since (i) a patch contains a lot of food and (ii) the value of additional food diminishes as reserves increase because of the accelerating metabolic and predation costs of energy reserves [41]. Furthermore, the benefit of sharing is high if the recipient's reserves are low because low reserves mean high probability of starvation, especially if food occurs in aggregated, hard-to-find patches. The above reserve-dependent strategy ensured that food is provided by those who pay the least for sharing and received by those who need it most.

This reserve-dependent strategy allows the efficient assortment of cooperators without any advanced cognitive ability. Individuals share food if they have high reserves, but they can only have high reserves if they have previously received food; in other words, they only help if they have been helped previously. Under this strategy, it is not important who provides help and who is the recipient. The only important point is that high reserves signal a cooperative social environment. It follows that food sharing in this setting can be considered a form of generalized reciprocity [42], rather than direct reciprocity [38]. Indeed, Barta et al. [43] showed that generalized reciprocity can spread in a population of cheaters if individuals base their decision to help or not on a state variable that increases by the amount of help received. Real organisms seem to follow this reserve-dependent food sharing strategy. For instance, Lendvai et al. [44] found that house sparrows (Passer domesticus) whose reserves were experimentally reduced played scrounger more frequently than sparrows in the control group.

(b). Parental care

Parental care improves the offspring's survival and reproductive success at a cost to the caring parent. As a consequence, a strong conflict of interest emerges, because each parent prefers the other to care more [45]. It seems that the details of the decision mechanism have a strong influence on the solution of this dilemma and hence the resulting pattern of care [30]. A crucial aspect of the decision process is the order of decision. Parents can decide about care simultaneously, i.e. the partner's decision is not known when a parent is making its own decision. On the other hand, the decision can be sequential, when the parent deciding second knows the decision of its partner who decided first. By developing a dynamic game model of parental care, McNamara et al. [46] found that the sex deciding first, e.g. males, can ‘force’ the other sex, e.g. females, to care by deserting first, even if the male would care in the simultaneous case. A completely different scenario emerged, however, when Barta et al. [47] introduced energy reserves in a similar game. In this case, an individual had to have reserves above a critical level in order to be able to care. If its reserves were below this level, then it had to desert the offspring to avoid starvation. The authors assumed that parents know their own reserves as well as their partner's reserves. In this model with energy reserves, the female circumvented the male's tactic: by keeping her reserves below the critical level she could not be forced to care if her partner deserted. Consequently, the male had to care and the female could desert [47]. The above result holds when the critical levels of reserves for uni- and biparental care were the same. An interesting pattern emerged if the critical limits for uni- and biparental care differed; individuals needed more energy to care alone than to care with a partner. In this case, the parents cooperated and biparental care emerged in the model [47]. This happened because the difference between the limits for uni- and biparental care allowed both parents to force the other to care. In order to force the male to care the female had to decrease her reserves below the uniparental limit, but not lower. This meant that she kept her reserves between the two limits, and so was still able to bear the cost of biparental care. This, in turn, allowed the male to lower his reserves below the limit of uniparental care and hence forced his partner to care as well.

(c). Partner's state unknown

As we have seen in §4(b) an individual should not pay attention to its own state only; in a social situation, the state of its partner(s) should also be considered. For instance, a high-quality parent might compensate for the less effective care of a low-quality partner. A problem, however, arises if a partner's quality cannot be known in advance of the focal individual's decision.

In a parental care dilemma (see §4b), McNamara et al. [48] assumed that individuals differ in their quality but only the partner's actions (i.e. its investment into the common goods, the offspring) and not its quality could be observed. As individuals differed in their cost of investment (low-quality individuals paid a higher cost), they would differ in their level of investment and there should be selection for responding to a partner's actions rather than choosing a fixed action. In other words, individuals should use not an evolutionarily stable action but rather an evolutionarily stable negotiation rule [48]. However, always choosing the action that best responds to a partner's action [49] cannot be evolutionarily stable because it is easily exploitable [48]. The authors were able to show that for a reasonable set of assumptions the evolutionarily stable negotiation rule is linear; an individual should increase its contribution to the common good if the contribution by its partner decreases [48]. Nevertheless, this compensation is only partial, as an individual increased its investment by less than the partner decreased it [50]. McNamara et al. [48] made two important observations. First, parents provided less total effort if they used the negotiation rule than if they used the evolutionarily stable action. Second, this difference between the amounts of effort invested remained even if the level of variation in quality became negligibly small. As a consequence, offspring may receive more care if only one parent cares for them than if both do [51,52].

In a context in which individuals meet different partners rather than having repeated interactions with the same partner McNamara & Doodson [53] found comparable results. In this model, individuals also differed in quality and the lower their quality was, the less they invested into the common good. Investment with previous partners determined an individual's reputation. Quality could not be directly observed, but current behaviour was correlated, although not perfectly, with an individual's reputation. It therefore paid off to take a partner's reputation into account when deciding about investment in the current round. As the strategy of responding to reputation spread in the population, individuals changed their behaviour to alter their future partners' behaviour through their changed reputation. This feedback mechanism changed the level of cooperation compared to the level that evolves in a population without consideration of reputation. The direction of change depended on the details of the payoff structure of the game. If an individual's best response investment increased as the partner's investment increased then the feedback mechanism increased the level of cooperation. The authors argued that this scheme may correspond to predator inspection in fishes. On the other hand, if the best response investment decreased with partner's increasing investment, reputation had an opposite effect: the level of cooperation decreased. Parental care usually falls into this category. McNamara & Doodson [53] highlight that variation in the quality of individuals was crucial for the above process. Variation made it worth responding to reputation and also guaranteed that reputation conveyed reliable information.

5. Social ties

Variation in an individual's social environment can also affect the evolution of cooperation, as a study of social networks by Santos et al. [54] indicates. Individuals in this model played a public goods game with their immediate neighbours in the network, i.e. in their neighbourhood. Individuals also took part in public goods games of the neighbourhoods centred on their neighbours. Cooperators invested a given amount into the public good, which was then multiplied by an enhancement factor and the resulting gain was equally divided between all members of the neighbourhood. The effect of variation was investigated by altering the network structure. Regular networks, where each individual has the same number of neighbours, served as the baseline of uniform population. Santos et al. [54] used scale-free networks to introduce variation in social ties. In a scale-free network, the number of neighbours follows a power distribution, meaning every individual can have a different number of neighbours.

Variation again had a dramatic effect on the evolution of cooperation. Cooperators spread at a significantly lower value of the enhancement factor in scale-free networks than in regular networks. In this model, a cooperator's gain increased with the number of its neighbours. Consequently, cooperators could occupy network positions with many neighbours (hubs) even if all of their neighbours were defectors. Moreover, they were able to invade neighbouring positions from hubs. Defectors gained more from being in hubs if these hubs were surrounded by cooperators. But this success worked against them because as they spread, they replaced neighbouring cooperators with defectors which in turn led to a significant reduction in their fitness. Then cooperators from neighbouring hubs could easily take over the defectors' hubs, from which they could spread further.

6. Task specialization

An important consequence of individual variation may be the possibility of task specialization. Individuals often have to perform several different activities, or tasks, to survive and reproduce. For instance, they have to search for food and be vigilant for predators at the same time. Similarly, in many bird species parents must feed, brood and defend their offspring [7]. Theory [55] predicts that in a single organism, division of labour, i.e. specialization for different tasks by different units (cells/organs), can be beneficial if (i) different units are predisposed for different tasks, (ii) specialization accelerates effectiveness of task performance, or (iii) there are synergistic effects between differently specialized units. One would expect that task specialization may also pay off for individuals living in groups or caring for common offspring. Nevertheless, to reap the benefits of task specialization individuals must cooperate, for instance by sharing food or information about predators or providing biparental care [56]. In turn, task specialization may boost the benefit of cooperation. Therefore, it is reasonable to assume that cooperation can evolve more easily under conditions promoting task specialization. Large inter-individual variation, when different individuals can perform different activities with different efficiencies, may provide such a condition.

Barta et al. [56] investigated this proposition in a parental care game. In the model, individuals could be either single (available to mate) or engaged (not able to mate because they were caring for offspring) [57]. Reproduction fulfilled the Fisher condition, i.e. each young had exactly one mother and one father [57]. This generated a self-consistent density-dependent process of mating where the sex in the minority enjoyed a mating advantage. As a consequence, any asymmetry, for instance in level of sexual selection or mortality between the sexes, quickly led to uniparental care. Caring in this model [56] meant performing two separate activities such as feeding the young and defending the nest. The young's survival was the highest if they received equal amounts of both types of care. Caring parents could decide (i) their total amount of care and (ii) the allocation of their effort between the two types of care. Cost of care monotonically increased with its total amount and it also depended on the pattern of allocation. The authors considered three scenarios: (i) for a given total level of effort, allocation had no effect on cost; (ii) sexes differed in their skills, i.e. one sex paid less cost for performing one type of care, while the other was more efficient in the other type of care, and (iii) simultaneously providing both types of care incurred an additional, synergistic cost. In this last case, the sexes were the same; they paid the same synergistic cost for allocating into both types of care.

Sexual selection was strong on males and allocation did not affect the cost of care in the baseline case. This resulted in unspecialized female care, an uncooperative solution. When skill differences were introduced, males and females provided only those types of care in which they were skilled and the pattern of care became biparental despite the maintenance of strong sexual selection on males. Recalling the problem of bootstrapping above (§3) [27], one may wonder how this can happen since strong sexual selection means that males should desert the young and remate. However, skill differences meant that a deserted female suffered an additional risk of mortality because she had to perform both tasks to successfully raise the young. Therefore, there were fewer single females in the population, decreasing the males' benefit from desertion. As a result, males started to devote more time to care. This, in turn, allowed females and males to specialize. Increasing specialization further decreased the gain from desertion because if a specialized partner was deserted it could not provide both types of care, leading to increased offspring mortality. This again acted to increase the frequency of biparental care which, in turn, strengthened specialization further. This self-reinforcing coevolutionary process then quickly settled down in a stable population where specialized individuals permanently cooperated with each other. Employing the synergistic cost scenario led to the same result: a stable population of cooperating individuals who were specialized in one type of care. This happened for basically the same reason as in the case of skill differences. Synergistic cost of care reduced the number of single females in a population where most males desert. This then increased the frequency of caring males, allowing specialization to start and leading to the further increase of biparental care. Here, interestingly, the possibility of cooperation created inter-individual variation in a population of uniform individuals, a variation which cultivated and then stabilized cooperation.

A crucial aspect of the model presented here was that offspring need two types of care. If benefits from care types did not combine synergically, no task specialization and, in turn, no cooperation would evolve [56]. Task specialization may occur even if only one task is considered in the sense that parents become more and more efficient at performing the given task. Nevertheless, allowing an increase of efficiency can easily result in uniparental care as McNamara & Wolf [58] have pointed out. It still remains to be seen what happens if the two scenarios, (i) two tasks and (ii) evolving cost of care, are combined.

7. Conclusion

This review of selected models illustrates that inter-individual variation can influence the evolution of cooperation in many ways. It can change the future expectation [26]. It can also open up new behavioural options; for example, partner choice only becomes meaningful in a variable population [28]. Interaction between energetic state and environmental stochasticity can tip the cost-to-benefit ratio towards favouring cooperation [38]. Allowing individuals to differ according to state variables further broadens the possibilities for the evolution of cooperation. State can serve as a signal about the cooperativeness of the social environment [40,43]. This assumes that state is easy to change, like readily mobilizable energy reserves. If state can only change on a much longer time-scale, like the accumulation of nutrition for reproduction, then state can serve as ‘credible threat’, which alters the information structure of the social dilemmas facilitating cooperation [59]. Differences in individuals' ability and skills can advance task specialization which, in turn, can promote the emergence of cooperation [56].

These models demonstrate that it is not necessary for variation to have a well-defined characteristic to facilitate the emergence of cooperation. For instance, variation should be inconsistent, that is the direction and magnitude of individual differences should change frequently and unpredictably, for variation in state to serve as a signal of cooperativeness. Nevertheless, when skill differences, credible threats or differences in cooperativeness drive the evolution of cooperation, then differences between individuals should be stable and consistent. This raises the possibility that animal personality might facilitate the evolution of cooperation. As a consequence, one may expect more strongly expressed personality traits in more cooperative populations.

Given that errors in games of reciprocal helping can greatly influence the outcome of the evolution of cooperation [60], one may wonder to what extent the effect of variation depends on the ability of organisms to reliably assess inter-individual differences [61]. For instance, in parental care games where one parent tries to force the other to care by its strategic regulation of reserves [47], the success of this strategy critically depends on how reliably the partner can estimate the state of the strategic regulator. In this case, however, it is in the regulator's best interest to convey honest information about its own state, and therefore accurate information transfer is expected. McNamara et al. [26] explicitly modelled the effect of phenotypic noise in their exit strategy model of cooperation. They found that as long as there is some genetic variance behind the behavioural variation, phenotypic noise does not affect how variation drives the evolution of cooperation. Similarly, McNamara & Doodson [53] found that the quality of the data on the partner's previous behaviour and hence its state did not influence the outcome of evolution considerably. In games where the evolution of cooperation is influenced by variation in the individuals' own state [40,43], it is reasonable to expect that individuals can accurately estimate their own reserves. As a consequence, one might safely conclude that the accuracy of assessment of inter-individual differences does not seriously affect the results presented here.

All but the food sharing and social tie models reviewed here consider pairwise interactions, where pairs are randomly chosen from large, often infinitely large populations. As a by-product, no population structure is considered in these models. Nevertheless, natural populations are usually structured, frequently into groups. Group structure may, in turn, permit several processes that act against inter-individual variation. For instance, group living can facilitate social learning, leading to reduced behavioural variation within groups. Group-level selection may also result in reduced within-group variation. At the moment, however, it is unclear how population structure influences the evolution of cooperation through its effect on inter-individual variation. To investigate this issue, we need further models where population structure and inter-individual variation are considered together.

To summarize, inter-individual variation, whether consistent or inconsistent, can play a major role in the evolution of cooperation. This is well supported by theoretical models, but interesting questions still remain. For instance, we do not know, apart from the case of task specialization, whether circumstances favouring cooperation, e.g. low cost-to-benefit ratio, could lead to the increase of inter-individual variation. Even less is known about the relationship between variation and cooperation in the real world. This is a difficult question because to empirically investigate the effect of variation, the composition of whole groups should be compared or manipulated. Nevertheless, studying alternative routes to cooperation, like the role of variation, seems to be a promising future avenue of research.

Competing interests

I declare I have no competing interests.

Funding

The publication was supported by the SROP-4.2.2.B-15/1/KONV-2015–0001 project. The project has been supported by the European Union, co-financed by the European Social Fund.