Negotiation and appeasement can be more effective drivers of sociality than kin selection

Abstract

Two alternative frameworks explain the evolution of cooperation in the face of conflicting interests. Conflicts can be alleviated by kinship, the alignment of interests by virtue of shared genes, or by negotiation strategies, allowing mutually beneficial trading of services or commodities. Although negotiation often occurs in kin-structured populations, the interplay of kin- and negotiation-based mechanisms in the evolution of cooperation remains an unresolved issue. Inspired by the biology of a cooperatively breeding fish, we developed an individual-based simulation model to study the evolution of negotiation-based cooperation in relation to different levels of genetic relatedness. We show that the evolution of negotiation strategies leads to an equilibrium where subordinates appease dominants by conditional cooperation, resulting in high levels of help and low levels of aggression. This negotiation-based equilibrium can be reached both in the absence of relatedness and in a kin-structured population. However, when relatedness is high, evolution often ends up in an alternative equilibrium where subordinates help their kin unconditionally. The level of help at this kin-selected equilibrium is considerably lower than at the negotiation-based equilibrium, and it corresponds to a level reached when responsiveness is prevented from evolving in the simulations. A mathematical invasion analysis reveals that, quite generally, the alignment of payoffs due to the relatedness of interaction partners tends to impede selection for harsh but effective punishment of defectors. Hence kin structure will often hamper rather than facilitate the evolution of productive cooperation.

1. Introduction

Cooperation constitutes the basis of all higher forms of biological organization. However, it is not straightforward to explain why an individual would help another when this is associated with fitness costs [1]. One explanation for the spread of a cooperative behaviour in a population is that the benefits of cooperation are more frequently directed towards other cooperators than towards defectors [2,3]. Such assortment arises naturally at the genetic level in populations with limited dispersal, or when individuals interact preferentially with relatives [1,2]. Alternatively, cooperation can arise when individuals respond to the actions of others [4–6]. Responsive strategies can favour cooperation through a range of different mechanisms; for example, when individuals reciprocate help received from others [4,5], when individuals choose their interaction partner based on its previous actions [7–9] or when individuals punish uncooperative partners [10]. Genetic assortment and responsive strategies are central to the two most prominent frameworks for explaining the evolution of cooperative behaviours: kin selection theory [1,2] and the theory of reciprocal altruism [5,11]. Most studies on cooperative behaviour among animals focus on either one or the other explanatory concept, but the two mechanisms are not mutually exclusive and, in fact, often act simultaneously [12,13]. Moreover, the coexistence and collaboration of both related and unrelated individuals within breeding groups is widespread in social animals [13,14].

In the theoretical literature, there is a lack of consensus about the consequences of the simultaneous action of relatedness and responsive strategies for the evolution of cooperation. Marshall & Rowe [15] suggested that relatedness prevents the evolution of reciprocal cooperation because relatedness weakens selection for effective retaliation against defectors. By contrast, Van Veelen et al. [16] found that relatedness increases the prevalence of reciprocal cooperation, and explained this by the fact that assortment of strategies prevents the ‘indirect invasion’ of defectors; that is, when cooperative but unresponsive strategies pave the way for defectors. Mengel [17], finally, argued that relatedness does not have a monotonic effect on the prevalence of cooperation when strategies are responsive. A common feature of these models is that they use the game-theoretical framework of the Iterated Prisoners Dilemma (IPD), a generic, abstract model of cooperation, in which cooperative interactions are detached from their ecological and life-history context [18]. Therefore, it is not straightforward to determine which of the contrasting theoretical models is applicable to a given biological example of cooperation. To address this problem, we here model cooperative interactions of which the fitness costs and benefits derive explicitly from the life histories of individuals, inspired by a well-studied biological system that is very suitable to analyse how kin selection and responsive strategies interact when generating cooperation. To complement our simulations for this particular model system, we also develop a general mathematical argument to illustrate the formal logic behind our main results.

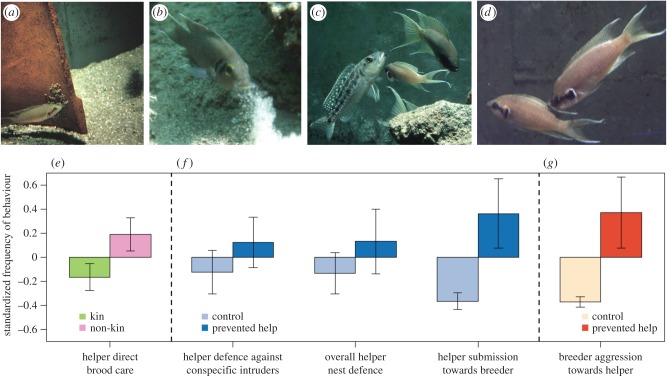
We first present an individual-based simulation model that is inspired by the cooperatively breeding cichlid Neolamprologus pulcher, where dominants and subordinates negotiate their levels of aggression and help [19]. This system is particularly well suited to understand the interaction of kin selection and responsive strategies [19–23]. Neolamprologus pulcher live in social groups in which related and unrelated individuals interact repeatedly with one another [21,24]. A group typically consists of a dominant breeding pair that largely controls reproduction, and several subordinates. Subordinates help in tasks related to nest maintenance and offspring care [23] (figure 1a–c). Small subordinates help in egg cleaning (figure 1a). Large subordinates dig out sand (figure 1b), in order to maintain or enlarge the size of the nest, and fight away egg predators (figure 1c). The observed alloparental care is not easily explained by kin selection. In fact, N. pulcher subordinates provide less (rather than more) care when they help a related dominant [22] (figure 1e). A plausible alternative hypothesis is that helping results from a negotiation between the dominant and the subordinate, involving responsive strategies on both sides [19,26]. According to this ‘pay-to-stay’ interpretation [26,27], the breeder allows the helper to use vital resources in a safe territory in exchange for the provided help [19,28]. The other side of the bargain, which is more difficult to demonstrate, is that helping is enforced by aggression and threats of eviction on the side of the dominant [29]. In fact, aggressive enforcement of help by breeders is rarely observed, and the overall level of aggression is low [19] unless aggression is provoked by experimentally preventing subordinates from helping [25] (figure 1g).

Figure 1.

Helping and aggression in the cooperatively breeding cichlid Neolamprologus pulcher. Subordinate helpers show brood care by cleaning the eggs of breeders (a), by performing nest maintenance such as digging out sand (b), and by defending the territory against predators, such as Lepidiolamprologus elongatus (c). Presumably, these helping behaviours are mediated by aggression from the breeder. In (d), a breeder (right) shows aggression towards a subordinate, and the subordinate responds with submissive behaviour (tail quiver). Panels (e–g) summarize results from experimental manipulations reported in previous studies. Bars show the mean of the standardized frequency of behaviour. Standardization was done by subtracting the mean from each data point and dividing by the standard deviation. Error bars are given by the standard error of the standardized frequency of behaviours. (e) Unrelated helpers (purple) provide more help than related ones (green; [22]). (f) After subordinates have been prevented from giving help (dark blue), they compensate by increasing their previous help and submission level (light blue), presumably in an attempt to appease the breeder [19,25]. (g) Aggression levels in the group are normally very low (cream), but they increase considerably when subordinates are experimentally prevented from helping (red; [25]).

Cooperative breeding in N. pulcher is no exception among other well-studied examples of cooperative behaviours in the wild, in that the roles of kin selection and responsive strategies in shaping the social system cannot easily be disentangled. It is not clear if and how the interaction between them has contributed to the evolution of cooperation. To bridge this gap, we model the evolution of behavioural mechanisms by which individuals respond to social partners in repeated interactions, in group-structured populations with varying degrees of relatedness. The interaction between group members in our model is captured by a negotiation process, where partners respond to each other by exchanging offers and counter-offers.

2. The model

(a). Overview

We consider a population with a large number of breeding territories each of which can harbour at most one breeder and at most one potential helper. Only breeders produce offspring. In the absence of helping, the presence of another individual on the territory reduces the fecundity of the breeder; therefore, a breeder will have the tendency to evict other individuals that are not willing to help. For non-breeders, it is beneficial to stay on a breeding territory, since otherwise they have to become floaters, and the survival probability of floaters is considerably lower than the baseline survival probability on a territory. However, being allowed to stay on a territory may require a ‘payment’ to the breeder in terms of helping (‘pay-to-stay’ [19,26]), and helping has a negative effect on the helper's survival.

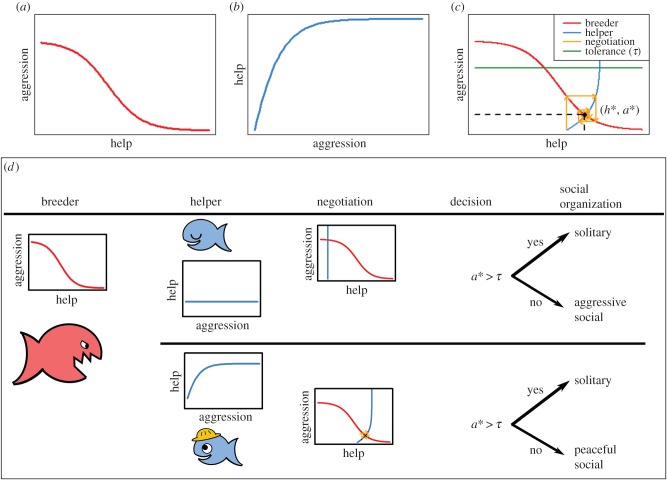
Whether a breeder accepts a helper in the territory depends on the outcome of a negotiation process at the time that a vacant helper position becomes available. The course and outcome of the negotiation process is determined by the ‘behavioural norms of reaction’ [17,30] of the breeder and the prospective helper (figure 2). The reaction norm of the breeder specifies the breeder's level of aggression in response to the level of help offered by the prospective helper (figure 2a). Conversely, the prospective helper's reaction norm specifies the helper's level of helping in response to the level of aggression received from the breeder (figure 2b). Thus, a change in the helping effort of the helper will evoke a change in the aggression exerted by the breeder, which in turn will induce an adjustment of the level of help provided by the helper. In the process of repeatedly responding to each other's actions, the two individuals typically converge to a stable equilibrium of aggression and help (figure 2c, [30,31]). At that stage the helper can decide to either stay in the territory or to become a floater (figure 2d). This decision depends on whether or not the aggression level of the breeder is higher than the aggression tolerance threshold of the helper.

Figure 2.

Model for the negotiation of help between a dominant breeder and a subordinate helper. (a) The behaviour of the breeder is determined by a reaction norm that defines the breeder's level of aggression in response to the level of help received. (b) The behaviour of the helper is determined by a reaction norm that defines the helper's level of help in response to the level of aggression received. Both reaction norms are heritable strategies that evolve in the course of the generations. (c) Plotting both reaction norms in one graph (thereby swapping the axes of graph b) gives a graphical illustration of the negotiation process. After a sequence of moves and counter-moves, the breeder and the helper settle at a negotiation equilibrium (h*,a*). The green line indicates the inherited tolerance level τ of the helper; the helper leaves if the negotiated aggression a* exceeds this threshold. (d) Different outcomes of the negotiation process. Depending on the helper's reaction norm, the same breeder can be more or less aggressive; helpers can stay or leave depending on their tolerance level and on how much aggression they receive.

Both behavioural reaction norms and the aggression tolerance threshold of the helper are heritable, and they evolve subject to mutation, genetic drift and natural selection. The question is whether a pair of reaction norms will evolve that leads to a high level of helping, and how much aggression is necessary to maintain helping behaviour. Furthermore, we investigate how genetic relatedness between the two partners affects the evolution of these reaction norms.

(b). Negotiation strategies

The responsive behaviours of the individuals in the negotiation phase are governed by two reaction norms, which are modelled as logistic functions

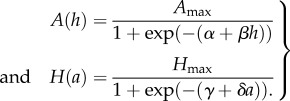2.1

The amount of aggression A(h) elicited by a helper providing an amount h of help is determined by the three heritable parameters A_max, α and β. A(h) is a sigmoidal function that varies between 0 and A_max. If β is positive, the aggression level increases with the amount of help provided; if β is negative, A(h) decreases with h. The slope parameter β determines the steepness of the breeder's reaction norm, and together the two parameters α and β determine the point of inflection of the sigmoidal curve A(h) (which is located at h = −α/β). Likewise, the amount of help H(a) elicited by a breeder with aggression level a is a sigmoidal function that is determined by the three heritable parameters H_max, γ and δ.

For a given pair A(h) and H(a) of reaction norms, the dynamics of the negotiation process is governed by the pair of recurrence equations

2.2

Depending on the reaction norms, the negotiation process may converge to a stable equilibrium level of helping that satisfies the equation h* = H(A(h*)), and an associated level of aggression satisfying a* = A(H(a*)).

The decision of the helper to stay or to leave depends on the heritable aggression tolerance τ of the helper. We assume that a helper will leave when

2.3

where ɛ_a is drawn from a normal distribution with mean 0 and standard deviation σ_a. Hence, we assume that aggression tolerance is subject to some error of size ɛ_a.

(c). Survival and reproduction

Our model is implemented as a stochastic, individual-based computer simulation. The simulation programme keeps track of a population of individuals, who are followed through their individual life histories. Generations are overlapping, and proceed in discrete steps, corresponding to distinct events in the life cycle. Each cycle starts with the removal of individuals by mortality, followed by the renewed colonization of sites that have become vacant and, finally, the production of offspring.

Floaters survive with probability S_F per time step. The survival probability of a breeder (S_B) depends on the costs associated with exhibiting aggressive behaviour, while the survival probability of a helper (S_H) depends on the cost of helping and the cost of being the target of aggression. In the case of a level of aggression a and a level of helping h, these survival probabilities are given by

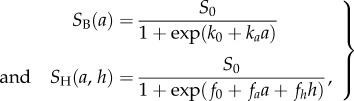2.4

where S₀ is the baseline survival probability on a territory, k_a is a parameter that quantifies the cost of aggression for the breeder; f_a and f_h are parameters determining how costly aggression and help are for the helper, respectively. The use of a logistic function for the survival functions reflects a scenario where survival is weakly affected when aggression and help levels are low, but where the fitness costs increase sharply beyond a certain level that can be set by modifying the parameters k₀ and f₀, for breeders and helpers, respectively.

Reproduction is monopolized by the breeder in a territory. The breeder's baseline fecundity F₀ is affected by the presence of a helper according to the function

2.5

where B quantifies the fecundity benefits gained from help provided by the helper, while C represents the fecundity costs that are incurred by accepting another individual in the territory.

Parameter values of the survival and fecundity functions were chosen in agreement with life-history data from N. pulcher. However, in the view of the uncertainty of some empirical estimates and their indirect correspondence to model parameters, we performed a sensitivity analysis to evaluate the robustness of our results (for details see the electronic supplementary material and figure S4).

(d). Recruitment and relatedness

Breeder mortality creates empty breeding positions that can be filled by helpers (on any territory) or by floaters. The two types of individuals compete for a vacant breeder position. We allow for the possibility that helpers and floaters differ in competitive ability, and we denote the relative competitive ability of a helper (in comparison to a floater) by η. If η is larger than one, a helper has a higher probability than a floater of obtaining a vacant breeder position, while the opposite is the case if η is smaller than 1. More precisely, the probability that a given vacant breeder position is taken by a helper is

2.6

where u_F and u_H are the relative frequencies of floaters and helpers, respectively. Accordingly, the probability that a floater occupies the vacant breeder position is given by p_F = 1 − p_H. Local helpers are allowed to fill the vacant breeder position on their territory, but they are not more likely to do so compared with other helpers. Thus in our model, helping evolves only for the survival benefits that helpers gain from the safe haven, irrespective of their chances to inherit the local territory.

Helper mortality and the decision of helpers to leave create empty helper positions. Such a position is filled either by a floater or by an offspring of the local breeder. The probability that the new helper is recruited from the local offspring will be denoted by φ. The relatedness between breeders and floaters depends on the parameter φ and on the rate of replacement of breeders and helpers, which depends on the mortality of the individuals in the two classes. In order to assess the degree of relatedness between the interaction partners in our simulations, we use the regression coefficient of a linear regression of a neutral quantitative trait of the helper individuals on the trait value of the breeder [32]. We will systematically vary φ in order to investigate the importance of kin selection for the evolution of helping.

(e). Inheritance

The six parameters of the reaction norms, together with the tolerance threshold, are evolving parameters that are genetically determined by seven loci, one for each parameter. For simplicity, we assume that individuals are haploid and that they reproduce asexually. Offspring faithfully inherit the alleles carried by their parent at the seven loci, except when a mutation occurs. Mutations occur independently at each of the loci, at a low rate μ per locus and reproduction event. A mutation changes the value of an allele by a small amount drawn from a normal distribution with mean 0 and small s.d. σ_μ; hence the allelic value in the offspring is close to that of the parental allele.

3. Results

(a). Kin-selected helping in the absence of negotiation

In order to characterize the interaction of kin selection and responsive strategies, we first investigated the sole effects of relatedness by allowing the evolution of unresponsive strategies. To this end, the parameters β and δ that determine responsiveness in the reaction norms (equation (2.1)) were initialized at zero and not allowed to mutate. As a consequence, individuals express a fixed level of aggression or help, irrespective of the behaviour expressed by their partner. Figure 3 shows the level of aggression and help, averaged over the last 500 generations of each simulation, characterized by four different levels of philopatry (φ = {0,1/10,1/6,1/3). With low levels of philopatry, populations evolve high levels of aggression and no helping behaviour. In this equilibrium, breeders are aggressive in an attempt to evict idle helpers. It is only with the highest level of philopatry (φ = 1/3) that populations evolve to an equilibrium characterized by the presence of helping behaviour, and no aggression. Hence, in line with the predictions of kin selection theory, helping can evolve once there is sufficiently high genetic relatedness between actor and recipient. Notice that the evolved aggression level of the breeder is negatively related to the degree of philopatry and reduced to zero in case of the highest level of philopatry: there is no point in harming relatives that are increasing the breeder's fecundity.

Figure 3.

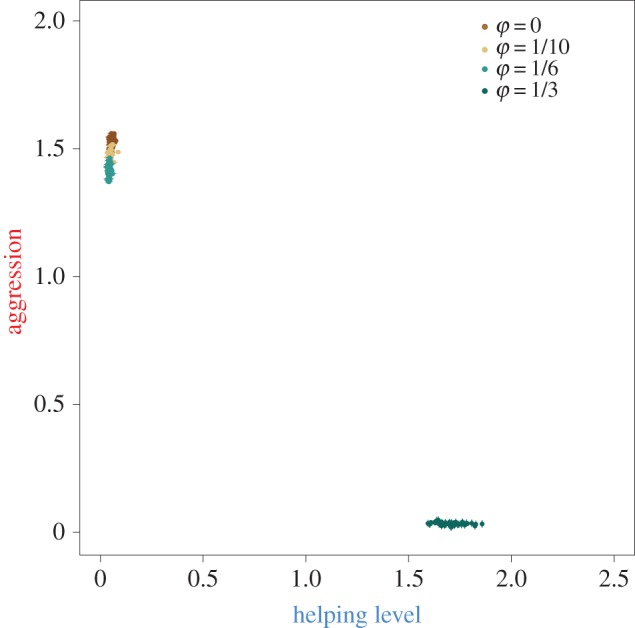
Evolution of kin-selected help in the absence of negotiation. Each point represents the evolved level of help and aggression in one, out of 50, replicate simulations when individuals are unresponsive. For each simulation, the levels of help and aggression were averaged over the last 500 generations; error bars represent standard errors. Colours discriminate different levels of philopatry used for the simulations. Helping only evolves under the highest level of philopatry (φ = 1/3), thus with the highest level of relatedness between interacting partners. All the other levels of philopatry (φ = {0,1/10,1/6}) yield populations with high levels of aggression and no help. The level of aggression is negatively related to the level of philopatry.

(b). Negotiation among unrelated individuals

If breeders and helpers can employ responsive strategies (i.e. if β and δ are allowed to evolve to non-zero values), helping does evolve, even if breeders and helpers are unrelated (φ = 0). As shown in figure 4, the behavioural reaction norms of breeders and helpers eventually evolve to a configuration where the amount of aggression elicited by the helper (A(h)) decreases with the help level h, while the amount of help elicited by the breeder (H(a)) increases with the breeder's level of aggressiveness a. Hence, the helpers are eventually prepared to pay an amount h* of help in order to be allowed to stay, and they actually do stay, since their evolved aggression tolerance τ is above the actual level of aggression a*.

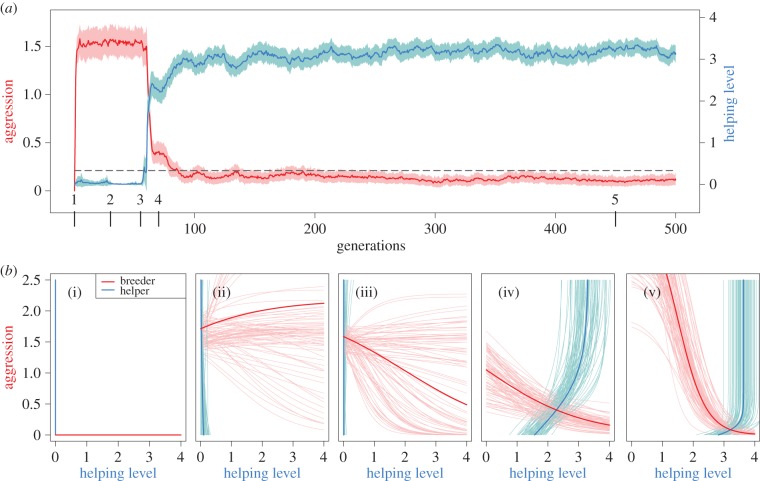
Figure 4.

Evolution of negotiated help. (a) Evolutionary dynamics of aggression (red line, left y-axis) and helping level (blue line, right y-axis) in a representative simulation run. Coloured bands represent 1 s.d. of the within population variation, above and below the mean. (b) Reaction norms of breeders (red) and helpers (blue) at five different points in time. (b(i)) Simulations start with unresponsive strategies that provide no help, and impose no aggression. (b(ii)) Breeders rapidly evolve high levels of aggression, thereby driving idle helpers out of their territories. (b(iii)) At some point in the simulation, the average reaction norm of the breeder (thick red line) becomes a decreasing function; (b(iv)) helpers in response evolve higher levels of help. Finally (b(v)), an evolutionary equilibrium results where helpers provide a high level of help, and breeders impose low levels of aggression.

As illustrated by figure 4, the negotiated pay-to-stay equilibrium is reached in several steps, with characteristic evolutionary transitions. Initially, individuals are unresponsive, but breeders quickly evolve high levels of aggression to evict lazy helpers (figure 4b(ii)). At this stage, there is little variation in helping behaviour, and only that part of the breeder's reaction norm A(h) that determines the breeder's response to small values of h is actually subject to selection. As a consequence, the other parts of the reaction norm start to vary under the influence of genetic drift. As soon as the slope of the breeder's reaction norm becomes negative on average (with considerable variation at the population level; figure 4b(iii)), helpers can reduce the amount of received aggression by providing help (figure 4b(iv)). As soon as some help is provided, there is selection in favour of a negative slope of the breeder's reaction norm. This in turn triggers the evolution of the helper's reaction norm to appease the breeder by providing sufficient help (figure 4b((v)).

Selection thus favours the evolution of responsive negotiation strategies that enable helpers providing more help to avoid the cost of aggression by appeasing the breeder, while allowing breeders to profit from the help induced by the threat to impose costs through aggression. The appeasement of aggression leads to an evolutionarily stable equilibrium in the population at which the breeder enjoys a net benefit from the presence of a helper. Moreover, because the mere threat of aggression suffices to secure help, the realized level of aggression during interactions is low. Thus, the two partners reach a compromise that satisfies their mutual interests. Contrary to expectations previously proposed [29], the evolutionarily stable negotiation equilibrium is characterized neither by high eviction rates nor by high levels of aggression.

(c). Negotiation among related individuals

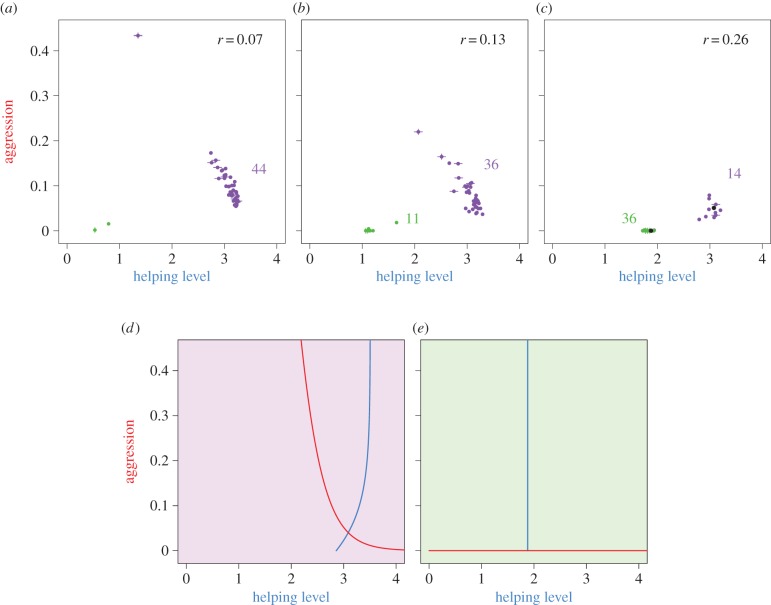
Next we allowed individuals to interact with relatives (φ > 0). We assessed the effect of genetic relatedness between the breeder and the helper on the evolutionary process by systematically varying the degree of philopatry of helpers. When the probability that helpers are recruited from their natal territory is low (figure 5a), resulting in a low degree of relatedness between helpers and breeder (r = 0.07), the reaction norms evolve in a similar way as shown in figure 4 (cf. figures 4b(v) and 5d). Breeders evolve a decreasing reaction norm, which allows helpers to appease the breeders' aggression by providing high levels of help. The interaction partners reach a negotiated compromise characterized by high helping levels and low aggression (figure 5d). However, when relatedness between interacting partners is higher, some simulations reach an alternative equilibrium (green points in figure 5b,c). The levels of help and aggression in this alternative equilibrium are very similar to the levels evolved under high relatedness in the unresponsive case (figures 3 and 5d). They both differ from the negotiated compromise by exhibiting lower levels of help and aggression; in fact, in both cases breeders do not show aggression at all.

Figure 5.

Effect of relatedness on the evolution of aggression and helping. Each point in (a–c) represents the evolved level of help and aggression in one, out of 150, replicate simulations. For each simulation, the levels of help and aggression were averaged over the last 500 generations; error bars represent standard errors. (a) When the relatedness between partners is low (r = 0.07), most simulations evolve to an equilibrium with a high level of help and a low but positive level of aggression. As relatedness is increased (b, r = 0.13; c, r = 0.26) an increasing number of simulations end up in an alternative equilibrium (green points), with a lower level of help and zero aggression. Simulation outcomes were classified as negotiated (purple) or kin-selected (green) on the basis of a k-means clustering algorithm [33]. (d) Evolved reaction norms in case of a negotiation equilibrium (black dot in the purple cluster in c); breeders and helpers respond to each other. (e) Evolved reaction norms in case of a kin-selected equilibrium (black dot in the green cluster in c); the two types of individuals are unresponsive.

The ‘kin-selected’ equilibrium, unveiled by high levels of relatedness, is the same equilibrium obtained in the unresponsive case (figure 3). Both sets of simulations are characterized not only by lower levels of help and the absence of aggression, but also by flat reaction norms: the interacting partners are unresponsive (figure 5e). The lack of responsiveness means that help is provided voluntarily by the helper rather than enforced by aggression. The benefits of helping at this equilibrium are indirect: helpers increase their inclusive fitness by boosting the productivity of a related breeder with their help. Likewise, there are indirect costs: the breeders refrain from attacking a related helper, as this would reduce their inclusive fitness.

Negotiation can evolve too under high levels of relatedness (figure 5b,c) but relatedness makes it less likely for the population to reach the ‘negotiated’ equilibrium. This can be seen in the higher proportion of simulation runs that end up in the ‘kin-selected’ equilibrium as relatedness is increased (figure 5b,c). The behaviours achieved at the ‘negotiated’ equilibrium give rise to groups that enjoy a higher reproductive output, even when correcting for the added mortality due to higher levels of aggression and helping. Kin-structured populations can, therefore, be trapped at an evolutionary equilibrium that is suboptimal with respect to productivity. Eventually, a population may escape from the ‘kin-selected’ equilibrium (see the electronic supplementary material, figure S1). This happens apparently if the fluctuations in reaction norms due to genetic drift are sufficiently large to push the population into the domain of attraction of the ‘negotiated’ equilibrium. This is supported by the increased number of simulations that reach the ‘negotiated’ equilibrium when we systematically increase the phenotypic effect size of mutations (electronic supplementary material, figure S3).

(d). Evolutionary invasion analysis

In the electronic supplementary material, we present a general mathematical analysis giving additional insights into the effect of relatedness on negotiation-based helping. To this end, we derive the invasion fitness of mutants with slightly different levels of expressed behaviour (aggression or help) in the negotiation. We take into account that a slight change in an individual's behaviour entails a change in the behaviour of their partner, owing to the negotiation dynamics. With the invasion fitness of the two types of mutants, we can assess the conditions for selection to favour an increase in aggressive and helping behaviour.

We find that the effect of selection can be captured by looking at the shape of the reaction norms in the vicinity of the behavioural equilibrium of aggression and help. As shown in the electronic supplementary material, the invasion fitness of a breeder with genetic trait y (slightly modifying the shape of the reaction norm and thereby inducing a different level of aggression) in a population of residents with genetic trait 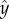and helping level is given by

3.1

where, the numerator of the term outside the brackets captures the marginal effect of the trait y on the level of aggression, and β_B and β_H are the slopes of the reaction norms of the breeder and helper, respectively, in the vicinity of the behavioural equilibrium. The product of the slopes (β_B and β_H) corresponds to the leading eigenvalue of the Jacobian matrix associated with the negotiation dynamics (equation (2.2)). If the product of the slopes has an absolute value smaller than 1, the negotiation dynamics converge to a stable equilibrium (see the electronic supplementary material), and the denominator is positive. If the marginal effect of y on aggression is also positive, the first term on the right-hand side of equation (3.1) is positive. Therefore, invasion fitness w_y has the same sign as β_Hb−d, that is, the difference between the marginal benefit of helping (b), multiplied by the slope of the reaction norm of the helper (β_H), and the marginal damage on the breeder caused by exerting aggression (d). Hence selection favours increased levels of aggression if the slope β_H of the helper's reaction norm in the vicinity of the residents' level of aggressiveness 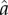exceeds the critical value d/b.

The above derivation was based on the assumption that breeder and helper are not related with each other. When we allow breeders and helpers to be related, we find that selection favours increased levels of aggression if:

3.2

where r denotes the coefficient of relatedness between breeder and helper, c is the marginal cost to the helper of providing help and d′ is the marginal damage to the helper from receiving aggression. Condition (3.2) implies that the evolution of breeder aggression is contingent on a sufficiently strong positive response (i.e. increased helping) of the helpers to aggression. The condition is more stringent in kin-structured populations for two reasons. First, relatedness increases the inclusive fitness effect of the damage caused by aggression, because aggression by the breeder reduces the fitness of a relative (i.e. the numerator on the right-hand side of inequality (3.2)). Second, relatedness reduces the net inclusive fitness benefit of help (in the denominator), because such help comes at a cost to the related individual that is providing it. Therefore, the position of the breeder in the negotiation process is compromised by a higher relatedness with the helper [15]. The conclusion that kin interactions weaken selection for aggression is in line with our simulation results, which also indicate that the level of aggression in the negotiation-based equilibrium decreases with relatedness (electronic supplementary material, figure S2).

A similar analysis of the selection gradient of genetic traits affecting the helping level reveals that there is selection in favour of helping if the slope β_B of the breeder's reaction norm in the vicinity of the residents' level of helping is smaller than a threshold value

3.3

If the net inclusive fitness benefit of helping rb − c is positive, inequality (3.3) implies that helping is selected even if β_B = 0, that is, even if helping is not enforced by aggression. By contrast, if helper and breeder are unrelated, helping evolves only if β_B < −c/d′ < 0, that is, if breeders respond to increasing levels of help by substantially reducing their aggression towards the helper.

Taken together, inequalities (3.2) and (3.3) indicate that the kin-selected and the negotiated equilibrium represent two distinct stable states of the social system. At the kin-selected equilibrium, breeders exert no aggression (β_B = 0) and they unconditionally accept helpers in their territory; voluntary help then evolves up to a level that balances the inclusive fitness components rb and c. By contrast, the negotiated equilibrium is characterized by responsive strategies (β_B < 0 and β_H > 0), so that at equilibrium the net inclusive fitness benefit of helping rb − c is negative. Consequently, under the plausible assumption that the benefits of help are diminishing or the costs are accelerating, negotiated levels of help must be higher than kin-selected help, even though such negotiated help can be enforced by minimal levels of aggression.

4. Discussion

We have shown here that both kin selection and negotiation can lead to the evolutionary emergence of helping behaviour. When responsiveness is prevented from emerging, helpers only evolve helping behaviour under high levels of genetic relatedness, and dominants restrain from harming helpers. When responsiveness is allowed to evolve but the partners are unrelated, helping behaviour evolves as a consequence of the negotiation between partners. Both types of equilibria arise in our simulations when responsive reaction norms evolve in the presence of genetic relatedness. However, the higher the relatedness between the partners, the more simulations end up in a ‘kin-selected’ equilibrium, where cooperation levels are lower than at the more productive ‘negotiated’ equilibrium. This happens because relatedness compromises the position of the dominant in the negotiation, both by increasing the cost of aggression and reducing the net benefit of help (see expression (3.2)); thus, it keeps the population trapped at a state with low productivity. By contrast, negotiations between unrelated partners provide a highly effective social mechanism to channel a conflict of interest towards a mutually beneficial outcome. The high productivity of the population at the negotiated equilibrium is fuelled by asymmetries in the fitness effects of help and aggression between the two interacting partners [34]: the pay-to-stay mechanism mediates an exchange of cheap services in return for valuable ones, allowing both partners to fully realize their comparative advantage [35].

The few earlier models that addressed the joint effect of relatedness and responsiveness arrived at contradictory results [3,15–17,36]. Our simulation results are in line with earlier finding that relatedness inhibits the evolution of reciprocal cooperation [15,17]. Moreover, our invasion analysis shows that this effect is not restricted to specific nonlinearities in the pay-off matrix [37]. The condition for selection to favour helping behaviour also confirms, contrary to earlier claims [36], that relatedness and responsiveness cannot be summarized by simple measures of phenotypic assortment [3]. More importantly, we show that these two processes can lead populations to attain alternative equilibrium states of the social system that differ in their levels of productivity.

Models of social evolution that explain the evolution of cooperation among unrelated individuals have mostly focused on the IPD, however, conditions of such a game are rarely met in nature [18,38,39]. For example, the IPD makes strict assumptions about the information exchange between individuals. The action of an individual has fitness consequences before there is information exchange [39]. Alternatively, negotiation models assume that individuals go through a long series of mutual exchanges before there are fitness consequences to their actions [30,31]. These are two extreme points of the separation of timescales between behavioural and evolutionary dynamics. Another consideration is the set of inputs that individuals use to make decisions. In IPD models, individuals typically use information about their partner's and their own actions [6]. In our negotiation model, individuals respond to each other through reaction norms, thus they only react to their partner's behaviour. However, individuals in nature could potentially have more complex decision-making mechanisms that account for other inputs, such as internal states (e.g. condition, emotions), partner's responsiveness or outside options [39,40]. Therefore, future models of negotiation would profit from more empirically informed representations of the negotiation process, thus favouring an integration of the proximate and ultimate perspectives in biology [6,41–43].

In order to capture the consequences of genetic relatedness in an interaction between responsive partners, we ignore some biological complexity. In N. pulcher, dominants live in groups containing several subordinates, and subordinates vary in size, age, sex, cooperation propensity and capability, and in their competitive abilities [44]. Variation in the condition of the interacting partners, even if small, is known to be important in negotiation dynamics [31]. Moreover, it is not straightforward to extrapolate our simple negotiation process to larger groups. The dominant could either keep track of each subordinate's helping effort, or rely on an overall measure of help in the group. More importantly, female and male dominants have different potential fitness costs due to reproductive participation of subordinates [45–47] causing different incentives in the two genders to express aggression and help. For instance, subordinate males can fertilize some of the eggs [48]; therefore, dominant males might use aggression not only to maintain help, but also to discourage subordinates from attempting fertilization [47,49]. Understanding the role of these group-level dynamics is an important challenge for future research in the field of social evolution [47].

Our results show that high levels of negotiated help and low levels of aggression are maintained by an implicit threat of aggression and the possibility of appeasement by increasing help levels. This outcome is in close agreement with experimental results in cooperatively breeding N. pulcher groups, where punishment is rarely observed even if subordinates are artificially prevented from helping [19]. Populations where negotiation has been shown to drive helping behaviour are taxonomically diverse [19,50–52]. However, the power of negotiation to stabilize helping behaviour is probably underestimated [53], as such experimental manipulations have rarely been performed in other cooperative breeders. Our model stresses the importance of hidden parts of behavioural reaction norms in strategic interactions [29]; the outcome of a social interaction is not only determined by the actions taken by each player at the equilibrium of a strategic game, but also by the full repertoire of conditional behaviours specified by their reaction norms [31]. Accordingly, it may be difficult to infer behavioural strategies without manipulative experiments that explore the full strategy space of individuals [19,22].

Competing interests

The authors have no competing interests.

Funding

G.S.v.D. was supported by Starting Independent Researcher grant no. 309555 of the European Research Council and Vidi grant 864.11.012 of The Netherlands Organization for Scientific Research (NWO). M.T. was supported by SNF grant nos. 310030B 138660 and 31003A_156152. F.J.W. was supported by a grant no. (823.01.006) of NWO.

Authors' contributions

A.E.Q. and G.S.v.D. contributed equally to this work. A.E.Q., G.S.v.D., I.P., F.J.W. and M.T. designed the research. A.E.P. coded for the individual-based simulations and analysed the output. G.S.v.D. derived the general mathematical analysis. A.E.Q., G.S.v.D., I.P., F.J.W. and M.T. wrote the paper.