Abstract
Neurons in the lateral prefrontal cortex (LPFC) encode sensory and cognitive signals, as well as commands for goal-directed actions. Therefore, the LPFC might be a good signal source for a goal-selection brain-computer interface (BCI) that decodes the intended goal of a motor action previous to its execution. As a first step in the development of a goal-selection BCI, we set out to determine if we could decode simple behavioral intentions to direct gaze to eight different locations in space from single-trial LPFC neural activity. We recorded neuronal spiking activity from microelectrode arrays implanted in area 8A of the LPFC of two adult macaques while they made visually guided saccades to one of eight targets in a center-out task. Neuronal activity encoded target location immediately after target presentation, during a delay epoch, during the execution of the saccade, and every combination thereof. Many (40%) of the neurons that encoded target location during multiple epochs preferred different locations during different epochs. Despite heterogeneous and dynamic responses, the neuronal feature set that best predicted target location was the averaged firing rates from the entire trial and it was best classified using linear discriminant analysis (63.6–96.9% in 12 sessions, mean 80.3%; information transfer rate: 21–59, mean 32.8 bits/min). Our results demonstrate that it is possible to decode intended saccade target location from single-trial LPFC activity and suggest that the LPFC is a suitable signal source for a goal-selection cognitive BCI.
Keywords: brain-computer interface, Macaca fascicularis, neural trajectory, prefrontal cortex
individuals with motor impairments following central nervous system trauma or disease may use a brain-computer interface (BCI) to translate the electric signals from the brain into prosthetic limb control (Aflalo et al. 2015; Collinger et al. 2013; Hochberg et al. 2006; Wang et al. 2013). Most neuroprosthetic BCIs continuously decode effector trajectories from the activity of a population of neurons in motor cortex (Hatsopoulos and Donoghue 2009; Pohlmeyer et al. 2007; Schwartz 2004). Alternatively, neural signals in upstream brain areas from motor cortex that are engaged in cognitive aspects of movement such as attention, decision-making, planning, learning, memory, expected reward, and visuomotor transformation may be used to drive a goal-selection BCI (Andersen et al. 2014; Musallam et al. 2004). However, to date, this approach has been mainly limited to parietal cortex.
Other brain areas that are known to be involved in decision-making and goal-directed behavior might also be reliable signal sources for goal-selection BCIs. The lateral prefrontal cortex (LPFC), anterior to the arcuate sulcus and posterior to the principal sulcus (Petrides 2005), is one such area. Previous single unit studies have implicated the LPFC in attention (Everling et al. 2002; Lennert and Martinez-Trujillo 2013), working memory (Fuster and Alexander 1971; Goldman-Rakic 1995; Jacobson 1936; Kubota and Niki 1971; Mendoza-Halliday et al. 2014; Miller et al. 1996), task rule representation (Bongard and Nieder 2010; Buschman et al. 2012; Wallis et al. 2001; White and Wise 1999), and the integration of information for decision making (Kim and Shadlen 1999). It might therefore be possible to decode behavioral goals, i.e., decision outcomes, from LPFC neural activity. However, because most of our understanding of LPFC comes from electrophysiological studies averaging single neuron recordings across many trials, the encoding of intention in single realizations of LPFC neural activity remains poorly understood.
Recently, simultaneous recording of multiple LPFC neurons using chronic multielectrode array (MEA) implants has enabled examination of single realizations of LPFC ensemble activity that may support BCI implementations. MEA recordings from populations of neurons provide statistical redundancy that enable the estimation of latent network structure (Cunningham and Yu 2014; Yu et al. 2009) that may underlie behavior and constrain learning (Chase et al. 2012; Sadtler et al. 2014). These features of population recordings can be exploited to decode behavior from single realizations of neural activity (Georgopoulos et al. 1986; Kao et al. 2015; Wessberg et al. 2000). A previous study using multiple electrodes showed that it is possible to decode the intention of a saccade from multiunit activity and local field potentials in superficial layers of macaque LPFC (Markowitz et al. 2011). More recently we have shown that using single unit activity recorded with a surface MEA chronically implanted in the LPFC it is also possible to decode the allocation of covert attention to different visual field quadrants on a single trial basis (Tremblay et al. 2015). Here, we expand this work and further investigate whether it is possible to decode intended saccade goals to single targets in many (n = 8) different spatial locations from LPFC single neuron activity recorded with chronic surface MEAs. Importantly, we describe the neural dynamics that contribute to the representation of intended saccade goals, then quantify and compare the decoding performance of different algorithms that exploit these dynamics.
MATERIALS AND METHODS
Animals.
Two adult male monkeys (Macaca fascicularis; monkey “JL” and monkey “M”) participated in this study. All procedures complied with the Canadian Council of Animal Care guidelines and were approved by the McGill University Animal Care Committee. Animals were pair-housed in enclosures, and interactive environmental stimuli were provided for enrichment. During experimental days, fluid was controlled (minimum of 35 ml·kg−1·day−1) in such a manner that the animals could earn any amount additional to the minimum through successful performance of the task. Fluid intake was supplemented to reach this quantity if it was not achieved during the task, and restriction was lifted during nonexperimental days.
Surgical procedures.
Surgical procedures were carried out under general anesthesia with endotracheal intubation. During the initial procedure, the animals were implanted with three titanium head posts—one was placed posterior to the supraorbital ridge in the midline and the other two on the petrosal bones superior to the occipital protuberance behind each ear. The head posts interfaced with a head holder to maintain fixed head position during the experimental tasks and recordings.
In a subsequent procedure, we chronically implanted a 10 × 10 MEA (Blackrock Microsystems) in each monkey's left LPFC anterior to the knee of the arcuate sulcus and caudal to the posterior end of the principal sulcus (Brodmann area 8a) (Fig. 1A). The scalp was incised and the incision was electrocauterized. The scalp was retracted and the pericranium excised to limit biological reaction around the implant. A high-power drill (Anspach) was used to create a craniotomy over the left LPFC. Wet gelfoam was applied to the epidural edges for hemostasis. The electrode array connector was fixed to the skull with cranial screws and the array wires were bent in anticipation of the electrode positioning; then the array wires were secured with Silastic sealant (silicon polymer, World Precision Instruments). The dura was opened with a no. 11 blade and Reynold scissors. The electrode was placed over the target such that it lay with the plane of the array parallel to, and just touching the cortex with no tension in the wire, and inserted 1 mm into the cortex using a pneumatic inserter (Blackrock Microsystems). The dural flap was laid atop the array and a synthetic dura placed over (Durepair, Medtronic, Minneapolis, MN). The bone flap was replaced and secured using cranial fixation plates and screws (Synthes). Gaps in the bone were filled with Silastic and the scalp was released from retraction. A small incision was made in the scalp to allow the connector to be percutaneous. The scalp was closed in layers with buried vicryl suture in the galea and staples to the skin. The animal fully recovered from the surgery within 1 wk.
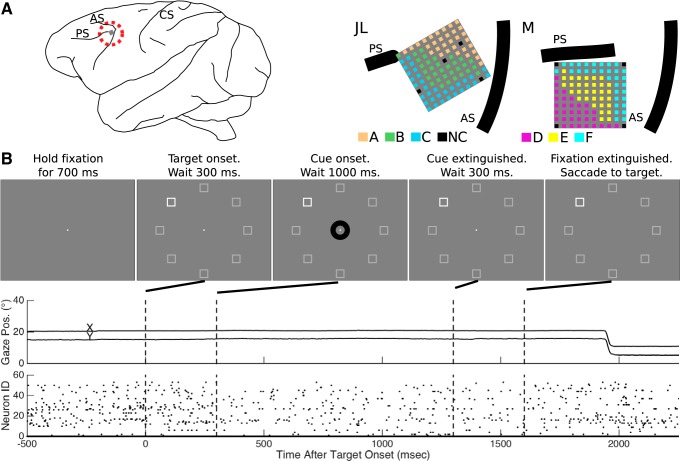
Fig. 1.
Experimental setup. A: microelectrode arrays were implanted in the left hemisphere, anterior to the knee of the arcuate sulcus (AS) and caudal to the posterior end of the principal sulcus (PS). The central sulcus (CS) is also indicated. Each recording session collected data from a block of 32 electrodes. For each monkey, electrode sites are colored according to membership in a block (A, B, or C for monkey JL; and D, E, or F for monkey M; NC, not connected). B: in each trial, the monkey maintained fixation through the presentation of the target stimulus until the central fixation point extinguished at which time the monkey made a saccade to the target. Example behavioral eye position data and neural spiking data for a single trial are presented in the middle and bottom panes, respectively. Note that the screen y-axis origin was at the top of the screen, and down was positive.
Electrophysiological recordings.
Data from 32 electrodes per session were recorded using a Cerebus Neuronal Signal Processor (Blackrock Microsystems). The signals were buffered at the headstage (1 × amplification; ICS-96) then band-pass filtered (0.3 Hz/1-pole, 7.5 kHz/3-pole, analog) and digitized (16 bit, 1 μV/bit) at 30 kHz. The occurrence of a spike was detected whenever the digitally high-pass filtered (250 Hz/4-pole) raw data passed a threshold (manually adjusted to −4 ∼ −4.5 × noise amplitude). Spike times and waveforms (48 samples at 30 kHz, ∼1.6 ms) were saved to disk for later offline analysis.
Task.
A custom computer program controlled the stimulus presentation and monitored eye position signals (SR Research, Ottawa, Canada). Visual stimuli were back-projected on a screen using a video projector (NEC WT610, 1024 × 768 pixels, 85 Hz). The screen was positioned 100 cm from the animal's eyes. The animal initiated a trial by maintaining fixation on a central fixation point—a square of length 0.2° located in the middle of the screen—for 700 ms. Then a target box of length 5.1° appeared in one of eight locations. The potential target locations were the 45° steps arranged radially 12.7° away from the middle of the screen. To maintain consistency with other experiments in which the monkeys were participating, an annulus of radius 1.3° appeared around the fixation point 300 ms after target onset and remained on the screen for another 1,000 ms. The annulus had no meaning in this study. After the annulus disappeared, the monkey continued to maintain fixation on the central fixation point for another 300 ms until the fixation point disappeared, when the monkey had to make a saccade to the target box to receive the reward. The trial progression and an example of behavioral and neural data from a single trial are shown in Fig. 1B. For each task event, the stimulus presentation software sent digital signals to both the neurophysiology and eye tracker systems for offline synchronization.
Behavioral analysis.
Saccades were automatically extracted from eye position data (Armstrong et al. 2006). Trials with erroneous or no saccades were eliminated (total = 20.0% eliminated) including those with any saccades detected between target onset and fixation offset, with no saccade detected within 500 ms after fixation offset. Additionally, for all analyses except the prediction of saccade angle, trials were eliminated if the saccade end point was not within the target bounds (0.4%).
Neuron characterization.
We analyzed each experimental session independently. We manually sorted spike waveforms from each session using MKSort (Ripple, Salt Lake City, UT). Sorted waveforms were presumed to come from unique neurons. As each session is analyzed independently, we made no attempt to track neurons across sessions.
We first sought to characterize the neuronal population recorded in each session by quantifying the task-related firing rate modulations of the individual neurons. Trials were segmented into four nonoverlapping epochs: baseline (−250 to 0 ms relative to target stimulus onset), cue (0 to +250 ms relative to target stimulus onset), delay (600 to +850 ms relative to target stimulus onset), and response (−50 to +200 ms relative to saccade onset). We chose 250 ms as the duration of the response epoch because this length captured the majority of the available post-saccade onset activity while still avoiding noise due to reward delivery or visual stimulus clearing. The baseline, cue, and delay epochs were set to the same duration (i.e., 250 ms). Neural spiking events were counted in each epoch. Spike count variances were proportional to the means, as is commonly observed (Shadlen and Newsome 1998), so we applied the square root transform to stabilize variances across target locations (Kihlberg et al. 1972).
To determine if neural activity varied significantly between target locations, we calculated mutual information (MI) between neuronal spike counts and target locations using the MIToolbox for Matlab (Brown et al. 2012). MI is a useful metric to analyze tuning because it is not sensitive to sample size and because its interpretation of information in bits is intuitive. MI is calculated using:
| (1) |
where s is the target location, r is the response (e.g., spike counts), and the log is base 2. Spike counts were quantized using a maximum of 8 quantiles (Musallam et al. 2004), but often fewer quantiles were needed to represent all unique spike count values, especially when analyzing neurons with low firing rates and short epochs. The quantile indexes were used as r in Eq. 1.
MI was compared against a null distribution obtained by shuffling target locations and calculating MI for 1,000 different shuffles. We labeled neurons as having significant target location information within an epoch if the MI was greater than 99% of the null values for that epoch. Neurons with significant MI during the baseline epoch were excluded from further neuron characterization because these neurons may possess spurious correlations between recording quality and target location probability, and any significant MI in later epochs cannot be trusted to be task-related. Further, some neurons were excluded from characterization if there was zero variance across trials, which typically only occurs in neurons with very low firing rates.
Trials were then grouped by target location and average firing rates were calculated for each location for baseline, cue, delay, and response epochs. For each neuron-epoch with significant location information, the preferred target location was defined as the location associated with the highest firing rate that was also significantly different from the average firing rate for all other locations. The frequencies of leftward (up-left, down-left, and left) and rightward (up-right, down-right, and right) preferred locations were compared against a uniform distribution using a χ2 goodness of fit test.
We next examined with greater temporal precision how the location dependence of neural activity evolved over the course of the trial. Trials were segmented into 250-ms windows with 40% overlap (i.e., 100-ms steps); then we performed the MI test on spike counts for each segment spanning −249 to 2,400 ms locked to target onset and again for segments spanning −2,449 to 200 ms locked to saccade onset. The population MI at each segment was tested for significantly greater MI than the baseline-epoch MI using paired t-tests and the Bonferroni correction for multiple comparisons.
Neural trajectories.
Multidimensional neural time series data can be represented as trajectories through multidimensional space. Neurons with zero variance across trials in any single epoch were excluded from the calculation of the neural trajectories. We constructed neural trajectories by first segmenting data from the trajectory epoch (i.e., −250 to 1,250 ms after target onset) into 50-ms windows and then extracting the square roots of the spike counts within each window. Extracted features were smoothed by convolution with a Gaussian kernel (σ = 50 ms). The transformed and smoothed spike counts constituted the most basic form of neural trajectories with dimensionality equal to the number of sorted neurons in the session and are thus referred to as “full trajectories.”
We used five different dimensionality reduction techniques to project full neural trajectories into lower dimensional space, limited to a maximum of eight dimensions. We used the DataHigh analysis toolbox (Cowley et al. 2013) to do the principal components analysis (PCA), factor analysis (FA), and Gaussian process factor analysis (GPFA; Yu et al. 2009) dimensionality reductions. PCA returns trajectories with fewer orthogonal dimensions that maximally account for the total variance in the full trajectories. FA returns trajectories that represent a latent process or structure underlying the observed full trajectories. GPFA extends FA by simultaneously optimizing smoothing timescales and identification of the latent structure (Yu et al. 2009). Unlike for all other dimensionality reduction techniques, the full trajectories were not smoothed before applying GPFA. For GPFA, we used the default parameters specified by DataHigh: the GPFA model is initialized with the Gaussian process covariance structure set to use the radial basis function, the Gaussian process timescales set to 200 ms, and the noise variances set to 0.001. We used demixed principal components analysis (dPCA) to reduce the data into dimensions that highlighted and separated the influences of target location and task time (Brendel et al. 2011; Kobak et al. 2014). For dPCA, we used a constant regularization parameter lambda of 0.0025 and we used the target-location and its interaction with time as the first marginalization and time as the second marginalization.
Finally, we created three different “canonical trajectories.” The first step was to calculate the first eight canonical correlation basis vectors (i.e., the coefficients that map all neurons to a reduced vector of eight canonical variates). Each set of eight basis vectors were calculated using the square root transformed spike counts from a single epoch. The projection of the original data onto the first basis vector yields the canonical variate that maximizes separation between target locations. Subsequent basis vectors maximize remaining target location separation but are subject to being orthogonal to the previous basis vector. The full neural trajectory, comprising many time-windows spanning multiple epochs, was then projected onto the basis vectors to get an 8-dimensional canonical variate that varies over time, hereafter referred to as a canonical trajectory. We applied this technique to each of the cue, delay, and response epochs to yield the “canonical cue,” “canonical delay,” and “canonical response” trajectories, respectively.
Population characterization.
We calculated the Euclidian distances between the GPFA trajectories and each of the canonical trajectories after swapping and negating the dimensions of the canonical trajectories to minimize the distance to the GPFA trajectories. We then performed a repeated-measures ANOVA on the distances between the GPFA trajectories and each of the canonical trajectories using “epoch” as the within-subjects factor.
Classifying intended saccade target.
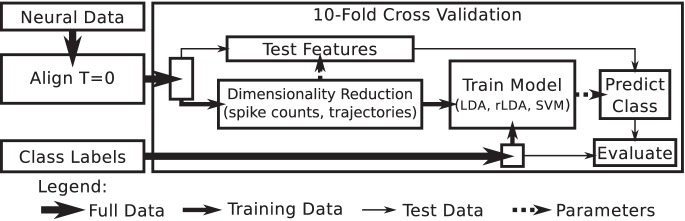
We predicted intended saccade targets from neural data independently for each recording session. An outline of the classification procedure is presented in Fig. 2. For each session, 14 different feature sets were extracted and analyzed independently. The feature sets included the square root of spike counts in each of the baseline, cue, delay, and response epochs (feature sets 1–4), the concatenation of the square-root transformed spike counts from each of the baseline, cue, delay, and response epochs (feature set 5), the average spike rate from the entire trial (feature set 6), and the full and reduced neural trajectories (feature sets 7–14: full, PCA, FA, GPFA, dPCA, canonical cue, canonical delay, and canonical response).
Fig. 2.
Classification analysis outline. Full neural data from all trials were aligned to target onset as time 0. Within 10 iterations of a cross-validation loop, trials were separated into training and test trials. Training trials were used to generate the parameters for dimensionality reduction and to train the model relating the reduced feature set to the target locations. Trained parameters were used to reduce the test data set and to predict test target locations. Predicted test target locations were compared with true target locations to determine classification accuracy. LDA, linear discriminant analysis; rLDA, regularized LDA; SVM, support vector machines.
For each of the 14 feature-sets, we tested three different classification algorithms. We tested linear discriminant analysis (LDA; Friedman 1989) and its regularized counterpart (rLDA) using the BCILAB toolbox for Matlab (Kothe and Makeig 2013). The LDA classifier was chosen because LDA is common, straightforward, and computationally efficient. We added regularization because some feature sets possess more features than there are realizations, and regularization is necessary to reduce overfitting. The regularization parameter lambda was computed analytically in closed-form (Ledoit and Wolf 2004). We also tested multiclass support vector machines (SVM; Cristianini and Shawe-Taylor 2000; Hastie et al. 2009) using the Matlab Statistics Toolbox. SVM was chosen because it uses regularization and we used a linear kernel because many of our feature sets already include sophisticated feature extraction that is unlikely to benefit from a different kernel.
We used 10-fold cross-validation to assess classifier performance. For each fold of the cross-validations, trials were divided into training (90%) and test (10%) sets such that each target location was proportionally represented in both sets and each trial only appeared in a test set once. Any features that had zero variance across training trials were excluded from both the training and test data. For the reduced neural trajectories, the feature reduction parameters were calculated using only the training data, then applied to the test data sets. The training data, comprising a neural feature set and target locations from 90% of the trials, were supplied to the supervised learning algorithm to create a model that predicted target location from the neural features. The model was then applied to each trial in the unlabeled test feature set to yield the predicted target locations. Predicted target locations were compared with the true target locations to determine the classification accuracy. For each feature set, we compared classification accuracy to the accuracy obtained in the baseline epoch using the same machine-learning algorithm using paired t-tests and Bonferroni corrections for multiple comparisons. We prefer using baseline accuracy instead of chance accuracy (theoretically 12.5% or 1/8 targets) because the baseline accuracy will capture any boost in classifier performance that may be due to uneven probabilities of target location presentation that coincide with changes in neural recording quality.
Predicting saccade end point may allow for an arbitrary number of targets or dynamically changing targets in an assistive communication application. To determine if the neural data can be used to predict saccade end points independent of target location, we used regularized least-squares regression using the lasso algorithm (l1 norm) from the Matlab Statistics Toolbox to correlate saccade end-point coordinates (x,y positions) with each of the 14 feature sets. We first used 10-fold cross-validation to determine the regularization parameter lambda that yielded the minimum least-squared error among all trials. We then used this value of lambda in a separate 10-fold cross-validation analysis that used the training data to calculate the coefficients that relate the feature set to saccade end point coordinates and then applied these coefficients to the test data to predict the saccade end point for the test trials. We then correlated the predicted saccade end points with the saccade end points measured with the eye tracker and calculated the square of Pearson's correlation coefficient (R2) that corresponds to the proportion of variance in measured saccade end point accounted for by the neural data.
In an application with fixed target locations, like the task in the present study, the intended target can be decoded from either a multiclass target-location classifier or a saccade end-point predictor. For all feature sets, we compared target-location prediction accuracies between the target locations nearest the predicted saccade end point and the target locations predicted by the best-performing machine-learning algorithm.
Using the full trial average firing rate feature set and linear discriminant analysis, we examined the impact of trajectory epoch duration on classification accuracy and information transfer rate (ITR). We calculated classification accuracy for trial durations ranging from 50 ms to 2,650 ms, in 50-ms steps, beginning at 250 ms before target onset. We calculated ITR by first calculating the average bits per selection (Pierce 1980), then dividing that by the total trial duration. ITR was calculated in two steps. First we calculate the bits per trial using
| (2) |
where N is the number of possible targets, and P is the classification accuracy. The ITR is then scaled by the trial duration using
| (3) |
where B is the bits per trial from Eq. 2, tp is the pretrial duration of 0.45 s, tt is the variable-duration neural trajectory, and tr is 0.7 s comprising the combined durations of the behavioral response, reward delivery, and system reset. The ITR is positively related to accuracy and negatively related to duration and can be used to find the optimum trade-off between data length and classification accuracy that maximizes information throughput. ITR is a useful metric to compare BCI performance between studies because it guards against inflating accuracy at the expense of speed and vice versa.
To examine the impact of ensemble size on classifier performance, we constructed neuron-adding curves. In the greedy neuron adding analysis, for each session, the individual neuron whose average firing rate provided the best classification accuracy using LDA was used to initialize the feature set. Each remaining neuron was then tested and the neuron that increased classification accuracy the most was added to the feature step. This process was repeated until no neurons remained. In the random neuron adding analysis, for each session, neurons were added to the model stepwise in a randomized order. The process was repeated 20 times for each session after rerandomizing the order in which neurons were added. For both the greedy and random neuron-adding analyses, the classification accuracy was recorded after the addition of each neuron.
RESULTS
Single-neuron characterization.
We recorded from 247 neurons across 12 sessions. Three neurons with significant MI in the baseline period and five neurons with zero variance across trials in at least one epoch were excluded from further single-neuron characterization.
We observed neurons with statistically significant mutual information (MI) among target locations and firing rates during each epoch. Significant MI was found in 78 neurons during the cue epoch (14 were significant in only the cue epoch), 97 (25) in the delay epoch, and 116 (38) in the response epoch. Summary statistics for the individual recording sessions are presented in Table 1. Peristimulus time histograms (PSTHs) and location-dependent firing rate profiles for exemplar neurons are shown in Fig. 3.
Table 1.
Summary of single-neuron recordings
| Tuned Units |
|||||||
|---|---|---|---|---|---|---|---|
| Subject | Block | Trials (Excluded) | Units (Excluded) | Total | Cue | Delay | Response |
| JL | A | 431 (133) | 21 (0) | 19 | 9 | 14 | 19 |
| 229 (33) | 26 (0) | 22 | 16 | 10 | 17 | ||
| B | 258 (99) | 27 (0) | 21 | 9 | 13 | 17 | |
| 266 (78) | 23 (1) | 19 | 13 | 15 | 11 | ||
| C | 259 (40) | 17 (0) | 13 | 5 | 6 | 9 | |
| 234 (61) | 22 (0) | 14 | 8 | 8 | 7 | ||
| M | D | 228 (46) | 21 (1) | 10 | 4 | 5 | 7 |
| 328 (79) | 28 (1) | 14 | 8 | 9 | 9 | ||
| E | 231 (25) | 14 (0) | 10 | 1 | 8 | 5 | |
| 208 (31) | 13 (3) | 7 | 1 | 3 | 5 | ||
| F | 184 (17) | 15 (0) | 9 | 2 | 4 | 6 | |
| 200 (34) | 20 (2) | 7 | 2 | 2 | 4 | ||
For each monkey, for each electrode block, two recording sessions were included in the analysis. For each session (n = 12), the number of trials (and excluded trials), and the number of single neurons identified with spike sorting (and single neurons excluded) are provided. Among the single neurons not excluded, the number of single neurons with significant tuning in total and in each of the individual trial epochs is provided.
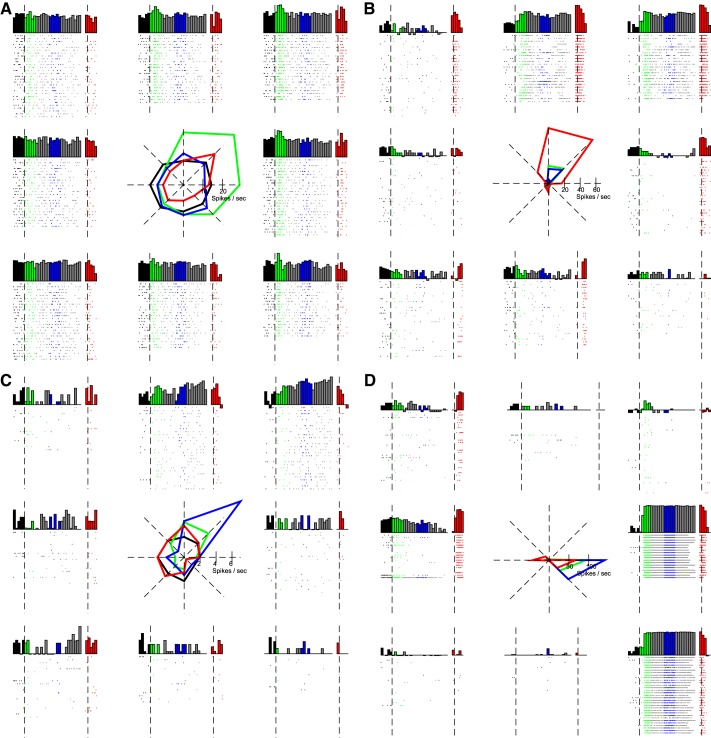
Fig. 3.
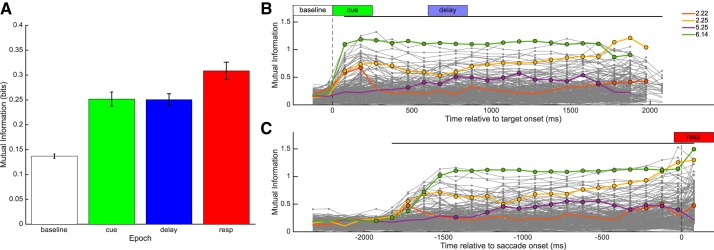
Locational dependence of firing rates for 4 exemplar neurons: neuron 2.22 (2nd session, 22nd neuron) (A); 2.25 (B); 5.25 (C); 6.14 (D). Note that these same neurons are highlighted in Fig. 5. For each neuron, the raster plots and peristimulus time histograms (PSTH) for each target location are in the outer 8 panes; the position of each plot is congruent with the target location used in the trials represented in the plot. PSTH plots are log-transformed and scaled between 0 and the per-neuron maximal firing rate: 59, 140, 16, and 167 spikes/s for neurons 2.22, 2.25, 5.25, and 6.14, respectively. The central pane shows the average firing rate to each direction for each trial epoch. Black, baseline; green, cue; blue, delay; red, response; gray, other.
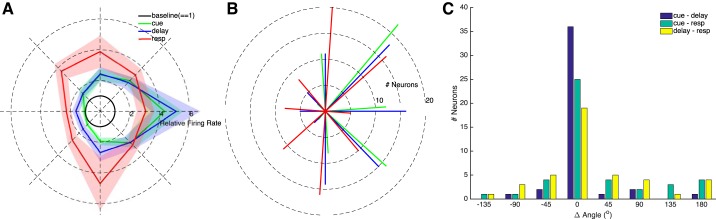
The summary of location-dependent firing rate profiles for each epoch is shown in Fig. 4A. For neurons with significant mutual information in a given epoch, we estimated the preferred target location as the location associated with the highest average firing rate that was also significantly different from the average firing rate for all other target locations. Of the 289 neuron-epochs with significant tuning, 244 (84.4%) met this criterion across 129 neurons. The summary of preferred target locations is shown in Fig. 4B. There was a great variety of firing rate profiles and preferred target locations across neurons. Many of the neurons with significant mutual information in multiple epochs had different preferred target locations across epochs (49 of 129, 39.3%; Fig. 4C). When grouping target locations within left and right hemifields, the frequencies of preferred locations were not evenly distributed between hemifields in the cue (χ2 = 36.8, P < 0.001) and delay (χ2 = 20.9, P < 0.001) epochs (response χ2 = 0.3, P = 0.60). For these epochs, more neurons modulated their activity to targets located in the contralateral visual hemifield (right) than to targets located in the ipsilateral visual hemifield (left).
Fig. 4.
Target-locational dependence of task-related neural activity for the entire population of neurons. A: firing rates (solid lines) ± SE (shaded regions) during each analysis epoch normalized by the firing rate during baseline (unit circle, black) to each of the 8 target locations. B: the distribution of preferred target locations among neurons with significant mutual information. Bar lines for the different analysis epochs are colored as in A. C: distribution of differences in preferred target locations for pairs of analysis epochs among neurons with significant mutual information in both analysis epochs. In B and C, the angles of some bars are offset to aid visualization; true angles for all epochs (B) and epoch-pairs (C) are the same as the central bar.
The temporal dependence of MI is shown in Fig. 5. Averaged across neurons, MI was significantly greater during cue, delay, and response epochs than during the baseline epoch (paired t-tests, Bonferroni-corrected P ⪡ 0.001). Further, MI was significantly greater during the response epoch than during the cue epoch (Fig. 5A; Bonferroni-corrected P value < 0.01) but the difference between response and delay was not significant (P = 0.055). Examining MI at each time step gave similar results; across all recorded neurons MI was significantly different from baseline from 75 to 2,075 ms relative to target onset, and MI was significantly different from baseline from −1,925 to 75 ms relative to saccade onset (all Bonferroni-corrected P values < 0.001). Individual neurons were significantly different from baseline during an individual epoch, during any combination of epochs, or no epochs. We reanalyzed MI after subtracting baseline values, and the results did not change (data not shown).
Fig. 5.
Mutual information (MI) between each neuron's firing rate and target location. A: average mutual information ± SE across neurons for each analysis epoch. Mutual information was significantly different between each pair of analysis epochs. Mutual information time-series relative to target onset and relative to saccade onset are presented in B and C, respectively. Time windows used for analysis epochs baseline, cue, delay, and response (resp) are indicated in white, green, blue, and red, respectively. Data points with a circle indicate time points for individual neurons for which MI was significantly different from baseline. The black bars above the individual traces indicate time points over which the population MI was significantly different from baseline. Traces from the 4 individual neurons presented in Fig. 3 are highlighted.
Population dynamics.
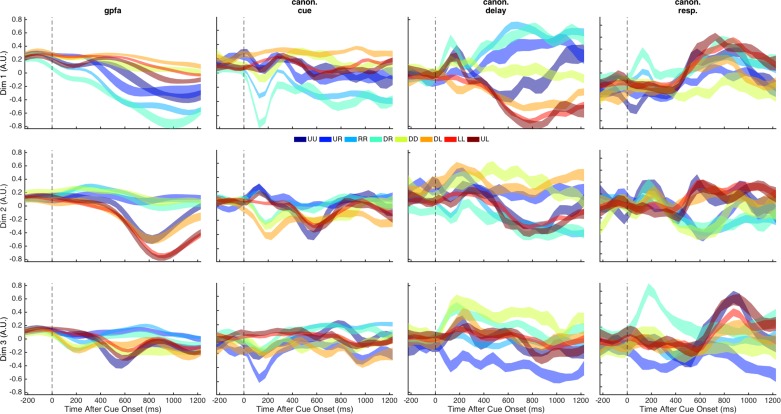
We extracted neural trajectories with reduced dimensionality using several techniques. The first column of Fig. 6 displays the neural activity projected into the space defined by the top three GPFA dimensions for one example session. Although the calculation of the GPFA weightings is unsupervised, some separation of trajectories according to target location was apparent in the top GPFA factors. This suggests that the neural activity arising from the latent network structure defined by the GPFA weightings participates in task performance.
Fig. 6.
Neural activity projected into the top 3 dimensions for different trajectories. Each column corresponds to a different neural trajectory (gpfa, Gaussian process factor analysis; canon. cue, canonical trajectories with component weightings calculated using cue epoch activity only; canon. delay, canonical trajectories based on delay epoch activity; canon. resp., canonical trajectories based on response epoch activity). Each row corresponds to a different dimension of the neural trajectory, ordered by decreasing variance. Each trace corresponds to the mean ± SE trajectory values (A.U., arbitrary units) of trials grouped by target location for a given trajectory and dimension. The different colors indicate the different target locations (UU: up-center; UR: up-right; RR: middle-right; DR: down-right; DD: down-center; DL: down-left; LL: middle-left; UL: up-left). The vertical dashed line indicates the time of cue onset.
We also projected the neural activity into the space defined by the canonical components calculated from each of the cue, delay, and response epochs (Fig. 6, columns 2–4, respectively). As expected, the canonical components that, by definition, maximized target-location separation based on neural activity in a specific epoch resulted in neural trajectories that had larger separation between target locations during the epoch than outside the epoch.
The average distance between GPFA trajectories and canonical trajectories varied between epochs [F(2, 22) = 5.63, P = 0.01]. Overall, the distance between GPFA trajectories and canonical delay trajectories was less than for the other canonical trajectories, but the difference was only significant compared with the canonical response trajectories (Bonferroni-corrected P = 0.015).
Classification.
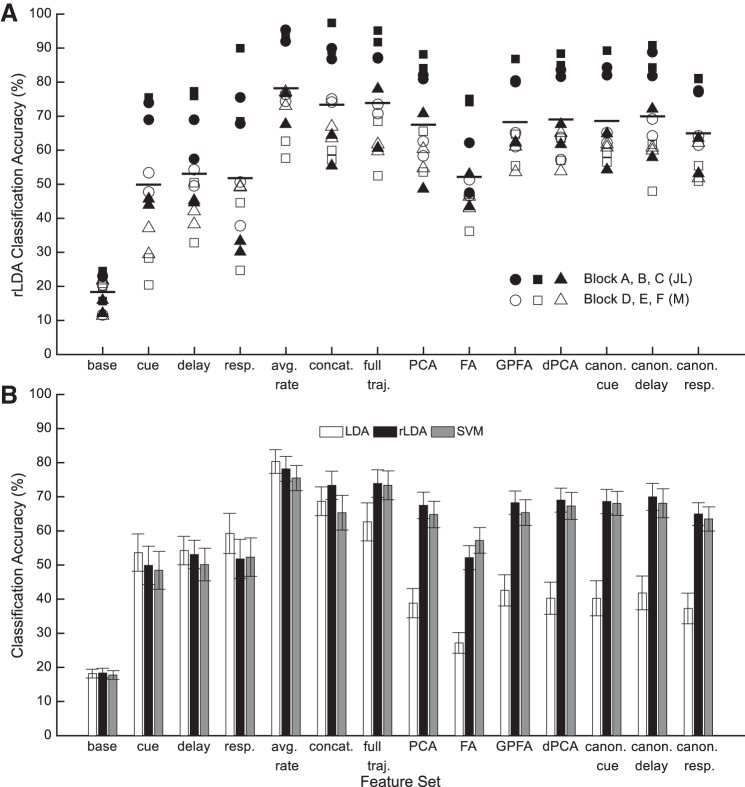
We predicted intended saccades from LPFC neuronal spiking activity separately for each session, for each of the 14 feature sets (baseline, cue, delay, and response epoch square root transformed spike counts, all epochs together, average firing rate throughout the full trial, full neural trajectories, PCA, FA, GPFA, dPCA and three canonical reduced neural trajectories), and for each machine-learning algorithm (LDA, rLDA, and SVM) (Fig. 7). Using rLDA, all feature sets predicted target location more accurately than the baseline feature set [Fig. 7A; baseline (chance) accuracy = 18.4%; repeated measures ANOVA F(13,78) = 116.5, P ⪡ 0.001, Bonferroni-corrected P < 0.01 for each feature set].
Fig. 7.
Classification results. A: classification accuracies for each session across all feature sets using rLDA. Subjects JL and M are represented with closed and open symbols, respectively. The different symbol shapes represent the electrode block used for the session (circle, square, triangle represent blocks A, B, C for monkey JL and blocks D, E, F for monkey M). For each feature set, the horizontal line indicates the mean. B: average classification accuracies across the 12 sessions for each feature set (n = 14 bar groups) and each machine-learning algorithm (m = 3 bar shadings within a group). The error bars indicate the standard error across sessions within the feature set and machine-learning combination.
Classification accuracy was strongly impacted by the block of electrodes used in a given session. For example, sessions using block A or B from monkey JL yielded classification accuracies much greater than sessions using block C or any sessions from monkey M. In general, there was no topographical association between block location and classification accuracy; classification was best for monkey JL using block B located in the middle of the intersection between the principal and arcuate sulci, whereas classification was best for monkey M using block D located more laterally. If we separate the sessions into two groups—the accurate group comprising monkey JL blocks A and B, and the inaccurate group comprising the remaining blocks—there is no significant difference in the number of trials [t(10) = 0.7, P = 0.50] or in the number of sorted neurons [t(10) = 2.0, P = 0.07].
Averaged across all sessions, the best overall feature set and machine-learning combination was the average firing rate with LDA (Fig. 7B; 80.3%; range: 63.6–96.9%). Indeed, the average firing rate yielded the best classification accuracy across feature sets for all machine-learning algorithms. For the other feature sets, lower dimensional feature sets worked best with LDA, and higher dimensional feature sets, containing data from multiple time points, benefited from regularization so rLDA was best. The lower dimensional cue, delay, and response feature sets, which each use data from only a 250-ms segment of the trial, all yielded worse classification accuracies than the feature sets that used the entire trial duration.
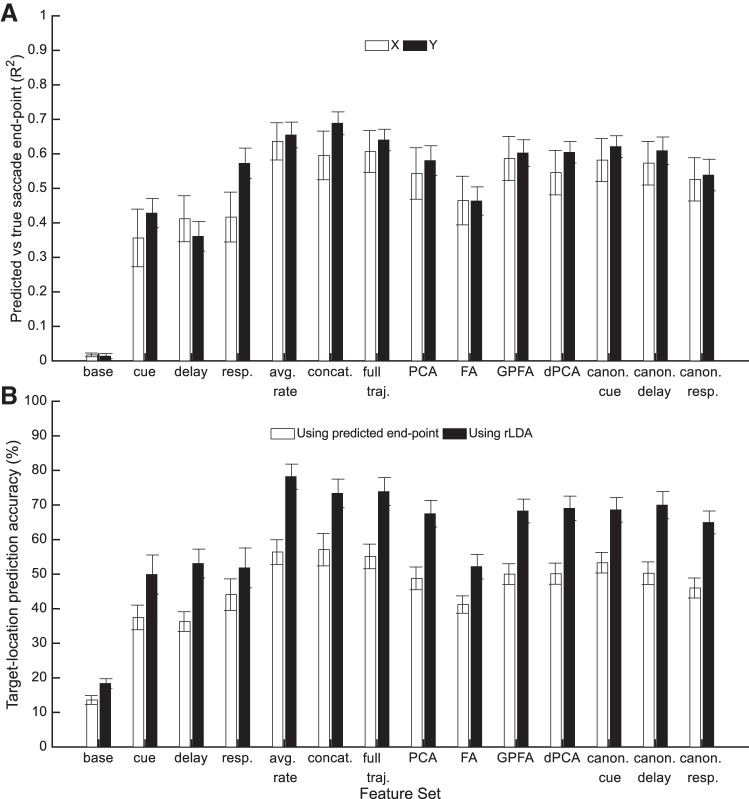
For each feature set, we used lasso regression to predict saccade end point coordinates. The average firing rate feature set accounted for 64 and 65% of the variance in saccade end point for x and y coordinates, respectively (Fig. 8A). Predicted saccade end-point was used to predict the target location as the target nearest to the saccade end point, but accuracy was 4–22% worse than predicting target location from the neural features directly [Fig. 8B; F(13,143) = 64.9, P < 0.001].
Fig. 8.
Correlation results. A: the correlation between actual saccade end point measured with the eye tracker and the predicted saccade end point from cross-validated lasso regression using each of the feature sets. The saccade end point X- and Y-coordinates were predicted independently. B: target location classification accuracies using either the target location nearest the predicted saccade end point or using regularized linear discriminant analysis on the neural activity to predict the saccade directly (same data as Fig. 7B). PCA, principal components analysis; dPCA, demixed PCA; FA, factor analysis; GPFA, Gaussian process factor analysis.
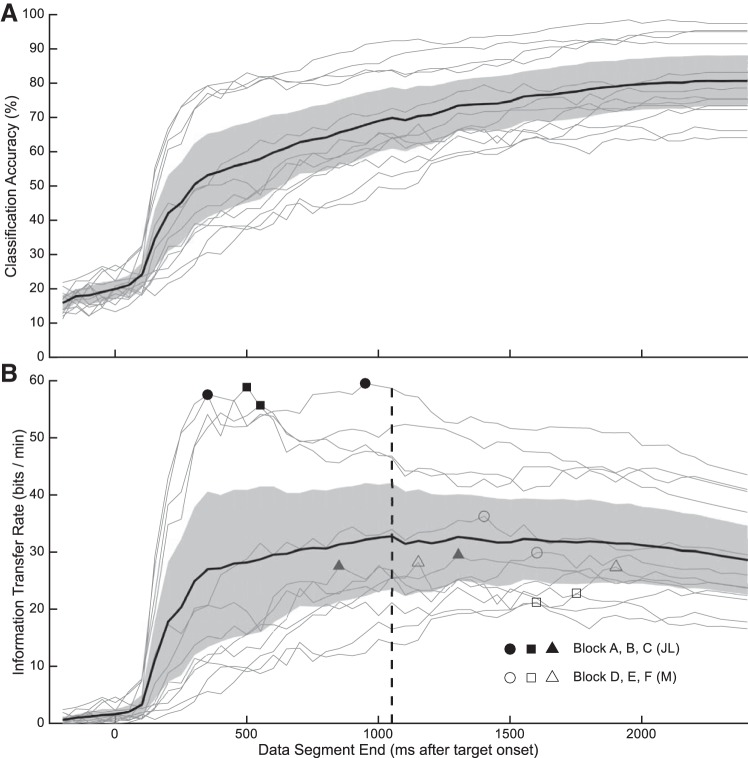
We used the average firing rate and LDA to calculate classification accuracy and information transfer rate (ITR) for different trial durations. Classification accuracy increased sharply 100 ms after target onset and continued to increase slowly as the duration of the neural trajectory increased (Fig. 9A). The average ITR peak value was 32.8 bits/min at 1,050 ms after target onset. Individual sessions had peak ITR values ranging from 21 to 59 bits/min from 350 to 1,600 ms after target onset (Fig. 9B).
Fig. 9.
Classification accuracy (A) and information transfer rate (ITR) (B) as a function of neural trajectory length. Individual sessions are plotted with thin lines, the average across sessions is plotted with the thick black line, and the gray shaded region is the 95% confidence interval. Symbols indicate the peak ITR for each session and the vertical dashed line indicates the trajectory duration that yielded the optimal ITR averaged across sessions.
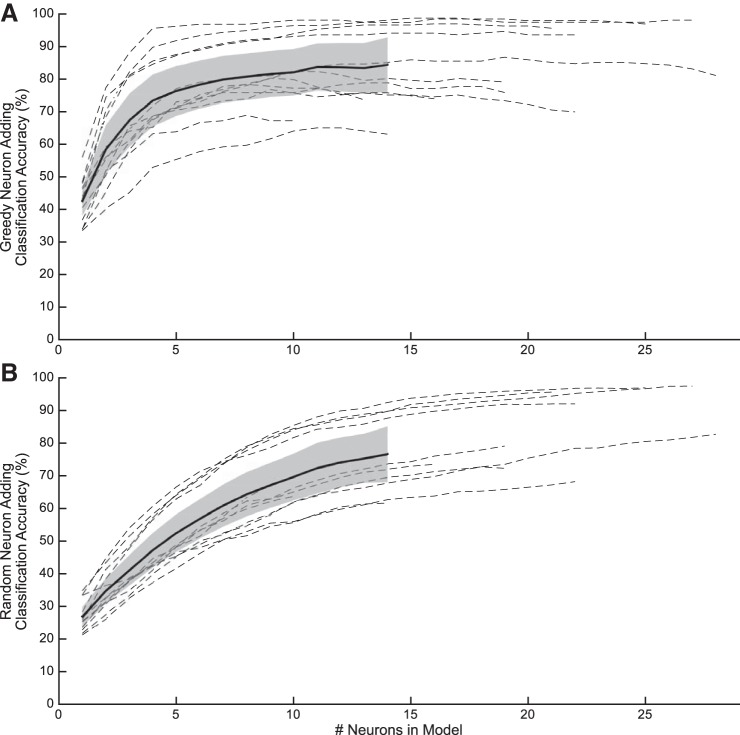
The greedy neuron-adding analysis demonstrated that LDA classifier performance using average firing rates improved as a function of the number of neurons included in the model until plateau accuracy was reached (Fig. 10A). Across sessions, classification accuracy surpassed baseline epoch classification after the single most informative neuron was added to the model [paired-t(11) = 11.1, corrected P value ⪡ 0.001]. Classification accuracy was significantly worse than the best accuracy, i.e., the accuracy obtained using average firing rate and LDA, until 6 neurons were added to the model [paired-t(11), corrected P value < 0.05 for <6 neurons in the model].
Fig. 10.
Greedy and random neuron adding. Classification accuracy improved as neurons were added to the model for each session (dashed line corresponds to individual sessions; solid line and shaded error corresponds to average across sessions ± SE). A: using average firing rates and linear discriminant analysis, the neuron that improved classification the most was added to the model stepwise until no neurons remained. B: for each session, neurons were added to the model in random order; presented data represent the average result after 20 random shuffles.
The random neuron-adding analysis demonstrated an increase in classifier performance as a function of the number of neurons included in the model that was shallower than the greedy analysis (Fig. 10B). Similar to the greedy analysis, classifier performance outperformed baseline performance with the inclusion of a single neuron [paired-t(11) = 5.95, corrected P < 0.05]. Unlike the greedy analysis, classification accuracy was significantly worse than the best accuracy until 16 neurons were added to the model (corrected P value < 0.05 for <16 neurons in the model).
DISCUSSION
The present study demonstrates accurate prediction of saccade target locations from single-trial dorsolateral prefrontal cortex (LPFC) neural activity. Despite the large heterogeneity of responses among individual neurons, lower-dimensional representations of the population of LPFC neurons demonstrated that saccade target location was encoded shortly after target presentation and was maintained throughout the delay epoch until the monkey made the saccade to the target. In our offline analyses of these data, classification accuracy and theoretical information transfer rates approached those of state of the art BCIs (Nuyujukian et al. 2014), suggesting these techniques may support a goal-based cognitive BCI.
Individual LPFC neurons are modulated by multiple task components.
LPFC neurons are involved in working memory and sensorimotor transformations, especially for visual input (Goldman-Rakic 1990), with a subpopulation of “visual” responses supporting covert attention (Tremblay et al. 2015). LPFC neurons are also involved in decision making for multiple modalities (Brody et al. 2003; Cunningham and Yu 2014; Machens et al. 2010; Mante et al. 2013) and for multiple aspects of the task (Hernández et al. 2010; Rigotti et al. 2013). Our observations of temporal and functional heterogeneity in task-related modulation of firing rates among individual LPFC neurons were consistent with the previous work. We identified neurons with location-dependent firing rate increases just after the onset of the target, during the delay epoch, around saccade onset, and every combination thereof. For many of the neurons with significant location-dependent firing rate modulation in more than one epoch, the locational dependence of such modulation was different between epochs.
The change in locational dependence from cue to response epochs may be representative of a flexible substrate that permits mapping of arbitrary stimulus information to arbitrary saccade locations. While the mechanism underlying this flexibility is unknown, it is a phenomenon commonly observed in antisaccade paradigms or scenarios where the cue is dissociated from the movement goal. These results add to a growing consensus that task representation in the activity of neurons in sensorimotor integration areas like the LPFC is perhaps more complicated than in the activity of neurons in sensory and motor cortices.
While we are confident that our spike sorting isolated individual neurons, it is always possible that some of the heterogeneity in single-neuron task involvement was due to multiple neurons contributing to a single neuron's response.
Target location is decoded accurately from single-trial LFPC population activity.
We were able to predict single-trial saccade target location with better-than-chance accuracy in all recording sessions. The classification accuracies in this study (64–97%) were somewhat similar to those obtained by Markowitz et al. (2011) using LFPs and multiunit activity recorded from multiple single electrodes at likely shallower cortical depths during an oculomotor delay response task. While it is likely that our classification results may improve with the addition of LFPs or unsorted neurons, we did not test this explicitly because we were interested specifically in single neuron and ensemble dynamics.
Classification accuracy varied substantially across sessions with different electrode blocks. The different electrode sites for each electrode block were not distributed evenly across the MEAs and it is likely that the blocks did not sample equally the spatially distinct subnets underlying the task (Kiani et al. 2015). We did not observe any relationship between classification accuracy and electrode position relative to the gyral anatomy.
Among the different feature extraction techniques implemented here, simple averaging of firing rates across the entire trial provided the best classification accuracy across sessions. This was surprising because the average firing rates over the entire trial would be expected to have a diluted response due to the inclusion of the baseline epoch, during which there cannot be any target-specific activity. Further, “specialist” neurons that respond robustly during one epoch but not others and neurons with different locational dependence of modulation between epochs will have a diluted response when averaged over an individual trial compared with their response during a single epoch. We expected that feature sets that accommodated these types of dynamic responses by including temporal information (i.e., concatenated epochs and all of the neural trajectories) would perform better.
There are at least two nonmutually exclusive explanations for why the simple averaged firing rates may allow for better classification than the more dynamic feature sets. First, the temporal feature sets may be subject to the “curse of dimensionality” as they have many more features and are more likely to overfit the training data. We used regularization to mitigate this problem, and indeed regularization improved classifier performance substantially for feature sets with high dimensionality, although we would have preferred to have many more trials than features. The second possible explanation for the better performance of averaged firing rates over the more dynamic features is that the task-related modulations of neuronal activity may not have been strongly time-locked to target onset, despite the simple nature of the task. That is, “specialist” neurons, if present, were not critical for classification.
Although the averaged firing rate provided the best classification accuracy, the neural trajectory feature sets were not far behind. Among the neural trajectories, dynamical modeling and data reduction (e.g., PCA, GPFA, dPCA) did not improve classifier performance probably because we only used data from 17 neurons per session (range 9–26), and the feature selection property intrinsic to both SVM and rLDA classifiers was adequate to handle these dimensionalities and prevent overfitting. Recordings with many more electrodes and many more task conditions may benefit from combined data reduction and feature selection.
Further, it is likely that the task in the present study was too simple to benefit from the incorporation of a dynamical model. We expect classification may benefit from feature reduction techniques that incorporate temporal dynamics in a decision-making task where the monkey may have to accumulate information prior to planning their behavior (Kiani et al. 2014), unlike the present task. Similarly, classification of such data may benefit from machine-learning techniques that are sensitive to temporal information [e.g., dynamic Bayesian networks (Bielza and Larrañaga 2014; Dean and Kanazawa 1989; Eldawlatly et al. 2010), dynamic time warping (Gupta et al. 1996) with template matching] unlike the machine-learning techniques used here that ignore the temporal relationship among predictors.
Decoding target location benefits from LPFC sensorimotor transformations.
There are several pieces of evidence that, taken in aggregate, suggest that sampling the sensorimotor transformations that occur during the delay epoch is critical for accurately decoding target location from LPFC neuronal activity.
The neuronal activity emerging from the latent network structure (i.e., GPFA trajectories) was more similar to the representation of activity that maximized target location separation during the delay epoch than representations that maximized separation during the response epoch. This suggests that the networks from which the ensemble activity arises are involved more in the sensorimotor transformation than they are in executing saccades.
Information transfer rate (ITR) optimizes the tradeoff between shorter trials to increase speed and longer trials to increase information. The stimulus presentation duration that maximized ITR across all sessions was 1,050 ms. This suggests that the improvement in classification from the addition of the neuronal data from the delay epoch to the early visually evoked response data more than compensated for the added time required to collect these data, but this was not true for the response epoch data.
Target prediction accuracy using targets nearest predicted saccade end points was worse than classifying target location directly. This suggests that the classifier is picking up an abstract representation of targets that does not depend on a continuous spatial coordinate system or the motor output to such a system.
Taken together, these results suggest that classification of target locations from LPFC neurons does not depend entirely on either the visual response or the motor output. Rather, the sensorimotor transformations that occur during the delay epoch are critical for good classifier performance. However, the task in the present study is too simple to differentiate visual processing from behavioral planning and it remains possible that the neuronal activity in the delay epoch is due to continued visual processing rather than sensorimotor transformations or behavioral planning. Future studies remain to be done that use different tasks (e.g., memory-guided saccades) to disambiguate these processes.
The classifiers performed poorly for trials with targets located in the ipsilateral visual field. This result was anticipated, as LPFC neurons are known to have a greater representation of stimuli and responses in the contralateral visual field (Goldman-Rakic 1990). However, we expect the neural activity recorded from a single hemisphere to be sufficient to drive a BCI with targets in both visual hemifields because the network underlying the recorded activity should adapt to the BCI decoder when rewarded directly in a closed-loop BCI (Graf and Andersen 2014). Furthermore, the target arrangement, distance, and spacing were predetermined prior to array implementation in the present study, and not dependent on the receptive fields of the recorded neurons. Classification performance would likely be much better if the targets were optimally selected for the recorded neurons. This strategy could be utilized to boost performance in a classification-based BCI from LPFC.
Despite array implantation that was based on relatively crude anatomic markers, the neuron-adding analysis demonstrated that either a random sampling of 16 neurons or a subsampling of the 6 best of 20 neurons was sufficient to achieve near-plateau classification accuracy. These results suggest that high-performance LPFC-based BCIs may be attainable with the implantation of small electrode arrays and subsequent selection of even fewer electrodes. It is desirable to use fewer electrodes because it reduces the device footprint in the brain and it facilitates the use of low-power embedded electronics for amplification, signal processing, and classifier output transmission.
Towards a cognitive BCI.
A cognitive neural prosthesis, or cognitive BCI, decodes goals and decisions in real time, then commands a computer or robot to achieve those goals. Unlike a motor cortical BCI, cognitive BCI users do not provide continuous control signals to the effector while monitoring its actions; they issue only the goals and rely on the effector's ability, whether driven by artificial intelligence or supplemented by a motor cortical BCI, to achieve that goal. A cognitive BCI may be more intuitive than a motor cortical BCI because the users do not need to continually attend to the effector and because the control signals emerge from the natural decision-making process (Andersen et al. 2014). A cognitive BCI may also be used to enhance motor cortical BCIs to be more efficient and compatible with the cognitive state of the individual. For example, the cognitive BCI could constrain neuroprosthetic movements to motor plans that involve the cognitively salient object or goal.
Most work on cognitive BCIs has used parietal cortex as a signal source (Andersen et al. 2014; Klaes et al. 2014; Musallam et al. 2004). The prefrontal cortex may also be a good signal source for cognitive BCIs (Vansteensel et al. 2010) because it is involved in integrating perceptual information, making decisions, and directing behavior toward goals (Buschman and Miller 2014; Everling et al. 2002; Heekeren et al. 2008; Tremblay et al. 2015). In the present study, we demonstrated that it is possible to decode goals from single-trial LPFC neural activity, at least for this simple task. Future studies remain to be done that investigate single-trial decoding during decision-making, how decoding of decision outcomes is affected by contextual learning, and how online feedback of decoded decision outcomes affects neural activity.
GRANTS
This study was supported by the Canadian Institutes for Health Research (CIHR) and the Natural Sciences and Engineering Research Council of Canada (NSERC).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
Author contributions: C.B.B. analyzed data; C.B.B. and J.M.-T. interpreted results of experiments; C.B.B. prepared figures; C.B.B. drafted manuscript; C.B.B., J.M.-T., and A.J.S. edited and revised manuscript; C.B.B., M.L., J.M.-T., and A.J.S. approved final version of manuscript; F.P., M.L., J.M.-T., and A.J.S. conception and design of research; M.L. and A.J.S. performed experiments.
REFERENCES
- Aflalo T, Kellis S, Klaes C, Lee B, Shi Y, Pejsa K, Shanfield K, Hayes-Jackson S, Aisen M, Heck C, Liu C, Andersen RA. Decoding motor imagery from the posterior parietal cortex of a tetraplegic human. Science 348: 906–910, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen RA, Kellis S, Klaes C, Aflalo T. Toward more versatile and intuitive cortical brain-machine interfaces. Curr Biol 24: R885–R897, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong KM, Fitzgerald JK, Moore T. Changes in visual receptive fields with microstimulation of frontal cortex. Neuron 50: 791–798, 2006. [DOI] [PubMed] [Google Scholar]
- Bielza C, Larrañaga P. Bayesian networks in neuroscience: a survey. Front Comput Neurosci 8: 131, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bongard S, Nieder A. Basic mathematical rules are encoded by primate prefrontal cortex neurons. Proc Natl Acad Sci USA 107: 2277–2282, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brendel W, Romo R, Machens CK. Demixed principal component analysis. Adv Neural Inf Process Syst 24: 2654–2662, 2011. [Google Scholar]
- Brody CD, Hernández A, Zainos A, Romo R. Timing and neural encoding of somatosensory parametric working memory in macaque prefrontal cortex. Cereb Cortex 13: 1196–1207, 2003. [DOI] [PubMed] [Google Scholar]
- Brown G, Pocock A, Zhao M, Luján M. Conditional likelihood maximisation: a unifying framework for information theoretic feature selection. J. Machine Learning Res 13: 27–66, 2012. [Google Scholar]
- Buschman TJ, Denovellis EL, Diogo C, Bullock D, Miller EK. Synchronous oscillatory neural ensembles for rules in the prefrontal cortex. Neuron 76: 838–846, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buschman TJ, Miller EK. Goal-direction and top-down control. Philos Trans R Soc Lond B Biol Sci 369 20130471, 2014. doi: 10.1098/rstb.2013.0471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase SM, Kass RE, Schwartz AB. Behavioral and neural correlates of visuomotor adaptation observed through a brain-computer interface in primary motor cortex. J Neurophysiol 108: 624–644, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collinger JL, Wodlinger B, Downey JE, Wang W, Tyler-Kabara EC, Weber DJ, McMorland AJ, Velliste M, Boninger ML, Schwartz AB. High-performance neuroprosthetic control by an individual with tetraplegia. Lancet 381: 557–564, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowley BR, Kaufman MT, Butler ZS, Churchland MM, Ryu SI, Shenoy KV, Yu BM. DataHigh: graphical user interface for visualizing and interacting with high-dimensional neural activity. J Neural Eng 10: 066012, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cristianini N, Shawe-Taylor J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. New York: Cambridge Univ. Press, 2000. [Google Scholar]
- Cunningham JP, Yu BM. Dimensionality reduction for large-scale neural recordings. Nat Neurosci 17: 1500–1509, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean T, Kanazawa K. A model for reasoning about persistence and causation. Comput Intell 5: 142–150, 1989. [Google Scholar]
- Eldawlatly S, Zhou Y, Jin R, Oweiss KG. On the use of dynamic Bayesian networks in reconstructing functional neuronal networks from spike train ensembles. Neural Comput 22: 158–189, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everling S, Tinsley CJ, Gaffan D, Duncan J. Filtering of neural signals by focused attention in the monkey prefrontal cortex. Nat Neurosci 5: 671–676, 2002. [DOI] [PubMed] [Google Scholar]
- Friedman JH. Regularized discriminant analysis. J Am Stat Assoc 84: 165–175, 1989. [Google Scholar]
- Fuster JM, Alexander GE. Neuron activity related to short-term memory. Science 173: 652–654, 1971. [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science 233: 1416–1419, 1986. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Neocortical memory circuits. Cold Spring Harb Symp Quant Biol 55: 1025–1038, 1990. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Cellular basis of working memory. Neuron 14: 477–485, 1995. [DOI] [PubMed] [Google Scholar]
- Graf ABA, Andersen RA. Brain-machine interface for eye movements. Proc Natl Acad Sci USA 111: 17630–17635, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta L, Molfese DL, Tammana R, Simos PG. Nonlinear alignment and averaging for estimating the evoked potential. IEEE Trans Biomed Eng 43: 348–356, 1996. [DOI] [PubMed] [Google Scholar]
- Hastie TJ, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer, 2009. [Google Scholar]
- Hatsopoulos NG, Donoghue JP. The science of neural interface systems. Annu Rev Neurosci 32: 249–266, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heekeren HR, Marrett S, Ungerleider LG. The neural systems that mediate human perceptual decision making. Nat Rev Neurosci 9: 467–479, 2008. [DOI] [PubMed] [Google Scholar]
- Hernández A, Nácher V, Luna R, Zainos A. Decoding a perceptual decision process across cortex. Neuron 66: 300–314, 2010. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, Branner A, Chen D, Penn RD, Donoghue JP. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature 442: 164–171, 2006. [DOI] [PubMed] [Google Scholar]
- Jacobson CF. Studies of cerebral functions in primates. I. The functions of the frontal association areas in monkeys. Comp Psychol Monogr 13: 1–30, 1936. [Google Scholar]
- Kao JC, Nuyujukian P, Ryu SI, Churchland MM, Cunningham JP, Shenoy KV. Single-trial dynamics of motor cortex and their applications to brain-machine interfaces. Nat Commun 6: 7759, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Cueva C, Reppas J, Newsome WT. Dynamics of neural population responses in prefrontal cortex indicate changes of mind on single trials. Curr Biol 24: 1542–1547, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Cueva C, Reppas J, Peixoto D. Natural grouping of neural responses reveals spatially segregated clusters in prearcuate cortex. Neuron 85: 1359–1373, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kihlberg J, Herson J, Schotz W. Square root transformation revisited. Appl Stat 21: 76–81, 1972. [Google Scholar]
- Kim JN, Shadlen MN. Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat Neurosci 2: 176–185, 1999. [DOI] [PubMed] [Google Scholar]
- Klaes C, Shi Y, Kellis S, Minxha J, Revechkis B, Andersen RA. A cognitive neuroprosthetic that uses cortical stimulation for somatosensory feedback. J Neural Eng 11: 056024, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobak D, Brendel W, Constantinidis C, Feierstein CE, Kepecs A, Mainen ZF, Romo R, Qi XL, Uchida N, Machens CK. Demixed principal component analysis of population activity in higher cortical areas reveals independent representation of task parameters. arXiv 1410.6031v1, 2014. [Google Scholar]
- Kothe CA, Makeig S. BCILAB: a platform for brain-computer interface development. J Neural Eng 10: 056014, 2013. [DOI] [PubMed] [Google Scholar]
- Kubota K, Niki H. Prefrontal cortical unit activity and delayed alternation performance in monkeys. J Neurophysiol 34: 337–347, 1971. [DOI] [PubMed] [Google Scholar]
- Ledoit O, Wolf M. A well-conditioned estimator for large-dimensional covariance matrices. J Multivar Anal 88: 365–411, 2004. [Google Scholar]
- Lennert T, Martinez-Trujillo JC. Prefrontal neurons of opposite spatial preference display distinct target selection dynamics. J Neurosci 33: 9520–9529, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machens CK, Romo R, Brody CD. Functional, but not anatomical, separation of “what” and “when” in prefrontal cortex. J Neurosci 30: 350–360, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mante V, Sussillo D, Shenoy KV, Newsome WT. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503: 78–84, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowitz DA, Wong YT, Gray CM, Pesaran B. Optimizing the decoding of movement goals from local field potentials in macaque cortex. J Neurosci 31: 18412–18422, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendoza-Halliday D, Torres S, Martinez-Trujillo JC. Sharp emergence of feature-selective sustained activity along the dorsal visual pathway. Nat Neurosci 17: 1255–1262, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK, Erickson CA, Desimone R. Neural mechanisms of visual working memory in prefrontal cortex of the macaque. J Neurosci 16: 5154–5167, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musallam S, Corneil BD, Greger B, Scherberger H, Andersen RA. Cognitive control signals for neural prosthetics. Science 305: 258–262, 2004. [DOI] [PubMed] [Google Scholar]
- Nuyujukian P, Kao JC, Fan JM, Stavisky SD, Ryu SI, Shenoy KV. Performance sustaining intracortical neural prostheses. J Neural Eng 11: 066003, 2014. [DOI] [PubMed] [Google Scholar]
- Petrides M. Lateral prefrontal cortex: architectonic and functional organization. Philos Trans R Soc Lond B Biol Sci 360: 781–795, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce JR. An Introduction to Information Theory: Symbols, Signals & Noise. New York: Dover, 1980. [Google Scholar]
- Pohlmeyer EA, Solla SA, Perreault EJ, Miller LE. Prediction of upper limb muscle activity from motor cortical discharge during reaching. J Neural Eng 4: 369–379, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang XJ, Daw ND, Miller EK, Fusi S. The importance of mixed selectivity in complex cognitive tasks. Nature 497: 585–590, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadtler PT, Quick KM, Golub MD, Chase SM, Ryu SI, Tyler-Kabara EC, Yu BM, Batista AP. Neural constraints on learning. Nature 512: 423–426, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz AB. Cortical neural prosthetics. Annu Rev Neurosci 27: 487–507, 2004. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci 18: 3870–3896, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay S, Pieper F, Sachs A, Martinez-Trujillo JC. Attentional filtering of visual information by neuronal ensembles in the primate lateral prefrontal cortex. Neuron 85: 202–215, 2015. [DOI] [PubMed] [Google Scholar]
- Vansteensel MJ, Hermes D, Aarnoutse EJ, Bleichner MG, Schalk G, van Rijen PC, Leijten FSS, Ramsey NF. Brain-computer interfacing based on cognitive control. Ann Neurol 67: 809–816, 2010. [DOI] [PubMed] [Google Scholar]
- Wallis JD, Anderson KC, Miller EK. Single neurons in prefrontal cortex encode abstract rules. Nature 411: 953–956, 2001. [DOI] [PubMed] [Google Scholar]
- Wang W, Collinger JL, Degenhart AD, Tyler-Kabara EC, Schwartz AB, Moran DW, Weber DJ, Wodlinger B, Vinjamuri RK, Ashmore RC, Kelly JW, Boninger ML. An electrocorticographic brain interface in an individual with tetraplegia. PLos One 8: e55344, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessberg J, Stambaugh CR, Kralik JD, Beck PD, Laubach M, Chapin JK, Kim J, Biggs SJ, Srinivasan MA, Nicolelis MAL. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature 408: 361–365, 2000. [DOI] [PubMed] [Google Scholar]
- White IM, Wise SP. Rule-dependent neuronal activity in the prefrontal cortex. Exp Brain Res 126: 315–335, 1999. [DOI] [PubMed] [Google Scholar]
- Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, Sahani M. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J Neurophysiol 102: 614–635, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]