The temporal dynamics of heading perception in the presence of moving objects

Abstract

Many forms of locomotion rely on the ability to accurately perceive one's direction of locomotion (i.e., heading) based on optic flow. Although accurate in rigid environments, heading judgments may be biased when independently moving objects are present. The aim of this study was to systematically investigate the conditions in which moving objects influence heading perception, with a focus on the temporal dynamics and the mechanisms underlying this bias. Subjects viewed stimuli simulating linear self-motion in the presence of a moving object and judged their direction of heading. Experiments 1 and 2 revealed that heading perception is biased when the object crosses or almost crosses the observer's future path toward the end of the trial, but not when the object crosses earlier in the trial. Nonetheless, heading perception is not based entirely on the instantaneous optic flow toward the end of the trial. This was demonstrated in Experiment 3 by varying the portion of the earlier part of the trial leading up to the last frame that was presented to subjects. When the stimulus duration was long enough to include the part of the trial before the moving object crossed the observer's path, heading judgments were less biased. The findings suggest that heading perception is affected by the temporal evolution of optic flow. The time course of dorsal medial superior temporal area (MSTd) neuron responses may play a crucial role in perceiving heading in the presence of moving objects, a property not captured by many existing models.

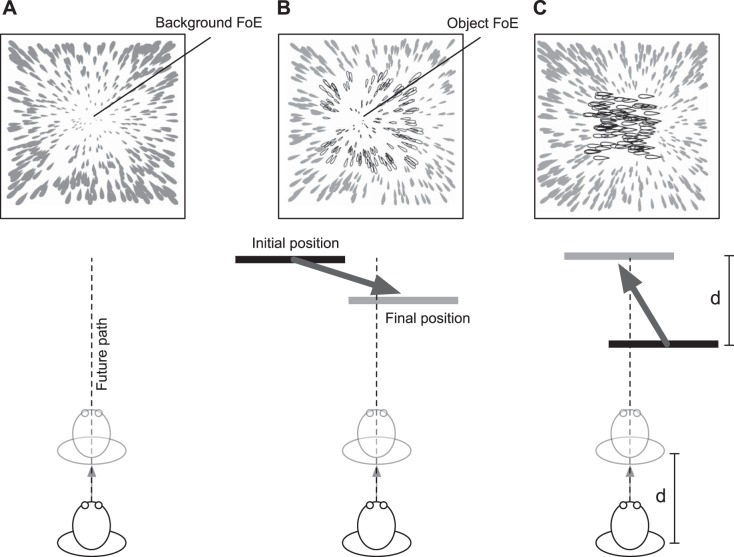
gibson (1958, 1961, 1979) proposed that sighted animals use optic flow to guide self-motion. To move forward, the animal should “contract the muscles so as to make the optic array flow outward,” and to stop, the animal should “make the flow cease” (Gibson 1958). Gibson's strategy for navigation requires the accurate perception of heading from optic flow, which prompted psychophysical studies to investigate how well humans judge their heading using visual information alone. In the typical psychophysical experiment, human observers passively view computer displays that simulate forward self-motion along a straight path in an environment defined by dots (Fig. 1A; Cuturi and MacNeilage 2013; Van Den Berg 1992; Warren and Hannon 1988). Judgments are accurate within ±2°, indicating that humans are capable of estimating heading from optic flow alone, which supports Gibson's hypothesis.

Fig. 1.

Illustration of an observer's self-motion (bottom panels) and the corresponding optic flow (top panels) in a static environment (A), with a laterally moving object that approaches in depth (B), and with a laterally moving object that does not approach in depth (c). Top, gray and black drops indicate the instantaneous optic flow vectors due to the background and moving object, respectively. The background focus of expansion (FoE) is the singularity that specifies the observer's heading direction, and the object FoE indicates the object's direction of travel. Bottom, the observer's initial (black) and final (gray) positions along a straight path (dashed line) are shown.

However, the optic flow patterns routinely experienced by animals are far more complex than the simple radial case, which makes Gibson's simple approach insufficient to explain the visual control of self-motion. One source of complexity is independently moving objects, which complicate the optic flow by introducing ambiguity about the heading direction. Moving objects locally alter the optic flow (Fig. 1, B and C) that would otherwise be experienced in a static environment and may occlude the focus of expansion (FoE), which specifies the observer's direction of travel in a static environment (background FoE, Fig. 1A). Unless the depth between a moving object and observer remains constant over time, the moving object will appear to approach or recede relative to the observer and generate a secondary FoE (object FoE, Fig. 1B) or focus of contraction (FoC), respectively, that specifies the direction of self-motion relative to the object. Thus independently moving objects introduce a conflict between the global flow from the stationary background, which is informative about heading, and the local flow from the object, which is not informative about heading.

Heading Perception in the Presence of Moving Objects

Despite how frequently humans encounter other moving vehicles while driving and other pedestrians while walking, there are presently only two studies that have investigated human heading perception during linear self-motion in the presence of moving objects (Royden and Hildreth 1996; Warren and Saunders 1995).¹ Warren and Saunders (1995) assessed heading judgments in the presence of an object moving perpendicularly to the path of a forwardly translating observer (Fig. 1B). Dots belonging to the square object occupied a closer depth than those belonging to the background frontoparallel plane. Because the object approached the observer in depth, the optical size of the object increased throughout the trial. They found that when the moving object obscured the background FoE for much of the trial, heading judgments were strongly biased in the direction opposite of object motion. For example, human heading judgments were biased toward the right when the moving object approached from the right and moved leftward across the observer's heading direction. On average, the magnitude of the bias was 3.7° when the object was opaque and 2.3° when the object was transparent. When the object moved on the side of the screen opposite of the observer's heading and did not approach the observer's future path, no heading bias occurred.

Royden and Hildreth (1996) focused on heading perception in the presence of a moving object that maintains a fixed depth with respect to the observer. The pattern of motion produced by a moving object that retreats such to maintain its depth to the observer appears planar (Fig. 1C). For example, an object that moves to cross the observer's heading direction from the left and preserves the relative depth between it and the translating observer will result in uniform, constant speed motion within the contours of the object. Under these conditions, Royden and Hildreth found a small ∼1°, but reliable, bias in the direction of the object's motion.

Modeling the Influence of Moving Objects on Heading Perception

Several attempts have been made to account for the origin of these biases in heading perception by developing biological models of heading perception that function in environments containing moving objects. These models fall into two classes based on whether they rely on differential motion or spatial pooling mechanisms.

Differential motion models exploit a mathematical “trick” involving the first-order optic flow equations when combined with a planar camera model to model the projection of optic flow on the primate retina, first described by Longuet-Higgins and Prazdny (1980). Instantaneous optic flow can be expressed in terms of the observer's translation and rotational velocity. In a rigid environment, the observer's translational and rotational velocity vectors fully characterize the optic flow when traveling along a straight path (Fig. 1A; Longuet-Higgins and Prazdny 1980). Several models have leveraged the fact that the translational component depends on depth in the world, but the rotational component does not. Therefore, subtraction of two nearby samples with different depths (e.g., at a depth discontinuity) cancels out the rotational term and yields a scaled version of the translational term, from which heading can be recovered (Hildreth 1992; Rieger and Lawton 1985; Royden 1997, 2002). One such model introduced by Royden (2002) simulates the previously described pattern of human heading bias in the presence of independently moving objects (Royden and Hildreth 1996; Warren and Saunders 1995).

Raudies and Neumann (2013) introduced a model that differs from the aforementioned models in that it segments object and background flow before estimating heading. Raudies and Neumann's model analytically combines different optic flow segmentation cues, such as accretion/deletion, expansion/contraction, and curvature, to detect heading during self-motion along straight or curved paths in the presence of moving objects.

The other main class of models relies on motion pooling mechanisms to estimate heading from optical motion rather than differential motion. In static environments, these models estimate heading by matching optic flow against a basis of radial motion pattern templates (Perrone 1992; Perrone and Stone 1994), a process inspired by the properties of neurons in the dorsal medial superior temporal area (MSTd) in the primate brain (Ben Hamed et al. 2003; Duffy 1998; Duffy and Wurtz 1991). To account for moving objects, Warren and Saunders (1995) introduced a simplified template model with pooling and template matching stages. In the presence of laterally moving objects that approach the observer in depth, the model's heading estimate is equivalent to a spatial average of the locations of the background and object FoE. The model explains the human heading bias in the presence of laterally moving objects that approach the observer in depth, but not when the object moves laterally and does not approach in depth (Royden 2002).

Although the aforementioned models differ in terms of the mechanism used to account for the influence of moving objects, an implicit assumption shared by all of these models is that heading perception is based on a snapshot of the instantaneous optic flow field at a single instant. The optic flow before or after this instant does not influence the estimate of heading recovered by these models. We refer to this as the instantaneous flow assumption. We emphasize that this is not an explicit assumption of these models. Nevertheless, none of these models contain mechanisms for capturing how heading perception might depend on the temporal evolution of the optic flow field.

Layton et al. (2012) recently introduced a neural model that captures heading perception as a process that evolves over time and is refined through competitive interactions between neural units. The model simulates the dynamical interactions between populations of neurons in primate areas V1, MT, and MSTd. Similar to the models of Warren and Saunders (1995) and Royden (2002), the model matches the optic flow against a number of radial templates to estimate heading. In the case of an object approaching in depth that occludes the observer's heading direction (Fig. 1B), the relative position between the object and background FoE does not change and the model exhibits “averaging” behavior among the FoE, similar to the model of Warren and Saunders (1995). The heading estimate from the model MSTd population is a function not only of the optic flow at the present moment but also of the time history of optic flow. As an approaching object occludes the observer's future path for an extended period of time, MSTd units responding to the salient object FoE suppress units that responded to the once visible background FoE. As a result, the heading bias increases over time in the direction of the object FoE. In the case of a laterally moving nonapproaching object (Fig. 1C), there is greater uncertainty about the heading estimate because it does not have a defined FoE/FoC. The confidence in the heading estimate increases over time, and like the human data (Royden and Hildreth 1996), the heading estimate is influenced by the object's motion.

Aims of the Present Study

Although competing models have been compared on the basis of motion pooling versus differential motion mechanisms (Royden 2002) and biological plausibility (Layton et al. 2012), the question of whether heading perception is based on an instantaneous snapshot of optic flow or depends on how the flow field unfolds over time has not yet been investigated. The primary aim of the present study was to test these competing assumptions. We assume that if the instantaneous flow assumption is correct, heading perception is based on the instantaneous optic flow field within some window of time prior to when heading is perceived. A significant challenge in testing this assumption is knowing when this window occurs. This is an important consideration because the position of the moving object relative to the background FoE changes over time. Previous models are ambiguous about this: they make no explicit assumptions about whether heading perception is based on the optic flow at the last instant or at some previous instant. Because previous experiments were not designed to investigate this issue, they are not particularly informative for the purposes of narrowing down the window of time within which heading is estimated. For example, in the study by Warren and Saunders (1995), the object either obscured the background FoE for most or all of the trial or moved on the opposite side of the screen and never obscured the background FoE. As such, it is not possible to draw any conclusions about when or for how long the object must obscure the background FoE to bias heading perception.

Experiments 1 and 2 were designed to narrow down the window of time during which the critical instantaneous optic flow field occurred. To anticipate, the findings reveal that moving objects influence heading perception when they obscure or approach the background FoE during the last 500 ms of the trial, but not when they obscure or approach the background FoE earlier in the trial. Thus, if the instantaneous flow assumption is correct, then heading perception must have been based on the optic flow at some moment within the last 500 ms, and the optic flow prior to this moment should not influence heading perception. We tested this prediction in Experiment 3 by manipulating trial duration and varying the portion of the earlier part of the trial leading up to the last frame that was presented to subjects. That is, the instantaneous optic flow at the end of the trial remained the same, but subjects viewed a varying amount of the same event leading up to that point in different conditions. The influence of moving objects on heading judgments was weaker when trial duration was longer and the stimulus included more than the last 500 ms of the event. These findings challenge the instantaneous flow assumption and suggest that heading perception depends on the temporal evolution of the optic flow field.

EXPERIMENT 1

The first aim of Experiment 1 was to replicate the results of Warren and Saunders (1995), which is a worthwhile first step given the paucity of data on heading perception in the presence of moving objects. The second aim was to characterize more precisely than in Warren and Saunders how the period of time during which the object occludes the background FoE relates to the bias in heading perception. In Warren and Saunders, the object either moved on the same side of the screen as the heading direction and always occluded the background FoE or moved on the opposite side as the heading direction and never occluded the background FoE. As such, it remains unclear whether the heading bias reported by Warren and Saunders (1995) arose due to the object's initial placement near the background FoE or the fact that the object obscured the background FoE throughout most of the trial.

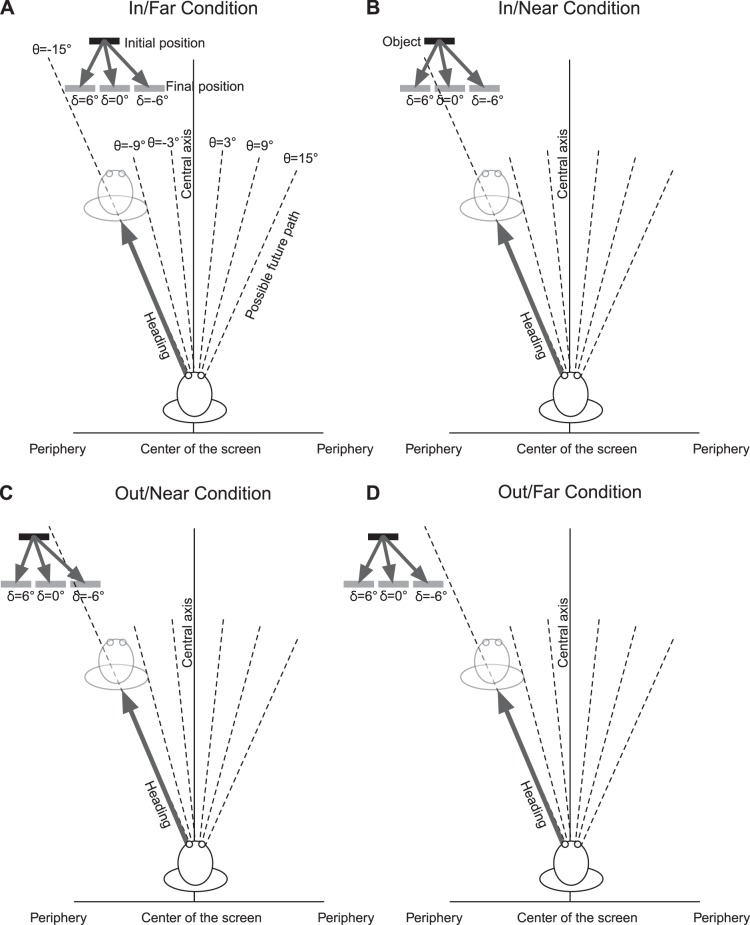
To address this issue, we independently manipulated the starting position of the object and its trajectory relative to the observer's future path, which was always linear. Object starting position was manipulated by varying the proximity of the object relative to the observer's path (Near vs. Far) and the side of the path on which the object initially appeared (In vs. Out) (Fig. 2). Specifically, the object initially appeared on the side of the observer's path closer to the central axis (i.e., toward the inside) or closer to the periphery (i.e., to the outside). As in Warren and Saunders (1995), the object moved parallel to, toward, or away from the heading direction. By manipulating these three variables, we were able to test how the proximity and direction of motion of the object relative to the observer's future path affected heading perception.

Fig. 2.

Illustration of the conditions in Experiment 1. In A–D, the observer's headings (θ) are depicted as dashed lines to either side of the central axis, which refers to the center of the screen and is aligned with the 0° heading direction. The initial and final positions of the observer and moving object (rectangle) are schematically depicted in black and gray, respectively. The object moves in depth relative to the observer along a trajectory specified by the angle δ. Note that the path angles depicted are exaggerated. “In” indicates that the object starts on the inside of the heading vector (i.e., toward the central axis), and “Out” indicates that the object starts on the outside of the heading vector. “Near” and “Far” indicate whether the object started near and far from the observer's path, respectively.

If the conclusions of Warren and Saunders (1995) generalize to the conditions tested in the present study, heading judgments should be affected only when the object moves along an oblique path and occludes the background FoE. Such conditions were satisfied when the object started in the In/Near position and the path angle was positive (+6° trajectory in Fig. 2B) and when the object started in the Out/Near position and the path angle was negative (−6° trajectory in Fig. 2C). If the object must obscure the background FoE to influence heading, then judgments should not be affected in any of the Far conditions since the background FoE was always visible. Likewise, judgments should not be affected in conditions in which the object moved parallel to the observer (i.e., 0° path angle).

The design of Experiment 1 also allowed us to test the claim that occlusion of the background FoE by the moving object is a necessary condition for the object to influence heading perception. This claim is based on the finding that heading judgments in Warren and Saunders (1995) were biased when the moving object crossed the observer's future path but not when the object moved on the opposite side of the screen. However, they did not test conditions in which a moving object approached but did not cross the observer's future path. If, in fact, the visual system relies on center-weighted spatial pooling, then judgments of heading should be affected by objects that move near the observer's future path even if they do not occlude the background FoE. This occurred when the object started in the In/Far position and path angle was positive (+6° in Fig. 2A) and when the object started in the Out/Far position and path angle was negative (−6° in Fig. 2D).

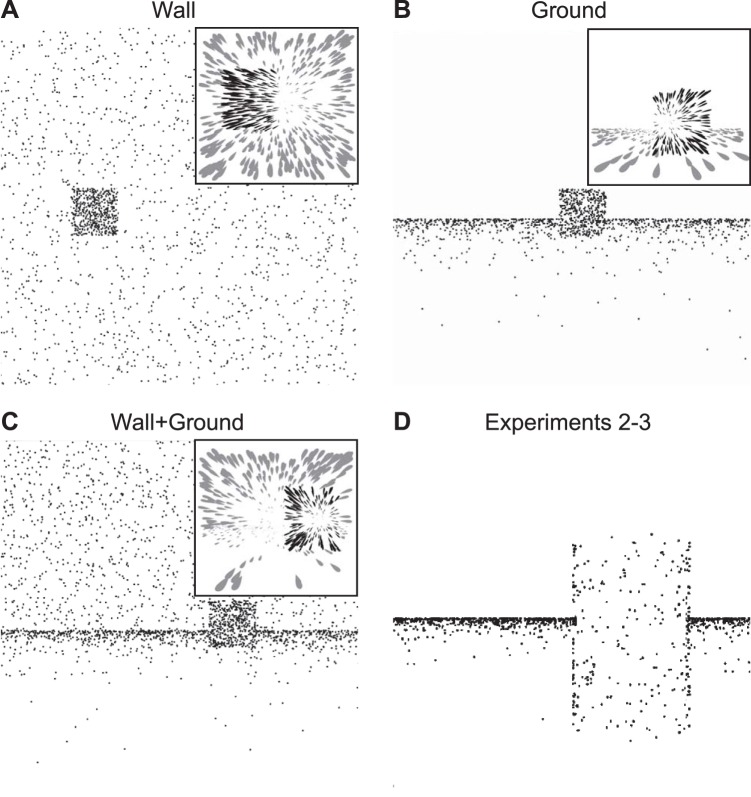
Last, Experiment 1 was designed to determine whether moving objects influence heading perception in environments with more natural depth structure than the environments used in previous studies (i.e., a frontoparallel plane). In Experiment 1, the stationary background consisted of a frontoparallel back plane similar to the design of Warren and Saunders (1995) (Wall condition; Fig. 3A), a ground plane (Ground condition; Fig. 3B), and a ground and back plane (Wall+Ground condition; Fig. 3C).

Fig. 3.

Views of the visual environments used in Experiment 1 (A–C) and in Experiments 2–3 (D). In Experiment 1, dots are distributed along either a frontoparallel plane (Wall condition; A), a ground plane (Ground condition; B), or both (Wall+Ground condition; C). Sample optic flow experienced by the observer is depicted in the insets. In Experiments 2–3, a ground plane was used with a cylindrical object (D).

Methods

Participants.

Fourteen naive subjects (9 males, 5 females) from Rensselaer Polytechnic Institute between the ages of 18 and 22 yr participated in the study for course credit. All subjects had a valid driver's license and normal or corrected-to-normal vision. The data from two subjects (1 male, 1 female) were excluded due to poor performance on a basic heading task completed during the warm-up phase (>10° heading error; see Procedure for details about the warm-up phase). We believe that the poor performance resulted from an inability to understand the directions for the task. Thus the final group consisted of 12 subjects (8 males, 4 females).

Visual displays.

Subjects viewed displays (100° W × 80° H) of simulated self-motion (heading angle θ = ±3°, ±9°, ±15° relative to the central axis) along a straight path. Negative and positive heading angles correspond to simulated self-motion toward the left and right sides of the screen, respectively (Fig. 2). The simulated observer had an average human eye height of 1.8 m. Translation of the observer and object was simulated at 5 and 7 m/s, respectively. The moving object initially subtended 11° × 11°, consisted of 500 dots superimposed on a plane that matched the black sky, and was initially positioned 20 m in depth relative to the observer. We selected the object speed and position to approximate the 3.33-s time to contact between the observer and moving object used by Warren and Saunders (1995). Because the object was opaque, it occluded background dots in the environment behind the object within the observer's field of view.

The object (3 m × 3 m) started in one of four positions relative to the observer's future path: 1) −2.5 m (In/Far condition), 2) −0.5 m (In/Near condition), 3) 0.5 m (Out/Near condition), and 4) 2.5 m (Out/Far condition). Each value indicates the horizontal displacement of the center of the moving object from the observer's future path, where negative and positive values correspond to displacements toward or away from the central axis, respectively. In the In/Far condition, the object started between the observer's path and the central axis and did not cross the observer's path throughout the trial, although it did become close when the object moved along a +6° path angle (Fig. 2A). In the In/Near condition, the object initially occluded the background FoE and the object's center was on the side of the path that was closer to the central axis. The object either occluded the background FoE for the entire trial or moved to either side to clear the observer's future path (Fig. 2B). The Out/Near condition was identical to the In/Near condition, except that the center of the object was positioned toward the periphery, on the opposite side of the path as the central axis (Fig. 2C). In the Out/Far condition, the moving object did not occlude the background FoE at any point during the trial and was positioned toward the periphery, far from the central axis (Fig. 2D).

The object moved along one of three trajectories relative to that of the observer, specified by the path angle δ (−6°, 0°, 6°). Path angles that implicate object movement toward the central axis were negative, and angles that implicate object movement away from central axis were positive (i.e., toward the periphery). In the Near conditions, when δ = 0°, the observer's future path was occluded by the object for the entire trial because the object moved along a parallel path with respect to the observer. In the Far conditions, the observer's future path was never occluded when δ = 0°. When the object approached the observer's future path in the Far conditions, with δ = −6° and δ = 6°, respectively, the leading edge of the object almost intersected the path (Fig. 2).

We simulated three different environments: 1) the Wall condition, 2) the Ground condition, and 3) the Wall+Ground condition. The Wall condition resembled the two-dimensional (2D) frontoparallel dot plane (55 m W × 55 m H; 25-m depth) display used by Warren and Saunders (1995). The ground plane in the Ground condition had a depth range of 50 m. In the Wall+Ground condition, the edges of the ground and wall planes intersected 50 m away from the observer's initial position. Each plane in the environment was opaque and consisted of 5,000 dots (Fig. 3). The dot density of the object (∼4 dots/deg²) and the environment (∼0.6 dots/deg²) in the present study was considerably greater than that used by Warren and Saunders (∼0.25 dots/deg² and ∼0.2 dots/deg², respectively).

The visual displays were generated in the WorldViz Vizard 3.0 environment on an Alienware Area 51 desktop computer equipped with two NVIDIA GeForce GTX 480 graphics cards, a 3.2-GHz Intel Core i7 processor, and 6GB of memory running Microsoft Windows 7 x64. The displays were projected on a large rear-projection screen using a Barco Ciné 8 projector (1,280 × 1,024 resolution; 60-Hz refresh rate). Subjects sat in a chair ∼1 m away from the rear-projection screen (100° W × 80° H) and viewed the visual displays binocularly in a dark room. Subjects were allowed to freely move their eyes during the experiment.

Procedure.

At the beginning of the experiment, subjects completed a short (10 trials) basic heading judgment task that consisted of simulated travel along a straight path toward a backplane defined by dots. The practice block contained no independently moving objects and allowed subjects to become familiar with the experimental instructions. The first frame of the trial appeared for 0.5 s at the outset of each trial. At the end of each 1.5-s trial of simulated self-motion, a blue rectangular postmotion probe (4° V) appeared on the screen at a random horizontal position along with the final frame of the optic flow sequence. Subjects aligned the horizontal position of the probe with their perceived heading by manipulating a steering wheel. Turning the wheel left or right moved the probe in the corresponding direction, and subjects confirmed their probe placement by pressing a button located on the front of the steering wheel. Before the main experiment, subjects were notified about the presence of a moving cluster of dots that may appear similar to a moving object. Subjects were instructed to ignore the object as much as possible and base their heading judgment on the direction they are moving through the environment. No feedback was given during the practice or experimental trials.

The main experiment consisted of three blocks that corresponded to each of the visual environments (Wall, Ground, Wall+Ground). Each block contained 216 trials (6 headings × 3 path angles × 4 object starting positions × 3 repetitions). Trials with the same object path angle and starting position repeated three times within each block. For each repetition, the heading angle was randomly jittered around the specified angle [θ + X, X ∼ U(−2°, 2°)]. Experimental blocks were counterbalanced across subjects, and the whole experiment lasted less than 75 min.

The experimental protocol for Experiment 1 and subsequent experiments was approved by the Institutional Review Board at Rensselaer Polytechnic Institute and is in compliance with the Declaration of Helsinki. All subjects gave informed consent in writing before participating in the experiment.

Eye movement control experiment.

Although it is generally assumed that moving objects bias heading perception due to discrepant optic flow, it is also possible that observers may track moving objects with their eyes and that such pursuit eye movements (and not discrepant optic flow) could be the cause of any heading bias. To rule out this possibility, we also performed a control experiment similar to the main experiment but with gaze restrictions. The experiment was run under two conditions that differed in terms of fixation requirements. In the Moving Fixation condition, we removed the moving object and replaced it with a fixation point that moved across the screen in the same way as the moving object in the main experiment. If any heading biases that are found in the main experiment are due to pursuit eye movements rather than discrepant optic flow, a similar pattern of biases should be observed in the Moving Fixation condition. In the Stationary Fixation condition, the moving object was present as in the main experiment, but subjects were instructed to maintain gaze on a fixation point that remained stationary on the screen. If heading biases in the main experiment are due to pursuit eye movements, such biases should disappear (or, at least, differ) in the Stationary Fixation condition.

In addition to the gaze restrictions, there were a few other minor differences between the control experiment and the main experiment. First, we used a SMI RED 500 eye tracker to record gaze location in screen coordinates at 500 Hz. Second, stimuli were presented to subjects on a 22-in. LCD monitor, which subtended a horizontal visual angle of ∼36° when subjects viewed the display with their head in a chin rest. Third, subjects used a mouse to position the probe at the end of the trial to indicate perceived heading. Fourth, we ran the experiment in the Ground condition only.

The experiment was blocked by fixation condition, consisted of 288 trials (2 fixation conditions × 4 headings × 3 path angles × 4 object starting positions × 3 repetitions), and took less than 30 min to complete.

Twelve subjects (3 females, 9 males) participated in the control experiment. This included nine naive students from Rensselaer Polytechnic Institute who were paid for their participation, one naive volunteer, and the authors. All subjects had a valid driver's license and normal or corrected-to-normal vision. Subjects completed 10 practice trials of each fixation condition before the beginning the experiment to become familiar with the instructions.

The eye movement data were low-pass filtered at 6 Hz and then used to exclude trials in which subjects did not follow the fixation instructions. In the Moving Fixation condition, we compared the eye movement trajectory on each trial with that of the fixation point and computed a pursuit gain. Data from trials were excluded if the pursuit gain fell below 0.66 or exceeded 1.2 (Wilkie and Wann 2003). We excluded data from Stationary Fixation trials if the standard deviation of the gaze position exceeded 1°. These criteria resulted in the mean exclusion of 10.6% Moving Fixation trials and 7.8% Stationary Fixation trials.

Analyses and bias correction.

The data were analyzed using repeated-measures analysis of variance (ANOVA). Mauchly's test was used to confirm sphericity in the data and was not significant for any of the analyses.

Consistent with other heading experiments (Royden and Hildreth 1996; Warren and Hannon 1988; Warren and Saunders 1995), subject responses tended to exhibit a constant bias toward the center of the screen (central axis). Except for the data presented in Fig. 4, we report heading bias after correcting for the center screen bias. We calculated a center screen bias correction for each subject, environment, and heading angle by averaging all subject judgments garnered for a set of trials with the same environment and heading angle, and subtracting that value from the data. That is, we computed the corrected response R̄:

$${\overline{R}}_{s,e,\theta ,\delta ,a,r}=R_{s,e,\theta ,\delta ,a,r}-E_{\delta ,a,r}\left[R_{s,e,\theta ,\delta ,a,r}\right],$$ (1)

Fig. 4.

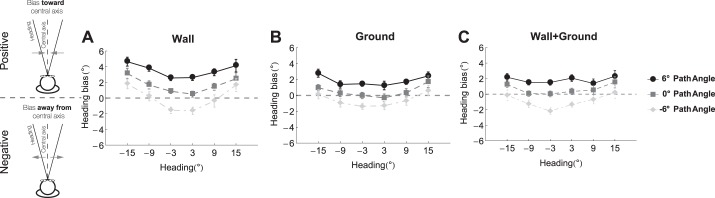
Mean bias in heading judgments in the Wall (A), Ground (B), and Wall+Ground (C) conditions from Experiment 1. Each graph shows the heading bias as a function of the heading direction. Positive bias indicates that errors in heading judgments were toward the center (central axis), negative bias indicates that errors were away from center, and the constant zero function corresponds to veridical judgments. Black, dark gray, and light gray curves in each plot correspond to performance when the object moved toward the center (δ = −6°), parallel to the observer (δ = 0°), and toward the periphery (δ = 6°), respectively. Error bars indicate ±SE. Note that unlike subsequent figures, these data are plotted without correction for the center screen bias.

where R is the response of subject s to environment e, heading θ, path angle δ, starting position a, and repetition r. The E[] symbol corresponds to the mean, taken with respect to δ, a, and r.

Results and Discussion

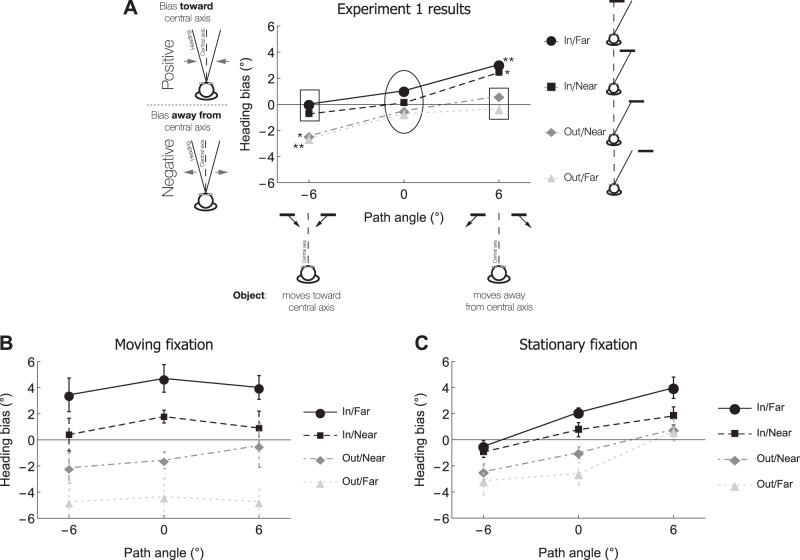
Figure 4 plots the heading bias from the main experiment averaged across all 12 subjects for each heading direction, when the moving object approached the central axis (δ = −6°), traveled parallel to the trajectory as the observer (δ = 0°), and moved away from the central axis (δ = 6°). Note that Fig. 4 presents the data without the center screen bias correction (see Analyses and bias correction above). Positive and negative heading bias indicates a bias toward and away from the central axis, respectively. We observed an overall bias toward the center of the screen (center screen bias) that was most pronounced in the Wall condition (Fig. 4A). That is, subjects tended to place the response probe closer to the center of the screen, independently of the object motion, which is consistent with the findings of other heading studies (Royden and Hildreth 1996; Warren and Hannon 1988; Warren and Saunders 1995). For this reason, we corrected for the center screen bias using the method described in Analyses and bias correction. Note that the bias correction assumes that the center screen bias is the same regardless of whether the object moved toward or away from the central axis. This assumption is validated by the symmetry of the curves in Fig. 4, that is, the fact that the curves for the +6° and −6° path angle conditions are vertically shifted from the 0° path angle condition by roughly the same amount. In addition to correcting for the center screen bias, we also collapsed across heading angle in subsequent analyses and figures.²

Effects of environmental depth structure.

A three-way (environment × path angles × starting positions) repeated-measures ANOVA revealed no significant main effect (F < 1) of environment and no significant interactions involving environment. Thus Experiment 1 provides no evidence that the heading bias reported by Warren and Saunders (1995) was due to the use of an unnatural frontoparallel plane or insufficient accretion/deletion around the borders of the moving object.

Effects of object-path proximity and path angle.

As expected, there was a significant path angle × starting position interaction [F(6, 66) = 3.11, P < 0.01, η_partial² = 0.20; see Fig. 5A]. To better understand the nature of this interaction, let us begin with conditions in which the object moved parallel to the observer's path, which occurred when path angle was 0° (Fig. 5A, symbols within oval). As expected on the basis of the findings of Warren and Saunders (1995), heading judgments were at most weakly affected by the moving object, with mean heading biases within about one degree of zero in all four starting position conditions.

Fig. 5.

Heading bias from Experiment 1 as a function of the path angle of the moving object. Positive bias indicates that errors in heading judgments were toward the central axis, and negative bias indicates that errors were away toward the periphery. Positive path angles signify that the object moved toward the periphery, negative path angles signify object movement toward the central axis, and a zero path angle signifies movement along a parallel trajectory with respect to the observer. The curves in each plot indicate performance for different starting object positions. The center screen bias has been removed. A: symbols within oval indicate conditions wherein the object moved parallel to the observer, symbols within the rectangular boxes indicate conditions wherein the object started far from the observer's future path and moved away, symbols labeled with a single asterisk indicate conditions wherein the object crossed the future path, and markers labeled with a double asterisk indicate conditions wherein the object approached, but did not cross, the future path. B: heading bias from the control experiment in which subjects maintained gaze on a moving fixation point that replaced the moving object (Moving Fixation condition). C: heading bias from the control experiment in which subjects maintained gaze on a centrally positioned fixation point that was stationary in the observer's frame of reference (Stationary Fixation condition).

Next, we consider conditions in which the object moved away from the observer's path (Fig. 5A; symbols within the 2 rectangular boxes). This occurred when the object started on the inside of the observer's path (In/Far and In/Near) and moved toward the central axis (−6° path angle) or started on the outside (Out/Near and Out/Far) and moved toward the periphery (+6° path angle). Again, the effect of the moving object was quite weak, with mean heading biases within one degree of zero.

The third set of conditions that we consider include those in which the object crossed the observer's future path, which occurred in the In/Near 6° and Out/Near −6° conditions (Fig. 5A; symbols labeled with single asterisk). Consistent with the findings of Warren and Saunders (1995), we observed a much stronger effect of the moving object in these two conditions (mean ± SE: 2.44° ± 0.21° in the In/Near 6° condition and 2.42° ± 0.21° in the Out/Near −6° condition). The heading bias was in the direction opposite the object's direction of motion, which is also consistent with the findings of Warren and Saunders (1995).

Last, we examine conditions in which the object started far away from the observer's path and moved toward but did not cross the path (i.e., the In/Far 6° and Out/Far −6° conditions; Fig. 5A, symbols labeled with double asterisks). Interestingly, the heading bias in these conditions was significantly different from zero (P < 0.001) and comparable to the bias that was observed when the object crossed the observer's path (3.04° ± 0.23° in the In/Far 6° condition and 2.60° ± 0.26° in the Out/Far −6° condition). This is inconsistent with the claim that the object must obscure the background FoE to influence heading perception, but is consistent with the hypothesis that the visual system relies on center-weighted spatial pooling (Layton et al. 2012; Warren & Saunders 1995).

Influence of eye movements.

Next, we consider the results of the eye movement control experiment, which was designed to determine whether heading perception in the main experiment was biased due to eye movements generated while tracking the object rather than discrepant optic flow generated by the object. By this account, the same pattern of bias observed in the main experiment should be found in the Moving Fixation condition, but the bias in the Stationary Fixation condition should differ or there should be no bias at all.

The results were not consistent with either prediction. When subjects maintained gaze on a fixation point that replaced the moving object (Moving Fixation condition), the pattern of heading bias was qualitatively different from that of the main experiment (Fig. 5B). Unlike the main experiment, the path angle × starting position interaction was nonsignificant [F < 1]. The bias was largest and in the direction of motion of the fixation point when the fixation point was eccentrically located (Far conditions). Furthermore, the pattern of heading bias in the Stationary Fixation was quite similar to that in the main experiment (Fig. 5C). There was a significant path angle × starting position interaction [F(6, 66) = 2.31, P < 0.05, η_partial² = 0.17] as in the main experiment, and the effects of path angle and starting position were quite similar across the two experiments. Taken together, the results indicate that the heading bias garnered in the main experiment cannot be attributed to eye movements generated while tracking the object.

Summary.

To summarize, the results of Experiment 1 confirm that when a moving object approaches an observer and crosses the observer's future path, heading perception is biased in the direction opposite the direction of object motion (Warren and Saunders 1995). Similar results were obtained when subjects were required to fixate a point that remained stationary on the screen, which indicates that the pattern of heading bias was due to discrepant optic flow introduced by the moving object rather than eye movements. Experiment 1 also revealed several important new findings. First, objects that initially appear on the future path and move away to reveal the background FoE do not influence heading perception. This suggests that the influence of moving objects is more pronounced when they approach or cross the future path toward the end of the trial. Second, moving objects that approach but do not cross the observer's future path can also influence heading perception. This is consistent with center-weighted spatial pooling and rules out the possibility that the influence of moving objects is gated by the visibility of the background FoE. Third, the effect of moving objects does not depend on depth structure in the environment. Regardless of whether the observer is moving toward a frontoparallel plane or over a ground plane, their ability to perceive heading is influenced by the presence of moving objects.

EXPERIMENT 2

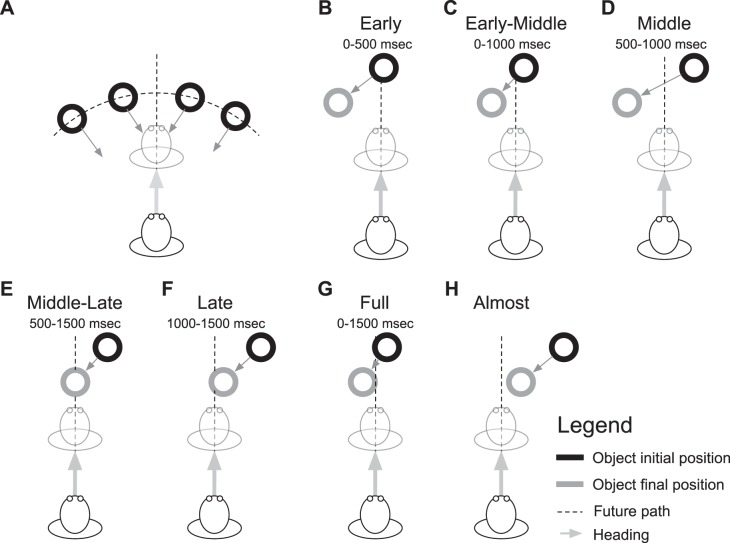
Experiment 2 was designed to further investigate precisely when a moving object must occlude the background FoE to influence heading perception. We divided each trial into early, middle, and late periods. The object occluded the observer's path for the first third (0–500 ms) of the trial (Early condition; Fig. 6B), the middle third (500-1,000 ms) of the trial (Middle condition; Fig. 6D), the end (1,000-1,500 ms) of the trial (Late condition; Fig. 6F), the first two-thirds (0–1,000 ms) of the trial (Early-Middle condition; Fig. 6C), the last two-thirds (500-1,500 ms) of the trial (Middle-Late condition; Fig. 6E), or the entire (0–1,500 ms) trial (Full condition; Fig. 6G). For example, in the Middle condition, the background FoE was visible at the outset of the trial, but the object crossed and subsequently cleared the path by the end of the trial. We also included an Almost condition (Fig. 6H), which was similar to the scenario in Experiment 1 whereby the object approached, but did not cross, the path of the observer.

Fig. 6.

Schematic depiction of the conditions used in Experiment 2. In all conditions, a cylindrical object moved for the entire duration of the trial (1,500 ms). The object was initially positioned along a semicircle, equidistant to the observer's initial position (A). The conditions are named at the top of each panel B–H, and the times during which the object occluded the path are shown beneath. 0 ms corresponds to the beginning of the trial, and 1,500 ms corresponds to the end of the trial. The object either occluded the future path for one-third of the trial (e.g., Early; B), two thirds of the trial (e.g., Early-Middle; C), the entire trial (Full; G), or none of the trial (Almost; H). The object always approached the observer's future path (δ > 0).

With a 6° path angle as in Experiment 1, it is possible for the moving object to occlude the observer's future path at the beginning, end, or throughout the entire trial. However, some of the other object occlusion conditions in Experiment 2 are not feasible with a 6° path angle without also increasing object speed or trial duration. For example, when traveling at 6° relative to the heading direction in the Middle condition (Fig. 6D), the object cannot start on one side of the observer's path and move at a moderate speed to cross and clear the path by the end of the trial. In Experiment 2, we also manipulated path angle (δ = 7.5°, 15°, 35°) to create the full range of object occlusion conditions in Fig. 6.

Methods

Participants.

Fourteen naive subjects (8 males, 6 females) from Rensselaer Polytechnic Institute between the ages of 18 and 20 yr participated in Experiment 2.

Visual displays.

The simulated environment used in Experiment 2 was identical to the Ground condition used in Experiment 1, except that the object was cylindrical rather than planar (Fig. 3D). We used a cylindrical object to ensure that the visual angle subtended by the object at the beginning of the trial was the same regardless of its initial position (Fig. 6A). The cylinder had a 1-m radius and was 3 m tall. The object moved along one of three possible trajectories relative to the observer (δ = 7.5°, 15°, 35°). In Experiments 2 and 3, the object always moved toward the observer's future path, so there was no need to designate a sign (+ or −) for path angle.

To ensure that the initial projected size of the object was the same across conditions, we distributed the object starting positions along an arc centered on the observer's initial position such that the object was initially 21 m away (Fig. 6A). We specified object starting positions with respect to the angular deviation α from the observer's future path. Negative α values indicate that the object started on the opposite side of the path as those with positive values, and α = 0° indicates the object began centered on the future path. Starting positions were selected in positive and negative angle pairs such that the object approached the observer's future path symmetrically from either side. The values for α are listed in Table 1.

Table 1.

Initial position of moving object for each occlusion condition

	Early	Early-Middle	Middle	Middle-Late	Late	Full	Almost
δ = 7.5°	−1.5°	−0.25°	N/A	4°	5.25°	1.75°	6.5°
δ = 15°	−0.25°	2.25°	N/A	5°	7.5°	N/A	10.25°
δ = 35°	2.5°	N/A	8°	N/A	14°	N/A	19.75°

Values are the initial position (α) of the moving object to either side of heading in Experiment 2 along a semicircle centered on the observer's initial position (r = 21 m) for each of the different occlusion conditions (see text) at different path angle conditions (δ). Negative α values indicate that the object started on the opposite side of the path as those with positive values. N/A signifies that an object placement is not feasible for a particular condition and path angle. A total of 15/21 occlusion time/path angle pairs were tested.

We computed the required starting position α of the object along the circle for a particular occlusion condition (e.g., Early, Full, etc.) given the amount of time the object occluded the path (occlusion time o) and path angle of the object (δ). For example, in the Early condition (Fig. 6B), α was computed such that the moving object occluded the future path for only the first third of the 1.5-s trial (o = 500 ms), at which point the trailing edge of the object cleared the observer's future path. To find values for α that satisfied the above conditions, we numerically solved for intersections between a line (Eq. 2), which defined the observer's trajectory, and a circle (Eq. 3), which represented the object.

$$z=\cot \left(\theta \right)x$$ (2)

$$r^2={\left\{x-\left[x_0-\text{st}\hspace{0.17em}\sin \left(\theta +\delta \right)\right]\right\}}^2+{\left\{z-\left[z_0-st\hspace{0.17em}\cos \left(\theta +\delta \right)\right]\right\}}^2$$ (3)

Equation 2 defines the observer's locomotor path in the XZ plane with slope cot(θ). Equation 3 specifies the perimeter of the object with radius r. The object moves away from the initial location (x₀, z₀) at a speed s and angle δ, and arrives at the position {[x₀ − st·sin(θ + δ)], [z₀ − st·cos(θ + δ)]} at time t. The coordinates of the object's starting position are given by x0 = d·sin(θ + α) and z₀ = d·cos(θ + α), where d indicates the initial distance of the object from the observer (21 m). We sampled different values for α to find the times at which intersections occurred, i.e., the intervals of time during which the object crossed the locomotor path. Table 1 presents the values for α that were used in each object occlusion condition.

Design.

The experiment did not have a fully crossed design because it was not possible to create each combination of occlusion condition and path angle while also keeping object speed constant. For example, the Middle condition was not feasible when the object moved at the smallest path angle (δ = 7.5°), since the object could not start on one side of observer's path and cross and clear the path by the end of the trial. Likewise, the Early-Middle, Middle-Late, and Full conditions were not feasible when the object moved at the largest path angle (δ = 35°). Table 1 shows the 15 of 21 combinations of occlusion condition and path angle that were feasible. Subjects completed a total of 540 trials, blocked by 3 repetitions of the experimental conditions.

Sign of the heading bias.

For Experiment 1, we adopted the conventions of Warren and Saunders (1995) in defining the sign of the heading bias: bias toward the central axis was positive, and bias away from the central axis was negative. Because heading judgments are consistently biased in the direction of the object FoE, it is more intuitive from this point forward to define the sign of the heading bias with respect to the direction of the object FoE. Thus, in Experiments 2 and 3, positive heading bias indicates heading error in the direction of the object FoE (i.e., opposite the direction of object motion), and vice versa.

Results and Discussion

As in Experiment 1, the data were corrected for the center screen bias prior to the main analysis.³ Inspection of Fig. 7 clearly shows that there is an overall increase in the magnitude of the bias from left to right, as the object occludes (or almost occludes) the background FoE later in the trial. To confirm this, we ran three separate one-way repeated-measures ANOVAs, one for each path angle condition. The effect of occlusion time was significant in the 7.5° [F(5, 65) = 4.69, P < 0.001, η_partial² = 0.34] and 15° [F(4, 52) = 2.59, P < 0.05, η_partial² = 0.30] conditions. Curiously, occlusion time was not statistically significant in the 35° condition [F(3, 39) = 2.13, P = 0.11, η_partial² = 0.19], although the ordering of means was similar to the ordering in the other path angle conditions.

Fig. 7.

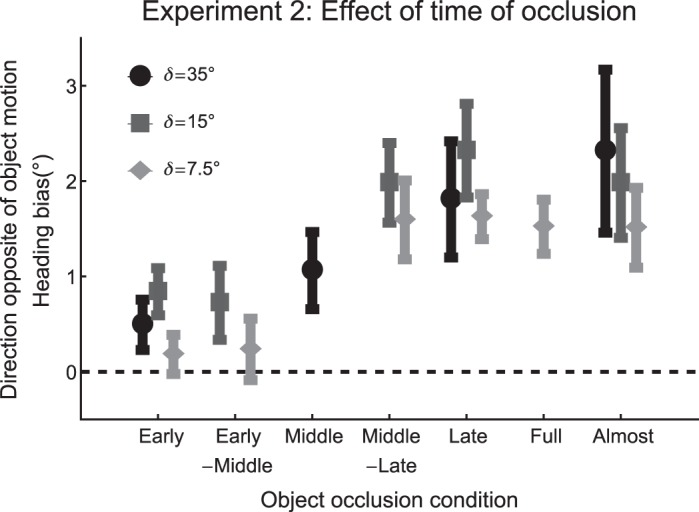
Mean heading bias obtained in Experiment 2. Positive heading bias indicates heading error in the direction opposite of object motion. The heading bias is plotted for each time of occlusion condition. The data are horizontally scattered in each condition for visual clarity. Note that not all path angles are not feasible some conditions and do not have data values (see Table 1). Error bars indicate ±SE.

Figure 7 also suggests that the heading bias is greatest in conditions in which the object occluded the path during the last third of the trial (i.e., in the Middle-Late, Late, and Full conditions) or approached but did not cross the path (i.e., in the Almost condition). It also appears that heading perception may be biased, albeit more weakly, when the object crosses the path during the middle third of the trial. To more precisely quantify the contribution of occlusion during each third of the trial, we performed a hierarchical multiple regression analysis with early, middle, and late as predictors. Fitting the heading bias using a linear model with a term for late occlusion accounted for a large portion of the variance (R² = 0.802). The coefficients for the late nominal predictor and the intercept were 1.26 and 0.59, respectively (P < 0.001). Next, we added a term for the middle period of the trial, but the fit to the data did not improve (R² = 0.803, R_change² = 0.001, P = 0.81). Subsequently adding a term for the early portion of the trial did not improve the fit either [R² = 0.84, R_change² = 0.037, F(1, 13) = 2.52, P = 0.14]. The results from the regression analysis confirm that occlusion (or near occlusion) of the observer's future path in the late period of the trial influences heading judgments the most. Interestingly, occlusion in the middle third of the trial had no additional impact on the model fit, suggesting that disocclusion of the background FoE for 0.5 s is sufficient time to yield accurate heading judgments.

In summary, Experiment 2 revealed that moving objects influence heading perception when they occlude or almost occlude the background FoE during the last 500 ms of the trial. When occlusion takes place earlier in the trial and the background FoE is revealed before the trial ends, heading perception is unaffected or weakly affected. On the basis of these findings, it can be assumed that, if the instantaneous flow assumption is correct, heading perception is most likely based on the optic flow at some moment that occurred during the last 500 ms of the trial. The fact that moving objects begin to influence heading perception shortly before they occlude the background FoE slightly complicates this interpretation. At first glance, it would seem to leave open the possibility that heading perception is based on the instantaneous optic flow during a window that begins prior to the last 500 ms. However, if that were the case, we would expect a moderate-to-strong (rather than weak) bias in the Early-Middle and Middle conditions and a weak-to-moderate (rather than strong) bias in the Almost condition. Neither prediction is consistent with the human data.

EXPERIMENT 3

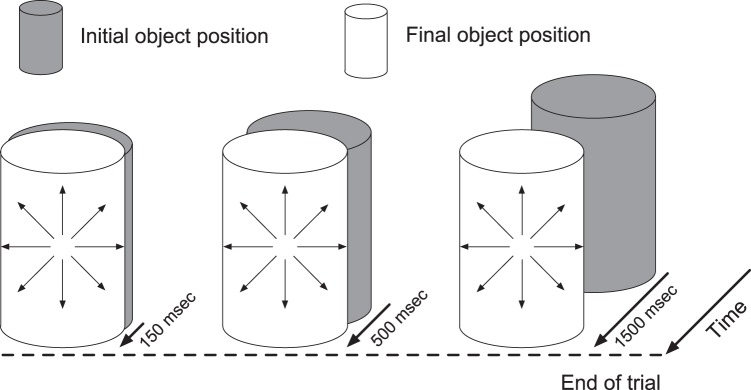
Having established that moving objects influence heading perception only when they occlude or almost occlude the background FoE during the last 500 ms of the trial, we can now turn to the question of whether heading perception is based on a snapshot of the instantaneous optic flow field or depends on the temporal evolution of the flow field. Our approach was to vary the duration of the earlier part of the trial leading up to the last frame that was presented to subjects. That is, for each observer/object trajectory condition, there were 6 conditions that varied in duration between 150 and 1,500 ms. The last 150 ms were the same across conditions; however, conditions with longer durations also included the earlier part of the event leading up to the last 150 ms (see Fig. 8).⁴

Fig. 8.

Illustration of the trial duration conditions of Experiment 3. The instantaneous optic flow field at the end of the trial (horizontal dashed line) in each condition was the same, despite the varying trial duration (150-, 500-, and 1,500-ms durations are shown). The object approached the locomotor path at a 15° path angle, and trajectories were horizontally shifted by 1 of 5 displacements (see text for details).

Let us first consider how the manipulation of trial duration should affect judgments if the instantaneous flow assumption is correct and if heading perception is based on the instantaneous optic flow field during some window of time prior to the end of the trial. As long as trial duration is long enough to include this window of time, the heading bias should be the same regardless of whether trial duration is the full 1,500 ms or just barely long enough to include the window. Based on the results of Experiment 2 (and the assumed validity of the instantaneous flow assumption), the window takes place within the last 500 ms of the trial. Thus the heading bias should be unaffected by increases in trial duration beyond 500 ms.

On the other hand, if heading perception depends on the temporal evolution of the optic flow field, the bias should vary with trial duration. The Layton et al. (2012) model, which was designed to capture the temporal dynamics of heading perception in the presence of moving objects, makes specific predictions about how heading perception should be affected by the manipulation of trial duration. In conditions in which the object comes in contact with the future path at the end of the trial, shorter trials yield larger heading bias in the model because the large optical size of the object dominates the optic flow field. As trial duration increases (i.e., as more of the earlier part of the trial before occlusion is also included), heading estimates are based to a larger extent on the background FoE, which means that the influence of moving objects is reduced.

Experiment 3 also included trials without a moving object so that we could characterize the temporal dynamics of heading perception in static environments.⁵ No Object trials were randomly interspersed among With Object trials.

Methods

Twelve naive subjects (8 males, 4 females) from Rensselaer Polytechnic Institute between the ages of 18 and 20 yr participated in Experiment 3. The visual displays were similar to those in the Full condition in Experiment 2, except the trial duration was 150, 300, 500, 750, 1,050, or 1,500 ms. Note that the trial duration used in Experiments 1 and 2 and by Warren and Saunders was 1,500 ms, the longest of the 6 durations in Experiment 3. The With Object condition contained the cylindrical object that moved to a final position 4 m away, centered on the observer's future path. The object moved at a 15° path angle, starting from either side of the observer's path (δ = 15°). Four object trajectories were introduced by rigidly displacing the object trajectory laterally compared with when its final position coincided with the center of the observer's future path. The trajectory was displaced by −1.75, 0.0, 1.0, or 2 m, where positive values indicate displacements to the right and negative values indicate displacements to the left. For example, compared with when the object moved to the center of the observer's future path (0.0 m) from the right side of the screen (δ = 15°), a lateral displacement of 2 m results in the final position of the object shifting to the right side of the observer's path. A lateral displacement of 1.0 m corresponds to the Almost condition.

Subjects completed 648 trials, blocked by 3 repetitions of experimental conditions. Each block consisted of 24 trials of the No Object condition (4 headings × 6 trial durations) and 192 trials of the With Object condition (4 headings × 2 symmetric object starting positions to either side of the heading × 6 trial durations × 4 lateral displacements).

Results and Discussion

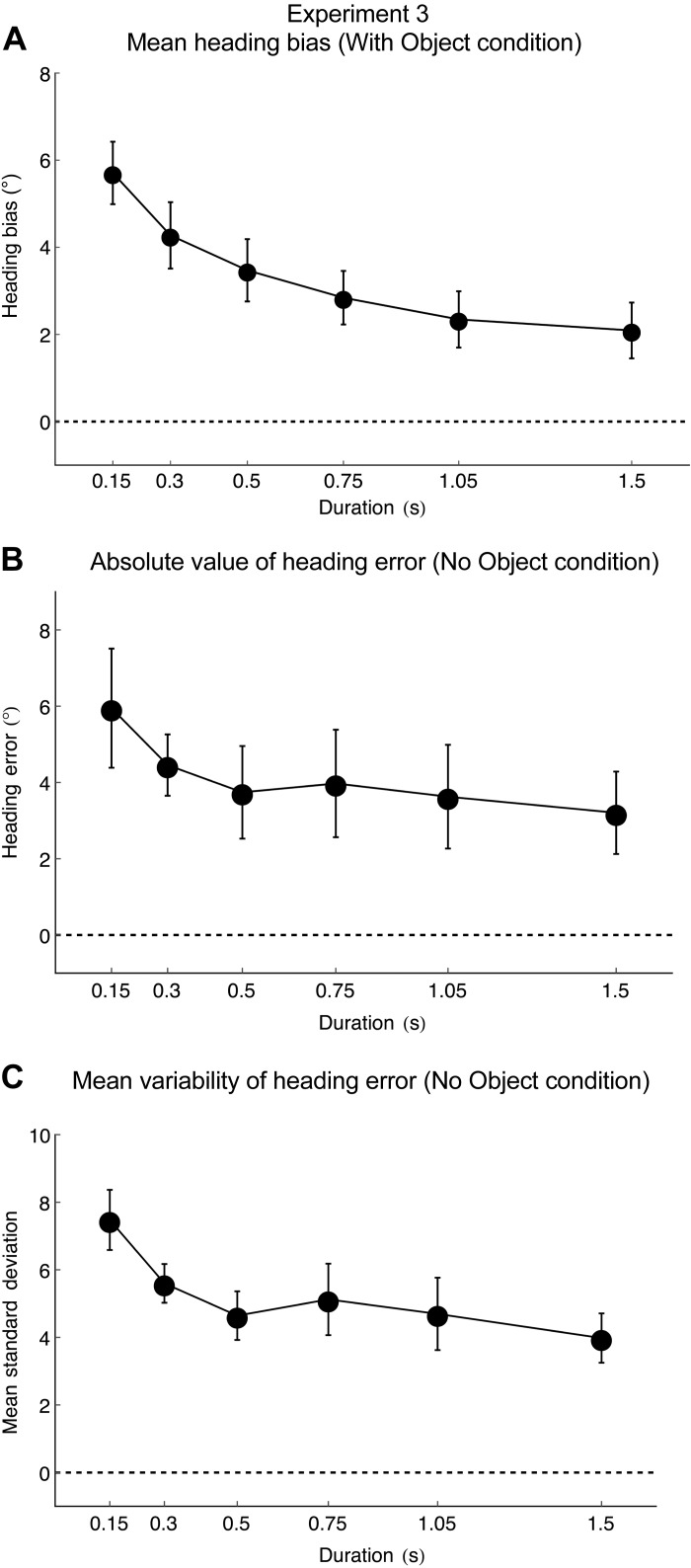
Heading bias in the With Object condition was significantly affected by trial duration [F(5, 55) = 32.3, P < 0.001, η_partial² = 0.74], with the greatest bias reaching ∼6° observed when trial duration was 150 ms (see Fig. 9A). This is approximately three times larger than the largest bias garnered in Experiment 2. As trial duration increased, the magnitude of the bias steadily decreased down to ∼2° in the 1,500-ms condition. Neither the main effect of lateral displacement (F < 1) nor the lateral displacement × trial duration interaction [F(15, 165) = 1.27, P = 0.23] were statistically significant. To further investigate the effect of trial duration, we ran planned comparisons using the 1,500-ms condition as the baseline. This analysis revealed significant (P < 0.05) differences between the 150- and 1,500-ms, 300- and 1,500-ms, 500- and 1,500-ms, and 750- and 1,500-ms conditions. The difference between 1,050 and 1,500 ms did not reach significance (P = 0.11). Recall that the instantaneous flow assumption together with the results of Experiment 2 predict that the heading bias should be unaffected by manipulations of trial duration beyond 500 ms. The findings of Experiment 3 do not support this prediction, since the heading bias was significantly reduced when subjects were able to see the earlier part of the trial before the object approached the observer's future path. Instead, the findings support the hypothesis that heading perception depends on the evolution of the optic flow field.

Fig. 9.

Mean bias in the With Object condition, which contained a moving object (A), the absolute value of the heading error in the No Object condition, which did not contain a moving object (B), and mean variability in heading judgments in the No Object condition (C) are plotted as a function of trial duration from Experiment 3. Note that whereas A depicts heading bias, B depicts heading error. Positive bias indicates a heading error in the direction of the object's FoE, and a negative bias indicates a heading error in the direction away from the object's FoE. The absolute values in B correspond to errors to either side of the heading direction. Error bars indicate ±SE. The mean standard deviation (i.e., variability) across subjects is plotted in C.

Note that the results cannot be attributed to a simple bias to indicate a heading direction closer to the center of the screen on shorter duration trials. The positive bias in Fig. 9A corresponds to a bias in the direction opposite object motion, which was toward the center of the screen on 50% of trials and toward the periphery on the other 50% of trials. Hence, judgments were biased toward the periphery on some trials and toward the center on other trials, depending on the direction of object motion. This rules out an explanation in terms of a decreasing center screen bias as trial duration increases.

Instead, heading judgments were strongly biased toward the object FoE when trial duration was short. As more of the earlier part of the event leading up to the last frame was included in the stimulus, heading judgments were less biased by the moving object and became more closely aligned with the background FoE. Thus, although moving objects bias heading perception when they occlude the background FoE, humans are able to rely on their perception of heading prior to occlusion of the background FoE to reduce the influence of the moving object.

Heading perception was also affected by trial duration in the No Object condition. Both mean absolute heading error (Fig. 9B) and mean standard deviation of heading error (Fig. 9C) were greatest when trial duration was short and gradually decreased as trial duration increased up to about 500 ms [F(5, 55) = 11.57, P < 0.01, η_partial² = 0.51 and F(5, 55) = 11.39, P < 0.01, η_partial² = 0.50 for absolute error and standard deviation, respectively]. Thus, even in static environments, heading perception is a dynamic process that evolves over time.

Together, these findings suggest that the visual system continuously integrates the optic flow field and forms a reliable heading estimate even for short durations. Although the estimate may be biased due to the object's motion for short durations, viewing the optic flow for longer periods of time greatly reduces the bias. The susceptibility to bias due to the object motion (object FoE) at short durations when the background FoE may not be visible is an expected outcome of a system that detects and depends on radial motion.

GENERAL DISCUSSION

The primary aim of the present study was to determine whether heading perception is based on the instantaneous optic flow field or depends on the evolution of the optic flow field. In Experiment 1, we showed that heading perception is influenced by objects that move along an oblique path and intersect or almost intersect the observer's future path, but not by objects that move parallel to or away from the observer's path. The results from Experiment 2 revealed that the influence of moving objects on heading perception depends on the object being in close proximity to the future path just prior to the moment at which the heading judgment is made. Moving objects, even those that initially occlude the background FoE, cease to influence heading perception shortly after they move away from the future path. This suggests that if heading perception is based on the instantaneous optic flow field, it must rely on the optic flow that occurs sometime during the 500 ms prior to when heading is estimated.

In Experiment 3, however, we found that heading judgments were less biased when the display included the period of the event before the moving object was in close proximity to the observer's path. This would not be expected if heading perception is based on the instantaneous optic flow sometime during the last 500 ms but is consistent with a process that relies on the temporal evolution of optic flow to estimate heading.

Experiments 1 and 2 also demonstrated that a moving object does not need to cross the observer's future path to bias heading perception. This finding is not consistent with the conclusions of prior studies that a moving object must cross the path for a large portion of the trial to yield heading bias (Royden and Hildreth 1996; Warren and Saunders 1995) and suggests that the bias occurs due to long-range interactions within the visual system. When the object approached but did not occlude the observer's future path, the object occupied a large portion of the visual field. We would not expect to observe bias if heading depends on local mechanisms because the background FoE remained visible throughout the trial. Proximity to rather than occlusion of the background FoE may represent a necessary condition for an object to influence heading perception.

Modeling Temporal Dynamics of Heading Perception

As a dynamical system, the Layton et al. (2012) model provides a natural framework for understanding the temporal evolution of optic flow signals in the primate visual system. The motion signal arrives to model MSTd after being matched with a number of radial templates. Neural units compete with one another as the network integrates the changing optic flow signal, implicitly maintaining a “memory” of the signals in recent history across the population. The recurrent competition between units in the network occurs through divisive normalization, which results in winner-take-all behavior. If the pattern of optic flow is unchanging for a long period of time (i.e., self-motion in the absence of a moving object), the most active unit whose receptive field is centered on the background FoE suppresses other units and thereby refines the network's heading estimate.

In the presence of a moving object, the network dynamics are more complex. When an object approaches the observer in depth and crosses the path near the end of the trial, the most active units that respond to the background FoE compete with those that respond to the object FoE. Once the background FoE is no longer visible, the response to the background FoE remains, but confidence in the heading estimate dwindles and an increasing number of units between the background FoE and object FoE become active. The longer the background FoE is occluded, the more likely peak activity in the network will spread toward the object FoE to yield an increasingly biased heading estimate.

Figure 10 shows a comparison between the heading bias garnered in Experiment 3 and that obtained by simulating the Layton et al. model under similar conditions. The model successfully reproduces the decreasing heading bias with longer optic flow viewing durations obtained in Experiment 3. When the viewing duration is short, the heading estimate necessarily depends on the brief optic flow history. If the object is crossing the observer's future path and the viewing duration is short, then the object FoE is visible, but the background FoE is occluded for the entire trial. The object FoE dominates heading estimates by the model, due to its salience for most or all of the trial, which yields a large bias in the model. High variability in the heading estimate occurs at shorter durations. In the absence of a temporal history over which to integrate, a robust heading estimate cannot develop in the model. Therefore, the bias fluctuates more greatly when the optic flow duration is short. On the other hand, if the trial duration is longer, units that respond to the background FoE establish a more stable heading estimate. Given the longer integration of the optic flow, these units will suppress other activity in the network, which reduces variability. The heading bias produced by the model is smaller at longer durations because evidence builds up about the position of the background FoE before the moving object begins to influence the model.

Fig. 10.

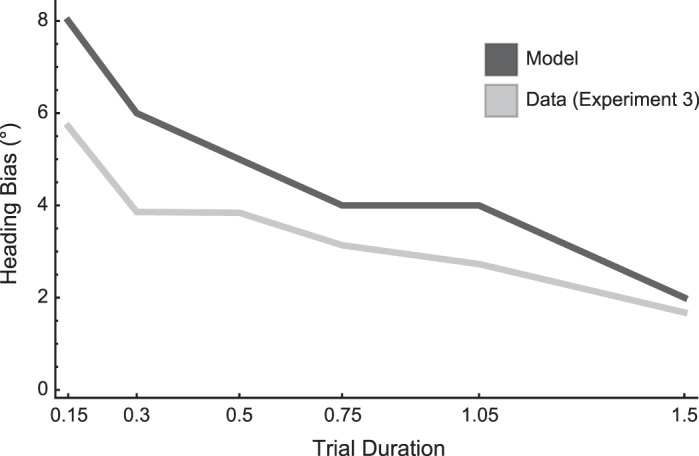
Heading bias produced by simulation of the Layton et al. (2012) model (black curve) compared with that from the corresponding conditions in Experiment 3 (gray curve). The input to the model closely mimicked the conditions of Experiment 3 and the dot environment. The object (initially 10° × 10°) was simulated to move along a 15° trajectory with a 2 m lateral offset with respect to the observer's heading direction (0°). In the model dorsal medial superior temporal area (MSTd) template matching layer, 100 MSTd units were simulated with regularly spaced receptive fields centered along the extent of the 100° screen. Viewing duration was simulated by progressively removing input frames leading up to the end of the original sequence in proportions that matched those used in Experiment 3.

Conclusions

Heading perception is robust in the presence of moving objects, except when the object moves along an oblique path and occludes or almost occludes the observer's future path immediately prior to the heading estimate. Nonetheless, when observers can perceive heading prior to the object occluding their future path, judgments are less biased by the moving object. This is because the visual system does not rely on the instantaneous optic flow field. Rather, heading perception is a process that evolves over time and is influenced by the time history of the optic flow field.

GRANTS

This work was supported by Office of Naval Research Grants ONR N00014-11-1-0535 and N00014-14-1-0359.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

O.W.L. and B.R.F. conception and design of research; O.W.L. performed experiments; O.W.L. analyzed data; O.W.L. and B.R.F. interpreted results of experiments; O.W.L. prepared figures; O.W.L. drafted manuscript; O.W.L. and B.R.F. edited and revised manuscript; O.W.L. and B.R.F. approved final version of manuscript.