Abstract
Perceptual decision making is fundamental to a broad range of fields including neurophysiology, economics, medicine, advertising, law, etc. Although recent findings have yielded major advances in our understanding of perceptual decision making, decision making as a function of time and frequency (i.e., decision-making dynamics) is not well understood. To limit the review length, we focus most of this review on human findings. Animal findings, which are extensively reviewed elsewhere, are included when beneficial or necessary. We attempt to put these various findings and data sets, which can appear to be unrelated in the absence of a formal dynamic analysis, into context using published models. Specifically, by adding appropriate dynamic mechanisms (e.g., high-pass filters) to existing models, it appears that a number of otherwise seemingly disparate findings from the literature might be explained. One hypothesis that arises through this dynamic analysis is that decision making includes phasic (high pass) neural mechanisms, an evidence accumulator and/or some sort of midtrial decision-making mechanism (e.g., peak detector and/or decision boundary).
Keywords: drift diffusion, signal detection, threshold
this review focuses primarily on perceptual decision-making dynamics. For simplicity, we refer to “perceptual decision making” as “decision making” throughout. Thorough definitions and descriptions follow later in this review; we begin by briefly defining decision-making dynamics as the study of time variations in the signals leading to individual decisions, including with the impact of stimulus frequency (i.e., studies of the frequency response of the decision-making system). We provide an illustrative example in the following paragraph. To keep the review focused on decision making, our primary focus is on those processes that contribute to (and occur before) each individual decision; we specifically choose not to cover all the processes and/or processing that occur in conjunction with decision making [e.g., confidence in a decision (Stankov et al. 2012), evidence accumulation after a decision boundary is reached (Huk and Shadlen 2005), etc.] or interactions between sequential decisions. To help raise an awareness of the importance of dynamics, our primary goal is to present and discuss a variety of findings that pertain to decision-making dynamics. To preview the endpoint, we provide our final thesis here: perceptual decision-making data across multiple sensory domains using various psychophysical tasks appear consistent with the hypothesis that decision-making processes include dynamic elements (i.e., phasic neural mechanisms). Furthermore, evidence also suggests that one or more midtrial decision mechanisms (described later) may also be essential. More specifically, we discuss the hypothesis that decision making may reflect high-pass filtering of the relevant information leading to an individual decision, but this review does not hinge on the veracity of that hypothesis. Alternate hypotheses (e.g., attentional influences, the increasing prevalence of drift-diffusion boundary crossings with time, shifting decision boundaries, including costs of accumulating evidence) are described elsewhere in the manuscript and assembled in discussion, Other Plausible Considerations.
We begin with an illustrative example. Recent studies (e.g., Grabherr et al. 2008) have shown that direction-recognition thresholds for whole body rotations, primarily evoked by signals from the vestibular system (Valko et al. 2012), vary with frequency. Specifically, thresholds for lower frequency (longer duration) rotation have been shown to have higher thresholds than for higher frequency (shorter duration) rotation. Rotation perception assayed using psychophysical techniques that do not utilize the standard discrete decision-making techniques does not show the same frequency dependence (Bertolini et al. 2011; Bronstein et al. 2008; Okada et al. 1999; Sinha et al. 2008). As will be discussed in much greater detail later, the variation of rotation thresholds with frequency have led to a hypothesis that the brain might high-pass filter the available perceptual signals as part of the decision-making processes. The plausibility of this hypothesis is bolstered by data showing that 1) visual motion thresholds show similar variations with frequency, and 2) speed-accuracy trade-offs provide evidence suggesting similar dynamic processes.
As defined in more detail later, perceptual decision making is the process of making a choice or judgment resulting in perceptual categorization (e.g., deciding if an object is hot or cold). Decision making is challenging because the nervous system does not perfectly represent information. For example, various forms of noise can arise externally (i.e., static noise heard and/or seen while “skyping”), during transduction, and/or internally in the neural circuitry. Decision making becomes especially challenging when stimuli are small in comparison to noise, such as hearing a whisper at a loud party. When decision making is studied in the laboratory, one of two experimental paradigms is typically used. For one task, the subject is provided stimuli and told that he/she must respond when signaled by the operator after the stimulus is complete (often called “forced choice”). For the second task, the subject is instructed to respond as soon as a decision is reached (often called “response time” or “time to respond”). Such experimental tasks are typically accompanied by one of two classes of standard theoretic frameworks (Gold and Shadlen 2007): 1) signal detection or 2) drift diffusion (formally referred to as sequential analysis). Multiple reviews and books focused on decision making have been published relatively recently (e.g., Bogacz 2007; Bogacz et al. 2006; Gold and Shadlen 2007; Heekeren et al. 2008; Macmillan and Creelman 2005; Purcell et al. 2010; Ratcliff and McKoon 2008; Ratcliff and Starns 2013; Sanfey et al. 2006; Shadlen and Kiani 2013; Sugrue et al. 2005). The focus of this review on decision-making dynamics differs from the earlier reviews.
Review “Roadmap”
To provide an overview and to help readers with different interests and backgrounds navigate this review efficiently, we provide an outline of the remaining sections. The first section immediately following this roadmap (Defining Terms, Experimental Tasks, and Models) thoroughly defines terms, tasks, and models. This section is primarily included for nonexperts to introduce how terms, tasks, and models are commonly used. It is not our intent to provide a comprehensive review of advanced topics related to these definitions and descriptions, which could be the topic of an entire review not focused on dynamics. Rather, we focus on basic definitions and descriptions that capture the most common ways the terms are defined and the tasks and models that are most commonly used.
Next, since the topic of dynamics may not be familiar to many readers, we provide a short primer on dynamics (Filtering Dynamics) that provides a basic introduction to first-order, linear analog, continuous-time high-pass and low-pass filters. Some readers prefer that this primer be provided before the data sections that immediately follow. Other readers prefer the context provided by the data to help them focus on the important aspects of this filtering section. To accommodate both styles, we provide the section just before the data sections. Individuals who prefer having context provided by experimental findings before reading about simple filtering might consider skimming this section when first reading this review and then returning to read this section more thoroughly after reading the data sections that follow.
As noted, several sections after the filtering dynamics primer describe published findings. Some readers interested primarily in empirical findings (and less in theory and modeling) may consider these the key sections of this review. In the first data section, we discuss the vestibular threshold literature that demonstrates frequency responses consistent with high-pass filtering; these data first suggested to us that dynamic elements may be contributing to decision making (Vestibular Threshold Frequency Responses). In the second data section, we discuss data from several visual perception studies that appear to show similar patterns of thresholds vs. frequency (Visual Perceptual Responses). In the third data section, we present data showing how speed and accuracy of decision-making co-vary depending on experimental constraints (Speed-Accuracy Trade-offs). These three data sections appear to support the hypothesis that perceptual decision-making processes include mechanisms that have dynamic characteristics that mimic high-pass filter characteristics.
We then include two sections focused on drift-diffusion models (and variants). Such models have long been used to model time-to-respond data, so there is an immense literature that we have reviewed and could draw upon. However, much of this literature has been reviewed (Bogacz et al. 2006; Busemeyer and Townsend 1993; Ratcliff 1978; Ratcliff and Starns 2013; Usher and McClelland 2001), and most of this literature does not consider dynamic elements beyond integration/accumulation. Furthermore, this literature does not appear to clearly support or refute any specific dynamics theory, high-pass filtering or other. Therefore, we provide an overview of diffusion models with a focus on system dynamics (Dynamic Decision-Making Modeling). we then present several recent studies (Drift-Diffusion Studies Investigating Dynamics) that specifically investigate dynamic contributions to decision making, with differing conclusions. The penultimate section describes different ways that the brain might accumulate information for decision making (Relating High-Pass and Low-Pass Filtering), and the last section is a standard discussion section wherein we consider several additional issues related to decision-making dynamics.
Defining Terms, Experimental Tasks, and Models
Before proceeding, we need to define and introduce “dynamics” and then “decision-making” before we can precisely define “decision-making dynamics.” We close this section with a brief description of “magnitude estimation.”
Dynamics.
System dynamics is the mathematical approach that helps explain and understand the behavior of systems over time. The genesis of dynamics can be traced to Newton's invention of differential equations to help explain planetary motion using his models of gravity and motion. Dynamic systems can be 1) electrical, mechanical, chemical, social, economic, biologic, etc., 2) discrete time or continuous time (or both), and/or 3) linear (e.g., Kailath 1980; Ogata 2004) or nonlinear (e.g., Shelhamer 2006; Strogatz 1996; Thompson and Stewart 2002). Simple dynamic systems include high-pass filters and low-pass filters (e.g., moving averages) that are commonly employed during physiological data acquisition. Dynamic analyses are commonly used to help describe time-varying changes in biological processes such as sensory transduction, sleep cycles, and muscle actuation. System dynamics are typically investigated experimentally and analyzed using one of two complementary approaches, time-domain or frequency-domain approaches (e.g., Bendat and Piersol 1971, 1980; Ljung 1987; Oppenheim and Willsky 1997). Both time- and frequency-domain approaches will yield the same resultant model of the system dynamics when properly applied to a linear system, but dynamic analyses are not limited to linear systems.
To investigate system dynamics in the time domain, system input signals are typically impulses, ramps, steps (or approximations thereof; e.g., trapezoids), random noise, or pseudorandom noise with the system output measured as a function of time. The frequency-domain approach often utilizes finite-duration sinusoidal inputs having an integer number of cycles at various frequencies, but frequency-domain approaches do not necessarily require sinusoidal inputs (e.g., Soyka et al. 2011, 2012). When sinusoidal inputs are utilized, the amplitude and/or phase of the steady-state sinusoidal output is often quantified. If a system is (or can be approximated as) linear and time invariant, both time- and frequency-domain analyses can be used to deliver a transfer function that models (i.e., represents) the input-output relationship of that linear system. In the event that significantly different models result from these two analyses, it shows that we do not have a satisfactory understanding of the system. In general, neither the time- or frequency-domain approach is “better,” nor does either provide a more fundamental understanding.
Decision making.
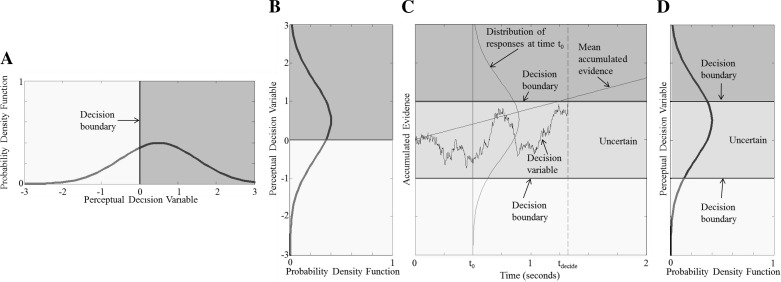
Decision making is studied using several different approaches. Because these approaches are somewhat different, we briefly describe several common approaches. Decision making studied with the use of the signal detection approach assumes that a forced-choice binary decision (e.g., left/right or yes/no) is made and requires an answer after each trial is complete, often without penalty for deliberation time. These studies almost always assume that there is a single decision boundary (e.g., Fig. 1, A and B) that separates inputs into one of two categories. Let us consider a standard motion direction-recognition task (also sometimes called a direction-discrimination task), where the subject's task is to decide if motion was leftward or rightward. If the decision variable is “positive” relative to the decision boundary (i.e., is greater than the decision boundary), the subject will decide “positive” (e.g., motion to the right), whereas if the decision variable is less than the decision boundary, the subject will report “negative” (e.g., motion to the left).
Fig. 1.
Decision-making models applied to perceptual motion direction-recognition tasks. We emphasize that the models shown all apply to tasks whereby subjects are asked to classify the direction of motion (e.g., left vs. right), which is a type of motion direction discrimination sometimes referred to as direction recognition. A: for untimed forced-choice tasks, the signal detection model assumes that a physical stimulus is contaminated with noise to yield a perceptual decision variable distribution. One sample from this distribution for each trial yields the decision variable for that trial. If the sampled decision variable for a given trial falls to the left of the decision boundary, “left” is reported. If the decision variable falls to the right of the decision boundary, “right” is reported. B: to allow a direct comparison with C and D, we rotate the same decision variable and signal detection model from A by simply swapping the abscissa and ordinate. C: for response-time tasks, a drift-diffusion model is often used to help model the time dependencies of the data. A time plot for a drift-diffusion model shows a decision variable for a single trial plotted against time. When the decision variable crosses a decision boundary, a decision is made: “left” for top decision boundary and “right” for bottom decision boundary. The time of the decision is indicated as tdecide. Before the decision variable crosses a decision boundary, the subject is undecided. The distribution of the decision variables across many trials at time 0 (t0) is also shown. The average evidence accumulation corresponds to the physical stimulus and in this example is assumed to be constant over time. D: a signal detection model that includes uncertainty as one of the options provides a simple extension to the signal detection model shown in A and B. Here the same decision variable is sampled but with 2 decision boundaries. If the sampled decision variable falls to the left of the most leftward decision boundary, “left” is reported. If the sampled decision variable falls to the right of the most rightward decision boundary, “right” is reported. If the sampled decision variable falls between the 2 decision boundaries, “uncertain” is reported. Note the intentional similarity of the probability distribution at t0 in C and the probability distribution in D.
Thresholds are often the measure resulting from the application of signal detection theory to human perceptual decision making. A threshold is a representation of the ratio of signal to noise; signal detection thresholds are always defined with respect to noise. In fact, when the noise is zero mean (or near-zero mean as is often assumed and/or found for direction-recognition tasks), one way to define a direction-recognition threshold is as the signal level that equals the standard deviation of the noise (T = σ). Using this definition of a direction-recognition threshold, a subject should get 84% of binary forced-choice trials correct when stimuli having this magnitude are presented (Merfeld 2011). For example, see Merfeld (2011), which is focused on vestibular system “self-motion” sensing applications.
This signal detection approach assumes that signals are contaminated by the presence of noise and lends itself directly to a temporal frequency domain approach via the use of stimuli that vary sinusoidally with time (e.g., Benson et al. 1986, 1989; Grabherr et al. 2008; Lim and Merfeld 2012; Soyka et al. 2011). Analysis with signal detection theory yields a threshold corresponding to the smallest stimuli the subject can categorize with a defined level of reliability, and thus includes decision-making processes when subjects decide how to categorize their perceptions of physical stimuli. Thresholds measured using the signal detection approach are influenced by the characteristics of the physical stimuli (i.e., frequency content and/or time course) as well as the dynamics of the transduction processes, sensory processing, and decision-making processes. Thus measuring thresholds as a function of frequency can elucidate the dynamic properties of these components. Decision-making dynamics can be isolated if transducer dynamics are known (e.g., through neural recordings or behavioral studies) and if behaviorally relevant stimulus frequencies overlap with frequencies influenced by decision-making dynamics. In the past, thresholds have often been measured as a function of stimulus frequency without necessarily improving our understanding of decision-making dynamics. For example, hearing (e.g., Von Békésy and Wever 1960) and tactile (e.g., Lofvenberg and Johansson 1984; Von Bekesy 1959) thresholds change with the frequency of the applied pressure variations, and visual thresholds vary with the temporal frequency of light (Cornsweet 1970). Given the dynamic ranges (i.e., frequency ranges) investigated, these measured threshold variations as a function of frequency typically reflect peripheral transduction processes and typically have not told us much about decision-making dynamics. With the exception of some vestibular threshold studies (e.g., Benson et al. 1986, 1989; Grabherr et al. 2008; Haburcakova et al. 2012; Karmali et al. 2014; Lewis et al. 2011a, 2011b; Lim and Merfeld 2012; Mardirossian et al. 2014; Priesol et al. 2014; Soyka et al. 2011, 2012; Valko et al. 2012), decision-making studies using signal detection methods have rarely focused on dynamics (e.g., perceptual decisions as a function of frequency, where the frequency is in a range relevant to decision-making as opposed to sensory transduction). As discussed later in this review, such vestibular threshold studies may help inform us about decision-making dynamics because behaviorally relevant stimulus frequencies overlap with frequencies influenced by decision-making dynamics.
Decision making is also often studied using a response-time task, in which subjects are asked to indicate their decision as soon as they make it. Data from such tasks are often analyzed using a drift-diffusion (i.e., sequential analysis) approach. In this model, evidence from a noisy signal is accumulated over time. It is generally assumed that the input (i.e., stimulus) as a function of time is constant. This noisy accumulation process leads to “drift” of a decision variable. When this decision variable crosses one of two decision boundaries, a decision is made. This task requires that the subject respond as soon as possible. For more comprehensive reviews, see Gold and Shadlen (2007), Ratcliff and McKoon (2008), and Smith and Ratcliff (2004). Implicitly, this approach adds a third “uncertain” categorization between the two decision boundaries (Fig. 1C). Drift-diffusion modeling almost always focuses on time-domain analyses because the subject is instructed to register his/her choice as soon as he/she makes a decision, which means that the stimulus duration at the time of the decision, and hence, the frequency content of the stimuli, cannot be controlled by the experimenter.
For both signal detection and response-time approaches, real-life decisions and laboratory tasks come in many varieties; we list a few (but far from all) varieties below. We first consider decisions where time to respond is not a critical variable. Experimentally, such decisions are typically investigated using tools and approaches provided by signal detection theory. One relatively simple binary decision is “am I moving?” Another binary decision is “am I moving to the right or left?” Although both are binary decisions, these are fundamentally different from the perspective of signal detection theory. Binary discrimination tasks that require yes/no answers are classically referred to as detection tasks as suggested by Swets (1996), who wrote that “The task of detection is to determine whether a stimulus of a specified category (call it category A) is present or not.” Binary recognition tasks that classify stimuli into one of two categories (e.g., leftward or rightward motion, faces vs. houses) are a second form of discrimination as suggested by Swets (1996), who wrote that “The task of recognition is to determine whether a stimulus known to be present, as a signal, is a sample from signal category A or signal category B.” For further details on the differences between these different binary tasks, see Chaudhuri et al. (2013), Macmillan and Creelman (2005), and Swets (1973). Such tasks are often called forced-choice tasks, because subjects are instructed that they must provide an answer after each trial. Note that for such binary forced-choice tasks, the subjective probability of category A (pA) by definition equals 1 minus the subjective probability of the alternative category (pB), i.e., pA = 1 − pB. Hence, from a statistical viewpoint, a single variable can encapsulate all probabilistic information regarding such binary forced-choice decisions.
We next consider decisions where time to respond is important. For example, time to respond is critical when deciding whether “I am starting to fall to the right or left.” Relevant time-to-respond tasks that have a binary classification goal have been analyzed (e.g., Laming 1968; Ratcliff 1978; Stone 1960). Such paradigms cannot strictly be considered “forced choice” because a third category of “I don't know” is implicit in the categorization before the subject provides their response. Specifically, beginning with stimulus presentation, there is a period of time during which the subject is uncertain (i.e., until he/she makes the decision). Hence, a third subjective probability, that of being uncertain (pU), is applicable prior to the subjective decision. With the sum of the three probabilities equaling 1 (1 = pA + pB + pU), at least two variables are required to encapsulate all probabilistic information regarding such decisions until the decision is made. Drift-diffusion models often include two independent variables that accumulate information pertinent to the decision [or a single accumulation variable that can be interpreted as the difference of these two accumulation variables (Bogacz et al. 2006)]. Since the subject is (strongly) encouraged to choose one of two options, we will call this a binary “response-time” (or time to respond) task.
A signal detection model might be considered as a snapshot of an evolving process that results from a drift-diffusion model. In fact, a signal detection task, where time to respond is not a factor, that includes these same three categorizations (signal category A, signal category B, or uncertain) has recently been reintroduced (e.g., Fechner 1966; García-Pérez and Alcalá-Quintana 2011, 2012). This might be considered a snapshot at time t̃ from Fig. 1C. This too cannot be considered a binary forced-choice task, because the uncertain option means that subjects are not forced to make binary decisions (Fig. 1D). As for the time-to-respond task described in the previous paragraph, at least two variables are required to encapsulate all probabilistic information regarding such decisions. Figure 1, B and D, depicts probability density on the x-axis and the perceptual decision variable on the y-axis. Although not the focus of this review, this graphically shows the similarity of the signal detection approach with an uncertainty option (Fig. 1D) to the time-to-respond approach prior to crossing a decision boundary (Fig. 1C).
Decision-making dynamics.
Having introduced and defined both “dynamics” and “decision making,” we now combine these definitions to define the focus of our review, which is “decision-making dynamics.” We succinctly define the study of decision-making dynamics as the study of how decision making systemically varies with frequency and/or time. We emphasize that while we investigate decision-making dynamics by varying the frequency content and/or the time course of stimuli, the dynamic characteristics of decision making are fundamental characteristics of the neural pathways that contribute to decision making.
Magnitude estimation.
Magnitude estimation is a standard psychophysical method in which subjects provide values according to perceived stimulus magnitude (e.g., Stevens 1974; Wolfe et al. 2014). Such responses can involve tasks that match one modality with another. For example, subjects can be asked to vary the brightness of a light to match their perception of sound loudness. Magnitude estimation tasks do not utilize the forced-choice or time-to-respond techniques described before that are typically utilized for studies of decision making. Hence, perceptual responses assayed using these methods presumably avoid the neural mechanisms associated with decision making. If, as hypothesized above, high-pass filtering impacts decision making, this impact should not be observed when perception is assayed using magnitude estimation techniques that do not utilize these decision-making mechanisms.
Filtering Dynamics
As mentioned in the Introduction (and detailed in subsequent sections), it has been suggested that a high-pass filter (HPF) might help explain why thresholds increase as frequency decreases (Fig. 2). Here, as background for that section, we discuss filter responses. A high-pass filter passes high-frequency signals and noise (i.e., those frequency components above the cutoff frequency) while attenuating low-frequency signals and noise (i.e., drift). For simplicity, we refer to signal components below a cutoff frequency as low frequency and signal components above the cutoff as high frequency. The steady-state output of such a filter always includes some noise. For simplicity, we will assume that the noise present on the filter output is zero-mean Gaussian [N(0, σ)] and stationary (i.e., not changing with time). Note that the frequency characteristics of the noise are assumed to be broad and independent of the signal, so the noise characteristics are the same regardless of the signal frequency. In other words, the primary influence of this filter is on the sensed stimuli/information (i.e., the signal) with little or no impact on the noise.
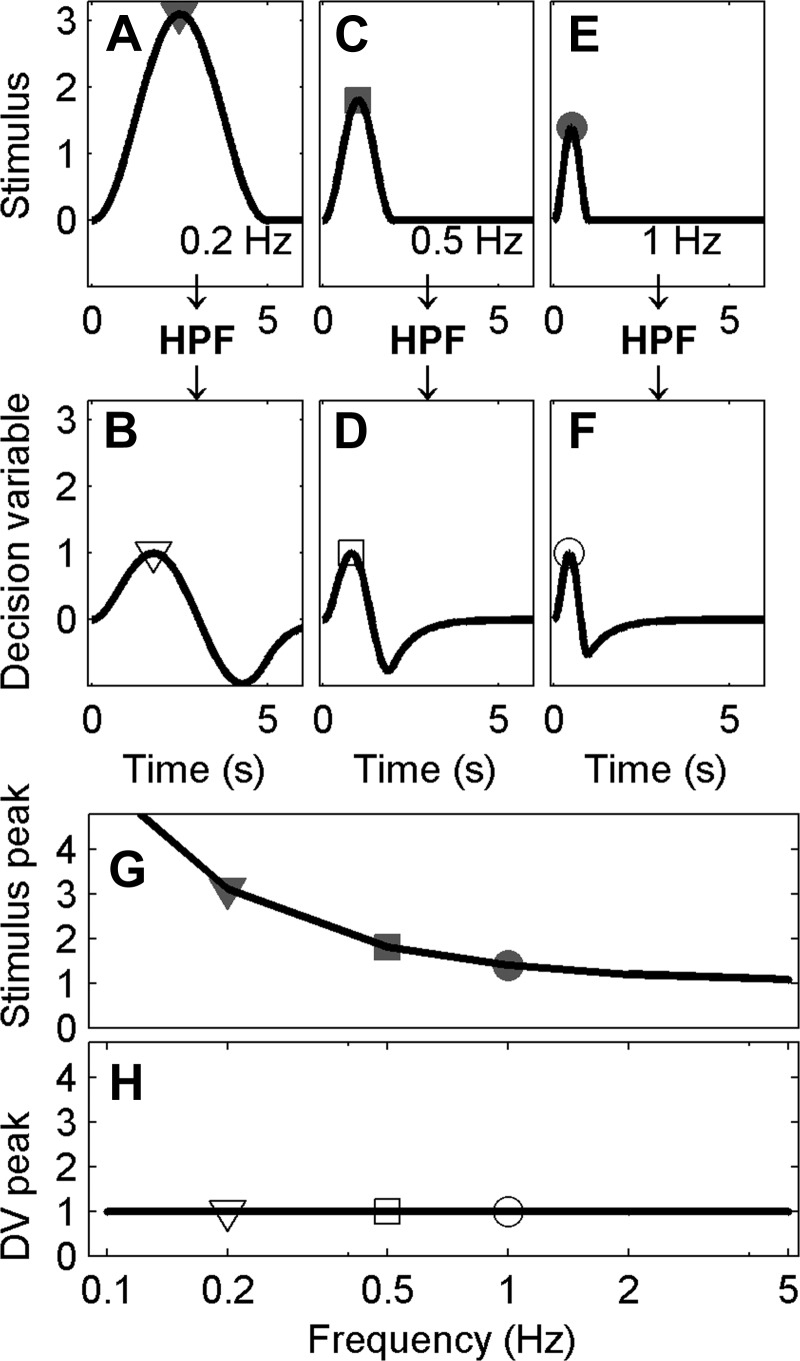
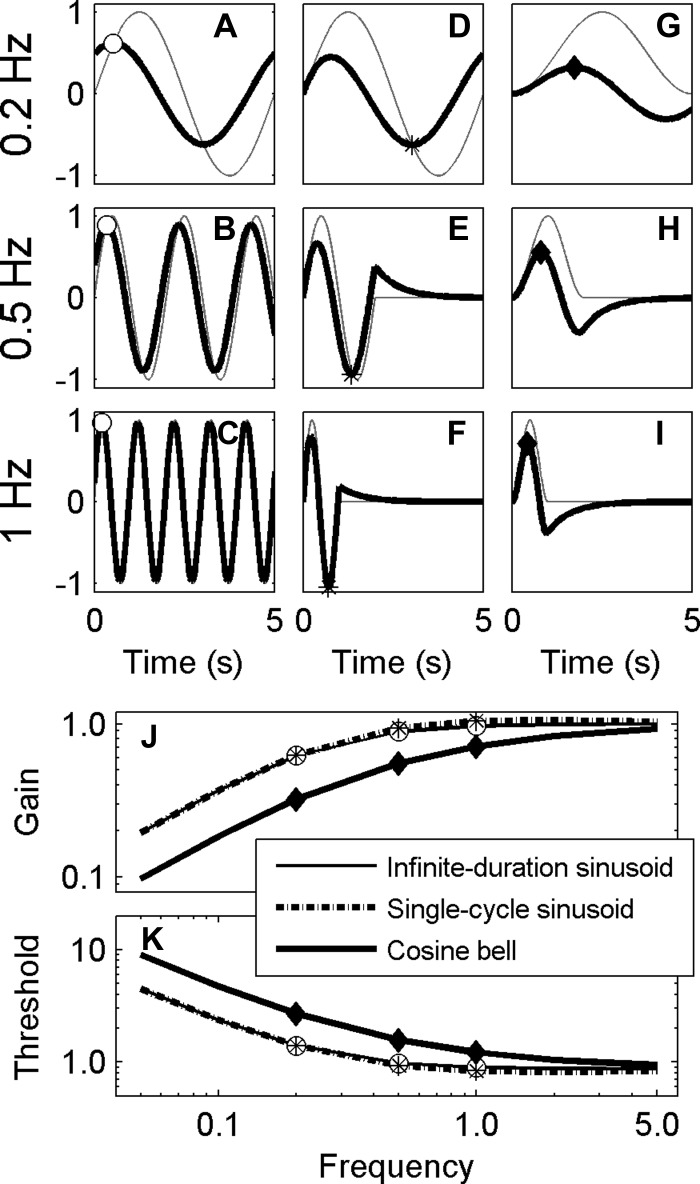
Fig. 2.
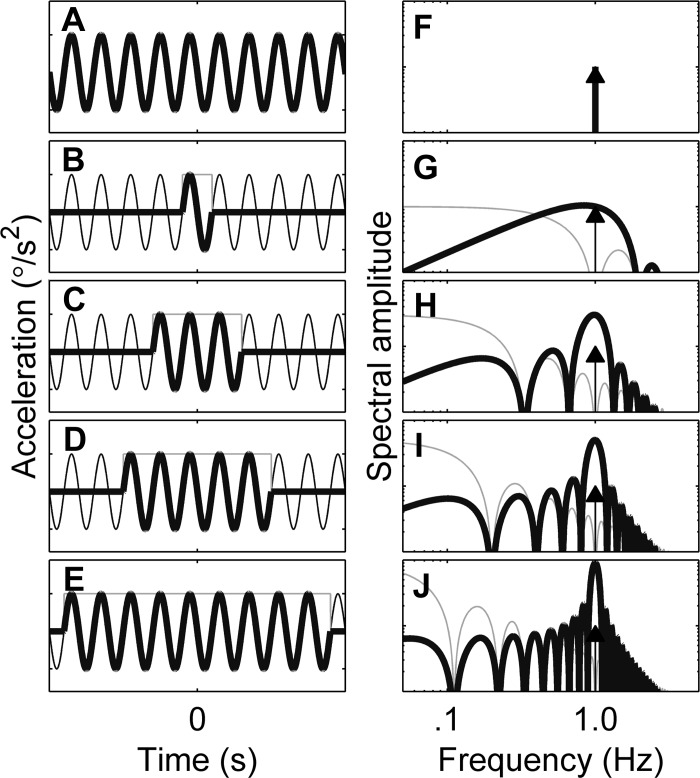
The high-pass filter (HPF) hypothesis predicts that thresholds increase at low frequencies. A: a typical cosine bell physical stimulus with a frequency of 0.2 Hz, corresponding to a period of 5 s, with the peak signal indicated by the gray filled triangle. B: high-pass filtered version of the 0.2-Hz signal, which yields the hypothesized decision variable, with the peak signal indicated by the open triangle. Similarly, 0.5- and 1-Hz signals are shown before (C, E) and after HPF (D, F). For illustration purposes, stimulus amplitudes have been selected so that the decision variable always has a peak of 1. This requires lower frequency stimuli to have larger amplitudes to yield the same peak decision variable after filtering. G: stimuli peak at a range of frequencies, with gray filled symbols indicating the peak for the examples shown by corresponding symbols in A, C, and E. H: the peak decision variable (DV) across a range of frequencies, with the open symbols representing the peaks shown by corresponding symbols in B, D, and F. High-frequency signals are relatively unaffected by an HPF; low-frequency signals are attenuated. Thus larger signals are required at low frequencies to yield the same signal amplitude after a high-pass filter compared with high frequencies.
As discussed earlier, one common representation of a perceptual threshold is when the decision-making signal equals the standard deviation of the noise (i.e., σ). Therefore, if a high-pass filter is processing a given cognitive or sensory signal as part of a decision-making process, the resultant high-pass-filtered output signal amplitude should equal σ at threshold, independent of the frequency content and amplitude of the original input signal. (For simplicity, we assume that downstream noise is small relative to the noise on the perceptual input signal.) To keep the resultant output signal constant as a function of frequency, the input signal amplitude will need to vary with frequency. Since a high-pass filter attenuates low-frequency signal components, a high-pass filter will require a larger input signal at low frequencies (Fig. 2G) to deliver the same output amplitude (Fig. 2H). Hence, under this simple model, thresholds would be predicted to increase at frequencies below the cutoff frequency of a high-pass filter (Fig. 2G).
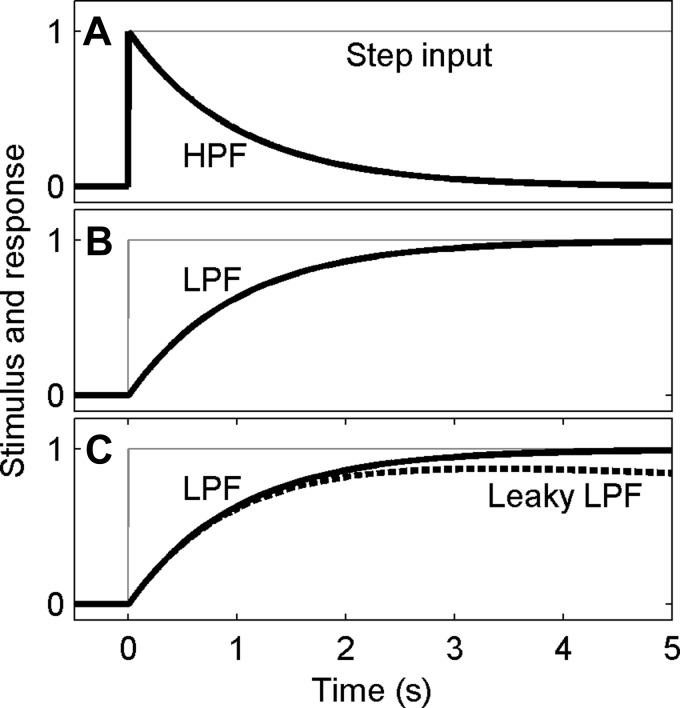
For a linear, first-order, continuous-time system, the cutoff frequency (f) of a high-pass filter is inversely related to its time constant (τ; i.e., τ = 1/2πf). Hence, a 1-s time constant corresponds to a cutoff frequency of 0.16 Hz for a first-order linear filter. Given an input step signal at time 0, a high-pass filter responds with an output (oHPF) that includes a step at time 0 in the same direction as the input, followed by a decaying exponential with time constant τ, oHPF(t) = Ke−t/τ for t ≥ 0 (Fig. 3A). This equation defines what is called the step response of this high-pass filter.
Fig. 3.
Relationship between low- and high-pass filters in the time domain. A: in response to a step input (gray line), an HPF responds (thick black line) with an initial step, followed by an exponential decay with a time constant of 1 s. B: since an integrator followed by an HPF is equivalent to a low-pass filter (LPF), we show that an LPF responds (thick black line) to a step input (gray) with an exponential rise with a time constant of 1 s. C: when an HPF is combined with a leaky integrator with a time constant of 30 s, a leaky LPF (thick dashed black line) results. It has a response that differs little from the LPF (thick black solid line) for the first second or two.
In contrast to our earlier description for high-pass filters, low-pass filters (LPF) attenuate frequency components above the cutoff frequency and pass input frequency components below the cutoff frequency. Given a step signal as an input, a linear, first-order, continuous-time low-pass filter responds with an output (oLPF) that demonstrates a gradual rise with a time constant τ, oLPF(t) = K′(1 − e−t/τ) for t ≥ 0. (This gradual exponential response of a low-pass filter is considered later when we discuss speed-accuracy trade-offs.) This equation defines what is called the step response of this low-pass filter. The time constant of a first-order low-pass filter and its cutoff frequency are directly related to one another using the same relationship shown above.
If we combine a linear, first-order, continuous-time high-pass filter and an integrator, a linear, first-order, continuous-time low-pass filter results (Fig. 3B). Because each of the elements is linear and time invariant, the relative order of the filtering does not matter; high-pass filtering followed by integration is the same as integration followed by such high-pass filtering.
As just one example, it is straightforward to show that that the integral of the output of our linear, first-order high-pass filter for a step input [∫oHPF(t′)dt′] equals the output of our linear, first-order low-pass filter output (oLPF) shown above, i.e.,
In summary, a low-pass filter can be achieved by integration followed by high-pass filtering (or high-pass filtering followed by integration), and all yield leaky integration. We also note that this section introduces stationary linear, first-order, continuous-time filters. We do so for simplicity but explicitly note that the filtering performed by the brain may not be stationary, linear, first order, and continuous time.
But perfect integration is difficult to achieve; what if integration were imperfect? Specifically, what if a high-pass filter were combined with a leaky integrator instead of a perfect integrator? Since there are a number of neural leaky integrators (Bogacz et al. 2006; Raphan et al. 1979), such as the oculomotor integrator (e.g., Kamath and Keller 1976; Robinson 1975) and velocity storage integrator (e.g., Raphan et al. 1979), with time constants of 20 s or more, here we consider a “leaky integration” time constant of 30 s. Figure 3C shows the response of a high-pass filter combined with a leaky integrator, demonstrating that it differs little from the response of a simple low-pass filter. This is generally true when the time constant of the leaky integrator is substantially larger than the time constant of the high-pass filter.
Vestibular Threshold Frequency Responses
The studies described in this section use a signal detection model/approach to analyze data obtained using what we sometimes refer to as a direction-recognition task (e.g., Chaudhuri et al. 2013), which means that the subject experienced a single motion and then needed to decide which of two directions (e.g., left vs. right) he/she moved and must indicate that decision after being informed that the stimulus was complete. Typically, subjects were in complete darkness during motion, to eliminate visual cues (Chaudhuri et al. 2013). Sound contributions were typically minimized via sound-reducing earpieces or auditory masking noise (or both). Tactile contributions were often minimized via the use of padding to distribute any such cues as much as possible. That the vestibular system is the predominant contributor for at least some motions has been demonstrated via elevated thresholds in patients having total bilateral vestibular loss (Valko et al. 2012).
As noted earlier, measuring how the response of a system varies with frequency (i.e., the “frequency response”) provides one way to study system dynamics. Benson and colleagues first explicitly measured human vestibular perceptual thresholds as a function of frequency nearly 30 years ago (Benson et al. 1986, 1989) using single cycles of sinusoidal acceleration. These single-cycle stimuli allow accelerations to be focused near a specific frequency by simply varying the period (i.e., duration) of the sinusoidal stimuli. For example, a single cycle of sinusoidal acceleration having a 2-s period has most of its energy focused near 0.5 Hz. (See Appendix for theoretic analysis of frequency content in single-cycle sinusoids.) Benson et al. (1986) first measured interaural (y-axis) translation thresholds across a range of frequencies and reported that the thresholds monotonically decreased as frequency increased (i.e., duration decreased) from 0.14 to 1.02 Hz. A few years later, Benson et al. (1989) reported a similar threshold response pattern for yaw rotation thresholds for frequencies between 0.05 and 1.11 Hz.
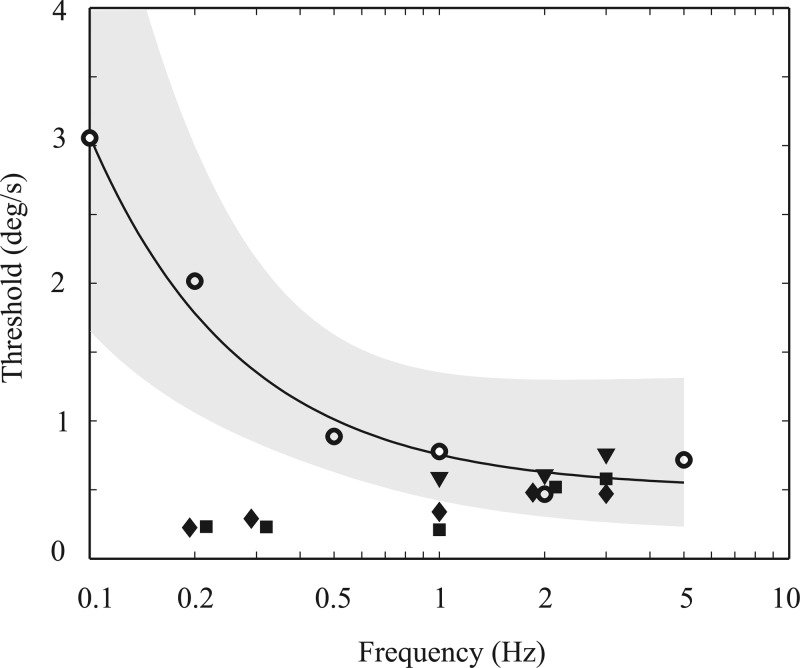
Recently, Benson's study of yaw rotation thresholds vs. frequency was repeated utilizing a broader range of frequencies (Grabherr et al. 2008) covering two full decades between 0.05 and 5 Hz. By extending the frequency range above 1 Hz, this study reported a plateau in thresholds at higher frequencies but noted the same pattern previously reported by Benson and colleagues for frequencies below 1 Hz (Fig. 4). Grabherr and colleagues suggested that these data appeared consistent with high-pass filtering of a decision-making variable. Specifically, Grabherr and colleagues suggested noise should be relatively unaffected by the stimulus characteristics and that the plateau could be rationalized as the passband (i.e., above the cutoff frequency) of a high-pass filter with the rise at lower frequencies caused by signal attenuation of the signal at lower frequencies by the high-pass filter (Fig. 2G).
Fig. 4.
Comparison of monkey vestibulo-ocular reflex (VOR) thresholds and human perceptual thresholds as a function of frequency. Open symbols show the average human perceptual thresholds from Grabherr et al. (2008) converted to “one-sigma” thresholds. Note the plateau in human perceptual thresholds for frequencies above 1 Hz and substantive threshold increase as frequency decreases below 1 Hz. The solid curve shows the least-square fit to the human threshold data, with the shaded area indicating 1 SD from the mean. Filled symbols show the VOR thresholds for each of 3 monkeys. [Modified from Haburcakova et al. (2012), where details can be found.]
Comparing these perceptual threshold decision-making dynamics with motor responses originating from the same sensory organs can help separate transduction effects from the effects of decision making. For example, yaw rotation vestibulo-ocular reflex (VOR)1 thresholds were measured in rhesus monkeys (Fig. 4). The monkey VOR thresholds at 1 through 3 Hz were roughly the same as human perceptual thresholds at these frequencies (Haburcakova et al. 2012), which is suggestive of a common noise source determining threshold performance. However, unlike human perceptual thresholds, the measured VOR thresholds did not show the same pattern of increasing thresholds with decreasing frequency. Specifically, the measured pattern of monkey VOR thresholds as a function of frequency (Haburcakova et al. 2012) does not mimic the human perceptual threshold pattern (Grabherr et al. 2008), which shows a substantial threshold increase as frequency decreased from 0.2 to 0.05 Hz (Fig. 4). The study concluded that one explanation is that perceptual thresholds are influenced by high-pass filter contributions to the perceptual decision-making process. However, other effects, including a difference between humans and nonhuman primates, could not be ruled out (Haburcakova et al. 2012).
The perceptual threshold data of Grabherr et al. (2008) were later quantitatively fit (Lim and Merfeld 2012) using several modeling approaches. This modeling study reported that Grabherr et al.'s threshold data were best fit via a first-order high-pass filter. The average threshold plateau across subjects was 0.5°/s, and the fitted high-pass filter cutoff frequency was 0.26 Hz, which corresponds to a time constant of 0.6 s. The cutoff frequency was specifically noted as being well above the cutoff frequency of the semicircular canals (around 0.03 Hz; Fernandez and Goldberg 1971) and also well above the cutoff frequency associated with velocity storage (around 0.01 Hz; Raphan et al. 1977; Robinson 1977a). Lim and Merfeld specifically wrote that “threshold dynamics do not match the dynamics of human yaw rotation perception measured using magnitude estimation (Bertolini et al. 2011; Bronstein et al. 2008; Okada et al. 1999; Sinha et al. 2008), which show decay time constants between 10 and 25 s, corresponding to cutoff frequencies between 0.006 and 0.016 Hz.” Since the perceptual dynamics assayed using magnitude estimation techniques show a passband that is much wider than that measured via thresholds, Lim and Merfeld suggested that a high-pass filter could contribute to decision making but did not rule out other contributions (e.g., attention or other cognitive or decision-making elements).
The basic frequency effect first reported by Grabherr and colleagues for yaw rotation has since been confirmed experimentally for yaw rotation by two independent studies (Soyka et al. 2012; Valko et al. 2012) that each also extended these findings in different ways. Valko et al. (2012) showed that qualitatively similar frequency characteristics applied for other transient stimuli, specifically, inferior-superior (z-axis) translation as well as interaural (y-axis) translation, and Soyka et al. (2012) were the first to show that the dynamic high-pass filtering effect generalized to other stimulus shapes (e.g., triangles and trapezoids). For yaw rotation, the cutoff frequency that best fit Soyka's data was 0.23 Hz, which corresponds to a time constant of 0.68 s, similar to the time constant fit by Lim and Merfeld to a different data set. In fact, Soyka et al. (2011) had previously applied these fitting methods to interaural (y-axis) translation thresholds before investigating yaw rotation thresholds. They reported frequency characteristics for y-translation that mimicked those for yaw rotation. The fitted cutoff frequency they reported was 0.26 Hz, corresponding to a time constant of 0.62 s. This model fit appears consistent with Valko's interaural translation thresholds described above. The dynamics of translation perception are not as well established as for yaw rotation. When studied using magnitude estimation tasks, translation perception appears transient in nature (Seidman 2008), so it is more difficult to separate translation perception dynamics as assayed via magnitude estimation techniques from decision-making dynamics quantified via threshold studies for y-translation than for yaw rotation. Nonetheless, the similarity of these various fitted high-pass filter parameters for both yaw rotation and y-translation across two laboratories certainly are not inconsistent with the hypothesis that vestibular perceptual threshold decision making can be modeled by high-pass filtering velocity with a time constant of around 0.5–0.7 s.
Consistent with these findings, vestibular response-time tasks have suggested that when the acceleration rate is small, subjects often do not make a decision regarding their motion direction (Arrott et al. 1990; Melvill Jones and Young 1978). For example, for an acceleration of 0.005 G, humans were reported to either be incorrect or not respond at all on over half of the trials (Melvill Jones and Young 1978). This would be consistent with the influence of high-pass filter that would inhibit the decision variable from reaching the decision boundary for small acceleration rates, even when the acceleration is maintained constant for around 5 s, but also may be consistent with drift-diffusion analyses that predict boundary crossings due to integration of a noisy signal for extended periods of time.
Finally, we note that several recent vestibular threshold studies (Coniglio and Crane 2014; Crane 2012a, 2012b; Roditi and Crane 2012) reported aftereffects on threshold processes when a threshold motion was presented shortly after another motion. Specifically, these studies reported a bias in a direction-recognition task; subjects were more likely to report that a second motion was in the direction opposite a prior motion. The papers reported that this effect was largest just after a stimulus was provided and that the effect decreased with a time constant of about 1 s that was explicitly noted to be independent of velocity storage. We note that this is exactly the effect that one would predict if a high-pass filter contributed to decision making, since a high-pass filter would yield an aftereffect in the opposite direction immediately after a unidirectional stimulus. We further note that the estimated aftereffect time constant (∼1 s) is near that reported to explain frequency-dependent threshold variations.
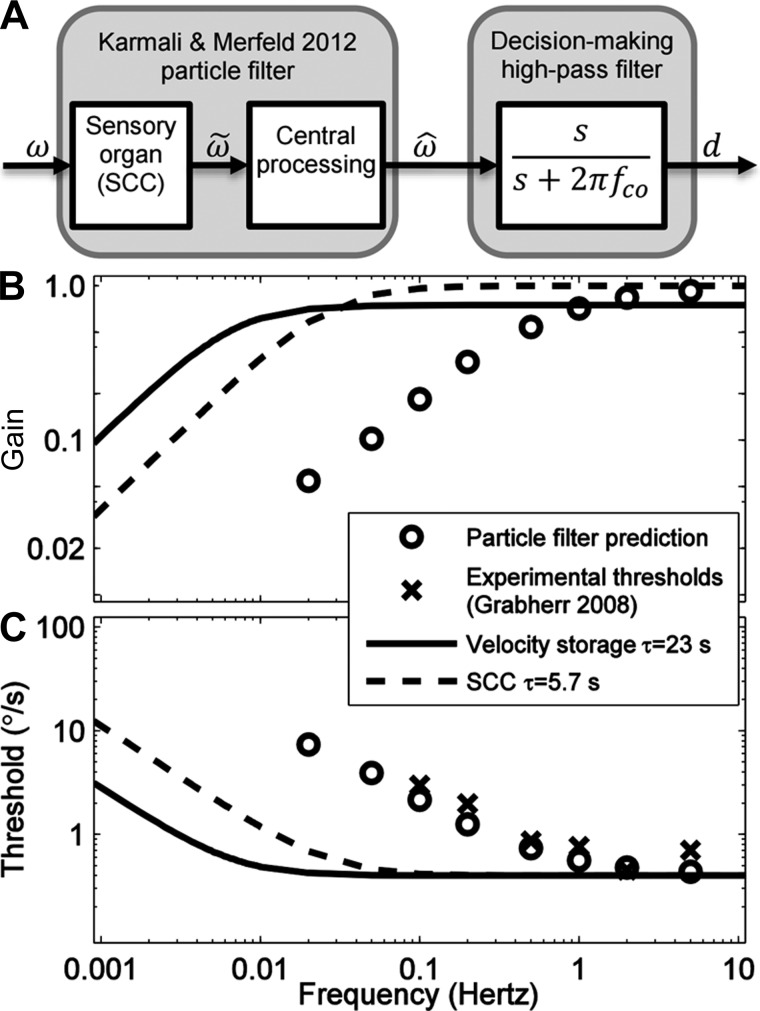
To demonstrate the relationship between noise, signal detection theory, and dynamics, we developed a computational model using a technique called particle filtering (Karmali and Merfeld 2012). This study showed that Bayesian optimal processing of rotational cues from the semicircular canals could model rotation perception and that processing could be implemented using a parallel computational structure that resembles the underlying physiology. When the rotation perception predicted by this model is processed by a high-pass filter decision-making element that was added to the previously published model to represent decision-making dynamics, we find that the model is able to predict dynamics of a human decision-making process. Specifically, the predicted thresholds closely match experimental (× symbols in Fig. 5) results (Grabherr et al. 2008). For example, at frequencies above 1 Hz, the particle filter predicts a plateau in threshold, which becomes larger as frequency decreases. To confirm that the observed dynamics originate in decision making and not transduction or other central processes, we also show the dynamics of two other high-pass filters that impact rotation perception. First, the frequency response of a common first-order model of the semicircular canal (SCC; the peripheral organ that senses rotation) is shown (dashed line) with a time constant of 5.7 s (Fernandez and Goldberg 1971; Melvill Jones and Milsum 1971). Also, the frequency response of “velocity storage” (Raphan et al. 1977; Robinson 1977b) (solid line) is shown, which is the frequency response measured when humans are asked to indicate how much they have moved via a magnitude estimation task (e.g., Bertolini et al. 2011; Okada et al. 1999; Sinha et al. 2008) rather than which direction they have moved.
Fig. 5.
A relationship between noise, signal detection theory, and dynamics is demonstrated by a parallel, dynamic particle filter model (Karmali and Merfeld 2012). A: a block diagram showing the relationship between the particle filter and the decision-making filter. The only addition made to the published model was the addition of linear, first-order high-pass filtering of the estimated angular velocity. The input to the particle filter is physical angular velocity ω, and an output is estimated angular velocity ω̂. This model includes both sensory and central processes, including ω̃, the afferent signals carried from the periphery. The decision-making process high-pass filters ω̂ to determine the decision variable, d. The cutoff frequency (fco) of the filter was 0.25 Hz, which corresponds to a time constant of 0.6 s. SSC, semicircular canal. B: simulated gain of the system as a function of frequency. C: the same data plotted as threshold as a function of frequency. The predicted threshold for each frequency (circles) is determined by determining the signal-to-noise ratio for an input at that frequency. “Signal” is the peak estimated angular velocity when the filter is simulated with no noise and an input of a single cycle of a sinusoid in acceleration at the indicated frequency, equivalent to a cosine bell in velocity; this ensured that transient effects of filtering a single-cycle signal were taken into account (Lim and Merfeld 2012). “Noise” is the standard deviation of the estimated angular velocity when the filter is simulated with noise but no signal. As detailed in the text, experimental data (crosses; Grabherr et al. 2008) are inconsistent with the frequency response of the semicircular canals and perceived angular velocity, suggesting that another process, such as a high-pass filter decision-making mechanism, may be a better explanation for the results.
Visual Perceptual Responses
A few studies have examined dynamics for visual motion perception using signal detection theory approaches. Nakayama and Tyler (1981) determined the threshold as a function of the temporal frequency of motion. In their study, subjects detect horizontal linear motion of dots in the simultaneous presence of random dot motion. The display specifically removed displacement cues and provided only motion cues. They found that threshold decreased with a slope consistent with a first-order high-pass filter (e.g., Figs. 2 and 3) between 0.1 and 1 Hz, and then flattened before climbing again above 2 Hz.
The Nakayama and Tyler study differed somewhat from other studies mentioned in this review, since they used the method of adjustment in which the subjects turned a dial to adjust the motion amplitude until they perceived the continuous sinusoidal motion. A second study (de la Malla and López-Moliner 2010), using forced-choice procedures, found similar results between 0.3 and 3.3 Hz. A third study (Lagacé-Nadon et al. 2009) tested roll motion (i.e., about the line of sight) using a forced-choice recognition approach for continuous sinusoids between 0.25 and 2 Hz and also reported similar results, with a slope consistent with a high-pass filter up to 1 Hz, with a possible flattening at around 2 Hz.
Karmali et al. (2014) recently tested visual motion perception using a direction-recognition rather than motion-detection task and single-cycle acceleration motions rather than multiple sinusoidal cycles, over a broad frequency range of 0.05 to 5 Hz. The study also used a “natural” visual scene that included typical objects seen in daily life rather than random dot patterns. Karmali et al. (2014) found that, again, consistent with a high-pass filter, thresholds decreased as frequency increased up to 1 Hz and then flattened between 2 and 5 Hz.
Between 0.1 and 5 Hz these responses are consistent with a high-pass filter and broadly similar to the results described above for vestibular thresholds (Benson et al. 1989; Grabherr et al. 2008; Lim and Merfeld 2012; Valko et al. 2012). It is important to note that the transduction and processing dynamics are much more complex for vision than for the vestibular system, which, as noted earlier, are known (Bertolini et al. 2011; Bronstein et al. 2008; Fernandez and Goldberg 1971; Okada et al. 1999; Raphan et al. 1977; Robinson 1977a; Sinha et al. 2008) to have a relatively constant response over a broad frequency range. Thus it is harder to attribute visual motion perception dynamics to a decision-making filter. Nonetheless, the similarity in dynamic responses is notable. Although separating visual processing dynamics from decision-making dynamics is not trivial, such analyses could provide tests for the specific decision-making filtering hypothesis discussed herein. While speculative, one plausible approach is suggested by analogy to the vestibular studies described above. Specifically, visual motion perception assayed via techniques that do not require binary decision making (e.g., magnitude estimation) might be unaffected by decision-making dynamics, so a large difference in dynamics assayed via visual motion decision making from those assayed using other psychophysical techniques that do not invoke decision making might provide one way to isolate decision-making dynamics from other visual processing dynamics.
Studies examining how the ability to correctly determine motion direction of a moving random dot scene improves with viewing duration have found that there are neuronal correlates of this improvement (Britten et al. 1992; Gold and Shadlen 2000), which are well-described by models that incorporate dynamics (Grossberg and Pilly 2008). An examination of these results suggests an increase in performance with time that reaches a plateau in a little less than 0.5 s, which is consistent with the behavior of a dynamic decision-making element but likely reflects visual transduction and visual processing dynamics, as well.
Speed-Accuracy Trade-Offs
A number of studies (e.g., Corbett 1977; Corbett and Wickelgren 1978; Dosher 1976; Hintzman and Curran 1997; Ratcliff 1981, 2006; Reed 1973, 1976; Schouten and Bekker 1967; Wickelgren 1977; Wickelgren et al. 1980) have utilized speed-accuracy trade-off methods to study cognitive and perceptual dynamics. Such studies typically measure response accuracy as a function of stimulus duration, where the operator controls stimulus duration. Subjects almost always become more accurate with increasing stimulation duration. Often, an exponential growth function that asymptotes over time fits the data. In fact, a modeling summary (Ratcliff 2006) reported that “the exponential function generally provides good fits to response signal data” and also reported that an exponential function with a time constant around 300–400 ms fit their data, as well: in this case, data representing binary categorization of the number of visible dots as either a “small” or “large.” The article further noted that “The major problem with the exponential function . . . is that it is not theoretically based. There is no model . . . that gives rise to the exponential function. . . . ” As described earlier (and below), our recent analysis suggests a model that gives rise to these predicted exponential functions. Specifically, such exponential functions are exactly what a linear, first-order low-pass filter (i.e., integration followed by high-pass filtering) predicts. Several exemplar findings are briefly described in the following paragraphs.
Reed (1976) studied the accuracy with which subjects could recognize whether a probe consonant was on a previously presented list of consonants and reported that accuracy increased with probe presentation duration. d-prime (d′), a standard signal detection measure representing the ability to distinguish stimuli, increased from zero (or near zero) at 0.2 s toward a plateau for stimulus duration >1 s. The time course appeared exponential. This time course is consistent with the behavior of a linear, first-order low-pass filter having a time constant <1 s.
Corbett and Wickelgren (1978) used a semantic memory retrieval task to test how rapidly associations between examples and a predefined category develop. Using the same d′ measure as Reed, this study showed a similar exponential approach to an asymptotic accuracy. These speed-accuracy trade-off data were consistent with an exponential growth function having a time constant of around 250 ms. Dosher (1976) used the speed-accuracy trade-off method to study the retrieval dynamics for recognition memory for parts of sentences. Recognition accuracy increased with time to an asymptotic accuracy at about 3 s, with the rate of accuracy increase similar across conditions.
Using a visual dot motion discrimination task, Ratcliff and McKoon (2008) studied the speed-accuracy trade-off in a time-to-respond task. On separate blocks of trials, human subjects were instructed to respond “as quickly as possible” or “as accurately as possible.” The effect of the instructions was fit by altering only the separation of the decision boundaries in the extended drift-diffusion model (details of this model are discussed in Dynamic Drift-Diffusion Modeling). This suggests that the accumulation process (e.g., drift rate and variability) and non-decision components are unaffected by the speed-accuracy trade-off. The precise shape of an exponential growth function could not be demonstrated with only two conditions (“quickly as possible” or “accurately as possible”), but the data are qualitatively consistent with the exponential growth reported above since the instructions emphasizing accuracy led to longer response times that yielded improved accuracy. A very recent study (Hanks et al. 2014) in monkeys yielded results more or less consistent with these human findings, except that neural recordings showed little evidence of a shift in the decision boundary, but instead suggested an increase in the neural firing rate prior to evidence accumulation at the beginning of each trial. Another recent speed-accuracy trade-off study has shown that an urgency signal might contribute to both “deciding” and “acting” (Thura et al. 2014).
Swensson (1972) studied the speed-accuracy trade-off in a visual discrimination task of shape orientation by manipulating subject rewards (i.e., encouraging faster or more accurate responses by providing payouts that reward each of these strategies). As for studies discussed above (e.g., Corbett and Wickelgren 1978; Ratcliff 2006; Reed 1976), accuracy improved with increasing time to respond, but accuracy did not approach perfect performance (i.e., a performance asymptote was evident), and data (Swensson 1972) were again consistent with an exponential growth function that asymptotes over time. Also, as shown in Filtering Dynamics, exponential growth in evidence accumulation is the predicted output of a low-pass filter (i.e., leaky integrator), which can be modeled as an integrator followed by a high-pass filter (or vice versa).
Dynamic Decision-Making Modeling
This section provides a brief overview of several decision-making models. All of these models accumulate noisy evidence over time and make a decision once sufficient confidence has been established. They differ primarily in the specific ways that the evidence is accumulated.
For example, the so-called “race model” separately integrates evidence favoring each of the two alternatives and makes a decision as soon as one of the integrators reaches a given threshold (e.g., Boucher et al. 2007). In contrast, the drift-diffusion models (DDM) only maintain a single abstract integrator, accumulating the difference between the evidence supporting either of the alternatives. A decision is then made once the integrated difference crosses a positive or a negative threshold. Such DDMs have long been used to model accuracy and reaction time datasets (e.g., Laming 1968; Ratcliff 1978; Stone 1960). In statistical decision theory, DDM may be regarded as an instance of a standard sequential probability ratio test, which is optimal in the sense that it is the test that provides the quickest decision under a given accuracy requirement. (The trade-off between accuracy and decision delay can be achieved by varying the decision thresholds.) In a recent article (Bitzer et al. 2014), the authors have also established an interesting connection between the DDM and a Bayesian model for decision making.
The DDM and its various extensions (e.g., extended DDM) provide good fits to available data, albeit at the cost of requiring several parameters that have yet to be directly verified. Specifically, because decision making is not simple, the extended DDM2 includes free parameters that represent mean drift rate, drift rate variability, the initial value of the drift-diffusion variable, and physiological noise variance. Additional assumptions include distribution of the physiological noise and distribution of the initial conditions.
Bogacz et al. (2006) have provided a comprehensive analysis of seven models of dynamic decision making. Models analyzed there include those that have a single accumulation variable (i.e., DDM, extended DDM, and Ornstein-Uhlenbeck models) and those that have more than one parallel variable to accumulate evidence in support of each hypothesis (i.e., race models, mutual inhibition models, feedforward inhibition models, and pooled inhibition models). In their analysis, Bogacz et al. showed that, with the exception of the race model, all the models mentioned above can be reduced to DDM under suitable parameter choices. In the following paragraphs, we briefly summarize aspects of their analysis that directly relate to decision-making dynamics. (For those interested in details, we recommend the article.)
From the perspective of decision-making dynamics, Bogacz et al. (2006) note that neither the DDM (e.g., Bogacz et al. 2006; Ratcliff 1978) nor the extended DDM (e.g., Bogacz et al. 2006; Ratcliff 1978; Ratcliff et al. 1999) include dynamic elements beyond integration/accumulation of evidence. Similarly, race models and feedforward inhibition models include simple integration as the primary dynamic element (Bogacz et al. 2006). Therefore, the following paragraphs focus on the three models that include dynamic elements beyond integration and accumulation. Diffusion models lend themselves to time-domain rather than frequency-domain analyses because, as noted earlier, the investigator cannot control frequency content of the stimuli at the time that the subject responds during a typical time-to-respond task.
The simplest of these models (called the Ornstein-Uhlenbeck model) includes a feedback term controlled by an additional rate parameter (Busemeyer and Townsend 1993; Busemeyer and Townsend 1992). The equation for the standard DDM can be written as simple diffusion equation:
where x represents the accumulated evidence, A is the evidence being accumulated, and the last term represents Gaussian white noise with variance c2.
For the Ornstein-Uhlenbeck model, the above equation is modified as
where λ represents a feedback parameter. The introduction of the factor λx allows one to introduce several new effects. For example, as described by Busemeyer and Townsend (1993), when the feedback parameter is between 0 and 1, this parameter produces “recency effects so that the recent samples have greater impact.” When negative, this parameter produces “primacy effects so that earlier samples have greater influence.” These statements seem to require the assumption that the information being accumulated is constant following an abrupt on-transition, assumptions that were met by the experiments being modeled, but such assumptions are not generally true, even in laboratory conditions. From a dynamic systems perspective, the sign of the feedback parameter (λ) affects the stability of the model. Positive feedback yields an unstable system; negative feedback yields leaky integration, which, as noted earlier (see Filtering Dynamics), is the same as low-pass filtering (and both are the same as integration combined with high-pass filtering). Since there is little evidence that perceptual decision making is unstable, from this point forward we consider only systems with negative feedback that are stable and do not consider unstable variants.
The mutual inhibition model (e.g., Bogacz et al. 2006; Usher and McClelland 2001) can be considered as two parallel Ornstein-Uhlenbeck models with additional mutual inhibition terms that link these two models. More specifically, the positive strengthening of evidence in favor of one alternative will inhibit (i.e., reduce) the accumulated evidence for the other alternative. Given this, it seems understandable that detailed analyses (Bogacz et al. 2006; Usher and McClelland 2001) show that the difference between the competing accumulators mimics the Ornstein-Uhlenbeck model dynamics. Similarly, the pooled inhibition model can be shown to be equivalent to an Ornstein-Uhlenbeck model (Bogacz et al. 2006). Hence, all three models reviewed by Bogacz and colleagues that include dynamic elements can be considered, from a dynamics perspective, nearly equivalent. Each essentially low-pass filters the available information, a concept also previously proposed and investigated by Smith (1995, 2000). To summarize, we emphasize that when the rate parameter is negative, this leaky integration model low-pass filters the available information. As noted earlier, low-pass filtering is nothing more than integration combined with high-pass filtering.
Finally, we note a few variations on these models that impact dynamic analysis. For most models in the DDM family, the decision thresholds are kept fixed. However, one can consider the use of time-varying thresholds that, for example, “collapse” over time (Churchland et al. 2008; Ditterich 2006; Drugowitsch et al. 2012; Ratcliff and Frank 2012). This can be used to model the “urgency” effect in decision making. Also, whereas the models we describe in this section all involve some kind of random walk or diffusion processing during the decision-making process at each trial, there are other decision-making models proposed in the literature that are not based on this random-walk formulation. One prominent example is the LATER model (Carpenter et al. 2009; Carpenter and Williams 1995; Reddi et al. 2003), which accumulates evidence at a fixed rate during a trial, with stochastic variations appearing across different trials.
Drift-Diffusion Studies Investigating Dynamics
Recent studies have investigated whether drift-diffusion models that combine an integrator with an information accumulation bound better explain data than the same model with leaky integration and no accumulation bound. As summarized below, some found that data were best explained by the presence of “leaky integration” alone (i.e., high-pass filtering combined with integration), whereas others found more support for the presence of an information accumulation bound alone.
Consistent with reports from the earlier Speed-Accuracy Trade-offs section, an article using data acquired from two monkeys confirmed that monkey visual motion direction-discrimination thresholds measured with different levels of random dot motion coherence demonstrate a roughly exponential time course when display duration is varied between 80 and 1,000 ms (Fig. 3 in Kiani et al. 2008). This study (Kiani et al. 2008) then further investigated whether the leveling off exhibited by the exponential function described in detail in the previous section might be due to the presence of leaky integration alone (i.e., high-pass filtering combined with integration) or to the presence of an information accumulation bound alone (i.e., without high-pass filtering). (This study did not investigate leaky integration combined with an accumulation bound.) These modeling analyses show that information provided earlier in the trial is more important for the bounded information accumulation mechanism than for the leaky integration mechanism. On the other hand, modeling also showed that later information was more pertinent for a leaky integration mechanism without bounded information accumulation than for bounded information accumulation alone.
The study yielded two experimental findings, both of which supported bounded information accumulation. One result derived from a reverse correlation analysis that was performed for those trials in which the stimulus had no available motion information (0% motion coherence). When this analysis was performed for the model simulations, both the experimental data and the bounded accumulation model showed that early information correlated best with the final decision, whereas the leaky integration model diverged, showing that late information correlated best with the final decision. The second finding was that pulses of information provided early in the viewing period had a greater influence on the final decision than pulses of information provided late in the viewing period. As noted above, this finding best corresponds to the predictions from the bounded accumulation model and is opposite to predictions from the leaky integration mechanism. On the surface, these results appear to contradict the high-pass filter hypothesis.
On the other hand, a previous human study (Experiment 3 presented in Usher and McClelland 2001) did not come to the same conclusion. In that study, humans viewed an interleaved stream of S's and H's and reported at the end of the stream which letter had appeared the most. When the number of S's and H's were the same, one of the letter's might appear more often early in the trial with the other appearing later. Of the six subjects tested, two showed an effect indicating a larger influence of the early information, two showed an effect indicating a larger influence of the late information, and two showed about the same impact of early and late information. At a minimum, this suggests that any such primacy/recency influence might vary in humans (e.g., depend on subject and/or perceived task constraints).
Given these apparent discrepancies, a recent study (Tsetsos et al. 2012) mimicked the methods used by Kiani et al. (2008) except that human subjects were tested. Specifically, a moving dot display with varying motion coherence, like that used by Kiani et al., was employed to test highly trained subjects. Furthermore, the time-pressure to respond was manipulated across conditions. The article reported a replication of the Kiani findings when the participants were pressured to respond quickly (i.e., data best mimicked a bounded accumulation model without high-pass filtering), but when the task explicitly provided less time pressure, influence of early information was much weaker. For 2 of 10 subjects, late information was more influential than early information when the time pressure to respond quickly was lessened. (A full summary of the 4 experiments exceeds the space available here; see the original paper for details.) In summary, Tsetsos et al. (2012) wrote that their studies showed that the influence of earlier information is equally consistent with the bounded accumulation model and the leaky competing accumulator model.
We are not in a position to adjudicate. We observe that these comparisons reflect a view that the explanation is either bounded accumulation or leaky integration. Given this observation, we return to the vestibular threshold frequency responses described above. The reported increase in thresholds at lower frequencies cannot be explained by bounded accumulation alone. Bounded accumulation in the total absence of any dynamic mechanisms would predict that the thresholds would be constant as a function of frequency (or perhaps even increase with frequency under some assumptions) with the bound crossed at the same velocity independently of frequency. However, the reported thresholds are also inconsistent with a leaky integration mechanism in isolation (i.e., without boundary crossings or some other similar mechanism). Specifically, since the motion trajectories used continuous velocity waveforms that first increased and then decreased back to zero just before the response was requested, it would be meaningless in this context to ignore boundary crossings and/or the peaks in the decision variable expected to occur transiently near the middle of the motion trajectory. In fact, analysis of the vestibular thresholds implicitly assumed both 1) a filtering mechanism and 2) a decision mechanism that would reflect the decision variable found near the middle of the trial when the peak velocity occurred. Such a midtrial decision mechanism could be a boundary crossing, a latch that records/maintains peaks in the decision variable, or a mechanism that provides a post hoc assessment of recent decision-variable peaks. Since we are unaware of drift-diffusion analyses that have combined leaky integration with any such midtrial decision mechanism, this may remain an open issue that requires new analyses and explicit experimental investigations.
Before proceeding, it is important to note that the DDM (and variants) include a substantial number of free parameters that provide the freedom to match data from a wide variety of studies quite well. This is good as this provides the freedom to match the complex behavior reported/observed. However, this freedom may come at the cost of not always providing direct hypothesis testing. As explicitly shown in the previous paragraph, the frequency-domain approaches provide an alternative approach that can provide useful information that might sometimes help resolve discrepancies.
Relating High-Pass and Low-Pass Filtering
We have noted that the dynamics of decision making found for vestibular direction-recognition tasks were consistent with a filtering element having a time constant on the order of one-half second (see Vestibular Threshold Frequency Responses), as are the reported frequency responses for visual perception (see Visual Perceptual Responses). Furthermore, literature suggests that speed-accuracy trade-offs for semantic decision-making yielded similar time constants (see Speed-Accuracy Trade-offs). We did not highlight earlier that the vestibular threshold frequency responses were fitted using a high-pass filter whereas the speed-accuracy trade-off data were consistent with a low-pass filter. We now describe one explanation for how these results could arise from a single mechanism. We specifically note that the goal of this review is to present relevant data and to provide plausible hypotheses, not to provide definitive proof for any single hypothesis or viewpoint. More data, alongside more thorough dynamic analyses of decision making, are needed to reach definitive conclusions.
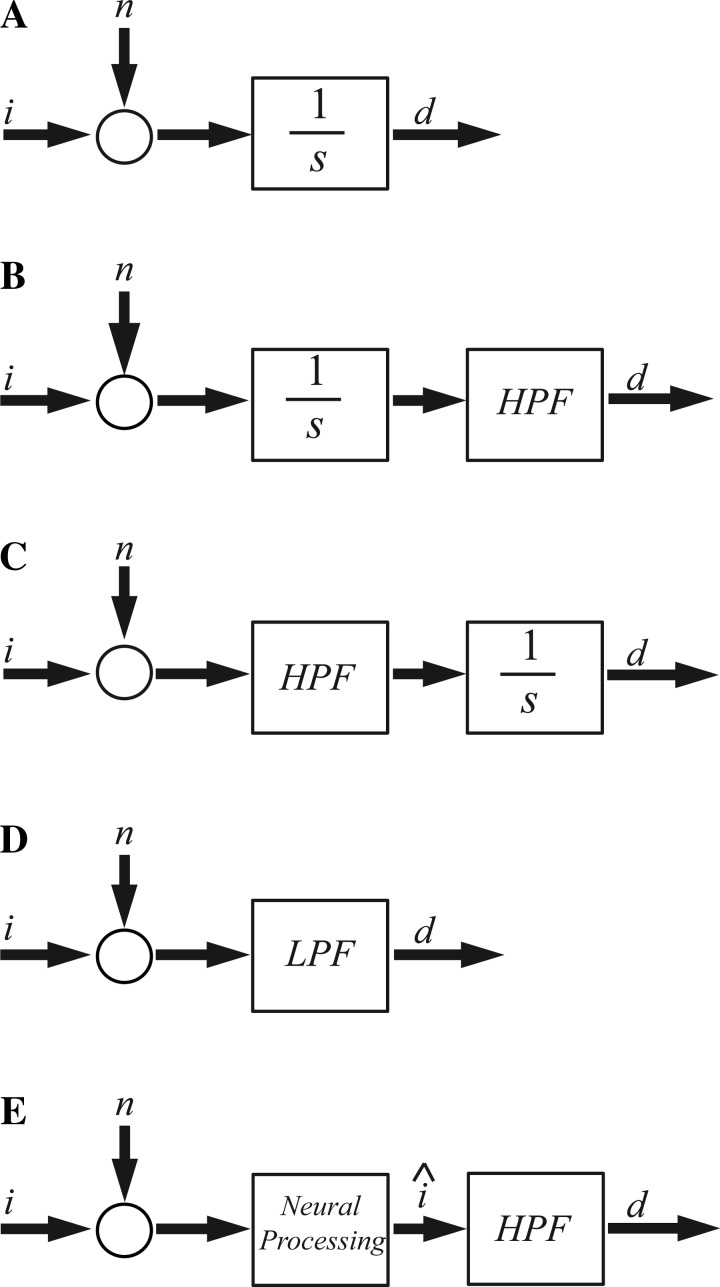
The information for speed-accuracy assays is obtained by turning the stimulus on for each trial. This initiates the start of evidence accumulation, which proceeds until the stimulus is turned off or the subject provides a response. As described earlier, it is commonly assumed that the information being accumulated is constant as a function of time, and such accumulation is often modeled using an integrator (Fig. 6A), which can be shown to be a statistically optimal process (Bitzer et al. 2014; Bogacz et al. 2006). If decision making includes the additional contributions of a first-order high-pass filter, this would be represented by adding a first-order high-pass filter to the integration process (Fig. 6B). As noted earlier, since both integration and high-pass filtering can be represented as linear time-invariant processes, the order of these processes is irrelevant, so we could reverse the order of these processes to indicate high-pass filtering of information followed by evidence accumulation (Fig. 6C). Either way, from a functional input/output perspective, this integration and high-pass filtering can be combined into a single first-order low-pass filter (Fig. 6D) that can (as discussed earlier) explain the exponential relationship commonly reported for such speed-accuracy trade-offs.
Fig. 6.
Evidence accumulation models. A: standard evidence accumulation is represented by a simple integration of noisy information, represented in the diagram as the sum of noise (n) and information (i). The output is the decision variable (d). As noted in the text, such integration might provide optimal processing for information sources that begin abruptly. B: if an HPF contributes to decision making, it would filter the accumulated evidence. C: alternatively, information could be accumulated following high-pass filtering. D: an LPF can represent the processes shown in B and C, because, as presented earlier, integration combined with high-pass filtering, in either order, is equivalent to low-pass filtering. Stated explicitly, from an input-output perspective, B, C, and D are identical. E: when information is continually processed optimally, integration of such information is suboptimal under many conditions, because integration of optimally processed information yields suboptimal processing. More generally, the continual processing shown in E could also represent the integration included in A–D, since integration is a form of continual processing that is particularly pertinent when a transient information source is turned on.
In contrast, we note that “vestibular” stimuli cannot be turned on or off. Even in the absence of motion, the vestibular system encodes that the motion is “zero” (e.g., Fernandez and Goldberg 1971, 1976; Goldberg and Fernandez 1971). This is different from the absence of incoming information as occurs when visual (or other) stimuli are turned off. In fact, the brain continuously processes vestibular information (e.g., Angelaki and Cullen 2008; Goldberg et al. 2011; Merfeld 2014; Raphan et al. 1977; Robinson 1977b), yielding underlying motion and orientation states (e.g., Angelaki et al. 2004; Clark et al. 2014; Glasauer 1992; Karmali and Merfeld 2012; Laurens and Droulez 2007; Macneilage et al. 2008; Merfeld et al. 1999; Zupan et al. 2002) that contribute to perception and reflexive responses. Furthermore, a number of studies suggest that the brain optimally processes this information (Borah et al. 1988; Butler et al. 2010; de Winkel et al. 2010; Fetsch et al. 2009, 2010, 2011; Gu et al. 2008; Jurgens and Becker 2006; Karmali et al. 2014; Karmali and Merfeld 2012; Laurens and Droulez 2007; Paulin et al. 1989; Selva and Oman 2012; Young 2011). If the information is, in fact, being optimally processed to yield optimal motion and orientation estimates, additional integration as part of the decision-making process might not make sense. (If integration yielded “better” information, then integration might have been included as part of the original optimal processing.) When information is continually processed optimally, integration would be suboptimal under at least some conditions, because integration of optimally processed information would yield suboptimal information.
Instead, we hypothesize that it would make sense for decision making to utilize the optimal information (î in Fig. 6E) already available rather than to integrate the incoming sensory information (i) or to integrate the optimally processed information (î). Schematically, we represent such neural processing using a block labeled “neural processing” in Fig. 6E. For vestibular responses, this could represent the optimal processing of vestibular information. In a general sense, the neural processing shown in Fig. 6E could also represent the integration explicitly included in Fig. 6, A–C (and implicitly included in D), since integration is a form of processing that seems particularly pertinent and may even be near-optimal when constant transient information is provided (Bitzer et al. 2014; Bogacz et al. 2006) for short periods of time.
More generally, such neural processing could represent other processing dynamics. For example, auditory (Burbeck and Luce 1982) or visual (Smith 1995) response times may be better modeled by including transient processes in addition to constant sustained accumulation. Furthermore, the drift rate may be time-varying when the stimulus is continuous but time-varying (e.g., Drugowitsch et al. 2014) or when the stimulus is discrete (e.g., tone bursts in an auditory discrimination task; Brunton et al. 2013). Thus we emphasize that many sensory information sources just may not be turned on and/or may not have constant, sustained accumulation; future models should aim to account for these variations. In particular, these cases may help illuminate dynamic mechanisms that contribute to the decision-making process.
DISCUSSION
In this article, we have reviewed literature that seems relevant to the development of an understanding of decision-making dynamics. As presented, both data and models suggest that a dynamic decision-making element having a time constant <1 s appears consistent with available data. At the same time, it is important to note that definitive evidence for such a dynamic element is lacking. Although neural recordings have shown phasic decision-making response components consistent with a high-pass filter (Aston-Jones and Cohen 2005a, 2005b), this is far from a proof that the phasic component represents decision-making dynamics. What other factors could explain these reported results that appear consistent with dynamic filtering?
Other Plausible Considerations
We briefly discuss a few explanations that might be considered instead of or in addition to high-pass-filtering of the decision variable.
1) It is certainly possible that attentional mechanisms contribute to decision making. As one example, threshold decision-making tasks require attentional resources to monitor the stimuli to avoid missed stimuli. It is possible that these mechanisms have limits that manifest with characteristics that mimic filtering dynamics when stimuli lasting more than a second (or so) are provided. We are unaware of studies that specifically study attentional contributions to threshold decision making, except to minimize lapses wherein a subject misses a stimulus (or several stimuli). To avoid excessive speculation in the absence of data, we simply note this as an area deserving study.
2) If the drift-diffusion model (i.e., without high-pass filtering) is an accurate representation of response-time decision making, it predicts that diffusion will lead to decisions even when no stimuli are presented. Similarly, such diffusion would contribute to incorrect decisions for subthreshold stimuli. Such diffusion contributions presumably increase with time. If true, longer duration (loosely equivalent to “lower frequency”) small stimuli would lead to more incorrect decisions due to diffusion, which could lead to higher thresholds for long-duration than short-duration (loosely equivalent to “higher frequency”) stimuli. This would mimic the general characteristics of a high-pass filter illustrated in Fig. 2, but would not explain (at least without further development and/or information) the similar time constants reported for a) vestibular thresholds as a function of frequency and b) vestibular aftereffects as well as c) visual thresholds as a function of frequency and d) speed-accuracy trade-offs (each presented above). Furthermore, for constant input stimuli, the drift-diffusion model predicts that accumulated information would increase with time3 in an unbounded manner that is not consistent with the performance plateaus reported earlier after about 1 s or so for speed-accuracy trade-offs.
3) We have posited that high-pass filtering of a decision variable accompanied by a constant decision boundary could explain some of the findings reported earlier. Are there alternatives that yield the same functional effect without high-pass filtering the decision variable? One alternative would be that the decision variable is unfiltered but that the decision boundary increases with a time course that yields the same relative spacing between the decision variable and decision boundary. As mentioned earlier, recent neural recordings (Hanks et al. 2014) provide little evidence of an increased decision boundary, despite looking explicitly for decision boundary changes. We cannot identify another mechanism equivalent to high-pass filtering of the decision variable at this time, but that does not mean that another such mechanism may not exist.
4) The cost of accumulating evidence could also impact perceptual decision making (Drugowitsch et al. 2012). This modeling work shows that such costs could help explain speed-accuracy trade-offs, but explicit prediction of frequency effects, like those reported earlier for both vestibular and visual stimuli, have not yet been published. For time-to-respond tasks like those investigated, it is certainly plausible that time could be seen as a cost, but it is not clear that forced-choice signal detection tasks should include such a cost, since a subject's responses have no impact on stimuli presentation in such tests. Adding a phasic dynamic element, like a high-pass decision-making filter, to such a model could also help improve these model predictions.
Drift-Diffusion Considerations
It has been noted that the drift-diffusion model suffers a shortcoming (e.g., Usher and McClelland 2001) in that it predicts that accuracy can improve without limit, whereas data (and our own personal experience) show imperfect performance even when participants are given unlimited time to respond. To address this concern, in his extended drift-diffusion model, Ratcliff (1978) assumed that the average drift rate is not the same on each trial, even when identical stimulation is provided (i.e., drift rate variations exist across trials) and showed that when such drift rate variations exist, accuracy does not improve without limit.
As an alternative, Usher and McClelland (2001) described a leaky accumulator model, which, as noted earlier, is the same as a low-pass filter model and the same as a high-pass filter combined with an integrator. Usher and McClelland specifically noted that accumulated information might decay. In response to Ratcliff's (1978) use of an additional free parameter, variability across trials in the information accumulation rate (i.e., drift rate), they wrote, “While not denying such a factor [i.e., accumulation variability] is likely to play a role . . . , limitations on discriminability may also arise from characteristics of the information accrual process itself. Specifically, we suggest that information that has been accumulated may be subject to leakage or decay.” Usher and McClelland also specifically noted that leakage imposes limits on the temporal window over which information can be accumulated.
Usher and McClelland (2001) provide a number of direct comparisons for how well their leaky accumulator model compares to the extended drift diffusion model. For one forced-choice experiment in which subjects judged which side of a nearly square rectangle was longer, they reported “small but systematic advantages” of the fit of their model relative to the drift-diffusion model for fitting the experimental time-accuracy curves. For a difficult time-to-respond experiment, Usher and McClelland reported that their leaky integration model could fit experimental skewed reaction time distributions as well as the drift-diffusion model. Also, Ratcliff and Smith (2004) reported that performance of the diffusion model with leaky integration is about the same as that of the extended drift-diffusion model across three experiments. Given these findings, it would seem reasonable to think that such dynamic “leakage” effects would typically be considered, but that does not seem widely true. One explanation may be that the predicted differences between the models were small relative to variability in the data. In fact, Ratcliff and Smith (2004) showed that the extended drift-diffusion model and one with leaky integration have substantial mimicry in many simulations. Another explanation is that adding the complexity of dynamic “leakage” to the already complex drift-diffusion model does not endear itself to experimental scientists (but this is probably no less true of the extended drift-diffusion model).
A third explanation could be that people are content to study forms of decision making where the existing drift-diffusion model is adequate. For example, Ratcliff and McKoon (2008) have correctly noted that the drift-diffusion model is generally appropriate for periods of up to only 1 or 2 s. If one is content to accept such limitations, then the influence of the dynamic effects, like those reported by Usher and McClelland (2001), are small. It is only when the time period of interest is large relative to the decision-making time constant that these dynamic influences become evident. As just one example, our self-motion threshold studies (e.g., Grabherr et al. 2008) sometimes used motions having periods on the order of 5–10 s. Such longer duration stimuli may demonstrate the dynamics of decision making more readily than stimuli lasting only a second or so, but this is far from proven and may only hold true for some forms of decision making. Finally, the presence of dynamic “leaky” integration vs. the trial-to-trial variability of drift rate in the extended drift-diffusion model may depend on the specifics of the experimental task. Usher and McClelland (2001) suggest that the concept of “drift variance is a plausible one, particularly when it is applied to experiments involving highly inhomogeneous items, such as items from a memory experiment. In such cases, item differences could easily arise from a number of sources, includes adequacy of study or relative similarity of a test item with other studied items, and these would likely play an important role.” This further suggests that the experimental design and task may be critical for cleanly observing the presence (or lack of presence) of dynamic elements such as “leaky” integration.
Potential Behavioral Benefits of High-Pass Filtering
Since a high-pass filter as part of decision making has been suggested by previous studies, we next consider some potential functional benefits that such a high-pass filter could contribute to decision making. Without such a high-pass filter, the influence of a previous stimulus could linger for many seconds or longer. For example, we consider a relatively dramatic vestibular example. “Velocity storage” has a time constant of 10–20 s that that typically yields an illusory rotation aftereffect lasting up to a minute following unidirectional rotation. High-pass filtering perceptual signals as part of the decision-making process could help reduce the impact of such lingering perceptual aftereffects on perceptual decision making.
We do not suggest that this potential behavioral benefit does not come without costs. Specifically, high-pass filtering may impair our ability to make accurate decisions in response to low-frequency stimuli. In the case of vestibular processing, this could impair our ability to recognize motion direction at low frequencies in the dark. Thus the utilization of a high-pass filter in the decision-making process may help de-emphasize older information that may no longer be relevant, at the expense of suboptimal decisions for longer duration stimuli (i.e., low-frequency stimuli). (This relates to material presented earlier in Drift-Diffusion Studies Investigating Dynamics.)
As discussed in an earlier paper (Haburcakova et al. 2012), there is another potential rational role for such a high-pass filter in decision making. Almost every signal that contributes to decision making will include noise. The accumulation of such noise via integration leads to a random walk (Fig. 7A) having variance that grows with time (Fig. 7B). For example, if we assume that the noise is Gaussian white noise, the integration of this noise leads to Brownian noise. One characteristic of Brownian noise is that the standard deviation grows with the square root of time in an unbounded manner. Such unbounded signal variance with time would not form an optimal decision variable. One way to create bounded variance is to high-pass filter the decision signal. For example, high-pass filtering Brownian noise leads to a constant value of the standard deviation after just a couple of filter time constants (Fig. 7C).
Fig. 7.
Effect of a linear, first-order HPF on drift-diffusion trajectories. All simulations have a drift rate of zero and include no decision boundaries to show the effect of accumulation of noise over time. A: an example diffusion trajectory with (gray line) and without (black line) the HPF. The HPF has little effect early but later draws the trajectory back toward the starting level. B: mean ± 2SD of 100 diffusion simulations without filtering over time. These could represent either ensemble parallel population coding or the expected outcome of sequential trials. Whereas the mean remains near the starting level, the SD of the trajectories grows without bound. C: the same trajectories as in B, but with the addition of the HPF with a time constant (τ) of 0.5 s. The HPF causes the SD of the trajectories to remain relatively constant after roughly 2 time constants and to remain strictly bounded in time even for long periods of time.
Other Dynamic Considerations
We note that different decision-making processes could share common decision-making dynamics, for example, a high-pass filter. When true, such common dynamics would be reflected in the data, which is why we compare visual, vestibular, and speed-accuracy dynamics herein. At the same time, it is important to remember that other dynamic elements, beyond just the decision-making dynamic element focused on herein, likely contribute to decisions. For example, sensory transduction dynamics contribute to decision making, as do central processing mechanisms. (For example, see Fig. 8 of Haburcakova et al. 2012). Such dynamic elements might need to be modeled to represent the pertinent dynamics of other transduction and/or physiological/cognitive processes performed as part of the decision-making response being studied.
One reason that decision-making dynamics could be implicated to help explain yaw rotation thresholds measured as a function of frequency (Benson et al. 1989; Grabherr et al. 2008; Lim and Merfeld 2012; Valko et al. 2012) is that the transduction processes (Fernandez and Goldberg 1971) and central processing elements (e.g., Karmali and Merfeld 2012; Merfeld et al. 1993; Raphan et al. 1977; Robinson 1977b) are known (or at least believed) to demonstrate dynamics that are relatively constant over the range of frequencies where thresholds show relatively large changes with frequency (i.e., between 0.1 and 1 Hz in Fig. 4). Certainly, as noted earlier, rotation perception measured using magnitude estimation has been shown on several occasions using a variety of methods (Bertolini et al. 2011; Bronstein et al. 2008; Okada et al. 1999; Sinha et al. 2008) to have dynamics that demonstrate a broad frequency range wherein the perceptual response is constant (i.e., “velocity storage”).
This minimal impact of transduction and processing dynamics is certainly not universally true for all sensory modalities, since other dynamic elements (e.g., transduction dynamics and/or neural processing dynamics) impact the overall dynamics measured when studying decision making. Hence, one does not necessarily predict identical overall decision-making dynamics for different decision-making processes even if the decision-making element in isolation is identical across systems. As a simple extreme example, imagine that sensory transduction could be modeled as a low-pass filter with a time constant of 1 s for system A and 0.01 s for system B. When true, such transduction dynamics would impact the information signal sent to the decision-making mechanisms. Even if the two systems had identical dynamics in their decision-making element (e.g., a high-pass filter with time constant ∼0.5 s), this would lead to not-so-subtle differences in the overall measured decision-making dynamics. Specifically, the overall decision-making dynamics for sensory system A that included the relatively slow dynamic transduction processes would be predicted to be slower than for system B unless the transduction dynamics were quantitatively factored into the analysis.
Dynamic Decision Making is Not the Same as the Dynamics of Decision Making
To avoid confusion, we clearly distinguish the dynamics of decision-making (also called decision-making dynamics), which is our focus herein, from dynamic decision-making, which has been defined (Fox et al. 2013) as the process of 1) recognizing when a decision is needed, 2) determining the options, 3) establishing the relevant criteria, 4) resolving conflicts, etc. Standard examples of dynamic decision-making include firefighting, emergency medical care, sports, military command, and air traffic control. As early as 1962 (Edwards 1962), dynamic decision-making had been characterized as achieving a goal in real-time via a series of decisions that are not independent where the problem changes with time. In other words, dynamic decision-making includes the entire process of framing what is being decided as well as how to make the decision. In contrast, we have defined decision-making dynamics as the time course (or frequency response) by which each specific individual well-defined decision is made.
A collection of papers on subtopics related to dynamic decision-making has recently been published, including integrative approaches (Fox et al. 2013; Trueblood and Busemeyer 2012), preference-based decisions (Fiedler and Glöckner 2012; Krajbich et al. 2012; Wollschläger and Diederich 2012), and adaptive decision making (Dutt and Gonzalez 2012; Knox et al. 2012; Lange et al. 2012; Osman and Speekenbrink 2012; Yu and Lagnado 2012). The editorial (Usher et al. 2013) that accompanies these articles as part of this decision making collection summarizes these contributions in much greater detail than is appropriate for this review of decision-making dynamics.
Moving Forward
We want to emphasize that this review is written with an incomplete understanding of decision-making dynamics, because our understanding beyond simple integration remains rudimentary. As such, our goal in writing this review is to accelerate progress by bringing together different perspectives that, to our knowledge, have never before been gathered together. Given the state of the field, we expect some specific topics included in this review may eventually be found to be only indirectly pertinent. We hope that such inconsistencies will not detract from our central thesis that advances in our understanding of decision making will likely accrue with advances in our understanding of the dynamics of decision making.
Summary
The various signal detection and sequential analysis decision-making models (e.g., the DDM family) have contributed to our understanding of decision making. It seems likely that future progress will be enhanced by additional theoretical and experimental approaches that augment the measurements and approaches previously utilized. For example, neural recordings in animals will continue to expand our understanding of decision making; simultaneous recordings of multiple neurons relevant to a decision-making task in different brain areas could provide a large step toward our understanding of nonhuman decision-making dynamics. Advances in our understanding of human decision-making dynamics also seem likely to arise from new techniques and/or new measurements that augment traditional measures like those focused on herein. For example, human evoked response potential recordings that simultaneously include response components representing sensory information, decision making, and motor responses (e.g., Kelly and O'Connell 2013; O'Connell et al. 2012) provide great promise for future advances in our understanding of decision-making dynamics, as do recordings of confidence (e.g., Kepecs et al. 2008; Kiani and Shadlen 2009; Kunimoto et al. 2001; Ratcliff and Starns 2013; Rolls et al. 2010) with, of course, appropriate considerations (Galvin et al. 2003) depending on task specifics.
Future psychophysical experiments are likely also required. These studies should focus on perceptual decisions involving sensory systems for which we have at least an approximate understanding of peripheral/sensory dynamics such that central decision-making dynamics can adequately be distinguished on the basis of psychophysical responses (such as we suggest can be done in the vestibular system). In general, an emphasis should be placed on designing studies in which the “frequency” of the stimuli is well controlled but varies across trials or sessions. The role of phasic mechanisms (i.e., high-pass filtering) is difficult, if not impossible, to identify if all of the presented stimuli have similar frequency content or if that content is not well controlled by the experimenter. With these experimental considerations, then the appropriate application of a formal dynamics analysis could help identify the role of phasic mechanisms in the decision-making process that exist across sensory systems.
GRANTS
This work was supported by National Institute on Deafness and Other Communication Disorders Grants R01 DC04158 (to D. M. Merfeld) and R03 DC013635 (to F. Karmali) as well as National Space Biomedical Research Institute Grant NCC9-58 (to T. K. Clark).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
D.M.M., T.K.C., and F.K. prepared figures; D.M.M., T.K.C., Y.M.L., and F.K. drafted manuscript; D.M.M., T.K.C., Y.M.L., and F.K. edited and revised manuscript; D.M.M., T.K.C., Y.M.L., and F.K. approved final version of manuscript.
Appendix: Frequency Characteristics of Truncated Sinusoids
One way to understand the dynamics of physiological systems is to characterize the frequency response. Experimentally, frequency characterization often consists of measuring responses to finite-duration sinusoidal stimuli over a range of frequencies and reporting gains or thresholds as a function of frequency. For simplicity, such frequency analyses often assume infinite-duration sinusoids. In this Appendix we explore the quantitative effects of finite-duration sinusoids and the theoretic impact on measurements.
Finite duration sinusoids can be represented as the product (multiplication) of an infinite-duration sinusoid (Fig. A1A) with a square window having unity amplitude and a finite duration. The magnitude of the frequency-domain representation (determined using Fourier analysis) of the infinite-duration sinusoid is zero everywhere except for a positive impulse at frequency +f0 and a negative impulse at frequency −f0 (Fig. A1F; only positive frequencies shown). These impulses are usually represented using Dirac's delta functions, each having an area of one-half: δ(f − f0)/2 and δ(f + f0)/2. The frequency-domain representation of the square window of width T is the sinc function T: sinc (Tf) = sin (πfT)/(πf) (Fig. A1G, gray line). For our single-cycle stimuli (Fig. A1B), the window length (gray line) is one period of our acceleration stimuli (T = 1/f0), so the sinc function for single-cycle stimuli is 1/f0·sinc (f/f0) = sin (πf/f0)/(πf). Since multiplication in the time domain corresponds to convolution in the frequency domain, the frequency-domain representation of the truncated sinusoid (Fig. A1G, thick black line) is the convolution of the sinc function and the impulses. Whereas the peak frequency is near that of the infinite-duration sinusoid, the square-wave windowing causes some spreading of frequency content around the fundamental frequency. For more cycles, the window becomes larger. For example, for three cycles, the window is T = 3/f0, which corresponds to a frequency-domain sinc function 3/f0·sinc (3f/f0) = 3 sin (3πf/f0)/(πf). Thus spreading of frequency content occurs even with three, five, nine (Fig. A1, C–E, and H–J) or more cycles; no finite-duration sinusoid is immune to this effect.
Fig. A1.
Frequency characteristics of truncated sinusoids. A: temporal representation of an infinite-duration sinusoid with frequency f = 1 Hz and period T = 1 s. Acceleration is shown, but the analysis is general for any sinusoid. B–E: finite-duration sinusoids ranging between 1 and 9 cycles; these are mathematically realized by multiplying an infinite-duration sinusoid (thin black line) with a square window (gray line). F: the frequency -domain representation for an infinite-duration sinusoid has all its energy represented by impulses at +1 and −1 Hz. G–J: the square window in time corresponds to the sinc function (gray line) in frequency. Multiplication in time corresponds to convolution in frequency; convolving the impulse (thin black line) with the sinc function (gray line) yields the frequency spectrum of the finite-duration sinusoid (thick black line). These finite-duration sinusoids exhibit small but significant frequency distortions.
Fig. A2.
A: a portion of a 0.2-Hz infinite-duration sinusoid (thin gray line) and the steady-state response after application of an HPF (thick black line) with a cutoff of 0.25 Hz, corresponding to a time constant of 0.6 s. Peak output magnitude is indicated with an open circle. B and C: the same as A for 0.5 and 1 Hz, respectively. D–F: single-cycle sinusoids (thin gray line) and the result of high-pass filtering (thick black line), with peak output magnitude indicated with an asterisk. G–I: cosine bells (thin gray line), which are the integral of single-cycle sinusoids, and the result of high-pass filtering (thick black line), with peak output magnitude indicated with a filled diamond. J: gain, measured as the ratio of peak output magnitude to peak input magnitude, for infinite-duration sinusoids, single-cycle sinusoids, and cosine bells. K: the corresponding threshold for the gains shown in J.
The ultimate goal of measuring physiological frequency responses is often to characterize a filter in the brain, such as the velocity storage filter (Raphan et al. 1977; Robinson 1977) or the perceptual decision-making filter (Grabherr et al. 2008; Lim and Merfeld 2012; Soyka et al. 2011). We now describe differences in how filtering impacts truncated sinusoids in comparison to infinite-duration sinusoids. In this example, we use a first-order high-pass filter with a cutoff of 0.25 Hz (corresponding to a time constant of 0.6 s), the cutoff frequency estimated for yaw rotation threshold decision making (Lim and Merfeld, 2012). Figure A2A shows a portion of an infinite-duration 0.2-Hz sinusoid (thin gray line) and the result of high-pass filtering (thick black line). Because the sinusoid frequency is below the cutoff of the filter, the output is an attenuated sinusoid with the same frequency as the input motion and with a phase lead present. We emphasize that this is the steady-state response, which is reached after a few time constants of the filter. Less attenuation occurs at higher frequencies such as 0.5 and 1 Hz (Fig. A2, B and C), resulting in larger peak amplitudes (open circles). When the corresponding 0.2-Hz single-cycle sinusoid is filtered (Fig. A2D), the output (thick black line) is not a pure sinusoid, but its largest magnitude (asterisk) is similar to that of the filtered infinite-duration sinusoid, albeit in the negative direction. The same is true for higher frequencies (Fig. A2, E and F), although with less attenuation. In terms of a direction-recognition task, a stimulus that incorporates two equal half cycles in opposite directions is usually nonsensical for subjects to interpret. This is especially true after filtering, since the peak filtered signal occurs in the direction opposite of the initial stimulus direction, and the peak signal is the most likely cue for decision making (Lim and Merfeld 2012; Soyka et al. 2011). Velocity, rather than acceleration, has been suggested as the salient cue in many facets of vestibular (e.g., Melvill Jones and Young 1978) and visual sensation (e.g., Nakayama and Tyler 1981). Thus a stimulus in which acceleration is a single-cycle sinusoid, which after integration means that velocity is a cosine bell, is often more appropriate for direction-recognition tasks, because the cosine bell never reverses polarity. Frequency for a cosine bell is often defined as the inverse of the period of the underlying single-cycle acceleration. Filtering a cosine bell with a frequency of 0.2 Hz (Fig. A2G, thin gray line) using the high-pass filter described before (time constant of 0.6 s corresponding to a cutoff frequency of 0.25 Hz) yields a highly attenuated output (thick black line) that is almost symmetric, but with the largest magnitude (filled diamond) always in the direction of the stimulus. For higher frequencies (Fig. A2, H and I), less attenuation occurs, and the largest magnitude is clearly in the same direction as the stimulus. Whereas the DC component (i.e., the non-zero mean signal) at lower frequencies is almost completely removed by filtering, at higher frequencies it is less affected.
The peak magnitudes after filtering of the infinite-duration sinusoid (thin black line and open circles), single-cycle sinusoid (dash-dot line and asterisks), and cosine bell (thick black line and filled diamonds) over a broad range of frequencies are compared in Fig. A2J. We note that the infinite-duration sinusoid and single-cycle sinusoid have similar peak amplitudes across frequencies. However, the cosine bell differs from the sinusoids both in peak output and qualitative shape. From this we can conclude that the difference between sinusoid and cosine bell responses is not a frequency effect per se, but rather the effect of the high-pass filter on the DC offset present in the cosine bell.
If one assumes that noise is constant regardless of stimulus characteristics, the stimulus required to reach threshold is larger when the stimulus undergoes greater attenuation (Lim and Merfeld 2012). When a low-frequency stimulus is high-pass filtered, the decision variable will be highly attenuated, and a large stimulus will be required to reach threshold level (Fig. 2 in main body of this article), resulting in a higher threshold. Likewise, for a high-frequency stimulus in which little attenuation occurs, the threshold is lower. Thus the gain relationship in Fig. A2J can be used to determine the relationship between frequency and threshold shown in Fig. A2K for infinite-duration sinusoids, single-cycle sinusoids, and cosine bells.
When determining filter parameters using experimental data, analysis is often easiest if one assumes that results are the responses to infinite-duration sinusoids even when the stimuli are of finite duration. Since this introduces some error (Fig. A2, J and K), techniques have been developed to determine filter parameters for cosine bell stimuli (Lim and Merfeld 2012; Soyka et al. 2011). In choosing an approach, investigators should determine whether the fitting error is large compared with intersubject, intrasubject, and measurement variability (e.g., Chaudhuri et al. 2013; Karmali et al. 2014; Valko et al. 2012).
Footnotes
Angular vestibulo-ocular reflexes are reflexive eye movements evoked by the vestibular system's semicircular canals that rotate the eyes to help compensate for head rotation.
Because the distinction between the standard drift-diffusion model and the extended drift-diffusion model is not critical to our review of dynamics, we do not expound on the differences herein. We simply note that the extended drift-diffusion model includes two added assumptions required to better fit data: 1) the drift rate for a given stimuli included variability across trials (instead of always having the same drift rate for the same stimuli), and 2) the initial value of the drift-diffusion variable was selected from a uniform distribution (instead of always starting at zero). We refer the interested reader to Bogacz et al. (2006; p. 704-705) for more details.
If the noise is assumed to be zero-mean, white Gaussian noise, the integral of this noise yields a Brownian noise random walk whose standard deviation increases unbounded with the square root of time. If the information being accumulated is constant, the integral yields a decision-variable that increases linearly with time. The ratio of these (i.e., the signal divided by the noise) determines a threshold, so under these conditions, thresholds would be expected to decrease as the square root of time in an unbounded manner, which is not what is typically found experimentally. See Speed-Accuracy Trade-Offs for references and descriptions of some relevant data.
REFERENCES
- Angelaki DE, Cullen KE. Vestibular system: the many facets of a multimodal sense. Annu Rev Neurosci 31: 125–150, 2008. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Shaikh AG, Green AM, Dickman JD. Neurons compute internal models of the physical laws of motion. Nature 430: 560–564, 2004. [DOI] [PubMed] [Google Scholar]
- Arrott AP, Young LR, Merfeld DM. Perception of linear acceleration in weightlessness. Aviat Space Environ Med 61: 319–326, 1990. [PubMed] [Google Scholar]
- Aston-Jones G, Cohen JD. Adaptive gain and the role of the locus coeruleus-norepinephrine system in optimal performance. J Comp Neurol 493: 99–110, 2005a. [DOI] [PubMed] [Google Scholar]
- Aston-Jones G, Cohen JD. An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu Rev Neurosci 28: 403–450, 2005b. [DOI] [PubMed] [Google Scholar]
- Bendat J, Piersol A. Engineering Applications of Correlation and Spectral Analysis. New York: Wiley-Interscience, 1980. [Google Scholar]
- Bendat J, Piersol A. Random Data: Analysis and Measurement Procedures. New York: Wiley-Interscience, 1971. [Google Scholar]
- Benson A, Hutt E, Brown S. Thresholds for the perception of whole body angular movement about a vertical axis. Aviat Space Environ Med 60: 205–213, 1989. [PubMed] [Google Scholar]
- Benson AJ, Spencer MB, Stott JR. Thresholds for the detection of the direction of whole-body, linear movement in the horizontal plane. Aviat Space Environ Med 57: 1088–1096, 1986. [PubMed] [Google Scholar]
- Bertolini G, Ramat S, Laurens J, Bockisch CJ, Marti S, Straumann D, Palla A. Velocity storage contribution to vestibular self-motion perception in healthy human subjects. J Neurophysiol 105: 209–223, 2011. [DOI] [PubMed] [Google Scholar]
- Bitzer S, Park H, Blankenburg F, Kiebel SJ. Perceptual decision making: drift-diffusion model is equivalent to a Bayesian model. Front Hum Neurosci 8: 102, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogacz R. Optimal decision-making theories: linking neurobiology with behaviour. Trends Cogn Sci 11: 118–125, 2007. [DOI] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol Rev 113: 700–765, 2006. [DOI] [PubMed] [Google Scholar]
- Borah J, Young L, Curry R. Optimal estimator model for human spatial orientation. Ann NY Acad Sci 545: 51–73, 1988. [DOI] [PubMed] [Google Scholar]
- Boucher L, Palmeri TJ, Logan GD, Schall JD. Inhibitory control in mind and brain: an interactive race model of countermanding saccades. Psychol Rev 114: 376–397, 2007. [DOI] [PubMed] [Google Scholar]
- Britten KH, Shadlen MN, Newsome WT, Movshon JA. The analysis of visual motion: a comparison of neuronal and psychophysical performance. J Neurosci 12: 4745–4765, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bronstein AM, Grunfeld EA, Faldon M, Okada T. Reduced self-motion perception in patients with midline cerebellar lesions. Neuroreport 19: 691–693, 2008. [DOI] [PubMed] [Google Scholar]
- Brunton BW, Botvinick MM, Brody CD. Rats and humans can optimally accumulate evidence for decision-making. Science 340: 95–98, 2013. [DOI] [PubMed] [Google Scholar]
- Burbeck SL, Luce RD. Evidence from auditory simple reaction times for both change and level detectors. Percept Psychophys 32: 117–133, 1982. [DOI] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychol Rev 100: 432–459, 1993. [DOI] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Fundamental derivations from decision field theory. Math Soc Sci 23: 255–282, 1992. [Google Scholar]
- Butler JS, Smith ST, Campos JL, Bulthoff HH. Bayesian integration of visual and vestibular signals for heading. J Vis 10: 23, 2010. [DOI] [PubMed] [Google Scholar]
- Carpenter RH, Reddi BA, Anderson AJ. A simple two-stage model predicts response time distributions. J Physiol 587: 4051–4062, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter RH, Williams ML. Neural computation of log likelihood in control of saccadic eye-movements. Nature 377: 59–62, 1995. [DOI] [PubMed] [Google Scholar]
- Chaudhuri SE, Karmali F, Merfeld DM. Whole body motion-detection tasks can yield much lower thresholds than direction-recognition tasks: implications for the role of vibration. J Neurophysiol 110: 2764–2772, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland AK, Kiani R, Shadlen MN. Decision-making with multiple alternatives. Nat Neurosci 11: 693–702, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark TK, Newman MC, Oman CM, Merfeld DM, Young LR. Human perceptual overestimation of whole-body roll tilt in hyper-gravity. J Neurophysiol 113: 2062–2077, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coniglio AJ, Crane BT. Human yaw rotation aftereffects with brief duration rotations are inconsistent with velocity storage. J Assoc Res Otolaryngol 15: 305–3017, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett AT. Retrieval dynamics for rote and visual image mnemonics. J Verbal Learning Verbal Behav 16: 233–246, 1977. [Google Scholar]
- Corbett AT, Wickelgren WA. Semantic memory retrieval: analysis by speed accuracy tradeoff functions. Q J Exp Psychol 30: 1–15, 1978. [DOI] [PubMed] [Google Scholar]
- Cornsweet T. Visual Perception. New York: Academic, 1970. [Google Scholar]
- Crane BT. Fore-aft translation aftereffects. Exp Brain Res 219: 477–487, 2012a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane BT. Roll aftereffects: influence of tilt and inter-stimulus interval. Exp Brain Res 223: 89–98, 2012b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de la Malla C, López-Moliner J. Detection of radial motion depends on spatial displacement. Vision Res 50: 1035–1040, 2010. [DOI] [PubMed] [Google Scholar]
- de Winkel KN, Weesie J, Werkhoven PJ, Groen EL. Integration of visual and inertial cues in perceived heading of self-motion. J Vis 10: 1, 2010. [DOI] [PubMed] [Google Scholar]
- Ditterich J. Stochastic models of decisions about motion direction: behavior and physiology. Neural Netw 19: 981–1012, 2006. [DOI] [PubMed] [Google Scholar]
- Dosher BA. The retrieval of sentences from memory: a speed-accuracy study. Cogn Psychol 8: 291–310, 1976. [Google Scholar]
- Drugowitsch J, DeAngelis GC, Klier EM, Angelaki DE, Pouget A. Optimal multisensory decision-making in a reaction-time task. Elife 3: 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drugowitsch J, Moreno-Bote R, Churchland AK, Shadlen MN, Pouget A. The cost of accumulating evidence in perceptual decision making. J Neurosci 32: 3612–3628, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutt V, Gonzalez C. The role of inertia in modeling decisions from experience with instance-based learning. Front Psychol 3: 177, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards W. Dynamic decision theory and probabilistic information processings. Hum Factors 4: 59–74, 1962. [Google Scholar]
- Fechner G. Elements of Psychophysics: Volume 1, translated by Adler HE, edited by Howes DH, Boring EG. New York: Holt, 1966. [Google Scholar]
- Fernandez C, Goldberg J. Physiology of peripheral neurons innervating the otolith organs of the squirrel monkey. I. Response to static tilts and to long-duration centrifugal force. J Neurophysiol 39: 970–984, 1976. [DOI] [PubMed] [Google Scholar]
- Fernandez C, Goldberg JM. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. II. Response to sinusoidal stimulation and dynamics of peripheral vestibular system. J Neurophysiol 34: 661–675, 1971. [DOI] [PubMed] [Google Scholar]
- Fetsch CR, Deangelis GC, Angelaki DE. Visual-vestibular cue integration for heading perception: applications of optimal cue integration theory. Eur J Neurosci 31: 1721–1729, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetsch CR, Pouget A, Deangelis GC, Angelaki DE. Neural correlates of reliability-based cue weighting during multisensory integration. Nat Neurosci 15: 146–154, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetsch CR, Turner AH, DeAngelis GC, Angelaki DE. Dynamic reweighting of visual and vestibular cues during self-motion perception. J Neurosci 29: 15601–15612, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiedler S, Glöckner A. The dynamics of decision making in risky choice: an eye-tracking analysis. Front Psychol 3: 335, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox J, Cooper RP, Glasspool DW. A canonical theory of dynamic decision-making. Front Psychol 4: 150, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galvin SJ, Podd JV, Drga V, Whitmore J. Type 2 tasks in the theory of signal detectability: discrimination between correct and incorrect decisions. Psychon Bull Rev 10: 843–876, 2003. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Interval bias in 2AFC detection tasks: sorting out the artifacts. Atten Percept Psychophys 73: 2332–2352, 2011. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Shifts of the psychometric function: distinguishing bias from perceptual effects. Q J Exp Psychol (Hove) 66: 319–337, 2012. [DOI] [PubMed] [Google Scholar]
- Glasauer S. Interaction of semicircular canals and otoliths in the processing structure of the subjective zenith. Ann NY Acad Sci 656: 847–849, 1992. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci 30: 535–574, 2007. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Representation of a perceptual decision in developing oculomotor commands. Nature 404: 390–394, 2000. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. I. Resting discharge and response to constant angular accelerations. J Neurophysiol 34: 635–660, 1971. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Wilson VJ, Cullen KE, Angelaki DE, Broussard D, Büttner-Ennever J, Fukushima K, Minor L. The Vestibular System. A Sixth Sense. New York: Oxford University Press, 2011. [Google Scholar]
- Grabherr L, Nicoucar K, Mast FW, Merfeld DM. Vestibular thresholds for yaw rotation about an earth-vertical axis as a function of frequency. Exp Brain Res 186: 677–681, 2008. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Pilly PK. Temporal dynamics of decision-making during motion perception in the visual cortex. Vision Res 48: 1345–1373, 2008. [DOI] [PubMed] [Google Scholar]
- Gu Y, Angelaki DE, Deangelis GC. Neural correlates of multisensory cue integration in macaque MSTd. Nat Neurosci 11: 1201–1210, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haburcakova C, Lewis RF, Merfeld DM. Frequency dependence of vestibuloocular reflex thresholds. J Neurophysiol 107: 973–983, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks T, Kiani R, Shadlen MN. A neural mechanism of speed-accuracy tradeoff in macaque area LIP. Elife 3: e02260, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heekeren HR, Marrett S, Ungerleider LG. The neural systems that mediate human perceptual decision making. Nat Rev Neurosci 9: 467–479, 2008. [DOI] [PubMed] [Google Scholar]
- Hintzman DL, Curran T. Comparing retrieval dynamics in recognition memory and lexical decision. J Exp Psychol Gen 126: 228, 1997. [Google Scholar]
- Huk AC, Shadlen MN. Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. J Neurosci 25: 10420–10436, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurgens R, Becker W. Perception of angular displacement without landmarks: evidence for Bayesian fusion of vestibular, optokinetic, podokinesthetic, and cognitive information. Exp Brain Res 174: 528–543, 2006. [DOI] [PubMed] [Google Scholar]
- Kailath T. Linear Systems. Englewood Cliffs, NJ: Prentice-Hall, 1980. [Google Scholar]
- Kamath BY, Keller EL. A neurological integrator for the oculomotor control system. Math Biosci 30: 341–352, 1976. [Google Scholar]
- Karmali F, Lim K, Merfeld DM. Visual and vestibular perceptual thresholds each demonstrate better precision at specific frequencies and also exhibit optimal integration. J Neurophysiol 111: 2393–2403, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karmali F, Merfeld DM. A distributed, dynamic, parallel computational model: the role of noise in velocity storage. J Neurophysiol 108: 390–405, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly SP, O'Connell RG. Internal and external influences on the rate of sensory evidence accumulation in the human brain. J Neurosci 33: 19434–19441, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepecs A, Uchida N, Zariwala HA, Mainen ZF. Neural correlates, computation and behavioural impact of decision confidence. Nature 455: 227–231, 2008. [DOI] [PubMed] [Google Scholar]
- Kiani R, Hanks TD, Shadlen MN. Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J Neurosci 28: 3017–3029, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science 324: 759–764, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knox WB, Otto AR, Stone P, Love B. The nature of belief-directed exploratory choice in human decision-making. Front Psychol 2: 398, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krajbich I, Lu D, Camerer C, Rangel A. The attentional drift-diffusion model extends to simple purchasing decisions. Front Psychol 3: 193, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunimoto C, Miller J, Pashler H. Confidence and accuracy of near-threshold discrimination responses. Conscious Cogn 10: 294–340, 2001. [DOI] [PubMed] [Google Scholar]
- Lagacé-Nadon S, Allard R, Faubert J. Exploring the spatiotemporal properties of fractal rotation. J Vis 8: 3, 2009. [DOI] [PubMed] [Google Scholar]
- Laming D. Information Theory of Choice Reaction Time. New York: Willey, 1968. [Google Scholar]
- Lange ND, Thomas RP, Davelaar EJ. Temporal dynamics of hypothesis generation: the influences of data serial order, data consistency, and elicitation timing. Front Psychol 3: 215, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Droulez J. Bayesian processing of vestibular information. Biol Cybern 96: 389–404, 2007. [DOI] [PubMed] [Google Scholar]
- Lewis RF, Priesol AJ, Nicoucar K, Lim K, Merfeld DM. Abnormal motion perception in vestibular migraine. Laryngoscope 121: 1124–1125, 2011a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis RF, Priesol AJ, Nicoucar K, Lim K, Merfeld DM. Dynamic tilt thresholds are reduced in vestibular migraine. J Vestib Res 21: 323–330, 2011b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim K, Merfeld DM. Signal detection theory and vestibular perception: II. Fitting perceptual thresholds as a function of frequency. Exp Brain Res 222: 303–320, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ljung L. System Identification: Theory for the User. Englewood Cliffs, NJ: Prentice-Hall, 1987, p. 519. [Google Scholar]
- Lofvenberg J, Johansson RS. Regional differences and interindividual variability in sensitivity to vibration in the glabrous skin of the human hand. Brain Res 301: 65–72, 1984. [DOI] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection Theory: A User's Guide. Mahwah, NJ: Erlbaum, 2005. [Google Scholar]
- Macneilage PR, Ganesan N, Angelaki DE. Computational approaches to spatial orientation: from transfer functions to dynamic Bayesian inference. J Neurophysiol 100: 2981–2996, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardirossian V, Karmali F, Merfeld D. Thresholds for human perception of roll tilt motion: patterns of variability based on visual, vestibular, and mixed cues. Otol Neurotol 35: 857–860, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melvill Jones G, Milsum JH. Frequency-response analysis of central vestibular unit activity resulting from rotational stimulation of the semicircular canals. J Physiol 219: 191–215, 1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melvill Jones G, Young LR. Subjective detection of vertical acceleration: a velocity-dependent response? Acta Otolaryngol 85: 45–53, 1978. [DOI] [PubMed] [Google Scholar]
- Merfeld D. The vestibular system and our sense of equilibrium. In: Sensation & Perception. Sunderland MA: Sinauer, 2014. [Google Scholar]
- Merfeld D, Zupan L, Peterka R. Humans use internal models to estimate gravity and linear acceleration. Nature 398: 615–618, 1999. [DOI] [PubMed] [Google Scholar]
- Merfeld DM, Young L, Oman C, Shelhamer M. A multi-dimensional model of the effect of gravity on the spatial orientation of the monkey. J Vestib Res 3: 141–161, 1993. [PubMed] [Google Scholar]
- Nakayama K, Tyler CW. Psychophysical isolation of movement sensitivity by removal of familiar position cues. Vision Res 21: 427–433, 1981. [DOI] [PubMed] [Google Scholar]
- O'Connell RG, Dockree PM, Kelly SP. A supramodal accumulation-to-bound signal that determines perceptual decisions in humans. Nat Neurosci 15: 1729–1735, 2012. [DOI] [PubMed] [Google Scholar]
- Ogata K. System Dynamics (4th ed.). Upper Saddle River, NJ: Pearson Prentice Hall, 2004. [Google Scholar]
- Okada T, Grunfeld E, Shallo-Hoffmann J, Bronstein AM. Vestibular perception of angular velocity in normal subjects and in patients with congenital nystagmus. Brain 122: 1293–1303, 1999. [DOI] [PubMed] [Google Scholar]
- Oppenheim AV, Willsky AS. Signals and Systems. Upper Saddle River, NJ: Prentice-Hall, 1997. [Google Scholar]
- Osman M, Speekenbrink M. Prediction and control in a dynamic environment. Front Psychol 3: 68, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulin M, Nelson M, Bower J. Dynamics of compensatory eye movement control: an optimal estimation analysis of the vestibulo-ocular reflex. Int J Neural Syst 1: 23–29, 1989. [Google Scholar]
- Priesol AJ, Valko Y, Merfeld DM, Lewis RF. Motion perception in patients with idiopathic bilateral vestibular hypofunction. Otolaryngol Head Neck Surg 150: 1040–1042, 2014. [DOI] [PubMed] [Google Scholar]
- Purcell BA, Heitz RP, Cohen JY, Schall JD, Logan GD, Palmeri TJ. Neurally constrained modeling of perceptual decision making. Psychol Rev 117: 1113–1143, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raphan T, Matsuo V, Cohen B. Velocity storage in the vestibulo-ocular reflex arc (VOR). Exp Brain Res 35: 229–248, 1979. [DOI] [PubMed] [Google Scholar]
- Raphan T, Matsuo V, Cohen B. A velocity storage mechanism responsible for optokinetic nystagmus (OKN), optokinetic after-nystagmus (OKAN) and vestibular nystagmus. In: Control of Gaze by Brain Stem Neurons (Developments in Neuroscience, Vol. 1), edited by Baker R, Berthoz A. Amsterdam: Elsevier/North Holland Biomedical, 1977, p. 37–47. [Google Scholar]
- Ratcliff R. Modeling response signal and response time data. Cogn Psychol 53: 195–237, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychol Rev 85: 59–108, 1978. [Google Scholar]
- Ratcliff R. A theory of order relations in perceptual matching. Psychol Rev 88: 552, 1981. [Google Scholar]
- Ratcliff R, Frank MJ. Reinforcement-based decision making in corticostriatal circuits: mutual constraints by neurocomputational and diffusion models. Neural Comput 24: 1186–1229, 2012. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput 20: 873–922, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev 111: 333–367, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Starns JJ. Modeling confidence judgments, response times, and multiple choices in decision making: recognition memory and motion discrimination. Psychol Rev 120: 697–719, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Connectionist and diffusion models of reaction time. Psychol Rev 106: 261–300, 1999. [DOI] [PubMed] [Google Scholar]
- Reddi BA, Asrress KN, Carpenter RH. Accuracy, information, and response time in a saccadic decision task. J Neurophysiol 90: 3538–3546, 2003. [DOI] [PubMed] [Google Scholar]
- Reed AV. List length and the time course of recognition in immediate memory. Mem Cognit 4: 16–30, 1976. [DOI] [PubMed] [Google Scholar]
- Reed AV. Speed-accuracy trade-off in recognition memory. Science 181: 574–576, 1973. [DOI] [PubMed] [Google Scholar]
- Robinson D. Vestibular and optokinetic symbiosis: an example of explaining by modelling. In: Control of Gaze by Brain Stem Neurons (Developments in Neuroscience, Vol. 1), edited by Baker R, Berthoz A. Amsterdam: Elsevier/North-Holland Biomedical, 1977a, p. 49–58. [Google Scholar]
- Robinson DA. Linear addition of optokinetic and vestibular signals in the vestibular nucleus. Exp Brain Res 30: 447–450, 1977b. [DOI] [PubMed] [Google Scholar]
- Robinson DA. Oculomotor control signals. In: Basic Mechanisms of Ocular Motility and their Clinical Implications, edited by Lennerstrand G, Bach-y-Rita P. Oxford: Pergamon, 1975, p. 337–374. [Google Scholar]
- Roditi RE, Crane BT. Suprathreshold asymmetries in human motion perception. Exp Brain Res 219: 369–379, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolls ET, Grabenhorst F, Deco G. Decision-making, errors, and confidence in the brain. J Neurophysiol 104: 2359–2374, 2010. [DOI] [PubMed] [Google Scholar]
- Sanfey AG, Loewenstein G, McClure SM, Cohen JD. Neuroeconomics: cross-currents in research on decision-making. Trends Cogn Sci 10: 108–116, 2006. [DOI] [PubMed] [Google Scholar]
- Schouten JF, Bekker JA. Reaction time and accuracy. Acta Psychol (Amst) 27: 143–153, 1967. [DOI] [PubMed] [Google Scholar]
- Seidman SH. Translational motion perception and vestiboocular responses in the absence of non-inertial cues. Exp Brain Res 184: 13–29, 2008. [DOI] [PubMed] [Google Scholar]
- Selva P, Oman CM. Relationships between observer and Kalman Filter models for human dynamic spatial orientation. J Vestib Res 22: 69–80, 2012. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Kiani R. Decision making as a window on cognition. Neuron 80: 791–806, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shelhamer M. Nonlinear Dynamics in Physiology. River Edge, NJ: World Scientific, 2006. [Google Scholar]
- Sinha N, Zaher N, Shaikh AG, Lasker AG, Zee DS, Tarnutzer AA. Perception of self motion during and after passive rotation of the body around an earth-vertical axis. Prog Brain Res 171: 277–281, 2008. [DOI] [PubMed] [Google Scholar]
- Smith PL. Psychophysically principled models of visual simple reaction time. Psychol Rev 102: 567, 1995. [Google Scholar]
- Smith PL. Stochastic dynamic models of response time and accuracy: a foundational primer. J Math Psychol 44: 408–463, 2000. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends Neurosci 27: 161–168, 2004. [DOI] [PubMed] [Google Scholar]
- Soyka F, Giordano PR, Barnett-Cowan M, Bulthoff HH. Modeling direction discrimination thresholds for yaw rotations around an earth-vertical axis for arbitrary motion profiles. Exp Brain Res 220: 89–99, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soyka F, Robuffo Giordano P, Beykirch K, Bulthoff HH. Predicting direction detection thresholds for arbitrary translational acceleration profiles in the horizontal plane. Exp Brain Res 209: 95–107, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stankov L, Pallier G, Danthiir V, Morony S. Perceptual underconfidence: a conceptual illusion? Eur J Psychol Assess 28: 190–200, 2012. [Google Scholar]
- Stevens SS. Perceptual Magnitude and Its Judgment. New York: Academic, 1974, p. 361–387. [Google Scholar]
- Stone M. Models for choice-reaction time. Psychometrika 25: 251–260, 1960. [Google Scholar]
- Strogatz SH. Nonlinear Dynamics and Chaos. Cambridge, MA: Perseus Books, 1996. [Google Scholar]
- Sugrue LP, Corrado GS, Newsome WT. Choosing the greater of two goods: neural currencies for valuation and decision making. Nat Rev Neurosci 6: 363–375, 2005. [DOI] [PubMed] [Google Scholar]
- Swensson RG. The elusive tradeoff: speed vs accuracy in visual discrimination tasks. Percept Psychophys 12: 16–32, 1972. [Google Scholar]
- Swets J. Signal Detection Theory and Roc Analysis in Psychology and Diagnostics: Collected Papers. Mahwah, NJ: Erlbaum, 1996, p. 328. [Google Scholar]
- Swets JA. The relative operating characteristic in psychology: a technique for isolating effects of response bias finds wide use in the study of perception and cognition. Science 182: 990–1000, 1973. [DOI] [PubMed] [Google Scholar]
- Thompson JMT, Stewart HB. Nonlinear Dynamics and Chaos (2nd ed). New York: Wiley, 2002. [Google Scholar]
- Thura D, Cos I, Trung J, Cisek P. Context-dependent urgency influences speed-accuracy trade-offs in decision-making and movement execution. J Neurosci 34: 16442–16454, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trueblood JS, Busemeyer JR. A quantum probability model of causal reasoning. Front Psychol 3: 138, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsetsos K, Gao J, McClelland JL, Usher M. Using time-varying evidence to probe decision dynamics. Front Neurosci 6: 79, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychol Rev 108: 550–592, 2001. [DOI] [PubMed] [Google Scholar]
- Usher M, Tsetsos K, Lagnado DA, Yu E. Dynamics of decision-making: from evidence accumulation to preference and belief. Front Psychol 4: 758, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valko Y, Priesol AJ, Lewis R, Merfeld D. Vestibular labyrinth contributions to human whole-body motion discrimination. J Neurosci 32: 13537–13542, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Bekesy G. Similarities between hearing and skin sensations. Psychol Rev 66: 1, 1959. [DOI] [PubMed] [Google Scholar]
- Von Békésy G, Wever EG. Experiments in Hearing. New York: McGraw-Hill, 1960. [Google Scholar]
- Wickelgren WA. Speed-accuracy tradeoff and information processing dynamics. Acta Psychol (Amst) 41: 67–85, 1977. [Google Scholar]
- Wickelgren WA, Corbett AT, Dosher BA. Priming and retrieval from short-term memory: a speed accuracy trade-off analysis. J Verbal Learning Verbal Behav 19: 387–404, 1980. [Google Scholar]
- Wolfe J, Kluender K, Levi D, Bartoshuk L, Herz R, Klatzky R, Lederman S, Merfeld D. Sensation & Perception (4th ed). Sunderland, MA: Sinauer, 2014. [Google Scholar]
- Wollschläger LM, Diederich A. The 2N-ary choice tree model for N-alternative preferential choice. Front Psychol 3: 189, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young LR. Optimal estimator models for spatial orientation and vestibular nystagmus. Exp Brain Res 210: 465–476, 2011. [DOI] [PubMed] [Google Scholar]
- Yu EC, Lagnado DA. The influence of initial beliefs on judgments of probability. Front Psychol 3: 381, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zupan L, Merfeld D, Darlot C. Using sensory weighting to model the influence of canal, otolith and visual cues on spatial orientation and eye movements. Biol Cybern 86: 209–230, 2002. [DOI] [PubMed] [Google Scholar]