Slow maturation of planning in obstacle avoidance in humans

Abstract

Complex gait (e.g., obstacle avoidance) requires a higher cognitive load than simple steady-state gait, which is a more automated movement. The higher levels of the central nervous system, responsible for adjusting motor plans to complex gait, develop throughout childhood into adulthood. Therefore, we hypothesize that gait strategies in complex gait are likely to mature until adulthood as well. However, little is known about the maturation of complex gait from childhood into adolescence and adulthood. To address this issue, we investigated obstacle avoidance in forty-four 8- to 18-yr-old participants who walked at preferred speed along a 6-m walkway on which a planar obstacle (150% of step length, 1 m wide) was projected. Participants avoided the obstacle by stepping over this projection, while lower body kinematics were recorded. Results showed that step length and speed adjustments during successful obstacle avoidance were similar across all ages, even though younger children modified step width to a greater extent. Additionally, the younger children used larger maximal toe elevations and take-off distances than older children. Moreover, during unsuccessful trials, younger children deployed exaggerated take-off distances, which resulted in obstacle contact upon the consecutive heel strike. These results indicate that obstacle avoidance is not fully matured in younger children, and that the inability to plan precise foot placements is an important factor contributing to failures in obstacle avoidance.

gait is rarely unobstructed in daily life, as we need to continuously adjust to our environment, including going up and down curbs, avoiding people, making turns, and stepping over holes or puddles. While studies on unobstructed gait reveal that adult-like gait patterns exist around the age of 8 yr, it is not yet fully understood whether these mature gait patterns hold in more complex gait at that age. More specifically, studies on unobstructed gait have shown that the normalized step speed reaches adult-like levels around the age of 4 yr (Dusing and Thorpe 2007; Vaughan et al. 2003), while the temporal variability of step cycle duration seems to mature until after 7 yr (Hausdorff et al. 1999). Additionally, normalized step length and stride length develop rapidly in the first 4 years of life, remain relatively stable between 4 and 8 yr (Dusing and Thorpe 2007) and continue to develop thereafter until ∼13–15 yr (Froehle et al. 2013). Additionally, Pryde et al. (1997) found that movement times on an unobstructed straight pathway were similar for children of 5–16 yr; however, signs of immature gait emerged in younger children when the gait task became more complex. More specifically, younger children (5–11 yr) decreased their movement time on a winding pathway with obstacles compared with a similar pathway without obstacles, while older children (12–16 yr) did not. This possibly indicates persistent development of complex gait after the age of 8 yr. Moreover, Pryde et al. (1997) showed that children below 8 yr made significantly more errors compared with older children and showed more signs of overcompensation while clearing the obstacles (i.e., taking larger than necessary safety margins when crawling under or stepping over the obstacles). Therefore, Pryde et al. (1997) suggested that, during more challenging gait, higher demands are placed on motor control and sensory information processing than during unobstructed gait, and that the required cognitive abilities might not yet be fully developed in these younger children. It has indeed been shown that cortical contributions are higher during more challenging gait. For instance, Malouin et al. (2003) found that the imagery of obstacle avoidance during gait increased cortical activity compared with imagery of unobstructed gait, and Bakker et al. (2008) found increased cortical activity during motor imagery of a precision stepping paradigm. Additionally, it has been shown that the maturation of cortical structures continues until adulthood and stabilizes between ∼20 and 30 yr of age (Herting et al. 2015; Ostby et al. 2009; Raznahan et al. 2011, 2014). Thus it is likely that the sensorimotor system responsible for performance during complex gait tasks matures into adulthood as well. In accordance, a review of Quatman-Yates et al. (2012) summarized that motor control does not reach full maturity in 12- to 15-yr-old children, due to immaturity of the sensorimotor system.

Unfortunately, except for Pryde et al. (1997), only very few other studies have investigated the maturation of complex gait. McFadyen et al. (2001) were among the first to describe in detail the presence of immature muscle activation patterns in children (aged 7–9 yr) while traversing an obstacle, despite their use of adult-like lower limb coordination. More specifically, the authors found no differences for toe and hip trajectories during the obstacle-crossing step between children and adults; however, the children did decrease (or even eliminate) knee flexor power bursts and antagonistic knee extensor power preceding take off. Therefore, it was suggested that the children used these immature muscle activation patterns to generate the adult-like toe clearances. Later, Berard and Vallis (2006) investigated the approaching phase before obstacle crossing, in addition to the actual obstacle-crossing step. They found that children took wider steps during both the lead- and trail-crossing steps compared with the two preceding steps, while adults held consistent step widths throughout the obstacle avoidance task. In contrast, no differences between children and adults were reported for the adjustments made to step length and step speed. To explain these results, Berard and Vallis (2006) proposed that the children increased the step width as part of a “squaring-up” strategy, while step length and speed were part of a cautious strategy that is similarly deployed by children and adults. The purpose of the “squaring-up” strategy, as deployed by children, is to increase the medial-lateral base of support to improve medial-lateral stability just prior to obstacle crossing. Additionally, Berard and Vallis (2006) investigated the lower limb control during obstacle crossing in more detail by examining take-off distance, landing distance and toe clearances. They reported that children used more variable take-off distances between different obstacle conditions (1 or 2 obstacles), and that they used larger lead toe clearances which reached peak height further from the anterior edge of the obstacle [horizontal toe displacement at apex (HDA)] than adults did. Taken together, the results of Berard and Vallis (2006) suggest that children used a more cautious strategy by adjusting their gait pattern to gain stability, but also by increasing the distance between the obstacle and their feet when crossing it to prevent tripping, while adults deployed a more consistent strategy with fewer adjustments to their preferred gait pattern. In summary, these studies of McFadyen et al. (2001) and Berard and Vallis (2006) confirm the existence of immature avoidance strategies in complex gait in children aged 7–9 yr, which cannot solely be explained by anthropometrics (e.g., leg length).

Thus, while maturation of unobstructed overground gait is well investigated, the continuous development of complex gait from childhood into adulthood is less well understood. However, such information would be useful for determining the effectiveness of therapies on restoring gait in both unobstructed and more complex environments in children with neuromotor disabilities. For example, children with a (mild) traumatic brain injury who restored their normal gait pattern might still experience persistent difficulties when navigating through more complex environments (Chiu et al. 2013; Katz-Leurer et al. 2011a, 2011b; McFadyen et al. 2009). Therefore, the aim of the present study was to elucidate the development of complex gait in a healthy population of children from 8 to 18 yr old, particularly regarding obstacle avoidance. Previously, Heijnen et al. (2012) showed the importance of studying both successful and unsuccessful trials to elucidate what factors lead to incidental failures. To identify these factors in our population, we assessed avoidance behavior over a virtual planar obstacle during both successful and unsuccessful obstacle avoidance trials. Moraes and Patla (2006) previously compared the use of a virtual planar obstacle and a real planar obstacle and confirmed that they provoked similar avoidance strategies regarding foot placements.

In accordance to the findings of Berard and Vallis (2006), we expected that step width of the step prior to the obstacle and the crossing step itself would mature slowly into adolescence. This would result in greater step width adjustments in younger children than in older children, while step length and speed would already be more consistent at younger ages. Additionally, we expected that younger children would prefer to create more space between their feet and the virtual obstacle, to decrease the risk of obstacle contact. Therefore, they would likely deploy larger take-off and landing distances, possibly resulting in obstacle contact in unsuccessful trials.

METHODS

Participants

Forty-four healthy children (age range 8 yr 6 mo to 18 yr 7 mo, height 1.22–1.98 m, 19 females), without any self-reported neurological or musculoskeletal problems, participated in this study. Visual acuity was tested using the Freiburg Vision Test (Bach 1996, 2007) and was on average 1.57 ± 0.40 visual acuity. Stereopsis was on average 40.34 ± 32.22 arcsec (Randot Stereotest, Stereo Optical). Detailed demographics regarding leg length and hip width can be found in Table 1.

Table 1.

Descriptive summary measures of the participant demographics

	Age, yr	Visual Acuity	Stereopsis, arcsec	Leg Length, mm	Height, mm	Hip Width, mm	%Unsuccessful Obstacle Trials
Means (SD)	14.19 (2.68)	1.57 (0.40)	40.34 (32.22)	891 (90)	1,657.5 (151)	229 (28)	22.4 (22)
Range	8.64–18.67	0.25–2.00	20–200	650–1,080	1,220–1,980	177–299	0–100

Total no. of participants = 44 (19 females).

Parents of all participants, and participants 12 yr of age and older, gave their written, informed consent. The experimental protocol was approved by the local ethics committee in accordance with the guidelines of the Declaration of Helsinki.

Experimental Protocol

In this experiment, two conditions were assessed: an obstacle gait condition (OBS) and an unobstructed gait condition [i.e., no obstacle (NO)], of which 10 trials were performed each. The conditions were presented in randomized order to prevent learning effects. Before the start of the experiment, participants familiarized themselves with the task setup. Participants wore comfortable, flat-soled shoes and walked at self-selected speed along a 6 × 1 (length by width; units of meters) walkway (Fig. 1). To control for accelerations and decelerations during the start and end of each trial, walking started at 2 m before the origin of the walkway and stopped 2 m after the walkway. Participants were instructed to maintain a constant speed throughout the experiment and to avoid stepping on a virtual planar obstacle in the OBS condition.

Fig. 1.

Experimental setup. A virtual obstacle (150% of step length) was projected on a black walkway (6 × 1 m, length by width) at a distance of 5 step lengths. Walking started (black dotted line) and ended at 2 m from the walkway. The obstacle appeared when the participant was at 1 m from the walkway (gray dotted line). Steps that were analyzed separately were obstacle (Obs)−2, Obs−1, Cross, Obs+1, and Obs+2.

Subsequently, the average step length (horizontal distance between the heel markers on consecutive steps; also see below) of three baseline NO trials was obtained to calculate the obstacle's position and depth. This virtual planar obstacle (a red rectangle) was projected (Hitachi CP-A100 projector) at approximately 5× the step length from the beginning of the walkway. The width of the obstacle was 1 m by default (covering the width of the walkway), while the obstacle length (1.5× step length − 1× foot length) forced the participants to cross it with at least 150% of their step length.

The projection of the obstacle started when the participant was at 1 m from the walkway to prevent motor or visual planning before the trial started. Only the steps on the walkway were analyzed. Lower body three-dimensional kinematics were recorded using a 16-marker lower body plugin gait model, with 10 infrared cameras sampling at 150 samples/s (Vicon Nexus version 1.8.5).

Participants were not explicitly informed about whether or not they made an error by stepping onto the obstacle to prevent overcompensation in the subsequent trials, which were previously shown to emerge after failures during three-dimensional obstacle avoidance (Heijnen et al. 2012). Lighting in the test room was kept constant during the entire experiment. In between trials, breaks were allowed to prevent fatigue and to improve attention.

Data Processing

Step speed, step length and step width.

Steps were based on subsequent heel strikes of the two feet, which were identified when the vertical velocity of the toe markers (m/s) reached their local minima (Pijnappels et al. 2001). Subsequently, the horizontal distance between the x- and y-coordinates of the heel markers on consecutive heel strikes defined the step length (x) and step width (y), respectively. Given that anthropometrics influence gait characteristics (Froehle et al. 2013; Hof 1996; Moosabhoy and Gard 2006), we normalized the step length (nSL) to leg length (step length/distance between the trochanter and medial malleolus) and the step width (nSW) to hip width (step width/bicristal breadth). Furthermore, normalized step speed (nSS) was expressed as the dimensionless Froude number (Hof 1996). According to the methods of Hof (1996), we calculated this Froude number by dividing the nonnormalized step speed (nonnormalized step length divided by the time between subsequent heel strikes) by the square root of g (acceleration of gravity) times leg length.

To assess the adjustments made to the preferred gait pattern in the OBS condition, we calculated the “absolute deviation from preferred gait” (DP) for each gait variable (i.e., nSL, nSW or nSS) by DP_X = mean |X_NO − X_OBS|, in which X is a given gait variable measured in the NO trials or the OBS trials. Similar, but not identical, measures were previously used by Nordin et al. (2010) to detect dual-task costs by subtracting the gait measures during a single task from those during a dual task.

For the NO condition, the characteristics of all steps (i.e., nSL, nSW and nSS) were averaged over all trials. For the OBS condition, we categorized the steps into five individual steps, Obs−2, Obs−1, Cross, Obs+1 and Obs+2 (Fig. 1), and averaged the characteristics per step over all trials. This method was previously used by Lowrey et al. (2007), who examined anticipatory gait adjustments during obstacle avoidance, which are likely to emerge two steps prior to obstacle avoidance (Vallis and McFadyen 2005).

Take-off distance, landing distance and toe elevation.

To evaluate the ability to precisely plan foot placements, crucial to prevent obstacle contact, we evaluated the foot placements in closest proximity of the obstacle, namely the take-off distance of the trailing limb (TO_TRAIL) and the landing distance of the leading limb (LA_LEAD), which were previously used to examine obstacle avoidance strategies (Chen et al. 1991; Weerdesteyn et al. 2008). The take-off distance of the leading limb and the landing distance of the trailing limb were not individually assessed, as these did not directly reflect precision control of the lower limb, and because possible age-related effects on these distances were already captured by evaluating the step lengths of Obs−1 and Obs+1. The TO_TRAIL was defined as the horizontal distance between the heel marker of the trailing limb + foot length and the anterior edge of the obstacle, while LA_LEAD was defined as the distance between the heel marker of the leading limb and the posterior edge of the obstacle. Take-off distance and landing distance were normalized to leg length (nTO_TRAIL and nLA_LEAD), since a closer look into our data revealed a significant partial correlation between leg length and TO_TRAIL in successful trials when corrected for age (r = 0.437, P = 0.004).

Additionally, although a planar obstacle was used, it was considered informative to also analyze the toe elevation from the floor, as it could indirectly provide information about trajectory control of the lower limb during obstacle avoidance. Toe elevation was defined as the maximal vertical elevation from the ground of the toe marker during the crossing step over the planar obstacle, after subtracting the vertical position of this marker during a static stance trial. We subsequently normalized maximal toe elevation to leg length for all trials (nTE_LEAD and nTE_TRAIL, respectively) to eliminate possible leg length-related effects from this data. Additionally, we calculated when the peak toe elevation was reached with regard to the anterior edge of the obstacle (HDA; adapted from Berard and Vallis 2006). By setting the anterior edge of the obstacle at 0%, and the posterior edge at 100%, we determined when the peak toe elevation occurred; e.g., when the obstacle was halfway, the HDA was 50%, while a HDA of 120% indicated that this peak toe elevation appeared at 20% of the obstacle length behind its posterior edge.

Successful and unsuccessful OBS trials.

OBS trials were divided into successful and unsuccessful trials. In unsuccessful trials, either the TO_TRAIL (nTO_TRAIL), the LA_LEAD (nLA_LEAD), or both, were equal to or smaller than 0, indicating a step onto the obstacle. For some participants, we experienced data loss due to marker invisibility or technical issues, and, additionally, not all participants performed an equal amount of unsuccessful trials. Table 1 provides an overview of the averaged percentage of unsuccessful trials in the OBS condition.

Statistical Analyses

Unobstructed gait.

For the NO condition, we evaluated the age-related effects on the general gait characteristics by performing separate univariate analyses of covariance (ANCOVAs) on the dependent variables nSL, nSW and nSS with covariate age.

Age-related success of obstacle avoidance and potential learning effects.

For the OBS condition, we verified whether the number of unsuccessful trials was the same for all ages. Hereto, we performed a univariate ANCOVA on error percentage with age as covariate. This was required to support the separate analyses of unsuccessful and successful OBS trials on age-related gait adjustments. Next, we assessed possible learning effects between successive OBS trials. Hereto, we performed a generalized estimation equation model with covariate trial number and five-level factor steps (Obs−2, Obs−1, Cross, Obs+1, Obs+2) with exchangeable correlation matrix, on the nSL, nSW and nSS of successful trials. This was done to verify whether we could average the variables of interest over all trials, without it being biased by learning-related effects.

Adjustments in spatiotemporal gait characteristics during obstacle avoidance.

Subsequently, we investigated whether gait pattern adjustments during successful or unsuccessful OBS trials were age dependent. To this end, we performed a repeated-measures ANCOVA on the dependent variables DP of nSL (DPnSL), nSW (DPnSW) and nSS (DPnSS), using the five-level repeated factor steps (Obs−2, Obs−1, Cross, Obs+1, Obs+2) and covariate age.

Lower limb control during obstacle avoidance.

Next, to assess age-dependent foot placement accuracy around the obstacle and limb trajectory during the crossing step, we performed a univariate ANCOVA on the dependent variable nTO_TRAIL with covariate age. Additionally, we performed a similar analysis on the dependent variable nLA_LEAD with two covariates, age and nTO_TRAIL. Similarly, we assessed the dependent variables nTE_LEAD and nTE_TRAIL and the HDA of the leading and trailing limb, with covariates age and take-off distance of the ipsilateral limb.

Greenhouse-Geisser corrections for assumptions of sphericity were used when needed. All statistical tests were performed using SPSS (IBM SPSS Statistics for Windows, version 22.0. IBM, Armonk, NY), and effects were reported as significant at P < 0.05.

RESULTS

Unobstructed Gait

First, we evaluated the gait characteristics during normal, unobstructed gait. Here, neither nSL [F_(1,42) = 1.38, P = 0.247] nor nSW [F_(1,42) = 3.68, P = 0.062] revealed any developmental changes between 8 and 18 yr. However, older children did walk faster compared with younger children in this condition [F_(1,42) = 11.57, P = 0.001, r = 0.46]. See Table 2.

Table 2.

F-values (significance) for main and interaction effects of age and steps

	Age	Steps	Age × Steps
Unobstructed gait
Normalized step width	3.68 (0.062)
Normalized step length	1.38 (0.247)
Normalized step speed	11.57 (0.001)†
Obstacle successful
DP step width	11.95 (0.001)†	7.74 (<.001)†	3.86 (0.020)*
DP step length	2.37 (0.131)	35.61 (<.001)†	2.28 (0.082)
DP step speed	0.086 (0.770)	0.857 (0.439)	2.37 (0.092)
Obstacle unsuccessful
DP step width	2.54 (0.121)	2.84 (0.055)	1.43 (0.244)
DP step length	4.67 (0.039)*	18.99 (<.001)†	2.11 (0.116)
DP step speed	0.098 (0.756)	1.771 (0.172)	2.115 (0.121)

The statistics are depicted for the gait characteristics normalized step width, step length, and step speed in the unobstructed condition, and the deviation from preferred gait (DP) in the obstacle condition.

^*P < 0.05.

^†P < 0.005.

Obstructed Gait: Validating Our Approach

Second, to validate our approach to analyze the successful trials separately from the unsuccessful trials, without the impact of any a priori grouping effects of age, we assessed whether age affected the distribution of unsuccessful and successful trials in our population.

When the obstacle avoidance was unsuccessful, either the trailing take-off distance (19% of all unsuccessful trials), the leading landing distance (78%) or both (2%) were too small, resulting in stepping onto the obstacle. This distribution was similar for all ages, i.e., younger children did not contact the obstacle more often with their leading limb than older children did [F_(1,30) = 3.15, P = 0.086]. Additionally, the total percentage of successful trials was evenly distributed among all ages [F_(1,42) = 2.51, P = 0.121]. Thus this allowed for individual evaluation of successful and unsuccessful trials, without it being affected by a priori age-biased grouping effects.

Furthermore, we averaged the data of all successful trials and of all unsuccessful trials, since no learning-related improvements were found between consecutive trials for nSL [Wald χ² = 0.30, degrees of freedom (df) = 1, P = 0.583], nSW (Wald χ² = 1.25, df = 1, P = 0.264), or nSS (Wald χ² = 3.31, df = 1, P = 0.069).

Obstructed Gait: Step Width, Length and Speed Adjustments

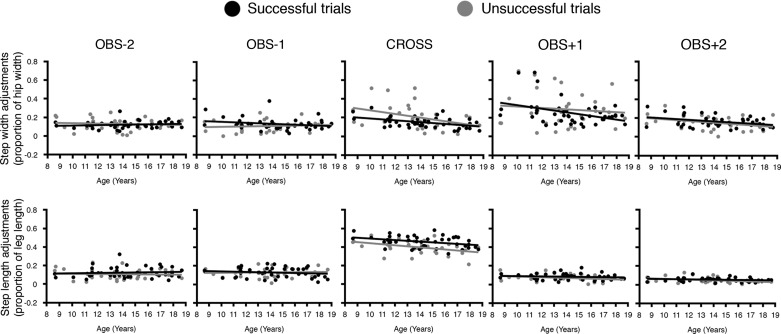
Subsequently, we evaluated the adjustments made to preferred gait characteristics during the OBS condition, which are shown in Fig. 2 and Table 2.

Fig. 2.

The absolute deviation from the preferred gait pattern (DP) for normalized step width (top) and normalized step length (bottom).

Step width adjustments.

In successful trials, all participants changed their DPnSW between consecutive steps, regardless of their age [F_(2.30,94.46) = 7.74, P < 0.001]. More specifically, contrast showed that all participants adjusted their step width less in Obs−2 (mean (± SD) = 0.12 ± 0.038) than in Obs−1 (mean = 0.13 ± 0.062) [F_(1,41) = 5.59, P = 0.023], less in Cross (mean = 0.15 ± 0.057) than Obs+1 (mean = 0.25 ± 0.131) [F_(1,41) = 5.53, P = 0.024], but adjusted their step width more in Obs+1 compared with Obs+2 (mean = 0.16 ± 0.06) [F_(1,41) = 5.56, P = 0.023]. However, although all participants adjusted their step widths between steps, the size of these step width adjustments within a step significantly depended on the participant's age [F_(1,41) = 11.95, P = 0.001], i.e., younger children made larger adjustments to preferred step width than older children did in the Cross (r = −0.45, P = 0.002), Obs+1 (r = −0.388, P = 0.010) and Obs+2 step (r = −0.352, P = 0.021). Additionally, an interaction effect existed between age and steps [F_(2.30,94.46) = 3.86, P = 0.020], indicating that, while the DPnSW increased with age in the Obs−2 step, it decreased with age in the Obs−1 step [F_(1,41) = 4.86, P = 0.033]. For unsuccessful trials, however, these results were not found, as here, neither an age effect, an effect of steps, nor an interaction between the two were found for DPnSW (all P > 0.055). See Table 2.

Step length adjustments.

In successful trials, all participants changed their DPnSL between consecutive steps, regardless of their age [F_{(3.07,125.82)} = 35.61, P < 0.001]. Not surprisingly, the adjustments made to preferred step length were larger in the Cross step (mean = 0.46 ± 0.061) compared with Obs−1 (mean = 0.13 ± 0.052) [F_(1,41) = 49.74, P < 0.001] and Obs+1 (mean = 0.08 ± 0.033) [F_(1,41) = 109.48, P = 0.000]. Also, the size of these adjustments in step length was similar for all ages, and no interactions were found between age and steps on DPnSL (all P > 0.082). Similarly to successful trials, also in the unsuccessful trials all participants changed their deviation from preferred step length, depending on the specific step, regardless of their age [F_(2.50,75.12) = 18.99, P = 0.001]. This was, again, due to a great adjustment of step length during the Cross step (mean = 0.40 ± 0.072) compared with Obs−1 (mean = 0.13 ± 0.050) [F_(1,30) = 27.83, P = 0.001] and Obs+1 (mean = 0.07 ± 0.037) [F_(1,30) = 42.35, P = 0.001]. However, in contrast to what was found in the successful trials, the size of these step length adjustments depended on the age of the participant [F_(1,30) = 4.67, P = 0.039], i.e., younger children made larger step length adjustments in the Cross step (r = −0.415, P = 0.018), and a similar trend was detected in Obs+2 (r = −0.348, P = 0.051). No interaction was found between age and steps in unsuccessful trials (P = 0.116). See Table 2.

Step speed adjustments.

In contrast to step width and step length, and likely due to the instructions to walk in a pace similar to preferred unobstructed walking, the DPnSS did not differ between steps or age. Additionally, there were no interactions between steps and age in successful OBS trials or in unsuccessful trials (all P > 0.092). See Table 2.

Take-Off Distance, Landing Distance and Toe Elevation During Obstacle Avoidance

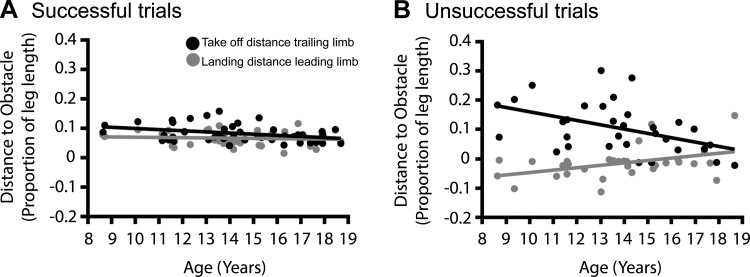
Take-off and landing distance.

We already indicated that the adjustments to step length in the cross step were larger in younger participants (see previous section), and this might be related to the inability to place the feet closer to the obstacle (Fig. 3 and Table 3). It was found that during obstacle crossings in successful trials, younger children indeed used larger TO_TRAIL compared with older children [F_(1,41) = 5.72, P = 0.021]. However, these larger take-off distances did not result in smaller leading landing distances [F_(1,40) = 2.30, P = 0.137], and the leading landing distance was the same at all ages [F_(1,40) = 0.00, P = 0.988]. Similarly, the trailing take-off distance was larger in younger children compared with their older peers during obstacle crossings in unsuccessful trials [F_(1,30) = 8.05, P = 0.008], but here, an increased trailing take-off distance was significantly correlated with a shortened leading landing distance [F_(1,29) = 8.73, P = 0.006], which resulted in obstacle contact of the leading limb in the majority of unsuccessful trials (78%). However, age did not directly affect the leading landing distance [F_(1,29) = 1.40, P = 0.25]. See Table 3.

Fig. 3.

Normalized take-off distances of the trailing limb were negatively correlated with age, whereas landing distances of the leading limb were not, in both successful trials (A) and unsuccessful trials (B).

Table 3.

F-values (significance) for main effects of age and take off distance of the trailing limb

	Age	Take-off Distance Trailing Limb
Obstacle successful
Take-off distance trailing limb	5.72 (0.021)*
Landing distance leading limb	0.00 (0.988)	2.30 (0.137)
Maximum toe elevation trailing limb	2.23 (0.144)
Maximum toe elevation leading limb	9.62 (0.004)†
Obstacle unsuccessful
Take-off distance trailing limb	8.05 (0.008)†
Landing distance leading limb	1.40 (0.247)	8.73 (0.006)†
Maximum toe elevation trailing limb	0.61 (0.440)
Maximum toe elevation leading limb	6.03 (0.020)*

The statistics are depicted for the take-off distance, landing distance, and toe elevation in the successful and unsuccessful obstacle trials.

^*P < 0.05.

^†P < 0.005.

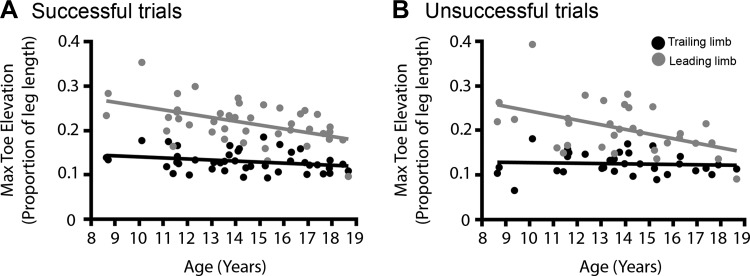
Toe elevation.

Finally, the toe elevation and the HDA of the leading limb and trailing limb during successful and unsuccessful OBS trials were investigated to determine trajectory control of the lower limb (Fig. 4 and Table 3). In both successful trials and unsuccessful trials, the nTE_LEAD decreased in older children [F_(1,40) = 9.62, P = 0.004, and F_(1,29) = 6.03, P = 0.020, respectively]. However, the toe elevation of the trailing limb was similar in all ages during both the successful trials and unsuccessful trials (all P > 0.143). Additionally, we did not find evidence that age affected the moment at which the toe elevation of either the trailing or the leading limb reached its peak during the cross step (HDA), neither in successful nor in unsuccessful trials (all P > 0.148).

Fig. 4.

Normalized maximal toe elevation of the leading limb decreased with increasing age, while the maximal toe elevation of the trailing limb did not, in both successful (A) trials and unsuccessful trials (B).

DISCUSSION

The aim of the present study was to investigate the maturation of obstacle avoidance during gait in children from 8 to 18 yr. It was observed that obstacle avoidance develops into adolescence, well beyond the ages explored in former studies. More specifically, we found that, during obstacle avoidance, younger children modified step width more so than older children, likely to improve medial-lateral stability during and after obstacle crossing. Additionally, our results showed that younger children cross the obstacle with larger lead limb toe elevations, which might be used to create a larger safety margin between themselves and the obstacle. Additionally, younger children used larger trailing take-off distances, which possibly increased the risk of obstacle contact in the subsequent heel strike. Indeed, unsuccessful trials revealed that excessively large take-off distances were followed by obstacle contact upon the next heel strike. Nevertheless, the failure rates were not higher in these younger children, but the sizes of the errors were larger (i.e., the part of the landing foot onto the obstacle).

Adjustments Prior to Obstacle Crossing

All participants in our study, regardless of their age, increasingly modified their step width in the consecutive steps from Obs−2 to Obs+1 during both successful and unsuccessful avoidance trials. Surprisingly, the highest deviation from preferred step width emerged in the Obs+1 step, which indicates the need of all participants to regain medial-lateral stability immediately after obstacle crossing. Additionally, during and after obstacle crossing, younger participants deviated more from their preferred step width than older participants did.

Why step width was adjusted in these steps may be explained by the “squaring up strategy,” as previously proposed by Berard and Vallis (2006). In accordance with our results, these authors found that participants increased their step width in anticipation of crossing an obstacle and interpreted these step width adjustments as being part of a “squaring-up” strategy, in which the medial-lateral stability is increased when the feeling of instability or the need for caution increases. It is likely that the feeling of instability emerged in our experiment as well, as the planar obstacle forced the participants to lengthen their crossing step with at least 150% of their preferred step length, therefore likely resulting in stability disruptions during and after obstacle crossing. Indeed, our results showed that the obstacle evoked larger adjustments to preferred step length in the crossing step, which were of similar size at all ages during successful trials, while being increased in younger children relative to their older peers during unsuccessful trials. These greater step-length adjustments in unsuccessful trials in younger children possibly intensified the feeling of instability, as the compensatory response of step-width adjustments during unsuccessful crossings in younger children seemed to be larger, albeit nonsignificant (P = 0.055).

In summary, the step-length, width and speed adjustments were not strikingly different during the anticipation phase before obstacle crossing between participants of different ages and successful or unsuccessful trials. Therefore, the cause of obstacle contact in the unsuccessful trials did not seem to be due to an improper anticipatory strategy before crossing the obstacle. Alternatively, failing to avoid the obstacle might have been related to improper planning of the foot placements during obstacle crossing. Therefore, the lower limb control during obstacle crossing will be discussed next.

Lower Limb Control During Obstacle Crossing

Heijnen et al. (2012) investigated the likely causes of unsuccessful obstacle avoidance in a three-dimensional obstacle paradigm in adults and found that, while 70% of failures in obstacle crossings were due to progressive decrease of the minimal trailing toe clearance, 20% of failures were due to incidental misjudgments in foot elevation, and 10% were due to misjudgment of trailing take-off distance. Toe clearance thus appears to be one of the most important variables that people control to cross a three-dimensional obstacle successfully and might, therefore, be prioritized in obstacle avoidance strategies. In our experiment, however, we did not use a three-dimensional, but a planar obstacle (i.e., without height dimensions). The toe clearance could therefore not have had a direct effect on obstacle contact. Instead, the incidental misjudgment of foot placements around the obstacle was likely the main reason for obstacle contact in our experiment. We indeed found that a misjudgment in take-off distance was often followed by too-short landing distances, resulting in obstacle contact, while in successful trials, younger children already deployed larger take-off distances than older children, but this did not yet lead to obstacle contact. Similarly, other studies have reported such misjudgments in foot placements around the obstacle as an important cause of failure in adults and elderly during three-dimensional obstacle avoidance trials (Chen et al. 1991; Chou and Draganich 1998; Patla and Greig 2006; Weerdesteyn et al. 2008). One might argue that the age-related differences in take-off and landing distances are a result of differences in preferred step length, as Froehle et al. (2013) found that immature walkers took relatively longer steps than mature walkers did. However, we controlled for this by adjusted the obstacle's size to 150% of individual preferred step length. Additionally, we did not find any indication of such an age-related difference in nSL in the NO condition, nor did we find age-related differences in the size of step length adjustments during successful and unsuccessful OBS trials in the approaching phase. We, therefore, believe that, in our population, the effect of the preferred step length on take-off and landing distances does not interfere with our interpretations.

As accurate foot placements require great planning skills (Smid and den Otter 2013), preferably with online visual information (Lee et al. 1982; Patla and Greig 2006), our results provide evidence that the younger children were less skilled in planning their obstacle crossing step as their foot placements seemed immature. This idea is substantiated by Berard and Vallis (2006), who showed that foot placements of children were less consistent than those of adults when planning a more complex avoidance strategy. This indicates that, when planning behavior becomes more important, children fail to form a consistent and efficient avoidance strategy. Interestingly, literature on bimanual motor control indicates that children develop the ability to build an accurate internal model regarding upcoming motor actions throughout childhood and adolescence (Caeyenberghs et al. 2009), as well as the use of feed-forward control when time pressure increases (van Roon et al. 2008). Translating these findings to our results, this would indeed support our notion that younger children are less able to accurately plan their avoidance strategy well in advance, resulting in inadequate foot placements near the obstacle.

Why young children are less skilled in planning their avoidance strategies may be explained by the immaturity of the responsible cortical and subcortical structures, as these are developing throughout childhood into mid-adulthood (Herting et al. 2015; Ostby et al. 2009; Raznahan et al. 2011, 2014). Indeed, a review of Quatman-Yates et al. (2012) summarized the evidence that sensory integration processes in the brain are not yet fully matured around the age of 11 yr, and processes such as inhibition of previously planned motor output and the ability to accurately plan movements even mature into adulthood. Additionally, interesting parallels to our findings have been reported in animal literature (Armstrong and Marple-Horvat 1996; Beloozerova and Sirota 1993; Friel et al. 2007; Lajoie and Drew 2007), in which limb (or paw) placement accuracy and obstacle clearance were affected when the maturation of cortical structures was interrupted in cats (i.e., motor cortex), or when cortical structures were lesioned (i.e., motor cortex, parietal cortex, cerebellum), stressing the importance of these structures in obstacle avoidance behavior. As these cortical structures mature into adulthood in humans (Herting et al. 2015; Ostby et al. 2009; Raznahan et al. 2011, 2014), this might be the underlying mechanism for the changes in age-related avoidance strategies, as found in the present study.

Additionally, our results showed that younger children used larger leading toe elevations (i.e., elevation from the floor) during obstacle crossing than their older peers in both successful and unsuccessful OBS trials. Similar results were found by Berard and Vallis (2006), who showed that children increased their leading limb toe clearances compared with adults when crossing a three-dimensional obstacle. However, in our experiment, inadequate foot elevation could not be the direct cause of obstacle contact, since we used a virtual planar obstacle. Therefore, these greater toe elevations in younger children might not be the result of a strategy to avoid the obstacle.

A possible interpretation is that higher toe elevation would result from the hip, knee and/or ankle flexion required to move the limb forward quickly to achieve the greater horizontal distance required. Younger children may lift the limb higher due to overcompensation or perhaps the lower leg mass results in greater flexion. Greater flexion will reduce the inertial load and increase ability to move the limb quickly, so they could be overcompensating, or this may be required to move the limb with the less mature motor system. This interpretation questions whether the biomechanical constraints posed by the obstacle were different for younger, smaller children, than for older, larger children/adolescents. However, we adjusted the obstacle length to 150% of the individual's preferred step length, as measured in three baseline unobstructed level walking trials. With this, we attempted to evoke similar biomechanical changes in all participants, irrespective of the leg lengths. Indeed, we did not find any differences in step-length adjustments during the successful obstacle crossing steps, nor did we find age-related differences in the moment at which the maximal toe elevation was reached relative to the anterior “edge” of the obstacle (HDA). This indicates that the toe trajectory during the leading crossing step was not altered in younger children. Additionally, we analyzed whether the relative adaptations in step speed during the crossing step compared with the preferred step speed were the same in all participants. We did not find differences between younger and older participants in their step speed adjustments. Therefore, the available evidence does not support the notion that the increased leading toe elevation was solely used to overcome the length of the obstacle as part of some kind of overcompensation.

Another possibility is that the lower leg mass results in greater flexion, resulting in greater toe elevation. This would predict that the mass of the lower leg is proportionally smaller in younger children. However, to our knowledge, there are no indications for this in the literature. A study of Sheehan and Gottschall (2014) did show that a longer shank length decreases the relative step length during level walking in healthy adults. However, to control for possible effects of leg length-related differences, we normalized the obstacle length to 150% of the preferred step length, and we normalized toe elevation to leg length.

This leaves open a third possibility, namely that the increased toe elevation is the result of a larger safety margin used by the young children. Since not touching the floor was the objective, it may have appeared safer for the children to produce higher toe elevations than strictly needed. Evidence for this hypothesis comes from work of Berard and Vallis (2006), who similarly found higher toe clearances in children compared with adults when crossing multiple three-dimensional obstacles. Furthermore, Michel et al. (2010) showed that, while both children of ages 9–12 yr and adults decrease their foot clearance during repeated presentations of an obstacle, the younger children of ages 6–8 yr were not capable of improving their foot clearance. In other words, they produced higher clearances than needed. Additionally, Heijnen et al. (2012) showed that minimal toe clearance progressively decreases in successive obstacle trials in adults, but, after an obstacle hit, toe clearances were again enlarged to increase the safety margin and decrease the risk of contacting the obstacle again. Considering this evidence and our efforts to prevent interindividual obstacle differences due to leg length, we think that the increased leading maximal toe elevation in our younger participants is likely due to an age-specific strategy to overcome the planar obstacle with a large safety margin.

Another possible contributing factor that could explain the increased toe elevation in younger children might be the maturity of the neuromotor system. As animal studies have previously revealed that lesions in the posterior parietal cortex could influence obstacle clearance in cats (Drew et al. 2008; Lajoie and Drew 2007), an immature cortex in humans could possibly lead to different clearance strategies as well. Although speculative, this might be a possible explanation for why younger children took crossing steps with higher toe elevations than older children. Younger children might have used a more generic avoidance strategy, which is not yet customized to the specific obstacle needs, whereas older, more experiences children are capable of adjusting their strategy to the requirements of the specific obstacle dimensions.

Limitations

While many studies on obstacle avoidance have used three-dimensional obstacles to investigate anticipatory strategies, we and others (Chen et al. 1991) utilized a virtual planar obstacle without height dimension. This was justified by the observation of Moraes and Patla (2006), who showed that the obstacle avoidance strategies were quite comparable between real and virtual obstacles, especially regarding the alternate foot placement strategies compared with a real obstacle. Nevertheless, when comparing the avoidance strategies found in our study to those found in studies which used three-dimensional obstacles (Berard and Vallis 2006; McFadyen et al. 2001), caution should still be taken considering that small differences in strategies might be evoked by the two distinctive obstacle types. Using this paradigm, however, we could specifically investigate the planning and selection of foot placements during obstacle avoidance, while being able to easily and efficiently adjust the obstacle size to the individuals step length. Additionally, to calculate the HDA, we used a slightly different approach than Berard and Vallis (2006). While Berard and Vallis (2006) calculated the HDA as the absolute distance between the obstacle and the point at which peak height was reached, we calculated the HDA as the actual distance (as a percentage of obstacle length, including positive and negative directions) between the peak toe elevation and the beginning of the obstacle. This possibly explains the discrepancy found between the results of Berard and Vallis (2006), who showed that children reached their maximal toe clearance further away from the obstacle's anterior edge than adults, while we did not find any age-related effects for this particular measure.

Conclusions

In conclusion, we have found that the ability to avoid obstacles continues to develop in children between 8 and 18 yr of age, specifically regarding the fine tuning of foot placements near the obstacle and the maintenance of medial-lateral stability during obstacle crossing. The immaturity of the avoidance behavior was particularly clear in unsuccessful trials, and we, therefore, would like to stress the importance of investigating unsuccessful in addition to successful trials to specifically identify the factors leading to failures. Analogies with other literature on motor planning in children suggest that the planning during obstacle avoidance is dependent on cortical maturity. Future research should, therefore, try to elucidate the direct relation between the maturation of involved cortical and subcortical structures (and/or function thereof), on the one hand, and the avoidance strategies in complex gait in children, on the other hand.

GRANTS

This work was supported by KU Leuven Research Fund Grant (OT/11/071), Flanders Fund for Scientific Research (FWO) Grants (G.A114.11, G0721.12, G0708.14), and the Interuniversity Attraction Poles Program initiated by the Belgian Science Policy Office (P7/11), awarded to S. P. Swinnen. Furthermore, J. Duysens is the recipient of a National Council for Scientific and Technological Development visiting professorship, and S.H.A. Corporaal is supported by an aspirant fellowship of the Research Foundation-Flanders (FWO). S. M. Bruijn is supported by a VENI grant (NWO no. 451-12-041) from the Netherlands Organization for Scientific Research (NWO).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.H.A.C., S.P.S., J.D., and S.M.B. conception and design of research; S.H.A.C. performed experiments; S.H.A.C. and S.M.B. analyzed data; S.H.A.C., J.D., and S.M.B. interpreted results of experiments; S.H.A.C. prepared figures; S.H.A.C. drafted manuscript; S.H.A.C., S.P.S., J.D., and S.M.B. edited and revised manuscript; S.H.A.C., S.P.S., J.D., and S.M.B. approved final version of manuscript.