Coherent and intermittent ensemble oscillations emerge from networks of irregular spiking neurons

Abstract

Local field potential (LFP) recordings from spatially distant cortical circuits reveal episodes of coherent gamma oscillations that are intermittent, and of variable peak frequency and duration. Concurrently, single neuron spiking remains largely irregular and of low rate. The underlying potential mechanisms of this emergent network activity have long been debated. Here we reproduce such intermittent ensemble oscillations in a model network, consisting of excitatory and inhibitory model neurons with the characteristics of regular-spiking (RS) pyramidal neurons, and fast-spiking (FS) and low-threshold spiking (LTS) interneurons. We find that fluctuations in the external inputs trigger reciprocally connected and irregularly spiking RS and FS neurons in episodes of ensemble oscillations, which are terminated by the recruitment of the LTS population with concurrent accumulation of inhibitory conductance in both RS and FS neurons. The model qualitatively reproduces experimentally observed phase drift, oscillation episode duration distributions, variation in the peak frequency, and the concurrent irregular single-neuron spiking at low rate. Furthermore, consistent with previous experimental studies using optogenetic manipulation, periodic activation of FS, but not RS, model neurons causes enhancement of gamma oscillations. In addition, increasing the coupling between two model networks from low to high reveals a transition from independent intermittent oscillations to coherent intermittent oscillations. In conclusion, the model network suggests biologically plausible mechanisms for the generation of episodes of coherent intermittent ensemble oscillations with irregular spiking neurons in cortical circuits.

local field potential (LFP) recordings from cortical tissue have long revealed short epochs of periodic voltage fluctuations (Buzsáki et al. 1992; Csicsvari et al. 1999). Such recorded voltage fluctuations reflect the superposition of synchronized oscillatory local extracellular currents from spiking neurons and/or synaptic inputs within the recording volume determined by the LFP reach (Buzsáki et al. 2012; Linden et al. 2011).

The LFP oscillations are ubiquitous across different cortical areas, species, and behavioral and cognitive context (Buzsáki et al. 2013; Fries et al. 2007; Jensen et al. 2007; Prechtl 1994). Despite this diversity in origin, cortical LFP oscillations tend to share four commonly observed features. First, for the population of neurons located within the LFP recording volume of an electrode, single neuron spiking is sparse (i.e., firing rate is smaller than oscillation frequency) (Lehky et al. 2005; Rolls et al. 2004, 2006; Treves et al. 1999) and irregular, both during epochs of oscillations and in the absence of oscillations (Fries et al. 2001). Second, throughout an epoch of elevated spectral power, the phase of the oscillation is not conserved, i.e., not autocoherent (Burns et al. 2010, 2011). Third, the duration and the power spectral density (PSD) distribution of LFP oscillations vary from epoch to epoch (Csicsvari et al. 1999; Xing et al. 2012), as well as for different conditions of sensory stimulation (Barbieri et al. 2014; Engel et al. 1990; Jia et al. 2011). Fourth, the fluctuating aspects of LFP oscillations covary across spatially separate cortical recording sites (Roberts et al. 2013).

The ubiquity of LFP oscillations raises the question as to what these mesoscopic emergent phenomena reveal about the underlying cortical microcircuits. In other words, what combination of biophysical ingredients of a model network can generate the four common features of emergent cortical oscillations? Numerous network models of varying levels of complexity have reproduced subsets of the listed four features of cortical LFP oscillations (Bartos et al. 2007; Buzsáki and Wang 2012; Traub and Whittington 2010). For instance, detailed model networks of irregularly and sparsely spiking neurons generated oscillations (Brunel 2000; Brunel and Hakim 1999; Brunel and Wang 2003; Geisler et al. 2005). However, these important investigations did not address intermittency and autocoherence. At a higher level of abstraction, a recurrent network consisting of one excitatory and one inhibitory node generated intermittent oscillations of variable durations and peak frequencies (Xing et al. 2012), but, by design of a rate model, these investigations did not speak to the nature of neuronal spiking. To the best of our knowledge, despite the vast literature on the mechanisms of cortical oscillations (Wang 2010), no computational model has captured simultaneously the four important features of observed cortical oscillations, i.e., irregular and sparse spiking, phase drift, epoch-to-epoch variations, and coherence across multiple networks.

Here, we propose underlying mechanisms for cortical oscillations that explain all observed features simultaneously. To this end, we investigated a model network consisting of regular-spiking (RS) pyramidal neurons, fast-spiking (FS) interneurons, low-threshold spiking (LTS) interneurons, and stochastic external inputs. With the use of biologically plausible parameters, the model network spontaneously generated intermittent epochs of activity oscillations with evolving phase, while model neurons spiked sparsely and irregularly. Durations and peak frequencies varied from epoch to epoch, but covaried for two networks with sufficient coupling.

MATERIALS AND METHODS

Model Network

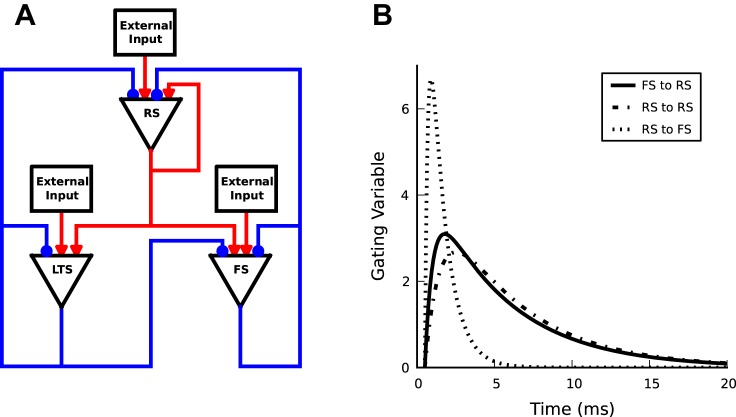
We consider a model network of 2,000 RS pyramidal neurons, 250 FS interneurons, 250 LTS interneurons and external inputs (Fig. 1A). The network structure resembles cortical feedback triads (Caudill et al. 2009). Specifically, each RS and LTS neuron can connect to all other neurons. In contrast, FS neurons can connect to other RS and FS neurons, but not to LTS neurons (Banks et al. 2000). The main differences between the two groups of interneurons, besides projecting to different targets, are 1) LTS neurons operate on much longer time scales (Banks et al. 2000; Goldberg and Yuste 2005; Silberberg and Markram 2007), and 2) LTS neurons tend not to spike as frequently as FS neurons, since they need coordinated input from RS cells (Beierlein et al. 2003; Kapfer et al. 2007). We implemented these distinctions through different synaptic time constants and leak conductances. Of the possible connections, constrained by the network structure, a subset of connections is chosen with probability, P_c, thus generating a network with sparse and random connectivity. As a result, each model neuron obtains on average 400 excitatory and 100 inhibitory connections from within the network. In addition, each neuron has 800 excitatory connections from private external inputs with a given total firing rate (Brunel and Wang 2003). Membrane potentials and action potentials of model neurons of each type are simulated as leaky integrate-and-fire neurons, with the subthreshold dynamics of the membrane potential V_i of neuron i given by C[dV_i(t)/dt] = −I_ext − I_leak − I_syn, where C is the membrane capacitance, I_leak = g_leak(V − V_leak) is the leak current (g_leak is leak conductance), and I_syn = g_synS(t)(V − V_syn) is the synaptic current due to excitatory and inhibitory inputs from within the network (g_syn is synaptic conductance and S is the gating variable) (Table 1). The external excitatory input, I_ext, is conductance based and has the same dynamics as the excitatory synapses of connections within the network. The synaptic gating variable S(t) = [τ_m/(τ_d − τ_r)](exp{−[(t − τ_l)/τ_d]} − exp{−[(t − τ_l)/τ_r]}) describes the time course of synaptic conductance change (Fig. 1B). The normalization constant ensures that the time integral of the synaptic gating variable equals the membrane time constant, and thus varying the synaptic time constant does not affect the time integral of the synaptic current. This normalization ensures the balance of excitation and inhibition. When the membrane potential of a neuron exceeds a threshold, the neuron fires an action potential, and the membrane potential resets and stays at the rest value for duration of the refractory period. The spike train of neuron i is given by the time series η_i(t). The numerical values in Table 2 are matched with experimental values for synaptic time scales (Angulo et al. 1999; Bartos et al. 2001; Gupta et al. 2000; Xiang et al. 1998; Zhou and Hablitz 1998) and conductances (Buhl et al. 1997; Markram et al. 1997). A model neuron receives external inputs with total firing rate of 6 and 8 kHz to RS and FS/LTS neurons. This external input can be delivered using a different number of synaptic connections. Considering 800 excitatory synaptic inputs makes each synapse to deliver an independent Poisson pulse train with mean rate of 7.5 Hz for RS and 10 Hz for FS and LTS neurons. For simplicity, the Poisson to Binomial distribution approximation is used. Synaptic conductance for external inputs is 1.75 nS for RS and 2.0 nS for FS and LTS neurons. All model parameters are defined, and their values are given in Tables 1 and 2. Simulations were performed using Euler's method with a time step of 0.05 ms. Simulations were carried out for 4 s in real time unless stated otherwise.

Fig. 1.

Model network with recurrent connections and synaptic dynamics. A: schematic representation of network structure. Each regular-spiking (RS) and low-threshold spiking (LTS) neuron can connect to all other neurons. In contrast, fast-spiking (FS) neurons can inhibit RS and FS but not LTS neurons. B: gating variable dynamics for three selected synapses. They are normalized in such a way that the area under the curve equals the membrane time constant.

Table 1.

Neuron and network properties

Parameter	Description	Value
Vleak, mV	Leakage reversal potential	−70
Vthr, mV	Threshold membrane potential	−59
Vreset, mV	Reset membrane potential	−52
VE, mV	Excitatory reversal potential	0
Vl, mV	Inhibitory reversal potential	−80
τrefE, ms	RS refractory time	2
τrefI	FS and LTS refractory time	1
τl, ms	Delay time constant	0.5
τmE, ms	Excitatory membrane time constant	20
τmI, ms	Inhibitory membrane time constant	10
CE, nF	Excitatory membrane capacitance	0.2
CI, nF	Inhibitory membrane capacitance	0.1
dt, ms	Simulation time step	0.05
t, ms	Time bin size	0.5
NRS	Number of RS pyramidals	2,000
NFS	Number of FS interneurons	250
NLTS	Number of LTS interneurons	250
Pc	Connection probability	0.2

RS, regular spiking; FS, fast spiking; LTS, low-threshold spiking.

Table 2.

Synaptic parameters

Pre/Post	RS	FS	LTS
Synaptic conductance, nS
RS	0.25	3.8	3.8
FS	0.30	4.00	4.00
LTS	0.30	0	4.00
Rise time constant, ms
RS	1.00	0.50	5.0
FS	0.20	0.50	5.0
LTS	0.20		5.0
Decay time constant, ms
RS	5	5	50
FS	1	5	50
LTS	1		50
Leakage conductance, nS	10	12.5	20

Analysis of Simulation Results

Single-neuron spike trains.

The sparseness of spiking is evaluated by comparing the distribution of single-neuron mean firing rates with the dominant frequency of the oscillation. The irregularity of spiking is evaluated via the interspike interval (ISI) distribution of the spike trains η_i(t). For a Poisson pulse train we expect an exponential decay of the ISI distribution (for ISIs larger than the refractory period) and a coefficient of variation (CV) with a value near one. The CV is defined as the SD divided by the mean ISI. For a bursting spike train, the CV can be larger than one because of two completely different time scales present in the spike train. In contrast, a regular spike train has a CV value near zero.

Synchrony.

To quantify the level of synchrony among the spike trains η_i(t) within the model network we bin the time, Δt = 0.5 ms. From the spike train of neuron i, we get the instantaneous firing rate r_i(t), i.e., the number of spikes within a time bin divided by the bin size. From this, the network instantaneous firing rate is r(t) = ${\sum }_{i=1}^N$ r_i(t). Operationally, this quantity is derived by summing the number of spikes from all neurons within a time bin. We then compare the variance var[r(t)/N] of the network instantaneous firing rate normalized by the network size against the population-averaged variance 1/N${\sum }_{i=1}^N$var[r_i(t)] of the variance of instantaneous firing rates from individual spike trains (Ginzburg and Sompolinsky 1994; Hansel and Sompolinsky 1992). Thus, we define the synchrony measure

$${\text{κ}}^2\left(N\right)=\left\{\mathrm{var}\left[\text{r}\left(t\right)/N\right]\right\}/\left\{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\mathrm{var}\left[{\text{r}}_i\left(t\right)\right]}\right\}\mathrm{.}$$

For fully synchronous spike trains this measure equals one and is independent of network size. In contrast, for asynchronous spike trains, κ(N) takes on values between zero and one and, importantly, varies linearly with the inverse of the square root of the network size, κ(N) ∼ κ(∞) + α/$\sqrt{N}$ where α is a constant (Golomb et al. 2006).

Oscillations.

We evaluate the level of oscillations in the network activity from the PSD via Fourier transform of the network instantaneous firing rate. Calculations are performed using the multitaper method (Henri and Shapley 2005; Mitra and Pesaran 1999). In general, time bins, Δt, must be much larger than the simulation time steps and much smaller than the period of the oscillations in network activity. Results are robust for time bins between 0.5 and 2 ms. To identify an episode of oscillation in network instantaneous firing rate signal, we first took the points in the time-frequency space that have at least one-half of the maximum power at any frequency between 20 and 100 Hz. Among these, points are accepted that are above three times the SD of a 5-Hz frequency band around it. Now neighboring points form an epoch. This procedure allows us to estimate the time duration and peak frequency of an oscillation episode.

Autocoherence.

Complementary to evaluating the amplitude of a frequency component, it is informative to evaluate its residual phase, which is the difference between the phase of the analyzed frequency component and the phase of a pure sinusoidal function of the same frequency. To obtain the phase of the analyzed frequency component, the network instantaneous firing rate r(t) is convolved with a Gabor filter

$$\psi \left(t;\tau ,f\right)=\frac{1}{\sigma \sqrt{2\pi }}\hspace{0.17em}\exp \left[-{\left(t-\tau \right)}^2/\left(2{\sigma }^2\right)\right]\exp \left(-j2\pi ft\right)$$

and the resulting function is Fourier transformed (j is the square root of −1 not an index)

$$G\left(\tau ,f\right)={\displaystyle {\int }_{-\infty }^{\infty }\text{ds}\hspace{0.17em}\text{r}\left(s\right)\psi \left(\text{s}-t;\tau ,f\right)=\text{R}\left(\tau \text{,}f\right)\exp \left[j\varphi \left(\tau ,f\right)\right]}\mathrm{.}$$

This “continuous Gabor transform” (Mallat 1999) yields the amplitude R(τ, f) and the phase ϕ(τ, f) of the network instantaneous firing rate r(t) in each time-frequency point. The circular variation

$$\text{CiV}\left(f\right)=1-\left|\frac{{\displaystyle {\sum }_{\tau }\text{R}\left(\tau ,f\right)\exp \left[\text{j}{\varphi }_r\left(\tau ,f\right)\right]}}{{\displaystyle {\sum }_{\tau }\text{R}\left(\tau ,f\right)}}\right|$$

where phase residual ϕ_r(τ, f) is the difference between phase of the signal and phase of a pure sinusoidal signal with that frequency, ϕ_r(τ, f) = ϕ(τ, f) − ϕ_sinusoidal(τ, f) where ϕ_sinusoidal(τ, f) = 2πf mod[τ,(1/f)]. As an example, complex Gabor transform of a pure sinusoidal (autocoherent) signal results in a circle trajectory phase portrait. Time evolution of the signal manifest itself in the circular counterclockwise rotation of the state on that circle around the origin. Subtracting ϕ_sinusoidal, which corresponds to a clockwise rotation in the reference coordinate, will result in one single point in the phase space as expected, since we started with an autocoherent signal. Circular variation (CiV) quantifies the localization of the residual phase in the phase portrait and is a criterion for the degree of autocoherence of that frequency component (Mardia 1972). The values of CiV are bounded by zero and one, with zero for the most coherent oscillation (pure sinusoidal) and one for random signals (Burns et al. 2010).

RESULTS

Overview

To gain insight into what combination of cellular and/or circuit mechanisms can generate cortical oscillations, we investigated a model network motivated by cortical neurons, synapses, and circuits. Here we focus on four important features of experimentally observed cortical oscillations: irregular and sparse spiking, intermittent network oscillations with phase drift, epoch-to-epoch variations in network oscillations, and coherence across multiple networks. The model network consists of 2,000 RS excitatory neurons, 250 FS interneurons, 250 LTS interneurons, and excitatory external inputs (Fig. 1A). Connectivity is sparse and random (see materials and methods) such that each model neuron receives on average 400 excitatory and 100 inhibitory connections from within the network, plus 800 excitatory connections from private external inputs. Each external input is simulated as an independent Poisson pulse train with mean rate of 7.5 Hz to pyramidal neurons and 10 Hz to interneurons.

Single-Neuron Spiking is Sparse, Irregular, and Asynchronous

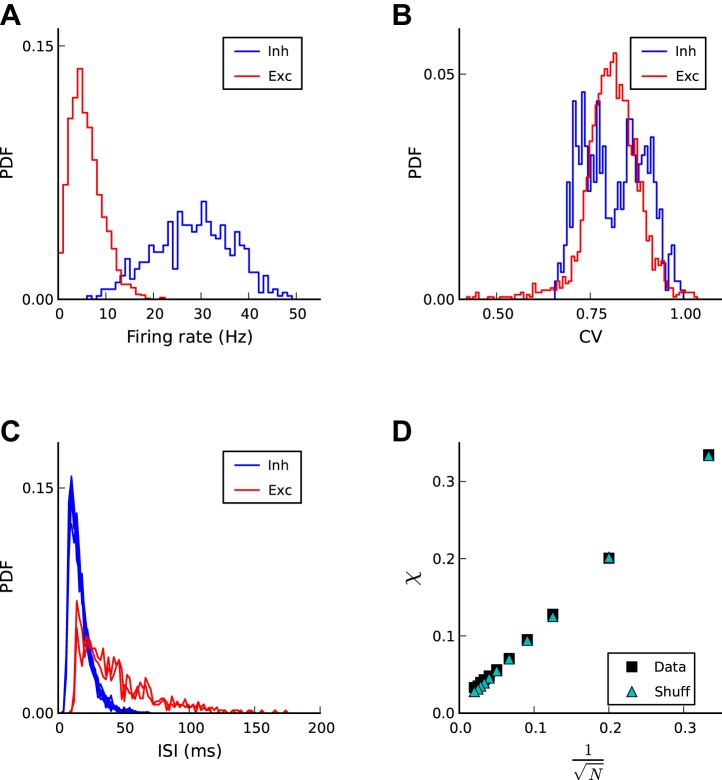
In response to the continuing external stochastic inputs and the inputs from the resulting spiking activity of other neurons from within the network, all neurons spike sparsely and irregularly (Figs. 2 and 3A). Time-averaged firing rates vary from neuron to neuron. Firing rates are distributed within the range of ∼1 and 20 Hz (mean = 6 Hz; maximum = 25 Hz) for RS excitatory neurons, whereas firing rates for inhibitory neurons range from ∼10 to 50 Hz (mean = 23 Hz for LTS and 34 Hz for FS; maximum = 50 Hz) (Fig. 2A). The CV values are distributed around slightly below one (Fig. 2B). The interspike interval distributions for all neurons decay approximately exponentially (Fig. 2C), as expected for Poisson pulse trains, thus indicating irregular spiking. To evaluate the level of correlation among the spike trains, we use the synchrony measure κ(N) (see materials and methods). This measure is defined as the ratio of the variance of the population-averaged instantaneous firing rate and the average variance of the instantaneous firing rates from individual spike trains. Simulated spike trains in our model yield values of κ(N) <1 and, importantly, scale with network size according to κ(N) ∼κ(∞) + (α/$\sqrt{N}$) (Fig. 2D). Both observations are characteristics of asynchronous spiking. This conclusion is further corroborated by the similarity of the results for network spike trains and shuffled spike trains. It is important to note, however, that the synchrony measure κ(N) is a time-averaged (total simulation time) measure and thus does not speak to transient correlations among spike trains.

Fig. 2.

Spiking is irregular and asynchronous on average. A: distribution of time-averaged firing rates for excitatory (red) and inhibitory (blue) neurons. For clarity, the distributions of inhibitory LTS and FS neurons are merged. Average firing rates are 6 Hz for RS, 23 Hz for LTS, and 34 Hz for FS neurons. B: distribution of coefficients of variation (CVs) for excitatory (red) and inhibitory (red) neurons. The mean CVs are 0.80 for RS and 0.81 for LTS and FS neurons combined. C: interspike interval (ISI) distributions for a few excitatory (red) and inhibitory (blue) neurons on the right tail of time-averaged mean rate distribution in A. D: synchrony measure κ(N) as a function of network size N. The linear increase with the inverse of the square root of the network size indicates the asynchrony of individual spike trains.

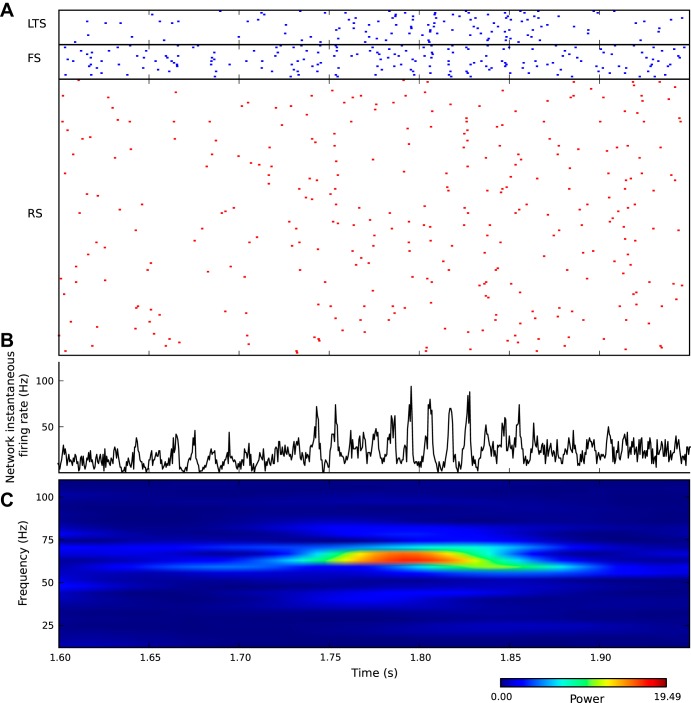
Fig. 3.

Irregular asynchronous spiking is consistent with intermittent oscillations of network activity. A: raster plots of spikes for 160 RS, 20 FS, and 20 LTS neurons, respectively. Irregular spiking for all three types of neurons is apparent by visual inspection. B: network instantaneous firing rate r(t) = ${\sum }_{i=1}^N$ r_i(t) reveals oscillations in this continuous variable. An episode of oscillation starts at around 1.75 s and lasts for about 100 ms. C: power spectrum of the network instantaneous firing rate shows an episode of elevated power between 1.75 and 1.85 s in time and around 70 Hz in frequency.

Network Oscillations Are Intermittent

To evaluate the possibility of transient epochs of oscillations, we looked beyond the individual spike trains η_i(t) (Fig. 3A) and analyzed the network instantaneous firing rate. Unlike the individual spike trains, this measure of network activity reveals significant oscillatory temporal structure (Fig. 3B). A time-resolved Fourier transform (see materials and methods) reveals elevated power in narrow frequency bands for short periods of time (Fig. 3C). Importantly, however, spiking remains sparse. Even at the highest peak in network instantaneous firing rate near 70 Hz, <5% of the neurons spiked during a given time bin (0.5 ms). Thus, visual inspection of a subset of spike trains (Fig. 3A) offers little information about epochs of network oscillations.

In contrast, the network instantaneous firing rates for the RS and FS populations of neurons (fast time scale), and the dynamics of inhibitory synaptic conductance (slow time scale), are informative about the underlying mechanisms of the population dynamics (Fig. 4). Qualitatively, the intermittent oscillations of network activity arise through the following sequence of biophysical interactions. First, stochastic fluctuations in the spike occurrence of the external inputs to the RS and FS neurons activate these groups of neurons. Second, from the thus transiently increased RS/FS activity and the recurrent interaction between RS/FS neurons, an oscillation in network activity emerges. Third, the increased synchrony of RS excitatory inputs to LTS neurons causes an increased activity of this group of inhibitory neurons during the oscillation. Fourth, the long synaptic decay time (50 ms) of LTS inhibitory synaptic conductances (Fig. 1B) causes a gradual build-up of inhibitory synaptic conductances in all neurons. Fifth, the increasing inhibitory synaptic conductance has two biophysical effects: 1) all membrane potentials drift closer to the inhibitory reversal potential of −80 mV and away from the spiking threshold of −59 mV; and 2) all effective membrane time constants decrease. Sixth, both effects reduce the spiking probabilities in all neurons and thus terminate the epoch of network oscillation.

Fig. 4.

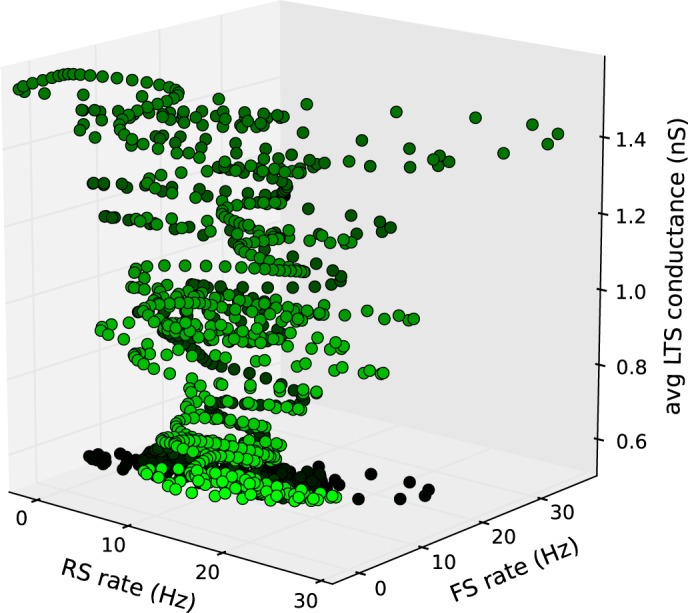
Dynamics of intermittent oscillations represented in three continuous model variables. A fluctuation in external inputs (data not shown) increases the RS and FS population-averaged instantaneous firing rates (dark green). The recurrent interaction between RS and FS neurons mediates oscillations. The coordinated activity of RS neurons activates LTS neurons. Because of the long decay of LTS synaptic conductances in other neurons, the population-averaged conductance accumulates. This accumulation causes a decline in RS and FS activity, which in turn terminates the oscillatory RS and FS activity. The vanishing coordinated activity in RS neurons causes a decline in LTS activity (light green). In this parametric plot the state of the network at a certain time is represented by a dot within 3-dimensional space spanned by the 150-Hz low-pass-filtered RS and FS instantaneous firing rates and the population-averaged LTS conductance in all neurons. Dots are plotted for 500 ms with time increments of Δt = 0.5 ms. Time increases from dark green to light green.

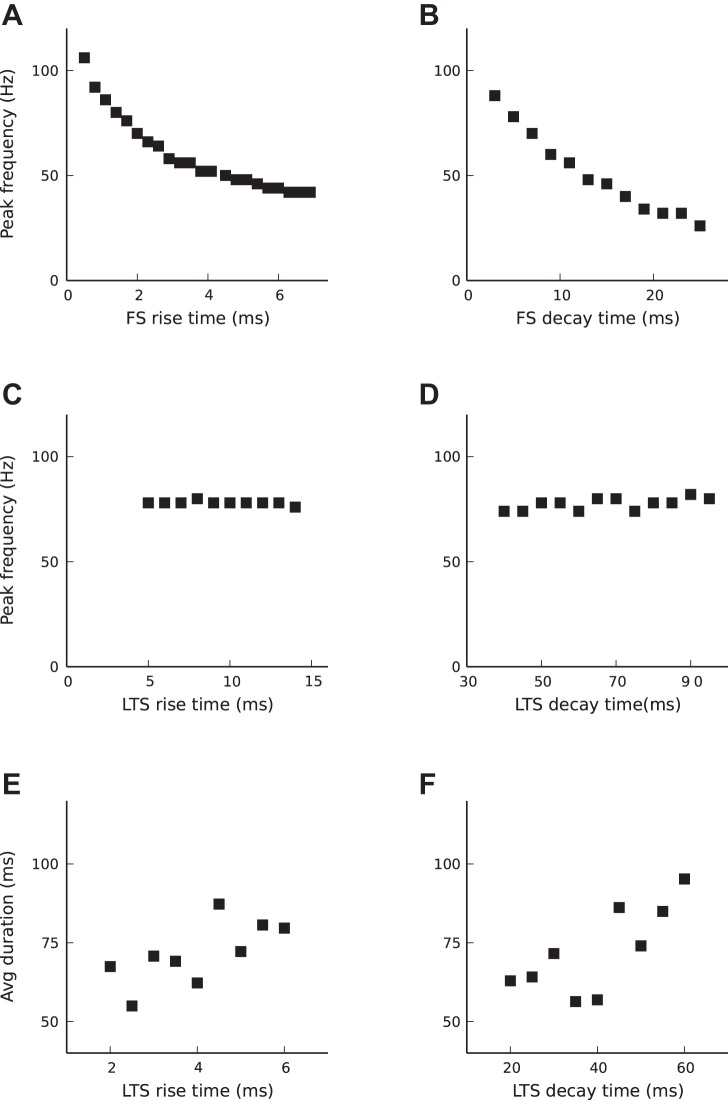
Consistent with this description of mechanisms, the oscillation peak frequency decreases with increasing FS synaptic rise or decay time constant (Fig. 5, A and B), whereas LTS synaptic rise and decay time constants do not impact the oscillation peak frequency (Fig. 5, C and D). However, LTS biophysical parameters determine the duration of oscillatory epochs (Fig. 5, E and F). LTS decay time impacts the duration of episodes in the following way. Synaptic current is defined by I_syn = g_synS(t)(V − V_syn), where the gating variable, S(t) (see materials and methods), includes the normalization constant, τ_m/(τ_d − τ_r), which is chosen so that the time integral of the gating variable is equal to the membrane time constant (Brunel and Wang 2003). This normalization was adopted to keep the balance between excitation and inhibition. Varying the synaptic time constants does not affect the time integral of a postsynaptic current but reduces the peak postsynaptic current. Thus, increasing synaptic time constants of LTS neurons, either τ_r or τ_d, reduces the LTS peak postsynaptic current. Therefore, more spikes in LTS are needed to terminate oscillations. Thus increasing synaptic time constants of LTS neurons leads to longer-lasting oscillations.

Fig. 5.

Dependence of oscillations on synaptic time constants. A and B: peak frequency decreases with increasing FS rise time and with increasing decay time. For time constants used in this work see Table 2, except τ_rise^FS = 1.5 ms in B. C and D: LTS synaptic time constants do not impact peak frequency. Parameters are based on Table 2, except τ_rise^FS = 1.5 ms. E and F: average duration of oscillation epochs increases with increasing LTS rise time and decay time.

The Phase Drifts Within an Epoch of Oscillation

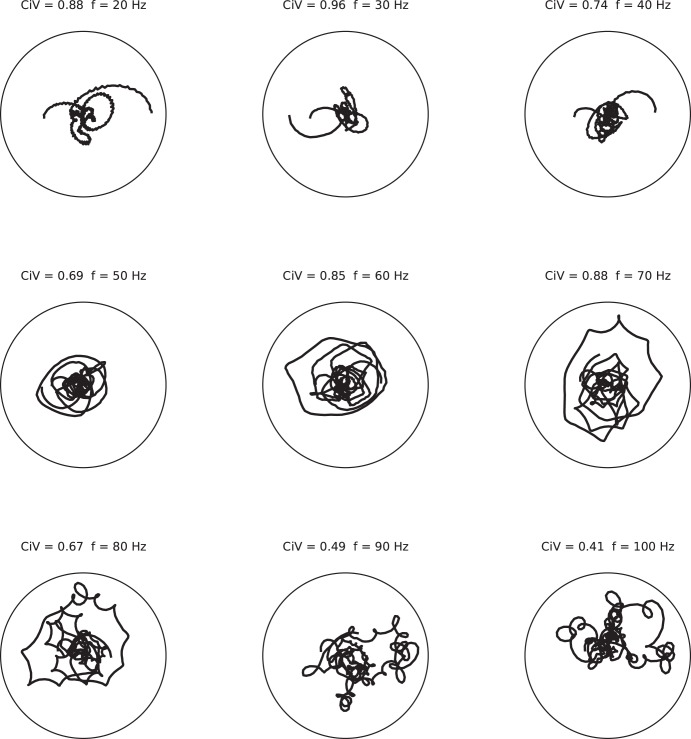
The stochastic nature of the generation of network oscillations in this model raises the question whether a resulting epoch of network oscillation resembles a sinusoid with a fixed phase. To address this question, we employed the continuous Gabor transform (see materials and methods) to evaluate the difference between the phase of the analyzed frequency component and the phase of a pure sinusoidal function of the same frequency. We use CiV to quantify the localization of residual phase in the phase portrait. The CiV is a measure for the degree of phase drift of that frequency component, with zero for the most coherent oscillation (pure sinusoidal) and one for signals with random phase. For all epochs of network oscillations tested, phase portrait trajectories for given frequency bands between 20 and 100 Hz fill out the space with a significant nonzero CiV (Fig. 6). This observation indicates that, over the time window of a given epoch of network oscillation, the phase is not constant. The network oscillation is not autocoherent.

Fig. 6.

The phase is not constant within an epoch of oscillation. Displayed are “phase portraits” of one oscillation epoch for frequencies in the gamma range (20–100 Hz). The oscillation epoch had a peak frequency of 70 Hz and a duration of 200 ms. A phase portrait for a given frequency value is a parametric plot of the residual phase (represented by the angle) and the amplitude (radius) at consecutive points in time (parameter). Circular variation (CiV) is a measure for the degree of phase drift of that frequency component. The CiV values and the given frequency are shown above each graph. For comparison, a perfect sine wave at the given frequency would result in a point on this graph and a vanishing CiV value. In contrast, signals with a random phase result in a CiV value of 1.

Epochs of Oscillations Are Variable

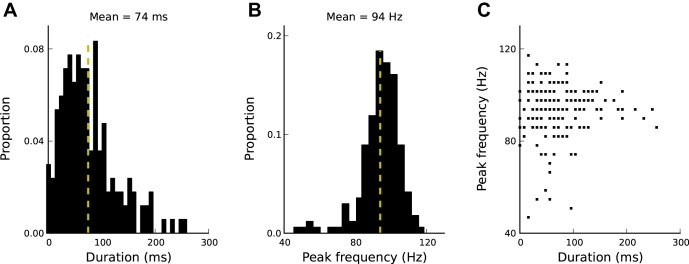
To what extent do the features of network oscillations vary from epoch to epoch? This question too is motivated by the stochastic nature of network oscillation generation. To address this question, we detected epochs of oscillations in a long simulation (60 s) and characterized each epoch in terms of its duration and peak frequency (see materials and methods). For the model parameters chosen, the epoch durations are normally distributed with a mean of 74 ms (Fig. 7A). The duration distribution depends on LTS biophysical parameters (Fig. 5, E and F). The peak frequencies are normally distributed around a mean of 94 Hz (Fig. 7B). As described above (Fig. 5, A and B), peak frequencies depend on the FS synaptic rise or decay time constants. Epoch duration and peak frequency of network oscillations are not correlated (Fig. 7C).

Fig. 7.

Epochs of oscillations vary in duration and peak frequency. A: epoch durations are distributed around 74 ± 51 ms (mean ± SD; the mean is indicated by the vertical yellow broken line). B: epoch peak frequencies are distributed around 94 ± 11 Hz (mean ± SD). C: epoch peak frequency and duration are unrelated. Values for a total number of 200 epochs are shown.

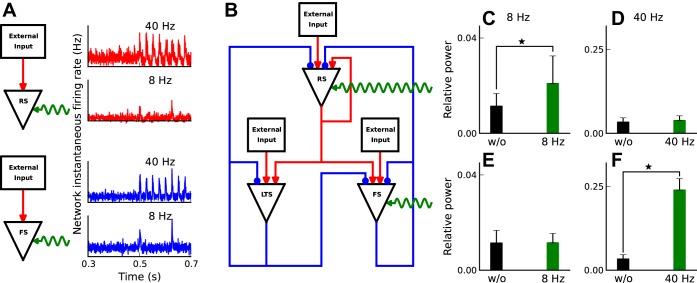
The Role of FS Neurons in Rhythmogenesis

The recurrent interaction between RS and FS neurons has long been thought to be the core mechanism for the generation of network oscillations (Borgers and Kopell 2005; Mann and Paulsen 2007; Wang and Rinzel 1992; Wang et al. 1995). To evaluate the role of each neuron type in this model (Fig. 1A), we stimulated RS or FS neurons through a 40% decrease in their leak conductance (pulses with 0.5- and 5-ms rise and decay time) repeated at regular intervals of 8 or 40 Hz frequency (Fig. 8A). First, we verified that this level of leak conductance modulation is sufficient to cause a corresponding increase in the network instantaneous firing rate in isolated RS and FS neurons (Fig. 8A). We then evaluated the impact of the imposed leak conductance modulation on network activity in the network with all possible connections intact (Fig. 8B). Modulating RS leak conductance at 8 Hz caused a small, but significant (P = 0.002; 2-sample t-test distribution), increase in network activity in the 6- to 10-Hz frequency band (Fig. 8C). Modulation of RS leak conductance at 40 Hz had no significant effect (P = 0.23) on network activity in the 38- to 42-Hz frequency band (Fig. 8D). Qualitatively, the modulation-induced correlated RS activity triggers LTS spiking, which, in turn, produces extended inhibition (50-ms decay time) of both RS and FS neurons. As a result, the LTS inhibition largely suppresses the drive-evoked RS spiking response. Modulating FS leak conductance, in contrast, evokes a different set of biophysical mechanisms. Periodic modulation of FS leak conductance at 8 Hz has little effect (P = 0.91) on the network activity in the 6- to 10-Hz range (Fig. 8E). With the short decay time (5 ms) of FS inhibition, the impact of FS inhibition on RS spiking is much shorter than the period of modulation (120 ms), thus leaving most of the RS spiking to be dominated by stochastic external input. The situation changes for 40-Hz modulation of FS leak conductance. This rate of modulation significantly (P << 0.01) increased the power of the network activity in the 36- to 42-Hz range (Fig. 8F). Qualitatively, at 40 Hz modulation and with the decay time (5 ms) of FS inhibition, the external input-evoked RS spiking undergoes sinusoidal fluctuations. This observation highlights the impact of periodic FS activity on network rhythmogenesis.

Fig. 8.

The role of RS/FS neurons in network rhythmogenesis. A: alpha function leak conductance modulation pulses with 0.5- and 5-ms rise and decay times modulate network spontaneous firing rate of uncoupled networks. B: schematic representation of the periodic leak conductance modulation of RS and FS neurons. C: low-frequency modulation of RS cells causes a significant relative power increase (P = 0.002) in a 4-Hz frequency band around stimulation frequency, 8 Hz. To compute the power we use multitaper power spectral density with 3 tapers, 500-ms time window sliding by 50 ms. Relative power in the given frequency is defined as the ratio of power in a 4-Hz frequency range around the given frequency to the total power from 0 to 100 Hz. Black bar is for no modulation case (baseline), and green is in the presence of periodic modulation. Error bars are calculated over 25 repetitions of the simulation. D: 40 Hz modulation of RS neurons does not have a significant (P = 0.23) impact of the relative power at high frequencies centered around 40 Hz. E: low-frequency leak conductance modulation of FS interneurons does not cause a significant (P = 0.91) change in relative power around 8 Hz. F: stimulating FS neurons at gamma-band frequencies significantly (P < < 0.01) increases relative power in gamma-band frequencies. ^⋆Significant difference between two bars or values.

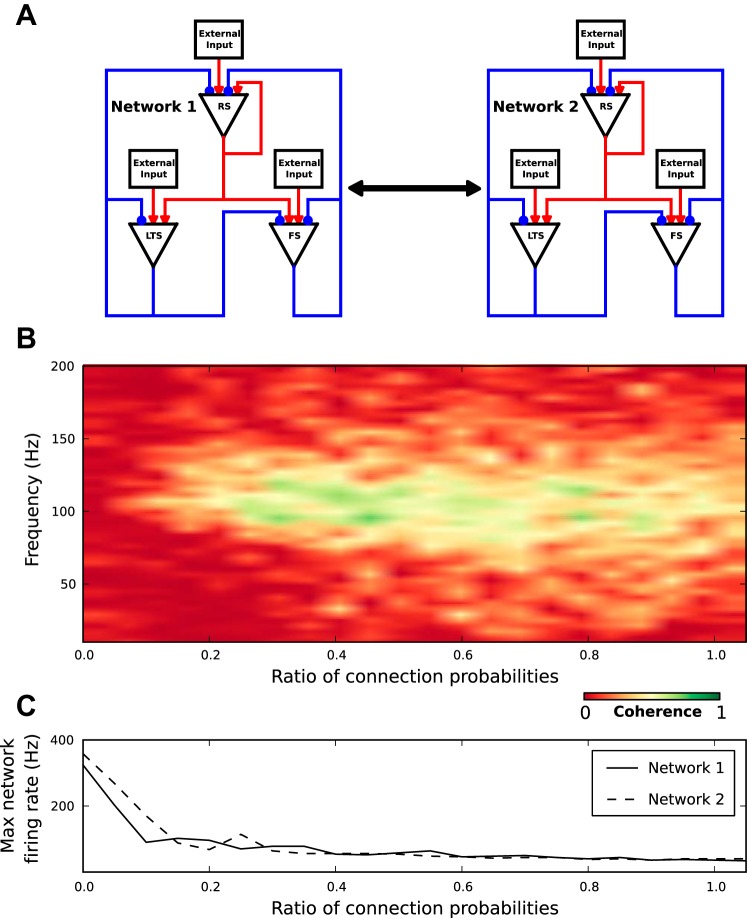
Coherent Oscillations Emerge Dynamically in Coupled Networks

As described above, the stochastic nature of rhythmogenesis causes fluctuations in occurrence, phase, duration, and frequency content of oscillation episodes. Such fluctuations raise the question to what extent intermittent oscillations in two networks covary. To address this question, we constructed two identical networks but with independent external inputs and varied the coupling between the two networks (Fig. 9A).

Fig. 9.

Oscillations covary in networks with modest coupling. A: schematic representation of two networks with all possible connections and internetwork coupling. Internetwork coupling is similar to intranetwork connection, but with different connection probability. B: coherence plot between two networks as a function of frequency and the ratio of inter- to intranetwork probabilities for a 4-s simulation. C: maximum amplitude of network instantaneous firing rate as a function of the ratio of inter- to intranetwork probabilities.

Within each network, of all possible connections, constrained by the network structure (Fig. 1A), a subset of connections is chosen with probability, P_c = 0.2. This procedure generates sparse and random connectivity within each network. Parameters are tuned (Fig. 5, A and B) so that each network generates intermittent oscillations at frequencies around 100 Hz. Coupling between the two networks is constrained by the same rules of the network structure. A subset of connections between the two networks is chosen from the possible connections with internetwork probability that ranges from 0 to 0.2. The coupling between the two networks, quantified as the ratio of inter- to intranetwork connection probability, ranges from zero (two independent networks of 2,500 neurons each) to one (one network of 5,000 neurons).

As expected, in uncoupled networks local activity fluctuations within each network trigger independent episodes of ensemble oscillations resulting in vanishing coherence values, which were calculated over the 4-s simulation time (Fig. 9B). However, a small increase in the coupling between the two networks causes a sharp rise in the coherence of the two network activities in the frequency range around 100 Hz. This is despite the fact that the two networks receive independent external inputs. In conclusion, coherent oscillations emerge dynamically in two networks with modest reciprocal coupling.

Above some intermediate coupling, the coherence decreases with increasing coupling. This is because, in our model, inhibitory (FS and LTS) neurons have a larger time-averaged firing rate than excitatory (RS) neurons (Fig. 2A). Thus the coupling between the two networks decreases the overall excitation-to-inhibition ratio, which in turn decreases the overall network activity (Fig. 9C) and thus reduces coherence.

DISCUSSION

In this model investigation we have shown that intermittent ensemble oscillations can arise from the interaction of excitatory RS and inhibitory FS and LTS neurons, while single neuron spiking remains largely irregular and sparse. The recurrent interaction between the RS and FS neurons provides a generative mechanism of oscillation. Periodic activation of FS, but not RS, model neurons causes enhancement of gamma oscillations. The emerging correlated RS spiking during an oscillation activates LTS neurons. The long LTS synaptic decay time causes an accumulation of inhibitory synaptic conductances in all neurons, which eventually terminates the ensemble oscillation. The stochastic nature of ensemble oscillation causes a phase drift during an epoch of oscillation, and a large variability in durations and peak frequencies from epoch to epoch. Importantly, however, oscillations largely covary for two networks with sufficient coupling.

Discrete and Continuous Variables Interact in the Network

The dichotomy between discrete irregular single-neuron spiking and continuous network activity lies at the core of cortical oscillations (Brunel 2000; Brunel and Hakim 1999; Brunel and Wang 2003). First, the firing rate of individual neurons is typically much smaller than the dominant oscillation frequency (Csicsvari et al. 1999, 2003; Destexhe et al. 1999; Engel et al. 1990). Second, discrete spike events are transformed into continuous variables, such as the synaptic gating variable and the membrane potential. Third, the continuous variables determine the probability of single-neuron spiking. Fourth, in a large population of neurons, the probability of single-neuron spiking translates into network instantaneous firing rates. In conclusion, at the level of continuous variables, the network dynamic is fully described within the three-dimensional state space spanned by the instantaneous firing rates of RS, FS neurons, and LTS-mediated slow inhibitory conductances in all neurons (Fig. 4).

Fast Negative Feedback Generates Oscillations

The biophysical mechanisms of sparse pyramidal neuron spiking during gamma oscillation have been explored in recent studies emphasizing the role of spike frequency adaptation and global inhibition (Kilpatrick and Ermentrout 2011) as well as shunting inhibition (Kotani et al. 2014; Krupa et al. 2014). Pharmacological blockade of inhibition disrupts oscillations (Borgers and Kopell 2005; McMahon et al. 1998; Mann and Paulsen 2007; Traub et al. 2004; Wang and Rinzel 1992; Wang et al. 1995). Our model results (Fig. 8F) corroborate the need for inhibition in rhythmogenesis and further predict how the FS synaptic rise and decay time constants impact the oscillation frequency (Fig. 5, A and B). The oscillation of the continuous variables is, however, the result of the convolution of discrete and stochastic spike events. The stochastic nature of rhythmogenesis results in phase drifts during an epoch of oscillation (Fig. 6). In other words, the phase of an oscillation is not conserved during the elevated power of an oscillation. This lack of autocoherence has been observed in LFP recordings from primary visual cortex of monkeys (Burns et al. 2010; Xing et al. 2012). In addition, the stochastic nature of rhythmogenesis results in a large epoch-to-epoch variability in peak frequencies (Fig. 7B), largely similar to the variability examined in primary visual cortex (Xing et al. 2012).

Optogenetic manipulation of barrel cortex in vivo showed that light-driven periodic (40-Hz) activation of FS neurons amplifies oscillations in the gamma range, whereas similar activation of RS had no such effect (Cardin et al. 2009). Our model reproduces this experimental observation (Fig. 8, D and F) and thus, consistent with investigations of a more complex model (Vierling-Claassen et al. 2010), emphasizes the role of FS neurons in rhythmogenesis.

Slow Negative Feedback Terminates Oscillations

Synchronous RS activity during an oscillation recruits LTS neurons, and their slowly accumulating inhibition eventually terminates the oscillation (Fig. 4). Because of the underlying stochastic spiking, accumulation of activity too is stochastic, which translates into a distribution of oscillation epoch durations (Fig. 7A). Such duration variability is qualitatively similar to what has been observed in primary visual cortex (Xing et al. 2012). On average, the duration of an oscillation epoch increases with increasing LTS synaptic time constants (Fig. 5, E and F). With biologically plausible LTS synaptic time constants, the model generated oscillation durations of up to a few hundred milliseconds (Fig. 7A). Because the network stops fulfilling all four features for very large LTS synaptic time constants, additional mechanisms would have to be explored for longer durations. Importantly, our model makes the experimentally testable prediction that optogenetic activation of LTS neurons after the onset of an oscillation will shorten the duration of that oscillation epoch.

Finally, our model investigation raises an important question about the FS and LTS connectivity (Fig. 1A). Our simulations show that, in the presence of FS-to-LTS connections of sufficient strength, spontaneously started oscillations continue indefinitely, while the peak frequency distribution remains largely unchanged (data not shown). The qualitative change in network behavior from intermittent to continuous as a function of FS-to-LTS synaptic conductance occurs within a narrow range between 4.0 nS (intermittent oscillations) and 4.7 nS (continuous oscillations).

The key mechanisms of oscillation termination are the accumulation of activity and the resulting negative feedback. The LTS neurons are but one biophysical implementation of the termination mechanism. Alternatively, oscillation termination can be accomplished by nonlinear transfer functions (Memmesheimer 2010), possibly implemented by the nonlinear properties of dendrites and synapses (Gasparini and Magee 2006; Nevian et al. 2007). Memmesheimer (Memmesheimer 2010) has shown that incorporating supralinear dendritic enhancement of synchronous inputs leads to the generation of intermittent sharp-wave ripples (200 Hz). This poses the question for future studies whether coexistence of these two mechanisms, slow inhibition and nonlinear transfer function, renders intermittent oscillations more robust. The model presented here shows that intermittency can arise due to the network structure rather than single-neuron property. However, the model is not robust. Intermittent oscillations arise from small volumes within the multidimensional parameter space.

For completeness, we discuss two important features of network models with nonlinear components, robustness and degeneracy. First, an exhaustive scan of the ∼25-dimensional parameter space is computationally extremely expensive and is beyond the scope of the present paper. Nevertheless, network behavior is robust with respect to small variations of connection probability (from 30% up to 50%) and synaptic conductances for AMPA and GABA channels (∼10% around the values given in Table 2). Second, the fact that, in networks with nonlinear elements multiple combinations of parameters can give rise to the same output, is well established in network theory and nonlinear dynamics, was introduced in neuroscience with a detailed model simulation (Prinz et al. 2004), and received further intellectual support in the analytic investigation of a simple model (Caudill et al. 2009). An exhaustive scan of the parameter space in search for degeneracy is beyond the scope of this manuscript.

Oscillations Covary for Coupled Networks

The stochastic nature of rhythmogenesis and the resulting variability in phase, peak frequency, and duration raise questions as to the potential coordination of oscillations across multiple networks. Regardless of the observed variability and the fact that phase does not unfold linearly with extended time, it is thought crucial for two networks to be able to offset differences in oscillation frequencies. In this manner, networks can initiate and maintain oscillations as communication means between distant neuronal groups (Fries 2005; Miller and Buschman 2013; Nikolić et al. 2013; Roberts et al. 2013; Salinas and Sejnowski 2001). We have shown that oscillations between distant regions remain robustly coordinated despite significant variations in their internal dynamics. Our results indicate that a wide range of frequencies could be exploited as mechanisms for information transmission between two networks with recurrent connections during perceptual and cognitive processing.

Simulating Important Features of Cortical Oscillations

Numerous previous theoretical investigations have offered physical intuition about individual aspects of rhythmogenesis in cortical circuits (Bathellier et al. 2008; Gerstner and van Hemmen 1993; Geisler et al. 2005; van Vreeswijk et al. 1994; Vierling-Claassen et al. 2010; Wang and Rinzel 1992). Here we highlight selected examples. 1) A spiking model was designed to generate ensemble oscillations in the presence of irregular and sparse spiking, but did not reproduce the intermittency of rhythms (Brunel and Wang 2003). 2) Another spiking model included spike timing-dependent plasticity and displayed the transition between different frequency bands (Izhikevich 2006). However, the degree of synchronization of spikes during network oscillations was inconsistent with the experimentally observed irregular and sparse spiking. 3) Clustered connections have been proposed to generate slow dynamics and high variability in a network of spiking neurons (Litwin-Kumar and Doiron 2012). This model, however, does not reproduce intermittent ensemble oscillations with variable peak frequencies. 4) electroencephalogram (EEG) model networks (not spiking) generate intermittent oscillations (Goodfellow et al. 2011; Jia et al. 2013; Lopes Da Silva et al. 1974, 1975; Wendling et al. 2002; Xing et al. 2012). However, by design (not spiking), these EEG models do not speak to irregular and sparse spiking.

In contrast, the spiking model proposed here, for the first time, reproduces five important features of observed cortical oscillations: 1) irregular and sparse spiking, 2) phase drift during an epoch of oscillation, 3) intermittent oscillations, 4) epoch-to-epoch variations in peak frequency and duration, and 5) coherence across multiple networks.

In addition, the model makes two testable predictions. First, our model predicts a lack of connections from FS to LTS neurons. Experimental observations in hippocampus (Banks et al. 2000; Miles et al. 1996) support this prediction. In cortex, the connectivity from FS to LTS neurons could be tested experimentally in the following two ways: 1) search for physiological connections via dual whole cell recordings in a slice of cortex and 2) search for anatomical connections via electron microscopic survey (connectomics) of a piece of cortical tissue. Second, the model predicts that optogenetic hyperpolarization of LTS neurons would transform oscillations from intermittent to more continuous. This experiment could be refined by triggering the optogenetic manipulation of LTS neurons on a detected oscillation (for online oscillation detection, see, for instance, Rutishauser et al. 2013). The prediction is that oscillation-triggered hyperpolarization of LTS neurons would increase oscillation episode duration, whereas oscillation-triggered depolarization of LTS neurons would decrease oscillation episode duration.

GRANTS

This research was supported by a Whitehall Foundation Grant no. 20121221 and National Science Foundation CRCNS Grant no. 1308159 to R. Wessel.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: M.S.H. and R.W. conception and design of research; M.S.H. analyzed data; M.S.H. prepared figures; M.S.H. drafted manuscript; M.S.H. and R.W. edited and revised manuscript; M.S.H. and R.W. approved final version of manuscript.