Estimation of the phase response curve from Parkinsonian tremor

Abstract

Phase response curves (PRCs), characterizing the response of an oscillator to weak external perturbation, have been estimated from a broad range of biological oscillators, including single neurons in vivo. PRC estimates, in turn, provide an intuitive insight into how oscillatory systems become entrained and how they can be desynchronized. Here, we explore the application of PRC theory to the case of Parkinsonian tremor. Initial attempts to establish a causal effect of subthreshold transcranial magnetic stimulation applied to primary motor cortex on the filtered tremor phase were unsuccessful. We explored the possible explanations of this and demonstrate that assumptions made when estimating the PRC in a traditional setting, such as a single neuron, are not arbitrary when applied to the case of tremor PRC estimation. We go on to extract the PRC of Parkinsonian tremor using an iterative method that requires varying the definition of the tremor cycle and estimating the PRC at multiple peristimulus time samples. Justification for this method is supported by estimates of PRC from simulated single neuron data. We provide an approach to estimating confidence limits for tremor PRC and discuss the interpretational caveats introduced by tremor harmonics and the intrinsic variability of the tremor's period.

recent interest in adaptive or “closed-loop” forms of neuromodulation for movement disorders has generated a need for greater understanding of how oscillatory activity within the nervous system is generated, propagated, and potentially suppressed (Little et al. 2013; Rosin et al. 2011). To develop novel sites or approaches to neuromodulation or to optimize existing approaches, such as deep brain stimulation, an intuitive model, based on biologically informed parameters, would provide a framework from which novel hypotheses could be tested. In the physical sciences, a broad range of biological oscillators, ranging from circadian rhythms to the cardiac pacemaker rhythm, has been characterized using a mathematical approach, known as dynamical systems theory (Hoppensteadt and Izhikevich 1997). More specifically, the phase response curve (PRC), which characterizes an oscillator's response to perturbation as a function of its phase, provides an intuitive insight into how the oscillation is generated, how it becomes entrained by other oscillators, and how it may be desynchronized (Lücken et al. 2013; Smeal et al. 2010). A central concept to the insights that PRC estimation provides to understanding oscillatory network dynamics is the idea of weakly coupled oscillators (Hoppensteadt and Izhikevich 1997; Smeal et al. 2010). This assumes that a network of coupled oscillators, interacting via weak coupling, only affects each other through phase shifts defined by the PRC. The attractiveness of this theoretical framework is in the ability to incorporate the PRC estimates into a greatly simplified model, such as a phase reduction, which in turn, can predict the entrainment and potentially, the existence of phase perturbations that predict the “sudden death” of the oscillating system (Kuramoto 1984; Strogatz 2000; Winfree 2001). The appeal in applying this framework to the design of a phase-resetting approach to suppressing pathological rhythms, such as tremor, motivated our interest in estimating the tremor PRC.

The PRC, when estimated from oscillators, such as single neurons, typically involves the comparison of the effect of a perturbing stimulus (such as a current pulse) on the neuron's interspike interval (ISI) at the time of the perturbation (Gutkin et al. 2005). The effect of this perturbation is then compared with the ISI preceding the stimulus and the response to stimuli applied at different points in the neuron's firing cycle used to derive the PRC (Reyes and Fetz 1993; Tsubo et al. 2007). Our hypothesis was that subthreshold motor cortex stimulation, using transcranial magnetic stimulation (TMS), could modify the ongoing phase of the tremor in a manner that was consistent with a PRC. An intuitive approach to derive the tremor PRC would be to filter the tremor signal and compare the length of the tremor cycle before and during the TMS pulse in a manner analogous to that for the single neuron case described above (see Fig. 1, A–C). Despite initial attempts, this approach did not yield any meaningful PRC estimates. We considered three possible explanations for this failure to estimate the tremor PRC. Firstly, when estimating the PRC from a filtered signal, precise timing information is lost, which results in underestimation of the eventual PRC. Secondly, by restricting the estimate of the tremor PRC to the precise time point at which the TMS pulse is delivered, underestimation may result from a priori assumptions about the point at which the stimulus acts on the tremor. Finally, in contrast to the process of estimating a single neuron PRC, where the start and finish of the neuron's cycle are intuitively defined by the onset of the action potential, the definition of the start and end of tremor cycle arbitrarily may result in falsely under-representing the tremor PRC.

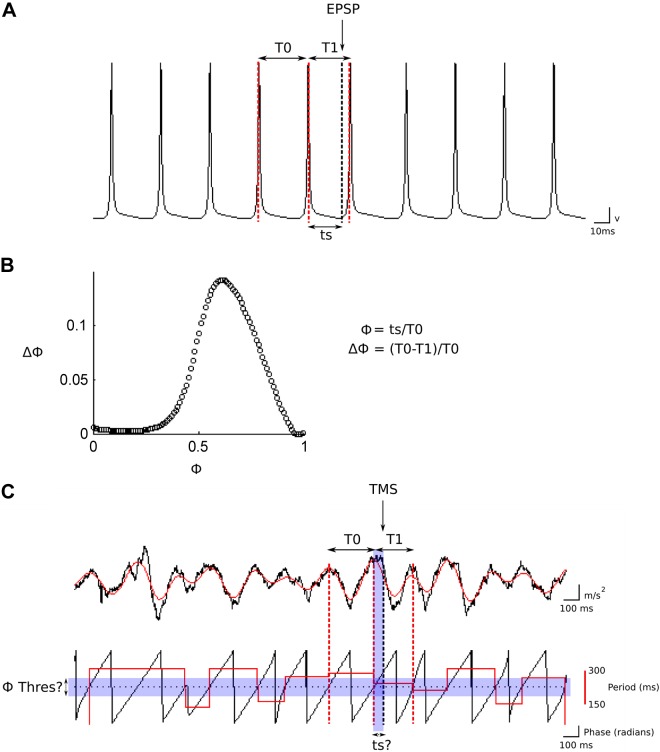
Fig. 1.

Analytical approach to estimating the traditional phase response curve (tPRC) and filtered PRC (fPRC). The tPRC is calculated by comparison of the interspike interval (ISI) preceding the stimulus (A; T0), with the ISI, which is perturbed by the stimulus [in this case, an excitatory postsynaptic potential (EPSP)], T1. The effect of presenting stimuli repeatedly though the firing cycle of the neuron allows plotting of the PRC (B), which is a plot of the phase response (PR; Δϕ) against the phase of the stimulus (ϕ). C: approach to estimating the tremor PRC. The tremor (sample accelerometer trace recorded from the patient's hand), represented by the black trace, is band-pass filtered (3–7 Hz), illustrated by the superimposed red line. The panel below this illustration of the raw tremor signal and filtered estimate represents the tremor phase (sawtooth black line) following Hilbert transformation of the filtered tremor signal. The tremor cycle length is then extracted from the tremor phase time series and is defined according to the threshold crossing points defined by the phase threshold [Φ Thres (Φ_thres)]. The superimposed red line illustrates this conversion process that results in a time series that represents an instantaneous estimate of the tremor cycle length. In this example, Φ_thres is 0 (dotted line). To estimate the tremor PRC (in an analogous manner to that illustrated in A), T0 and T1 are then defined using the instantaneous cycle-length estimate. A critical difference between the single neuron case and the estimation process for tremor PRC is that the time at which the transcranial magnetic stimulation (TMS) pulse perturbs the tremor (ts) and how to define Φ_thres are unknown (shaded areas).

To explore how these caveats might make the filtered PRC (fPRC) tremor more prone to underestimation, we simulated neuron spike trains (Morris and Lecar 1981) and compared the PRC estimated from the precise timing of the simulated action potentials with the PRC derived from filtering the spike train. The motivation behind this model choice was simply for convenience of simulation rather than driven by biological relevance to tremor (other than being a neural model). The aim of these simulations was simply to generate known PRCs to explore mechanisms behind the failure of our initial pragmatic approach and to inform the development of a more reliable technique to estimating the tremor PRC.

With the use of a method informed from the results of these simulations, we demonstrate in two patients with Parkinsonian tremor that TMS at subthreshold intensity to primary motor cortex modulates the phase of the tremor in a manner that would be consistent with a PRC. Detection of this filtered tremor PRC relied on the need to generate iteratively PRCs across multiple peristimulus time points while defining the tremor cycle over multiple phases to prevent “missing” the true PRC.

METHODS

Tremor TMS experiments.

We recruited two patients with idiopathic Parkinson's disease (PD; man: aged 72 yr, right handed, 5 yr disease duration, right-hand rest tremor, treated with 562.5 mg levodopa/day; woman: aged 68 yr, right handed, 7 yr disease duration, bilateral-hand rest tremor, treated with 475 mg levodopa/day and 1 mg rasagiline/day), who had given written, informed consent to participate in the experiments. The study had been approved by the local ethics committee. We recorded rest tremor while cortical stimuli were delivered at below motor threshold to primary motor cortex. Motor cortex was chosen as the site of stimulation due to its recognized involvement in the Parkinsonian tremor circuit (Timmermann et al. 2002). Electromyography recordings were made from the abductor pollicis brevis (APB), first dorsal interossei, and abductor digiti minimi muscles of the right side. Test responses in the target muscles were evoked by TMS of the left primary motor cortex, applied through Magstim 200 magnetic stimulators (Magstim, Witland, Carmarthenshire, Wales) with a monophasic current waveform, connected to a figure-of-eight coil (mean loop diameter, 9 cm). The coil was held tangentially to the skull with the handle pointing backwards and laterally at an angle of 45° to the sagittal plane and was optimally positioned to obtain motor-evoked potentials (MEPs) in the APB. TMS pulses were delivered at regular intervals with an interstimulus interval of 1 s. The stimulus intensity was set to 80% of the resting motor threshold. Tremor was recorded using a triaxial accelerometer (Biometrics, Newport, UK) attached to the dorsum of the hand. This signal was amplified and digitized using a 1401 AD converter [Cambridge Electronic Design (CED), Cambridge, UK], running Spike version 2 (CED). All signals were acquired at a sampling rate of 1,000 Hz.

Offline, the tremor signal was then epoched with a peristimulus time window of 1 s, pre- and poststimulus, and then filtered [second-order Butterworth filter (Parks and Burrus 1987), band pass 3–7 Hz, corresponding to the peaks of 3.5 and 7 Hz in the tremor power spectrogram]. We performed filtering in the forward and reverse directions using the Matlab filtfilt function to ensure zero-phase distortion (Matlab; MathWorks, Natick, MA). The filtered tremor signal phase was then derived using the Hilbert transform (Fig. 1C). We used the point at which the phase crossed 0 radians [henceforth, known as the phase threshold (Φ_thres)] to define the cycle length of the tremor and calculated the phase response (PR) accordingly.

PR = (T0 − T1)/T0 (1)

where T1 is the length of the tremor cycle at the time of the TMS pulse, and T0 is the length of the tremor cycle preceding the stimulus. The plotting of the PR as a function of the phase of the TMS pulse within T1 derives the PRC. A PR was estimated for each TMS pulse, and the PR was averaged within 10 equally spaced bins across the tremor cycle. PR values that were >0.75 or less than −0.75 were excluded from this average, as they corresponded to nonphysiological phase slips caused by gross movement artefacts or large fluctuations in the tremor amplitude (on visual inspection of the tremor trace).

Single neuron simulations.

Our initial attempts to derive the tremor PRC using the method described above did not produce any clear effect of the TMS pulse on the tremor phase or averaged peristimulus amplitude. To establish if this approach was valid, we wanted to test the method while applying it to an oscillatory signal where the PRC was known. By simulating “known” PRCs, any deficiencies and assumptions in our approach to tremor PRC estimation could thus be highlighted. These, in turn, could be used to derive a more robust method that could be reapplied to the tremor recordings.

Simulations were performed using the Morris-Lecar (ML) neuronal model (Morris and Lecar 1981). It is important to emphasize that the choice of this model was not motivated by any biological relevance to tremor other than its neural basis. The intention of these simulations was not to imply that tremor could be modeled by a single neuron firing but rather, to derive neuron-based PRCs that could be re-estimated using our filtering approach and compared with PRCs derived from the exact timing of the neuron's spikes. The membrane potential for the ML model V is defined as

$$\begin{array}{l}c\frac{dV}{dt}=-g_{Ca}{m}_{\infty }\left(V\right)\left(V-V_{Ca}\right)-g_K\omega \left(V-V_K\right)-g_L\left(V-V_L\right)+I+\epsilon \\ \frac{dw}{dt}=\varphi \frac{\left[{\omega }_{\infty }(V)-\omega \right]}{{\tau }_{\omega }},\\ m_{\infty }\left(V\right)=0.5\ast \left[1+\tanh \left\{\left(V-V_1\right)/V_2\right\}\right],\\ {\omega }_{\infty }\left(V\right)=0.5\ast \left[1+\tanh \left\{\left(V-V_3\right)/V_4\right\}\right],\\ {\tau }_{\omega }\left(V\right)=1/\cosh \left[\left(V-V_3\right)/\left(2\ast V_4\right)\right],\end{array}$$ (2)

where g_K = 8, g_L = 2, V_Ca = 120, V_K = −84, V_L = −60, V₁ = −1.2, V₂ = 18, and c = 20 are constants. Changing V₃ from 12 to 2, V₄ from 17.4 to 40, ϕ from 0.0667 to 0.04, and g_Ca from 4.0 to 4.4 switches the model's bifurcation type from class I to class II excitability (producing types I and II PRCs, respectively). For all simulations, dt = 1 ms. We simulated steady-state firing at ∼10 Hz using an input current I of 45 and 130 μA/cm² for each class. Where simulations were performed to produce variable spiking, this was achieved by adding Gaussian noise ε to the neuron's current with the same mean value of I as above for each class but with an SD σ that would produce 15 and 25% ISI variance (for type 1 excitability, σ = 10 for 15%, σ = 20 resulted in 25%; for type 2 excitability, σ = 10 for 15%, σ = 25 resulted in 25%). The resultant PRC was calculated following perturbation with a 5-ms square current pulse. Pulse amplitudes (A) of between 15 and 30 μA/cm² were required to produce an approximately similar magnitude of PR for types I and II PRCs, respectively, in the absence of noise.

The single neuron PRC was then derived by measuring the effect of the current pulse on the neuron's ISI, T (Fig. 1A). The effect of a current pulse on this interval (T1) is compared with the ISI preceding the stimulus (T0), and the PR is defined as for Eq. 1. The spike times of the ML neuron were defined as the point at which the membrane potential crossed 0 mV. Estimates using this “traditional” approach are henceforth referred to as the “tPRC.”

Plotting the PR as a function of the phase of the stimulus within the ISI derives the PRC. Any positive PR value represents a shortening of the ISI by the stimulus (phase advance), whereas PR values with negative values represent a lengthening (phase delay) of the ISI by the stimulus (see Fig. 1B). We then used the same simulated spike trains and applied the filtering approach described above. Spike trains were filtered (bandpass 4–16 Hz) with a second-order Butterworth filter (i.e., the same filter as for the patient tremor recordings). The instantaneous phase of the filtered signal was then derived with the Hilbert transform, resulting in a time series with amplitude between −π and π. The ISIs of the neuron were then defined from this filtered signal as the Φ_thres crossings, where the phase was greater than zero. This aligned the instantaneous phase with the start of the firing phase of the neuron, where a phase of 0 corresponded to the first point at which the neurons membrane rose above 0 mV. The resultant time series, a representation of the ISIs of the neuron, derived from this filtered spike train, was then used to extract the fPRC.

To allow comparison of the morphology of the PRC estimates at different peristimulus time samples, we correct the phase at which the stimulus is delivered phase by the time difference in radians relative to the stimulus presentation (t = 0) so that the corrected phase ${\Phi }_{\text{corr}}\left(\text{t}\right)=\Phi \left(\text{t}\right)-\left(\left[\frac{2\pi }{\mu }\right]\ast t\right)$, where μ is the mean ISI at time t in milliseconds. To allow for phase wraparound following correction, ${\Phi }_{\text{corr}}=\{\begin{array}{l}{\Phi }_{\text{corr}}+2\pi ,\hspace{0.17em}{\Phi }_{\text{corr}}<-\pi \\ {\Phi }_{\text{corr}}-2\pi ,\hspace{0.17em}{\Phi }_{\text{corr}}>\pi \end{array}$. For simulations in the presence of noise, PRCs were estimated for peristimulus time samples between −100 and 100 ms. For these estimates, Φ_thres remained constant at 0 radians. As with the tremor PRC estimates, the PR was averaged within 10 equally spaced bins across the neuron's cycle.

All single neuron simulation and signal processing were performed in Matlab version 2012 (MathWorks).

Estimating confidence limits.

As a consequence of results from the single neuron simulations, we developed an iterative approach to capture the tremor PRC. This required the estimation of the fPRC from multiple peristimulus time periods and the use of variable definitions of Φ_thres, which defined the start and finish of the tremor cycle. This approach resulted in a multiple comparisons problem. Our approach to circumventing this issue relied on the observation that the PRC can be estimated from multiple peristimulus samples rather than a single or discrete infrastimulus sample. This property of the PRC means that any “true” estimate of the PRC will result in a cluster of positive (corresponding to phase advance) and negative (corresponding to phase delay) values when estimated across multiple contiguous time samples. We designate this estimate of the PRC across multiple contiguous time samples from the filtered time series as the fPRC(t). We performed a shuffling procedure by selecting random epochs of tremor signal (number of “trials” matched the number collected in the real experiment) and repeating the same analysis as above (i.e., for the same values of Φ_thres and peristimulus time samples) to this resampled data. These shuffled data sets were generated 100 times [generating an n-by-100 fPRC(t), where n is the number of Φ_thres]. We then looked for clusters of PRs in the shuffled fPRC(t), which were above or below a predefined PR threshold [defined by the peak or trough value of the PR estimated from the fPRC(t)]. Clusters were defined using algorithms from FieldTrip and SPM2 (Friston et al. 1994; Oostenveld et al. 2011), based on a nearest-neighbor approach (Thurfjell et al. 1992). Each cluster was then summed to generate a single value [∑fPRC(t)], which was then used to generate a probability density function fitted with a nonparametric Gaussian kernel (Bowman and Azzalini 1997) after values for both positive and negative clusters were combined. This distribution was used to define the 95% confidence limits.

Simulated tremor spectra.

To explore further the contribution of tremor harmonics bias in the confidence limit estimates, we re-estimated these using the same procedure above on simulated tremor spectra. We varied the spectral composition of the signal to explore how harmonics may interact to bias the confidence limit estimates. Simulated tremor was calculated according to the sum of two sine waves, y(t) = a_Xsin(tπf_X) + a_Ysin(tπf_Y) + 0.1ε, where a_X and a_Y are the amplitude of the two harmonics X and Y, with values between 1 and 0.1. The frequency of the harmonics f_X and f_Y remains constant at 3.5 and 7 Hz, respectively. Added Gaussian noise is represented by ε. With the use of a Φ_thres of 0.001 and 20 shuffled estimates of the resampled data, the confidence limit of the positive and negative clusters was derived after fitting with a nonparametric Gaussian kernel as above.

RESULTS

Initial tremor PRC estimates.

We recorded limb tremor with an accelerometer [triaxial accelerometer transducer (sensitivity ± 100 mV/G) attached to the dorsal surface of the proximal phalanx of the right thumb] while delivering submotor threshold cortical stimuli to contralateral primary motor cortex in two patients with idiopathic PD. In total, 961 and 1,421 stimuli were included in the final estimate of the tremor PRC for each patient, respectively. The mean cycle length at the time of the TMS pulse was 245 ± 49 ms and 267 ± 62 ms for each patient. Peristimulus tremor was filtered and the pre- and poststimulus tremor cycle length defined for each trial so that the PRC could be estimated in each patient to establish the effect of the TMS pulse on the tremor phase. In both patients, no clear peak (or trough) in the resulting PRC was observed, and PR values compared with those estimated from shuffled data could not be explained outside chance levels (results not shown). A possible explanation for this failure to demonstrate a tremor PRC was that in the context of the noisy tremor signal, a weak cortical TMS pulse was insufficiently small to result in any meaningful phase perturbation. However, before accepting this null hypothesis (i.e., that the TMS pulse had no effect on the tremor phase), we considered possible explanations that may have contributed to the absence of a measurable PRC.

Possible confounds in the estimation of tremor PRC: insights from simulated PRC estimates.

A fundamental assumption when deriving the PRC is that the timing of the oscillator's cycle is precisely known. The aim of filtering the tremor was to eliminate spurious low- and high-frequency noise; however, this process may have inadvertently eliminated this precise temporal information and therefore, prevented PRC estimation. To test this possible confound, we performed a series of simulations using the ML model neuron (Morris and Lecar 1981) and compared the PRC derived from the filtered spike train (fPRC) with those derived from the unfiltered action potential times (tPRC).

By varying the pulse intensity (A) and the parameters of the model, we could produce PRCs of various amplitudes and of both type I (strictly monophasic) and II (biphasic) forms. The corresponding fPRC morphology was broadly similar (Fig. 2A; compare the plots of the fPRC with the plots of the tPRC), however with a tendency for the peak of the PR to be underestimated in all cases (for all values of A and for types I and II PRC types). Visual inspection of the filtered neuron spike trains demonstrated that this could be explained by limitation in the filter's temporal resolution (Fig. 2B). In this illustrative example (simulation with type I PRC parameters; A = 30), the precision with which the phase is estimated from the filtered spike train degrades around the time of the pulse (compare where the 0 phase precisely corresponds to 0 mV with the phase estimate where the filtered estimate is less temporally resolved). This error in the filtered phase estimate results in a fPRC peak of 0.22, in contrast to the true tPRC peak PR of 0.26 (Fig. 2A), defined from the unfiltered, precise spike times. These corresponded to a phase advance of 22 and 26 ms, respectively, i.e., an ∼15% underestimation. An additional source of error that cannot be discounted is the effect of performing the Hilbert transform on a discrete time series. The “boundary” or “edge” effects introduced by this additional step of processing may have caused further underestimation of the fPRC estimate, further corrupting the filtered spike time series and deviating this from the original (unfiltered), simulated action potential trace. Nevertheless, despite these additional processing steps and the consequent corruption introduced to the filtered time series, a range of PRCs with varying forms and amplitudes could still be recovered. Therefore, these simulations supported the basic principle that the PRC could still be recovered, albeit with a tendency for the fPRC to be underestimated but without significant corruption in its form or shape.

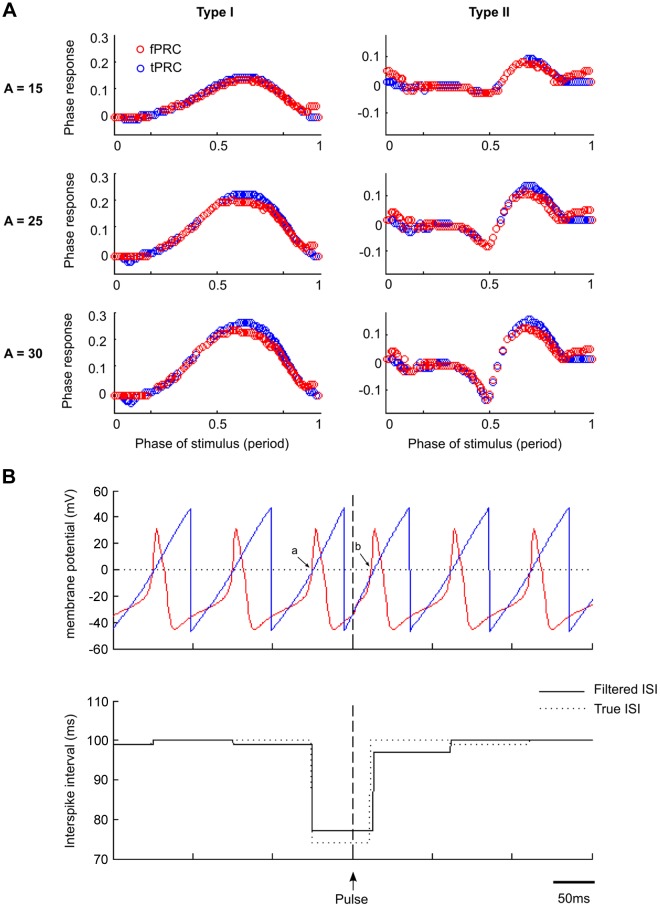
Fig. 2.

Comparison of tPRC and fPRC estimates from single neuron stimulations. A: varying the amplitude (A) of the EPSP and model parameters produces different PRC shapes and classes (Type I and Type II). The tPRC (defined from the single neuron spike times), represented by blue circles, is plotted alongside the fPRC (derived from the same spike train but after filtering the spike train), represented by red circles. Estimates using the fPRC approach were similar in form and captured much of the “true” tPRC with a tendency for the fPRC to underestimate the real PR. The mechanism for this underestimation is explored further (B). The effect of filtering can, at least in part, be understood by the temporal distortion introduced by the filtering process. The Morris-Lecar (ML) neuron (top), firing at 10 Hz, receives a perturbing pulse at the time illustrated by the vertical, dashed lines (top and bottom). This results in a phase advance of ∼0.26. The ISI estimates, derived from the phase of the filtered ML neuron membrane potential, under-represents this phase advance (solid line; bottom) by 4 ms, with the resulting PR equaling 0.22. Close inspection of the filtered phase estimate (sawtooth blue line; top), superimposed on the ML model membrane potential (red line; top), illustrates that under steady-state conditions, the filter estimates the 0-crossing threshold at the start of the action potential (arrow labeled “a”), whereas following the pulse, the 0-crossing point is represented at the down stroke of the simulated neuron action potential (arrow “b”). Although this jitter introduced by filtering appears trivial (i.e., 4 ms), as a proportion of the PR to a weak stimulus, it results in a disproportionately large (15%) underestimate of the phase advance introduced by the pulse at this point in the neuron firing cycle.

In performing the single neuron simulations, it became apparent that a further assumption, when estimating the tremor PRC, was in the definition of the start and finish of the tremor cycle. In contrast to the single neuron firing cycle, where the start of the ISI is defined intuitively by the onset of the action potential, our definition of the tremor cycle was arbitrarily defined by a threshold crossing value (Φ_thres) of 0 radians. Could the inappropriate definition of this threshold value have prevented the subsequent recovery of the tremor PRC? To test this confound, we returned to the ML neuron simulations and estimated the fPRC from single neuron PRC while varying threshold used to define the action potential timing (Fig. 3). For these simulations, the model neuron was simulated to produce a type I PRC, with A = 30. We compared the effect of inappropriately defining the action potential timing [e.g., defining the start of the action potential as −1 radians rather than the true onset of the action potential (0 radians)] and comparing the PRC estimated with the real PRC (Fig. 3A). The use of the incorrect Φ_thres resulted in the corruption of the PRC morphology and underestimation of the PRC (Fig. 3, A and B). The reason for this corruption and underestimation of the PRC can be understood by looking at the effect that the inappropriate definition of the firing cycle has on how T0 and T1 are measured (Fig. 3B). If the start and end of the firing cycle of the neuron are defined as occurring before the action potential (i.e., −1 radians), then this has the effect of inadvertently incorporating the shortening effect of the pulse on T1 into the T0 estimate, which results in the phase delay slip, illustrated in Fig. 3A. In contrast, if the firing cycle is defined inappropriately after the action potential (Φ_thres = +3), then T0 becomes shortened (as it has become contaminated by the real effect of the pulse on T1), and T1 is lengthened, as its estimate is contaminated by the subsequent unperturbed ISI (T₂; see Fig. 3B for an expanded illustration of this effect). Overall, this inappropriate definition of the neuron's cycle results in the artificially diminished PR [e.g., from Fig. 3B, the maximal PR_{(Φthres = 0)} = (100 − 73)/100 = 0.23; PR_{(Φthres = +3)} = (92 − 82)/92 = 0. 11] and an underestimation of the true PRC by ∼50%. These simulations emphasized that the definition of the firing cycle of the neuron is critical to recovery of the fPRC. Therefore, an additional explanation for our failure to recover the tremor PRC may have been that the arbitrary definition of the tremor cycle using Φ_thres = 0 may have caused a similar degradation of the PR estimate and prevented the recovery of the tremor PRC. These simulations would therefore further justify the need to estimate the tremor PRC across a range of Φ_thres values to prevent missing the tremor PRC through a priori assumptions as to the start and finish of the tremor cycles.

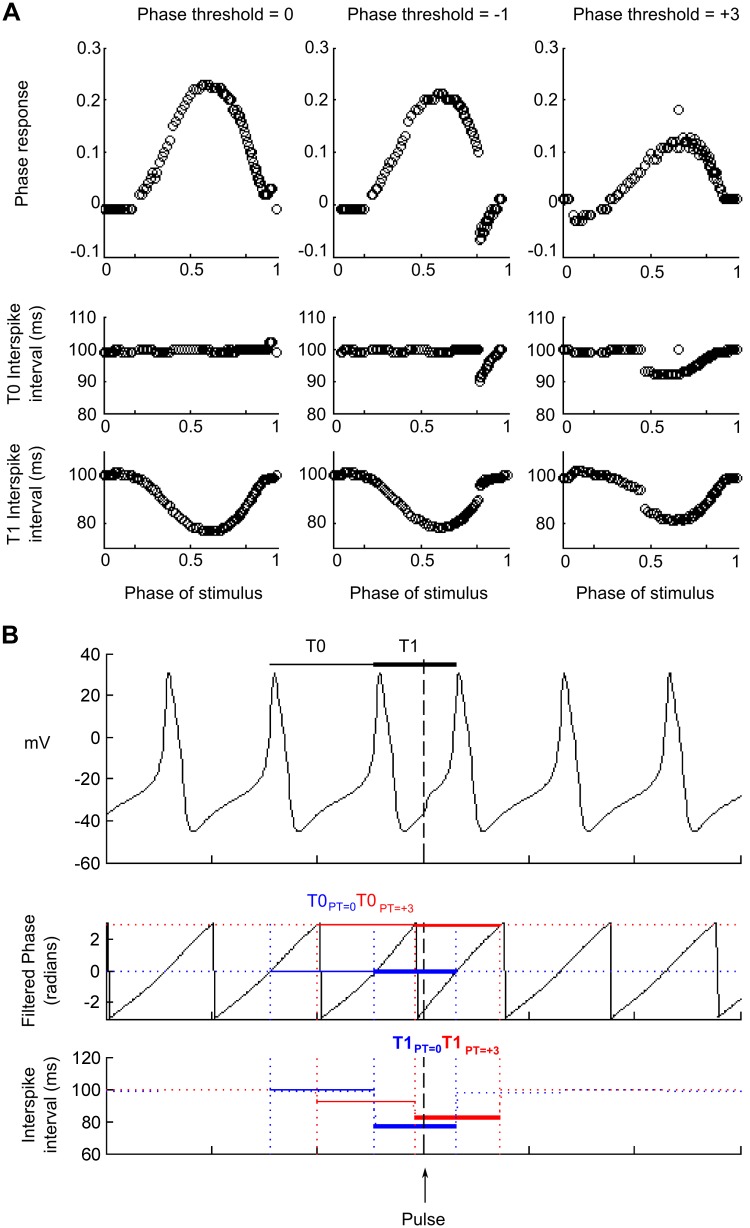
Fig. 3.

Effect of varying Φ_thres on the morphology of the fPRC and fPRC across multiple contiguous time samples [fPRC(t)]: single neuron simulations. A: attributing a different value of Φ_thres alters the ISI length estimate of T0 and T1. The correct Φ_thres = 0 aligns the Φ_thres, crossing to the point of action potential generation. Changes in Φ_thres, i.e., to −1 or +3 radians (middle and right), result in inaccuracies in the fPRC estimates. To understand this effect, an illustrative example of a PR estimate from the same neuron is provided (B). As illustrated (top), the effect of the pulse (dashed, vertical line) is to shorten T1 (thick black line) relative to T0 (thin black line), resulting in a relative phase advance (and positive PR of ∼0.22). The phase, derived from the Hilbert transform of the bandpass-filtered neuron, is illustrated (middle and bottom). With the assumption that the T0 and T1 are defined by the point at which the phase is >0 [i.e., Φ_thres (PT) = 0], the same PR can be measured (0.22), as T0 and T1 (thin and thick blue lines, respectively) are representative of the true T0 and T1 (derived from the actual spike time of the neuron). In contrast, if the Φ_thres is defined at +3 radians, then the definition of T0 and T1 becomes corrupted (bottom): T0 becomes shorter (thin red line) and T1 relatively longer (thick red line); the PR [PR = (T0 − T1)/T0] is correspondingly reduced (∼0.12). The same effect of misappropriation of the Φ_thres can explain the corrupted form of the PRC (A, middle) for stimuli occurring between 0.8 and 1 of the neuron period and the artificial reduction in the estimate for values between 0.5 and 0.8, where Φ_thres = +3.

In our initial estimates of the tremor PRC, we estimated a single PRC by extracting the PR of the tremor at a single time sample—that at which the TMS pulse is delivered. In the absence of noise, it is reasonable to assume that the PRC could be estimated from any sample within the length of a single tremor cycle. To test this assumption, we estimated multiple peristimulus fPRCs from the ML neuron spike trains. We also looked at how the Φ_thres definition corrupted the temporal evolution the fPRC(t). The results of this simulation are illustrated in Fig. 4. The expected corruption and underestimation of the PRC, when Φ_thres is defined inappropriately, are unsurprisingly identical to that when the PRC estimates are constrained to a single peristimulus time sample (as in Fig. 3). The graphical representation is simply complicated by the additional temporal dimension of the analysis. The temporal evolution of the true fPRC(t) (Fig. 4; Φ_thres = 0) illustrates an important property of this analysis; nevertheless, although the PRC is shifted in phase across the course of a single cycle, the PRC remains intact across all samples within the cycle of the oscillator (in this case, the 100-ms ISI). This positive “cluster” of PR values, dispersed across the ISI, illustrates an important statistical property of the PRC that could be used to estimate the PRC in the presence of noise: the effect of a stimulus pulse on the neuron is to produce multiple peristimulus PRCs. Therefore, we reasoned that the temporal stability of the PRC across multiple peristimulus time samples could be used to capture the tremor PRC in the presence of noise and under circumstances where unknowns, such as conduction delays, are present.

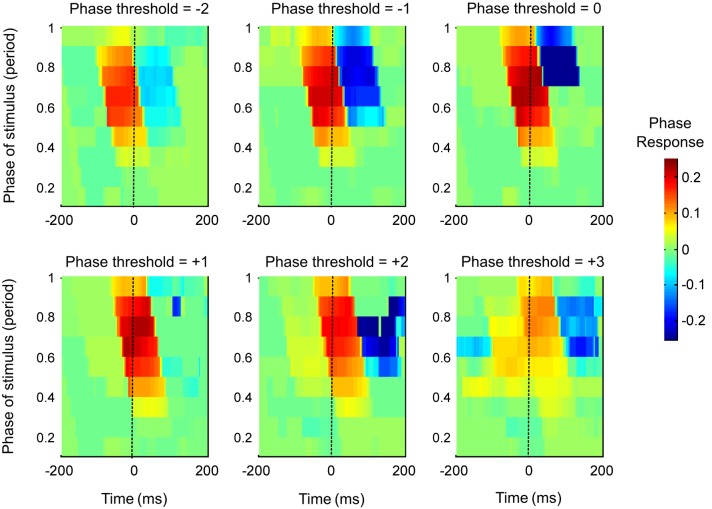
Fig. 4.

Temporal evolution of the fPRC estimated for multiple peristimulus time periods. fPRC estimates for the ML model neuron firing at 10 Hz (parameters set for type I PRC, with A = 30) were estimated every 3 ms, from −200 to +200 ms, relative to the stimulus. Varying the Φ_thres caused underestimation in the PRC (e.g., compare the true PRC Φ_thres = 0, where the peak PRC = 0.22, with PRC for Φ_thres = −2, −1, +2, and +3 radians).

Tremor PRC estimation informed from single neuron simulations.

With the use of these insights gained from the single neuron simulations, we re-examined our original data set from the patient tremor recordings by using an adapted approach. The fundamental difference to this re-analysis was to perform estimates of the tremor PRC at multiple peristimulus samples to find a cluster of PRCs and to perform estimates using different values of Φ_thres throughout the tremor cycle to prevent arbitrary allocation of this variable and underestimation of the tremor PRC.

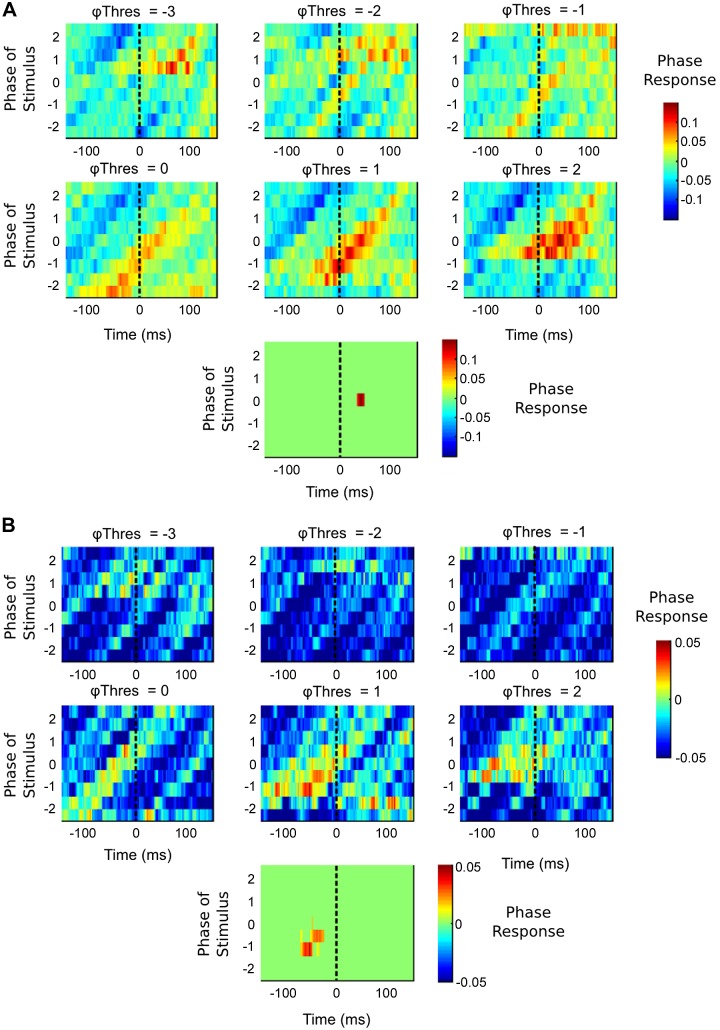
The estimation of the fPRC(t) at multiple peristimulus time samples (150 ms pre- and post-TMS pulse) and at 6 Φ_thres variables between −3 and 3 radians resulted in a clear, positive PR (phase advance) in both patients (with Φ_thres set to 1 and 2 radians for both patients). In contrast, for values of Φ_thres between −3 and 0 radians, no clear cluster of positive (or negative) PRs is seen (Fig. 5A, patient M; Fig. 5B, patient G). The dependency of these estimates on Φ_thres was analogous to that of the simulated ML neuron data (Fig. 4). A similar relationship, with both corruption and underestimation of the “real” fPRC(t) for Φ_thres not equaling 0 (the true Φ_thres), was observed. A clear contrast between the simulated fPRC(t) and the tremor fPRC(t) is the absence of noise in the simulated estimates. To establish if the PR clusters estimated from the patient experiments were expected to occur at a greater than chance level, we performed a series of shuffled fPRC(t) estimates (n = 100). These estimates were then thresholded according to the individual's maximal PR (for patient M, this was set to 0.1; for patient G, 0.01). Clusters of PR values outside of the interval (−0.1,0.1) were then summed to produce a probability density function for the “positive” and “negative” clusters, respectively. The results of fitting data derived from this procedure are illustrated (see Fig. 7A) for each patient. The maximum significant cluster ∑fPRC(t) was identified at +46 ms, Φ_thres = 2 radians [upper bounds of 99% confidence limit (CL) = 0.46], for patient M (Fig. 5A). No significant negative clusters (phase delays) were identified (lower bounds of 99% CL = −17.7). A similar peak was found in patient G (Fig. 5B) but at an earlier latency ∑fPRC(t) = 0.66, −50 ms, Φ_thres = 1 radian (upper bounds of 99% CL = 0.24). Again, no significant negative clusters were found (lower bounds of 99% CL = −48.2).

Fig. 5.

fPRC estimates for 2 patients with Parkinsonian tremor. A: fPRC(t) estimates for patient M following (n = 961) subthreshold TMS pulses to primary motor cortex. Maximal PRC estimate at Φ_thres = 2, +46 ms poststimulus (represented by the dotted vertical lines). A similar PRC was estimated at −50 ms (prestimulus), Φ_thres = 1 (n = 1,421), for patient G (B). The significant cluster of PR values after estimating the chance levels with a shuffling procedure (A and B, bottom).

Fig. 7.

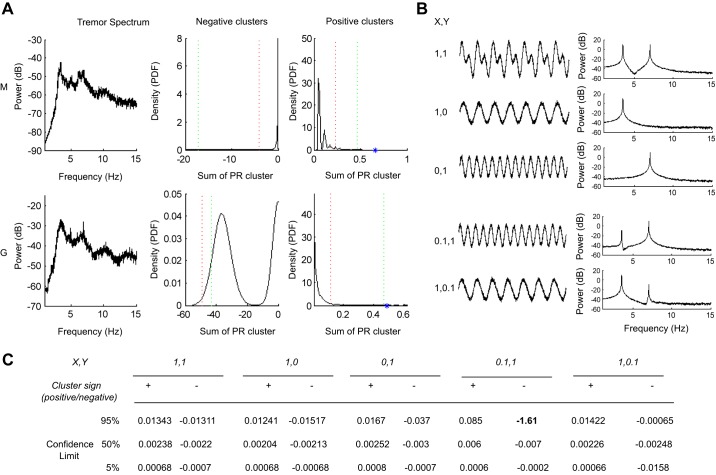
Confidence limit estimation for real and simulated tremor spectra. A: power spectrum from patients M and G with corresponding 99% (green) and 95% (red) confidence limits derived after bootstrapped estimates of the tremor spectrum for positive and negative clusters of PR. Note the large asymmetry in the confidence limits for negative PR clusters (99% confidence limits −17.7 and −48.2, respectively, for negative and 0.46 and 0.66 for positive clusters). Blue asterisks (right, top and bottom) illustrate individual patient cluster estimates that lie outside of the 99% confidence limit for positive clusters. PDF, probability density function. Simulated spectra (B) produced a similar bias when spectra consisted of a low-amplitude, 3.5-Hz harmonic relative to the first harmonic of the tremor spectra at 7 Hz [patients' spectral estimates (A), simulated spectral estimate figure (B) = 0.1,1]. C: table illustrates the fitted confidence limits for estimates derived from the different simulations in B. The bold number highlights the bias in the negative cluster confidence limit caused by interaction between the high- and low-frequency harmonic (in the simulated data).

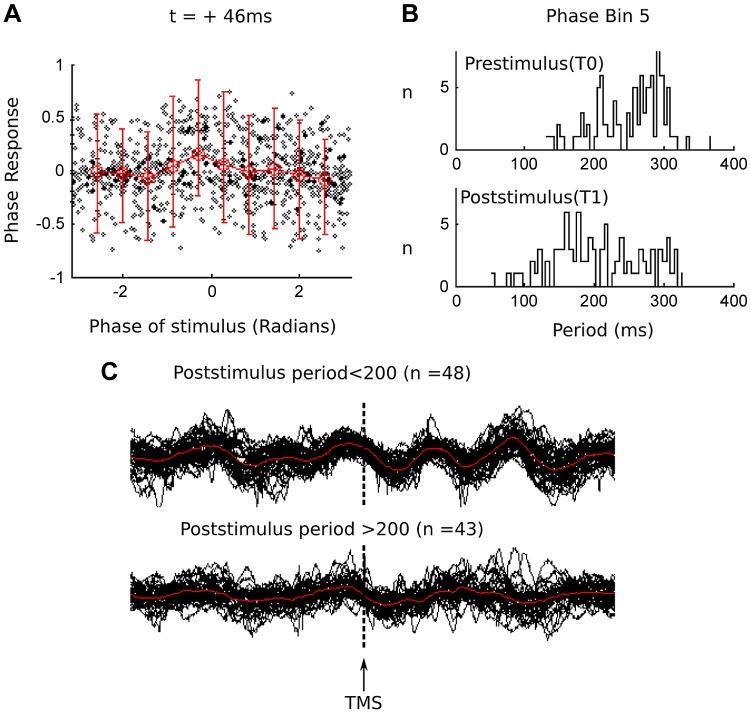
To explore the properties of the tremor's PR further, we examined the PRC at +46 ms post-TMS pulse (Fig. 6) in patient M. The effect of the TMS pulse on the tremor cycle is illustrated in Fig. 6. As expected from the positive PRC form, the effect on the poststimulus tremor cycle length is to shorten this and result in a phase advance or frequency modulation (to a higher tremor frequency). The comparison of the instantaneous cycle length of the tremor before and after the TMS pulse, during trials where this phase advance occurred (Fig. 6A; phase of stimulus, −1.25 to −0.62 radians), demonstrated a shortening of the cycle length from 246.7 ± 55 ms to 204.7 ± 65 ms (Fig. 6B). The further examination of the raw data of trials, where this “interval shortening” occurred, demonstrated a phase advance of the tremor in ∼50% of trials and corresponding frequency modulation to a higher instantaneous frequency (Fig. 6C).

Fig. 6.

Parkinsonian PRC: single trial analysis. A: single trial PRs plus superimposed average (across 10 phase bins) in red ± SE. Significant response at +46 ms in patient M (n = 961), pre- and poststimulus histogram of tremor period. B: expected shortening of tremor period (phase advance) when trials are sorted into T0 and T1 (mean interval 246.7 + 55 ms to 204.7 + −65 ms). C: to examine the mechanism of this phase advance produced when the TMS pulse coincides with this phase of the tremor, we examined the raw accelerometer trace for trials from T1. The plotting of the trials (n = 48), where there was clear phase advancement (indexed by an instantaneous cycle length of <200 ms), illustrates the frequency-modulating effect of the TMS pulse on the tremor trace (top). In contrast, ∼50% (n = 43) of the TMS pulses did not affect the tremor phase when stimulated at this point in the tremor cycle (bottom).

In all, these patient experiments demonstrated the validity and reproducibility of the iterative approach outlined above. An unexpected feature of the confidence limit estimate, however, was the considerable asymmetry in the confidence limits for positive and negative PR “clusters.” There was a strong bias in the negative cluster estimates to find “false positive” clusters with large negative values. As this result has implications for the ability of our method to extract PRCs with negative values (e.g., type II or PRCs derived from inhibitory input), we went further to explore the potential mechanisms of this effect. A possible explanation lies in the potential interaction between harmonics of the tremor spectrum. In both patients, the tremor was characterized by a 3.5-Hz dominant peak with a secondary harmonic at ∼7 Hz (Fig. 7A). These spurious clusters of PR may have resulted as a direct consequence of natural fluctuations in the amplitude of these two harmonics. We tested this hypothesis by performing confidence limit estimations on simulated tremor spectra while varying the spectral content of the signal (Fig. 7). “Asymmetrical” confidence limits with a 10-fold bias toward negative clusters were only observed when a spectrum consisted of a dominant, 7-Hz harmonic (a_X = 0.1; a_Y = 1; 95% CL for negative clusters = −1.61; 95% CL for positive clusters = 0.085). In contrast, the confidence limits remained relatively symmetrical for all other variations tested, including the spectrum where both harmonics are equally represented (a_X = 1; a_Y = 1; 95% CL for negative clusters = −0.0134; 95% CL for positive clusters = 0.0131). This simple simulation provides an intuitive explanation for the bias in our confidence limits from the patient PRC estimates: pseudo-phase delays will naturally occur, due to the nonstationarity of the tremor signal. During episodes where the first harmonic becomes dominant, pseudo- phase delays will occur when the threshold crossing estimate (and the instantaneous period of the tremor) is modulated by the weak, low-frequency oscillation of the fundamental frequency of the tremor.

Estimates of simulated PRC in the presence of noise.

A critical assumption of our approach is that it remains valid to define the PRC by comparing the effect of a perturbation on the pre- and poststimulus cycle when these are fluctuating in response to noisy (unknown) inputs. This additional noise in the tremor PRC estimates could be considered to violate the basic assumption of PRC theory—that the oscillator returns to a stable limit cycle following the perturbing stimuli (Smeal et al. 2010). Previous approaches to estimating the “noisy PRC,” such as the infinitesimal PRC (where Fourier components are fitted to the cycle-to-cycle variation in the ISI of neurons), rely implicitly on knowledge of the input to the neuronal oscillator. As this is unknown in the case of the tremor, a perturbation-based approach remains the only feasible option to recover the PRC. Although perturbation-based PRCs have been estimated from noisy data [e.g., Mattei and Schmied (2002)], the variance in the tremor cycle in our estimates (upwards of 20% of the tremor cycle) exceeds the conventional accepted threshold of ∼10% (Galán et al. 2005). This raises the question as to whether the PRC form can still be recovered using a perturbation approach when noise levels are high. To address this question, we performed further simulations to establish if the PRC could be recovered in the presence of noise at levels comparable with that in the tremor PRC estimates.

We simulated spiking using the ML model, while adjusting the parameters of the model to produce both types I and II PRCs, characterized by monophasic and biphasic (both positive and negative) PRC forms (see Fig. 8, D and G). We then incorporated noisy input into the model neuron to produce variability in the ISI of neurons and repeated the PRC estimation procedure after filtering the neuron spike train. Each PRC estimate consisted of 1,000 stimulus presentations, constituting a single “experiment.” We performed 10 separate simulated “experiments” with the intention of establishing the reproducibility of PRC estimates in the presence of noise. With 25% variability in the ISI (analogous to the tremor estimates)—the extraction of the PRC at t = 0 (pulse delivery) for type I excitability was not possible—the PRC was poorly reconstructed and bore little resemblance to the original PRC (compare Fig. 8, D with E). In contrast, the biphasic form of the type II PRC could be recovered, despite the variability in the ISI, and could be replicated consistently across “experimental” sessions (see Fig. 8H, where an estimate from 1,000 perturbations is represented). Consistent with this observation, the correlation coefficient between the values of the true PRC (unfiltered estimate in the absence of noise) and the fPRC with 25% ISI variation was low, r = 0.06 ± 0.31 (mean ± SD across the 10 experiments), for the type I PRC and higher for the type II, 0.77 ± 0.11. These simulations demonstrated that the PRC can be recovered for the ML, with type II excitability using a perturbation approach, despite high levels of intrinsic variability in the firing rate of neurons.

Fig. 8.

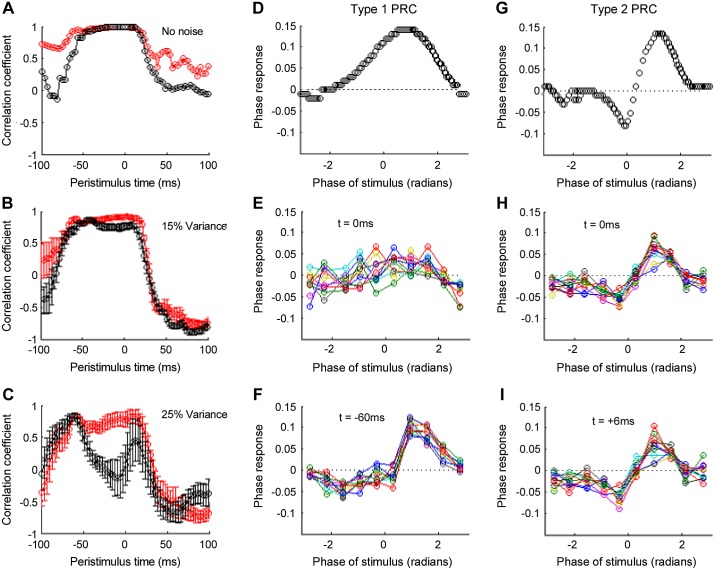
PRC estimates form the ML model in the presence of noise. The PRCs for types I and II excitability for regular spiking (No noise) are illustrated (D and G, respectively). The PRCs following the addition of noise to the simulations (25% ISI variability) are illustrated (E and F), following filtering of the spike train and application of the same method used to estimate the tremor PRC. Each colored line represents a single “experimental estimate,” based on 1,000 stimulus presentations. The PR values are averaged within 10 evenly spaced bins across the firing cycle (defined between −π and π). Note the lack of reproducible estimate of the type I PRC (E) compared with type II when the PRCs are extracted from t = 0, the time the perturbing pulse is delivered. The biphasic properties of the type II PRC are still reproduced using our approach, despite the 25% variability of the ML firing rate. A: the temporal evolution of the PRC(t) is represented by correlating the ideal PRC (No noise) at t = 0 against itself for peristimulus estimates between −100 and +100 ms. For both types I (black line) and II (red line) PRCs, the correlation coefficient tends toward 1 for samples between −60 to +20 ms with respect to the stimulus presentation. With the addition of noise, ∼15% ISI variability (B), the PRC estimates from samples close to the stimulus presentation become corrupted for type I, represented by the reduction in the correlation coefficient (black line). Simulations in the presence of 25% ISI variability (analogous to that seen in the tremor estimates) produce a substantial reduction in the reliability of the type I PRC estimate (C), whereas the type II estimates remain relatively robust. The PRC estimate for type I excitability at the point of the maximal correlation coefficient (t = −60 ms) is illustrated for each of the 10 estimates (F). The corresponding maximal estimate for type II (t = +6 ms) is illustrated (G) for comparison. Note that the type I estimate form −60 ms represents the original PRC (D) well, from 1 to π radians, but the original form of the PRC is under-represented for the remainder of the cycle (an artificial negative region is introduced).

This analysis constrained the fPRC estimates to t = 0, the point of the current pulse delivery. To what extent could the underestimation of the type I PRC, in the presence of noise, be a consequence of assuming that under noisy conditions, the estimate is most robust at the point of stimulus delivery? We tested this assumption by estimating the fPRC at peristimulus time samples around the stimulus presentation. With 25% variability in the ISI, simulated PRC estimates that time samples in close proximity to the stimulus became unrepresentative of the original PRC (Fig. 8C) for type I estimates. The correlation coefficient, between the “ideal,” noiseless PRC and the noisy estimates, tended to increase for estimates between −100 and −50 ms for both excitability types but peaked at −60 ms (r = 0.82 ± 0.06) for type I and +6 ms (r = 0.83 ± 0.10) for type II. The plotting of the PRC estimates from 10 experimental sessions for the type I estimates at t = −60 ms illustrates the extent to which the additional peristimulus estimates augment the ability to delineate the PR in the presence of noise. The type I PRC at t = −60 ms (Fig. 8F) is both reproducible across experimental session and representative in terms of the position of the peak and amplitude of the PR. Differences nevertheless exist between the original PRC and the noisy PRC extracted from t = −60 ms. Specifically, there is corruption of the form of the type I PRC, with a negative region in the PRC for stimuli between −2 and −1 radians.

Overall, these simulations would suggest that in levels of noise, comparable with those seen in the tremor PRC estimates, the PRC can be recovered from the ML model, providing that estimates from peristimulus samples are included in the estimation process. Although this causes minor corruption of the type I PRC form, the salient features of this PRC can still be recovered. These simulations therefore both rejected the possibility that the PRC cannot be recovered from noisy “real-world” biological data (using a perturbation approach). They also provided further justification for transforming tremor PR estimation from a single dimensional problem (phase of stimulus) to a three-dimensional problem, following the addition of further two degrees of freedom (i.e., latency and Φ_thres).

DISCUSSION

The aim of this report was to demonstrate that the PRC could be recovered from an oscillatory signal (in this case, tremor), the basis of which is (in part) the consequence of a rhythmic population of synchronized neuronal firing. The PRC has been estimated previously from a broad range of oscillating biological systems, including single motor units (Mattei and Schmied 2002) and epileptic slow-wave discharges (Perez Velazquez et al. 2007), and from the gamma oscillation in vitro hippocampal slices (Akam et al. 2012). This is the first report of a PRC estimate for tremor. The unknown relationship of the neuronal firing to the population neuronal oscillation, the precise timing of the perturbing pulse, and the inherent variability of the tremor period make recovery of the tremor PRC challenging. With the use of simulated neuronal data (with known PRCs), we demonstrate here that when estimating the PRC, the definition of the firing cycle of the neuron is nonarbitrary and when unknown (as in the case of tremor PRC estimation), requires multiple estimates to ensure that the PRC can be extracted. Furthermore, to capture the tremor PRC reliably, this must be estimated at multiple peristimulus time points: if we had restricted our PRC analysis to the time point at the onset of the TMS pulse or at +20 ms (i.e., allowing for corticospinal conduction), the resultant PRC would have been underestimated (in case M) or absent (in case G). The disadvantage of a “blind,” iterative approach is the potential to find false-positive PRC estimates. This, in turn, requires substantial computational time to derive a confidence limit for the real estimate. Future work may be required to approach this with alternative methods that may prove more efficient.

Several limitations to this method must be considered when estimating the tremor PRC (or applying this method to any other physiological oscillating system). Firstly, the process of filtering the tremor signal loses information about the PRC. This has the effect of underestimating the eventual PRC. Different forms of PRCs could be extracted reliably and their features retained from the filtered spike trains in our simulated data, despite the inherent limitations of filtering. Despite this, we found an unexpected bias when estimating the tremor PRC for falsely detecting “negative troughs,” which represent phase delays when the confidence limits were estimated. We found that this could be explained by an epiphenomena of the spectral content of the tremor (which contains a significant first harmonic). In practical terms, this places an important interpretational limitation on the PRC tremor estimate. Firstly, this bias will result in the potential to “miss” small troughs that characterize biphasic type II PRCs (Gutkin et al. 2005). Furthermore, in the theoretical case of an oscillating neuronal population receiving inhibitory input, the PRC would also be in danger of falling within the confidence limits. These observations reinforce the importance of cautious interpretation of the PRC estimated from tremor (or any neuronal oscillatory population) that has more than monotonic spectral composition.

Although PRCs from noisy experimental data (such as single neurons) have been estimated, the variability of the tremor cycle, ∼25% in these estimates, exceeds that for previous estimates in single neurons, where a 10% variation in the ISI was accepted (Galán et al. 2005; Mattei and Schmied 2002). This additional noise in the tremor PRC estimates could be considered to violate the basic assumption of PRC theory—that the oscillator returns to a stable limit cycle following the perturbing stimuli (Smeal et al. 2010). Despite observing a phase-dependent advance of the tremor phase by the TMS pulse in both patients (suggestive of type I PRC), to what extent is it possible to classify the tremor PRC correctly, given these caveats? The fact that we were able to recover the ML PRC in the presence of equivalent levels of noise, using the same procedure applied to the tremor estimates, would argue that PRC form can still be delineated through a perturbation-based approach. The key limitation to perturbation-based estimates, therefore, becomes the signal-to-noise ratio, necessitating large numbers of stimuli, which may or may not be feasible, depending on the experimental context. Our observation that the type I PRC estimated from the ML model is less resistant to noise is consistent with previous theoretical studies (Ermentrout et al. 2011). Neuronal models with type I excitability and strictly positive type I PRCs exhibit far greater PR variance than type II models (Ermentrout et al. 2011). Our ability to “capture” a corrupted version of the type I PRC at 60 ms before the stimulation implies that the deleterious effects of noise on the type I PRC estimate are not constant in time. This recovery of the PRC from a sample, 60 ms before the stimulus, further justifies the iterative approach that we applied to the tremor estimates; however, the corruption of the PRC's form (these estimates were consistently biphasic, with an erroneous negative region introduced) emphasizes that strictly for the basis of PRC classification, estimates from time samples outside of the stimulus presentation are likely to be unclassifiable. Overall, the answer to the question of whether the PRC can be estimated and classified in the presence of high levels of noise is a binary one: for samples at the time of stimulus presentation, the PRC can be recovered and classified. In contrast, estimates recovered from peristimulus samples can be used to confirm a causal effect of the stimulus on the oscillating system, but the resulting PRC is unclassifiable. Given the latencies at which the tremor PRCs were estimated (+46 and −50 ms) for the patients, we can only conclude that for these two examples, weak perturbing stimuli were able to modify the ongoing phase of the tremor in a manner consistent with a PRC. We cannot conclude with any certainty which bifurcation type or excitability class to which the oscillator underpinning these tremor PRC estimates belongs. Certainly, for these two example cases, this inability to classify the PRC type would preclude the integration of these estimates into a reduced-phase model (i.e., to develop a closed-loop stimulation device informed by the PRC class). From a purist's perspective, this interpretational limitation may seem insurmountable; however, in practical terms, the very existence of a PRC estimate (irrespective of whether it can be classified) provides an important and novel functional insight into tremor physiology: weak external stimulation to motor cortex can modulate the tremor's phase (and frequency). On a practical level, the PRC can be estimated in individual patients with tremor and therefore, represents a novel biomarker that could be used clinically to predict response to pharmacological treatments or establish novel sites at which neurostimulation may access the tremor network. This personalization of the treatment approach may be increasingly important in PD tremor, given the recognition that tremor genesis involves multiple oscillating sources and may be clinically heterogeneous (Brittain et al. 2015).

Although the aim of this study was not to explore the physiological significance or basis of the PD PRC, it is difficult not to comment at this stage on the latencies at which the “maximal” PRC was estimated in the two patients studied. These are remarkable for both their long latency with respect to the onset of the stimulus (∼50 ms) and their discordance between the two subjects (+46 ms in patient M; −50 ms in patient G). On one hand, these are reassuring, as a simple effect of superimposition of the MEP on the tremor (in a phase-dependent manner) would be expected to be maximal at ∼20 ms, in line with the central motor conduction time. The concordance with these latencies and the estimate for the ML PRC with type I excitability (maximal at −60 ms before the stimulus) illustrate that the maximal PRC estimate may not necessarily be at the time at which the stimulus is delivered. If these latencies, at which the PRC estimates were maximal, do represent the time at which the stimulus perturbed the tremor cycle, then we believe that long delays and discordance between subjects are not irreconcilable with a physiologically oscillating system. A similar situation has been observed when estimating corticospinal conduction time of oscillation corticomuscular coherence estimates. In these estimates of beta coherence (cycle ∼50 ms), systematic phase differences among +20, 0, and −20 ms have been observed in different subjects. It is thought that differences in the balance of feedback between afferent and efferent systems to the oscillatory system contribute to this discrepancy (Witham et al. 2011). The latency differences in our PRC estimates may therefore reflect similar differences in the relative contribution of afferent (feedback) and efferent (feedforward) processes that contribute to the genesis of the tremor. One further aspect that we cannot discount is the possibility of anticipation of the stimulus, particularly in the case of the −50-ms estimate. Parkinsonian patients are recognized for their attention sensitivity to external cues (Brown and Marsden 1988). As the TMS pulses were delivered at regular intervals (1 Hz), the PRC that preceded the TMS pulse may therefore have resulted, not from the effect of the TMS pulse directly on motor cortex but from anticipation of the pulse as an external auditory cue at some unknown site. Nevertheless, although we cannot discount this as mechanistic confound, the effect of the stimulus is a PR, irrespective of how or where the stimulus acts.

To what extent can the PRC estimated from PD tremor be considered analogous to the classical PRC or tPRC? A basic assumption of the PRC is that perturbing stimuli advance or delay the phase of the oscillating system. Although one mechanism of the tremor PRC observed is an increase in the tremor frequency as a consequence of the phase advance produced by the stimulus, we cannot discount the possibility of an interaction between the tremor fundamental frequency and its first harmonic. For example, a phase-dependent modulation (increase) in the amplitude of the first harmonic of the tremor could equally have produced the same result. The consequence of this phase-dependent augmentation of the first harmonic would be to produce a pseudo-frequency modulation (and phase advance) in the tremor when taken as a whole. We performed further estimates of the tremor PRC while attempting to narrow the bandwidth and exclude the first harmonic (results not shown); however, the PRC could not be recovered without including the whole of the spectrum (i.e., from 3 to 7 Hz). This could be considered to support the idea that the PRC observed is the consequence of an interaction between the harmonics of the tremor spectrum. However, the filtering of the first harmonic could equally remove a genuine frequency modulation of the fundamental frequency of the tremor. Therefore, this approach cannot be used to exclude definitively a harmonic interaction.

Irrespective of the potential mechanism of the PRCs recovered with our methodology, this result demonstrates that subthreshold stimuli to primary motor cortex can frequency modulate the tremor in a phase-dependent manner. Despite the interpretational caveats of our approach to tremor PRC estimation, we hope that this paper stimulates further efforts to estimate the tremor PRC reliably. Such an approach is likely to be critical to informing the development of closed-loop stimulation therapeutic devices for patients with movement disorders.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: T.A.S. and T.G. conception and design of research; T.A.S. and P.K. performed experiments; T.G. analyzed data; T.G. interpreted results of experiments; T.G. prepared figures; T.A.S., M.J.E., and T.G. drafted manuscript; T.A.S., M.J.E., P.K., and T.G. edited and revised manuscript; T.A.S., M.J.E., P.K., and T.G. approved final version of manuscript.