Prediction suppression in monkey inferotemporal cortex depends on the conditional probability between images

Abstract

When monkeys view two images in fixed sequence repeatedly over days and weeks, neurons in area TE of the inferotemporal cortex come to exhibit prediction suppression. The trailing image elicits only a weak response when presented following the leading image that preceded it during training. Induction of prediction suppression might depend either on the contiguity of the images, as determined by their co-occurrence and captured in the measure of joint probability P(A,B), or on their contingency, as determined by their correlation and as captured in the measures of conditional probability P(A|B) and P(B|A). To distinguish between these possibilities, we measured prediction suppression after imposing training regimens that held P(A,B) constant but varied P(A|B) and P(B|A). We found that reducing either P(A|B) or P(B|A) during training attenuated prediction suppression as measured during subsequent testing. We conclude that prediction suppression depends on contingency, as embodied in the predictive relations between the images, and not just on contiguity, as embodied in their co-occurrence.

human infants and adults are able to learn rapidly, through passive experience, the statistical relations governing the transition from one element to the next in a structured stream of visual images (Bulf et al. 2011; Fiser and Aslin 2002; Howard et al. 2008; Kim et al. 2009; Kirkham et al. 2002; Turk-Browne et al. 2005, 2008) or auditory stimuli (Pelucchi et al. 2009; Romberg and Saffran 2010; Saffran et al. 1996). The neuronal mechanisms underlying this capacity are not yet well understood (Gavornik and Bear 2014; Meyer and Olson 2011; Summerfield and Egner 2009; Wacongne et al. 2012). Single-neuron recording studies in monkeys have, however, begun to cast light on this issue. Repeated viewing of two images in fixed sequence, so that the leading image becomes a strong predictor for the trailing image, induces prediction suppression among neurons of inferotemporal area TE. They respond weakly to a trailing image when it follows the leading image that preceded it during training and respond strongly when it follows some other leading image (Meyer and Olson 2011; Meyer et al. 2014). For ease of reference, we term this phenomenon prediction suppression although it remains to be determined whether the effect arises from suppression of neural responses when the trailing image is predicted or from enhancement of neural responses when it is unpredicted.

In humans, transitional statistical learning depends not just on the repeated pairing between successive elements in a stimulus stream but also on their conditional probability (Aslin et al. 1998; Fiser and Aslin 2001; Meyer and Baldwin 2011). For instance, infants exposed to a syllable stream learn a particular syllabic sequence as legitimate if the leading syllable is always followed by a particular trailing syllable. However, the effect is abolished by inserting additional instances in which the leading syllable is followed by a different trailing syllable (Aslin et al. 1998). Whether similar principles apply to prediction suppression in TE is unknown. To resolve this issue, we measured prediction suppression in monkeys exposed repeatedly to displays in which leading and trailing images were paired with equal frequency but their conditional probability varied.

MATERIALS AND METHODS

Subjects.

We studied two adult rhesus macaques: monkey 1 (male; laboratory designation Tu) and monkey 2 (female; laboratory designation Ec). Procedures were in accordance with guidelines set forth by the United States Public Health Service Guide for the Care and Use of Laboratory Animals and were approved by the Carnegie Mellon University Institutional Animal Care and Use Committee.

Task.

The monkeys were required, during both the training and testing phases of the experiment, to engage in passive viewing of pairs of images presented in sequence. The succession of events in each trial was as follows: fixation spot (300 ms), leading image at screen center (503 ms), an 18-ms delay, trailing image at screen center (503 ms), an 18-ms delay, fixation spot (300 ms), and reward delivery (Fig. 1A). A trial was aborted without reward if, at any point from onset of fixation to offset of the fixation spot at the end of the trial, the monkey failed to maintain fixation within a 4 × 4° central window. The use of a relatively large fixation window was required because, during presentation of the images, which spanned 4°, the fixation spot was absent.

Fig. 1.

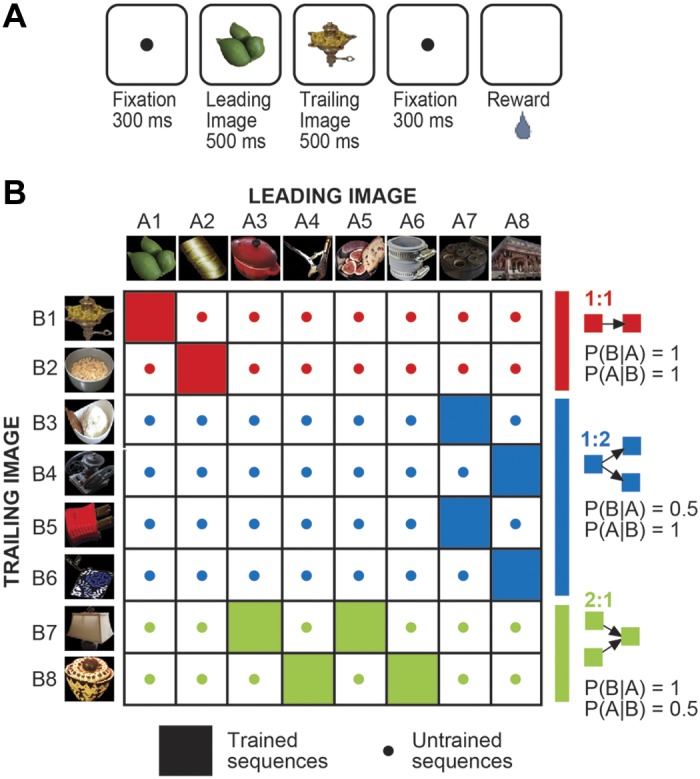
During the training period, the conditional probability of sequentially presented images was manipulated independently of the frequency with which they were paired. A: timing of events within each trial during training and subsequent neuronal data collection sessions. B: 8 leading and 8 trailing images were employed. During training, 10 sequences were presented repeatedly with equal frequency (filled cells). In the 1:1 condition (red) a given leading image (A) always preceded a given trailing image (B) so that P(B|A) = P(A|B) = 1. In the 1:2 condition (blue) a given leading image could be followed by either of 2 trailing images so that P(B|A) = 0.5 and P(A|B) = 1. In the 2:1 condition (green) a given trailing image could follow either of 2 leading images so that P(B|A) = 1 and P(A|B) = 0.5. During neuronal recording, each of the 10 trained sequences was presented 8 times and each of the 54 untrained sequences was presented once. Prediction suppression took the form of a reduction in the strength of the neuronal response elicited by a trailing image when it was in a trained sequence (filled cell) than when it was in an untrained sequence (dotted cell). The trained and untrained sequences used to assess prediction suppression in the 1:1, 1:2, and 2:1 conditions are rendered in red, blue, and green, respectively.

Training.

On each training day, the monkey completed one or more runs. A run consisted of 60 successfully completed trials. The trials conformed to 10 conditions representing all allowable pairings of leading and trailing images (filled cells in Fig. 1B). Each condition was imposed six times during a run. The conditions were interleaved randomly subject to the constraint that within each block of 10 successfully completed trials each condition had to be imposed once. The number of runs completed on a day ranged from 1 to 12 in monkey 1 and from 1 to 3 in monkey 2. Monkey 1 viewed each sequence 834 times during 139 runs extending over 27 days. Monkey 2 viewed each sequence 408 times during 68 runs extending over 40 days.

Although the number of trials completed successfully was, by design, identical across the 10 image sequences, the number of unsuccessful trials was not subject to control because the monkeys introduced errors arbitrarily by breaking fixation. If a fixation break occurred after presentation of the second image, then, although the trial was aborted, the monkey still experienced the two-image sequence. The percent increase in exposures due to the occurrence of such trials was 3.2% (3.7 and 2.7% in monkey 1 and monkey 2, respectively) in the 1:1 condition (red in Fig. 1B), 5.0% (3.8 and 6.3% in monkey 1 and monkey 2, respectively) in the 1:2 condition (blue in Fig. 1B), and 5.2% (4.4 and 6.0% in monkey 1 and monkey 2, respectively) in the 2:1 condition (green in Fig. 1B). Inasmuch as these occurrences were rare and inasmuch as their trend was to be more numerous under conditions in which prediction suppression was weaker, it is appears unlikely that they contributed substantially to the observed results.

Testing.

During neuronal data collection, the monkeys completed trials identical to training trials with regard to the timing of events (Fig. 1A). The status of the images as leading or trailing was the same as during training. However, any leading image might be followed by any trailing image. A run consisted of 134 trials encompassing 80 trained sequences (each of 10 trained sequences occurring 8 times) and 54 untrained sequences (each of 54 untrained sequences occurring once). The conditions were imposed in random order with replacement on error.

Images.

All stimuli were digitized images of background-free objects. When presented on an LCD monitor 32 cm from the monkey's eyes, each image subtended 4° of visual angle along whichever axis, vertical or horizontal, was longer. The full stimulus set for monkey 1 consisted of eight leading images and eight trailing images paired according to rules summarized in Fig. 1B. The same images were used in monkey 2 but with their sequential status (leading or trailing) reversed and the pattern of pairing altered so that no images paired in monkey 1 were paired in monkey 2. The images shown in Fig. 1 are representative of the images used in training but are not identical.

Recording.

An electrode was introduced through a vertical guide tube into left (monkey 1) or right (monkey 2) temporal lobe. We determined the locations of the recording sites by extrapolation from MRI-visible fiducial markers within the chamber. The identified locations, as judged by reference to standard maps of cytoarchitecturally defined areas in the temporal lobe, lay within area TE (Bonin and Bailey 1947) in the ventral bank of the superior temporal sulcus and on the inferior temporal gyrus and lateral to the perirhinal cortex (Suzuki and Naya 2014). They lay at levels anterior to the interaural plane by 16–19 mm in monkey 1 and 13–16 mm in monkey 2.

Database.

We monitored neuronal activity at one site during each recording session. Following the recording session, neuronal spikes were classified offline by use of a hierarchical clustering algorithm (Plexon Offline Sorter) with the requirement that spikes, to be considered as deriving from separate neurons, form clearly distinct clusters. We classified a neuron as visually responsive if, for either the leading or the trailing image, the mean firing rate in a window 50–300 ms following image onset exceeded the mean firing rate in a 100 ms baseline window centered on image onset (one-tailed t-test, α = 0.05). Eighty-six neurons meeting this criterion were recorded from 51 sites (30 and 21 in monkeys 1 and 2, respectively). Sites yielding 1, 2, and 3 neurons numbered 23, 21, and 7, respectively. Traces from the same 51 sites passed through a low-pass filter with a high-frequency cut-off of 170 Hz formed the local field potential (LFP) database.

Statistical analysis.

To determine whether prediction suppression occurred under a given condition (1:1, 1:2 or 2:1) required assessing whether a corresponding measure (spike rate or peak-to-peak LFP amplitude) differed significantly between trials when the trailing image was unpredicted (U) and when it was predicted (P). To make this determination, we computed the mean of U and the mean of P for each neuron or LFP site. The distribution of means across observations (86 neurons or 51 recording sites) in some cases deviated from normalcy (Jarque-Bera test). To correct for this problem, we conducted all analyses on log-transformed values. Following log transformation, no distribution deviated from normalcy. Comparison between U and P was based on a two-tailed paired t-test (α = 0.05). To determine whether prediction suppression (S = U-P) differed significantly between condition A (for example 1:1) and condition B (for example 1:2), we computed S for each neuron or recording site. We then log-transformed the values. Following log transformation, no distribution deviated significantly from normalcy. We then carried out a two-tailed paired t-test (α = 0.05) comparing the means of S under the two conditions.

RESULTS

The experiment began with a training period during which the monkeys passively viewed pairs of images presented in fixed sequence (Fig. 1A). For each monkey, the training set consisted of eight leading images and eight trailing images (Fig. 1B). These were presented in 10 sequences (filled cells in the matrix of Fig. 1B). The sequences were presented with equal frequency. Thus the 16 individual images were matched for absolute probability and the 10 training pairs were matched for joint probability. However, the relations of conditional probability pertaining between the leading and trailing images were different. Across the two sequences highlighted in red in Fig. 1B, one leading image (A) and one trailing image (B) always appeared in sequence. Accordingly, we designate this as the 1:1 condition. Under this condition, the appearance of A guaranteed that B would follow: P(B|A) = 1. Likewise, the appearance of B guaranteed that A had preceded: P(A|B) = 1. Across the four sequences highlighted in blue, a given leading image could precede either of two trailing images. We term this the 1:2 condition. Under this condition, P(A|B) = 1 but P(B|A) = 0.5. Across the four sequences highlighted in green, either of two leading images could precede a particular trailing image. We term this the 2:1 condition. Under this condition, P(B|A) = 1 but P(A|B) = 0.5. Training of each monkey extended over multiple weeks and included more than 400 exposures to each of the 10 image sequences.

After completion of training, we measured the responses of 86 visually responsive neurons in anterior TE (56 in monkey 1 and 30 in monkey 2) to leading and trailing images presented in both trained and untrained sequences. During each run, the 10 trained sequences appeared 8 times each and 54 untrained sequences, representing all other possible combinations of the leading and trailing images, appeared once each for a total of 134 trials. If prediction suppression were present, then we would expect a trailing image to elicit a weaker response when it occurred in a trained sequence than when it occurred in an untrained sequence. Cells in the matrix of Fig. 1B indicate the trained conditions (filled) and untrained conditions (dotted) that were compared to measure prediction suppression under the 1:1 condition (red), the 1:2 condition (blue), and 2:1 condition (green). All analyses were conducted on data combined across the two monkeys. Every effect subsequently described as significant in the combined data either achieved significance in both monkeys or achieved significance in one monkey while the trend in the other monkey was of matching sign although insignificant.

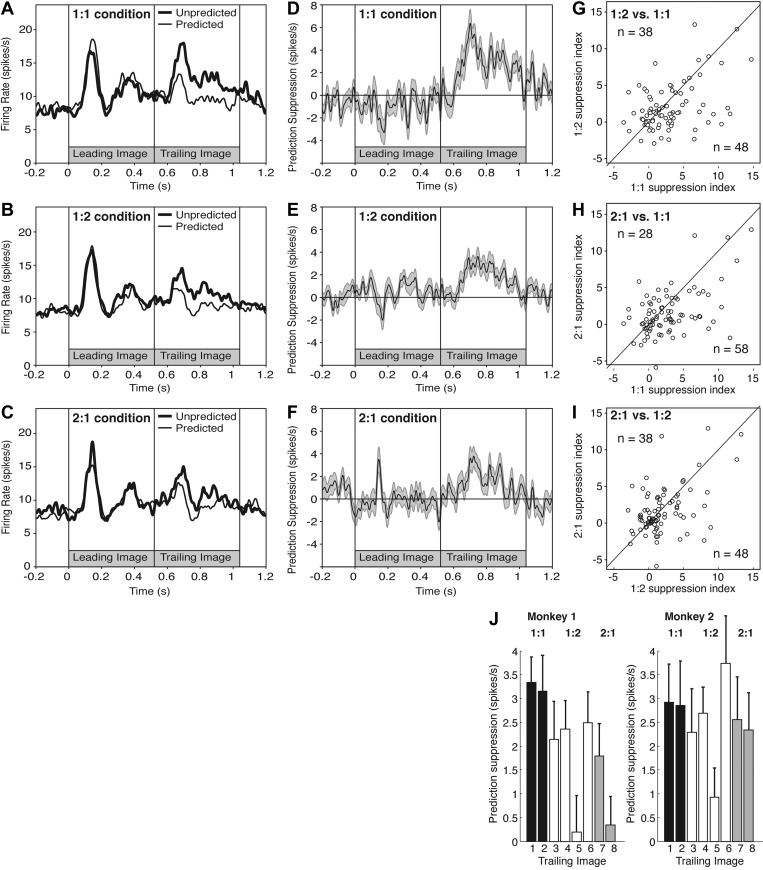
Population histograms representing the mean firing rate during trials in which the trailing images were unpredicted (thick line) or predicted (thin line) revealed prediction suppression after all three training procedures (Fig. 2, A–C). Prediction suppression is evident as an excursion of the difference signal (response to trailing image on unpredicted trials minus response to trailing image on predicted trials) into the positive range under each condition (Fig. 2, D–F). Note that this measure is based exclusively on the response to the trailing image and not on the response to the leading image. The mean difference signal 100–500 ms after trailing-image onset was significantly greater than zero under all three conditions (1:1 mean = 3.1 spikes/s, P = 3.0 E-8, T = 6.11; 1:2 mean = 2.0 spikes/s, P = 2.7 E-5, T = 4.44; 2:1 mean = 1.6 spikes/s, P = 0.0066, T = 2.78; two-tailed paired t-test; n = 86).

Fig. 2.

Prediction suppression, measured at the level of population spiking activity, was stronger in the 1:1 condition than in the 1:2 and 2:1 conditions. A–C: mean firing rate of 86 neurons stimulated with trailing images from the 1:1 set (A), the 1:2 set (B), and the 2:1 set (C). In each plot, the thin curve represents activity on trials in which the trailing image was presented in a trained sequence and therefore was predicted, while the thick curve represents activity on trials in which the trailing image was presented in an untrained sequence and therefore was unpredicted. D–F: mean prediction suppression signal (firing rate on unpredicted trials minus firing rate on predicted trials) of 86 neurons stimulated with trailing images from the 1:1 set (D), the 1:2 set (E), and the 2:1 set (F). Ribbon represents means ± SE. G: prediction suppression signal for the 1:2 condition (firing rate on unpredicted trials minus firing rate on predicted trials) is plotted against the prediction suppression signal for the 1:1 condition. H: 2:1 signal plotted against the 1:1 signal. I: 2:1 signal plotted against the 1:2 signal. J: means ± SE of prediction suppression for trials involving each trailing image. G–I: count n indicates the number of neurons in the corresponding sector of the plot (either above or below the identity line).

Although the net effect at the level of the population took the form of prediction suppression, some neurons might have exhibited prediction enhancement. To explore this issue, we repeated the statistical analysis on each neuron. Despite the limit on power arising from the small number of trials, we found, under each condition, that the percentage of neurons exhibiting significant (α = 0.05) prediction suppression was significantly greater than the percentage (2.5%) expected by chance (1:1 count = 10, P = 3.8 E-7; 1:2 count = 9, P = 1.2 E-5; 2:1 count = 11, P = 8.1 E-9; χ² test with Yates correction). In contrast, under no condition was the number of neurons exhibiting significant prediction enhancement significantly greater than expected by chance (1:1 count = 3, P = 0.81; 1:2 count = 5, P = 0.10; 2:1 count = 4, P = 0.35). Our data thus provide no support for the idea that some neurons exhibited prediction enhancement.

To determine whether prediction suppression was attenuated by manipulations reducing the conditional probability between the leading and trailing images, we plotted, across all neurons, the suppression index measured under each condition against the suppression index measured under each other condition. We defined the suppression index as the mean firing rate 100–500 ms after trailing-image onset on unpredicted trials (U) minus the same measure on predicted trials (P). The suppression index under the 1:1 condition was greater than under the 1:2 condition (mean difference = 0.91 spikes/s, P = 0.017, T = 2.44; two-tailed paired t-test; n = 86) and the 2:1 condition (mean difference = 1.40 spikes/s, P = 0.0022, T = 3.16). The 1:2 and 2:1 conditions did not differ significantly from each other (mean difference = 0.49 spikes/s favoring 1:2, P = 0.16, T = 1.44). We conclude that a training procedure reducing either P(A|B) or P(B|A) attenuates prediction suppression at the level of spiking activity.

The population response to an unpredicted image (U) and the population response to the same image when predicted (P) were found in a previous study to be related by a scaling factor of ∼1.5 (Meyer and Olson 2011). To determine whether, in the present study, the scaling factor U/P varied across conditions, we computed the population means of U and P under each condition and then computed their ratio. The ratio was 1.32, 1.22, and 1.16 under conditions 1:1, 1:2, and 2:1, respectively. The rank ordering of conditions with regard to U/P was thus identical to their rank ordering with regard to the standard measure U-P.

Training in the 1:1, 1:2, and 2:1 conditions involved multiple trailing images. We designed the task so that the number of trials under each condition would be adequate for data analysis if results were combined across all relevant trailing images. We now turn to the question of whether the results were consistent across the images, with the qualification that measures were noisy due to the low number of trials. We measured prediction suppression independently for each of the 16 trailing images used in the 2 monkeys using the standard measure of firing rate on unpredicted trials minus firing rate on predicted trials. The strength of prediction suppression varied across images within each training condition (Fig. 2J). However, only in one case did prediction suppression measured after 1:2 or 2:1 training exceed prediction suppression measured after 1:1 training. That the five cases of strongest prediction suppression should have included all four 1:1 cases is unlikely to have arisen by chance (upon random ranking of the 16 cases, the probability that 4 selected cases would occupy the top 5 ranks is only 0.0027). Subtle differences between the monkeys (Fig. 2J) could have arisen from the fact that the recording sites were at slightly different AP levels, as described in materials and methods, but could also reflect noise in the neuronal data or differences in the physical properties of the images. We conclude that the tendency for prediction suppression to be stronger in the 1:1 than in the 1:2 and 2:1 conditions was genuinely associated with training condition as distinct from trailing-image identity.

In the analyses described above, we computed the strength of the response when the image was unpredicted by averaging across all available unpredicted conditions (dotted cells in the matrix of Fig. 1B). This design had the consequence that, in computing the strength of the unpredicted response to a trailing image associated with the 1:1 condition, we made disproportionate use of leading images associated with the 1:2 and 2:1 conditions, and so on. To be sure that the outcome did not depend on this imbalance, we repeated the analysis with a corrective step. For each trailing image, we computed the strength of the unpredicted response when it followed a leading image with 1:1 training status, when it followed a leading image with 1:2 training status, and when it followed a leading image with 2:1 training status. Then we averaged the three values. This step did not alter the pattern of results. Prediction suppression under the 1:1 condition (mean = 2.95 spikes/s) was greater than under the 1:2 condition (2.04 spikes/s) and the 2:1 condition (1.55 spikes/s). The comparison between the 1:1 and 1:2 conditions no longer attained statistical significance (P = 0.66, T = 0.43; two-tailed paired t-test; n = 86) but the comparison between the 1:1 and 2:1 conditions did remain significant (P = 0.0086, T = 2.69; two-tailed paired t-test; n = 86).

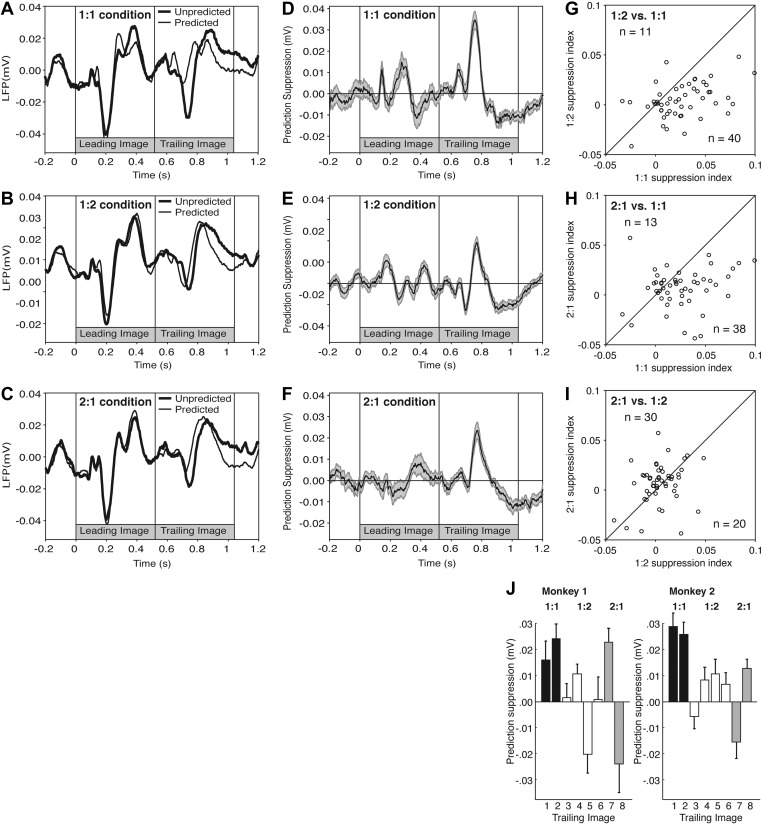
Analysis at the level of the LFP is a useful adjunct to analysis at the level of neuronal spiking activity. Arising from synaptic events spanning thousands of neurons, the LFP provides a low-noise window on events common to a local population. Reflecting primarily synaptic events, it provides a window on a processing stage distinct from that reflected in spiking activity. It does not go without saying that a reduction of spiking activity will be accompanied by a reduction of the LFP since the reduction of neuronal firing might result from an increase in activation of inhibitory synapses. Accordingly, we analyzed data collected from the 51 sites at which we had monitored neuronal activity (30 and 21 sites in monkeys 1 and 2, respectively). Previous reports have indicated that prediction suppression is manifest as a reduction in the magnitude of the excursion from maximal negativity at ∼200 ms to maximal positivity at ∼300 ms in the LFP response to trailing-image onset (Meyer and Olson 2011; Meyer et al. 2014). In the present study, in plots representing the raw voltage (Fig. 3, A–C) and the difference between predicted and unpredicted voltages (Fig. 3, D–F), this effect appears strong for images trained under the 1:1 condition but weak for images trained under the 1:2 and 2:1 conditions. As a basis for statistical analysis, we computed a suppression index for each site as U-P where U and P represented the magnitude of the voltage excursion 100–500 ms after trailing-image onset on unpredicted and predicted trials, respectively. To measure the excursion, we computed the average across all trials of voltage as a function of time and then took the difference between the maximum and the minimum within the window. We chose this measure so as to allow for possible differences from site to site in the timing of the response. Upon comparing the suppression indices measured under each condition to the suppression indexes measured under each other condition (Fig. 3, G–I) we found that the mean under the 1:1 condition was significantly greater than the mean under the 1:2 and 2:1 conditions (P = 3.9 E-5, T = 4.51 and P = 0.01, T = 2.62; two-tailed paired t-test; n = 51) whereas the 1:2 and 2:1 conditions did not differ significantly from each other (P = 0.57, T = 0.57). Upon breaking down the results according to the identity of the trailing image, we found that prediction suppression occurred consistently for images associated with the 1:1 condition whereas it was inconsistent for images associated with the 1:2 and 2:1 conditions. In conclusion, results obtained at the level of the LFP are concordant with neuronal results indicating that training under the 1:1 condition induces stronger prediction suppression than training under the 1:2 and 2:1 conditions.

Fig. 3.

Prediction suppression, measured at the level of the local field potential (LFP), was stronger in the 1:1 condition than in the 1:2 and 2:1 conditions. LFP responses from 51 sites. A–J: format and conventions are as in Fig. 2.

DISCUSSION

The aim of this experiment was to determine whether prediction suppression (Meyer and Olson 2011; Meyer et al. 2014) depends solely on the contiguity between the leading and the trailing images, as determined by their repeated pairing, or also on their mutual contingency, as determined by the ability of one to predict the other. Our results indicate that contingency matters. Prediction suppression is reduced if the contingency between the images is degraded.

In manipulating the conditional probabilities P(A|B) and P(B|A) while holding joint probability P(A,B) constant, we unavoidably altered certain other display statistics. These included the absolute probabilities P(A) and P(B) and the conditional probability P(A|∼B). In the 1:1 condition P(A) and P(B) were both 0.1 in the sense that each image appeared on one-tenth of training trials. In the 1:2 condition, P(A) and P(B) were 0.2 and 0.1, respectively. In the 2:1 condition, P(A) and P(B) were 0.1 and 0.2, respectively. Images with an absolute probability of 0.2, were presented twice as often as other images during training. Making images familiar reduces the strength with which TE neurons respond to them (Meyer and Olson 2011; Meyer et al. 2014). Trailing images with an absolute probability of 0.2 might conceivably have elicited particularly weak responses because they were particularly familiar. If so, then prediction suppression might have been correspondingly low as a result of proportional scaling. This mechanism could potentially explain weak prediction suppression in the 2:1 condition but not in the 1:2 condition. In the 1:1 and 1:2 conditions, P(B|∼A), the conditional probability of a given trailing image following the nonoccurrence of a given leading image, was 0 for trained pairs and 1/9 for untrained pairs. The corresponding probabilities for the 2:1 condition were 1/9 and 2/9. Inasmuch as P(B|∼A) distinguishes the 1:1 and 1:2 conditions from the 2:1 condition, it cannot easily account the fact that prediction suppression was uniquely strong in the 1:1 condition.

We suggested previously that prediction suppression in TE serves to reduce the salience of a predicted and therefore uninformative trailing image (Meyer and Olson 2011; Meyer et al. 2014). If so, then prediction suppression can be seen as a specific phenomenon arising from the general ability of the neocortex to predict future events (Bar 2009; Friston 2005; Hawkins and Blakeslee 2005). It is natural to think of prediction as giving rise to an active representation of an impending event. However, it is equally plausible to imagine it as producing a passive state conducive to filtering out the predicted event. Damped responding to predicted events is frequently observed at the level of perceptual, cognitive, and motivational systems (den Ouden et al. 2012). Filtering out could be adaptive both in preventing the capture of attention by things that require no processing (Foley et al. 2014) and in allowing the refinement of the very brain mechanisms that mediate prediction making. The idea that surprising events (prediction errors) fine tune the predictive apparatus lies at the heart of animal learning theory (Courville et al. 2006; Kamin 1969; Pearce and Hall 1980; Schultz and Dickinson 2000).

If prediction suppression indeed arises from the tendency of the visual system to filter out the representation of a predicted event, then it should be possible to reduce the strength of prediction suppression by reducing the predictability of the trailing image during training. That is exactly what we accomplished in the 1:2 condition. Reducing P(B|A) to 0.5 induced a corresponding reduction in prediction suppression relative to the 1:1 control. The outcome of the 2:1 condition is difficult, however, to explain in this framework. In the 2:1 condition, following a leading image, the probability of the paired trailing image, P(B|A), was 1.0 just as in the 1:1 control condition. Nevertheless, prediction suppression was reduced. The feature distinctive of the 2:1 condition was the low probability of the leading image given the trailing image: P(A|B) = 0.5. To explain this result requires considering an alternative framework.

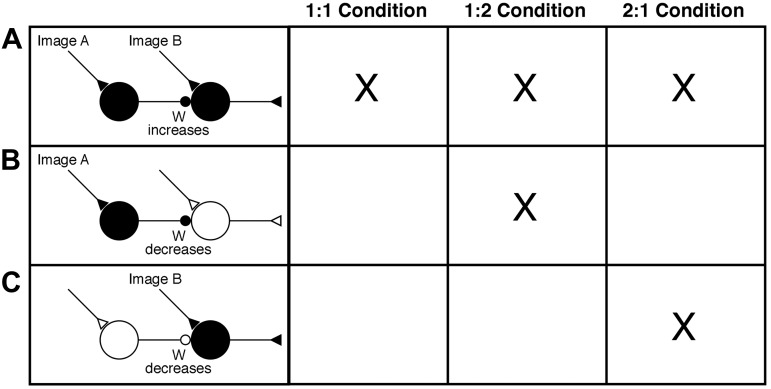
The dependence of prediction suppression on both P(B|A) and P(A|B) can be explained parsimoniously in terms of a covariance-based synaptic learning rule (Courville et al. 2006; Kamin 1969; Pearce and Hall 1980; Schultz and Dickinson 2000; Sejnowski 1977; Sejnowski et al. 1989). Consider a network in which a neuron responsive to leading image A inhibits a neuron responsive to trailing image B (Fig. 4). Inhibition serves here as a proxy for the unknown mechanism underlying prediction suppression. The learning rule governing the strength of the inhibitory synapse is given by:

$${\Delta \mathrm{W}}_{B,A}(t)=e\hspace{0.17em}\times [Y_A(t)\hspace{0.17em}-\hspace{0.17em}<Y_A>]\hspace{0.17em}\times \hspace{0.17em}[Y_B(t)\hspace{0.17em}-\hspace{0.17em}<Y_B>]$$

where e is the learning rate constant, ΔW_B,A(t) is the change in the weight at time t, Y_A(t) and Y_B(t) are the firing rates of neurons A and B at time t, and <Y_A> and <Y_B> are the mean firing rates over some prior interval. Under all three training regimens, there are trials in which image A is paired with image B. Coactivation of neurons responsive to A and B induces an increase of the weight (W) of the inhibitory synapse between them (Fig. 4A). Under the 1:2 condition, there are also trials involving the sequence A,∼B where ∼B is the other trailing image paired with A. On these trials, the neuron responsive to A is active but the neuron responsive to B is not. This induces a decrease in the weight W (Fig. 4B). Under the 2:1 condition, there are trials involving the sequence ∼A,B where ∼A is the other leading image paired with B. On these trials, the neuron responsive to B is active but the neuron responsive to A is not. This induces a decrease in the weight W (Fig. 4C). Thus the asymptotic level of W is lower under the 1:2 and 2:1 conditions than under the 1:1 condition. Whether plasticity actually conforms to a covariance-based rule in the most commonly studied form of cortical plasticity, long-term potentiation, has been subject to debate (Kerr and Abraham 1993; Paulsen et al. 1993; Stanton and Sejnowski 1989). Insertion of trials in which postsynaptic activity occurs without presynaptic activity (Fig. 4C) has been reported to weaken LTP in accordance with the covariance principle (Bauer et al. 2001; Christofi et al. 1993; Pockett et al. 1990), but insertion of trials in which presynaptic activity occurs without postsynaptic activity (Fig. 4B) has been reported not to do so (Buonomano and Merzenich 1996).

Fig. 4.

A covariance-based model of experience-dependent plasticity can account for the fact that prediction suppression is stronger in the 1:1 than in the 1:2 and 2:1 conditions. A: successive activation of neurons responsive to images A and B induces an increase in the weight (W) of a synaptic link allowing A neurons to suppress B neurons. This occurs under all 3 training conditions. B: activation of A neurons in the absence of B neuron activation induces synaptic weakening. This occurs under the 1:2 condition. C: activation of B neurons in the absence of A neuron activation induces synaptic weakening. This occurs under the 2:1 condition.

Explanations of prediction suppression based on the ability of the leading image to predict the trailing image and on a covariance-based learning rule are not necessarily incompatible. It may be that TE relies, in learning to suppress responses to predicted images, on a mechanism that generally is sensitive to the predictability of the trailing image but that employs computations not perfectly suited to doing so. It is useful in considering this point to note that there are parallel quirks in the process by which, in Pavlovian conditioning, the association between the conditioned stimulus (CS) and the unconditioned stimulus (US) is acquired. The strength of the CS-US association does not depend simply on the joint probability P(CS,US) as would be expected from isolated operation of the rule depicted in Fig. 4A. It also depends on the conditional probability P(US|CS) as expected from operation of the rule depicted in Fig. 4B. This is evident in the induction of an acquisition deficit by partial reinforcement (Miguez et al. 2012). Finally, and critically, it also depends on the conditional probability P(CS|US) as expected from operation of the rule depicted in Fig. 4C. This is evident in the induction of an acquisition deficit by contingency degradation (Bermudez and Schultz 2010; Rescorla 1968).

GRANTS

This study was supported by National Institutes of Health Grants R01-EY-018620, R01-EY-024912, P50-MH-103204, and K08-MH-080329 and Pennsylvania Department of Health's Commonwealth Universal Research Enhancement Program. Technical support was provided by National Institutes of Health Grants P30-EY-008098 and P41-RR-03631.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.R., T.M., and C.R.O. conception and design of research; S.R. and T.M. performed experiments; S.R. and C.R.O. analyzed data; S.R., T.M., and C.R.O. interpreted results of experiments; S.R. and C.R.O. prepared figures; S.R. and C.R.O. drafted manuscript; S.R., T.M., and C.R.O. edited and revised manuscript; S.R., T.M., and C.R.O. approved final version of manuscript.