Are microsatellite fragment lengths useful for population-level studies? The case of Polygala lewtonii (Polygalaceae)

Abstract

Premise of the study:

Microsatellites, despite being commonly used population-level markers, contain biases because scoring relies solely on fragment length. Their complexity can lead to homoplasy, the effects of which are poorly understood. We investigated the impact of using fragment lengths, repeats, or flanking region sequences on common population-level analyses.

Methods:

Five polymorphic microsatellite markers amplified across the central Florida scrub endemic Polygala lewtonii (Polygalaceae) and its close, widespread congener P. polygama. We genotyped 147 individuals of P. lewtonii and 156 of P. polygama, and sequenced the amplicons of four markers across all individuals. We ran basic statistics, spatial clustering analysis, historical demographics, and migration tests.

Results:

One population of intermediate morphology was genetically clearly identified as P. polygama, making it the southernmost population of this species. Statistics were comparable between the fragment length and repeat numbers, with some notable differences. Flanking regions exhibited surprisingly high polymorphism between species, and between geographically distant conspecific populations.

Discussion:

The increasing use of markers developed in one species and amplified in another is only a good practice if precautions are taken, notably the sequencing of the fragments between species and populations. Flanking region sequences are a useful marker at the interspecific level.

Genetic diversity is one of the three forms of biodiversity recognized by the International Union for the Conservation of Nature (IUCN) and is linked to the fitness of a species, as well as its capacity to adapt to future environmental changes (Reed and Frankham, 2003). Especially in the case of species from endangered habitats, genetic diversity and its geographical partitioning can be important for sound conservation planning (Ellstrand and Elam, 1993; Petit et al., 1998; Crandall et al., 2000; Frankham, 2003, 2005; Reed and Frankham, 2003).

The genetic study of plants at the inter- or intraspecific level has often been hampered by a lack of molecular markers. Recombining nuclear DNA encompasses a much larger pool of genetic variation than the plastid genome, with information for reconstructing coalescence and recent evolutionary history. Nuclear microsatellites (simple sequence repeats [SSRs]) have therefore become popular due to their abundance, high polymorphism, codominance, and Mendelian inheritance (Morgante and Olivieri, 1993). Despite the recent surge in single-nucleotide polymorphism (SNP)–based studies, microsatellites are still favored, not only because of their lower cost of development, but also because they are useful for the study of species with shallow evolutionary history and restricted ranges (Putman and Carbone, 2014). Still, microsatellites can present some problems (Selkoe and Toonen, 2006). Several studies have examined the different biases in the practice of microsatellite genotyping, namely the sole reliance on fragment length, despite the complex composition of the repeats (Culver et al., 2001; Ramakrishnan and Mountain, 2004; Anmarkrud et al., 2008), and the influence of flanking region polymorphism on results (Blankenship et al., 2002; Selkoe and Toonen, 2006; Vali et al., 2008). In general, the extent of homoplasy among alleles at different scales (within the same population, among different populations of the same species, and between closely related species) is still not well understood, and the effects of homoplasy have seldom been evaluated (Adams et al., 2004; Shirai et al., 2009).

Homoplasy occurs when identical fragment lengths result from different evolutionary histories. Numerous studies have examined the impact of homoplasy on evaluations of genetic diversity and found that mutations in the repeat or the flanking region can “lead to false inference in phylogenetic, taxonomical and diversity studies if small numbers of microsatellites are used” (Stágel et al., 2009). Depending on the number and nature of the loci and organism, homoplasy has resulted in underestimations of population subdivision and genetic divergence between populations (Goldstein et al., 1995; Hedrick, 1999; Makova et al., 2000; Selkoe and Toonen, 2006), inflated levels of gene flow between populations (Rousset, 1996; Epperson, 2005; Selkoe and Toonen, 2006), overestimation of hybridization between species (Shirai et al., 2009), or no significant effect (Estoup et al., 2002). One study detected noticeably more variation in the flanking region sequences than in the microsatellite repeats between closely related species (Queloz et al., 2010).

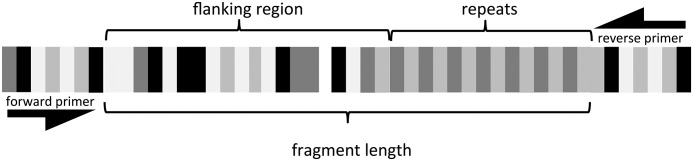
One way to detect and address homoplasy is to sequence the flanking regions of the microsatellite loci and subsequently infer the number of repeats. The flanking region is the stretch of approximately 100–150 bp of nonrepeated nucleotides on each side of the SSR tandem repeat between the priming sites and the repeat (Fig. 1). Nucleotide substitution in these regions is believed to evolve more slowly than repeat-number evolution of the microsatellite itself, but the flanking regions can still exhibit some degree of polymorphism, and in some cases significantly so (Vali et al., 2008). Identifying different haplotypes in the nonrepeat flanking sequences enables researchers to identify homoplasious microsatellite alleles (Blankenship et al., 2002; Vali et al., 2008). At the intraspecific level, very few studies have used microsatellite flanking regions, but some have been able to resolve homoplasy (Grimaldi and Crouau-Roy, 1997; Waters and Wallis, 2000; Mogg et al., 2002; Won et al., 2005; Ablett et al., 2006; Queloz et al., 2010), and one has found the insertions/deletions (indels) in the flanking regions to be a source of homoplasy (Matsuoka et al., 2002). Several studies have investigated this problem in nonmodel animal species (Adams et al., 2004; Reyes et al., 2012), but only one so far in plants (Stágel et al., 2009), which addresses varieties of the commercial species of Capsicum L.

Fig. 1.

Schematic representation of the repeats, flanking regions, and fragment length—the basis of the three data sets in this study. The four shades of gray correspond to the four different nucleotides. The number of repeats is calculated as the difference between the fragment length (from genotyping) and the flanking region (from sequencing).

In this study, the U.S. federally listed endangered species and Florida endemic Polygala lewtonii Small and its more widespread sister species, P. polygama Walter, were chosen as a test case for the study of microsatellite flanking regions as potential markers at the population level and to assess the impact of indels on homoplasy and the estimation of genetic diversity. The inclusion of the more widespread sister species, P. polygama, will allow for an objective interpretation of the results in the context of the evolutionary history of this group (Gitzendanner and Soltis, 2000). We analyzed and compared the flanking region sequence, the fragment length (as would be used in most population-level studies using microsatellites), and strict numbers of tandem repeat numbers (inferred from those two data sets).

METHODS

Sample collection

Leaves of 148 and 118 individuals from 10 and eight populations were collected between 2006 and 2009 for P. lewtonii and P. polygama, respectively, encompassing the range of each species, although sampling of P. polygama was more focused on the southern United States and is sparse throughout the remainder of its range (Table 1 and map in Fig. 2). We collected from four to 16 and eight to 16 individuals per population for P. lewtonii and P. polygama, respectively (Table 1). Permits were obtained from the Florida Division of Plant Industry (permit numbers 714 and 954). Leaves were dried and stored in silica gel, and DNA was extracted following a modified cetyltrimethylammonium bromide (CTAB) extraction protocol (Doyle and Doyle, 1987; Cullings, 1992).

Table 1.

Populations, locations, number of plants genotyped for fragment length, number of plants sequenced, and population vouchers for Polygala lewtonii and P. polygama.

Species	Population no.	Location	Latitude (°N)	Longitude (°W)	Genotypeda	Sequencedb	Voucher (Herbarium)c
P. lewtonii	102	LWRSF, Polk Co., FL	27.704	−81.475	16	13	CGA 11 (FLAS)
P. lewtonii	105	Clermont, Lake Co., FL	28.546	−81.701	16	16	JRA 22703 (FLAS)
P. lewtonii	107	TNC Tiger Creek, Polk Co., FL	26.644	−81.443	16	15	JRA 22685 (FLAS)
Polygala sp.	108	TNC Saddle Blanket, Polk Co., FL	28.018	−81.383	16	8	JRA 22690 (FLAS)
P. lewtonii	115	ADBCCSP, Polk Co., FL	26.677	−81.493	16	12	CGA 50 (FLAS)
P. lewtonii	118	ADBCCSP, Polk Co., FL	26.670	−81.494	4	0	—
P. lewtonii	124	ONF, Salt Spring, Marion Co., FL	29.331	−81.782	16	19	—
P. lewtonii	125	ONF, Hughes Island, Marion Co., FL	29.256	−81.760	16	12	—
P. lewtonii	126	ONF, Hughes Island, Marion Co., FL	19.250	−81.757	16	15	—
P. lewtonii	127	ONF, Hughes Island, Marion Co., FL	29.254	−81.707	16	0	—
P. polygama	102	Citrus Co., FL	27.704	−81.475	13	11	JRA 24633 (FLAS)
P. polygama	1301	Mansfield, CT	41.750	−72.183	8	0	B. Connelly s.n.
P. polygama	1801	Anoka Co., MN	45.252	−93.232	16	13	O. Gockman s.n.
P. polygama	1802	St. Louis Co., MN	47.359	−92.109	16	0	O. Gockman s.n.
P. polygama	601	Richland Co., WI	43.359	−90.431	15	19	T. Cochrane s.n.
P. polygama	602	Sauk Co., WI	43.393	−89.955	16	18	T. Cochrane s.n.
P. polygama	805	Lauderdale Co., MS	32.232	−88.862	10	10	L. Majure s.n.
P. polygama	301	Ashtabula Co., OH	41.889	−80.786	8	0	J. Bissell s.n.

Note: FLAS = Florida Museum of Natural History, Gainesville, Florida, USA; LWRSF = Lake Wales Ridge State Forest; TNC = The Nature Conservancy; ADBCCSP = Allen David Broussard Catfish Creek State Park; ONF = Ocala National Forest.

^aNo. of samples genotyped for fragment length.

^bNo. of samples sequenced.

^cWhere voucher information is missing, authorities did not grant permission for vouchering.

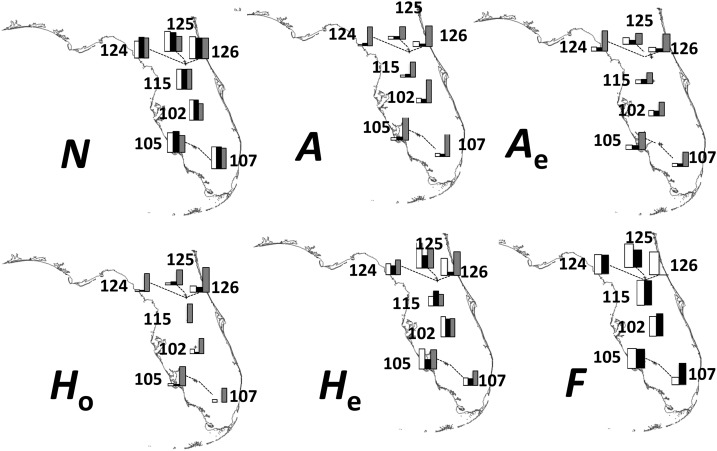
Fig. 2.

Geographical distribution of the genetic diversity of Polygala lewtonii. Different maps represent measures of diversity for the fragments (white bar), repeat number (black bar), and flanking regions (gray bar). N = number of individuals; A = number of alleles/number of polymorphic sites for sequence data; A_e = effective number of alleles/number of haplotypes; F = fixation index; H_e = expected heterozygosity; H_o = observed heterozygosity. Graphs are based on Appendix S6 ^{(94KB, docx)} .

Species identification for the Saddle Blanket population

Population 108, in The Nature Conservancy’s (TNC) Saddle Blanket site, was labeled as P. lewtonii at the time of collection, although there were doubts about its identity. The morphology of the plant combines traits of P. lewtonii and P. polygama, and looks like a dwarfed P. polygama, an unexpected species so far south. Normally, the ranges of P. lewtonii and P. polygama do not overlap and P. polygama is significantly larger than the Florida endemic. Further investigation involving measurement of seed sizes resulted in a size range overlapping both P. lewtonii and P. polygama. Ploidy was checked by comparing genome sizes of individuals from population 108 with those of other P. lewtonii and P. polygama populations using flow cytometry (Doležel et al., 2007; Hare and Johnston, 2011).

Microsatellite development and genotyping

A microsatellite library was constructed using the voucher for population 107 and biotinylated (CA)₈ and (GA)₈ probes following a protocol optimized in the Soltis laboratory (Edwards et al., 2007, 2008; Lopez-Vinyallonga et al., 2010; Germain-Aubrey et al., 2011). Because we were interested in the variation in flanking regions, we designed a primer to encompass a long flanking region (ca. 300 bp) on the 5′ end of the repeat, while the primer on the 3′ end was close to the repeat, so as to minimize the amount of variation on that end to a negligible amount, and allowing sequencing to be unidirectional. The primers amplified a comparable region in the sister species, P. polygama.

Loci were amplified in all samples of both P. lewtonii and P. polygama in a 10-μL solution containing 1× buffer, 1 M betaine, 1.5 mM MgCl₂, 0.1 μM dNTPs, 0.5 μM forward and reverse primers, 0.5 μM of either 6-FAM-, VIC-, NED-, or PET-labeled M13 primer (Life Technologies, Carlsbad, California, USA), and 0.2 unit Taq polymerase. PCR amplification conditions were 3 min at 95°C, followed by 35 cycles of 45 s at 95°C, 1 min 15 s at 52°C, and 1 min 15 s at 72°C, with a final step of 20 min at 72°C. PCR products were pooled in a NED/PET:VIC/FAM 2:1 ratio and then genotyped on an ABI 3730 DNA analyzer (Applied Biosystems, Carlsbad, California, USA) at the Interdisciplinary Center for Biotechnology Research at the University of Florida. Microsatellites were scored automatically and then checked by eye using GeneMarker version 1.6 (Soft Genetics, State College, Pennsylvania, USA). PCR products were sequenced on an ABI 3130 DNA sequencer (Applied Biosystems) from the long flanking region (5′-end) toward the repeat. Sequences were visualized and edited using Geneious Pro version 5.3.4 (Biomatters, http://www.geneious.com/). For all genotyping and sequencing, four positive controls per 96-well plate were used to ensure consistency in the scoring. In the case of clear and unambiguous sequences, flanking regions were considered homozygous, and any fragment length difference was attributed to a difference in repeat number (Fig. 1). Sequences with more than two or three ambiguous sites in the flanking region were cloned and the clones sequenced. We were then able to score precise nucleotide substitutions and attribute any fragment length difference to either an insertion/deletion event in the flanking region or a difference in repeat number between the two alleles. Also, when sequence polymorphism could not be resolved for each allele through clean sequences from the clones, only fragment length could be retrieved. This can lead to differences between the number of individuals in the fragment length and flanking regions data sets. Sequences at loci Poly1, PolyD12, PolyE01, PolyB08, and Poly5 were edited manually and aligned in Geneious Pro version 5.3.4.

Characterization of markers

MICRO-CHECKER version 2.2.3 (van Oosterhout et al., 2004) was used to test potential genotyping errors, selection biases of loci, and the presence of null alleles. GenAlEx 6.41 (Peakall and Smouse, 2006) was used for statistics to characterize the loci and for conversions of data formats for other software packages. GENEPOP (Excoffier et al., 2005) was used for tests of Hardy–Weinberg equilibrium and linkage disequilibrium. SPAGeDi version 1.3a (Hardy and Vekemans, 2002) was used to perform a randomization test with 10,000 permutations of R_ST (a genetic distance measure that assumes the stepwise mutation process in microsatellites; Slatkin, 1995) on alleles, for each locus separately and averaged over all loci to find the best-fitting evolutionary model for the data set. Because Polygala L. is a perennial with a few to dozens of annual stems, GenoDive version 2.0b17 (Meirmans and Van Tienderen, 2004) was used to detect any clones in the data set.

All subsequent analyses were repeated using three data sets: the fragment length, the repeat number, and the flanking region sequence—hereafter referred to as fragments, repeats, and flanking regions, respectively (Fig. 1). The data set consists of the three loci common to all data sets, which were all genotyped and sequenced: Poly1, PolyE01, and PolyB08. The goal of this comparison of the three data sets is to evaluate their impact on several population-level genetic analyses.

Genetic diversity

GenAlEx 6.501 (Peakall and Smouse, 2006) was used to infer statistics at the population level: observed and expected heterozygosity (H_o and H_e), mean number of individuals (N), mean number of alleles per locus (both absolute [A] and effective [A_e]), and fixation index (F). Also, an exact Hardy–Weinberg equilibrium test was implemented with a 1,000,000-generation Markov chain (including a 100,000 burn-in) in GENEPOP. All statistics were averaged over all loci for each population for an analysis of P. lewtonii alone, and averaged over all populations within each species for a comparison of the endemic and its widespread sister species. For the flanking regions, Arlequin version 3.1 (Excoffier et al., 2005) was used to infer the number of haplotypes, heterozygosity, and nucleotide diversity within each population.

Spatial genetic structure

TESS version 2.3.1 (Durand et al., 2009) was used to infer the number of clusters (K) based on allelic identity and frequency. TESS uses a Bayesian method to minimize departure of populations from Hardy–Weinberg equilibrium and includes a decay of correlation of membership coefficients with geographical distance within clusters. As advised in the manual, the analysis of the true number of clusters has to be assessed on the basis of the Deviance Information Criterion (DIC) and bar plots. In all, 100,000 generations encompassing 10,000 burn-in, with admixture, were replicated 10 times per K = 2–6 for the two Polygala species combined, and per K = 2–8 for P. lewtonii alone. All runs were permuted within each K, “averaged” in CLUMPP (Jakobsson and Rosenberg, 2007), and then visualized in DISTRUCT (Rosenberg, 2004).

AMOVA analyses with 9999 permutations were implemented in GenAlEx, partitioning variation within individuals, among individuals within populations, among populations within species, and between species to infer gene flow between populations and ridges. For conservation applications, the genetic contribution of each population of P. lewtonii relative to other populations was calculated using CONTRIB (Petit et al., 1998). This allelic contribution was then broken down into its contribution to total allelic diversity and divergence from other populations.

Historical demography and migration

The mutation rates for each of the loci were used in an isolation-with-migration model in IMa2 (Hey and Nielsen, 2007; Hey, 2010). For the microsatellites, several mutation rates were considered from previous studies, with the conservative range of 0.0001–0.001 mutation per allele per generation being retained (Thuillet et al., 2002; Vigouroux et al., 2002; O’Connell and Ritland, 2004). Mutation rates of the flanking regions were estimated as 0.002 for PolyB08, 0.00035 for PolyE01, 0.00037 for Poly5, and 0.0010 for Poly1 (Appendix S1 ^{(100.8KB, docx)} ). We employed the HKY model for the DNA sequences and for the microsatellites used a stepwise mutation model, as advised in the program manual. We ran 20 chains under a geometric heating scheme. Runs consisted of 3 million steps with the first 300,000 steps of burn-in. Histograms were compared, effective sample size (ESS) values (correcting sample size for autocorrelation) checked to evaluate the runs, and correlations between parameters checked. Generation time was set to three years (Weekley and Menges, 2012).

RESULTS

Characterization of markers

Ten novel microsatellites were amplified across populations and species; of these, eight showed polymorphism for the microsatellite data set. Due to budget restrictions, five were selected for sequencing (Appendix S2 ^{(74.4KB, docx)} ). Of the latter five, PolyD12 and PolyE01 were found to be linked based on the linkage disequilibrium test implemented in GENEPOP (Raymond and Rousset, 1995; Rousset, 2008), so the two were concatenated for the flanking regions data set, but only PolyE01 was kept for the fragments and repeats data sets, leaving four unlinked loci. Locus Poly5 was difficult to amplify for fragment scoring and was therefore deleted from subsequent comparative analyses due to excessive missing data. However, the sequences of the flanking region of Poly5 are reported in Appendix S3 ^{(116.4KB, docx)} and the Discussion, as one large indel is particularly relevant to our question of homoplasy. Three loci were therefore used for the comparative analysis. No scoring error or null alleles were detected for any of the loci, and the R_ST permutation tests on the P. lewtonii data set revealed a stepwise mutation model for all loci (both with fragments and repeats) after a sequential Bonferroni correction (Rice, 1989). We therefore performed R_ST for the AMOVA, as well as F_ST as it is widely used in microsatellite studies.

Flanking regions

All loci exhibited polymorphism. PolyB08 (100 individuals of P. lewtonii and 65 P. polygama) is 211 bp long with three nucleotide substitutions; PolyD12 (66 P. lewtonii and 49 P. polygama) is 280 bp long with five substitutions, two points indels, and one 4-bp indel; PolyE01 (48 P. lewtonii and 51 P. polygama) is 367 bp long with five substitutions and three indels; Poly1 (108 P. lewtonii and 61 P. polygama) is 222 bp long with seven substitutions and two deletions; and Poly5 (135 P. lewtonii and 87 P. polygama) is 169 bp long with three nucleotide substitutions, one deletion, and a 30-bp insertion inside of which are one substitution and one deletion. Of those 32 polymorphisms, 12 delimited species, and only six showed within-population variation (Appendix S3 ^{(116.4KB, docx)} ).

Homoplasy

Combining the information from the flanking regions and fragment lengths, we can identify homoplasy due to variation in flanking regions, or even due to repeat differences in all loci. As an example, position 207 at locus PolyB08 shows all individuals in P. polygama population 102 having an A (allele A) while all other individuals in the species have a G (allele G). The scoring for this population is uniformly 414/414. While only five P. polygama individuals from populations other than population 102 have the same fragment length (and sequences for allele G), 74 individuals from several populations of P. lewtonii have fragment lengths scored at 414. In the absence of indels in the flanking region, it means they also have the same number of repeats. However, the 414-bp allele is homoplasious, and the 74 individuals of P. lewtonii all have the allele G. This homoplasy and the differentiation of population 102 would not be picked up by fragment length alone. Subsequently, the estimated rates of gene flow between those populations will be artificially increased. Table 2 represents the mutations in flanking regions PolyB08, PolyE01, and Poly1 and the homoplasy created subsequently within populations, within species, and across species. The vast majority of homoplasy is created across species, although it occurs even among populations within species and between individuals in the same population.

Table 2.

List of mutations and their impact on homoplasy at different levels.

						Homoplasy created in same
Locus	Population	Individualsa	Nature of mutation	Fragment length score also present in other individuals	No. of individuals with same score	Population	Species	Across species
PolyB08	L 108 + all P	All	Substitution	414, 418	74 out of 100 scored L	No	No	Yes
	P 102	All	Substitution	414	5 P + 74 L	No	Yes	Yes
Poly1	P 805, 1301, 102, L 108	All	Substitutions (3 separate)	214, 226, 230, 224	21 P + 100 L	No	Yes	Yes
	P + L 108	All	Substitutions (3 separate)	215, 226, 232	101 L	No	No	Yes
	P 805, 1301, L 108	All	Substitution	214, 226, 230, 224	28 P + 100 L	No	Yes	Yes
	L 120	1	Indel	216	1 L	No	Yes	No
	L 105	1	Indel	214	99 L + 18 P	Yes	Yes	Yes
	L 124	1	Indel	214	99 L + 18 P	Yes	Yes	Yes
PolyE01	P 1801, 601, 602	All	Substitutions (2 separate)	472, 474, 478, 416	20 L + 70 P	No	Yes	Yes
	L 108	1	Indel	474	10 L + 65 P	Yes	Yes	Yes
	L 102, 115	3	Indel + substitution	470, 476, 478	102 L + 2 P	Yes	Yes	Yes
	P 805	All	Substitutions (2 separate)	474	10 L + 58 P	No	Yes	Yes
	P + L 108	All	Substitutions (2 separate)	474, 416, 482, 468, 464, 470, 472, 478, 488	17 L	No	No	Yes
	L 105	1	Substitution	476	101 L	Yes	Yes	No
	L (but 102)	All but 2	Insert (×2 for 107)	470, 476, 470, 474, 472, 478, 456, 480, 434	In text and Fig. 3	Yes	Yes	Yes

Note: L = Polygala lewtonii; P = Polygala polygama.

^aNot all mutations apply to all individuals in the population at all loci and mutations.

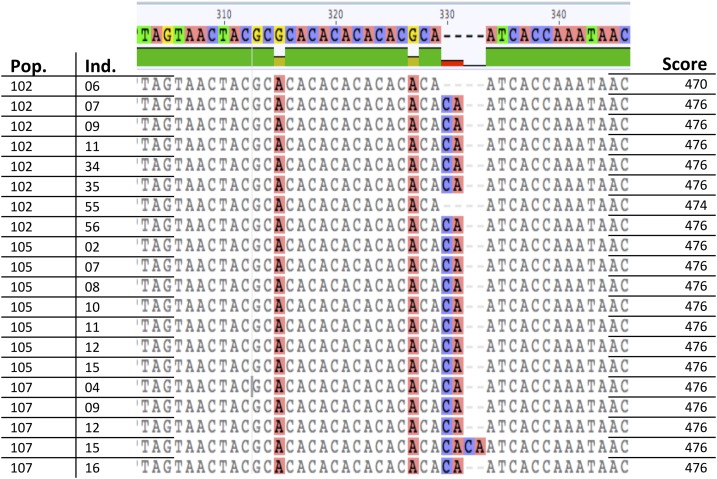
Rarer, but still possible, differences in the flanking region can hide similarities in the number of repeats in the microsatellite. For example, for locus PolyE01, individuals 7, 9, 10, 11, 34, 35, and 56 in population 102 of P. lewtonii are all scored with a fragment length of 476 and individual 55 with 474. However, at base position 330, a CA insert differentiates these former individuals from individual 55. The difference in fragment length is therefore only due to the flanking region; the number of repeats is the same for all individuals. This will lead to an apparent increase in genetic diversity that is not due to differences in the number of repeats. To take this further, at the same insertion in population 107, all individuals have the same 476 fragment-length score. However, individual 15 has two CA insertions, and therefore has one less repeat in its microsatellite, but this difference is compensated by the extra 2-bp insertion in the flanking region. This will decrease the apparent genetic diversity detected in this population for this locus (Fig. 3).

Fig. 3.

Examples of creation and obstruction of fragment length differences with inserts in the flanking region at locus PolyE01 for Polygala lewtonii. The topmost sequence is the 50% consensus sequence over both species (more than are included in the frame presented here). Ind. = individual; Pop. = population.

Genetic diversity

Between sister species, P. lewtonii has a higher number of alleles per population than its widespread congener P. polygama, but a lower number of effective alleles (Table 3), which could imply the presence of rare or unique alleles. Those numbers are generally higher for repeats than they are for fragment length. The expected heterozygosity differs significantly between fragments and repeats (lower for fragments), as does the observed heterozygosity (higher for fragments). Lastly, the fixation index also showed noticeable differences, with the repeats giving higher estimates of inbreeding than the fragments.

Table 3.

Overall genetic diversity in Polygala lewtonii and P. polygama.^a

Statistics	P. lewtonii	P. polygama
N
Fragment	148	118
Repeats	139	87
A
Fragment	2.127 (0.120)	1.966 (0.162)
Repeats	6.333 (1.202)	5.667 (2.404)
Ae
Fragment	1.363 (0.048)	1.339 (0.090)
Repeats	1.702 (0.142)	2.225 (0.683)
He
Fragment	0.199 (0.020)	0.213 (0.026)
Repeats	0.405 (0.048)	0.423 (0.215)
Ho
Fragment	0.100 (0.016)	0.090 (0.020)
Repeats	0.060 (0.041)	0.011 (0.011)
F
Fragment	0.410 (0.046)	0.564 (0.055)
Repeats	0.845 (0.104)	0.972 (0.023)

Note: A = number of alleles; A_e = effective number of alleles; F = fixation index; H_e = expected heterozygosity; H_o = observed heterozygosity; N = number of individuals.

^aResults for all but N are means per population and are presented with SE in brackets.

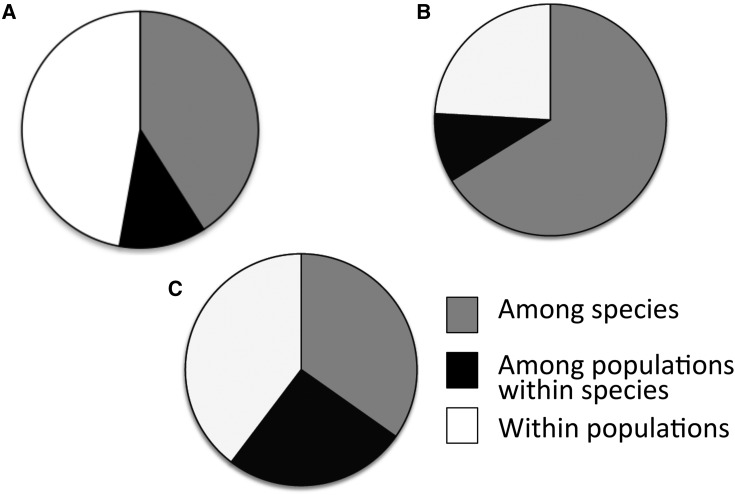
Using AMOVA, most of the variation in repeat number is partitioned between species, whereas most of the variation in fragment lengths is maintained within populations. The flanking regions show nearly equal variance components between species, among populations, and among individuals within populations (Fig. 4).

Fig. 4.

Portion of molecular variance between species, among populations within species, and within populations for both Polygala lewtonii and P. polygama using fragment lengths (A), repeat number (B), and flanking region sequence (C) for the three overlapping loci.

Within P. lewtonii, the number of individuals per population for each data set is summarized in Table 1 (columns “Genotyped” and “Sequenced”). Low numbers can interfere with statistical analyses, so populations 108, 118, and 127 were removed from the data set for the comparative analyses. The variation per population based on flanking regions was higher than the estimates from both fragments and repeats for A_e and H_e. Within P. lewtonii, the sample sizes, A, and A_e were comparable for the repeats, flanking regions, and fragments. H_o, however, was higher for the fragments than the repeats for all populations except 105. Finally, the fixation index was comparable for all populations except 107 and 126. The variation among populations in the number of polymorphic sites, number of haplotypes, and nucleotide diversity was not correlated with the variation in A, A_e, and H_o, respectively (Fig. 2).

The fragments data set shows only population 102 (Lake Wales Ridge State Forest) to have a positive contribution to the overall allelic richness. Repeats, however, reveal populations 102, 115 (ADB Catfish State Preserve SP), and 127 (Ocala National Forest) all positively contribute to the allelic richness of the species. Flanking regions show populations 115 and 127 as positive contributors (Appendix S4 ^{(499KB, pdf)} ).

Spatial genetic structure

Population 108

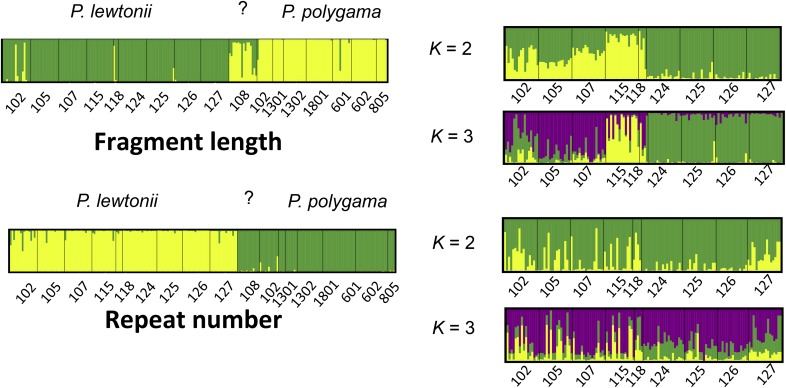
TESS detected clear structure, clustering population 108 with P. polygama based on both fragments and repeat number (Figs. 3, 5, Appendix S5 ^{(990.1KB, pdf)} ). Population 108 was therefore excluded from analyses of P. lewtonii only. Flow cytometry did not detect any difference in genome size between population 108 and any population of P. lewtonii. All mutations that are specific to P. polygama are also found in population 108 (Appendix S3 ^{(116.4KB, docx)} ). Population 108 in The Nature Conservancy’s Saddle Blanket site is hereafter identified as P. polygama, making it the southernmost population of this species.

Fig. 5.

Genetic and geographic clustering of data for both Polygala species (left) and P. lewtonii only (right), using TESS, with the number of clusters (K) shown in the center for fragment length (above) and repeat number (below).

Bayesian clustering

Both fragment length and repeats delimit both Polygala species clearly, with the fragments showing less distinction between the two, and a less clear-cut population 108 in P. polygama. Within P. lewtonii, the DIC curves detect an optimal number of clusters of K = 3 for both the fragments and repeats, but only the fragments show a clear structure in the bar plots: one cluster in the southern Lake Wales Ridge (populations 102, 105, 107), one on Mount Dora (populations 124–127), and the smallest one for populations in central/north Lake Wales Ridge (Fig. 5) (populations 115 and 118). K = 3 is therefore the optimal number of clusters for the fragments within P. lewtonii. The repeat numbers analyses show no structure at any K values (Fig. 5).

Gene flow

F_ST permutations among populations reveal low population differentiation in fragments, with less differentiation between geographically close populations, such as those in the Ocala National Forest (populations 124–127), while the repeats show a proportionally high differentiation in the Ocala National Forest cluster (Table 4). Also, populations 105 and 102, in central and northern Lake Wales Ridge, seem isolated from everything else. Finally, populations 115 and 107, which are geographically close, at the southern tip of the Lake Wales Ridge, show low levels of differentiation, perhaps due to ongoing gene flow. Generally, fragment lengths showed a high level of significance in F_ST while repeats were not significant. On the other hand, R_ST tended to be more consistent between fragments and repeat numbers, with population 105 being more isolated from other populations; some populations on Mount Dora were also genetically isolated despite being geographically very close (Table 4). Because the data set has proven to follow a stepwise mutation model, the consistency in the R_ST might be due to a better fit overall.

Table 4.

Among-population F_ST/R_ST values for Polygala lewtonii.^a

Population	102	105	107	115	124	125	126
102		0.122/0.189*	0.126/0.000	0.142/0.010	0.262/0.097*	0.038/0.000	0.135/0.067
105	0.130*/0.000		0.029/0.177*	0.091/0.184*	0.201/0.107*	0.056/0.235*	0.133/0.095*
107	0.090*/0.006	0.165*/0.096*		0.119/0.000	0.159/0.047	0.041/0.000	0.070/0.048
115	0.080*/0.104*	0.098*/0.192*	0.084*/0.000		0.079/0.000	0.088/0.001	0.158/0.031
124	0.082*/0.002	0.081*/0.091*	0.044/0.000	0.056/0.000		0.203/0.111*	0.193/0.013
125	0.104*/0.000	0.102*/0.000	0.117*/0.104*	0.058/0.218*	0.061/0.097*		0.034/0.098*
126	0.121*/0.000	0.106*/0.005	0.079*/0.000	0.062/0.000	0.034/0.000	0.040/0.027

Note: F_ST = genetic distance measure assuming an infinite allele model; R_ST = genetic distance measure assuming a stepwise mutation model.

^aInformation presented: values for repeats/values for fragments.

^*Indicates significance of permutation test (P < 0.05).

Population contributions

The fragment data set shows three populations that distinguish themselves from the rest. Populations 124 and 126, in the Ocala National Forest, have high diversity, but no significant divergence from other populations, while population 102, at the southernmost tip of the Lake Wales Ridge, does not exhibit a positive contribution to overall diversity, but is highly differentiated from other populations, most likely in the form of private alleles. Overall, fragment lengths had a higher degree of differentiation between the highest and lowest contributions, followed by the flanking regions, and then the repeats data set.

Historical demography and migration

Runs in IMa2 (repeats only, whole fragments, and sequences only) all showed ESS values higher than 70 (up to 436), with no significant correlations between parameters, and most histograms exhibited a strong sharp peak, as expected in reliable analyses. This isolation-with-migration Bayesian model uses mutation rates and a priori relationships between groups of individuals to reconstruct present and past effective population sizes and gene flow between those populations in time. Population sizes are relative to each other and should not be compared from one run to another.

For the repeats only, the size of the P. polygama population (including population 108 of P. lewtonii) was larger (value of 1.8 relative to other values within the repeats analysis) than that of the Lake Wales Ridge (0.752) and the Mount Dora (0.446) populations of P. lewtonii combined. The ancestral P. lewtonii population is thought to have been large (2.0), similar to the ancient Polygala complex (2.0). In terms of relative population migration (2Nm), there is no gene flow between P. polygama and either of the P. lewtonii populations. The Lake Wales Ridge populations, however, contributed largely to migrants toward P. polygama (relative value of 0.499), while the Mount Dora populations contributed less (0.049). The exchange of migrants from the Lake Wales Ridge to Mount Dora is larger than in the opposite direction (0.167 vs. 0.1). The ancestral P. lewtonii population contributed migrants toward P. polygama (0.268), while the opposite was not true (0.00).

For the data set of fragment lengths, P. polygama was also larger (4.7) than the Lake Wales Ridge (1.8) and Mount Dora (2.5) populations, even when combined. The ancestral P. lewtonii, however, was larger (83.6) than the ancestral Polygala complex (43.0). These last values are much larger than those from the repeats. For the relative gene flow between populations, the strongest exchange of genes was between Mount Dora and the Lake Wales Ridge (0.6 from Mount Dora toward the Lake Wales Ridge, and almost double in the other direction: 1.00). The Lake Wales Ridge also served as a source of gene flow toward P. polygama with 0.7, with only 0.2 in the opposite direction, contrary to the absence of such flow with the repeats.

Using flanking region sequences gives us a completely different view of the past history of population sizes and gene exchange. No gene exchange was detected between any of the populations at any point in time. Also, the P. polygama population (3.6) is larger than either of the P. lewtonii populations (Mount Dora and Lake Wales Ridge), as is the case with the other data sets, but the Mount Dora population is larger than the Lake Wales Ridge population (0.5 and 0.04, respectively). Finally, the ancestral populations are much smaller than the present ones, which is not the case with the other data sets (0.01 for the ancestral P. lewtonii population and 0.02 for the ancestral P. polygama/P. lewtonii population).

DISCUSSION

This study is the first to sequence the microsatellite flanking regions for a full set of populations for two closely related species, nearing 200 individuals sequenced for four loci. Moreover, the distinction between the fragment length and the repeat numbers provides an exceptional data set to measure the impact of mutations in the flanking region on estimates of genetic diversity. Although the number of independent loci sequenced is small, it is still superior to studies using only chloroplast regions to infer levels and partitioning of genetic diversity, as they are inherently linked and only rarely variable (Ouborg et al., 1999).

The increasingly diverse utilization of microsatellites (Selkoe and Toonen, 2006; Kalia et al., 2010) and rapidity with which microsatellites can now be developed make it easy to overlook issues at individual loci. Our findings reinforce the idea that careful consideration of each locus is essential, especially when using loci developed and characterized in related taxa, or when comparing several related species in the same study (as is common in studies of crops and their wild relatives, or hybrids, among other examples).

Homoplasy

Homoplasy was detected with the use of flanking region sequencing and the discovery of substitutions and even-number one indel at the locus Poly5. The latter case is the most problematic because it will go undetected when only fragment length is being considered, as it mimics the addition or deletion of one or more repeats. Also, in rare cases, indels in the flanking region can create homoplasy (a repeat shorter by two repeats of 2 bp, “compensated” by a 4-bp insertion in its flanking region). Estoup et al. (2002) estimated that homoplasy problems in studies of populations with “shallow” history and/or smaller effective population size, as is the case for P. lewtonii, did not affect overall results. Indeed, recently diverged populations have had less time to accumulate mutations in their flanking regions. However, we show that even in recently diverged species and populations, complex mutations have accumulated in the flanking regions at all loci. Most mutations within P. lewtonii were substitutions, but some were indels, with the case of locus Poly1 exhibiting variation within populations. Also, Fig. 3 exhibits several consequences for the same indel in different populations, and within populations. We therefore believe that mutations in the flanking region should not be underestimated in small or young species and populations.

This trend was only accentuated when considering related taxa. Between P. lewtonii and P. polygama, the presence of insertions, substitutions, and a single-base-pair insertion specific to P. polygama means that risks of homoplasy are significantly higher between closely related species than within either one alone. Commonly, journals require loci to be amplified in related species. The cross-amplification in related species can be useful for studies in the same clade, but loci should be used carefully, and sequencing should be systematic when comparing across species.

Consequences for genetic diversity measures

Several indices of molecular variance are affected by differences between fragment length and number of repeats. The most important differences in molecular variance were observed when comparing the two species. Number of alleles (observed or effective) was much higher in the fragment lengths, possibly due to the added variation in the flanking regions compared to the number of repeats. Expected heterozygosity was higher than observed heterozygosity in both the fragment length and repeats data sets, but inbreeding was higher in the repeat numbers than the fragment length, also perhaps due to the generally higher diversity in the latter. These conclusions support other studies (Blankenship et al., 2002; Vali et al., 2008), even though the direction of the differences might not be the same as here. For example, Epperson (2005) and Rousset (1996) found that allelic diversity was underestimated with fragment lengths compared to repeat number, and that gene flow was overestimated. In Polygala, allelic diversity was higher when estimated with fragment lengths than with repeat numbers, as was gene flow (especially between species in the Lake Wales Ridge and Mount Dora populations).

The differences in estimates from the three data sets were less substantial, however, within P. lewtonii. Values were comparable, but the directionality of variation between populations within the species varied between repeats and fragments. Also, some analyses yielded very different results (as in Appendix S4 ^{(499KB, pdf)} ). Noticeably, the estimations of gene flow were affected by the data set used. Fragment lengths showed substantial gene flow between populations, while the repeats themselves showed none. This might be due to the separation of homoplasious repeats with variations in the flanking regions, in accordance with several studies (Goldstein et al., 1995; Hedrick, 1999; Makova et al., 2000; Selkoe and Toonen, 2006). Possibly for similar reasons, the clustering of populations within a rare endemic is only feasible with the fragment lengths, and not the repeats only. Furthermore, we ran analyses to detect bottlenecks and, consistent with the migration results, the fragments data set showed signs of bottlenecks in the Mount Dora populations, whereas the repeats data set showed no signs of recent bottleneck.

It is important to note that flanking regions evolve at a different rate than repeat number, and so reflect a different evolutionary history. The past history and gene flow reflect this difference and can be used to address different questions. For example, the use of flanking regions for the delimitation of closely related species is useful in our study and can be extended to systematics studies at shallow levels, as well as to conservation planning.

Recommendations for the use of microsatellites within and between closely related taxa

We recommend that microsatellite studies include the sequencing of one or two individuals per population. A careful design of microsatellite primers, close to the repeats, could also prevent sequence variation in the flanking regions from being interpreted as variation in repeat number. However, in view of the high polymorphism in the flanking regions, this strategy could increase the risk of null alleles. Sequencing of the flanking regions could be particularly useful for population-level studies between species, species delimitation, and phylogeographic studies of a clade of closely related taxa. Low-level phylogenetic studies could also benefit from targeting the microsatellite flanking regions, as has proved useful for resolving relationships among closely related species (Zardoya et al., 1996; Rossetto et al., 2002; Chatrou et al., 2009). The strongest recommendation this study conveys is the absolute necessity of sequencing several individuals when using markers developed in a related species to the focal species. The added cost and time will be small, and will avoid potential major underlying problems further in the study that could jeopardize the legitimate use of one or more loci.

CONCLUSIONS

Our study shows that the risk of homoplasy in microsatellites is real, with different types of mutations present at all three loci. The directionality of those mutations in the flanking regions of the microsatellites is inconsistent with past studies, and so the substitution of fragment length for repeat number should not be assumed. Overall, it seems that most mutations create homoplasy across species, as well as between populations within the same species. A lower but significant proportion of mutations in the flanking region also created homoplasy between individuals within the same population. The overwhelming majority of mutations will lead to a decrease in the estimation of the genetic diversity of populations and species, but an increase in the estimation of gene flow between populations that share homoplasious alleles. Our recommendations, especially for sequencing fragments when using markers developed in one species to study or compare a close relative, are relatively quick and inexpensive and will ensure that the researcher avoids any major indels in the flanking region that are likely to skew results.