Significance
We present 3D acoustic tweezers, which can trap and manipulate single cells and particles along three mutually orthogonal axes of motion by recourse to surface acoustic waves. We use 3D acoustic tweezers to pick up single cells, or entire cell assemblies, and deliver them to desired locations to create 2D and 3D cell patterns, or print the cells into complex shapes. This technology is thus shown to offer better performance over prior cell manipulation techniques in terms of both accurate and precise motion in a noninvasive, label-free, and contactless manner. This method offers the potential to accurately print 3D multicellular architectures for applications in biomanufacturing, tissue engineering, regenerative medicine, neuroscience, and cancer metastasis research.
Keywords: 3D acoustic tweezers, cell printing, 3D cell manipulation, cell assembly, 3D particle manipulation
Abstract
The ability of surface acoustic waves to trap and manipulate micrometer-scale particles and biological cells has led to many applications involving “acoustic tweezers” in biology, chemistry, engineering, and medicine. Here, we present 3D acoustic tweezers, which use surface acoustic waves to create 3D trapping nodes for the capture and manipulation of microparticles and cells along three mutually orthogonal axes. In this method, we use standing-wave phase shifts to move particles or cells in-plane, whereas the amplitude of acoustic vibrations is used to control particle motion along an orthogonal plane. We demonstrate, through controlled experiments guided by simulations, how acoustic vibrations result in micromanipulations in a microfluidic chamber by invoking physical principles that underlie the formation and regulation of complex, volumetric trapping nodes of particles and biological cells. We further show how 3D acoustic tweezers can be used to pick up, translate, and print single cells and cell assemblies to create 2D and 3D structures in a precise, noninvasive, label-free, and contact-free manner.
The ability to precisely manipulate living cells in three dimensions, one cell at a time, offers many possible applications in regenerative medicine, tissue engineering, neuroscience, and biophysics (1–3). However, current bioprinting methods are generally hampered by the need to reconstruct and mimic 3D cell-to-cell communications and cell–environment interactions. Because of this constraint, bioprinting requires accurate reproduction of multicellular architecture (4, 5). Several approaches have been developed to produce complex cell patterns, clusters, assembled arrays, and even tissue structures. These approaches use many disparate technologies which include optics, magnetic and electrical fields, injection printing, physical or geometric constraints, or surface engineering (6–11). However, there is currently a paucity of a single method that can facilitate the formation of complex multicellular structures with high precision, high versatility, multiple dimensionality, and single-cell resolution, while maintaining cell viability, integrity, and function. As a result, there is a critical need to develop new methods that seek to overcome these limitations.
“Acoustic tweezers,” which manipulate biological specimens using sound waves, offer several unique advantages (12, 13) in comparison with other techniques. First, the acoustic tweezers technology is the only active cell-manipulation method using gentle mechanical vibrations that do not alter cell characteristics. Acoustic vibrations create a pressure gradient in the medium to move suspended microobjects and cells, thereby resulting in a contamination-free, contact-less, and label-free method for cell manipulation. Sound waves are preferred for cell manipulation for the following reasons: (i) cells maintain their native state (e.g., shape, size, reflective index, charge, or polarity) in the absence of surface modification or labeling; and (ii) cells can remain in their original culture medium or extracellular matrix gel solution. Furthermore, acoustic tweezers are safe tools for biological manipulation. Acoustic tweezers involving sound waves have a power intensity that is ∼10 million times lower than that of optical tweezers. Therefore, acoustic tweezers have minimal impact on cell viability and function. Moreover, acoustic tweezers operate at a power intensity and frequency similar to the widely used medical ultrasound method that is well known as a safe technique for sensitive clinical applications such as imaging of a fetus in the mother’s womb. Finally, the acoustic tweezers platform can be constructed as a single, integrated microdevice without any moving parts or complicated setup procedures. This feature offers additional advantages for ease of use and versatility.
Thus far, sound waves have been demonstrated to successfully perform many microscale functions such as the separation, alignment, enrichment, patterning, and transportation of cells and microparticles (12–17). None of these acoustic approaches, however, has hitherto demonstrated controlled 3D manipulation of single cells. The lack of these manipulation methods is mainly attributable to the limited understanding of the relationship between a 3D acoustic field and the induced acoustic streaming. Using 2D acoustic waves often results in insufficient control of a single cell in 3D space. Here, we report a standing surface acoustic wave (SSAW)-based technique that is able to create and independently manipulate an array of stable 3D trapping nodes.
In this work, we illustrate the relation between the acoustic vibrations, the acoustic field produced by SSAWs, and the resulting streaming in a microfluidic chamber by recourse to both modeling and controlled experimental validation. Unlike Rayleigh streaming in bulk acoustic wave devices, the unique acoustic streaming (i.e., streaming motion caused by acoustic oscillation) pattern in a SSAW device determines how objects are lifted up from the substrate surface. By regulating the 3D distributed acoustic field and acoustic streaming, induced by two superimposed pairs of orthogonally placed SSAWs, we achieved an array of 3D trapping nodes in a microfluidic chamber. By independently tuning the relative phase angle of each SSAW or by varying the input power, the position of these 3D trapping nodes can be precisely controlled in a 3D environment. Using this concept, we demonstrate 3D trapping and three-axis manipulation of single microparticles and single biological cells. Finally, we illustrate how this 3D acoustic tweezers technique can be used for printing with live cells and for producing prescribed cell culture patterns.
Results
Working Mechanism of Three-Dimensional Acoustic Tweezers.
To manipulate suspended objects along three orthogonal axes with surface acoustic waves (SAWs), it is necessary to form 3D trapping nodes and to move these nodes precisely in three dimensions. To achieve this objective, we created a 2D displacement field on a lithium niobate (LiNbO3) piezoelectric substrate by superimposing two mutually orthogonal pairs of interdigital transducers (IDTs) that produce SSAWs. The propagation of these waves through a microfluidic chamber produces an acoustic field distributed in three dimensions and induces acoustic streaming which creates stable 3D trapping nodes within the fluid-filled chamber. The positions of these 3D trapping nodes were precisely manipulated in the transverse (x), longitudinal (y), or vertical (z) directions by adjusting the phase angle of each individual IDT pair (x or y axis motion control) or the input acoustic power (z axis motion control), respectively.
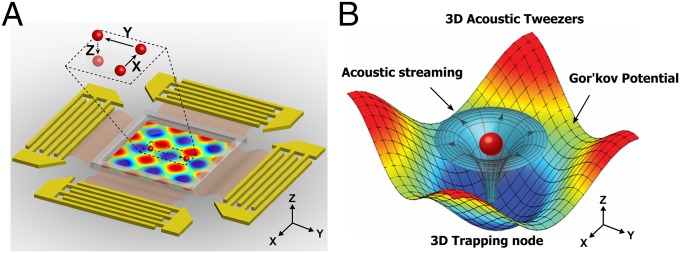
Two orthogonal SSAWs were used to perform particle/cell manipulation in a microfluidic chamber. Two pairs of IDTs were deposited onto a 128° YX-cut LiNbO3 substrate, which were positioned along the x and y axes. The IDTs were made up of 40 pairs of electrodes with a 75-μm width of each finger electrode and a 75-μm spacing between fingers, and a 1-cm aperture. A polydimethylsiloxane (PDMS) layer with a 1.8 mm × 1.8 mm × 100 μm fluidic chamber was bonded to the substrate, at the center of the two orthogonal pairs of IDTs. Fig. 1A shows a schematic diagram of the device. Each pair of IDTs was individually connected to a double-channel radio-frequency (RF) signal generator and two amplifiers, which generated SSAWs with different frequencies and independent SSAW phase angle control. Once the pairs of IDTs were activated, a 2D displacement field (including both longitudinal and transverse vibrations) was produced on the surface of the LiNbO3 substrate (18). The acoustic waves induced by these surface vibrations propagated in the fluid, reflected by the chamber walls, and established a 3D, differential Gor’kov potential field (19). Meanwhile, these surface vibrations also induced 3D acoustic streaming in the microfluidic chamber. The interaction of the fluidic and acoustic fields produced 3D trapping nodes within the chamber (Fig. 1B). Along the vertical direction, suspended microobjects were pushed and levitated to a stable trapping node because of the competitive interaction of the acoustic radiation force, the gravitational force, the buoyancy force, and the Stokes drag force induced by acoustic streaming. After increasing the input acoustic power, the vertical trapping position was raised because of a rebalancing of these forces. Along the horizontal plane (x-y plane), the objects were pushed toward the center of the 3D trapping node. These trapping positions can be independently manipulated along the transverse (x) or longitudinal (y) directions by relocating the 2D displacements via changing the input phase angle. As a result, microobjects were trapped into a 3D node and manipulated along three axes within a microfluidic chamber (Fig. 1A).
Fig. 1.
Illustration of our 3D acoustic tweezers. (A) Configuration of the planar surface acoustic wave generators, used to generate volumetric nodes, surrounding the microfluidic experimental area. The Inset indicates a single particle within a “3D trapping node,” which is independently manipulated along the x, y, or z axes. (B) Numerical simulation results mapping the acoustic field around a particle that shows the physical operating principle for the 3D acoustic tweezers. The 3D trapping node in the microfluidic chamber is created by two superimposed, orthogonal, standing surface acoustic waves and the induced acoustic streaming.
SAW Vibrations Induce Three-Dimensional Acoustic and Fluidic Fields.
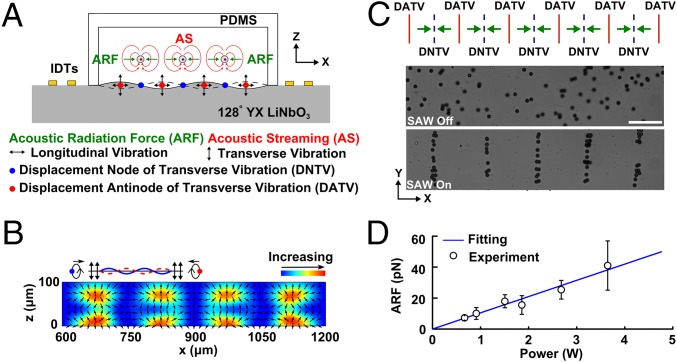
To create a 3D trapping node in a microfluidic chamber, the mechanism by which SSAWs manipulate objects within such a chamber must be understood. A simple acoustic tweezers device, consisting of a PDMS chamber and a pair of IDTs (positioned along the x axis of a 128° YX LiNbO3 substrate), was used to investigate this mechanism. Two sets of SAWs, traveling toward each other, were produced after applying a RF signal to the IDTs. A SSAW was formed via the superposition of these SAWs. This type of resulting wave is considered a Rayleigh wave. These waves confine most of the energy to the surface because of the exponential decay of their amplitude with the depth of the substrate. In addition, these waves include both longitudinal and transverse vibrations with a phase lag on the substrate. Once the waves interfere with the liquid in the microfluidic chamber, periodically distributed vibrations are created which lead to periodically distributed acoustic fields and acoustic streaming in the microfluidic chamber (Fig. 2A). We developed a numerical model that could account for the Gor’kov potential and acoustic streaming in a lateral plane (x-z plane) as well as the acoustic radiation force acting on suspended particles. The model considers the effects of the transverse and longitudinal vibrations on the liquid, and the acoustic reflection and transmission at the interface between the fluid and PDMS. A detailed description of the numerical model can be found in SI Text, Theoretical Framework and Model Setup (see also Fig. S1 and Table S1).
Fig. 2.
Study of the acoustic radiation force. (A) Illustration showing how a standing surface acoustic wave enables particle manipulation in a microfluidic chamber. The longitudinal and transverse vibrations are generated by the propagation of standing waves along the x axis on a 128° YX lithium niobate substrate, which enables displacement motions along the surface. These displacements introduce an acoustic field and acoustic streaming in the microfluidic chamber which can push and levitate suspended objects. Numerical simulation results show the distribution of Gor’kov potential and the acoustic radiation force along the x-z plane induced by the transverse vibrations (B). The red regions indicate a high Gor’kov potential, whereas the blue regions indicate a low Gor’kov potential, and the arrows from the red region to the blue region show the direction of the acoustic radiation forces. (C) Diagram of the radiation force distribution between the periodic array of nodes and antinodes and the correlated experimental manipulation of 10.1-μm polystyrene particles along the x-y plane without, and then with, an applied standing surface acoustic wave. (D) The experimental results show the dependence of the acoustic radiation force on the input power. (Scale bar: 100 μm.)
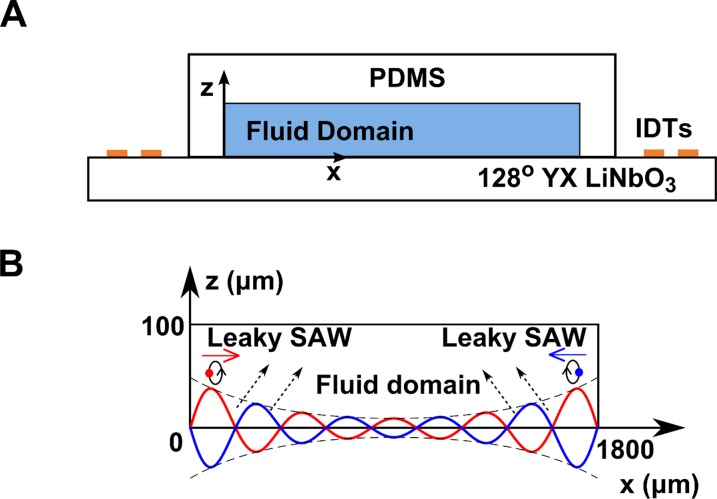
Fig. S1.
Scheme of 1D SSAW device and 2D fluid domain for modeling. (A) Cross-section of the 1D SSAW device, comprising a 128° YX LiNO3 substrate with one pair of IDTs on its surface and a PDMS chamber filled with fluid. (B) Two-dimensional fluidic domain used for numerical modeling. Two decaying LSAWs propagate in opposite directions to form the actuation boundary at the bottom. The other boundaries are lossy-wall boundaries. The dimensions of this 2D modeled domain are 1,800 × 100 µm (width × height).
Table S1.
Parameters used in the numerical simulations
| Material properties | Symbol | Value |
| Water | ||
| Density | ρ0 | 997 kg⋅m−3 |
| Speed of sound | c0 | 1,495 m⋅s−1 |
| Viscosity | µ | 1 × 10−3 Pa⋅s |
| Bulk viscosity | µB | 2.4 × 10−3 Pa⋅s |
| Ethanol | ||
| Density | ρ0 | 789 kg⋅m−3 |
| Speed of sound | c0 | 1,144 m⋅s−1 |
| Viscosity | µ | 1.082 × 10−3 Pa⋅s |
| Bulk viscosity | µB | 1.4 × 10−3 Pa⋅s |
| Polystyrene | ||
| Density | ρp | 1,050 kg⋅m−3 |
| Speed of sound | cp | 2,350 m⋅s−1 |
| 128° YX lithium niobate | ||
| Density | ρs | 4,650 kg⋅m−3 |
| Longitudinal wave speed | cl | 7,158 m⋅s−1 |
| Transverse wave speed | ct | 4,260 m⋅s−1 |
| Phase velocity of SAW | cR | 3,990 m⋅s−1 |
| Phase velocity of LSAW | cL | 3,900 m⋅s−1 |
The periodically distributed transverse vibrations are considered as the primary perturbation source for generating an acoustic field in a liquid chamber, whereas the longitudinal vibrations decay very fast and have little impact on the acoustic field. Fig. 2B predicts the distribution of the Gor’kov potential along the x-z plane. The regions of maximum Gor’kov potential (in red color), known as pressure antinodes (ANs), are located atop places with a displacement antinode of the transverse vibrations (DATVs), whereas minimum regions (in blue color), known as pressure nodes (PNs), occur atop a displacement node of transverse vibrations (DNTVs). The distribution of PNs and ANs coincide with the location of DNTVs and DATVs on the substrate’s surface; therefore, the distance between adjacent PNs or ANs is half-wavelength of a SAW. Because of the gradient of the Gor’kov potential, an acoustic radiation force was generated to push the suspended cells or microparticles from ANs to PNs. The experimental results show that all of the suspended 10.1-μm diameter polystyrene particles were pushed to the parallel PNs by the acoustic radiation force (Fig. 2C). The dependence of the acoustic radiation force on input power was investigated, and the results were plotted (Fig. 2D and SI Text, Data Analysis).
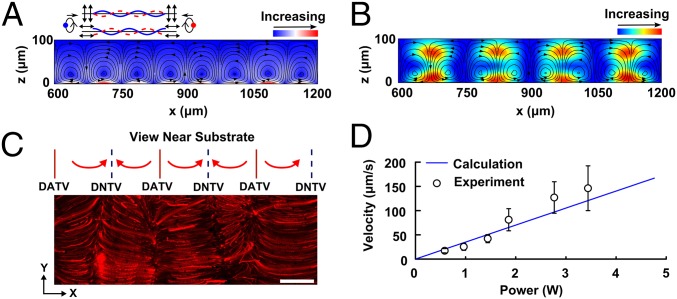
In addition to the aforementioned acoustic field, the vibrations also induced acoustic streaming. Both the transverse and longitudinal vibrations attenuate in a thin boundary layer close to the substrate and result in a particular streaming pattern in the microfluidic chamber (Fig. 2A). Our numerical results describe the streaming vortices and the periodic distribution of the acoustic streaming in the x-z plane, as shown in Fig. 3A. The streaming flows rise up from DNTVs on the substrate, rotate clockwise or counter clockwise to the two nearby DATVs, and then rise up again from the original DNTVs. In contrast to Rayleigh streaming (18, 20), which is driven by standing bulk acoustic waves, this streaming, which is induced by SSAWs, has a reversed direction with respect to the streaming vortices. However, these streaming processes share the same spatial distribution with four vortices in one wavelength. This particular streaming plays an important role in the vertical manipulation of microparticles/cells. Fig. 3B plots the numerical streaming pattern over Gor’kov potential in the x-z plane. The streaming flows rise vertically from DNTVs on the substrate toward the PNs where particles are trapped.
Fig. 3.
Study of acoustic streaming. (A) Simulation results showing the acoustic streaming patterns in the x-z plane, as induced by both the longitudinal and transverse vibrations. The streaming lines rotate clockwise or counterclockwise from a displacement node to two neighboring displacement antinodes. The arrows indicate the rotation directions. The red color nearby the substrate surface indicate the high magnitudes of the streaming velocities, whereas the blue color shows low velocities. (B) Simulation results of the distribution of Gor’kov potential overlaid on top of the acoustic streaming results in the microfluidic chamber along the x-z plane. (C) Visualization of the acoustic streaming pattern along the periodic array of displacement nodes and antinodes and the overlapped experimental acoustic streaming lines along the x-y plane, under a standing surface acoustic wave. Path lines formed from 1-μm red fluorescent polystyrene particles as they flow up from the premarked displacement nodes and rotating as our simulations predicted. (D) Experimental results showing the dependence of the magnitudes of the streaming velocities on the input power. (Scale bar: 100 μm.)
To validate our modeling prediction, we performed an experiment to investigate SSAW-induced acoustic streaming within the microfluidic chamber. We started the experiment by premarking the location of DNs by patterning 10.1-μm polystyrene particles into parallel lines. Then, we fixed the focal plane of the microscope near the substrate. Once the SSAW was applied, the 1-μm fluorescent particles, used as the markers to trace streaming lines, flowed up from the DNTVs, defocused, and then flowed down to the neighboring DATVs in the x-y plane (Movie S1). A time series of frames, captured from the movie, was superimposed to show the streaming pattern (Fig. 3C). The magnitude of streaming velocity increases linearly with the input power (Fig. 3D and SI Text, Data Analysis). Based on the quantitative values of the acoustic radiation force and acoustic streaming, we calculated the quantitative relationship between the input powers and the amplitudes of the transverse vibrations (∼several nanometers) on the substrate (Fig. S2 and SI Text, Calibration of Vibration Amplitude).
Fig. S2.
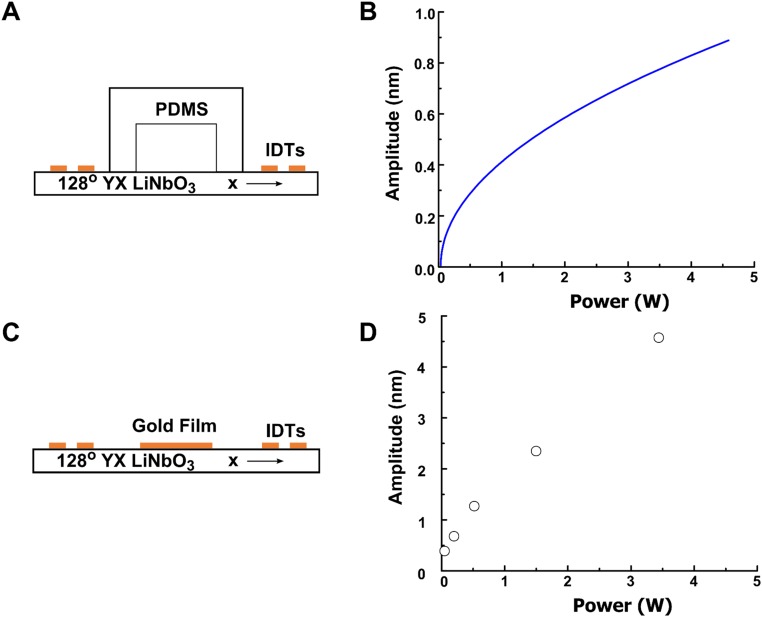
Calibration of vibration amplitude. (A) Schematic of the 1D SSAW microfluidic device. Two traveling waves are propagating toward each other and superposed to form a standing wave along the x axis of a 128° YX-cut lithium niobate substrate. Before entering into the microfluidic chamber, each wave propagates through a PDMS chamber wall which results in a decay of the vibration amplitude. (B) The curve shows the calibrated dependence of the amplitude of the LSAW (in the fluidic chamber) on the input power. (C) The figure illustrates the setup for directly measuring the amplitude of the longitudinal vibration of the SSAW. An additional 4 × 4 mm gold film with a thickness of 200 nm was deposited in the middle of the pair of IDTs to reflect light during the optical measurement. (D) The results graph the amplitude of the longitudinal vibrations under different input powers by directly measuring the SAW vibrations on the substrate with an optical vibrometer system.
Manipulation in the Vertical Direction.
Based on our model of the vertical distribution of the acoustic and fluidic fields induced by a SSAW, we explored the vertical manipulation of trapped objects. Using the aforementioned device with one SSAW, we examined the forces acting on 10.1-μm polystyrene particles in detail. Along the horizontal plane (x-y plane), the suspended particles experience a greater acoustic radiation force than the Stokes drag force (induced by the acoustic streaming), causing the particles to be pushed toward the PNs. Along the vertical direction, the particle experiences acoustic radiation force, Stokes drag force, gravitational force, and buoyancy force as shown in Fig. 4A. Because of the minimal Gor’kov potential and small gradient within the PNs, the acoustic radiation force in the PNs is comparable to the opposing forces. Once these forces are balanced, the suspended object will be trapped in a stable, vertical position. By adjusting the vibration amplitude along the substrate through tuning the input power of the SAWs, the acoustic radiation force and the Stokes drag force along the z direction can be regulated accordingly. As a result, the trapped object will move to a new stable position along the z axis.
Fig. 4.
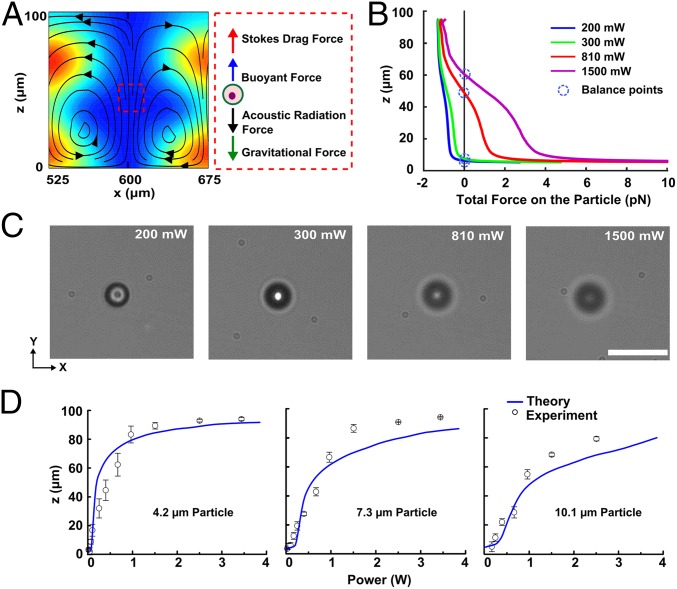
Vertical (z axis) acoustic manipulation. (A) Calculated trapping node induced by a standing acoustic wave in the x-y plane within the microfluidic chamber and an illustration of the forces along the z direction in the trapping node. (B and C) The theoretical calculations (B) and experimental demonstration (C) of vertical position control of a single 10.1-μm polystyrene particle by varying the input power. The images taken in the x-y plane show the stable trapped single particle was lifted up and through the fixed microscope’s focal point by increasing the input power from 200 to 1,500 mW. (D) Experimental results showing the vertical positions of particles with different sizes (4.2, 7.3, 10.1 μm) under different input powers, which is consistent with the predictions from our numerical model. (Scale bar: 20 μm.)
In addition, the forces acting on a single 10.1-μm polystyrene particle along the vertical direction are quantitatively investigated by our model (SI Text, Theoretical Framework and Model Setup). Fig. 4B shows the total force acting on the particle along the z direction in the chamber (x = 600 µm) as a function of the input power (Fig. 4B). The stable trapping positions, where the net force is zero, are marked with blue circles. The trap position rises as the input power increases. To validate our model, we conducted additional experiments in the vertical direction of the chamber. By applying SSAW with a frequency of 13 MHz and an input power of 200 mW, the particles were levitated to the PNs. A single trapped particle can be levitated toward the top of the microfluidic chamber by increasing the input power from 200 to 1500 mW (Fig. 4C and Movie S2). The focal plane of the microscope was kept at the same position in Fig. 4C; therefore, defocusing indicated that a single particle was levitated vertically as the input power increased. The absolute position of the trapped particle in the vertical direction was calibrated to a reference plane and could be readily obtained by measuring the change in focal planes while tracking the particle. With this method, we quantitatively characterized the vertical trapping position of the particle as a function of input power. Fig. 4D shows the experimental results of the trapping position of single particles with a diameter of 4.2, 7.3, and 10.1 µm, respectively, under different input powers (Fig. 4D). The datasets shown in Fig. 4D were obtained by averaging 10 repeated experimental measurements. The model predictions of the vertical position versus input power are seen to match the experimental results. This method can thus levitate single particles to any vertical position within the chamber.
Three-Dimensional Trapping and Manipulation.
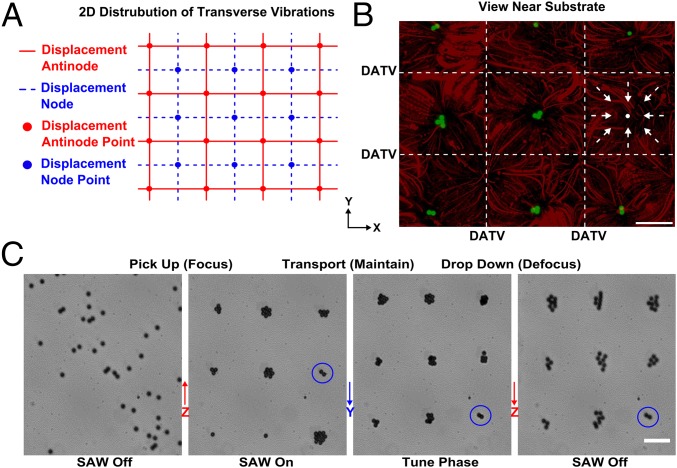
With an understanding of the actuation mechanism for the 1D SSAW, we investigated 3D trapping and manipulation by using orthogonally arranged 2D SSAWs. Fig. 5A illustrates the 2D distribution of transverse vibrations from the 2D SSAWs on a substrate: the interaction of DATVs (blue lines) formed node points (blue filled circles) with minimum Gor’kov potentials, and the interaction of DNTVs (red lines) formed antinode points (red filled circles) with maximum Gor’kov potentials. Vibrations from 2D SSAWs exhibit characteristics similar to those of 1D SSAW and can induce acoustic fields and streaming into the liquid of the microfluidic chamber. The interaction of these two fields forms an array of 3D trapping nodes in the microfluidic chamber with each node superposed on each displacement node of the transverse vibrations.
Fig. 5.
Three-dimensional acoustic manipulation. (A) Illustration of the 2D distribution of transverse vibrations on the substrate. Blue lines represent displacement nodes of transverse vibrations that have minimal vibration amplitudes; red lines represent displacement antinodes. (B) Superimposed images of 3D trapping and streaming patterns; 10-μm green fluorescent polystyrene particles were trapped into a suspended array of single dots, and 1-μm red fluorescent polystyrene particles tracked the motion of the acoustic streaming vortex (the arrows indicate the direction of the streaming near the substrate surface). (C) The image sequence shows the 3D trapping and manipulation of particles with a stable array configuration. A trapping node (blue circle) can levitate particles along z axis (moving into focus) and pushing particles together, transporting them along y axis and dropping them back toward the substrate (moving out of focus). (Scale bar: 100 μm.)
Next, we used the acoustic tweezers device with two orthogonal pairs of IDTs to experimentally demonstrate 3D trapping and manipulation. By applying two different RF signals (13 and 12 MHz/810 mW) to the two pairs of IDTs (along the x and y axes, respectively), 3D trapping was achieved as shown in Fig. 5B. The square trapping region (marked with white lines) consists of a displacement node point and four nearby antinode points from the transverse vibrations. The 10.1-μm green fluorescent polystyrene particles were levitated to a 3D trapping node above a displacement node point in the microfluidic chamber. Close to the substrate, the trajectories of the 1-μm red fluorescent polystyrene particles indicate that the streaming flows come from the edges of the square-like region (DATVs) and stream toward the center. There, the flow rises up and rotates back toward the edges. Combining the effects of the acoustic radiation force and acoustic streaming induced by 2D SSAWs, we have demonstrated that a 3D trapping node can be generated in the volumetric space above this cubic region within a microfluidic chamber.
To achieve 3D manipulation, we need to precisely move the trapping nodes along the x, y, and z directions. We have demonstrated that the vertical (z direction) movement of the trapped particles can be achieved by tuning the input power on the IDTs. To move trapped particles in the horizontal plane (x-y plane), we used a phase shift strategy: changing the relative phase angle lag (Δϕ) of the RF signals applied to each pair of IDTs can move the DNTVs on the substrate as well as the PNs in the fluid. The change in distance of the DNs (ΔD) along the x or y direction is given as ΔD = (λ/4π)Δϕ. As a result, the trapped particles in the PNs are moved the same distance along the same direction. For example, at a relative phase angle lag of π/2, the trapped particles move over a distance of λ/8. With our 3D acoustic tweezers, the randomly distributed 10.1-μm-diameter polystyrene particles were first pushed and levitated to 3D trapping nodes in a dot-array configuration. Gradually increasing the relative phase angle lag of the RF signal from 0 to 3π/2 along the y axis, while keeping all other parameters fixed, we found that all of the trapped particles moved along the y direction while in the dot-array formation. By decreasing the input power of the RF signals to zero, all of the trapped particles settled to the bottom but kept the dot-array formation. The entire process was recorded and is shown in Fig. 5C (Movie S3). Focusing and defocusing indicates that our 3D acoustic tweezers are capable of manipulating microparticles along the z direction. The manipulation of particles along the x direction can be achieved in a similar way. With the wide tuning range of the relative-phase-angle lag, we can translocate microobjects to any desired location within the entire microfluidic chamber and maintain any desired formation of the trapping array, which results in a significant improvement in manipulation dexterity, compared with our previous work (14). By demonstrating a vertical range from the substrate surface to the ceiling of the microfluidic chamber, our approach can manipulate microparticles within the entire volume of a microfluidic chamber. Our 3D acoustic tweezers provide new possibilities for massively parallel and multiaxis manipulation.
Cell Printing with Three-Dimensional Acoustic Tweezers.
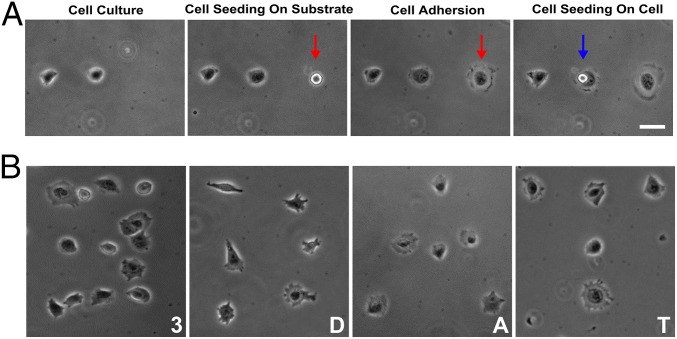
To explore potential practical applications of this technology, we performed 3D printing of living cells onto a substrate with customized cell patterns using our 3D acoustic tweezers. Our earlier work (14, 15) demonstrated that the use of acoustic tweezers had no discernible effect on cell viability, functionality, and gene expression (14, 15). When an acoustic field was applied, living single cells were captured into the 3D trapping nodes. Then, cells were transported along the x or y directions in a horizontal plane by tuning the phase angle of each IDT pair accordingly. After the delivery of the cells above the target locations, the trapped cells were lowered onto the substrate or onto other cells that were already in place, by tuning the input power of the acoustic field. As a result, the cells were printed with precise control of the cell number, spacing, and configuration. To demonstrate 3D printing of live cells, we captured a single suspended 3T3 mouse fibroblast and transported it to a desired location on the substrate after injecting a cell suspension into the microfluidic chamber (Fig. 6A, indicated with red arrow). Following placement via our 3D acoustic tweezers, the cells started to adhere and then spread on to the substrate. In this way, a linear cell array was created by depositing cells one by one (Fig. 6A). We could also position another 3T3 cell on top of the previously adhered cells by using the precise control of 3D acoustic tweezers (Fig. 6A, indicated with blue arrow) to form a 3D cell assembly. To further demonstrate the capabilities of the 3D acoustic tweezers, we applied our technology to print living cells into complicated configurations, such as numbers and letters. Through single-cell seeding of HeLa S3 cells using acoustic control, we printed cells into the following patterns: “3” “D” “A” “T,” as an acronym for “Three-Dimensional Acoustic Tweezers” (Fig. 6B). Cells were able to adhere to the surface and then spread along the surface (Fig. 6B). We also demonstrated that the adhered cells were able to split and proliferate in the prescribed morphological patterns (Fig. S3). Hence, we have demonstrated a versatile acoustic cell printing technique that is capable of single cell resolution and has the ability to manipulate multiple cell types without affecting cell viability.
Fig. 6.
Printing living cells with 3D acoustic tweezers. (A) Single-cell printing. After previously deposited 3T3 cells were attached to the substrate, another single cell was picked up, transported, and dropped at the desired location on the substrate (indicated by red arrow) or on top of another cell (indicated by blue arrow). The single cell adhered and spread along the surface. (B) Formation of arbitrary cell culture patterns forming a “3” “D” “A” and “T” by printing of single HeLa S3 cells via 3D acoustic tweezers. (Scale bar: 20 μm.)
Fig. S3.
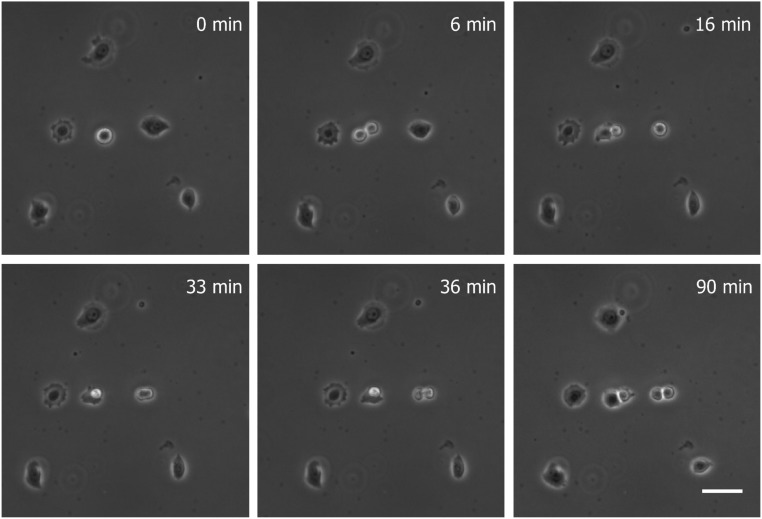
Viability of cells after 3D acoustic printing. Image sequences show that the HeLa S3 cells are splitting and proliferating after being printed into the cell culture pattern of the letter “A.” (Scale bar: 50 μm.)
Discussion
In this work, we have demonstrated 3D manipulation of microparticles and biological cells in a microfluidic chamber with 2D SSAWs. We investigated, through modeling and experiment, the mechanism behind 3D trapping with acoustic tweezers. We showed that 3D trapping originates from the interactions between induced acoustic fields and acoustic streaming in a microfluidic chamber via acoustic vibrations of the substrate. The transverse vibrations of SSAWs induce longitudinal waves into the liquid and establish a Gor’kov potential distribution within the microfluidic chamber. Both the longitudinal and transverse vibrations of SSAWs contribute to the acoustic streaming in the microfluidic chamber; this SSAW-induced streaming differs from Rayleigh streaming associated with bulk acoustic waves, which are only induced by longitudinal vibrations. The vibration amplitude regulates the transverse, out-of-plane position of the trapped objects by rebalancing the acoustic radiation force, the Stokes drag force, the gravitational force, and the buoyancy force. The predictions of the model are validated by our experimental results. This model accounts for the spatial distribution of the Gor’kov potential and acoustic streaming and rationalizes the dependence of acoustic manipulation on vibration parameters. We created 3D trapping node arrays in the microfluidic chamber by superimposing two orthogonal displacement nodes and antinodes. These 3D trapping nodes were then translated horizontally or vertically by tuning the location of the displacement nodes or vibration amplitudes. We further demonstrated 3D manipulation by lifting and pushing microparticles into 3D trapping node arrays, translating them horizontally, and finally allowing them to sink to the surface. In our current IDT design, 3D trapping nodes are created and manipulated in a massively parallel formation. However, the independent operation of a 3D node could be realized with dynamic regulation of the vibrations on the substrate through IDT design and RF signal control. Because it uses gentle acoustic vibrations, our method offers several advantages such as dexterous 3D manipulation, digitally programmable and potentially automatable operation, as well as contactless and label-free handling of cells. Finally, these processes are all done in a simple, low-cost device without any moving parts.
With the current setup and experimental condition used, we can manipulate a single cell or particle and place it at a desired location down to 1-µm accuracy in the x-y plane and 2-µm accuracy in the z direction. Because the acoustic wavelength and input power are both instantaneously tunable during experiments, the spatial accuracy (along x, y, or z direction) of cell/particle placement is in principle only limited by the optical or imaging resolution of the experimental setup. The cell or particle transport time achieved in the present study was in the range of several seconds to a couple of minutes, depending on both the moving velocity and the distance between the cells/particles starting location and the target location. We were able to move a 10-µm particle or a single cell with an average speed of ∼2.5 µm/s.
Using these 3D acoustic tweezers, we verified the printing of living cells with acoustic manipulation. We demonstrated that single cells could be picked up, delivered to desired locations, and allowed to adhere and spread on the surface or on top of previously deposited cells (Fig. 6A). We printed cells into prescribed adherent patterns by acoustic-based single cell seeding. Three-dimensional acoustic tweezers were used to pattern cells with control over the number of cells, cell spacing, and the confined geometry, which may offer a unique way to print neuron cells to create artificial neural networks for applications in neuron science and regenerative neuron medicine. For example, during peripheral nervous repair, Schwann cells are naturally aligned into structures, “bands of Büngner”, which guide regenerating neurons to reconnect to their peripheral targets (21). Our method may offer a unique way to control the spatial distribution of Schwann cells for optimal nerve regeneration. With spatial resolution control down to a single cell, this technology shows the potential to enable layer-by-layer positioning of living cells to create 3D tissue-like structures. This technology could provide new pathways for 3D bioprinting, because the technology addresses the central challenge of replicating tissue structures or even fabricating artificial organs that are made up of multiple cell types and complex geometries, but with single-cell control resolution (4). In addition, we expect this technology to rebuild the 3D architecture of a tumor, which will aid in the investigation of heterogeneous genetic alterations during tumor growth and metastasis process (22). The ability to precisely transport single cells along three axes using our 3D acoustic tweezers may facilitate investigations of a number of challenging problems in biology, particularly those involved in the spatial regulation of cells in 2D or 3D environments (23).
In addition to bioprinting, our 3D acoustic tweezers can aid in the imaging and analysis of biological specimens. Taking a confocal microscope as an example, the implementation of our device can provide precise transportation of a target cell or small tissue to the focal area of the microscopic lens. Then, the vertical position of the target object can be moved with respect to the focal plane to generate a confocal image (24). In addition, we demonstrated the rotation of stable trapped objects with the acoustic streaming patterns discussed above (Movie S4), which enables the reconstruction of 3D cells or small tissue images. Furthermore, these 3D acoustic tweezers could serve as building blocks in future integrated imaging and analysis systems including microscopes or fluorescent-activated cell sorter (FACS).
Materials and Methods
Theoretical Model.
We use perturbation theory to model the acoustic fields and second-order acoustic streaming in the microfluidic channel, to assess two main forces acting on the particles: acoustic radiation force and Stokes drag force. With the perturbation theory, continuity and Navier–Stokes equations are asymptotically expanded into two sets of equations in different order based on a small perturbation. The solution to the first-order equations, together with given boundary conditions that contain SSAWs vibration and partial acoustic radiative losses at the PDMS/fluid interface, yields the acoustic fields. The first-order equations lead to the determination of the Gor’kov potential and the acoustic radiation force, whereas the solution to the second-order equations identify acoustic streaming. The forces on microparticles are evaluated based on the two solutions. Detailed formulation, model description, force analysis, and parametric assessment can be found in SI Text, Theoretical Framework and Model Setup, Fig. S1, and Table S1.
Device Fabrication and Experiment Setup.
The procedure for device fabrication was described in our previous work (14, 15). Details of the experimental setup and the operating procedures are given in SI Text, Experimental Setup and SI Text, Calibration of Vibration Amplitude.
Data Analysis.
The velocity of the microparticles was measured using Nikon NIS Elements Advanced Research (AR) software (Nikon). Details of the analysis steps are described in SI Text, Data Analysis.
On-Chip Cell Culture.
Cell culture in the acoustic tweezers device was conducted with a customized cell-culture chamber. Details about handling and culturing cells are described in SI Text, Cell Preparation and Culture.
SI Text
Theoretical Framework and Model Setup.
The acoustic radiation force and the hydrodynamic drag force induced by nonlinear acoustic streaming are the main forces driving the movement of microparticles in this system. To consider these nonlinear effects, a perturbation approximation was used to analyze the aforementioned forces associated with the acoustic fields and the resulting steady acoustic streaming patterns induced in the fluid. The basic assumption is that the perturbations induced by these acoustic vibration amplitudes should be much smaller than the characteristic length scale of the fluid domain, which also means that the vibrating velocity of the surface attributable to acoustic waves is much smaller than the acoustic phase velocity. For a surface acoustic wave, its amplitude is typically in the range of 0.1–10 nm, whereas the length scale of SAW-driven microfluidic devices is on the order of 10–1,000 µm. This condition allows us to use the perturbation approximation to numerically investigate the motion of microparticles driven by standing surface acoustic waves (SSAWs).
The general governing equations for a fluid are the continuity and the Navier–Stokes equations, respectively,
| [S1a] |
and
| [S1b] |
where ρ, v, p, µ, and µB are the density, velocity, pressure, dynamic viscosity, and bulk viscosity, respectively. By linearizing the Eq. S1 using a perturbation approximation, we can obtain the first-order equations for an acoustic field and the time-averaged second-order equations for steady acoustic streaming. The detailed derivation of the two sets of equations can be found in ref. 13. Here, we give the resulting first-order equations directly:
| [S2a] |
| [S2b] |
The parameters with subscript 1 denote the first-order terms, whereas the subscript 0 indicates constant properties of a quiescent fluid. c0 is the speed of sound in the fluid and is related to the first-order pressure p1 with density ρ1 through the equation of state p1 = ρ1. Substituting the equation of state into Eq. S2, the first-order equations can be transformed into linear wave equations with viscous attenuation. p1 and v1 are the acoustic pressure and the velocity of the acoustic particles, respectively, which give rise to the acoustic radiation force on the particles within the streaming fluid. Assuming a single harmonic time dependence of eiωt on all of these fields, the time-dependent Eq. S2 can be transformed into the frequency domain, which is much more efficient for numerical simulations than directly using the time-dependent Eq. S2. Substituting harmonic time-dependent terms into Eq. S2, we arrive at
| [S3a] |
| [S3b] |
where i is an imaginary term, and ω is the angular velocity of acoustic vibrations. The physical fields are the real part of the complex fields in Eq. S3. For instance, [v1] = Re(v1eiωt), where [v1] on the left side is the physical field, and the v1 on the right side is the complex field obtained from Eq. S3.
The second-order time-averaged equations are given as
| [S4a] |
| [S4b] |
Similarly, the parameters with subscript 2 denote the second-order terms. By time-averaging both sides of Eq. S4, the time-dependent second-order terms on the left hand side disappear and the time-averaged second-order equations, after rearrangements, are
| [S5a] |
| [S5b] |
The angled brackets 〈•〉 denote a time average over an oscillation period. It can be seen from Eq. S5 that the equations are actually the continuity and the Navier–Stokes equations with source terms, which drive the flow fields of v2 and p2. The source terms, such as the mass source term (−∇⋅〈ρ1v1〉) in Eq. S5a and the force source term (ρ0〈∂v1/∂t〉 + ρ0〈(v1⋅∇) v1〉) in Eq. S5b, are products of first-order terms. To solve Eq. S5, the first-order equations of Eq. S4 should be solved first. Physically, the nonzero velocity 〈v2〉 is the acoustic streaming velocity.
Applying a perturbation analysis, we use a 2D model to analyze the motion of microparticles in a PDMS chamber actuated by a 1D SSAW. The device used in our experiments is composed of a 128° YX LiNO3 substrate with two pairs of orthogonally positioned IDTs on the substrate surface. The PDMS chamber is aligned to be parallel to the IDTs and is bonded on the substrate. To simplify the experimental system and the associated theoretical model for SSAW-based acoustophoresis in the PDMS chamber, only one pair of parallel IDTs was used to actuate the fluidic domain within the PDMS chamber. When RF signals are applied to the IDTs, the excited surface acoustic waves (SAWs) travel toward the channel as plane waves. This result means that the wave fronts of the SAWs are parallel to the IDTs and are nearly uniform in the direction parallel to the IDTs. Therefore, a 2D model that approximates the phenomena, in a cross-section (as shown in Fig. S1A) perpendicular to the IDTs, can be used to simplify the verification analysis of the motion of microparticles in such a fluidic device. Because the dimensions of the PDMS chamber walls are much larger than the acoustic wave amplitudes, and the wave absorption and damping within PDMS layer is strong, its effect on the acoustic fields in the fluidic domain can be modeled as a lossy-wall boundary condition (20), which describes the partial radiative acoustic losses at the liquid/PDMS boundaries, to further simplify the model. Conversely, the effects of the motion of the fluid on the surface vibrations generated by the piezoelectric device are neglected. Instead, a commonly imposed leaky SAWs (LSAWs) boundary condition is used to model the actuation of the SSAW at the interface between the substrate and the fluid. The final simplified 2D model is illustrated in Fig. S1B. Only the fluidic domain is numerically solved. The dimensions of the PDMS chamber bonded on the device are 1,800 × 1,800 × 100 µm (length × width × height), and the size of the 2D modeled fluidic domain is 1,800 × 100 µm (width × height).
The first-order acoustic fields are determined by Eq. S3 and the aforementioned boundary conditions. For the LSAWs boundary at the substrate, the surface particles move in ellipses and the motion is retrograde, that is, the in-plane motion of the particles is counterclockwise when the LSAW propagates from left to right and vice versa. This type of motion means that the vibration of the LSAW consists of both longitudinal and transverse vibrations, and these two motions are separated by a phase lag of 3π/2. Meanwhile, the LSAW decays as it propagates along the interface between the substrate and the fluid domain because of the continuous energy radiation into the fluid. Therefore, by assuming a harmonic time dependence (eiωt) for the LSAW vibrations, the vibrating velocities of the bottom boundary of the fluidic domain, when two LSAWs propagate in opposite directions, can be modeled as
| [S6a] |
| [S6b] |
where ε is the amplitude ratio between the longitudinal and transverse vibrations; A is the amplitude of the transverse vibration; α is the decay coefficient of the amplitude along x; k is the wave number of the LSAW; and x0 is the width of the fluidic domain. The ratio ε can be determined from analytical solutions of the Rayleigh wave displacement in the longitudinal (x) and transverse (z) directions, given as (2)
| [S7a] |
| [S7b] |
where A0 is a constant; kR is the wave number of Rayleigh wave. In Eq. S7 qR and sR are given by and , respectively, where kl and kt are the wave numbers for the longitudinal and transverse modes, respectively. According to the parameters given in Table S1, the amplitude ratio ε (i.e., the ratio between amplitude of UR to WR) is 0.7428 in our model. For the decay coefficient α, it is induced by the acoustic energy continuously being attenuated by the fluid, and can be obtained from a dispersion relation for LSAWs, given as (18)
| [S8] |
where k* is the complex wave number of the LSAW; ρs is density of the substrate; k0 is the wave number of the longitudinal wave in the fluid; i is the imaginary unit; and . By using the relationships between wave numbers and acoustic phase velocities, Eq. S8 can be transformed into an equation which is independent of the frequency, yielding (25)
| [S9] |
where cl, ct, and cf are the acoustic phase velocities of the longitudinal and transverse modes in the 128° YX LiNO3 substrate, and in the fluid, respectively. in Eq. S9 is the complex acoustic phase velocity of the LSAW. Using the parameters listed in Table S1, Eq. S9 has the solution = 3,900 – 32.7i (m·s−1). The corresponding wave number is k* = 20,940 + 176i (m−1). Physically, the imaginary part of k* is the coefficient of decay for the LSAW. Thus, α in Eq. S6 is calculated as 176 m−1 in our model.
The other three boundaries in contact with the walls of the PDMS are modeled as lossy walls to account for the acoustic reflection and transmission at the interface between the fluid and the PDMS. This is expressed as (20)
| [S10] |
where n is the normal vector with respect to the boundary; ρw and cw are the density and speed of sound of the PDMS channel material, respectively.
For a spherical particle suspended in an acoustic wave-actuated fluid, the acoustic radiation force, the Stokes drag force induced by acoustic streaming, the gravitational force, and the buoyancy force all need to be taken under consideration. In our model, the first two forces can be obtained from solving the first-order and the second-order equations with the aforementioned boundary conditions.
The acoustic radiation force on an incompressible spherical particle, with a diameter that is smaller than the wavelength of sound can be evaluated using the expression given by Gor’kov (19):
| [S11] |
with
| [S12a] |
| [S12b] |
where Vp is the volume of the sphere particle, and ρp and cp are its density and acoustic phase velocity. Here, the p1 and v1 in Eq. S11 are the real part of the complex fields in Eq. S3.
Normally, the Stokes drag force is given by
| [S13] |
where R is the radius of the particle, and v is the particle’s velocity. Particularly, when a particle moves perpendicularly toward a wall, the Stokes drag formula Eq. S13 needs to be corrected by an analytical factor to take into account the wall effect. The Stokes drag force with a wall-effect-correction factor is (26, 27)
| [S14a] |
| [S14b] |
| [S14c] |
where χ is the wall-effect-correction factor, and H is the distance from the bottom wall to the center of the particle. By combining these forces, we can obtain the dynamic motion equation for the microparticle, which can be expressed as
| [S15] |
where m, Fb, and Fg are the mass of the particle, the buoyance force, and the gravitational force acting on the particle, respectively.
A finite-element method-based software package, COMSOL version 4.4 (COMSOL), was used to solve the abovementioned 2D boundary value problem. The numerical procedure is similar to the one described in ref. 28. First, the first-order Eq. S4, together with the boundary conditions of Eq. S6 and Eq. S10, is solved in the frequency domain by the predefined thermoacoustics solver module in COMSOL. Then, the second-order Eq. S5 is solved by the laminar flow solver module within COMSOL, which is modified to add a mass source term to the right side of Eq. S5a and a body force term to the right side of Eq. S5b from the products of first-order acoustic fields. The acoustic radiation force and the Stokes drag force acting on a spherical particle can be determined by inputting the corresponding solutions from the calculations of the second-order equations into Eq. S11 and Eq. S14. A mesh-independence test has also been done. To confirm the accuracy of the numerical solution, the grid near the bottom boundary was finely meshed, and the distance between nodes in this mesh is much smaller than the thickness of the so-called Stokes layer or the shear viscosity decay layer, which has a thickness of . The parameters used in these calculation are summarized in Table Sl.
Experimental Setup.
The acoustic device was mounted either on a motorized stage or inside the cell culture chamber (INUBTFP-WSKM-GM2000A; Prior Scientific) on an inverted microscope (TE2000U; Nikon). The particle or cell solution was manually injected into the acoustic tweezers device. The images and the videos of the particles or cells were acquired with a 10× microscope objective and a charge-coupled device (CCD) camera (CoolSNAP HQ2; Photometrics) or a high-speed camera (SA4; Photron) connected to a computer. Two controllable alternating current signals generated by a double-channel function generator (AFG3102C; Tektronix) and amplified by two amplifiers (25A100A; Amplifier Research) were connected to one pair of IDTs. The other pair of orthogonally arranged IDTs were powered by a similar setup.
Data Analysis.
For the acoustic radiation force analyzed in our experiments, all of the 10.1-μm polystyrene particles were suspended in ethanol and were pushed toward pressure nodes by the acoustic radiation force. During this process, the induced Stokes drag force counteracts with this acoustic radiation force so that the acoustic radiation force can be determined by examining the velocity of the particles. The movements of 10.1-µm microparticles under different input powers were recorded in individual videos with a frame rate of 500/s. The velocity of each single particle can be determined using Nikon NIS Elements AR software (Nikon). To better compare with the theoretical predictions, we used a function f(x) = Vmaxsin(x − x1) + f0 to fit the moving speed data of each microparticle based on the fact that the acoustic radiation force has a wave form distribution in the horizontal direction. Through the fitting, the Vmax of each microparticle, which corresponds to the peak of acoustic radiation force along the trajectory, can be found. Then, the peak of acoustic radiation force can be calculated using Frad = 6πRµVmax, where R is the radius of the particles and µ is the dynamic viscosity of the medium. Following this equation, the acoustic radiation force acting on the microparticle under different input powers was evaluated. The data were used to match with the corresponding peak horizontal acoustic radiation force in the theoretical model. The detailed parameters used are available in Table S1.
We analyzed the acoustic streaming velocity as the following. After applying SSAW, 1.3-µm microparticles suspended in ethanol were flowed into the paralleled distributed vortex patterns in the microfluidic chamber, which indicates the induced acoustic streaming. Using the same method, the movements of these small particles (within the x-y plane: x ∼915–960 µm; z ∼1–10 µm) under different input powers were recorded in individual videos, and the velocity of each single particle was processed with respect to different input powers.
Calibration of Vibration Amplitude.
To correlate the experimental results with the theoretical predictions, the vibration amplitude of the LSAW (A in Eq. S6) at different input powers has to be determined. We have characterized the vibration amplitude using two different methods.
Method 1.
We calibrated the vibration amplitude in the fluidic chamber as a function of the input power by fitting experimental data of acoustic radiation force and acoustic streaming measured (Figs. 2D and 3D) and comparing with the ones calculated by the theoretical model at certain vibration amplitudes. Because the input power P ∼A2 and Frad ∼A2, theoretically, the acoustic radiation force Frad is linearly dependent on the input power P. Thus, a linear line through the origin can be used to fit the experimental data of the acoustic radiation force, as shown in Fig. 2D. To calibrate the vibration amplitude, this fitted line is considered to be the magnitude of the acoustic radiation force at different input powers and was used as reference to compare with the one calculated by the theoretical model until finding the equal one at certain vibration amplitude, which was considered as the vibration amplitude at that input power. The calibrated vibration amplitude curve is shown in Fig. S2B, matching with the theoretical prediction that A ∼ After calibrating the vibration amplitudes, the values were again inputted into the theoretical model to find the acoustic streaming magnitude at different input powers. The theoretically predicted linear line is shown in Fig. 3D, which matches with our theoretical prediction. This method accounts the attenuation effects of the PDMS channel wall and the liquid in the microfluidic chamber. In the 1D SSAW microfluidic device, acoustic waves are propagating along the x axis of a 128° YX-cut lithium niobate substrate. They travel through the PDMS chamber wall and then encounter the liquid in the microfluidic chamber (Fig. S2A).
Method 2.
We also directly measured the vibration amplitude on a bare SAW substrate using an optical method. Fig. S2C illustrates the 1D SAW substrate for directly amplitude measurement with an optical vibrometer system (MSA-500 Micro System Analyzer; Polytec). An additional 4 × 4 mm gold film with a thickness of 200 nm was deposited into the middle of the IDT pair (along the x axis of a 128° YX-cut lithium niobate substrate) to reflect right during the optical measurement. Fig. S2D show the measurement of the longitudinal vibration under different input powers, which are within the same order of magnitude as the aforementioned calculated results.
Furthermore, we performed our analysis with the result using method 1, which is closer to the actual experimental conditions than that from method 2. The amplitude given by method 1 (Fig. S2B) is smaller than the value obtained using method 2 (Fig. S2D). This is because method 1 considers the losses due to the PDMS channel walls and the attenuation effect of the liquid in the microfluidic chamber.
Cell Preparation and Culture.
We purchased all of the cell lines from American Type Culture Collection (ATCC); 3T3 (CRL-1658) cells were cultured in Dulbecco’s modified Eagles medium (DMEM; ATCC) supplemented with 10% (vol/vol) FBS and a 1% penicillin–streptomycin solution. HEK 293T (CRL-3216) cells were cultured using Earle’s minimum essential medium (EMEM) (Cellgro; Corning) supplemented with 10% (vol/vol) FBS and a 1% penicillin–streptomycin solution. Both adherent cell lines were kept in T-25 cell culture flasks and subcultured twice per week. HeLa S3 cells (CCL-2.2) were cultured in a medium (F-12K medium; ATCC) supplemented with 10% (vol/vol) FBS and a 1% penicillin–streptomycin solution. The cells were kept in this suspension within shaker flasks (VWR, minishaker) at 100 rpm and subcultured twice per week. All of the cells are cultured in a 37 °C cell culture incubator with a 5% (vol/vol) CO2 atmosphere. Before the on-chip experiments, cells were harvested and resuspended into fresh medium at the desired concentration (0.8–1.2 × 106 cells/mL). After seeding cells into the device [coating with 2% (vol/vol) fibronectin overnight], cells were cultured inside the customized cell-culture chamber. This chamber can provide a stable 37 °C and 5% CO2 atmosphere for cell culture. In addition, the humid environment necessary for cell culture was maintained by the evaporation of deionized water inside the sealed chamber.
Supplementary Material
Acknowledgments
We thank Dr. John Mai for helpful discussions. We also acknowledge financial support from NIH Grants 1R33EB019785-01 and 1 R01 GM112048-01A1, the National Science Foundation, and the Penn State Center for Nanoscale Science (Materials Research Science and Engineering Center) under Grant DMR-0820404. M.D. also acknowledges partial support from NIH Grant U01HL114476.
Footnotes
Conflict of interest statement: F.G., Z.M., M.D., S.S., and T.J.H. have filed a patent based on the work presented in this paper.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1524813113/-/DCSupplemental.
References
- 1.Bao G, Suresh S. Cell and molecular mechanics of biological materials. Nat Mater. 2003;2(11):715–725. doi: 10.1038/nmat1001. [DOI] [PubMed] [Google Scholar]
- 2.Berthiaume F, Maguire TJ, Yarmush ML. Tissue engineering and regenerative medicine: History, progress, and challenges. Annu Rev Chem Biomol Eng. 2011;2:403–430. doi: 10.1146/annurev-chembioeng-061010-114257. [DOI] [PubMed] [Google Scholar]
- 3.Wang J, et al. Microfluidics: A new cosset for neurobiology. Lab Chip. 2009;9(5):644–652. doi: 10.1039/b813495b. [DOI] [PubMed] [Google Scholar]
- 4.Murphy SV, Atala A. 3D bioprinting of tissues and organs. Nat Biotechnol. 2014;32(8):773–785. doi: 10.1038/nbt.2958. [DOI] [PubMed] [Google Scholar]
- 5.Guo F, et al. Probing cell-cell communication with microfluidic devices. Lab Chip. 2013;13(16):3152–3162. doi: 10.1039/c3lc90067c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang H, Liu KK. Optical tweezers for single cells. J R Soc Interface. 2008;5(24):671–690. doi: 10.1098/rsif.2008.0052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pan Y, Du X, Zhao F, Xu B. Magnetic nanoparticles for the manipulation of proteins and cells. Chem Soc Rev. 2012;41(7):2912–2942. doi: 10.1039/c2cs15315g. [DOI] [PubMed] [Google Scholar]
- 8.Albrecht DR, Underhill GH, Wassermann TB, Sah RL, Bhatia SN. Probing the role of multicellular organization in three-dimensional microenvironments. Nat Methods. 2006;3(5):369–375. doi: 10.1038/nmeth873. [DOI] [PubMed] [Google Scholar]
- 9.Calvert P. Materials science. Printing cells. Science. 2007;318(5848):208–209. doi: 10.1126/science.1144212. [DOI] [PubMed] [Google Scholar]
- 10.Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE. Geometric control of cell life and death. Science. 1997;276(5317):1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 11.Zhang K, Chou CK, Xia X, Hung MC, Qin L. Block-Cell-Printing for live single-cell printing. Proc Natl Acad Sci USA. 2014;111(8):2948–2953. doi: 10.1073/pnas.1313661111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ding X, et al. Surface acoustic wave microfluidics. Lab Chip. 2013;13(18):3626–3649. doi: 10.1039/c3lc50361e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Friend J, Yeo LY. Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev Mod Phys. 2011;83(2):647–704. [Google Scholar]
- 14.Guo F, et al. Controlling cell-cell interactions using surface acoustic waves. Proc Natl Acad Sci USA. 2015;112(1):43–48. doi: 10.1073/pnas.1422068112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li P, et al. Acoustic separation of circulating tumor cells. Proc Natl Acad Sci USA. 2015;112(16):4970–4975. doi: 10.1073/pnas.1504484112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gesellchen F, Bernassau AL, Déjardin T, Cumming DRS, Riehle MO. Cell patterning with a heptagon acoustic tweezer--application in neurite guidance. Lab Chip. 2014;14(13):2266–2275. doi: 10.1039/c4lc00436a. [DOI] [PubMed] [Google Scholar]
- 17.Bourquin Y, et al. Rare-cell enrichment by a rapid, label-free, ultrasonic isopycnic technique for medical diagnostics. Angew Chem Int Ed Engl. 2014;53(22):5587–5590. doi: 10.1002/anie.201310401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Viktorov IA. Rayleigh and Lamb Waves: Physical Theory and Applications. Springer; New York: 1967. [Google Scholar]
- 19.Gor’kov LP. On the forces acting on a small particle in an acoustic field in an ideal fluid. Sov Phys Dokl. 1962;6:773–775. [Google Scholar]
- 20.Bruus H. Acoustofluidics 2: Perturbation theory and ultrasound resonance modes. Lab Chip. 2012;12(1):20–28. doi: 10.1039/c1lc20770a. [DOI] [PubMed] [Google Scholar]
- 21.Fex Svennigsen A, Dahlin LB. Repair of the peripheral nerve-remyelination that works. Brain Sci. 2013;3(3):1182–1197. doi: 10.3390/brainsci3031182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Waclaw B, et al. A spatial model predicts that dispersal and cell turnover limit intratumour heterogeneity. Nature. 2015;525(7568):261–264. doi: 10.1038/nature14971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Manz BN, Groves JT. Spatial organization and signal transduction at intercellular junctions. Nat Rev Mol Cell Biol. 2010;11(5):342–352. doi: 10.1038/nrm2883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McDermott G, Le Gros MA, Knoechel CG, Uchida M, Larabell CA. Soft X-ray tomography and cryogenic light microscopy: The cool combination in cellular imaging. Trends Cell Biol. 2009;19(11):587–595. doi: 10.1016/j.tcb.2009.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vanneste J, Buhler O. Streaming by leaky surface acoustic waves. Proc Math Phys Eng Sci. 2011;467(2130):1779–1800. [Google Scholar]
- 26.Brenner H. The slow motion of a sphere through a viscous fluid towards a plane surface. Chem Eng Sci. 1961;16(3-4):242–251. [Google Scholar]
- 27.Ryu S, Matsudaira P. Unsteady motion, finite Reynolds numbers, and wall effect on Vorticella convallaria contribute contraction force greater than the stokes drag. Biophys J. 2010;98(11):2574–2581. doi: 10.1016/j.bpj.2010.02.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Muller PB, Barnkob R, Jensen MJH, Bruus H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab Chip. 2012;12(22):4617–4627. doi: 10.1039/c2lc40612h. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.