Chemotaxis toward phytoplankton drives organic matter partitioning among marine bacteria

Significance

Microscale interactions between bacteria and phytoplankton underpin ocean biogeochemistry and frequently involve bacterial chemotaxis to phytoplankton dissolved organic matter (DOM). Yet, it remains unclear how the effects of this interaction propagate to ecosystem scales. We address this gap through a hybrid approach where high-resolution observations of chemotaxis toward a diatom are directly used in a resource utilization model. We find that chemotactic bacteria consume most diatom DOM under resource-rich or bacteria-rich conditions, that DOM is partitioned among distinct populations based on diffusivity, and that consumption is skewed toward very few cells. Nonmotile oligotrophic bacteria dominate when productivity is low. Motile copiotrophs dominate during blooms. Ocean chemotaxis thus partitions resources spatially, by molecular size, and temporally through seasonal and episodic blooms.

Abstract

The microenvironment surrounding individual phytoplankton cells is often rich in dissolved organic matter (DOM), which can attract bacteria by chemotaxis. These “phycospheres” may be prominent sources of resource heterogeneity in the ocean, affecting the growth of bacterial populations and the fate of DOM. However, these effects remain poorly quantified due to a lack of quantitative ecological frameworks. Here, we used video microscopy to dissect with unprecedented resolution the chemotactic accumulation of marine bacteria around individual Chaetoceros affinis diatoms undergoing lysis. The observed spatiotemporal distribution of bacteria was used in a resource utilization model to map the conditions under which competition between different bacterial groups favors chemotaxis. The model predicts that chemotactic, copiotrophic populations outcompete nonmotile, oligotrophic populations during diatom blooms and bloom collapse conditions, resulting in an increase in the ratio of motile to nonmotile cells and in the succession of populations. Partitioning of DOM between the two populations is strongly dependent on the overall concentration of bacteria and the diffusivity of different DOM substances, and within each population, the growth benefit from phycospheres is experienced by only a small fraction of cells. By informing a DOM utilization model with highly resolved behavioral data, the hybrid approach used here represents a new path toward the elusive goal of predicting the consequences of microscale interactions in the ocean.

Bacteria in the ocean compete for organic matter to support growth. Strategies for the acquisition of organic matter span a continuum whose extremes are oligotrophy and copiotrophy (1–3). Oligotrophic taxa thrive in low-nutrient conditions and dominate bacterial assemblages in most oceanic provinces, whereas copiotrophs are adapted for growth in resource-rich conditions, such as coastal phytoplankton blooms (4), and can account for much of the carbon uptake by a microbial assemblage (5). However, the growth advantages of coexisting populations of marine bacteria with different adaptations, in relation to realistic resource landscapes, is challenging to study and frequently neglected in microbial oceanography, reflecting the need for a quantitative ecological framework for the foraging of marine microorganisms and its ecosystem consequences (6).

One adaptation frequently differentiating copiotrophs from oligotrophs is motility (2), which typically entails chemotaxis, the ability to sense and move toward a chemical source. Phytoplankton and detrital particles exude dissolved organic matter (DOM), creating strong localized hotspots that fall off through steep gradients into background levels of DOM in bulk seawater (7). For phytoplankton, this microenvironment is called the “phycosphere” (8) and its composition will vary for healthy, stressed, or dead phytoplankton. Chemotaxis allows some copiotrophic bacteria to accumulate in resource-rich locations and significantly increase their exposure to DOM in transient microscale hotspots (9–13). However, the long-term value of chemotaxis for populations may depend on environmental conditions, because the prevalence of motile cells varies widely in natural communities (14, 15), and genes associated with chemotaxis can be sparse in typical seawater (16) yet abundant and highly expressed in enriched waters (17). Copiotrophs exhibiting chemotaxis may frequently outcompete oligotrophs that do not swim, and vice versa, yet we have a poor understanding and no predictive tools to determine the conditions under which either strategy is favored. To understand the ecological consequences of bacterial competition for DOM in the phycosphere, a link is needed between the microscale, where chemotaxis unfolds, and the ecosystem scale, where microbial activities integrate into the marine food web.

Here we examine the fate of diatom DOM using a hybrid approach that integrates high-resolution analysis of bacterial dynamics in phycospheres with a mathematical model that bridges microscale observations to ecosystem consequences. Experimentally, we created reproducible, controlled hotspots and attained the most detailed view of phycosphere hotspot dynamics to date. Mathematically, we used this observational data to model the consumption competition between a motile copiotrophic population and a nonmotile oligotrophic population, including an examination of the ocean conditions under which chemotaxis affects the consumption of DOM. This approach allowed us to predict the partitioning of DOM among and within bacterial populations and the effects of DOM consumption on bacterial population dynamics.

Results and Discussion

Natural Hotspots.

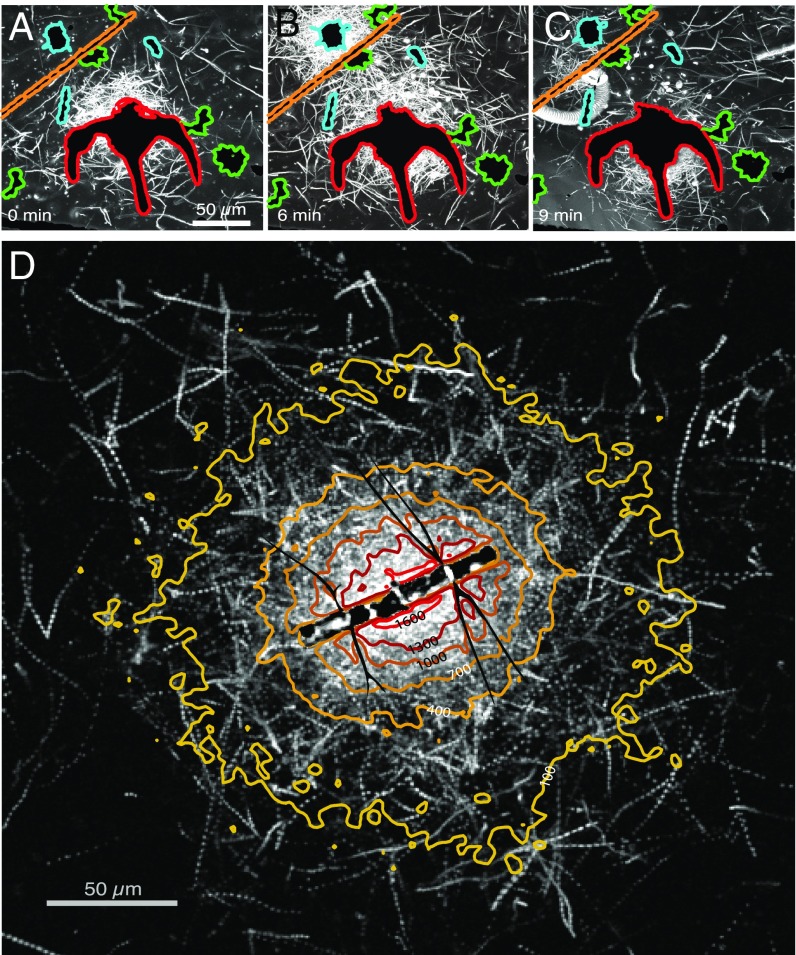
Using time-lapse video microscopy, we repeatedly observed that the motile fraction of bacteria from an enriched coastal ocean community formed clusters around individual phytoplankton cells of different genera (Fig. 1 A–C and Movie S1) and other planktonic particles, including dead copepods and fecal pellets (Movie S2), all collected from the same samples as the bacteria. The clusters were often ephemeral, lasting from a few minutes to >1 h (Fig. 1 and Movie S2). For example, over 6 min a Chaetoceros diatom (Fig. 1 A–C, upper left) attracted a strong cluster of bacteria that was completely dissipated 3 min later. We interpret these accumulations as the chemotactic response of motile bacteria to the chemical gradients surrounding the phytoplankton cells and organic particles (10).

Fig. 1.

Seawater bacteria respond to ephemeral DOM gradients from phytoplankton. (A–C) Swimming trajectories (white) of bacteria demonstrate ephemeral accumulations or ‟clusters” around natural phytoplankton including Chaetoceros sp. (aqua outline), Ceratium sp. (red), Asterionella sp. (green), and Skeletonema sp. (orange). The image at each time point is the maximum intensity projection from a movie (Movie S1). (D) Chemotactic cluster formation around the cultured diatom C. affinis. Contours show the enhancement of motile bacteria over background concentration during the 30 s immediately following cell lysis (Fig. S4). White tracks are bacterial trajectories over 2 s.

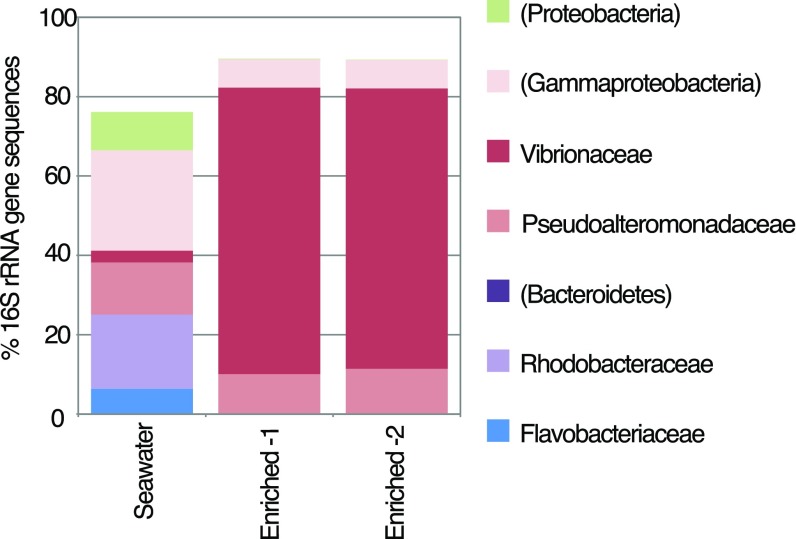
Community 16S rRNA gene analysis revealed that the enriched bacterial community used in experiments was dominated by Vibrio spp. and Pseudoalteromonas spp. (Fig. S1). These genera are frequently observed in coastal seawater, and the cultured isolates Vibrio alginolyticus and Pseudoalteromonas haloplanktis exhibit strong and rapid chemotaxis toward artificial microscale DOM plumes (18, 19). These genera also grow in response to short-term enrichments (20, 21), demonstrating their copiotrophic nature. Thus, enrichment with planktonic particles predictably stimulated growth of copiotrophic taxa, as occurs during natural resource enrichments such as phytoplankton blooms (4), and our analysis of phycosphere dynamics therefore focused on the responses of these copiotrophic genera.

Fig. S1.

Taxonomic composition of natural microbial communities enriched from seawater and used in the experiments, as determined via 16S rRNA gene analyses of the V4 region. OTU identifications were made to the family level if possible (level 6 in GreenGenes 12_10 database); parentheses indicate phylum- or subphylum-level identification. Only taxa with ≥5% representation in any one of the samples are shown. ‟Enriched-1” and ‟Enriched-2” are analytical replicates of particle-enriched water. ‟Seawater” was a control that did not contain concentrated particles.

Controlled Hotspots.

To quantitatively characterize the spatiotemporal dynamics of a prototypical chemotactic cluster, we devised an approach to create microscale DOM hotspots on demand using the diatom Chaetoceros affinis (CCMP160), owing to its cosmopolitan distribution and frequent occurrence in natural samples (Fig. 1 A–C). We induced the lysis of individual C. affinis chains by 5- to 10-min exposure to fluorescent light (350 nm, 7 mW/mm²) under the microscope, resulting in reproducible DOM pulses that mimic those naturally occurring in the ocean as a result of viral lysis (22) or “sloppy feeding” by zooplankton (23). Multiple cells in the diatom chains typically underwent lysis; whereas the diatom frustule usually remained intact, the plasma membrane collapsed (Fig. S2 and Movie S3).

Fig. S2.

Controlled lysis of individual diatoms to create DOM hotspots. One part of a C. affinis chain is shown at selected times, taken from a sequence of time-lapse images captured every 15 s via epifluorescence microscopy (488-nm excitation, 535-nm emission) and phase microscopy (Inset) (see also Movie S3). Time labels denote minutes:seconds. Before image capture, the diatom had been exposed to continuous fluorescent light for ∼5 min to stimulate cell lysis. The cell suspension was amended with a polar fluorescent dye (SYTOX Green) that permeates compromised cell membranes. Plasmolysis was confirmed by the intracellular accumulation of SYTOX Green signal coinciding with the membrane collapse visible by phase contrast (Inset).

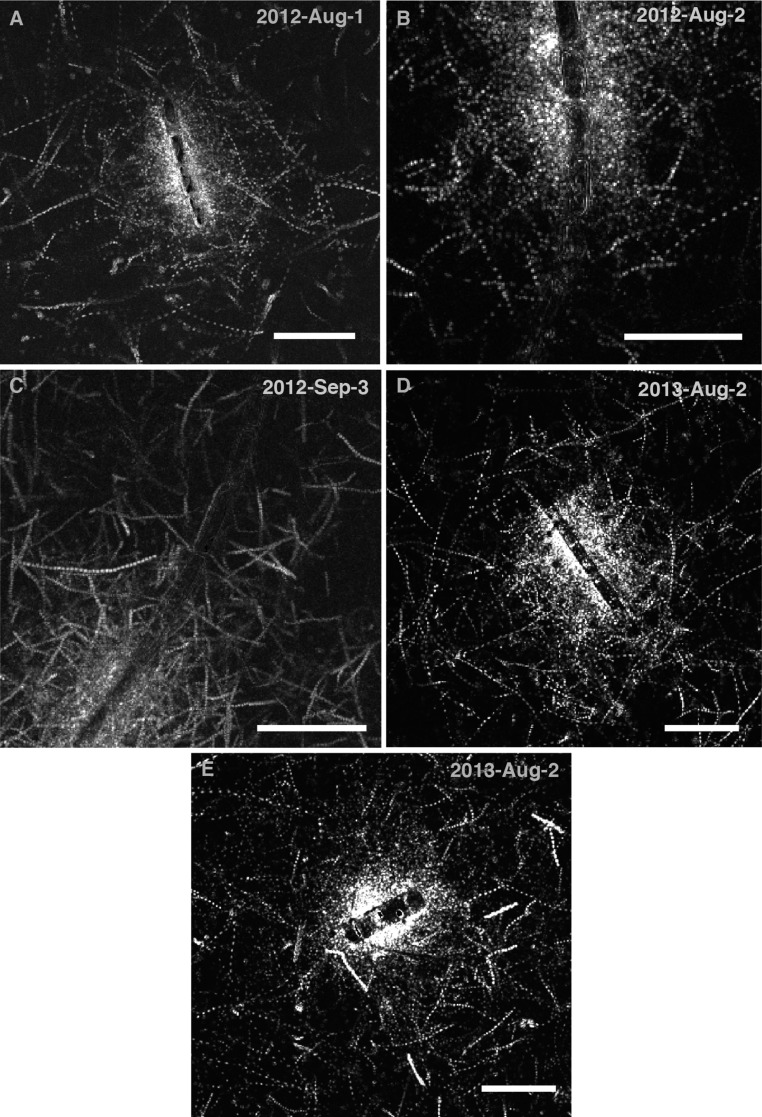
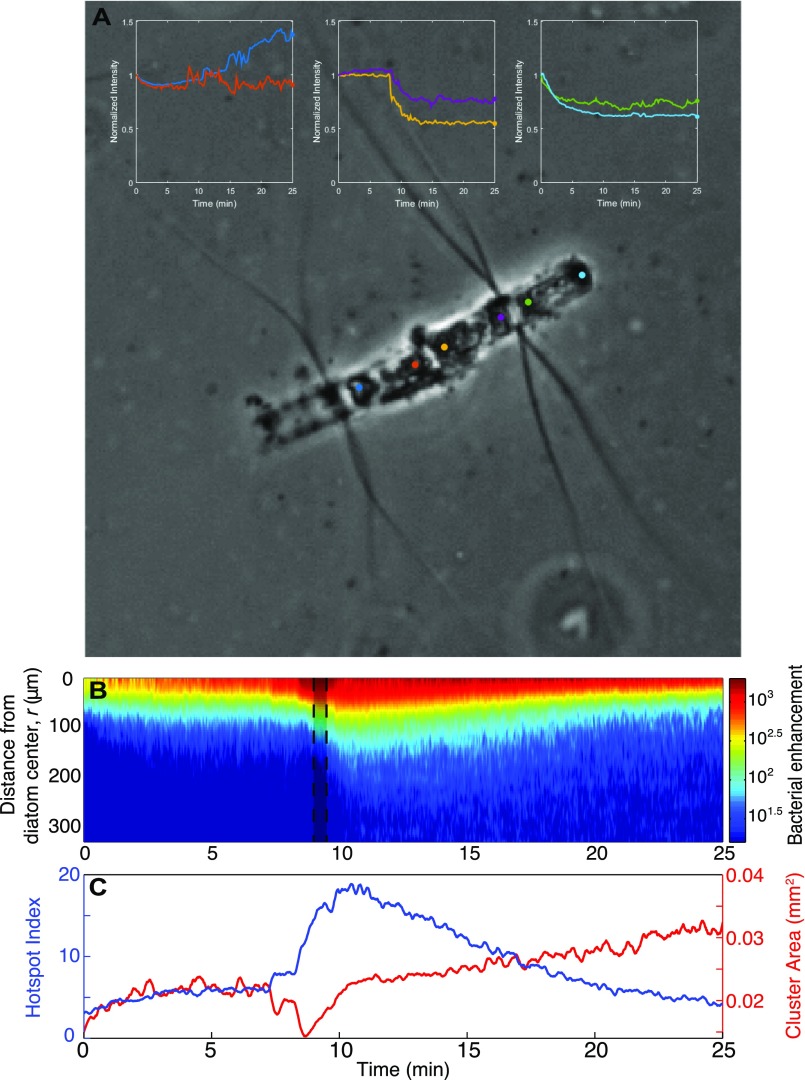
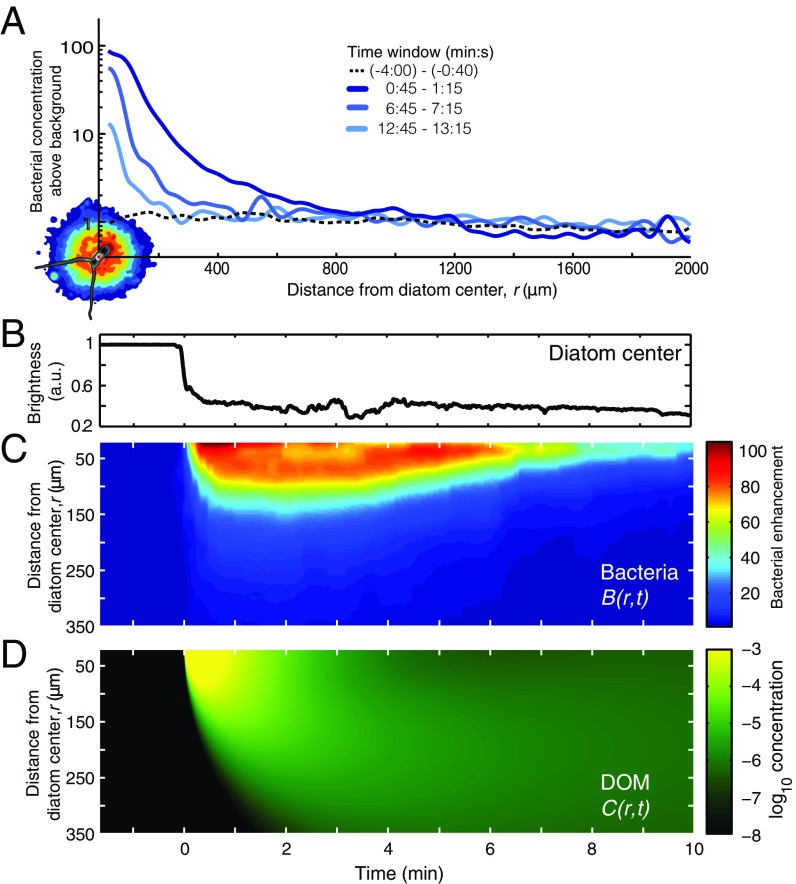
Upon diatom lysis, motile bacteria exhibited strong chemotaxis. A representative example (Fig. 1D) of six replicate experiments (Fig. S3) illustrates a bacterial cluster within the phycosphere, as determined from the quantification of individual bacterial positions with ∼1-µm resolution from time-lapse images acquired every 0.05 s (SI Materials and Methods). The enhancement of bacteria relative to the background concentration, B(r,t), where r is the distance from the diatom center and t is time (SI Materials and Methods), shows an initial accumulation toward the diatom, followed by a sharp increase in intensity reaching greater than 1,000-fold above background (Fig. 1D and Fig. S4B). Quantitative metrics for cluster intensity and size (Fig. S4C) as well as coincident changes in diatom brightness (Fig. S4A) indicate that this accumulation occurred in response to more than one DOM release event, with the response to some individual releases reflected by brief contractions in the area of the bacterial cluster.

Fig. S3.

(A–E) Chemotactic clusters around different chains of C. affinis undergoing lysis, captured on different days with different bacterial communities enriched from coastal seawater, demonstrating experimental replication of the dynamics shown in Fig. 1D and Fig. S4. Shown are bacterial swimming trajectories captured over 1–2 s at a time close to peak cell accumulation. (Scale bars, 50 μm for all images.)

Fig. S4.

Diatom chain lysis and the quantified bacterial response. (A) The color-coded profiles demonstrate the changing brightness (normalized by initial value) of points at each end of diatom cells corresponding to Fig. 1D. The sudden change in intensity at one end of the middle cell at 7 min indicates the point at which a sharp lysis event occurred. In contrast, the more gradual change in the left and right cells points to gradual changes in the diatom structure and a more prolonged DOM leakage. (B) Bacterial enhancement relative to the background concentration, B(r,t), as a function of distance from the diatom center, r, and time, t. The shaded region at t = 9 min corresponds to the section of the movie depicted in Fig. 1D. (C) Two metrics characterizing the cluster dynamics: the hotspot index, H, measures the mean motile cell concentration near the diatom (r < 100 μm) relative to the mean background concentration, and the cluster area represents the area of the 2D region where the bacterial concentration was greater than 0.5H.

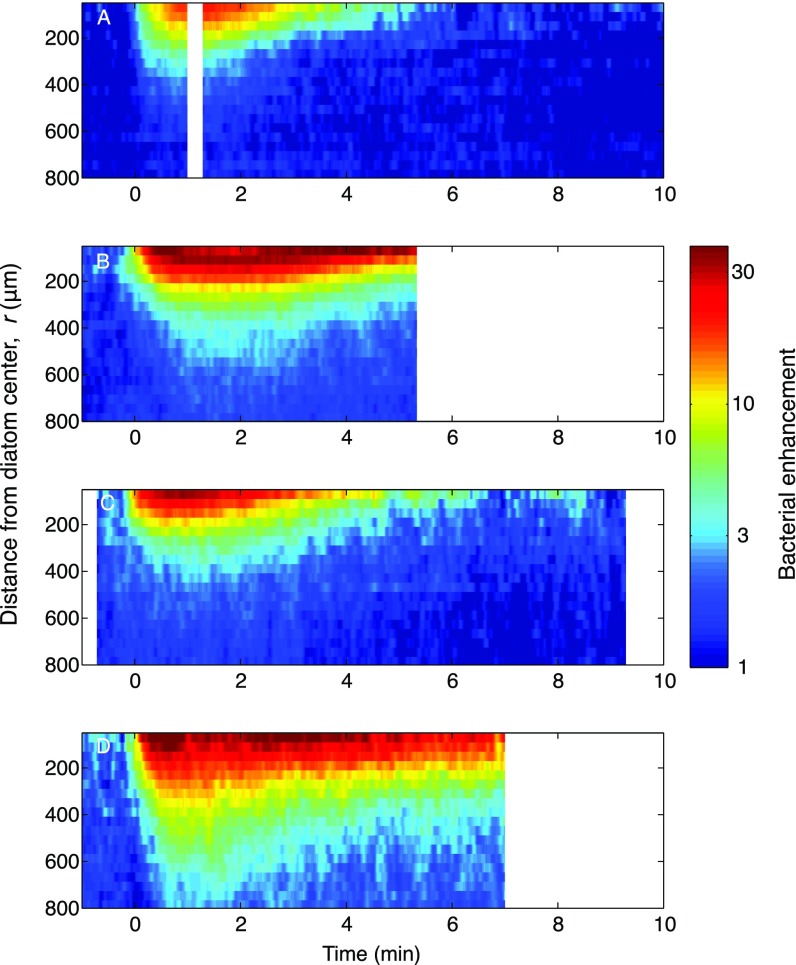
To determine the prototypical cluster response, and sidestep the complexity of multiple sequential lysis events, we repeated experiments on single, isolated C. affinis cells (Movie S4). The resulting bacterial distribution was nearly radially symmetric (Fig. 2A). The time course of the cell enhancement, B(r,t), illustrates that the cluster formed within ∼1 min and dissipated after ∼10 min (Fig. 2 B and C), characteristics that were robustly observed across replicate single-cell lysis events (n = 5; Fig. S5) and consistent with previous studies (10, 24). Shortly after lysis, the cluster intensified substantially. An increase in bacterial concentration over background at distances of r = 1.2–1.8 mm from the diatom (Fig. S6; 3–6 min after lysis) indicates that detectable levels of released DOM reached these distances. Thus, for the purposes of modeling we define 2 mm as the radius of the phycosphere.

Fig. 2.

Chemotactic accumulation in the phycosphere lasts ∼10 min and extends ∼2 mm from the diatom. All panels (A–D) show results for a prototypical radially symmetric cluster in response to lysis of a single C. affinis diatom. (A) Bacterial concentration above background as a function of distance from the diatom center, r, for three 30-s time windows after lysis. The prelysis background is also shown. An image of the lysed diatom (bottom left) shows relative bacterial concentration (color contours) at peak accumulation (t = 1 min), with the same scale as the x axis. (B) Brightness of the diatom center (in arbitrary units) showing the moment at which lysis occurred, t = 0. (C) Bacterial enhancement relative to the background concentration, B(r,t). (D) Relative concentration of the effective chemoattractant as a function of distance and time, C(r,t), determined from a mathematical simulation.

Fig. S5.

(A–D) Spatiotemporal distribution of motile bacteria, B(r,t), for chemotactic clusters around four different single cells of C. affinis undergoing lysis, demonstrating experimental replication by showing dynamics similar to those in Fig. 2. B(r,t) represents the bacterial enhancement relative to the background concentration (color bar). The positions of hundreds of bacteria were simultaneously captured by video microscopy with a spatial resolution of 1 μm and a temporal resolution of 0.05 s and smoothed with Gaussian filters, using a 10-μm SD in the radial direction and a 2-s SD in the temporal direction. Blank spaces indicate gaps in the video capture. Note that these ‟clean” accumulations around single diatom cells contrast with the more complex accumulation dynamics around diatom chains (Figs. S3 and S4).

Fig. S6.

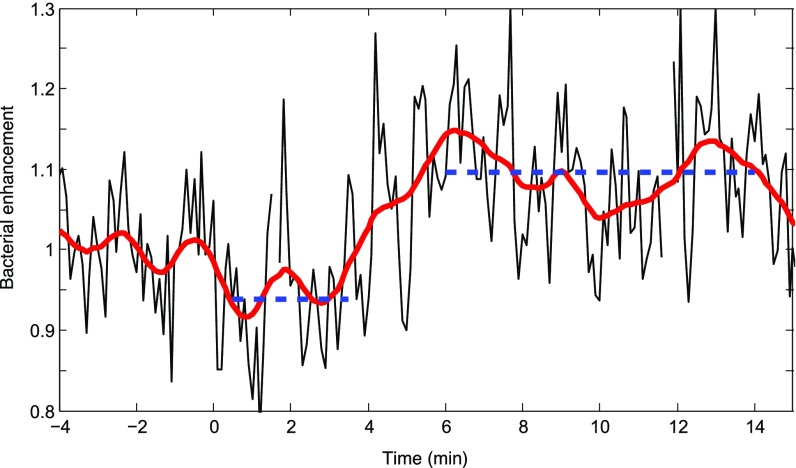
The phycosphere extends to ∼2 mm, as seen in a higher-resolution view of data displayed in Fig. 2A. Diatom lysis occurred at t = 0. The black line shows the average cell concentration every 6 s, as the fold difference normalized by the average concentration before lysis (−4 min to −40 s), for the region contained between r = 1.2 and r = 1.8 mm from the diatom center. The concentration initially decreased from 0.5 to 3.5 min after lysis (one-sided t test, P < 0.001) then increased significantly from 6 to 14 min after diatom lysis (one-sided t test, P < 0.001). This corresponds to an initial loss of 10³ cells, and a subsequent gain of 2.5 × 10³ cells, in the volume that comprises this region. The red line is a running mean with 1-min averaging window.

DOM Consumption Model.

We used the observed bacterial enhancement, B(r,t), in a mathematical model to quantify DOM consumption and predict the implications of hotspot exploitation on the competition for DOM between motile and nonmotile bacteria. Although DOM is often a complex mixture of molecules, we model it here for simplicity as a single compound, whose concentration C(r,t) varies in space (r) and time (t) as a result of diffusion and consumption, that is,

$$\frac{\partial C}{\partial t}=D{\nabla }^{2}C-\left[4\pi a_{\text{NM}}D{B}_0+4\pi a_{\text{M}}DB\left(r,t\right)\gamma B_0\right]\hspace{0.17em}C.$$ [1]

The first term on the right-hand side represents molecular diffusion with diffusivity D. We identified the diffusivity of the effective chemoattractant as that which best corresponded to the observed bacterial response, recognizing that release of chemoattractant may not have been instantaneous (SI Materials and Methods). The two terms in square brackets express diffusion-limited DOM consumption by a population of nonmotile bacteria (25), having bulk concentration B₀ and individual-cell radius a_NM,, and a population of motile bacteria having bulk concentration γB₀ and individual-cell radius a_M. Radii are equivalent-spherical-cell radii for ecologically relevant cell sizes (26) and are different between motile and nonmotile populations as a simple means to account for differences in uptake kinetics. The parameter γ represents the relative concentration of motile and nonmotile bacteria in bulk seawater. We chose a baseline value of ∼10% motility, typical of natural seawater communities, but explored the effect of this parameter over a broad range, representative of the variability observed in nature (14, 15, 27). Nonmotile bacteria maintain their uniform bulk concentration B₀ at all times, lacking the ability to behaviorally respond to the DOM. Thus, the model extends our observations by including a nonmotile population (SI Materials and Methods) and the quantification of the consumption by each population, obtained from the model, is the basis for determining the outcome of the competition for the diatom’s DOM.

Fate of Diatom-Derived DOM.

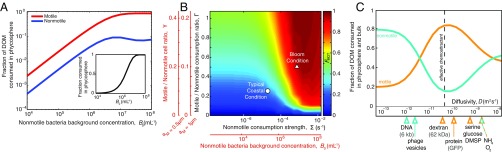
When the bulk bacterial concentration is high, a large fraction of the DOM released by lysis is consumed locally within the phycosphere, mostly by motile cells. Assuming a 1:10 ratio of motile to nonmotile bacteria (γ = 0.1) and that motile bacteria are larger (a_M = 0.5 µm > a_NM = 0.2 µm), we used the model to compute the fraction of DOM consumed by all cells within a single phycosphere (r < 2 mm) and the partitioning of this consumption between motile and nonmotile bacteria (Fig. 3A). For B₀ < 10⁵ cells per mL, consumption in the phycosphere is negligible and most DOM diffuses past the clustered bacteria and out of the phycosphere (Fig. 3A, Inset). Conversely, when B₀ = 10⁶ cells per mL then 25% of the DOM is consumed within the phycosphere, and when B₀ = 10⁷ cells per mL—as can occur during phytoplankton blooms (28)—this fraction increases to 92% (Fig. 3A, Inset). Phycosphere consumption is dominated in all cases (for B₀ = 10⁴ to 10⁸ cells per mL) by motile bacteria, which obtain greater than fivefold more DOM in the phycosphere than nonmotile bacteria (Fig. 3A).

Fig. 3.

Motile bacteria often dominate consumption of DOM released from phycospheres. (A) Fraction of DOM released in a lysis that is consumed within the phycosphere (r < 2 mm from the diatom center), and within the duration of accumulation (10 min), by motile (red) and nonmotile (blue) bacteria, as a function of the background concentration of nonmotile bacteria, B₀. (Inset) Fraction of DOM consumed in the phycosphere by both populations together. (B) Fraction of DOM consumed by motile bacteria (F_MOT; color bar), calculated for a broad range of motile to nonmotile cell number ratios γ, background bacterial concentrations B₀, and cell sizes a_M and a_NM. Red axes show F_MOT for two selected values of motile cell size, a_M, with nonmotile cell size fixed at a_NM = 0.2 μm. Black axes shows F_MOT as a function of the nonmotile consumption strength, Σ = 4π a_NM D B₀,[s⁻¹], and the dimensionless consumption ratio, Γ = a_M/a_NM γ. Two scenarios are identified by the white symbols (discussed in the main text). (C) Fraction of DOM consumed overall by motile (orange) and nonmotile (cyan) bacteria as a function of the diffusivity D (for B₀ = 10⁷ cells per mL). The diffusivity of the effective chemoattractant in the experiments is indicated by the dashed line (D = 3 × 10⁻¹¹ m²/s). Values of D for some biomolecules are indicated by arrowheads and color-matched to the population that dominates consumption of that molecule. For A, B, and D: γ = 0.1, a_M = 0.5 μm, and a_NM = 0.2 μm.

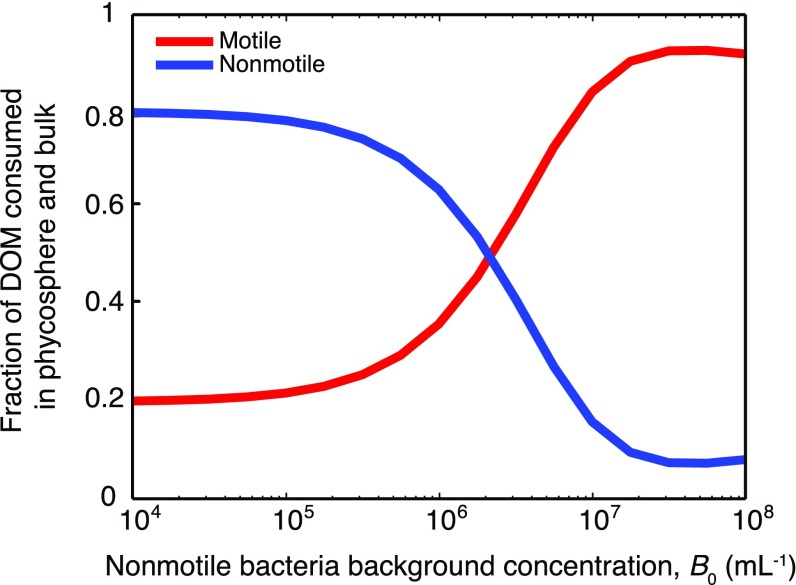
DOM not consumed in the phycosphere diffuses into bulk seawater (r > 2 mm), where it becomes homogeneously distributed and consumed over time by homogeneously distributed motile and nonmotile bacteria. The sum of each population’s consumption in the two regimes—the phycosphere and the bulk—determines the outcome of the competition, and when phycosphere consumption is negligible, then each population’s consumption is determined solely by its uptake rate in the bulk, irrespective of behavior. Accounting for this (SI Materials and Methods), we find that motile bacteria consume 22–36% of released DOM at bulk bacterial concentrations typical of seawater (B₀ = 10⁵ to 10⁶ cells per mL), 50% at slightly elevated bulk concentrations (B₀ = 2.2 × 10⁶ cells per mL), and a striking 82% at high bulk concentrations (B₀ = 10⁷ cells per mL) (Fig. S7).

Fig. S7.

Overall partition from a single phycosphere. The fraction of DOM consumed overall (i.e., in phycosphere and bulk) by motile (red) and nonmotile (blue) bacteria is shown. Bulk consumption occurs on the DOM that escapes the phycosphere as shown in Fig. 3A and favors the nonmotile oligotrophs.

An analysis of the resource competition equation (Eq. 1) shows that DOM partitioning can be predicted for a broad range of different bulk bacterial concentrations B₀, cell sizes a_NM and a_M, and proportion of motile cells γ, using only two lumped parameters, Σ = 4πDa_NMB₀ and Γ = γa_M/a_NM (Fig. 3B). The nonmotile consumption strength parameter, Σ (an inverse timescale), represents the uptake rate of the population of nonmotile bacteria, whereas the consumption strength ratio, Γ (dimensionless), measures the uptake rate of the motile population (4πDa_MγB₀) over that of the nonmotile population (4πDa_NMB₀), both computed assuming a uniform distribution of bacteria. For low consumption strengths (Σ < ∼10⁻⁵ s⁻¹, Γ < ∼1; Fig. 3B), the fraction of the DOM consumed overall by motile bacteria, F_MOT, is set by Γ alone, because consumption is negligible within the phycosphere and occurs almost entirely in the bulk (Fig. 3A). This “bulk limit” represents the traditional view of bacterial consumption in the ocean, in which microscale resource heterogeneity is not considered. For Σ > ∼10⁻⁴ s⁻¹, consumption occurs primarily in the phycosphere and is dominated by the motile population for all but the smallest values of Γ. For example, we find that motile bacteria consume F_MOT = 29% of released DOM in typical coastal seawater conditions (Fig. 3B, white circle; Σ = 4.0 × 10⁻⁵ s⁻¹, Γ = 0.25; i.e., B₀ = 5 × 10⁵ cells per mL, a_M = 0.5 µm, a_NM = 0.2 µm, γ = 0.1). This value jumps to F_MOT = 93% in typical diatom bloom conditions (Fig. 3B, white triangle; Σ = 7.9 × 10⁻⁴ s⁻¹, Γ = 0.5; i.e., B₀ = 10⁷ cells per mL, a_M = 1.0 µm, a_NM = 0.2 µm, γ = 0.1). These results reveal that under typical coastal conditions the partitioning of DOM among bacterial populations is largely unaffected by motility, and this is consistent with the variable and often low prevalence of swimming cells observed in natural waters (14, 27). In contrast, in hotspot-rich conditions such as blooms, chemotaxis can play a disproportionate role in the fate of DOM from phytoplankton, even when the fraction of motile bacteria is small.

A Bountiful Yet Risky Phycosphere?

By bringing bacteria in close proximity to the diatom and each other, cluster formation can influence the exchange of substances beyond the chemoattractant(s). These can include other molecules from the diatom but also biological entities originating from the accumulated bacteria themselves, for example signaling molecules, phages, or vesicles (29), the release of which can be approximated as originating from the diatom lysis. We quantified the potential for exchange enhancement for different substances by running the model for different values of the diffusivity D and the observed cluster dynamics quantified by B(r,t). Molecules with intermediate diffusivities (D = 3.2 × 10⁻¹² to 3.2 × 10⁻⁹ m²s⁻¹), characteristic of many that can be released during diatom lysis, are consumed predominately (>50%) by motile cells (Fig. 3C). For example, consumption of proteins similar in size to GFP [D = 9 × 10⁻¹¹ m²s⁻¹ (30)] will be strongly dominated by motile bacteria (83%), which is consequential because phytoplankton are composed of >50% protein (31). In contrast, molecules with very high diffusivity (D > 10⁻⁸ m²s⁻¹) escape from the phycosphere before being consumed. Meanwhile, substances with very low diffusivity (D < 10⁻¹² m²s⁻¹) disperse much more slowly than the ∼10-min duration of a cluster, hence they are not preferentially captured by motile bacteria. A consequence of this last result is that, although clustering allows motile bacteria to dominate DOM consumption in the phycosphere, it does not enhance their exposure to low-diffusivity entities that may be present in high concentrations in the cluster, such as phages (Fig. 3C). Based on this prediction, we speculate that motile bacteria take advantage of DOM hotspots while minimizing the risk of “dangerous exchanges” within them. Moreover, enzyme activity among clustered bacteria may degrade low-diffusivity DOM to create high-diffusivity hydrolysates (32, 33), further enhancing uptake by chemotactic cells in the phycosphere.

From a Single Phycosphere to the Phycoscape.

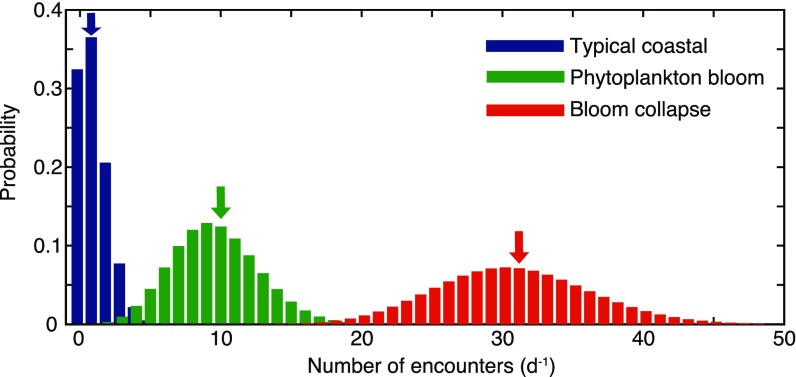
The importance of phycospheres for bacterial populations will depend on consumption by individual bacteria over multiple phycosphere encounters in the ocean resource landscape. To scale up predictions of consumption from a single phycosphere to this “phycoscape,” we consider an ocean in which diatom lysis hotspots are the sole carbon source for two competing bacterial populations under three scenarios: typical coastal conditions, a phytoplankton bloom, and a bloom collapse, corresponding to 34, 312, and 912 lyses per mL per d, respectively (SI Materials and Methods). Assuming that lysis events are uncorrelated and bacteria never experience overlapping phycospheres, individual bacteria encounter phycospheres as a Poisson process with average encounter rates of 1 per d, 10 per d, and 31 per d, respectively (Fig. S8 and SI Materials and Methods). In this model ocean, bacteria consume DOM both within phycospheres and in the bulk, where the bulk, steady-state DOM concentration is determined by the amount of DOM escaping from phycospheres and by the concentration of bacteria (Fig. 3A, Inset).

Fig. S8.

Frequency distribution for the encounter rate of single bacteria (either motile or nonmotile) with diatom lysis events, for three assumed diatom lysis rates corresponding to typical coastal conditions (1.4 lysis events per mL per h), a phytoplankton bloom (13 lysis events per mL per h), and a bloom collapse (38 lysis events per mL per h). These conditions correspond to a mean encounter rate of 1 per d, 10 per d, and 31 per d, respectively (as indicated by the arrows). Given the independent random occurrence of lysis events, all locations are equally likely to experience phycospheres. Thus, under our assumptions, the encounter rate with phycospheres is the same for motile and nonmotile cells.

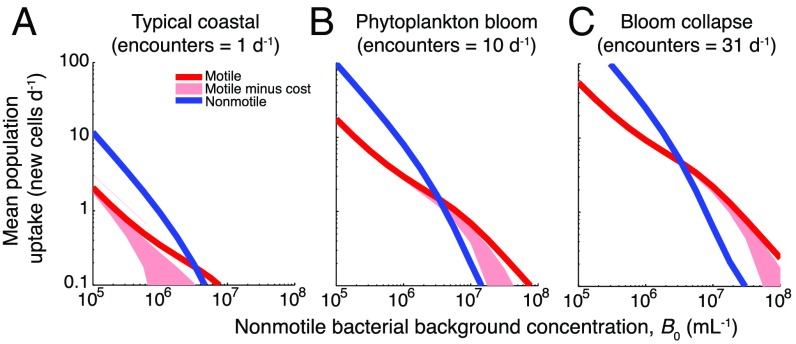
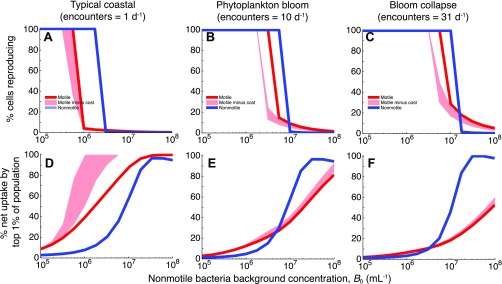
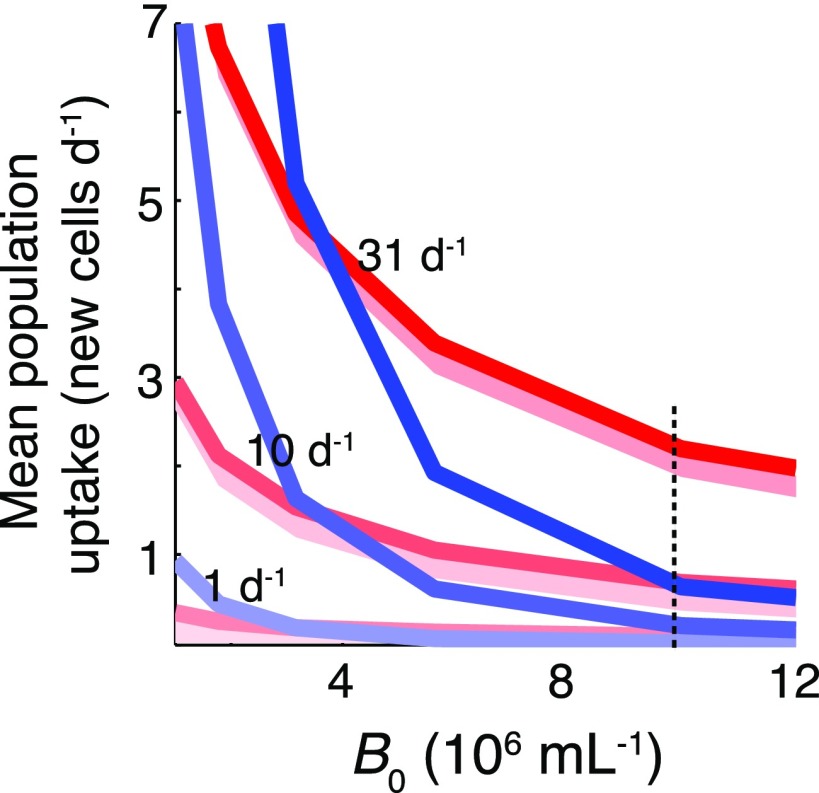
At the phycoscape level, there is a distinct transition in bacterial growth between bulk-dominated and phycosphere-dominated regimes (Fig. 4 and Fig. S9), mirroring the behavior observed in the partitioning of DOM from a single diatom. At low bacterial concentrations (B₀ < 10⁶ cells per mL), elevated levels of carbon in the bulk drive growth, giving an advantage to the nonmotile population. At high bacterial concentrations (B₀ > 10⁷ cells per mL), carbon consumption occurs primarily within phycospheres and little leaks into the bulk, which strongly favors motile bacteria. The point of transition between the two regimes depends on the ratio γ of motile to nonmotile bacteria: For a 1:10 ratio, the transition occurs at B₀ = 5 × 10⁶ cells per mL (Fig. 4), whereas for a 1:1 ratio it occurs at B₀ = 0.8 × 10⁶ cells per mL. In the typical coastal scenario considered, carbon from lysis events supports growth of less than one new motile cell per day, insufficient to sustain the population under a characteristic assemblage turnover time of 1 d (34). In contrast, in the phytoplankton bloom or bloom collapse scenarios, growth benefits for both bacterial populations become substantial as cells encounter more lysis events (Fig. 4), and a higher percent of cells reproduce (Fig. S10 A–C). Even while both populations grow better, motility yields a >300% growth advantage in the bloom collapse scenario when B₀ = 10⁷ cells per mL, a difference that remains conspicuous even after accounting for the cost of swimming (Fig. S11 and SI Materials and Methods).

Fig. 4.

Bacterial growth in a seascape of lysing diatom, illustrating the advantage of motility at high lysis encounter rates and high bacterial concentrations. Three characteristic environmental conditions are shown: typical coastal seawater, a phytoplankton bloom, and a bloom collapse. (A–C) Mean population uptake for motile and nonmotile cells, expressed in new cell carbon equivalents per day, as a function of the background concentration of nonmotile bacteria, B₀. For all panels, the motile:nonmotile cell number ratio was 1:10 (γ = 0.1). Shaded pink areas indicate motile population benefits after subtracting costs for swimming, for a range of assumed swimming velocities and efficiencies (SI Materials and Methods).

Fig. S9.

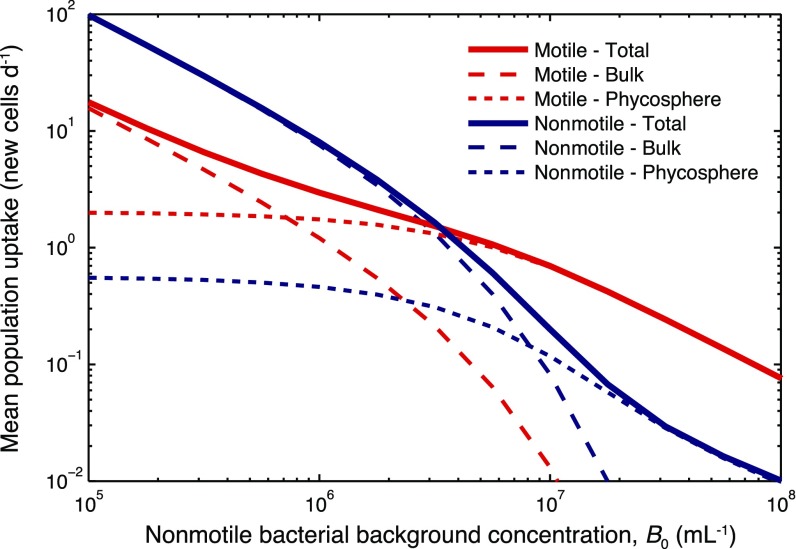
Uptake of diatom DOM by a motile (red) and a nonmotile (blue) population in a phytoplankton bloom (10 lysis encounters per d). The contribution to ‟Total” uptake by uptake in the ‟Bulk” and uptake in the ‟Phycosphere” are indicated (see legend), where the latter indicates consumption within r = 2 mm from the diatom center that occurs during the 10-min duration of the lysis accumulation (Fig. 2).

Fig. S10.

Percentage of cells reproducing within a population (A–C) and contribution to DOM consumption by the top 1% of cells in a population (D–F), for a motile population (red), a nonmotile population (blue), and a motile population for which swimming costs have been accounted (pink shading). Results are shown for three assumed diatom lysis encounter rates, corresponding to typical coastal conditions (A and D), a phytoplankton bloom (B and E), and a bloom collapse (C and F). ‟Reproducing cells” were those that consumed more than one new cell carbon equivalent over 1 d. For all panels the ratio of motile to nonmotile cells in the total population was γ = 0.1. Costs of motility were computed as the envelope of results obtained for a range of swimming velocities (40–60 μm/s) and swimming efficiencies (1–2%) (SI Materials and Methods).

Fig. S11.

Bacterial growth comparison under different phycoscapes. This is a direct comparison of motile copiotrophs (red) and nonmotile oligotrophs (blue) plotted in Fig. 4, but with linear axes. The advantage for motile cells (i.e., the ratio of motile to nonmotile uptake expressed as a percentage for each encounter rate) when B₀ = 10⁷ cells per mL (indicated by a dashed line) is <40% for typical coastal conditions (lysis encounter rate of 1 per d), 190–310% for a phytoplankton bloom (10 per d), and 300–340% for a bloom collapse (31 per d).

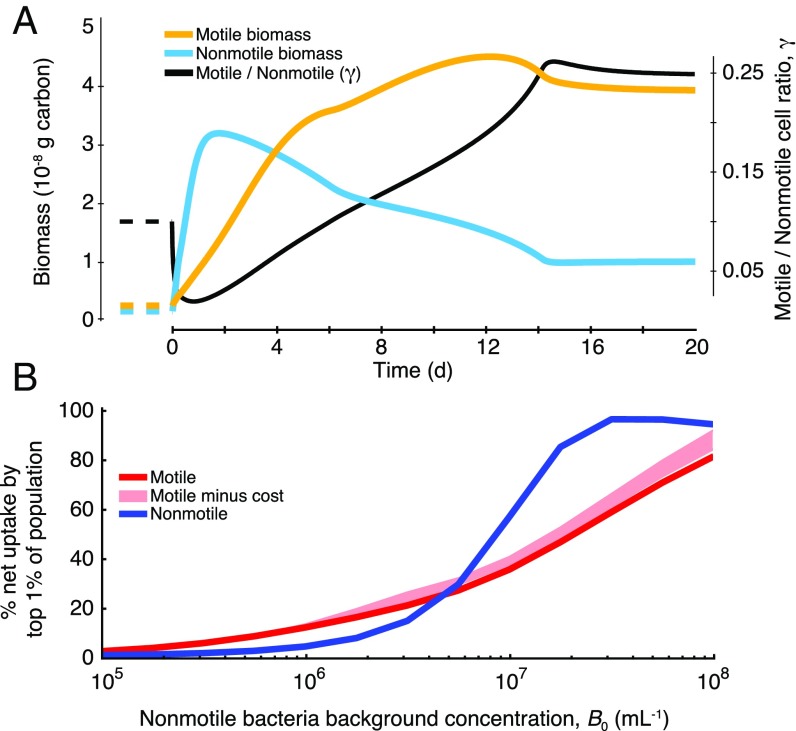
The increased role of motile copiotrophs in DOM consumption under increased cell concentration, B₀ (Fig. 4), provides a mechanism for the initiation of bacterial succession in phytoplankton blooms. This is revealed by a simulation of the first several days of a bloom, starting from bacterial abundances typical of coastal conditions (B₀ = 0.5 × 10⁶ bacteria per mL, ref. 35; γ = 0.1) and accounting for losses due to viral infection and protistan grazing (SI Materials and Methods). The simulation predicts a turnover in biomass from nonmotile oligotrophs to motile copiotrophs (Fig. 5A): Populations increase after the bloom begins, heightening the competition for DOM and thus the importance of phycosphere consumption, and triggering the dominance of bacterial biomass by motile bacteria after ∼4 d (Fig. 5A). In this scenario, nonmotile bacteria still dominate numerically (γ_MAX = 0.25), but the larger cell size of motile bacteria and their dominance of phycosphere consumption triggers the biomass “inversion.” This inversion will amplify during a bloom collapse, when phycosphere encounters increase even further.

Fig. 5.

Bacterial growth during a phytoplankton bloom, illustrating the effects of phycospheres on the initiation of succession among populations of bacteria. (A) Biomass of motile (yellow) and nonmotile (cyan) cells and motile:nonmotile cell number ratio γ (black). The bloom was simulated by exposing both populations over several days to a constant lysis encounter rate of 10 per d. Before bloom initiation (dashed lines), conditions for the bacteria populations were set at γ = 0.1, nonmotile background bacterial concentration B₀ = 5 × 10⁵ cells per mL, and cell sizes a_M = 0.5 μm and a_NM = 0.2 μm. (B) Contribution by the top 1% of cells to the overall population consumption of DOM by each population. For B, results are for 1-d exposure to a bloom where B₀ was fixed (accordingly) and γ = 0.1, and shaded pink areas indicate motile population benefits after subtracting costs for swimming (Fig. 4).

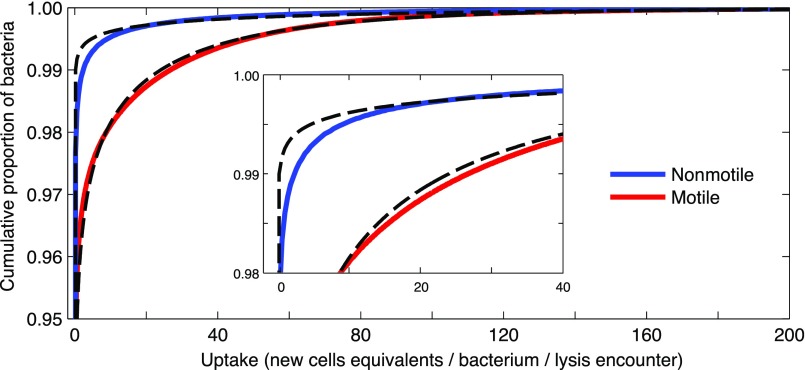
During a bloom, when consumption is phycosphere-driven, the statistical nature of phycosphere encounters by individual bacteria results in a strong skew in uptake among motile bacteria as well as among nonmotile bacteria. Quantifying single-cell uptake in these conditions (SI Materials and Methods) revealed that a few “superconsumer” cells, those that happen to encounter multiple phycospheres and/or to be in a favorable location within a phycosphere, consume vastly more DOM than the average cell. For example, during a single lysis event (for B₀ = 10⁷ cells per mL) the top 1% of motile cells consume enough DOM to each produce >30 new cells (Fig. S12). Scaling this up to the phytoplankton bloom scenario, the top 1% of motile cells account for 40% of the population’s total DOM consumption (Fig. 5B and Fig. S10E). This reveals that population reproduction may be largely driven by a small number of superconsumer cells. Consumption inequality during a bloom is even greater among nonmotile bacteria, where the 1% superconsumers account for 60% of the population’s total consumption (for B₀ = 10⁷ cells per mL; Fig. 5B and Fig. S10 E and F), owing to the absence of cell redistribution within the phycosphere.

Fig. S12.

DOM uptake in the phycosphere for motile (red) and nonmotile (blue) bacteria, shown as a cumulative distribution function for individuals in each population. (Inset) A magnified view. The calculation used the distribution of motile bacteria, B(r,t), and the simulated diffusion of diatom DOM following lysis, C(r,t) (Supporting Information), for B₀ = 10⁷ cells per mL. These distributions were fitted with gamma distributions (dashed lines) matching the mean and variance, which were subsequently used to determine the top 1% consumers for three characteristic environmental conditions (Fig. 5B and Fig. S10).

Impacts on the Microbial Ocean.

DOM in the surface ocean often becomes available to microbes as microscale hotspots, in the form of organic particles (33), leakage or lysis of phytoplankton, and microscale filaments originating from the turbulent stirring of larger DOM patches (36). However, consumption of DOM is not always correspondingly heterogeneous: Consumption can occur within the hotspots but also in the bulk. Our hybrid observation-modeling framework enables one to predict the conditions under which bacterial DOM consumption is bulk-dominated versus hotspot-dominated (Fig. 3B). We find that consumption among free-living bacteria is bulk-dominated under typical coastal ocean conditions, when most DOM released as microscale patches diffuses past bacteria that have accumulated by chemotaxis into bulk seawater, where consumption is dominated by nonmotile oligotrophs. In contrast, consumption becomes hotspot-dominated in phytoplankton blooms and bloom collapse conditions, when bacterial concentrations are high, cells are large, and/or the percentage of motile cells is elevated (Fig. 3B).

When the environment shifts toward a higher frequency of hotspots, the growth of motile cells creates positive feedback by hastening the development of hotspot-dominated conditions, which in turn skews consumption toward motile cells. In addition to chemotaxis, the growth of motile cells will be strengthened by other copiotrophic adaptations, including diversified membrane transporters and higher ribosome content (2), as well as multiphasic uptake kinetics (37). Chemotaxis then enables copiotrophs to deploy these adaptations with great effectiveness within hotspots, even when phycospheres are distorted by fluid flow (SI Discussion), potentially further increasing the per capita utilization of DOM compared with that found in our analysis.

The accumulation of copiotrophs in the phycosphere marks the initial stage in a continuum of events following a phytoplankton’s lysis. Chemotaxis may favor and precede attachment of some bacteria to the diatom surface, enabling colonization of nascent phytodetrital particles. Attached bacteria that produce hydrolytic enzymes can degrade particulate organic matter embedded in the diatom (38), releasing additional DOM. Because the timescale of attachment can be much greater than the initial ∼10-min-long response to lysis, the enzymatic activity of attached cells may create long-term gradients, prolonging the effect of the phycosphere on bacterial competition. Our observations demonstrate that clusters are mostly dissipated after 10 min (Fig. 2), suggesting that DOM gradients become too weak to trigger substantial accumulation and that DOM exuded from phytodetritus on longer timescales should partition primarily to nonmotile oligotrophs. In contrast, attached copiotrophs will have prolonged individual benefits.

Growth of motile cells in hotspot-dominated conditions will modify the composition of bacterial assemblages by leading to greater prevalence of copiotrophic taxa. Despite observational evidence that major perturbations to the DOM environment trigger succession among bacteria, with a dominance of copiotrophic groups (4), no quantitative framework has been available for these observations. Our analysis provides such a framework, for the simplified case of two bacterial populations, for which it predicts both the trends and the turning points for bacterial succession, in particular revealing that the initial phase of succession is driven by competition for DOM that becomes increasingly localized (Fig. 5A). Importantly, the model predicts the dynamics of the relative concentration of motile and nonmotile bacteria (γ), a parameter analogous to the relative representation of motility and chemotaxis genes in metaomic datasets (17, 39). The model therefore provides context for interpreting relative gene data and potentially converting such data post hoc to an empirical ratio for motile to nonmotile cells.

For motile bacteria and nonmotile bacteria, the effect of “being in the right place at the right time” has large consequences for individual uptake when DOM appears as ephemeral hotspots. Uptake distributions are strongly skewed within a population (Fig. S10) and a small number of superconsumer individuals, belonging to the long tail of the per-cell consumption curve, are responsible for most of the total population uptake. This hetereogeneity is commonly averaged out in bulk sampling approaches and seldom appreciated in marine microbial ecology. Intriguingly, long-tailed distribution curves also characterize single-cell activity rates in coastal seawater (40, 41), suggesting a relationship between the uptake heterogeneity resulting from hotspots and skewed rates in standing bacterial stocks, which may extend to the level of individual phylotypes.

The concept of the phycosphere has evolved from theory (7–9, 12) to observation (10, 11, 13) and, with this study, to controlled generation and high-resolution quantification, indispensable steps to permit up-scaling its consequences for consumption and growth among bacterial populations. The hybrid approach introduced here opens the door to its application for other studies of microscale patch dynamics and provides a blueprint for studying bacterial competition in heterogeneous environments. Different resource hotspots—including diverse groups of phytoplankton, particles, and oil droplets, as well as different release rates spanning from slow leakage to sudden lysis—will result in different microscale resource seascapes and thus different outcomes of the competition. The extension of both the laboratory approach and the modeling framework to the spectrum of microscale hotspots making up the ocean’s chemical seascape will provide a fertile avenue toward a deeper understanding of the foraging ecology of microorganisms and their effects on microbial competition, genetic diversity, and ocean biogeochemistry.

SI Discussion

Phycospheres are subject to fluid flow in the ocean. At the length scale of the phycosphere, all but the most intense turbulence primarily manifests itself as a time-varying linear shear flow (13, 42). At shear rates >0.05 s⁻¹, the phycosphere will form isolated filaments (36), diverging from the symmetric geometry assumed here (Fig. 2). Stronger shear rates could also alter uptake dynamics (43) and very high rates (>2.5 s⁻¹) may hinder chemotaxis (44). However, in calm to moderate ocean conditions, wind-driven shear (0.005–0.05 s⁻¹) would only stretch the phycosphere to an ellipsoid during the 10-min phycosphere interaction discussed here (11), and we thus expect clustering and the associated competitive advantage for motile cells to persist. Weak shear may even increase the chemotactic signal volume of the phycosphere and thus its utilization by motile copiotrophic bacteria (36, 45).

SI Materials and Methods

Seawater Sampling and Diatom Culture Maintenance.

Seawater samples were collected at Canoe Beach (Nahant, MA) or Revere Beach (Revere, MA) via a net tow (63-µm mesh size) to concentrate planktonic particles. The particles and entrained seawater (∼40 mL) were incubated for 22 h at room temperature then filtered to remove particles (5-µm pore size, 47-mm-diameter polycarbonate membrane). The resulting filtrate containing enriched bacteria was washed once by centrifugation (5,000 × g, 1 min), resuspended in f/2 media, then added to aliquots of diatom cultures (20 µL bacteria with 40 µL diatoms) for microscopic observation.

Cultures of C. affinis CCMP160 were acquired from the National Center for Marine Algae and maintained in f/2 media in a light incubator (70–90 µE m⁻²s⁻¹). Cell aliquots in midlog phase were used for all experiments.

Microscopy.

Experimental conditions for diatom lysis are described in the main text. Bacteria–diatom mixtures (20 µL of enriched bacteria mixed with 40 µL of diatom culture) were viewed in a custom-made observation chamber. The chamber consisted of a glass slide and coverslip (24 × 54 mm, no. 1 thickness) separated by rubber gasket material (1-mm thickness) along the long edges of the coverslip. The cell mixture was applied to the coverslip as a “hanging drop,” which was then set gently atop the gasket material. This setup minimized fluid motion and enhanced gas exchange with ambient air. Diatoms settled to the glass slide surface within 5–10 min; lysis and visualization were performed only on settled diatoms (Materials and Methods). In contrast to naturally occurring hotspots where lysis occurred sporadically (Fig. 1A), the controlled approach permitted capture of the full time course of the bacterial response associated with diatom lysis.

Videos were captured on a Nikon TE-2000 microscope with a CMOS camera (Nikon Zyla, 2,560 × 2,160 pixels, with a region of interest set at 2,000 × 2,000 pixels) controlled through Nikon Elements software (version 5) on a desktop with RAID 0 hard drive storage. Capture frame rates ranged from 15 per s to 60 per s for different movies. Cells were imaged in phase contrast using a 10× (N.A. 0.30) objective with a 1.5× magnifier lens; the field of view was 0.9 × 0.9 mm².

Lysis of the plasma membrane in diatom cells was confirmed experimentally in the absence of bacteria. Aliquots of cultured C. affinis were amended (5 µM final concentration) with the polar fluorescent dye SYTOX Green (Invitrogen). This charged, DNA-intercolating dye permeates only compromised cell membranes, leading to intracellular accumulation within lysed diatom cells as detected via epifluorescence imaging (488-nm excitation, 535-nm emission). Photobleaching was minimized by capturing fluorescent images at 15-s intervals, rather than continuously. Before imaging (e.g., for Movie S3, before the start of the movie), diatom lysis was initiated by applying blue fluorescence light (350-nm excitation, ∼7 kW/m²) for 5–10 min while maintaining continual broad-spectrum LED white-light illumination (∼200 µmol m⁻² s⁻¹). In separate trials, plasmolysis occurred more slowly with application of green fluorescence light (488-nm excitation, ∼7 kW/m²) or in the absence of continual LED white light.

Bacterial Community Composition.

For DNA analyses, samples of enriched seawater were filtered to remove particles (5-µm pore size, 47-mm-diameter polycarbonate membrane) then collected on a membrane (Supor-200, 0.2-µm pore size, 25-mm diameter) and stored in a sterile tube at −20 °C. DNA was extracted from membranes via a modified bead-beating technique. Community taxonomic composition was determined via high-throughput parallel sequencing of 16S rRNA genes (Illumina) and analyses with the QIIME software package (46). There were >1,000 reads per sample, and operational taxonomic units (OTUs) were reported to the level 6 taxonomy assignment. Data shown here (Fig. S1) correspond to the community quantified in the prototypical single diatom example (Fig. 2).

Dominance of Vibrionaceae in the enriched seawater, rather than other copiotrophic taxa, was likely influenced by the presence of highly concentrated phytoplankton and zooplankton particles, which may have been a source for attached Vibrio spp., as well as the relatively warm temperature (22 °C) of the overnight incubation (21).

Image Analysis.

The positions of moving bacteria were extracted in each video frame through image analysis. To isolate swimming bacteria, each frame was compared against its adjacent neighbors. Large objects such as diatoms and small, slow-moving particulates are deemphasized in this approach. Individuals were identified by thresholding the resulting image and locating centroids. Subsequently, objects that were too small (approximately one pixel) or that were moving slowly by Brownian motion were rejected as noise or nonmotile. All of the positions of motile bacteria were then binned in 5-µm increments of radial distance from a point centered in the diatom. This image processing was accomplished using custom MATLAB (The MathWorks) scripts. Finally, the distributions of bacteria over time were filtered with Gaussian filters, using a 10-µm SD in the radial direction and a 2-s SD in time. The resulting smoothed distribution was normalized by the average concentration in the 3 min before lysis occurred, which matched the unaffected far-field concentration. The resulting normalized distribution, denoted B(r,t), captures the enhancement over the background concentration caused by chemotaxis in response to a diatom lysis. Image intensity time series of the diatom center were separately extracted to identify the time of lysis, corresponding to abrupt changes in the diatom phase image (Fig. 2B). For the bacterial enhancement B(r,t), t = 0 corresponds to the time of lysis.

Coupled DOM–Bacteria Consumption Model.

Numerical models for evaluating the distribution of diatom DOM in the presence of motile and nonmotile bacteria were implemented in COMSOL Multiphysics (version 4.2.a; COMSOL Inc.). The model in Eq. 1 (main text) was implemented using a general form PDE module with radial symmetry in a 2-mm-radius sphere. Making use of the symmetry, the mesh consisted of a line with 1,000 segments, progressing geometrically from 0.16 µm near the diatom to 8 µm at the outer boundary. The outer boundary of the model was pinned to have zero DOM concentration and the internal point had zero flux due to symmetry.

The experimentally measured enhancement of motile bacteria, B(r,t), was linked to the numerical model as a MATLAB function that interpolated the spatiotemporal bacterial enhancement. Nonmotile bacteria were assumed to be uniformly distributed in the numerical model. By using the function B(r,t) measured in the absence of this second population, we assume that the behavior of motile cells is not affected by the presence of nonmotile cells, and that the normalized motile cell distribution B(r,t) will not vary with the background concentration of motile bacteria γB₀. This assumption may break down when overall consumption is very strong.

All bacteria were excluded from the central 15-µm radius where the simulated diatom was positioned; within this region, the video data gave highly variable estimates of B(r,t) due to bacterial crowding, surface attachment, and optical interference from the diatom biomass itself. Thus, consumption was set to zero for r < 15 µm. Simulating diatom lysis, the DOM is initially evenly distributed within the diatom only but able to diffuse outward without restraint. The initial distribution has a smoothed transition to zero over 2 µm centered at the 15-µm point. Owing to the resulting transient sharp gradients, the first second was simulated in 0.01-s increments and the remaining 10 min was simulated in 30-s increments. Comsol simulations were performed using a backward differentiation formula (BDF) solver, with an intermediate setting in time stepping. The remaining parameters of the time-dependent solver remained as the default for the BDF solver. The Comsol simulations of DOM diffusion were compared against analytical solutions of spherically diffusing compounds (47) to verify that the mesh, time-stepping, and solver choices were adequate. The DOM distribution at each time step was exported, and subsequently the calculations for consumption were performed in MATLAB.

The model assumes that a single chemoattractant drives the response of motile bacteria. This is a simplification, because diatoms contain and release upon lysis a broad range of chemical compounds spanning a range of diffusivities. In the absence of an ability to experimentally identify the dominant chemoattractant, and the possibility of multiple attractants stimulating the motile cells’ response, we identified the effective chemoattractant diffusivity as the value of D that best corresponded to the observed bacterial response. To do this, the coupled DOM–bacteria model was tested under conditions closely replicating the laboratory experiments for a range of DOM diffusivities. Under these conditions, there were no nonmotile bacteria, and the motile bacteria had an equivalent radius (a_M = 0.94 µm) and a background concentration (γB₀ = 1.18 × 10⁶ cells per mL) representing those observed in the experiments. Determination of when a simulation was a good match to the experiment was based on several metrics. First, the DOM could not escape the 2-mm-radius model geometry too quickly or remain adjacent to the diatom during the 10-min chemotactic response, because both extremes could not be reconciled with the 10-min duration of the transient clustering. Second, we evaluated the timing of the initial accumulation by comparing the DOM gradient near the diatom (15–30 µm from the diatom center) with the onset of bacteria accumulating in that same region. Third, considering the direct interaction between bacteria and DOM, we examined the length of time until the DOM gradient flattened near the diatom (as a rough measure of the duration of attraction to the diatom). Fourth, the total DOM consumed by the motile bacteria was compared for different DOM diffusivities. Although the bacterial response is not necessarily optimizing the overall amount of chemoattractant DOM consumed by the bacteria, one expects the total consumed DOM to be comparatively high at the effective diffusivity.

Factoring these metrics in with our understanding of potential attractive components of diatom DOM, an effective diffusivity of 3.16 × 10⁻¹¹ m²s⁻¹ (Fig. 2D) best satisfied all four metrics, and this value was used in all subsequent analyses. This value is low relative to known, small-molecule chemoattractants (e.g., D = 9 × 10⁻¹⁰ m²s⁻¹ for serine), likely because it captures the noninstantaneous release of multiple attractants with a single diffusivity value. More specifically, the diatom surface likely acted as a sieve and the release of different DOM constituents through openings in the sieve occurred at some unknown rate. Additionally, ectohydrolytic enzyme activity among clustered bacteria may have degraded large DOM molecules, leading to additional gradients of small molecules, and clustering may also reflect attraction to and consumption of these small hydrolysates. For example, diffusivity for the representative protein GFP is ∼3.16 × 10⁻¹¹ m²s⁻¹ (Fig. 3C), so clustering may reflect chemotaxis toward dissolved free amino acids created by hydrolysis of similarly sized proteins released from diatoms during lysis.

To quantify the consumption partitioning of different molecules released from diatoms upon lysis, and to constrain the potential for interbacterial exchange enhancement of biological entities, we used the same consumption model described above with both motile and nonmotile bacteria. However, rather than using a single effective diffusivity, D, we iterated the model for 23 assumed diffusivity values (10^−13.5, 10^−13.25, ..., 10^−8.25, 10⁻⁸ m²s⁻¹), making it possible to calculate the quantities consumed within the phycosphere by both bacterial populations at each diffusivity. The fraction of DOM consumed by each population resulted from a combination of this local consumption and bulk consumption (discussed below).

Bulk Consumption of DOM from a Single Lysis Phycosphere.

DOM that escaped the bounds of the numerical simulation domain or that remained after the 10-min chemotactic response was treated as being in the bulk environment. In the bulk, both motile and nonmotile bacteria as well as the DOM are assumed to be uniformly distributed. Under these assumptions, uptake of a diatom’s DOM is partitioned by each population’s consumption strength and therefore dependent on the cell sizes and background concentrations of the two populations.

Multiple Lysis Encounters.

Three phycoscape scenarios were considered: typical coastal conditions (100 diatoms per mL, 3-d population turnover time), phytoplankton bloom conditions (1,000 diatoms per mL, 3-d turnover time), and bloom collapse conditions (loss of 900 diatoms per mL per d) (SI Materials and Methods). These conditions correspond, respectively, to 1.4, 13, and 38 lyses per mL per h. To convert the lysis rates of diatoms under three ocean conditions into bacterial encounter rates, we made some assumptions. Given the brevity of the lysis response (10 min), and the spatial extent of the phycosphere (2-mm radius), it was assumed that negligible numbers of bacteria begin outside the phycosphere, enter the phycosphere during the lysis response, and differ significantly in terms of consumption from the consumption they would have had in the bulk. Therefore, an encounter occurs if a bacterium is within a phycosphere radius of a diatom when it lyses. We also assumed that diatom lysis events are uncorrelated in time and space. This is a simplification, in particular for Chaetoceros spp., because diatoms can form chains of cells that can each lyse. Finally, we assumed that independent lysis events do not have overlapping phycospheres. For the three lysis rates considered here, this is a minor assumption [at the highest lysis rate (38 events per mL per h), the expected minimum distance between lysis events within a 10-min period is ∼3.2 mm, less than the phycosphere radius]. With these assumptions, we can view lysis encounters as random, independent events occurring with a constant probability at any location. Therefore, a bacterium encounters lysis events as a Poisson process with a rate determined by the occurrence of lysis in a ball of equal radius to the phycosphere, centered at the bacterium. The distributions of the number of daily encounters for bacteria in different environments are shown in Fig. S8. It is important to note that under the independent lysis assumptions there is no difference in encounter rates between motile and nonmotile bacteria. Because all locations are equally likely to be a DOM source, swimming does not change the encounter probability. The advantage of motile bacteria therefore is limited to being able to closely cluster near the DOM source within a phycosphere.

In the treatment of bacteria in phycoscapes of intermittent lysis events, we shift from considering general DOM consumption to carbon consumption, which is more directly related to bacterial growth. This assumes the DOM is the sole source of carbon in the modeled environment, and that carbon uptake is proportional to DOM uptake.

Uptake Distribution Among Bacteria.

To create a bacteria-centric population model, it was necessary to specify the consumption distribution of bacteria in the phycosphere. The experimental procedure for capturing the bacterial distribution B(r,t) was tailored to evaluate the entire phycosphere and therefore does not have the resolution necessary to track individual bacteria, particularly in the dense concentrations near the diatom. As a result, it is not possible to obtain a direct estimate of the distribution in bacterial uptake determined by the changing position of each bacterium over the duration of the lysis event. Instead, we used the observed enhancement distribution of motile bacteria and a uniform distribution for nonmotile bacteria; we approximated the consumption distribution by evaluating the magnitude of consumption at a given radius, weighted by the proportion of bacteria at that radius during the chemotactic response (Fig. S12). The additional motility of individual bacteria would result in a smoothing of these distributions. Although in both cases these distributions indicate that the majority of bacteria consume very little DOM, the key distinction between the motile and nonmotile populations is apparent in the differing higher consumption tails (i.e., top 2% consumers, Fig. S12).

We subsequently estimated the uptake distribution among individuals in a population after multiple phycosphere encounters. When combined with the assumed independence of lysis event encounters, the overall probability distribution of bacterial uptake over some time T can be expressed by $f_{U|T}\left(u|t\right)={\displaystyle {\sum }_n}{f}_{U|N}\left(u\right|n)P_{N|T}\left(n\right|t)$, where $f_{U|N}$ is the distribution of uptake for a bacterium that has interacted with N lysis events but is conditionally independent on the length of time T. P_N|T is the probability of encountering N lysis events over a time T, determined by a Poisson process (Fig. S8). To simplify this calculation and avoid numerical artifacts, the approximate phycosphere consumption distributions were fitted with the two-parameter gamma probability distribution (dashed lines, Fig. S12), which has a closed form for $f_{U|N}$. These distributions are necessary for evaluating the skewness of the uptake from diatom lyses, but the population means (Fig. 4) only require the mean consumption.

Bulk Carbon Concentrations in Multiple Lysis Encounters.

Consistent with the simplified model environment of diatom-only carbon sources and bacteria-only carbon sinks, the bulk carbon concentration was determined by the amount of carbon escaping phycospheres. Because the consumption by bacteria is proportional to the carbon concentration, it is possible to solve the partial differential equation for bulk carbon levels for a steady-state solution of the bulk concentration, $C_{\text{b}}=\frac{\phi R{C}_{0}V}{4\pi D{B}_0\left(a_{\text{NM}}+a_{\text{M}}\gamma \right)}$, where $\phi$ is the fraction escaping from the phycosphere (Fig. 3A, Inset), R is the diatom lysis rate, C₀ is the concentration of carbon inside the diatom, and V is the diatom volume. Because the equations governing bacterial uptake are linear in concentration, the bulk consumption can be directly added to any uptake bacteria experience from interacting with diatom phycospheres (Fig. S9).

Bacteria Biomass and Energetics.

The uptake quantities determined by the population models (Fig. 4) were divided by a reference amount of carbon required to make an individual bacterium. Following Taylor and Stocker (36), this carbon biomass was calculated based on the cell volume (0.2-µm equivalent radius for nonmotile cells, 0.5-µm radius for motile cells) and an assumed carbon concentration of 0.1 g cm⁻³.

For both motile and nonmotile bacteria, the bacterial growth efficiency (BGE) determines the fraction of carbon taken up that goes into biomass, with the remainder going to respiration. Although large ranges of BGE are quoted in the literature, we chose a moderate 20% value for BGE for both types of bacteria. Although we here assumed the same BGE for both populations, motile copiotrophs may actually have a higher BGE than nonmotile oligotrophs, because copiotrophs generally grow faster than oligotrophs and there is evidence that BGE increases with growth rate. If this assumption is correct, then the total fraction of a diatom’s DOM transferred into bacterial biomass, and thus presumably to higher trophic levels, would be higher when robust chemotactic accumulations respond to lysis events and lower when the response is weak.

Finally, for motile bacteria, the energetic cost of swimming was translated into a carbon cost. The power required for swimming, following Taylor and Stocker (36), is $P_{\text{C}}=c_{\text{L}}{v}^2/\eta C_{\text{c}}$, where c_L is the effective drag coefficient for a 0.5-µm-radius bacterium (4.1 × 10⁻⁸ N s m⁻¹; ref. 15), v is the swimming velocity, η is the swimming efficiency, and C_C is a conversion factor for carbon to energy. In our analysis, we assumed a range of swimming velocities (40–60 µm/s) and efficiencies (1–2%) and results for the envelope of conditions are given (Fig. 4). Because the cost of swimming is not drawn from the cell biomass, the model exacted the cost of swimming from the total carbon taken up (i.e., before the BGE was applied).

Population Dynamics.

To investigate the effects of the transition from bulk- to phycosphere-dominated consumption in multiple lysis phycoscapes (Fig. 4), the population dynamics of motile and nonmotile populations were computed over several days (Fig. 5A). Starting from a fixed position with a motile to nonmotile population ratio γ = 0.1, and a nonmotile background population of B₀ = 0.5 × 10⁶ cells per mL, the bacterial populations were exposed to sustained bloom conditions (∼10 lysis encounters per d). The growth was determined by interpolating the population-averaged uptake between a series of simulations done over a range of 11 nonmotile background concentrations (B₀ = 10^4.0, 10^4.5, …, 10^8.5, 10^9.0 cells per mL) and five population ratios (γ = 0.01, 0.1, 0.3, 0.5, 1.0). Additionally, each hour, a fixed fraction of bacteria was removed to account for losses by protists and viruses, tuned so that for steady populations full turnover occurred in 1 d. In this population dynamics analysis, a fixed swimming cost corresponding to 40 µm/s and 2% swimming efficiency was deducted from the motile population. Additionally, the motile and nonmotile cells in this analysis had 0.5-µm and 0.2-µm equivalent radii, respectively. This size difference accounts for the finding that biomass can be comparable (Fig. 5A) when numerical abundance is very different.

Materials and Methods

Experimental Conditions for Diatom Lysis and Chemotactic Bacterial Response.

We developed an approach to stimulate chemotactic cluster formation by inducing the lysis of individual chains or cells of the diatom C. affinis. In a mixture of enriched bacteria and diatom culture, a diatom was centered within the microscope’s field of view and the iris constricted to shine fluorescent light only on the diatom and its immediate vicinity, over a circular area of ∼10-µm radius. To initiate diatom lysis, blue fluorescence light (350 nm excitation, 7 kW/m²) was applied for 5–10 min while maintaining continual broad-spectrum light-emitting diode (LED) white-light illumination (∼200 µmol m⁻² s⁻¹). This procedure stimulated diatom plasmolysis, which was followed by chemotactic accumulation of motile bacteria 3–4 min after the fluorescence light was turned off. Image capture via video microscopy occurred during light exposure and through the chemotactic clustering response for up to 60 min.

Other Methods.

Seawater sampling, diatom maintenance, microscopy, image analysis, and mathematical modeling are described in Supporting Information.