Significance
Understanding sea-level change is of paramount importance because it reflects climate-related factors, such as the ocean heat budget, mass changes in the cryosphere, and natural ocean/atmosphere variations. Furthermore, sea-level rise directly affects coastal areas, which has ramifications for its population and economy. From a novel combination of Gravity Recovery And Climate Experiment and radar altimetry data we find over the last 12 y: (i) a larger global steric sea-level rise as previously reported, (ii) a mass contribution to global sea level consistent with mass loss estimates from the world’s ice sheets, glaciers, and hydrological sources, and (iii) regionally resolved sea-level budget components which differ significantly from that of the global sea-level budget.
Keywords: sea level, budget, steric, GRACE, altimetry
Abstract
Dividing the sea-level budget into contributions from ice sheets and glaciers, the water cycle, steric expansion, and crustal movement is challenging, especially on regional scales. Here, Gravity Recovery And Climate Experiment (GRACE) gravity observations and sea-level anomalies from altimetry are used in a joint inversion, ensuring a consistent decomposition of the global and regional sea-level rise budget. Over the years 2002–2014, we find a global mean steric trend of 1.38 0.16 mm/y, compared with a total trend of 2.74 0.58 mm/y. This is significantly larger than steric trends derived from in situ temperature/salinity profiles and models which range from 0.66 0.2 to 0.94 0.1 mm/y. Mass contributions from ice sheets and glaciers (1.37 0.09 mm/y, accelerating with 0.03 0.02 mm/y2) are offset by a negative hydrological component (−0.29 0.26 mm/y). The combined mass rate (1.08 0.3 mm/y) is smaller than previous GRACE estimates (up to 2 mm/y), but it is consistent with the sum of individual contributions (ice sheets, glaciers, and hydrology) found in literature. The altimetric sea-level budget is closed by coestimating a remaining component of 0.22 ± 0.26 mm/y. Well above average sea-level rise is found regionally near the Philippines (14.7 4.39 mm/y) and Indonesia (8.3 4.7 mm/y) which is dominated by steric components (11.2 3.58 mm/y and 6.4 3.18 mm/y, respectively). In contrast, in the central and Eastern part of the Pacific, negative steric trends (down to −2.8 1.53 mm/y) are detected. Significant regional components are found, up to 5.3 2.6 mm/y in the northwest Atlantic, which are likely due to ocean bottom pressure variations.
Global sea-level rise has been identified as one of the major threats associated with global climate change (1, 2). However, from the perspective of assessment- and decision-making, regional estimates of sea-level rise are even more important to formulate meaningful adaptation plans on a national or international level. Besides the magnitude of the total sea-level rise itself, identifying dominant drivers, and their corresponding uncertainties, may also prove beneficial for projection studies.
Historical records from tide gauges indicate a sea-level rate of about 1.7 mm/y over the period 1900–2009, where it must be noted that tide gauges indicate an acceleration (0.009–0.017 mm/y2) over the last century (3–5). Besides the steric expansion of sea water due to temperature changes, the ongoing melting and ablation of ice sheets in Greenland and Antarctica and other land glaciers cause the sea level to rise. Hydrological mass variability on land and reservoir construction have been found to cause a negative trend (6–9). Furthermore, meltwater, precipitation, or evaporation result in regional salinity changes, leaving steric signatures in sea level once the barotropic component has been compensated (10). For an observer at the coast, crustal movement, caused by glacial isostatic adjustment (GIA), tectonics, or local subsidence may also significantly affect the relative sea level. Finally, sea level may be altered regionally by long-term changes in wind stress, atmospheric pressure, and changes in heat and freshwater fluxes at the ocean surface and boundaries (e.g., ref. 11).
It is well known that sea level does not rise uniformly across the ocean basins, but exhibits regional variations (12). Global mean sea level provides an excellent metric to monitor global change, and ample studies exist which attempt to close the global mean sea-level budget in terms of the different contributions (12–15). Unfortunately, the components of the sea-level budget still exhibit significant differences across studies depending on the chosen corrections, datasets, methods, and time periods (16, 17).
Understanding sea-level rise requires a well-established monitoring network, preferably covering long timespans. Besides important historic measurements from reprocessed tide gauge measurements (18), spaceborn techniques have become increasingly important over the last decades. Satellite radar altimetry enabled monitoring of geometric sea level with unprecedented coverage, and more recently, satellite gravimetry from the Gravity Recovery And Climate Experiment (GRACE) provided invaluable information on mass contributions to sea level. Because altimetry and gravimetry measure different contributions of sea-level change, i.e., total versus mass-driven, combining them allows one to resolve for volumetric (steric) sea-level changes.
Independently, steric sea level can also be resolved by integrating volumetric anomalies over a water column, from measured temperature and salinity changes. Hydrographic profiles of temperature and salinity can be derived from expendable bathythermography (XBT), conductivity/depth/temperature and, in more recent times, from Argo floats (e.g., ref. 19).
Here, we decompose global and regional sea level into different components (steric, glaciers and ice sheets, hydrology, GIA) by combining sea-level anomalies from Jason-1/2 and gravimetric observations from GRACE, over the period 2002 (April)–2014 (June). An additional nonrandom, deterministic sea-level component is estimated, which is used to separate remaining signals in large-scale sea level, e.g., residual mass variations due to ocean circulation, from observational noise. The sea-level budget is considered globally and for a set of dedicated coastal zones (see the colored polygons in Fig. 2). Our simultaneous least-squares inversion allows for a consistent closure of the sea-level budget, taking into account technique errors and coverage (Materials and Methods and SI Appendix). Another advantage is that no additional filtering of the GRACE data is required in our method. Such filtering is commonly applied to reduce the typical north–south errors of the GRACE products, but it attenuates the spatial content of the signal, with a decrease of spatial resolution as a result.
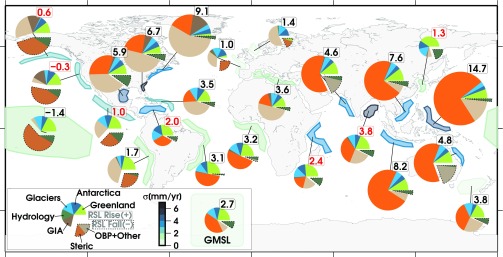
Fig. 2.
Relative sea-level rise in mm/y in selected coastal zones. The associated polygons are colored according to the estimated total error (Materials and Methods). Wedge areas reflect the absolute magnitude of the different contributions, and negative wedges are shaded. Trends with red numbers indicate nonsignificant (1-σ) total trends, although the individual components may have significant contributions (SI Appendix, Table S4).
Global Mean Sea-Level Budget
The different contributions to global mean relative sea-level rise are computed by aggregating the relevant inversion results and are plotted in Fig. 1. In addition, trends, significant accelerations, annual amplitudes and phases are tabulated in Table 1.
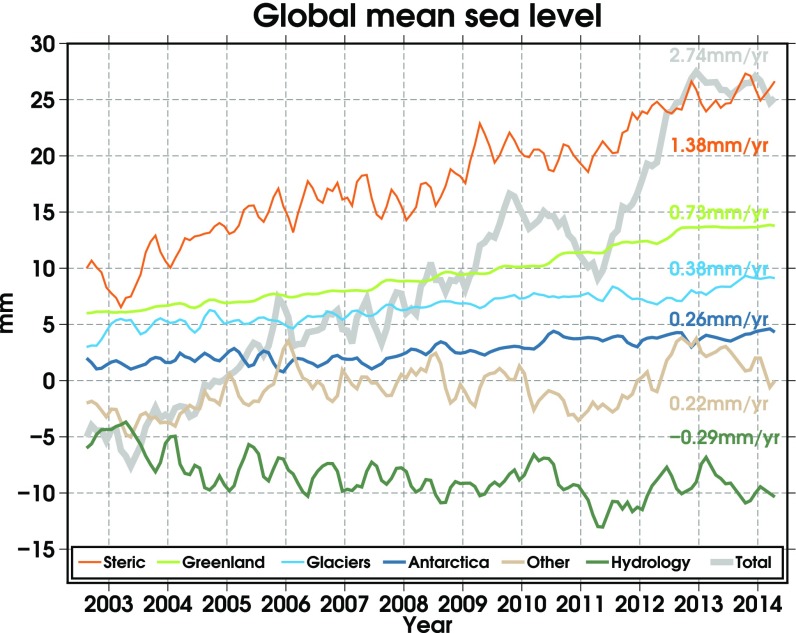
Fig. 1.
Global mean relative sea level, divided into different contributions. Annual and semiannual harmonics have been fitted and removed and the resulting curves are smoothed with a 3-month running mean (trends are derived from the unsmoothed data). The curves have been offset for clarity.
Table 1.
Estimated annual amplitudes, phases (indicating day of maximum), trends, and accelerations of the different contributions to global mean sea level in the period 2002–2014
| Contribution | Annual | Trend | Acceleration | rms | |
| A, mm | , doy | mm/y | mm/y2 | post., mm | |
| Gr + An + Gl | 1.3 ( 0.36) | 281 ( 17) | 1.37 ( 0.09) | 0.03 ( 0.019) | 0.9 |
| Antarctica | 0.3 ( 0.18) | 83 ( 32) | 0.26 ( 0.04) | 0.01 ( 0.009) | 0.6 |
| Greenland | 0.5 ( 0.07) | 285 ( 8) | 0.73 ( 0.02) | 0.02 ( 0.004) | 0.3 |
| Glaciers | 1.2 ( 0.25) | 276 ( 14) | 0.38 ( 0.07) | — | 0.6 |
| Hydrology | 11.0 ( 0.98) | 270 ( 6) | −0.29 ( 0.26) | — | 1.9 |
| Steric | 4.6 ( 0.71) | 51 ( 9) | 1.38 ( 0.16) | — | 1.7 |
| Other | 3.3 ( 1.03) | 82 ( 20) | 0.22 ( 0.26) | — | 2.0 |
| Total | 6.1 ( 2.20) | 303 ( 22) | 2.74 ( 0.58) | — | 2.7 |
| Steric (Ishii, 1,500m) | 3.6 ( 0.76) | 87 ( 12) | 0.66 ( 0.17) | — | 1.2 |
| Thermo | 3.4 ( 1.08) | 94 ( 18) | 0.59 ( 0.25) | — | 1.1 |
| Halo | 0.4 ( 0.30) | 18 ( 42) | 0.07 ( 0.07) | — | 1.1 |
| Steric (ORAS4) | 3.6 ( 0.38) | 80 ( 6) | 0.94 ( 0.08) | — | 1.2 |
| Thermo | 3.2 ( 0.44) | 78 ( 8) | 1.43 ( 0.09) | — | 1.0 |
| Halo | 3.7 ( 0.28) | 79 ( 4) | −0.53 ( 0.05) | — | 0.9 |
The estimate from Ishii and Kimoto (20) only contains data up to Dec. 2012. Accelerations are only estimated when significant (1-σ). The last column denotes the rms of the residuals. doy, day of year.
Striking is that the estimated steric sea-level trend, 1.38 0.16 mm/y (April 2002–June 2014 or 1.36 mm/y over April 2002–December 2012), is significantly larger compared with an independent estimate obtained from the upper 1,500 m of the ocean, which stands at 0.66 0.17 mm/y (using gridded in situ data from ref. 20 over the period 2002–2012). In another study, an even smaller steric trend derived from Argo data indicates 0.5 0.1 mm/y (2005–2012) of thermosteric sea level in the first 1,500 m, where it must be noted that Argo potentially underestimates steric sea-level trends due to sampling problems (19). Similarly, the thermosteric component of sea level in the first 2,000 m has been estimated at 0.54 mm/y (21) (1955–2010).
In the abyssal ocean (below 4,000 m), a significant thermosteric warming trend of 0.053 0.017 mm/y has been found over the 1990s and 2000s, with an additional 0.093 0.081 mm/y, when the Southern Ocean between 1,000 and 4,000 m is considered too (22). Somewhat later, a steric trend of 0.095 mm/y for the layers below 3,000 m has been found from observations (23). However, in light of our results, the trend in the first 1,500 m and in the abyssal ocean cannot explain the 1.39 mm/y we found from the GRACE and altimetry data.
The operational ocean reanalysis system (ORAS4), assimilating various hydrographic datasets and altimetry, can provide estimates of the steric trend in the entire ocean column (24). Over the time period considered here, global mean thermosteric and halosteric trends of 1.43 mm/y and −0.53 mm/y (combined 0.94 mm/y) are derived, respectively, from the ORAS4 data (see also Table 1). It is interesting to note that the thermosteric trend from ORAS4 is much more consistent with our estimate, especially when considering that the strong negative halosteric trend is considered spurious and linked to the assimilation of recent Argo data (24).
GIA has no direct contribution in terms of mean relative sea level, although it indirectly does significantly influence the estimate for the Antarctic mass loss contribution. It is common to subtract a GIA correction of −0.3 mm/y from the altimetry record (e.g., ref. 25) to convert from global mean geocentric sea level to relative sea level. From the estimated GIA signal from this study, we find a smaller correction (−0.1 mm/y). To put this number into perspective, compared with an ensemble of GIA runs from (26), our estimate lies at the upper bound of the spread of the GIA models (−0.1 to −0.5 mm/y). This smaller correction can be partly explained by a weaker GIA signal found in the Antarctic (SI Appendix, Tables S1 and S2), implying a decreased mantle flow from the ocean basin to the Antarctic continent, which in its turn causes a smaller volumetric change of the mean ocean basin. A relatively weak present-day GIA signal in the Antarctic is also confirmed by 3D Earth models (27).
Fig. 1 and Table 1 also show that some components exhibit considerable interannual variations. The residual variations, 3.3 mm in terms of root-mean-square (rms), are mostly determined by the hydrological, steric, and “other” component (Materials and Methods). The contribution of Greenland to sea level contains the smallest residual variations (0.3-mm rms), indicating the robustness of its mass loss signal. Besides the trend, 0.73 mm/y, a significant acceleration of about 0.02 0.004 mm/y2, can also be found over the considered period.
Table 1 indicates that the annual steric sea level (peaking end of February) is partly compensated by the hydrological component (reaches its minimum in the end of March), similar to what has been observed by ref. 28.
Regional Sea-Level Budget
The regional contributions differ significantly from those of the global mean sea level. For a selection of coastal zones (the inversion results have been evaluated in areas as indicated by colored polygons), regional sea-level trends and their contributions are graphically depicted in Fig. 2 (trends are tabulated in SI Appendix, Table S4). The coastal zones were selected to cover a wide set of different characteristics [e.g., vulnerability (2), occurrence of upwelling regions, coastal shelves]. To avoid contamination by land effects, and errors from interpolation of steric fields, the regions have been hand-drawn while avoiding regions with too much variations in the altimetric sea level. It should be noted that effects from local subsidence and tectonics are not considered in this study, but these may be added for local studies. In the western Pacific and Indian Ocean, sea-level rise is dominated by the steric contribution (up to 75%), most notably the 14.7 4.4-mm/y rise in the vicinity of the Philippines, and trends of 7.6 3.17 mm/y (South China Sea) and 8.3 4.7 mm/y (Indonesia). At the same time, the contribution from glaciers and ice sheets (Gr + An + Gl) is also relatively strong as these coastlines are positioned far away from the melting sources. On the other hand, negative steric contributions (down to −2.8 1.5 mm/y) are found in the central and eastern part of the Pacific.
For most coastlines, in particular around the Atlantic Ocean, we find significant contributions which cannot be explained by either steric changes or land–ocean mass exchange (indicated by OBP + other in the figures and tables, where “OBP” is ocean bottom pressure). For example, near the east coast of the United States and in the North Sea, more than 50% of the trend is attributed to the “OBP + other” component. On regional scales, this contribution is expected to be strongly influenced by internal mass variations of the ocean (e.g., bottom pressure change caused by wind stress forcing) (29, 30). In the deeper parts of the ocean it is also possible that these reflect remaining steric signal which cannot be absorbed by the chosen parameterization of the steric parameters (SI Appendix).
For most coastlines, the hydrological contribution is found to be zero or negative (the lowest component amounts to −0.7 0.27 mm/y in the Gulf of Mexico).
Compared with other contributions, GIA-related relative sea level remains fairly small, except for regions closer to the former ice sheets. The largest GIA trends (1.3 0.25 mm/y) take place in the coastal zone at the northeast United States, which is located on the subsiding peripheral bulge of the former Laurentide ice sheet.
Accelerations and Interannual Changes at Regional Scales
Regional sea-level variations are generally more variable compared with the global mean. The trends provided in this paper are based on a short timespan (2002–2014) because of the limited availability of GRACE data. Uncertainties in the trends are based on empirical autoregressive models of order 1 and therefore reflect mainly the correlated interannual signals in the residuals. To visualize the interannual variability of the different contributions, we have plotted the time-varying components of sea level in Fig. 3 for the case of the Philippines. Plots of the other zones can be found in the SI Appendix.
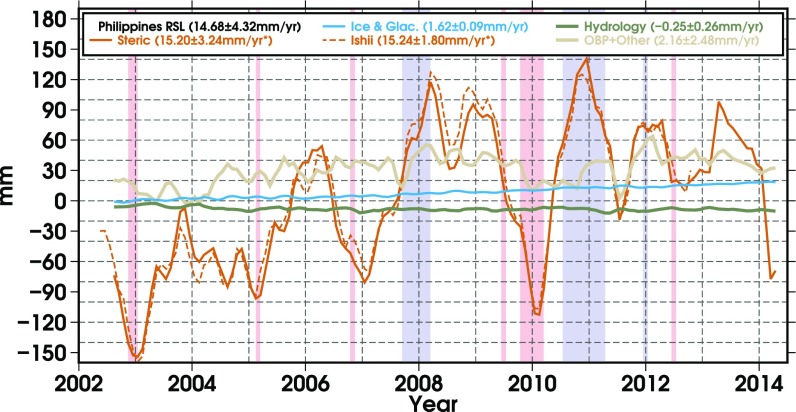
Fig. 3.
Time-variable sea-level contributions to the east of the Philippines. Warm (El Niño, red) and cold (La Niña, blue) phases are highlighted whenever the MEI gets larger than 1 or smaller than −1, respectively. The asterisk indicates that the trend is computed over the period where there are Ishii data available (2002–2012). Plots of other regions can be found in the SI Appendix.
Fig. 3 shows that the steric component and the component related to OBP and other signals contain by far the strongest interannual signals. In stark contrast stand the much smoother contributions from the ice sheets, glaciers, and hydrology. Consequently, the accuracy of the sea-level trend, and the ability to extrapolate such trends in the future, is severely limited by variations of the steric contribution. It is well known that total (global and regional) sea level is sensitive to large interannual variations, such as the El Niño Southern Oscillation (ENSO) (31, 32). This can also be seen in Fig. 3. A regression with the Multivariate ENSO Index (MEI) removes 30% of the SD of the steric series (maximum correlation occurred at zero lag), but a significant interannual component remains nonetheless and cannot be easily explained by the ENSO.
For other coastal zones, it can generally be said that interannual variations in the steric component are the main cause of uncertainties in the trends. One exception is the North Sea, where the shallow water column cannot accommodate large steric variations. Consequently, components related to wind stress and other effects introduce the largest interannual variations that play a larger role there.
Discussion
The simultaneous combination of sea-level anomalies from satellite altimetry and data from satellite gravimetry allows a partitioning of the sea-level rise into the different contributions. The estimated global mean sea-level rise over the past 12 y (2002–2014) amounts to 2.74 0.58 mm/y, which can be attributed to glaciers and ice sheets (1.37 0.09 mm/y), terrestrial hydrology (−0.29 0.26 mm/y), steric sea-level rise (1.38 0.16 mm/y), and a remaining nonrandom component of 0.22 0.26 mm/y, which is needed to close the global mean sea-level budget. The enigma is that the steric component is more than two times as large compared with the estimate derived from hydrographic data from the first 1,500 m in the ocean (0.66 0.17 mm/y), and is also larger than other similar estimates of steric sea-level rise (19, 21). It has to be mentioned that signals in the deeper ocean (1,500-m bottom) and in regions not frequently visited by Argo floats are not well resolved by the hydrographic data, and may potentially cause a low bias (19), although it is commonly expected that warming at intermediate depths is relatively small (33). Furthermore, although the halosteric signal should not give rise to large steric signals, salinity errors may potentially influence the steric trends as well.
Another possibility is that the inversion scheme used here significantly underestimates the combined mass losses from the major ice sheets, glaciers, and hydrology. This leads to the larger steric trend, because the closure of the sea-level budget is respected in the inversion. Using an ocean basin averaging technique, another study found a significantly larger mass trend from GRACE data (2.0 0.1 mm/y) over a shorter period (2005–2013) (15). However, we would like to emphasize that the smaller mass trend we found here (1.08 0.3 mm/y) is consistent with published estimates of mass loss in the ice sheets, glaciers, and hydrology. For Greenland we find −270 7 Gt/y, which is comparable to −230 33 Gt/y (34), and more recently −278 19 Gt/y (17). For Antarctica, our estimate (−96 15 Gt/y) is consistent with the most recent estimates which use smaller GIA corrections [−92 26 Gt/y (17) and −114 23 Gt/y (35)]. Furthermore, land glaciers (in this study −141 26 Gt/y) agree within the error bars with the −148 30 Gt/y found in ref. 36. Finally, the remaining hydrological contribution to sea level is slightly negative (here −0.29 0.26 mm/y) and agrees with the −0.22 0.05 mm/y from ref. 9, and −0.1 0.3 mm/y (8) (see SI Appendix, Table S3 for additional comparisons).
The interannual variability of the steric and hydrological component is responsible for about 50% of the interannual variations of the total sea level; this is in line with ref. 37, which used hydrologic and steric corrections to reduce the interannual variability of the global mean sea level.
On regional scales, the relative contributions to the sea-level budget depend strongly on the coastline location (see also SI Appendix, Table S4). The most extreme case can be found at the Philippines, where a trend of 14.7 4.4 mm/y was found. The steric component is largely responsible for this rate (11.2 3.6 mm/y).
On the other hand, negative rates have been found in the Central Pacific and at the west coast of the United States.
At regional scales, we find significant components which cannot be simply attributed to steric changes or land–ocean mass exchange. These trends are most likely related to trends in the OBP, but may also contain residual steric signals. This holds in particular for coastlines bordering the North Atlantic. It is known that in shallow regions such as the North Sea, wind-driven Ekman transport plays a large role at decadal scales (11). Although its magnitude depends on the location, the trends from glaciers and ice sheets exhibit a relatively smooth and similar behavior over time, and an acceleration over the last decade can be observed at the majority of the coastlines.
Although the time period of this study is still relatively short, we expect that the observational results from this study are important for model validation and identifying regional sea-level drivers. Because our inversion results are not dependent on data from Argo floats and other hydrographic data, they shed new light on the discussion of “missing heat” in the Earth system (38–40) and the consistent closure of the sea-level budget.
Materials and Methods
Inversion Methodology.
In our forward modeling–least-squares approach (41, 42), the different contributions are parameterized by predefined spatial patterns, each scaled with an unknown time-varying magnitude. The spatial information for each pattern, coined “fingerprints,” originates from a priori data, whereas the time evolution is estimated from altimetry and GRACE data. In this study, 200 empirical orthogonal functions (EOF) are used as steric sea-level fingerprints. These are computed from integrating, over the full ocean column, volume changes from temperature and salinity variations from the Finite Element Sea Ice–Ocean Model (FESOM) (10, 43), and explain more than 99% of the modeled variance of steric sea level. Because FESOM uses variable-size finite elements, it is possible to obtain steric values close to the coast, and in shallow areas. These steric heights are then interpolated on a 0.5 × 0.5-degree grid, which is used as input for the EOF analysis (area-weighted).
Continental hydrological mass changes, and mass variations of the glaciers and ice sheets (Gr + An + Gl) are discretized by 119 global patterns, which include a passive ocean response, mass-consistent with the applied land load and accounting for the effect of rotational feedback (see SI Appendix for the discretization used). This involves solving the so-called “Sea-Level Equation” (44), which, in our case, is performed in the spherical harmonic domain (41, 45). In addition, contributions from five separate GIA patterns, each representing the effect of a former glacial mass (Laurentide, Antarctica, Greenland, Fennoscandia, and auxiliary glacial masses), are used as fingerprints. To account for possible frame offsets of the radar altimeters, satellite-specific unconstrained mean reference system offsets are introduced and solved for simultaneously.
After the initial inversion step, significant large-scale geophysical residuals remain in the altimetry residuals. We therefore decided to fit an additional set of fingerprints to the data, to separate unexplained but significant nonrandom sea-level signals from pure noise. These fingerprints are constructed by extracting the 100 leading EOF modes of the gridded and Gaussian-smoothed (200-km half width) altimetry residuals from the first inversion step. In the final inversion step, these parameters are then estimated together with the other parameters. Throughout the paper, this component is referred to as “other,” as it contains a mix of signals (deep and shallow steric changes, which are not accounted for by the steric fingerprints, and internal ocean mass variations as deviations from the background model).
Sea-Level Anomalies.
To link the sought-for parameters to the binned along-track sea-level anomalies, , we consider the following observation equation:
| [1] |
The vector contains the monthly contributions of the ice sheets, glaciers, hydrology, and steric heights. In contrast to those, the GIA parameters, , and the altimeter-specific offsets, , are estimated with data over the entire timespan as they are modeled as trends and a bias, respectively (42). The computed fingerprints, expressed in terms of geocentric sea level, are contained in matrix B and C. The fingerprints in B are expressed in terms of spherical harmonic coefficients, which are mapped to the altimeter tracks with matrix Y. The steric EOF modes from FESOM are provided on 0.5 × 0.5-degree grids, which are bilinearly interpolated to the altimeter tracks using matrix K. Matrix P projects the satellite offset onto the radial direction of the measurement.
Along-track radar altimetry data are taken from the Radar Altimeter Database System [RADS (46)], and averaged into along-track bins of about 1-s length (roughly 6 km). All standard range corrections are applied to the data before averaging, and large outliers are removed.
Satellite Gravimetry.
Similarly, the observation equation for the GRACE Stokes coefficients, , looks like
| [2] |
Obviously, no steric changes can be observed by GRACE and Eq. 2 is described in the spherical harmonic domain. The columns of matrix D contain the fingerprints, but are here expressed in terms of Stokes coefficients. In this study, we have used monthly GRACE RL05 data processed by the GFZ German Research Centre for Geosciences (47). The data are provided in the form of full (unsolved) normal equation systems, expressed in terms of residual Stokes coefficients, from which we use the information up to spherical harmonic degree and order 150. These systems are transformed with matrix D while avoiding an intermediate (ill-posed) solving step (42).
Background Model.
Besides the standard corrections, both the GRACE data and altimetry have been reduced with modeled variations of monthly averaged OBP variations [ECMWF + OMCT (48)]. Here, we use the ocean–atmosphere product (GAC) from the GRACE standard processing, except that we apply an additional monthly correction over the ocean, which ensures that the background model contains no mean ocean signal for each time step. OBP variations from the background model, , are thus modified over the ocean domain (ocean function O) to obtain :
| [3] |
Because the GRACE normal equation systems are already reduced with the GRACE dealiasing product, we only need to update the background model with the last term above.
Regional Trend Correction.
It was found that the background model introduces spurious regional sea-level trends, which consequently contaminate trends in the regional inversion results. To mitigate this, we restored the trends of to the “other” component of the inversion in a postprocessing step. The resulting component, denoted as OBP + other, therefore additionally reflects the complete OBP trend signal. This correction is not necessary for the global mean estimates, as the ocean mean of , and consequently its trend is zero per definition.
External Steric Sea Level.
For the computation of the external estimate of the steric height evolution, we use temperature and salinity data from ref. 20 (V6.13) in the first 1500m of the ocean, in combination with the thermodynamic equation of seawater (TEOS) (49).
Constraints.
During the solving step, two types of (weak) constraints are needed to avoid instabilities in the solution (see also the SI Appendix). The first is a Tikonov constraint which pushes the GIA secular scale factors toward the a priori GIA model. The other constraint is applied to selected combinations of small and neighboring ice sheet drainage basins, and constrains the equivalent water height in them toward a common value.
Error Estimates.
Although we propagate instrumental errors from GRACE and altimetry (range errors) to the sea-level heights, these are unrealistically small because of the dramatic reduction of the solution space (only 400 parameters are estimated each month compared with >10,000 gravity coefficients). For the error estimates of the trends and seasonal components, we therefore use empirical autoregressive models of order 1, which are computed from the postfit residuals of each time series. The errors therefore also reflect correlated errors in time, which arise due to interannual variability.
Errors in the secular GIA component are even harder to quantify, especially because we apply constraints. We decided to apply a worst-case error, where we took the magnitude of the estimated GIA corrections itself, and applied it as an error. Although we believe that the data do have some resolving power and this error is too large, it does reflect the spread in current GIA models.
Global Mean Sea Level and Coastal Zones.
To estimate a time-varying contribution for the mean sea level, , we compute from the estimated and relevant components, :
| [4] |
where the time-invariant factors correspond to the ocean average of the associated fingerprint, which can be found from matrices B and C (using an area-weighted average).
For the regional coastline estimates, we evaluate the inversion results in terms of relative sea level as area averages over the hand-drawn polygons shown in Fig. 2. Mass components and GIA are evaluated as spectral basin averages (the results have been validated with spatial methods), whereas the gridded components were obtained by area weighting the cells in the region.
Supplementary Material
Acknowledgments
We thank three reviewers whose comments improved the manuscript considerably. Magdalena Balmaseda is thanked for providing global mean steric trends from the ORAS4 model. Valentina Barletta is thanked for providing modeled glacial isostatic adjustment (GIA) trends from her ensemble runs. Furthermore, we are grateful to Volker Klemann for providing the GIA modeling results, and thank the German Space Operations Center of the German Aerospace Center for providing continuously and nearly 100% of the raw telemetry data of the twin GRACE satellites. We also acknowledge Radar Altimeter Database System (RADS) for providing up-to-date and flexible along-track altimetry products. All figures are made using the Generic Mapping Tools. This research has been funded by the German Research Foundation under Grants KU1207/9-2 and SCHR779/6-2 and by the German Federal Ministry of Education and Research Support Code 03F0654A.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The data reported in this paper have been deposited in the PANGAEA database, www.pangaea.de (doi: 10.1594/PANGAEA.855539).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1519132113/-/DCSupplemental.
References
- 1.Stocker TF, et al. Intergovernmental Panel on Climate Change, Working Group I Contribution to the IPCC Fifth Assessment Report (AR5) Cambridge Univ Press; New York: 2013. Climate change 2013: The physical science basis. [Google Scholar]
- 2.Nicholls RJ, Cazenave A. Sea-level rise and its impact on coastal zones. Science. 2010;328(5985):1517–1520. doi: 10.1126/science.1185782. [DOI] [PubMed] [Google Scholar]
- 3.Church JA, White NJ. Sea-level rise from the late 19th to the early 21st century. Surv Geophys. 2011;32(4):585–602. [Google Scholar]
- 4.Hay CC, Morrow E, Kopp RE, Mitrovica JX. Probabilistic reanalysis of twentieth-century sea-level rise. Nature. 2015;517(7535):481–484. doi: 10.1038/nature14093. [DOI] [PubMed] [Google Scholar]
- 5.Jevrejeva S, Moore J, Grinsted A, Woodworth P. Recent global sea level acceleration started over 200 years ago? Geophys Res Lett. 2008;35(8):L08715. [Google Scholar]
- 6.Jensen L, Rietbroek R, Kusche J. Land water contribution to sea level from Grace and Jason-1 measurements. J Geophys Res: Oceans. 2013;118(1):212–226. [Google Scholar]
- 7.Chao BF, Wu YH, Li YS. Impact of artificial reservoir water impoundment on global sea level. Science. 2008;320(5873):212–214. doi: 10.1126/science.1154580. [DOI] [PubMed] [Google Scholar]
- 8.Riva REM, Bamber JL, Lavallée DA, Wouters B. Sea-level fingerprint of continental water and ice mass change from grace. Geophys Res Lett. 2010;37(19):L19605. [Google Scholar]
- 9.Llovel W, Becker M, Cazenave A, Crétaux J-F, Ramillien G. Global land water storage change from Grace over 2002–2009; inference on sea level. C R Geosci. 2010;342(3):179–188. [Google Scholar]
- 10.Brunnabend S-E, Schröter J, Timmermann R, Rietbroek R, Kusche J. Modeled steric and mass-driven sea level change caused by Greenland ice sheet melting. J Geodyn. 2012;59-60:219–225. [Google Scholar]
- 11.Dangendorf S, Calafat FM, Arns A, Wahl T, Haigh ID, Jensen J. 2014. Mean sea level variability in the north sea: Processes and implications. J Geophys Res: Oceans 119(10):JC009901.
- 12.Cazenave A, Llovel W. Contemporary sea level rise. Annu Rev Mar Sci. 2010;2:145–173. doi: 10.1146/annurev-marine-120308-081105. [DOI] [PubMed] [Google Scholar]
- 13.Lombard A, et al. Estimation of steric sea level variations from combined Grace and Jason-1 data. Earth Planet Sci Lett. 2007;254(1):194–202. [Google Scholar]
- 14.Gregory J, et al. Twentieth-century global-mean sea level rise: Is the whole greater than the sum of the parts? J Clim. 2013;26(13):4476–4499. [Google Scholar]
- 15.Llovel W, Willis J, Landerer F, Fukumori I. Deep-ocean contribution to sea level and energy budget not detectable over the past decade. Nat Clim Change. 2014;4(11):1031–1035. [Google Scholar]
- 16.Chen J, Wilson C, Tapley B. Contribution of ice sheet and mountain glacier melt to recent sea level rise. Nat Geosci. 2013;6(7):549–552. [Google Scholar]
- 17.Schrama E, Wouters B, Rietbroek R. 2014. A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from Grace data. J Geophys Res: Solid Earth 119(7):6048–6066.
- 18.Holgate SJ, et al. New data systems and products at the permanent service for mean sea level. J Coast Res. 2012;29(3):493–504. [Google Scholar]
- 19.Von Schuckmann K, et al. Monitoring ocean heat content from the current generation of global ocean observing systems. Ocean Sci Discuss. 2013;10:923–949. [Google Scholar]
- 20.Ishii M, Kimoto M. Reevaluation of historical ocean heat content variations with time-varying XBT and MBT depth bias corrections. J Oceanogr. 2009;65(3):287–299. [Google Scholar]
- 21.Levitus S, et al. World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys Res Lett. 2012;39(10):L10603. [Google Scholar]
- 22.Purkey SG, Johnson GC. Warming of global abyssal and deep southern ocean waters between the 1990s and 2000s: Contributions to global heat and sea level rise budgets. J Clim. 2010;23(23):6336–6351. [Google Scholar]
- 23.Kouketsu S, et al. 2011. Deep ocean heat content changes estimated from observation and reanalysis product and their influence on sea level change. J Geophys Res: Oceans (1978–2012) 116(C3):C03029.
- 24.Balmaseda MA, Trenberth KE, Källén E. Distinctive climate signals in reanalysis of global ocean heat content. Geophys Res Lett. 2013;40(9):1754–1759. [Google Scholar]
- 25.Nerem R, Chambers D, Choe C, Mitchum G. Estimating mean sea level change from the Topex and Jason altimeter missions. Mar Geod. 2010;33(S1):435–446. [Google Scholar]
- 26.Barletta VR, Sorensen LS, Forsberg R. Scatter of mass changes estimates at basin scale for Greenland and Antarctica. The Cryosphere. 2013;7(5):1411–1432. [Google Scholar]
- 27.van der Wal W, Whitehouse PL, Schrama EJ. Effect of GIA models with 3D composite mantle viscosity on GRACE mass balance estimates for Antarctica. Earth Planet Sci Lett. 2015;414:134–143. [Google Scholar]
- 28.Chen J, Wilson C, Tapley B, Chambers D, Pekker T. Hydrological impacts on seasonal sea level change. Global Planet Change. 2001;32(1):25–32. [Google Scholar]
- 29.Bonin JA, Chambers DP. Evaluation of high-frequency oceanographic signal in Grace data: Implications for de-aliasing. Geophys Res Lett. 2011;38(17):L17608. [Google Scholar]
- 30.Johnson GC, Chambers DP. Ocean bottom pressure seasonal cycles and decadal trends from GRACE release-05: Ocean circulation implications. J Geophys Res: Oceans. 2013;118(19):4228–4240. [Google Scholar]
- 31.Böning C, Willis JK, Landerer FW, Nerem RS, Fasullo J. The 2011 La Niña: So strong, the oceans fell. Geophys Res Lett. 2012;39:L19602. [Google Scholar]
- 32.Cazenave A, et al. Estimating ENSO influence on the global mean sea level, 1993–2010. Mar Geod. 2012;35:82–97. [Google Scholar]
- 33.Dieng HB, Palanisamy H, Cazenave A, Meyssignac B, von Schuckmann K. The sea level budget since 2003: Inference on the deep ocean heat content. Surv Geophys. 2015;36(2):209–229. [Google Scholar]
- 34.Velicogna I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by Grace. Geophys Res Lett. 2009;36(19):L19503. [Google Scholar]
- 35.Sasgen I, et al. Antarctic ice-mass balance 2003 to 2012: Regional reanalysis of GRACE satellite gravimetry measurements with improved estimate of glacial-isostatic adjustment based on GPS uplift rates. The Cryosphere. 2013;7:1499–1512. [Google Scholar]
- 36.Jacob T, Wahr J, Pfeffer WT, Swenson S. Recent contributions of glaciers and ice caps to sea level rise. Nature. 2012;482(7386):514–518. doi: 10.1038/nature10847. [DOI] [PubMed] [Google Scholar]
- 37.Cazenave A, et al. The rate of sea-level rise. Nat Clim Change. 2014;4:358–361. [Google Scholar]
- 38.Trenberth KE, Fasullo JT. Climate change. Tracking Earth’s energy. Science. 2010;328(5976):316–317. doi: 10.1126/science.1187272. [DOI] [PubMed] [Google Scholar]
- 39.Lyman JM, et al. Robust warming of the global upper ocean. Nature. 2010;465(7296):334–337. doi: 10.1038/nature09043. [DOI] [PubMed] [Google Scholar]
- 40.Loeb N, et al. Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty. Nat Geosci. 2012;5(2):110–113. [Google Scholar]
- 41.Rietbroek R, Brunnabend SE, Kusche J, Schröter J. Resolving sea level contributions by identifying fingerprints in time-variable gravity and altimetry. J Geodyn. 2012;59:72–81. [Google Scholar]
- 42.Rietbroek R. 2014. Retrieval of sea level and surface loading variations from geodetic observations and model simulations: An integrated approach. PhD thesis (University of Bonn, Bonn, Germany)
- 43.Timmermann R, et al. Ocean circulation and sea ice distribution in a finite element global sea ice-ocean model. Ocean Model. 2009;27(3):114–129. [Google Scholar]
- 44.Woodward R. On the form and position of mean sea level. Geol Surv Bull. 1888;48:87–170. [Google Scholar]
- 45.Dahlen FA. The passive influence of the oceans upon the rotation of the earth. Geophys J R Astron Soc. 1976;46(2):363–406. [Google Scholar]
- 46.Scharroo R, et al. 2013. RADS: Consistent multi-mission products. Proceedings of the Symposium on 20 Years of Progress in Radar Altimetry, Venice, 20–28 September 2012, ESA SP-710 (ESA, Noordwijk, The Netherlands). Vol 20.
- 47.Dahle C, et al. 2013. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 12/02 - Data (Deutsches GeoForschungsZentrum GFZ, Potsdam, Germany), Scientific Technical Report STR12/02 − Data, Revised Ed, January 2013.
- 48.Dobslaw H, et al. Simulating high-frequency atmosphere-ocean mass variability for dealiasing of satellite gravity observations: AOD1B RL05. J Geophys Res: Oceans. 2013;118(7):3704–3711. [Google Scholar]
- 49.McDougall TJ, Barker P. 2011. Getting started with TEOS-10 and the Gibbs seawater (GSW) oceanographic toolbox. SCOR/IAPSO WG 127:1–28. Version 3.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.