Observation of femtosecond X-ray interactions with matter using an X-ray–X-ray pump–probe scheme

Significance

Understanding ultraintense light–matter interactions is an intriguing subject from viewpoints of basic science and practical applications. For the X-ray region, such research fields have opened up with the emergence of X-ray free-electron lasers (XFELs). By using an X-ray–X-ray pump–probe scheme, we firstly measured atomic response to XFEL light with femtosecond–ångstrom time–space resolutions. It was found that the atomic position is freezing until 20 fs after the XFEL irradiation, which supports the feasibility of damageless structural determinations with ultraintense XFEL pulses. The pump–probe scheme demonstrated here is an effective way to capture X-ray–matter interactions, and would contribute to verify and improve theory of X-ray interactions with matter, and stimulate advanced XFEL applications.

Abstract

Resolution in the X-ray structure determination of noncrystalline samples has been limited to several tens of nanometers, because deep X-ray irradiation required for enhanced resolution causes radiation damage to samples. However, theoretical studies predict that the femtosecond (fs) durations of X-ray free-electron laser (XFEL) pulses make it possible to record scattering signals before the initiation of X-ray damage processes; thus, an ultraintense X-ray beam can be used beyond the conventional limit of radiation dose. Here, we verify this scenario by directly observing femtosecond X-ray damage processes in diamond irradiated with extraordinarily intense (∼10¹⁹ W/cm²) XFEL pulses. An X-ray pump–probe diffraction scheme was developed in this study; tightly focused double–5-fs XFEL pulses with time separations ranging from sub-fs to 80 fs were used to excite (i.e., pump) the diamond and characterize (i.e., probe) the temporal changes of the crystalline structures through Bragg reflection. It was found that the pump and probe diffraction intensities remain almost constant for shorter time separations of the double pulse, whereas the probe diffraction intensities decreased after 20 fs following pump pulse irradiation due to the X-ray–induced atomic displacement. This result indicates that sub-10-fs XFEL pulses enable conductions of damageless structural determinations and supports the validity of the theoretical predictions of ultraintense X-ray–matter interactions. The X-ray pump–probe scheme demonstrated here would be effective for understanding ultraintense X-ray–matter interactions, which will greatly stimulate advanced XFEL applications, such as atomic structure determination of a single molecule and generation of exotic matters with high energy densities.

Since W. C. Röntgen discovered X-rays emitted from vacuum tube equipment in 1895, scientists have continuously endeavored to develop brighter X-ray sources throughout the 20th century. One of the most remarkable breakthroughs was the emergence of synchrotron light sources, which were much more brilliant than the early lab-based X-ray sources. Such dramatic increase in X-ray brilliance provided a pathway to obtain high-quality X-ray scattering data. This, in turn, enabled one to solve the structures of complex systems such as proteins, functional units of living organisms, and viruses. However, the increase in the brilliance is also accompanied by a severe problem of X-ray radiation damage to the samples being examined (1). X-rays ionize atoms and generate highly activated radicals that break chemical bonds and cause changes in the structures of the samples. To achieve structure determination precisely, a sufficient scattering signal should be recorded before the samples are severely damaged. Radiation damage was considered to be an intrinsic problem associated with X-ray scattering experiments, which imposed a fundamental limit on the resolution in X-ray structure determination (2).

The recent advent of X-ray free-electron lasers (XFELs) (3–5), which emit ultraintense X-ray pulses with durations of several femtoseconds, may totally avoid the problem of radiation damage. The irradiation of intense XFEL pulses generates highly ionized atoms, and the strong Coulomb repulsive force leads to evaporation of the samples. Meanwhile, it has been predicted theoretically (6) that atoms do not change their positions before the termination of the femtosecond X-ray pulse owing to inertia, thus enabling the use of X-ray radiations beyond the conventional X-ray dose limit. This innovative concept, called a “diffraction-before-destruction” scheme (6, 7), has paved a clear way to high-resolution structure determinations of weak scattering objects, including nanometer-sized protein crystals (8), noncrystalline biological particles (9), and damage-sensitive protein crystals (10).

Despite the potential impact of XFELs, detailed understanding of the ultrafast XFEL damage processes has been missing. As a pioneering work, Barty et al. (11) measured the diffraction intensities of protein nanocrystals by changing the XFEL pulse durations from 70 to 300 fs at intensities of ∼10¹⁷ W/cm². They found that the diffraction intensities greatly decrease for longer durations, clearly indicating sign of structural damage, i.e., X-ray–induced atomic displacements within the XFEL pulse durations. For further understanding of ultraintense X-ray interactions with matter, we need to directly measure the temporal changes of the structural damage. In particular, measuring the ignition time of the atomic displacements is crucial for realizing advanced applications with greatly intense XFELs. Although improving our knowledge of the X-ray damage processes is essential for all aspects of XFEL science, the experimental verifications have been missing because of the extreme difficulty in observation with ultrahigh resolutions in space (ångstrom) and time (femtosecond).

As a new approach to investigate the femtosecond X-ray damage processes, we here propose an X-ray–X-ray pump–probe experiment using double X-ray pulses; a pump X-ray pulse excites a sample and a probe X-ray pulse with a well-controlled time delay characterizes the change in the sample. In this approach, it is highly useful to exploit two-color double pulses with tunable temporal separations (12–15), which have been developed at SPring-8 Angstrom Compact free-electron LAser (SACLA) (4) and Linac Coherent Light Source (3). In this article, we measured the X-ray damage processes of diamond by using an X-ray–X-ray pump–probe diffraction experiment at SACLA. As the carbon–carbon bond is one of the most fundamental bonds in biomolecules, our results should provide a benchmark for XFEL-induced damage to practical samples.

Results

X-Ray–X-Ray Pump–Probe Experiment at SACLA.

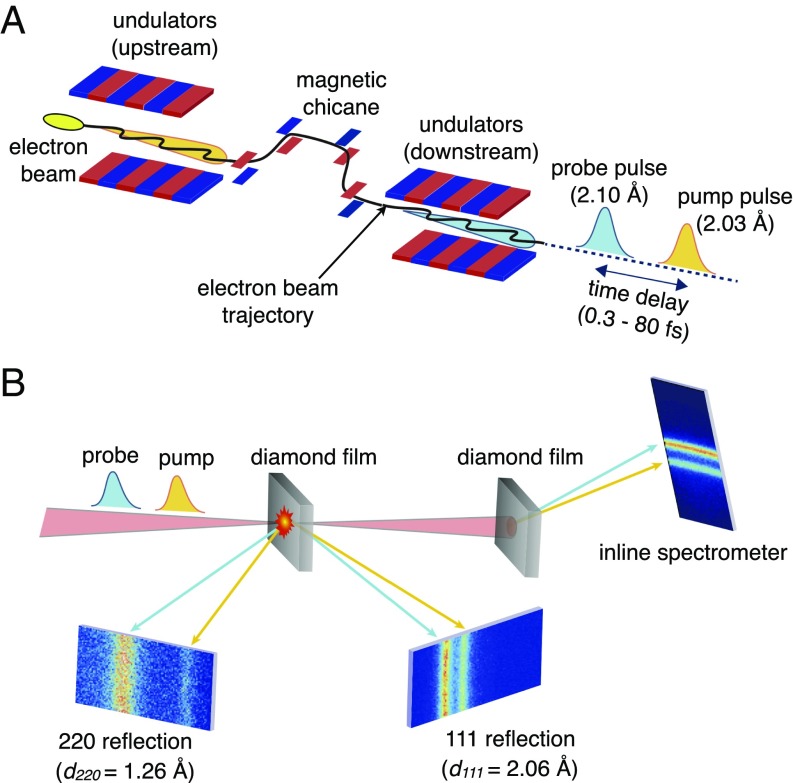
The experiment was performed at SACLA BL3 (4, 16), as schematically shown in Fig. 1 (Materials and Methods). We operated the XFEL source in the two-color double-pulse mode (12). Here, the eight upstream undulators were tuned to generate pump X-ray pulses with a wavelength of 2.03 Å. The remaining downstream undulators generated probe X-ray pulses with a wavelength of 2.10 Å. The time interval was controlled by a magnetic chicane located downstream of the eighth undulator. The temporal durations of the two pulses were estimated to be ∼5 fs by autocorrelation measurements (17), which was consistent with the estimation based on spectral spike width measurement (18). The X-ray intensities of the two pulses were increased up to ∼10¹⁹ W/cm² by using a two-stage focusing system (19), and the pulse energies were determined shot-by-shot by an inline spectrometer. Typical photon numbers in the pump and the probe X-ray pulses at the focus point were 9 $\times$ 10⁹ and 2 $\times$ 10¹⁰, respectively. The X-ray fluences of the pump and probe pulses were ∼3 $\times$ 10⁴ J cm⁻² and ∼7 × 10⁴ J cm⁻², respectively. We set a thin film of diamond nanocrystals at the focal point, and measured the Debye Scherrer rings of the 111- and 220 reflections, which correspond to the lattice plane distances of d₁₁₁ = 2.06 Å and d₂₂₀ = 1.26 Å, in the horizontal direction with two multiport charge-coupled device (MPCCD) detectors (20). To avoid the influence of the X-ray–induced damage, we scanned a fresh part of the diamond film surface to every XFEL shot. We performed the X-ray–X-ray pump–probe experiment by changing the relative time delay between the pump and the probe pulses from 0.3 to 80 fs.

Fig. 1.

Schematic illustration of the X-ray–X-ray pump–probe experiment at SACLA. (A) XFEL pulses were generated at a repetition rate of 30 Hz in the two-color double-pulse operation mode of SACLA. The eight upstream undulators generated pump X-ray pulses with a wavelength of 2.03 Å, and the downstream undulators generated probe X-ray pulses with a wavelength of 2.10 Å. The time interval between the pump and the probe pulses was tuned by a magnetic chicane located just after the eighth undulator, which controlled an additional path length of the electron beam with respect to the straight trajectory. (B) Two-color double pulses with time intervals, which were focused to 130 nm (horizontal) × 200 nm (vertical), irradiated a thin film of diamond nanocrystals. Debye Scherrer rings of the diamond 111- and 220 reflections in the horizontal direction were measured using two MPCCD detectors. The pulse energies of the incident pump and probe pulses were determined in a shot-by-shot manner using an inline spectrometer that combined a diamond foil and an MPCCD detector.

Analysis of Pump and Probe Diffraction Intensities.

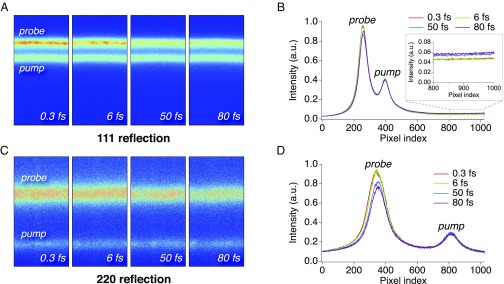
Fig. 2 A and C shows MPCCD images of the 111- and 220 reflections, respectively, at different time delays, which are averaged for multiple shots with the specific fluences of the pump and the probe pulses. In this condition, the pump fluence corresponds to an X-ray dose of 320 MGy to carbon atoms, which is much higher than the conventional tolerable dose limit for protein crystals of 30 MGy at cryogenic temperatures (1). In both diffraction patterns of the 111- and 220 reflections, we can observe two well-separated diffraction peaks, reflecting the differences in Bragg angles for the pump and the probe pulses. Fig. 2 B and D shows the line profiles corresponding to Fig. 2 A and C, respectively. In these figures, we corrected the effect of XFEL polarization on the diffraction intensity (Materials and Methods). For both 111- and 220 reflections, the probe diffraction intensities gradually decrease as the time delay increases. We can consider these changes indicative of the femtosecond X-ray–induced damage in diamond. In addition, we found that the diffuse scattering intensity around the 111 reflection increases with the time delay (Fig. 2B, Inset). The increase in the diffuse scattering intensity is also considered indicative of the X-ray–induced damage in the femtosecond time scale. For more quantitative analyses of the X-ray damage processes, we calculated the averaged line profiles of the 111- and 220 reflections at the respective fluences of the pump and the probe pulses. Then, we fitted each profile to the summation of two Lorentzian functions and a baseline:

$$L\left(i\right)=\hspace{0.17em}\frac{I_{pump}}{\pi {\gamma }_{pump}\left[1+{\left(\frac{i-i_{pump}}{{\gamma }_{pump}}\right)}^2\right]}+\frac{I_{probe}}{\pi {\gamma }_{probe}\left[1+{\left(\frac{i-i_{probe}}{{\gamma }_{probe}}\right)}^2\right]}+B.$$

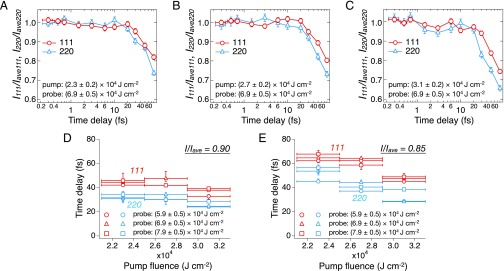
Here, $i$, $\gamma$, $I$, and $B$ represent the index of pixels, the widths and integrated diffraction intensities of Bragg reflections, and the baseline, respectively. We analyzed the dependence of the integrated probe diffraction intensities of the 111- and 220 reflections ($I_{111}$ and $I_{220}$) on the time delay after correcting the inhomogeneity of the sample and the differences in the probe pulse energies (Materials and Methods). Fig. 3 A–C shows the dependence of $I_{111}$ and $I_{220}$ on the time delay for three different fluences of the pump pulses. In these figures, $I_{111}$ and $I_{220}$ are normalized by the averaged values of those at the four shortest time delays (0.3, 0.5, 0.7, and 1.5 fs), $I_{ave111}$ and $I_{ave220}$. Here we note that $I_{111}$ and $I_{220}$ in the case of the shortest time delays were almost the same as those when the diamond film was moved to a defocused position [10 mm apart from the focus along the beam axis. The beam size at the position was 250 µm (H) and 400 µm (V)]. This result indicates that X-ray damage during irradiations of the pump or the probe pulses was negligibly small in the conditions of the present pump–probe experiment. Interestingly, $I_{220}$ decays faster than $I_{111}$, as shown in Fig. 3 D and E, which represent the time delays at which $I_{111}$/$I_{ave111}$ and $I_{220}$/$I_{ave220}$ decrease to 0.9 (Fig. 3D) and 0.85 (Fig. 3E), respectively.

Fig. 2.

Images and line profiles of the diffraction from diamond. (A and C) MPCCD images of the 111- and 220 reflections at time intervals between the pump and the probe pulses of 0.3, 0.6, 50, and 80 fs, which are averaged over multiple shots with specific fluences of the pump [(3.1 ± 0.2) $\times$ 10⁴ J cm⁻²] and the probe [(6.9 ± 1.1) $\times$ 10⁴ J cm⁻²] pulses. (B and D) Line profiles of A and C after compensating for the effect of XFEL polarization on the diffraction intensity (Materials and Methods). (B, Inset) An enlarged figure that represents diffuse scattering around the 111 reflection.

Fig. 3.

Temporal changes of the probe diffraction intensities of the diamond 111- and 220 reflections after irradiation of the pump pulse. (A–C) Dependence of the probe diffraction intensities of the 111- and 220 reflections on the time delay at specific fluences of the pump [(A) (2.3 ± 0.2) $\times$ 10⁴ J cm⁻², (B) (2.7 ± 0.2) $\times$ 10⁴ J cm⁻², and (C) (3.1 ± 0.2) $\times$ 10⁴ J cm⁻²] and the probe [(6.9 ± 0.5) $\times$ 10⁴ J cm⁻²)] pulses. (D and E) Time delays for $I_{111}$ (red) and $I_{220}$ (blue) decreasing to be, respectively, 90% and 85% of $I_{ave111}$ and $I_{ave220}$ for different fluence conditions of the pump [(2.3 ± 0.2) $\times$ 10⁴ J cm⁻², (2.7 ± 0.2) $\times$ 10⁴ J cm⁻², and (3.1 ± 0.2) $\times$ 10⁴ J cm⁻²] and the probe [(5.9 ± 0.5) $\times$ 10⁴ J cm⁻², (6.9 ± 0.5) $\times$ 10⁴ J cm⁻², and (7.9 ± 0.5) $\times$ 10⁴ J cm⁻²] pulses. After evaluating $I_{111}$ and $I_{220}$ for the respective conditions, we performed the linear interpolation of $I_{111}$ and $I_{220}$ between the measured conditions of time delays and determined the values of the time delays shown in D and E.

Evaluation of Temporal Changes of X-Ray-Induced Damage in Diamond.

The decreases in $I_{111}$ and $I_{220}$ could be explained by two factors: electronic damage (21) and structural damage (11). The former is attributed to the increase in the number of ionized carbon atoms with longer time delays. As the atomic form factor of carbon that corresponds to the 111- and 220 reflections of diamond is almost proportional to the number of electrons occupying the core shell (K shell) (22), the generation of core holes by pump X-ray irradiation and subsequent excitation processes, such as electron impact ionization, leads to decreases in $I_{111}$ and $I_{220}$. However, in our experimental conditions, such electronic damage is negligible because the percentage of core hole atoms generated by the entire excitation processes is evaluated to be ∼1% at most, which corresponds to a decrease in diffraction intensities much less than 1% (Materials and Methods). Therefore, we can assume that the latter, the atomic displacement caused by strong Coulomb interactions between ionized atoms, is the main mechanism that explains our observation. In this case, the diffraction intensities from smaller lattice spacing should decrease faster because the atomic displacement leads to a larger phase mismatch between scattered X-rays from each atom. In fact, this tendency agrees with our observation (Fig. 3 D and E).

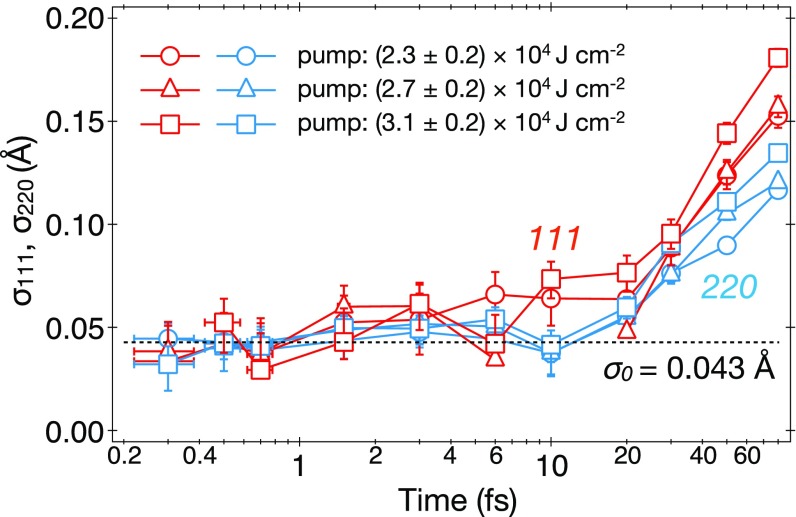
To quantitatively verify the assumption, we evaluated the temporal development of the atomic displacement using Barty et al.'s simple model (11). We assume that the displacements of carbon atoms in diamond are independent and random with a mean of zero. A change in the diffraction intensity with such random displacements is mathematically equivalent to the Debye–Waller factor in crystallography, which represents the effect of thermal motion on the diffraction intensity. The diffraction intensity of Bragg reflection is reduced by a factor of $\text{exp}(-q^2{\sigma }^2)$, where $q$ is a scattering vector given by $q=4\pi \hspace{0.17em}\text{sin}\theta /\lambda$ for wavelength $\lambda$ and scattering angle $2\theta$, and $\sigma$ is the root-mean-square (rms) displacement perpendicular to the lattice plane. In our experiment, the diffraction intensities of the 111- and 220 reflections are almost constant for time delays shorter than 1.5 fs (Fig. 3 A–C). This result indicates that the atomic displacement does not increase in this time scale, and the rms displacement is considered the same as that of undamaged diamond at room temperature. Then, $I_{111}$/$I_{111ave}$ and $I_{220}$/$I_{220ave}$ can be expressed as $\exp \left(-q^2{\sigma }_{111}^2\right)/\exp \left(-q^2{\sigma }_0^2\right)$ and $\exp \left(-q^2{\sigma }_{220}^2\right)/\exp \left(-q^2{\sigma }_0^2\right)$, respectively. Here, ${\sigma }_0=0.043\hspace{0.17em}\AA$ are the rms displacements of carbon atoms perpendicular to the (111)- and (220) planes in the undamaged state (23), and ${\sigma }_{111}$ and ${\sigma }_{220}$ are those of atoms interacting with intense X-rays. Based on the above representations of the diffraction intensities, the temporal changes of ${\sigma }_{111}$ and ${\sigma }_{220}$ were evaluated for three different pump pulse energies (Fig. 4). ${\sigma }_{111}$ and ${\sigma }_{220}$ rapidly increase from 20 fs after irradiation of the pump pulse, indicating that the critical time for the ignition of the X-ray–induced structure change is 20 fs for the present pump pulse fluences. Interestingly, σ₁₁₁ is larger than σ₂₂₀ after the ignition of the atomic movement. Although it is difficult to conclusively explain the mechanism using only the presently available data, it may be caused by higher-order atomic displacement beyond the simple Debye–Waller model. The rates of ${\sigma }_{111}$ and ${\sigma }_{220}$ are of the order of 10⁻³ Å/fs, which is comparable to the unidirectional velocity of isolated carbon atom at room temperature ($v=\sqrt{k_{B}T/M}$ = 4 $\times$ 10⁻³ Å/fs, where $k_B$ is the Boltzmann constant, $T$ = 300 K, and $M$ is the mass of carbon atom). This similarity of the rate of rms atomic displacement and the velocity of isolated atoms is a general feature in the nonthermal melting processes of semiconductors pumped by optical lasers (24, 25), where interatomic potential changes by excitation of valence electrons lead inertial dynamics. Such interatomic potential changes might be caused by the electronic damage processes in the present experiment.

Fig. 4.

Temporal changes of the atomic displacements of carbon atoms perpendicular to the (111)- and (220) planes in diamond (σ₁₁₁, σ₂₂₀) after irradiation of the probe pulses. We assumed that the atomic displacements did not depend on the fluence of the probe pulse, and estimated the atomic displacements for different fluence conditions of the pump [(2.3 ± 0.2) $\times$ 10⁴ J cm⁻², (2.7 ± 0.2) $\times$ 10⁴ J cm⁻², and (3.1 ± 0.2) $\times$ 10⁴ J cm⁻²] pulses to be the average values of those for fluences of the probe pulses being (5.9 ± 0.5) $\times$ 10⁴ J cm⁻², (6.9 ± 0.5) $\times$ 10⁴ J cm⁻², and (7.9 ± 0.5) $\times$ 10⁴ J cm⁻². Here, data for certain conditions of time delays and fluences are missing because the overestimation of the diffraction intensities of the probe pulses owing to artifacts made it impossible to evaluate the atomic displacement [i.e., $I_{111}/I_{ave111}\hspace{0.17em}>\text{exp}\left(q_{111}^2{\sigma }_0^2\right)$ or $I_{220}/I_{ave220}\hspace{0.17em}>\text{exp}\left(q_{220}^2{\sigma }_0^2\right)$]. The atomic displacement of carbon atoms in diamond in the undamaged state (${\sigma }_0$ = 0.043 Å) is also shown for comparison.

Discussion

Finally, we discuss the maximum X-ray intensity that is acceptable for X-ray structure determination. We compare the degree of X-ray damage induced by the pump 5-fs XFEL pulse used in the present experiment (fluence of 3 $\times$ 10⁴ J cm⁻², which corresponds to a photon density of 3 $\times$ 10³ photons Å⁻², an intensity of ∼10¹⁹ W cm⁻², and a radiation dose of 320 MGy to carbon atoms) and an XFEL pulse with duration of 20 fs at the same fluence. Although the total number of photoelectrons at the termination of the XFEL pulse is the same for both cases, the 5-fs XFEL pulse generates more photoelectrons than the 20-fs XFEL pulse at any time within 20 fs after beginning of the XFEL irradiation. As each photoelectron takes some time to ionize surrounding atoms, the X-ray damage induced by the 5-fs XFEL should obviously become faster. In our experiment, structural changes were not prominent within 20 fs after pump pulse irradiation. Thus, we can consider that structural determination is feasible with 20-fs XFEL pulses at the same fluence of 3 $\times$ 10⁴ J cm⁻² as in our experiment. According to molecular dynamics simulations of protein crystals, which predict that the rms displacement of atoms at the termination of the XFEL pulse is proportional to $F^{1/2}T$ for X-ray fluence of $F$ and pulse duration of $T$ (7, 11), our results indicate that the atomic displacements are also expected to be negligible for 2-fs XFEL pulses with fluence of $F=3\times {10}^4\hspace{0.17em}{\text{J}\hspace{0.17em}\text{cm}}^{-2}\times {\left(20\hspace{0.17em}\text{fs}/2\hspace{0.17em}\text{fs}\right)}^2=3\times {10}^6\hspace{0.17em}{\text{J}\hspace{0.17em}\text{cm}}^{-2}$. This condition of XFEL pulses, a pulse duration of 2 fs and a fluence of $3\times {10}^6\hspace{0.17em}{\text{J}\hspace{0.17em}\text{cm}}^{-2}$ (i.e., a photon density of 3 $\times {10}^5$ photons Å⁻², an intensity of ∼10²¹ W cm⁻², and a radiation dose of 32 GGy to carbon atoms), would allow us to collect sufficient scattering signals from single protein molecules for determination of molecular orientation (26), which enables structural determination with atomic scale from multiple scattering images. As sub-10-fs XFEL pulses are routinely used in the current XFEL facilities (18, 27), increasing the photon density by two orders higher than the value currently achieved would enable the X-ray scattering experiment of single protein molecules. Precisely shaped X-ray mirrors (28) producing an X-ray spot comparable to the size of protein molecules (although the spot size sets an upper limit of the molecule size to be analyzed) and increases in the number of emitted photons from XFELs by optimizing accelerator parameters for production of high-current and low-emittance electron beams, would provide a platform for scattering experiments of single molecule without X-ray–induced structural damage.

The experimental results presented here support the feasibility of molecular imaging with sub-10-fs XFEL pulses with fluence of 10⁶∼10⁷ J cm⁻², which has long been desired by scientists. To realize this ultimate measurement, we need further understanding of the interaction of high-intensity X-rays with matter. Simulation studies predict (29, 30) that the effect of electronic damage for sub-10-fs hard XFEL pulses becomes prominent above the photon density of 10⁶∼10⁷ photons Å^-2, which corresponds to fluence of 10⁷∼10⁸ J cm⁻² and intensity of 10²¹∼10²² W cm⁻². Although this threshold value of fluence is slightly larger than that required for molecular imaging, the margin is small. Thus, one may need to consider modification of the conventional scattering theory, which assumes all atoms being ground state, for analyzing scattering from molecules with intense XFEL pulses. To achieve accurate analysis, new scattering theory that incorporates the effect of electronic damage (31) would become a promising way. Understanding and modeling of the X-ray–induced electronic damage and matter in extreme conditions with high energy densities (32, 33) would be helpful for constructing this new framework of scattering theory with ultraintense X-rays. The experimental investigations of the XFEL-induced electronic damage are the next intriguing subjects for the X-ray–X-ray pump–probe experiment.

Materials and Methods

X-Ray–X-Ray Pump–Probe Experiment at SACLA.

The experiment was performed in EH5 at SACLA BL3. Double XFEL pulses were generated at a repetition rate of 30 Hz in the two-color double-pulse operation mode of SACLA. By tuning the undulator gaps, we generated pump X-ray pulses with a wavelength of 2.03 Å (i.e., a photon energy of 6.1 keV) and probe X-ray pulses with a wavelength of 2.10 Å (i.e., a photon energy of 5.9 keV). The time interval between the pump and the probe pulses was controlled with ultrahigh accuracy of less than 0.1 fs using a magnetic chicane located just after the eighth undulator. The spectral bandwidths of the pump and the probe pulses were ∼50 eV. The intensity profile of the double pulse measured at the optical hutch was almost identical and round-shaped for the different delay times and shots.

The XFEL pulses were focused using a two-stage reflective focusing system (19). The focused spot size of the pump and the probe pulses measured by a knife-edge scan method was 130 nm (horizontal) $\times$ 200 nm (vertical). We also measured the focus size of the double pulses after transmission of a 25-µm chromium film. Because the absorption K edge of chromium is 5.99 keV and only the probe pulse selectively transmitted the film, we were able to measure the focus size of the probe pulse. The focus size of the probe pulse was the same as that of the double XFEL pulses, which indicates that the pump and the probe pulses perfectly overlapped in space.

We used a nanocrystal diamond film prepared by plasma-enhanced chemical vapor deposition as a sample for the X-ray–X-ray pump–probe experiment. This diamond film is the same as that used for monitoring the position and intensity of XFEL beam (34). The film thickness was 15 µm and the crystal grain size was ∼30 nm. The X-ray transmittances at the wavelengths of the pump and the probe pulses were above 95%. We set the diamond film at the focal point and measured the diffraction patterns of the 111- and 220 reflections in the horizontal direction with two MPCCD detectors at 30 Hz. The distances between the sample and the MPCCD detectors were 205 mm for the 111 reflection and 260 mm for the 220 reflection. The pulse energies of the pump and the probe pulses were determined using a calibrated intensity monitor (34) installed at SACLA and a spectrometer located 5.5 m downstream of the focal point, consisting of the same diamond foil as the sample and an MPCCD detector to measure the diffraction intensities of the 111 reflection.

We performed the experiment for the condition of time delays of 0.3, 0.5, 0.7, 1.5, 3, 6, 10, 20, 30, 50, and 80 fs. For each condition, we measured ∼12,000 shots by scanning the sample so as to use a fresh surface for every shot to avoid the influence of XFEL-irradiation-induced damage.

Procedure for Calculating Line Profiles of Diffraction Intensities.

To calculate the line profiles of the diffraction intensities as shown in Fig. 2 B and D, we first extracted MPCCD images for specific fluences of the pump and the probe pulses. For each image, we converted the digital signals at respective pixels into the number of detected X-ray photons in a photon-counting manner (20). Then, we averaged the number of detected photons over all extracted images for each pixel. Next, to compensate for the effect of the X-ray polarization on the diffraction intensity, the averaged number of detected photon at each pixel was divided by the polarization factor, which was determined under the assumption of the XFEL pulse having completely horizontal polarization. Finally, by integrating the compensated diffraction intensities along the shorter directions of the MPCCD images, we calculated the line profiles of the diffraction intensities.

Evaluation of Integrated Diffraction Intensities of Probe Pulses.

To compare the probe diffraction intensities for different time delays, we calculated the normalized probe diffraction intensities of the 111- and 220 reflections, $I_{111}$ and $I_{220}$, defined as

$$I_{111}=\frac{I_{probe}\left(111\right)/I_0\left(probe\right)}{I_{pump}\left(111\right)/I_0\left(pump\right)}\hspace{0.17em},$$ [1]

$$I_{220}=\frac{I_{probe}\left(220\right)/I_0\left(probe\right)}{I_{pump}\left(220\right)/I_0\left(pump\right)}\hspace{0.17em},$$ [2]

where $I_{pump}$ and $I_{probe}$ represent the integrated diffraction intensities determined by the fitting of the line profiles for specific fluences of the pump and the probe pulses, and $I_0\left(probe\right)$ and $I_0\left(pump\right)$ are the pulse energies of the incident pump and probe pulses, which are averaged over the XFEL shots extracted for the calculation of the line profiles. The denominators of Eqs. 1 and 2 are considered proportional to the number of crystals contributing to the 111- and 220 reflections of the pump pulses, respectively. As the Bragg diffraction angles are almost the same for the pump and the probe pulses, the denominators should compensate for the effect of the inhomogeneity of the sample on the probe diffraction intensity. In addition, $I_{probe}\left(111\right)$ and $I_{probe}\left(220\right)$ are divided by $I_0\left(probe\right)$ in Eqs. 1 and 2 to compensate for the differences of the incident probe pulse energies for different time delays.

Effect of Ionization of Carbon Atoms on Diffraction Intensity.

During the irradiation of a pump X-ray pulse with a fluence of ∼3$\times$ 10⁴ J cm⁻², ∼0.7% of all irradiated carbon atoms are photoionized (35), and the same number of photoelectrons with energies almost the same as the pump X-ray photon energy (∼6 keV) are emitted mostly from the inner shell. Each photoelectron collides with the bound electrons in the surrounding carbon atoms, leading to the emission of electrons from the outer and inner shells of the carbon atoms, which is called the electron-impact ionization process. The ejected electrons also collide with the bound electrons, leading to the cascade ionization of carbon atoms. In such electronic damage processes, the inner shell ionization terminates at ∼1 fs after the generation of photoelectrons, at which time the energies of the cascade electrons become lower than the binding energy of the inner shell electron of carbon (273 eV) (21). By the time of the termination, ∼30 bounded electrons are emitted per 6-keV photoelectron (21). For electron energies ranging from 273 eV to 6 keV, the cross-section of the electron-impact inner shell ionization of carbon is almost the same as or less than 1% of that of the total electron-impact ionization (36), indicating that the number of emitted electrons from the inner shell via impact ionization is less than 0.3 per single 6-keV photoelectron. Therefore, the percentage of core hole atoms generated by the irradiation of the pump pulse over all carbon atoms is ∼1% at most. As this value corresponds to a decrease in diffraction intensity of much less than 1%, the electronic damage is considered negligible for the accuracy of our experiment.