Greenhouse−icehouse transition in the Late Ordovician marks a step change in extinction regime in the marine plankton

Significance

In the graptoloids, a major group of early Paleozoic plankton, extinction selectively removed young species during times of background (low intensity) extinction. Age-independent extinction was confined to high extinction rate spikes of short duration that were related to environmental perturbations. During the extreme Late Ordovician Mass Extinction, old species were selectively removed. Graptoloids provide a sensitive indicator of marine environmental change and suggest that age selectivity of extinction in oceanic pelagic ecosystems switched rapidly and repeatedly from one mode to another and back again, a pattern that can be detected only when temporal resolution and species turnover rates are exceptionally high.

Abstract

Two distinct regimes of extinction dynamic are present in the major marine zooplankton group, the graptolites, during the Ordovician and Silurian periods (486−418 Ma). In conditions of “background” extinction, which dominated in the Ordovician, taxonomic evolutionary rates were relatively low and the probability of extinction was highest among newly evolved species (“background extinction mode”). A sharp change in extinction regime in the Late Ordovician marked the onset of repeated severe spikes in the extinction rate curve; evolutionary turnover increased greatly in the Silurian, and the extinction mode changed to include extinction that was independent of species age (“high-extinction mode”). This change coincides with a change in global climate, from greenhouse to icehouse conditions. During the most extreme episode of extinction, the Late Ordovician Mass Extinction, old species were selectively removed (“mass extinction mode”). Our analysis indicates that selective regimes in the Paleozoic ocean plankton switched rapidly (generally in <0.5 My) from one mode to another in response to environmental change, even when restoration of the full ecosystem was much slower (several million years). The patterns observed are not a simple consequence of geographic range effects or of taxonomic changes from Ordovician to Silurian. Our results suggest that the dominant primary controls on extinction throughout the lifespan of this clade were abiotic (environmental), probably mediated by the microphytoplankton.

The importance of the marine plankton in both the carbon cycle and in the food web that supports the diversity of marine life is undisputed. However, the evolutionary dynamics of planktic species and the factors controlling their diversity and evolutionary turnover are still poorly known (1, 2). This is particularly so for the Paleozoic, where problems of preservation and sampling bias, and poor time resolution, have precluded detailed analysis. How does the marine plankton respond to environmental perturbations arising from climate change over geological time? How does background extinction differ from episodic and mass extinction in the pelagic realm? Is the risk of plankton species extinction dependent on the amount of time since the species originated (3)? These questions have important implications for macroevolutionary process, stability of marine ecosystems, and modern biodiversity conservation (3–5). Here, using a new global data set of unparalleled temporal resolution, we attempt to answer these questions.

The graptoloid clade (order Graptoloidea) constituted the main component of the early Paleozoic macrozooplankton from the beginning of the Ordovician to the Early Devonian (6). Graptoloids were colonial filter-feeding protochordates, generally ranging from a few millimeteres up to ∼200 mm in maximum dimension, which lived suspended in the water column in a range of depth zones. They have been used extensively for correlation and zonation (7–10), and the stratigraphic distributions of species are well documented. Thus, their observed stratigraphic ranges commonly are inferred to be good approximations of their true ranges in time, and empirical graptoloid range data have been used as examples of, or tests for, macroevolutionary rates (3, 4, 11–13). Like most of the marine macroplankton, their evolutionary dynamics are interpreted to have depended closely on those of the microphytoplankton and bacterioplankton (13–16), the primary producers in the food web and which, in the modern oceans, are sensitive indicators of oceanic circulation, nutrient flux, and global climate (1, 17); in addition, they depended on physical properties of the water mass such as temperature and chemistry.

Most previous studies of taxonomic survivorship using the fossil record have been limited by the relatively coarse time resolution of the analyses, generally no better than 7- to 11-My time bins (5, 18–20). We use the constrained optimization (CONOP) global graptolite composite developed by Sadler et al. (10) that has been calibrated directly by radiometric dating and provides the basis for the Ordovician and Silurian global time scales (21). This composite has been constructed from >18,000 local records of the stratigraphic ranges of 2,045 species in 518 published stratigraphic sections distributed globally; it resolves 2,031 discrete temporal levels through the 74-My span of the graptoloid clade, yielding a mean resolution of 37 kya between levels (13). The first- and last-appearance events of all species in all sections have been used to optimally order, and proportionally space in time, the earliest first appearance and latest last appearance of each taxon using a simulated annealing optimization heuristic (10, 22) (see SI Text, Construction of the Global Composite Sequence). The raw extinction and origination rates of the 2,045 graptolite species have been smoothed with a 0.25-My moving window centered at each resolved level, providing, in effect, instantaneous rate curves, each with 2,031 control points. Extinction and origination rates, and the derivative measures such as faunal turnover (origination + extinction), have thus been estimated with a precision that is orders of magnitude better than in most previous studies of global extinction. Uncertainty bounds have been estimated by bootstrapping. Our data set spans the entire lifespan of the graptoloid clade; the uppermost part, in the earliest Devonian, is omitted from further analysis because species diversity is very low and analytical uncertainty becomes unacceptably large. For similar reasons, the basal 4 My of the clade history is not included in the analysis.

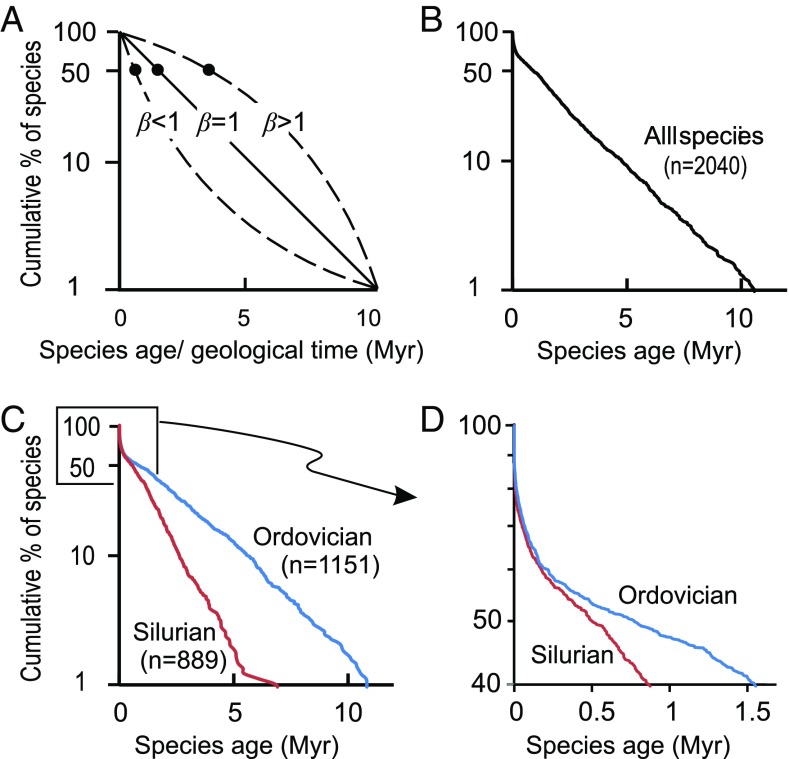
To test if extinction depends on species age, we use taxon survivorship of birth cohorts (23) (Fig. 1A) and AIC-based model selection (Figs. S1–S6). Birth cohorts are comprised of all species originating in a short interval of time; we use time bins of 0.25 million years, 0.5 million years, and 1 million years. A survivorship curve, produced by plotting the age of species in a cohort against the proportion of species still extant as the cohort decays over time, is exponential when the probability of extinction is uniform through the life of the cohort. In a semilog plot, this results in a linear distribution (3) (Fig. 1A, β = 1). Significant deviations from an exponential relationship indicate age dependency of extinction and yield curves in semilog space that are either convex up or concave up, which are approximated by Weibull distributions with shape parameters (β-values) greater than or less than unity, respectively (24). A concave-upward curve indicates a decreasing extinction probability with species age (Fig. 1A, β < 1). A convex-upward curve indicates increasing extinction probability with taxon age (Fig. 1A, β > 1). To produce Fig. 2C, on which each cohort is represented by a single point plotted at its β-value, we varied the cohort durations and start times in successive iterations using time bin durations of 0.25 million years, 0.5 million years, and 1 million years, and offsets of bin start equal to one-fifth of the bin duration. This produces, in effect, a series of moving windows of different duration and boundary ages, and, for this reason, points shown are not statistically independent of each other. This approach, however, maps out patterns of survivorship that are robust to arbitrary variations in cohort size and start time, and robust results are indicated by clustering of points in the figure. In contrast, isolated points in the plot are idiosyncratic to a particular combination of bin duration and starting time, and are ignored during subsequent interpretation. Gaps in coverage indicate intervals where species richness is low and cohorts fail to meet the qualifying threshold of at least 20 taxa.

Fig. 1.

(A) Semilog plot showing idealized taxon survivorship curves for a cohort commencing at 0 My; β = 1, linear survivorship curve indicating exponential decay rate (constant extinction probability); β < 1, decreasing decay rate, extinction probability decreases with taxon age; β > 1, increasing decay rate, extinction probability increases with taxon age). Black dots indicate median cohort age in each curve. (B−D) General age structure curves for all species (B) and for all Ordovician and all Silurian species (C and, detail, D). The life expectancy of a Silurian species is half that of an Ordovician species.

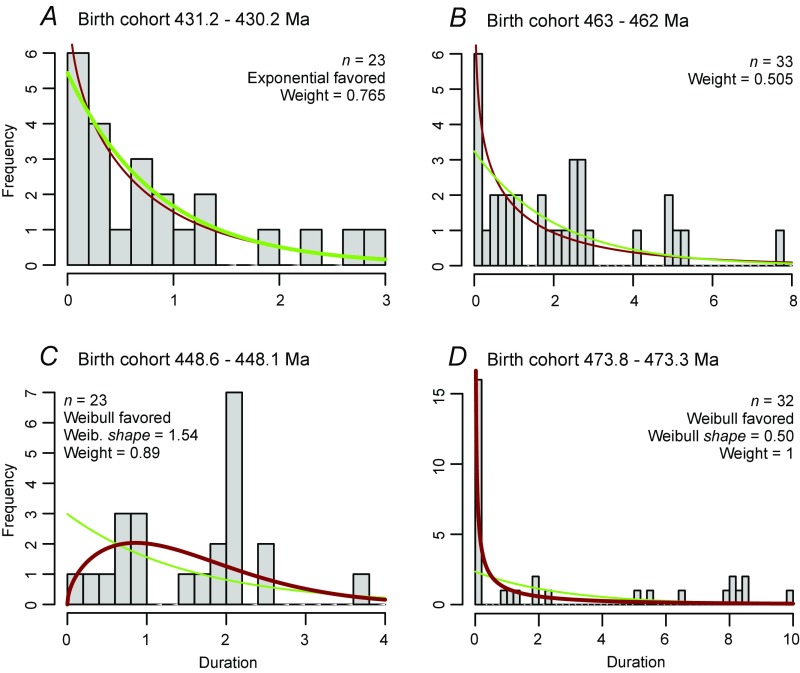
Fig. S1.

Examples of model fits for individual cohorts taken from our data. In all cases, the green curve is the best-fit exponential distribution, the red curve is the best-fit Weibull distribution, and the heavier line indicates the favored fit. “Weight” indicates Akaike weight of the best-fitting model. (A) Cohort for which an exponential fit is favored. (B) Cohort for which there is no preferred fit. (C) Cohort for which a Weibull fit, with shape parameter β > 1, is favored. (D) Cohort for which a Weibull fit, with β < 1, is favored.

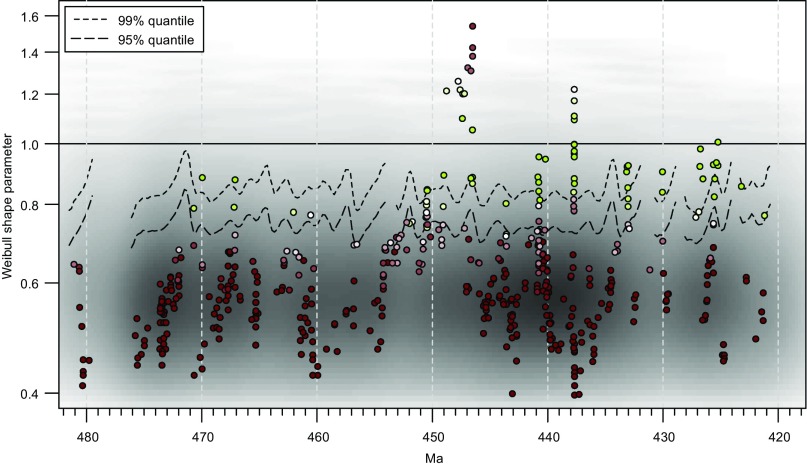
Fig. S6.

Test of the impact of uneven distribution of first appearances. Time series of fitted Weibull shape parameters (β) for the graptolite data, superimposed on gray-scale map of fitted β from data in which observed durations have been randomized with respect to observed first-appearance ages; density of gray shading is proportional to density of points. Dashed lines are the one-tailed, 95% and 99% quantiles on the distribution of the randomized data; fluctuations in the levels of these lines are a consequence of uneven distribution of first-appearance ages in time. See Fig. 2 for explanation of symbol colors, etc.

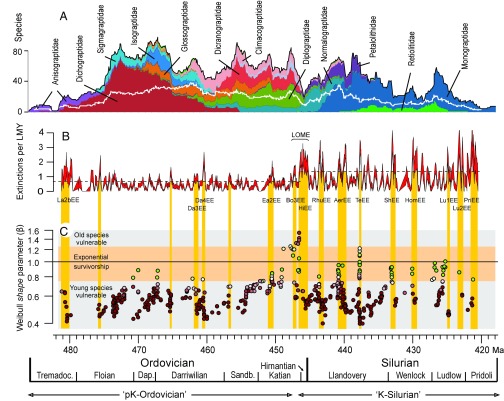
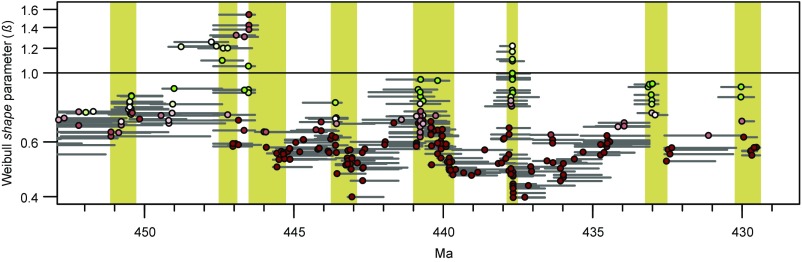
Fig. 2.

(A) Graptoloid standing species richness, main families shown. The white line is level-by-level generic richness. (B) Extinction rate (extinctions per lineage-million-years), 0.25-My moving window, centered at each level in the composite. The band represents ±1 SE from bootstrap means (1,000 iterations) of median values for each 0.25-My bin. The main extinction episodes, those exceeding the 75th percentile for each period (dashed lines) are: La2bEE, Lancefieldian 2; Da3EE, Darriwilian 3; Da4EE, Darriwilian 4; EaEE, Eastonian; BoEE, Bolindian; HiEE, Hirnantian; RhuEE, Rhuddanian; AerEE, Aeronian; ShEE, Sheinwoodian; HomEE, Homerian; Lu1EE, Ludfordian (early); Lu2EE, Ludfordian (late); and PriEE, Pridolian. (C) Weibull shape (β) value for each cohort survivorship curve is plotted at the median age, in geological time, of the last appearances of its constituent species. Red points, Weibull model preferred; green points, exponential model preferred; the darker the tone, the greater the AIC weight of the preferred model. Age bands with clusters of green points indicate fields with cohorts in which extinction is not dependent on species age; 498 points are shown.

Results and Discussion

Graptoloid Extinction Rate Curve.

The graptolite per lineage-million-years (Lmy) species-level extinction rate curve (Fig. 2B) fluctuates throughout the time series but nevertheless shows a step change that demarks two contrasting levels of intensity: (i) low amplitude and low median rate in the Floian to mid-Katian (“pK-Ordovician”) referred to as predominantly “background” extinction and (ii) a higher median rate with much greater variance in the late Katian to end-Silurian (“K-Silurian”), labeled “episodic” extinction. The transition between the two regimes is relatively sharp and takes place in the late Katian, when there was a coincident transition in global climate regime and in the marine carbon isotope ratios (25, 26). Following Cooper et al. (13), we treat these two parts of the extinction rate curve independently in setting threshold levels for identifying major extinction episodes. The threshold levels are somewhat arbitrary, and we have chosen the 75th percentile, equal to 0.72 species per Lmy in the pK-Ordovician and 1.46 species per Lmy in the K-Silurian (see Fig. 2). The graptolite extinction rate reached extreme levels of intensity (greater than 1.5 species per Lmy) repeatedly through the K-Silurian, including during the Late Ordovician Mass Extinction (LOME) (13, 27). These severe extinction episodes are interpreted to have been triggered by abiotic, environmental perturbations of the graptolite ecosystem related to rapid changes in the marine climate (13, 28, 29). The link between Ordovician−Silurian evolutionary dynamics of the marine fauna and global climatic events is well supported (30–36), especially for the LOME and the Sheinwoodian climatic−evolutionary events and their accompanying perturbations in the carbon cycle. The clade survived these catastrophic extinction rates, among the highest recorded for any marine group (11), by virtue of the correlated, equally intense, spikes in origination rate (13); extinction otherwise would have been sufficient to almost extinguish the clade in less than a million years. The high species turnover rate reflects the exceptionally short median life span of a graptoloid species—0.89 My in the pK-Ordovician and 0.48 My in the K-Silurian. In comparison with other groups (means only are available), ammonites (∼1 My) are comparable but planktonic foraminifera [6−9.5 My (37) or ∼12–15 My (11)] have much longer mean durations than graptoloids (0.65–1.00 My).

Birth Cohort Survivorship Analysis.

The great majority of cohorts throughout the Ordovician and Silurian periods (423 out of 498 measured values) are best fit by Weibull distributions with β < 1, and most of these have β < 0.75. For these cohorts, extinction risk decreases with taxon age. Most cohorts with β > 0.75 are of Katian or younger age and are confined largely to very short time intervals with elevated extinction rate (Fig. 2). This pattern, combined with the contrast in extinction intensity described above, defines a distinctive extinction regime that distinguishes the K-Silurian from the pK-Ordovician. The probability of finding the observed correspondence of β > 0.75 with extinction episodes by chance is << 0.001 (one-tailed test based on randomizing the age of cohorts 10,000 times and calculating the proportion of cohorts with β > 0.75 that lie within our extinction episodes). For most of these cohorts with β > 0.75, an exponential fit is favored, except for a number of cohorts at ∼447 Ma, for which a Weibull distribution with β > 1.2 is favored and extinction risk increases with taxon age. The clustering of points indicates that the observed highly nonrandom distribution is robust to variations in both time bin duration and start time.

We further tested the robustness of our results as follows (details in SI Text, Tests for Sensitivity and Bias in the Analyses and Tests for Bias in the Data and Figs. S5 and S7). The analysis was repeated after removing the shortest-ranging species (12% of the total) and, again, after first combining the ranges of consecutive congeneric species for which the last appearance of one was coeval with the first appearance of the other; these tests showed that neither undersampling nor pseudoextinction are likely to influence the observed pattern significantly.

Fig. S5.

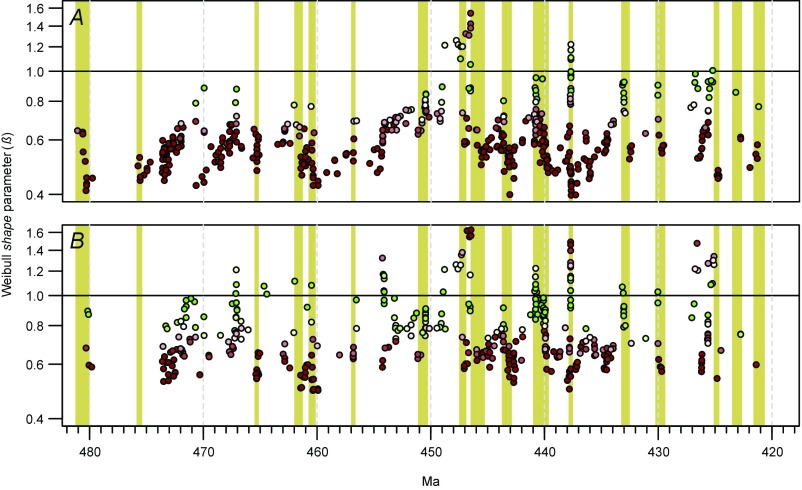
Test of bias related to poorly sampled species. Results for the full dataset (A) and with the 253 shortest ranging species removed (B). Yellow bars denote extinction episodes discussed in the main text. See Fig. 2 for explanation of symbol colors, etc.

Fig. S7.

Test for the impact of pseudoextinction. Results of modeling following the elimination—by combining ranges of candidate ancestor−descendant pairs—of potential instances of pseudoextinction. (A) Result with no instances of pseudoextinction removed (compare Fig. 2). (B) Result following removal of 160 instances of potential pseudoextinction. (C) Result following removal of 654 instances (∼30% of species) of potential pseudoextinction. Yellow bars denote extinction episodes discussed in the main text. See Fig. 2 for explanation of symbol colors, etc.

Patterns of survivorship revealed by our analyses are not detected at the genus level (Fig. S8A). The generally low β-values are recovered by species-level analyses at the temporal resolution of stages (average duration 4.6 My) and biostratigraphic zones (average duration 1.1 My), but the fine-scale structure visible in our results is entirely (stages) or largely (zones) invisible at these resolutions (SI Text, Genus, Stage, and Zone Resolution Analyses and Fig. S8B).

Fig. S8.

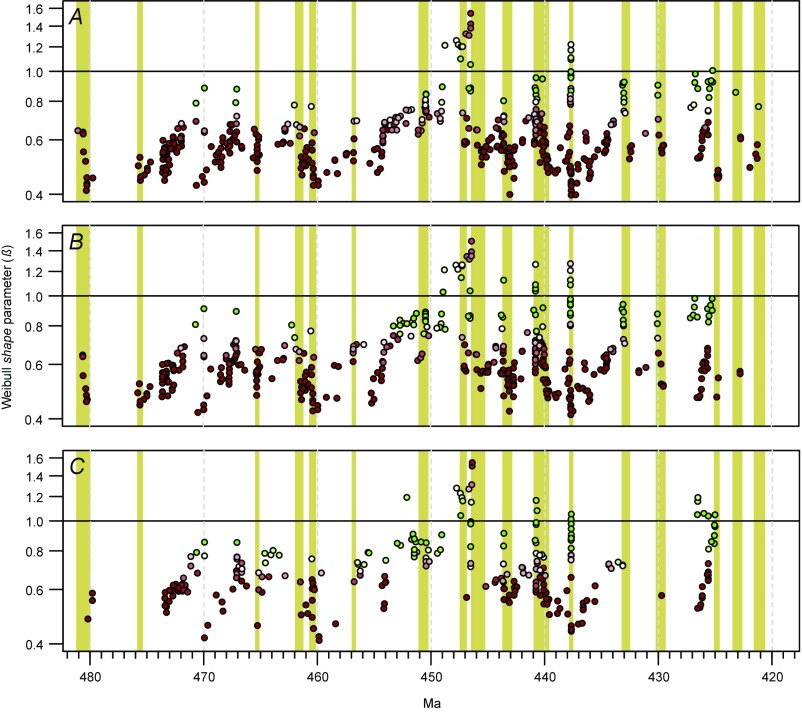
Analyses using genera, stages, and zones. (A) Patterns of survivorship at the taxonomic level of genera, showing fitted Weibull shape parameters (β) for genus cohorts and interquartile ranges of cohort last-appearance ages (compare Fig. S3). (B and C) Patterns of species survivorship at the temporal resolution of stages (B) and graptolite zones (C), showing fitted Weibull shape parameters (β) for species cohorts and interquartile ranges of cohort last-appearance ages (compare Fig. S3). Yellow bars denote extinction episodes discussed in the main text. See Fig. 2 for explanation of symbol colors, etc.

Discussion

From these results, we infer that the background mode of survivorship for graptoloid species was extinction risk that decreased with taxon age (β < 0.75). At any given time, extinction risk was higher for new species than for old species, reflected in the excess of short-lived species above the expectation of constant extinction (Fig. 1D). This applied during both times of relatively low background extinction rate in the pK-Ordovician and times of more volatile, but not peak, extinction rate in the K-Silurian. It also applied during times of adaptive radiation of the graptoloid clade, in the Floian Age, and refilling the same ecospace in the Llandovery Epoch after the LOME diversity crash (13). A negative dependence of extinction on taxon age, previously reported in marine, mainly benthic, genera (5), is here shown to also apply to marine zooplanktic species. This finding points to the importance of abiotic factors in driving extinction; old species and genera tend to be more widely distributed and represented by more local populations, rendering them less susceptible to environmentally driven extinction (38–40), although Finnegan et al. (5) found that additional, unexplained, factors were involved for their data. Note that survivorship trajectories for short-lived taxa (taxon durations <0.2 My) are identical in the pK-Ordovician and K-Silurian (Fig. 1D); the shorter median duration of K-Silurian taxa therefore results from fewer long-lived species than in the pK-Ordovician, rather than from a surfeit of short-lived species.

The age-independent fields represent brief excursions into selectively neutral territory (0.75 < β < 1.3), in which extinction risk was essentially random with respect to taxon age. They lie within, or close to, major graptoloid extinction episodes (Fig. 2) that previously have been linked to environmental changes (13, 29, 35). For this reason, it seems plausible that the age-independent fields resulted ultimately from abiotic processes rather than the kinds of biotic interactions that were initially proposed as part of Van Valen’s (3) “Red Queen hypothesis” to help explain age-independent survivorship. Thus, during both background and episodic extinction, extrinsic, abiotic factors appear to be the primary drivers in graptoloid evolution.

An alternative interpretation of these neutral excursions during the K-Silurian is that they could reflect simply a quantitative consequence of the overall intensification of extinction (38). If this were the case, then we would expect to see a significant positive association between extinction rate and β during the K-Silurian, but, in fact, this relationship is negligible (Spearman rank-order correlation coefficient: r_s = 0.071; P = 0.10; see SI Text). Indeed, by eye, we see that there are many times of elevated extinction that are marked by vulnerability of young species. To further test this, we used logistic regression to characterize the relationship between taxon age and survival within cohorts (cf ref. 5) and compared the slopes of these regressions to their corresponding extinction rates. Contrary to the idea that intensification of extinction itself weakens selectivity during the K-Silurian, the correlation between extinction rates and regression coefficients is small and nonsignificant (details in SI Text). We therefore conclude that the excursions to selectively neutral extinction during the K-Silurian, identified herein, cannot be explained as a simple consequence of elevated extinction intensity alone.

During the extreme perturbation of the LOME (447−445 Ma), β-values > 1.3 indicate positive dependence of extinction risk on taxon age: Old species became vulnerable to extinction and were selectively removed. The change in age selectivity mode suggests that, like the selectively neutral fields, the LOME did not result simply from scaled up background extinction (39, 41). The LOME marks the largest depletion in species diversity (77% loss) in the history of the clade and the complete, or near-complete, removal of many long-standing families, genera, and species, including the Diplograptidae, Climacograptidae, and Dicranograptidae (27, 28). It was associated with major positive excursions in the carbon isotope (δ¹³C_carb) ratio (25, 29, 42), global continental glaciation (43, 44), changes in oceanic circulation, water mass properties, and microphytoplankton populations (42, 45), and the deep-water graptoloid biotope was severely degraded or destroyed (13, 29). The main surviving group after the LOME, the cold-adapted normalograptids (46), diversified rapidly in the early Silurian, driving a rapid recovery in species richness of the clade. Our findings suggest that the LOME was a unique event that marks the transition to a new regime in which frequent extinction episodes disturbed the age structure of the entire clade, prevented the accumulation of long-lived species in the Silurian, and reduced the median species duration to half its Ordovician value (Fig. 2B). It is not clear whether the positive dependence of extinction risk on taxon age during the LOME indicates that a novel extinction mechanism was operating during this event or whether it represents simply an extreme expression of the processes operating during other severe extinction episodes. One possible mechanism for the high β-values is that when environmental change is severe and rapid enough, old species that were adapted to a previous environment become maladapted in the new environment, compared with newly evolving species, and are selectively removed (4).

The LOME caused an almost complete turnover in the graptoloid clade, raising the possibility that the contrast in extinction rate from Ordovician to Silurian might result from this turnover and be an intrinsic property of the taxonomic groups themselves rather than the result of extrinsic environmental factors. Only one family, the Normalograptidae, is represented by a significant number of species in both the Ordovician and Silurian. Interestingly, the median duration of an Ordovician normalograptid species (1.20 My) is significantly longer than that of a Silurian species (0.33 My; Mann Whitney-U, two tailed, P = 0.02). Therefore, the change in extinction regime takes place within a single family and suggests that the higher extinction probability of Silurian species is not due simply to changed taxonomic composition (updated from ref. 47).

Notably, the high temporal resolution of the present data set reveals that changes in age selectivity associated with extinction episodes were short lived and sharp (Fig. 2), and the graptoloid survivorship regime returned rapidly (within 0.5 My) to its background state after each extinction episode, even though diversity itself was much slower to recover (e.g., ∼5 My in the case of the LOME).

Previous studies of taxonomic survivorship, which dominantly consider benthic marine genera and are resolved to time units of 7- to 11-My duration or longer, generally show extinction to be negatively age-dependent (i.e., β < 1) and negatively correlated with geographic range (5). The planktic foraminifera, in contrast, generally show taxon age to be positively related to extinction [β > 1 (4, 24, 48, 49)]; Doran et al. (49) found, for the planktic foraminifera, significant positive age dependency of extinction in the long recovery periods following mass extinctions. The graptolites seem to show features of both these patterns. Through most of their history, extinction risk decreases with taxon age, as seen in the benthos. In contrast, during many extinction episodes, graptolite extinction probability is independent of taxon age. Extinction risk that increases with taxon age, as observed in the planktic foraminifera, is confined, in the graptolites, to a single short interval of extreme environmental stress (the LOME).

An outstanding question remains: Why is survival age-dependent? Presumably, the causal agent is a correlate of species age, such as increasing organismal fitness (which we cannot test) or some aspect of the “ecological footprint” of a species, such as geographic range, that is commonly observed to increase with species age (40 and references therein). To assess the possible role of geographic range, we assigned each species occurrence to an equal-area map cell of ∼5 × 10⁴ km² and measured the geographic range of each species in each time interval (i.e., not aggregated over its lifetime) as the number of cells in which it is found. Given uncertainties with paleogeographic reconstructions, we based these assignments on present-day coordinates; because most species are confined to single paleocontinents, cell occupancy in paleocoordinates generally agrees well with that based on modern coordinates (50). We then carried out logistic regressions of survival with respect to range (see SI Text). Consistent with previous studies, range enhances survival; median regression coefficients are 0.26 ± 0.031 for the entire time series and 0.27 ± 0.036 for the K-Silurian. Selectivity with respect to range during the K-Silurian appears to be somewhat stronger with increasing extinction intensity (correlation between extinction rate and regression coefficient: r_s = 0.28; P = 0.009).

Importantly, although geographic range and age both predict survival, age is not merely a proxy for range. Range and age correlate positively but not very strongly (median r_s within intervals: 0.20 ± 0.019 for the entire time series; 0.10 ± 0.017 for the K-Silurian). Moreover, the effect of age on survival is virtually the same in a simple logistic regression as in a multiple logistic regression incorporating both age and range. The linear relationship between multiple (B_mult) and simple (B_simp) age coefficients is given by B_mult = 0.94 B_simp − 0.034 (r² = 0.93). Thus, species age evidently contributes to survival above and beyond its possible contribution to geographic range. The reason for this remains unresolved.

Conclusions

Our results suggest that, in planktic groups such as the graptolites, where species turnover rates and temporal and taxonomic resolution are all high enough, age selectivity of extinction is seen to be tightly linked with, and highly responsive to, extinction episodes associated with severe changes in marine climate. We recognize three alternative, and qualitatively distinct, modes of selectivity: background extinction mode, where extinction rates are low and newly evolved species are most vulnerable; high extinction mode, where extinction rates are elevated and all species are equally vulnerable; and mass extinction mode, where extinction rates are extreme and old species are the most vulnerable. Graptoloids provide a sensitive indicator of marine environmental change and suggest that selective regimes in oceanic pelagic ecosystems switched rapidly from one mode to another and back again. The reversion to background evolutionary turnover rates and mode, following environmental perturbations, was rapid even in cases where the full ecosystem recovery took several million years. The distinctive dynamics revealed here suggest the existence of a threshold in the severity of environmental change in the marine environment below which young species of zooplankton were selectively removed and above which old species became increasingly vulnerable to extinction. This threshold was crossed repeatedly in the Late Ordovician to end-Silurian icehouse climate.

Methods

The CONOP analysis was performed using the software CONOP9, as reported elsewhere (10). The initial ordinal composite was scaled using mean rock thickness separating event levels in the local sections after all these sections had been rescaled to mitigate the effects of their different accumulation rates (for procedures and protocols, see ref. 10 and SI Text). The resultant scaled composite was then age-calibrated by means of 23 radiometrically dated volcanogenic beds that are present in local graptolite-bearing sections and integrated into the global graptolite composite. All subsequent analyses were undertaken in R (51). Survivorship analysis of successive birth cohorts used a maximum likelihood, model-fitting approach and the corrected Akaike Information Criterion (AICc; see ref. 52) for model selection. For each observed cohort distribution of species durations, we identified the best-fitting exponential and Weibull distributions, determined which of these two had the overall best fit to the data, and recorded the best-fit Weibull shape parameter (β). These analyses accounted for the fact that the exponential distribution is a special case of the Weibull, and used the method of Hirose to reduce bias in the maximum likelihood estimation of the Weibull β-parameter (53) (see SI Text for details).

SI Text

Construction of the Global Composite Sequence of Species Ranges in Time.

The sections and faunal lists used have been compiled from the literature and have been screened for taxonomic and biostratigraphic reliability as explained in Sadler et al. (ref. 10, with supplementary online data), who also discuss the completeness of geographic and stratigraphic coverage. Forty-three percent of species are found in no more than one section, and, although they are a valid component of species richness, they do not assist in the correlation procedure. The density and overlap in ranges of the sections is such that, except for the very basal and top-most portion of the clade range, every level in the composite is spanned by at least 10, and up to 80, sections, with an average of over 50.

The methodology for building, scaling, and calibrating a global composite sequence of stratigraphic first, and last, appearance events by CONOP has been fully discussed by Sadler et al. (10). The species’ stratigraphic ranges in many local range charts are composited into a single global, best-fit ordinal composite spanning the entire lifespan of the graptoloid clade (base Ordovician to Early Devonian), by computer optimization using the simulated annealing heuristic. Refinements introduced by Sadler et al. (22) include greatly increasing the weight of taxa known from five or more sections during the compositing procedure, thus ensuring that the stratigraphically best-controlled and best-sampled taxa have the greatest influence in building the composite. The ordinal composite was scaled using mean rock thickness separating event levels in the local sections after all local sections were rescaled to mitigate the effects of their different accumulation rates (for procedures and protocols, see ref. 10). The resultant scaled composite was then calibrated by means of 23 radiometrically dated volcanogenic beds, present in local graptolite-bearing sections and integrated into the global graptolite composite. The radiometric dates serve not only to calibrate the scaled composite sequence but also to test for its linearity. The final product—a scaled and calibrated composite—is a timeline for the Ordovician and Silurian global succession of graptolite first- and last-appearance events, and is the basis for the geological time scale (GTS 2012) for these periods (21) (tests for sampling bias, robustness, and plausibility of the CONOP composite are presented in refs. 10 and 22). The time scale used herein has been calibrated by polynomial regression rather than spline fitting (compare figures 20.11 and 20.13 in ref. 54).

The optimization procedure assumes that locally observed taxon ranges may match the true global time span of the species, but more likely underestimate it as a result of migration and extirpation or failures of preservation and collection. Local species successions are made to match the emerging global timeline by stretching the observed ranges to the minimum extent necessary. The optimal timeline is the compromise that requires the least net stretching. Taxon ranges in the global timeline are naturally a little longer than their preserved ranges at individual sites. This effect would be exaggerated by any variance in practice between taxonomists. Fortunately, taxonomic practices tend to be relatively uniform for clades used in international correlation, such as the graptolites, and composite timelines examined during construction of the composite used here readily expose disjunct ranges.

The 2,045 graptoloid species yield 4,090 range-end events and produce a composite with 2,031 steps (“event levels”). There is, therefore, an average of two events per level, equivalent to 55 events per million years. The 2,031 levels span 74 My and have an average spacing of 37 thousand years (kya). This is the limiting resolution of our raw (unbinned) rate and richness curves. Spacing between levels is widest at the top and bottom of the composite sequence where species richness is lowest. The composite sequence of range-end events enables a direct reading of the precise species origination and extinction rates, as recorded in stratigraphic sections.

During subsequent analyses, we have assumed that the first appearance of a taxon lies at the sample level below its first-recorded occurrence and, likewise, the last appearance lies at the level above its last-recorded occurrence. This minor adjustment reflects the fact that observed first and last appearances represent positive evidence for the presence of a given taxon, and, therefore, the true events must lie beyond these points. This adjustment was not applied to events at the limits of the time series, which would imply extrapolation of the composite. Also, we did not place events midway between their recorded range limit and the levels beyond, because this would have required creation of synthetic event levels and implied unrealistic and unobserved increases in temporal resolution.

The CONOP analysis described above was performed using the software CONOP9 (see ref. 10). All other analyses discussed in this paper were undertaken in R (51). Where relevant, we cite specific R packages and functions.

Model-Fitting Methods.

Our method takes successive birth cohorts (details below) of species through the Ordovician and Silurian, and uses a maximum likelihood, model-fitting procedure to determine whether the distribution of species durations for each cohort is best fitted by an exponential or a Weibull distribution. Because of issues of statistical power (discussed below; see also ref. 49), we avoid formal hypothesis testing approaches. Instead, for each cohort, we simply ask the question, “Given a choice between an exponential and a Weibull distribution, which of these best describes our species duration distribution?” This approach is predicated on the expectation that, to a first approximation, the Weibull should provide a reasonable description of the distribution of species (24), remembering that the exponential is a special case of the Weibull. The Weibull distribution is described by two parameters, the shape (β) and the scale; an exponential distribution can be parameterized as a Weibull distribution with β = 1. Deviations of β from unity indicate deviations from exponential behavior and, in the context of survivorship curves, reflect age selectivity of extinction. Thus, β < 1 indicates preferential survival of older taxa relative to younger taxa, a positive relationship between taxon age and survivorship. Conversely, β > 1 indicates preferential removal of older taxa, a negative relationship between taxon age and survivorship.

The model-fitting procedure searches the parameter space and selects the two distributions, one exponential and one Weibull, that best fit the empirical data. The search for the best exponential distribution uses the R function “optimize” and the method of Brent (55). The search for the best Weibull distribution employs the “L-BFGS-B” optimization routine of Byrd et al. (56), as implemented in the R function “optim.” For both, we use the corrected AICc to select the best distributions (see ref. 52). Out of the two candidate model distributions for each cohort, the overall best model is selected using the AICc, and the difference in AICc between the two alternatives, expressed as the Akaike weight, is used to indicate the relative strength of preference for one over the other. Note that, because the exponential is a special case of the Weibull, with one fewer parameter, the Akaike weight in favor of the exponential will not be equal to 100% even if the data fit the exponential model perfectly, in which case the value of β would be unity and both models would have equal likelihoods. For large (effectively infinite) samples, a perfect fit to the exponential would yield an Akaike weight of ∼0.73; for smaller cohort sizes of 20 species, a perfect fit would yield a higher weight of ∼0.78, because the small-sample-size adjustment in the corrected AICc penalizes the two-parameter model more than the one-parameter model. Examples of various model fits for individual cohorts, taken from our data, are illustrated in Fig. S1.

During calculation, we use the method of Hirose to reduce bias in the maximum likelihood estimation of the Weibull β-parameter (53),

$${\beta }_u=\frac{{\beta }_b}{1.0115+\frac{1.278}{r}+\frac{2.001}{r^2}+\frac{20.35}{r^3}-\frac{46.98}{r^4}}$$

where β_b is the biased estimate of the Weibull shape, and β_u is the corrected estimate. Simulation demonstrates that some bias remains when sample sizes are small (Fig. S2A), but this bias is negligible for sample sizes of ≥20, as used here, and for the range of β inferred for our data. This simulation, and others reported below, employs the “rweibull” function in R to generate random deviates from the Weibull distribution that are used as model species durations. Where relevant, we distribute these model durations through time using random deviates from the uniform distribution and the R function “runif.” Unless otherwise specified, all simulations assume a Weibull scale parameter of 1.

Fig. S2.

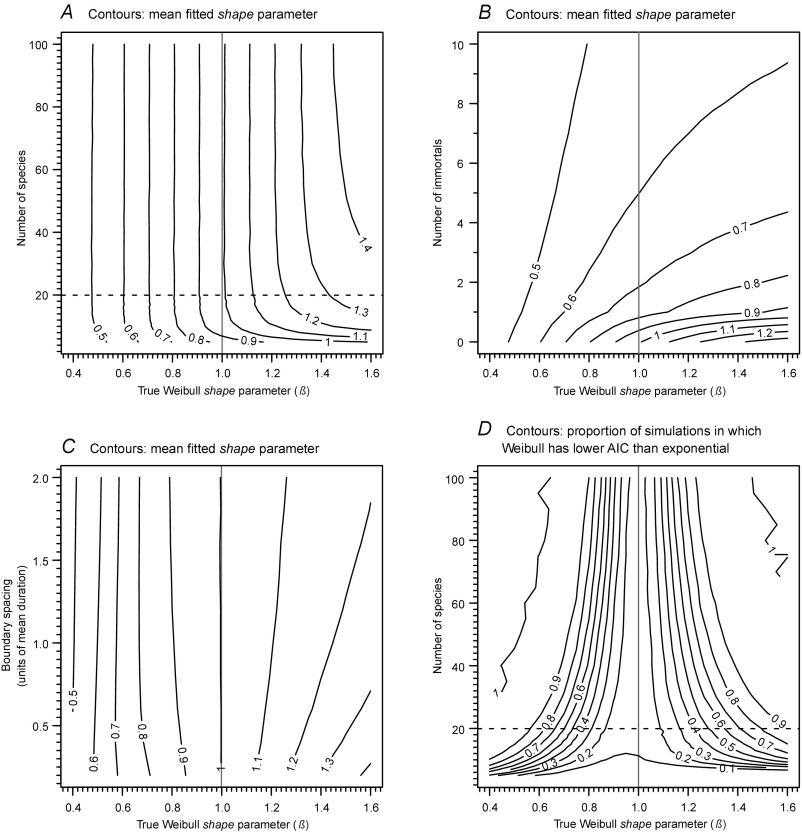
Simulations for assessing sensitivity of, and biases in, model-fitting method. (A) Contours on the mean Weibull shape parameter (β) recovered using our fitting approach from simulated data of known β, and showing the effect of increasing cohort size. (B) As for A, but showing the effect of adding increasing numbers of immortal taxa to the cohort. Simulation is based on starting cohorts of 20 species (to mimic the smallest cohorts used in our analyses) and immortals that have durations 10 times the mean duration of the starting cohort. (C) As for A, but showing the effect of using boundary-crossing birth cohorts and varying boundary spacing. In this simulation, a cohort is defined as the group of taxa that originated in the preceding time bin and crossed the younger boundary of that bin, the focal boundary. Duration of the birth time bin to the focal boundary (boundary spacing) is expressed in units of mean duration of the birth cohort. For the model fitting, taxon duration is recorded as the forward duration from the focal boundary (23). The use of boundary-crossing cohorts biases the recovered β, and, for β > 1, this bias increases with boundary spacing. Simulation is based on cohorts of 100 species. (D) Contours on the proportion of simulations, of known Weibull shape (β), for which a Weibull fit is preferred over an exponential fit using our approach, showing the effect of increasing cohort size. The plot demonstrates that, with modest cohort sizes and realistic deviations from exponential distribution, it can be relatively difficult to favor a Weibull distribution over an exponential. In all plots, the central vertical line is for a true β = 1 (i.e., an exponential distribution); where shown, the horizontal dashed line shows the minimum cohort size threshold of 20 that is used in our main analyses. In all plots, the contours are based on 10,000 replications.

Here we use simple birth cohorts as used in other studies, these being taxa that originate during a discrete interval (bin) of time. We have experimented with two alternative cohort assembly protocols: boundary-crossing birth cohorts, taxa that originate during a discrete time bin and cross the younger boundary of that bin, and simple boundary-crossing cohorts, the taxa that cross a given boundary, irrespective of time of origin. Each of these methods has some intuitive appeal. However, we favor the use of birth cohorts to ensure that very long-lived taxa are not counted in multiple cohorts, thereby gaining undue weight in the analysis; the bias introduced by just a small proportion of such “immortal” taxa is readily demonstrated by simulation (Fig. S2B). Moreover, analysis of boundary-crossing cohorts would tacitly assume that extinction risk is age-independent, whereas our main goal is to test whether this is the case. In contrast, the use of boundary-crossing cohorts appeals because these isolate groups of taxa that truly coexisted at an instant of time, whereas a birth cohort may include many short-lived taxa that ranged sequentially through time and never actually coexisted (a problem that decreases as bin size decreases). In reality, simulations demonstrate that cohorts assembled using boundary-crossing protocols yield biased estimates of β (Fig. S2C) because they undersample short-duration taxa that, compared with long-duration taxa, have a low probability of crossing any particular boundary.

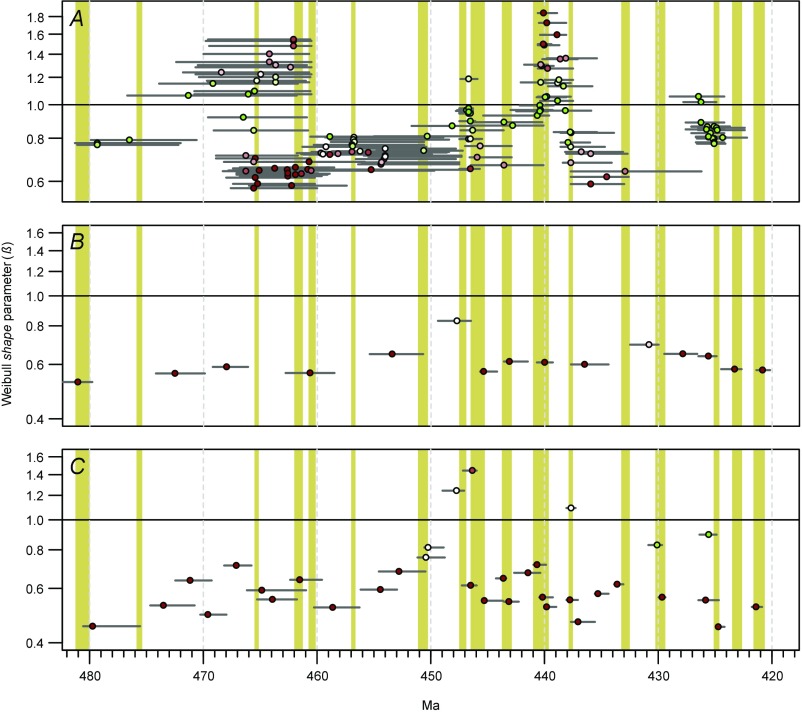
In Fig. S2C, therefore, each point corresponds to a particular birth cohort that contains at least 20 species, its position on the x axis records the age of the cohort in geological time (Fig. S3), and its value on the y axis indicates the best-fit Weibull β-parameter. The color of points indicates whether an exponential or Weibull model is preferred (green and red, respectively), and density of color gives a sense of Akaike weight, such that the darker the color, the stronger the preference for a given model. For plotting purposes, we take the age of a cohort to be the median of the constituent last-appearance events; in reality, of course, each cohort has an age span, as illustrated in Fig. S3 as the interquartile ranges of the last-appearance event ages.

Fig. S3.

The meaning of cohort ages. Segment of our time series of fitted Weibull shape parameters (β) for the graptolite data. Points are plotted at the median last-appearance age for each cohort; horizontal bars span the interquartile ranges of cohort last-appearance ages. Yellow bars denote extinction episodes discussed in the main text. See Fig. 2 for explanation of symbol colors, etc.

The composition of a particular birth cohort, and thus the resulting modeled β, depends on the span of the cohort bin and its starting point. Given that any time binning is arbitrary, we have chosen to map out and superimpose results for many combinations of bin length and starting ages of bin time series. Thus, for all our main results, we have used birth cohort bins of 1-My, 0.5-My, and 0.25-My duration and, for each, have started the time series at five different positions, each offset by one-fifth of the bin duration (i.e., these are moving windows). In total, therefore, our result maps 15 passes through the data. For this reason, points shown are not statistically independent of adjacent points. Clusters of points (Fig. S2C) indicate places where the modeled β is robust to variations in bin duration and starting time, and therefore robust to small changes in cohort assembly and composition. In contrast, isolated points in the plot are particular to a single bin duration and starting time combination, and are ignored during subsequent interpretation.

Tests for Sensitivity and Bias in the Analyses.

Exploratory analyses by us using a range of survivorship approaches (see also below), and results from other studies (e.g., ref. 49), demonstrate that attempts to discriminate exponential behavior from age-dependent extinction selectivity are limited by issues of statistical power. For this reason, and as noted above, we have avoided a formal hypothesis testing framework. In the context of the modeling approach described above, the challenge of low statistical power is illustrated in Fig. S2D, which reveals that it can be relatively difficult to reject an exponential model in favor of a Weibull when dealing with modest cohort sizes and realistic deviations from an exponential distribution. If one regards exponential survivorship as the null model, then this means that inferences of Weibull behavior will be conservative and are likely to be robust. In any case, we present our main results (Fig. 2C) as plots of modeled, best-fitting β, and the strength of preference for exponential or Weibull distributions is a secondary consideration and is indicated by color density.

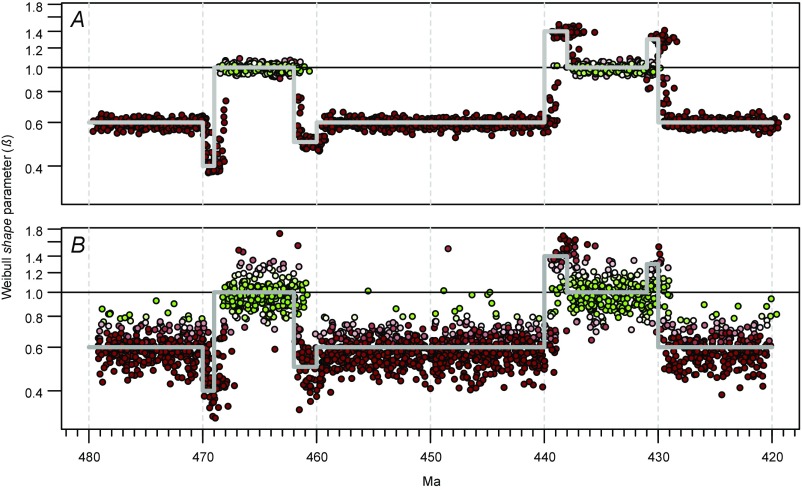
Despite the caveat noted above, simulations demonstrate that our modeling approach can extract meaningful signals from the type of data available. For Fig. S4, synthetic species first appearance ages were sampled at random from a uniform distribution and, for each, a species duration was sampled from a Weibull distribution, with the β-parameter varying through time and the scale parameter drawn at random from the values observed in the graptolite data. The magnitude of variation in the generating β mimicked the variation observed in the graptolite data (compare Fig. S4 and Fig. 2C). With these synthetic data, we used our modeling approach to recover the fitted β-parameter. Fig. S4A shows results for a very large dataset of 100,000 species and minimum cohort size of 100 species. In this case, the fitted β is very close to the generating β, with the expected small lag between a given perturbation in generating β, which was determined according to first-appearance ages of cohort species, and the matching perturbation in fitted values, which are positioned at the median last-appearance ages of species in each cohort. Fig. S4B shows results for a synthetic dataset that is comparable in size to our graptolite dataset, with 2,045 species and a minimum cohort size of 20. Although the scatter of fitted values is much greater and the signal is less clear than for the large dataset, the fitted values still recover key features of the generating β-curve, suggesting that our approach will be able to identify major variations in extinction selectivity in the graptolite dataset.

Fig. S4.

Tests of our model-fitting method using synthetic data sets. Time series of fitted Weibull shape parameters (β) based on entirely synthetic data. In both plots, the heavy gray line indicates the β that was used to generate the synthetic species ranges through different intervals of the time series; this parameter was perturbed within the range of values observed in the graptolite data. (A) Results based on a very large dataset of 100,000 species and a minimum of 100 species per cohort. (B) Results based on a dataset of 2,045 species and a minimum of 20 species per cohort—values that match our graptolite dataset—and five repetitions. See Fig. 2 for explanation of symbol colors, etc.

Tests for Bias in the Data.

To test the potential impact of poorly sampled or undersampled species, we reanalyzed our data after culling all species with the shortest stratigraphic ranges (total range spans < three adjacent levels, equivalent to 70 kya on average). This removed 253 species, 12.3% of our dataset. These are mostly species recorded at one level in one local section. They are likely to include those species whose stratigraphic range is significantly affected by any undersampling of the data (57). If the recorded stratigraphic range of a species is shortened by one or two event levels as a result of undersampling, it will make little difference to long-ranging species but will represent a much larger proportion of the recorded range of very short-ranging species, which could fail detection altogether. As expected, the removal of the shortest-ranging species shifts the whole population of cohorts toward higher β-values, and more cohorts lie in the exponential band where age selectivity is not significant, especially in the Ordovician (Fig. S5). From the Katian to the end of the Silurian, however, the pattern is essentially similar to that of the full dataset: Clusters of exponential cohorts, and a few high-β-cohorts, tend to lie on or near the major extinction episodes; the selection regime takes short sharp “excursions” into higher-Weibull territory. The imprint of the major extinction episodes on the pattern of age-selective, and age-independent, extinction described in this paper is not significantly affected by undersampling of stratigraphic ranges by up to three event levels in the composite.

To determine whether the perturbations in β that we observe could result from an uneven distribution of first appearances, we shuffled the observed durations with respect to the observed first-appearance ages, to create a new, randomized time series of graptolite durations. This time series was subjected to our model-fitting procedure, and the whole process was repeated 1,000 times. Results of this randomization are shown in Fig. S6. In this figure, the distribution of randomized results is summarized as a gray-scale map, where density of shading indicates density of fitted points. In addition, the one-tailed, 95% and 99% quantiles were estimated for a 1-My moving window, moving in 0.2-My increments, and requiring at least 5,000 points to lie within each window. The uneven distribution of randomized results, shown by both variations in density of shading and fluctuations in the quantiles, results from uneven distribution of first-appearance events in time. Most of the estimates of β fall well within the range of randomized values, which is to be expected given that we have maintained the observed, generally age-dependent distribution of species durations. However, the positive excursions in β at ∼437 Ma and ∼447 Ma are extreme relative to the distribution of randomized values, suggesting that they do not simply reflect an uneven distribution of first occurrences and are therefore robust features of our data.

Pseudoextinction, extinction resulting from the within-lineage, gradual phyletic evolution of one species to another, has the potential to corrupt patterns of true lineage extinction and thereby affect our results. Gradual phyletic evolution has, however, been demonstrated in very few lineages in the Graptoloidea. Successive subspecies in a lineage are sometimes interpreted as examples of “phyletic evolution” [for example, by Urbanek et al. (58)], but gradual morphological transitions in time, that can be demonstrated by population analysis, are rare. One exception is the Ordovician complex with Isograptus victoriae and its derivatives; in this complex, species and subspecies populations change gradually, progressively, and globally (59). More commonly among the graptoloids, however, the mode of speciation is undetermined.

In any case, to test a scenario of widespread phyletic gradualism and pseudoextinction, we ran a series of experiments by combining the ranges of consecutive species of the same genus for which the last appearance of one was coeval, within some tolerance, with the first appearance of the other. This rather crude attempt to identify and remove pseudoextinctions will undoubtedly have removed valid extinctions that are not within-lineage terminations, and we make no claim that the cases identified represent true instances of phyletic gradualism—to determine this would require careful, quantitative analysis of many large populations spanning each transition. Here we report the result of two such experiments (Figs S7 B and C): one that required the first appearance of a species to be exactly coincident with the last appearance of its putative ancestor, and the other that allowed an overlap or gap between biostratigraphic ranges of up to three composite levels. In both cases, if multiple candidate ancestors are available, one was chosen at random. These experiments reveal that our major patterns of extinction selectivity are robust to even widespread apparent pseudoextinction affecting ∼30% of the species in our dataset. Hence, given the lack of empirical evidence for widespread phyletic gradualism in the graptolites, and the results of these experiments, we conclude that the presence of pseudoextinction is unlikely to have a significant effect on our conclusions.

Relationships Between Survivorship, Extinction, and Geographic Range.

To examine relationships between β and extinction rate, we first calculated extinction rates centered on the age of each of the β-points shown in Fig. 2C, using a temporal window of 0.25 My as in Fig. 2B, and then quantified the correlation between the two time series (see Discussion). This analysis pertains to age dependence of survival throughout the history of cohorts. To confirm this, we analyzed age dependence of survival within discrete time intervals, as in ref. 5. We divided the entire Ordovician–Silurian time span into 0.25-My intervals, using nonoverlapping time windows to allow independence of data points. For each interval containing at least 20 species, we tabulated the time since first appearance of all extant species and used logistic regression to assess whether the odds of survival beyond the interval are a function of species age. Consistent with the results of ref. 5, age generally has a positive effect on survival: Median regression coefficients (±1 SE, based on bootstrap resampling) are r_s = 0.13 ± 0.028 for the entire time series and r_s = 0.16 ± 0.036 for the K-Silurian (note that, in contrast to the Weibull shape parameter β, higher regression coefficients imply stronger selectivity in favor of older species). However, contrary to the idea that intensification of extinction itself weakens selectivity during the K-Silurian, the rank-order correlation between extinction rates and regression coefficients is, in fact, slightly positive, although nonsignificant (r_s = 0.16; P = 0.11).

To assess the possible role of geographic range on survivorship, we assigned each species occurrence to an equal-area map cell and measured the geographic range of each species in each time interval, as explained in the Discussion. We then carried out logistic regressions, as described above for species age, and compared results of simple and multiple logistic regressions in which the effects of range and age on survival were assessed separately and together; results of these analyses are explained in the Discussion.

Genus, Stage, and Zone Resolution Analyses.

We are interested to know how our patterns of survivorship would manifest at the taxonomic level of genera or at a coarser temporal resolution that is more typical of other studies. To this end, we calculated β for birth cohorts of genera in exactly the same way as for species (Fig. S8A). From comparison of Fig. 2C and Fig. S8A, we see that the genus-level analysis does not detect the dominantly negative dependence of extinction on taxon age that is observed at the species level. In addition, there is, at best, only partial correspondence between excursions into high β-space in the two sets of analyses. Full exploration of this question—the relationship between selective regimes at different levels of the taxonomic hierarchy—is beyond the scope of the present paper. From this preliminary investigation, however, it is clear that analysis at the genus level does not recover either the overall pattern or, perhaps less surprisingly, the detailed structure of analysis at the species level.

Finally, we examined species-level survivorship patterns that are resolved at the temporal scale of stages of the international geological time scale and biostratigraphic zones, using these units as birth cohort bins (Fig. S8 B and C, respectively). For the Ordovician and Silurian, stages have an average duration of 4.6 My and graptolite zones have an average duration of 1.1 My. For both these analyses, the dominantly negative dependence of extinction on taxon age is recovered, but, again unsurprisingly, the short-term excursions to high-β-values are not detected in the stage-level analysis. The zone-resolution analysis does identify the LOME and hints at the structure and form of our full-resolution results; however, working at the resolution of zones fails to reveal the distinctiveness and brevity of the excursions into selectively neutral space.