Parallel Transmission Pulse Design with Explicit Control for the Specific Absorption Rate in the Presence of Radiofrequency Errors

Abstract

Purpose

A new framework for the design of parallel transmit (pTx) pulses is presented introducing constraints for local and global specific absorption rate (SAR) in the presence of errors in the radiofrequency (RF) transmit chain.

Methods

The first step is the design of a pTx RF pulse with explicit constraints for global and local SAR. Then, the worst possible SAR associated with that pulse due to RF transmission errors (“worst-case SAR”) is calculated. Finally, this information is used to re-calculate the pulse with lower SAR constraints, iterating this procedure until its worst-case SAR is within safety limits.

Results

Analysis of an actual pTx RF transmit chain revealed amplitude errors as high as 8% (20%) and phase errors above 3° (15°) for spokes (spiral) pulses. Simulations show that using the proposed framework, pulses can be designed with controlled “worst-case SAR” in the presence of errors of this magnitude at minor cost of the excitation profile quality.

Conclusion

Our worst-case SAR-constrained pTx design strategy yields pulses with local and global SAR within the safety limits even in the presence of RF transmission errors. This strategy is a natural way to incorporate SAR safety factors in the design of pTx pulses.

Introduction

Specific absorption rate (SAR) management is one of the major concerns in parallel transmission (pTx) MR applications at high field. PTx coils provide additional degrees-of-freedom (DOFs) for excitation of the nuclear spins, which allows fine control of the transverse magnetization (1–6). More recently, it has also been shown that the additional transmit (Tx) DOFs of these coils can be used in the pulse design process to reduce the SAR, both global (2,7–10) and local (11–18). Agreement between the actual SAR and the SAR predicted by the monitoring system depends on the accuracy of the electromagnetic (EM) simulation by which the electric fields are computed as well as on the fidelity of the radiofrequency (RF) Tx chain (i.e., its capacity to accurately reproduce the desired RF waveforms). The first issue (i.e., accuracy of the EM simulation) is being studied from different perspectives. In particular, promising advances in the estimation of the in vivo permittivity and conductivity maps using so-called electrical property tomography (19–21) offer the promise of accurate patient-specific EM simulations, which is considered the gold standard for safety evaluation. However, most previously published techniques for SAR control in pTx assume that the RF transmit channel does not introduce any error in the pulses. In other words, they assume that the RF pulse being played at the coil plug (we refer to this pulse as the “pulse actually played”) is exactly the same as the pulse calculated by the pulse design algorithm (the “reference pulse”). Some strategies have been proposed to reduce RF fidelity errors, such as the use of Frequency-Offset Cartesian feedback (22), which improves the original Cartesian feedback approach for RF power amplifier (RFPA) linearization (23), and the design of smooth RF pulses with intrinsically lower amplifier distortions (24); however these approaches are not perfect and are not always applicable.

Several authors have proposed direct monitoring of the RF waveforms played on each Tx element using small pick-up coils (25,26) or by analysis of the reflected signal from the directional couplers (DiCos) (27–30). Such strategies can be used to abort the scan when significant deviations are detected between the pulse actually played and the reference pulse. The performance of these monitoring systems has been increased by patient specific real-time calculations of local SAR caused by deviations based on SAR matrices databases with different patient models and scenarios (31,32). A major drawback of such strategies is that they can unnecessarily stop the scan even if the RF deviations being detected do not cause an SAR in excess of the tolerated limit. A recent improvement in the real-time SAR monitoring is the approach developed by Gumbrecht et al (30), which calculates local SAR with a safety margin to take into account the latency of RF measurements. However, this real-time SAR monitoring strategy may also result in frequent scan interruptions for high-SAR protocols with power levels close to the tolerated limit. Ideally, the pTx RF pulse should be designed with knowledge of the worst-case SAR estimation error to guarantee the safety of the patient and that the scan is not interrupted.

In this work, we propose a predictor-corrector pulse design strategy producing RF pulses that will satisfy the SAR limits in the presence of potentially large RF fidelity errors. There are two basic components to our approach: (i) an RF pulse design algorithm with explicit global SAR and local SAR constraints (17) and (ii) an optimization method to compute the maximum possible local and global SAR (“worst-case SAR”) produced by possible RF deviations that are within the expected performance of the RF Tx chain. Based on these two tools, we design RF pulses for which the worst-case SAR is within the SAR limits even if RF fidelity errors are large. This is done by iterating between (i) computation of an RF pulse subject to fixed local and global SAR limits and (ii) adjustment of these SAR limits based on the worst-case SAR of the previous pulse. We show in this work that the worst-case SAR is a theoretical upper bound that is extremely unlikely to be reached in practice. However, it is a useful metric that we propose to use for the incorporation of the safety margins in the SAR monitoring process.

To our knowledge, only two previous works, Neufeld et al (33) and Gumbrecht (34), have performed similar worst-case analysis. In Neufeld et al (33), worst-case local and global SAR amplifications were computed in realistic body models using an eigenvalue-based analysis of SAR matrices. On the other hand, Gumbrecht (34) calculated the worst-case SAR in the case of bounded errors in a similar formulation to the one used in this study. However, this information was not used in the pulse design, but only for SAR monitoring (30,35).

In this work, we measured the RF fidelity of an actual eight-channel 7 Tesla (T) pTx system using a real-time monitoring system based on measurement from DiCos (29). We then evaluated our pulse design approach in EM simulations of a 3T (eight Tx channels) and a 7T (eight Tx channels) pTx coil for torso and head imaging, respectively, using the RF fidelity performance measured previously. We show in these simulations that our approach yields pulses with excellent SAR properties even in the face of RF fidelity errors for both magnitude least-squares (MLS) slice-selective spokes (RF-shimming and two-spoke) and nonselective spiral pulses, while achieving high quality flip-angle excitations.

Methods

Measurements of RF Chain Errors

We measured the forward and reflected power in an eight-channel pTx coil array (Magnetom 7T, Siemens Healthcare, Erlangen, Germany) using DiCos. The DiCos were placed as close to the transmit coil elements as possible. The received monitoring signals were attenuated by 60 dB at the receiver, which was the level necessary to allow transmission at 200 V simultaneously on all eight channels without clipping artifacts. The value of 200 V was the maximum voltage that each of the eight RFPA could deliver. A dedicated calibration sequence, with scan time of less than 10 s, estimated the complex-valued 8 × 8 coupling matrices (designated by α_FWD and α_REF for the forward and reflected measurements) that transform the transmitted power waveform for each channel set by the digital pulse waveform to the forward or reflected power at each 50 Ω matched coil. Given a designed pulse b played at a maximum transmit voltage TX_vol, we define the pulse actually played (b_m) as the difference between the forward and reflected RF signals for the DiCos. This pulse is compared against the reference pulse (b_r) defined as b_r = TX_vol · b · (α_FWD — α_REF).

We measured the fidelity of the RF transmit chain of our eight-channel pTx system for both a four-spoke pulse and a spiral pulse. The first dataset consists of the prescribed RF pulse (reference pulse, b_r) and the measured RF values on the scanner (pulse actually played, b_m) of a four-spoke pTx excitation for a designed flip angle of 30°. The length of the pulse (L_RF) was 4.1 ms, the maximum voltage was 170 V, with a repetition time (TR) of 7.82 ms and 64 repetitions. The second dataset consists of a measured spiral-shaped pTx excitation of 40° (L_RF = 6.42 ms, TX_vol = 180 V, TR = 18.9 ms, 64 repetitions).

RF measurements with amplitude smaller than the 1% of the maximum voltage were not included in the analysis. The amplitude and the phase information from these pulse samples have a relatively small impact on the excited magnetization profile and SAR.

Worst-Case SAR Constrained Pulse Design

Our pulse design strategy is a predictor-corrector approach that iterates between (i) design of a pTx pulse subject to strict SAR limits and (ii) adjustment of these SAR limits based on an estimation of the worst-case SAR amplification due to RF transmit errors.

The problem of designing a pTx RF pulse subject to strict global and local SAR constraints was described previously (11,17). In summary, we solve a constrained optimization problem that minimizes the magnitude least-squares (MLS) difference between the target magnetization and the magnetization distribution created by the RF pulse. Quadratic, hermitian, semidefinite positive SAR matrices and power constraints are added that guarantee that the pulse being designed is safe (SAR constraints) and can be played on the scanner (power constraints) (17). To speed up the pulse optimization, we compress the original set of SAR matrices (one SAR matrix per voxel of the body model) using the virtual observation points (VOPs) algorithm (14). This speeds up the constrained optimization procedure considerably while guaranteeing that local SAR does not exceed the tolerated safety limit (17). The MLS optimization problem, in the small tip-angle regime where the magnetization and the RF pulse are linearly related, is formulated as follows:

$$\begin{array}{c}\underset{b}{min}{\Vert |\mathit{\text{Ab}}|-{\mathit{m}}_{\mathit{t}}\Vert }_2^{2}s.t.\\ a)\frac{d_c}{N_t}\sum _{i=1}^{N_t}{\mathit{b}}^H(t_i){\mathit{Q}}_v\mathit{b}(t_i)\le \mathit{\text{ISAR}},\forall V\\ b)\frac{d_c}{N_t}\sum _{i=1}^{N_t}{\mathit{b}}^H(t_i)\langle \mathit{Q}\rangle \mathit{b}(t_i)\le \mathit{\text{gSAR}}\\ c){\mathit{b}}_c^2(t_i)\le 8Z_0{P}_{\mathit{\text{peak}}},\forall t_i,c=1\dots C\\ d)\frac{1}{N_t}\sum _{i=1}^{N_t}{\mathit{b}}_c^2(t_i)\le 8Z_0{P}_{\mathit{\text{aver}}.},c=1\dots C\end{array}$$ [1]

where A represents the gradient matrix as described in Guérin et al (17), b is the designed pulse, N_t is the total number of samples in the pulse, Q_v is the v^th VOP matrix, 〈Q〉 is the global SAR matrix, lSAR and gSAR are the local and global SAR regulatory limits, d_c accounts for the duty-cycle, C is the number of channels, Z₀ is the reference impedance of the coil while P_aver and P_peak are the average and peak power limits on each channel. The source is assumed to be an ideal voltage source V with a Z₀ = 50 Ω internal resistance outputting power into the coil, which is represented by the load Z_L.

The pulse designed in the previous step (denoted by b₀) does not account for any possible error in the transmitted RF waveform. Therefore, in the presence of RF waveform distortions due to imperfections of the power amplifiers, it is possible that the SAR actually exceeds the safety limits. To avoid this scenario, we compute the worst possible local and global SAR (“worst-case SAR”, or SAR_WC) that may be caused by such distortions. We then adjust iteratively the SAR constraints to ensure that the worst-case SAR is below the safety limit. For a given RF pulse, the worst-case SAR is computed as follows:

$${\mathit{\text{SAR}}}_{\mathit{\text{WC}}}=\underset{\mathit{b}}{max}\frac{1}{N_t}\sum _{i=1}^{N_t}{\mathit{b}}^H(t_i)\mathit{Q}\mathit{b}(t_i)s.t.$$ [2]

$$||\mathit{b}(t_i)|-{\mathit{b}}_0(t_i)||\le \varepsilon |{\mathit{b}}_0(t_i)|\text{and}|\angle \mathit{b}(t_i)-\angle {\mathit{b}}_0(t_i)\le \delta ,\forall t_i$$ [2a]

where Q is a generic SAR matrix (i.e., the global SAR matrix or one of the VOPs), b₀ is the reference RF pulse computed in the previous step, ε and δ are the maximum percent RF magnitude error and the maximum absolute RF phase error, respectively. ε and δ characterize the accuracy of the RF transmit chain and must be provided to the algorithm. These parameters can be given by the technical specifications of the vendors, measured directly on the scanner or set by the user. If the worst-case SAR associated with the initial pulse b₀ exceeds the SAR limit, we then re-design the pulse by scaling the limit using the worst-case SAR information (see the pseudo code in Figure 1). Once a new pulse is designed the process is repeated until the worst-case SAR in case of errors is below the initial safety limit.

Fig. 1.

Pseudocode of the algorithm to design worst-case SAR constrained pulses.

This procedure is summarized in Figure 2 for a spoke pulse.

Fig. 2.

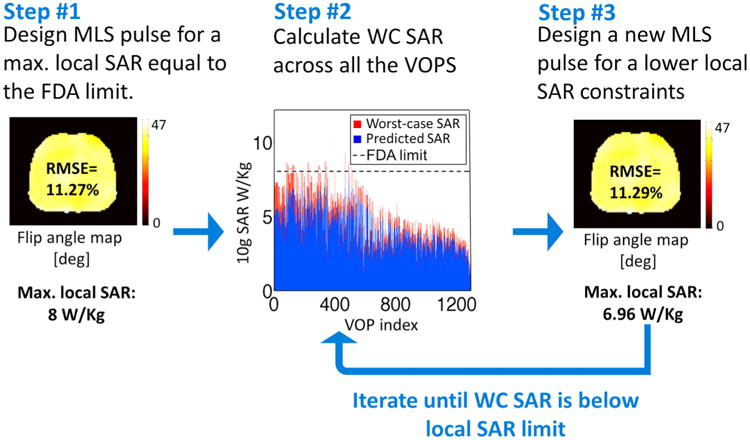
Flowchart of the robust pulse design process. A first pulse is designed while constraining SAR to the FDA limit (Step 1). The worst case SAR (SAR_WC) for every SAR (and the global SAR matrix) is then calculated for maximum RF amplitude and phase chain errors (Step 2). If SAR_WC exceeds the SAR limit, a new pulse is designed with a reduced SAR constraint (Step 3). This process is iterated until we obtain an RF pulse with a worst-case SAR (global and local) below the safety limit. This guarantees that the SAR is never exceeded, even in the presence of error in the transmitted RF waveform.

We used two different implementations of the pulse design algorithm in Eq. [1] (17). A magnitude least squares algorithm was coded in Matlab® (Mathworks, Natick, MA) for the design of spokes pulses using the interior-point method available in Matlab (36) (because the number of unknown in spoke pulses is not large, we used the standard implementation). For the design of the spiral pulses subject to local and global SAR constraints, we used a least squares interior-point design approach implemented in C++ using parallel computing (multithreading on multiple CPU cores) and optimized linear algebra libraries (37) for maximum performance.

Notice that due to the linearity of the SAR calculation in Eq. [2], solving the optimization problem for the pulse b is equivalent to solve it for each time sample b(t_i) separately. In the specific case that the designed pulse b₀ is a spokes-type pulse, the worst-case SAR calculation in Eq. [2] becomes much simpler. For instance, for a one-spoke pulse (RF-shimming), fixing any particular time point t_j, we have that ∀t_i it exists a complex scalar d_i such that b₀ (t_i) = d_i · b₀(t_j). Then, if we denote b_WC(t_j) to the solution of the problem in Eq. [2] and D_j = b_WC(t_j) – b₀ (t_j), we have that ∀t_i, we obtain b_WC(t_i) = b₀(t_i) + d_i · D_j. Hence, we just need to solve the optimization problem in Eq. [2] only for one time sample instead of doing it for all the points. This relation can be generalized for the case of more than one spoke pulses, with the need in that case to solve only one optimization problem for each spoke.

The interior-point algorithm (38), as implemented in Matlab® (Mathworks, Natick, MA), was applied to solve an equivalent unconstrained formulation of Eq. [2] written in terms of the indicator function of the convex set of constraints appearing in Eq. [2a]. The resulting optimization problem is then solved separately for each SAR matrix. The Parallel Computing Toolbox in Matlab® (Mathworks, Natick, MA) was used to speed up the code implementation by exploiting the multicore architecture of the machine.

All the algorithms were run on a machine with 16 Intel Xeon E52670 cores and 128 GB of memory.

Electromagnetic Simulations

We evaluated our method using EM simulations of a 3T body and 7T head pTx coil. Both coils have eight transmit (Tx) channels and were loaded with the 33 tissue types Ansys (Ansys, Canonsburg, PA) realistic male body model. Simulation of these arrays was performed using a co-simulation strategy based on HFSS (Ansys, Canonsburg PA) and the circuit simulator ADS (Agilent, Santa Clara, CA) described previously (17,36). Coupling between the Tx channels was modeled. Tuning, matching, and decoupling capacitors were optimized in the circuit simulator using the gradient routine of ADS so as to yield −30 dB matching at all ports (at 128 MHz and 297 MHz for the 3T and 7T coils, respectively) and better than −15 dB coupling between any pair of channels. B1+ maps were computed from the magnetic field created by each coil element. The 10-g average SAR matrices were computed from the electric fields as well as the conductivity and density distribution, as explained in Guérin et al (37).

The original SAR matrices obtained from the co-simulation step were subsequently compressed into a smaller set of control matrices using the VOP algorithm (14). For the 3T simulation (eight-channel body coil), the VOP algorithm was run with an SAR overestimation factor of 1% of the maximum possible 10-g average SAR, yielding 1289 VOPs. For the 7T simulation (eight-channel head coil), the algorithm was run with an SAR overestimation factor of 5%, yielding 484 VOPs.

Evaluation of the Pulse Design Strategy

For all the simulated scenarios, we compare the results obtained by designing the pulse using, and not using, the proposed algorithm: (i) MLS RF-shimming sinc-shaped pulse design of a uniform slice with flip angle equal to 45° for both the body (3T pTx) and head models (7T pTx) (duty-cycle equal to 10% and 20%, respectively). The time-bandwidth product (TBW) is 4 for both scenarios and the length of the RF pulse (L_RF) is 1.4 ms and 1.6 ms for the body and the head models, respectively. (ii) MLS two-spoke sinc-shaped pulse design of a uniform slice with flip angle equal to 45° for both body and head models (duty-cycle equal to 10% and 20%, respectively). TBW is 8 and Lrf is 2.3 ms and 2.7 ms for the body and the head models, respectively. (iii) LS spiral pulse design for a 20° excitation of the liver for the body model (duty-cycle = 20%, L_RF = 4 ms). (iv) LS spiral pulse design for a 20° excitation of the brain for the head model (duty-cycle = 20%, L_RF = 2.4 ms).

In all cases, the predicted 10-g average SAR and the worst-case SAR in the case of RF errors are calculated for all the VOPs as well as the actual 10-g average SAR for the complete body or head model. Worst-case SAR was calculated by solving Eq. [2] using the errors bounds (ε, δ) = (5%, 2.5°) for the RF-shimming and the two-spoke pulse and (ε, δ) = (15%, 12.5°) for the spiral pulse. These values were chosen as a proof of concept from the 94th–97th percentiles of the measured error distribution of the spokes and spiral pulses correspondently.

Generation of SAR Histograms Using Random RF Perturbations

To test the effect of random errors on SAR, we simulated ten thousand perturbations of an RF-shimming and a spiral pulse and computed the SAR of each randomly perturbed pulse. SAR histograms were created from this data. Random perturbations of the original RF-shimming and spiral pulses were created by drawing random numbers from the nonparametric probability distributions (PDF) of RF errors shown in Figures 3 and 4 and measured on our pTx system. To draw random numbers from these nonparametric PDFs, we used the so-called inverse transform sampling whereby uniformly distributed random numbers are generated and are converted into the desired PDF by inversion of the cumulative distribution. SAR histograms were generated for two of the pulse cases presented in the previous section: RF-shimming (MLS RF-shimming 3T body) and spiral (LS spiral excitation of the liver at 3T). SAR histograms for the RF-shimming (spiral) pulse were obtained using error distributions measured for the four-spoke (spiral) pulse.

Fig. 3.

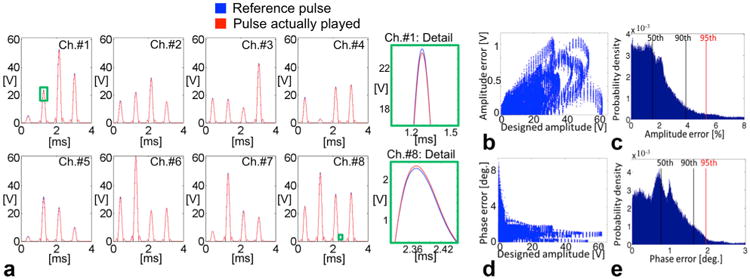
a: Four-spoke pulse played on eight Tx channels (reference pulse is in blue, the pulse actually played in red). A zoom-in detail of channels 1 and 8 is displayed to better visualize the differences. b: Difference between the desired and played RF amplitude as a function of the desired RF amplitude (linear correlation coefficient equal to 0.75). c: Histogram of the RF amplitude errors (SD = 2%). d: Difference between the desired and played RF phase as a function of the desired RF amplitude. e: Histogram of the RF phase errors (SD = 0.7°). In c and e, the 50th, 90th, and 95th percentiles are indicated with vertical lines.

Fig. 4.

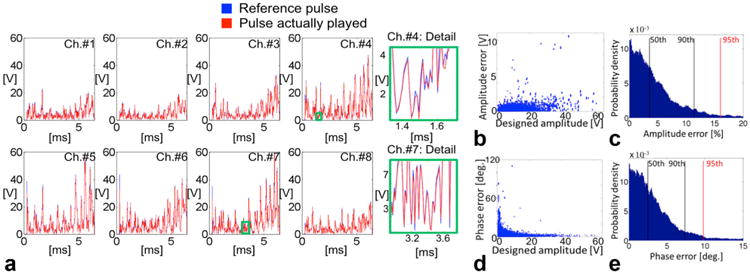
a: Spiral pulse played on eight Tx channels (reference pulse is in blue, the pulse actually played in red). A zoom-in detail of channels 4 and 7 is displayed to better visualize the differences. b: Difference between the desired and played RF amplitude as a function of the desired RF amplitude (linear correlation coefficient equal to 0.44). c: Histogram of the RF amplitude errors (SD = 6.5%) d: Difference between the desired and played RF phase as a function of the desired RF amplitude. e: Histogram of the RF phase errors (SD = 4.4°). In c and e, the 50th, 90^th, and 95th percentiles are indicated with vertical lines.

Worst-case SAR, as explained in the previous subsection, was calculated for a maximum amplitude error of 5% (15%) and a maximum phase error of 2.5° (12.5°) for the spokes (spiral) pulse, consistently with the measured errors reported in the Results section.

Results

Measurements of RF Accuracy

Errors in amplitude and phase were analyzed for values of the four-spoke pulse where the voltage was over the 1% of the maximum amplitude value (see Figure 3). Phase errors are especially high (> 8°) for small voltage values of the pulses while the amplitude errors increase with the nominal voltage getting above 1 V. Error histograms show that a 95% of total errors are below the 6% of the prescribed voltage and 2° in phase (see Figures 3c and 3e).

The second pulse analyzed was a spiral shaped pulse (Fig. 4). This kind of pulse is of special interest for this study, as they are challenging for the RF system because of their high frequency contents and they are known to generate high SAR values. Errors in both amplitude and phase are considerably higher than the ones obtained for the spokes pulses (Fig. 3). Punctual errors of ∼10 V in amplitude were found for prescribed values in the range 20–40 V (see Figure 4b.). Indeed, more than 50% of the measured values show deviations of more than 3 V and 2.5° (Figs. 4c, e.).

Effect of Random RF Errors in SAR Predictions

We generated SAR histograms using different values of the small signal rejection threshold (i.e., 2% and 3% of the maximum RF waveform in addition to the value of 1% used to generate the SAR histograms of Figure 5) and have found that the resulting histograms were almost identical. This indicates that the specific manner in which the small samples of the input RF waveform are rejected is not crucial, as long as we prune these deviations in small signals that can artificially bias the error distribution. Histograms of the maximum 10 g local SAR for the original VOPs are plotted for an RF-shimming (Fig. 5a) and a spiral pulse (Fig. 5b). As explained in the Methods section, these histograms were obtained by generating ten thousand random perturbations of the original pulses by drawing random numbers from the error probability distributions shown of Figures 3 and 4.

Fig. 5.

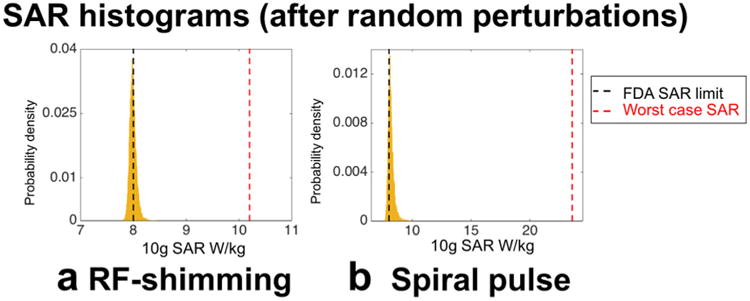
a: Distribution of the maximum local SAR of 10,000 random perturbations of an RF-shimming slice-selective excitation of 45° in the body (duty-cycle = 10%). b: Maximum local SAR distribution of 10,000 perturbed versions of a spiral pulse excitation of the liver for a flip angle of 20° (duty-cycle = 20%). Both pulses were originally designed to produce a maximum peak local SAR of 8 W/kg. Random perturbations of the original pulses were generated from the RF amplitude and phase error distributions of Figure 3 for the RF-shimming and Figure 4 for the spiral pulse. In both scenarios, worst-case SAR is far from the SAR values obtained in the VOPs for the perturbed pulses. However, errors as measured in the pTx system produce pulses exceeding SAR limits.

We observe in Figure 5a that 41% of the randomly perturbed pulses produced SAR values above the safety limit. However, all perturbed pulses had SAR values far below the worst-case SAR (which was 10.2 W/kg for the RF-shimming pulse). In fact, 99% of the pulses had an SAR below 8.17 W/Kg and the maximum local SAR obtained for all pulses was 8.42 W/Kg. For the spiral pulse, 76% of the perturbed pulses exceeded the local SAR limit. The perturbed pulse with the greatest SAR reached 9.86 W/kg, which is 123% of the local SAR limit (8 W/kg). Still, this value was much smaller than the worst possible SAR consistent with bounded RF errors, which was 23.6 W/kg for this spiral pulse. Furthermore, 99% of the pulses reached a maximum SAR below 8.85 W/kg. In both cases, although it is clear that reaching the worst-case SAR becomes practically impossible, errors in RF fidelity can cause SAR problems, if these errors are not taken into account when designing the pulse.

Spokes Pulses Design

Figures 6 and 7 show the performance of our approach for RF-shimming and two-spoke pulses in the body and head models, respectively. The optimization details together with the total time spent for the pulse and the worst-case SAR calculations are displayed in Table 1. Notice that for the spokes pulses, the time spent in the worst-case SAR calculation is significantly shorter than the time spent in the MLS pulse design. This is due to the fact that worst-case calculations are not performed for all the time samples, but only for one and two time samples in the RF-shimming and the two-spoke cases, respectively. Using the realistic knowledge obtained from the error distribution for spokes pulses showed in Figure 3, the maximum amplitude error was fixed to the 5% of the designed pulse amplitude and a maximum deviation of 2.5° in the phase was allowed.

Fig. 6.

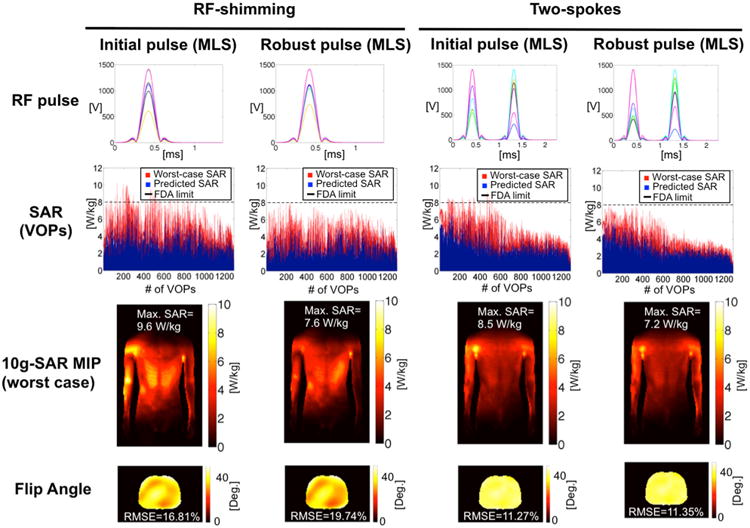
Evaluation of our approach in 3T body simulations (eight Tx channels) for MLS design of spoke pulses. The worst case SAR was calculated for a maximum deviation of 5% for the amplitude and 2.5° in the phase. The first row shows the original pulses as well as those modified to be robust in the presence of transmit errors. The second row shows the SAR distribution across VOPs of the original pulse (in blue) and its worst-case SAR version (in red). Horizontal black lines indicate the FDA SAR limits. The third row shows MIPs of the worst-case SAR distribution of all pulses. In the last row the achieved flip angle maps are displayed. These results show that our method produces RF pulses that are robust even in the presence of worst-case errors in the transmit RF chain. The price to pay for this additional safety-margin is a small loss in the flip-angle distribution that becomes almost negligible for the two-spoke pulse design.

Fig. 7.

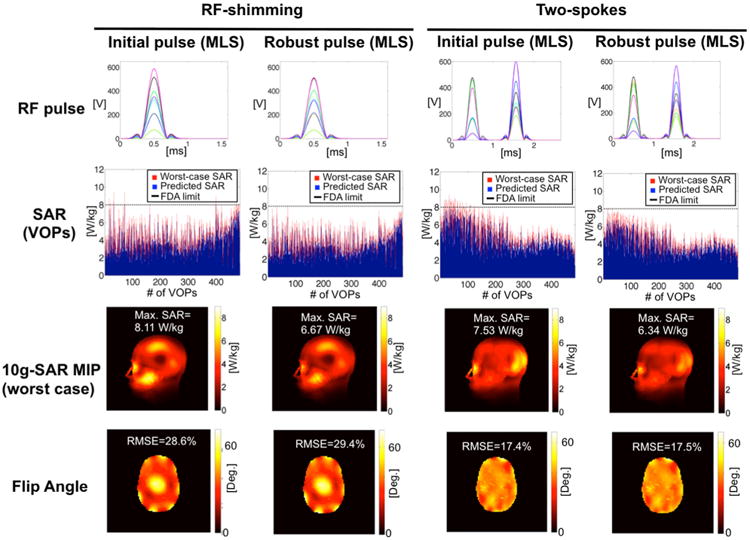
Evaluation of the proposed method for MLS spokes pulse design for head simulations in a 7T scanner. The worst-case SAR was calculated for a maximum deviation of 5% for the amplitude and 2.5° in the phase. The first row shows the original pulses as well as those modified to be robust in the presence of transmit errors. The second row shows the SAR distribution across VOPs of the original pulse (in blue) and its worst-case SAR version (in red). Horizontal black lines indicate the FDA SAR limits. The third row shows MIPs of the worst-case SAR distribution of all pulses. In the last row, the produced flip angle maps are displayed. The proposed algorithm design pulses that never exceed the safety limits with a minimum difference in the flip-angle distribution. Notice the large errors in the flip-angle maps due to the high target flip-angle value (45°).

Table 1. Number of RF Time Samples (N_t), Number of VOP of the Model (N_VOP), Size of the Magnetization ROI, Number of Iterations of the Predictor-Corrector Strategy (N_P-C), Total Time Spent in the Pulse Design (T_PD), and Total Time Spent in the Worst-Case Calculations (T_WC).

	Nt	NVOP	ROI size	NP-C	TPD [s]	TWC [s]
3T 8Ch Body: MLS RF-shimming	135	1289	80×120	3	1,467	132
3T 8Ch Body: MLS Two-spoke	225	1289	80×120	3	2,199	199
3T 8Ch Body: LS spiral	398	1289	80×120	4	1,168	37,600
7T 8Ch Head: MLS RF-shimming	159	484	100×100	2	248	36
7T 8Ch Head: MLS Two-spoke	265	484	100×100	2	476	62
7T 8Ch Head: LS spiral	243	484	100×100	4	316	8,184

In the cases considered, the worst possible SAR calculated for all the VOPs shows that it exceeds the safety limits in several locations when the errors in the RF chain are not taken into account in the pulse design. This problem was found to be more severe for the RF-shimming pulses than for the two spokes design, leading to a worst-case SAR higher than 10 W/kg in the RF-shimming design for body excitation. Robust pulses have a very similar performance in terms of excitation fidelity while the worst-case SAR is controlled to be under the safety limits for both RF-shimming and two-spoke pulses in the 3T and 7T simulated scenarios (see Figures 6, 7). The corresponding loss in the excitation accuracy becomes almost negligible for the two-spoke pulses design because of its better behavior in terms of worst possible SAR after errors, as can be easily seen in the third row of the figures. To force the SAR limits, we set a high target flip angle (45°), which provoked large errors in the flip angle maps for the 7T head model (Fig. 7).

Spiral Pulses Design

The same strategy was also applied in the design of a spiral pulse for tailored excitation in the body and in the head models (optimization details and total calculation times can be found in Table 1). This case is especially interesting because spiral pulses were found to be more affected by errors in the Tx chain in the experiments carried out (Fig. 4). Following the error distribution showed in Figure 4, a maximum deviation of 15% in the amplitude and a maximum error of 12.5° in the phase were set.

The spiral pulse was used for the excitation of the liver in the body model; these results are shown in the two first columns in the Figure 8. The feasible big deviations in this type of pulse lead to a worst-case SAR three times higher than the predicted 10-g average SAR in the VOPs, exceeding the 20 W/kg for some locations. The proposed method achieves reducing the worst-case SAR to be under the limits with a tolerable loss in the excitation fidelity (12.5% RMSE versus an initial RMSE of 6.4%).

Fig. 8.

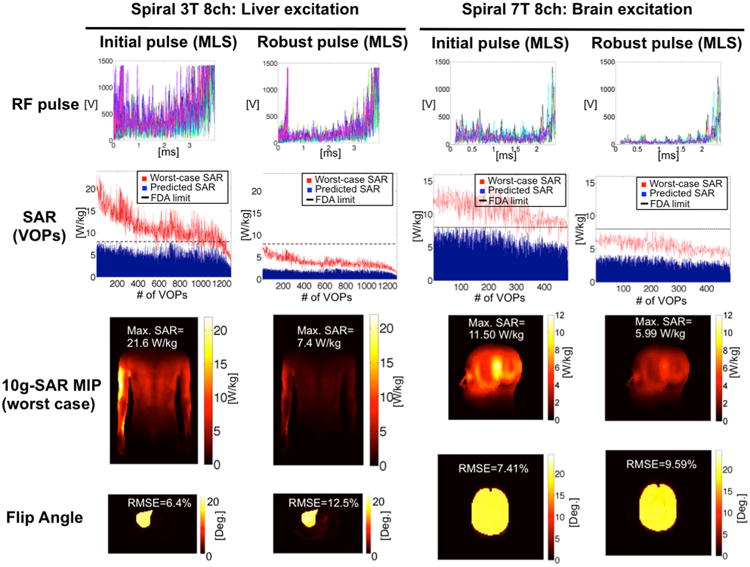
Evaluation of the proposed method for LS design of spiral pulses. The two first columns correspond to the tailored excitation of the liver in the 3T eight-channel body model. The last columns show the result of the technique for brain excitation in the 7T head model. The worst case SAR in both scenarios was calculated for a maximum deviation of 15% for the amplitude and 12° in the phase. The first row shows the original pulses as well as those modified to be robust in the presence of transmit errors. The second row shows the SAR distribution across VOPs of the original pulse (in blue) and its worst-case SAR version (in red). Horizontal black lines indicate the FDA SAR limits. The third row shows MIPs of the worst-case SAR distribution of all pulses. In the last row the achieved flip angle maps are displayed. Worst possible SAR values because of errors are severe when the proposed strategy is not applied. In cases where the worst-case SAR is large compared with the tolerated SAR limit, incorporation of the worst-case SAR information in the pulse design may result in a significant worsening of the flip-angle excitation profile. However, in the examples studied in this work we found that the quality of all excitation profiles remained acceptable even after scaling the SAR constraints using the worst-case SAR information.

The two last columns of the Figure 8 display the results for the brain excitation in the head model simulation. In this case the proposed method reduces the worst possible 10-g average SAR from values over 15 W/kg to values below the FDA limit (8 W/kg) with a small loss in terms of excitation fidelity.

Discussion and Conclusion

We presented a framework for the design of pTx pulses that uses information about the fidelity of the RF transmit chain to avoid exceeding local SAR safety limits even in the presence of potentially large, but bounded, RF transmission errors. This strategy is based on the computation of the maximum possible local and global SAR (i.e., “worst-case SAR”) produced by bounded RF deviations from the prescribed RF waveforms. We used the worst-case SAR to re-compute the RF pulse to ensure that it does not violate the SAR limit even in the presence of maximally constructive RF errors. We showed the efficacy of our method in simulations of 3T body and a 7T head imaging. We showed in this work that the worst-case SAR is a theoretical upper bound that is highly unlikely to be reached in practice. Indeed, actual SAR values obtained by random perturbation of the reference pulse were much lower than the worst-case SAR. Despite this, we believe this metric is very useful to derive safety margins to be incorporated in the pulse design process to ensure safety even in the presence of RF transmission errors.

The price to pay for introducing a new safety margin is a decrease in the excitation performance of the RF pulses. If the original pulse reaches the tolerated limit, worst-case SAR constraints become more constraining than FDA regulations. As expected, decreasing the maximum local SAR limits may drive the designed pulse solution to a different minimum in the optimization problem and increase the excitation error. Figure 8 shows how our method produces good excitation maps even when very large deviations were considered (a 15% of the original amplitude and 12° in the phase). This framework is independent of the type of pulse designed and of the specific pulse design algorithm used, as long as it explicitly constrains global and local SAR, other alternative approaches, e.g. the methods proposed in (11,15,16) can be applied. This strategy can be used in the same way in the design of SAR constrained high flip angle pulses (18,39), where SAR limitations are much more problematic.

The goal of this preliminary study is to demonstrate the validity of the proposed approach. RF measurements were performed in a single pTx system for two particular RF pulses (Figures 3, 4). Then, errors bounds were estimated from this measured data under the assumption that pulses within the same class will suffer from similar RF fidelity errors. In this work, we characterized the RF fidelity of the transmit chain using spoke and spiral pulses played at relatively large duty-cycles (52% for the spoke pulse and 34% for the spiral pulse). Most MRI sequences are played with smaller duty-cycle (which is the ratio of the TR and the excitation pulse duration). Because we expect the fidelity of the RF system to worsen as the duty-cycle increases, the errors estimated in this work are likely to be upper-bound of the actual errors that can reasonably be expected for most MRI sequences. As a consequence, the worst-case SAR values computed in this work are conservative values that are guaranteed to be robust for less demanding duty-cycles. Errors in spiral pulses were experimentally found to be more severe (Fig. 4) than the ones measured for the spokes pulse (Fig. 3). The proposed method is finally applied to certain pulse design scenarios with duty-cycles of 10% and 20%. The SAR increase results due to RF phase and amplitude errors were obtained for an individual system. These results cannot be generalized and should be individually studied for specific systems and pulse design scenarios.

In this work, we characterized the fidelity of the RF transmit chain using a relative amplitude and an absolute phase error metrics. In the work of Zanchi et al (22), RF fidelity was also characterized in terms of relative magnitude and absolute phase errors for correction of amplifier nonlinearities. Gumbrecht (34), also used this representation for real-time analysis of the impact of RF errors on SAR (Sections 7.1 and 7.2). To prevent the small signal to artificially skew our error histograms, we rejected from our analysis those RF samples with a magnitude smaller than 1% of the pulse peak voltage. The entire error analysis contained in this work could have been carried out using a real/imaginary representation of RF pulses. Similar to magnitude/phase representation, one needs to be very careful not to skew the RF error histograms with artificially large errors associated with RF samples with small magnitude. Therefore, small signals should always be rejected for a worst-case SAR analysis.

The relative RF amplitude error that we use in this work can be seen as a linear approximation of the amplifiers fidelity and it is, therefore, a first-order approximation to the full nonlinear RFPA behavior (see References (22,24,40–44)) for more information on amplifiers nonlinearities). The complex fidelity response of RFPAs can be better modeled using the transfer function approach (42); however, it is not straightforward to calculate explicit transfer functions for each amplifier which could be easily included in the calculation of the worst-case SAR. The linear model of the RFPAs deviations, which we use in this work, is approximate, but yields a formulation of the worst-case SAR that can be evaluated using standard optimization algorithms and can also account for other random errors in the RF chain. Therefore, we retain this error metric as a practical compromise between accuracy and computational feasibility. We will study in future work how to include more complex model of RFPA fidelity in the computation of the worst-case SAR. Furthermore, a benefit of using a relative magnitude error metric expressed in percent of the input RF waveform is that this avoids the need for performing a complete error analysis for every new pulse. Indeed, if we had chosen to compute the worst-case SAR using error bounds expressed in absolute units (i.e., Volts) as opposed to percentages, we would have to recompute the RF fidelity histogram for every new pulse being studied. This would render the worst-case SAR metric impractical to use in actual scans. A fundamental assumption behind the use of a relative error metric to characterize the fidelity of the RF transmit chain is that this error bound does not vary dramatically for different pulses in the same class. As we showed in Figures 3 and 4, the percent RF error is different for spokes and spiral pulses. However, we assume in this work that the percent error computed using a specific spoke (spiral) pulse is roughly constant for all spoke (spiral) pulses.

The optimization problem presented in Eq. [2] is not convex. Indeed, it consists in maximizing a quadratic form (convex) while enforcing that the solution (i.e., the unknown RF perturbations yielding the worst-case SAR) lays in a convex set. According to the general theory of maximization of convex functions (45), solutions to this type of problems lie at the boundary of the constraint set. In this case, there exist no theorems proving that a solution is the globally optimal one (theorem only exists for the minimization of a convex function within a convex set). The only way to verify this is by comparison of the optimized solution with all possible pulses laying on the constraint set boundary (i.e., pulses that reach the maximum allowed amplitude and phase deviations), which is an NP-hard problem. In this work, we solve the worst-case SAR optimization (Eq. [2]) using an interior-point approach, which converges quickly but does not guarantee convergence to the global optimum. Despite the lack of guarantee of global optimality, we have found in practice that the pulse solutions found by this approach are associated with values of the objective function equal or greater than other pulses laying on the boundary of the constraint set of Eq. [2] (Eq. [2a]). In other words, we were not able to find pulses that outperformed the interior-point solutions (the constraint set boundary is continuous, therefore, we checked all pulses laying at vertices of the boundary). We also compared the solutions provided by interior-point with solutions obtained using sequential quadratic programming (SQP), which has been suggested as a good alternative for nonlinear nonconvex problems before (46), and found that the two approaches yielded the same worst-case SAR. These observations tend to indicate that, in practice, the worst-case SAR computed by solving Eq. [2] using the interior-point method is close to the global optimum.

In a general pulse design scenario, the worst-case SAR is calculated for each time point of the RF discretization and each SAR matrix. As explained before, we do not have to solve an optimization problem for each time point when spokes pulses are considered. Because there exists a linear relation between every two pulse samples, it is enough to perform the calculations for one time point of each spoke. This leads to a very fast worst-case SAR calculation for spokes-type pulses so providing an attractive method to be implemented in practice (Table 1). For the spiral pulse design, total processing time increases linearly with the length of the pulse and the number of SAR matrices (see Table 1). On the other hand, all these problems are completely independent one from the other, which facilitates a faster parallel implementation using multiple threads or GPU programming. Current code was implemented using the multi-threads options of the Parallel Computing Toolbox in Matlab® (Mathworks, Natick, MA). Compared with sequential code, the parallel implementation is more than 6 times faster on average.

The iterative process that we use in this work to generate robust pulses in the presence of RF transmit errors may not be optimal. Direct incorporation of the worst-case SAR as constraints in the SAR-constrained pulse design calculation may be taken into account. However, such a problem involves adding as new constraints as much optimization sub-problems as SAR matrices are involved, and, therefore, may be hard to solve and very time consuming. In this sense, our approach is a practical strategy that seems a reasonable trade-off between SAR safety, pTx excitation performance and computational complexity. We also point out that there are many other errors that could be modeled in the pulse design process in addition to RF transmit errors, such as B1 maps and gradient trajectory errors. Including these effects in the pulse design would increase the robustness of pTx pulses.