Abstract
Azimuthal movement of tropomyosin around the F-actin thin filament is responsible for muscle activation and relaxation. Recently a model of αα-tropomyosin, derived from molecular-mechanics and electron microscopy of different contractile states, showed that tropomyosin is rather stiff and pre-bent to present one specific face to F-actin during azimuthal transitions. However, a new model based on cryo-EM of troponin- and myosin-free filaments proposes that the interacting-face of tropomyosin can differ significantly from that in the original model. Because resolution was insufficient to assign tropomyosin side-chains, the interacting-face could not be unambiguously determined. Here, we use structural analysis and energy landscapes to further examine the proposed models. The observed bend in seven crystal structures of tropomyosin is much closer in direction and extent to the original model than to the new model. Additionally, we computed the interaction map for repositioning tropomyosin over the F-actin surface, but now extended over a much larger surface than previously (using the original interacting-face). This map shows two energy minima— one corresponding to the “blocked-state” as in the original model, and the other related by a simple 24 Å translation of tropomyosin parallel to the F-actin axis. The tropomyosinactin complex defined by the second minimum fits perfectly into the recent cryo-EM density, without requiring any change in the interacting-face. Together, these data suggest that movement of tropomyosin between regulatory states does not require interacting-face rotation. Further, they imply that thin filament assembly may involve an interplay between initially seeded tropomyosin molecules growing from distinct binding-site regions on actin.
Keywords: Actin; Coiled-coil; Electron microscopy, Molecular Dynamics; Tropomyosin
Introduction
Tropomyosin is a 284 amino acid dimeric protein that forms a coiled-coil structure and plays a key role in the control of muscle contraction. 40 nm long coiled–coiled tropomyosin molecules link end-to-end to form a superhelical cable that wraps around the F-actin filament and thereby follows the filament’s helical trajectory (Lorenz et al. 1995; Hitchcock-DeGregori 2008; Li et al. 2014; Orzechowski et al. 2014a). In striated muscles, the azimuthal position of the tropomyosin cable on F-actin is under the dual control of Ca2+ binding to troponin and myosin binding to F-actin. The changing location of tropomyosin regulates myosin cross-bridge actin interactions, cross-bridge cycling and consequently contraction (Gordon et al. 2000; Poole et al. 2006; Holmes and Lehman 2008; Lehman et al. 2013). At low-Ca2+, tropomyosin is trapped in an inhibitory B-state “blocking” position over the myosin-binding site on actin by a C-terminal regulatory domain of troponin-I (TnI) (Potter and Gergely 1974; Galińska-Rakoczy et al. 2008; Yang et al. 2014). At high-Ca2+, Ca2+-saturated troponin-C (TnC) attracts the TnI-extension away from actin, releasing the steric constraint on tropomyosin and allowing tropomyosin to move azimuthally across actin to a “closed” C-state position. This tropomyosin movement partly uncovers the myosin-binding site, increasing the probability of myosin binding. The ensuing binding of small numbers of myosin heads to F-actin causes further tropomyosin movement to an “open” M-state position, which exposes the myosin-binding site completely and results in full filament activation (Lehman et al. 1994; Vibert et al. 1997). By contrast, when F-actin and tropomyosin are reconstituted in the absence of troponin and myosin (in the “apo” A-state), tropomyosin is still localized very near to the B-state position, but with increased azimuthal variance (Lehman et al. 2009; Li et al. 2011). The structural and biochemical evidence that has led to our current understanding of mechanisms for tropomyosin movement over the surface of actin to control myosin-binding and muscle activity, however, still remains incomplete. Indeed, a new structural model (von der Ecken et al. 2014) appears to invalidate the consensus view of how tropomyosin movement happens, and a further analysis of this structure is the principal subject of this study.
The binding of a single tropomyosin molecule to the F-actin filament is very weak; estimates of Ka are in the ~3000 M−1 range, making straightforward binding determination problematical (Wegner 1980). In fact, tropomyosin molecules only remain on F-actin because the end-to-end linked tropomyosin cable wraps many times around the F-actin filament (Monteiro et al. 1994; Hitchcock-DeGregori 2008; Holmes and Lehman 2008). Since the total binding energy of the cable derives from the sum contribution of about 25 molecules per micron of thin filament, it follows that collective binding association of the tropomyosin cable on F-actin will be tight while locally interactions between tropomyosin and actin will remain weak, thus providing low energy costs for azimuthal transitions between regulatory states. In fact, energy maps of the interactions between actin and tropomyosin on troponin- and myosin-free filaments yield a broad and relatively flat energy basin (Orzechowski et al. 2014b), centered around the A/B-position. The breadth of this basin indicates that, when tropomyosin is not pinned down by troponin or myosin, the protein can then oscillate between the B- and C-positions, as has been previously proposed (McKillop and Geeves 1993; Lehman et al. 2000; Pirani et al. 2005; Maytum et al. 2008).
A full molecular description of thin filament assembly and regulation requires information defining the longitudinal, azimuthal and rotational positioning of tropomyosin on F-actin in all physiological states. In fact, three geometric parameters are necessary to unambiguously determine the average position of tropomyosin on F-actin: (1) the azimuthal angle of tropomyosin around the central axis of F-actin, (2) its longitudinal position parallel to that axis, and (3) the pseudo-rotation of tropomyosin that determines which face of tropomyosin (subsequently referred to as the “interacting-face”) is turned towards the actin filament (cf. Fig. 5 in Lorenz et al. 1995). Electron microscopy and 3D reconstruction are well suited for determining the azimuthal rotation angle of tropomyosin on actin. However, tropomyosin densities in current ~8 A° resolution cryo-EM reconstructions lack the resolution to discriminate sidechains. Therefore, the longitudinal position and the interacting- face of tropomyosin on actin cannot be fully defined; viz., any longitudinal displacement of the tropomyosin backbone can be fitted into a given EM density by a compensating change in the interacting-face (cf. Fig. 9 in the extended data of von der Ecken et al. (2014)). To determine all three geometric parameters pertaining to the EM-density of the A-state, Li et al. (2011) performed a computational search to optimize the electrostatic energy of interaction between F-actin and tropomyosin. This led to a model of tropomyosin in the A-state for which the longitudinal position and the interacting-face are both well defined. Later, a high-resolution cryo-EM reconstruction by Behrmann et al. (2012) of myosin-decorated F-actin used flexible fitting of crystal structures of tropomyosin fragments to match the EM contours. This led to a detailed model of tropomyosin in the M-state, whose interactingface was identical to that of the Li et al. (2011) model of the A-state. This lent credence to the notion that tropomyosin has the same internal conformation in the A/B- and M-regulatory states, and thus that this conformation is likely to be retained as tropomyosin slides across actin throughout the B → M transition as well (Orzechowski et al. 2014b).
Recently, von der Ecken et al. (2014) published a cryo- EM reconstruction for the A-state, where tropomyosin position differed significantly from that in the EM data of Li et al. (2011), presumably because of the dissimilar conditions of filament preservation. A model of tropomyosin proposed by von der Ecken and co-workers to fit their densities involves a radical change in the interacting-face compared to that in the Li et al. model. This implies that tropomyosin might easily assume different super-helical shapes, which led these authors to propose that tropomyosin might roll instead of slide on the surface of actin.
Figure 1 illustrates how tropomyosin rolling versus sliding could modify the interacting-face presented to actin. The major goal of the present study is to help decide which of these two possibilities is the more likely, a tropomyosin model that can change its interacting-face and therefore can roll, or one that always presents the same face to actin and therefore must slide. For this purpose, we compared tropomyosin models to known crystal structures, and we computed the energy map of the electrostatic interactions between tropomyosin and F-actin for a much larger region of the actin surface than done in our earlier studies (Orzechowski et al. 2014). We find that the Li et al. (2011) model fits better to crystal structures than the model by von der Ecken et al. (2014) does. Moreover, the extended energy landscape reveals the existence of a second region of low (i.e., favorable) interaction energy, whose center is related to the Li et al. model by a simple translation of 24 Å parallel to the F-actin axis (without changes in the interacting-face). The actin-tropomyosin structure at the center of this region fits well into the actintropomyosin cryo-EM density of von der Ecken et al. (2014), which can now be fully explained without having to invoke a change in the interacting-face of tropomyosin.
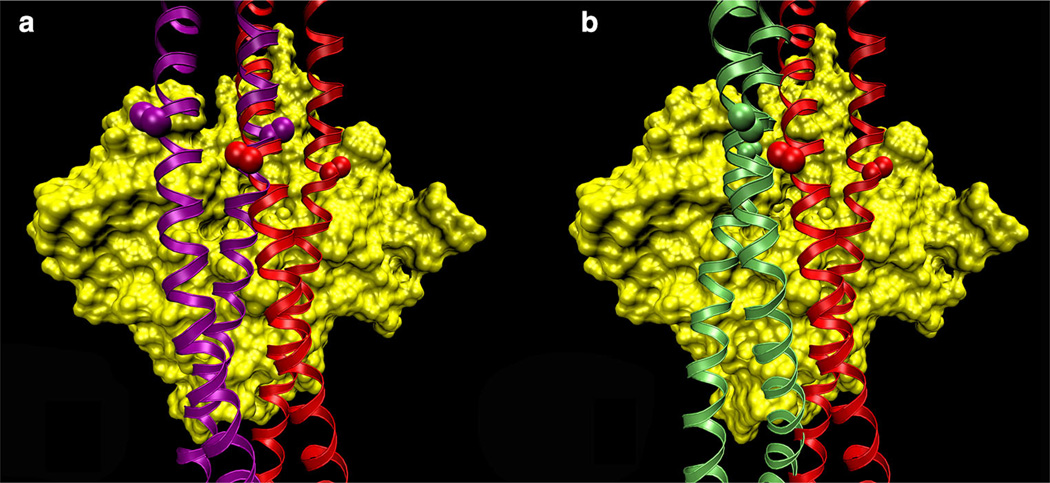
Fig. 1.
Binding-mode possibilities of tropomyosin on F-actin. Models of tropomyosin (ribbons) superposed on an actin subunit (surface rendered in yellow). a The Li et al. (2011) structure (red) was translated longitudinally and rotated azimuthally to a new position (purple), keeping the interacting-face unchanged. Note how the side chains of residues 118 (marked by spheres) are parallel to the surface of actin in both structures. b The von der Ecken et al. (2014) model (green) presents a different face to F-actin than the Li et al. (2011) model does. Note how the residue 118 side-chains are perpendicular to the surface of F-actin, thus the interacting-face is different between the two models
Methods
Structural analysis
All calculations were performed with the program CHARMM (version c35b2; Brooks et al. 2009). von der Ecken et al. (2014) fitted tropomyosin onto an F-actin model that is marginally different from the one used here (Oda et al. 2009), and which has a slightly different helical twist. We therefore adjusted the coordinates of their tropomyosin model (PDB code 3J8A) to match the helical symmetry of the Oda structure to allow a better superposition of models (Fig. 2) and RMSD comparisons (Table 1).
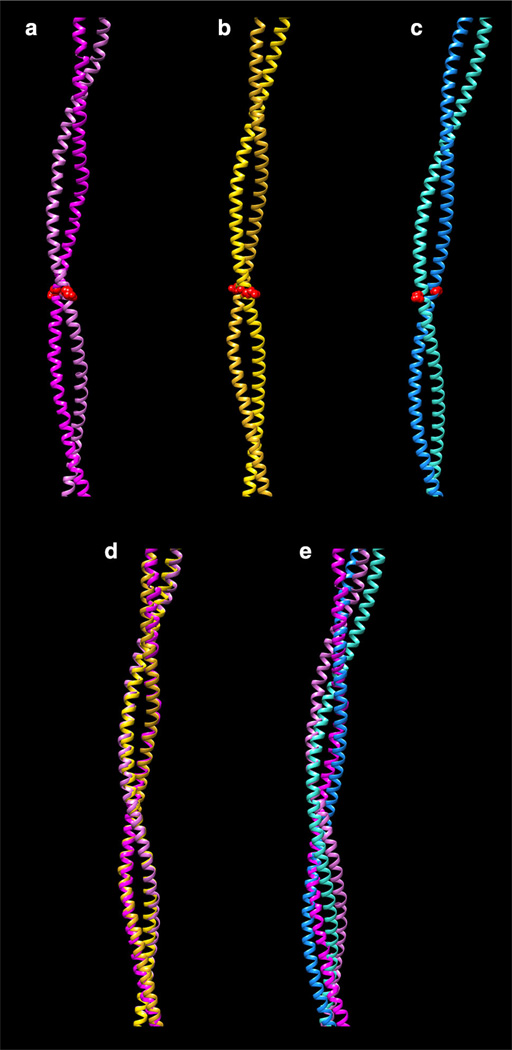
Fig. 2.
Fitting of different tropomyosin models to crystal structures. a Whitby and Phillips (2000) 7 Å resolution structure (PDB ID:1C1G). b Li et al. (2011) model. c von der Ecken et al. (2014) model (PDB ID:3J8A). Only residues in which the crystal structure remains super-helical are shown (residues 50–175). Note that the interacting-face is the same in (a) and (b), but differs from that in (c); for example, compare the orientation of the side-chain 104 (shown as red spheres). d Superposition of (a) and (b). e Superposition of (a) and (c). Note that the match in d is considerably better than in e. All structures are viewed with their concave side (i.e., the F-actin interacting-face) towards the right. Alignment of structures was performed using the MatchMaker tool of the program Chimera (Pettersen et al. 2004)
Table 1.
RMS deviations (Å) between crystal structures and tropomyosin models
| PDB IDa | Li et al. model (2011)b |
von der Ecken et al. model (2014)c |
|---|---|---|
| 1C1G | 1.91 | 4.76 |
| 1IC2 | 1.15 | 1.39 |
| 1KQL | 1.26 | 1.71 |
| 3U1A | 0.89 | 1.46 |
| 3U59 | 1.51 | 1.92 |
| 2D3E | 1.65 | 2.85 |
| 2B9C | 1.31 | 1.56 |
Root-mean-square deviation (RMSD) for the Cα-backbone atoms between tropomyosin models and crystal structures, after alignment with the rmsd-plugin of the program VMD (Humphrey et al. 1996)
The splayed or non-coiled-coil ends of the crystal structures were truncated prior to RMSD calculation, the employed residues are: 1C1G, Whitby-Phillips model (2000), residues 50–175 (same as segment shown in Fig. 2a). 1IC2, N-terminal 81 residues (striated muscle α-tropomyosin, Brown et al. (2001)). 1KQL, C-terminal 31 residues (rat striated muscle α-tropomyosin, Li et al. (2002)). 3U1A, N-terminal 81 residues (chicken gizzard smooth muscle α-tropomyosin, Rao et al. (2012)). 3U59, N-terminal 98 residues (chicken gizzard smooth muscle α-tropomyosin, Rao et al. (2012)). 2D3E, 134 C-terminal residues (rabbit striated muscle α-tropomyosin, Nitanai et al. (2007)). 2B9C, residues 98–175 (rat striated muscle α-tropomyosin, Brown et al. (2005))
Li et al. (2011) model, shown in Fig. 1a, 2b and 3a
von der Ecken et al. (2014) model, shown in Fig. 1b and 2c
Energy map calculations
An extended energy map, in which tropomyosin is translated longitudinally and rotated azimuthally on a cylindrical grid around the actin filament, was computed as described previously (Orzechowski et al. 2014b) with some minor modifications: The F-actin filament consisted of 21 actin molecules (Oda et al. 2009), each with bound ADP and Mg2+. One tropomyosin molecule (composed of a twochained coiled-coil) was placed on one of the helical strands of F-actin, always using the same interacting-face as in Li et al. (2011). (A second tropomyosin over the “back side” strand of the filament was not used, because it would be redundant for the measurements made here). To preserve the integrity and the symmetry of the actin filament during energy minimizations, some parts of F-actin were not allowed to move (i.e. they were “fixed”), including: (1) the ten actin monomers on the back side of the filament, (2) one actin monomer at each end of the “front” helical strand, (3) any actin residue with at least one atom inside of a 20 Å radius from the center of the F-actin helical axis and (4) residues with less than 4 Å2 of accessible surface area (using a 2 Å probe radius), which were regarded as buried. The F-actin was extensively energy minimized (in the absence of tropomyosin), while iteratively transferring the coordinates of the moving atoms of one actin monomer to the corresponding atoms of the other actin monomers, in order to preserve the helical symmetry between actin monomers. The resulting structure was used as the starting F-actin structure for each point on the map.
Side-chain orientations in the starting structure used for tropomyosin were described previously by Li et al. (2010, 2011); viz., side chains were oriented in accord with high-resolution crystal structures of tropomyosin fragments then available. Because there is no suitable crystal structure for fragments containing residues 76–97, these side chains were now built based on sequence similarity to other tropomyosin fragments: side chains 76–87 were modeled on residues 76–87 of a recent crystal structure of smooth muscle tropomyosin (PDB ID-2U59; Rao et al. 2012); the side chain conformation of Leu88 and Asn89 were taken from Leu207 and Glu208 in the 2B9C PDB (Brown et al. 2005), and side chains for residues 90–97 were taken from residues 11–18 of a non-muscle tropomyosin structure (PDB ID-3AZD; Meshcheryakov et al. 2011). N- and C-terminal ends of tropomyosin make an overlap complex with each other when tropomyosin associates end-to-end to form a cable on actin filaments. In previous analyses of the overlap domain (Orzechowski et al. 2014a), it was shown that residues 1–24 and 254–284 do not have a typical coiled-coil conformation. Therefore, the ends of the tropomyosin molecule were truncated, keeping only residues 25–253. This tropomyosin model was then extensively energy minimized (in the absence of actin), while being subjected to two constraints, in order to maintain the superhelical shape of the coiled-coil: (1) Harmonic constraints were placed on the distance between the centers-of-mass of each quarter of the molecule, as well as between the N- and C-termini, in order to preserve the overall bending of tropomyosin. (2) Cylindrical distance constraints were applied to the center of mass of each of the seven pseudo-repeats (~40 residues long), to keep each pseudo-repeat at a distance of 39 Å from the actin central axis [to be consistent with thin filament fiber diffraction studies (Lorenz et al. 1995)]. The resulting structure was then placed on F-actin, for all points represented by the map.
For each point of the energy map, the minimized tropomyosin was rotated azimuthally and translated parallel to the F-actin axis in steps of 2° and 2.5 Å, respectively. The F-actin filament composed of 21 actin monomers is long enough to always extend beyond each end of tropomyosin by at least two actin units for any point of the present map. A positive longitudinal displacement in the interaction energy map corresponds to movement of tropomyosin towards the “pointed end” of F-actin. The [azimuth, longitude] point [0,0] on the map is arbitrarily chosen to correspond to the Li et al. (2011) model, relative to which the displacements are measured here. Ridges occur at the lateral edges of the actin monomer interface that would result in severe steric clashes with the tropomyosin cable. These regions were not sampled. The energy of each map point assessed was minimized. Initially, harmonic constraints to the starting position of actin and tropomyosin were applied and gradually released. However, the fixing of F-actin atoms and the geometrical constraints described above were maintained throughout the minimization. The steepest descent and conjugate gradient algorithms were used, until the potential energy gradient was less than 0.05 kcal/mol.
Results and discussion
Preferred bending of tropomyosin inferred from crystal structures
The tropomyosin model proposed by Li et al. (2011) was constructed to match the helical contours of F-actin. Comparison of the Li et al. model (Fig. 2) to crystal structures of tropomyosin suggests that the tropomyosin super-helix bends with a naturally preferred curvature and shape. For example, the Whitby-Phillips 7 Å resolution crystal structure (Fig. 2a) of full length tropomyosin (Whitby and Phillips 2000) aligns to the Li et al. model very well (Fig. 2d). The corresponding RMSD is only 1.9 Å (Table 1), which is low for the long molecular stretch (185 Å) tested. In addition, RMS deviations between the Li et al. model and high resolution crystal structures of tropomyosin fragments from both striated and smooth muscles are small (Table 1). This good agreement results from the fact that tropomyosin and these crystal structures are bent in the same direction and with comparable curvature. Note that this preferred bending is conserved across crystal structures despite differences in tropomyosin construct, crystallization conditions, and lattice constraints. This common bending is a strong indication that tropomyosin has a natural inherent tendency to bend in a way that yields a preferred interacting-face when bound to actin filaments. In marked contrast, the von der Ecken et al. (2014) model (Fig. 2c) yields a structure that fits poorly to the 7 Å resolution crystal structure (Fig. 2e), with an RMSD of 4.76 Å (Table 1). Likewise, its fit to high resolution tropomyosin fragments is poorer when compared to the corresponding fitting of the Li et al. model for all crystal structures examined (Table 1). This suggests that the model proposed by von der Ecken et al. is not a preferred stable conformation of tropomyosin, and perhaps is an unsatisfactory accounting of tropomyosin binding to F-actin.
A new binding mode is found in the interaction map and validated by cryo-EM
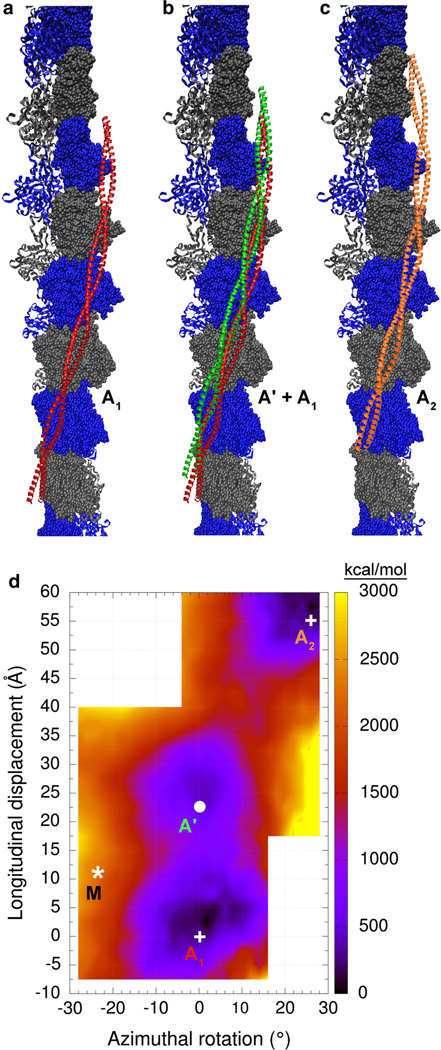
An extended surface of actin was probed to measure the Coulombic interaction between F-actin and tropomyosin. An interaction map was calculated starting from the previously published F-actin-tropomyosin model (Li et al. 2011). Each point in the map was generated by applying azimuthal rotations and longitudinal translations in 2° and 2.5 Å steps, respectively, to tropomyosin in the model, then minimizing the resulting complex and calculating the Coulombic interaction energy. The Li et al. (2011) model in this map is arbitrarily placed at point [0°, 0 Å]. The region of F-actin surveyed by tropomyosin through these rotations and translations is illustrated in Fig. 3a–c. Note that tropomyosin was repositioned super-helically in azimuthal and axial directions, and without changing its interacting-face, to examine interactions over eight contiguous actin subunits, covering a larger surface of F-actin than in previous studies (Orzechowski et al. 2014b). Ridges occur at the lateral edges of the actin monomer interface that would result in severe steric clashes with the tropomyosin cable; therefore, these regions were not sampled. The resulting energy landscape is shown in Fig. 3d. It reveals that there are two distinct and prominent minima. One minimum (marked A1 in Fig. 3d) has been previously described (Orzechowski et al. 2014b). Its center corresponds to the position and conformation of tropomyosin described by Li et al. (2011) (Fig. 3a). The other minimum, which was previously unknown, is centered on the coordinates [0°, 24 Å], marked by a white circle and denoted here as A’. It corresponds to the green tropomyosin structure on F-actin shown in Fig. 3b. The difference in Coulombic interaction energy between the two minima is 407 kcal suggesting that the A site is preferred over the A’ location of tropomyosin on actin.
Fig. 3.
Coulombic interaction energy landscape of actin-tropomyosin. Shown are tropomyosin positions on F-actin (surface with alternating gray and blue colors). a the Li et al. (2011) tropomyosin model (red). b the Li et al. (2011) model in red and a tropomyosin model in green that corresponds to energy minimum A’ in d. c the Li et al. (2011) model (orange) shifted helically by one actin unit relative to its position in a. Note that the models shown here cover a large portion of the actin surface accessible to tropomyosin. d Each point in the energy landscape on this map gives the electrostatic energy of interaction between F-actin and one tropomyosin coiled-coil, which has been longitudinally and azimuthally repositioned while showing the same interacting-face to F-actin (see “Methods” section). The lower right hand and upper left hand corners of the graph were not sampled, since ridges on F-actin in those locations would result in severe steric clashes with the tropomyosin cable. Positions at the energy minima of the landscape are labeled A1, A’ and A2 (and with white circles and crosses) and correspond to the structures shown in a–c, respectively. The asterisk marked M indicates the position of the M-state model of Behrmann et al. (2012) for comparison. The energies [in kcal/mol] are given relative to the minimum energy position
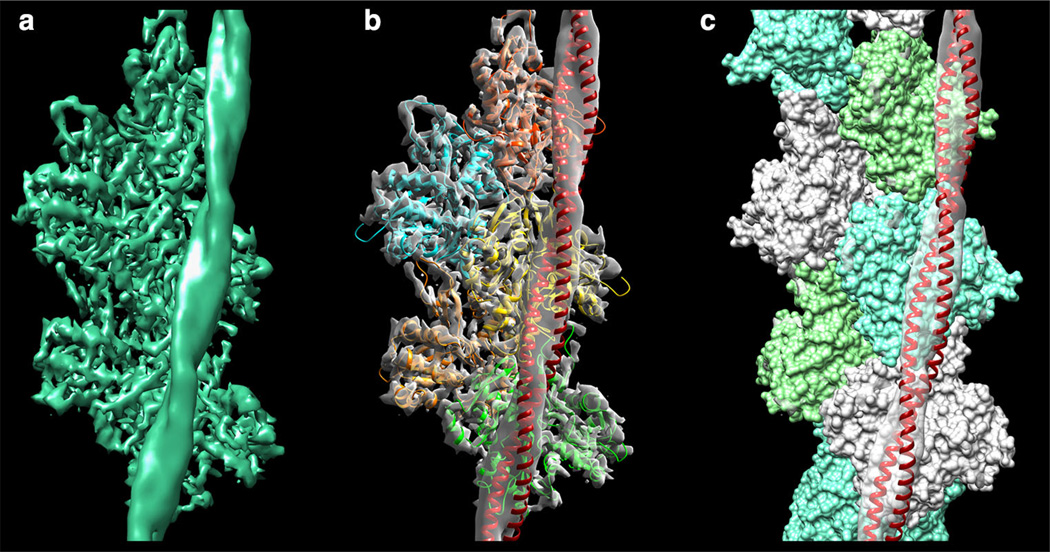
When this A’ actin-tropomyosin structure is fitted rigidly into the von der Ecken et al. (2014) cryo-EM density, it yields a near perfect match (see Fig. 4). Note that the entire actin-tropomyosin structure was fitted as a unit, and not actin and tropomyosin separately. It is remarkable that this excellent agreement of both actin and tropomyosin with the cryo-EM density can be achieved without any flexible fitting. In this newly found binding mode, tropomyosin presents the same interacting-face to F-actin as in the model of the A/B-states of Li et al. (2011) as well as in the cryo-EM model for the M-state of Behrmann et al. (2012). This is further evidence that tropomyosin is likely to always present the same interacting-face to F-actin during the muscle regulation. If this is true, then it follows that during tropomyosin’s transitions between B-, C- and M-regulatory states, tropomyosin does not roll over the surface of F-actin (which would involve changes in the interacting-face), but more than likely slides over the surface, as previously proposed (Behrmann et al. 2012; Orzechowski et al. 2014b). In fact, additional energy landscapes performed indicate that pseudo-rotated tropomyosin positioned and displayed on actin as in von der Ecken et al. (2014) is not at a deep energy minimum (data not shown).
Fig. 4.
Fitting the new tropomyosin model into the cryo-EM structure. a The cryo-EM density of F-actin-tropomyosin (von der Ecken et al. 2014; EM Data bank ID-6124). b, c Rigid body fitting of the actin-tropomyosin structure defined by point A’ on the map in Fig. 3d (consisting of F-actin and a tropomyosin configuration shown in green in Fig. 3b) into the cryo-EM density of a made translucent. The tropomyosin coiled-coil is shown as a red ribbon, actin subunits are shown as b ribbons or c in space-filling format
Lacking information on side-chain orientation as cues to locate tropomyosin residues on actin in EM-reconstructions, any longitudinal displacement of the tropomyosin backbone can be equally well fitted into a given EM density by a compensating change in its interacting-face without any such longitudinal shift, as already pointed out by von der Ecken et al. (2014) and shown schematically in their extended data [see Fig. 9 in von der Ecken et al. (2014)]. Because of the ambiguity between longitudinal positioning and interacting-face orientation of tropomyosin in such moderate resolution data, alternative tropomyosin models are equally plausible without further information available. The model proposed in von der Ecken et al. (2014), in which tropomyosin has a different interactingface, fits the cryo-EM data well; however, it does not match the crystal structures tested above. The alternative structure we have presented here, where the Li et al. model is shifted longitudinally by ~24 Å (as illustrated in Fig. 3b), accurately fits to the cryo-EM maps (Fig. 4b, c), as well as matches the crystal structure and energy landscape data. This again suggests that the model proposed by Li et al. (2011) is a more satisfactory accounting of tropomyosin binding to F-actin.
Longitudinal movement of tropomyosin on actin
The newly found binding position (A’ in Fig. 3d) raises the question whether or not an A → A’ transition of the tropomyosin cable is a probable event physiologically. The large 24 Å longitudinal shift between A and A’ tropomyosin position would require the simultaneous disruption of about 30 electrostatic interactions per tropomyosin molecule (i.e. between one tropomyosin molecule and the seven corresponding actin units). In order to occur over the entire tropomyosin cable, this would need to be repeated simultaneously 25 times (along 1 µm long thin filaments), resulting in a very high energetic cost. Thus, it is unlikely that the cable could undergo an A → A’ transition within the time-scale of muscle activation. Moreover, the troponin and/or myosin bound to actin-tropomyosin in muscle might further impede such a transition. However, our results suggest that in the absence of troponin and myosin, the initial nucleation event of the first tropomyosin molecules binding to F-actin can occur in the A or the A’ position. During elongation, a stable chain may then be formed in either the A or the A’ locations. Different experimental conditions appear to readily affect the relative stability of the A and the A’ positions, which is a likely explanation why the negative staining procedures yielded the A binding mode (Li et al. 2011) and cryo-EM yielded the A’ mode (von der Ecken et al. 2014).
Our results raise the question whether axial and azimuthal diffusion of tropomyosin may be a factor in the formation of the tropomyosin cable. Indeed, if the initial association of tropomyosin with seven successive actin subunits along filaments is random (Wegner 1980; Schmidt et al. 2015), then the chains growing from initially seeded molecules will likely be out-of-register with regard to neighboring seven-actin units, resulting in gap formation. However, gaps are not observed on muscle filaments. One explanation is that after nucleating at a single site of F-actin (e.g. the filament ends), nascent tropomyosin chains grow uniformly from that point (Johnson et al. 2014; Hsiao et al. 2015; Gunning et al. 2015). Alternatively, tropomyosin may initially bind at multiple sites, and followed either by a stochastic mechanism of nucleation/annihilation or by means of axial diffusion, gaps are filled between growing tropomyosin chains on F-actin (Holmes and Lehman 2008; Schmidt et al. 2015). Although axial motion of a whole cable appears unlikely as discussed above, a short “train” comprised of a few tropomyosin molecules might be able to diffuse axially, “jumping” between A-and A’-states, and then coalesce into a longer train at a lowest energy position. Moreover, the additional presence of myosin or troponin may distort the actin-tropomyosin landscape and serve to select between A- and A’-state tropomyosin during filament assembly. Higher resolution imaging of tropomyosin comparable to that already achieved for the actin subunits in F-actin will help to discriminate among these interesting possibilities.
Our observations imply that thin filament assembly involving the 40 or so different tropomyosin isoforms in non-muscle cells may necessarily be even more complex than originally thought (see excellent review by Gunning et al. 2015). Cellular actin-binding proteins not only might bias tropomyosin to one or another positional state, but sequence-specific differences in the isoforms might also define new tropomyosin-actin landscape minima. The resulting isoform-specific thin filament properties may bias or restrict co-assembly of the tropomyosin isoforms on single filaments. Similarly, diverse filament initiators, such those in the formin family (Johnson et al. 2014), might select out tropomyosin isoforms with particular favored binding locations on actin.
Acknowledgments
These studies were supported by NIH grant R37HL036153 to W.L. The Massachusetts Green High Performance Computing Center and the IWR (University of Heidelberg) provided computational resources.
Contributor Information
William Lehman, Email: wlehman@bu.edu.
Stefan Fischer, Email: stefan.fischer@iwr.uni-heidelberg.de.
References
- Behrmann E, Müller M, Penczek PA, Mannherz HG, Manstein DJ, Raunser S. Structure of the rigor actin–tropomyosin–myosin complex. Cell. 2012;150:327–338. doi: 10.1016/j.cell.2012.05.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks BR, Brooks CL, MacKerell AD, Nilsson L, Petrella RJ, Roux B, et al. CHARMM: the biomolecular simulation program. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JH, Kim KH, Jun G, Greenfield NJ, Dominguez R, Volkmann N, Hitchcock-DeGregori SE, Cohen C. Deciphering the design of the tropomyosin molecule. Proc Natl Acad Sci USA. 2001;98:8496–8501. doi: 10.1073/pnas.131219198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JH, Zhou Z, Reshetnikova L, Robinson H, Yammani RD, Tobacman LS, Cohen C. Structure of the mid-region of tropomyosin: bending and binding sites for actin. Proc Natl Acad Sci USA. 2005;102:18878–18883. doi: 10.1073/pnas.0509269102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galińska-Rakoczy A, Engel P, Xu C, Jung H, Craig R, Tobacman LS, Lehman W. Structural basis for the regulation of muscle contraction by troponin and tropomyosin. J Mol Biol. 2008;379:929–935. doi: 10.1016/j.jmb.2008.04.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon AM, Homsher E, Regnier M. Regulation of contraction in striated muscle. Physiol Rev. 2000;80:853–924. doi: 10.1152/physrev.2000.80.2.853. [DOI] [PubMed] [Google Scholar]
- Gunning PW, Hardeman EC, Lappalanien P, Mulvihill DP. Tropomyosin—master regulator of actin filament function in the cytoskeleton. J Cell Sci. 2015 doi: 10.1242/jcs.172502. (in press). doi: 10.1242/jcs.172502. [DOI] [PubMed] [Google Scholar]
- Hitchcock-DeGregori SE. Tropomyosin: function follows form. Tropomyosin and the steric mechanism of muscle regulation. Adv Exp Med Biol. 2008;644:60–67. doi: 10.1007/978-0-387-85766-4_5. [DOI] [PubMed] [Google Scholar]
- Holmes KC, Lehman W. Gestalt-binding of tropomyosin to actin filaments. J Muscle Res Cell Motil. 2008;29:213–219. doi: 10.1007/s10974-008-9157-6. [DOI] [PubMed] [Google Scholar]
- Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J Mol Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Hsiao JY, Goins LM, Petek NA, Mullins RD. Arp2/3 complex and cofilin modulate binding of tropomyosin to branched actin filaments. Curr Biol. 2015;25:1573–1582. doi: 10.1016/j.cub.2015.04.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson M, East DA, Mulvihill DP. Formins determine the functional properties of actin filaments in yeast. Curr Biol. 2014;24:1525–1530. doi: 10.1016/j.cub.2014.05.034. [DOI] [PubMed] [Google Scholar]
- Lehman W, Craig R, Vibert P. Ca2+-induced tropomyosin movement in Limulus thin filaments revealed by three- dimensional reconstruction. Nature. 1994;368:65–67. doi: 10.1038/368065a0. [DOI] [PubMed] [Google Scholar]
- Lehman W, Galińska-Rakoczy A, Hatch V, Tobacman LS, Craig R. Structural basis for the activation of muscle contraction by troponin and tropomyosin. J Mol Biol. 2009;388:673–681. doi: 10.1016/j.jmb.2009.03.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehman W, Hatch V, Korman V, Rosol M, Thomas L, Maytum R, Geeves MA, Van Eyk JE, Tobacman LS, Craig R. Tropomyosin and actin isoforms modulate the localization of tropomyosin strands on actin filaments. J Mol Biol. 2000;302:593–606. doi: 10.1006/jmbi.2000.4080. [DOI] [PubMed] [Google Scholar]
- Lehman W, Orzechowski M, Li XE, Fischer S, Raunser S. Gestalt-binding of tropomyosin on actin during thin filament activation. J Muscle Res Cell Motil. 2013;34:155–163. doi: 10.1007/s10974-013-9342-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li XE, Holmes KC, Lehman W, Jung H-S, Fischer S. The shape and flexibility of tropomyosin coiled-coils: implications for actin filament assembly and regulation. J Mol Biol. 2010;395:327–399. doi: 10.1016/j.jmb.2009.10.060. [DOI] [PubMed] [Google Scholar]
- Li XE, Tobacman LS, Mun JY, Craig R, Fischer S, Lehman W. Tropomyosin position on F-actin revealed by EM reconstruction and computational chemistry. Biophys J. 2011;100:1005–1013. doi: 10.1016/j.bpj.2010.12.3697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li XE, Orzechowski M, Lehman W, Fischer S. Structure and flexibility of the tropomyosin overlap junction. Biochem Biophys Res Commun. 2014;446:304–308. doi: 10.1016/j.bbrc.2014.02.097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Mui S, Brown JH, Strand J, Reshetnikova L, Tobacman LS, Cohen C. The crystal structure of the C-terminal fragment of striated-muscle alpha-tropomyosin reveals a key troponin T recognition site. Proc Natl Acad Sci USA. 2002;99:7378–7383. doi: 10.1073/pnas.102179999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz M, Poole KJV, Popp D, Rosenbaum G, Holmes KC. An atomic model of the unregulated thin filament obtained by X-ray fiber diffraction on oriented actin-tropomyosin gels. J Mol Biol. 1995;246:108–119. doi: 10.1006/jmbi.1994.0070. [DOI] [PubMed] [Google Scholar]
- Maytum R, Hatch V, Konrad M, Lehman W, Geeves MA. Ultra short yeast tropomyosins show novel myosin regulation. J Biol Chem. 2008;283:1902–1910. doi: 10.1074/jbc.M708593200. [DOI] [PubMed] [Google Scholar]
- McKillop DFA, Geeves MA. Regulation of the interaction between actin and myosin subfragment-1: evidence for three states of the thin filament. Biophys J. 1993;65:693–701. doi: 10.1016/S0006-3495(93)81110-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meshcheryakov VA, Krieger I, Kostyukova AS, Samatey FA. Structure of a tropomyosin N-terminal fragment at 0.98 Å resolution. Acta Crystallogr D. 2011;67:822–825. doi: 10.1107/S090744491102645X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monteiro PB, Lataro RC, Ferro JA, Reinach Fde C. Functional alpha-tropomyosin produced in Escherichia coli. A dipeptide extension can substitute the amino-terminal acetyl group. J Biol Chem. 1994;269:10461–10466. [PubMed] [Google Scholar]
- Nitanai Y, Minakata S, Maeda K, Oda N, Maéda Y. Crystal structures of tropomyosin: flexible coiled-coil. Adv Exp Med Biol. 2007;592:137–151. doi: 10.1007/978-4-431-38453-3_13. [DOI] [PubMed] [Google Scholar]
- Oda T, Iwasa M, Aihara T, Maéda Y, Narita A. The nature of the globular- to fibrous-actin transition. Nature. 2009;457:441–445. doi: 10.1038/nature07685. [DOI] [PubMed] [Google Scholar]
- Orzechowski M, Li XE, Fischer S, Lehman W. An atomic model of the tropomyosin cable on F-actin. Biophys J. 2014a;107:694–699. doi: 10.1016/j.bpj.2014.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orzechowski M, Moore JR, Fischer S, Lehman W. Tropomyosin movement on F-actin during muscle activation explained by energy landscapes. Arch Biochem Biophys. 2014b;545:63–68. doi: 10.1016/j.abb.2014.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera–a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Pirani A, Xu C, Hatch V, Craig R, Tobacman LS, Lehman W. Single particle analysis of relaxed and activated muscle thin filaments. J Mol Biol. 2005;346:761–772. doi: 10.1016/j.jmb.2004.12.013. [DOI] [PubMed] [Google Scholar]
- Poole KJ, Lorenz M, Evans G, Rosenbaum G, Pirani A, Tobacman LS, Lehman W, Holmes KC. A comparison of muscle thin filament models obtained from electron microscopy reconstructions and low-angle X-ray fibre diagrams from non-overlap muscle. J Struct Biol. 2006;155:273–284. doi: 10.1016/j.jsb.2006.02.020. [DOI] [PubMed] [Google Scholar]
- Potter JD, Gergely J. Troponin, tropomyosin, and actin interactions in the Ca2+ regulation of muscle contraction. Biochemistry. 1974;13:2697–2703. doi: 10.1021/bi00710a007. [DOI] [PubMed] [Google Scholar]
- Rao JN, Rivera-Santiago R, Li XE, Lehman W, Dominguez R. Structural analysis of smooth muscle tropomyosin α and β isoforms. J Biol Chem. 2012;287:3165–3174. doi: 10.1074/jbc.M111.307330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt WM, Lehman W, Moore JR. Direct observation of tropomyosin binding to actin filaments. Cytoskeleton. 2015;72:292–303. doi: 10.1002/cm.21225. doi: 10.1002/cm.21225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vibert P, Craig R, Lehman W. Steric-model for activation of muscle thin filaments. J Mol Biol. 1997;266:8–14. doi: 10.1006/jmbi.1996.0800. [DOI] [PubMed] [Google Scholar]
- von der Ecken J, Müller M, Lehman W, Manstein DJ, Penczek PA, Raunser S. Structure of the F-actin-tropomyosin complex. Nature. 2014;519:114–117. doi: 10.1038/nature14033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wegner A. The interaction of alpha, alpha-and alpha, beta-tropomyosin with actin filaments. FEBS Lett. 1980;119:245–248. doi: 10.1016/0014-5793(80)80263-8. [DOI] [PubMed] [Google Scholar]
- Whitby FG, Phillips GN., Jr Crystal structure of tropomyosin at 7 Angstroms resolution. Proteins. 2000;38:49–59. [PubMed] [Google Scholar]
- Yang S, Barbu-Tudoran L, Orzechowski M, Craig R, Trinick J, White H, Lehman W. Three-dimensional organization of troponin on cardiac thin filaments in the relaxed state. Biophys J. 2014;106:855–864. doi: 10.1016/j.bpj.2014.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]