Markov state models of protein misfolding

Abstract

Markov state models (MSMs) are an extremely useful tool for understanding the conformational dynamics of macromolecules and for analyzing MD simulations in a quantitative fashion. They have been extensively used for peptide and protein folding, for small molecule binding, and for the study of native ensemble dynamics. Here, we adapt the MSM methodology to gain insight into the dynamics of misfolded states. To overcome possible flaws in root-mean-square deviation (RMSD)-based metrics, we introduce a novel discretization approach, based on coarse-grained contact maps. In addition, we extend the MSM methodology to include “sink” states in order to account for the irreversibility (on simulation time scales) of processes like protein misfolding. We apply this method to analyze the mechanism of misfolding of tandem repeats of titin domains, and how it is influenced by confinement in a chaperonin-like cavity.

I. INTRODUCTION

Recently, Markov state models (MSMs) have become one of the tools of choice for the analysis of molecular dynamics (MD) simulations in the study of biological systems.^1,2 In this type of model, the dynamics of the biomolecule are modeled as a stochastic network of transitions between metastable conformational states. Although MSMs were first introduced in the study of peptide folding,^3–7 and they continue to reveal new insights into small systems,^8–10 their principal applications have been extended to include protein folding,^11–20 the native dynamics of protein structures,^21,22 ligand binding,^23–26 the dynamics of nucleic acids,^27–29 and even the study of large macromolecular machines like dynamin.³⁰ In spite of their versatility, and the availability of dedicated software packages such as MSMbuilder³¹ or Emma³² that automate their generation, there are nonetheless still challenges in deriving MSMs from simulation data. Here we focus on two of these issues: the discretization of the conformational space sampled during the simulation, and the ergodicity of the resulting stochastic network. We analyze a coarse-grained simulation model for the misfolding via domain swapping of titin^33,34 as a biologically relevant example where these two problems are manifested.

When constructing an MSM, the atomic coordinates of the biomolecule in the myriad of conformations visited during the simulation are typically clustered into thousands of discrete states. Although novel methods are being derived for the clustering,³⁵ many times the root-mean-square deviation between the cartesian coordinates of pairs of structures (RMSD) is employed as a structural metric to identify these clusters. However, a global RMSD suffers from the problem that structures separated by a large energy barrier may nonetheless be separated by a very small RMSD; on the other hand, using a very small RMSD cutoff can lead to an unmanageable number of states, and difficulty in determining their connectivity from equilibrium simulations. Recent work suggests that alternative similarity metrics, based on the contact map of the protein^18,20 or the backbone dihedral angles³⁶ may perform better in identifying kinetically connected states. These metrics have the advantage of being closely correlated with local minima in the energy landscape, i.e., rotameric states in the case of dihedrals and formation/breaking of atomic contacts in the case of contact maps. Still, the number of states based on possible dihedral angle combinations (2^N in the simplest description, considering just 2 possibilities α and β for each of the N protein residues⁷) or alternative contact maps (naively, 2^n_c, where n_c is the number of contacts in the contact map²⁰) can make the use of these discretizations challenging. Here, we introduce coarse contact maps³⁷ in the context of MSMs, as a means of alleviating the clustering problem.

A second difficulty is that strong connectivity within the network of microstates is usually assumed in the dynamical model. In other words, the conformational dynamics of the protein are modelled as an ergodic Markov chain, where for every pair of microstates i and j one can define a path from i → j and from j → i. In practice this is done by identifying ergodic subgraphs in the clustered data and then restricting the analysis to the maximal ergodic subgraph.³¹ However, this presents a problem for systems where there exist very stable states or traps, from which the system never (or very rarely) escapes on the simulation time scale. In these situations, trimming the network so that its largest ergodic part is retained may severely distort the results if some of the discarded states turn out to be important for the system properties. In our case, for example, they may be very long-lived misfolded states that appear to be traps (experimental evidence suggests these states to be stable on a time scale of days³³). While one possibility would be to obtain additional data in order to sample the reverse transitions (out of traps), if such transitions only occur on a much longer time scale they may not be of practical interest anyway. Here, we present an approach to including such states in the model, where a standard analysis is done for the largest ergodic subgraph, but absorbing states are also included in the final model, resulting in alternative stationary distributions. For this type of Markov state model with absorbing states the solution can be calculated analytically, for given initial conditions. The resulting method is generally applicable to scenarios where the condition of ergodicity is not fulfilled.

In this study we focus on the misfolding of tandem immunoglobulin domains from the giant protein titin. This system has been studied extensively using both experiments³³ and simulations.^38,39 In this work we use a simple model for protein folding/misfolding that successfully predicted the formation of domain-swapped structures.³³ Here we probe multiple misfolding scenarios by analyzing simulations of the tandem repeat protein in isolation and in different confinement conditions, which we have reported before.⁴⁰

This paper is organized as follows. First, we very briefly describe the simulation model. Second, we introduce the Markov state model methodology. Then, we describe the details in the construction of the MSM, with particular detail in the description of the two main contributions of this work, the new coarse contact map discretization, the construction of a transition matrix that does not require ergodicity and the calculation of the infinite time population of the Markov state model with absorbing states. Finally, we show the analysis of the MSM for the titin domain swapping.

II. METHODS

A. Molecular system and MD simulations

We analyse coarse-grained molecular simulations of titin, including the possibility of domain-swapped misfolding. The protein simulation model, described in an earlier publication,³³ is summarized briefly here. The protein representation was generated using the 1tit PDB structure, using the Cα-based Gō model of Karanicolas and Brooks.⁴¹ An additional linker with sequence RSEL was introduced between the domains, as in the experiment. Linker-protein interactions were treated by short-ranged repulsive potentials. In addition to the standard Gō-like contacts within each domain, we introduced additional native-like contacts between domains, i.e., if (i, j) was an intra-domain native contact, the contacts (i + N, j) and (i, j + N) were added as interdomain contacts, where N = 93 is the length of one domain plus linker.

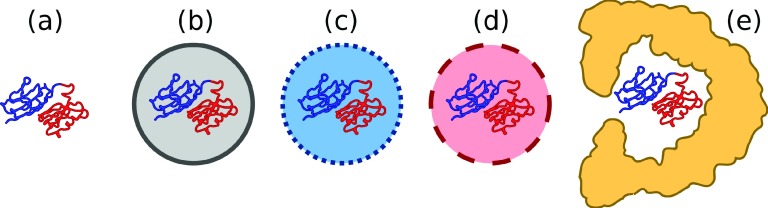
In addition to free titin (see Fig. 1(a)), we considered several additional scenarios of titin under confinement similar to those described in our previous study.⁴⁰ The titin was confined within a spherical cavity with an additional short range contact potential between the protein residues and the boundary, such that the energy for a residue contacting the wall was −ε. We considered the following scenarios: essentially repulsive walls (ε = 10⁻⁴ kJ mol⁻¹, Fig. 1(b)), “weakly” attractive walls (ε = 0.5 kJ mol⁻¹, Fig. 1(c)), or “strongly” attractive walls (ε = 1.0 kJ mol⁻¹, Fig. 1(d)). A cavity radius of 35 Å was used to provide a volume comparable to that of the GroEL interior. In the interest of investigating the robustness of our MSM analysis to potentially complex folding scenarios, simulations were also performed of titin inside a residue-level coarse-grained model of GroEL, analogous to previous simulations of rhodanese in GroEL⁴² (Fig. 1(e)). Interactions between titin and GroEL were described using the Kim-Hummer protein-protein interaction model, rescaled appropriately for the simulation temperature.⁴³ Long first passage time simulations were run, 50 per folding scenario, starting from a high-temperature unfolded state, at a temperature of 270 K, using Langevin dynamics with a friction of 0.1 ps⁻¹. Simulations were carried out using a modified version of GROMACS 4.0.5 software package.⁴⁴ Further details may be found in our earlier work.^33,42

FIG. 1.

Cartoons of the titin folding scenarios. (a) Free titin, (b) repulsive cavity, (c) “weakly” attractive cavity, (d) “strongly” attractive cavity, and (e) GroEL. The two repeat domains of titin are shown in different colours.

B. MSM theory

Here, we give a brief overview of relevant MSM theory; more detailed descriptions are available elsewhere.^5,6,45 We describe the dynamics of the system as a Markov chain, where memory-less transitions occur between non-overlapping regions of configurational space, which we term microstates. The probability of finding the system in a certain microstate at time t + Δt hence depends only on the microstate of the system at time t and not on the previous history. The time evolution of the system can be described by a transition matrix T(Δt) through the equation

$${\displaystyle \mathbf{p}\left(n\mathrm{\Delta }t\right)=\mathbf{T}\left(n\mathrm{\Delta }t\right)\mathbf{p}\left(0\right)={\left[\mathbf{T}\left(\mathrm{\Delta }t\right)\right]}^n\mathbf{p}\left(0\right),}$$ (1)

where p(t) is a vector of microstate populations at time t and p(0) the set of initial populations. The matrix T has a set of eigenvalues {λ}, that outline the transition modes of the system and the time scales {τ} on which they occur through the relation

$${\displaystyle {\tau }_i=-\frac{\mathrm{\Delta }t}{ln{\lambda }_i}.}$$ (2)

The corresponding set of left ({ϕ}) and right ({ψ}) eigenvectors describes the transitions associated with each mode.

C. Coarse contact map discretization

To define the microstates of the model, the continuous conformational space explored in the titin simulations was discretised using a novel approach. As mentioned above, using the pairwise RMSD can prove problematic when the configuration space to be covered becomes large. Residue contact maps are a more intuitive and concise way to distinguish individual structures, especially for the native-centric modelling used here. Residue-level contact maps were calculated for each structure as follows:

$${\displaystyle C_{ij}^{\mathrm{structure}}=\{\begin{array}{ll}1\hfill & \mathrm{if}{r}_{ij}<\lambda r_{ij}^{\mathrm{native}}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array},}$$ (3)

where r_ij is the separation between residues i and j in the structure of interest and $r_{ij}^{\mathrm{native}}$ is the native or domain-swapped contact separation, as defined by the inter-residue distance in the native structure of titin. λ was a scaling factor set to 1.2, allowing for fluctuations about the minimum energy contact distance.

Initially, we attempted to cluster these residue-level contact maps using the leader algorithm,⁴⁶ which generates a number of clusters of fixed radius r_c. The distance metric for clustering was the difference between contact maps (L₁ norm)

$${\displaystyle d(A,B)=\sum _{\mathrm{contacts}i,j}\left|C_{i,j}^A-C_{i,j}^B\right|.}$$ (4)

However, d(A, B) is highly sensitive to noise arising from small differences in individual contacts and therefore, at small cluster sizes, structures that were essentially the same were separated into distinct clusters; on the other hand, increasing the cluster radius resulted in dissimilar structures being placed in the same cluster.

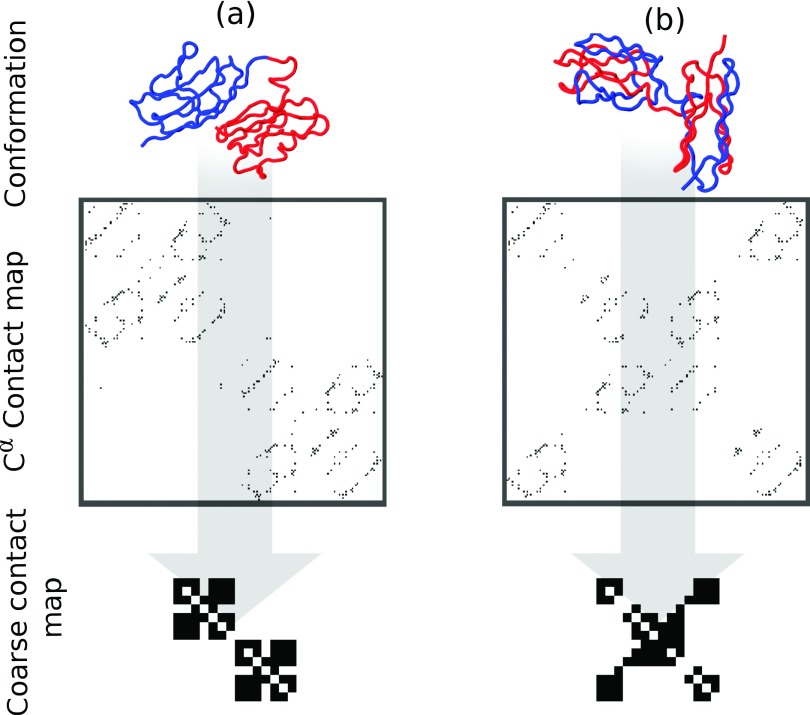
In order to reduce the sensitivity of the clustering to individual contacts, we exploited the observation that the structures of folded and misfolded titin mostly differ in the positioning of individual β strands on the titin domains. We subsequently calculated coarse-grained, strand-based contact maps S by defining a contact between two strands as being present when at least half of the native or domain-swapped contacts between those strands were formed (see Figure 2)

$${\displaystyle S_{ij}=\{\begin{array}{ll}1\hfill & \mathrm{if}{q}_{ij}/q_{ij}^{\mathrm{native}}>0.5\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}.}$$ (5)

Here, q_ij is the total number of native and native-like misfolded contacts between residues in strand i and strand j and $q_{ij}^{\mathrm{native}}$ is the number of contacts between these strands in the native structure. A total of 14 β strands were defined, 7 on each domain, reducing the contact map size from 182²/2 to 14²/2 elements, significantly reducing the amount of data stored and the variation seen between identical states due to thermal fluctuations of individual residue-residue contacts. The strand-based contact maps also made it easier to identify folded and misfolded states since domain-swapped contacts between entire strands were now more clearly distinguishable from the correctly formed intradomain contacts (see Fig. 2).

FIG. 2.

Coarse-grained representation of titin misfolding. (a) Natively folded titin; (b) domain-swapped, misfolded titin. Top row shows structures with the N-terminal domain coloured blue and the C-terminal coloured red. Middle row shows residue-residue contact maps corresponding to each structure and bottom row shows the contact maps defined between secondary structure elements (β-strands).

A strand-based contact map was calculated for every frame of the 250 trajectories, maintaining a count for the number of times each unique map appeared. Maps seen fewer than 50 times over all the simulations were discarded as they were considered to be highly unstable or transient states. The contact maps were then clustered based on similarity using the leader algorithm with the d(A, B) metric, as described above, so that structures differing by fewer than the cluster radius of r_c = 5 strand-strand contacts were classed into the same microstate. Any conformation with fewer than 8 strand-strand contacts was considered to be in a separately defined unfolded cluster. The clusters generated by this scheme defined a consistent set of conformational microstates for constructing the MSM, shared between the folding scenarios.

D. Constructing the Markov state model

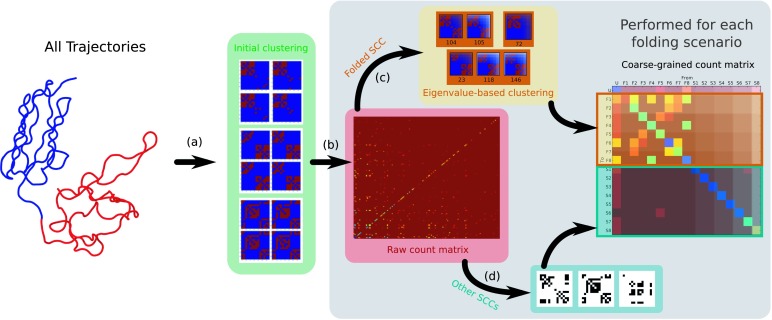
For the system of interest a number of innovations have been introduced within the traditional set of steps (i.e., assignment, estimation, and lumping) involved in producing a Markov state model from the discretized simulation data.⁶ A general scheme of the procedure we introduce here is shown in Figure 3. In summary, first, the simulation trajectories are assigned to the microstate space defined above using coarse contact maps (a). Then, the raw count matrix is calculated. At this point the ergodic and non-ergodic subgraphs are separated (b), and the largest ergodic subgraph (Folded SCC) is aggregated into conformational macrostates via the Perron cluster analysis (c). The folded and remaining subgraphs (d) are finally combined into a global model that combines detailed information about the folding mechanism as well as information about the events that may result in the molecule getting stuck into a misfolded conformation.

FIG. 3.

Schematic of algorithm for deriving Markov state models. In step (a), structures from the simulations are mapped to coarse-grained contact maps, which are further reduced by clustering. In (b), the initial assignment to coarse contact maps is used to count transitions between states after a fixed lag time, Δt. The strongly connected network is coarse-grained via a standard PCCA procedure in (c), and by adding back the disconnected states (sinks), (d), the final set of coarse grained states is defined and used to construct a coarse-grained transition matrix.

1. Constructing the microstate transition matrix

For each folding scenario a count matrix N was generated by iterating over the frames of the trajectory using non-overlapping windows of width Δt. The lag time Δt used was 1 ns, which was sufficient to identify transitions to the folded and misfolded states via intermediates, while ignoring unimportant processes that occurred on shorter time scales. The transition matrix T (Figure 3), giving the probability of making a transition from microstate j to i was calculated using the maximum likelihood estimator⁴⁵

$${\displaystyle T_{ij}=\frac{N_{ij}}{{\sum }_i{N}_{ij}}.}$$ (6)

2. Separation of ergodic and non-ergodic sub-graphs

In order to gain a more intuitive description of the processes corresponding to the slow dynamics of the system we further coarse grain the microstate MSM by lumping the microstates into a few macrostates.⁶ An eigenvector-based clustering method using the microstate MSM would be an obvious way to reduce the overall number of states. However, the standard PCCA clustering analysis requires an ergodic transition matrix,⁴⁷ while our microstate transition matrix includes sinks such as the fully folded and misfolded states (Fig. 2).

In order to circumvent this problem we treated the transition matrix as an adjacency matrix defining a directed graph, and then identified the strongly connected components (SCCs) of the graph. Following the methods used in previous work,⁴⁸ Tarjan’s algorithm⁴⁹ was used to identify the SCCs from the transition probability matrix T. The SCCs of a directed graph are subgraphs which satisfy the property that from every node in the subgraph there is a path to every other node in both the forward and reverse directions, i.e., each subnetwork is an ergodic Markov chain.

In general, the analysis yields one large strongly connected subnetwork including the folded state, and this can be further clustered using PCCA (see Section II D 3). Each of the other subnetworks represents a potential sink in the full MSM with the unfolded state as a common source, and once entered into by the system, there is no escape except via the unfolded state. The next step was generating a subset of the transition matrix T^F, which corresponded to the SCC containing the folded state. Note that by design the folded SCC did not contain the unfolded state as this was a commonly shared state that potentially exchanged with states in all the SCCs, not just the folded SCC.

3. PCCA of the folding subgraph

In practice, the eigenspectrum of the transition matrix for the folded SCC, T^F, was first calculated. This provides a good indication of the number of significant processes taking place within the native folding subnetwork. The relative time scales {τ} were calculated in order to determine the existence of a large separation in time scale after a certain number of modes, M − 1; based on the first M − 1 modes, a “macrostate” model with M coarse-grained states could be constructed.

Next, the Perron-cluster cluster analysis (PCCA) method was applied to hierarchically lump the microstates in the native folding subnetwork together into a set of M macrostates in order to maximise the metastability of each macrostate.^6,50 For M expected macrostates, the right eigenvectors {ψ} associated with the M slowest modes (ignoring the first, stationary mode) were inspected in order to lump the microstates based on their participation in the transition. Specifically, microstates were progressively lumped based on the sign of each ψ_k, for k = 1, …, M, i.e., for each k, all states where ψ_k < 0 were separated from those states where ψ_k > 0. The procedure was repeated for each eigenmode until the desired number of macrostates, M had been obtained.

4. Merging the SCCs

Transitions from the unfolded state (a source) and to the other SCCs (sinks) were now incorporated into the simplified transition matrix. In order to generate the coarse-grained count matrix, the trajectory frames were reassigned based on their corresponding lumped macrostate if they were part of the native folding subnetwork (labelled F_i in the figures) or based on the non-folded SCC of which they were a member (labelled S_i in the figures). The folded state was sampled far more frequently in the simulations than any misfolded states, and therefore some transitions were observed leaving the folded state while this was not the case for most misfolded states, which we presume is due to their lower population. Therefore, the transition rates out of the folded state PCCA cluster were set to zero, in order to obtain p(∞) populations of the folded state. Thus, our infinite time solution really corresponds to the situation after a few minutes in experiment, where the protein has initially folded to the native or domain-swapped dimer. Subsequent equilibration via unfolding (of either misfolded, or native states) occurs on a much longer time scale of days³³ and is not sampled here.

E. Infinite time solution

In order to determine the ultimate fate of the system at long times the population distribution p(∞) can be calculated for an absorbing Markov chain using the solution devised by Kemeny.⁵¹ The criterion that a Markov chain be absorbing is that there exists a state which cannot be escaped even at infinite times and that it is possible to access an absorbing state in the chain from any non-absorbing state (potentially via intermediate states). Since there was always at least one absorbing (sink) state, the native state PCCA cluster (see Subsection II D 4), this solution could be universally applied to all the folding scenarios.

For a system with r absorbing states and t transient states (those that are not sinks), the transition matrix can be arranged as follows:

$${\displaystyle \mathbf{P}=\left(\begin{array}{cc}\hfill \mathbf{Q}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{R}\hfill & \hfill \mathbf{I}\hfill \end{array}\right),}$$ (7)

where Q is a t × t matrix, R a t × r matrix, 0 an r × t zero matrix and I an r × r identity matrix. We know that the expected probability of making a transition from transient state i to transient state j after n steps is $Q_{i,j}^n$. Summing the matrix Qⁿ quantity over all n gives the fundamental matrix N,⁵² which we later use to determine the remaining properties of the absorbing Markov chain,

$${\displaystyle \mathbf{N}=\sum _{k=0}^{\infty }{\mathbf{Q}}^k={({\mathbf{I}}_t-\mathbf{Q})}^{-1},}$$ (8)

where I_t is a t × t identity matrix. The elements of N denote the expected number of times the system enters state j given it started in state i. From there it is simple to obtain the probability of entering an absorbing state j from transient state i as each element of the matrix

$${\displaystyle \mathbf{B}=\mathbf{R}\mathbf{N}.}$$ (9)

III. RESULTS AND DISCUSSION

A. Assignment of the titin misfolding datasets to the coarse contact maps

Coarse-grained simulations of titin, based on native and native-like interactions, have given powerful insights into the types of misfolded species which may be formed at long times, with the results being very consistent with experimental FRET data when available.^33,40 However, a detailed analysis of the intermediates involved in both folding and misfolding is currently lacking. Part of the reason is that it is difficult to find simple reaction coordinates which capture the diverse range of species that can be populated. Therefore, we set out here to analyze the pathways for misfolding by constructing a representative Markov state model. The main questions we seek to answer are: (i) what are the major pathways and metastable states of folding and misfolding? and (ii) is there a possibility of rescue from misfolding pathways via reversible transitions.

Here, we analyze Gō model MD simulations of titin that have previously been performed under a range of folding scenarios: the unconfined protein “free in solution”, and within confining spheres having (i) repulsive walls, (ii) moderately attractive walls, or (iii) strongly attracting walls, as well as an explicitly atomistic model for the GroEL chaperonin cavity (see Figure 1).⁴⁰ For each folding scenario, frames from the simulation trajectories were assigned to different microstates defined using strand-based contact maps, and transitions between pairs of these states after a lag time of 1 ns were counted, producing a matrix of transition counts N, Fig. 2. In Figure S1 of the supplementary material,⁵³ we show the dependence of the slowest modes on the lag time for the unconfined case. We observe a variation of a factor of ∼2 in the slowest modes for a change in lag time of more than two orders of magnitude, suggesting that the Markovian approximation is quite reasonable, and we use the shortest lag of 1 ns in order to retain the most detailed kinetic information. We have also tested the sensitivity of the results to the amount of data used. When using only half the data (Figure S2⁵³), the observed relaxation times are very similar.

In Table I, we can see that at the chosen lag time of 1 ns, over a million unique states in total are visited over all the folding scenarios, a substantial number of which have very low population and would be highly transient intermediates on a (mis)folding pathway. These are first pruned by discarding those contact maps which were visited fewer than 50 times over all the simulations, and then clustering the surviving states. States that differed by fewer than 5 contacts in their contact maps were placed in the same cluster, and some representative clusters are shown in Figure 3(a). Evidently, not all the microstates obtained in this global clustering procedure are visited by the trajectories of every folding scenario.

TABLE I.

Clustering statistics for the individual titin folding scenarios, where n is the total number of unique contact maps, n_p is the number of contact maps seen more than 50 times, n_c the total number of microstates, post-clustering, n_v the number of microstates visited under each folding scenario, n_f is the number of states in the folded SCC, M the number of PCCA clusters, and n_CG the number of final coarse-grained states.

Scenario:	Unconfined	Repulsive	Weak	Strong	GroEL
n	1 149 021
np	9 520
nc	153
nv	88	53	64	102	56
SCCs	9	21	16	5	20
nf	30	28	28	31	31
M	8	5	7	9	7
nCG	17	26	23	14	32

While the folding mechanism is unlikely to change drastically for different confinement conditions, the relative populations of the misfolded microstates may be affected by excluded volume effects and protein-cavity interactions. Looking at the number of states visited by each folding scenario, n_v (Table I), allows us to get some preliminary ideas about the effect each type of confinement has on the folding pathways of titin. Relative to the unconfined case, the repulsive sphere and GroEL cavity reduce the number of unique microstates visited by the system. Introducing attractive interactions increases n_v, to a degree proportional to the strength of the interaction. A possible cause for this is stabilisation of the folded and misfolded states due to the volume exclusion effects of repulsive confinement, thereby accelerating folding towards these stable states and restricting exploration of the conformational space.

To reduce the number of states visited, such that the transition network is more comprehensible, we would like to construct a coarse-grained transition network reflecting only the populations of the important metastable states. To do so, we first decompose the transition network of each folding scenario into individual subnetworks, i.e., the strongly connected components (SCC’s) of the graph represented by the global transition matrix combining the data from all simulation trajectories. The largest SCC is designated the folded SCC, as the majority of transitions occurs around the native state and its intermediates. All the SCCs are connected via the unfolded state and therefore it is isolated as a source for the derivation of the coarse-grained transition matrix T (also since the unfolded state, defined using a simple maximum threshold on the number of contacts formed, is already highly coarse-grained).

B. Clustering the folded SCC

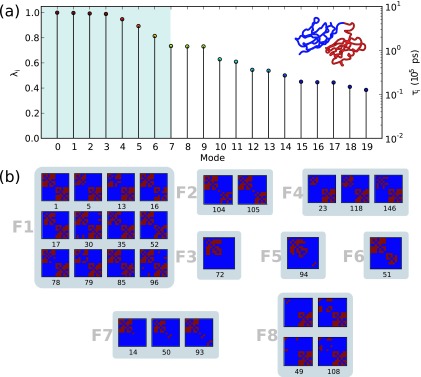
Next, we set out to simplify the states in the folded SCC so that only metastable states are represented. The first 20 eigenvalues of the folded SCC for the unconfined folding scenario are shown in Figure 4(a). The corresponding eigenvalues for the other confinement scenarios are shown in Figure S3.⁵³ As an outcome of separating the global transition network into its constituent SCCs, the native folding subnetwork for each scenario has only one stationary eigenmode (λ_i = 1), corresponding to the equilibrium distribution of states within the subnetwork. The remaining eigenvalues shown in Figure 4 correspond to the 19 slowest processes in the system. Naturally, only the slowest modes are of concern, as they represent the transitions taking place between the most metastable states in the system. By examining the eigenspectrum of each folding scenario, the slowest modes can be identified and an appropriate number of clusters, M, can be chosen for the PCCA lumping (see Table I). As an example, the PCCA macrostates obtained for the unconfined titin are shown in Figure 4. Notably, all the folding scenarios have roughly the same number of states in their folding SCCs and, more importantly, similar macrostates are obtained for all the folding scenarios, comprising the native folded state and the intermediates corresponding to either domain being folded.

FIG. 4.

PCCA clustering. (a) Eigenvalue spectrum for the folded SCC of unconfined titin and (b) corresponding PCCA clusters from the strongly connected clusters (SCCs).

The coarse-grained transition matrix is generated by defining each of the PCCA-derived macrostates of the folded SCC as separate states, with the other misfolded SCCs, and the unfolded cluster, each being described by a single state. The PCCA cluster containing the native folded state (F1, F1, F3, F3, and F2 for the unconfined, repulsive sphere, weakly attractive sphere, strongly attractive sphere, and GroEL, respectively) is enforced to be a sink by setting all rates for leaving it to zero.

C. Graphing the networks

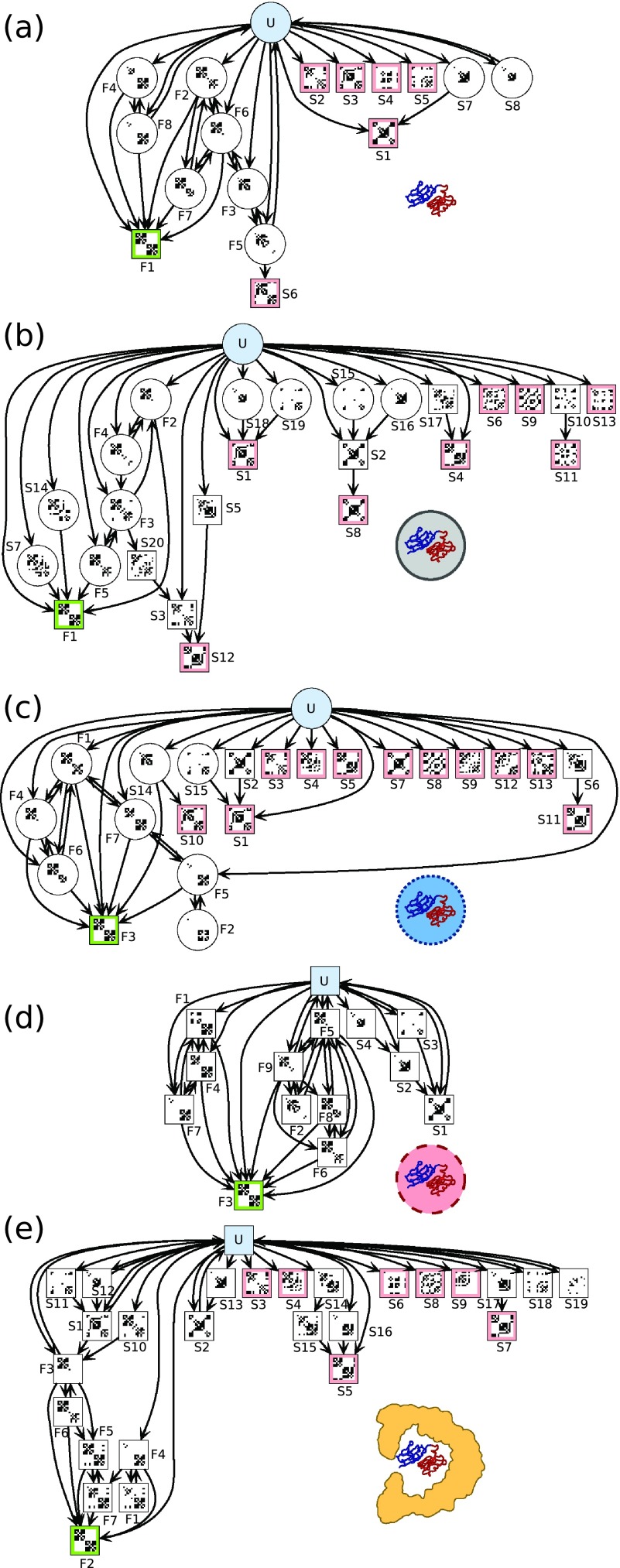
The transition matrix represents a directed graph, which is plotted for each of the folding scenarios in Figure 5. The graphs allow us to see the complexity of the transition network under each type of confinement, with the width of the graph roughly corresponding to the number of parallel sinks that the system can enter and the height of the graph to the complexity of the native folding subnetwork. Note that in these graphs, states of the MSM which are part of the folded-state SCC are labelled F1, F2,…, while the remaining states are labelled S1, S2,…. While many of the “S” states are sinks, several are merely misfolded intermediates en route to the sink states.

FIG. 5.

Connectivity graphs describing coarse-grained Markov state models for different scenarios. (a) Unconfined, (b) repulsive cavity, (c) weakly attractive cavity, (d) strongly attractive cavity, and (e) GroEL. Each state is represented by the average coarse-grained contact map over its members. Unfolded and folded are highlighted in cyan and green, respectively, while states with a pink border are misfolded sink or trap states.

For the unconfined scenario (Fig. 5(a)), the majority of the misfolded sink states are isolated from the native folding subnetwork, though the system can irreversibly enter the misfold S6 via the F5 intermediate. Interestingly, few of the intermediates are able to make transitions back to the unfolded state at the lag time with which we make observations; only F5 and F8 make reversible transitions with the unfolded state. However, once the system has entered the native folding subnetwork, there are numerous parallel pathways to the native state via the intermediates, and in fact at the chosen lag time there are transitions directly from the unfolded to the folded state (although a small number).

For the repulsively confined scenario (Figure 5(b)) the emerging picture is more complicated. Notably, we see macrostates that are not part of the folded SCC and yet are not true sinks (S7 and S14), indicating the possibility of transitioning to the native state from an apparently initially misfolded state. In addition, the reversibility of transitions towards the folded state is reduced, with only states F2-F4 and F3-F5 able to exchange with one another and, unlike the unconfined case, no transitions are made back into the unfolded state, presumably due to the stronger bias towards folded or misfolded states arising from the excluded volume effect. Some interesting features include the existence of both terminal-end and central domain nucleating misfold intermediates, for example S18, S19 → S1 and S15, S16 → S2.

In the weakly attractive cavity (Figure 5(c)), titin displays a somewhat more diverse set of folding pathways within the folded SCC, compared with the repulsive case, and many of those transitions are reversible — an effect which can be understood in the context of attractive interactions, which have an overall slight destabilizing effect on more folded or ordered states. However, interactions with the cavity are clearly insufficient to rescue titin from the numerous and diverse misfolded sinks, as reverse transitions to the unfolded state are never observed on the time scale of the simulations.

Upon increasing the strength of attractive interactions with the cavity (Figure 5(d)) we see a striking difference in the transition network of titin. Above all, there are no sink states sampled, apart from the native folded state, and the single misfolded state is not a trap and can unfold. It is unclear why only one type of misfolded conformation is observed within the strongly attractive spherical cavity, but one possibility is that the folding nuclei for state S1 (S2, S3, and S4) are particularly favoured by strong interactions with the wall due to attachment of the termini on the cavity wall. The termini are still able to diffuse until they come in contact and form the intermediate shown in S3; however, it is also possible, and potentially more likely, that the misfold nucleates in the central region, indicated by states S2 and S4, before the termini come into contact and the system enters S1. The native folding subnetwork is similar to that produced in the weakly attractive cavity, though transitions show more reversibility.

The transition network of titin in the GroEL cavity (Figure 5(e)) is similar to that of the weakly attractive scenario. The native folding subnetwork is complex and can be entered not only via native folding intermediates but also via the misfolded SCCs S1 and S10. Some misfolded states (S2, S18, S19) are able to return to the unconfined state but clearly, when compared with the strongly attractive spherical cavity, the GroEL cavity is unable to rescue trapped misfolded states to the same degree.

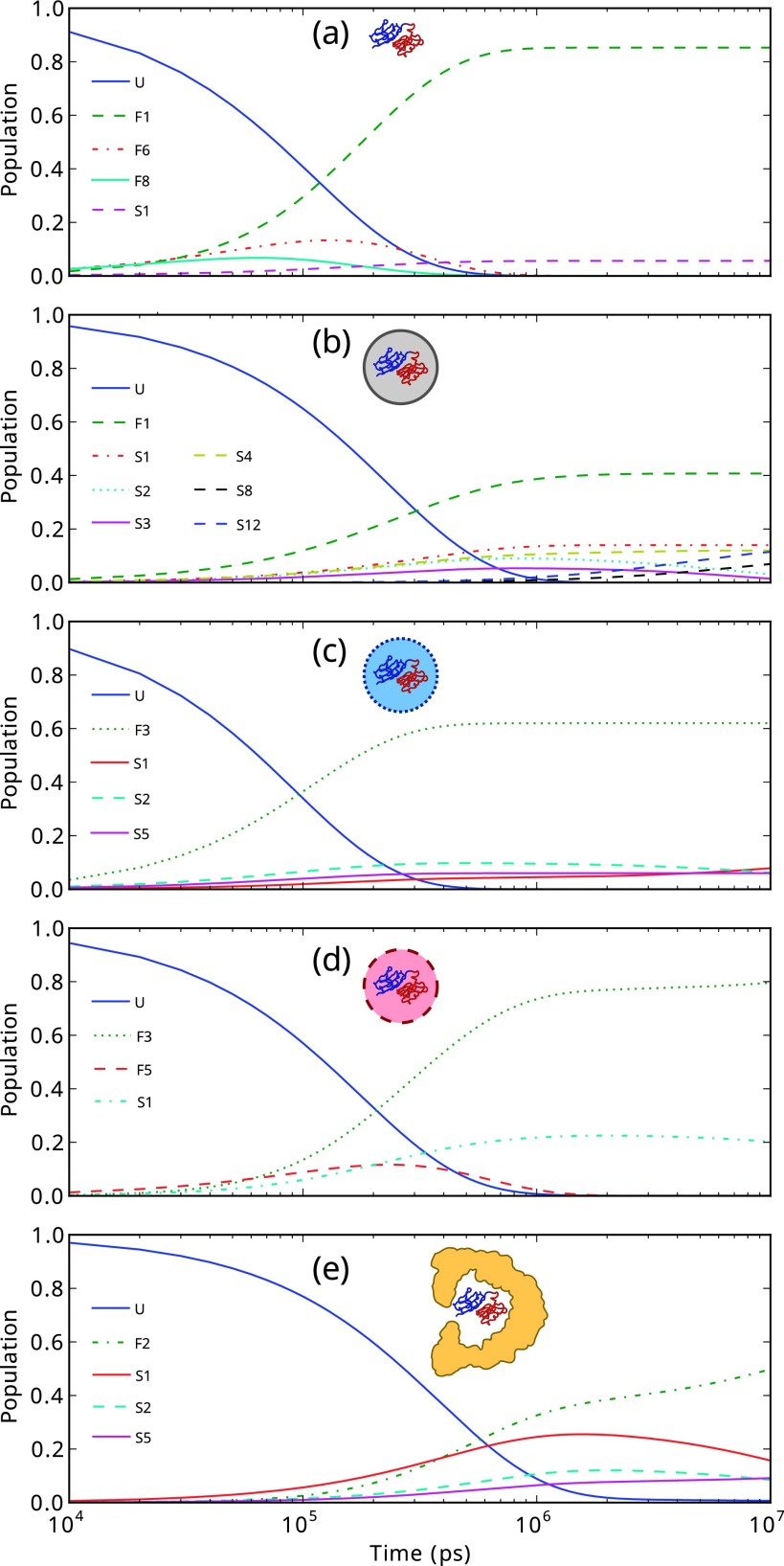
D. Simulating the time evolution

Mechanistic information can also be obtained from the evolution of the populations of states in time. Time-dependent populations p(t) were simulated using Equation (1), where p(0) was initialised with 100% of the population in the unfolded state (see Figure 6). As expected, the unfolded state population decays with time, while the native folded state population increases. In the unconfined case (Figure 6(a)), folding clearly progresses via the native-like intermediates F6 and, to a lesser degree, F8. The misfolded state S1 is the next most dominant state at long time scales but the populations of other states are negligible.

FIG. 6.

Evolution of populations as a function of time. (a) Unconfined, (b) repulsive cavity, (c) weakly attractive cavity, (d) strongly attractive cavity, and (e) GroEL. Definitions of states are given in Figure 5.

When placed in the repulsive cavity (Figure 6(b)), the time scale on which the folded state F1 appears is comparable to that of the unconfined case, although the final population of the folded state is significantly decreased. The misfolded sink S12 can be seen increasing towards the end of the time series as the populations of states S3 and S5 decay and has not equilibrated at the final time step.

In the weakly attractive sphere, the folded state population at long time scales is recovered, relative to the repulsive case, and convergence toward the final populations occurs more rapidly than in the repulsive or unconfined scenarios. Also evident is the early growth of the population of state S2, which decays as it makes transitions to sink S1. Additionally, the populations of numerous intermediates in the native folding subnetwork can be seen to increase and decay at early time scales as population drains into the native folded state F3.

The strongly attractive cavity recovers a significant amount of the folded state population observed in the unconfined scenario at long time scales and at the end of the time series is still increasing. Folding occurs predominantly via the F5 intermediate, since this plays a central role in the native folding subnetwork, as is evidenced by the network graph, and filters into numerous other folded intermediates as well as the native state. The continual increase in the population of state F3 is due to the reversibly formed misfolded state S1 which can make transitions back to the unfolded state and therefore feed population back into the folding subnetwork. The time scale on which the folded state population equilibrates is somewhat slower in the strongly attractive cavity than in the unconfined, repulsive and weakly attractive cases due to the initial division of population between the native folding subnetwork and intermediate states of the S1 misfold.

Surprisingly, in the GroEL cavity the picture we have is more complex. Folding is significantly slower within GroEL and, at time scales of 100 ns, there is competition between the native state F2 and misfolded state S1, with the population of S1 initially being larger. However, since S1 in fact makes transitions to states within the native folding subnetwork, its population eventually decays while that of the folded state grows.

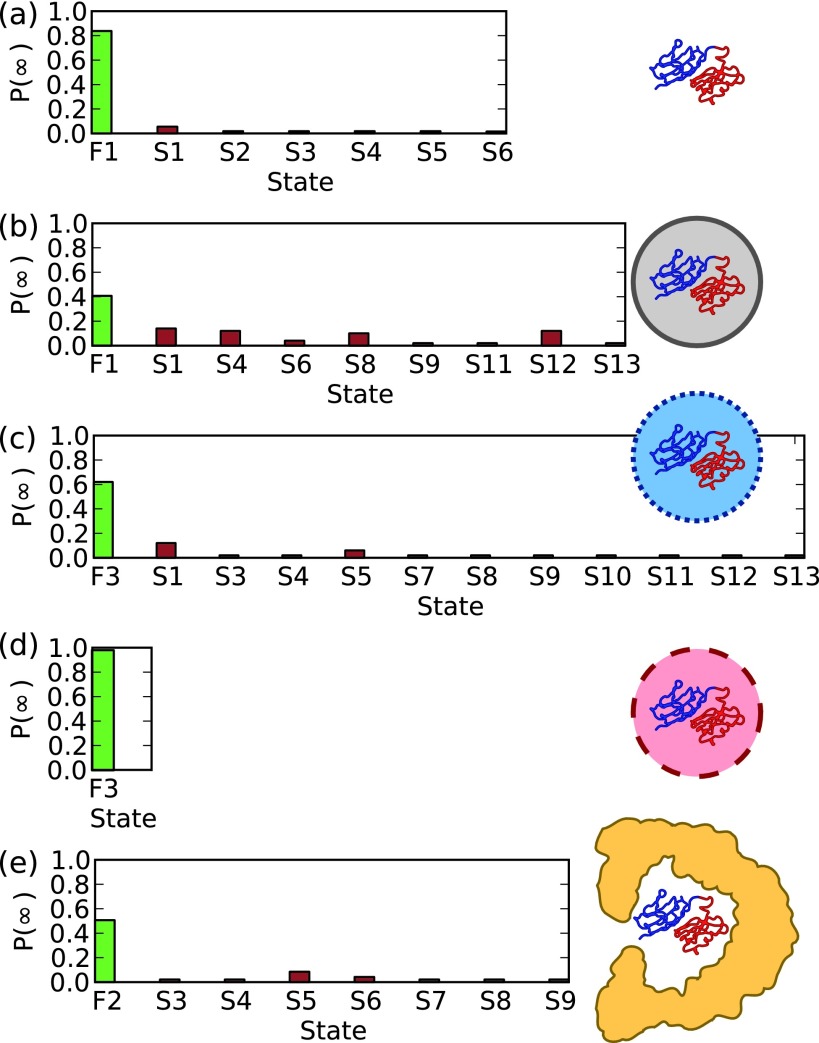
E. State populations at infinite time

The infinite-time probabilities p(∞) for each confinement scenario were calculated using the analytical solution presented in Section II E and are shown in Figure 7. Most importantly, note that under all confinement conditions the probability of being in the folded state is considerably larger than the other states, suggesting that misfolding is not as probable as correct folding. In the case of the strongly attractive sphere, the system will always be found in the folded state at t = ∞, since all the misfolded states can unfold. The repulsive spherical cavity results in approximately equal probabilities for being in a number of misfolded states, whereas the weakly attractive and GroEL cavities tend to favour only one or two misfolded states. The folded state is most disfavoured by the repulsive cavity since it indiscriminately stabilises misfolded states and prevents the system from escaping once trapped in a misfolded state.

FIG. 7.

Long-time populations for each model. The different scenarios are (a) unconfined, confined in (b) repulsive, (c) weakly attractive, (d) strongly attractive cavities, and (e) confined in GroEL.

An important point to highlight is that the results shown here for the unconfined scenario and the spherical cavities shown in Figure 7 are qualitatively similar to the previous population distributions obtained via naive clustering of the final frames of each simulation, while the results in Figure 7 were derived from an MSM. In both cases, there is an increased population of misfolded states caused by repulsive confinement and a partial reduction in these populations by the introduction of attractive interactions. For the strongly attractive cavity, misfolded states have a non-zero population in the distributions obtained from naive clustering, whereas the long-time solution provided by the MSM suggests that all the misfolded states would eventually convert to the folded state. This may be because the dynamics in the strongly attractive cavity is slowed down such that this situation is never reached in the direct simulations. The origin of the slowdown can be attributed partially to slower diffusion on the folding coordinate⁴⁰ but is also probably related to the destabilization of folded states (and misfolded states) relative to the unfolded state, due to the greater number of interactions the latter can make with the cavity wall.

The results reveal a complex transition network for titin, which is very sensitive to the confinement scenarios presented here. While repulsive confinement is generally thought to increase folding rates via volume exclusion, the nonspecific nature of repulsive interactions means misfolded states are stabilised alongside the native state and the ergodicity of the system is reduced, as progress towards a (mis)folded state is mostly one-way. The addition of attractive interactions with the cavity walls is able to counteract the effects of volume exclusion and, due to binding with the walls, disfavours the majority of misfolded states observed in repulsive confinement. An intriguing result, evident from the network graphs (Fig. 5) and the simulated time evolution (Fig. 6), is the ability for some misfolded states to make transitions towards the folded state, suggesting that nucleation of a misfold does not resign titin to forming a stable misfold. In fact, sufficiently strong interactions are able to completely rescue the system from being trapped in any misfolded states. However, it is also clear that the interactions between titin and the GroEL cavity are not directly comparable to those with the strongly attractive cavity and are therefore unable to completely rescue misfolded titin; the results are more consistent with the weakly attractive cavity.

IV. CONCLUSIONS

We have used a Markov-state model to condense a large quantity of simulation data into networks of transitions between discrete states in order to analyze the folding and misfolding mechanisms of a titin dimer. MSMs provide a useful tool for extracting kinetic details from simulation data in situations where projecting a one- or two-dimensional energy landscape on a set of chosen reaction coordinates cannot easily resolve all relevant intermediates. In order to apply MSMs to the folding landscape of titin, in which transitions to some important states were not reversible, we needed to construct an MSM with these sink states included. This yields populations at long times which are completely consistent with the results of our previous analysis of titin folding.^40,42

However, the MSM approach can give us insight into the complex folding and misfolding pathways of titin, and the degree to which various confinement scenarios are able to influence those pathways, especially with respect to reversing the trapping of titin in misfolded states. An interesting finding from this analysis was that it was possible for partially misfolded intermediates to interconvert directly with partially folded intermediates, without going via the unfolded state. In retrospect, this seems reasonable, since both types of partially folded/misfolded species share a large number of contacts. This mechanism is in contrast to a simplified view in which folded and misfolded states are considered to be reached from the unfolded state via alternative “pathways.”

We anticipate that the methodology for clustering states by coarse contact maps between secondary structure elements, and for constructing MSMs having sink states, will be applicable to a wide range of problems involving protein folding, binding and misfolding.