Physiologically Based Modelling of Darunavir/Ritonavir Pharmacokinetics During Pregnancy

Abstract

Pregnant women are usually excluded from clinical trials. Physiologically based pharmacokinetic (PBPK) modelling may provide a method to predict pharmacokinetics in pregnant women, without the need to perform extensive in vivo clinical trials. Here, we used mechanistic modelling to delineate the potential impact of drug transporters on darunavir pharmacokinetics and to identify current knowledge gaps that limit accurate PBPK modelling of darunavir/ritonavir (darunavir/r) exposure in pregnancy. Simcyp (version 13.2) was used for PBPK modelling, using physicochemical and in vitro pharmacokinetic parameters of darunavir and ritonavir from the literature. The Michaelis–Menten constant (K_m) and the maximum rate of metabolite formation (V_max) for cytochrome P450 3A4-mediated darunavir biotransformation and inhibition by ritonavir were determined experimentally, while the contributions of hepatocyte influx and efflux transporters were assessed by sensitivity analysis. The simulations were compared with previously published clinical pharmacokinetic data. We found that use of a well-stirred liver model overestimated darunavir exposure substantially. A permeability-limited liver model, including hepatic uptake and efflux transporters and an efficient enterohepatic circulation step, resulted in an acceptable description of darunavir/r exposure. For the 600/100 mg darunavir/r twice-daily dose and the 800/100 mg once-daily dose, the estimated pharmacokinetic parameters were within a 2-fold range of the reported data. The predicted decreases in the area under the concentration–time curve (AUC) values during pregnancy for the twice- and once-daily doses were 27 and 41 %, respectively, which were in line with the observed decreases of 17–22 and 33 %. In conclusion, our data support a clinically relevant role of hepatic transporters in darunavir pharmacokinetics. By including them in our model, we successfully approximated the increase in darunavir exposure mediated by ritonavir co-administration and the decrease in darunavir exposure observed during pregnancy.

Electronic supplementary material

The online version of this article (doi:10.1007/s40262-015-0325-8) contains supplementary material, which is available to authorized users.

Key Points

Our data support a clinically relevant role of hepatic transporters in darunavir pharmacokinetics.

We successfully approximated the increase in darunavir exposure mediated by ritonavir co-administration and the decrease in darunavir exposure during pregnancy, using physiologically based pharmacokinetic modelling.

Introduction

Pregnant women are generally excluded from clinical trials during the development phase of new drugs, for obvious ethical and safety reasons [1–3]. However, medication use during pregnancy is not uncommon [4]. Most information regarding safety, pharmacokinetics and placental transfer is collected after drugs have become available on the market. The implication of this is that pregnant women often use medication for which the treating physicians have no knowledge of the systemic drug exposure, the placental transfer and hence the safety of the unborn child. On the other hand, physicians may withhold beneficial medication from pregnant women because they lack this critical information. It would be a tremendous advantage if in silico modelling could be applied to prediction of maternal and fetal exposure of (new) drugs that are possibly being prescribed during pregnancy. Such models would be particularly relevant in the treatment of human immunodeficiency virus (HIV). To prevent mother-to-child transmission, pregnant HIV-infected women should use combination antiretroviral treatment (cART) [5, 6]. Pregnancy-induced reductions in maternal exposure to these drugs may lead to subtherapeutic levels, eventually leading to virological failure and/or resistance, thus requiring dose adjustment [7].

Physiologically based pharmacokinetic (PBPK) modelling is a mechanistic approach to predict the absorption, distribution, metabolism and excretion (ADME) of drugs on the basis of the anatomy and physiology of the human body, as well as physicochemical properties and in vitro data on transport and biotransformation of the drug. In this way, the handling of a drug by the body can be simulated, taking molecular processes as a starting point. A PBPK model can take into account the numerous physiological changes that occur during pregnancy, affecting the volume of distribution, plasma protein binding and metabolic clearance of drugs [8–10]. In addition, PBPK modelling can allow quantitative assessment of the impact of concomitantly prescribed interacting drugs. This is particularly useful in HIV-infected pregnant women, who typically use a cocktail of drugs, with drug–drug interactions even being intentionally employed to optimize treatment. For example, ritonavir, a strong cytochrome P450 (CYP) 3A4 inhibitor, is used as a booster to increase the exposure of antiretroviral drugs that are metabolized by CYP3A4. Finally, PBPK modelling provides an effective manner to integrate the currently available mechanistic drug disposition data and to obtain a better understanding of the pharmacokinetic behaviour of a compound.

Simcyp has developed a PBPK modelling platform, which includes physiological changes in relation to the duration of pregnancy (a p-PBPK model) [11, 12]. Exposure to drugs during pregnancy at any gestational age may be predicted, provided that in vitro pharmacokinetic data on all processes relevant to drug disposition are available [11]. To study the feasibility of such a p-PBPK modelling approach, we focused in this study on the antiretroviral compound darunavir, co-administered with ritonavir.

We developed and evaluated a mechanistic model to predict darunavir exposure resulting from the treatment regimens 600/100 mg darunavir/ritonavir (darunavir/r) twice daily and 800/100 mg darunavir/r once daily, both given with two nucleoside/nucleotide reverse transcriptase inhibitors (NRTIs) to provide a complete cART regimen. These efforts also aimed to elucidate whether the appropriate in vitro pharmacokinetic parameters that are required in such a model are currently available. Another aim was to identify current knowledge gaps that limit the accuracy of PBPK modelling of darunavir/r exposure, thereby generating new hypotheses and hence directions for future mechanistic studies to provide better understanding of darunavir/r disposition.

Methods

PBPK Modelling Platform

Simcyp Population-Based Pharmacokinetic Simulator version 13 release 2 (Simcyp Limited, a Certara company, Sheffield, UK) was used as a PBPK platform. [13–16] Simulations were performed using Simcyp virtual populations of healthy volunteers and pregnant women. For each simulation, the number of patients, gender, age range and gestational age of the virtual population were matched with clinical data sets used for validation.

Physicochemical and In Vitro Pharmacokinetic Parameters of Darunavir

Darunavir physicochemical properties (e.g. molecular weight, log P) and blood and protein binding properties were obtained from the literature (Table 1). Holmstock et al. [17] reported a 2.7-fold increase in darunavir intestinal permeability (in mice and Caco-2 monolayers) of darunavir in the presence of ritonavir, as a result of the strong P-glycoprotein (P-gp) inhibitory effect of ritonavir [17], which was in line with the findings of other studies [18]. Therefore, when modelling the pharmacokinetics of darunavir alone, we used a reported in vitro Caco-2 permeability of 7 × 10⁻⁶ cm s⁻¹ for darunavir alone and 18.6 × 10⁻⁶ cm s⁻¹ when simulating combined darunavir/r administration. Darunavir is mainly eliminated by hepatic metabolism; therefore, no renal clearance component was included in our simulations [19]. To determine the Michaelis–Menten constant (K_m) and the maximum rate of metabolite formation (V_max) for CYP3A4-mediated darunavir metabolism, we performed in vitro tests using human liver microsomes (HLMs) and baculosomes overexpressing human recombinant CYP3A4. See the corresponding paragraph below for a more detailed description of these experiments.

Table 1.

Physicochemical and in vitro pharmacokinetic parameters of darunavir

Parameter	Value	References
Physicochemical
Molecular weight	548 g mol−1	Pubchem [52]
Log Po:w	1.8	http://www.antimicrobe.org/d94.asp (February 2015) [53]
		http://www.drugbank.ca/drugs/db01264 (February 2015) [54]
Compound type	Weak base
pKa		http://www.drugbank.ca/drugs/db01264 (February 2015) [54]
Strongest basic	2.39
Strongest acidic	13.59
Physiological charge	0
Blood:plasma ratio	0.64	EMA scientific discussion [19, 55]
Fraction unbound in plasma	0.06	EMA scientific discussion [19, 55]
Main plasma binding protein	AAG	EMA scientific discussion [19, 55]
Absorption
Absorption model	ADAM
Permeability predicted via	Caco-2
Apical pH:basolateral pH ratio	6.5:7.4
Activity	Passive and active
P app Caco-2 (10E−06 cm s−1)	7 (in the absence of ritonavir)	Holmstock et al. [17]
	18.9 (in the presence of ritonavir)	Holmstock et al. [17]
Scalar	1
Dosage form	Immediate release, dissolution over 2-h period (fed condition)
Available for reabsorption after biliary excretion	Sensitivity analysis 0–100, 80 % was optimal
Distribution
Distribution model	Full PBPK model
Predicted V ss (L h−1)	1.23	Prediction method by Rodgers and Rowland [56]
K p scalar	6	Empirically determined [19, 55]
Metabolism/elimination
Clearance type	Enzyme kinetics
Test system	Human liver microsomes
Enzyme kinetics CYP3A4	V max = 181 pmol min−1 mg−1 microsomal protein	Determined
	K m = 1.1 µM	Determined
	Protein concentration = 0.25 mg mL−1	Determined
	F u,mic = 0.96 (pH 7.4)	Calculated
Transport
Passive diffusion clearance	0.1 mL min−1 million cells−1	Simcyp default value
Pooled basolateral hepatocyte uptakea, CLint,T	Sensitivity analysis 0–500 µL min−1 million cells−1
	100 µL min−1 million cells−1 used in final model
Canalicular hepatocyte efflux (P-gp) CLint,T	Sensitivity analysis 0–500 µL min−1 million cells−1
	100 µL min−1 million cells−1 used in final model

ADAM advanced absorption and dissolution model, AAG α1-acid glycoprotein, CL _int,T in vitro transporter-mediated intrinsic clearance, CYP cytochrome P450, EMA European Medicines Agency, F _u ,mic fraction of unbound drug in the in vitro microsomal incubation (calculated), K _m Michaelis–Menten constant, K _p partition coefficient, P _app permeability coefficient, PBPK physiologically based pharmacokinetic, P-gp P-glycoprotein, pKa acid dissociation constant, Po:w Partition coefficient octanol:water, V _max maximum rate of metabolite formation, V _ss volume of distribution at steady state

^aReflecting various organic anion transporting polypeptides

For darunavir simulations, the Simcyp full PBPK distribution model was applied, which makes use of a number of time-based differential equations in order to simulate the concentrations in various organ compartments. Initially, we used a well-stirred liver model without hepatic basolateral uptake, canalicular excretion or intestinal reabsorption of darunavir. In subsequent steps, modelling with a permeability-limited liver model was performed, exploring various degrees of hepatic uptake and efflux clearance, while also addressing the impact of various efficiencies of intestinal reuptake of the drug that was excreted unchanged into bile. With respect to the modelling of enterohepatic recycling, contraction of the gall bladder (resulting in release of the drug into the duodenum) is included as a periodic event corresponding to the Interdigestive Migrating Motor Complex (IMMC) cycle time and set at 1.55 h (coefficient of variation [CV] 55 %). During contraction of the gall bladder, release of the drug from the gallbladder was defined by release constants of 0.18 h⁻¹ (CV 30 %) in the fasting state and 0.48 h⁻¹ (CV 19 %) in the fed state.

Physicochemical, In Vitro and Clinical Pharmacokinetic Parameters of Ritonavir

The ritonavir model used to simulate CYP3A4 and transporter inhibition (boosting) was a semi-mechanistic pharmacokinetic model, based on physicochemical parameters, in vitro data and clinical pharmacokinetic data. Absorption was based on first-order kinetics (absorption rate constant [k_a] = 0.24 h⁻¹ and fraction absorbed [f_a] = 1) and a volume of distribution at steady state (V_ss) of 0.41 L kg⁻¹, in line with data that has been derived from clinical studies [20]. Oral ritonavir clearance of the 100 mg dose is 16 L h⁻¹ in healthy volunteers [21]. For the pregnant situation, a CL/F value of 20 L h⁻¹ was used, as derived from clinical observations [22, 23]. The interaction potential of ritonavir was based on competitive inhibition of CYP2C9, CYP2D6 and CYP3A4. We performed in vitro tests in HLMs to corroborate and, if necessary, update the ritonavir concentration producing 50 % inhibition (IC₅₀) on CYP3A4-mediated darunavir biotransformation (see below). In addition to competitive inhibition, Fahmi et al. [24] and Kaspera et al. [25] described mechanism-based inhibition of CYP3A4 by ritonavir, which was also included in the model. Inductive properties of ritonavir on CYP3A4 have also been described and were added to the model, on the basis of the work by Kirby et al. [26] We included reported in vitro inhibitory potencies of ritonavir on P-gp (hepatic canalicular efflux), as well as on the pooled hepatic basolateral influx process, reflecting the involvement of organic anion transporting polypeptides (OATPs) in darunavir uptake. For the latter, we used the reported IC₅₀ of ritonavir on OATP1B3 (solute carrier organic anion transporter family member 1B3 [SLCO1B3]) of 2.5 µM [27, 28].

In Vitro Testing

A range of darunavir concentrations (1–25 µM) was incubated with HLMs and, at the end of the incubations, final darunavir concentrations were determined by high-performance liquid chromatography (HPLC) via a method adapted from the protocol described by Droste et al. [29] (lower limit of quantification: 50 nM or 0.027 mg L⁻¹). Incubations depleted darunavir concentrations on average by 30 %. A prerequisite for conducting Michaelis–Menten analysis is that no significant substrate depletion should occur; however, it has been described that via this method, a reasonable estimate of K_m and V_max can be still made, which is suitable for our purposes [30]. The same protocol was used to analyse the results obtained from incubations with baculosomes overexpressing human recombinant CYP3A4 (20 pmol mL⁻¹), over a darunavir concentration range of 1–10 µM. Enzyme-mediated darunavir bioconversion was analysed by non-linear regression analysis according to the Michaelis–Menten equation, using GraphPad Prism 5 (version 5.02; GraphPad Software Inc.).

To determine the inhibitory effect of ritonavir on darunavir biotransformation, incubations with HLMs were performed as described above, in the presence of 1 µM darunavir (substrate) and ritonavir (inhibitor) concentrations ranging from 0.01 to 0.3 µM. The IC₅₀ was estimated by fitting a one-binding site inhibition model with a variable slope to the data, using GraphPad. Derived IC₅₀ values from three separate experiments, each performed in duplicate, were subsequently converted to a K_i value (the binding affinity of the inhibitor) using the Cheng–Prusoff equation (IC₅₀/(1 + [darunavir]/K_{m, darunavir})).

PBPK Workflow and Statistical Analysis

We first simulated the pharmacokinetics of darunavir in healthy volunteers, when it was administered as a single dose without ritonavir. We then verified the interactions of darunavir with ritonavir, first for a single dose of darunavir, after Sekar et al. [31] and after Rittweger and Arasteh [19], and then for the steady-state situation for the clinical dosing regimens of 600/100 mg darunavir/r twice daily [32, 33] and 800/100 mg once daily. [34, 35] Before application of the ritonavir semi-mechanistic model in the darunavir PBPK modelling approach, the ritonavir model performance was validated against data available from interaction studies between ritonavir and midazolam (a probe substrate for CYP3A4) [26, 36]. Acceptance criteria were defined as follows: both the geometric mean maximum concentration (C_max) and the area under the concentration–time curve (AUC) should not deviate more than 2-fold from the observed pharmacokinetic parameters, as is commonly applied in assessing PBPK model performance. After modelling of darunavir/r exposure in healthy volunteers, we proceeded to model darunavir/r pharmacokinetics during pregnancy. Simulations of twice-daily 600/100 and once-daily 800/100 darunavir/r were performed during the second and third trimesters (the same gestational ages as those reported in published clinical studies). For the non-pregnant situation, simulations were performed using the healthy volunteer population (females, matched for age where reported). An independent-samples t test (SPSS 20) was performed on the log-transformed AUCs, comparing the pregnant situation with the non-pregnant situation, resulting in geometric mean ratios (pregnant:non-pregnant) and 90 % confidence intervals (CIs). Finally, we performed simulations with higher darunavir/r dosages: 900/100 mg darunavir/r once daily, as well as 800/100 and 900/100 mg darunavir/r twice daily during pregnancy (in the third trimester), to predict which dose would compensate for the observed decrease in exposure. These dosages were chosen because darunavir is available as 300, 400, 600 or 800 mg film-coated tablets for oral use.

Comparison of Physiological Parameters of the Simcyp Pregnant Population with a Real-Life HIV-Infected Pregnant Population

Within a clinical study coordinated by our institution (the Pharmacokinetics of Newly Developed Antiretroviral Agents in HIV-Infected Pregnant Women [PANNA] study; www.pannastudy.com), several physiological parameters (the haematocrit and serum creatinine, α1-acid glycoprotein [AAG] and albumin concentrations) were collected from HIV-infected women during pregnancy and after delivery. We compared these physiological parameters with those used to define the Simcyp virtual healthy pregnant population as described by Abduljalil et al. [10]. The data were compared with the mean values summarized by Abduljalil et al. to investigate if there were any differences between HIV-infected and non-infected pregnant women, using an independent-samples t test (SPSS 20).

Results

In Vitro Metabolic Clearance of Darunavir

A literature search yielded values for a substantial number of mechanistic pharmacokinetic parameters related to absorption and distribution of darunavir (Table 1). Because quantitative data on in vitro darunavir metabolic clearance by CYP enzymes (K_m and V_max values) were not available, we determined the in vitro metabolic K_m and V_max using HLMs.

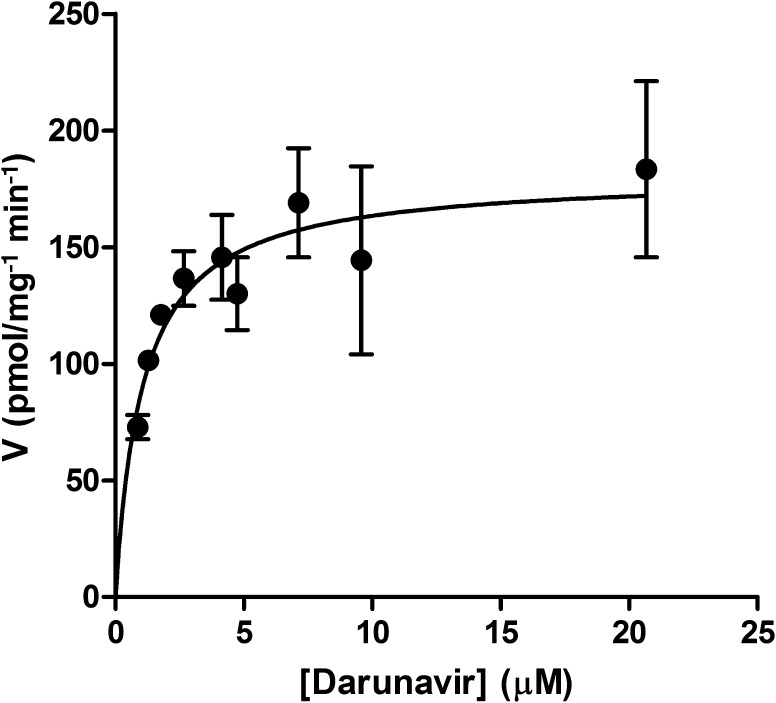
Enzyme kinetics were determined at a protein concentration of 0.25 mg·mL⁻¹ over a 30-min time period. We found that darunavir bioconversion was saturable with increasing concentrations (Fig. 1), characterized by a K_m value (95 % CI) of 1.1 (0.3–1.8) µM and a V_max value (95 % CI) of 180 (150–210) pmol min⁻¹ mg⁻¹ protein. The K_m value (95 % CI) derived from the experiments performed in the baculosome CYP3A4-overexpression system was 0.80 (0.17–1.43) µM (intrinsic metabolic clearance [CL_int,met] 2.25 µL min⁻¹ pmol⁻¹ CYP3A4).

Fig. 1.

Rate of darunavir disappearance (V) from human liver microsomal incubations at increasing substrate concentrations. The data represent a typical experiment; from a total of 3 experiments, performed in duplicate, the mean ± range (minimum/maximum) values are presented. A Michaelis–Menten equation was fitted to the data as described in the “Methods” section. The calculated Michaelis–Menten constant (K _m) and the maximum rate of metabolite formation (V _max) for the indicated study are 1.1 µM and 180 pmol min⁻¹ mg⁻¹ microsomal protein

Simulation of Darunavir Pharmacokinetics Without Ritonavir

We simulated the concentration–time curve of a single oral 600 mg dose of darunavir in plasma with a well-stirred liver model, hence assuming passive partitioning of the drug from the plasma into the liver tissue, instantaneous homogeneous distribution across the liver mass and CYP3A4-mediated metabolic clearance as the only relevant clearance mechanism. As can be seen in Fig. 2, the simulations overestimated the total exposure of darunavir when compared with the clinical data presented by Sekar et al. [31] and by Rittweger and Arasteh [19].

Fig. 2.

Simulation of darunavir plasma concentration (conc)–time curves after a single oral dose of 600 mg, using the well-stirred liver model on a linear scale (a) and on a semi-logarithmic scale (b). The black circles represent the observed concentrations [19], the dashed line represents the simulated mean concentrations and the dotted lines represent the associated 95 % confidence intervals of the simulated concentrations. The simulated plasma concentration data were derived from 8 healthy subjects (3 female, 5 male) aged 27–37 years, matching the subjects in the reported trial as far as possible

Inclusion of Hepatic Influx and Efflux Transport via Sensitivity Analyses

According to the general workflow of PBPK modelling and simulation [12], we refined the model by taking clues from in vitro pharmacokinetic studies as a starting point. Visual inspection of the curves indicated that the simulated absorption phase was in line with the observed data. The known interaction of darunavir with the basolateral OATP1B1, 2B1, 1B3 and canalicular P-gp hepatocyte membrane transporters [18, 28, 37] might influence darunavir clearance. Therefore, we investigated whether inclusion of a basolateral influx or a canalicular efflux component in the model could improve the simulations. The simulations performed for this sensitivity analysis are reported in Supplementary Table 1. In Fig. 3, the effects of different intrinsic uptake and efflux clearances on model fit was examined. In Fig. 4, it can be seen that inclusion of both a canalicular efflux and a basolateral uptake step allows for better model fits at lower intrinsic transport clearance values (CL_int,T; µL min⁻¹·million cells⁻¹).

Fig. 3.

Darunavir single-dose (600 mg oral) simulation of plasma concentration (conc)–time curves at increasing intrinsic transport clearance (CL_int,T) uptake values (a) and CL_int,T efflux values (b), using the permeability-limited liver model. The black circles represent the observed concentrations [19], the solid line reflects the data obtained with the well-stirred liver model and the dashed lines represent the simulated mean concentrations with application of the permeability-limited liver model at increasing CL_int,T values: 100, 200, 300, 400 and 500 µL min⁻¹ million hepatocytes⁻¹

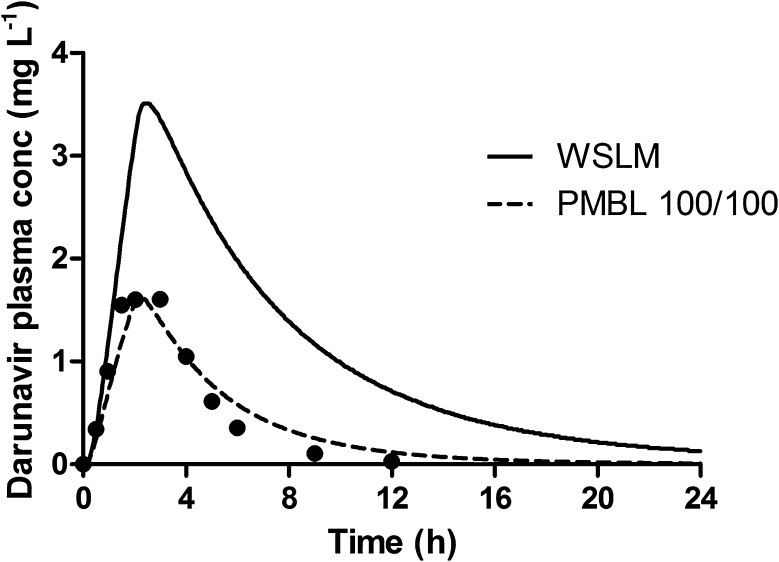
Fig. 4.

Darunavir single-dose (600 mg oral) simulation of plasma concentration (conc)–time curves, assuming combined influx and efflux processes, using the permeability-limited liver model (PMBL). The black circles represent the observed concentrations [19], the solid line reflects the data obtained with the well-stirred liver model (WSLM) and the dashed line represents the simulated mean concentrations with application of the PMBL with optimal CL_{int,T uptake}/CL_{int,T efflux} values of 100/100 µL min⁻¹·million hepatocytes⁻¹, respectively. CL_int,T intrinsic transport clearance

In vitro transport parameters (K_m, V_max or CL_int,T) for darunavir in human hepatocytes or recombinant overexpression systems of drug transporters were not available in the literature. However, when uptake and efflux clearance rates that have been measured for other drugs are considered, it can be seen that the required CL_int,T values are in a pharmacologically feasible range (Table 2). This is particularly the case when combined hepatocellular influx and efflux processes are assumed to take place.

Table 2.

Intrinsic transport clearance (CL_int,T) influx and efflux values reported in the literature

	Mean (SD)
Compound	CLint,T uptake [µL min−1 million cells−1]	CLint,T efflux [µL min−1 million cells−1]	References
Bosentan	17.9		Ménochet et al. [44]
	9.1	7.4	Jones et al. [43]
Cerivastatin	9.6 (2.7)	6.2 (1.8)	Jones et al. [43]
Fluvastatin	45 (21)	17	Jones et al. [43]
Pitavastatin	40.7		Ménochet et al. [44]
Pravastatin	2.77		Ménochet et al. [44]
	1.8	1.2	Jones et al. [43]
Repaglinide	79.0a		Ménochet et al. [44]
	30 (16)	0	Jones et al. [43]
Rosuvastatin	9.21		Ménochet et al. [44]
	9.3 (2.6)	1.5 (0.088)	Jones et al. [43]
Telmisartan	95.2a		Ménochet et al. [44]
Valsartan	2.88		Ménochet et al. [44]
	2.1 (0.5)	96a	Jones et al. [43]

SD Standard deviation

Jones et al. [43] reported in vitro parameters estimated from sandwich culture human hepatocyte parameters at a single substrate concentration; mean from multiple replicates of 1–2 donors. Ménochet et al. [44] performed uptake kinetics in cryopreserved human hepatocytes at 7 concentrations; the uptake parameters were estimated using a mechanistic 2-compartment model

^aReported parameter close to simulated estimate for darunavir

Inhibitory Effect of Ritonavir on CYP3A4

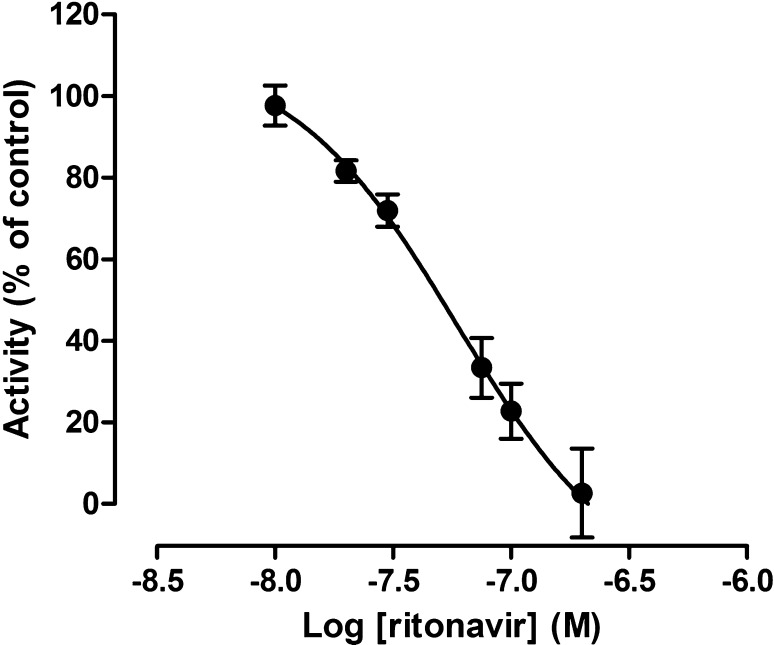
In clinical practice, darunavir is always administered together with ritonavir. In order to simulate this effect on a mechanistic level, the ritonavir IC₅₀ for inhibiting CYP3A4-mediated darunavir metabolism is required. As can be seen in Fig. 5, ritonavir completely inhibited darunavir bioconversion, with an IC₅₀ (95 % CI) of 0.06 (0.04–0.10) µM, which was equivalent to a mean K_i value of 0.03 µM. This value was included in the ritonavir model, together with other parameters listed in Table 3. The performance of the ritonavir PBPK model was then validated in simulations with midazolam, a probe substrate for CYP3A4. Figure 6 presents the results of these simulations, demonstrating that the model could predict the increase in midazolam exposure within a 2-fold difference of the reported clinical C_max and AUC ratios.

Fig. 5.

Ritonavir inhibition of darunavir metabolism in human liver microsomal preparations. The data represent the mean ± standard error of the mean of three separate experiments, each performed in duplicate. A 1-site binding model with a variable slope was fitted to the data in order to estimate the ritonavir concentration producing 50 % inhibition (IC₅₀). The calculated IC₅₀ was 0.06 µM

Table 3.

Physicochemical and in vitro pharmacokinetic parameters of ritonavir

Parameter	Value	References
Physicochemical
Molecular weight	720.95 g mol−1	Pubchem [57]
Log Po:w	4.3	Simcyp compound library
Compound type	Monoprotic base
pKa	2	Simcyp compound library
Blood:plasma ratio	0.587	Simcyp compound library
Fraction unbound in plasma	0.02	http://www.drugbank.ca/drugs/DB00503 [58]
Main plasma binding protein	AGP
Absorption
Absorption model	First-order absorption
Fraction absorbed	1	Simcyp compound library
k a (1 h−1)	0.24	Simcyp compound library
Distribution
Distribution model	Minimal PBPK model
V ss (L kg−1)	0.41	Simcyp compound library
Metabolism/elimination
Clearance type	In vivo clearance
CLpo (L h−1)	16 non-pregnant; 20 pregnant	Product characteristics Norvir [21], Colbers et al. [22]
CLr (L h−1)	0.32
Interaction CYP
CYP2C9 K i (µM)	4 (F u,mic 0.29)
CYP2D6 K i (µM)	10 (F u,mic 0.29)
CYP3A4 K i (µM)	0.03 (F u,mic 0.976)	Determined
CYP3A4 K app (µM)	0.1 (F u,mic 0.91)	Kaspera et al. [25]
CYP3A4 K inact (1 h−1)	0.32 (F u,mic 0.91)	Kaspera et al. [25]
Interaction transporters
ABCB1 (P-gp) K i (µM)	0.2 (F u,inc 0.233)	Drewe et al. [27]
Pooled basolateral uptakea K i (µM)	2.5 (F u,inc 1)	Annaert et al. [28]

AGP α1-acid glycoprotein, ABCB1 ATP-binding cassette, subfamily B, member 1, CL _po clearance after oral administration, CL _r renal clearance, CYP cytochrome P450, F _u ,inc fraction of unbound drug in the in vitro hepatocyte incubation, F _u ,mic fraction of unbound drug in the in vitro microsomal incubation (calculated), k _a absorption rate constant, K _app concentration of mechanism-based inhibitor associated with half-maximal inactivation rate, K _i concentration of inhibitor that supports half-maximal inhibition, K _inact inactivation rate of the enzyme, PBPK physiologically based pharmacokinetic, P-gp P-glycoprotein, pKa acid dissociation constant, Po:w Partition coefficient octanol:water, V _ss volume of distribution at steady state

^aBased on reported K _i for organic anion transporting polypeptide 1B3 (2.5 µM)

Fig. 6.

Scatter plot representing the area under the plasma concentration–time curve (AUC) ratio (AUC_{with inhibitor}/AUC_without) values of simulated and clinical drug-interaction studies between midazolam and different ritonavir (RTV) doses, as reported by Katzenmaier et al. [51], Kirby et al. [26] and Mathias et al. [36]. The dashed lines represent a 2-fold difference from the observed values

Simulation of Combined Darunavir/Ritonavir Administration

Next, simulations of the interaction of darunavir with ritonavir were performed. First, the influence of ritonavir on single-dose darunavir (600 mg) was simulated and the data were compared with those reported by Rittweger and Arasteh [19]. As can be seen in Fig. 7, a strong increase in darunavir exposure could be simulated when darunavir was combined with ritonavir, but only if it was assumed that unchanged drug excreted via the bile was readily available for enteric reabsorption. Reducing the percentage available for reabsorption to 0 % abolished enterohepatic cycling, and the effect of ritonavir was lost (see also Supplementary Table 1). In contrast, it followed from our simulations that enterohepatic recirculation does not appear to be a major player in determining exposure of single-dose darunavir without ritonavir, as inclusion of the intestinal reabsorption of biliary-excreted darunavir was not necessary to describe these clinical data (Fig. 7).

Fig. 7.

Linear plasma concentration (conc)–time curves (a) and semi-logarithmic plasma concentration–time curves (b) for a single oral dose of darunavir (600 mg) after 2 days of pre-treatment and in combination with 100 mg ritonavir twice daily (black dashed lines), or as a single oral dose of 600 mg darunavir alone (grey dashed line). A permeability-limited liver model was simulated, with combined influx and efflux processes taking place, both at a clearance rate of 100 µL min⁻¹ million cells⁻¹. For the darunavir/ritonavir simulations, the response of the model to varying percentages of biliary-excreted unchanged drug available for enteric reabsorption are indicated (reflecting the maximum possible degree of enteric hepatic recirculation). The black circles and grey circles are observed concentrations taken from Rittweger and Arasteh [19]

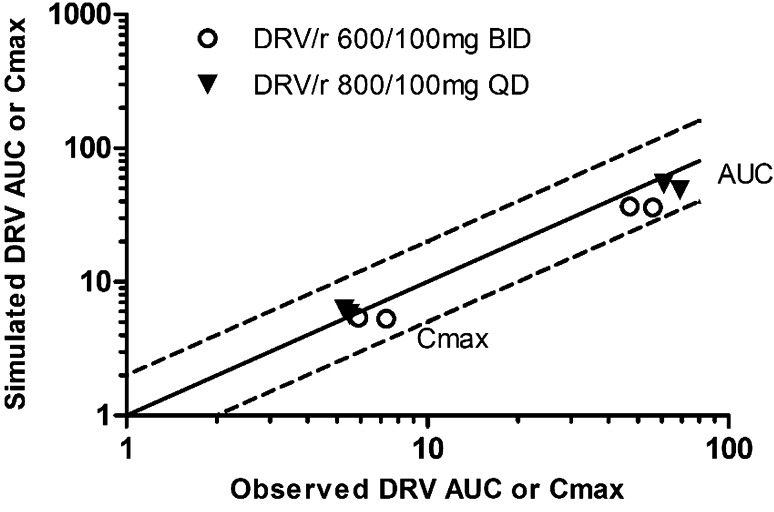
We also assessed whether the model predicted the steady-state pharmacokinetics of relevant clinical dosage regimens of 600/100 mg darunavir/r twice daily and 800/100 mg darunavir/r once daily [33–35, 38]. For this situation, darunavir/r pharmacokinetics could also be simulated successfully with indicated CL_int,T uptake, CL_int,T efflux and efficient enteric reuptake (80 %) values in place. The simulated geometric mean darunavir AUC and C_max values were within a factor of 2 from the observed parameters (Fig. 8).

Fig. 8.

Scatter plot representing the area under the concentration–time curve (AUC) and maximum concentration (C _max) from simulated and clinical darunavir/ritonavir (DRV/r) trials at steady state. For the 600/100 mg darunavir/r twice-daily (BID) dose, two studies by Sekar et al. [32, 33] were used, and for the 800/100 mg darunavir/r once-daily (QD) dose, results reported by Boffito et al. [34] and Kakuda et al. [35] were used. The dashed lines represent a 2-fold difference from the observed values

Simulation of Darunavir and Ritonavir During Pregnancy

With the same model, simulations for both regimens at steady state were performed during the second and third trimesters of pregnancy. Figures 9 and 10 show that the prediction of the shape of the curves for both the non-pregnant and pregnant situations was accurate. The exposure was somewhat underestimated for the 800/100 mg darunavir/r once-daily dosing regimen. In Table 4, the simulated pharmacokinetic parameters are compared with the observed parameters from several studies [22, 39]. The AUC decreases for the 600/100 mg darunavir/r twice-daily dose were predicted to be 27 versus 24 % observed in the second trimester and 27 % predicted versus 17–22 % observed in the third trimester. For the 800/100 mg darunavir/r once-daily dose, a decrease in the AUC of 41 % was predicted versus an observed decrease of 33 % in the third trimester. The simulations with increased dosages are also described in this table.

Fig. 9.

Simulation of darunavir plasma concentration (conc)–time curves at steady state after 14 days of treatment with twice-daily (BID) 600/100 mg darunavir/ritonavir (DRV/r) in the third trimester of pregnancy (gestational week 36, n = 11, age 20–35 years) (a) and in postpartum/non-pregnant subjects (n = 11, age 20–35 years) (b). The black circles represent the observed concentrations [39], the solid line represents the simulated mean concentrations and the dashed lines represent the 95 % confidence interval of the simulated concentrations

Fig. 10.

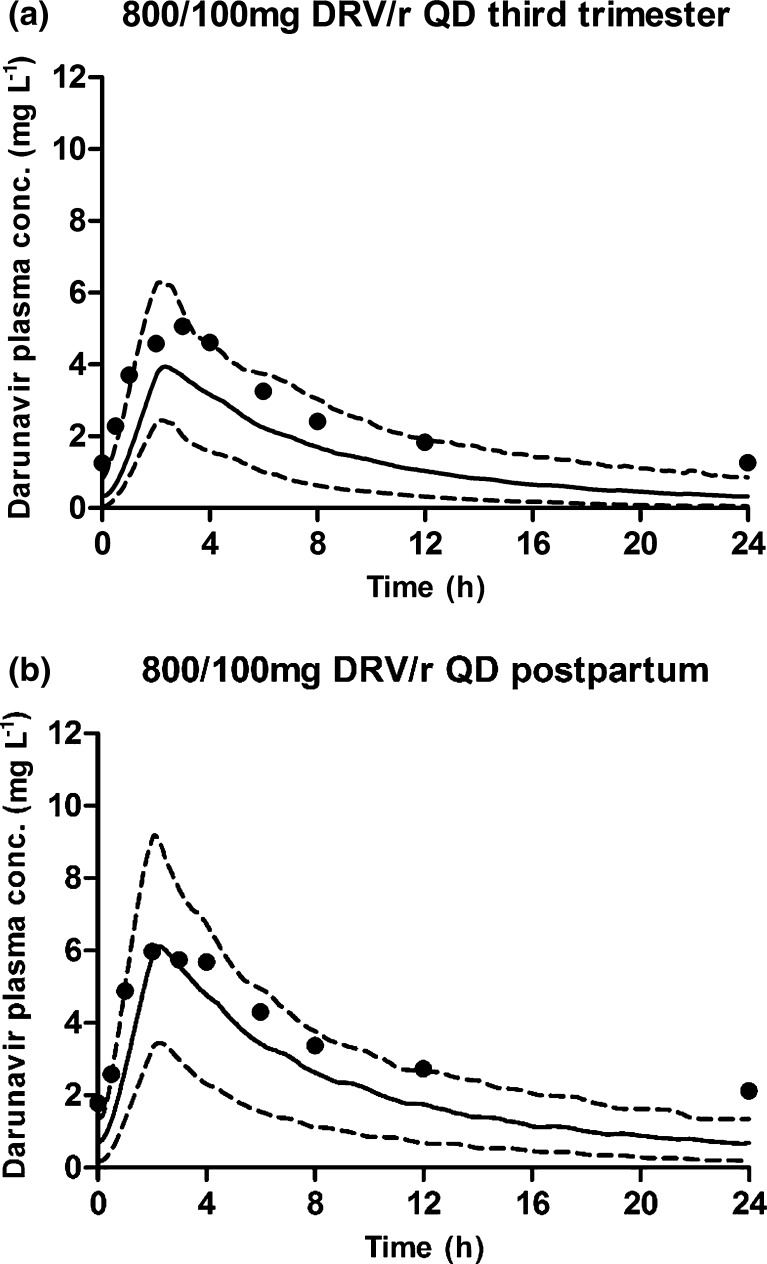
Simulation of darunavir plasma concentration (conc)–time curves at steady state after 14 days of treatment with once-daily (QD) 800/100 mg darunavir/ritonavir (DRV/r) in the third trimester of pregnancy (gestational week 34, n = 16, age 20–44 years) (a) and in postpartum/non-pregnant subjects (n = 8, age 20–44 years) (b). The black circles represent the observed concentrations [22], the solid line represents the simulated mean concentrations and the dashed lines represent the 95 % confidence interval of the simulated concentrations

Table 4.

Pharmacokinetic parameters of darunavir in pregnancy

Observed vs simulated AUC and C max values
	95 % CI (SD)
Dosage, parameter and reference	2nd trimester	3rd trimester	Postpartum	GM ratio (90 % CI)
				2nd trimester/postpartum	3rd trimester/postpartum
600/100 mg darunavir/ritonavir BID
AUC [mg h L−1]
Zorrilla et al. [39]	39 (10)	44 (16)	55 (27)	0.76 (0.63–0.90)	0.83 (0.72–0.97)
Colbers et al. [22]		41 (27–62)	53 (38–73)		0.78 (0.60–1.00)
Simulation	34 (25–46)	34 (26–45)	47 (36–61)	0.73 (0.51–1.02)	0.73 (0.53–1.02)
C max [mg L−1]
Zorrilla et al. [39]	4.6 (1.1)	5.1 (0.5)	6.5 (2.4)	0.72 (0.61–0.86)	0.81 (0.69–0.96)
Colbers et al. [22]		5.0 (3.2–7.8)	6.5 (4.4–9.7)		0.76 (0.53–1.11)
Simulation	4.7 (3.7–6.1)	4.6 (3.7–5.8)	6.6 (5.3–8.3)	0.71 (0.53–0.96)	0.70 (0.53–0.93)
800/100 mg darunavir/ritonavir QD
AUC [mg h L−1]
Colbers et al. [22]		53 (44–63)	76 (65–90)		0.67 (0.56–0.82)
Simulation		29 (23–37)	49 (37–65)		0.59 (0.42–0.83)
C max [mg L−1]
Colbers et al. [22]		5.3 (4.5–6.2)	6.8 (5.9–7.8)		0.78 (0.65–0.95)
Simulation		3.8 (3.3–4.5)	5.9 (4.7–7.5)		0.65 (0.51–0.82)

Simulations of increased doses in the 3rd trimester
Dosage	AUC simulation	Non-pregnant AUC		GM ratio: 3rd trimester/non-pregnant (90 % CI)
		BID	QD	BID	QD
800/100 mg BID	44 (33–58)	47 (36–61)		0.93 (0.67–1.29)
900/100 mg BID	50 (38–66)	47 (36–61)		1.05 (0.76–1.47)
600/100 mg BID × 2a	69 (53–90)		49 (37–65)		1.41 (1.00–1.98)
900/100 mg QD	39 (30–51)		49 (37–65)		0.80 (0.57–1.12)

AUC area under the plasma concentration–time curve, AUC _0–xh AUC from 0 to x hours, BID twice daily, CI confidence interval, C _max maximum concentration, GM geometric mean, QD once daily, SD standard deviation

^a600/100 mg AUC_0–12h × 2 to compare the AUC with the AUC_0–24h

Physiological Parameters in the Simcyp Virtual Population Library Versus a Real-Life HIV-Infected Pregnant Population

Figure 11 shows the comparison of the haematocrit and the serum creatinine, albumin and AAG concentrations between HIV-infected and non-infected healthy pregnant women (parameters used for the Simcyp p-PBPK model) [10]. The haematocrit and the creatinine and albumin concentrations were significantly lower in HIV-infected women during pregnancy, but also postpartum. The levels of the main darunavir binding protein in plasma, AAG, did not differ between the two populations. Updating the Simcyp model with the indicated parameters did not significantly alter the simulation outcomes (data not shown).

Fig. 11.

Physiological parameters compared between healthy women without human immunodeficiency virus (non HIV) and HIV-infected pregnant women (HIV+). The data represent the mean ± standard deviation per week of gestation for non HIV as reported [10] and for HIV+ women from the PANNA Network. Asterisk Significant difference between HIV+ and non HIV women (unrelated samples t test). AAG α1-acid glycoprotein

Discussion

We developed and evaluated a mechanistic model to predict darunavir exposure, both in non-pregnant and in pregnant women. Particularly, these efforts also focused on elucidating the availability of crucial mechanistic in vitro pharmacokinetic parameters that need to be incorporated into such a model. Recently, Siccardi et al. [40] published a paper on simulation of the pharmacokinetics of several antiretrovirals co-administered with antidepressant drugs. The pharmacokinetics of darunavir/r were also briefly described in terms of a PBPK model, which included only CYP3A4-mediated metabolism as a clearance mechanism. However, our literature search (Table 1) revealed that darunavir pharmacokinetics are known to be also determined by P-gp transport. Various in vitro studies have demonstrated altered disposition of darunavir during co-administration or co-incubation with P-gp inhibitors, one of which is ritonavir [17]. Moreover, there is also possible involvement of active hepatocellular uptake in the disposition of darunavir. In the rat, high concentrations of darunavir were found in the liver [41]. This would be in line with active hepatic uptake, which has been confirmed by in vitro studies showing that darunavir can interact with OATPs [28]. Therefore, we argued that an accurate PBPK model describing darunavir/r should at least take into account these active hepatic transport processes.

Only an accurate determination of metabolic clearance could allow us to begin delineating to what extent uptake and efflux transporters may be important to describe darunavir pharmacokinetics mechanistically. Therefore, we first conducted extensive studies on in vitro metabolic darunavir clearance. The values we found were in the same order of magnitude as the data described by Mamidi et al. [42] and yielded similar metabolic intrinsic in vitro clearances, i.e. 164 (in this study) versus 147 µL mg⁻¹ min⁻¹. The consistent overestimation of exposure with only metabolic clearance in our models further underlined the need to include drug transporters.

The well-stirred liver model performance could be improved substantially when uptake and efflux transport mechanisms were included against the background of a permeability-limited liver model. Quantitative transport kinetic data for darunavir are missing, but what is crucial in our findings is that the simulation outcome improved with CL_int,T values in the range of what is found to be pharmacologically feasible for liver uptake of other comparable drug substrates [43, 44]. Nevertheless, our findings now urge more detailed quantitative studies on darunavir transport kinetics in cultures of hepatocytes or overexpression systems, in order to validate whether CL_int,T, uptake and CL_int,T efflux values are in line with the values that we predicted with our simulations. These studies should also include measurements of membrane transporter abundance to allow accurate extrapolation from in vitro to in vivo. As the in vivo abundance of several hepatic transporters has already been reported in the literature [45], it is of particular relevance that new studies on the transporter kinetics of darunavir should also include quantification of absolute transporter expression in in vitro incubation systems.

The ritonavir-mediated increase in darunavir exposure could be adequately simulated if efficient enterohepatic recycling was assumed, i.e. when 80–100 % of the darunavir that was excreted unchanged via the bile was set to be available for enteric reabsorption. Enterohepatic circulation of darunavir has been suggested previously [46], but, to our knowledge, we are the first to capture this in a mechanistic model. However, for the unboosted darunavir dose, inclusion of enterohepatic cycling resulted in slightly overpredicted exposure. Possibly, this discrepancy can be explained by unexpected non-linearity in intestinal absorption at very low luminal darunavir concentrations in the gut, resulting from biliary excretion of darunavir. Low permeability could be due to effective P-gp-mediated efflux of darunavir from enterocytes at these concentrations. This would indeed not be expected in the presence of ritonavir, as this inhibits P-gp, maintaining high darunavir permeability and effective enterohepatic circulation even at very low concentrations. Additional measurements of darunavir permeability in Caco-2 cells, covering a wider/lower range of apical darunavir concentrations, may reveal whether this effect does indeed take place.

Pending the outcome of the proposed experiments to test the hypotheses generated by the PBPK modelling work described here, it is not possible to definitively separate the contributions of uptake, efflux, metabolism and enterohepatic cycling to darunavir pharmacokinetics.

With regard to the data used for input into the ritonavir model, it should be taken into account that mechanism-based inhibition of ritonavir by definition also played a role in the described HLM experiments, which were primarily designed to assess the competitive aspect of CYP3A4 inhibition by ritonavir. This is virtually unavoidable, but, as a result, the competitive CYP3A4 inhibitory component of the ritonavir interaction model may have been slightly overestimated. Despite this drawback, inclusion of the data as an estimate of competitive CYP3A4 inhibition led to a useful model, since the effect of ritonavir on midazolam exposure was adequately predicted. An additional limitation of the ritonavir model is that physiological changes in pregnancy did not affect the ritonavir concentrations in the current model, whereas in real life, this is the case [22, 39]. We compensated for this in our simulations by adjusting the oral ritonavir clearance used for simulations in non-pregnant individuals to reported values during pregnancy. In general, a 50 % decrease in ritonavir exposure is described in pregnancy, which could lead to a smaller effect on darunavir exposure [22, 47]. However, clinical studies have demonstrated that a 50 mg ritonavir dose also increased darunavir concentrations almost as powerfully as the 100 mg dose [48]. Therefore, we considered it unnecessary to develop a full mechanistic ritonavir PBPK model on the basis of in vitro metabolic clearance parameters. Future studies may address this in more detail.

As can be seen in Figs. 10 and 11, particularly for 800/100 mg darunavir/r once daily, the model overpredicted the elimination rate. We hypothesize that a possible explanation for the discrepancies between the observed and simulated data is that the Simcyp pregnancy PBPK model is based on physiological changes described for ‘healthy’ pregnant women, whereas the pregnancy pharmacokinetic curves we used were taken from HIV-infected pregnant women. The levels of the main darunavir binding protein (AAG) did not differ between the two populations. Although the haematocrit and albumin concentrations were lower in the HIV-infected women, the effect of pregnancy was similar for both physiological parameters. Anaemia, with a decreased haematocrit, is common in HIV-infected patients, as a result of the disease, or possibly resulting from certain antiretroviral agents [49]. We do not expect the decreased serum creatinine concentration at the end of pregnancy, pointing to an increased glomerular filtration rate, to be relevant for darunavir/r, as the renal clearance is very low [41]. Nevertheless, our findings are important for mechanistic pharmacokinetic modelling of other drugs that are excreted renally, have high albumin binding or exhibit high distribution into red blood cells.

Finally, we used the pregnancy PBPK model to predict the alternative dose levels that may compensate for the decreased exposure observed in pregnancy. It remains questionable whether it is necessary to increase the dose during pregnancy [22]. Nevertheless, two alternative dosages (800/100 mg twice daily and 900/100 mg twice daily), one of which was also predicted via our approach, are indeed currently being investigated clinically in a P1026 protocol by the International Maternal Pediatric Adolescent AIDS Clinical Trials Group (IMPAACT) group. The outcome will allow further validation of the model described here [50]. Ultimately, PBPK model predictions may also be helpful in choosing the most optimal dose in more complex cases—for example, when women taking darunavir/r are not only pregnant but also use various medications that may additionally alter darunavir pharmacokinetics via DDIs.

Conclusion

A PBPK model that takes the involvement of hepatic drug transporters and enterohepatic circulation into account could adequately simulate darunavir/r pharmacokinetics for several dosage regimens and patient populations. To improve the mechanistic basis of the model, we propose that future studies should address hepatic—but also intestinal—transporter-mediated darunavir disposition in more detail. The current model predicted decreased exposure during pregnancy to be compensated for by 600/100 mg darunavir/r twice-daily dosing for women who initially took the 800/100 mg darunavir/r once-daily dose. For the 600/100 mg twice-daily dose (used in treatment-experienced patients), the reduction in exposure can be compensated for by an 800/100 mg darunavir/r twice-daily dosing regimen.

Compliance with Ethical Standards

The PANNA study was conducted in compliance with the principles of the Declaration of Helsinki. Informed consent was obtained from each participant before they entered the study. The study was approved by the medical ethical committee from each individual centre involved, and by the national authorities if applicable. The study was registered at ClinicalTrials.gov under study ID Number NCT00825929.

The PANNA Network is financially supported by the European AIDS Treatment Network (NEAT), Bristol-Myers Squibb, Merck and Janssen Research BV. The PBPK modelling was supported by door Health~Holland, Top sector Life Sciences & Health.

AC, RG, CL, DB and FR have no conflicts of interest to declare.