Mechanistic Models Predict Efficacy of CCR5‐Deficient Stem Cell Transplants in HIV Patient Populations

Abstract

Combination antiretroviral therapy (cART) effectively suppresses viral load in HIV‐infected individuals, but it is not a cure. Bone marrow transplants using HIV‐resistant stem cells have renewed hope that cure is achievable but key questions remain e.g., what percentage of stem cells must be HIV‐resistant to achieve cure?. As few patients have undergone transplants, we built a mechanistic model of HIV/AIDS to approach this problem. The model includes major players of infection, reproduces the complete course of the disease, and simulates crucial components of clinical treatments, such as cART, irradiation, host recovery, gene augmentation, and donor chimerism. Using clinical data from 172 cART‐naïve HIV‐infected individuals, we created virtual populations to predict performance of CCR5‐deficient stem‐cell therapies and explore interpatient variability. We validated our model against a published clinical study of CCR5‐modified T‐cell therapy. Our model predicted that donor chimerism must exceed 75% to achieve 90% probability of cure across patient populations.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC? ☑ In 2008, the Berlin patient underwent a bone marrow transplant from a CCR5Δ32 donor. Since then, he has shown no signs of active HIV‐1 replication in the absence of cART. This approach was recently shown to reduce viremia and to return T cell counts to normal levels in pigtail macaques, however, clinical data remains limited, as few patients have undergone transplants. • WHAT QUESTION DOES THIS STUDY ADDRESS? ☑ The following questions were addressed: (i) given that patients will have a chimeric immune system after the transplant, what percentage of stem cells must be HIV‐resistant for a cure to work? and (ii) what is the minimal level of anti‐HIV activity needed in these cells to achieve cure? WHAT THIS STUDY ADDS TO OUR KNOWLEDGE ☑ The mechanistic model introduced in this work reproduces the complete course of HIV/AIDS, captures variations in clinical measurements across patient subpopulations, and simulates crucial components of stem cell transplants. The model predicts the probability of cure for CCR5‐deficient stem cell therapy across patient populations. • HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS ☑ Bone marrow transplants using HIV‐resistant stem cells have renewed hope that cure is achievable but key questions remain to be answered. Our model will help answer those questions, design stem cell‐based therapies, and predict clinical studies.

Thirty‐two years after the discovery of human immunodeficiency virus (HIV), there has been only one reported case of a functionally cured HIV‐infected individual. This individual, known as the “Berlin patient,” was treated in 2008 with myeloablative irradiation and hematopoietic stem cell transplant from a donor with a homozygous CCR5Δ32 mutation conferring resistance to HIV.1, 2 Since then, the recipient has not used combination antiretroviral therapy (cART) and the virus seems to be eliminated. Two “Boston patients” seemed HIV‐free after reduced‐intensity conditioning hematopoietic stem cell transplant from donors without the rare CCR5Δ32 mutation; however, their new immune systems were vulnerable to reinfection and the virus rebounded after 7 and 15 weeks.3 Thus, irradiation and transplant are likely insufficient for cure without anti‐HIV activity in the immune system. Since 2008, at least six other patients received a graft from a donor with a homozygous CCR5Δ32 mutation.4, 5 However, none survived for longer than one year, suggesting that other key factors, such as graft‐vs‐host effects, are involved in the success of the therapy.

Finding a rare matched donor who also has a homozygous mutation in CCR5 for each patient with HIV is very challenging. However, the HIV‐resistance conferred by the CCR5Δ32 mutation could be recapitulated in donor cells by ex vivo knockout or editing of CCR5 before transplant. This could provide HIV‐resistance to the new immune system, assist in viral elimination from the recipient's system (Figure 1 a), and lead to a functional HIV cure.6 This approach was recently shown to reduce plasma viremia and to return T cell counts to normal levels7 in pigtail macaques that underwent bone marrow transplants augmented with mC46,8, 9 a virus fusion inhibitor. However, key questions remain: (a) given that patients will have a chimeric immune system after the engraftment, what percentage of the cells must be HIV‐resistant in order to clear the system? (b) what is the minimal level of anti‐HIV activity needed in these cells to achieve cure? Given the small number of patients with HIV who have undergone bone marrow transplants10 and the limited number of animal experiments,7, 11, 12, 13 we built a novel mechanistic model of HIV infection to answer these questions. Using the model, we study the complex pathogenesis of HIV, design and test CCR5‐based therapies, and explore interpatient variability in response to these therapies.

Figure 1.

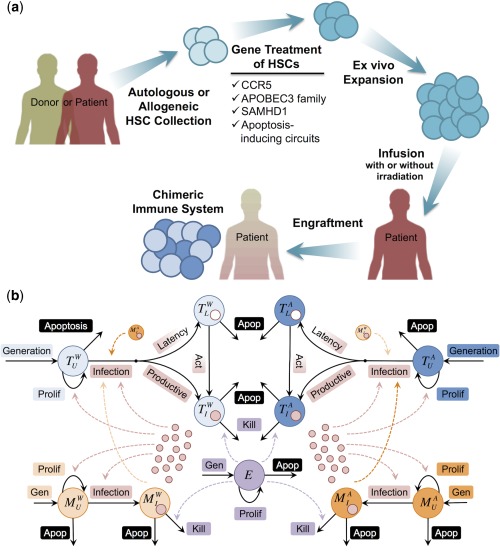
Anti‐HIV stem cell therapy and mechanistic model of HIV infection. (a) Finding matched donors with homozygous CCR5 mutation is challenging. Instead, hematopoietic stem cells can be collected from the patient (autologous) or a matched donor (allogeneic) and treated to become HIV‐resistant. This can be done by knocking out CCR5 or by inserting anti‐HIV genes, such as APOBEC3 family, SAMHD1, or on‐demand apoptosis‐inducing circuits. Treated stem cells expanded ex vivo are re‐infused into the patient after bone marrow or total body irradiation to kill the patient's own stem cells. Irradiation does not eliminate 100% of the recipient's stem cells or immune system. Therefore, the post‐engraftment immune system will be chimeric (i.e., a mixture of immune cells that are progenies of the donor and recipient stem cells). (b) The model includes key components of the infection: the virus (red circles), and multiple immune cell types: CD4+ T cells (blue), monocytes/macrophages (orange), and CD8+ cytotoxic T lymphocytes (purple). We also track wild type (light colors) and augmented (dark colors) CD4+ T cells and macrophages, in which CCR5 has been rendered dysfunctional (e.g., knocked out or edited). Blue circles with a small red or white circle inside them represent productive and latently infected CD4+ T cells, respectively. Solid arrows demonstrate the mechanisms included for each cell type in the model, whereas dashed arrows pointing out of cells or viruses indicate which mechanisms they impact. More details, including differential equations and detailed model description, are provided in Supplementary Method S1.

METHODS

Description of the model

Our model is built using components of previous well‐established models of HIV dynamics by others14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 and models of host‐pathogen molecular interaction and therapy from our laboratory.26, 27 Previous models of HIV dynamics could predict some features of in vivo HIV/AIDS, such as the biphasic viral decay after starting cART. However, they also have shortcomings (e.g., most models assume that the disease is at a steady state, do not reproduce the late‐stage viremia, focus only on acute or chronic infection, fail to reproduce the clinical results for both treated and untreated patients, have some unrealistic parameter values, and/or are trained with limited viral load or CD4+ data). To address these issues, we built a mechanistic model of HIV/AIDS that captures the complete course of the disease, reproduces both treated and untreated patients, has constant parameters that take biologically relevant values, is trained with viral load, CD4+ and CD8+ data, uses cohort data to capture interpatient variability, and has the ability to test anti‐HIV CCR5‐based therapies. The model includes key components of the infection: the virus, and multiple immune cell types: CD4+ T cells, monocytes/macrophages, latently infected CD4+ T‐cells, and CD8+ cytotoxic T lymphocytes. We also track wild type (WT) and augmented cells, in which CCR5 has been rendered dysfunctional (e.g., knocked out or edited; Figure 1 b). The model was developed in SimBiology (MathWorks, Natick, MA). See Table 1 for parameters used in the model and Supplementary Method S1 for model equations and detailed description.

Table 1.

Parameters of the model, definitions, and the mechanism they represent

Parameter	Mechanism	Definition
sT	T cell generation	Production rate of uninfected CD4+ T cells
fT	T cell generation	Percentage of augmented stem cells, which produce CCR5−/− CD4+ T cells
rT	T cell proliferation	Proliferation rate of uninfected CD4+ T cells in the absence of infection
pT	T cell proliferation	Max. proliferation rate of uninfected CD4+ T cells due to infection
cT	T cell proliferation	Conc. of virus, at which the proliferation rate of uninfected CD4+ T cells due to infection is half of pT
dT	T cell apoptosis	Death rate of uninfected CD4+ T cells
kVT	T cell infection	Rate constant for infection of CD4+ T cells by HIV
kMT	T cell infection	Rate constant for infection of CD4+ T cells by infected macrophages
αCCR5	T cell infection	Reduction in kVT for CCR5−/− CD4+ T cells
εCCR5	T cell infection	Reduction in kMT for CCR5−/− CD4+ T cells
kL	T cell latency	Fraction of infected CD4+ T cells that become latently infected.
aL	Act of latent T cells	Activation rate of latently infected CD4+ T cells
dTI	Infected T cell death	Death rate of infected CD4+ T cells
kET	Infected T cell kill	Rate constant for killing of infected CD4+ T cells by CD8+ T cells
dL	Latent T cell death	Death rate of latently infected CD4+ T cells
sM	Mφ generation	Production rate of uninfected macrophages
fM	Mφ generation	Percentage of augmented stem cells, which produce CCR5−/− macrophages
pM	Mφ proliferation	Maximum proliferation rate of uninfected macrophages due to infection
cM	Mφ proliferation	Concentration of virus, at which the proliferation rate of uninfected macrophages due to infection is half of pM
dM	Mφ apoptosis	Death rate of uninfected macrophages
kVM	Mφ infection	Rate constant for infection of macrophages by HIV
βCCR5	Mφ infection	Reduction in kVM for CCR5−/− macrophages
dMI	Infected Mφ death	Death rate of infected macrophages
kEM	Infected Mφ kill	Rate constant for killing of infected macrophages by CD8+ T cells
sE	CD8+ T cell gen.	Production rate of CD8+ T cells
pE	CD8+ T cell prolif.	Maximum proliferation rate of CD8+ T cells due to infection
cE	CD8+ T cell prolif.	Conc. of CD4+ T cells, at which the proliferation rate of CD8+ T cells due to infection is half of pE
dE	CD8+ T cell death	Death rate of CD3+ CD8+ T cells
dV	Virus clearance	Clearance rate of free virus
nT	Virus production	Burst size of infected CD4+ T cells
nM	Virus production	Burst size of infected macrophages

RESULTS

Clinical data

To train and validate our model, we used the publicly available dataset (release P20 at http://www.ntis.gov/) of the Multicenter AIDS Cohort Study, which includes longitudinal semiannual clinical measurements of patients from 1984–2007. The dataset has information from 6,972 individuals, including seronegatives, seropositives, and seroconverters. In this study, we were interested in cART‐naïve HIV‐infected individuals, whose date of HIV seroconversion and date of initial AIDS diagnosis were (approximately) known. This resulted in 172 patients (see Supplementary Method S2). We categorized patients based on their progression time to AIDS into 4 subgroups: AIDS occurring before 3.5 years (rapid progressors, N = 32), between 3.5 and 7 years (N = 61), between 7 and 9 years (N = 39), and after 9 years since seroconversion (slow progressors, N = 40). There are significant variations in the clinical measurements, e.g., plasma viremia, CD3+CD4+ and CD3+CD8+ T cell counts among individuals within each subpopulation of patients with HIV (Figure 2 a,b,c and Supplementary Figure S1); for example, one year post‐seroconversion, CD4+ T cell count ranges from 100 to 1,200 cells/μL in rapid progressors (Figure 2 b). There is also substantial variability in the baseline levels of CD4+ T cells before infection (day 0 in Figure 2 b and Supplementary Figure S1e,f,g,h). Between subpopulations, there is a high degree of overlap; however, rapid progressors have the highest viral loads in the shortest period of time with rapid decline in the CD4+ T cell counts, whereas slow progressors show relatively stable viral load and CD4+ T cell counts for a longer time compared with other populations. We also observed that CD8+ T cell count increases until the midchronic stage of HIV and then tends to drop (Figure 2 c and Supplementary Figure S1i,j,k,l), suggesting homeostasis failure before the onset of AIDS.28 Most published models of HIV dynamics only reproduce the average profiles of viral load and CD4+ T cell counts and use that model to predict the efficacy of treatments. This gives a limited view of treatment efficacy, as the huge interpatient variability is neglected. In this work, we build models to capture the range of variability observed in patients and use that information to run virtual clinical trials and predict the interpatient variability of treatment performances. See Supplementary Table S1 for more information on patient characteristics and their clinical measurements.

Figure 2.

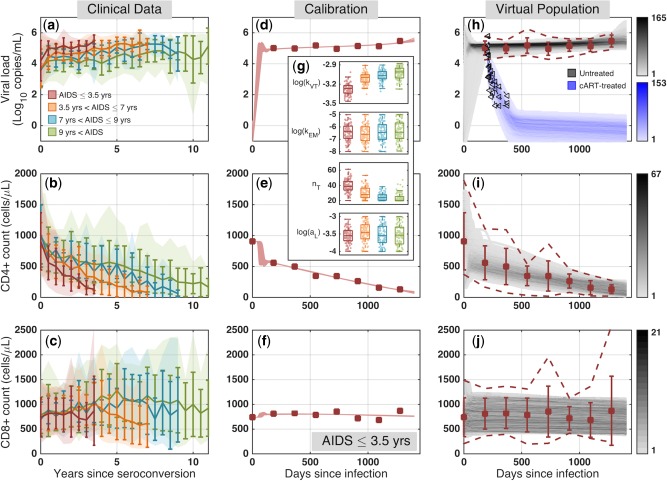
Clinical data, model calibration, and generation of virtual population. (a–c) From the Multicenter AIDS Cohort Study (MACS) cohort, we collated viral load, CD4+ and CD8+ T cell counts from combination antiretroviral therapy (cART)‐naïve HIV‐infected individuals with known dates of HIV seroconversion and initial AIDS diagnosis; shaded regions: 5th and 95th percentiles of the aggregated data; dark colored lines: average and standard deviation. (d–f) We calibrated the model to match the average clinical data in rapid progressors; see Supplementary Figure S3 for all subpopulations; symbols: average clinical profiles; curves: 100 best fits. (g) The boxplots represent parameters values corresponding to the 100 best curves. See Supplementary Figure S4 for all parameters; (h–j) Virtual patient population captures the observed variability in clinical measurements of cART‐naïve rapid progressors and is validated against clinical data from decay of plasma viremia in another group of cART‐treated patients who received cART at 208 dpi³⁰; symbols: average clinical profiles; dashed lines: 5th and 95th percentiles of the aggregated data; black symbols: clinical data for the viral load decay; gray regions: temporal histograms of cART‐naïve patients; blue region: cART‐treated virtual patient profiles.

Average clinical profiles can be reproduced using multiple different parameter sets with biologically relevant values

To train our model, we used average profiles of viral loads, CD4+ and CD8+ T cell counts in each subpopulation. We used the scatter‐search based optimization method29 to find the parameter values that generate curves with the best fit (the lowest error) to the clinical data (Supplementary Figure S2). Parameter values were confined to biologically relevant ranges and consistent with previously published measurements (see Supplementary Table S2). Parameter optimization is discussed in detail in Supplementary Method S3. The 100 best curves matching the average viral load, CD4+ and CD8+ T‐cell counts for rapid progressors, are shown in Figure 2 d,e,f (see Supplementary Figure S3 for all subpopulations). These 100 best curves produce good fits to the clinical data and are tightly placed on top of each other. Inspecting the values of the 23 parameters across the 100 best parameter sets, we observe that some parameters (e.g., p_M and k_VT) have values in a relatively tight range and therefore the model is more sensitive to these and we have greater confidence in their values, whereas others (e.g., k_EM) take values in a wider range (Figure 2 g; also see Supplementary Figure S4 for parameter values generating the 100 best fits in each subpopulation). Although none of these curves represents a real patient (only the population average), this observation suggests that there might be patients with very similar longitudinal viral loads and T cell counts who might have very different immune systems and HIV infections (as represented by the different parameter values) and hence respond differently to treatments. We calculated Spearman correlations to test for trends across populations (Supplementary Figure S4). For example, we found that n_T, the burst size of infected T cells, takes statistically smaller values as we transition from rapid progressors to slow progressors, whereas a_L, activation rate of latently infected T cells, does not take significantly different values across populations (Figure 2 g). We also studied the correlation coefficients between the system parameters in all populations (Supplementary Figure S5). In most cases, there is a weak correlation between parameters of the system, suggesting that these parameters act relatively independently. However, in all populations, we observed strong negative correlations between n_T and k_VT and between n_M and k_VM, suggesting that the burst size of infected T cells and macrophages are inversely associated with the infection rate of T cells and macrophages by free virus, respectively. The parameter values for the 100 best curves matching the average clinical profiles are provided in Supplementary File S1.

The model also predicts other metrics of the disease (Supplementary Figures S6 and S7). In the first 500 days, the predicted percentage of infected CD4+ T cells remains under 15% in rapid progressors and this percentage is substantially lower for slower progressors (Supplementary Figure S6). This is consistent with the low values for clinical measurements of infected CD4+ T cells during chronic infection.30, 31, 32 The model also suggests that the percentage of infected macrophages remains <5% for most of the infection and that the number of macrophages rises at the late stage of the disease, explaining the rise in viral load during AIDS (Supplementary Figure S7). Finally, the model indicated that the majority of viral load is due to infected T cells during the acute/early chronic infection and, as the disease progresses, viruses released from infected macrophages play a more important role and eventually constitute the majority of viral load during AIDS (Supplementary Figure S7). This is consistent with the experimental evidence that macrophages produce large amounts of simian immunodeficiency virus (SIV) even after CD4+ T cells are depleted in macaques.33

Virtual patient populations capture the range of variability observed in the clinical data

To facilitate capturing the observed clinical variability in measurements from HIV‐infected individuals, we created four virtual patient populations using the 5th and 95th percentiles of the clinical data for each subpopulation. We used a virtual population development methodology, introduced in ref. 34, which includes three main steps: (1) patient generation: to explore uncertainty by creating parameter sets locally randomized around the 100 best fits; (2) patient selection: to select those generated patients whose simulated profiles lie within the range of clinical data for the corresponding subpopulation; and (3) patient validation: to validate the virtual populations against another clinical dataset (which was not used for training). The details of virtual population development are discussed in Supplementary Method S4. Figure 2 h,i,j show, respectively, the temporal histogram of viral load, CD4+ and CD8+ T cell profiles of the 1,000 virtual patients for rapid progressors, completely capturing the range of clinical measurements (see Supplementary Figures S8 and S9 for the virtual patient profiles and the temporal histograms in all subpopulations, respectively). For validation, we used the viral decay data (black symbols in Figure 2 h and Supplementary Figure S8) from cART‐treated patients, who started taking cART approximately 208 days after infection and were monitored for 48 weeks.30 After receiving cART, all the virtual patient populations display a biphasic decay, consistent with the viral decay from cART‐treated patients (Figure 2 h and Supplementary Figure S8). The decay is followed by a plateau in viral load, which is due to occasional activation of latently infected CD4+ T cells and is below the detection level of clinical assays. The temporal histogram of virtual patient profiles also demonstrates a good match between average clinical patterns and the high intensity regions, where a higher proportion of the patient profiles lies (Figure 2 h,i,j and Supplementary Figure S9). The parameter values for the 1,000 virtual patients in each population are provided in Supplementary File S2 and the parameter trends across populations (Supplementary Figure S10) are similar to Supplementary Figure S4. Correlations between parameters (Supplementary Figure S11) have changed only slightly compared to parameters reproducing the average profiles (Supplementary Figure S5). The average percentage of infected CD4+ T cells in the first 500 days remains under 10 percent and is lower for slower progressors (Supplementary Figure S12), consistent with our current understanding that infected CD4+ T cells constitute a small fraction of CD4+ T cells during the chronic infection. The average percentage of infected macrophages in this period is <3 percent in all populations (Supplementary Figure S13). Also, in cART‐treated patients, the ratio of latently infected CD4+ T cells is in the range 10⁻⁶−10⁻³ (Supplementary Figure S12), which is consistent with our current knowledge of the size of the latent reservoir.35

Virtual clinical trials predict the efficacy of CCR5‐based stem cell therapy

CCR5‐deficient stem cell therapy has appeared to functionally cure the Berlin patient of HIV, but one key question is whether CCR5‐based therapy would be successful at stopping the disease in other HIV‐infected individuals. To predict the efficacy of CCR5‐based stem cell therapy, we simulated the complex clinical procedure for the Berlin patient as closely as possible and ran a virtual clinical trial using our validated virtual populations. As illustrated for rapid progressors (Figure 3), the simulated protocol is as follows. (1) Infection at day 0: CD4+ T cells quickly drop while plasma viremia rapidly increases in these patients. (2) cART 208 days postinfection (dpi): patients start taking cART, which stops the infection of CD4+ T cells and macrophages, and hence reduces the viral load in a biphasic way and returns T cell counts to normal levels. Eventually, the viral load plateaus and becomes undetectable. (3) Bone marrow transplant at 500 dpi: this procedure consists of bone marrow irradiation over seven days, followed by the engraftment of new stem cells (six months). During the irradiation, stem cells are killed and hence no more immune cells are produced. Also, cytotoxic T lymphocytes, uninfected and infected CD4+ T cells are killed, and the size of the latent reservoir is reduced by three orders of magnitude.36, 37 However, macrophages remain intact as they mostly reside in tissues. Note that even after the irradiation is complete, some residual WT stem cells are left behind. This leads to donor chimerism after infusion of CCR5‐modified stem cells. During engraftment (507–687 dpi), a percentage of stem cells are CCR5‐deficient and the rest are WT (donor chimerism, 50% in Figure 3). Also, the production levels of immune cells return to pretransplant values. All patients remain on cART during irradiation and engraftment. (4) No cART (687 dpi): six months after engraftment, CD4+ T cells are back to normal levels (except many CD4+ T cells are CCR5‐deficient) and viremia is below the detection level. These patients cease taking cART; infection rates of CD4+ T cells and macrophages return to pre‐cART values.

Figure 3.

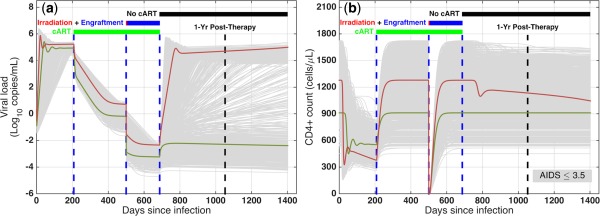
Performance prediction of CCR5‐deficient stem cell therapy in rapid progressors. (a) Viral load and (b) CD4+ T cell counts in a virtual clinical trial simulating rapid progressors to predict the efficacy of CCR5‐modified stem cell transplants. The virtual clinical trial includes: (1) infection at day 0; (2) combination antiretroviral therapy (cART) from 208 days postinfection (dpi); (3) bone marrow transplant at 500 dpi, including irradiation and six months of engraftment; and (4) cART cessation at 687 dpi. A patient is functionally cured if posttherapy CD4+ level >95% of preinfection level and viral load <50 copies/mL and decaying; gray curves: individual patients; green curves: cured patient; red curves: patient not cured.

We observe that some patients (e.g., individual in green, Figure 3) maintain their CD4+ T cell levels and keep their viremia below the level of detection, whereas for other patients (e.g., individual in red), viral load rapidly increases and CD4+ T cells start to decline, suggesting that CCR5‐deficient cells slowed the infection but were not able to completely stop it. If we only had one model with one parameter set, our answer to the question of whether CCR5‐based therapy is successful at stopping HIV infection would be an all‐or‐none response. In reality, there is huge variability among patients and the significance of using virtual populations is that, similar to running a clinical trial, we are able to look at the interpatient variability in response to new anti‐HIV therapies in a virtual clinical trial.

To calculate probability of cure, we define an HIV‐infected patient as functionally cured if, one year post‐therapy: (1) CD4+ level >95% of baseline and (2) viral load <50 copies/mL and decaying. Figure 4 a,b show one year post‐therapy viral load and normalized CD4+ T cell counts, respectively, for any level of donor chimerism (percentage of CCR5‐modified stem cells) in rapid progressors. The model predicts that if augmented stem cells are <10%, post‐therapy viral load is at about 10⁵ copies/mL for almost all patients and normalized CD4+ levels are between 10% and 80%. As the donor chimerism increases, the post‐therapy viral load drops and CD4+ T cell count rises, however, we observe a broad spectrum. For augmented stem cells >80%, the viral load is below the level of detection and CD4+ T cell counts are back to normal levels for almost all patients. Using the post‐therapy viral load and CD4+ levels and based on the two conditions that we defined, we calculated the probability of cure for rapid progressors (Figure 4 c, red curve). Surprisingly, the model predicts that if the donor chimerism is <20%, the probability of cure is zero, suggesting that high levels of chimerism and transfection efficiencies are needed to achieve meaningful ranges for the probability of cure in patients. Comparing rapid progressors with the other populations, we observe that the post‐therapy viral load decreases faster and CD4+ T cell counts rise to normal levels more quickly (Supplementary Figure S14), and hence the probability of cure is higher in these populations for a given percentage of CCR5‐modified stem cells (Figure 4 c and Supplementary Figure S14). For example, if the percentage of stem cells transfected is 60%, the probability of cure will be 51% and 83% in rapid progressors and slow progressors, respectively. The model also crucially suggested that most of the difference is between rapid progressors and the rest of the HIV‐infected individuals (Figure 4 c). To achieve 90% probability of cure in all patient populations, our model predicted that the level of donor chimerism must be at least 75%. In our model, we assume a partial inhibition of HIV infection (92.5%, consistent with experimental data38) for CCR5‐modified CD4+ T cells and macrophages, but these cells can still get infected. Virtual clinical trials varying this level of anti‐HIV activity (85% and 100%, Supplementary Figure S15) illustrate how to evaluate multiple therapeutic design parameters to achieve desired cure rates. For example, with 60% donor chimerism in slow progressors, the probability of cure increases to 91% if CCR5‐modified cells are completely resistant to infection.

Figure 4.

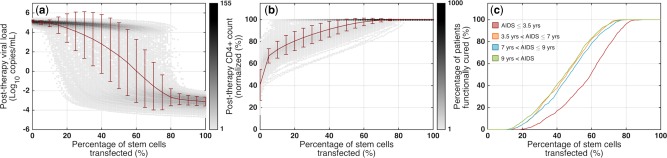
Probability of cure for CCR5‐deficient stem cell therapy. (a) Viral loads and (b) normalized CD4+ levels at one year post‐therapy in rapid progressors for different percentages of stem cells transfected (i.e., different levels of donor chimerism). (c) Using the one‐year post‐therapy simulation results and the two conditions for a functional cure, we calculated the probability of cure in all patient populations; red: AIDS ≤3.5 years; orange: 3.5 < AIDS ≤7 years; blue: 7 < AIDS ≤9 years; green: 9 years < AIDS.

Validation of the virtual populations against clinical data from CCR5‐based autologous T cell therapy in HIV‐infected patients

Recently, Tebas et al.39 investigated the infusion of CCR5‐modified autologous CD4+ T cells to 12 patients, who were receiving cART and had chronic aviremic HIV infection. Six of these patients, who had baseline CD4+ T cell counts >450 cells/μL (546–1123 cells/μL) and a documented nadir of not lower than 300 cells/μL, underwent a 12‐week cART interruption four weeks after the single dose infusion of 10¹⁰ cells (∼2,000 cells/μL), with 20% of those cells being CCR5‐modified on average. Plasma viremia, CCR5‐modified, and total CD4+ T cell counts were monitored in these patients for 36 weeks (symbols in Figure 5 represent median results). For two of these patients, the treatment interruption was terminated prematurely at week eight of the interruption period.

Figure 5.

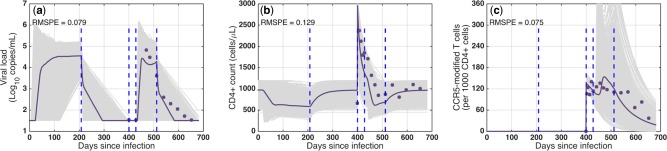
Validation of virtual populations against clinical data from CCR5‐modified autologous T cell therapy in HIV‐infected patients. (a) Viral load, (b) total CD4+ T cell count, and (c) CCR5‐modified CD4+ T cell count in virtual patients for virtual clinical trial simulation compared to clinical data from an infusion of CCR5‐modified CD4+ T cells to HIV infected individuals. Gray curves: individual patients; purple curves: median of virtual patients; symbols: median of clinical data; RMSPE: root mean square prediction error.

To validate our model against this data, we selected virtual patients with baseline CD4+ T cells levels <1,200 cells/μL from all subpopulations. In our model, these patients began cART at 208 dpi, had undetectable viral load by 400 dpi, and received a single infusion of 2,000 cells/μL (WT: 1,600 cells/μL; CCR5‐modified: 400 cells/μL). Four weeks postinfusion (428 dpi) cART was ceased for 12 weeks, and they resumed cART at 512 dpi. Figure 5 shows the individual virtual patients (gray curves) and the median of the simulation results (purple curves), which predicts the clinical data (symbols) with low RMSPE (root‐mean square prediction error) values. The details for each subpopulation are shown in Supplementary Figure S16.

DISCUSSION

In this article, we introduced a novel mechanistic model of HIV/AIDS that reproduces the complete course of the disease from acute infection to AIDS. Unlike most models in the literature, our model is not running at a steady state; this challenges the HIV RNA setpoint theory, which assumes a stable viral load during chronic infection. We use the model to create virtual patient populations that capture the variations in clinical measurements of cART‐naïve HIV‐infected patients, who progressed to AIDS 1.5–12 years post‐seroconversion in the Multicenter AIDS Cohort Study cohort (Supplementary Table S1 and Supplementary Figure S1). Although CD4+ T cells are thought to be the driving force in HIV infection and the role of macrophages is debated in the field,33, 40, 41 this model suggests that macrophages are required to reproduce the clinical data in cART‐naïve patients (Supplementary Figure S3); without macrophages, the calibration failed and the model could not fit the data. The model also predicts that in late stage disease, when the viral load increases and CD4+ T cells are almost depleted, infected macrophages play a major role in producing viruses (Supplementary Figures S7 and S13). In this study, the immune response to HIV infection is represented by CD8+ cytotoxic T lymphocytes, as there is a strong negative association between the strength of the immune response and progression to AIDS.42 We also included latently infected CD4+ T cells, as they present the major obstacle to achieve HIV cure.43 We validated the model against clinical data for the biphasic viral decay in cART‐treated patients (Supplementary Figure S8).

To test the efficacy of CCR5‐modified stem cell therapies in blocking HIV, we considered two separate populations of WT and CCR5‐modified cells for CD4+ T cells and macrophages. The model has the capability to simulate events in an HIV clinical trial (e.g., taking patients on and off cART, bone marrow, and total body irradiation, engraftment and host recovery, gene modifications, and donor chimerism). Using virtual populations, our model successfully predicted the results for a clinical study of infusion of autologous CCR5‐modified CD4+ T cells to HIV‐infected individuals (Figure 5 and Supplementary Figure S16). However, both the simulation and clinical results indicated that augmented CD4+ T cell therapies do not lead to cure, as there is no source for constant production of these cells in patients. Instead, we used the virtual patients to predict whether the CCR5‐deficient stem cell therapy performed on the Berlin patient can be replicated in other HIV‐infected individuals (Figure 4 c; Supplementary Figures S14 and S15). The simulations suggested some key insights: (1) for donor chimerism <10%, the probability of cure is zero; (2) high levels of donor chimerism is required to achieve meaningful success rates in patients (e.g., at least 75% of stem cells must be CCR5 modified to achieve cure in 90% of patients); and (3) most of the difference in the success rate of the stem cell therapy lies between rapid progressors (AIDS ≤3.5 years) and other HIV‐infected individuals (AIDS >3.5 years). A major barrier in stem cell therapies has been low efficiency of gene transfections into stem cells, leading to low levels of augmented cells in vivo.44, 45, 46 To make anti‐HIV stem cell therapies more successful in clinical trials, the results indicate that more efforts should be undertaken to increase ex vivo transfection/selection efficiencies and in vivo post‐transfection selection of augmented cells,7, 47 and to suppress the host immune system sufficiently for achieving high levels of donor chimerism.

Including other disease‐relevant tissue compartments in addition to the blood in the model (e.g., lymphoid and mucosal tissues), could represent a more comprehensive picture of the immune system during the course of infection. For example, some studies have suggested that damage in lymphoid tissues as a consequence of HIV infection leads to limited reconstruction of T cells after cART. In humans, the blood compartment contains 1–2% of the total T cells, whereas the mucosal tissues contain at least 50% of the T cells. Recent clinical data indicates that the percentages of CCR5‐modified CD4+ T cells in the blood and mucosal tissues vary substantially after the infusion of CCR5‐modified CD4+ T cells to HIV‐infected individuals. Therefore, understanding the dynamics of cell trafficking could improve the predictions of efficacy for stem cell therapies. In order to correctly account for infection in the tissues and cell trafficking between them, more complex models involving multiple compartments are needed. However, in the absence of longitudinal biopsy data from untreated patients, it becomes increasingly difficult to constrain and validate these complex models, which questions the predictability and applicability of such models. Because the single‐compartment model introduced in this work accurately predicts clinical data, it remains unknown whether increasing model complexity by adding other compartments is needed to explain the current clinical measurements.

One major issue with blocking or knocking out CCR5 alone is that it could lead to selection of CXCR4‐tropic virus.5, 48 However, a recent study demonstrated that although the Berlin patient had a minor population of CXCR4‐tropic virus before transplantation, this population was not able to reestablish HIV infection because of its dependence on CCR5 for replication and high genetic barrier toward CXCR4 usage.49 Nonetheless, inclusion of CXCR4‐tropic virus would be a useful extension to the model. Multiple layers of protection against HIV will likely be required for reliable cure. Therefore, in addition to knocking out CCR5, other restriction factors, such as members of the APOBEC family and SAMHD1 or gene circuits that induce apoptosis in HIV‐infected cells,27 could be used50 (Figure 1 a). Our model can be extended to design and test the performance of new CD4+ T cell or stem cell therapies with multiple genes added or edited. Finally, gene‐augmented stem cell therapies have recently been tested in nonhuman primate models of AIDS.7, 11, 13 and, hence, the model should be translated to a mathematical model of nonhuman primates to be able to use preclinical data, validate against it, and use the refined model to predict the results in humans.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information