On sample size and power calculation for variant set-based association tests

Summary

Sample size and power calculations are an important part of designing new sequence-based association studies. In this paper, we explore an efficient and accurate approach to computing sample size and power (particularly at small significance level, e.g., 10⁻⁶) for the sequence kernel association test (SKAT), which is a powerful and widely used approach for testing variant set association. The recently developed SEQPower (Wang et al., 2014) and SPS programs (Li et al., 2015) adopted random Monte Carlo simulations to empirically estimate power for a series of variant set association test methods including the SKAT, which could be very computing intensive and time consuming. It is desirable to develop methods that can quickly and accurately compute power without intensive Monte Carlo simulations. To our knowledge, the only analytical approach to computing power for SKAT was proposed by at Lee et al. (2012), who used an approximate non-central χ² distribution to efficiently compute sample size and power for SKAT and related methods. However we will show that the computed power based on the analytical approach of Lee et al. (2012) could be inflated especially for a small significance level, which is often of primary interest for large-scale whole genome and exome sequencing projects. We propose a new non-central χ² approximation based approach to accurately and efficiently compute sample size and power. In addition we study and implement a more accurate “exact” method to compute power, which is more efficient than the Monte Carlo approach though generally involves more computations than the χ² approximation method. The exact approach could produce very accurate results and be used to verify alternative approximation approaches. We implement the proposed methods in publicly available R programs that can be readily adapted when planning sequencing projects.

Introduction

Sample size and power calculations are a crucial step for designing sequence-based association studies. Software programs exist for single SNP based association tests in the genome-wide association studies (GWAS) (see, for example, Purcell et al., 2003; Skol et al., 2006). Single variant based association tests have proven useful in discovery of hundreds of disease-associated common variants (Welter et al., 2014). However these identified common variants only explain a small proportion of most human trait variance and disease heritability (Manolio et al., 2009), which indicates more variants with small to moderate effects or rare variants with large effects may yet to be discovered. Recently there is growing interest in detecting the joint association of a set of variants in a gene or region, which can aggregate multiple weak effects to boost detection power. Many methods have been proposed for detecting variant set association (VSA). Among them, the two widely used approaches are the burden test (BT) and sequence kernel association test (SKAT) (see, for example, Morgenthaler and Thilly, 2007; Li and Leal, 2008; Kwee et al., 2008; Madsen and Browning, 2009; Morris and Zeggini, 2010; Price et al., 2010; Liu and Leal, 2010; Lin and Tang, 2011; Wu et al., 2010; Neale et al., 2011; Wu et al., 2011; Lin et al., 2011; Lee et al., 2012; Schaid et al., 2013; Wang et al., 2013; Zhang et al., 2014; Lee et al., 2014; Wu et al., 2015; Wang et al., 2015).

Compared to the well developed VSA test methods, sample size and power calculation methodology for VSA tests is greatly lacking in the literature. This is partly due to two challenges: the complicated population dependent genetic variant distribution and the mathematical intractability of most VSA test methods. A common strategy to overcome the first challenge is to simulate sequence data based on, for example, the Wright-Fisher formula, forward-time simulation, or coalescent theory (Hudson, 2002; Schaffner et al., 2005; Hellenthal and Stephens, 2007; Peng and Liu, 2010). With the availability of well characterized reference panels of outside samples (for example, the HapMap and 1000 Genome Projects) and more and more real-word sequencing datasets, for example, the National Heart, Lung, and Blood Institute Exome Sequencing Project (Tennessen et al., 2012), we can also efficiently simulate sequence data by resampling from the real data (Li and Li, 2008). As for the second challenge, a straightforward solution is the Monte Carlo approach. For example, the recently developed SEQPower (Wang et al., 2014) and SPS programs (Li et al., 2015) adopted the random Monte Carlo simulations to empirically estimate power for a series of rare variant set association test methods including the SKAT. In general, these simulations are very computing intensive and time consuming. It is desirable to develop methods that can quickly and accurately compute power without intensive Monte Carlo simulations. To our knowledge, the only analytical approach to computing power for SKAT is studied at Lee et al. (2012), who used an approximate non-central χ² distribution to efficiently compute sample size and power for SKAT and related methods. However we will show that the computed power based on the analytical approach of Lee et al. (2012) could be inflated especially for a small significance level, which is of primary interest for large-scale whole genome and exome sequencing projects. We study a new non-central χ² approximation based approach to accurately and efficiently compute sample size and power. In addition we also study and implement a more accurate “exact” method to compute power, which is more efficient than the Monte Carlo approach though generally involves more computations than the χ² approximation method. The exact approach could produce very accurate results and be used to verify alternative approximation approaches. We implement the proposed methods in R programs that can be readily adapted when planning sequencing projects.

Sample size and power calculation for sequence-based association study

For illustration we consider a continuous trait with no covariates. We note that the following results can be easily extended to accommodate covariates and various outcomes (for example, disease status) following the approach of Lee et al. (2012). Consider n unrelated individuals. Denote the n outcomes as Y = (y₁, …, y_n)^T, and the m-vector of genotype scores as G_i for individual i = 1, …, n. We assume the linear regression model, y_i = β₀ + μ_i + ε_i, where ε_i is a zero mean normal random variable with variance σ², ${\mu }_i=G_i^T\mathit{\beta }$ is the contribution from the variant set, and β is a m-vector of regression coefficients. Without loss of generality, we assume the genotype scores have been centered and the outcome is standardized with unit variance σ = 1.

We can write the SKAT test statistic as Q = (Y − Ȳ)^TGWWG^T (Y − Ȳ)/n, where $\overline{Y}={\sum }_{i=1}^n{y}_i/n$, G = (G₁, …, G_n)^T, and W = diag(w₁, …,w_m) is a diagonal matrix of weights pre-specified for each variant (typically determined by the variant MAF). Here we have scaled the typical SKAT statistic by n for ease of derivation. Let $Z=\mathit{W}{\mathit{G}}^T(Y-\overline{Y})/\sqrt{n}$. We have Q = Z^TZ. Our sample size and power calculation will be based on the m-vector Z (typically m ≪ n).

Note that G is centered, therefore $Z=\mathit{W}{\mathit{G}}^{T}Y/\sqrt{n}$, and hence Z follows a multivariate normal distribution with mean $\mathit{\eta }=\mathit{W}{\mathit{G}}^T\mathit{G}\mathit{\beta }/\sqrt{n}$ and covariance matrix Σ = WG^TGW/n. Note that G^TG/n is the pairwise covariance matrix of the m genotype scores. Σ can be readily computed from simulated sequencing data or existing real-world sequencing data. Denote the eigen decomposition Σ = UDU^T, where U is an orthogonal matrix and D = diag(λ₁, …, λ_m) consists of the eigen values. Note that UU^T equals to the identity matrix, hence we can write Q = (U^TZ)^T (U^TZ). Here U^TZ follows a multivariate normal distribution with mean U^Tη and covariance matrix U^TΣU = D. So Q is essentially the sum of squares of m independent normal random variables. Therefore Q asymptotically follows a mixture of one degree of freedom (DF) non-central χ² distributions, ${\sum }_{j=1}^m{\lambda }_j{\chi }_1^2({\delta }_j)$, where the vector of non-centrality parameter (δ₁, …, δ_m) equal to the square of $D^{-1/2}{U}^T\mathit{\eta }=\sqrt{n}{D}^{1/2}{U}^T{\mathit{W}}^{-1}\mathit{\beta }$.

Conditional on the genotype scores G, Lee et al. (2012) approximated the distribution of Q using the non-central χ² distribution under the null and alternative derived by matching the first four moments of Q based on the approach of Liu et al. (2009). This moment-matching based non-central χ² approximation enables us to analytically and quickly compute the sample size and power. As shown in Duchesne and Lafaye De Micheaux (2010), the computed probabilities from the non-central χ² approximation of Liu et al. (2009) could be very far from the true values. For small significance level in the magnitude of 10⁻⁶, which is typically of our main interest in whole genome and exome sequencing studies, the approach of Lee et al. (2012) can lead to over-estimated power as we show in the following. To account for the randomness of G, we can easily average over randomly generated sequence data, or approximately replace η and Σ with their expected values following Lee et al. (2012), which often leads to accurate results for relatively large sample size.

In the following we first derive a general formula to calculate power for SKAT and then discuss various computation approaches.

Power calculation

Denote the p-value function P(Y ; n,β,G) which computes the significance p-value for n individuals with observed outcome Y and genotype G. Here β is the postulated standardized genotype regression coefficients. For a given significance level α and genotype G, the power can be computed as S(α; n,β,G) = E_Y {I[P(Y; n,β,G) ≤ α]}, where the expectation is with respect to the outcome distribution conditional on G. Then we can compute the power as θ = E_G[S(α; n,β,G)], where the expectation is with respect to the genotype distribution.

The SEQPower (Wang et al., 2014) and SPS programs (Li et al., 2015) computed θ by Monte Carlo simulation of both sequence data and outcomes to approximate E_Y and E_G. Lee et al. (2012) computed S(α; b,β,G) analytically based on the non-central χ² distributions, and then approximately computed E_G(S) by evaluating S at the expected genotype covariance matrix and non-centrality parameters based on simulated sequence data. We can invert the power formula to compute the sample size.

Exact and approximation approaches

We can analytically compute S(α; n,β,G) for given genotype using the Davies’ method (Davies, 1980), which is based on the numerical integration to invert the characteristic function of Q. The Davies’ method can achieve very high accuracy but generally requires very large number of integration terms. It has been implemented in the R package CompQuadForm (Lafaye De Micheaux, 2013). To accurately compute small p-values using the Davies’ method, we set the error bound as 10⁻¹² and maximum number of integration terms as 10⁸. For a given significance level α, sample size n, and G, we first numerically solve the quantile under the null hypothesis (setting β = 0) based on the Davies’ method, which is then used to compute the corresponding power for the given β. Specifically we use the R ‘uniroot()’ function to numerically solve the null quantile. We need to calculate the expectation E_G to compute the exact power, which can be approached by averaging over randomly simulated G to estimate the power. We will also evaluate a more computationally efficient approach where we use E_G(Σ) and E_G(η) to compute the corresponding power to approximate the exact average power.

For fast and accurate computation of more extreme significance p-values, we use the the non-central χ² approximation approach of Wu and Pankow (2015), which is based on matching the higher moments of Q to achieve more accuracy, while Lee et al. (2012) matched the first four moments as in Liu et al. (2009). Specifically we approximate the distribution of Q using a k-DF non-central χ² distribution ${\chi }_k^2(\gamma )$ with non-centrality parameter γ ≥ 0. Following the approach of Liu et al. (2009), we compute

$$\begin{array}{l}Pr(Q>t)=Pr\left(\frac{Q-{\mu }_Q}{{\sigma }_Q}>\frac{t-{\mu }_Q}{{\sigma }_Q}\right)\\ \approx Pr\left(\frac{{\chi }_k^2(\gamma )-{\mu }_{\chi }}{{\sigma }_{\chi }}>\frac{t-{\mu }_Q}{{\sigma }_Q}\right)=Pr\left({\chi }_k^2(\gamma )>\frac{t-{\mu }_Q}{{\sigma }_Q}{\sigma }_{\chi }+{\mu }_{\chi }\right),\end{array}$$

where ${\mu }_Q={\sum }_{i=1}^m{\lambda }_i,{\sigma }_Q=\sqrt{2{\sum }_{i=1}^m{\lambda }_i^2}$, μ_χ = k + γ, and ${\sigma }_{\chi }=\sqrt{2(k+2\gamma )}$. Here k and γ can be estimated by moment-matching. Specifically Liu et al. (2009) matched the skewness and minimized the kurtosis difference. Lee et al. (2012) proposed to match the kurtosis to improve the tail probability estimation. Both approaches lead to analytical solutions for k and γ. We can check that the jth cumulant of Q is ${\kappa }_j=2^{j-1}(j-1)!\left[{\sum }_{i=1}^m{\lambda }_i^j(1+j{\delta }_i)\right]$ (see, for example, Liu et al., 2009), and the jth cumulant of ${\chi }_k^2(\gamma )$ is κ̃_j = 2^j−1(j − 1)!(k + jγ). From the cumulants, we can easily compute their central moments denoted as ν_j and ν̃_j for Q and ${\chi }_k^2(\gamma )$ respectively (see, for example, Lange, 2010). Let $s_1={\kappa }_3/{\kappa }_2^{3/2}$ and $s_2={\kappa }_4/{\kappa }_2^2$. When $s_1^2>s_2$, let $a=1/(s_1-\sqrt{s_1^2-s_2})$, both the Liu and Lee method have γ = s₁a³ − a² and k = a² − 2λ. When $s_1^2>s_2$, the Liu method has γ = 0 and $k=1/s_1^2$, and the Lee method has γ = 0 and k = 1/s₂. Both methods provide poor approximation to small tail probabilities (Wu and Pankow, 2015). To improve the tail probability approximation accuracy, we can match higher moments. Specifically we follow the approach of Wu and Pankow (2015) to minimize the standardized (J − 1)th and Jth moments differences

$$\underset{k,\gamma }{min}\left[{\left(\frac{{\nu }_J}{{\nu }_2^{J/2}}-\frac{{\stackrel{\sim }{\nu }}_J}{{\stackrel{\sim }{\nu }}_2^{J/2}}\right)}^2+{\left(\frac{{\nu }_{J-1}}{{\nu }_2^{(J-1)/2}}-\frac{{\stackrel{\sim }{\nu }}_{J-1}}{{\stackrel{\sim }{\nu }}_2^{(J-1)/2}}\right)}^2\right].$$

We set J = 12 to accurately compute small tail probabilities under the null hypothesis following Wu and Pankow (2015). For approximating relatively large tail probabilities under alternative, setting J = 6 leads to an overall good performance in our numerical studies. Note that both k and γ just need to be solved once and can be stored for power calculation for any significance level.

For a given sample size n and genotype G, denote the estimated non-central χ² distribution parameters as k₀, γ₀ under the null hypothesis (β = 0), and k₁, γ₁ under the alternative hypothesis. Under significance level α, the power can be computed as $1-F\{F^{-1}[1-\alpha ;{\chi }_{k_0}^2({\gamma }_0)];{\chi }_{k_1}^2({\gamma }_1)]$, where $F[·;{\chi }_k^2(\gamma )]$ is the cumulative distribution function of ${\chi }_k^2(\gamma )$. To compute the average power over genotype distribution E_G, we can average over randomly simulated genotype G to compute the power. Generally we need relatively small number of simulations (for example, 100) to obtain accurate power estimate. Instead of computing the average of power over random sequence data, we can estimate E_G(Σ) and E_G(η) and use them to compute the corresponding power to approximate the exact average power.

In the following we evaluate the numerical accuracy of various approaches for computing power.

Numerical example

We compared the performance of the the analytical approach of Lee et al. (2012), the proposed non-central χ² approximation and Davies’ method. We compared their estimated power over 1000 simulated sequencing datasets, and the approximate power based on the average genotype covariance matrix. For a benchmark, we also included the Monte Carlo approach of estimating power over 10⁸ simulations. Specifically each time we simulate both outcomes and genotypes, and compute the SKAT p-values. The collection of 10⁸ p-values are then used to estimate power at a given significance level α.

For illustration we analyze common and rare variant sets in the gene G6PC2 using data from the Atherosclerosis Risk in Communities (ARIC) Study (The ARIC Investigators, 1989). The ARIC study is a prospective investigation of atherosclerotic disease with a total of 15792 individuals recruited from four U.S. communities participating in the baseline examination in 1987–1989. G6PC2 is a glucose-6-phosphatase gene. Both common and rare G6PC2 variants have shown significant associations with fasting glucose in large scale GWAS and sequencing studies (see, for example, Dupuis et al., 2010; Service et al., 2014; Mahajan et al., 2015; Wessel et al., 2015). First, we study a selected set of eighteen common G6PC2 variants, which have squared pairwise correlation smaller than 0.8 based on the GWAS data from 5947 non-diabetic white ARIC participants (Dupuis et al., 2010). Second, we study a set of nine rare G6PC2 variants measured using the illumina exome chip in 5866 non-diabetic white ARIC participants (Wessel et al., 2015). We treat the subset of measured ARIC genotypes G as the true population and use Bootstrap resampling to generate random sequencing data for any given sample size. We compute the standardized residuals from regressing the measured fasting glucose levels on the covariates (age, gender, and study center). We then regress the standardized residuals on genotypes to estimate β, which is treated as the true values.

We set weight $w_i=1/\sqrt{p_i(1-p_i)}$ for common variants and w_i = (1 − p_i)²⁴ for rare variants, where p_i is the MAF of the ith variant. We plug in the population genotype MAF and covariance matrix to approximate the average of Σ and η for a finite sample. Generally there is large variation associated with rare variants, and it is possible that we do not observe a rare variant in a finite sample. Following Lee et al. (2012), we compute an “observation probability” r_i = 1 − (1 − p_i)²ⁿ for the ith rare variant in a finite sample of n individuals. We then adjust the average of Σ and η as follows. Denote the population genotype covariance matrix as R with its (i, j)th element being σ_ij. Define a matrix R̃ with its (i, j)th element being ${\stackrel{\sim }{\sigma }}_{ij}={\sigma }_{ij}{r}_i{r}_j^{I(i\ne j)}$. We approximate the average of Σ with WR̃W, and the average of η with $\sqrt{n}\mathit{W}\stackrel{\sim }{\mathit{R}}\mathit{\beta }$.

Table 1 and 2 summarize the estimated power at significance level 2.5 × 10⁻⁶ for the common and rare variant sets respectively. Overall we can see that the Lee et al. (2012) approach over-estimated power. The proposed non-central χ² approximation and Davies’ method lead to very similar results and both agree with the Monte Carlo approach very well. In general we need a very large number of simulations for the Monte Carlo approach to obtain stable estimates especially for the rare variant set. For the common variant set, the approximate powers computed at the expected genotype covariance matrix are very close to the average power computed from 1000 simulations. Due to the large variation of sampling the rare variant set, the approximate approach generally under-estimated the power for a relatively small sample size, but the approximation improved with increased sample size.

Table 1.

Estimated power (%) at significance level 2.5 × 10⁻⁶ for the set of eighteen common G6PC2 variants: listed within parenthesis are the standard errors (%) of the estimated average powers over 1000 simulations for Davies, Lee and WP methods, and 10⁸ simulations for the Monte Carlo (MC) approach. The Davies₁, Lee₁, and WP₁ are the approximate powers computed at the expected genotype covariance matrix.

n	MC	Davies	Davies1	WP	WP1	Lee	Lee1
1000	1.09 (0.001)	1.09 (0.02)	1.00	1.07 (0.02)	0.99	1.49 (0.02)	1.40
2000	15.8 (0.004)	15.8 (0.11)	15.5	15.6 (0.11)	15.3	19.0 (0.12)	18.9
3000	51.2 (0.005)	51.1 (0.16)	51.2	50.8 (0.16)	50.8	56.3 (0.16)	56.4
4000	82.0 (0.004)	82.0 (0.10)	82.3	81.8 (0.10)	82.0	85.3 (0.09)	85.5
5000	95.6 (0.002)	95.7 (0.03)	95.8	95.6 (0.04)	95.7	96.8 (0.03)	96.8
6000	99.2 (0.001)	99.3 (0.01)	99.3	99.2 (0.01)	99.3	99.5 (0.01)	99.5

Table 2.

Estimated power (%) at significance level 2.5 × 10⁻⁶ for the set of nine rare G6PC2 variants: listed within parenthesis are the standard errors (%) of the estimated average powers over 1000 simulations for Davies, Lee and WP methods, and 10⁸ simulations for the Monte Carlo (MC) approach. The Davies₁, Lee₁, and WP₁ are the approximate powers computed at the expected genotype covariance matrix.

n	MC	Davies	Davies1	WP	WP1	Lee	Lee1
4000	6.70 (0.003)	6.58 (0.12)	5.44	6.49 (0.11)	5.35	8.20 (0.13)	7.11
6000	25.7 (0.004)	25.4 (0.27)	23.8	25.2 (0.27)	23.5	29.6 (0.28)	28.3
8000	53.2 (0.005)	52.9 (0.35)	52.4	52.6 (0.35)	52.0	58.1 (0.34)	58.0
10000	77.1 (0.004)	77.1 (0.26)	77.4	76.8 (0.26)	77.1	81.0 (0.23)	81.5
12000	91.1 (0.003)	91.1 (0.14)	91.7	90.9 (0.15)	91.6	93.1 (0.12)	93.7
15000	98.5 (0.001)	98.5 (0.03)	98.8	98.5 (0.04)	98.8	99.0 (0.03)	99.2

Effect of variant weight on rare variant set association test power

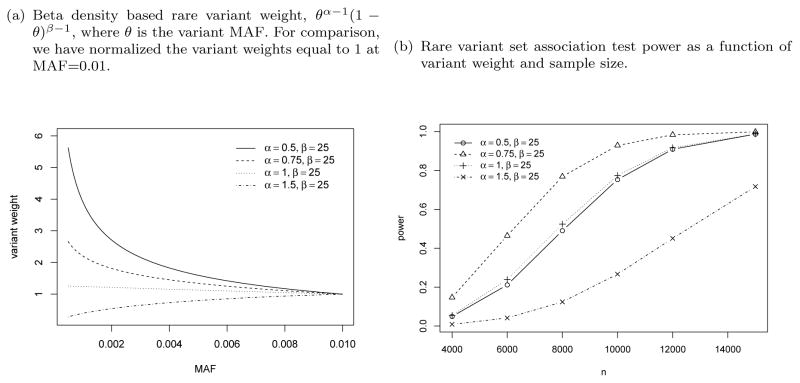
For SKAT of rare variant set, rarer variants are typically up-weighted to increase the detection power, which is based on the assumption that rarer variants tend to have larger effect sizes. Here we empirically investigate the SKAT power as a function of variant weight. Figure 1 compares four choices of variant weights based on the Beta density function, θ^α−1(1−θ)^β−1, where θ is the variant MAF. For comparison, we have normalized the variant weights equal to 1 at MAF=0.01. The default weight of SKAT is (α = 1, β = 25) following Wu et al. (2011). Here we fix β = 25 and set α at 0.5, 0.75, 1 and 1.5. In general rarer variants get more weights with smaller α. For the first three sets of weights with α ≤ 1, the weight is decreasing with variant MAF, hence we are assigning more weights to rarer variants. For the last set of weights with α = 1.5, the weight is increasing with variant MAF, hence we are down-weighting rarer variants. Figure 1(b) compares the empirical power (computed using the Davies method) using previous G6PC2 rare variant set under different sample size and variant weights. Overall we can see that up-weighting rarer variants (α ≤ 1) does improve the SKAT power compared to down-weighting rarer variants (α = 1.5). And there are appreciable power difference between the first three sets of weights: α = 0.75 has the overall best power, and α = (0.5, 1) have similar performance. We expect that correct rare variant weighting can boost power, but generally the correct weights depend on the data and are unknown. It is worthwhile to study methods that can adaptively assign variant weight based on the data.

Figure 1.

Effects of rare variant weight and sample size on the variant set association test power.

Discussion

In this paper, we studied sample size and power calculations for designing sequencing studies for variant set association tests. Methods to perform these calculations are widely available for single SNP tests, but have been less well developed for variant set association tests, which are likely to increase in importance with the advent of whole exome or whole genome sequencing projects. Our numerical studies have suggested that care should be taken when computing and reporting power at a small significance level especially for rare variant sets due to their inherent large variations. The non-central χ² distribution based analytical approximation method of Lee et al. (2012) in general over-estimated the power. We developed alternative approaches based on a new non-central χ² approximation and Davies’ method to efficiently and accurately estimate sample size and power. We recommend computing/verifying sample size and power at those small significance level by using alternative methods, e.g., computationally intensive Monte Carlo simulation or the proposed methods.

We have implemented the proposed methods in R programs posted at http://www.umn.edu/~baolin/research/katsp_Rcode.html. They can be readily adapted to help investigators optimally design sequencing studies. Our proposed methods and results will offer important insights into the design of appropriately powered sequencing studies to maintain study power and reduce costs.